GroEL/S Overexpression Helps to Purge Deleterious Mutations and Reduce Genetic Diversity during Adaptive Protein Evolution

Abstract

Chaperones are proteins that help other proteins fold. They also affect the adaptive evolution of their client proteins by buffering the effect of deleterious mutations and increasing the genetic diversity of evolving proteins. We study how the bacterial chaperone GroE (GroEL+GroES) affects the evolution of green fluorescent protein (GFP). To this end, we subjected GFP to multiple rounds of mutation and selection for its color phenotype in four replicate Escherichia coli populations, and studied its evolutionary dynamics through high-throughput sequencing and mutant engineering. We evolved GFP both under stabilizing selection for its ancestral (green) phenotype, and to directional selection for a new (cyan) phenotype. We did so both under low and high expression of the chaperone GroE. In contrast to previous work, we observe that GroE does not just buffer but also helps purge deleterious (fluorescence reducing) mutations from evolving populations. In doing so, GroE helps reduce the genetic diversity of evolving populations. In addition, it causes phenotypic heterogeneity in mutants with the same genotype, helping to enhance their fluorescence in some cells, and reducing it in others. Our observations show that chaperones can affect adaptive evolution in more than one way.

Highlights.

• GroE reduces genetic diversity.

• GroE enhances the effect of deleterious (activity reducing) mutations.

• GroE helps to intensify purifying selection and leads to higher activity of client proteins.

Introduction

In most proteins, the majority of amino acids help provide a stable structural scaffold, whereas fewer amino acids are directly responsible for catalysis or other protein activities (Todd et al. 2002). Protein evolution is thus constrained by mutations that destabilize a protein’s 3D fold (DePristo et al. 2005; Zeldovich et al. 2007). Such mutations can reduce protein activity and organismal fitness, for example, by reducing the amount of correctly folded and thus active protein. They can also increase a protein’s propensity to form toxic aggregates of misfolded proteins (Fersht 1997; Winklhofer et al. 2008; Hartl 2017). Mutations that create a new protein activity are especially often destabilizing (Wang et al. 2002; Tokuriki et al. 2008; Fromer and Shifman 2009; Studer et al. 2014).

Cells encode multiple proteins called chaperones that help other proteins to fold correctly and to maintain their fold. Chaperones act via various mechanisms, such as the stabilization of newly synthesized polypeptides, the acceleration of the folding process, and the refolding of misfolded proteins. This diversity of mechanisms is reflected in a diversity of chaperone structures (Kim et al. 2013; Saibil 2013; Ries et al. 2017). Prominent chaperone classes include the protein family Hsp60 (heat shock protein with a molecular weight of 60 kDa), the Hsp70, Hsp90, and Hsp100 families, as well as the trigger factor. Chaperones from all these families exist in both bacteria and eukaryotes (Kim et al. 2013; Saibil 2013; Ries et al. 2017).

The GroEL/S complex (GroE) is one of the major chaperones in bacteria. It is composed of the essential proteins GroEL and GroES (Fayet et al. 1989; Li and Wong 1992), and belongs to the Hsp60 family. Eukaryotes also express GroE homologs, which help mitochondrial and chloroplast proteins fold. Structurally, GroE belongs to a class of chaperones known as chaperonins, which form a cylindrical cage that entraps an unfolded polypeptide molecule and allows it to refold (Horwich et al. 2007).

During adaptive evolution, chaperones can facilitate the evolution of various organismal traits, including the evolution of proteins with new functions (Rutherford and Lindquist 1998; Cowen and Lindquist 2005; Tokuriki and Tawfik 2009a; Wyganowski et al. 2013; Agozzino and Dill 2018; Phillips et al. 2018; Alvarez-Ponce et al. 2019). For example, Hsp90 accelerates the evolution of drug resistance in fungi (Cowen and Lindquist 2005). In addition, chaperones can prevent the erosion of organismal fitness when deleterious mutations accumulate in an evolving population. For example, overexpressing GroE in Escherichia  coli (Fares et al. 2002) and Salmonellla typhimurium (Maisnier-Patin et al. 2005) populations with large numbers of random genomic DNA mutations, can improve bacterial population growth. Relatedly, overexpressing GroE in E.  coli populations subject to periodic bottlenecking reduces the likelihood of population extinction (Sabater-Muñoz et al. 2015).

A main mechanism by which chaperones may facilitate adaptive evolution is the buffering of deleterious mutational effects on protein stability, and in consequence, on organismal fitness (Fares et al. 2002; Wyganowski et al. 2013; Karras et al. 2017; Phillips et al. 2018). It is caused by a chaperone’s ability to help a protein with a destabilizing mutation fold correctly. This mechanism is especially well documented for GroE (Tokuriki and Tawfik 2009a; Bershtein et al. 2013; Sadat et al. 2020). For example, GroE directly improves the folding rate and the fluorescence of a green fluorescent protein (GFP) variant whose fluorescence is compromised by the mutation K45E (a lysine [K] to glutamate [E] change at position 45) (Sadat et al. 2020). Additionally, GroE overexpression can promote the evolution of new protein functions by stabilizing proteins (Tokuriki and Tawfik 2009a; Wyganowski et al. 2013). For example, the F306L mutation that improves the catalytic activity of the enzyme phosphotriesterase on a novel substrate, destabilizes the protein, but this destabilizing effect can be mitigated by GroE (Wyganowski et al. 2013).

Despite the plausibility of this buffering mechanism, several reports on Hsp90 suggest that this chaperone can also have the opposite effect. That is, it can “potentiate” or enhance the effect of a mutation (Xu et al. 1999; Cowen and Lindquist 2005; Whitesell et al. 2014; Geiler-Samerotte et al. 2016; Dorrity et al. 2018). For example, Hsp90 can help amplify the oncogenic activity of the viral oncogene v-Src (Xu et al. 1999). More generally, Hsp90 has been reported to both buffer (Rutherford and Lindquist 1998; Queitsch et al. 2002; Sangster, Salathia, Lee, et al. 2008; Sangster, Salathia, Undurraga, et al. 2008; Karras et al. 2017) and potentiate (Cowen and Lindquist 2005; Whitesell et al. 2014; Geiler-Samerotte et al. 2016; Dorrity et al. 2018) mutational effects. This is possible because a chaperone that promotes protein folding can increase the stability and foldability both of protein variants with a new phenotype and of variants with an ancestral phenotype. Existing work aiming to distinguish Hsp90-mediated buffering from potentiation focuses on complex morphological traits in the yeast Saccharomyces cerevisiae (Geiler-Samerotte et al. 2016). Here, we take a complementary approach by studying the influence of a chaperone on the directed evolution of a single protein.

One related previous study has used saturation mutagenesis and selection to exhaustively understand the effect of Hsp90 on mutations in a yeast transcription factor that controls the two mutually exclusive organismal phenotypes of mating and invasion (Dorrity et al. 2018). The study showed that temperature stress enhances invasion in some Hsp90 dependent mutants. It does so at the expense of mating, suggesting that buffering and potentiation are context dependent. Our experiments are superficially similar in that they combine mutagenesis, high-throughput sequencing, and protein engineering to study a chaperone’s effects at the molecular level. However, they are also fundamentally different from single step high-throughput screening experiments, because they aim to understand how a chaperone can affect the dynamics of protein evolution over multiple cycles of mutation and selection. In addition, they focus on the bacterial chaperone GroE, for which buffering but not potentiation has been demonstrated.

Most existing experiments on GroE buffering in individual proteins rely on single amino acid mutations (Bershtein et al. 2013; Sadat et al. 2020) or on small populations of protein variants (Tokuriki and Tawfik 2009a; Wyganowski et al. 2013). In contrast, we maintained large populations of more than 10⁵ individuals in which many variants can segregate during multiple rounds of directed evolution. The large population size allows many different variants to compete. In addition, it also reduces the effect of genetic drift and enhances that of selection on evolution.

Specifically, we studied the influence of GroE on the adaptive evolution of GFP in E. coli cells that overexpress GroE. We subjected GFP to directed evolution experiments in which we alternated cycles of (PCR-mediated) mutation with selection imposed by fluorescence-activated cell sorting (FACS), both with and without overexpression of GroE. In phase 1 of our experiments, we performed five rounds (generations) of evolution under stabilizing selection on the ancestral green fluorescent phenotype. We followed this phase 1 by a phase 2, in which we imposed directional selection on the new color phenotype of cyan fluorescence during an additional five generations. We studied both stabilizing and directional selection, because a chaperone might have different effects under different types of selection.

We chose GFP in this study for several reasons. First, its light-emission phenotype can be easily measured at single cell resolution in a high-throughput manner using flow cytometry. Second, it allows us to exert selection in a highly controlled manner via FACS. Third, GFP is non-native to the E.  coli host, and interferes less with the host’s cell physiology, growth, and metabolism than native proteins would. Fourth, GFP is a known GroE client, that is, the chaperone can promote GFP folding (Makino et al. 1997).

We studied the genotypic and phenotypic evolution of GFP via high-throughput single molecule real time (SMRT) sequencing, protein engineering, and phenotypic analysis. We focused on a key prediction that distinguishes the buffering and potentiation hypotheses: if a chaperone helps to buffer the deleterious effects of mutations, then it should help increase genetic diversity in a population over time, because some mutations that would otherwise be deleterious can be tolerated in its presence. Conversely, if a chaperone helps to enhance the effect of such mutations, it should lead to a loss of genetic diversity, because it renders such mutations more deleterious. We note that a chaperone may buffer the effect of some mutations and potentiate that of others. We also note that the observed effect of chaperone on a mutation may be categorized as either buffering or potentiating, depending on the point of view of the observer. For example, mutations can simultaneously suppress a phenotype and enhance another (Dorrity et al. 2018). At the molecular level, a chaperone may either promote folding of a protein, or in some cases, help target the misfolded protein for degradation (Kriegenburg et al. 2014). In our study, we focus on the molecular phenotypes of fluorescence intensity and spectrum. To avoid potential confusion between the terms buffering and potentiation, we instead describe the effect of GroE on fluorescence. Specifically, we say that GroE may either enhance the fluorescence of a GFP variant or reduce it. Likewise, it may enhance or suppress the color change associated with a GFP variant, relative to the ancestral protein.

Our experiments show that GroE can both enhance and suppress the effects of GFP mutants that coexist in the same population. However, GroE-mediated enhancement of deleterious (fluorescence-reducing) mutational effects far outweighs the suppression of such effects during directed evolution.

Results

Experimental Design

To evolve GFP under conditions of varying GroE (GroEL + GroES) expression, we first constructed an E.  coli plasmid (supplementary fig. S2, Supplementary Material online) that expresses GFP constitutively, and that allowed us to vary chaperone expression via an arabinose-inducible promoter. With this expression system, we studied GFP evolution at different chaperone expression levels. We note that GroEL and GroES are essential proteins, such that the chromosomal genes groS and groL, cannot be deleted. Thus, when we refer to GroE expression throughout, we strictly refer to overexpression of GroE from the expression plasmid. Consistent with a previous demonstration that GFP is a client of GroE (Makino et al. 1997), we found that chaperone expression affects the fluorescence of our ancestral GFP protein (supplementary fig. S4A, Supplementary Material online).

We performed directed evolution in four replicate populations that overexpressed GroE (condition G⁺) and in four other populations that did not (G⁻). In each round (generation) of evolution and for each population, we introduced random mutations into GFP via error-prone PCR at a rate of approximately one nucleotide substitution per GFP-coding gene, corresponding to approximately 0.95 amino acid changes per GFP protein (see Materials and Methods). Our populations comprised at least $\sim {10}^5$ individuals, such that genetic drift plays a negligible role on the time scale of the experiment.

We selected cells for survival using FACS (fig. 1) under two selection regimes that distinguish phase 1 from the later phase 2 of our experiments. In phase 1, we selected cells for survival that showed the native (ancestral) GFP phenotype of green fluorescence. In phase 2, we selected for the new phenotype of cyan fluorescence. Each phase consisted of five rounds (generations) of mutagenesis and selection. In both phases, we applied weak rather than strong selection for high fluorescence, because we reasoned that strong selection may favor mutants that fold well on their own, may thus not require chaperone assistance, and would thus subvert the intent of our study. Specifically, for each selection step, we only required that cells fluoresce more intensely than the autofluorescence of cells not expressing GFP. Each phase consisted of five rounds (generations) of mutagenesis and selection. After each round, we recorded the phenotype of surviving cells using flow cytometry, and sequenced population samples using SMRT sequencing (Pacific Biosciences 2015).

Fig. 1.

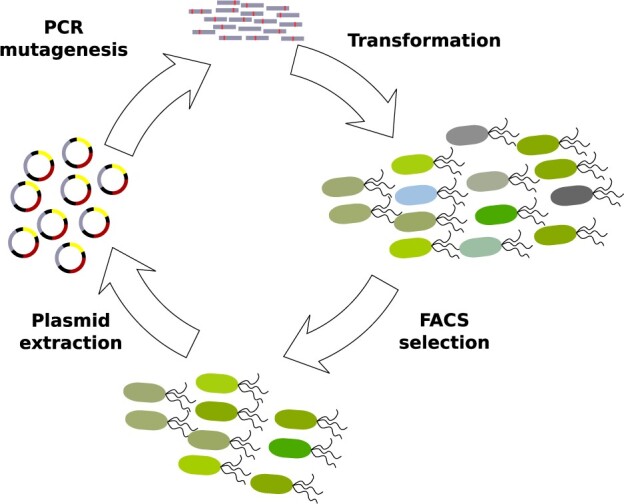
Experimental design. We selected cells for green fluorescence in phase 1 and cyan fluorescence in phase 2. Each phase consisted of five rounds (generations) of directed evolution. We sequenced the GFP gene from plasmids that survived each round of directed evolution using SMRT sequencing.

GroE Expression Slows the Decay of Fluorescence under Weak Stabilizing Selection

The vast majority of protein mutations that affect protein evolution are deleterious to protein activity (Bershtein et al. 2006; Eyre-Walker and Keightley 2007; Tokuriki and Tawfik 2009b). We emphasize that we here use the term “deleterious” to strictly mean a reduction in protein activity, that is, in fluorescence, although the term is often used to describe a reduction in cellular growth and fitness (Fares et al. 2002; Maisnier-Patin et al. 2005). When describing mutations that affect both protein activity and cellular fitness (see Materials and Methods), we use the terms “growth-enhancing” or “growth-reducing” for the latter effect.

Because phase 1 evolution involved only weak selection on our ancestral green fluorescence phenotype, we would expect that deleterious mutations accumulate in our phase 1 populations. This was indeed the case. We measured the distribution of green fluorescence of 10⁵ single cells from G⁺ and G⁻ populations at the end of each round of phase 1 evolution. During all five generations, green fluorescence consistently declined in all populations relative to the ancestor (fig. 2). However, the median fluorescence of G⁺ populations declined significantly more slowly than that of G⁻ populations ($P={10}^{-7}$, linear mixed effects model [LMM], type-III analysis of variance [ANOVA] using Satterthwaite’s method; see Materials and Methods). As a result, at the end of phase 1 evolution, all G⁺ populations showed significantly higher median green fluorescence than G⁻ populations (P = 0.0088, one-tailed Mann–Whitney U test).

Fig. 2.

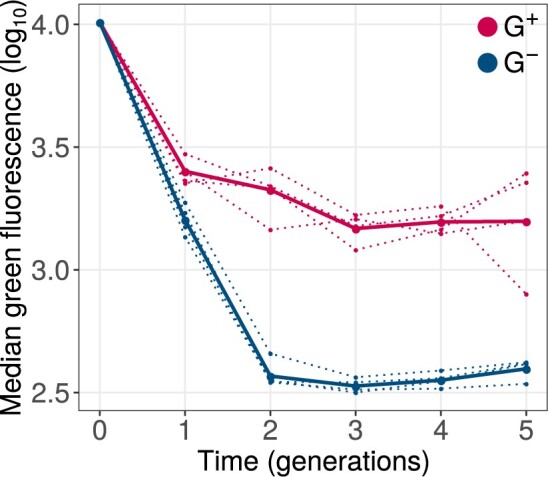
GroE expression reduces the decay of green fluorescence during phase 1 evolution. The vertical axis denotes logarithmically (base 10) transformed median green fluorescence (arbitrary units) of G⁺ (red) and G⁻ (blue) populations. The horizontal axis indicates time in generations (rounds of evolution), with zero referring to the ancestral GFP protein. Dotted lines denote the median fluorescence of individual replicate populations. Solid lines denote the median fluorescence when all four replicate populations are pooled.

GroE Slows Genetic Diversification under Weak Stabilizing Selection

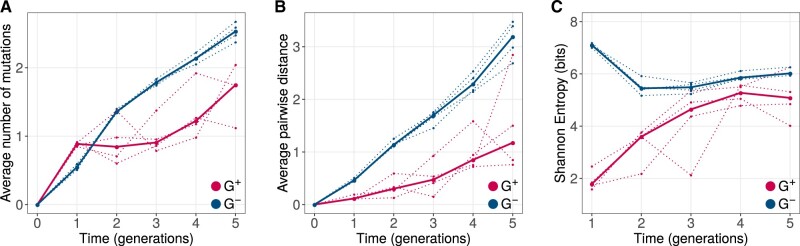
We next turned to the question how the chaperone helps slows down the decay of green fluorescence. If chaperone expression helps to suppress the effects of deleterious (fluorescence-reducing) mutations, then it should help increase genetic diversity over time, because some mutations that would otherwise be eliminated by purifying selection could remain in the population. Conversely, if chaperone expression mostly helps to enhance the effect of deleterious mutations, it should help to reduce genetic diversity, because more such mutations would be subject to purifying selection. We note that both these effects may occur simultaneously in the same population, that is, GroE may enhance the effect of some mutations while suppressing the effect of others. To find out which process dominates in its effect on genetic diversity, we sequenced the GFP coding regions from each of the phase 1 populations to a coverage of 1,000–3,300 (average 2,155) single molecule reads, depending on the population (supplementary table S6A, Supplementary Material online). From the sequencing reads, we calculated the frequencies of point mutations and multimutant genotypes at the amino acid level.

Although synonymous mutations may affect cotranslational folding (Buhr et al. 2016), they are unlikely to affect post-translational folding. Thus, our main analyses focus on nonsynonymous mutations because GroEL is known to bind to proteins after translation (see section 10, Supplementary Material online for an analysis of synonymous mutations). Figure 3A shows how the mean number of amino acid changes in GFP relative to ancestral GFP, evolves over time. Not surprisingly, both G⁺ and G⁻ populations diverged significantly from the ancestor during evolution (LMM: ANOVA, $P<{10}^{-15}$). However, the rate of increase of divergence of G⁺ populations was significantly lower than that of G⁻ populations (LMM: ANOVA, $P<{10}^{-5}$). We performed analogous analyses for the average pairwise distance between the genotypes in the same population (fig. 3B), and for the Shannon entropy (fig. 3C), an information-theoretic measure of genetic diversity. We found that both these diversity metrics also increase more slowly in G⁺ populations (LMM: ANOVA, P < 0.0012).

Fig. 3.

GroE expression leads to reduced genetic diversity during phase 1 evolution. Genetic diversity metrics (A) average distance from the ancestral GFP, (B) average pairwise distance between genotypes, and (C) Shannon entropy are shown on the vertical axes. Horizontal axes denote time in generations of evolution, where generation zero corresponds to the ancestral GFP sequence. G⁺ and G⁻ populations are color coded as red and blue, respectively. For all three metrics, G⁺ populations showed significantly lower genetic diversity (LMM: ANOVA, P < 0.0012).

In sum, GroE reduces genetic diversity in our evolving populations. This supports the view that it predominantly helps to enhance rather than suppress the effects of deleterious mutations, and thus helps purge such mutations.

In addition to affecting the overall amount of genetic diversity, GroE may cause different kinds of genotypes to accumulate. To find out whether this is the case, we randomly sampled 200 sequences from each population, and displayed the location of these sequences in genotype space using principal component analysis (PCA), a widely used dimensionality reduction method (Bratulic et al. 2017). This analysis shows that G⁺ and G⁻ populations cluster in different regions of genotype space (supplementary fig. S9A, Supplementary Material online). A complementary PCA on the frequencies of individual amino acid alleles shows analogous differences (supplementary fig. S9B, Supplementary Material online). Populations evolving with and without GroE expression, harbor different sets of GFP variants.

GroE Helps to Suppress the Effect of at Least Some Deleterious Mutations in Phase 1 Populations

Our preceding analyses do not address the question whether GroE enhances the effects of all deleterious mutations, or whether it may suppress the effects of at least some such mutations. To find out, we focused on another likely observation if GroE helps to suppress the effects of deleterious mutations. In this case, the fluorescence intensity of phase 1 populations should increase with GroE expression, and deleterious mutations would be more likely to remain in the population. If many such mutants persist in the populations, the net fluorescence of populations at the end of phase 1 should also increase with GroE expression. That is, if we quantify the fluorescence intensity of G⁺ populations during phase 1 in two conditions, one where the chaperone is not overexpressed and one where it is, then fluorescence should be higher when the chaperone is overexpressed. This is not necessarily expected if a chaperone helps to enhance the effect of deleterious mutations. In that case, the chaperone may have simply helped eliminate deleterious mutations, and the activity of the remaining variants may or may not be chaperone dependent. In addition, the chaperone may also decrease the fluorescence of some of the GFP variants that remain in the final population.

To find out whether fluorescence at the end of phase 1 evolution is chaperone dependent, we measured the fluorescence of those populations that had evolved while GroE was overexpressed, both with and without the induction of the chaperone (fig. 4), and compared their median fluorescence using a Mann–Whitney U test. In three out of four populations chaperone expression increased fluorescence ($P<1.5\times {10}^{-4}$), and in one (replicate 3) it decreased fluorescence ($P<{10}^{-15}$). Although these differences are statistically highly significant because of the large number of individuals we analyzed (N > 77,000), we also note that they are small in magnitude, ranging from 2% to 11%. They contrast with the much greater differences that emerge in fluorescence during evolution (fig. 2), most of which must be caused by GroE-mediated enhancement of deleterious mutational effects. In sum, GroE may mitigate the effect of some deleterious mutations in evolving populations but its effect on overall fluorescence is small. This conclusion is reinforced by specific candidates for buffered mutants that we engineered and analyzed phenotypically (section 9, Supplementary Material online).

Fig. 4.

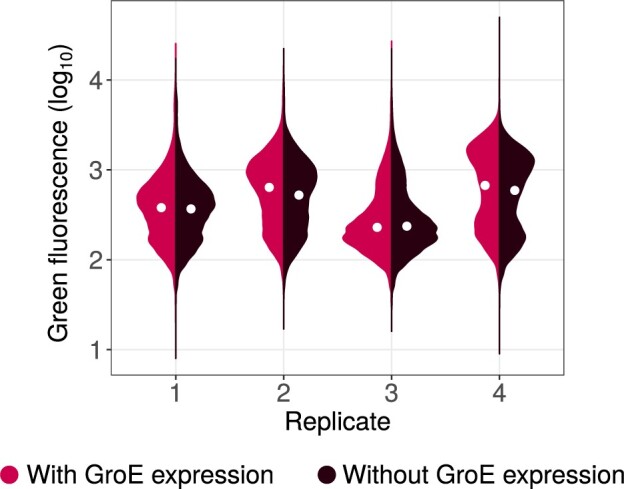
Violin plots denoting the distribution of logarithmically (base 10) transformed green fluorescence (arbitrary units) for each replicate G⁺ population at the end of phase 1 evolution (generation 5), with (red) or without (brown) the expression of GroE. The white circle in the center of the distribution denotes the median. The medians are significantly different for each pair of distributions shown (Mann–Whitney U test, $P<1.5\times {10}^{-4}$).

GroE Disfavors the Accumulation of Deleterious Mutations

To further validate the hypothesis that GroE helps purge deleterious mutations by enhancing their phenotypic effects, we examined our sequence data for single amino acid variants that attained significantly lower frequency in G⁺ than in G⁻ populations at the end of phase 1 (see Materials and Methods). To keep this analysis tractable, and to restrict ourselves to those mutations that are likely to affect fluorescence most strongly, we restricted this analysis to variants whose frequency exceeded 3.5% at the end of evolution in at least one replicate population (supplementary fig. S11, Supplementary Material online). We note that this frequency threshold is higher than the expected frequency of any one variant due to mutation pressure alone ($N={10}^5,P<{10}^{-5}$, Monte–Carlo simulations).

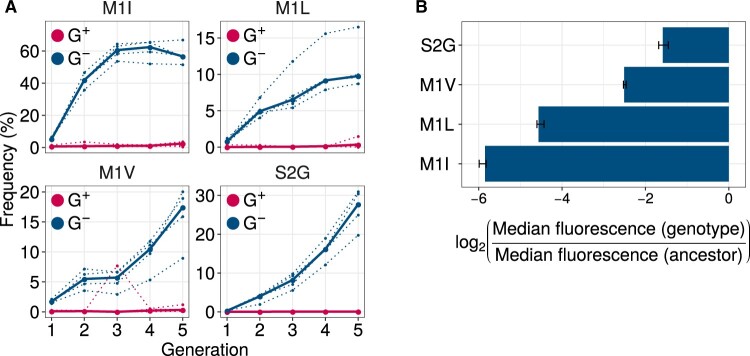
In total, we identified seven such variants (generalized linear model [GLM]: likelihood ratio test [LRT], $P<{10}^{-15}$ for the null hypothesis that they have equal frequency in G⁺ and G⁻ populations). Specifically, these are the variants: M1I, M1L, M1V, S2G, K52R, I128T, and N198D. Of these seven variants, the first four had consistently high frequency (8.5–67%) in every replicate G⁻ population (fig. 5A). More than 87% of individuals in every population had at least one of these four mutations. In contrast, the other three mutations: K52R, I128T, and N198D, had comparatively lower frequencies (0.7–5.5%; supplementary fig. S11, Supplementary Material online). Therefore, we chose to further investigate the mutations M1I, M1L, M1V, and S2G.

Fig. 5.

GroE expression disfavors accumulation of deleterious (fluorescence-reducing) mutations in phase 1. (A) Rise of deleterious mutations in evolving populations. The vertical axes show the frequency of deleterious mutations M1I, M1L, M1V, and S2G in evolving G⁺ (red) and G⁻ (blue) populations during phase 1, at different generations (horizontal axes). The dotted lines denote the frequency of a mutation in individual replicate populations. The solid lines denote the median frequency over all replicates. (B) Effect of the mutations on green fluorescence. The horizontal axis shows the ${\hspace{0.17em}\text{log}\hspace{0.17em}}_2$-transformed ratio of median green fluorescence for a given GFP variant (vertical axis) and ancestral GFP. A negative value denotes a deleterious effect whereas a positive value denotes a beneficial effect. The length of the bar denotes the median value of the ${\hspace{0.17em}\text{log}\hspace{0.17em}}_2$-transformed fluorescence ratios in the three replicate measurements whereas the error bar spans the range of minimum and maximum values.

To prove that these mutations indeed reduce fluorescence, we engineered them individually into the ancestral GFP using site directed mutagenesis, and measured their fluorescence. They caused a 2.7- to 64-fold reduction in median green fluorescence relative to ancestral GFP (fig. 5B), and are thus strongly deleterious to fluorescence. Their lower frequency in G⁺ populations suggests that GroE enhances the effects of individual deleterious mutations, and causes their elimination from these populations. These individual mutations do not simply hitchhike to fixation with other, beneficial mutations, as shown by experimental data on multimutant genotypes (section 8, Supplementary Material online). In a complementary analysis, we show that most frequent mutations in G⁺ are rarely deleterious or GroE-dependent for their fluorescence (section 9, Supplementary Material online).

These observations raise the question why mutations that are strongly deleterious to fluorescence, can become highly abundant in G⁻ populations in the first place. Since these mutations do not increase a cell’s probability of survival by enhancing GFP activity, we hypothesized that they provide a growth advantage to cells harboring them. For example, three of these mutations (M1I, M1L, M1V) are start codon mutations. Such mutations can reduce a protein’s translation initiation rate (Hecht et al. 2017), the amount of synthesized protein, and hence also the protein’s expression cost (Kafri et al. 2016). Cells carrying these mutations in GFP might have a lower metabolic burden and can outgrow other cells that synthesize more GFP (Kafri et al. 2016). To find out whether this is the case, we measured the maximum growth rate of cells carrying the mutations M1I, M1L, M1V, and S2G, relative to that of ancestral GFP (see Materials and Methods). We found that these mutations indeed provide a significant growth advantage (Mann–Whitney U test, P < 0.013). Thus, growth-enhancing mutations that are deleterious to fluorescence can accumulate when GroE is not overexpressed. We note that our choice of weak selection helps detect strongly fluorescence-reducing mutations that are eliminated under GroE overexpression, because such mutations can persist only under weak selection.

GroE Expression Increases Phenotypic Heterogeneity in Fluorescence Irrespective of the Genotype

Next we asked why deleterious (fluorescence-reducing) mutations may be disfavored under GroE expression. GroE might have an overall negative effect on fluorescence irrespective of the mutation, or it might affect strongly deleterious mutations differently from weakly deleterious mutations. To distinguish these possibilities, we measured the fluorescence of 15 differentially enriched mutations that we had engineered into ancestral GFP, and did so also under GroE overexpression (section 12, Supplementary Material online). We observed that for all mutants and for ancestral GFP, GroE overexpression caused the members of an isogenic population expressing a GFP variant to become increasingly heterogeneous in their fluorescence (supplementary fig. S18A, Supplementary Material online). Most strikingly, the distribution of the log-transformed fluorescence intensity became bimodal under GroE overexpression. One peak showed a higher, and the other a lower fluorescence than the peak of the unimodal, Gaussian distributed ($\mathcal{N}({\mu }_{{}^{-}},{\sigma }_{{}^{-}})$) fluorescence intensity without GroE overexpression.

The bimodal distribution of log transformed fluorescence intensity can be expressed as a sum of two Gaussian distributions ($\mathcal{N}({\mu }_{+\mathrm{L}},{\sigma }_{+\mathrm{L}})$ and $\mathcal{N}({\mu }_{+\mathrm{H}},{\sigma }_{+\mathrm{H}})$), where the mean fluorescence at the lower peak (${\mu }_{+\mathrm{L}}$) and at the higher peak (${\mu }_{+\mathrm{H}}$) amount to an average of 93% and 107% of the mean log-fluorescence in the absence of GroE overexpression (${\mu }_{-}$), respectively (supplementary fig. S20 and table S5, Supplementary Material online). These results suggest that GroE can both help to enhance and reduce fluorescence of the same GFP variant, depending on the cell where it is expressed.

Phenotypic Heterogeneity Increases the Fitness of Some Deleterious Mutations but Reduces That of the Others

To understand how this phenotypic heterogeneity may affect the selection of deleterious mutations, we developed a statistical model that relates fluorescence to fitness, as quantified by the likelihood to survive experimental selection. Specifically, we define the fitness of a genotype as the fraction of cells in an isogenic (genotypically homogeneous) population whose fluorescence intensity lies above the selection threshold we used in our directed evolution experiments. Without GroE overexpression, individual cells of a given genotype show a unimodal Gaussian fluorescence distribution with a mean ${\mu }_{-}$ and variance ${\sigma }_{-}$ that we can estimate from our engineered mutants (supplementary fig. S18 and table S5, Supplementary Material online). In the presence of GroE expression, this distribution changes to a bimodal distribution whose parameters we can also estimate from data (supplementary fig. S18 and table S5, Supplementary Material online). With this information in hand, we calculated the change in fitness of a genotype under GroE expression as the average difference in its fitness with and without GroE expression ($\mathrm{\Delta }\mathrm{F}={\mathrm{F}}^{+}-{\mathrm{F}}^{-}$; see Materials and Methods). A deleterious mutation with positive $\mathrm{\Delta }\mathrm{F}$ has a higher chance of surviving selection when GroE is expressed than when it is not. Conversely, a mutation with a negative $\mathrm{\Delta }\mathrm{F}$ has reduced chance of selection under GroE expression.

Using this data-driven model, we found that GroE improved the likelihood of selection of deleterious mutations whose fluorescence mean (${\mu }_{-}$) lies no more than 5% above the threshold value that is needed for survival in our experiment. In contrast, GroE reduced the fitness of moderately deleterious mutations whose ${\mu }_{-}$ lies between 5% and 35.6% above this threshold (fig. 6). Outside this range, the value of $\mathrm{\Delta }\mathrm{F}$ is zero, and GroE does not affect the fluorescence-based selection of the variants.

Fig. 6.

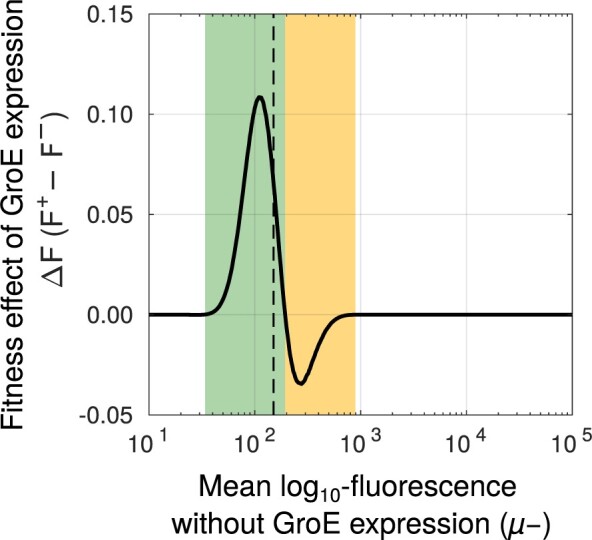
GroE increases the fitness of some mutants while reducing the fitness of the others. Change in fitness (ΔF, vertical axis) due to GroE expression predicted by our statistical model (see Materials and Methods), as a function of mean ${\hspace{0.17em}\text{log}\hspace{0.17em}}_{10}$ transformed fluorescence (${\mu }_{-}$, horizontal axis) in the absence of GroE expression. The black-dashed vertical line denotes the selection threshold (150 arbitrary units of fluorescence). A positive value of ΔF indicates increased fitness (green area) whereas a negative value indicates reduced fitness (orange area), in response to GroE expression.

This model can explain several of our experimental observations, if one keeps in mind that our populations evolved under weak selection for fluorescence, and that individuals can accumulate deleterious (fluorescence-reducing) mutations and survive selection as long as they fluoresce above a low fluorescence threshold. Even mutants whose mean fluorescence lies slightly below the threshold can persist at low frequency, because a few individuals may cross the selection threshold every generation due to phenotypic heterogeneity (supplementary fig. S18, Supplementary Material online). Since most new mutations are deleterious (Bershtein et al. 2006; Eyre-Walker and Keightley 2007), fluorescence in our populations declines continually (fig. 2; G⁻ populations) until most genotypes fluoresce barely above the threshold. Our model predicts that GroE reduces the fitness of such deleterious but above-threshold genotypes, causing them to become depleted in G⁺ populations. This prediction is supported by our genetic diversity analysis (fig. 3). The model also correctly predicts that mutations which are less deleterious and reduce fluorescence by a smaller amount, can persist in G⁺ populations (section 9, Supplementary Material online), because GroE has no effect on the fitness of these mutations.

In addition, the model can help explain that some highly deleterious mutations become enriched in G⁺ populations, because GroE improve the survival of such mutations during selection for fluorescence. One such mutation is a start-codon mutation M1T (discussed in section 9, Supplementary Material online), which becomes enriched in G⁺ populations, even though its mean fluorescence lies 5% below the selection threshold.

GroE Leads to Evolution of Higher Fluorescence Intensity but Lower Color Shift during Directional Selection toward a New Phenotype

Since mutations that bring forth a new protein phenotype often destabilize a protein (Wang et al. 2002; Tokuriki et al. 2008; Fromer and Shifman 2009; Studer et al. 2014), we also asked how GroE may affect the adaptive evolution of a new phenotype. We thus conducted a phase 2 of our evolution experiment, in which we selected for the new phenotype of cyan fluorescence. Since green and cyan fluorescence are correlated phenotypes (supplementary fig. S5, Supplementary Material online), a green-fluorescing variant with high expression or stability could have a higher absolute cyan fluorescence than a cyan-fluorescing variant with low expression or stability. To avoid this problem, we selected cells whose cyan fluorescence increased relative to green fluorescence (supplementary fig. S5, Supplementary Material online). Phase 2 started with populations from the end of phase 1 (round zero of phase 2). We subjected these populations to five additional rounds of directed evolution toward cyan fluorescence.

After every generation of phase 2 evolution, we measured cyan and green fluorescence of 10⁵ cells from G⁺ and G⁻ populations, and observed that median cyan fluorescence significantly increased in all populations during phase 2 (linear model [LM]: ANOVA, P < 0.005; supplementary fig. S6A, Supplementary Material online) with a concomitant decrease in median green fluorescence (LM: ANOVA, $P<3.6\times {10}^{-4}$; supplementary fig. S6B, Supplementary Material online). Thus, our populations can evolve increased cyan fluorescence.

Next, we asked if GroE expression influences the rate of evolution toward the new color. To this end, we compared the cyan fluorescence of G⁺ and G⁻ populations. During every generation (including the starting population derived from the end of phase 1), G⁺ populations had higher median cyan fluorescence than G⁻ populations (Mann–Whitney U test, P < 0.015; supplementary fig. S6A, Supplementary Material online).

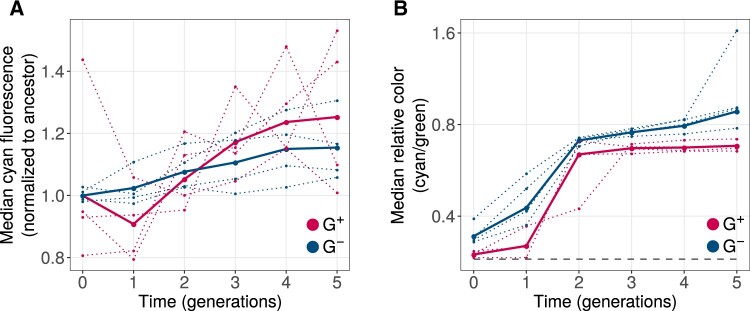
We next asked whether the faster evolution of cyan fluorescence in phase 2 G⁺ population originated during phase 2, or whether it might stem from the already higher fluorescence of the starting G⁺ populations from the end of phase 1 (supplementary fig. S6A, Supplementary Material online). To find out, we normalized the fluorescence of the phase 2 starting populations to the same value for G⁺ and G⁻ populations. Specifically, we pooled the fluorescence values of individual replicates of the initial G⁺ populations (round zero), calculated the median fluorescence of this pooled population, and divided the absolute fluorescence values from each replicate population by this median. We proceeded analogously for the G⁻ populations, dividing their fluorescence by the median of the initial fluorescence values from a pool of all G⁻ populations. Next, we compared the rate of increase of this normalized fluorescence for both G⁺ and G⁻ populations with a LM and found that GroE expression did not have a significant effect on this rate (fig. 7A). Moreover, at the end of evolution, normalized cyan fluorescence was not significantly higher in G⁺ than in G⁻ populations. This analysis suggests that the difference between G⁺ and G⁻ populations during phase 2 may result from differences accumulated during phase 1. However, we also note that after generation one of phase 2, median cyan fluorescence increased more rapidly during every generation and remained somewhat higher in each of the last three generations (fig. 7A and supplementary fig. S6A, Supplementary Material online).

Fig. 7.

GroE expression leads to evolution of higher fluorescence but reduced color shift. Vertical axes denote (A) median normalized cyan fluorescence (normalized to starting populations; see main text), and (B) the relative color (cyan/green; logarithmically scaled) during phase 2 of directed evolution. The dotted line denotes the median value of individual replicates and the solid line denotes the median fluorescence value when data from all populations is pooled. Horizontal axes denote time in generations, where generation 0 refers to populations at the end of phase 1 evolution. G⁺ and G⁻ populations are indicated by red and blue colors, respectively. The dashed horizontal line in panel (B) shows the relative color of ancestral GFP.

We also analyzed a different aspect of the phenotype, which is the extent of the spectral shift from green to cyan that occurred during phase 2. To find out whether GroE expression can affect the rate of this spectral shift, we calculated the ratio of cyan and green fluorescence for each cell in the different phase 2 populations. We refer to this ratio as relative color. Just like cyan fluorescence increased during phase 2 (fig. 7A), so did the spectral shift in both G⁺ and G⁻ populations (fig. 7B). However, this shift was lower for G⁺ populations than for G⁻ populations during every round of evolution (Mann–Whitney U test, P < 0.03). Our genotypic analysis of specific color shifting mutations supports this finding (section 12, Supplementary Material online; supplementary figs. S17 and S19, Supplementary Material online).

GroE Reduces Genetic Diversity during Evolution toward the New Phenotype

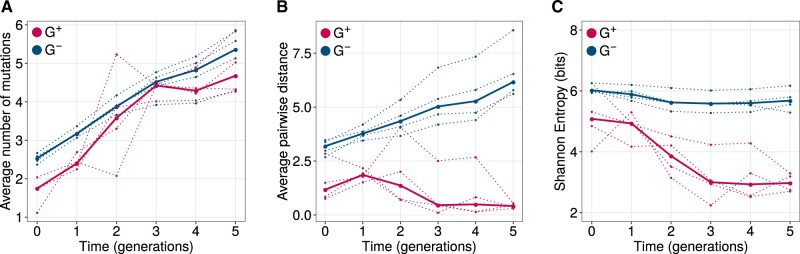
We next asked whether GroE helps reduce effects of deleterious mutations during phase 2, thus increasing a population’s genetic diversity, or whether it enhances their deleterious effects, thus reducing diversity. To find out, we sequenced the GFP coding region from each phase 2 population to an average coverage of 2,155 sequences per population (750–3,760 reads, depending on the population; supplementary table S6B, Supplementary Material online). Not surprisingly, the number of mutations per GFP coding sequence increased further during phase 2 evolution (LMM: ANOVA, $P<{10}^{-10}$; fig. 8A), but we observed no significant effect of GroE expression on the rate of this increase (LMM: ANOVA, P > 0.05).However, when we quantified the genetic diversity of a population by the average pairwise distance between genotypes (fig. 8B), the diversity of G⁺ populations decreased during phase 2, whereas the diversity of the G⁻ populations further increased (LMM: ANOVA, P = 0.00015). Likewise, the Shannon entropy also significantly decreased in G⁺ populations compared with G⁻ populations (fig. 8C; LMM: ANOVA, P < 0.002). In sum, like in phase 1, GroE helps reduce genetic diversity, which is inconsistent with a net suppression of deleterious mutational effects, and supports the notion that GroE helps purge deleterious mutations by enhancing their effects. We also found that G⁺ populations had lower phenotypic diversity than G⁻ populations in every generation of phase 2 (Mann–Whitney U test, P < 0.0015). Just like in phase 1, PCA shows that G⁺ populations accumulate different kinds of variants (supplementary fig. S10, Supplementary Material online). In addition, although GroE-mediated enhancement of deleterious mutational effects, dominates in its effect on genetic diversity, the chaperone enhances the fluorescence of at least some variants (supplementary fig. S7, Supplementary Material online).

Fig. 8.

GroE expression leads to reduction of genetic diversity during phase 2 evolution. Genetic diversity metrics (A) average distance from the ancestral GFP, (B) average pairwise distance between genotypes, and (C) Shannon entropy are shown on the vertical axes. Horizontal axes denote time in generations of evolution, where generation zero refers to the populations obtained after phase 1 evolution. G⁺ and G⁻ populations are color coded as red and blue, respectively. Average pairwise distance and Shannon entropy significantly reduced in G⁺ populations and were significantly lower than that of G⁻ populations (LMM: ANOVA, P < 0.002).

GroE Helps Purge Fluorescence Reducing Mutations during Evolution of the New Phenotype

G⁺ populations may acquire higher cyan fluorescence during phase 2 (fig. 7A) for two reasons. The first is that GroE may help spread mutations that convey the new phenotype. The observation that GroE overexpression delays evolutionary change in fluorescence color argues against this possibility (fig. 7B and supplementary fig. S6C, Supplementary Material online). A detailed analysis of specific mutants shows that this is indeed not the case (section 11, Supplementary Material online).

The second possible reason is that GroE may help purge deleterious mutations from these populations, as it did during phase 1. If so, G⁻ populations should show lower fluorescence, because they preferentially accumulate deleterious mutations. To test this hypothesis, we identified single mutations that were significantly more abundant in G⁻ populations (GLM: LRT P < 0.05) relative to G⁺ populations by the end of phase 2. We restricted this analysis to variants whose frequency exceeded 5% at the end of evolution in at least one replicate population (supplementary fig. S12, Supplementary Material online), and found 28 such mutations. Of these mutations, the most frequent were M1V, S2G, and T203A. Each of them exceeded a frequency of 40% in every replicate population. We here discuss the mutations M1V and S2G (supplementary fig. S17, Supplementary Material online; see section 11, Supplementary Material online for T203A). Both mutations reduce fluorescence (fig. 5B). Remarkably, they not only achieved a high frequency at the end of phase 2, but their frequency significantly increased during the five generations of phase 2 (generalized LM with mixed effects: LRT $P<{10}^{-15}$). In contrast, their frequency did not increase in G⁺ populations, where it remained below 0.5%. This suggests that these fluorescence-reducing mutations do not simply persist in G⁻ populations due to their higher abundance in the starting populations, that is, the populations at the end of phase 1. Instead, GroE continues to help purge these mutations during selection for a new phenotype.

Discussion

We used GFP as a model to understand how GroE affects protein evolution. More specifically, we tried to find out whether GroE predominantly helps to reduce or enhance the effect of deleterious (fluorescence-reducing) mutations during protein evolution. Buffering refers to the suppression of a mutant’s deleterious effect. It occurs when a chaperone facilitates the folding of the mutant protein (Fares et al. 2002; Wyganowski et al. 2013; Karras et al. 2017; Phillips et al. 2018). In contrast, the term potentiation is mostly used to describe the enhancement of a mutation’s (deleterious or beneficial) effect (Cowen and Lindquist 2005; Whitesell et al. 2014; Geiler-Samerotte et al. 2016; Dorrity et al. 2018). Chaperones, by facilitating protein folding, can both suppress the effect of deleterious mutations that affect protein folding, and enhance the effect of phenotype-altering mutations. More importantly, chaperones can simultaneously enhance a phenotype while suppressing another (Dorrity et al. 2018), hence making the terms buffering and potentiation highly contextual. In our study, we focused on deleterious mutations, because such mutations are most abundant during both stabilizing and directional selection (Bershtein et al. 2006; Eyre-Walker and Keightley 2007; Zheng et al. 2020). If chaperone-mediated suppression of deleterious mutational effects is prevalent during stabilizing selection for an ancestral phenotype, then genetic diversity should increase over time, because mutations that would otherwise be deleterious can accumulate in our evolving populations. In contrast, if chaperone-mediated enhancement of the effects of such mutations is prevalent, genetic diversity should decrease, because deleterious mutations become eliminated more rapidly.

We found that GroE overexpression reduces genetic diversity during experimental evolution, implying that it helps purge deleterious mutations. It has been proven beyond doubt that GroE can buffer the effects of deleterious or destabilizing mutations (Tokuriki and Tawfik 2009a; Bershtein et al. 2013; Wyganowski et al. 2013; Sadat et al. 2020). Our experiments do not challenge this fact, because we show that GroE can indeed increase the survival of some deleterious mutations. However, this kind of buffering is not the dominant phenomenon in our evolution experiments.

Chaperones can enhance the activity of neofunctionalizing mutations by increasing the folding and stability of such variants (Cowen and Lindquist 2005; Dorrity et al. 2018). However, the notion that a chaperone can help to exacerbate the effect of deleterious mutations is counter-intuitive, given that its protein folding assistance is expected to enhance protein function. However, it is not without precedent. For example, increasing the concentration of the chaperone Hsp70 can reduce a client protein’s folding yield (Morán Luengo et al. 2018). Furthermore, a chaperone can target misfolded proteins for degradation if they fail to refold (Kriegenburg et al. 2014). Misfolded protein variants also impose a metabolic burden on a cell. This burden may be further exacerbated by high chaperone expression. Relatedly, GroE assisted folding itself incurs a metabolic cost in the form of ATP consumption (Horwich et al. 2007). Additionally, an excessive amount of GroE may nonspecifically associate with endogenous proteins and interfere with their spontaneous folding and maturation. Together, these costs may reduce cellular growth and fitness, especially under GroE overexpression, which may lead to the purging of protein mutations that are prone to misfolding.

During our evolution experiments, GroE reduced genetic diversity both under stabilizing selection for the ancestral green fluorescence phenotype, and under directional selection for a new (cyan) phenotype. During directional selection, it not only helped purge deleterious mutations, but also prevented the accumulation of key mutations with the new phenotype. Furthermore, GroE helped to increase phenotypic heterogeneity in isogenic populations. That is, it enhanced fluorescence in a subset of a population, and decreased fluorescence in another subset. Thus, GroE can buffer or potentiate the activity even of a single genotypic variant, depending on the cell in which the variant is expressed.

Although the biochemical causes of this phenotypic heterogeneity remain to be determined, we discuss two possible explanations for it. The first is that the cellular machinery involved in gene expression is shared between the two overexpressed proteins GroE and GFP. If the two proteins compete for shared resources, then the subpopulation of cells that expresses more GFP may express less GroE and vice versa. This hypothesis posits that expression of GroE and GFP may be inversely correlated, which in turn suggests that phenotypic heterogeneity exists because cells can assume one of several GFP and GroE expression states. However, this hypothesis still does not explain why phenotypic heterogeneity manifests as a bimodal distribution. In addition, protein overexpression cost is probably not the only cause of fluorescence bimodality. The reason is that overexpression of another chaperone, Hsp90 (HtpG), with an even higher molecular weight (71.4 kDa compared with 57.3 + 10.4 kDa for GroEL and GroES), does not cause a bimodal distribution of fluorescence (supplementary fig. S4B, Supplementary Material online). Thus, this phenomenon specifically results from GroE overexpression, possibly through its consequences on the activity of the chaperone’s endogenous clients.

A second possible explanation of bimodality relates to the timing of GroE overexpression, and its effect on the growth of different cells that are dividing nonsynchronously. In the yeast S. cerevisiae, the timing of a growth perturbation can dictate its phenotypic outcome (Hartwell et al. 1974). Specifically, yeast cells carrying temperature sensitive mutants of two different cell cycle genes display heterogeneous phenotypes when shifted to nonpermissive temperature. They show two different cellular phenotypes which correspond to the mutational effects of the two cell cycle genes. Importantly, the phenotype that a cell exhibits after the temperature shift depends on its stage of the cell cycle before the shift. In unrelated work, the cell division inhibitor nocodazole caused the cell size of Wangiella dermatitidis (another yeast) to become bimodally distributed (Roberts and Szaniszlo 1980). In a similar manner, the bimodality of fluorescence in nonsynchronously dividing bacterial cells might result from growth perturbations caused by GroE overexpression. Relatedly, genome-independent replication of the plasmid (Chang and Cohen 1978) could be an additional source of asynchrony between cell division and gene expression that might help explain phenotypic heterogeneity.

Few detailed studies exist on the effect of GroE on the evolution of individual proteins. One of them provided evidence for the importance of buffering (Tokuriki and Tawfik 2009a). The study found that during stabilizing selection for an enzyme’s ancestral phenotype, about 20–30% of enzyme variants that had evolved under GroE overexpression lost their activity when the chaperone was no longer expressed. In addition, GroE dependent variants evolved higher catalytic activity toward a novel substrate during directional selection. These experiments differed from ours in at least three ways that may help explain the prevalence of buffering in them. Firstly, they evolved enzymes. An enzyme’s activity depends not just on protein expression, folding, and stability, but also on molecular motions that affect the rate of catalysis, whereas such motions play little role in our fluorescence phenotype. In addition, a mutation may simultaneously enhance an enzyme’s catalytic activity and reduce its stability, a frequent phenomenon for activity altering mutations in enzymes (Wyganowski et al. 2013). Since chaperones directly alter protein folding and stability but affect an enzyme’s catalysis only indirectly, it is possible to select mutations with such a stability-activity tradeoff. In contrast, no such tradeoff has been documented for fluorescent proteins. In its absence, GFP variants with high activity (fluorescence) may also be stable and thus chaperone-independent.

A further difference between our experiments and this previous work (Tokuriki and Tawfik 2009a) is that it used stringent selection, where survival required catalytic activities to exceed 70% of the ancestral activity. In contrast, we deliberately used relaxed selection to expose chaperone effects. Finally, the previous work evolved small populations of approximately 200 variants, whereas we evolved large populations of more than 10⁵ individuals. We were thus able to analyze GroE effects for a wider spectrum of variants.

A previous study that also speaks to our observations focused on the effect of the chaperone Hsp90 on morphology-altering mutations in the yeast, S.  cerevisiae (Geiler-Samerotte et al. 2016). It defined potentiation as an increase, and buffering as a decrease in the variation of a morphometric trait caused by a chaperone. The study showed that Hsp90-mediated potentiation far outweighs buffering, except for mutations that have undergone several generations of selection under Hsp90 expression, which are buffered. It appears that in this system, the chaperone predominantly exposes mutational effects rather than suppressing them. This observation is consistent with our finding that chaperone-mediated enhancement of mutational effects can be more widespread than their suppression.

In virtually every evolution experiment on growing cells, selection will act on cellular growth rate. A primary reason why we evolved GFP, a protein that is not native to E.  coli, and why we expressed GFP from a low-copy-number plasmid (see Material and Methods), was our intention to minimize interference of GFP mutations with host physiology, growth rate, and other aspects of host fitness. We emphasize, however, that such interference cannot be completely eliminated, and that selection in our experiments acted on both fluorescence and cell growth. This is a limitation of our work, and possibly of any in vivo evolution experiment. Evidence of selection on growth is the occurrence of GFP start-codon mutations that increased the host’s growth rate. Such mutations reduce the rate of protein synthesis and thereby increase the growth rate of cells. However, we emphasize that selection did not act exclusively on growth rate. First, if it had, start-codon mutations would have spread through both G⁻ and G⁺ populations. One would expect these mutations to be more important in G⁺ populations where they can mitigate the burden of GroE overexpression. However, their frequency remained low in G⁺ populations. Second, a different set of color changing mutations accumulated in G⁺ relative to G⁻ populations, during evolution toward a novel phenotype (section 12, Supplementary Material online). The two evolved populations also shifted their color to a different extent, in agreement with the frequency of the color shifting mutations (fig. 7). This difference is not consistent with the possibility that selection acted purely on growth. Although future experiments might restrict mutagenesis to exclude start-codon mutations, it may be difficult to eliminate growth-affecting mutations completely, because even some synonymous mutations may reduce a protein’s expression, and thus the associated energy cost on a host (Zwart et al. 2018). Relatedly, a chaperone may affect the evolution of any one protein directly, by interacting with this protein, or indirectly, if cellular physiology changes in response to chaperone expression. Indeed, recent work shows that even different cellular metabolic states can have different effects on protein folding and activity (Verma et al. 2020). Some of these physiological changes may even persist for many generations (Shaffer et al. 2020). Our experimental system and that of previous studies (Cowen and Lindquist 2005; Tokuriki and Tawfik 2009a; Wyganowski et al. 2013; Whitesell et al. 2014; Geiler-Samerotte et al. 2016) cannot distinguish between such direct and indirect effects of chaperone expression. Although these limitations might be overcome by evolution in vitro, a synthetic in vitro environment creates its own limitations that are even more serious. In sum, experiments that study how chaperones affect evolution in vivo should be interpreted with these caveats in mind.

Our study opens exciting directions for future work. For example, the prevalence of potentiation or buffering may depend on the chaperone, the client protein, and on multiple other factors, such as selection strength and population size. We reemphasize that the two terms buffering and potentiation are contextual, and do not represent distinct biochemical or genetic phenomena. Their usage, although frequent (Rutherford and Lindquist 1998; Xu et al. 1999; Queitsch et al. 2002; Cowen and Lindquist 2005; Sangster, Salathia, Lee, et al. 2008; Sangster, Salathia, Undurraga, et al. 2008; Tokuriki and Tawfik 2009a; Wyganowski et al. 2013; Whitesell et al. 2014; Geiler-Samerotte et al. 2016; Karras et al. 2017), can thus be misleading. However, it is important to investigate in greater detail if a chaperone can indeed facilitate the folding of some mutants while impairing the folding or causing degradation of others. A recent study shows how this decision is made for some eukaryotic proteins (Shao et al. 2017), but it is still unknown how this process affects protein evolution. More importantly, the observation that GroE induces phenotypic heterogeneity even among genetically identical cells calls for more detailed biochemical analysis of chaperone action. Experiments with synchronized bacterial cells (Ferullo et al. 2009) may help understand whether the timing of chaperone expression and its possible interaction with cell cycle proteins helps determine the cellular phenotype. This unexpected complexity shows that studies on proteins amenable to single-cell phenotyping will be crucial to understand the mechanisms behind chaperone action and their role in adaptive evolution.

Materials and Methods

Construction of the Expression System

Construction of the Expression Plasmid

We constructed a plasmid to express both GFP (constitutively) and GroE (inducibly). Our starting point for plasmid construction was the pGro7 plasmid designed by Takara (Takara Bio Inc. 2017) for arabinose inducible expression of the chaperone proteins GroEL and GroES. This is a low-to-medium copy number plasmid with the pACYC origin of replication. It encodes chloramphenicol acetyltransferase, the transcription factor araC from S.  typhimurium, and the groE operon consisting of GroEL and GroES downstream of the araBAD promoter from S. typhimurium. Because we did not know whether leaky expression of pGro7 might occur even in the absence of arabinose, we created a control plasmid that cannot express the chaperone proteins at all. To this end, we digested pGro7 with BamHI and religated the larger fragment corresponding to the plasmid backbone so as to eliminate the GroE operon. We named this control plasmid pΔGro7.

We next identified a region in pGro7 that can be used to place a GFP expression cassette. This region is a short stretch of DNA flanked by 5′-BglII and 3′-HindIII restriction sites downstream of the GroE operon. We use the GFPmut2 variant of GFP, which is distinguished by three amino acid changes from Aequorea victoria GFP (Cormack et al. 1996). This GFP variant is advantageous for our experiments because it is weakly dimerizing, has a single excitation peak (488 nm), and undergoes fast maturation (Balleza et al. 2018). We obtained the GFP expression cassette, which consists of a promoter followed by a ribosome binding site and the GFP coding sequence, from plasmid pMSs201 (Zaslaver et al. 2006). The GFP coding sequence is additionally flanked by 5′-XhoI and 3′-XbaI restriction sites. Since these sites already exist in pGro7 and are thus not useful for cloning, we engineered a 5′-SalI site and a 3′-SacI site flanking the GFP coding sequence in addition to the original restriction sites. We did so by PCR-amplifying the plasmid with the primers, pMS-Sal1-GFP-F and pMS-GFP-SacI-R (supplementary table S6, Supplementary Material online), and cloned the PCR-product back into the plasmid backbone. Next, we amplified the modified GFP expression cassette using the primers pMS-BglII-F and pMS-HindIII-R (supplementary table S6, Supplementary Material online), and cloned it into pGro7 and pΔGro7.

To identify the best promoters for GFP expression, we repeated this process with three variants of plasmid pMSs201, thus creating three pGro7 and three ΔGro7 plasmid variants that drive GFP expression from the ompA, rpsM, and rplN promoters (Zaslaver et al. 2006). We quantified GFP expression from each promoter as explained in the next section.

Estimating of Growth Rates Associated with Different Promoters

The host organism for our experiments is E. coli strain BW27784 (CGSC 7881), which cannot metabolize arabinose. We cultured all cells hosting our expression plasmids in LB with 25 µg/ml chloramphenicol (LB+chl). Visual inspection of plated cells under blue light yielded green colonies and showed that all constructed plasmids expressed GFP. We corroborated this observation by measuring fluorescence on a plate reader (Tecan Spark 10M; supplementary fig. S1A, Supplementary Material online). To this end, we diluted 200 µl of overnight (LB+chl) culture in 1 ml PBS, distributed the diluted suspension into a 96-well plate in triplicate, and measured fluorescence in the GFP channel (485 ± 10 nm excitation, 521 ± 10 nm emission). Applying this procedure to each of our three pGro7 plasmids showed that GFP expression (fluorescence) from ompA and rplN promoters was 4.5 and 2.35 times higher than that from the rpsM promoter (supplementary fig. S1A, Supplementary Material online), making these promoters better candidates for our experiments.

Next, we quantified the growth cost associated with GFP expression from the rplN and ompA promoters. To this end, we inoculated 30 µl of overnight cultures that carried the corresponding pGro7-GFP plasmid in 14 ml tubes containing 3 ml LB+chl. After 60 min of growth at 37 °C, we transferred 700 µl of each culture to separate tubes and added different amounts of l-arabinose (from a 20% w/v stock solution) for GroE induction, such that the final arabinose concentrations equaled 0, 1, and 4 mg/ml. Next, we transferred 200 µl from each culture to a 96-well plate (in triplicate). We measured optical density (OD at 600 nm) and GFP fluorescence every 12 min during a growth period of 24 h on a Tecan Spark 10M plate reader with temperature being maintained at 37 °C, and with the plate shaken constantly between measurements. We inoculated and measured the growth of cultures with the two ΔGro7-GFP plasmids in the same manner. Using the final OD as an indicator of the carrying capacity, we fitted a logistic growth equation to the OD data using the fminsearch function (unconstrained, derivative free optimization) from the Optimization Toolbox in MATLAB (2017b), and estimated the growth rate from the fitted equation. Under arabinose induction, the growth rate was higher for the rplN promoter strain (supplementary fig. S1B, Supplementary Material online), whereas the end point OD was comparable between the two promoter strains (supplementary fig. S1C, Supplementary Material online). Therefore, we chose the pGro7-rplN-GFP (supplementary fig. S2, Supplementary Material online) plasmid for all evolution experiments.

Measurement of GroE Expression Using SDS–PAGE

To determine the extent to which chaperone proteins are expressed from our plasmid at different concentrations of arabinose, we extracted total protein from the cells, performed SDS–PAGE of the protein extracts and observed the intensity of bands corresponding to proteins of the appropriate size. To this end, we first inoculated 30 µl of overnight culture of the pGro7-rplN-GFP strain in 3 ml of LB+chl and induced GroE expression with nine different concentrations of l-arabinose—0, 0.002, 0.004, 0.008, 0.016, 0.04, 0.1, 1, and 4 mg/ml—after 60 min of growth at 37°C. In these experiments, we also included the pΔGro7-rplN-GFP strain as an additional control for no plasmid-borne GroE expression. We allowed cell populations to grow for 8 h. For each population, we pelleted cells from 1 ml of cell suspension by centrifuging at 8,000 × g for 3 min. We resuspended each pellet in 300 µl of lysis buffer, which consists of 50 mM Tris–HCl pH 7.5, 100 mM NaCl, 5% (v/v) glycerol, 1 mM dithiothreitol (added fresh), 1× protein inhibitor cocktail (cOmplete, Roche; added fresh), 300 µg/ml lysozyme, 3 µg/ml DNAseI, and 16 mM MgCl₂. We then incubated this suspension for 4 h at 4°C. We lysed the cells by freezing the suspension in liquid nitrogen, followed by thawing it in a water bath, and repeated this freeze-thaw cycle ten times. Then, we centrifuged the suspension at 18,000 × g for 30 min at 4°C and collected the supernatant. We quantified protein concentration using the Bradford method (Bio-Rad Quick Start Bradford reagent). We then heated 10 µg of protein sample with suitable amounts of 4× SDS–PAGE loading buffer (250 mm Tris–HCl pH 6.8, 8% w/v SDS, 0.2% w/v bromophenol blue, 40% v/v glycerol, and 20% v/v 2-mercaptoethanol) at 95 °C for 5 min. We loaded the samples on a polyacrylamide gel (4% for stacking and 12% for resolving; TruPAGE precast gel, Sigma–Aldrich), and performed electrophoresis at 180 V for 45 min in 1× TruPAGE TEA-Tricine SDS buffer (Sigma–Aldrich). We fixed the gel for 30 min in fixing/destaining solution (50% v/v methanol, 10% v/v acetic acid), and stained it overnight in Coomassie brilliant blue staining solution (0.1% w/v Coomassie brilliant blue R-250, 50% v/v methanol, 10% v/v acetic acid). Next, we destained the gel with destaining solution until the background was clean and the bands were clear.

We observed no induction of GroEL (60 kDa) in the absence of arabinose (supplementary fig. S3, Supplementary Material online) but strong induction even at the lowest tested concentration of arabinose (0.002 mg/ml). The 60-kDa GroEL band was missing in both the pΔGro7-rplN-GFP sample and in the no-induction sample, suggesting that leaky expression is negligible. With these observations in mind, we chose a modest concentration of 0.1 mg/ml arabinose for induction in all subsequent experiments. We reasoned that at this concentration of arabinose the expression of GroE would be saturated, and small deviations from this chosen value during the experiments would not affect the expression.

Mutagenesis and Selection

Preparation of Electrocompetent Cells

To prepare electrocompetent cells, we performed every step of the procedure described below in detergent-free glassware. We cultured E.  coli strain BW27784 in 10 ml SOB medium overnight at 37 °C with shaking at 220 rpm. Subsequently, we inoculated 1 l of prewarmed (37°C) SOB in a 5-l flask with the overnight culture. We let cells grow for 2–3 h (37 °C + 220 rpm) until their OD reached 0.4–0.6. Then we transferred the flask to ice and let it cool for 20 min. Subsequently, we transferred the cell suspension to two 500 ml centrifuge bottles (Eppendorf), and centrifuged both bottles at 1,500 × g for 15 min at 4 °C with neither acceleration nor deceleration, on a swinging bucket rotor (Eppendorf). Next, we resuspended the cells in 90 ml of cold water per bottle by gently swirling the bottle, and distributed the suspension in six prechilled 50 ml tubes (30 ml per tube). We gently added 15 ml of cold glycerol–mannitol solution (20% w/v glycerol, 1.5% w/v mannitol) to the bottom of each tube. Then we centrifuged the tubes at 1,500 × g for 15 min at 4 °C without acceleration/deceleration. We removed the supernatant and resuspended the pellet of each tube in 1.5 ml of cold glycerol–mannitol solution. We combined the cell suspension from all tubes and aliquoted 100 µl into chilled 1.5 ml tubes. We snap-froze aliquots in liquid nitrogen bath and stored them at −80 °C.

Mutagenesis

For mutagenesis by error-prone PCR, we used the primers Gro-Mut-F and Gro-Mut-R to amplify GFP from pGro7-rplN-GFP (supplementary table S6, Supplementary Material online).

For the error-prone PCR itself, we used the following reaction mixture: 150 nM each of the nucleotide analogs 8-oxodeoxyguanosine triphosphate (8-oxo-dGTP, Trilink Biotechnologies) and 6-(2-deoxy-beta-d-ribofuranosyl)-3,4-dihydro-8H-pyrimido-[4,5-C] [1,2]oxazin-7-one triphosphate (dPTP, Trilink Biotechnologies), 200 nM each of forward and reverse primers, 400 µM of each dNTP (Thermo Scientific), 1× ThermoPol buffer (NEB), and 25 units/ml of Taq polymerase (NEB). We prepared 100 µl of the PCR reaction with 5 ng of plasmid DNA as the template (∼6$\times {10}^8$ molecules), and split the reaction mixture into two 50 µl aliquots for efficient heat transfer during PCR. We performed the PCR with the following program: initial denaturation at 95 °C for 5 min, 25 cycles of amplification with 95 °C for 30 s, 56 °C for 30 s, 72 °C for 1 min, and a final extension at 72 °C for 5 min. We optimized this protocol such that we obtained approximately one nucleotide mutation per amplicon corresponding to approximately 0.95 amino acid changes per GFP protein.

We purified PCR products using a QIAquick PCR purification kit (QIAGEN). Subsequently, we prepared 50 µl of restriction digestion reaction with 400 ng PCR product, 20 units each of the two restriction enzymes, SalI-HF and SacI-HF (NEB), 20 units of DpnI (NEB; for removing template plasmid), and 5 µl of 10×-CutSmart buffer (NEB). We carried out the digestion overnight and purified the digested products with the QIAquick PCR purification kit. We digested the plasmid in the same way using the restriction enzymes. Additionally, we treated the plasmids with Antarctic phosphatase (NEB) to minimize their self-ligation. We separated the digested plasmid backbones from the insert using agarose gel electrophoresis, and purified the excised band using a QIAquick gel extraction kit (QIAGEN). For ligation, we prepared a 30-µl ligation mixture consisting of 100 ng of the digested plasmid backbone, 55 ng of the digested amplicons (1:3 molar ratio of backbone and insert), 3 µl of 10× T4 DNA ligase buffer (NEB), and 1.5 µl (600 units) of T4 DNA ligase (NEB). We performed the ligation overnight at 16 °C. To separate salts from the ligation products, we added 70 µl water, 50 µg glycogen (Thermo-Fisher), 50 µl 7.5M ammonium acetate, and 375 µl ethanol to the ligation mix. After incubating the mixture for 20 min at −80 °C, we centrifuged it at 18,000 × g for 20 min at 4 °C. We decanted the supernatant and washed the pellet twice with 800 µl of 70% ethanol. We dried the pellet and resuspended it in 20 µl of sterile deionized water.

Transformation of the Mutant Library Using Electroporation

We thawed frozen electrocompetent cells on ice and added the purified ligation products to them. We transferred the resulting suspension into a 2-mm electroporation cuvette (EP202, Cell Projects, UK), and performed electroporation with a single 3 kV pulse using the Bio-Rad MicroPulser (program EC3). We immediately added 1 ml of warm (37 °C) SOC medium, transferred the suspension to a 35-ml glass tube (17 mm diameter), and incubated the cells for 1.5 h at 37 °C with shaking at 220 rpm. We plated 100 µl of a 512-fold diluted suspension (three 1:8 serial dilution) on an LB-chl agar plate and added 9 ml of LB-chl to the undiluted suspension. We incubated the plates and the tubes (with shaking at 220 rpm) overnight at 37 °C. We estimated the library size by counting the number of colonies on the LB-chl plate. Throughout our evolution experiments, we maintained a minimum library size of 10⁵ transformants.

Estimation of Mutation Rate

To estimate the mutation rate of our mutagenesis procedure, we performed mutagenesis on the ancestral GFP gene and transformed the mutants using electroporation as described in the previous section. We performed colony PCR with ten randomly picked colonies from the plate and sequenced the PCR products using Sanger sequencing to estimate the mutation rate. In this way, we determined the mutation rate of the ancestral GFP gene during every round of directed evolution to ensure that it stayed in the range of one to two mutations per amplicon throughout the evolution experiment. It is well-known that PCR-mutagenesis creates a biased mutation spectrum (Bratulic et al. 2017), and our protocol is no exception. From the combined Sanger sequencing data obtained from all rounds of evolution, we estimated the frequencies of different point substitutions as follows: AT$\to$GC: 0.755, GC$\to$AT: 0.144, AT$\to$TA: 0.072, AT$\to$CG: 0.025, GC$\to$CG: 0.004, and GC$\to$TA: 0. Thus, the protocol is biased toward AT$\to$GC transitions.

Selection of Transformed Cells Using FACS

We performed directed evolution in four replicate populations where GroE was expressed from our expression plasmid, along with four control populations in which it was not expressed from this plasmid. We applied the following selection protocol to each population. To prepare for selection, we inoculated 4 ml of LB-chl in a 20-ml glass tube with 80 µl of the appropriate transformed library. We allowed the cells to grow at 37 °C with shaking at 220 rpm for 60 min, and then induced GroE expression in G⁺ populations with 0.1 mg/ml of l-arabinose. We allowed cells to continue their growth for another 10 h. Subsequently, we transferred the tubes to ice and pelleted cells from 700 µl of the suspension by centrifuging at 8,000 × g for 3 min. We washed cells by resuspending them in cold PBS and centrifuging them again. We decanted the supernatant, resuspended the cells in 1 ml cold PBS, and transferred 100 µl of the suspension to 1 ml cold PBS in a 5-ml polystyrene tube (Falcon). We performed cell sorting on a BD FACSAriaIII cell sorter with the following photomultiplier tube (PMT) voltages for different channels—478 V for FSC, 282 V for SSC, 480 V for FITC, and 493 V for AmCyan. We excluded debris and other small particles by setting a threshold of 1,000 on FSC-H and SSC-H.

We used the FITC channel (488 nm excitation and 530 ± 15 nm emission) for measuring green fluorescence and the AmCyan channel (405 nm excitation and 510 ± 25 nm emission) for measuring cyan fluorescence. We quantified the autofluorescence of cells in each channel by measuring the fluorescence of untransformed cells. To select variants with green fluorescence, we sorted cells with a FITC-H value higher than the maximum FITC-H value of the untransformed cells. Because green and cyan fluorescence are correlated—wild-type GFP fluoresces in both the FITC (green) and the AmCyan (cyan) channel—we did not define the new phenotype merely as a higher fluorescence in the AmCyan channel. Instead, we required a relative shift toward cyan fluorescence that cannot be solely explained by higher green fluorescence. Specifically, we plotted the fluorescence of wild type GFP in the two channels (FITC-H and AmCyan-H) against each other, and designated the area that lay both above the regression line and the background fluorescence of the AmCyan channel as the selection gate (supplementary fig. S5, Supplementary Material online). This procedure ensures that surviving cells show cyan fluorescence that cannot be merely explained by enhanced green fluorescence.

We sorted 10⁵ cells into 1.5 ml tubes containing 500 µl of cold LB. We incubated the sorted cells at 37 °C for 30 min and then transferred them to 5 ml of LB-chl in a 20-ml glass tube. We let the cells grow overnight at 37 °C with shaking at 220 rpm. We inoculated 4 ml of LB-chl with 80 µl of the overnight culture and repeated the induction and the sorting procedure as described above. We performed the second sort to minimize possible contamination from cells that did not meet our selection criteria. We incubated the sorted cells at 37 °C for 30 min and transferred them to 10 ml LB-chl in a 50-ml tube. We allowed these cells to grow overnight and used 1 ml of the overnight culture for preparing glycerol stocks (15% glycerol). We used the remainder of the culture for extracting the plasmid library using a QIAprep Spin Miniprep kit (QIAGEN). The plasmid libraries thus isolated served as templates for the next round of mutagenesis.

Analysis of Fluorescence of Populations Using Flow Cytometry

We used flow cytometry to analyze the phenotype of evolving populations after every generation, that is, after every round of mutagenesis and selection. To this end, we first obtained an overnight culture either directly after the second round of sorting (previous section), or by reviving a glycerol stock. From this culture, we inoculated 40 µl of cell suspension in 4 ml LB+chl. After 1 h of growth at 37 °C with shaking at 220 rpm, we added l-arabinose to a final concentration of 0.1 µg/ml, and allowed the cells to grow for another 9 h. Next, we pelletted cells from 500 µl of the culture by centrifuging at 8,000 × g for 3 min at 4 °C. Then, we washed the cells by resuspending them in 1 ml cold PBS and pelletted them again. We resuspended the cells in 1 ml PBS and transferred 60 µl of this suspension into 1 ml of cold PBS in a 5-ml polystyrene tube (Falcon). We quantified green fluorescence using the FITC channel (488 nm excitation and 530 ± 15 nm emission), and cyan fluorescence using the AmCyan channel (405 nm excitation and 510 ± 25 nm emission) on a BD LSR FortessaII flow cytometer. The PMT voltages for the FITC and AmCyan channels were 480 and 493 V, respectively. We recorded 100,000 events and analyzed the data using both MATLAB (fca-Readfcs.m; Balkay 2018) and the R package flowCore (Ellis et al. 2019). We note that GroE expression led to an increase in number of nonfluorescent “events” (signals) even in an isogenic population (data not shown). We surmise that these nonfluorescent events could originate from nonviable cells which in turn could arise due to protein overexpression stress. Therefore, we excluded all nonfluorescent cells from our analyses.

We measured the fluorescence of evolved populations after every round of directed evolution. To analyze the temporal change in fluorescence, we fitted a linear mixed model using the R package lme4 (v1.1-21; Bates et al. 2015). In this analysis, we used median fluorescence (green in phase 1 and cyan in phase 2) as the response variable, with time (round of evolution) and state of GroE expression (condition: G⁺ or G⁻) as interacting predictors, and variation between replicates as random effects. Specifically, we used the following expression to define our statistical model: Fluorescence ∼ rounds*condition + (1|replicate). Because all phase 1 populations started with the same ancestral fluorescence, we forced a constant intercept for the LM. We analyzed the significance of the fit using the ANOVA function from the R package lmerTest (v3.1-0; Kuznetsova et al. 2017). This function performs a type III analysis of variance of the fitted coefficients and estimates degrees of freedom using Satterthwaite’s method (Kuznetsova et al. 2017). In the model we used, the factors (rounds of evolution and GroE expression) do not significantly affect the response variable (fluorescence), under the null hypothesis.

Analysis of DNA Sequencing Data

Preparation of Sequencing Libraries

We sequenced the GFP coding sequence from plasmid libraries isolated after every round of evolution using SMRT sequencing (Pacific Biosciences, PacBio).

For multiplexed sequencing, we generated barcoded libraries according to the instructions provided by PacBio (Pacific Biosciences 2015). To create these libraries, we performed two rounds of PCR. In the first round, we amplified the GFP coding region with primers carrying a “universal” sequence provided by PacBio. We amplified the GFP gene from the plasmid libraries obtained after every round of selection (see Selection of Transformed Cells using FACS), using the primers GLG_ORF_PacBio-F and GLG_ORF_PacBio-R (supplementary table S6, Supplementary Material online). These primers have a 5′ amino-C6 modification and had been PAGE purified before use. We prepared a 25-µl PCR mix with 5 ng of plasmid, 400 nM of each primer, 200 µM of each dNTP, 5 µl of 5× Phusion HF buffer (Thermo-Fisher), and 0.5 units of Phusion High-Fidelity polymerase (Thermo-Fisher). We then performed PCR using an initial denaturation at 95 °C for 5 min followed by 20 cycles of amplification with the following program: 95 °C for 30 s; 58 °C for 30 s, 72 °C for 30 s, and a final extension at 72 °C for 2 min. We added 8 µl of water, 1 µl of 10×-CutSmart buffer (NEB), 10 units each of DpnI (NEB), and ExoI (NEB) to the PCR products, and incubated the mixture for 30 min at 37 °C, followed by 10 min at 85 °C. After the reaction, we diluted the mixture by adding 70 µl of water.

We carried out a second round of PCR to barcode the different samples. We selected 36 barcode sequences from a list of 384 16 nt-barcode sequences from PacBio (Pacific Biosciences 2019a), and designed 18 barcoded forward and reverse primers. All these primers carry a 5′ phosphate modification and were HPLC purified before use. For this second PCR, we used 2 µl of the DpnI-ExoI treated first-round PCR product (diluted) as the template in a 50-µl PCR mix consisting of 200 nM of each of the barcoded primers, 200 µM of each dNTP, 10 µl of 5× Phusion HF buffer (Thermo-Fisher), and 1 unit of Phusion High-Fidelity polymerase (Thermo-Fisher). We performed PCR using an initial denaturation at 95 °C for 5 min, followed by 30 cycles of amplification using the following program: 95 °C for 30 s, 62 °C for 30 s, and 72 °C for 40 s, and a final extension at 72 °C for 2 min. We determined the purity of the PCR products through agarose gel electrophoresis, and found that most of the products were clean, without nonspecific bands or primer dimers. We purified these products using a QIAquick PCR purification kit (QIAGEN). For the few samples that contained large amounts of primer dimers, we purified the PCR products using gel extraction. We measured the concentration of the purified products using a Nanodrop 1000 (Thermo-Fisher) spectrophotometer and a Qubit 3.0 fluorometer (Life Technologies). For GFP libraries from each phase of evolution (1 and 2), we pooled 130 ng of every barcoded product and purified the two resulting pools using gel extraction.

For subsequent DNA sequencing two PacBio Sequel SMRT cells were used for the two pooled samples (phase 1 and phase 2), and sequencing was performed on the PacBio Sequel system (3.0 Chemistry) by the Functional Genomics Center Zurich.

Processing of Raw Data

We obtained approximately 600,000 raw zero mode waveguide (ZMW) reads from each of the SMRT cells. We determined the consensus of circular sequences (CCS) from the raw data (subreads) using the ccs (v3.4.1) application from the PacBio SMRTlink package (Pacific Biosciences 2019b), with the following parameters: minimum length = 750, maximum length = 1,500, minimum passes = 3, minimum predicted accuracy = 99%. We kept the other parameters at their default value. We obtained approximately 55% of the ZMW reads. We demultiplexed the post-CCS reads using lima (v1.9.0, SMRTlink), and aligned them to the reference sequence (GFPmut2) using minimap2 (v2.15-r905, SMRTLink). We analyzed the alignments in SAM format using a custom awk script. PacBio sequencing produces a high incidence of artifactual indels (Goodwin et al. 2016; Giordano et al. 2017; Watson and Warr 2019). Consistent with this observation, we found indels (mostly insertions) in the coding region of almost every read. To demonstrate that many of these must be false positives, we Sanger-sequenced 20 randomly chosen GFP variants. Not a single one of them contained an indel. Second, we also never found indels in preselection samples (again sequenced using Sanger sequencing), which suggests that our mutagenesis protocol does not produce indels. Thirdly, if these indels were not sequencing artifacts, then even our first-generation populations should have lost their fluorescence phenotype due to deleterious frameshifts. This was not the case (fig. 2). Therefore, we excluded any indels from further analysis. From the data thus filtered, we obtained lists of single mutations as well as genotypes with multiple mutations, along with their raw counts and frequencies.

Synonymous mutations can alter cotranslational folding (Buhr et al. 2016), but GroE-assisted folding occurs post-translationally. For this reason, we focused our analysis to nonsynonymous mutations. We discuss synonymous mutations in section 10, Supplementary Material online.

Estimation of Genetic Diversity

We used three measures of genetic diversity, all of which are based on the observed number of amino acid changes in our evolving GFP sequences. The first is the average distance of the genotypes in a population from the ancestor, defined as the average number of amino acid mutations in a population relative to the ancestral GFP sequence. The second is the average pairwise distance between two genotypes in a population, defined as the Hamming distance between their amino acid sequences. This metric is analogous to a widely used nucleotide diversity metric (Nei and Li 1979), except that we apply it to amino acid sequences. Specifically, we define:

$$\pi =\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j\ne i}{\pi }_{ij}$$ (1)

where π denotes the average pairwise distance between any two genotypes in a population, π_ij denotes the distance between the ith and the jth genotypes, and n is the total number of genotypes in the population.

The third metric is the Shannon entropy H of individual allele frequencies p_i in a population (Vajapeyam 2014), defined as:

$$H=\sum _i-p_i{\hspace{0.17em}\text{log}\hspace{0.17em}}_2(p_i).$$ (2)

This diversity measure is largest if all alleles have equal frequencies, and it decreases as an allele frequency distribution becomes increasingly peaked at one or few alleles that occur at much higher frequencies than the other alleles.

We used LMM implemented in the R package lme4 (v1.1-21; Bates et al. 2015) to analyze the effect of GroE overexpression on changes in genetic diversity between different populations. We represented diversity as the response variable, with time (rounds of evolution) and state of GroE expression (G⁺ or G⁺) as interacting predictor variables. We include differences between the replicate populations as random effects. Specifically, we used the following expression to define the model: diversity ∼ rounds*condition + (1|replicate). We tested the model’s goodness-of-fit to the sequence data using the ANOVA function from the R package, lmerTest (v3.1-0; Kuznetsova et al. 2017).

Principal Component Analysis of the Genotypes

We performed PCA (Bratulic et al. 2017) to visualize different genotypes accumulated in a population. To this end, we randomly sampled 200 sequences without replacement from every replicate population after the end of the final round of evolution. We converted the amino acid sequence of each genotype to a numerical sequence, assigning a numerical code to each amino acid. Specifically, we assigned the numbers 1–20 to amino acids in the following order: W, F, Y, I, V, L, M, C, D, E, G, A, P, H, K, R, S, T, N, and Q. This ordering of amino acid, in contrast to an alphabetical order, ensures that chemically similar amino acids have a small numerical difference between them (Kim et al. 2009). We assigned the number −10 to the stop codon, because effects of nonsense mutations are dramatically different from those of missense mutations.

We then performed PCA (supplementary figs. S9A and S10A, Supplementary Material online) on a matrix containing all these numerical sequences, using the prcomp function from the R package stats (v3.4.4; R Core Team 2018). The rows of this matrix harbor individual sequences (genotypes). Its columns correspond to individual positions in the sequence.

We also performed PCA on a matrix harboring allele frequencies of all single amino acid mutations from each population at the end of evolution (supplementary figs. S9B and S10B, Supplementary Material online). In this matrix, each row contains allele frequency data from a different population, and each column corresponds to a different observed mutant.

Monte–Carlo Simulations to Calculate Variant Frequencies Expected under Mutation Pressure Alone

We restricted this analysis to amino acid variants that attain a minimal threshold frequency in at least one replicate population at the end of evolution. We chose this threshold frequency to be 3.5% for phase 1, and 5% for phase 2 to keep the number of variants manageable for all subsequent analyses. No individual population had more than 56 variants exceeding these thresholds. For each of these variants, we performed Monte–Carlo simulations to test the null hypothesis that mutation pressure alone may be responsible for the variant’s frequency. Rejection of this null hypothesis for any one variant implies that selection must be involved in explaining its frequency. (Our experimental populations are sufficiently large that genetic drift is negligible on the time scales of our experiment.)

This numerical analysis consists of two parts. In the first part, we compute the probability π that a specific amino acid variant arises in the population. In the second part, the Monte–Carlo simulation proper, we simulate how the frequency of this variant changes over time due to mutation pressure alone.

We explain this procedure with the mutation S147P, which occurs at a frequency of less than 0.4% in all the G⁺ populations at the final (fifth) round of phase 1. After five additional rounds of evolution in phase 2 this mutation attained a frequency greater than 98% in all replicate populations. S147P is encoded by the codon CCA, which requires a T$\to$C change at the 439th position of the GFP coding sequence, which corresponds to the first position of the ancestral codon 147 (TCA$\to$CCA).

For an S147P mutation to occur, three events must take place. We calculate their probability as follows.

• At least one mutation must occur (somewhere) in the GFP coding sequence. Because mutations are rare, we model the probability $P_{\text{mut}}$ of this event with a Poisson distribution, such that

  $$P_{\text{mut}}=1-{\mathrm{e}}^{-\lambda }.$$

  Here, λ denotes the average number of mutations in each individual per round of mutagenesis. Because we had calibrated our mutagenesis protocol such that this number lies between 1 and 2 (see Estimation of Mutation Rate), we use a value of $\lambda =1.5$, which leads to $P_{\text{mut}}=0.777$

• One of the occurring mutations must affect the 439th nucleotide position, whereas all other mutations must occur outside codon 147. If only one mutation occurs in the GFP coding sequence, the probability of this event ($P_{\text{pos}}$) is equal to the probability of choosing this one position from the GFP coding sequence of length 717nt, which is $1/717=0.0014$. If two mutations occur in the coding sequence then $P_{\text{pos}}$ would be $1/717\times 715/716=0.001393$. If three mutations occur, $P_{\text{pos}}=1/717\times 715/716\times 714/717=0.001391$. Analogous expressions apply for (increasingly unlikely) higher numbers of mutations. Since the difference between the values of $P_{\text{pos}}$ for the above three cases is very small, we can conveniently approximate its value to be $P_{\text{pos}}=1/717=0.0014$. Because this value is a slight overestimate, our statistical inference would be conservative.

• This mutation must cause a T$\to$C change. From our estimation of mutation rates by Sanger sequencing experiments (see Estimation of Mutation Rate), we know that this probability ($P_{\text{sub}}$) is 0.75

The probability (π) that the mutation S147P occurs (i.e., all the above-mentioned events occur) in any one generation is the product of the above three probabilities: $P_{\text{mut}}\times P_{\text{pos}}\times P_{\text{sub}}=8.18\times {10}^{-4}$.

We note that we can neglect amino acid changes caused by double or triple nucleotide mutations, because our sequencing data showed that every amino acid variant that exceeded our threshold frequency was caused by a single nucleotide change.

We next turn to the second part of our numerical analysis, where we use the probability π that a specific variant arises to calculate how the expected mean frequency of this variant changes over time. To this end, we used a discrete time stochastic model of a population whose individuals mutate at a rate π, such that the number of unmutated individuals becomes progressively smaller. Our simulations neglect back-mutations to the wild-type allele, which will slightly overestimate the allele frequencies caused by mutation pressure. In consequence, our analysis below will be statistically conservative. That is, it might accept some variants as having a frequency consistent with mutation pressure alone, whereas they may actually be affected by selection.

Specifically, for each mutant whose frequency exceeded our threshold, we performed the following simulation 10⁵ times, with a starting population of $N_0={10}^5$ individuals. Each individual has a probability π (as described earlier) of acquiring a given mutation. The number of individuals mutated in the first round of evolution is thus given by a random variable that is binomially ($B(\pi ,N_0)$) distributed. In our simulations, we generated a pseudorandom number M₀ from this distribution, and computed the number of unmutated individuals after the first round of evolution as $N_1=N_0-M_0$. In the second round, the number of individuals experiencing the mutation is a random variable with binomial distribution, $B(\pi ,N_1)$. We also generated an instance M₁ of this random variate numerically, and calculated the number of unmutated individuals after the second round as $N_2=N_1-M_1$. We repeated this procedure for three more rounds/generations to obtain the frequency of the remaining wild-type alleles, and thus also the frequency of the mutant alleles at the end of phase 1. We repeated the procedure for an additional five rounds to obtain mutant allele frequencies at the end of phase 2 evolution. For each mutation, we performed 10⁵ such simulations and calculated the fraction of simulations in which the predicted frequency exceeded the threshold frequency of 3.5% for phase 1 and of 5% for phase 2.

For each variant whose frequency exceeded the threshold in our experimental populations, not a single one among 10⁵ simulation reached this threshold. Thus, if we consider the null-hypothesis that the observed frequency of any one variant can be explained by mutation pressure alone, our simulations reject this null-hypothesis at a P value of $P<{10}^{-5}$. Applying a Bonferroni correction to the number of such tests, we performed (<90 tests, i.e., variants, for each of the two threshold), we reject the null-hypothesis at a Bonferroni-corrected P value of P < 0.0009. In sum, the frequency of no mutation we consider here can be explained by mutation pressure alone. Since our populations are so large that we can neglect genetic drift at the time scale of this experiment, selection or hitchhiking with another high-frequency mutation must be invoked to explain their frequency.

Calculation of Mutation Enrichment

For each round of evolution, we compared the enrichment of mutations in G⁺ populations relative to G⁻ populations, using generalized LMs (GLM; R stats package v3.4.4; R Core Team 2018). Specifically, we fitted a GLM with a logit link function (binomial model) using mutation counts as the response variable, and the state of GroE expression (G⁺ or G⁻) as the predictor variable. We analyzed the goodness of fit of the full model (slope + intercept) with respect to a reduced (intercept only) model, using the ANOVA function from the R stats package v3.4.4. This function performs an analysis of deviance on the models, using a likelihood ratio test, and determines if the additional parameters (slope in our case) significantly improve the fit. Here, a positive value of the slope denotes enrichment of the mutation in G⁺ populations. We adjusted the P values thus obtained for multiple testing using a Bonferroni correction. We used the mutations with a corrected P value of P < 0.05 in subsequent analyses.

Estimating the Strength of Selection Acting on Mutations

For the variants that satisfied the frequency threshold criterion of Monte–Carlo simulations, we estimated the strength of selection in G⁺ and G⁻ populations by fitting generalized linear mixed-effects models (GLMM) using the function glmer from the R package lme4 (v1.1-21; Bates et al. 2015). We fitted two models, one each for GroE overexpression and control populations, using a logit link function with mutation counts as the response variable, time (round of evolution) as the predictor variable, and the variation between replicate populations as the random effect. Specifically, we defined the models with the following expression: Counts ∼ rounds + (1|replicate). We analyzed the goodness of fit of the full model (slope + intercept) with respect to a reduced (intercept only) model, using the ANOVA function from the R stats package v3.4.4. We adjusted the P values thus obtained for multiple testing using a Bonferroni correction. The estimated value of the slope denotes the strength and direction of selection. A positive value denotes positive selection, and a higher absolute value of the slope denotes stronger selection.

Construction and Analysis of Specific Mutants

Engineering-Specific Mutations

We used PCR-based site directed mutagenesis to engineer-specific mutations into the GFP gene. To this end, we first created a “minimal” plasmid that expresses GFP constitutively (pMini-GFP) from the rplN promoter, but that did not contain the chaperone genes and the araC gene. We designed primer pairs to amplify this entire plasmid from the site of the desired mutation (supplementary table S7, Supplementary Material online). Specifically, we designed these primer pairs with 15 complementary nucleotides at their 3′ end and a noncomplementary region that did not exceed 25 nucleotides in length. We included the desired mutation in the complementary region. Whenever the difference in melting temperature (Tm) of the primers exceeded 5 °C, we trimmed the noncomplementary region of the primer with higher Tm from the 5′ end. We used the software tool—melting (ver. 5.1) (Dumousseau et al. 2012) to calculate Tm. We designed the primers in this way to minimize inefficient amplification due to primer dimer formation.

We amplified pMini with different primer pairs for each mutation to be engineered (supplementary table S7, Supplementary Material online) using high-fidelity Q5 polymerase (NEB). We transformed the PCR products into E.  coli BW27784 cells made transformation-competent with the CaCl₂ method (Green et al. 2012), using a standard heat shock transformation method (Green et al. 2012). We isolated and purified plasmid from the clones thus obtained and sequenced the GFP gene to confirm the mutation. Next, we cloned each mutated GFP gene into the GroE expression plasmid, pGro7-rplN-GFP.

We generated double mutants via the same procedure, by engineering the mutations serially via two rounds of PCR. Next, we cloned the mutated GFP gene into pGro7-rplN-GFP.

Measurement of Growth Rates Associated with Different GFP Mutants

To measure whether selected mutations (M1I, M1L, M1T, M1V, and S2G) confer a growth advantage in the absence of GroE expression, we prepared 1:20 dilutions of an overnight culture of each mutant, as well as of the strain expressing ancestral GFP. We inoculated 10 µl of each diluted suspension into 1.4 ml of fresh LB+Chl, and aliquoted 200 µl of this inoculated medium into six wells (replicates) of a 96-well plate. Next, we measured OD (at 600 nm) every 10 min during 20 h on a Tecan Spark plate reader at 37 °C and with the plate shaken constantly between measurements.

All mutants reached stationary phase after 13 h of growth. Because the growth data fitted a logistic growth equation poorly (not shown), we calculated the maximum growth rate, another commonly used estimate of growth (Papkou et al. 2020). To this end, we first logarithmically (base 2) transformed the measured OD values for each mutant. Using a sliding window of six time points (corresponding to 1 h of growth), we calculated the rate of change of ${\hspace{0.17em}\text{log}\hspace{0.17em}}_2$-OD between consecutive time points using an LM (R stats package v3.4.4) (R Core Team 2018). Next, we calculated the maximum value of this slope for all time points, and for each of the six replicates for each mutant and the ancestor. We then compared the median maximum growth rate (of the six replicates) for each mutant to that of ancestral GFP using a one-tailed Mann–Whitney U test. Each of the five mutations conferred a significantly higher growth rate relative to that of ancestral GFP (Mann–Whitney U test, false discovery rate corrected P < 0.013).

Modeling the Effect of GroE Overexpression on Fitness

We define a genotype’s fitness based on its fluorescence rather than its growth rate, because this is the criterion we used during directed evolution. More specifically, we define a genotype’s fitness as the probability that a cell with this genotype exceeds the fluorescence threshold of 150 arbitrary units which we used during phase 1 selection. Cells with a given genotype can show a broad distribution of fluorescence due to phenotypic heterogeneity. Here, we show how we map this distribution onto fitness both without and with GroE overexpression. Our procedure consists of two steps. In the first, we estimate statistical parameters such as mean and variance of the fluorescence distribution of each genotype from flow cytometry data. In the second, we use these statistical parameters to predict the fluorescence distribution of genotypes with arbitrary mean fluorescence in the presence and absence of GroE overexpression.

Step 1. In the absence of GroE overexpression, all genotypes we engineered showed a Gaussian distribution of logarithmically (base 10) transformed green fluorescence ($\mathcal{N}({\mu }_{-},{\sigma }_{-})$, supplementary fig. S14A and B, Supplementary Material online). In contrast, in the presence of GroE overexpression this distribution became bimodal. In this bimodal distribution, the first mode (peak) ${\mu }_{+\mathrm{L}}$ has a lower fluorescence intensity than ${\mu }_{-}$ whereas the second mode ${\mu }_{+\mathrm{H}}$ has a higher fluorescence intensity than ${\mu }_{-}$ (supplementary fig. S14A, Supplementary Material online). The same holds for cyan fluorescence (supplementary fig. S14B, Supplementary Material online). We expressed this bimodal distribution as a sum of two Gaussian distributions. Specifically, we defined a bimodal probability density function $C_{+\mathrm{L}}\mathcal{N}({\mu }_{+\mathrm{L}},{\sigma }_{+\mathrm{L}})+C_{+\mathrm{H}}\mathcal{N}({\mu }_{+\mathrm{H}},{\sigma }_{+\mathrm{H}})$, where $C_{+\mathrm{L}}$ and $C_{+\mathrm{H}}$ denote weight coefficients for the Gaussian distributions representing the lower and the higher modes, respectively.

To estimate these parameters for each genotype, we fitted a kernel density function to the fluorescence distribution data from populations with GroE overexpression, using the fitdist function from the Statistics and Machine Learning Toolbox (ver. 11.5) of MATLAB (2019a). Then, we used the fmincon function (constrained nonlinear optimization) from the MATLAB (2019a) Optimization Toolbox (ver 8.3) to estimate a set of parameters for the bimodal distribution that minimize the square distance between the data and the fitted kernel density function. During this optimization, we constrained the weight parameters to have a value between zero and one. In addition, we fitted a (single) Gaussian density function to the fluorescence distribution of GFP mutants in the absence of GroE overexpression, using the fitdist function to estimate parameters ${\mu }_{-}$ and ${\sigma }_{-}$ for this distribution.

We performed these calculations for every biological replicate of ancestral GFP and all the engineered mutants, except for start codon mutants. We excluded the start codon mutations from this analysis for two reasons. Firstly, their range of fluorescence intensities (both in the presence and absence of GroE expression) overlapped with the range of cellular autofluorescence, making it difficult to accurately estimate the fluorescence distribution independently from this background. Secondly, for these mutations, the two fluorescence peaks that arose due to GroE expression were so close that bimodality was not clearly apparent. Their overlap with the autofluorescence distribution further hindered the discrimination of these peaks.

Our procedure resulted in an estimate of the parameters ${\mu }_{-},\hspace{0.17em}{\sigma }_{-},\hspace{0.17em}{C}_{+\mathrm{L}},\hspace{0.17em}{C}_{+\mathrm{H}},\hspace{0.17em}{\sigma }_{+\mathrm{L}},\hspace{0.17em}{\sigma }_{+\mathrm{H}},\hspace{0.17em}{\mu }_{+\mathrm{L}}$, and ${\mu }_{+\mathrm{H}}$, for each of the 19 mutants we analyzed, and for three biological replicates for each mutant (supplementary fig. S18, Supplementary Material online).

Across these mutants, the value of ${\mu }_{+\mathrm{L}}$ was on an average $\sim 93\%$ of that of ${\mu }_{-}$, and that of ${\mu }_{+\mathrm{H}}$ was on an average $\sim 107\%$ of that of ${\mu }_{-}$ (supplementary fig. S20A, Supplementary Material online). In addition, for any one mutation the values of ${\mu }_{+\mathrm{L}}$ and ${\mu }_{+\mathrm{H}}$ were clearly distinct from each other (supplementary fig. S20A, Supplementary Material online). For these reasons, we chose to express ${\mu }_{+\mathrm{L}}$ and ${\mu }_{+\mathrm{H}}$ relative to ${\mu }_{-}$. By doing that, one can obtain the absolute value of each peak by multiplying the relative values with ${\mu }_{-}$. We denote these relative values by the symbols ${\mu }_{+\mathrm{L}}^{\prime }$ and ${\mu }_{+\mathrm{H}}^{\prime }$, respectively.

The weight coefficients, $C_{+\mathrm{L}}$ and $C_{+\mathrm{H}}$, did not depend on ${\mu }_{-}$, and their values showed a nonoverlapping distribution across mutants, with means of 0.64 and 0.76, respectively (supplementary fig. S20B, Supplementary Material online). The SDs ${\sigma }_{-},\hspace{0.17em}{\sigma }_{+\mathrm{L}}$ and ${\sigma }_{+\mathrm{H}}$ also did not depend strongly on ${\mu }_{-}$ but their distributions across mutants overlapped (supplementary fig. S20C, Supplementary Material online). Below, we will refer collectively to $C_{+\mathrm{L}},\hspace{0.17em}{C}_{+\mathrm{H}},\hspace{0.17em}{\sigma }_{+\mathrm{L}},\hspace{0.17em}{\sigma }_{+\mathrm{H}},\hspace{0.17em}{\mu }_{+\mathrm{L}}$, and ${\mu }_{+\mathrm{H}}$ as the parameters of the bimodal distribution.

Step 2. To map fluorescence distributions of arbitrary mutants onto fitness, we first represented different mutants through different mean fluorescence values ${\mu }_{-}$ in the absence of GroE expression. We explored a range of ${\mu }_{-}$ values ranging from 10 to 10⁵, because this is the range of green fluorescence that we observed in libraries of GFP mutants before selection. We subdivided this range into 4,000 bins that are equally spaced on a logarithmic (base 10) scale, and chose a ${\mu }_{-}$ value from each bin for all subsequent analyses. (We will henceforth refer to all fluorescence values on this logarithmic scale).

We will first describe how we predicted the fitness of variants for each of these ${\mu }_{-}$ values in the absence of GroE expression. To do so, we first had to generate a distribution of expected log-fluorescence values for a variant with a given value of ${\mu }_{-}$. As mentioned earlier in this section, without GroE expression log-fluorescence is Gaussian distributed with mean ${\mu }_{-}$ and SD ${\sigma }_{-}$ ($\mathcal{N}({\mu }_{-},{\sigma }_{-})$). This means that we had to estimate ${\sigma }_{-}$ for any given ${\mu }_{-}$. Supplementary figure S20C (black dots), Supplementary Material online, shows that ${\sigma }_{-}$ spans a range of 0.15–0.25 and does not depend on ${\mu }_{-}$. We thus chose randomly choose different values of ${\sigma }_{-}$ from this range under the assumption that ${\sigma }_{-}$ itself has a Gaussian distribution. Specifically, we first calculated the mean ($M_{{\sigma }_{-}}$) and SD ($S_{{\sigma }_{-}}$) from the experimentally observed distribution of ${\sigma }_{-}$ values (supplementary table S5, Supplementary Material online).

We then chose for each value of ${\mu }_{-}$, 4,000 different pseudorandom variates ${\sigma }_{-}$ with the Gaussian distribution, $\mathcal{N}\left(M_{{\sigma }_{-}},S_{{\sigma }_{-}}\right)$. Each of the resulting 4,000 pairs of ${\mu }_{-}$ and ${\sigma }_{-}$ values defines a fluorescence distribution of cells with a given genotype, and we determined the fraction of cells in this distribution that exceeded the selection threshold of 150 arbitrary units (2.176 units on a logarithmic scale). We then averaged this fraction over all 4,000 ${\mu }_{-},{\sigma }_{-}$ pairs to obtain the expected fitness of a genotype with fluorescence mean ${\mu }_{-}$ (F⁻).

We then repeated this procedure for all 4,000 values of ${\mu }_{-}$ in the fluorescence interval (2, 5) to obtain a fitness estimate for each possible variant in this interval. In other words, our estimate of fitness in the absence of GroE is based on 4,000 × 4,000 pairs of ${\mu }_{-}$ and ${\sigma }_{-}$ values.

We next describe how we obtained the same fitness distribution in the presence of GroE expression. We again start with 4,000 values of ${\mu }_{-}$ in the fluorescence interval (2, 5), and perform the same procedure as just described for each such value, except that the distribution is more complex, and we thus need to estimate not just one parameter (${\sigma }_{-}$) but six of them: $C_{+\mathrm{L}},\hspace{0.17em}{C}_{+\mathrm{H}},\hspace{0.17em}{\sigma }_{+\mathrm{L}},\hspace{0.17em}{\sigma }_{+\mathrm{H}},\hspace{0.17em}{\mu }_{+\mathrm{L}}^{\prime }$ (${\mu }_{+\mathrm{L}}$ relative to ${\mu }_{-}$), and ${\mu }_{+\mathrm{H}}^{\prime }$ (${\mu }_{+\mathrm{H}}$ relative to ${\mu }_{-}$). Importantly, our experimental data show these values do not depend on the value of ${\mu }_{-}$ (supplementary fig. S20, Supplementary Material online). We thus estimated each of these parameters by sampling them from a Gaussian distribution whose parameters we estimated from the experimental data (supplementary table S5, Supplementary Material online), exactly as we described above for ${\sigma }_{-}$.

At the end of this procedure, we had obtained a total of $\mathrm{4,000}\times \mathrm{4,000}\times 6$ combinations of parameters. Each of them describes a bimodal fluorescence distribution from which we calculate the fraction of cells above the selection threshold (F⁺).

Overall, this procedure yields for each genotype (value of ${\mu }_{-}$) a value of fitness in the absence of GroE (F⁻) and in the presence of GroE (F⁺). We then also calculated the difference between these two fitness values (ΔF=F${}^{+}-$F⁻) which denotes the effect of GroE on fitness. A positive value of ΔF means higher fitness in the presence of GroE (buffering) and a negative value means lower fitness in the presence of GroE (potentiation).

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.