Beyond broadband: Towards a spectral decomposition of electroencephalography microstates

Abstract

Originally applied to alpha oscillations in the 1970s, microstate (MS) analysis has since been used to decompose mainly broadband electroencephalogram (EEG) signals (e.g., 1–40 Hz). We hypothesised that MS decomposition within separate, narrow frequency bands could provide more fine‐grained information for capturing the spatio‐temporal complexity of multichannel EEG. In this study, using a large open‐access dataset (n = 203), we first filtered EEG recordings into four classical frequency bands (delta, theta, alpha and beta) and thereafter compared their individual MS segmentations using mutual information as well as traditional MS measures (e.g., mean duration and time coverage). Firstly, we confirmed that MS topographies were spatially equivalent across all frequencies, matching the canonical broadband maps (A, B, C, D and C′). Interestingly, however, we observed strong informational independence of MS temporal sequences between spectral bands, together with significant divergence in traditional MS measures. For example, relative to broadband, alpha/beta band dynamics displayed greater time coverage of maps A and B, while map D was more prevalent in delta/theta bands. Moreover, using a frequency‐specific MS taxonomy (e.g., ϴA and αC), we were able to predict the eyes‐open versus eyes‐closed behavioural state significantly better using alpha‐band MS features compared with broadband ones (80 vs. 73% accuracy). Overall, our findings demonstrate the value and validity of spectrally specific MS analyses, which may prove useful for identifying new neural mechanisms in fundamental research and/or for biomarker discovery in clinical populations.

Originally applied to alpha oscillations in the 1970s, microstate (MS) analysis has since been used to decompose mainly broadband electroencephalography (EEG) signals (e.g., 1–40 Hz). We hypothesized that MS decomposition within separate, narrow frequency bands could provide more fine‐grained information for capturing the spatio‐temporal complexity of multichannel EEG. After decomposing a large open‐access dataset (n = 203) into four classical frequency bands, we observed strong informational independence of MS temporal sequences between spectral bands which may prove useful for identifying new neural mechanisms in fundamental research and/or for biomarker discovery in clinical populations.

1. INTRODUCTION

Multichannel electroencephalography (EEG) is a long‐established tool for exploring the human brain's spatio‐temporal activities. Microstate (MS) analysis (Michel & Koenig, 2018), first introduced by Lehmann (1971), takes advantage of EEG's high temporal resolution to segment EEG signals into short successive periods of time characterised by metastable scalp topographies. Initially applied to narrowband alpha oscillations (8–12 Hz)(Lehmann, 1971), MS analysis is nowadays usually performed on broadband EEG signals (1–40 Hz) (Michel & Koenig, 2018; Zanesco, King, Skwara, & Saron, 2020). Historically, only a limited number of studies (Javed, Croce, Zappasodi, & Del Gratta, 2019; Merrin, Meek, Floyd, & Enoch Callaway, 1990; Musaeus et al., 2020) have focused on applying MS analysis to the traditional frequencies associated with cortical oscillations (e.g., delta, theta, alpha, beta, etc.). For example, Merrin et al. (1990) were the first to report on a significant difference in MS segments between schizophrenic patients and controls specifically in the theta EEG band. On the other hand, more recent work in healthy subjects found that MS dynamics were independent of EEG power fluctuations across the frequency spectrum (Britz, Van De Ville, & Michel, 2010), which technically supported the rationale for performing broadband MS analysis. Neuroimaging studies have nevertheless emerged showing that anatomically distinct cortical regions display different dominant EEG frequencies, with occipitoparietal regions more active in the alpha band, and prefrontal regions being biased more towards delta or theta power (Groppe et al., 2013; Keitel & Gross, 2016; Mellem, Wohltjen, Gotts, Ghuman, & Martin, 2017). Moreover, ongoing cortical dynamics have been reported to fluctuate from a local resting/idling alpha oscillatory state to task‐specific active mode(s) dominated by other rhythms [e.g., theta (Ribary, Doesburg, & Ward, 2017) and gamma (Hipp, Engel, & Siegel, 2011)]. As a consequence, cortical regions could combine different frequencies for integrating/segregating information across large‐scale networks, a phenomenon termed ‘oscillatory multiplexing’ (Akam & Kullmann, 2014). Finally, of more clinical significance, a growing body of work has indicated abnormal EEG spectral power in distinct frequencies across cortical regions in a variety of brain disorders (Ros, Baars, Lanius, & Vuilleumier, 2014; Schulman et al., 2011). Therefore, given that different spatial topographies uncovered by MS analysis imply anatomically distinct cortical generators [according to the forward‐model of EEG generation (Michel & Koenig, 2018)], it is reasonable to hypothesise that distinct MS topographies may display different spatial and/or temporal profiles across the frequency spectrum.

To investigate this question as well as gain a deeper understanding of frequency‐specific MS signature(s), we sought to explicitly decompose MS spatio‐temporal dynamics within discrete, narrowband frequency bands (i.e., delta, theta, alpha and beta), with the aim of comparing them to the classical analysis of the broadband signal.

Here, we employed a validated, open‐source dataset (Babayan et al., 2019) of resting‐state EEG recordings from 203 healthy subjects during both eyes‐open (EO) and eyes‐closed (EC) conditions. These were then filtered in the classical EEG bands (delta: 0–4 Hz, theta: 4–8 Hz, alpha: 8–12 Hz and beta: 15–30 Hz) to obtain band‐specific signals. These narrowband signals, in addition to the broadband (1–30 Hz) signal, were then independently subjected to standard MS analysis (Pascual‐Marqui, Michel, & Lehmann, 1995). Map topography, mean duration (MeanDurs), occurrence, time coverage (TimeCov) and global explained variance (GEV) were used as quantitative measures of spatio‐temporal MS dynamics. In summary, and using spatial correlation analysis, we firstly demonstrate remarkably similar MS topographies across frequencies, closely matching the classical broadband maps. Interestingly, however, we observed strong informational independence of MS sequences between frequencies, in addition to significant differences in established measures of temporal dynamics (MeanDurs, occurrence and TimeCov).

In conclusion, our results support a more diverse, frequency‐specific application of MS analysis compatible with the narrowband MS analyses of early pioneers (Lehmann, 1971; Merrin et al., 1990). We anticipate this approach to provide a more fine‐grained spectral information not visible to the standard broadband analysis, for example, in the identification of biomarkers in clinical populations or for understanding the mechanisms underlying EEG MSs.

2. METHODS

2.1. Dataset

EEG recordings were obtained from 203 anonymized participants enrolled in the Mind‐Brain‐Body study (Babayan et al., 2019). Detailed protocol and inclusion criteria are reported in the literature (Babayan et al., 2019). The overall sample consisted of 227 participants divided into two groups: the younger adults group with participant age ranging between 20 and 35 years (N = 153, 45 females, mean age = 25.1 years and SD = 3.1) and an older adults group with age ranging between 59 and 77 years (N = 74, 37 females, mean age = 67.6 years and SD = 4.7). Medical and psychological screening was conducted on all participants at the Day Clinic for Cognitive Neurology of the University Clinic Leipzig and the Max Planck Institute for Human and Cognitive and Brain Sciences to include only healthy patients. The study protocol was approved by the ethics committee of the University of Leipzig (reference 154/13‐ff). Data were obtained in accordance with the Declaration of Helsinki.

2.2. Recordings

Resting‐state EEGs were recorded using 61 scalp electrodes (ActiCAP, Brain Products GmbH, Gilching, Germany), and one additional vertical electrooculography electrode for recording right eye activity. All electrodes were placed according to the international standard 10–20 extended localization system with FCz reference, digitised with a sampling frequency of fs = 2500 Hz, and an amplitude resolution of 0.1 microV, and bandpass filtered between 0.015 Hz and 1 kHz. The ground was located at the sternum, and scalp electrode impedance was kept below 5 kΩ. Recordings took place in an electrically shielded and sound‐attenuated EEG booth. Here, 60s blocks alternated between EO and EC conditions for a total recording of 16 min (eight blocks EC, eight blocks EO, starting with EC). During the EO condition, participants were asked to stay awake while fixating their eyes on a black cross presented on a white background.

2.3. Preprocessing

The preprocessing steps are extensively described in the literature (Babayan et al., 2019), which we summarise below. All EEG recordings were down‐sampled from 2500 to 250 Hz and filtered between 1 and 45 Hz (eighth order, Butterworth filter). Blocks sharing the same condition were concatenated leading to the creation of two datasets per subject. After visual inspection, outlying channels were rejected and EEG segments presenting noise and/or artefacts were removed (except eye movements and eye blinks that were kept for further prepossessing). Principal component analysis was used to reduce data dimensionality, by keeping PCs (N ≥ 30) that explain 95% of the total data variance. Then, independent component analysis (ICA) was performed using the Infomax (runica) algorithm. Retained independent components for EO (mean: 19.7, range: 9–30) and EC (mean: 21.4, range: 14–28). Components reflecting eye movement, eye blink, or heartbeat related artefacts were removed.

Before performing MS analysis, the following additional prepossessing steps were conducted using MNE‐python (Gramfort et al., 2013): missing/bad channels were interpolated using spherical spline interpolation, the reference was re‐projected to average, and recordings were down‐sampled to 100 Hz. Finally, each recording was filtered into broadband plus the five traditional EEG frequency bands: broadband (1–30 Hz), delta (1–4 Hz), theta (4–8 Hz), alpha (8–12 Hz) and beta (15–30 Hz). Filter design consisted of a two‐pass forward and reverse, zero‐phase, non‐causal bandpass finite‐impulse response filter with the following parameters.

• Broadband (1–30 Hz): Lower passband edge: 1.00; lower transition bandwidth: 1.00 Hz (−12 dB cut‐off frequency: 0.50 Hz); upper passband edge: 30.00 Hz; upper transition bandwidth: 7.50 Hz (−12 dB cut‐off frequency: 33.75 Hz); filter length: 331 samples (3.310 s).

• Delta (1–4 Hz): Lower passband edge: 1.00; lower transition bandwidth: 1.00 Hz (−12 dB cut‐off frequency: 0.50 Hz); upper passband edge: 4.00 Hz; upper transition bandwidth: 2.00 Hz (−12 dB cut‐off frequency: 5.00 Hz); filter length: 331 samples (3.310 s).

• Theta (4–8 Hz): Lower passband edge: 4.00; lower transition bandwidth: 2.00 Hz (−12 dB cut‐off frequency: 3.00 Hz); upper passband edge: 8.00 Hz; upper transition bandwidth: 2.00 Hz (−12 dB cut‐off frequency: 9.00 Hz); filter length: 165 samples (1.650 s).

• Alpha (8–12 Hz): Lower passband edge: 8.00; lower transition bandwidth: 2.00 Hz (−12 dB cut‐off frequency: 7.00 Hz); upper passband edge: 12.00 Hz; upper transition bandwidth: 3.00 Hz (−12 dB cut‐off frequency: 13.50 Hz); filter length: 165 samples (1.650 s).

• Beta (15–30 Hz): Lower passband edge: 15.00; lower transition bandwidth: 3.75 Hz (−12 dB cut‐off frequency: 13.12 Hz); upper passband edge: 30.00 Hz; upper transition bandwidth: 7.50 Hz (−12 dB cut‐off frequency: 33.75 Hz); filter length: 89 samples (0.890 s).

For all filters, a Hamming window with 0.0194 passband ripple and 53‐dB stopband attenuation was used to reduce border effects.

2.4. MS segmentation

2.4.1. Segmentation

MS segmentation was applied to each combination (case) of frequency band (broadband, delta, theta, alpha and beta) × behavioural condition (EO, EC) leading to the computation of optimal clusters using the methodology described below.

The first step (Figure S1—Step 1) consisted in computing within each case and for each individual, 20 clusters (each composed of k centroids (1 ≤ k ≤ 12). For this purpose, local maxima of the global field power (GFP) known to represent the portions of EEG data with highest signal‐to‐noise ratio (Koenig & Brandeis, 2016) were extracted from each individual recording. Twenty random subsamples each composed of 500 of those GFP peaks were independently submitted to a modified k‐means cluster analysis using the free academic software Cartool (Brunet, Murray, & Michel, 2011). This k‐means clustering algorithm is modified to change the way the similarity between samples is calculated, using the absolute spatial correlation instead of the more traditional Euclidean definition to extract spatial patterns that are invariant to polarity. The clustering process consisted of evaluating independently for each number of centroids k ranging from 1 to 12, 50 random initialisations of the modified k‐means algorithm. For each number of centroids k, initialisation with highest GEV was selected and kept for further processing. Finally, a meta‐criterion (Bréchet et al., 2019) was used to choose the optimal number of centroids among all possible value of k. At the end of this process, each individual recording had for each case (combination of filter parameters × behavioural condition) a set of 20 optimal clusters each composed of k centroids.

The second step (Figure S1—Step 2) of the processing consisted of merging individual optimal clusters within each case to form 10 set each composed of 4,060 individuals set of k centroids. Each set was then randomly resampled into 100 random subsets each composed of 5,000 centroids and submitted to the modified k‐means algorithm (50 initialisations, with meta criterion selection), leading to the extraction of 100 optimal set of centroids per case. Finally, the last step of the processing consisted of merging these 100 sets and submit them to the modified k‐means clustering algorithm to extract, for each number of all values of k between 1 and 12, a set of k centroids which best represent the spatio‐temporal variance of frequency‐specific EEG data within each condition.

2.4.2. Selection of ‘common’ MS maps

Given that we found high spatial correlations between MS maps across all frequencies and EO/EC conditions, we fitted the broadband maps directly to all the frequency bands to have a common reference. This may be considered a heuristic approach for the sake of simplicity. An alternative approach we explored was to perform subject‐level (i.e., first level) clustering on all data concatenated within‐subject (across frequencies and/or conditions), followed by group‐level (i.e., second‐level) clustering. We found this to once again produce identical maps to the broadband decomposition. This method could theoretically be used to find the most ‘common’ clusters across different datasets, in the case of variable k‐means outputs (e.g., visually similar MS maps at different k‐values). Since it is beyond the scope of this article, we leave it to future studies to validate this method more rigorously.

2.4.3. Back‐fitting of MS maps

The common topographic maps selected above were then assigned to every time point from all individual recordings using the traditional MS back‐fitting method (Van De Ville, Britz, & Michel, 2010). First, the spatial correlation was computed between every time point and map. Using the so‐called ‘winner takes all’ algorithm, each time point was labelled according to the map with which it shared the highest absolute spatial correlation. Time points were labelled as ‘non‐assigned’ when the absolute spatial correlation was below r < .5 threshold. To ensure temporal continuity of MS segmentation, a smoothing step (Brunet et al., 2011; Pascual‐Marqui et al., 1995) was applied. Finally, segments with duration shorter than three samples (30 ms) were assigned to neighbouring segments using the following rule: the segment was split into two parts, where each part was assigned to the neighbouring segment with the higher spatial correlation. With back‐fitting completed, we extracted three spatio‐temporal parameters for each MS map, namely:

• GEV described as the sum of variances of the original recording explained by the considered MS map weighted by the GFP at each moment in time. Units are percentages (%) between 0 and 1.

• MeanDurs defined as the mean temporal duration of segments assigned to each MS map. Units are in seconds (s).

• TimeCov is the ratio of time frames assigned to each MS map relative to the total number of time frames from the recording. Units are percentages (%).

2.5. Adjusted mutual information score

Scikit‐learn (Pedregosa et al., 2011) implementation of the adjusted mutual information score (AMI) (Vinh, Epps, & Bailey, 2010) was used to quantify the mutual information (MI) shared between different MS temporal segmentations, while simultaneously accounting for random overlap due to chance. This metric, bounded between 0 and 1, is used to evaluate the statistical (in)dependence of two variables. In our case, AMI is estimated between the symbolic sequences of two different MS segmentations (e.g., ABDCADB vs. ABDBDAC). A high score (approaching 1) indicates that the two segmentations agree on the temporal order of all labels while a low score (approaching 0) indicates that the segmentations' labels are not temporally aligned. We selected the corrected version of this metric to control for the impact of differences in label distribution due to chance (e.g., differences in overall TimeCov between labels). Time points assigned as ‘unlabelled’ in at least one of the two studied segmentations were ignored. Comparisons with more than 20% of total unlabelled time points were excluded from this analysis.

2.6. Frequency profiles of MS time courses

In an effort to further explore MS spectral signatures, the topography of each MS map was used as a spatial filter to compute instantaneous ‘microstate map time courses’. More specifically, for each MS, spatially filtered signals were computed by multiplying the multichannel EEG time series by the MS map electrode weights using the dot product, resulting in a one‐dimensional time series. Then, the relative power spectral density (PSD) of each MS time series was computed using Welch's method for frequencies ranging from 1 to 30 Hz.

2.7. Statistics

Statistical analyses were performed on the three main spatio‐temporal parameters (GEV, MeanDurs and TimeCov). Tests were conducted using a two‐sided permutation test for equality of means on paired samples (same subject, between condition, either between frequencies) under the H0 hypothesis that both frequencies (i.e., condition) share the same mean against the alternative H1 that the distributions come from two different populations. The p‐values were estimated by simulated random sampling with 10,000 replications. As many statistical tests were carried out without specific pre‐planned hypotheses (Armstrong, 2014), p‐values were corrected for multiple comparisons using the Bonferroni method. Corrected p‐values are reported in Section 4. Effect sizes are reported as the standardised difference of means using Cohen's d (d).

2.8. Neurobehavioural prediction models

2.8.1. Model

Linear support vector classification with ‘l2’ norm penalization and squared hinge loss function were used to discriminate EO versus EC states using MS parameters pertaining to broad‐ and narrowband EEG activity. Models were trained using 15 frequency‐specific features corresponding to the three spatio‐temporal MS metrics (GEV, MeanDurs and TimeCov) of each map (A, B, C, D and C′) of a given frequency. Band‐specific prediction models were fitted with standardised features (after removing their respective mean and scaling them to unit variance).

2.8.2. Evaluation

As suggested by Bouckaer (2003), 10 times repeated 10‐folds cross‐validation tests were used to assess classification results. For each of the 100 runs, ninefold of 20 subject's features each were used to train the model while onefold of 20 subject's features was used to evaluate the three diagnostic metrics:

• Accuracy defined as number of the number of correctly predicted samples out of all the testing Set.

• The receiver operating characteristic (ROC) which is a plot of true positive rate as a function of the false positive rate. It is used to illustrate the classification trade‐off for different discrimination thresholds.

• Area under the curve (AUC) defined as the area under the receiver‐operating characteristic (ROC) curve: it is an aggregate measure of performance for all possible classification thresholds. AUC values are in the range of 0–1. A model with 100% error in its predictions has an AUC of 0.0. If all its predictions are correct, its AUC is 1.0.

Ninety‐five percentage confidence intervals were evaluated on each of the three metric distributions with 10 degrees of freedom.

Statistical comparison between models was conducted on both accuracy and AUC using a two‐tailed permutation test for equality of means on paired samples under the H1 hypothesis that the alpha‐band (8–12 Hz) MS measures had a greater mean classification rate than the broadband (1–30 Hz) MS measures. The p‐values were estimated by simulated random sampling with 10,000 replications.

3. RESULTS

3.1. Spatial similarity of MS maps

Figure 1 illustrates the topographic results of MS segmentations in the different conditions and frequency bands. After visual inspection of optimal clusters at different cluster numbers (k), we identified that a value of k = 5 revealed five MS topographies that were similar across all EEG bands and behavioural conditions, consistent with recent findings from our laboratory (Bréchet et al., 2019; Bréchet, Brunet, Perogamvros, Tononi, & Michel, 2020; D'Croz‐Baron, Baker, Michel, & Karp, 2019). MS maps were designated in line with the canonical prototypes from the literature and their respective symbols, featuring a left–right orientation (A), a right–left orientation (B), an anterior–posterior orientation (C), fronto‐central maximum (D) and occipito‐central (C′) maximum.

FIGURE 1.

Spatial correlation between microstate (MS) topographies across behavioural conditions. Global cluster centroids of each frequency band within eyes‐open (EO) or eyes‐closed (EC) condition. Note that map polarity inversion is ignored in the classical analysis of spontaneous electroencephalography (EEG)

Given the additional frequency dimension, we labelled the MS maps firstly according to the Greek letters traditionally used for narrowband EEG (i.e., δ, θ, α and β) and then the Latin alphabet for the canonical map symbols (i.e., A, B, C and D). For example, αA denoted the left–right diagonal map from the alpha‐band (α) segmentation, and δC the anterior–posterior map from the delta band (δ) segmentation. The broadband segmentation was designated with the prefix ‘bb’.

As shown in Figure 2, when comparing topographies between broadband and each narrowband (i.e., the diagonal entries in the correlation matrix), all spatial correlations were r > .98. Consequently, we fitted the broadband maps directly to all the frequency bands to have a common reference.

FIGURE 2.

Spatial correlation between microstate (MS) topographies across frequencies. Spatial correlation of cluster centres of each sub‐frequency bands compared to broadband for eyes‐open (EO) and eyes‐closed (EC) condition

We similarly observed common MS maps when comparing broadband topographies between EO and EC conditions (Figure S2), with all intraclass spatial correlations exceeding r > .98, thus providing justification for comparing MS parameters between behavioural conditions while fitting condition‐specific broadband maps.

3.2. MI of MS sequences

Briefly, AMI is an index of how similar two separate MS segmentations are, by estimating the degree of shared information (i.e., the number of time points assigned with the same MS) between their symbolic sequences (e.g., ABCD vs. ABDA). The ‘adjusted’ aspect ensures that the measure is unbiased for symbolic overlap(s) due to chance (Vinh et al., 2010). Higher AMI (approaching 1) indicates nearly identical MS temporal sequences, while lower AMI (approaching 0) indicates temporally independent sequences (i.e., low overlap).

As shown in Figures 3, the AMI between broadband and narrowband segmentations in the EO condition showed a value of s = 0.09 for delta, s = 0.05 for theta, s = 0.07 for alpha and s = 0.02 for beta. These values are surprisingly low, and we can conclude that the broadband segmentation is comparatively independent of the narrowband one. Similar conclusions of temporal independence can be made by examining the AMI between the narrowbands themselves, with a maximum AMI value between theta and alpha bands (EO: s = 0.008, EC: s = 0.01), and a minimum AMI value of s = 0.002 for non‐adjacent EEG bands (delta‐alpha, delta‐beta and theta‐beta).

FIGURE 3.

Adjusted mutual information of microstate (MS) symbolic sequences. (a) Mean adjusted mutual information (AMI) is depicted, for each behavioural condition (EC, eyes‐closed; EO, eyes‐open) across n = 203 subjects. (b) Mean adjusted mutual information of MS symbolic sequences between all broadband and narrowband combinations. Mean (n = 203 subjects) AMI for all frequency pairs

As a sanity check, when inspecting the EO versus EC transition, the shared information with broadband decreased for the delta band (s = 0.03) but increased for the alpha band (s = 0.15). The latter is in line with expectations, as alpha oscillations are known to increase considerably during eye closure, which would amplify their contribution to the broadband signal and consequently their shared dynamics.

3.3. Between‐frequency comparison of classical MS measures

Here, we tested for significant differences between broadband and narrowband filtered EEG in the classical MS measures: GEV, TimeCov and MeanDurs. This was done by conducting paired t‐tests between broadband (bb) and respective narrowband (delta to beta) MS measures across all n = 203 subjects. For each MS measure and MS map, results were visualised using heat‐plots as the narrowband absolute difference from the broadband mean value. Here, a red/blue background indicated significant positive/negative differences at p < .05, while a white colour indicated non‐significant differences at p > .05. Exact p‐values and effect sizes are reported in Table S2 and Figure S3 of the Supplementary Results.

3.3.1. Global explained variance

Figure 4 illustrates the percentage differences in GEV between each narrowband versus broadband, demonstrating the presence of specific ‘fingerprints’ between frequencies (rows) or MS maps (columns), MS segmentation of delta band activity showed significantly higher GEV across most MS maps in both EO (+16%) and EC (+16%) conditions, compared to the broadband segmentation. A similar but less pronounced effect was found for the theta segmentation, suggesting that low‐frequency EEG fluctuations in the 1–8 Hz (delta‐theta) range may be accounted for more parsimoniously using the five canonical MS maps than 1–30 Hz (broadband) activity.

FIGURE 4.

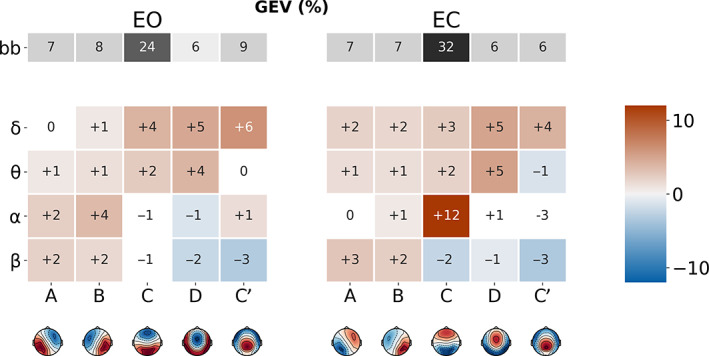
Microstate (MS) map differences in global explained variance (GEV) between broadband and narrowband filtered electroencephalography (EEG), for eyes‐open (EO) and eyes‐closed (EC) conditions. The first row (in grey) represents the mean GEV of the broadband segmentation. Coloured rows represent the mean GEV difference between the narrowband (δ, ϴ, α and β) and broadband segmentations, for each MS (A–C′). Significant differences have red/blue backgrounds, while non‐significant ones have a white/grey background

The profile of the alpha‐band segmentation depended on behavioural condition. During EC, MS C had significantly increased GEV (+12%) relative to broadband, indicating that distinct MS topographies have stronger behavioural specificity at narrowband frequencies (see section Statistical classification of EO versus EC behavioural states). Conversely, during EO, MSs A (+2%) and B (+4%), expressed significantly more GEV compared to broadband.

Conversely, or the beta band, GEV was significantly greater than broadband for maps A (EO: +2%, EC+3%) and B (EO: +2%, EC: +2%) while it was significantly reduced for maps D (EO: −2%, EC: −1%) and C′ (EO: −3%, EC: −3%). MS C explained less variance compared to broadband, but the comparison was significant only for EC (−2%).

3.3.2. Time coverage

During MS segmentation, each time point is assigned to only one of the five canonical MS topographies through a winner‐takes‐all process (i.e., the map with the highest spatial correlation with that time point wins). TimeCov refers to the average prevalence of each MS map over the whole EEG recording (Figure 5), expressed as a percentage (i.e., number of time points assigned to a particular MS map divided by the total number of time points).

FIGURE 5.

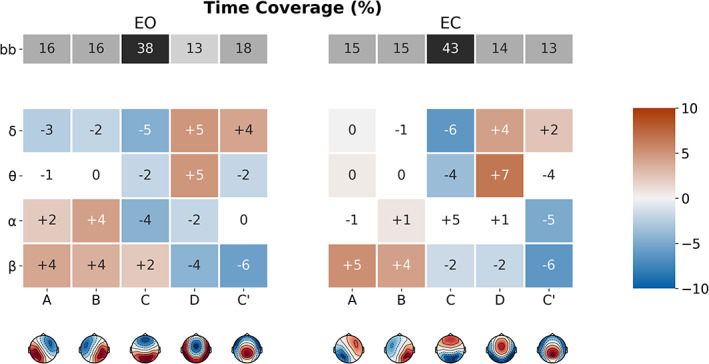
Microstate (MS) map differences in time coverage (TimeCov) between broadband and narrowband filtered electroencephalography (EEG), for eyes‐open (EO) and eyes‐closed (EC) conditions. The first row (in grey) represents the mean TimeCov of the broadband segmentation. Coloured rows represent the mean TimeCov difference between the narrowband (δ, ϴ, α and β) and broadband segmentations, for each MS (A–C′). Significant differences have red/blue backgrounds, while non‐significant ones have a white/grey background

Comparing the delta band segmentation to broadband, TimeCov was reduced for maps A (EO: −3%, EC: −0%), B (EO: −2%, EC: ns) and C (EO: 5%, EC: −6%), while it was increased for maps D (EO: +5%, EC: +4%) and C′ (EO: +4, EC: +2%).

Small differences were generally observed between theta and broadband MS distributions, with the notable exception of a significant increase in map D (EO: +5%, EC: +7%) and decrease in map C (EO: −2%, EC: −4%), consistently found across behavioural states. For the alpha band, TimeCov was particularly greater than broadband for maps A (EO: +2%, EC: ns) and B (EO: +4%, EC: +1%).

Finally, comparing the beta band to broadband, TimeCov was increased for maps A (EO: +4%, EC: +5%, p < .05), B (EO: +4%, EC: +4%, p < .05), while it was reduced for maps D (EO: −4%, EC: −2%, p < .05) and C′ (EO: −6%, EC: −6%, p < .05).

3.3.3. Mean duration

While analysing MS MeanDurs (Figure 6) we first observed that MS were significantly shorter in delta than broadband across all maps: map A (EO: −14 ms, EC: −13 ms), map B (EO: −14 ms, EC: −14 ms), map C(EO: −15 ms, EC: −17 ms, map D (EO: −7 ms, EC: −8 ms) and map C′ (EO: −8 ms, EC: −11 ms).On the contrary theta segments were significantly longer than broadband ones for map A (EO: +6 ms, EC: +11 ms), map B (EO: +6 ms, EC: +11 ms) and map D (EO: −7 ms, EC: −8 ms). Similar but non‐significant increases were also observed for maps C and C′.

FIGURE 6.

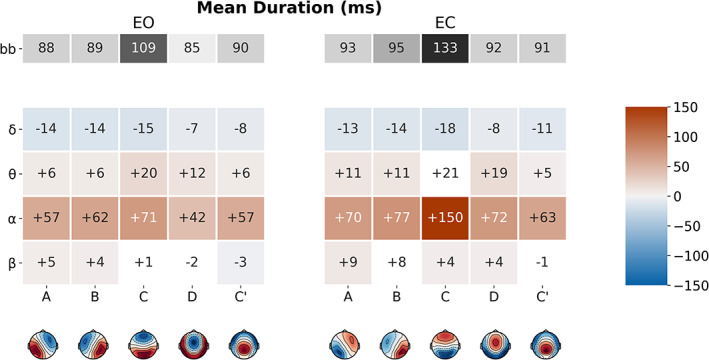
Microstate (MS) map differences in mean duration (MeanDurs) between broadband and narrowband filtered electroencephalography (EEG), for eyes‐open (EO) and eyes‐closed (EC) conditions. The first row (in grey) represents the mean MeanDurs of the broadband segmentation. Coloured rows represent the mean MeanDurs difference between the narrowband (δ, ϴ, α and β) and broadband segmentations, for each MS (A–C′). Significant differences have red/blue backgrounds, while non‐significant ones have a white/grey background

Notably, all MS maps had significantly increased duration in alpha band compared to broadband: map A (EO: +57 ms, EC: +70 ms), map B (EO: +62 ms, EC: +70 ms), map C (EO: +71 ms, EC: +150 ms), map D (EO: +42 ms, EC: +72 ms) and map C′ (EO: +57 ms, EC: +63 ms).

Less pronounced and less consistent differences were found for the beta band, which revealed a single significant increase of map A duration in the EC condition (EO: ns, EC: +9 ms).

3.4. Within‐frequency comparison of classical MS measures during EO versus EC

Here, we directly compared EO versus EC conditions within each frequency band, and only relevant cases where narrowband measures were salient compared to the broadband analysis are reported (Figure 7). Full results are documented in Table S3 and Figure S4 of the Supplementary Results.

FIGURE 7.

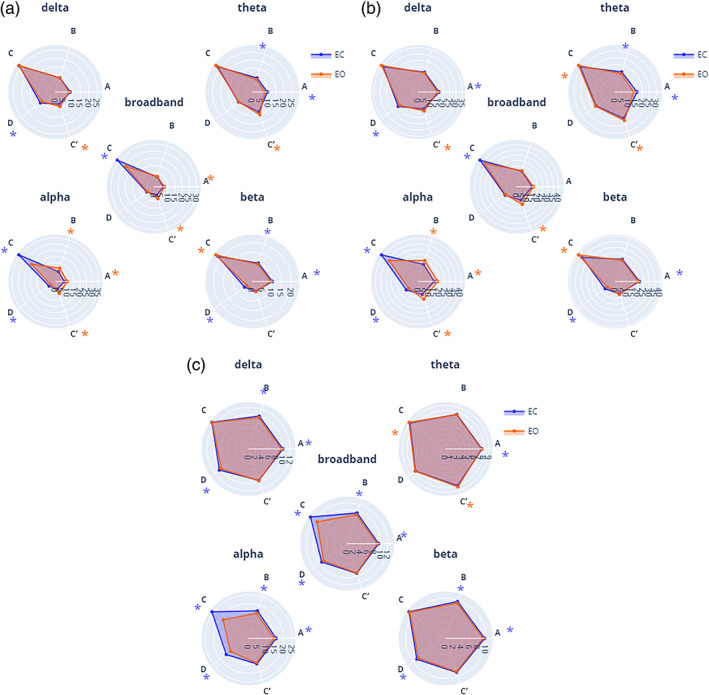
EO versus EC comparison using frequency‐specific microstate (MS) parameters. (a) Mean global explained variance (GEV, %), and (b) mean time coverage (time coverage, %) for each MS (A–C′) within each frequency band (broadband, delta, theta, alpha and beta) for both eyes‐closed condition (EC, blue) and eyes‐open condition (EO, red). Significance values are indicated from paired permutation test on mean between conditions: no asterisk: .05 > p, *p < .05, *colour indicates the condition with highest value

3.4.1. Global explained variance

Across frequencies, map C′ explained more variance during EC than during EO for all bands (bb: d = 0.59, p < .05; δ: d = 0.43, p < .05; θ: d = 0.35, p < .05; α: d = 0.35, p < .05; β: d = 0.67, ns) while map D expressed less variance(bb: d = −0.14, ns; δ: d = −0.07, ns; θ: d = −0.29, p < .05; α: d = −0.42, p < .05; β d = −0.73, p < .05). In contrast, the other MS maps had band‐specific modulations: during EC map C explained relatively less variance in alpha (d = −1.0, p < .05) and broadband (d = −0.7, p < .5), but expressed more variance in delta (d = 0.20, p < .05) and beta (d = 0.21, p < .05). In addition, statistically significant effects were detected in the narrowbands which were not evident in the broadband. For example, the GEV of map B decreased from EC to EO (d = −0.31, p < .05) in the beta band while no significant effect was found in broadband for this map.

3.4.2. Time coverage

Map C was relatively more prevalent in EC versus EO in alpha (d = −0.71, p < .05) and broadband (d = −0.48, p < .05), but the effect size was significantly stronger in the alpha band. In contrast, the opposite effect was observed in delta (d = 0.22, p < .05) and beta (d = 0.42, p < .05) bands, which showed increased coverage of map C during EO compared to EC. Diverging effects of TimeCov in narrow bands compared to broadband appeared across a number of MS maps and frequency bands, during the EO versus EC transition: βA—where TimeCov decreased prevalence (d = −0.20, p < .05), bbA and βC—TimeCov increased, respectively (d = 0.23, p < .05) and (d = 0.21, p < .05), while bbC TimeCov decreased (d = −0.71, p < .05). While non‐significant differences between EO and EC conditions were found for bbB coverage, βB (d = −0.17, p < .05) and ϴB (d = −0.35, p < .05) were significantly increased in the EC condition while αB (d = 0.57, p < .05) was decreased.

Overall, the EO versus EC comparison revealed significant differences between the broadband and narrowband segmentations, which were frequently map‐ and/or band‐specific.

3.5. Power spectral density (PSD) of MS time courses

Here, we first obtained MS‐specific time courses by spatial filtering (see Section 2). Then, the relative power spectral density (PSD) of each MS time course was calculated to compare the distribution of (percent) power of each MS across different frequency bands. As shown in Figure 8, we observed varying spectral signatures across MS time courses. Of note, under the EO condition, MS D exhibited greater relative power in the theta band than the other maps (A: d = 0.6; B: d = 0.7; C: d = 0.6; C′: d = 0.9, all p < .05). This is compatible with its relatively increased GEV or TimeCov in the theta band compared to broadband (see Figures 4 and 5).

FIGURE 8.

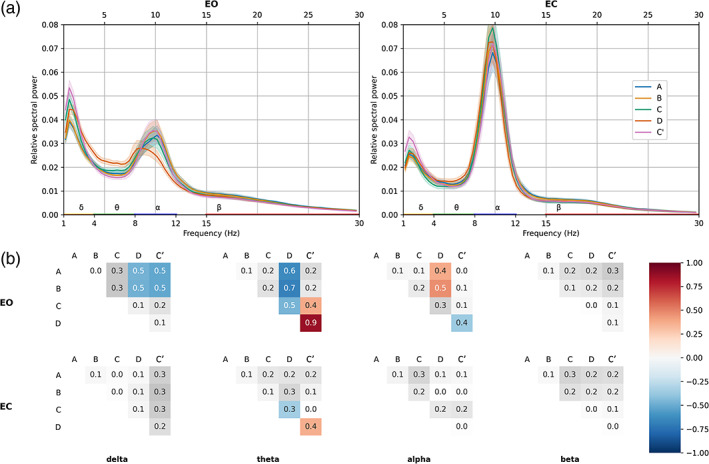
(a) Electroencephalography (EEG) relative power spectral densities of microstate (MS) time courses in EO and EC conditions. Solid lines represent mean value across subjects (n = 203); shaded areas represent 95% confidence intervals. Traditional frequency bands: delta (orange, 1–4 Hz), theta (green, 4–8 Hz), alpha (blue, 8–12 Hz) and beta (red, 15–30 Hz) are highlighted on the x‐axis. (b) Differences of effect size (Cohen's d) between the relative spectral powers of each spatially filtered MS time course, within each frequency band. Positive/negative differences represent the column–row variable subtraction. Bonferroni‐corrected significant differences have red/blue backgrounds, while non‐significant ones have a white/grey background

3.6. Statistical classification of EO versus EC behavioural states

As a proof of concept, we tested the applicability of band‐specific MSs in the context of behavioural prediction, that is, the binary discrimination of EO versus EC states using machine learning. Leveraging the well‐known effect of alpha‐band modulation during eye opening/closure (Barry, Clarke, Johnstone, Magee, & Rushby, 2007) we hypothesised that alpha‐band‐specific MS parameters would be stronger and more specific predictors of the EO/EC transition than those derived from the broadband segmentation. As we did not have any MS map‐specific hypotheses, we selected as features the basic set of classical MS measures from our study: 5 maps (A, B, C, D and C′) × 3 variables (GEV, TimeCov and MeanDurs). Then, using these 15 features, we applied a linear support vector machine (SVM) to classify EO versus EC recordings across all 203 subjects, separately for alpha‐band and broadband models.

Following 10‐fold cross‐validation, we observed higher accuracy (i.e., sensitivity) for the SVM model tested with alpha‐band MS parameters (80 ± 5%) than the one tested with broadband MS parameters (73 ± 6%). The superiority of the alpha‐band model was reinforced by a separate analysis of the AUC of the ROC, which also incorporates the false positive rate (i.e., specificity) (Figure 9). Here, alpha‐band (AUC: 87 ± 5%) outperformed broadband (77 ± 7%) by a full 10%. Finally, these differences were statistically significant for both accuracy (Cohen's d = 1.75, p < .001) and AUC (Cohen's d = 1.28, p < .001) demonstrating that a narrowband MS segmentation may provide higher sensitivity/specificity in differentiating behavioural state relative to a broadband one.

FIGURE 9.

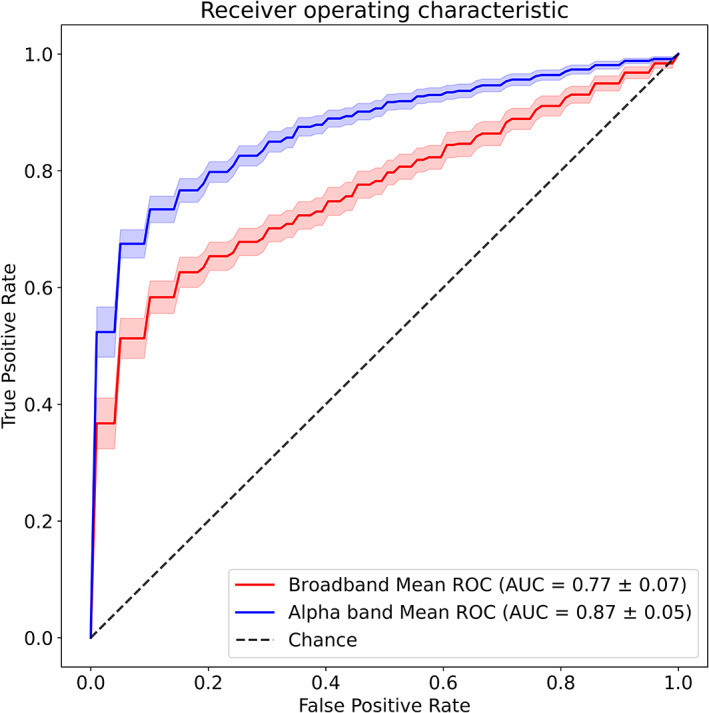
Classifying eyes‐open (EO) versus eyes‐closed (EC) states using classical microstate (MS) measures. Binary classification performance, computed as the area under the curve (AUC) of the receiver‐operating characteristic (ROC), for two support vector machine models. Input features of the first model (red) were broadband MS parameters (see text) while the second model (blue) was evaluated on alpha‐band MS parameters. Shaded areas represent 95% CI. Mean AUC ± SD is reported in the legend

4. DISCUSSION

Historically, the first MS analysis was applied by Lehmann and colleagues to narrowband alpha oscillations (Lehmann, 1971), yet this ‘frequency‐specific’ approach appears to have been overlooked during the last decades of MS research in favour of decomposing broadband EEG signals (e.g., 2–40 Hz) (Michel & Koenig, 2018; Pascual‐Marqui et al., 1995). Hence, the present study specifically explored the MS characteristics of narrowband EEG signals, their quantitative interrelationship, and whether they provide any novel information compared to their aggregate (i.e., broadband dynamics). This was done by simply filtering the broadband EEG signal into separate narrowband frequencies (delta, theta, alpha and beta), with the goal of comparing MS maps, symbolic sequences and classical measures (explained variance, MeanDurs and TimeCov) between each other, as well as across different behavioural conditions (EO vs. EC).

4.1. The spatial dimension: MS topographies

We first investigated whether analogous MS scalp topographies would be produced by segmenting broadband versus narrowband EEG signals [including the alpha band (Milz, Pascual‐Marqui, Achermann, Kochi, & Faber, 2017)]. Interestingly, we observed highly similar MS topographies (with minimum spatial correlations of r > .98) across all investigated broad‐ and narrowband frequencies (broadband, delta to beta), as well as between EO/EC conditions. This is compatible with studies of dipolar EEG generators, identified using ICA (Delorme, Palmer, Onton, Oostenveld, & Makeig, 2012), which are spatially fixed and known to simultaneously produce a spectrum of frequencies (e.g., the posterior cortex is known to generate both alpha and beta rhythms). These same generators would contain a mixture of oscillatory activities (rhythmic frequency ‘peaks’) as well as a background of 1/f distributed broadband aperiodic (Donoghue et al., 2020), which could explain the generation of a range of difference frequencies by the same anatomical region(s) (i.e., MS maps).

This is supported by recent work from Brechet and colleagues (Bréchet et al., 2020), who observed that states of sleep and wake exhibited significantly different spectral content (e.g., delta vs. beta power) but very similar MS maps. Secondly, maps derived in our analyses corresponded closely to the canonical (broadband) topographies previously described in the literature (Custo et al., 2017; Michel & Koenig, 2018). It may be therefore tempting to conclude that identical neuronal sources are involved in generating the same topographies across frequencies. However, technically speaking, although different maps imply different generators (forward problem), same topographies do not necessarily imply identical generators (inverse problem). Due to the ill‐posed nature of EEG signals (constructive and destructive electromagnetic fields), similar scalp potentials can still be generated by different underlying brain mechanisms (von Helmholtz, 1853). Hence, although we cannot unequivocally conclude that MS maps across the EEG spectrum are generated by the same anatomical sources, this would be the most probable and parsimonious interpretation. Moreover, we must juxtapose our findings with work from other groups (Musaeus et al., 2020) which applied a similar approach but did not necessarily find the same topographies across the EEG spectrum. Nevertheless, it should be kept in mind that narrowband MS analyses do not necessarily require similar topographies between frequencies. In this case, although cross frequency comparisons would not be possible due to dissimilar maps, it would remain valid to study and quantify spatio‐temporal MS parameters within each frequency band separately; for example, in the service of clinical biomarker discovery (Merrin et al., 1990). Reassuringly, the MS maps of our study replicate the ones derived from independent work utilising the same EEG dataset (Zanesco et al., 2020), further supporting the reproducibility of MS analysis despite methodological variations between studies (e.g., absence of resampling).

4.2. The temporal dimension: MI of MS sequences

Milz and colleagues (Milz et al., 2017) recently proposed that alpha oscillations were the major component driving MS dynamics. In general, AMI analyses reported in our work reveal low values (near or below 0.1) of information shared between the narrowband segmentations, including alpha, and that of the broadband decomposition. However, consistent with the work of Milz and colleagues (Milz et al., 2017), the alpha‐band during EC did indeed have the highest shared information with broadband (around 0.125). Importantly, however, this relationship did not necessarily hold during EO (delta being highest). This indicates specific narrowband contribution(s) to broadband dynamics heavily depend on behavioural state. Moreover, if narrowband(s) topographies were directly responsible for the origin of the spatial distribution of the broadband signal, one would expect much higher AMI values (at least 0.5) than those, we observed. In view of the results presented, it would be inaccurate to claim that alpha band or any other narrowband as the dominant source of broadband topographies.

In contrast, our results appear to support the ideas of Croce and colleagues (Croce, Quercia, Costa, & Zappasodi, 2020), who suggested that broadband MS dynamics could not be extrapolated from one or a subset of EEG frequency bands. It remains unclear how the interaction of several narrowband‐components leads to a substantially different broadband MS decomposition. We speculate that this might stem from the fact that (a) different narrow band signals could cancel each other at specific time points and (b) MS assignment is non‐linear given the winner‐takes all approach.

Lastly and most intriguingly, no significant informational interrelations were found between the narrowband topographical dynamics themselves (e.g., delta vs. beta, theta vs. alpha), indicating that each EEG band appears to have has its own independent dynamics. This may not be surprising, considering that spontaneous EEG oscillations have been reported to dynamically switch from a resting signature (e.g., alpha) to task‐specific active mode(s) dominated by theta (Ribary et al., 2017), beta (Fernández et al., 1995) or gamma activities (Hipp et al., 2011)). In this context, our observations of spatio‐temporal independence between narrowband EEG components support the operation of ‘oscillatory multiplexing’ (Akam & Kullmann, 2014) mechanisms in the cortex, whereby brain regions could combine different frequencies for integrating/segregating information across large‐scale networks (Le Van Quyen, 2011).

4.3. Classical MS measures: Explained variance, time coverage and mean duration

4.3.1. Global explained variance

Overall, MS segmentations of low‐frequency bands (delta and theta) explained more of the global topographical variance compared to the classical broadband segmentation. Since GEV is normalised by and therefore independent of GFP, this suggests that the goodness‐of‐fit (i.e., GEV) of the five‐map MS model is clearly greater in the delta/theta bands than broadband EEG. In higher frequencies, effects are more map‐specific, as for example we observed an increase in GEV for the diagonal maps (A and B) and a decrease for midline (D and C′) ones.

4.3.2. Time coverage

Different patterns of MS temporal coverage were observed according to frequency. The delta and theta bands seem to exhibit greater prevalence of map D and decreased incidence of maps A, B and C. This is remarkable insofar map D shares an intriguing overlap with the topography of the well‐known frontal‐midline theta‐rhythm (fm‐theta) (Scheeringa et al., 2008; Töllner et al., 2017). Conversely, beta band dynamics seem to favour the more frequent appearance of maps A and B in lieu of maps D and C′. The appearance of alpha‐band MS maps, on the other hand, appear to be more state‐dependent, as might be expected given the well‐known expression of the posterior alpha rhythm during EC. Accordingly, there was a strong behavioural dissociation particularly for map C, which displayed a relatively greater temporal prevalence during EC than EO.

The presence of such ‘spectral fingerprints’ suggests the existence of an 'affinity' between distinct MS topographies and EEG bands suggests that different cortical generators (i.e., topographies) may be activated preferentially in certain frequencies (Groppe et al., 2013; Keitel & Gross, 2016; Mellem et al., 2017).

4.3.3. Mean duration

MSs are defined as short periods of time during which the scalp electric field remains quasi‐stable. Traditional MS analysis does not suggest specific frequency filtering, thus resulting in various broadband filter settings across studies (Michel & Koenig, 2018). Our findings demonstrate that temporally stable states (around 80 ms or longer) are present within all classical EEG narrowbands (i.e., delta to beta). It is established that such spatio‐temporal structures do not appear for randomly shuffled EEG (Wackermann, Lehmann, Michel, & Strik, 1993). For most EEG narrowbands, mean MS durations were usually in the same range as the typically reported 70–120 ms, but often longer. For example, the average MS duration in the EO state was around 150 ms for the alpha‐band, compared to 90 ms for broadband. It will be therefore interesting for future studies to examine the mechanistic links between the aggregated dynamics of the broadband MSs and those of frequency‐specific modes.

4.4. Discriminating between behavioural states: EO versus EC

Within each EEG narrowband, between 8 Hz (for theta) and 14 Hz (for alpha) of the classical MS measures were found to be statistically significant. In comparison, classical MS measures derived from broadband EEG had a higher effect size for only one parameter (broadband MS B MeanDurs). For all other 14 parameters, at least one narrowband component showed a relatively stronger effect size.

Hence, the addition of the frequency dimension has the primary benefit of increasing both the number and the specificity of potential neural markers that could aid clinical prognosis or provide insight into brain mechanisms. We therefore conclude that the extra frequency dimension leads to a more fine‐grained decomposition of multichannel and multiplex EEG signals than the standard broadband analysis. Interestingly, we found that in a few cases the narrowband effects were opposite in directionality to the broadband results. Thus, limiting the analysis to only the latter could lead to incomplete (or even incorrect) interpretations of underlying brain dynamics.

A complementary analysis based on spatially filtered MS time courses, we illustrated different frequency profiles of relative power between MS topographies. These observations reinforce our main hypothesis that MS may be expressed to varying degrees across the frequency spectrum. Hence, although we found similar MS topographies to be shared across EEG frequencies, their temporal sequences will be influenced by the frequency band under investigation.

The value of narrowband MS decomposition is directly supported by our behavioural classification results, where we utilised alpha‐band versus broadband MS parameters to predict EO versus EC states using the recordings of all 203 subjects. The significant increase in overall accuracy (alpha‐band: 80% vs. broadband: 73%) and area under the ROC curve nicely demonstrate that frequency‐specific MS measures may provide higher behavioural predictive power than those derived from the broadband analysis. Although beyond the scope of this article, we expect that this approach to provide advantages in other contexts, such as event‐related potential analyses or for discriminating between different clinical populations.

Interestingly, we found that in a few cases the narrowband effects were opposite in directionality to the broadband results. Thus, limiting the analysis to only the latter could lead to incomplete (or even incorrect) interpretations of underlying brain dynamics.

5. POTENTIAL LIMITATIONS AND FUTURE WORK

The current study may technically be considered exploratory, given the large number of tests that were carried out and in the absence of well‐defined hypotheses; however, we carried out Bonferroni correction for all tests which may be considered the most conservative method for controlling for multiple comparisons. Several studies have thus far proposed explanations for the origins of broadband MS topographies (Britz et al., 2010). We feel it is still too early to make analogies or speculations between these results and those of the narrowband dynamics. However, we believe that the application of the methodology proposed here may lead to valuable insights to more fully understand the underlying spectral tapestry of EEG MSs.

6. CONCLUSION

Ultimately, we report several important and novel findings between the classical broadband MS analysis, generally performed in the EEG field, and its application to more narrow frequency bands relevant to cortical oscillatory activities. In a nutshell, it appears that each canonical EEG frequency band possesses its own independent spatio‐temporal dynamics, while the relative prevalence of MS topographies themselves differ across frequencies. Analysis of narrowband MS parameters revealed spatial and temporal characteristics that both converged and diverged from broadband MS findings. In other words, it seems that broadband MS sequences may not be a simple aggregate of individual narrowband MS sequences, either.

Analysis of narrowband MS parameters revealed that both spatial and temporal characteristics converged and diverged from broadband MS findings. Our results therefore indicate that both narrowband and broadband MS analyses are justified and complementary to each other. A narrowband decomposition into frequencies more specific for cortical oscillatory activity could not only advance and consolidate findings in clinical disorders (e.g., Merrin et al., 1990) (Musaeus et al., 2020) but also enable a better understanding of the organisation and functioning of large‐scale brain systems.

CONFLICT OF INTEREST

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

AUTHOR CONTRIBUTIONS

Victor Férat: Conceptualization; formal analysis; methodology; visualisation; writing – original draft; writing – review & editing. Martin Seeber: Writing – review & editing. Christoph M. Michel: Writing – review & editing. Tomas Ros: Writing – review & editing; conceptualization; formal analysis; methodology.

Supporting information

Figure S1: Detailed clustering pipeline

Figure S2: MS segmentation parameters of MS topographies.

Spatial correlation of broadband cluster centers between eyes opened (EO) and eyes closed (EC) condition.

Figure S3: MS segmentation parameters of MS topographies. Mean global explained variance (Gev), microstate time coverage (time coverage) and mean segment duration (MeanDurs, in s) within each microstate configuration (A – C′) for each frequency band (broadband, delta, theta, alpha, beta) for both eyes closed condition and eyes opened condition. Significance values are indicated from paired permutation test on mean between conditions. ns: 0.05 < p, * 0.01 < p < = 0.05. Boxplots consist of median (Q2), first quartile (Q1), third quartile (Q3), maximum (Q3 + 1.5*[Q3 ‐ Q1]), minimum (Q1–1.5*((Q3 ‐ Q1). Scales of Microstates C metrics are different from others states due to difference of order of magnitude.

Figure S4: MS segmentation parameters of different frequency bands. Mean global explained variance (Gev), microstate time coverage (time coverage) and mean segment duration (MeanDurs, in s) for each microstate (A –C′) within each frequency band (broadband, delta, theta, alpha, beta) for both eyes closed condition (EC, blue) and eyes opened condition (EO, red). Significance values are indicated from paired permutation test on mean between conditions. ns: 0.05 < p, * for 0.01 < p < = 0.05

Table S1: For both EO and EC condition, P values (p) and Cohen's d (d) are reported for each test between broadband and band segmentation on each studied metric (Global explained variance, Mean duration, time coverage).

Table S2: For both EO and EC condition P values (p) and Cohen's d (d) are reported for all comparisons (permutation test on mean) between subband (delta, theta, alpha, beta) and broadband metrics for all microstate topographies.

Table S3: For each between conditions (EO/EC) test P values (p) and Cohen's d (d) are reported for all combinations of band, map and metric.

Férat, V. , Seeber, M. , Michel, C. M. , & Ros, T. (2022). Beyond broadband: Towards a spectral decomposition of electroencephalography microstates. Human Brain Mapping, 43(10), 3047–3061. 10.1002/hbm.25834

DATA AVAILABILITY STATEMENT

The data and code supporting our results are openly available in the OSF repository and can be found at: https://osf.io/bfsge/ (DOI: 10.17605/OSF.IO/BFSGE). Other third‐party software and datasets used in this study can be found by following citations in the article.