Hippocampal‐amygdalo‐ventricular atrophy score: Alzheimer disease detection using normative and pathological lifespan models

Abstract

In this article, we present an innovative MRI‐based method for Alzheimer disease (AD) detection and mild cognitive impairment (MCI) prognostic, using lifespan trajectories of brain structures. After a full screening of the most discriminant structures between AD and normal aging based on MRI volumetric analysis of 3,032 subjects, we propose a novel Hippocampal‐Amygdalo‐Ventricular Atrophy score (HAVAs) based on normative lifespan models and AD lifespan models. During a validation on three external datasets on 1,039 subjects, our approach showed very accurate detection (AUC ≥ 94%) of patients with AD compared to control subjects and accurate discrimination (AUC = 78%) between progressive MCI and stable MCI (during a 3‐year follow‐up). Compared to normative modeling, classical machine learning methods and recent state‐of‐the‐art deep learning methods, our method demonstrated better classification performance. Moreover, HAVAs simplicity makes it fully understandable and thus well‐suited for clinical practice or future pharmaceutical trials.

In this article, we present an innovative MRI‐based method for Alzheimer disease (AD) detection and mild cognitive impairment (MCI) prognostic, using lifespan trajectories of brain structures. Compared to normative modeling and recent state‐of‐the‐art deep learning methods, our method demonstrated better classification performance. Moreover, it simplicity makes it fully understandable and thus well‐suited for clinical practice or future pharmaceutical trials.

1. INTRODUCTION

Finding early and specific biomarkers of Alzheimer disease (AD) clinical syndrome is of major interest to accelerate the development of new therapies. Among the potential structural biomarkers proposed for AD, neurodegeneration estimated using magnetic resonance imaging (MRI) is still a good candidate (Frisoni, Fox, Jack, Scheltens, & Thompson, 2010; Jack et al., 2016). From simple volume‐based approaches to advanced deep learning strategies, the development of new biomarkers able to detect anatomical alterations caused by AD has been the subject of much attention over the past decades (Feng & Ding, 2020; Leandrou, Petroudi, Kyriacou, Reyes‐Aldasoro, & Pattichis, 2018; Rathore, Habes, Iftikhar, Shacklett, & Davatzikos, 2017).

Nowadays, two main strategies are used to detect neurodegeneration caused by AD using MRI: normative modeling for abnormality detection (Marquand et al., 2019; Wolfers et al., 2020) and classification‐based approaches (Coupé et al., 2015; Wen et al., 2020).

On the one hand, normative modeling based only on cognitively normal (CN) subjects can be used to detect abnormality and therefore to distinguish AD patients from CN subjects. As explained in Marquand et al. (2019), normative lifespan modeling is similar to growth charts used in pediatric medicine to detect abnormal child development in terms of height or weight related to the age's subject. Indeed, such charts can be used to detect outliers considered as pathological. For AD detection, volume or thickness of key structures as a function of age is usually used. The main advantages of normative modeling are to robustly capture the heterogeneity of normal anatomy and to provide an easily interpretable distance between an individual and the normative range. Normative modeling is the approach used in most of the available software for quantitative brain analysis (in open access such as volBrain [Manjón & Coupé, 2016] or for commercial use as in Neuroquant [Ross et al., 2013], Qscore [Cavedo et al., 2020] or Qreport [Pemberton et al., 2021]). The added‐value in terms of diagnosis accuracy has been shown for several pathologies including AD (Cavedo et al., 2020; Hedderich et al., 2018; Pemberton et al., 2021; Ross et al., 2013). Due to its simplicity and easy understanding, normative modeling is the closest strategy to clinical practice with several CE‐marked and FDA‐approved software packages.

On the other hand, a classifier can be trained using features extracted from the two groups—one composed of CN subjects and another one composed of AD patients. The used features can be handcrafted as usually done in machine learning (ML) (Rathore et al., 2017) or automatically learned using deep learning (DL) (Jo, Nho, & Saykin, 2019). At the end of the training, a decision boundary is available to discriminate features of CN subjects from features of AD patients. Such a strategy is supposed to be more accurate than normative modeling since patients are used in addition to CN subjects during training. Consequently, the developed method is pathology specific. Moreover, by using advanced methods such as DL, a specific signature of a given pathology can be automatically and efficiently learned. However, such approaches suffers from a lack of generalization usually related to overfitting on the training database (Bron et al., 2021; Wen et al., 2020). Moreover, with the advent of DL methods, interpretation of the results and explanation of the underlying decision‐making process is far from being straightforward (Jo et al., 2019).

In this article, we present an alternative framework combining advantages of both strategies: an easy interpretation and an accurate classification. To this end, we propose a novel method able to detect patients with AD using both normal and pathological lifespan models. First introduced in Coupé, Manjón, Lanuza, and Catheline (2019), lifespan modeling of AD provides an useful and easily interpretable tool to capture the heterogeneity of AD signature. Moreover, by using multiple models (i.e., an AD model in addition to a CN model), the decision boundary is pathology specific and thus produces a more accurate detection of AD patients compared to usual normative modeling. Finally, we also propose an innovative framework to extract the most discriminant structures between both groups based on a fully automatic multiscale brain segmentation pipeline. Applied to AD, this framework led us to propose a novel Hippocampal‐Amygdalo‐Ventricular Atrophy score (HAVAs) based on multiple lifespan models.

2. MATERIAL AND METHOD

2.1. Dataset description

2.1.1. Training dataset

Our training dataset was composed of 3,032 T1‐weighted (T1w) MRI from seven open access databases (Table 1). This dataset was composed of 2,655 CN subjects (CN) and 377 patients with AD. As explained in the following, CN subjects younger than 55y (N = 1874) were used to estimate both CN and AD lifespan trajectories.

TABLE 1.

Training dataset description used for model constructions after quality control (N = 3,032)

Dataset	Group	N = 3,032	Gender	Age in years
C‐MIND	CN	236	F = 129/M = 107	8.44 (0.74–18.86)
NDAR	CN	382	F = 174/M = 208	12.39 (1.08–49.92)
ABIDE	CN	492	F = 84/M = 408	17.53 (6.50–52.20)
ICBM	CN	294	F = 142/M = 152	33.75 (18–80)
IXI	CN	549	F = 307/M = 242	48.76 (20.0–86.2)
OASIS	CN	298	F = 187/M = 111	45.34 (18–94)
ADNI	CN	404	F = 203/M = 201	74.81 (60–90)
OASIS	AD	45	F = 29/M = 16	77.04 (63–96)
ADNI	AD	332	F = 151/M = 181	75.13 (55–91)

Note: This table provides the name of the databases, the group, the number of considered subjects, the gender proportion, and the average age with the interval in brackets.

2.1.2. Testing dataset

To validate our model, we built a testing dataset based on two open access databases (AIBL and MIRIAD) to perform AD versus CN diagnosis task. Therefore, we validated the generalization capacity of our method and its robustness to domain shift. In addition, we used subjects with mild cognitive impairment (MCI) from ADNI to estimate the capability of our models on prognosis task (Table 2). Consequently, we validated the generalization of our models to unseen related tasks. As in Wen et al. (2020), the MCI group was split into stable MCI (sMCI) over 3 years and progressive MCI (pMCI) who will convert to AD within 36 months following the baseline visit. Finally, we used the ClinicaDL software (https://github.com/aramis-lab/clinicadl) (Wen et al., 2020) to define the groups of AD and CN groups in AIBL, and the pMCI and sMCI groups in ADNI. Therefore, we used the same selection criteria.

TABLE 2.

External dataset used for validation (N = 1,039)

Dataset	Group	N = 1,039	Gender	Age in years
AIBL	CN	467	F = 277/M = 190	73.4 (60.5–92.4)
MIRIAD	CN	23	F = 11/M = 12	69.7 (58.0–85.7)
ADNI	sMCI	255	F = 100/M = 155	72.3 (55–89.5)
AIBL	AD	82	F = 47/M = 36	74.8 (55.5–93.4)
MIRIAD	AD	46	F = 27/M = 19	69.3 (55.6–85.8)
ADNI	pMCI	235	F = 103/M = 132	74.0 (55–88.0)

Note: This table provides the name of the databases, the group, the number of considered subjects, the gender proportion, and the average age with the interval in brackets.

2.1.3. Sensitivity analysis

Finally, in order to test the consistency of our findings, we changed training and testing datasets: AIBL, OASIS, and MIRIAD databases were used for training and ADNI was used for testing.

2.2. Image processing

All the considered images were processed using AssemblyNet software (https://github.com/volBrain/AssemblyNet) (Coupé et al., 2020). Based on collective artificial intelligence, AssemblyNet is able to produce fine‐grained segmentation of the whole brain in 15 min. The AssemblyNet preprocessing pipeline was based on several steps: image denoising (Manjón, Coupé, Martí‐Bonmatí, Collins, & Robles, 2010), inhomogeneity correction (Tustison et al., 2010), affine registration to the MNI space, automatic quality control (QC) (Denis de Senneville, Manjón, & Coupé, 2020), a second inhomogeneity correction in the MNI space (Ashburner & Friston, 2005) and a final intensity standardization step (Manjón & Coupé, 2016).

After preprocessing, the brain was segmented into several structures using 250 DL models (see Coupé et al., 2020 for details). All the segmentations were based on the Neuromorphometrics protocol which comprises 132 structures (Klein & Tourville, 2012). In this protocol, the segmentation of the subcortical structures follows the “general segmentation protocol” as defined by the MGH Center for Morphometric Analysis (http://neuromorphometrics.com/Seg/). Moreover, the segmentation of the cortical structures follows the “BrainCOLOR protocol” (http://neuromorphometrics.com/ParcellationProtocol_2010-04-05.PDF) These structures are combined to create tissue segmentations (gray matter [GM], white matter [WM], and cerebrospinal fluid [CSF]), regional tissue segmentations (cortical GM, subcortical GM, ventricular CSF, and external CSF), and lobar segmentations (temporal, limbic, insular, parietal and frontal)—Figure 1.

FIGURE 1.

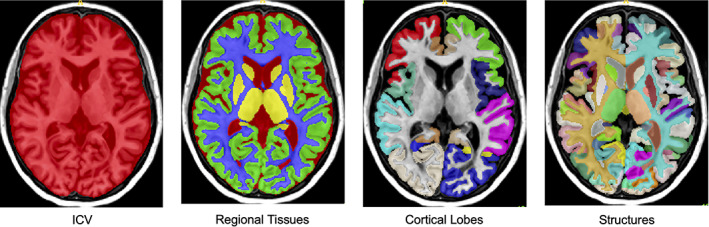
Illustrations of the AssemblyNet multiscale segmentations

Finally, we performed a QC procedure to carefully select subjects included in our training dataset. For all the training subjects detected as failure by the automatic QC RegQCNet (Denis de Senneville et al., 2020), a visual assessment was performed by individually checking the input images and the segmentations produced by AssemblyNet using a 3D viewer. If the failure was confirmed by our expert, the subject was removed from training dataset.

2.3. Volume normalization

To compensate for the inter‐subject variability, we normalized all the structure volumes using the intracranial cavity volume (ICV) (Manjón et al., 2014). Moreover, in order to be able to combine several structures with different sizes, we performed z‐score normalization of all the normalized volumes (in percentage of ICV). To do that, we first estimated the mean and the SD for each structures using all the CN subjects over the entire lifespan. Then, for a given structures, we applied the same z‐score normalization to all the subjects (i.e., CN, AD, and MCI). Therefore, by using z‐score of normalized volumes in % of ICV, we compensated for both inter‐subject and inter‐structure variabilities. In the following, all the volumes are expressed as z‐scores of normalized volumes.

2.4. Lifespan model estimation

To create our lifespan models, we estimated normal and pathological trajectories of structure volumes across the entire lifespan. To this end, for each considered structure, models were estimated on two different groups to generate CN and AD trajectories. For CN trajectories, we used the N = 2,655 subjects from 9 months to 94y of the training dataset as done in Coupé et al. (2017). For the AD trajectories, we used N = 2,251 subjects. As done in Coupé et al. (2019), we mixed AD patients with young CN. More precisely, we used 377 AD patients (from 55y to 96y) and all the CN younger than 55y available in the training dataset (i.e., 1874 subjects) assuming that neurodegeneration is a slow and progressive process.

To estimate the volume trajectories, we considered several low order polynomial models:

• Linear model

  $$\mathrm{vol}\left(\mathrm{Age}\right)={\mathrm{\beta }}_0+{\mathrm{\beta }}_1\mathrm{Age}+\mathrm{\epsilon }$$
• Quadratic model

  $$\mathrm{vol}\left(\mathrm{Age}\right)={\mathrm{\beta }}_0+{\mathrm{\beta }}_1\mathrm{Age}+{\mathrm{\beta }}_2{\mathrm{Age}}^2+\mathrm{\epsilon }$$
• Cubic model

  $$\mathrm{vol}\left(\mathrm{Age}\right)={\mathrm{\beta }}_0+{\mathrm{\beta }}_1\mathrm{Age}+{\mathrm{\beta }}_2{\mathrm{Age}}^2+{\mathrm{\beta }}_3{\mathrm{Age}}^3+\mathrm{\epsilon }$$

As in Coupé et al. (2017, 2019), a polynomial model was considered as a potential candidate only when simultaneously F‐statistic based on ANOVA (i.e., model vs. constant model) was found significant (p < .05) and when all its coefficients were also significant using T‐statistic (p < .05). Afterwards, to select the most relevant model between these potential candidates, we used the Bayesian Information Criterion (Schwarz, 1978). In addition, we estimated the distance between both AD and CN models as the Euclidean distance between trajectories. Finally, we estimated the confidence interval for each model at 95% and the lifetime period for which the two models diverged significantly (i.e., when confidence intervals do not overlap).

2.5. Classification using volume trajectories

Once the AD and CN lifespan trajectories were estimated for each structure using the training dataset, we used them to perform subject classification. To classify each subject of the testing dataset, we simply estimated the closest lifespan trajectory in terms of Euclidean distance to assign the class of the subject under study.

Moreover, in order to provide easily interpretable nonbinary scores to the user about the probability of the subject's status (and to be able to estimate area under curve), we proposed new scores of being an AD patient (respectively a CN subject) based on the distance to the models. This score was built to ensure that when AD score is higher than 50%, the closest model is the AD model. Moreover, we ensured that an AD score of 50% (i.e., CN score of 50%) is obtained for an equal distance between both models. To define these scores, we used the following approach.

First, for GM and WM structures, we defined a score $s_{\mathrm{CN}}$ to be CN (respectively $s_{\mathrm{AD}}$ to be AD) based on the distance to CN model (respectively to AD model) taking into account structure atrophy:

$$s_{\mathrm{CN}}=\mathrm{\Phi }\left(\mathit{vo}{l}_{\text{subject}},\mathit{vo}{l}_{\mathrm{CN}}\left(\mathrm{Age}\right),\mathrm{\delta }\right)$$

$$s_{\mathrm{AD}}=1-\mathrm{\Phi }\left(\mathit{vo}{l}_{\text{subject}},\mathit{vo}{l}_{\mathrm{AD}}\left(\mathrm{Age}\right),\mathrm{\delta }\right)$$

where $\mathrm{\Phi }\left(\mathrm{z},\mathrm{\mu },\mathrm{\sigma }\right)$ is the cumulative distribution function of the standard normal distribution of mean $\mathrm{\mu }$ and SD $\mathrm{\sigma }.$ In our case, we used $\mathrm{\delta }=\left|\mathrm{vo}{\mathrm{l}}_{\mathrm{CN}}\left(\mathrm{Age}\right)-\mathrm{vo}{\mathrm{l}}_{\mathrm{AD}}\left(\mathrm{Age}\right)\right|$ to take into account the increasing distance between the both models during aging.

For CSF structures, we adapted the estimation taking into account structure enlargement caused by AD (Nestor et al., 2008) as follows:

$$s_{\mathrm{CN}}=1-\mathrm{\Phi }\left(\mathrm{vo}{\mathrm{l}}_{\text{subject}},\mathrm{vo}{\mathrm{l}}_{\mathrm{CN}}\left(\mathrm{Age}\right),\mathrm{\delta }\right)$$

$$s_{\mathrm{AD}}=\mathrm{\Phi }\left(\mathrm{vo}{\mathrm{l}}_{\text{subject}},\mathrm{vo}{\mathrm{l}}_{\mathrm{AD}}\left(\mathrm{Age}\right),\mathrm{\delta }\right)$$

Finally, these scores were normalized to obtain the final scores. This normalization enables to get the sum of both scores equal to 1.

$$S_{\mathrm{CN}}=\frac{s_{\mathrm{CN}}}{s_{\mathrm{CN}}+s_{\mathrm{AD}}},S_{\mathrm{AD}}=\frac{s_{\mathrm{AD}}}{s_{\mathrm{CN}}+s_{\mathrm{AD}}}$$

Consequently, the proposed HAVAs (i.e., the S _AD score) reflects the probability for the subject under study to be a patient with AD (or a pMCI subject). The classification performance of the proposed method was validated using several metrics: balanced accuracy (BACC), specificity (SPE), sensibility (SEN) and area under the curve (AUC) based on HAVAs.

2.6. Comparison with state‐of‐the‐art methods

In this study, we compared the proposed multimodel HAVAs with normative model‐based strategy (i.e., using only CN model), state‐of‐the‐art deep learning methods and classical machine learning methods.

First, as usually done in normative modeling (Marquand et al., 2019) or in automatic quantitative software (Pemberton et al., 2021), we used $2\mathrm{\sigma }$ as threshold to detect abnormal values when using normative model‐based methods. To ensure that this threshold was suitable for our analysis, we tested multiple thresholds and we confirmed that $2\mathrm{\sigma }$ was the best one. We decided to evaluate lifespan normative approach using hippocampus (considered as the state‐of‐the‐art biomarker [Frisoni et al., 2010]), amygdala (also known to be a good candidate [Coupé et al., 2019]), inferior lateral ventricle (main part of lateral ventricle impacted by AD [Bartos, Gregus, Ibrahim, & Tintěra, 2019]) and the combination of the three as done for the proposed HAVAs (called Normative HAV model in the following).

Second, as shown in Wen et al. (2020), most of the proposed deep learning methods suffer from data leakage resulting in biased reported performances. In addition, most of the published studies used the same dataset for training and testing that produce over‐optimistic performance of the methods (Bron et al., 2021; Wen et al., 2020). Consequently, we decided to report the score of the well‐evaluated methods proposed in Wen et al. (2020) as state‐of‐the‐art deep learning methods since the training was well‐designed and that the proposed methods were well‐validated on external datasets. We selected a ROI‐based convolutional neural network (CNN) focused on hippocampal area, one subject‐based CNN method using the entire image and one patch‐based CNN processing the whole image patch by patch. These three strategies are a good representation of current deep learning frameworks for AD detection and prognosis. We used the ClinicaDL software proposed in Wen et al. (2020) to create the testing databases. Consequently, the selection criteria were similar although the number of subjects per cases were not exactly the same.

Finally, since (Wen et al., 2020) demonstrated that classical machine learning methods (i.e., SVM) can perform similarly and sometimes better than deep learning methods, we decided to include two classical classifiers in our comparison. First, we used the nonlinear SVM with RBF kernel of Matlab with default parameters. Second, we used the logistic regression with LASSO regularization of Matlab with default parameters. The z‐score of normalized volumes were used as input features.

3. RESULTS

3.1. Detection of the most discriminant structures

First, we selected all the multiscale brain areas (i.e., tissues, regional tissues, lobes, and structures) for which CN and AD models significantly diverged (i.e., confidence intervals stop overlapping at some point across lifespan). Thanks to this analysis, we obtained 33 areas. Using these 33 selected areas, we performed a screening to detect the most discriminant ones in terms of classification accuracy on the training ADNI dataset in order not to use testing data during method development. This analysis showed that amygdala, hippocampus, and inferior lateral ventricle were the most discriminant structures for AD vs. CN classification (Table 3). These three structures obtained AUC > 80% and thus were selected to build our AD‐specific hybrid lifespan models.

TABLE 3.

Performance of the classification using multiple lifespan models on the training ADNI dataset (404 CN vs. 332 AD) for the 33 selected structures

	BACC	SPE	SEN	AUC
WM	61	53	69	69
CSF	66	60	71	73
External CSF	59	53	64	64
Ventricular CSF	68	72	64	71
Inf. Lat. Vent	75	85	64	82
Lat. Vent	68	70	65	71
GM	66	64	68	70
Subcortical GM	70	66	73	75
Amygdala	82	85	79	88
Hippocampus	80	78	81	87
Accumbens area	59	52	66	64
Putamen	57	53	60	61
Thalamus	56	55	58	62
Pallidum	55	55	55	58
Caudate	57	52	62	61
Cortical GM	61	59	63	69
Temporal lobe	71	71	71	78
Middle temporal gyrus	66	66	66	63
Fusiform gyrus	63	61	66	72
Inferior temporal gyrus	62	60	64	68
Superior temporal gyrus	60	59	62	65
Temporal pole	61	60	63	67
Limbic cortex	64	61	67	68
Entorhinal area	64	64	63	71
Parahippocampal gyrus	64	65	63	70
Anterior cingulate gyrus	59	54	64	63
Insular cortex	60	57	63	63
Anterior insula	58	55	61	63
Posterior insula	58	56	59	63
Parietal lobe	57	53	60	59
Angular gyrus	59	55	64	63
Frontal lobe	n.s	n.s	n.s	n.s
Middle frontal gyrus	55	52	57	58

Note: The best results are indicated in bold and second best in italic. Finally, “n.s.” means that the divergence of frontal lobe was not significant.

3.2. Combination of the main AD MRI‐based biomarkers

Based on our screening, we decided to combine the volume of hippocampus, amygdala, and inferior lateral ventricle to propose a novel HAVAs. To do that, we simply added hippocampus and amygdala volumes and subtracted the inferior lateral ventricle volume. Indeed, contrary to hippocampus and amygdala showing lower volumes in AD model due to atrophy, inferior lateral ventricle exhibited larger volumes in AD model due to enlargement. As done before, HAVAs is also expressed as a z‐score of normalized volume. As shown in Figure 2, HAVAs exhibited an earlier divergence between CN and AD models (i.e., it can be used on younger subjects) and a larger distance between models (i.e., it is more discriminant) compared to single structure models.

FIGURE 2.

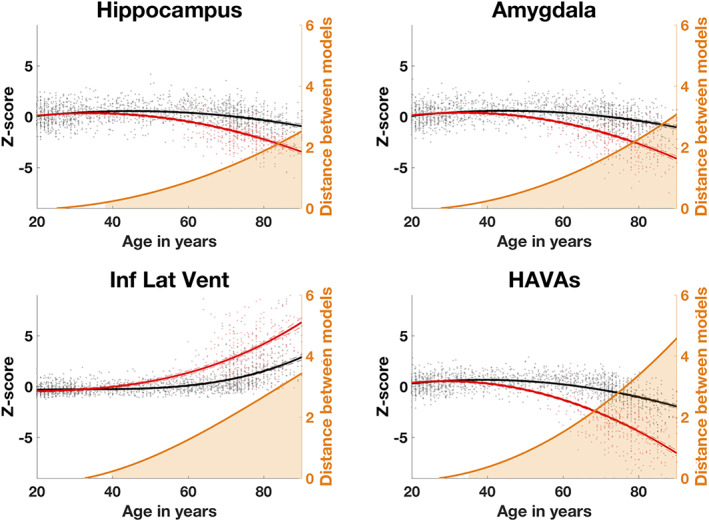
Trajectories based on z‐scores of normalized volumes (in % total intracranial volume) for the selected brain structures and the proposed HAVAs for both models (AD in red and CN in black) across the entire lifespan. The prediction bounds of the models are estimated with a confidence level at 95%. The orange curve is the distance between both models in SD. The orange area indicates the time period where confidence intervals of both models do not overlap

In Table 4, we present the statistical analysis of the estimated lifespan models for the selected structures. First, we can observe that most of the estimated models were quadratic. Only, the inferior lateral ventricle models were cubic. This is in line with previous lifespan studies (Coupé et al., 2017, 2019). Second, all the model statistics were highly significant (p < .0001), excepted for the inferior lateral ventricle model for AD which was only significant (p < .05).

TABLE 4.

Results of model analysis for hippocampus, amygdala, inferior lateral ventricle and HAVAs

	Selected model	F‐statistic	R 2	p‐Value of the T‐statistic	p‐Value of the F‐statistic based on ANOVA	BIC
Hippocampus for CN	Quadratic	202	0.13	β0: p < .0001; β1: p < .0001; β2: p < .0001	p < .0001	7,172
Hippocampus for AD	Quadratic	704	0.38	β0: p < .0001; β1: p < .0001; β2: p < .0001	p < .0001	6,346
Amygdala for CN	Quadratic	230	0.15	β0: p < .0001; β1: p < .0001; β2: p < .0001	p < .0001	7,120
Amygdala for AD	Quadratic	902	0.44	β0: p < .0001; β1: p < .0001; β2: p < .0001	p < .0001	6,598
Inf. Lat. Ventricle for CN	Cubic	685	0.44	β0: p < .0001; β1: p < .0001; β2: p < .0001; β3: p < .0001	p < .0001	6,031
Inf. Lat. ventricle for AD	Cubic	725	0.65	β0: p < .0001; β1: p < .05; β2: p < .05; β3: p < .0001	p < .001	6,968
HAVAs for CN	Quadratic	483	0.27	β0: p < .0001; β1: p < .0001; β2: p < .0001	p < .0001	6,720
HAVAs for AD	Quadratic	483	0.66	β0: p < .0001; β1: p < .0001; β2: p < .0001	p < .0001	6,827

3.3. Classification based on multiple lifespan models

To evaluate the classification performance of HAVAs on testing datasets, we performed a comparison with the three most discriminant structures. As shown in Table 5, in all the cases, HAVAs outperformed strategies based on a single structure, in terms of BACC and AUC, demonstrating its higher classification performance. In most of the cases, the second best one was the lifespan model of amygdala that confirmed the results previously obtained in Coupé et al. (2019). For diagnostic task (i.e., AD vs. CN), HAVAs obtained 88% of BACC and 94% of AUC on the AIBL database, and 89% of BACC and 96% of AUC on the MIRIAD database. Moreover, while developed using only AD and CN subjects, HAVAs obtained 73% of BACC and 78% of AUC for prognosis task (i.e., discriminating between sMCI and pMCI). These results demonstrate the good generalization capabilities of HAVAs on unseen databases and on unseen tasks.

TABLE 5.

Comparison of classification performance of HAVAs compared to individual structures on three unseen external datasets (N = 1,039)

	BACC	SPE	SEN	AUC
AIBL (467 CN/82 AD)
HAVAs	88	93	83	94
Amygdala	80	85	76	89
Hippocampus	80	78	82	88
Inferior lateral ventricle	79	91	67	89
MIRIAD (23 CN/46 AD)
HAVAs	89	87	91	96
Amygdala	88	83	93	95
Hippocampus	74	61	87	87
Inferior lateral ventricle	86	87	85	91
ADNI‐MCI (255 sMCI/235 pMCI)
HAVAs	73	72	74	78
Amygdala	68	69	68	74
Hippocampus	66	56	77	70
Inferior lateral ventricle	65	76	54	71

Note: The best results are indicated in bold and second best in italic.

During our experiments, we also tested several strategies to combine the selected structure volumes. First, we evaluated the hippocampal‐ventricle ratio (HVR)—defined as hippocampus/(inferior lateral ventricle + hippocampus). HVR has recently been proposed as a better alternative than hippocampus volume (Bartos et al., 2019; Schoemaker et al., 2019). During our experiments, we observed a drop of 7% point of BACC for diagnosis on AIBL and for prognosis on ADNI compared to the proposed HAVAs. Consequently, we found similar performance between using HVR or hippocampus z‐score normalized volume. Second, we tried to add the temporal lobe volume (the fourth best structure during our screening) in HAVAs. This reduced by 1% point of BACC the diagnosis performance and kept prognosis similar. Finally, we also evaluated the use of weights to combine HAV volumes (e.g., to give more importance to amygdala than hippocampus). Such strategy provided marginal improvement for diagnosis <1% point and 1% point of improvement for prognosis. However, for a sake of simplicity, we decided not to use weights in our approach.

Figure 3 presents the results of the classification produced by HAVAs on the external datasets. The boundary decision is simply the middle distance between both models. Consequently, false positive are CN subjects (green dots) below orange curve and false negative are AD patients (red dots) above orange curve. Visually, we observed that AD patients exhibited higher variability than CN subjects. Moreover, as expected, most of the MCI were between both models.

FIGURE 3.

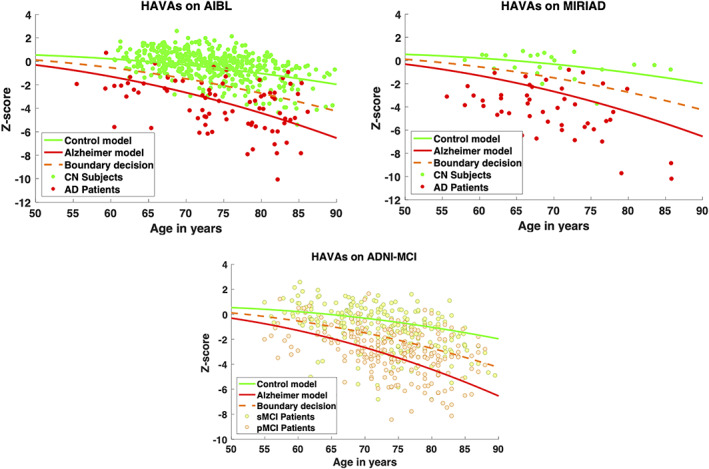
HAVAs classification results on three external testing datasets (ADNI was the training dataset). The CN trajectory is in green, the AD trajectory in red and the boundary decision in orange. For AIBL and MIRIAD datasets, CN subjects are in green and AD patients in red. For ADNI dataset, sMCI patients are in yellow and the pMCI patients in orange

3.4. Comparison with state‐of‐the‐art methods

In this section, we compared HAVAs with normative modeling strategy, classical ML and recent DL methods.

First, as shown in Table 6, HAVAs obtained the best results for both diagnostic and prognostic tasks. Compared to the second‐best methods, HAVAs produced an improvement of 3% point for diagnosis and for prognosis. Second, the second‐best methods were the ROI‐based CNN involving mostly the same structures as HAVAs and LASSO using the combination of HAV structures. We also observed using HAV structure combination was the best solution for SVM and normative modeling. Consequently, the proposed HAV combination based on z‐score was beneficial for all the compared strategies (multimodel, normative modeling, SVM, and LASSO). In addition, for all the considered structures, the proposed multimodel strategies outperformed single‐model‐based approaches (i.e., normative modeling). This result shows the interest of using multiple models for classification compared of using a single normative model. Moreover, the normative modeling and machine learning based on HAV combination obtained results similar to CNN‐based methods. These results are in line with the comparisons proposed in Bron et al. (2021 and Wen et al. (2020). Finally, while hippocampus volume is considered a hallmark of AD, normative modeling using hippocampus obtained the worst results (16% point lower than the proposed multimodel HAVAs). For all the considered strategies (multimodel, normative modeling, SVM, and LASSO), amygdala volume provided the best performance when using a single structure. These results are in line with previous studies dedicated to lifespan modeling of AD (Coupé et al., 2019).

TABLE 6.

Comparison with state‐of‐the‐art strategies based on normative modeling and recent deep learning methods

BACC on external datasets	AIBL (AD vs. CN)	ADNI (sMCI vs. pMCI)
Multimodel HAVAs	88	73
ROI‐based CNN (Wen et al., 2020)	84	70
LASSO HAV	85	67
Subject‐based CNN (Wen et al., 2020)	83	69
SVM HAV	82	70
LASSO amygdala	83	68
Normative HAV model	81	70
Patch‐based CNN (Wen et al., 2020)	81	70
LASSO hippocampus	81	67
Multimodel amygdala	80	68
SVM amygdala	80	66
Multimodel hippocampus	79	66
LASSO inf. lat. vent.	79	66
Multimodel inf. lat. vent.	79	65
SVM hippocampus	79	64
Normative amygdala model	75	63
SVM inf. lat. Vent.	75	63
Normative inf. lat. vent. model	71	61
Normative hippocampus model	70	58

Note: BACC is provided for each method for both datasets. For CNN‐based methods, the results published in Wen et al., 2020 are used. For normative modeling, a threshold of 2σ was used to detect abnormal volumes. Finally, for SVM and LASSO, the Matlab version with default parameters is used. The best results are indicated in bold and second best in italics.

3.5. Sensitivity analysis to training domain

Finally, as a sensitivity analysis, in order to evaluate the consistency and the robustness of HAVAs to training domain, we performed an additional experiment using AIBL, OASIS, and MIRIAD databases in the training dataset while removing the AD and CN subjects of the ADNI database from training and used them as testing dataset. First, Table 7 shows the results obtained by HAVAs, amygdala, hippocampus, and inferior lateral ventricles. The obtained results are similar to the results previously obtained on AIBL. This result highlights the robustness of the proposed HAVAs strategy to training domain selection and the good generalization capability of our method.

TABLE 7.

Sensitivity analysis

	BACC	SPE	SEN	AUC
ADNI (404 CN/332 AD)
HAVAs	87	87	86	93
Amygdala	82	81	83	89
Hippocampus	78	71	86	88
Inferior lateral ventricle	75	83	66	84

Note: Comparison of classification performance of HAVAs compared to individual structures using AIBL, OASIS and MIRIAD in the training and the AD and CN subjects ADNI as testing. The best results are indicated in bold and second best in italics.

Moreover, Figure 4 presents the graphical results obtained using HAVAs score in the same condition. As previously, we observed that most of the CN subjects well follow the CN model while most of the AD patients are below the decision bounds and exhibit higher variability. Finally, it is interesting to observe that HAVAs models estimated on AIBL, OASIS, and MIRIAD are very similar to HAVAs models estimated using ADNI (Figure 3). This result highlights the stability of the proposed HAVAs strategy to images used during training.

FIGURE 4.

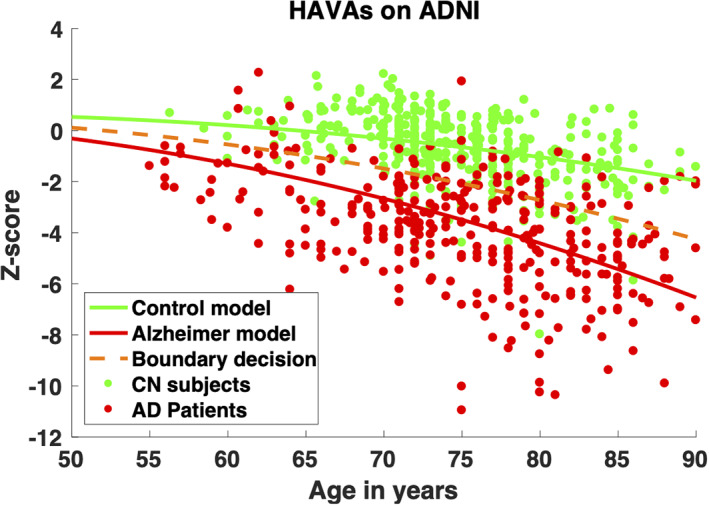
Sensitivity analyses. HAVAs classification results for AD and CN subjects of the ADNI database while using AIBL, OASIS, and MIRIAD in the training dataset. The CN trajectory is in green, the AD trajectory in red and the boundary decision in orange

4. DISCUSSION

In this article, we proposed a novel framework for AD detection based on lifespan modeling of the hippocampal‐amygdalo‐ventricular volume trajectory for both CN and AD. To this end, we first estimated volume trajectories for AD and CN models across the entire lifespan using a large number of subjects. In this study, we analyzed 132 structures, 5 lobes, 4 regional tissues, and 3 tissues. This whole brain analysis, in a multiscale fashion, enabled us to produce a full screening of the diverging brain areas across lifespan between CN and AD. Within the considered brain areas, only 33 showed significantly divergences between AD and CN models. For these 33 brain areas, we estimated the most discriminant lifespan model in terms of classification performance. We found that amygdala, hippocampus, and inferior lateral ventricle were the most discriminant structures. These results obtained using AssemblyNet were in line with recent studies based on other segmentation protocols, software or frameworks (Bartos et al., 2019; Coupé et al., 2019; Mu, Xie, Wen, Weng, & Shuyun, 1999; Pinaya et al., 2021; Qiu, Fennema‐Notestine, Dale, & Miller, 2009). Therefore, we proposed a new AD score based on hippocampal‐amygdalo‐ventricular volume called HAVAs. This score is based on the distances between the volume of the subject under study and the AD and CN lifespan trajectories. During the validation of HAVAs on three external datasets, we showed that our strategy enables accurate detection of subject having AD, or MCI who will convert to AD in the next 3 years (i.e., pMCI). Finally, we demonstrated the competitive performance of the proposed HAVAs compared to usual normative modeling, classical ML and recent DL methods.

During our experiments, we showed that models combining several structures (i.e., HAVAs and HAV) outperformed models based on a single structure. This demonstrates the advantage of combining volumes of key structures to improve AD detection. Moreover, our results suggests that methods based on amygdala provide higher accuracy than models based only on hippocampus. The important role of amygdala at the early state of AD has been already observed in the past (Coupé et al., 2019; Poulin, Dautoff, Morris, Barrett, & Dickerson, 2011; Qiu et al., 2009). Finally, we showed that using several models had beneficial impact for improving classification accuracy compared to single‐based model normative approach. We also found that DL methods were in general more accurate than normative modeling approach but not better than usual ML. Recently, it has been suggested that the combination of both could improve the performance by using normative modeling of learned features (Pinaya et al., 2021). We will investigate this strategy in future works.

To conclude, in addition to improving classification performance, the proposed HAVAs strategy has several advantages over recent DL approaches:

• First, HAVAs is conceptually very simple to understand since based on the distance to AD or CN trajectories. This aspect enables an easy interpretability of the results in terms of hippocampal‐amygdalo atrophy and concomitant ventricular enlargement. While current DL methods failed to produce relevant explanation on the used features for their decision making (Bron et al., 2021), HAVAs is fully interpretable and thus is well‐suited for clinical practice or pharmaceutical trials. Moreover, the simplicity of HAVAs makes it fast and easy to reimplement. A software package including AssemblyNet pipeline and HAVAs estimation will be made freely available as a downloadable Docker (https://github.com/volBrain/AssemblyNetAD) as well as an online pipeline on the volBrain platform (http://www.volbrain.net/).

• Second, HAVAs is based on a very low number of parameters and hyperparameters. The use of low order polynomial models for trajectory results in few learnable parameters per trajectory. Thus, using less than 10 parameters, HAVAs is able to outperform CNN models involving more than 10 million parameters. Moreover, thanks to our volume normalization procedure compensating for inter‐subject and inter‐structure variabilities, no hyper‐parameter is needed to combine hippocampus, amygdala, and inferior lateral ventricle volumes. As shown during our experiments, this enables HAVAs to generalize well by being robust to domain shift and efficient on prognosis task.

AUTHOR CONTRIBUTIONS

Pierrick Coupé developed the idea, the theoretical formalism, performed the analytic calculations, and performed the numerical experiments. Pierrick Coupé, José V. Manjón, and Boris Mansencal conceived and planned the experiments and Boris Mansencal prepared and processed the data. Pierrick Coupé took the lead in writing the manuscript. Thomas Tourdias, Gwenaëlle Catheline, and Vincent Planche aided in interpreting the results and worked on the manuscript. All authors provided critical feedback and helped shape the research, analysis and manuscript. All authors discussed the results and contributed to the final manuscript.

Coupé, P. , Manjón, J. V. , Mansencal, B. , Tourdias, T. , Catheline, G. , & Planche, V. (2022). Hippocampal‐amygdalo‐ventricular atrophy score: Alzheimer disease detection using normative and pathological lifespan models. Human Brain Mapping, 43(10), 3270–3282. 10.1002/hbm.25850

DATA AVAILABILITY STATEMENT

All the used MRI were from open access database and thus can be downloaded from the database provider website. AssemblyNet is freely available at https://github.com/volBrain/AssemblyNet. HAVAs will be made available through our online platform www.volbrain.net and as part of AssemblyNet‐AD at https://github.com/volBrain/AssemblyNetAD.