Abstract
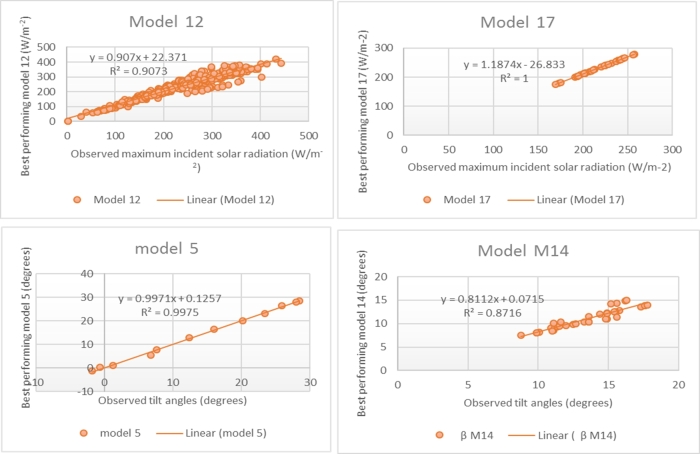
This research was designed to apply measured and theoretically derived models to estimate the optimal tilt angle (β), maximum incident solar radiation (HT), and global radiation index (GRI) in Lagos and 37 metropolitan cities in Nigeria. Six modules were mounted at different tilt angles with two modules north-facing, three south-facing, and one positioned horizontally to determine the orientation and tilt angle performance. Overall, the 16.8° module 4 south-facing tilted emerged as the best performing module for HT, with maximum output power, and much more than 6.174 annual earned energy reported on module 6 mounted horizontally. The GRI obtained from the six solar modules revealed a significant coefficient of 1.0269 for module 1 north-facing, 0.9923 for module 2 north-facing, 1.0217 for module 3 south-facing, 0.9609 for module 4 south-facing, and 1.0232 for module 5 south-facing for the values obtained from the horizontally positioned module 6. In-depth statistical analysis of the effectiveness of values observed against the predicted values to estimate the optimal and maximum inclination angle of incident solar radiation using error metrics and GPI revealed that model 5, model 12, model 14, model 17, and model 14 outperform the other estimation models in their respective categories. A similar statistical analysis of model 14 with the best performance was performed to estimate the best inclination angle in 37 metropolitan cities in Nigeria compared to two models consolidated in the literature; model 14 performed admirably in terms of accuracy compared to the two models obtained from the literature.
Keywords: Optimum tilt angle, Global radiation index, Maximum incident solar radiation, Orientation, Global solar radiation
Optimum tilt angle; Global radiation index; Maximum incident solar radiation; Orientation; Global solar radiation
1. Introduction
Although photovoltaic (PV) solar power generation is the fastest-growing power technology [1], terrestrial solar modules typically fall below their established performance rating under standard test conditions. In the context of responsiveness to following the direction of the sun during the day, an adequate tilt angle of a solar module can greatly affect its overall performance. Numerous plants possess natural tendencies to follow the movement of the sun to receive the maximum photosynthetically active radiation needed to maximize photosynthesis, most of Earth's solar energy systems, including solar photovoltaic (PV) modules, do not. In 1941, Hoyt Hottel revealed that “artificial flat converters of solar energy are too cheap to justify being mounted to follow the direction of the sun, but they can profitably be permanently tilted towards the equator [2]. Installation angles are necessary for solar photovoltaic design [3], energy use [4], and economic analysis [5]. In contrast, rooftop solar PVs are specifically designed to be mounted at the optimum angles which are a combination of tilt and orientation/azimuth angles to achieve maximum annual power generation. Solar PV technicians, manufacturers, technocrats, and researchers [6], [7], [8], [9] have tried different approaches or experiments to arrive at or work outside the optimum angle of inclination for incoming solar insolation to maximize for a flat surface. It seems like a simple challenge, but it is a complicated exercise that has not produced any global standardized results since 1956 researchers have begun to develop empirical models [10], expressions based on latitude [11], ideal loss equation [12], tilt angle optimization techniques [13], tilt angle analysis and photovoltaic performance orientation [14], long-term energy harvesting capacity for photovoltaic systems [15], optimal planning of the grid-connected photovoltaic system [16], multi-objective optimization criterion for standalone photovoltaic systems [17], analysis of methods for determining the daily direction of photovoltaic modules [18] and monitoring of photovoltaic solar surfaces [19] for mass a yield of solar energy. This is attributed to the fact that it is necessary to consider the rotation, obliquity, orbital eccentricity, and revolution around the Earth, as well as the climate and geographical features of the site.
In the context of global sustainability, the sophisticated tracking system is still considered expensive. The system also requires maintenance in addition to the energy system required for operation. They are equally prone to heavy snow or storm damage and are often not applicable to small-scale systems such as rooftop applications due to their heavy nature. Computation [20], algorithm [21], and optimization [22] are recent approaches by researchers to determine optimal tilt angles. Recently, Yadav and Chandel [13] examined these approaches by comparing the results of analytical, numerical, and experimental methods to determine the suitability of a technique for a particular location. The authors concluded that the optimal inclination is very site-specific due to the variability of climatic and geographic factors and must be carefully studied considering long-term observational datasets. Indeed, Jacobson and Jahdav [23] predicted two very different angular inclinations for almost the same geographic latitudes: 34° for London in the UK and 45° for Calgary, Canada.
As indicated in a recent review paper [11], a data-driven approach is thus emerging as a standard practice. Modarresi and Hosseinnia [24] employed datasets from 337 locations in the Northern hemisphere and 247 locations in the Southern hemisphere to estimate optimum tilt angle worldwide. The results show that daily optimum tilt angle changes in cosine form over a year. The authors equally revealed that the optimum tilt angle is independent of the longitude but can be estimated using parameters dependent on latitude and day number. Sharma et al. [25] employed diffuse and global solar irradiance datasets from 2012 to 2017 to estimate optimum tilt angle in Western Himalayan, India. The authors revealed that established mathematical approaches were capable of increasing the maximum incident solar radiation obtained in all the locations.
Numerous authors have started applying the “typical meteorological year” (TMY) as a type of hourly solar resources data, in which the entirety of original multi-year solar radiation and meteorological datasets is considered into one year's worth of the most usual conditions. However, albeit TMY data collection may enable the estimation of optimum tilt angle for all major cities globally [23], they ultimately are auxiliary datasets and cannot reflect the nonlinear dynamics of global climate change [26]. The actual solar spectrum remains the key indicator to understanding this because all other indicators are directly or indirectly dependent on it. The sunlight received by the terrestrial solar module is continuously changing as a result of the Earth's rotation and revolution. It equally depends on the changes in radicals and meteorological conditions of the atmosphere. This, in the long run, is subject to fluctuations on a minute summarization interval.
Since the data for the global solar spectrum are hardly available at this resolution. Bright et al. [27] suggested “stochastic generation of synthetic minute irradiance from mean hourly weather observation data”. Although, the model generates realistic irradiance profiles, however, it is non-spatial and is not intended to match real-world observational datasets because the individual simulations at near locations would not correlate [28], [29]. Conversely, according to the Union of Concerned Scientists [30], 700 satellites are recording datasets for Earth observation purposes. Among these databases, the National Aeronautics and Space Agency (NASA), National Renewable Energy Laboratory (NREL) as well as European Space Agency (ESA), offer wide-ranging resources down to a 1 min summarization interval. It is therefore recommended to combine such valuable information to model the optimum tilt angle at a specific site.
In Nigeria, there is a lack of adequate routinely and consistently measured datasets and research materials in optimum tilt angle and maximum incident solar radiation field. The reasons for this are not unrelated to the barriers to the application of solar photovoltaic modules in Nigeria that Okoye et al. [19] have enumerated to include technical, social, cultural and behavioral, economic and financial, institutional and political problems and market distortions. Some researchers determine the optimal tilt angle of solar panels in certain parts/regions of the country. Some of these include Eke [31] for Zaria in Kaduna, Oko et al. [32] for low latitudes of 4.86° - 13.02°N, Waziri et al. [33] for Kano, Idowu et al. [34] for the tropical low-latitude region, Udoakah et al. [35] for Enugu, Southeastern Nigeria, Okundamiya et al. [36] for Abuja, Benin City, and Katsina, and Ajao et al. [37] for Ilorin, Kwara state, among others.
These studies were more location-specific than generalized and as such could not seem applicable to other parts of the country. Many other parts of the country have not been exposed to the subject and there is a lack of data and literature; Lagos is one of them even though it may appear to have been included in that by Oko et al. [32]. Recently, Oladeji et al. [38] determined optimal tilt angles in selected cities in Nigeria for maximum extractable solar energy through simulation based on existing models between 0° and 42° throughout the year. The above studies did not use any existing theoretical/mathematical model or long-term 1 min time summarization interval datasets to model or estimate optimum tilt angles in Nigerian locations as recommended [39] or even validate the results obtained experimentally. This would have given more credit to their research and the results obtained from it.
Up till now, no field research has been conducted at any location in Lagos or any location in Nigeria since modeling and estimation of the optimal tilt angle, maximum incident solar radiation (HT) in addition to this study began. Numerous authors have models and estimates of the optimal HT tilt angle as well as HT from different parts of the world. However, these models differ from each other in simplicity [40], application [41], and accuracy [42]. According to Barbon et al. [43], these models can be separated into calculations using latitude angle and calculations that maximize total solar irradiance on inclined surfaces. Awan et al. [44] found the first approach (latitude angle) to be simple but appropriate. Barbon et al. [45] stated that the second approach is more accurate but has a strong dependence on the solar irradiation model and their application is more complex.
Numerous studies have evaluated the optimal tilt angle from different location approaches at different sites around the world. There is little information on evaluating the energy performance of solar PV systems for any orientation and angle of inclination that deviates from those of the idea. Chen et al. [12] have shown that a fairly wide range of installation angles of photovoltaic systems results in negligible energy losses annually. Sanchez et al. [46] present an experimental study showing that small deviations from the optimal tilt angle do not cause large energy losses.
This study is divided into three different parts. The first part explores the potential energy of solar energy systems in a non-contractual position for urban or rural applications (previously mounted models not suitable for the Nigerian environment). In the second part, with the help of the previous study, a practical application is presented to enhance the energy efficiency potential. In the third part, with the help of the previous study and practical application, theoretical models for determining the optimal inclination angles, the maximum incident solar radiation, and the global radiation index (GRI) of photovoltaic plants in Lagos, Nigeria, Africa, the Mediterranean region, and around the world the use of latitude-dependent parameters is presented. The study will also allow solar PV module manufacturers to incorporate specific orientation and tilt angles into their user manuals with corresponding maximum values of incident solar radiation and optimal tilt angles for semiconductor silicon photovoltaic technology. This is to allow users of such products to take full advantage of this product so that accurate sizing of solar PV systems is much easier. This research aimed to derive empirical and theoretical models for the estimation of the optimal inclination angle, HT, and GRI based on climatological and geographic factors, and to evaluate and compare them with the values of the models existing in the literature.
2. Materials and methods
2.1. Geography and climate of the location under study
The study was conducted in Lagos, a small but densely populated coastal state in Nigeria. Fig. 1 below shows Lagos on the political map of Nigeria. The geography and climate of Lagos are summarized in Table 1.
Figure 1.
Map of Nigeria showing the study area.
Table 1.
Summary of the geography and climate of Lagos State, Nigeria.
| Serial | Entity | Measure | Comments |
|---|---|---|---|
| 1. | Latitude | 6.6080°N (6.5° or 6.45°) | Low latitude |
| 2. | Longitude | 3.6218°E | Low |
| 3. | Elevation | 41 m | Ikeja as a reference point |
| 4. | Weather | Wet and dry seasons | a. Wet season. |
| Apr – Jul (heavy rain) | |||
| Oct – Nov (Light rains) | |||
| b. Dry season. Mid Dec – late Feb (with Harmattan) | |||
| 5. | Vegetation | Tropical rain forest | Dominated by swampy terrain |
| 6. | Temperature | High – 33 °C | a. Hottest months from Jan – Mar when average temp is 29 °C. |
| Low – 21 °C | b. Month of Jul is usually coldest with average temp of 25 °C |
2.2. Research strategy
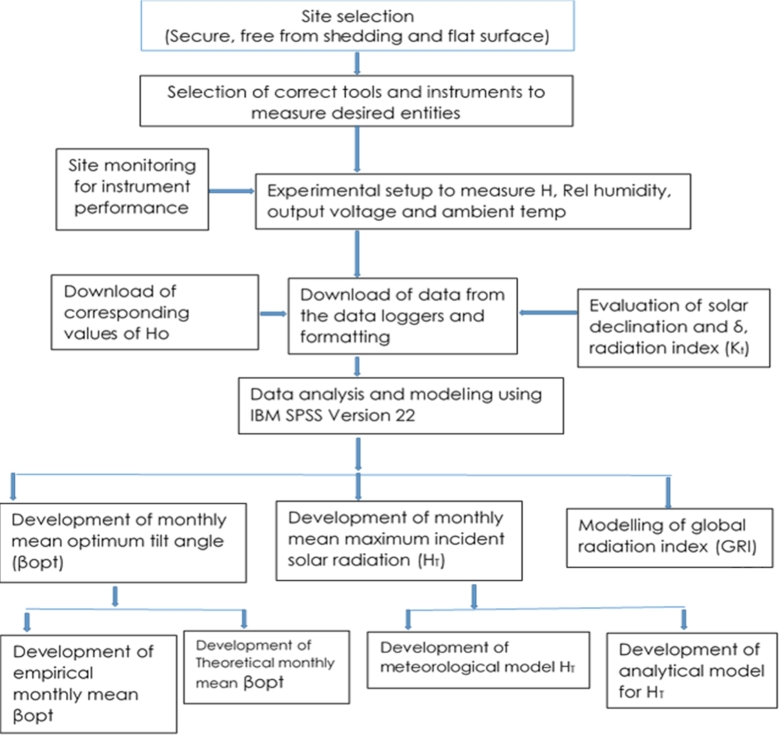
The strategy adopted in this work first implies a concise understanding of the aims and objectives of the work and the mapping of the most effective and convenient ways of achieving them. The overall aim of the research was to collect numerical/field data for use in determining which of the solar PV modules recorded the highest solar radiation. The measured data are used to develop and validate the models. To validate the development models, the results of the models were compared with the results of the models selected from the literature. Both assessment values were further compared to the assessment values using data downloaded from relevant NASA websites. Therefore, with clear and precise intent and thought of the research involved, the parameters to be measured and the tools and platforms required to achieve them were carefully considered and selected as shown in Fig. 2. Relevant measurement tools and accompanying software were purchased to run the purchased hardware.
Figure 2.
Flow chart of the methodology.
2.3. Approach
A key measure for the realization of research goals and objectives is an accurate determination of the tools and materials to be used and their correct design to ensure timely and accurate recording and data collection. The experimental setup worked unperturbed, with intermittent visits to the site and downloading of recorded data to a computer via USB cables. Consequently, the following tools were deemed most necessary for use in data collection at the research site: solar modules, the tilt angle of the metal frame 0 - 90° adjustable and rotatable for mounting the solar module, inclinometer; pyranometers for measuring global (diffuse) solar radiation; digital data logger for recording measured radiations and output voltages, hygrometer for simultaneous measurement of ambient temperature and relative humidity; power resistors; electric cables; digital compass; adjustable clips; markers and tapes.
The above tools were connected as expected in the search diagram using various types and sizes of electrical cables. The six photovoltaic modules used in the work were mounted as follows:
-
1.
Two of the photovoltaic modules were facing north tilted at 5.5° and 10.1° angles based on Lagos latitude (6.7°) as a general guide. It was intended to guide and provide information on some authors' general rule that photovoltaic solar modules located in the northern hemisphere must be oriented towards the equator (south).
-
2.
Three modules were oriented south and tilted at 6.7°, 16.8° and 26.8° angles respectively The modules were set at these angles according to Elsayed [47] and Qui and Riffat [48] (that and respectively).
-
3.
The sixth solar module was mounted horizontally (0°) to validate the measured data from the other five modules.
Solar noon was determined using the rule of thumb of the clock ray method. An electronic compass was also used while the digital inclinometer was used to set the various inclination angles. To dissipate the power generated by the solar modules and therefore the output voltage (Vo), four power resistors (100 W) that make up a low resistance network were connected in parallel to form a load R. This was connected to the ends of each of the six solar modules. The value of the resistive loads, the nominal powers and the number of resistors have been determined considering the I-V characteristic curve of the solar modules. This curve was generated using the open-circuit voltage, short-circuit current, maximum voltage, and maximum current at maximum module test power. Accordingly, the manufacturer's output power/peak output voltage rating and current were used to calculate the required resistance value and power ratings. These were connected to the two data loggers which were programmed to take readings with a summary interval of 5 minutes throughout the day, for a total of 288 (144 readings for the daylight period) output voltage records for each solar module per day. The ambient temperature/relative humidity data logger has been fixed outside and connected to the data loggers. The pyranometers, which measured global solar radiation, were each mounted on the side of each of the six solar modules, and their cables connected to the micro station's digital data logger which were also programmed to record at 5-minute summary intervals throughout the day (between 06:00 and 18:00). All data loggers have been presented to record various input data from all measuring devices with a summary interval of 5 minutes. All data loggers have been preset to record various input data from all measuring devices with a summary interval of 5 minutes as shown in Fig. 3.
Figure 3.
Measuring devices used for obtaining data used for analysis.
2.4. Data collection and analysis
The instruments for collecting the data measured during the research were all connected to the 4-channel micro-digital or analog 4-channel analogs. The loggers then have USB connectors to connect to a laptop to download previously recorded data. Therefore, weekly, the recorded data for the data loggers were downloaded and their memories checked to ensure that they were not full. Once the memories were filled in, they were quickly emptied and re-entered after careful synchronization with the timer's interval of the loggers. The downloaded data was subsequently formatted in Microsoft Excel into more comprehensible formats and headings and then entered into the relevant software for analysis and results. IBM SPSS version 22 software was used for data integrity testing, analysis, and modeling. Many models have been stimulated based on the exact fittings and application of dependent and independent parameters.
2.5. Descriptive statistics of input and output parameters
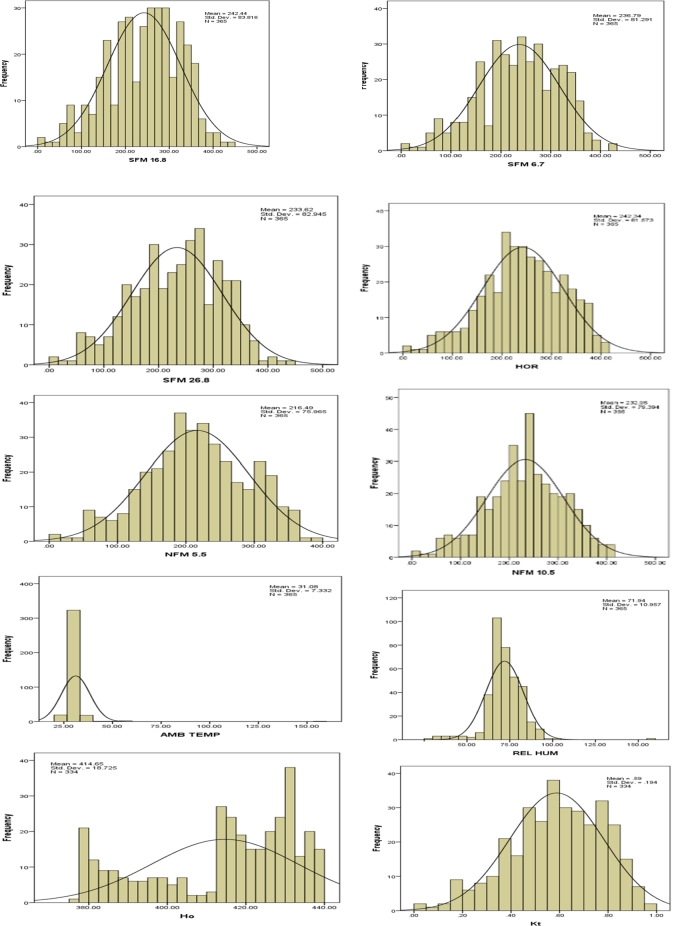
In this study, the methodology used to obtain data sets such as monthly mean H, output voltage (Vout), output power (Pout) for south-facing modules (SFM) (inclined at 6.7° for module 3, 16.8° or for module 4 and 26.8° or - module 5), north-facing modules (NFM) (inclined at 5.5° or for module 1 and 10.5° or module 2) and module 6 mounted horizontally at Lagos, as well as other measured parameters and data sets such as monthly mean RH and T are tabulated in Table 2 and graphically shown in Fig. 4. The monthly averages Ho and kt are evaluated using the equation (1) - (4) and their numerical description is presented equally in Table 2 and Fig. 2.
| (1) |
| (2) |
Table 2.
Monthly average H and other parameters at various tilts and orientations.
| Orientation | Tilt Angle | N | Minimum | Maximum | Mean |
|---|---|---|---|---|---|
| Monthly average H at various tilts and orientations | |||||
| SFM | 6.7 | 12 | 89.73 | 155.74 | 114.7583 |
| SFM | 16.8 | 12 | 88.39 | 158.58 | 123.0883 |
| SFM | 26.8 | 12 | 83.37 | 158.30 | 116.2667 |
| Horizontal | 0.0 | 12 | 92.39 | 145.80 | 116.1900 |
| NFM | 5.5 | 12 | 84.39 | 152.36 | 117.7375 |
| NFM | 10.1 | 12 | 89.51 | 161.78 | 120.9325 |
| Monthly average Vout at various tilts and orientations | |||||
| SFM | 6.7 | 12 | 4.11 | 8.32 | 6.1233 |
| SFM | 16.8 | 12 | 7.01 | 12.87 | 10.6067 |
| SFM | 26.8 | 12 | 5.31 | 9.41 | 6.6358 |
| Horizontal | 0.0 | 12 | 2.08 | 6.10 | 4.2992 |
| NFM | 5.5 | 12 | .09 | 2.73 | 2.1675 |
| NFM | 10.1 | 12 | 2.31 | 3.67 | 2.9667 |
| Monthly average Pout at various tilts and orientations | |||||
| SFM | 6.7 | 12 | 19.66 | 66.25 | 15.7425 |
| SFM | 16.8 | 12 | 11.28 | 35.42 | 45.8642 |
| SFM | 26.8 | 12 | 1.73 | 14.88 | 18.0942 |
| Horizontal | 0.0 | 12 | .00 | 2.98 | 8.0283 |
| NFM | 5.5 | 12 | 2.13 | 5.39 | 2.0675 |
| NFM | 10.1 | 12 | 19.66 | 66.25 | 3.5950 |
| Monthly average kt at various tilts and orientations | |||||
| SFM | 6.7 | 12 | .22 | .40 | .2817 |
| SFM | 16.8 | 12 | .21 | .41 | .3000 |
| SFM | 26.8 | 12 | .20 | .40 | .2842 |
| Horizontal | 0.0 | 12 | .21 | .37 | .2825 |
| NFM | 5.5 | 12 | .20 | .39 | .2850 |
| NFM | 10.1 | 12 | .22 | .38 | .2933 |
| Monthly average T, RH and Ho | |||||
| Parameter | Temperature (T) | 12 | 26.86 | 30.32 | 28.6325 |
| Parameter | Relative humidity (RH) | 12 | 69.13 | 85.83 | 78.4367 |
| Parameter | Extraterrestrial | 12 | 377.14 | 433.29 | 413.1433 |
| Radiation (Ho) | |||||
Figure 4.
Frequency distribution of monthly mean values of measured and calculated input parameters.
| (3) |
| (4) |
where all symbols retain their usual meaning.
2.6. Model development with experimental datasets
2.6.1. Monthly mean optimum tilt angles
The data sets obtained were divided into two categories. The first group consisted of data obtained from 3 SFMs and horizontally mounted modules. Whereas, the second group of datasets was generated by the two NFM solar models. These datasets were used to develop generalized empirical models for estimating optimal lean angles in Lagos, as shown in Table 3. These datasets were applied to test the developed generalized modules. Eight generalized empirical models were developed using data obtained from three SFMs and one horizontally skewed. Using a statistical confidence level of 95%, IBM SPSS statistical software was employed to generate the regression coefficients at an angle of 3°. This was used because it was initially anticipated that about fifteen solar photovoltaic modules tilted at various angles ranging from 0° to 30° would be used in the research. This is because the optimal tilt angle within the geographic location of the search was not expected to vary beyond this range of values. However, only six solar modules were ultimately used due to the cost of the panels and other associated instrumentation networks required. Two of the modules were tilted north, one was installed horizontally, while the remaining three were tilted at various angles within the variation of the expected south-facing tilt angle. Consequently, following the previous intention of having fifteen panels to cover the inclined angles from 0° - 30°, an extrapolation of the inclination angles in steps of 3° covering 3° - 30° was made to cover the angles that the solar modules are not available, they should have covered. Therefore, the inclination angles incorporating south-facing sloped modules such as 6.7°, 16.8°, and 26.8° were used together with the theoretically and realistically extrapolated inclination angles in the range of 0° to 30° (i.e. in steps of 3°). These were used as a dependent variable for the training datasets. Meanwhile, lean angles were employed that incorporate north-facing skewed modules such as 5.5° and 10.1° with the corresponding optimum lean angle extrapolated between 0° and 30° as a dependent parameter for testing the data sets. Monthly, climate parameters such as H, N, δ, T and RH were used as the independent variables for the training datasets incorporating climate parameters for south-facing sloped panels at 6.7°, 16.8°, and 26.8°, validating datasets incorporating climate parameters for North-facing sloped modules such as 5.5° and 10°. The implicit climatic and meteorological empirical models stimulated the evaluation of Lagos and other stations with similar latitudinal orientations.
Table 3.
Monthly mean empirical models for estimating optimum tilt angles in Lagos, Nigeria.
| S/N | Parameters | Regression Relations | Model |
|---|---|---|---|
| 1 | β,H,Ho,n,δ | β = −2.214 − 0.009(H)+0.015(Ho)+0.079(n)+0.014(δ) | M1 |
| 2 | β,H,n,δ | β = 4.998 − 0.018(H)+0.080(n)+0.021(δ) | M2 |
| 3 | β,H,n,δ,kt | β = 4.131 + 0.044(H)+0.080(n)−0.010(δ)−22.559(kt) | M3 |
| 4 | β,H,n,δ,kt,RH | β = 3.460 + 0.041(H)+0.079(n)+0.010(δ)−21.475(kt)+0.009(RH) | M4 |
| 5 | β,H,n,δ,kt,T | β = −29.085 + 0.016(H)−0.283(n)−0.661(δ)−12.379(kt) | M5 |
| 6 | β,n,δ,Ho | β = −5.102 + 0.079(n)+0.014(δ)+0.020(Ho) | M6 |
| 7 | β,n,δ,Ho,kt | β = 0.899 + 0.080(n)+0.013(δ)+0.009(Ho)−5.556(kt) | M7 |
| 8 | β,δ,n,kt | β = 5.084 + 0.080(δ)+0.016(n)−8.036(kt) | M8 |
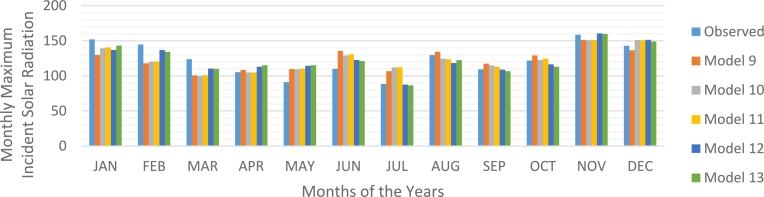
2.6.2. Monthly average HT
To develop regression models for the evaluation of the monthly mean HT for Lagos, Nigeria, the experimental training datasets of the monthly mean HT for the solar module 3 inclined at an angle were taken as target values (dependent variable) of 16.8° facing south. Other predictors such as the monthly mean H, Ho, kt, T, and RH were used as independent variables as presented in Table 4. The monthly mean kt (dimensionless parameter) and Ho on the horizontal surface in W/m2 are as indicated in the equations 1 - (4). Climate datasets such as monthly mean H, Ho, kt, T, RH and obtained from the NASA database [49] for Lagos, Nigeria, geographic coordinates were applied to validate the developed models.
Table 4.
Meteorological regression expressions for evaluating HT in Lagos, Nigeria.
| S/N | Parameters | Regression Relations | Model |
|---|---|---|---|
| 1 | HT,H | HT = 12.778 + 0.949(H) | M9 |
| 2 | HT,H,kt | HT = 49.157 − 0.741(H)+566.656(kt) | M10 |
| 3 | HT,H,Ho,kt | HT = 203.120 + 0.09(H)+195.989(kt)−0.353(Ho) | M11 |
| 4 | HT,H,Ho,kt,T | HT = 143.665 − 0.121(H)+457.007(kt)−0.3451(Ho)+0.125(T) | M12 |
| 5 | HT,H,Ho,kt,T,RH | HT = −906.628 − 3.108(H)+1838.411(kt)+1.713(Ho)+8.754(T)−1.109(RH) | M13 |
2.7. Theoretical model for estimating yearly optimum tilt angles
Theoretical models have also been developed to evaluate the optimal tilt angle for low- and high-latitude locations in both the northern and southern hemispheres of Earth. It has been established that the hour angle at sunrise and sunset for SFM in the Northern Hemisphere (degrees) is given mathematically and geometrically as:
| (5) |
When HT for a photovoltaic module is about the H for low latitude locations close to the equator, given in equation (6) is equally about for photovoltaic installed H for SFM in the Northern Hemisphere expressed by equation (5).
| (6) |
Hence, equating equations (5) and (6) gives:
| (7) |
But from trigonometric functions,
| (8) |
Substituting equation (8) into (7) gives equation (9)
| (9) |
| (10) |
| (11) |
Hence, Equation (10) is the theoretical model developed for evaluating β under low latitude locations (ϕ) () on Earth using only latitude as an input parameter as presented in Table 5. To simulate β a model applicable for locations farther from the equator on either Northern or Southern Hemisphere across the globe, boundary conditions were set up according to latitudinal (ϕ) classification as follows:
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
These boundary conditions were established because since any geographic location tends toward the North or South pole from the equator, the optimum angle of inclination tends to take on the actual latitude value of that location. These generalized models (equation (10)-(16)) were currently employed in this research to evaluate the optimal tilt angle for 37 metropolitan cities in Nigeria. Next, the optimal tilt angles evaluated for metropolitan cities in Nigeria were used as a dependent variable to establish two different linear models based on the latitude of the locations and elevation from sea level for the same locations as the independent variable for the sets of training data for two years or annual models for 37 metropolitan cities in Nigeria. Furthermore, Liu and Jordan's [50] model for estimating optimal tilt angles was equally used to validate the annual models developed using the dataset (global solar radiation) downloaded from NASA websites [49] for the Nigerian metropolitan cities by applying equations (1) - (4) and (17) - (24) as shown in Table 5. Theoretically, HT is given as:
| (17) |
where the monthly mean total incident solar radiation, the direct component of the solar radiation, the diffuse component of the solar radiation, the reflected component of the solar radiation.
Table 5.
Theoretical models for estimating yearly optimum tilt angles.
| S/N | Parameters | Regression Relations | Model |
|---|---|---|---|
| 1 | β,ϕ | β = 5.882 + 0.624(ϕ) | M14 |
| 2 | β,ϕ,h | β = 5.980 + 0.836(ϕ)+0.02(h) | M15 |
where h is the elevation.
β can be generated by differentiating equation (17) with respect to β, thereafter, expressing the equation in terms of zero so as to evaluate β as shown below:
| (18) |
The monthly mean direct normal irradiation (Hb) falling on the inclined surface is mathematically given as Liu and Jordan [50]:
| (19) |
The following relation was used to calculate the angle of declination Cooper [51]:
| (20) |
For SFM like Nigeria, , the value of beam conversion factor (Rb) is expressed as Liu and Jordan [50]:
| (21) |
| (22) |
The HD at the inclined surface is given by Erbs et al. [52]:
| (23) |
The HR on the inclined surface is given as:
| (24) |
where ρ is the ground reflectivity represented as 0.2 [53].
Thus, HT was evaluated using equation (17) for β.
2.8. Models for estimating yearly maximum incident solar radiation
To develop theoretical models for estimating the maximum incident solar radiation for 37 metropolitan cities in Nigeria, the derived optimal inclination angles for the various metropolitan cities in Nigeria were used to evaluate the empirical models of Liu and Jordan [50]. The resulting values were set as target values (dependent variable), while other predictors such as H, Ho, kt, ϕ, and h were used as independent variables as presented in Table 6. The maximum incident solar radiation values originally obtained using the models Liu and Jordan [50] were employed to test the newly established models.
Table 6.
Models for estimating yearly maximum incident solar radiation (HT).
| S/N | Parameters | Regression Relations | Model |
|---|---|---|---|
| 1 | HT,H | HT = −21.310 + 1.167(H) | 16 |
| 2 | HT,H,HO | HT = 235.791 + 1.120(H)−0.599(HO) | 17 |
| 3 | HT,H,kt | HT = −14.250 + 0.333(H)+330.139(kt) | 18 |
| 4 | HT,H,ϕ | HT = −6.083 + 1.049(H)+1.231(ϕ) | 19 |
| 5 | HT,H,ϕ,kt | HT = −5.888 + 0.500(H)+0.846(ϕ)+231.867(kt) | 20 |
| 6 | HT,H,ϕ,HO | HT = 207.117 + 1.058(H)+0.716(ϕ)−0.511(HO) | 21 |
| 7 | HT,H,ϕ,HO,h | HT = 182.214 + 1.043(H)+0.141(ϕ)−0.440(HO)+0.014(h) | 22 |
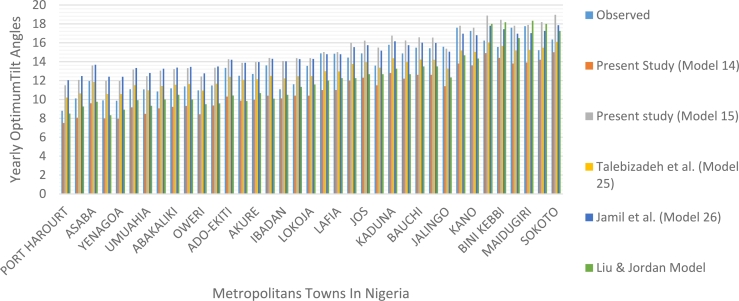
2.9. Comparison between the derived models for optimum tilt angle and those from literature
The two theoretical linear models established as presented in Table 5 were used to test and compare their workability with two linear models developed for Iran and India in the literature by applying statistical metrics presented in Table 7. This technique was used by evaluating the four linear models in 37 metropolitan cities of Nigeria, to establish the best performing model.
Table 7.
Comparison between the derived models for optimum tilt angle and those from literature.
2.10. Performance evaluation
In statistical modeling, performance evaluation can only be achieved by using statistical metrics to determine the influence of impact parameters on dependent variables. Therefore, statistical metrics such as mean bias error (MBE), mean percent error (MPE), mean squared error (RMSE), relative mean squared error (RRMSE), coefficient of determination (r2), and overall performance index were applied to calculate the variations between the measured and the estimated parameter for different empirical and theoretical models developed about HT and β for Lagos and Nigeria in general, as outlined in the procedures found in Jamil et al. [54] and on Table 8.
Table 8.
Details of the statistical tests.
| S/N | Abbreviation | Statistical test | Expression | Ideal value |
|---|---|---|---|---|
| 1. | MBE | Mean bias error | Zero | |
| 2. | MPE | Mean percentage error | Zero | |
| 3. | RMSE | Root mean square error | Zero | |
| 4. | RRMSE | Relative root mean square error | Zero | |
| 5. | R2 | Coefficient of determination | One | |
| 6. | GPI | Global performance indicator [55], [56] | Negative to positive |
2.11. Energy gain/loss assessment
Mathematically, the gain/loss percentage is the global solar radiation availability of the solar PV module or any inclined collector with an optimal tilt angle on the horizontally mounted PV module and is evaluated using equations (25) and (26) below:
| (25) |
| (26) |
2.12. Global radiation solar assessment
The global radiation index (GRI) is the fraction between HT (maximum incident solar radiation) and H (global solar radiation on the horizontal surface) minus one at a particular position expressed mathematically in equation (27) given below as:
| (27) |
| (28) |
| (29) |
| (30) |
3. Results and discussions
3.1. Diurnal and seasonal changes in 5 mins global solar irradiance
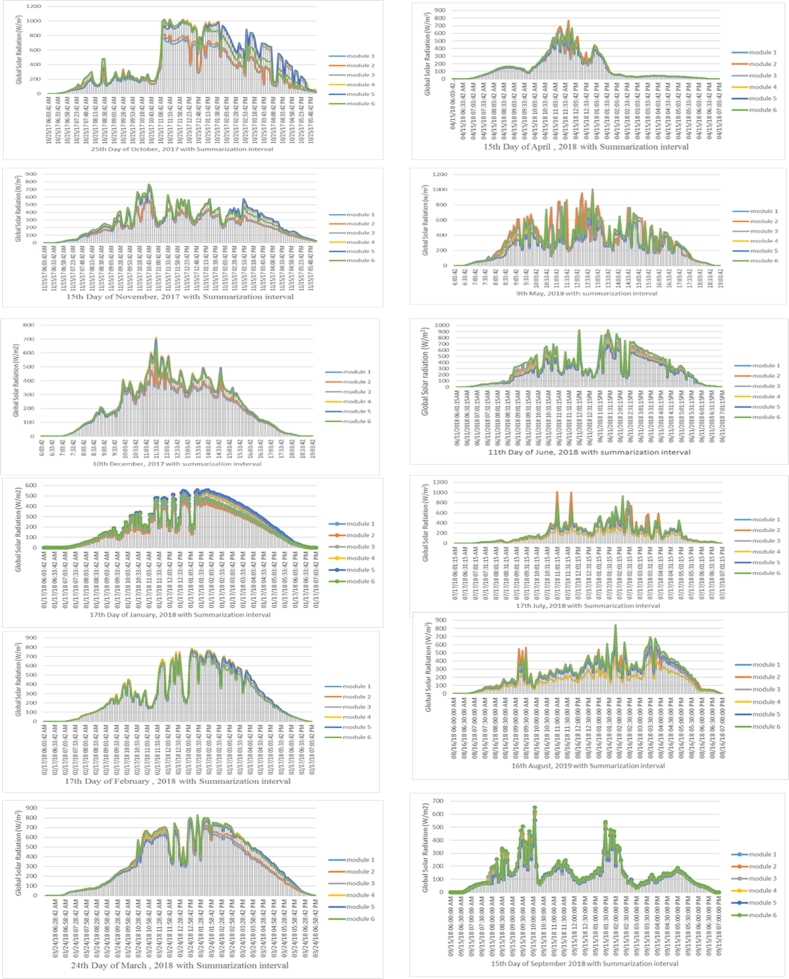
Fig. 5 presents the diurnal fluctuations of global solar irradiance over 5 minutes of internal summary under different inclination angles ranging from 0 - 1010 W/m2 in October, 0 - 880 W/m2 in November, 0 - 710 W/m2 in December, 0 - 565 W/m2 in January, 0 - 800 W/m2 in February, 0 - 820 W/m2 in March, 0 - 780 W/m2 in April, 0 - 1100 W/m2 in May, 0 - 920 W/m2 in June, 0 - 1000 W/m2 in July, 0 - 840 W/m2 in August, 0 - 660 W/m2 in September, 0 - 797.5 W/m2 in the dry season, and 0 - 883.3 W/m2 in the rainy season. This indicates that the mono-crystalline solar modules applied in this study are meteorologically and climatologically suitable to generate enormous solar energy within the Lagos environment as all modules produced over 800 W/m2 with a 5 minute summary throughout the year despite the humid nature of the Lagos environment and regardless of the tilt angles and orientation applied. From the general trend of distribution, global solar irradiance has maintained similar production, trends, and amplitude at different angles of inclination, months, and seasons of the year. The north-facing modules (1 and 2) monotonously produced around 200 W/m2 below the south-facing modules (3, 4, and 5) as well as module 6 mounted horizontally in October which represents one of the hottest periods in the dry season. This indicates that it is optically and meteorologically inadequate to orient the solar photovoltaic modules facing the Northern Hemisphere in October in Lagos.
Figure 5.
Fluctuation of global solar irradiance based on five minutes summarization interval on the 15th Day of September, 2018 at varying tilt angles (module 1 for 5.5°, module 2 for 10.1°, module 3 for 6.7°, module 4 for 16.8°, module 5 for 26.8°, and module 6 for 0.00°). Where module 1 and 2 are north facing panels whereas modules 3 – 5 are South-facing and module 6 is horizontal panel.
The 5-minute monthly mean diurnal fluctuation in global solar irradiance approached its maximum/minimum values (i.e. increase/decrease in amplitude) during sunrise or sunset for most months (October - February, April - September) as shown in Fig. 5. The daily fluctuations defined from June to September are evident in particular the month of August which represents the wettest period. Solar irradiance peaked in the morning and gradually decreased to a minimum towards solar noon (around 13:00 local station time (LST)), then gradually increased in the afternoon. This could be due to constant rainfall towards solar noon within the month which attenuates global solar irradiance. The maximum global solar irradiance was obtained for each month for various inclination angles towards solar noon representing 12:00 and 13:00 LST except for the months of November (reported at 10:18 LST) and October (recorded at 10:00 am LST). Meanwhile, September and November were recorded at around 10:30 and 11:30 LST respectively. The slight variations in these months could be attributed to conventional cloudiness, which usually occurs around solar noon and disappears in the afternoon. These results correspond to the results obtained in Ilorin, Nigeria [57], Lagos, Nigeria [58], Germany [59], Cairo, Egypt [60], Palestine [61]. From Fig. 5, it can be seen that from January to March and from October to December, when the sky was less cloudy and the Harmattan dust wave was starting, the amplitudes of the fluctuations are greater, while the smaller amplitudes occurred in April to September characterized with relative heavy cloudy and turbid months characterized due to abundant of rainfall within the period. Overall, the highest solar fluxes in Nigeria occurred in November, while the lowest solar fluxes occurred in July/August, as predicted for the southwestern region of Nigeria [57], [62].
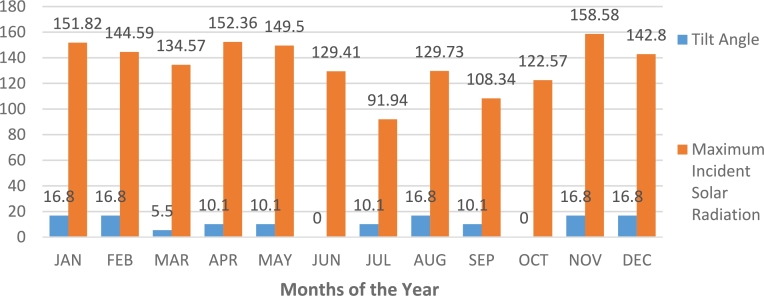
Based on the monthly and seasonal characterization, module 4 inclined at 16.8° facing south, recorded the highest solar fluxes of global solar irradiation during the months of the dry season (from October to December, and from January to February). This indicates that the optimal tilt angle for Lagos, Nigeria is approximately 16.8° as it produces the highest global solar irradiation in addition to other angular positioning and orientations employed in this study. However, a closer look at Fig. 5 reveals that module 6 installed horizontally (0.00 °) recorded the highest global solar irradiation in the wettest months of the rainy season (June, August, and September). It can also be seen that modules 1 and 2 tilted at 5.5° and 10.1° (modules facing north) reported the highest global solar irradiation respectively from March to May, when the sky was moderately foggy, cloudy, and the spell of the rainy season was just setting. This indicates that during these months (March, April, and May), as the earth rotates around the sun, the modules installed in the north are prone to receive more global solar radiation than the modules installed facing the south. Therefore, during the peak rainy seasons, solar installers are advised to install the modules horizontally (zero tilt angle) to receive the maximum global solar radiation for electricity generation. On an annual time scale, module 4 (16.8°) produced the highest global solar irradiation (123.09 W/m2) despite the numerous angular positioning and orientations employed in this study. This suggests that solar installers are advised to mount photovoltaic modules up to approximately 16.8° to achieve the maximum fluxes of global solar irradiation falling on the modules to generate electricity in Lagos, Nigeria.
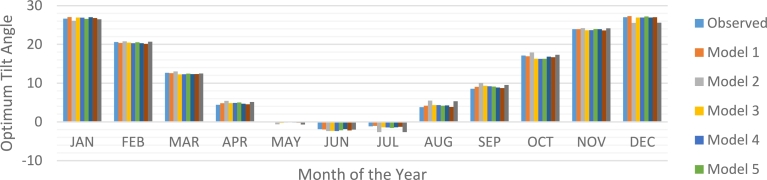
3.2. Monthly optimal tilt angle and orientation of solar modules in Lagos, Nigeria
The research involved six solar modules oriented in various directions and at different angles. Apart from module 6 which was positioned horizontally (0°), modules 1 and 2 were tilted respectively 5.5° and 10.1° north-facing (NFM), while modules 3, 4, and 5 south-facing (SFM) were inclined 6.7°, 16.8° and 26.8° respectively. Table 9 and Fig. 6 show the orientations, inclination angles, and modules having the maximum average levels of global solar irradiation (H) received by the listed modules. Analysis of Table 9 shows that module 4 received the highest H for January, February, August, November, and December. Module 2 (10.1° tilted) also received the highest irradiation in four months (April, May, July, and September) compared to the other modules. Module 1 (inclined at 5.5°) received the maximum irradiation in March while module 6 positioned horizontally recorded the maximum H in June and October. Module 4 recorded the maximum H in August despite still being in the peak of the rainy season in Nigeria, which could be attributed to the “August break (in Nigerian context)” (season in which the intensity of H is relatively higher in the last weeks of the month, while heavy rainfall usually occurs in the first two weeks of the month).
Table 9.
Optimum tilt angle (degrees) and maximum incident solar radiation (W/m2) at various orientation for 21st day of every month in Lagos, Nigeria.
| Month | Day of the month (n) | Solar Declination | Position of the Sun | Tilt Angles | Orientation | Radiation Level |
|---|---|---|---|---|---|---|
| JAN | 21 | −20.13 | From the tropic of Capricorn | 16.8 | SFM | 151.82 |
| FEB | 21 | −11.21 | From the tropic of Capricorn | 16.8 | SFM | 144.59 |
| MAR | 21 | 0.02 | At the equator | 5.5 | NFM | 134.57 |
| APR | 21 | 11.95 | Towards the tropic of Cancer | 10.1 | NFM | 152.36 |
| MAY | 21 | 20.35 | Towards the tropic of Cancer | 10.1 | NFM | 149.50 |
| JUN | 21 | 23.34 | At the tropic of Cancer | 0 | Horizontal | 129.41 |
| JUL | 21 | 20.23 | Towards the equator | 10.1 | NFM | 91.94 |
| AUG | 21 | 11.38 | Towards the equator | 16.8 | SFM | 129.73 |
| SEP | 21 | −0.63 | At the equator | 10.1 | NFM | 108.34 |
| OCT | 21 | −12.13 | Towards the tropic of Capricorn | 0 | Horizontal | 122.57 |
| NOV | 21 | −20.65 | Towards the tropic of Capricorn | 16.8 | SFM | 158.58 |
| DEC | 21 | −23.44 | At the tropic of Capricorn | 16.8 | SFM | 142.80 |
Optimum tilt angle and maximum incident solar radiation at various orientation (SFM represents the South facing module, NFM stands for North facing module) for 21st day of every month in Lagos, Nigeria.
Figure 6.
Optimum tilt angle (in degrees) and maximum incident solar radiation (in W/m2) at various orientation for 21st day of every month in Lagos, Nigeria.
It can be seen that module 4 received a higher intensity level of H in the dry season months and at the peak of the dry season. This is due to the position of the sun lying at the Tropic of Capricorn and towards the equator, while modules 1 and 2 (5.5° and 10.1°) received the maximum (HT) in March, April, May, July, and September due to the position of the sun - towards the Tropic of Cancer at the equator as shown in Table 9 and Fig. 6. This could also be attributed to the position of the sun - towards the Tropic of Cancer and the Equator. According to the general rule, solar modules located in the northern hemisphere should face south (towards the equator) and vice versa. However, Table 9 shows that the north-facing modules mostly recorded radiation in the rainy season (March - October). This fact contradicts the initial statement of the “rule of thumb” [63], [64]. Therefore, for better energy production in Lagos during the rainy season, the solar modules must be oriented towards the north. However, this may not be feasible if fixed year-round solar modules are planned. Energy loss from SFM in the rainy season can be increased by adding a few more solar modules facing south. The seasonality experienced in Lagos is attributed to the fact that the Earth is tilted by 23.45° with a corresponding rotation along its axis and around the sun. The declination angle, therefore changes more or less this numerical value (23.45°). From Table 9, it can be seen that only at the spring and autumn equinoxes δ is recorded zero.
3.3. Modeling and analysis of the global radiation index
From the classical theory of the orientation of the solar module about the position of the Sun anywhere on Earth to obtain the maximum incident solar radiation, the solar module cannot be placed facing East or West due to the rising and setting of the Sun. By convention, the Sun rises from the east in the morning at an initially low-frequency angle relative to Earth. The intensity of radiation received by the solar module is extremely minimal at this inclination. However, as the distance of daylight from the Sun and the Earth that orbits it constantly increases, the Sun reaches its antenna or aerial position between noonday and 1:00 LST. During this period, solar radiation is directly perpendicular to the solar module. However, because the solar modules are classically oriented in a north or south direction, depending on the location (northern or southern hemisphere). At any time from the first shift to the time the sun sets in the afternoon, the solar modules are constantly exposed to solar radiation as if they were facing east or west where it is only between 6:00 LST and 12:00 LST that the sun can receive solar radiation modules. By the time the Sun crosses around 12.00-13.00 LST to the other side moving backward, only the retrospective solar module can receive radiation and those facing east will no longer receive solar radiation. However, this is not the objective of solar energy installers when orienting or positioning solar modulators to receive solar radiation during the day without any type of obstruction, shading, or limitation in terms of solar exposure.
However, if the solar modules are oriented north or south, regardless of sunrise and sunset, the solar modules are exposed to solar radiation during the day. For example, in the morning when the sun rises, the frequency angle of the sun is very low. As the length of the day increases, so does the angle of incidence of the sun. That is why the frequency angle of the sun is almost perpendicular towards noon. For example, an object placed in an open field, that is, without shading effect, the shadow is often cast in the opposite direction. As the length of the day increases or when the sun rises, the shadow overlaps the object. When the sun is just perpendicular to the object, the image will be completely superimposed on the object. But the moment the sun crosses in the other direction, the image is projected back onto the object. The trend will continue until sunset. Therefore, to guarantee the maximum incident solar radiation anywhere on Earth. By convention, the module should be oriented to the south or north depending on its location about the northern or southern hemisphere.
According to this classical theory of solar radiation, the module must be oriented towards the equator. For locations in the Northern Hemisphere, the solar modules must face south to face the equator. Also, for the location in the Southern Hemisphere, the solar modules must be oriented north to face the equator to ensure maximum incident solar radiation generated by the solar modules. This is why different positions of the Earth receive different intensities of solar radiation simply because solar radiation is at its peak at the equator. That is, the sun's rays hit the earth's surface more directly at the equator. The wider the position from the equator, the less intense the solar radiation generated by the solar collectors. Therefore, the variation in the intensity of solar radiation is extended in different locations and seasons of the year as the earth rotates around the sun. Conventionally, since the sun's rays strike obliquely, the illuminated surface is less hot. The more the rays are focused, the more energy the surface receives, and the hotter it is, the less the rays are focused, the less energy the surface receives, and the colder it is. Therefore, since solar radiation is concentrated on a smaller surface, it causes warmer temperatures, culminating in more solar PV power generated by the solar module. At higher latitudes, the solar irradiation angle is smaller, which culminates in the energy being distributed over a larger surface and colder temperatures, resulting in less solar PV output power generated by the solar modules. This is also why locations in the northern hemisphere receive the maximum solar intensity of the sun's rays, while the maximum solar intensity decreases towards the southern hemisphere.
However, due to the seasonal and anthropological impact on the variation of solar radiation, as well as its overall effect in determining the optimal tilt angle of solar modules, the aforementioned classical theory of the orientation of solar modules relative to the position of the sun at any position on Earth differs slightly from the experimental results. Therefore, the authors developed a new model known as the global radiation index (GRI) to estimate and analyze solar radiation for modules tilted at certain angles to receive the maximum incident solar radiation.
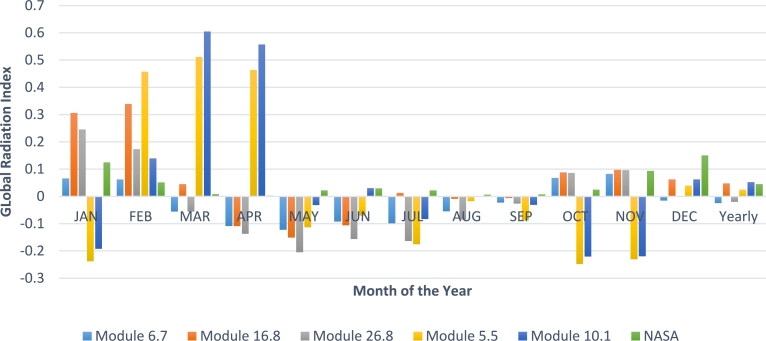
The GRI varies from month to month and from season to season as assessed using the experimental results of this study presented in Table 10. GRI varies from negative values to less than or equal to one, expressed as 0 < GRI ≤ 1. GRI is the ratio of HT (on a sloped or inclined surface at the optimal inclination. Mathematically, HT can be expressed as the fraction of optimal H on a sloped surface to H on the horizontal surface at all-sky conditions minus one at a particular location. This is different from the generally known kt which is calculated as the ratio of H to the horizontal plane on top of the atmosphere (Ho). The GRI is also different from the clear sky index (Kc) expressed as the ratio between Hc (H in clear sky conditions) and Ho.
Table 10.
Monthly and annual GRI for numerous modules tilted at various angles as well as comparison with NASA findings.
| Month | Module 3 (6.70) [SFM] | Module 4 (16.80) [SFM] | Module 5 (26.80) [SFM] | Module 1 (5.50) [NFM] | Module 2 (10.10) [NFM] | NASA GRI | NASA (β)/orientation | RH (%) | Conditions for GRI assessment | Concluding Remarks |
|---|---|---|---|---|---|---|---|---|---|---|
| JAN | 0.066185 | 0.305553 | 0.245418 | −0.23801 | −0.19178 | 0.124138 | 310 (S) | 69.13 | + GRI (0 – 1), higher GRI value greater performance, orientation South | NFM & NASA are rejected, SFM accepted in terms of orientation, Module 4 performed best in terms of higher magnitude compared to other SFM |
| FEB | 0.062128 | 0.339214 | 0.172638 | 0.456543 | 0.138543 | 0.050721 | 210 (S) | 76.84 | + GRI (0 – 1), higher GRI value greater performance, orientation North | SFM & NASA are rejected, NFM accepted in terms of orientation, Module 1 performed best in terms of higher magnitude compared to module 2 NFM |
| MAR | −0.05486 | 0.044341 | −0.05486 | 0.511358 | 0.604801 | 0.00772 | 8.50 (S) | 75.26 | + GRI (0 – 1), higher GRI value greater performance, orientation North | SFM & NASA are rejected, NFM accepted in terms of orientation, Module 2 performed best in terms of higher magnitude compared to module 1 NFM |
| APR | −0.10883 | −0.10863 | −0.13662 | 0.463104 | 0.557252 | 0.002704 | 050 (S) | 76.39 | + GRI (0 – 1), higher GRI value greater performance, orientation North | SFM &NASA are rejected, NFM accepted in terms of orientation, Module 2 performed best in terms of higher magnitude compared to module 1 NFM |
| MAY | −0.12186 | −0.1503 | −0.20447 | −0.11243 | −0.03137 | 0.021919 | 14.50 (N) | 75.83 | Module should be mounted horizontally. Otherwise, NASA SFM are accepted in terms of orientation and GRI magnitude | NFM are rejected in terms of orientation, as such Module should be mounted horizontally. Otherwise, NASA SFM are accepted in terms of orientation and GRI magnitude |
| JUN | −0.0918 | −0.10536 | −0.15617 | −0.06943 | 0.030162 | 0.029371 | 170 (N) | 81.09 | + GRI (0 – 1), higher GRI value greater performance, orientation North | SFM are rejected, NFM & NASA are accepted in terms of orientation, Module 2 & NASA datasets performed best in terms of higher magnitude compared to module 1 NFM |
| JUL | −0.09817 | 0.013199 | −0.16378 | −0.17549 | −0.08232 | 0.02227 | 150 (N) | 82.37 | Module should be mounted horizontally or tilted at 2.50 facing south | NFM and SFM are rejected, NASA accepted in terms of orientation, Module should face North titled at 150 |
| AUG | −0.05416 | −0.00862 | −0.08428 | −0.01715 | 0.001361 | 0.005642 | 7.50 (N) | 80.86 | + GRI (0 – 1), higher GRI value greater performance, orientation North | NFM and SFM are rejected, NASA accepted in terms of orientation, Module should face South titled at 7.50 |
| SEP | −0.02244 | −0.00612 | −0.02619 | −0.08722 | −0.03108 | 0.00687 | 2.50 (S) | 85.83 | Module should be mounted horizontally or tilted at 2.50 facing south | NFM and SFM are rejected, NASA accepted in terms of orientation, Module should face South titled at 2.50 |
| OCT | 0.068176 | 0.087654 | 0.085734 | −0.24781 | −0.21989 | 0.024707 | 15.50 (S) | 82.67 | + GRI (0 – 1), higher GRI value greater performance, orientation South | NFM are rejected, SFM accepted in terms of orientation, Module 4 performed best in terms of higher magnitude compared to other SFM |
| NOV | 0.082136 | 0.097196 | 0.09612 | −0.23035 | −0.21944 | 0.093273 | 280 (S) | 77.71 | + GRI (0 – 1), higher GRI value greater performance, orientation South | NFM are rejected, SFM accepted in terms of orientation, Module 4 performed best in terms of higher magnitude compared to other SFM |
| DEC | −0.01474 | 0.061744 | −0.00017 | 0.038991 | 0.062146 | 0.150514 | 33.50 (S) | 77.26 | + GRI (0 – 1), higher GRI value greater performance, orientation South | NFM and SFM are rejected, NASA accepted in terms of orientation, Module should face South titled at 33.50 |
| Yearly | −0.02402 | 0.047489 | −0.01889 | 0.024342 | 0.051531 | 0.044472 | 070 (S) | 78.43667 | Module should face North | SFM & NASA are rejected in terms of orientation. Module should face North titled at 10.10 or 11.480 obtained using theoretically determined optimum tilt angle for Lagos |
The essence of developing the GRI model (equation (28)) is to ascertain and validate the classical theory of the orientation of solar modules concerning the position of the sun anywhere on the Earth to receive the maximum incident solar radiation. This is because once a solar module is oriented incorrectly, reception of the maximum incident solar radiation can never be achieved during daylight. The GRI is also developed to determine the gain or loss of solar radiation by a given solar module relative to the global solar radiation at the horizontal surface. This indicates that the higher the GRI numerical values, the higher the PV output power received. Statistically, as the GRI takes negative and positive values, it, therefore, indicates that PV solar module installers can easily apply the formula to detect and determine the actual optimal tilt angle of a location when multiple solar modules with very tilt angles are used for field measurement in the absence of first-hand knowledge of the optimal angle of inclination of the location or to validate the classical theory of the orientation of the solar modules concerning the position of the sun in the location of study.
Accurate knowledge and understanding of the HT intensity obtained from a particular module are of the utmost importance for solar energy installers to generate the maximum incident solar radiation of the solar module. This is because GRI is a function of H, optimal angle of inclination (β), the latitude of the location, the position of the sun, and its corresponding angle of incidence to name but a few. As a result, several photovoltaic modules were used to determine the GRI located at numerous north and south-facing slopes on module 6 mounted horizontally. The highest GRI numerical values recorded were 0.604801 in March, 0.557252 in April, 0.031062 in June, 0.001361 in August, 0.150514 in December, and 0.051531 on an annual time scale compared to other modules. Whereas, module 1 NFM tilted at 5.1° produced the highest GRI compared to other modules only in February. This indicates that in the twelve months of the year, and on an annual time scale, the photovoltaic modules should be mounted towards the north from the experimental result obtained in this study.
However, from the GRI numerical value, as assessed by NASA datasets (NASA, 2020), the months April to August yielded 0.00270 for April, 0.021919 for May, 0.029371 for June, 0.02227 for July, and 0.005642 for August for photovoltaic solar modules facing the North Pole during the peak of the rainy season. Comparing the values and orientation of those obtained in this study as shown in Table 10. It can be seen that NASA's orientation corresponds favorably to the classical theory of solar radiation on a seasonal time scale. The experimental result obtained in this study, on the other hand, reveals that they differ slightly in July which reported the highest GRI numerical value (0.013199) for module 4 inclined by 16.8° facing south compared to other modules with different tilt angles and orientation. Additionally, in May, all modules reported negative GRI values regardless of different orientations indicating that the module must be installed horizontally.
It can also be observed that during the peak of the rainy season in Lagos, when global solar radiation is lower due to high relative humidity and other climatic and anthropological factors, as experienced in Beijing (Shen et al., 2018), the GRI obtained from the output of the experimental results (0.557252) surpassed those of the NASA datasets (0.002704) in April. This suggests that the module was suitably oriented and inclined to obtain the optimal solar radiation generated. Considering that in June equivalent values of 0.029371 for the NASA datasets and 0.030162 for the datasets measured in Lagos. This indicates that in June, the optimal tilt angle of the experimental result agreed favorably with the classical solar radiation theory of the orientation and tilt angle of photovoltaic to obtain the maximum incident solar radiation and NASA's predictions.
However, the GRI value of NASA's 0.005642 datasets tilted at 7.5° slightly exceeded those obtained from the NFM module 2 tilted at 10.1° in this study (0.001361) in August. This also indicates that the tilt angle employed for the five sloped modules in this study deviates slightly from the actual optimal tilt angle. Therefore, in August, the module should be oriented towards the south with inclination angles of about 7.5°.
From Table 10, the month of September reported the highest relative humidity of 85.83%, and five modules used in this study had negative GRI numerical values indicating that the module should be mounted horizontally. Given this, NASA's numerical value reported a positive value of 0.00687 and was 2.5° oriented toward the South Pole (equator) as prescribed by classical theory. This is equivalent to the fact that the tilt angle used for the five tilted modules in this study deviates slightly from the actual optimal tilt angle when negative GRI values emerged. Therefore, in September, the module should be oriented towards the south with inclination angles of about 2.5°.
In the months of the dry season which include January, February, March, October, November, and December, the magnitude of the GRI obtained in this study exceeded those reported by the NASA datasets except for December which registered 0.150514 with an optimal inclination of 33.5° compared to 0.062146 reported by module 2 NFM inclined at 10.1°. This could be attributed to a lower optimal tilt angle (6.7° to 26.8°) of the modules mounted in Lagos. Furthermore, it implies that NASA's orientation and optimal tilt angle should be accepted to determine the optimal tilt angle and maximum incident solar radiation in December in Lagos. Therefore, to receive the maximum incident solar radiation for December in Lagos, the solar modules must be mounted at approximately 33.5° towards the South Pole (equator) or facing south.
In November, the GRI numerical value of the experimental result (0.097196) generated in this research with the values measured by NASA (0.093273) reported values close but albeit of opposite orientation. The highest GRI numerical value obtained in this study was reported by the NFM module 2 tilted at 10.1°, while the NASA solar module was tilted at 28° facing south. This indicates that the orientation and optimal tilt angle of the NFM module 2 have significantly adapted the module to receive maximum incident solar radiation.
In February and March, NFM modules 1 and 2 produced higher GRI values than those of SFM modules 3, 4, and 5, as well as NASA datasets by a considerably high margin. During the months of the year, NFM module 2 tilted at 10.1° reported the highest GRI value of 0.604801 followed by 0.456543 reported by module 1 NFM tilted by 5.1° compared to the SFM and NASA datasets. This indicates that the modules were correctly oriented and tilted to receive maximum incident solar radiation, compared to other predicting modules, as well as NASA datasets.
In January, Module 4 SFM tilted at 16.8° reported the GRI 0.305553 higher than other SFMs, the NFM which produced negative GRI, and the GRI value 0.124138 for NASA datasets. This indicates that the module has been mounted about the optimal tilt angle and orientation in the experimentation site (Lagos) for January.
On the annual timescale, Module 2 (NFM) tilted at 10.1° produced the highest GRI value of 0.051531 compared to other modules including NASA's forecast value of 0.044472 mounted at a tilt angle of 7° regardless of orientation and the angles of inclination. The GRI value 0.051531 reported by module 2 indicates that the annual optimal tilt angle for Lagos has slightly exceeded 7° obtained by NASA and less than 16.8° and 26.8° fitted by modules 4 and 5, and exceeded 5.1° reported by the NFM module, but compliant to the theoretically determined value of 11.48° in this study. This indicates that module 3 (6.7°) and module 1 (5.5°) is tilted below the threshold of optimal tilt angles in Lagos, module 5 (26.8°) was tilted far above the optimal inclination angle of Lagos, Nigeria, as determined experimentally (16.8°) and theoretically (11.8°).
From the conditions for assessing the GRI presented in Table 10, it can be concluded that positive GRI values between zero and one are acceptable otherwise reject them. The greater the numerical value of GRI, the more efficient the performance of the photovoltaic system. Negative values during the months of the rainy season connote an inadequate orientation of the photovoltaic system, indicating that only positive GRI values are accepted. Negative GRI values during the months of the rainy season indicate that the modules must be positioned horizontally. However, in others to get positive numerical values and considerably GRI, the modules would be mounted facing the North Pole (equator) and tilted about 10.1°.
On the annual time scale, the module should be mounted facing north regardless of the classic solar photovoltaic orientation theory since module 2 (NFM) recorded higher GRI numerical values on the annual time scale and in six months out of twelve that make up the year. However, to follow the classic theory of solar photovoltaic orientation, the module must be mounted facing south with an optimal tilt angle between 11.48° to 16.8°. In May and September, it is preferable to tilt the modules horizontally as all five modules with different tilt and orientation angles produced negative GRI values. This indicates that the inclination of the modules by a certain angle as well as the change in orientation about the module mounted horizontally did not register any changes observed in increasing the solar radiation gain. Therefore, in these months, the assembly of the modules horizontally will culminate in the maximum incident solar radiation received, with the consequent appreciable energy efficiency of the solar photovoltaic output.
Therefore, from this study, the conditions for the evaluation of the global radiation index and models, as well as its concluding observations employed through the applicability of models 26a to 38a and values from Table 11 to estimate the monthly and yearly maximum incident solar radiation using the experimentally established tilt angle for Lagos, Nigeria, are shown in Fig. 7.
Table 11.
Models for estimating monthly and yearly maximum incident solar radiation employing global radiation index and global solar radiation and comparison with NASA numerical values in Lagos.
| Present Study |
NASA |
|||
|---|---|---|---|---|
| Month | Model # | Model | Model # | Model |
| JAN | 26a | HT = 1.3055(H) | 26b | HT = 1.1241(H) |
| FEB | 27a | HT = 1.4565(H) | 27b | HT = 1.0507(H) |
| MAR | 28a | HT = 1.6048(H) | 28b | HT = 1.0077(H) |
| APR | 29a | HT = 1.5573(H) | 29b | HT = 1.0027(H) |
| MAY | 30a | HT = H | 30b | HT = 1.0219(H) |
| JUN | 31a | HT = 1.0302(H) | 31b | HT = 1.0293(H) |
| JUL | 32a | HT = 1.0132(H) | 32b | HT = 1.0222(H) |
| AUG | 33a | HT = 1.0014(H) | 33b | HT = 1.0056(H) |
| SEP | 34a | HT = H | 34b | HT = 1.0068(H) |
| OCT | 35a | HT = 1.0877(H) | 35b | HT = 1.0247(H) |
| NOV | 36a | HT = 1.0972(H) | 36b | HT = 1.0937(H) |
| DEC | 37a | HT = 1.0621(H) | 37b | HT = 1.1505(H) |
| ANNUAL | 38a | HT = 1.0515(H) | 38b | HT = 1.0445(H) |
Figure 7.
Monthly and annual GRI at numerous tilt angle relative to horizontal installed module 6, and comparison with NASA values.
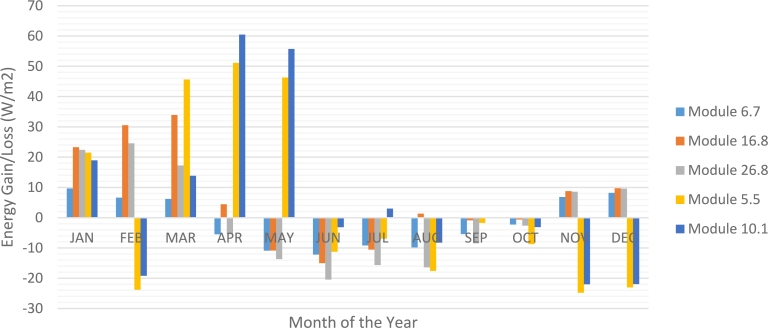
3.4. Energy Gain/Loss by the various tilted modules in Lagos, Nigeria
Generally, H was obtained during the experimentation period for the inclined modules (module 3, module 4, and module 5) at 6.7°, 16.8°, and 26.8° for the south-facing modules and module 1 and module 2 inclined respectively by 5.5° and 10.1° for the north-facing module, the solar radiation acquired/lost on both an annual and monthly basis on the horizontally mounted module 6. Modules 3-5 typically recorded the highest solar energy gain in the dry season months and the dry season peak as shown in Tables 12 and Fig. 8. This could be attributed to the fact that the dry season (winter) often accompanies the low altitude of the sun on the horizontal surface resulting in a wider optimal tilt angle and ultimately culminating in greater availability of solar energy gain. However, during the rainy season, these modules suffered solar energy losses due to the lower value of the optimal tilt angle and the higher altitude of the sun, thus culminating in a greater gain in solar energy availability on the horizontally mounted photovoltaic module about inclined photovoltaic modules. This could be attributed to the higher rainfall, RH, and cloudiness experienced in the rainy period as a result of the high altitude of the sun and angle of incidence on the PV module. This causes a low level of radiation on any solar photovoltaic module or any collector on Earth. In addition, the modules facing north (modules 1 and 2) recorded solar energy losses in all months of the year except for January, March, April, May, July, and September for the 10.1° tilted module (module 2). This may be due to the orientation of the module relative to the location of the measurement site far from the equator. From the data obtained in this research, solar energy installers must install solar photovoltaic modules facing south during the dry season months and facing north for the rainy season monthly, as seen for modules 4, 1, and 2 in Table 12, which yielded an annual solar gain of 6.174428961%, 3.89912995%, and 6.214631096% respectively. It can be seen that module 2 tilted 10.1o facing north reported the highest energy gain, followed by module 4 tilted 16.8o facing south, and finally, module 1 tilted 5.5° facing north. This result obtained from this research is consistent with the yearly average energy of 12.92% for the monthly time scale, 11.61% for the seasonal time scale, and 6.5% for the annual time scale concerning the horizontally fixed module recorded by Jamil et al. [65]. In another study by the same group of researchers, they observed that Jodhpur and Bangalore reported availability of 15.77% of the maximum incident solar radiation based on the optimal monthly tilt angle. A loss of 5.74% for cold weather, 7.49% for composite climate, 6.16% for the hot and dry climate, 4.30% for hot and humid climate, and 4.39% % for temperate climate for an optimal annual inclination with respect to a horizontal surface Jamil et al. [65]. This could be attributed to the fact that Lagos, Nigeria experienced seven months of the rainy season (March to September) compared to five months of the dry season (October to February). This implies that the angle of incidence in these rainy seasons (March to September) is relatively small due to the high altitude of the Sun from the measurement site in Lagos, Nigeria. Solar power installers may need to install north-facing solar photovoltaic modules during the rainy season months and inclined modules at certain angles for the dry season months. How feasible and cheap this is for year-round fixed solar modules is another issue.
Table 12.
Energy Gain/Loss (in MJm2day−1) versus monthly average and yearly optimal angles over horizontally installed module 6.
| Month | Module 3 (6.70) [SFM] | Module 4 (16.80) [SFM] | Module 5 (26.80) [SFM] | Module 1 (5.50) [NFM] | Module 2 (10.10) [NFM] |
|---|---|---|---|---|---|
| JAN | 9.663012586 | 23.28055217 | 22.43605359 | 21.47787251 | 18.95249695 |
| FEB | 6.618510158 | 30.55530474 | 24.54176072 | −23.8013544 | −19.1783296 |
| MAR | 6.212793592 | 33.92142007 | 17.26377314 | 45.65429159 | 13.85431324 |
| APR | −5.48556691 | 4.43408392 | −5.485566908 | 51.13580002 | 60.4801111 |
| MAY | −10.8827559 | −10.86318262 | −13.66216481 | 46.31043257 | 55.72519084 |
| JUN | −12.1860753 | −15.02975041 | −20.44664245 | −11.2433351 | −3.13731551 |
| JUL | −9.18016194 | −10.53643725 | −15.61740891 | −6.94331984 | 3.016194332 |
| AUG | −9.81724461 | 1.319900031 | −16.37769447 | −17.5492034 | −8.23180256 |
| SEP | −5.41594847 | −0.861834346 | −8.427832713 | −1.71459675 | 0.136079107 |
| OCT | −2.24361589 | −0.611895244 | −2.618911642 | −8.72154687 | −3.10842784 |
| NOV | 6.817558299 | 8.765432099 | 8.573388203 | −24.7805213 | −21.9890261 |
| DEC | 8.213599693 | 9.71955436 | 9.61198617 | −23.0349597 | −21.9439109 |
| Yearly | −1.47382456 | 6.174428961 | −0.01743834 | 3.89912995 | 6.214631096 |
Figure 8.
Energy Gain/Loss versus months of the year under various tilt angles over horizontal installed module 6.
However, due to space constraints in the city, most solar modules are installed on roofs, which makes it impossible to adapt to any desired direction at any time of the year. Consequently, the authors believe that solar energy engineers will have to consider a trade-off in installing the solar module to face the North (with a given number of solar modules in consideration of the solar energy already required to be generated by the modules) or to face the south using additional solar modules to provide the same previously determined amount of energy required in the rainy season. Table 12 and Fig. 8 show that modules 3 and 5 (6.7° and 26.8° respectively) facing South have experienced energy losses despite facing South. This is attributable to the fact that module 3 (6.7°) was tilted virtually at Lagos latitude which is far below the experimentally and theoretically determined optimal tilt angles of 16.8° and 11.48° respectively. In addition, module 5 (26.8°) has a much higher value than the experimentally and theoretically determined optimal angles of inclination.
3.5. Analysis of optimum tilt angle and maximum incident solar radiation under Nigeria climate
As presented in Table 13, Nigeria is located in the tropics between latitudes 4° to 14°N and longitudes 3° to 15°E with a corresponding elevation range of 4.06 - 992.55 m according to the metropolitan cities applied in this study. However, the highest attitude in Nigeria is Chappal Waddi at 2,419 m, while the Atlantic Ocean (0 m) is the lowest point. The Niger River and the Benue River are the two distinct rivers that flow through the country and eventually converge at Lokoja (Kogi State) in the Guinea savanna belt (north-central part of the country) and flow into the Niger Delta.
Table 13.
Evaluation of annual optimum tilt angles and maximum global solar radiation in metropolitan towns in Nigeria using Liu and Jordan [50] Isotropy model (L & J), theoretical models – Observed data, model 14 (M14), model 15 (M15), models from literature – Talebizadeh et al. [67] model (M23) and Jamil et al. [54] model (M24). Yearly maximum incident solar radiation and global radiation index with associated evaluation parameters.
| Station | Lat | Long | β Observed | β NASA | β (L&J) [50] | β M14 | β M15 | B M23 [67] | β M24 [54] | H NASA | NASA | (L&J) model [50] | model 38 | model 22 | GRI NASA | GRI Model 38 | GRI Model 22 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Port Harcourt | 4.4 | 7.2 | 8.8 | 4.5 | 8.5 | 7.5 | 11.5 | 10.2 | 12.0 | 172.8 | 179.2 | 177.0 | 178.9 | 179.6 | 0.037 | 0.040 | 0.045 |
| Uyo | 5.1 | 8.0 | 10.1 | 5.5 | 9.3 | 8.1 | 12.1 | 10.6 | 12.5 | 193.4 | 202.1 | 199.9 | 182.2 | 184.2 | 0.045 | 0.041 | 0.053 |
| Asaba | 6.8 | 6.8 | 12.0 | 7 | 9.8 | 9.6 | 13.6 | 11.9 | 13.7 | 197.3 | 207.4 | 204.3 | 207.5 | 210.0 | 0.051 | 0.041 | 0.053 |
| Calabar | 5.0 | 8.3 | 9.9 | 5 | 8.3 | 8.0 | 12.0 | 10.6 | 12.4 | 175.4 | 182.4 | 180.5 | 185.4 | 186.0 | 0.040 | 0.040 | 0.044 |
| Yenagoa | 4.9 | 6.3 | 9.9 | 5 | 8.9 | 8.0 | 12.0 | 10.6 | 12.4 | 169.5 | 175.9 | 174.2 | 177.5 | 177.4 | 0.038 | 0.040 | 0.040 |
| Benin Cty | 6.3 | 5.6 | 11.1 | 6.5 | 9.9 | 9.2 | 13.2 | 11.5 | 13.3 | 191.2 | 200.4 | 198.9 | 201.0 | 202.9 | 0.049 | 0.041 | 0.051 |
| Umuahia | 5.5 | 7.5 | 11.1 | 5.5 | 9.3 | 8.5 | 12.5 | 11.0 | 12.8 | 193.4 | 202.3 | 198.8 | 182.7 | 185.1 | 0.046 | 0.041 | 0.055 |
| Awka | 6.2 | 7.7 | 10.9 | 6.5 | 10.0 | 9.1 | 13.1 | 11.4 | 13.3 | 202.2 | 212.5 | 209.7 | 212.0 | 215.1 | 0.051 | 0.041 | 0.056 |
| Abakaliki | 6.4 | 8.1 | 11.2 | 6.5 | 10.5 | 9.2 | 13.2 | 11.5 | 13.4 | 207.4 | 218.3 | 214.9 | 216.7 | 220.3 | 0.053 | 0.041 | 0.058 |
| Enugu | 6.5 | 7.5 | 11.4 | 6.5 | 10.0 | 9.3 | 13.3 | 11.6 | 13.5 | 202.2 | 212.6 | 209.7 | 212.0 | 215.1 | 0.052 | 0.041 | 0.056 |
| Oweri | 5.5 | 7.0 | 11.0 | 5.5 | 9.5 | 8.4 | 12.4 | 10.9 | 12.8 | 193.4 | 202.3 | 197.2 | 200.0 | 202.0 | 0.046 | 0.041 | 0.051 |
| Lagos | 6.6 | 3.6 | 11.5 | 7 | 9.6 | 9.4 | 13.4 | 11.7 | 13.5 | 195.0 | 204.2 | 201.7 | 204.7 | 206.4 | 0.047 | 0.041 | 0.049 |
| Ado-Ekiti | 7.6 | 5.2 | 13.3 | 8 | 10.4 | 10.3 | 14.3 | 12.4 | 14.2 | 202.7 | 214.3 | 211.9 | 214.7 | 225.2 | 0.057 | 0.040 | 0.092 |
| Abeokuta | 7.2 | 3.3 | 12.5 | 7.5 | 9.8 | 9.9 | 13.9 | 12.1 | 13.9 | 201.5 | 212.2 | 208.0 | 211.0 | 214.8 | 0.053 | 0.041 | 0.060 |
| Akure | 7.3 | 5.2 | 12.7 | 7.5 | 10.7 | 10.0 | 14.0 | 12.1 | 14.0 | 202.7 | 214.0 | 212.1 | 214.7 | 220.4 | 0.056 | 0.041 | 0.068 |
| Osogbo | 7.8 | 4.6 | 13.6 | 8 | 10.1 | 10.4 | 14.4 | 12.5 | 14.3 | 200.8 | 211.9 | 208.2 | 210.7 | 218.0 | 0.055 | 0.040 | 0.077 |
| Ibadan | 7.4 | 3.9 | 11.1 | 7.5 | 10.5 | 10.1 | 14.1 | 12.2 | 14.0 | 201.5 | 212.3 | 209.0 | 211.0 | 215.1 | 0.054 | 0.041 | 0.061 |
| Makurdi | 7.7 | 8.5 | 11.6 | 8 | 11.3 | 10.4 | 14.4 | 12.5 | 14.3 | 213.2 | 226.0 | 223.8 | 223.8 | 227.2 | 0.060 | 0.041 | 0.057 |
| Lokoja | 7.8 | 6.8 | 13.6 | 8 | 11.6 | 10.4 | 14.4 | 12.5 | 14.3 | 209.3 | 221.4 | 219.9 | 219.5 | 224.0 | 0.058 | 0.041 | 0.062 |
| Ilorin | 8.5 | 4.6 | 14.9 | 8.5 | 12.0 | 11.0 | 15.0 | 13.0 | 14.8 | 211.6 | 224.5 | 224.4 | 224.2 | 231.0 | 0.061 | 0.041 | 0.072 |
| Lafia | 8.5 | 8.5 | 14.8 | 9 | 12.3 | 11.0 | 15.0 | 13.0 | 14.8 | 220.4 | 235.0 | 230.8 | 231.3 | 235.5 | 0.066 | 0.041 | 0.060 |
| Minna | 9.6 | 6.6 | 14.4 | 10 | 12.3 | 12.0 | 16.0 | 13.8 | 15.5 | 225.4 | 240.9 | 236.1 | 235.8 | 243.2 | 0.069 | 0.041 | 0.073 |
| Jos | 9.9 | 8.9 | 14.9 | 10.5 | 12.7 | 12.3 | 16.2 | 14.0 | 15.7 | 224.7 | 241.6 | 236.2 | 235.9 | 252.6 | 0.075 | 0.041 | 0.114 |
| Abuja | 9.1 | 7.5 | 13.6 | 9.5 | 12.7 | 11.5 | 15.5 | 13.4 | 15.2 | 224.0 | 239.5 | 401.9 | 234.4 | 242.9 | 0.069 | 0.040 | 0.078 |
| Kaduna | 10.5 | 7.4 | 15.8 | 11 | 13.3 | 12.8 | 16.8 | 14.4 | 16.2 | 231.9 | 249.5 | 246.9 | 246.1 | 257.9 | 0.076 | 0.041 | 0.090 |
| Yola | 9.9 | 11.9 | 14.9 | 10 | 12.7 | 12.2 | 16.2 | 14.0 | 15.7 | 239.7 | 257.9 | 245.8 | 246.2 | 253.0 | 0.076 | 0.041 | 0.069 |
| Bauchi | 10.3 | 9.8 | 15.5 | 10.5 | 13.5 | 12.6 | 16.6 | 14.2 | 16.0 | 236.9 | 254.4 | 252.3 | 253.0 | 264.9 | 0.074 | 0.041 | 0.090 |
| Gombe | 10.3 | 11.2 | 15.4 | 10.5 | 13.5 | 12.6 | 16.6 | 14.2 | 16.0 | 236.9 | 253.7 | 252.5 | 252.8 | 261.5 | 0.071 | 0.041 | 0.076 |
| Jalingo | 8.9 | 11.4 | 15.6 | 9.5 | 12.3 | 11.4 | 15.4 | 13.3 | 15.1 | 228.8 | 245.0 | 238.8 | 235.4 | 241.4 | 0.071 | 0.041 | 0.067 |
| Damaturu | 11.7 | 12.0 | 17.6 | 12 | 14.7 | 13.8 | 17.8 | 15.2 | 17.0 | 244.8 | 263.4 | 261.8 | 259.6 | 269.1 | 0.076 | 0.041 | 0.079 |
| Kano | 11.5 | 8.5 | 17.3 | 12 | 14.3 | 13.6 | 17.6 | 15.0 | 16.8 | 240.7 | 259.0 | 258.6 | 257.0 | 267.7 | 0.076 | 0.041 | 0.084 |
| Kastina | 13.0 | 7.6 | 16.2 | 13.5 | 18.0 | 14.9 | 18.9 | 16.0 | 17.8 | 257.8 | 279.8 | 270.0 | 260.8 | 272.5 | 0.086 | 0.041 | 0.087 |
| Bini Kebbi | 12.5 | 4.2 | 15.6 | 13 | 18.2 | 14.4 | 18.4 | 15.7 | 17.4 | 245.3 | 264.9 | 268.8 | 257.5 | 265.6 | 0.080 | 0.041 | 0.074 |
| Dutse | 11.7 | 9.3 | 17.6 | 12 | 16.5 | 13.8 | 17.8 | 15.2 | 17.0 | 242.1 | 260.4 | 266.2 | 257.9 | 268.1 | 0.076 | 0.041 | 0.082 |
| Maidugiri | 11.8 | 13.2 | 17.8 | 12 | 18.3 | 13.9 | 17.9 | 15.3 | 17.0 | 242.2 | 261.0 | 267.7 | 258.3 | 266.6 | 0.078 | 0.041 | 0.074 |
| Gusau | 12.2 | 6.7 | 15.2 | 12.5 | 18.0 | 14.2 | 18.2 | 15.5 | 17.3 | 246.6 | 266.1 | 270.5 | 261.5 | 272.4 | 0.079 | 0.041 | 0.085 |
| Sokoto | 13.1 | 5.2 | 16.3 | 13.5 | 17.3 | 15.0 | 19.0 | 16.1 | 17.9 | 256.2 | 278.1 | 276.6 | 267.1 | 276.8 | 0.085 | 0.041 | 0.078 |
| Average | 8.5 | 7.4 | 8.78 | 215.7 | 229.4 | 231.5 | 225.4 | 231.7 | 0.063 | 0.041 | 0.070 |
Here β is the optimum tilt angle, ϕ is the latitude of the location and theoretical optimum tilt angle model employed as the observed data were generated using equation (12) – (16), H represents yearly global solar radiation in 37 metropolitan towns in Nigeria, L & J [50] model represents Liu and Jordan model for estimating maximum incident solar radiation, GRI stands for the value of global radiation index obtained using datasets such as global solar radiation with associated values of maximum incident radiation obtained from Liu and Jordan model, model 39 represents maximum incident solar radiation evaluated using model 37, model 22 represents the best performing model for sets of computing models for evaluating HT in 37 metropolitan towns in Nigeria. Ho stands for the yearly extraterrestrial solar radiation in 37 metropolitan towns in Nigeria.
In terms of climatology, the climate and vegetation of the country are dry in the equator, tropical in the south, and dry in the far north. There are two major seasons in the country: the rainy season and the dry season. The dry season often occurs as a consequence of the emergence and influence of the Inter-Tropical Convergence Zone (ITCZ) along with the low altitude position of the sun producing Tropical Continental (TC) accompanied by dry and dusty northeasterly winds. The dry, dusty wind flows through the Sahara Desert, and eventually prevails over the entire country (but with a strong edge over the northern part of the country), thus creating dry weather conditions. Overall, the implication is that there is usually an extended dry season in the far north region of the country while the far south region experiences a short dry season period per year. This results in relatively high global solar radiation reported in the northern region (215 W/m2 to 256 W/m2) from Makurdi to Sokoto as presented in Table 13 and a higher optimal tilt angle (11.60° – 17.75°) on an annual time scale compared to the southern region experiencing lower global solar radiation (17.1 - 202.7 W/m2) and a lower optimal tilt angle as shown in Table 13 and vice versa in the rainy season.
From the theoretically derived model for estimating the optimal tilt angle as presented in equations (12)-(16) using the latitude and elevation of distinct places, the observed datasets were used to calculate the optimal tilt angle for 37 cities in Nigeria performed poorly as presented in Table 13. A close look at Table 13 indicates that as the latitude and altitude of the various localities increase from Port Harcourt (latitude 4.4°N) located in the equatorial ecological zone to Sokoto (latitude 13.07°N) located in the ecological level of the Sahel savannah, the annual optimal tilt angle, HT, H and kt increases as shown in Fig. 9, while the annual Ho decreases.
Figure 9.
Comparison between observed and best performing maximum incident solar radiation (model 12) in W/m2 in Lagos, Nigeria when compared with models in Table 4 and Table 14; Comparison between observed and best performing maximum incident solar radiation (model 17) in W/m2 over 37 metropolitan towns in Nigeria when compared to other models in Table 6 and Table 14; Comparison between observed and best performing optimum tilt angle (model 5) in degrees in Lagos, Nigeria when compared with models in Table 3 and Table 14; Comparison between observed and best performing optimum tilt angle (model 14) in degrees in 37 metropolitan towns in Nigeria when compared with model 15 (present study), Talebizadeh et al. [67], Jamil et al. [54] as presented in Table 7 and Table 14.
Geographically, locations on or near the equator are excepted to receive the highest annual average of global solar radiation HT, H, and Ho such as Port Harcourt - Ibadan (4.4°N - 7.38°N) concerning locations situated farther from the equator such as Makurdi - Sokoto (7.73°N - 13.07°N) as seen in Tables 13. On the contrary, due to the influence of the position of the sun, that is, the higher the altitude of a place relative to the sun, as the Earth rotates periodically in different months and seasons of the year, the lower the angle of incidence between the sun and any solar collectors in the location, thus contributing to the formation of heavy clouds in the lower atmosphere. It is also reinforced by the high rate of evaporation and condensation of large bodies of water located in the southern region. This generally culminates in high relative humidity, a low temperature and a low amount of global solar radiation received, and ultimately leads to a low maximum incident solar radiation and an optimal tilt angle received as seen in Tables 13.
3.6. Performance evaluation
Table 14 summarizes the comparative results of predictions in the eight empirical models for estimating optimal tilt angles using datasets from module 4 tilted to 16.8° with corresponding extrapolated values for the observed or dependent variable, while the monthly average H, Ho, n, δ, kt and T as an independent variable. It is clear that by applying the statistical evaluation techniques of Ertekin and Yaldiz [66] in the form of equations (28 - 41), the accuracy of the capacity of the best model estimated among the eight developed is evaluated. Table 14 revealed that Model 5 emerged as the best performing model due to its relatively small RRMSE values (0.827104%) employing all independent variables for modeling all eight models. This indicates that Model 5 performed excellently and therefore is recommended to estimate the optimal tilt angle in Lagos as shown in Fig. 9, while Model 8 which uses the solar declination, number of days of the features, and the clearness index produced the model with the poorest performance with the corresponding RRMSE values of 195.6545. Therefore, Model 8 is not recommended for estimating the optimal tilt angle in Lagos based on its high RRMSE value.
| (31) |
| (32) |
| (33) |
| (34) |
To validate the statistical relationship of Ertekin and Yaldiz [66], GPI introduced by Behar et al. [55] and Despotovic et al. [56] were equally applied to the eight developed models. Table 14 reveals that model 5 emerged as the highest GPI value by validating that model 5 emerged as the best performing model for evaluating β in Lagos, Nigeria, as shown in Fig. 10.
Table 14.
Scaled and unscaled error parameters for empirical and evaluation of β and HT in Lagos, Nigeria.
| Location | Parameter | statistics | Model | MBE | MPE | RMSE | RRMSE | R2 | GPI | Ranking |
|---|---|---|---|---|---|---|---|---|---|---|
| Lagos | β (evaluating) | Unscaled | model 1 | −0.00672 | 0.404409 | 0.069669 | 27.98666 | 0.989271 | ||
| model 2 | 0.008314 | 3.105855 | 0.189097 | 184.2403 | 0.972723 | |||||
| model 3 | −0.00042 | 1.970635 | 0.118075 | 101.683 | 0.97724 | |||||
| model 4 | −0.00526 | 1.303398 | 0.072961 | 74.02754 | 0.986858 | |||||
| model 5 | −0.01212 | −0.64945 | 0.067096 | 0.827014 | 0.995827 | |||||
| model 6 | −0.00287 | 1.617105 | 0.086884 | 80.53735 | 0.984327 | |||||
| model 7 | −0.00082 | 1.856794 | 0.11676 | 81.62941 | 0.982704 | |||||
| model 8 | 0.010382 | 3.727819 | 0.254774 | 195.6545 | 0.95710 | |||||
| Lagos | β (evaluating) | Scaled | model 1 | 0.464587 | 0.127463 | 0.387534 | 0.140156 | 0.907805 | −0.10154 | 2 |
| model 2 | 0.52731 | 0.204256 | 0.561238 | 0.223535 | 0.807827 | −0.58733 | 7 | |||
| model 3 | 0.50636 | 0.202153 | 0.525998 | 0.215693 | 0.821177 | −0.40396 | 6 | |||
| model 4 | 0.468508 | 0.144071 | 0.454559 | 0.157083 | 0.90613 | −0.15522 | 3 | |||
| model 5 | 0.416856 | 0.1249 | 0.231083 | 0.131566 | 0.980131 | −0.05289 | 1 | |||
| model 6 | 0.493515 | 0.145482 | 0.497636 | 0.16537 | 0.886344 | −0.22111 | 4 | |||
| model 7 | 0.497976 | 0.171837 | 0.51139 | 0.196646 | 0.88021 | −0.24752 | 5 | |||
| model 8 | 0.579824 | 0.70489 | 0.572317 | 0.690357 | 0.795714 | −0.59759 | 8 | |||
| Lagos | HT (evaluating) | Unscaled | model 9 | 0.035767 | −0.06543 | 4.129406 | 41.96881 | 0.859681 | ||
| model 10 | 0.00435 | −0.07427 | 3.617221 | 37.61502 | 0.861867 | |||||
| model 11 | −0.00276 | −0.14809 | 3.612718 | 37.4786 | 0.905978 | |||||
| model 12 | −0.00888 | −0.1742 | 2.54982 | 26.50075 | 0.993466 | |||||
| model 13 | −0.00384 | −0.16049 | 2.594963 | 26.71104 | 0.990466 | |||||
| Lagos | HT (evaluating) | Scaled | model 9 | 0.511442 | 0.681972 | 0.481565 | 0.574691 | 0.907000 | −0.28817 | 5 |
| model 10 | 0.511087 | 0.677396 | 0.479555 | 0.416253 | 0.912066 | −0.28322 | 4 | |||
| model 11 | 0.50942 | 0.549153 | 0.473442 | 0.413654 | 0.914123 | −0.1948 | 3 | |||
| model 12 | 0.360229 | 0.506984 | 0.337831 | 0.308652 | 0.916318 | −0.10663 | 1 | |||
| model 13 | 0.390297 | 0.53956 | 0.380116 | 0.309687 | 0.916011 | −0.11936 | 2 | |||
| Nigeria | β (evaluating) | Unscaled | model 14 | 0.000088 | -0.01289 | 0.115584 | 10.03103 | 0.975573 | ||
| model 15 | 0.133602 | −0.92624 | 0.812668 | 67.613 | 0.967767 | |||||
| Nigeria | β (evaluating) | Scaled | model 14 | 0.242356 | 0.519225 | 0.237879 | 0.234853 | 0.95991 | −0.31988 | 1 |
| model 15 | 0.50088 | 0.707063 | 0.412801 | 0.390925 | 0.953709 | −0.58440 | 2 | |||
| Nigeria | HT (evaluating) | Unscaled | model 16 | 0.002821 | −0.02223 | 1.715347 | 23.45524 | 0.961867 | ||
| model 17 | −0.00098 | −0.02186 | 1.688865 | 23.02892 | 0.993466 | |||||
| model 18 | −0.00249 | −0.02443 | 1.692862 | 23.0906 | 0.993466 | |||||
| model 19 | 0.004618 | −0.02129 | 1.716492 | 23.51276 | 0.905978 | |||||
| model 20 | −0.0002 | −0.02355 | 1.711004 | 23.39444 | 0.961867 | |||||
| model 21 | −0.00232 | −0.02411 | 1.69431 | 23.1283 | 0.98778 | |||||
| model 22 | 0.004857 | −0.02117 | 1.738694 | 23.78289 | 0.859681 | |||||
| Nigeria | HT (evaluating) | Scaled | model 16 | 0.941091 | 0.102087 | 0.064099 | 0.094775 | 0.969764 | −0.39174 | 5 |
| model 17 | 0.908147 | 0.064788 | 0.060842 | 0.090902 | 0.971789 | −0.10786 | 1 | |||
| model 18 | 0.930797 | 0.074064 | 0.063138 | 0.093731 | 0.970655 | −0.10888 | 2 | |||
| model 19 | 0.943435 | 0.104736 | 0.064481 | 0.095984 | 0.96961 | −0.44611 | 6 | |||
| model 20 | 0.938892 | 0.08984 | 0.064021 | 0.094737 | 0.969968 | −0.19967 | 4 | |||
| model 21 | 0.934378 | 0.081478 | 0.063273 | 0.093836 | 0.970044 | −0.1782 | 3 | |||
| model 22 | 0.946148 | 0.131657 | 0.065084 | 0.097035 | 0.96119 | −0.92157 | 7 | |||
| Nigeria | β (empirical) | Unscaled | model 14 | 8.80E-05 | −0.92629 | 0.115584 | 10.03103 | 0.993466 | ||
| model 15 | 0.133602 | 0.074862 | 0.812668 | 23.81 951 | 0.859681 | |||||
| model 23 | −0.0143 | −0.29953 | 0.153691 | 13.11089 | 0.961867 | |||||
| model 24 | 0.034463 | −0.01289 | 0.237445 | 67.613 | 0.905978 | |||||
| Nigeria | β (empirical) | Scaled | model 14 | 0.242356 | 0.519225 | 0.237879 | 0.320472 | 0.963907 | −0.06558 | 1 |
| model 15 | 0.506408 | 0.707063 | 0.437395 | 0.407484 | 0.953709 | −0.27418 | 4 | |||
| model 23 | 0.495119 | 0.608267 | 0.374856 | 0.390925 | 0.95991 | −0.12592 | 2 | |||
| model 24 | 0.50088 | 0.631054 | 0.412801 | 0.390926 | 0.955273 | −0.19248 | 3 |
Here HT stands for maximum incident solar radiation, and β represents the optimum tilt angle.
Figure 10.
Observed and evaluated developed empirical models for estimating optimum tilt angles for Lagos, Nigeria.
Similarly, using the rule of the RRMSE statistical indicator of Ertekin and Yaldiz [66], Behar et al. [55] and Despotovic et al. [56] GPI and the classification tools in Table 14 reveal that Model 12 emerged as the best performing model due to the lowest RRMSE value (26.50075) and the highest GPI value (−0.10663) for estimating the maximum incident solar radiation using monthly mean H, Ho, kt, and T as predictors in Lagos, Nigeria, as shown in Fig. 9 and Fig. 11.
Figure 11.
Observed and evaluated developed empirical models for estimating monthly maximum incident solar radiation for Lagos, Nigeria.
Furthermore, model 17 emerged as the best performing model for estimating maximum incident solar radiation, as shown in Tables 14 in 37 metropolitan cities in Nigeria, as shown in Fig. 9, and 13. From Table 14, it is shown that model 14 employing latitude as only the predictor outperformed model 15 by using elevation and location latitude as predictors to estimate the optimal annual tilt angle in 37 metropolitan cities in Nigeria, as shown in Fig. 9 and Fig. 12.
Figure 13.
Observed and evaluated developed empirical models for estimating monthly maximum incident solar radiation for Nigeria.
Figure 12.
Observed and evaluated developed empirical models for estimating optimum tilt angles for Nigeria.
To validate models 14 and 15 for the environment of Nigeria, two empirical models for estimating the optimal annual tilt angle developed in Iran and India were compared with established models 14 and 15 in 37 metropolitan cities in Nigeria. From the statistical indicators presented in Table 14, model 14 outperformed models 15, 23, and 24 with the following GPI values of −0.146, −0.23924, −0.52094 and −0.3657, respectively, and RRMSE values of 10.03103, 13.11089, 23.81951 and 67,613, using Ertekin and Yaldiz [66], Behar et al. [55], and Despotovic et al. [56] statistical tools as shown in Fig. 9 and Fig. 13.
3.7. Evaluation of optimum tilt angle and maximum incident solar radiation in Africa, Mediterranean region and selected cities across the globe
Table 15, Table 16, Table 17 present an overview of the annual optimum tilt angle (degrees) and maximum incident solar radiation (W/m2) for Africa, the Mediterranean region, and selected locations around the world. In general, the optimal annual tilt angle improves with increasing latitude. This result compares favorably with numerous results found in the literature [23], [38], [65], [69], [70], as the optimal angle of inclination often depends mainly on the latitude of the location. From Table 18, Darhmaoui and Lahjouji [70], Talebizadel et al. [67], and Jamil et al. [54] overestimated the optimal inclination angles in most of the places under study for the latitude of the places; while, model 14 developed in this study moderately adapted to the optimal angle of inclination in localities around the Mediterranean region and Africa. Furthermore, in Table 16, model 15 was also developed in this study using the latitude and altitude of the location as the input parameters overestimated the optimal tilt angle at various locations under consideration, while Talebizadel et al. [67] and Jamil et al. [54] estimated the parameter moderately. Meanwhile, model 14 used latitude only as the input variable fit the parameter better than the corresponding latitude values in different positions as presented in Table 16. Furthermore, the model [71] matched Jacobson's estimated values [23] in various locations around the globe while Talebizadel et al. [67] and Jamil et al. [54] overestimated the parameter due to the latitude magnitude of places as presented in Table 17.
Table 15.
Optimum tilt angle and maximum incident solar radiation for Mediterranean region using derived models and models from literature for comparison.
| Location details |
Optimum tilt angle models |
Maximum incident radiation model |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Country | City | latitude | Longitude | H | Darhmaoui and Lahjouji [70] | M14 (Present study) (M17) | Talebizadeh et al. [67] | Jamil et al. [68] | Darhmaoui and Lahjouji [70] | Present Study | Liu & Jordan [50] |
| Egypt | Luxor | 25.69 | 32.64 | 261.93 | 27.4 | 21.91 | 24.68 | 26.32 | 294.36 | 272.59 | 277.26 |
| Morocco | Smara | 26.73 | 11.67 | 250.44 | 28 | 22.56 | 25.39 | 27.02 | 277.306 | 260.63 | 265.1 |
| Egypt | SharmSheikkh | 27.86 | 34.36 | 240.12 | 29 | 23.27 | 26.16 | 27.78 | 295.238 | 249.89 | 254.18 |
| Morocco | Agadir | 30.41 | 9.6 | 241.51 | 31.3 | 24.86 | 27.89 | 29.49 | 266.666 | 251.34 | 255.65 |
| Libya | Sabha | 30.63 | 18.35 | 239.66 | 31.9 | 25 | 28.04 | 29.64 | 268.839 | 249.41 | 253.68 |
| Egypt | Alexandria | 31.2 | 29.92 | 217.96 | 31.9 | 25.35 | 28.43 | 30.02 | 276.054 | 226.83 | 230.72 |
| Palestine | Gaza | 31.41 | 34.31 | 231.3 | 32.1 | 25.48 | 28.57 | 30.16 | 274.061 | 240.72 | 244.84 |
| Libya | Tripoli | 32.9 | 13.19 | 226.32 | 33.1 | 26.41 | 29.59 | 31.16 | 265.445 | 235.53 | 239.56 |
| Syria | Damascus | 33.51 | 36.28 | 226.2 | 33.7 | 26.79 | 30 | 31.57 | 261.001 | 0235.4 | 239.44 |
| Algeria | Macharia | 33.55 | 0.28 | 223.18 | 33.7 | 26.82 | 30.03 | 31.6 | 265.033 | 232.27 | 236.25 |
| Lebanon | Beirut | 33.88 | 35.5 | 212.86 | 33.8 | 27.02 | 30.25 | 31.82 | 246.761 | 221.52 | 225.32 |
| Cyprus | Nicosia | 35.16 | 33.38 | 204.97 | 35 | 27.82 | 31.13 | 32.68 | 250.197 | 213.31 | 216.97 |
| Morocco | Larache | 35.18 | 6.15 | 198.13 | 35 | 27.83 | 31.14 | 32.69 | 253.164 | 206.19 | 209.73 |
| Greece | Heraklion | 35.32 | 25.14 | 197.08 | 35.1 | 27.92 | 31.23 | 32.79 | 243.941 | 205.1 | 208.62 |
| Syria | Latakia | 35.52 | 35.8 | 200.68 | 35.2 | 28.05 | 31.37 | 32.92 | 256.678 | 208.85 | 212.43 |
| Tunisia | Tunis | 35.41 | 10.18 | 209.73 | 35.2 | 27.98 | 31.3 | 32.85 | 255.527 | 218.26 | 222 |
| Malta | Vallella | 35.89 | 14.51 | 199.06 | 35.3 | 28.28 | 31.62 | 33.17 | 258.797 | 207.16 | 210.71 |
| Tunisia | Bizerte | 37.27 | 9.86 | 185.83 | 36.5 | 29.14 | 32.56 | 34.1 | 246.194 | 193.39 | 196.71 |
| Spain | Seville | 37.38 | 5.98 | 183.16 | 36.6 | 29.21 | 32.64 | 34.17 | 232.128 | 190.62 | 193.89 |
| Turkey | Isparta | 37.76 | 30.55 | 195.34 | 36.7 | 29.44 | 32.89 | 34.42 | 230.836 | 203.29 | 206.78 |
| Italy | Marsala | 37.8 | 12.44 | 187.8 | 36.7 | 29.47 | 32.92 | 34.45 | 246.906 | 195.45 | 198.8 |
| Greece | Anthen | 37.97 | 23.73 | 189.08 | 36.8 | 29.58 | 33.04 | 34.56 | 237.635 | 196.77 | 200.15 |
| Turkey | Bursa | 40.18 | 29.06 | 169.82 | 38.6 | 30.95 | 34.54 | 36.05 | 200.702 | 176.73 | 179.77 |
| Spain | Madrid | 40.4 | 3.7 | 181.42 | 38.6 | 31.09 | 34.69 | 36.2 | 225.494 | 188.81 | 192.04 |
| Albania | Vlore | 40.46 | 19.49 | 176.78 | 38.7 | 31.13 | 34.73 | 36.24 | 222.124 | 183.98 | 187.13 |
| Greece | Thessaloniki | 40.63 | 22.94 | 174.23 | 38.7 | 31.24 | 34.85 | 36.35 | 208.284 | 181.32 | 184.43 |
| Italy | Naples | 40.83 | 14.27 | 175.74 | 38.8 | 31.36 | 34.98 | 36.48 | 225.041 | 182.89 | 186.03 |
| Montenegro | Podgoria | 42.47 | 19.26 | 157.41 | 40 | 32.38 | 36.1 | 37.58 | 184.528 | 163.82 | 166.63 |
| Bosnia & Herzegovina | Sarajevo | 43.51 | 18.41 | 150.1 | 40.7 | 33.03 | 36.81 | 38.28 | 181.476 | 156.21 | 158.89 |
| Monaco | Monaco | 43.73 | 7.42 | 163.33 | 40.7 | 33.17 | 36.96 | 38.43 | 227.858 | 169.97 | 172.89 |
| Italy | Florence | 43.77 | 11.26 | 158.34 | 40.7 | 33.19 | 36.98 | 38.46 | 194.97 | 164.78 | 167.61 |
| Italy | Milan | 45.46 | 9.19 | 157.06 | 41.8 | 34.25 | 38.13 | 39.59 | 192.108 | 163.46 | 166.26 |
| France | Lyon | 45.76 | 4.84 | 153 | 41.9 | 34.44 | 38.34 | 39.79 | 183.742 | 159.23 | 161.96 |
| Croatia | Zagreb | 45.81 | 15.98 | 140.13 | 41.9 | 34.47 | 38.37 | 39.83 | 170.406 | 145.83 | 148.33 |
| Slovenia | Ljubljana | 46.05 | 14.51 | 136.76 | 42.3 | 34.62 | 38.54 | 39.99 | 169.247 | 142.33 | 144.77 |
| Average | 136.76 | 36.09 | 29.01 | 32.42 | 33.96 | 169.247 | 142.33 | 144.77 | |||
Table 16.
Optimum tilt angle and maximum incident solar radiation for Africa using derived models and models from literature for comparison.
| Location details |
Optimum tilt angle models |
Maximum incident radiation model |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Country | Capital | Lat | Long | Elevation | H (W/m2) | M14 (Present study) | M15 (Present study) | Talebizadeh et al. [67] | Jamil et al. [54] | Present Study [M17] | Liu & Jordan [50] |
| Algeria | Algiers | 38.75 | 3.06 | 424 | 199.7 | 30.062 | 46.855 | 33.5685 | 35.08825 | 207.873 | 212.5 |
| Angola | Luanda | 8.83 | 13.23 | 6 | 197.7 | 11.3919 | 13.4819 | 13.2109 | 15.01193 | 205.707 | 210.28 |
| Benin | Porto Novo | 6.5 | 2.63 | 38 | 175.5 | 9.938 | 12.174 | 11.6256 | 13.4485 | 182.649 | 186.71 |
| Botswana | Gaborone | 24.75 | 25.92 | 1014 | 243.8 | 21.326 | 24.91 | 24.0429 | 25.69425 | 253.753 | 259.4 |
| Burkina Faso | Ouagadougou | 12.37 | 1.52 | 305 | 233.5 | 13.6009 | 22.4213 | 15.6195 | 17.38727 | 243.009 | 248.41 |
| Burundi | Bujumbura | 3.61 | 29.36 | 774 | 194.4 | 8.13464 | 24.478 | 9.65924 | 11.50931 | 202.327 | 206.83 |
| Cameroon | Yaoundé | 3.84 | 11.5 | 726 | 184.3 | 8.27816 | 23.7102 | 9.81574 | 11.66364 | 191.824 | 196.09 |
| Cape Verde | Praia | 14.93 | 23.51 | 0 | 269 | 15.1983 | 18.4615 | 17.3614 | 19.10503 | 279.95 | 286.17 |
| Central African Republic | Bangui | 4.39 | 18.56 | 369 | 199.8 | 8.62136 | 17.03 | 10.19 | 12.03269 | 207.880 | 212.5 |
| Chad | N'Djamena | 12.15 | 15.06 | 298 | 247.7 | 13.4636 | 22.0974 | 15.4699 | 17.23965 | 257.737 | 263.47 |
| Comoros | Moroni | 11.7 | 43.25 | 29 | 243.9 | 13.1828 | 16.3412 | 15.1637 | 16.9377 | 253.874 | 259.52 |
| Democratic Republic of Congo | Kinshasa | 4.34 | 15.27 | 240 | 192.2 | 8.59016 | 14.4082 | 10.1559 | 11.99914 | 200.033 | 204.48 |
| Djibouti | Djibouti | 11.82 | 42.59 | 2028 | 254.5 | 13.2577 | 56.4215 | 15.2453 | 17.01822 | 264.86 | 270.75 |
| Egypt | Cairo | 30.03 | 31.24 | 23 | 234.2 | 24.6207 | 31.5451 | 27.6354 | 29.23713 | 243.734 | 249.15 |
| Equatorial Guinea | Malabo | 3.75 | 8.78 | 240 | 148.9 | 8.222 | 13.915 | 9.7545 | 11.60325 | 155.004 | 158.45 |
| Eritrea | Asmara | 15.32 | 38.93 | 2325 | 249.5 | 15.4417 | 65.2875 | 17.6267 | 19.36672 | 259.669 | 265.44 |
| Ethiopia | Addis Ababa | 8.98 | 38.76 | 2355 | 223.2 | 11.4855 | 60.5873 | 13.313 | 15.11258 | 232.265 | 237.43 |
| Gabon | Libreville | 0.42 | 9.47 | 159 | 178.5 | 6.14408 | 9.51112 | 7.48877 | 9.36882 | 185.788 | 189.92 |
| Gambia | Banjul | 13.45 | 16.58 | 0 | 252.9 | 14.2748 | 17.2242 | 16.3544 | 18.11195 | 263.169 | 269.02 |
| Ghana | Accra | 5.55 | −0.19 | 61 | 183 | 9.3452 | 11.8398 | 10.9792 | 12.81105 | 190.496 | 194.73 |
| Guinea | Conakry | 9.64 | 13.58 | 1752 | 224.3 | 11.8974 | 49.079 | 13.7621 | 15.55544 | 233.472 | 238.66 |
| Guinea-Bissau | Bissau | 11.8 | 15.18 | 0 | 239.7 | 13.2452 | 15.8448 | 15.2317 | 17.0048 | 249.407 | 254.95 |
| Ivory Coast | Yamoussoukro | 6.83 | 5.29 | 213 | 177.5 | 10.1439 | 15.9499 | 11.8501 | 13.66993 | 184.701 | 188.81 |
| Kenya | Nairobi | 1.28 | 36.82 | 1795 | 234.6 | 6.68072 | 42.9501 | 8.07391 | 9.94588 | 244.096 | 249.52 |
| Lesotho | Maseru | 29.3 | 27.49 | 1600 | 230.3 | 24.1652 | 62.4748 | 27.1387 | 28.7473 | 239.629 | 244.96 |
| Liberia | Monrovia | 6.31 | −10.81 | 174 | 168 | 9.81944 | 14.7352 | 11.4963 | 13.32101 | 174.802 | 178.69 |
| Libya | Tripoli | 32.87 | 13.19 | 81 | 226.3 | 26.3929 | 35.0793 | 29.5677 | 31.14277 | 235.525 | 240.76 |
| Madagascar | Antananarivo | 18.88 | 47.51 | 1276 | 276.2 | 17.6631 | 47.2837 | 20.049 | 21.75548 | 287.434 | 293.83 |
| Malawi | Lilongwe | 13.96 | 33.77 | 1050 | 246.7 | 14.593 | 38.6506 | 16.7014 | 18.45416 | 256.771 | 262.48 |
| Mali | Bamako | 12.64 | −8 | 350 | 230.3 | 13.7694 | 23.547 | 15.8033 | 17.56844 | 239.629 | 244.96 |
| Mauritania | Nouakchott | 20.17 | 57.5 | 7 | 259.8 | 18.4681 | 22.9821 | 20.9267 | 22.62107 | 270.413 | 276.43 |
| Mauritius | Port Louis | 20.35 | 57.55 | 133 | 259.8 | 18.5804 | 25.6526 | 21.0491 | 22.74185 | 270.413 | 276.43 |
| Morocco | Rabat | 33.97 | −6.85 | 160 | 212.3 | 27.0793 | 37.5789 | 30.3162 | 31.88087 | 220.917 | 225.83 |
| Mozambique | Maputo | 25.97 | 32.57 | 345 | 261.9 | 22.0873 | 34.5909 | 24.873 | 26.51287 | 272.586 | 278.65 |
| Namibia | Windhoek | 22.55 | 17.07 | 1655 | 268.2 | 19.9532 | 57.9318 | 22.546 | 24.21805 | 279.105 | 285.31 |
| Niger | Niamey | 13.515 | 2.13 | 207 | 248 | 14.3154 | 21.4185 | 16.3986 | 18.155565 | 258.099 | 263.84 |
| Nigeria | Abuja | 9.08 | 7.34 | 840 | 205.3 | 11.5479 | 30.3709 | 13.381 | 15.17968 | 213.674 | 218.43 |
| Republic of the Congo | Brazzaville | 0.23 | 15.83 | 320 | 189.7 | 6.02552 | 12.5723 | 7.35949 | 9.24133 | 197.377 | 201.77 |
| Rwanda | Kigali | 1.98 | 30.1 | 1567 | 205.7 | 7.11752 | 38.9753 | 8.55019 | 10.41558 | 214.036 | 218.8 |
| São Tomé and Príncipe | São Tomé | 0.33 | 6.73 | 137 | 183.5 | 6.08792 | 8.99588 | 7.42753 | 9.30843 | 190.979 | 195.23 |
| Senegal | Dakar | 14.73 | 17.47 | 22 | 263.9 | 15.0735 | 18.7343 | 17.2253 | 18.97083 | 274.638 | 280.74 |
| Seychelles | Victoria | 4.62 | 55.45 | 905 | 232.7 | 8.76488 | 27.9423 | 10.3464 | 12.18702 | 242.164 | 247.55 |
| Sierra Leone | Freetown | 8.48 | 13.23 | 26 | 220.1 | 11.1735 | 13.5893 | 12.9728 | 14.77708 | 229.006 | 234.1 |
| Somalia | Mogadishu | 2.04 | 45.32 | 9 | 250.6 | 7.15496 | 7.86544 | 8.59102 | 10.45584 | 260.755 | 266.55 |
| South Africa | Pretoria | 25.75 | 28.23 | 1339 | 265.3 | 21.95 | 54.287 | 24.7233 | 26.36525 | 276.087 | 282.23 |
| South Sudan | Juba | 4.86 | 31.57 | 550 | 205 | 8.91464 | 21.043 | 10.5097 | 12.34806 | 213.312 | 218.06 |
| Sudan | Khartoum | 15.51 | 32.56 | 381 | 261 | 15.5602 | 26.5664 | 17.756 | 19.49421 | 271.620 | 277.66 |
| Swaziland | Mbabane | 26.3 | 31.14 | 1243 | 263 | 22.2932 | 52.8268 | 25.0975 | 26.7343 | 273.672 | 279.76 |
| Tanzania | Dodoma | 6.16 | 35.75 | 1120 | 200 | 9.72584 | 33.5298 | 11.3943 | 13.22036 | 208.121 | 212.75 |
| Togo | Lomé | 6.14 | 1.23 | 10 | 183.7 | 9.71336 | 11.313 | 11.3807 | 13.20694 | 191.2207 | 195.47 |
| Tunisia | Tunis | 33.89 | 9.54 | 4 | 226.1 | 27.0294 | 34.392 | 30.2618 | 31.82719 | 235.283 | 240.51 |
| Uganda | Kampala | 0.34 | 32.58 | 1190 | 202.9 | 6.09416 | 30.0642 | 7.43434 | 9.31514 | 211.1396 | 215.83 |
| Zambia | Lusaka | 15.4 | 28.32 | 1279 | 272.9 | 15.4916 | 44.4344 | 17.6812 | 19.4204 | 284.0545 | 290.37 |
| Zimbabwe | Harare | 17.72 | 31.03 | 1490 | 269.6 | 16.9393 | 50.5939 | 19.2597 | 20.97712 | 280.5536 | 286.79 |
| Average | 225.4 | 14.0758 | 29.7886 | 16.1373 | 17.897913 | 234.5614 | 239.78 | ||||
Table 17.
Optimum tilt angle for selected locations across the globe using derived models and models from literature for comparison.
| Cities | Lat | Jacobson & Jadhav [23] | M14 (Present study) | Talebizadeh et al. [67] | Jamil et al. [54] | Cities | Lat | Jacobson & Jadhav [23] | M14 (Present study) | Talebizadeh et al. [67] | Jamil et al. [54] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Reykjavik | 64.1 | 43 | 46 | 51 | 52 | Innsbruck, Austria | 42.27 | 42.3 | 37 | 32 | 36 |
| Karachi, Pakistan | 24.9 | 25 | 21 | 24 | 26 | Kunas | 54.88 | 54.9 | 33 | 40 | 45 |
| S Maria Di Leuca | 39.7 | 30 | 31 | 34 | 36 | St Hubert | 50.03 | 50.0 | 35 | 37 | 41 |
| Algiers | 36.7 | 31 | 29 | 32 | 34 | Thessolonica | 40.52 | 40.5 | 33 | 31 | 35 |
| Gerona, Spain | 41.9 | 37 | 32 | 36 | 37 | Kuala Lumpur | 3.12 | 3.1 | 1 | 8 | 9 |
| Harare, Zimbabwe | −17.9 | −22 | −17 | −19 | −21 | Gan Island | 0.68 | 0.7 | −2 | −6 | −8 |
| Fort-De-France | 14.6 | 14 | 15 | 17 | 19 | Dakar, Senegal | 14.73 | 14.7 | 14 | 15 | 17 |
| Buenos Sires | −34.8 | −30 | −28 | −31 | −32 | CozzoSpadaro | 36.68 | 36.7 | 28 | 29 | 32 |
| Tabriz, Iran | 38.1 | 30 | 30 | 33 | 35 | Kwajelein Atoll | 8.73 | 8.7 | 12 | 11 | 13 |
| Darwin | −12.4 | −18 | −14 | −16 | −17 | Dakar, Senegal | 14.73 | 14.7 | 14 | 15 | 17 |
| Perth | −31.9 | −27 | −26 | −29 | −31 | Antananarivo | −18.8 | −18.8 | −18 | −18 | −20 |
| Sydney | −34.0 | −31 | −27 | −30 | −32 | Mexico City | 19.43 | 19.4 | 17 | 18 | 20 |
| Graz | 47.0 | 33 | 35 | 39 | 41 | Belize | 17.53 | 17.5 | 16 | 17 | 19 |
| Tabriz, Iran | 38.1 | 30 | 30 | 33 | 35 | Guam, Hi | 13.55 | 13.6 | 14 | 14 | 16 |
| Saua La Grande | 22.8 | 21 | 20 | 23 | 24 | Odessa, Ukraine | 46.45 | 46.5 | 31 | 35 | 39 |
| Riyaadh | 24.7 | 26 | 21 | 24 | 26 | Nice, France | 43.65 | 43.7 | 35 | 33 | 37 |
| Chittagong | 22.3 | 25 | 20 | 22 | 24 | Ulaanbaatar | 47.93 | 47.9 | 43 | 36 | 40 |
| Fort-De-France | 14.6 | 14 | 15 | 17 | 19 | Podgorica | 42.37 | 42.4 | 36 | 32 | 36 |
| Minsk | 53.9 | 32 | 39 | 44 | 45 | Casablance | 33.37 | 33.4 | 28 | 27 | 30 |
| Saint Hubert | 50.0 | 35 | 37 | 41 | 43 | Johannesburg | −26.1 | −26.1 | −29 | −22 | −25 |
| Belize | 17.5 | 16 | 17 | 19 | 21 | Bangkok, Thailand | 13.92 | 13.9 | 15 | 15 | 17 |
| Accra, Ghana | 5.6 | 6 | 9 | 11 | 13 | Cape Town | −34 | −34.0 | −30 | −27 | −30 |
| Pagri, China | 27.7 | 32 | 23 | 26 | 28 | Kwajelein Atoll | 8.73 | 8.7 | 12 | 11 | 13 |
| La Paz | −16.5 | −22 | −16 | −18 | −20 | Kathandu | 27.7 | 27.7 | 29 | 23 | 26 |
| Banja Luka | 44.8 | 33 | 34 | 38 | 39 | Beek | 50.92 | 50.9 | 34 | 38 | 42 |
| Johannestburg | −26.1 | −29 | −22 | −25 | −27 | Aukland | −37 | −37.0 | −30 | −29 | −32 |
| Manaus | −3.1 | −7 | −8 | −9 | −11 | Rivas | 11.42 | 11.4 | 14 | 13 | 15 |
| Rio De Janeiro | −22.9 | −22 | −20 | −23 | −24 | Accra, Ghana | 5.6 | 5.6 | 6 | 9 | 11 |
| Bandar Seri Begwa | 4.9 | 5 | 9 | 11 | 12 | Accra, Ghana | 5.6 | 5.6 | 6 | 9 | 11 |
| Plovdiv | 42.1 | 30 | 32 | 36 | 37 | Oslo | 59.9 | 59.9 | 40 | 43 | 48 |
| Accra, Ghana | 5.6 | 6 | 9 | 11 | 13 | Abu Dhabi, UAE | 24.43 | 24.4 | 25 | 21 | 24 |
| Kisii, Kenya | −0.7 | −3 | −6 | −8 | −10 | Karachi | 24.9 | 24.9 | 25 | 21 | 24 |
| Dkar, Senegal | 14.7 | 14 | 15 | 17 | 19 | Koror | 7.33 | 7.3 | 8 | 10 | 12 |
| Bangkok,Thailand | 13.9 | 15 | 15 | 17 | 18 | Jerusalem | 31.87 | 31.9 | 28 | 26 | 29 |
| Accra, Ghana | 5.6 | 6 | 9 | 11 | 13 | Rivas, Nicaragua | 11.42 | 11.4 | 14 | 13 | 15 |
| Calgari | 51.1 | 45 | 38 | 42 | 43 | Wiepa, Australia | −12.7 | −12.7 | −17 | −14 | −16 |
| Vancouver | 49.2 | 34 | 37 | 41 | 42 | Asuncion | −25.3 | −25.3 | −23 | −22 | −24 |
| Montreal | 45.5 | 37 | 34 | 38 | 40 | Lima | −12 | −12.0 | −7 | −13 | −15 |
| Accra, Ghana | 5.6 | 6 | 9 | 11 | 13 | Manila | 14.52 | 14.5 | 9 | 15 | 17 |
| Accra, Ghana | 5.6 | 6 | 9 | 11 | 13 | Bielsko-Biala | 49.67 | 49.7 | 31 | 37 | 41 |
| Antofagasta | −23.4 | −22 | −21 | −23 | −25 | Lisbon | 38.73 | 38.7 | 35 | 30 | 34 |
| Beijin | 39.9 | 37 | 31 | 34 | 36 | Abu Dhabi, UAE | 24.43 | 24.4 | 25 | 21 | 24 |
| Shanghai | 31.2 | 23 | 25 | 28 | 30 | Bucharest | 44.5 | 44.5 | 32 | 34 | 37 |
| Lhasa | 29.7 | 31 | 24 | 27 | 29 | St Petersburg | 59.97 | 60.0 | 40 | 43 | 48 |
| Kunming | 25.0 | 25 | 21 | 24 | 26 | Moscow | 55.75 | 55.8 | 37 | 41 | 45 |
| Bogota | 4.7 | 5 | 9 | 10 | 12 | Omsk | 54.93 | 54.9 | 42 | 40 | 45 |
| Antananarivo | −18.8 | −18 | −18 | −20 | −22 | Kisii, Kenya | −0.67 | −0.7 | −3 | −6 | −8 |
| Accra, Ghana | 5.6 | 6 | 9 | 11 | 13 | Charlotte Amilie | 18.35 | 18.4 | 18 | 17 | 20 |
| Harare, Zimbabwe | −17.9 | −22 | −17 | −19 | −21 | Fort-De-France | 14.6 | 14.6 | 14 | 15 | 17 |
| Rivas, Nicaragua | 11.4 | 14 | 13 | 15 | 17 | Nadi, Fiji | −17.8 | −17.8 | −18 | −17 | −19 |
| Ancona, Italy | 43.6 | 30 | 33 | 37 | 38 | Rimini, Italy | 44.03 | 44.0 | 31 | 33 | 37 |
| Sancti Spiritus | 21.9 | 21 | 20 | 22 | 24 | Accra, Ghana | 5.6 | 5.6 | 6 | 9 | 11 |
| Larnaca | 34.9 | 30 | 28 | 31 | 33 | Riyadh | 24.7 | 24.7 | 24 | 21 | 24 |
| Ostrava | 49.7 | 33 | 37 | 41 | 42 | Dakar | 14.73 | 14.7 | 14 | 15 | 17 |
| Copenhagen | 55.6 | 36 | 41 | 45 | 46 | Belgrade | 44.82 | 44.8 | 34 | 34 | 38 |
| Combolcha/Dessie | 11.1 | 15 | 13 | 15 | 17 | Lamu/MandaIslanda | −2.27 | −2.3 | −2 | −7 | −9 |
| Fort-De-France | 14.6 | 14 | 15 | 17 | 19 | Dakar, Senegal | 14.73 | 14.7 | 14 | 15 | 17 |
| AquadillaBorinquen | 18.5 | 20 | 17 | 20 | 22 | Singapore | 1.37 | 1.4 | 0 | 7 | 8 |
| Carasca Venezuela | 10.6 | 10 | 12 | 14 | 16 | Kosice | 48.7 | 48.7 | 33 | 36 | 40 |
| Quito | −0.2 | −3 | −6 | −7 | −9 | Ljubljana | 46.22 | 46.2 | 29 | 35 | 39 |
| Aswan | 24.0 | 24 | 21 | 24 | 25 | Wiepa, Australia | −12.7 | −12.7 | −17 | −14 | −16 |
| Ilopango | 13.7 | 18 | 14 | 17 | 18 | Marsabit, Kenya | 2.3 | 2.3 | 4 | 7 | 9 |
| Accra, Ghana | 5.6 | 6 | 9 | 11 | 13 | Lowdar, Kenya | 3.12 | 3.1 | 5 | 8 | 9 |
| Gondar, Ethiopia | 12.5 | 18 | 14 | 16 | 18 | Johannesburg | −26.1 | −26.1 | −29 | −22 | −25 |
| Helsinki | 60.3 | 39 | 44 | 48 | 50 | Cape Town | −34 | −34.0 | −30 | −27 | −30 |
| Gondar | 12.5 | 18 | 14 | 16 | 18 | Castellon | 39.95 | 40.0 | 36 | 31 | 34 |
| Nadi | −17.8 | −18 | −17 | −19 | −21 | Ceuta | 35.89 | 35.9 | 31 | 28 | 32 |
| Helsinki | 60.3 | 39 | 44 | 48 | 50 | Colombo | 6.82 | 6.8 | 9 | 10 | 12 |
| Lyon | 45.7 | 30 | 34 | 38 | 40 | Fort-De-France | 14.6 | 14.6 | 14 | 15 | 17 |
| Bordeaux | 44.8 | 33 | 34 | 38 | 39 | Gondar, Ethiopia | 12.53 | 12.5 | 18 | 14 | 16 |
| Accra, Ghana | 5.6 | 6 | 9 | 11 | 13 | Boa Vista Brazil | 2.83 | 2.8 | 6 | 8 | 9 |
| Dkar, Senegal | 14.7 | 14 | 15 | 17 | 19 | Johannesburg | −26.1 | −26.1 | −29 | −22 | −25 |
| Tabriz, Iran | 38.1 | 30 | 30 | 33 | 35 | Stockholm | 59.65 | 59.7 | 41 | 43 | 48 |
| Cologne | 50.9 | 32 | 38 | 42 | 43 | Geneva | 46.25 | 46.3 | 32 | 35 | 39 |
| Munich | 48.1 | 33 | 36 | 40 | 41 | Damascus | 33.42 | 33.4 | 29 | 27 | 30 |
| Accra, Ghana | 5.6 | 6 | 9 | 11 | 13 | Taipei | 25.07 | 25.1 | 17 | 22 | 24 |
| Ceuta, Spain | 35.9 | 31 | 28 | 32 | 33 | Tashkent | 41.27 | 41.3 | 32 | 32 | 35 |
| Athens | 37.9 | 29 | 30 | 33 | 35 | Makindu, Kenya | −2.28 | −2.3 | −4 | −7 | −9 |
| Guatemala City | 14.6 | 18 | 15 | 17 | 19 | Bangkok | 13.92 | 13.9 | 15 | 15 | 17 |
| Dakar, Senegal | 14.7 | 14 | 15 | 17 | 19 | Darwin, Asutralia | −12.4 | −12.4 | −18 | −14 | −16 |
| Dakar, Senegal | 14.7 | 14 | 15 | 17 | 19 | Accra, Ghana | 5.6 | 5.6 | 6 | 9 | 11 |
| Boa Vista (Civ/Mil) | 2.8 | 6 | 8 | 9 | 11 | Nadi, Fiji | −17.8 | −17.8 | −18 | −17 | −19 |
| Punta Maisi, Cuba | 20.3 | 19 | 19 | 21 | 23 | Fort-De-France | 14.6 | 14.6 | 14 | 15 | 17 |
| Catacamas | 14.9 | 15 | 15 | 17 | 19 | Tunis | 36.83 | 36.8 | 28 | 29 | 32 |
| Hong Kong | 22.3 | 20 | 20 | 22 | 24 | Ankara | 40.12 | 40.1 | 29 | 31 | 35 |
| Debrecen | 47.5 | 30 | 36 | 40 | 41 | Tabriz, Iran | 38.05 | 38.1 | 30 | 30 | 33 |
| Rajkot | 22.3 | 24 | 20 | 22 | 24 | Tehran Mehrabad | 35.41 | 35.4 | 31 | 28 | 31 |
| Chennai | 13.1 | 13 | 14 | 16 | 18 | Nadi, Fiji | −17.8 | −17.8 | −18 | −17 | −19 |
| Bandar Seri Begawan | 4.9 | 5 | 9 | 11 | 12 | Kisii, Kenya | −0.67 | −0.7 | −3 | −6 | −8 |
| Tehran | 35.4 | 31 | 28 | 31 | 33 | Kiev | 50.4 | 50.4 | 35 | 37 | 41 |
| Yadz | 31.9 | 26 | 26 | 29 | 30 | Odessa | 46.45 | 46.5 | 31 | 35 | 39 |
| Kilkenny | 52.7 | 30 | 39 | 43 | 44 | Rleigh, NC | 35.86 | 35.9 | 32 | 28 | 32 |
| Be'Er'Sheva | 31.3 | 29 | 25 | 28 | 30 | Bakershfirld,CA | 35.43 | 35.4 | 29 | 28 | 31 |
| Ctania | 37.5 | 27 | 29 | 33 | 34 | Austin,TX | 30.29 | 30.3 | 28 | 25 | 28 |
| Accra, Ghana | 5.6 | 6 | 9 | 11 | 13 | Abu Dhabi | 24.43 | 24.4 | 25 | 21 | 24 |
| Kingston De Cuba | 20.0 | 20 | 18 | 21 | 22 | Heemsby | 52.68 | 52.7 | 34 | 39 | 43 |
| Osaka | 34.8 | 30 | 28 | 31 | 32 | London | 51.15 | 51.2 | 34 | 38 | 42 |
| Jerusalem, Israel | 31.9 | 28 | 26 | 29 | 30 | Montevideo | −34.8 | −34.8 | −32 | −28 | −31 |
| Tashkent | 41.3 | 32 | 32 | 35 | 37 | Tashken | 41.27 | 41.3 | 32 | 32 | 35 |
| Nairobi | −1.3 | 4 | 7 | 8 | 10 | Nadi, Fiji | −17.8 | −17.8 | −18 | −17 | −19 |
| Kwajalein Atoll | 8.7 | 12 | 11 | 13 | 15 | Roma, Ciampino | 41.8 | 41.8 | 30 | 32 | 36 |
| Kwanju | 35.1 | 29 | 28 | 31 | 33 | Carascas | 10.6 | 10.6 | 10 | 12 | 14 |
| Pyongyang | 39.0 | 36 | 30 | 34 | 35 | Hanoi | 21.2 | 21.2 | 16 | 19 | 22 |
| Podgorica | 42.4 | 36 | 32 | 36 | 38 | Gondar, Ethiopia | 12.53 | 12.5 | 18 | 14 | 16 |
| Shira, Iran | 29.5 | 26 | 24 | 27 | 29 | Harare, Zimbabwe | −17.9 | −17.9 | −22 | −17 | −19 |
| Kashi, China | 39.5 | 35 | 31 | 34 | 36 | Damascus, Syria | 33.4 | 29 | 27 | 30 | 32 |
| Hanoi, Vietnam | 21.1 | 16 | 19 | 22 | 23 | Johannesburg | −26.1 | −29 | −22 | −25 | −27 |
| Kaunas, Lithuania | 54.9 | 33 | 40 | 45 | 46 | Dakar, Senegal | 14.7 | 14 | 15 | 17 | 19 |
However, from Table 15, Table 16, Table 17, it can be seen that global solar radiation and maximum incident solar radiation decreased simultaneously as the optimal location angle increased in most cities and varied considerably from site to site as well as for locations with the same latitude. For example, although Bujumbura and Yaounde reported the same latitudes (3.61°N and 3.84°N respectively), their annual global solar radiation recorded 194.4 W/m2 and 184.3 W/m2 as presented in Table 16. Similarly, Munich and Sarajevo recorded the same latitudes (43.73°N and 43.51°N respectively), their annual global solar radiation recorded 163.33 W/m2 and 150.1 W/m2 respectively as presented in Table 15. Furthermore, Darhmaoui and Lahjouji [70] overestimated the maximum incident solar radiation while model 37 (global radiation index derived in this study) moderately adapted the radiation parameter by comparing the values here with Darhmaoui and Lahjouji [70] as well as the values calculated using the Liu and Jordan [50] model often used by numerous researchers to calculate the maximum incident solar radiation due to its wide application coverage and accuracy as presented in Table 15, Table 16.
4. Conclusion
Understanding the newly discovered and developed simplified global radiation index employed to estimate maximum incident solar radiation using global solar radiation as the only predictive variable is required as long as maximum efficiency is achieved for the photovoltaic system. Before the development of the first-ever simplified global radiation index (GRI) report from the beginning of the estimation of renewable energy resources, there are two obvious techniques in the literature to obtain the maximum incident solar radiation: (1) mathematical approach using isotropic models and complex anisotropic that in most cases the meteorological and atmospheric variables needed for computation are not readily available in most weather stations around the world, coupled with the rigorous mathematical proficiency required that discourages some researchers (2) experimentation technique that most researchers are often discouraged from undertaking the necessary instrumentation network as a result which includes costs, expertise, among others. In this study, a simplified experimental report to evaluate maximum incident solar radiation (HT) on monthly and yearly time scales using global solar radiation as the only widely and globally available predictor in the NASA database [49] bypassed these anomalies.
However, knowledge of the optimal tilt angle is of utmost importance as it is essential to obtain the maximum incident solar radiation in photovoltaic for high energy utilization purposes. In this study, the authors used an experimental approach to determine the optimal monthly and yearly mean tilt angle using six differently oriented and tilted PV modules in Lagos. The result revealed that Module 4 tilted at 16.8° and oriented to the south emerged as the optimal tilt angle after careful evaluation of renewable energy and statistical analysis. The IBM SPSS statistical tool was employed to develop several empirical and theoretical models to assess β and its corresponding HT on monthly and annual time scales in Lagos (empirical models) and Nigeria (theoretical models). Modeling of the solar energy resource was employed to promote the first empirical and theoretical models in Lagos and Nigeria in general, where the application of renewable energy techniques, in particular the use of the solar photovoltaic module to generate electricity, appears to be highly limited, as a result of the wrong impression and approach of most inexperienced professionals when purchasing, mounting, installing, assembling, orienting and especially in determining the angle of inclination of the PV modules concerning their customers. Therefore, the authors meticulously developed eight monthly models to estimate the optimal tilt angle using the monthly average Ho, H, n, δ, kt, RH, and T in Lagos. Five models were developed to estimate the monthly maximum incident solar radiation using the monthly average Ho, H, kt, T, and RH in Lagos using experimentally measured datasets.
To extend the boundary of rationality about renewable energy resources and appreciate theoretical physical applications in renewable energy, the authors have likewise established a theoretical approach for determining the optimal tilt angle for low-latitude locations near the equator. Based on the established technique, two annual models of optimal tilt angle were established using the latitude and elevation of locations in 37 metropolitan cities in Nigeria. The meteorological and atmospheric datasets obtained from the NASA database were equally applied for the development of seven empirical models using the annual average Ho, H, kt, ϕ and the elevation of the 37 metropolitan cities in Nigeria. To ascertain the applicability and estimation capacity of these models, relevant statistical indicators such as MBE, MPE, RMSE, RRMSE, R2 and, GPI were applied to determine the best performing model in each category of the model developed. The Ertekin and Yaldiz [66] assessment tool using RRMSE and GPI introduced by Behar et al. [55] and Despotovic et al. [56] was further employed to select the model with the best performance using the aggregate evaluation of statistical indicators already set. From the statistical tools, model 5 outperformed seven other models for estimating the optimal tilt angle for Lagos (Table 14); model 12 produced the best of the remaining four models developed to predict the maximum incident solar radiation in Lagos (Table 14); model 17 emerged as the best relationship for estimating the maximum incident solar radiation in 37 metropolitan cities in Nigeria (Table 14); and model 14 developed in this study, outperformed models 15 (present study), model 23 [67] developed in Iran and model 24 [54] developed in India to estimate the optimal tilt angle in 37 metropolitan cities in Nigeria (Table 14). Furthermore, the models adapted to estimate the optimal tilt angle (model 14) and the maximum incident solar radiation (model 17) at these study sites were applied together with existing models and observed values in selected places in the literature in Africa, in the Mediterranean region and the world in general. The results were considerably appreciable concerning the magnitude of the values found in the literature, as well as the corresponding latitudes and global solar radiation recorded in those locations.
Declarations
Author contribution statement
Anthony Umunnakwe Obiwulu: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Nald Erusiafe: Conceived and designed the experiments; Performed the experiments.
Muteeu Abayomi Olopade: Conceived and designed the experiments.
Samuel Chukwujindu Nwokolo: Analyzed and interpreted the data; Wrote the paper.
Declaration of interests statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
Data included in article/supp. material/referenced in article.
Funding statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
The authors are grateful to the management of Army Barrack in Yaba (Lagos), Nigeria and NASA Power project for providing enabling environment and datasets respectively for conducting this research.
References
- 1.Hatipoglu E., Al Muhanna S., Efird B. Renewables and the future of geopolitics: revisiting main concepts of international relations from the lens of renewables. Russ. J. Econ. 2021;6:358–373. [Google Scholar]
- 2.Hottel H.C. A simple model for estimating the transmittance of direct solar radiation through clear atmospheres. Sol. Energy. 1976 [Google Scholar]
- 3.Ullah A., Imran H., Maqsood Z., Butt N.Z. Investigation of optimal tilt angles and effects of soiling on PV energy production in Pakistan. Renew. Energy. 2019 [Google Scholar]
- 4.Shaker Al-Sayyab A.K., Al Tmari Z.Y., Taher M.K. Theoretical and experimental investigation of photovoltaic cell performance, with optimum tilted angle: Basra city case study. Case Stud. Therm. Eng. 2019 [Google Scholar]
- 5.Yadav S., Panda S.K., Hachem-Vermette C. Optimum azimuth and inclination angle of BIPV panel owing to different factors influencing the shadow of adjacent building. Renew. Energy. 2020 [Google Scholar]
- 6.Mamun M.A.A., Islam M.M., Hasanuzzaman M., Selvaraj J. Effect of tilt angle on the performance and electrical parameters of a PV module: comparative indoor and outdoor experimental investigation. Energy Built Environ. 2021 [Google Scholar]
- 7.Le Roux W.G. Optimum tilt and azimuth angles for fixed solar collectors in South Africa using measured data. Renew. Energy. 2016;96:603–612. [Google Scholar]
- 8.Obiwulu A.U., Chendo M.A.C., Erusiafe N., Nwokolo S.C. Implicit meteorological parameter-based empirical models for estimating back temperature solar modules under varying tilt-angles in Lagos, Nigeria. Renew. Energy. 2020;145:442–457. [Google Scholar]
- 9.Obiwulu A.U., Erusiafe N., Olopade M.A., Nwokolo S.C. Modeling and optimization of back temperature models of mono-crystalline silicon modules with special focus on the effect of meteorological and geographical parameters on PV performance. Renew. Energy. 2020;154 [Google Scholar]
- 10.Hafez A.Z., Soliman A., El-Metwally K.A., Ismail I.M. Tilt and azimuth angles in solar energy applications – a review. Renew. Sustain. Energy Rev. 2017;77:147–168. [Google Scholar]
- 11.Danandeh M.A., Mousavi G. S.M. Solar irradiance estimation models and optimum tilt angle approaches: a comparative study. Renew. Sustain. Energy Rev. 2018;92:319–330. [Google Scholar]
- 12.Chen X.M., Li Y., Zhao B.Y., Wang R.Z. Are the optimum angles of photovoltaic systems so important? Renew. Sustain. Energy Rev. 2020 [Google Scholar]
- 13.Yadav A.K., Chandel S.S. Tilt angle optimization to maximize incident solar radiation: a review. Renew. Sustain. Energy Rev. 2013 [Google Scholar]
- 14.Babatunde O., Akinyele D., Akinbulire T., Oluseyi P. Evaluation of a grid-independent solar photovoltaic system for primary health centres (PHCs) in developing countries. Renew. Energy Focus. 2018 [Google Scholar]
- 15.Kuo P.H., Huang C.J. A green energy application in energy management systems by an artificial intelligence-based solar radiation forecasting model. Energies. 2018 [Google Scholar]
- 16.Khezri R., Mahmoudi A., Aki H. IEEE Trans. Ind. Appl. 2022. Resiliency-oriented optimal planning for a grid-connected system with renewable resources and battery energy storage. [Google Scholar]
- 17.Ridha H.M., Gomes C., Hizam H., Ahmadipour M., Heidari A.A., Chen H. Multi-objective optimization and multi-criteria decision-making methods for optimal design of standalone photovoltaic system: a comprehensive review. Renew. Sustain. Energy Rev. 2021 [Google Scholar]
- 18.Gardashov R., Eminov M., Kara G., Emecen Kara E.G., Mammadov T., Huseynova X. The optimum daily direction of solar panels in the highlands, derived by an analytical method. Renew. Sustain. Energy Rev. 2020 [Google Scholar]
- 19.Okoye C.O., Bahrami A., Atikol U. Evaluating the solar resource potential on different tracking surfaces in Nigeria. Renew. Sustain. Energy Rev. 2018 [Google Scholar]
- 20.Xu L., Long E., Wei J., Cheng Z., Zheng H. A new approach to determine the optimum tilt angle and orientation of solar collectors in mountainous areas with high altitude. Energy. 2021 [Google Scholar]
- 21.Yadav S., Hachem-Vermette C., Panda S.K., Tiwari G.N., Mohapatra S.S. Determination of optimum tilt and azimuth angle of BiSPVT system along with its performance due to shadow of adjacent buildings. Sol. Energy. 2021 [Google Scholar]
- 22.Chinchilla M., Santos-Martín D., Carpintero-Rentería M., Lemon S. Worldwide annual optimum tilt angle model for solar collectors and photovoltaic systems in the absence of site meteorological data. Appl. Energy. 2021;281 [Google Scholar]
- 23.Jacobson M.Z., Jadhav V. World estimates of PV optimal tilt angles and ratios of sunlight incident upon tilted and tracked PV panels relative to horizontal panels. Sol. Energy. 2018 [Google Scholar]
- 24.Modarresi J., Hosseinnia H. Worldwide daily optimum tilt angle model to obtain maximum solar energy. IETE J. Res. 2020 [Google Scholar]
- 25.Sharma A., Kallioğlu M.A., Awasthi A., Chauhan R., Fekete G., Singh T. Correlation formulation for optimum tilt angle for maximizing the solar radiation on solar collector in the Western Himalayan region. Case Stud. Therm. Eng. 2021 [Google Scholar]
- 26.Duffy P.B., Field C.B., Diffenbaugh N.S., Doney S.C., Dutton Z., Goodman S., Heinzerling L., Hsiang S., Lobell D.B., Mickley L.J., Myers S., Natali S.M., Parmesan C., Tierney S., Williams A.P. Strengthened scientific support for the endangerment finding for atmospheric greenhouse gases. Science. 2019;80 doi: 10.1126/science.aat5982. [DOI] [PubMed] [Google Scholar]
- 27.Bright J.M., Smith C.J., Taylor P.G., Crook R. Stochastic generation of synthetic minutely irradiance time series derived from mean hourly weather observation data. Sol. Energy. 2015 [Google Scholar]
- 28.Nwokolo S.C., Ogbulezie J.C. A qualitative review of empirical models for estimating diffuse solar radiation from experimental data in Africa. Renew. Sustain. Energy Rev. 2018;92 [Google Scholar]
- 29.Nwokolo S.C. A comprehensive review of empirical models for estimating global solar radiation in Africa. Renew. Sustain. Energy Rev. 2017;78:955–995. [Google Scholar]
- 30.Union of Concerned Scientists . 2017. UCS Satellite Database 2-1-14 Satellite Database. (Union Concerned Sci.). [Google Scholar]
- 31.Ben Eke A. Prediction of optimum angle of inclination for flat plate solar collector in Zaria, Nigeria. Agric. Eng. Int. CIGR J. 2011 [Google Scholar]
- 32.Oko C.O.C. Optimum collector tilt angles for low latitudes. Open Renew. Energy J. 2012 [Google Scholar]
- 33.Waziri N.H., Usman A.M., Enaburekhan J.S., Babakano A. Determination of optimum tilt angle and orientation of a flat plate solar collector for different periods in Kano. Sci. Res. J. 2014 [Google Scholar]
- 34.Idowu O.S., Olarenwaju O.M., Ifedayo O.I. Determination of optimum tilt angles for solar collectors in low-latitude tropical region. Int. J. Energy Environ. Eng. 2013 [Google Scholar]
- 35.Udoakah Y., Okpura N. Determination of optimal tilt angle for maximum solar insolation for PV systems in enugu-southern Nigeria. Niger. J. Technol. 2015 [Google Scholar]
- 36.Okundamiya M.S., Nzeako A.N. Influence of orientation on the performance of a photovoltaic conversion system in Nigeria. Res. J. Appl. Sci. Eng. Technol. 2011 [Google Scholar]
- 37.Ajao K.R., Ambali R.M., Mahmoud M.O. Determination of the optimal tilt angle for solar photovoltaic panel in Ilorin, Nigeria. J. Eng. Sci. Technol. Rev. 2013 [Google Scholar]
- 38.Oladeji S., Ayodele T.R., Ogunjuyigbe A.S.O. Determination of optimal tilt angles in some selected cities of Nigeria for maximum extractable solar energy. Int. J. Renew. Energy Technol. 2018;9:453. [Google Scholar]
- 39.Schuster C.S. The quest for the optimum angular-tilt of terrestrial solar panels or their angle-resolved annual insolation. Renew. Energy. 2020 [Google Scholar]
- 40.Wessley G.J.J., Narciss Starbell R., Sandhya S. Modelling of optimal tilt angle for solar collectors across eight Indian cities. Int. J. Renew. Energy Res. 2017 [Google Scholar]
- 41.Abdulmunem A.R., Mohd Samin P., Abdul Rahman H., Hussien H.A., Izmi Mazali I., Ghazali H. Numerical and experimental analysis of the tilt angle's effects on the characteristics of the melting process of PCM-based as PV cell's backside heat sink. Renew. Energy. 2021 [Google Scholar]
- 42.Conceição R., Silva H.G., Fialho L., Lopes F.M., Collares-Pereira M. PV system design with the effect of soiling on the optimum tilt angle. Renew. Energy. 2019 [Google Scholar]
- 43.Barbón A., Bayón-Cueli C., Bayón L., Carreira-Fontao V. A methodology for an optimal design of ground-mounted photovoltaic power plants. Appl. Energy. 2022 [Google Scholar]
- 44.Awan A.B. Optimization and techno-economic assessment of rooftop photovoltaic system. J. Renew. Sustain. Energy. 2019 [Google Scholar]
- 45.Barbón A., Bayón-Cueli C., Bayón L., Rodríguez-Suanzes C. Analysis of the tilt and azimuth angles of photovoltaic systems in non-ideal positions for urban applications. Appl. Energy. 2022 [Google Scholar]
- 46.Sánchez J.P., McInnes C.R., Marchis F. Optimal sunshade configurations for space-based geoengineering near the Sun-Earth L1 point. PLoS ONE. 2015 doi: 10.1371/journal.pone.0136648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Elsayed M.M. Optimum orientation of absorber plates. Sol. Energy. 1989 [Google Scholar]
- 48.Qiu G., Riffat S.B. Optimum tilt angle of solar collectors and its impact on performance. Int. J. Ambient Energy. 2003 [Google Scholar]
- 49.NASA . 2020. NASA Prediction of Worldwide Energy Resources: the power project. Data Access Viewer. [Google Scholar]
- 50.Liu B.Y.H., Jordan R.C. The interrelationship and characteristic distribution of direct, diffuse and total solar radiation. Sol. Energy. 1960 [Google Scholar]
- 51.Cooper P.I. The absorption of radiation in solar stills. Sol. Energy. 1969 [Google Scholar]
- 52.Erbs D.G., Klein S.A., Duffie J.A. Estimation of the diffuse radiation fraction for hourly, daily and monthly-average global radiation. Sol. Energy. 1982 [Google Scholar]
- 53.Muneer T., Saluja G.S. A brief review of models for computing solar radiation on inclined surfaces. Energy Convers. Manag. 1985 [Google Scholar]
- 54.Jamil B., Siddiqui A.T., Denkenberger D.C. Solar radiation on South-facing inclined surfaces under different climatic zones in India. Environ. Prog. Sustain. Energy. 2019 [Google Scholar]
- 55.Behar O., Khellaf A., Mohammedi K. Comparison of solar radiation models and their validation under Algerian climate - the case of direct irradiance. Energy Convers. Manag. 2015 [Google Scholar]
- 56.Despotovic M., Nedic V., Despotovic D., Cvetanovic S. Review and statistical analysis of different global solar radiation sunshine models. Renew. Sustain. Energy Rev. 2015 [Google Scholar]
- 57.Udo S.O., Aro T.O. Global PAR related to global solar radiation for central Nigeria. Agric. For. Meteorol. 1999 [Google Scholar]
- 58.Maduekwe A.A.L., Garba B. Characteristics of the monthly averaged hourly diffuse irradiance at Lagos and Zaria, Nigeria. Renew. Energy. 1999 [Google Scholar]
- 59.Kasten F., Czeplak G. Solar and terrestrial radiation dependent on the amount and type of cloud. Sol. Energy. 1980;24:177–189. [Google Scholar]
- 60.Hegazy A. Estimation of optimum tilt angles for solar collector and gained energy at Cairo, Egypt. Int. J. Innov. Sci. Eng. Technol. 2019 [Google Scholar]
- 61.Abdullah A.S., Omara Z.M., Ben Bacha H., Younes M.M. Employing convex shape absorber for enhancing the performance of solar still desalination system. J. Energy Storage. 2022 [Google Scholar]
- 62.Udo S.O., Aro T.O. Technical note measurement of global solar global photosynthetically-active and downward infrared radiations at Ilorin, Nigeria. Renew. Energy. 1999 [Google Scholar]
- 63.Li D.H.W., Lam T.N.T. Determining the optimum tilt angle and orientation for solar energy collection based on measured solar radiance data. Int. J. Photoenergy. 2007 [Google Scholar]
- 64.Tang R., Wu T. Optimal tilt-angles for solar collectors used in China. Appl. Energy. 2004 [Google Scholar]
- 65.Jamil B., Siddiqui A.T., Akhtar N. Estimation of solar radiation and optimum tilt angles for South-facing surfaces in Humid subtropical climatic region of India. Int. J. Eng. Sci. Technol. 2016 [Google Scholar]
- 66.Ertekin C., Yaldiz O. Comparison of some existing models for estimating global solar radiation for Antalya (Turkey) Energy Convers. Manag. 2000 [Google Scholar]
- 67.Talebizadeh P., Mehrabian M.A., Abdolzadeh M. Determination of optimum slope angles of solar collectors based on new correlations. Energy Sources, Part A Recover. Util. Environ. Eff. 2011 [Google Scholar]
- 68.Jamil B., Siddiqui A.T. Estimation of monthly mean diffuse solar radiation over India: performance of two variable models under different climatic zones. Sustain. Energy Technol. Assess. 2018 [Google Scholar]
- 69.Gharakhani Siraki A., Pillay P. Study of optimum tilt angles for solar panels in different latitudes for urban applications. Sol. Energy. 2012 [Google Scholar]
- 70.Darhmaoui H., Lahjouji D. Energy Procedia. 2013. Latitude based model for tilt angle optimization for solar collectors in the Mediterranean region. [Google Scholar]
- 71.Jafarkazemi F., Saadabadi S.A. Optimum tilt angle and orientation of solar surfaces in Abu Dhabi, UAE. Renew. Energy. 2013 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data included in article/supp. material/referenced in article.