The pH-dependent reactions in the sonochemical synthesis of luminescent fluorides: The quest for the formation of KY₃F₁₀ crystal phases

Graphical abstract

Highlights

• •We reveal the significance of sonochemistry in the design of luminescent fluorides.
• •The study offers the key to synthesizing both the α- and δ-phases of KY₃F₁₀.
• •A landmark methodology for the preparation of yttrium hydroxyfluorides is reported.
• •The reaction mechanisms underlying the formation of the compounds are unraveled.
• •The Eu³⁺-doping endows the materials with highly tunable optical properties.

Abstract

In this study Eu³⁺-doped yttrium fluorides were designed by ultrasound-assisted processes at different pH values (4.0–9.0). This novel strategy has enabled to obtain materials with intriguing morphologies and modulated crystal structures: α-KY₃F₁₀, δ–KY₃F₁₀·xH₂O, and Y(OH)_3–xF_x. To date, the literature has primarily focused only on the α-phase of KY₃F₁₀. Yet, explaining the formation of the mostly uncharted δ-phase of KY₃F₁₀ remains a challenge. Thus, this paper offers the key to synthesizing both the α and the δ-phases of KY₃F₁₀ and also reports the first ultrasound-assisted process for the preparation of yttrium hydroxyfluorides. It is also unraveled the connection between the different pH-dependent reactions and the formation mechanisms of the compounds. In addition to this, the unique features of the Eu³⁺ ion have allowed to conduct a thorough study of the different materials and have endowed the compounds with photoluminescent properties. The results underscore a highly tunable optical response, with a wide gamut of color emissions (from orangish to red hues), lifetimes (from 7.9 ms to 1.1 ms) and quantum efficiencies (98–28%). The study unveils the importance of sonochemistry in obtaining luminescent fluorides with controlled crystal structures that can open up new avenues in the synthesis and design of inorganic materials.

1. Introduction

Sonochemistry has emerged as a powerful strategy in the synthesis and design of novel inorganic materials by virtue of its unique features [1], [2]. Sonochemical reactions are induced by ultrasound radiations that generate local hot spots which can reach temperatures above 5000 K, pressures exceeding 1000 atm, and heating and cooling rates higher than 10¹⁰ K/s [3]. These extreme, transient conditions allow the synthesis of chemical compounds with controllable structures, shapes, and crystallinity at room temperature, without the need to use high pressures or high temperatures that would entail an important economic cost. It comes as no surprise, therefore, that ultrasound-assisted processes to develop nano/micron-sized materials at the expense of other conventional methods have aroused a great deal of enthusiasm [4], [5].

As a series of important luminescent materials, fluoride hosts doped with lanthanide ions (Ln³⁺) are attracting a growing amount of attention owing to their remarkable applications in photonics, solar energy, medicine, bioanalytics, or environmental science [6], [7], [8], [9], [10]. The extraordinary optical response of these materials arises from their electronic characteristics: sharp f-f transitions, low phonon energy (usually below 600 cm⁻¹), and high viability of energy transfers with other ions [11], [12]. Particularly, fluoride crystal lattices with trivalent yttrium cations are the most common due to the ease with which they replace Y³⁺ ions by isovalent Ln³⁺ ions [13]. Moreover, Eu³⁺ has been widely appreciated for its adequacy as a site-sensitive structural probe, while the great similarity of its ionic radius to that of Y³⁺ ensures a perfect incorporation of the Ln³⁺ ion into the host matrix [14].

To date, KY₃F₁₀ and its Ln³⁺-doped counterparts have gained much attention for their important applications in several fields of materials science [15], [16], [17], [18], [19]. However, the studies in the literature have only focused on the common α-phase of KY₃F₁₀ in detriment of the mostly unknown δ-phase, which was discovered in 2000 by Le Berre et al. [20]. These authors reported the crystallographic description of this new structure and performed a detailed analysis of its zeolitic and thermal behavior. As a drawback, it is important to note that a great amount of hydrofluoric acid (HF) was required during the synthesis process. Even so, as far as we are aware, no additional research about this material had been conducted until the results of a recent study by our laboratory were published [21]. It was reported a simple high-yield method based on a sonochemical approach to obtain the compound δ-KY₃F₁₀·xH₂O. For the first time, the growth mechanism of this structure and its perfect adequacy for optical applications were studied. Moreover, the alternative method did not require the use of HF, which greatly reduced the safety hazards.

Despite the aforementioned signs of progress, explaining the mechanism underlying the formation of such an uncharted and promising phase of KY₃F₁₀ remains a challenge. In addition, further studies to exploit the δ-phase as host lattice for luminescent ions are required. The zeolitic behavior of this compound could also be essential for different photonic applications since it could help to modulate the incorporation/substitution of different cations inside the structure. With this in mind, in this paper, the significance of sonochemistry in the design of Eu³⁺-doped fluorides is revealed. The ultrasound-assisted processes enabled to obtain materials with intriguing morphologies and modulated crystal structures: α-KY₃F₁₀, δ–KY₃F₁₀·xH₂O, and Y(OH)_3–xF_x. Hence, this study not only offers the key to synthesizing both the α- and δ-phases of KY₃F₁₀ but also reports a landmark methodology for the preparation of yttrium hydroxyfluorides. It also explains how the different pH–dependent reactions govern the formation mechanisms of the compounds. Further to this, the incorporation of Eu³⁺ into the host lattice endows the material with important optical properties that are also highly tunable, depending on the compound.

Therefore, this study can contribute to a further comprehension of the δ-phase of KY₃F₁₀, while at the same time opening up novel avenues in the synthesis and design of inorganic materials for important photonic and associated applications.

2. Experimental section

2.1. Materials

The reagents used were yttrium(III) nitrate hexahydrate [Y(NO₃)₃·6H₂O 99.9%, Alfa Aesar], europium(III) nitrate hexahydrate [Eu(NO₃)₃·6H₂O 99.9%, Strem Chemicals], potassium hydroxide [KOH 85%, Labkem], and potassium tetrafluoroborate [KBF₄ 96%, Sigma-Aldrich]. All reagents were used without further purification.

2.2. Synthesis of Eu³⁺-doped compounds

The powders were prepared following a sonochemical process based on some previous studies of our research group detailed in references [21], [22]. Calculations were performed in order to obtain approximately 0.25 g of the α/δ-phase of KY₃F₁₀. In the synthesis procedure, 1.5 mmol of Ln(NO₃)₃·6H₂O were dissolved in 30 mL of water (Ln = Y, Eu; 1 mol% Eu³⁺) with a resulting pH of 4.0. Then, 3.0 mmol of KBF₄ were added to the above solution and the pH of the medium was adjusted to the desired value (pH: 4.0, 6.0, 6.5, 7.0, 7.5, 8.0, 8.5, 9.0) by adding dropwise 0.1 or 2 M KOH aqueous solutions (for pH > 7.0, a whitish precipitate appeared and it underwent redissolution/‌precipitation processes with the reaction time). The mixture was stirred for 5 min and the final volume was adjusted to 50 mL with water. The whole system was transferred into a Bandelin Sonorex ultrasonic bath operating at a frequency of 35 kHz for 24 h. The as-formed precipitate was then centrifuged, washed several times with water, and dried under an infrared lamp. For convenience, the abbreviations used for the different samples were denoted as “S-n”, where n indicates the initial pH of the reaction medium. A general scheme of the experimental procedure can be found in Fig. 1 of the Supplementary Information.

Fig. 1.

Coordination polyhedra of Y³⁺ in the different crystal structures together with the corresponding coordination numbers (CN) and local symmetries (LS). Some symmetry elements have been included for clarification purposes. The labels F1, F2, F3… refer to fluoride anions situated at different Wyckoff positions.

2.3. Characterization

All the characterization was performed at room temperature. Powder X-ray diffraction (XRD) was performed using a Bruker-AX D8-Advance X-ray diffractometer with CuK_α1 radiation from 2θ = 15° to 90° at a scan speed of 2.25°/min. The microstructure of the samples was observed using a JEOL 7001F scanning electron microscope (SEM) operating with an acceleration voltage of 30 kV, a measuring time of 20 s, and a working distance of 10 mm. For the microstructural characterization, the powders were deposited on double-sided carbon stickers (previously adhered to the surface of aluminum stubs) and were sputtered with platinum. Moreover, the FT-IR spectra of the powders were recorded using an Agilent Cary 630 FT-IR spectrometer in transmission mode. Chemical equilibrium diagrams were generated with the Database-Spana software package, which is based on the SOLGASWATER and HALTAFALL algorithms [23], [24].

The optical properties were studied with an Eclipse Fluorescence Spectrophotometer (Varian). Excitation spectra were recorded in the range 250–500 nm with an emission wavelength of 593 nm, while emission spectra were performed upon excitation at 395/397 nm (depending on the compound) in the 500–750 nm range. All the spectra were normalized to unity. The asymmetry ratio $R$ and the Judd-Ofelt parameters (${\mathrm{\Omega }}_2$ and ${\mathrm{\Omega }}_4$) were calculated from the emission spectra. In addition, the CIE coordinates of the Eu³⁺-doped materials were calculated from the spectra using the GoCIE software package [25]. Time-resolved luminescence measurements were also performed to obtain the lifetimes and calculate the corresponding quantum efficiencies. In these experiments, the emission wavelength was set to 593 nm and the excitation was monitored at 395/397 nm (depending on the compound).

3. Results and discussion

3.1. Structural characterization

Prior to the discussion on the structural characterization, a brief description of the different crystal structures is provided in order to properly understand some concepts that can be helpful in this and subsequent sections of the paper. The compound α–KY₃F₁₀ crystallizes in a cubic structure belonging to the $\mathit{Fm}\overline{3}m(O_h^5)$ space group (SG) with 8 formula units per unit cell (Z = 8) [26], while δ-KY₃F₁₀·xH₂O presents a cubic crystal system with SG = $\mathit{Fd}\overline{3}m(O_h^7)$ and Z = 16 [27]. Conversely, Y(OH)_3–xF_x is a hexagonal structure with SG = $P{6}_3/m(C_{6h}^2)$ and Z = 2 [28]. The coordination polyhedra of Y³⁺ in the different crystal structures are depicted in Fig. 1. All structures were plotted with VESTA software [29]. The coordination number (CN) and the local symmetry (LS) of Y³⁺ are also shown. For the sake of clarity, different colors have been assigned to the crystal structures and have been maintained throughout all the graphics in the article: red (α-KY₃F₁₀), blue (δ-KY₃F₁₀·xH₂O), and green (Y(OH)_3–xF_x). When a mixture of α- and δ-phases exists, the color purple is used.

It is important to mention that the ideal LS of Y³⁺ in Y(OH)_3–xF_x is C_3h. Yet, this symmetry would only be strictly true for the fluoride-free compound, i.e., Y(OH)₃, since the partial substitution of OH^– by F^– generates some local distortions and a lack/descent in symmetry is expected. The C_3h point group is thus lowered to other subgroups of symmetry such as C_3v, C_s, or C₁, depending on the local environment of Y³⁺.

The XRD patterns of the Eu³⁺-doped powders prepared at different pH values following the sonochemical synthesis procedure are depicted in Fig. 2 and the results are summarized in Table 1. As can be appreciated, there is an extreme influence of the pH in the resulting crystal phase. Sample S-4.0 exhibits all the peaks corresponding to the single phase of cubic α-KY₃F₁₀ (ICSD card 00–040-9643). However, the increase in pH produces a coexistence between the α-KY₃F₁₀ and δ-KY₃F₁₀·xH₂O phases in samples S-6.0 and S-6.5. Indeed, the peaks corresponding to the cubic δ-phase of KY₃F₁₀ become more prominent as the pH increases (see the blue stars in Fig. 2). Surprisingly, as presented in a recent publication [21], when the initial pH of the synthesis is set to 7.0 (sample S-7.0) the XRD pattern exhibits only the peaks corresponding to δ-KY₃F₁₀·xH₂O (ICDD card 04–016-7073) [27], with no traces of α–KY₃F₁₀ secondary phase or other impurities.

Fig. 2.

XRD patterns for the Eu³⁺-doped compounds prepared at different pH values by a sonochemical process. The blue stars in samples S-6.0 and S-6.5 highlight the presence of peaks corresponding to the δ–KY₃F₁₀·xH₂O structure. For the sake of greater clarity, the crystal phases of each powder have been indicated in brackets as abbreviations: α for α-KY₃F₁₀, δ for δ-KY₃F₁₀·xH₂O, and YOHF for Y(OH)_3–xF_x. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 1.

Initial and final pH values of the reaction medium for the different Eu³⁺-doped compounds. The crystal phase and the weight of the synthesized powders are also indicated.

Sample	Initial pH	Final pH	Powder Weight (g)	Crystal Phase
S-4.0	4.0	1.0	0.24	α-KY3F10
S-6.0	6.0	1.0	0.24	α-KY3F10 + δ-KY3F10·xH2O
S-6.5	6.5	1.1	0.25	α-KY3F10 + δ-KY3F10·xH2O
S-7.0	7.0	1.1	0.25	δ-KY3F10·xH2O
S-7.5	7.5	6.4	0.22	Y(OH)3–xFx
S-8.0	8.0	6.5	0.14	Y(OH)3–xFx
S-8.5	8.5	6.6	0.06	Y(OH)3–xFx
S-9.0	9.0	7.2	0.05	Y(OH)3–xFx

For the rest of the samples synthesized with a pH ≥ 7.5, another substantial change occurs. At first glance, the most notable visual change is the absence of peaks between 20 and 25° 2θ (present in the previous samples), a fact that affirms that the crystal structure of these compounds is different and, probably, with a different spatial group and/or crystal system. The XRD patterns of samples S-(7.5–9.0) are in good agreement with the hexagonal structure Y(OH)_3–xF_x (ICDD card 00–080-2008, x  = 1.43). The reflection peaks of these powders are slightly shifted toward a higher angle relative to the JCPDS data (Figure S2, Supplementary Information), a behavior previously noted in several studies [30], [31], [32], [33], [34]. In this series of samples, it is important to note that the increase in the pH produces a broadening and a decrease in the intensity of the peaks, resulting in a more amorphous character.

In addition, the initial pH has an extreme influence not only on the crystal phase(s) obtained, but also on the weight of the final product and on the final pH of the reaction medium (measured at the end of the ultrasonic process, that is, 24 h after the reaction started), which are summarized in Table 1 as well. The results will be discussed in the following section because of their direct connection with the reaction mechanisms. To further characterize the materials, the FT-IR spectra of some representative compounds were recorded (Figure S3, Supplementary Information). All the spectra exhibited the characteristic bands associated with the internal vibrations of the different crystal structures. Besides, the presence of some absorbed water was noted.

3.2. Reaction mechanism

In order to elucidate the phenomena that govern the reaction mechanisms, some emphasis must first be placed on the equilibria that take place in the aqueous medium. Hence, it has been noted that one of the keystones is the hydrolysis of the tetrafluoroborate ion, which can be written as [35]:

BF₄^– + 3H₂O ⇄ 3H⁺ + 4F^– + B(OH)₃ (1).

In addition, the equilibrium reactions of hydrofluoric acid and the species formed with boric acid [36], [37] also have to be considered:

HF ⇄ H⁺ + F^– (2).

B(OH)₃ + xF^– + (x – 1)H⁺ ⇄ [BF_x(OH)_4-x]^– + (x – 1)H₂O (3).

Moreover, there is an equilibrium between the deprotonated [BF_x(OH)_4-x]^– species and their respective protonated forms HBF_x(OH)_4-x, although the latter compounds dissociate very quickly and only HBF₃(OH) has a significant concentration in the system at pH < 0, so they can be neglected. The equilibrium constant for the reverse reaction of (1), i.e., the formation of BF₄^–, takes the value K_f = 10^19.21 at 25 °C. Consequently, the hydrolysis of BF₄^– is not favored due to the small value of the equilibrium constant of the forward reaction (1), K_h = 10^–19.21, which has also been established to be very slow [35], [38].

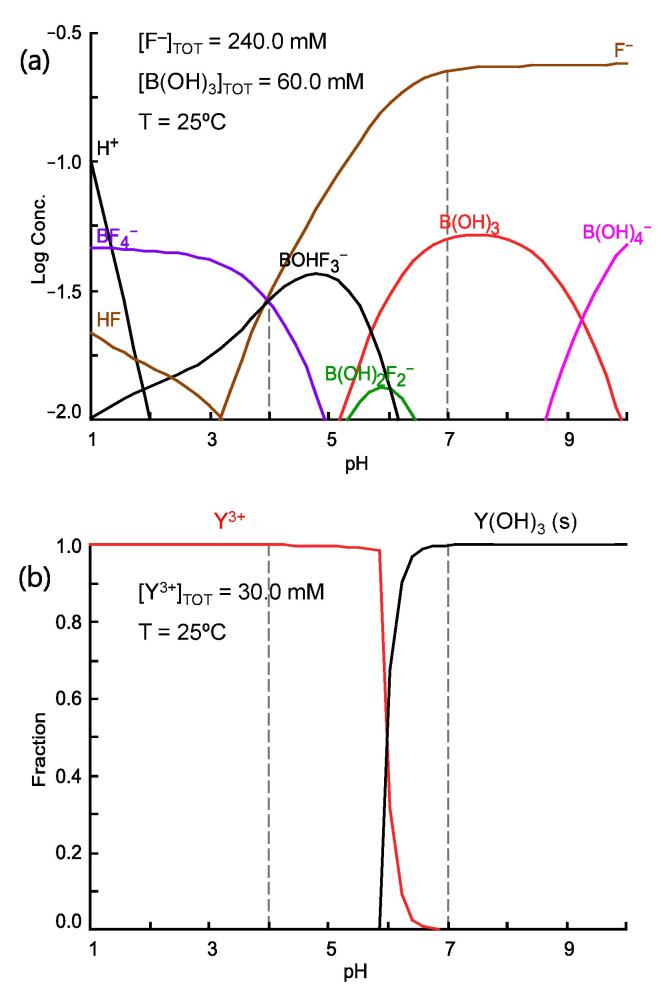
In order to properly understand the reaction mechanisms, the theoretical chemical equilibrium diagrams were generated with the Database-Spana software package and are presented in Fig. 3. Default parameter values (temperature and total concentrations) were set according to the experimental procedure followed in the synthesis of the materials. It should be noted that these diagrams take into account the thermodynamic behavior of the species, while neither the kinetics nor the sonochemical effects are contemplated. Hence, the diagrams can be useful to discuss some aspects of the reactions but they are not representative of the final products. Bearing this in mind, yttrium was considered separately because its reactivity with fluoride anions depends on the degree of hydrolysis of BF₄^–.

Fig. 3.

(a) Speciation in the boric acid–hydrofluoric acid system as a function of pH. (b) Fractions of the dominant species of yttrium as a function of pH.

Fig. 3(a) depicts the speciation in the B(OH)₃–HF system as a function of pH, see reactions (1)–(3). At pH ≈ 7, an inflection point in the F^– curve is observed with a plateau for pH > 7. By that stage BF₄^– hydrolysis should be completed. Fig. 3(b) presents the fractions of the dominant species of yttrium as a function of pH. It is clear that in the pH range 6–7, Y(OH)₃ starts to become the dominant species. In contrast to the hydrolysis and reactivity of BF₄^– (slow and requires activation by sonochemical processes), the solid formation of Y(OH)₃ is immediate. This fact is in clear agreement with the experimental procedure since in the basic medium a whitish precipitate was formed, thus indicating the formation of yttrium hydroxide, which will be redissolved, as highlighted in the following. As per the above considerations, it can be distinguished different reaction pathways (addressed in the following sections) that determine the formation of the final product. Furthermore, for a better comprehension of the results, the evolution of the final pH and the weight of the powders synthesized at different initial pH values are depicted in Fig. 4. This will also be discussed below because of their direct connection with the reaction mechanisms.

Fig. 4.

Evolution of the final pH and the weight of the powders synthesized at different initial pH values.

3.2.1. Formation of compounds with initial pH ≤ 7

As can be observed in Fig. 4, all the samples synthesized with an initial pH ≤ 7 had a very similar behavior taking into account the weight of the powders (0.24/0.25 g) and the final pH of the reaction medium (1.0/1.1). The amounts of the powders produced indicate that the reactions have a high yield since the calculations were performed so as to obtain approximately 0.25 g. The final pH values agree with the protons released during the successive hydrolysis of BF₄^–, see reaction (1). These facts lead to feel that the general reaction for these compounds must be very similar and can be represented as:

K⁺ + 3Y³⁺ + 10F^– + xH₂O → (α/δ)-KY₃F₁₀·xH₂O (4).

The most intriguing issue to understand is perhaps the evolution from the α-phase of KY₃F₁₀ toward the formation of the δ-phase as the initial pH is increased. It should be noted that both phases crystallize in a cubic system with very similar space groups ($\mathit{Fm}\overline{3}m$ for the α-phase, and $\mathit{Fd}\overline{3}m$ for the δ-phase). Therefore, these similarities may explain the possible coexistence of the two phases (as in samples S-6.0 and S-6.5) or the tendency of the system to form only one crystal structure in detriment of the other one (samples S-4.0 and S-7.0).

To explain the single-phase formation of δ-KY₃F₁₀·xH₂O (sample S-7.0), more focus must be put again on Fig. 3(b). As mentioned earlier, yttrium hydroxide precipitates at pH ≈ 7. Moreover, the equilibrium of reaction (1) is expected to be shifted to the right by the addition of OH^–, which partially neutralizes the H⁺. In fact, during the synthesis of this sample, when the pH value was initially set to 7.0, the solution became turbid, thereby indicating the precipitation of a whitish solid that corresponded to Y(OH)₃. However, within a few minutes after putting the mixture in the ultrasonic bath, the pH of the medium decreased (which is in agreement with the successive hydrolysis of BF₄^–) and the precipitate was redissolved (see our previous publication for further details [21]). It also has to be noted that for samples synthesized with pH ≤ 6.5, this effect was not observed and no precipitate was initially formed. Therefore, the incipient precipitation of Y(OH)₃ and its posterior redissolution could be crucial to control the fluoride and yttrium concentrations that would lead the system toward the formation of δ–KY₃F₁₀·xH₂O.

Additionally, the formation of [BF_x(OH)_4-x]^– species might also play a pivotal role because they could affect the solvation shell of Y³⁺ ions and make the reaction advance through different pathways. Indeed, at pH = 4, in Fig. 3(a) the confluence of curves corresponding to BF₄^–, [BF₃(OH)]^– and F^– can be appreciated.

3.2.2. Formation of compounds with initial pH > 7

The mechanistic explanations for these compounds are easier because all the samples present the same crystal structure: Y(OH)_3–xF_x. According to Fig. 3(b), Y(OH)₃ is the dominant species in a basic medium. During the synthesis procedure, the fast precipitation of Y(OH)₃ yields an amorphous solid that can progressively react with fluoride anions released by BF₄^– hydrolysis. The reaction that takes place to form the final product may be understood by means of an anion-exchange process [39]:

Y(OH)₃ + xF^– ⇄ Y(OH)_3–xF_x + xOH^– (5).

For these samples, at the initial stage (before being ultrasonicated), two phases were clearly distinguished in the reaction medium: a solid phase at the bottom of the bottle containing mainly the as-formed Y(OH)₃, and a transparent aqueous phase at the top of it. As time went by, the distinction between the two phases started to disappear and only one phase was appreciated at the end of the reaction with the final product dispersed (as in the rest of the samples in this work).

Nonetheless, the amount of product decreased as the medium became more basic (see Fig. 4). Hence, the sonochemical processes involved in the formation of crystalline yttrium hydroxyfluorides are not favored in highly basic media. A plausible account of it might be found considering that some redissolution processes can occur promoted by ultrasonication. Additionally, the decrease in the powder weight may also be explained considering the kinetics of reaction (5), which is influenced by the pH. Thus, further analysis about the formation of hydroxyfluorides at different reaction times could complement this work and be the scope of future studies. Be that as it may, it is important to note that, to the best of our knowledge, this is the first publication in which an ultrasound-assisted process is described for the fabrication of yttrium hydroxyfluorides. Particularly, these materials can be used as precursors to produce the greatly appreciated YOF compounds by topotactic transformations or thermal decompositions [40], [41].

3.3. Morphological characterization

Fig. 5 presents the SEM images of the different Eu³⁺-doped materials and a schematic representation to illustrate the evolution of the morphology in a simple way. Table 2 summarizes the morphological results (shapes and approximate sizes of the particles and their respective subunits).

Fig. 5.

SEM images of the Eu³⁺-doped samples prepared at different pH values by a sonochemical process, and schematic representation of the morphology of the particles.

Table 2.

Representative morphologies and approximate sizes of the different particles and subunits.

Sample	Morphology	Particle size (μm)a	Subunit	Subunit size (Ø nm)a
S-4.0	Spherical	0.2 – 0.7 (Ø)	Nanospheres	20
S-6.0	Spherical + Truncated Triangular Nanoplates	0.2 – 0.7 (Ø)	Nanospheres	20
S-6.5	Spherical + Truncated Triangular Nanoplates	0.2 – 0.7 (Ø)	Nanospheres	20
S-7.0	Truncated Triangular Nanoplates	0.1 (thickness), 0.2 (long edge)	–	–
S-7.5	Spheroidal	1.0 (long axis), 0.6 (short axis)	Nanorods	30
S-8.0	Spheroidal	0.8 (long axis), 0.3 (short axis)	Nanorods	40
S-8.5	Spheroidal	0.9 (long axis), 0.3 (short axis)	Nanorods	50
S-9.0	Amorphous	Aggregates	–	–

^aFor samples S-6.0 and S-6.5, the particle/subunit size refers to the spherical particles.

Sample S-4.0 (α-KY₃F₁₀ structure) consists of spherical particles. A close-up observation (Figure S4(a), Supplementary Information) shows that these particles resulted from the self-assembly of nano-sized subunits around 20 nm in diameter (Ø). The same morphology is representative of samples S-6.0 and S-6.5 (α-KY₃F₁₀ + δ–KY₃F₁₀·xH₂O structures), although some truncated triangular nanoplates were also observed in a very small proportion (Figure S4(b), Supplementary Information). The major particles (spherical) are attributed to the α-phase, while the minor ones (nanoplates) can be assigned to the δ-phase. These remarks suggest that the δ–phase is in the minority. In contrast, sample S-7.0 (δ-KY₃F₁₀·xH₂O structure) only exhibits truncated triangular nanoplates, which is consistent with the existence of a single-phase rather than a mixture as in samples S-6.0 and S-6.5. It was also noted that the aggregation of some nanoplates occurred in order to reduce their surface energy.

As explained in the previous sections, substantial changes take place in materials with a Y(OH)_3–xF_x structure. The SEM micrographs show that samples S-(7.5–8.5) exhibit spheroidal particles that are composed of aligned nanorods as subunits (a magnification can be found in Figure S4(c,d) of the Supplementary Information). These nanorods were observed both on the surface and in the interior of the architectures and they aggregated side-by-side. Similar morphologies were obtained by Xianghong et al. [34] for Y(OH)_3–xF_x compounds synthesized hydrothermally. Curiously, the spheroidal particles tend to elongate with an increase in the pH. Lastly, the particle aggregates of sample S-9.0 evidence its amorphous character, as observed in the XRD pattern. Hence, the evolution of the crystal phase is also linked to the evolution of the morphology of particles (from spherical to truncated triangular nanoplates and to spheroidal). This fact can be explained taking into account that the activation energy required to form each compound is different, so the ultrasound radiation affects the morphology in different manners as well.

3.4. Photoluminescence studies

3.4.1. Excitation and emission spectra

The room temperature excitation and emission spectra of the Eu³⁺-doped samples recorded with a delay time (DT) of 0.2 ms are shown in Fig. 6. All the excitation spectra present similar spectra profiles, exhibiting the common bands associated with the different transitions of Eu³⁺ from the ground ⁷F₀ level to higher excited levels with a clear dominance of the ⁷F₀→⁵L₆ transition. For samples S-(4.0–7.0), with (α/δ)–KY₃F₁₀·xH₂O structures, the maximum of the band corresponding to the above transition is observed at 395 nm, while for samples S-(7.5–9.0), with a Y(OH)_3–xF_x structure, the band is slightly shifted toward the low-energy side (397 nm). Therefore, the corresponding emission spectra were recorded upon excitation at 395/397 nm, depending on the sample.

Fig. 6.

Room temperature excitation and emission spectra obtained with a DT = 0.2 ms for samples prepared at different pH values. The blue stars in the emission spectra indicate bands associated with ⁵D₁→⁷F_J transitions from the higher excited level ⁵D₁. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The most significant differences are found in the emission spectra of the phosphors, the profiles of which depend on the crystal lattice of the materials and thus the resulting color emission is affected, as will be discussed later on. All the samples present the typical ⁵D₀→⁷F_J transitions of Eu³⁺ but interesting changes occur, taking into account the presence of transitions from higher excited levels, the splitting and relative intensities of bands, and their broadening.

Samples S-4.0 (α-KY₃F₁₀ structure) and S-(6.0, 6.5), with a mixture of α-KY₃F₁₀ + δ–KY₃F₁₀·xH₂O structures, have the same emission profile. These results suggest that Eu³⁺ ions are mainly incorporated into the crystal lattice of α-KY₃F₁₀ in samples where the coexistence of α/δ-phases exists (S-6.0 and S-6.5). For these first samples, S-(4.0, 6.0, 6.5), the whole spectra are dominated by the ⁵D₀→⁷F₁ magnetic dipole transition and notable contributions from transitions that take place from the higher excited state ⁵D₁ are observed (highlighted with blue stars in Fig. 6). The absence of the ⁵D₀→⁷F₀ transition is justified by its overlapping with the ⁵D₀→⁷F₁ band and because of its typical low intensity. The interpretation of the emission spectra recorded with a DT = 0.2 ms can be difficult due to the mixing of ⁵D_0,1→⁷F_J transitions. Therefore, the photoluminescence measurements of these samples were also carried out increasing the detector delay time to 10 ms, since the Eu³⁺ lifetimes associated with the transitions occurring from the ⁵D₁ higher energy level are lower than those corresponding to the ⁵D₀ ground level. As a result, these experiments allowed to observe only the contribution of ⁵D₀→⁷F_J transitions and ensure that the assignation of bands was accurate (Figure S5 of the Supplementary Information). Further information about the assignation of the emission bands to their respective transitions can also be found in Section 3 of the Supplementary Information.

A remarkable contrast is observed in sample S-7.0 (with a single δ-KY₃F₁₀·xH₂O phase). In this case, the spectrum is dominated by the ⁵D₀→⁷F₂ electric dipole transition, and ⁵D₁→⁷F_J transitions (blue stars) are almost absent, probably quenched by the existence of crystalline water molecules in the host lattice. However, although this contribution was very small and may not be of substantial importance for the subsequent calculation of physical parameters, the emission spectrum of sample S-7.0 was also collected with a DT = 10 ms.

The last series of samples S-(7.5–9.0) presents the typical photoluminescence profile of Eu³⁺-doped Y(OH)_3–xF_x compounds [34], and also exhibits broad bands and is dominated by the ⁵D₀→⁷F₂ electric dipole transition. For these samples, there is a complete absence of transitions from higher excited levels due to the presence of hydroxyl groups in the crystalline matrix. Besides, the observation of the ⁵D₀→⁷F₀ transition is clearer, albeit with low intensity.

Lastly, the CIE coordinates of the materials are plotted in Fig. 7. Interestingly, the color emissions of the phosphors can be tuned from orangish to red hues through the different crystal structures (higher pH values imply an evolution toward reddish tonalities). However, it is important to note that samples with the same crystal phase have virtually the same color emission regardless of the pH.

Fig. 7.

CIE chromaticity diagram of the Eu³⁺-doped samples prepared at different pH values.

3.4.2. Asymmetry ratio and Judd-Ofelt parameters

The ⁵D₀→⁷F₁ transition has a magnetic dipole character and is considered independent of the chemical surroundings of Eu³⁺ ions. Moreover, the ⁵D₀→⁷F₂ transition of Eu³⁺ presents an electric dipole character, and is therefore hypersensitive to the local symmetry of the dopant [42], [43]. As a consequence, the relative intensities of these transitions are widely used to obtain information about the site symmetry of Eu³⁺ ions [44]. For that purpose, it is usual to define the asymmetry ratio $R$ as the quotient between the integrated intensities of the ⁵D₀→⁷F₂ and ⁵D₀→⁷F₁ transitions.

On the other hand, the Judd-Ofelt (JO) parameters are extremely useful to characterize the local structure and bonding of lanthanide ions and, in the particular case of Eu³⁺, they can be calculated directly from the emission spectra [45]. In the literature, it is well known that the short-range JO parameter (${\mathrm{\Omega }}_2$) provides information about the polarizability and crystal environment of Eu³⁺ in the lattice, whereas the long-range JO parameter (${\mathrm{\Omega }}_4$) is sensitive to macroscopic properties of the hosts such as viscosity and rigidity [46]. A direct relation between ${\mathrm{\Omega }}_2$ and the asymmetry ratio $R$ can be established [47]. Hence, larger values of ${\mathrm{\Omega }}_2$ point to stronger polarizability and higher asymmetry of Eu³⁺ ions in the crystal lattice [48], [49]. The physicochemical parameters mentioned above are listed in Table 3, while the equations employed to calculate them are described in Sections 4 and 5 of the Supplementary Information.

Table 3.

Asymmetry ratio ($R$) values, Judd-Ofelt parameters (${\mathrm{\Omega }}_2$, ${\mathrm{\Omega }}_4$), ⁵D₀ lifetimes (${\tau }_{\mathrm{o}\mathrm{b}\mathrm{s}}$) and quantum efficiencies ($\eta$) for the different Eu³⁺-doped phosphors. For samples S-(7.5–9.0), ${\tau }_{\mathrm{o}\mathrm{b}\mathrm{s}}$ corresponds to the effective lifetime.

Sample	$R$	${\mathrm{\Omega }}_2$(10-20 cm2)	${\mathrm{\Omega }}_4$(10-20 cm2)	${\tau }_{\mathrm{o}\mathrm{b}\mathrm{s}}$(ms)	${\tau }_{\mathrm{r}\mathrm{a}\mathrm{d}}$(ms)	$\eta$(%)
S-4.0	0.99	1.77(2)	1.65(1)	7.88(1)	8.07(4)	98
S-6.0	0.97	1.74(2)	1.77(2)	7.73(2)	8.10(4)	95
S-6.5	0.97	1.72(2)	1.80(2)	7.52(2)	7.99(4)	94
S-7.0	1.43	2.52(3)	1.93(3)	4.93(1)	6.80(3)	73
S-7.5	1.84	3.17(4)	1.96(3)	1.82(5)	4.25(3)	43
S-8.0	1.79	3.09(4)	2.16(3)	1.40(6)	4.23(3)	33
S-8.5	1.71	2.95(4)	2.30(3)	1.20(4)	4.28(4)	28
S-9.0	1.85	3.19(4)	2.56(3)	1.11(3)	3.99(2)	28

The values of the asymmetry ratio are linked to the incorporation of Eu³⁺ ions in different crystal structures: $R$ ≈ 1.0 for α-KY₃F₁₀ as the main phase (pH ≤ 6.5), $R$ ≈ 1.4 for δ-KY₃F₁₀·xH₂O (pH = 7.0), and $R$ ≈ 1.8 for Y(OH)_3–xF_x (pH ≥ 7.5). The successive increase of $R$ indicates the higher asymmetry of Eu³⁺, which is in excellent agreement with the expected site symmetry for the dopant (see Fig. 1). The asymmetry ratio and ${\mathrm{\Omega }}_2$ are directly related, and therefore the same reasoning can be applied to this JO parameter. It is also observed that ${\mathrm{\Omega }}_4$ increases as the pH rises, which can be attributed to the different host lattices and morphologies of the particles, since ${\mathrm{\Omega }}_4$ is ascribed to bulk properties.

3.4.3. Time-resolved luminescence and quantum efficiencies

The decay curves for the ⁵D₀→⁷F₁ emission of Eu³⁺ were measured to allow further analysis of the luminescence properties of the samples (Figure S7, Supplementary Information) and to extract the observed lifetimes (${\tau }_{\mathrm{o}\mathrm{b}\mathrm{s}}$). Interestingly, a small rising part at the beginning of the decay profiles was observed for samples synthesized with pH ≤ 7.0 (samples with α/δ-phase of KY₃F₁₀). This effect is ascribed to the Eu³⁺ population feeding from the upper ⁵D₁ excited level. The rising phenomenon was more notable for samples S-(4.0–6.5), which also presented the most important contribution of ⁵D₁→⁷F_J emissions (see the emission spectra in Fig. 6). The decay curves were thus fitted using a single exponential model with a modified pre-exponential factor that modulates the population of Eu³⁺ ions [50], [51]. However, the decay curves of samples synthesized with a pH ≥ 7.5, Y(OH)_3–xF_x compounds, were best fitted with a double exponential model without the presence of a rising part. This change in the fitting expression might well be attributed to different local environments of Eu³⁺ affected by the surrounding OH^– and F^– anions.

In order to evaluate the quantum efficiencies (the intrinsic quantum yields,$\eta$) of the materials, the theoretical radiative lifetimes (${\tau }_{\mathrm{r}\mathrm{a}\mathrm{d}}$) of Eu³⁺ ions for the ⁵D₀ level were also calculated from the emission spectra. Extra details about all the equations used can be found in Section 6 of the Supplementary Information. The observed lifetimes, the calculated radiative lifetimes, and the quantum yields are presented in Table 3. All the parameters present a monotonic decrease with the rise in pH. Lifetimes vary from 7.9 ms to 1.1 ms, whereas extremely different quantum yields are also obtained (98–28%). The key point that allows these values to be obtained is the sequential evolution of the crystal phase. For instance, the crystalline water molecules in the host lattice of the δ-phase of KY₃F₁₀ (sample S-7.0) can partially quench the radiative emission, thus yielding notably lower quantum efficiencies in comparison to the α–phase of KY₃F₁₀ (sample S-4.0). Following the same line of reasoning, the presence of hydroxyls in Y(OH)_3–xF_x compounds has a strong impact on the quenching process. For this last series of samples, a higher degree of suppression also occurs while increasing the pH. This can be attributed to the increasing amorphous character of the particles (as noted in the lack of resolution in the photoluminescence spectra) and to the possible presence of residual hydroxyls in the surface of the particles.

By all accounts, the results underscore the highly tunable optical response of the materials, with a wide gamut of color emissions, lifetimes, and quantum efficiencies. These parameters have shown a direct connection with the modulated crystal structures and morphologies of the compounds. The detailed analysis of the photoluminescence properties has allowed to further confirm the formation of the different crystal structures due to the unique site-selective characteristics of the Eu³⁺ ion. Hence, the optical study has also corroborated the postulated formation mechanisms of the materials.

4. Conclusions

In order to shed some light on the formation of the different crystal phases of KY₃F₁₀, Eu³⁺-doped yttrium fluorides were designed by ultrasound-assisted processes at a wide range of pH values (4.0–9.0). The major conclusions that can be extracted are as follows:

• ▪The crystal phase and the morphology of the materials are critically dependent upon the initial pH of the reaction medium.
• ▪A description of plausible reaction mechanisms has underlined the fact that the hydrolysis of the tetrafluoroborate ion and the incipient precipitation of Y(OH)₃ and posterior redissolution/precipitation processes could play a crucial role.
• ▪The unique site-selective characteristics of the Eu³⁺ ion have allowed to describe the optical performance of the materials and to establish a relationship with their chemical structure, as has been observed with the calculations of the asymmetry ratio and the Judd-Ofelt parameters.
• ▪The emission profiles of the phosphors depend on the crystal lattice of the materials, which exhibit ⁵D_i→⁷F_J transitions with different splitting, broadening, and relative intensities of bands. The resulting color can thus be tuned from orangish to red hues.
• ▪The modulated optical response of the phosphors is also evidenced by the lifetime values (7.9–1.1 ms) and quantum efficiencies (98–28%).

Based on the aforementioned points, the present novel strategy can contribute to an in-depth comprehension of these materials, especially of the uncharted δ–KY₃F₁₀·xH₂O structure. Furthermore, the study unveils the importance of sonochemistry in obtaining luminescent fluorides with controlled crystal structures that can open up new avenues in the synthesis and design of inorganic materials for important photonic and associated applications.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: