Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2022 Jun 13.
Published in final edited form as: Clin Biomech (Bristol). 2014 Oct 12;30(2):121–128. doi: 10.1016/j.clinbiomech.2014.10.001

Effect of the metastatic defect on the structural response and failure process of human vertebrae: An experimental study

Ron N Alkalay 1
PMCID: PMC9190195  NIHMSID: NIHMS1811815  PMID: 25586264

Abstract

Background:

Pathologic vertebral fractures are associated with intractable pain, loss of function and high morbidity in patients with metastatic spine disease. However, the failure mechanisms of vertebrae with lytic defects and the failed vertebrae’s ability to retain load carrying capacity remain unclear.

Methods:

Eighteen human thoracic and lumbar vertebrae with simulated uncontained bone defects were tested under compression-bending loads to failure. Failure was defined as 50% reduction in vertebral body height. The vertebrae were allowed to recover under load and re-tested to failure using the initial criteria. Repeated measure ANOVA was used to test for changes in strength and stiffness parameters.

Findings:

Vertebral failure occurred via buckling and fracture of the cortex around the defect, followed by collapse of the defect region. Compared to the intact vertebrae, the failed vertebrae exhibited a significant loss in compressive strength (59%, p = 0.001), stiffness (53%, p = 0.05) and flexion (70%, p = 0.01) strength. Significant reduction in anterior-posterior shear (strength (63%, p = 0.01) and stiffness (67%, p = 0.01)) and lateral bending strength (134%, p = 0.05) were similarly recorded. In the intact vertebrae, apart from flexion strength (r2 = 0.63), both compressive and anterior-posterior shear strengths were weakly correlated with their stiffness parameters (r2 = 0.24 and r2 = 0.31). By contrast, in the failed vertebrae, these parameters were strongly correlated, (r2 = 0.91, r2 = 0.86, and r2 = 0.92, p = 0.001 respectively).

Interpretation:

Failure of the vertebral cortex at the defect site dominated the initiation and progression of vertebral failure with the vertebrae failing via a consolidation process of the vertebral bone. Once failed, the vertebrae showed remarkable loss of load carrying capacity.

Keywords: Pathologic vertebral fractures, Lytic Defects, Experimental, Failure mechanisms

1. Introduction

Annually, up to 1.5 million new cases of cancer are reported in the U.S (American-Cancer-Society, 2012) with thirty to sixty percent of this patient population presenting bony metastasis in the spine (Ratliff and Cooper, 2004; Toma et al., 2007; White, 2006). The migration of cancer cells to the highly vascular vertebrae often results in the destruction of the osseous tissues (Taneichi et al., 1997; Tschirhart et al., 2004; Whealan et al., 2000; Whyne et al., 2003). This pathological process exposes the patients to a high risk of catastrophic failure of the affected vertebra (Lad et al., 2007; Weber et al., 2011), with the resulting fractures often associated with intractable pain, loss of function and increased morbidity (Falicov et al., 2006; Walls et al., 1995; Weber et al., 2011), and in up to 30% of these patients, neurologic compromise from spinal cord compression (Roth et al., 2004; Taneichi et al., 1997). Pathologic vertebral fracture thus represents an important cause of disability with significant clinical and economic implications for the US healthcare system (Coleman, 2001; Lad et al., 2007; Weber et al., 2011).

The deleterious effect of lytic lesions on the risk of vertebral failure was recently demonstrated in an animal model for vertebral lytic metastasis (Hardisty et al., 2012; Hojjat et al., 2010). The occurrence of the lesion resulted in the doubling of compressive strains compared to the control vertebrae with the development of stress concentration at the dorsal aspects of the vertebrae indicating increased structural instability. Retrospective clinical studies have identified defect geometry, destruction of the pedicles, pain, age, anatomic site, lesion type, activity levels and, for thoracic vertebrae, costovertebral joint destruction, as significant risk factors for impending vertebral collapse (Bunting, 1985; Coleman and Stanley, 1994; Fidler, 1981; Taneichi et al., 1997; Weber et al., 2011). Experimental (Whealan et al., 2000; Windhagen et al., 1997, 2000) and computational (Tschirhart et al., 2004, 2006; Whyne et al., 2001, 2003) studies have further established measures of defect size and geometry, defect location within the vertebral body and bone density, to be predictors of vertebral risk of fracture. However, although most often used as a predictor of vertebral fracture risk (Carlson et al., 1995), relative lesion size has been shown to account for only 50% of the variation in vertebral body strength (Taneichi et al., 1997; Tokuhashi et al., 2005). At present, despite this extensive body of work and clinical reports, no clear guidelines have been established to allow prediction of fracture risk (Roth et al., 2004). Critically, the structural mechanisms underlying the initiation and progression of the failure process for vertebrae with uncontained lytic defects remain unclear.

The objectives of this study were twofold: The first was to investigate the effect of an uncontained defect within the body of thoracic and lumbar human vertebrae, on the failure process of the vertebrae in response to compression-flexion loading. Our hypothesis is that Failure of vertebral cortex in human vertebrae with significant, uncontained, osetoltic defects determines the initiation of vertebral failure. The second was to establish the degree to which the failed vertebrae, having been allowed to recover under load simulating bed rest, retained residual load carrying capacity.

2. Methods

2.1. Specimen preparation

Five thoraco-lumbar spines were obtained from donors aged 65–78 years. Each spine was radiographed (Faxitron, HP, McMinnville, OR) to exclude existing pathology or fractures, the spine submerged in a saline bath to simulate soft tissues and Bone Mineral Density (BMD) measured in the anterior-posterior (A-P) and lateral (LAT) anatomical axis of the vetebra using a DXA scanner (QDR 2000 +, Hologic Inc., Waltham, MA). Once dissected clean of all musculature, 18 individual vertebral levels were obtained by sectioning through the disc. The vertebrae were coded, wrapped in saline soaked gauze and stored at − 20 °C in double plastic bags until the day of testing. Anterior (HA) and posterior (HP) vertebral body heights were measured from the sagittal radiographs and the measurement verified along the vertebral sagittal midline using a mechanical caliper (Mitutoyo, Japan, accuracy 0.01 mm). The location of the measurement was prescribed on the vertebra to be used for subsequent measurements (failed and recovered). For each stage (intact, failed and recovered) a vertebral deformity index (VDI) was computed from the following formula, ((HP - HA)/HP)*100.

2.2. Metastatic defect creation

On the day of testing, the vertebra was thawed for four hours at room temperature, followed by a one-hour submersion in a 37 °C heated saline bath. Registration markers, identifying the vertebral body sagittal and coronal anatomical axes, were created on the vertebral cortex and the vertebra registered to an imaging device secured to a fluoroscopy unit (Mini 6600, GE medical). Sagittal and coronal radiographs were obtained with care to keep magnification errors to a minimum, the images transferred to transparencies and the outlines of a defect, corresponding to 40 % of the vertebral body, drawn on the transferred images (Fig. 1). The drawings were super-imposed on the screens of the fluoroscopy unit and a high speed drill (MultiPro, Dremel, WI) with an attached 3 mm ball-end burring bit used to create an entry hole in the vertebral cortical shell with a diameter ranging from 6–9 mm, a mean of 7.2 mm (standard deviation = 1.4 mm). Under continuous fluoroscopy control, the drill was used to create a cavity in the vertebral body to match the one planned in the sagittal and coronal planes (Fig. 1). Defects were created equally along the medial and lateral aspect of the vertebrae to avoid bias.

Fig. 1.

Fig. 1.

Open in a new tab

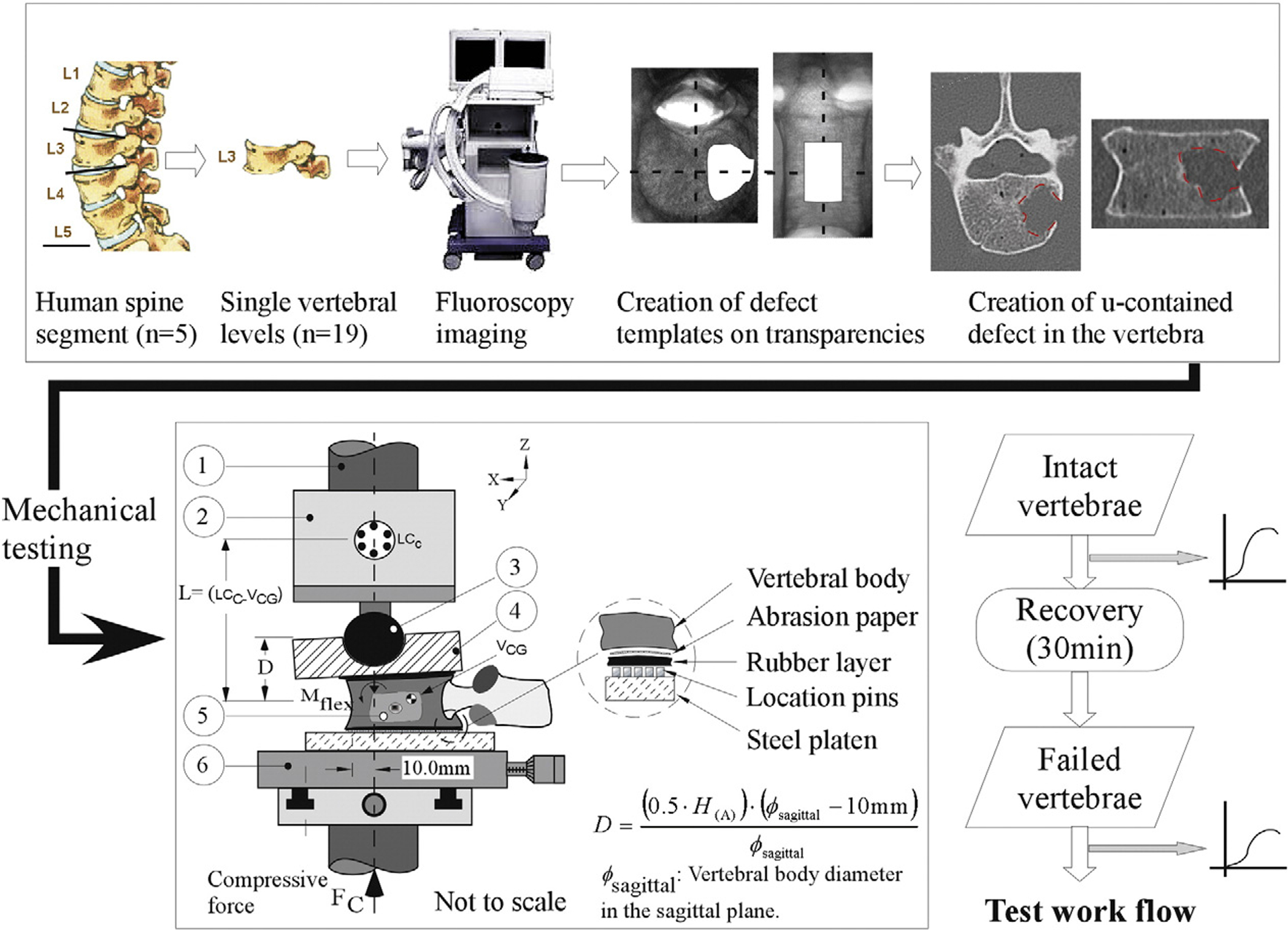
A schematic diagram of the testing device used to apply combined compression and flexion loads onto the vertebral specimens. 3 mm rubber sheets located on either side of the vertebra allowed a more uniform transfer of load between the test device and the vertebra. Coarse-grit sandpaper, bonded on the outer side of the rubber sheets (Fig. 1) provided containment of the vertebra to the testing assembly whilst keeping the strengthening effect of cement embedding of the vertebra on the resulting vertebral deformations to a minimum. Required test displacement at the actuator, D, of the material testing system was computed from the equation (Alkalay et al., 2008) with (H(A)): anterior height of the vertebra (intact, failed), Ø sagittal: the sagittal diameter of the upper endplate measured from the X-rays.

2.3. Mechanical testing

The testing methodology, previously detailed (Alkalay et al., 2008), is hereby described in brief.

2.4. Testing system

The vertebra was mounted and registered to a mechanical testing device (Fig. 1), secured to a servo-hydraulic test system (Instron 1331, Instron Co., Canton, MA). The location of the vertebra was adjusted such that the Instron’s long axis was located 10 mm posterior to the anterior-most boundary of the vertebra and a loading platen positioned on top of the vertebra. A ball indenter, articulating with a hemi-spherical socket on the loading platen, completed the test load pathway (Fig. 1) with a 6DOF load cell (MC-5000, AMTI, MA) used to measure the resulting forces and moments.

2.5. Intact vertebra

Under displacement control, the vertebra was subjected to a monotonically increasing compressive displacement at a rate of 5.0 mm/min until any of the following conditions occurred: a 50% reduction in the anterior height of the vertebral body, the load cell capacity (5000 N) was exceeded, or a vertebral failure, defined as a reduction of 10% in maximum load, occurred (Alkalay et al., 2008). With the test completed, the anterior and posterior heights of the vertebral body were re-measured and the vertebra re-radiographed.

2.6. Failed vertebra

The vertebrae were allowed to recover under a load of 200 N for a period of 30 min. Vertebral heights were re-measured and the required displacement for actuator re-computed by subtracting the failed vertebral heights from that of the intact vertebra, Eq. 2 (Fig. 1). The vertebra was co-registered to the test system, re-tested to failure and the change in its geometry post-failure re-measured once the test was completed. For both tests, the applied displacement and resulting forces and moments were recorded at a rate of 10Hz (V. 9.0, LabView, National Instruments, Austin, TX) with overestimation of the measured moments due to the difference between the coordinate systems of the load cell and the vertebrae corrected in software. Yield and ultimate failure values and displacement at yield were measured for each force and moment response curve. Linear models, fitted to the linear portion spanning between 20–80% of the curve, were used to compute corresponding stiffness values.

2.6. Statistical analysis

Repeated measure ANOVA (JMP 8.0, SAS, NC) was used to test for statistically significant changes in the anterior and posterior vertebral body heights between the intact, recovered and failed test stages. Tukey’s HSD (honestly significant difference) test was to evaluate the effects of individual test conditions. Paired t-test was used to test for difference in the structural parameter, i.e. ultimate strength and stiffness values computed from the force and moment curves of the intact vs. the failed vertebrae. Analysis of covariance (ANCOVA) was used to test for the effect of failure on the association between the strength and stiffness parameters underlying the force and moment structural response of the vertebrae. ANCOVA was similarly used to test for the effect of estimated BMD, obtained by averaging the values of the adjacent intact vertebrae, and that of vertebral level, on the ultimate strength of the vertebrae. Significance level was set at 5%.

3. Results

Though many of the vertebrae exhibited osteophyts on the radiographs, none exhibited pre-test fractures. Vertebral BMD showed a mean (standard deviation) of 0.54 (0.06)g.cm−2 with the values distributed normally (Table 1). Mean change in VDI index between the intact (_I), failed (_F) and recovered (_R) test conditions are presented in Fig. 2. Independent of vertebral level, vertebral failure yielded a significant reduction in the anterior 19.2(6.8)% and posterior 7.2(36.2)% vertebral heights (p b 0.001 respectively), resulting in a significant increase in computed VDI_F (460%, p < 0.001). Comparisons for individual levels, showed these differences to be significant for the L2 (p < 0.01), L4 (p < 0.05) and L5 (p < 0.05) levels. With recovery, both the anterior and posterior vertebral heights increased (6.5 (4.9)% and 2.4 (4.8)%), the difference being significant for the anterior height (p < 0.001). These changes yielded a significant restoration of vertebral geometry (VDI_R, p < 0.01), independent of level (p N 0.05). However, VDI_R values were significantly lower than VDI_I, (p < 0.001), independent of level (Fig. 2). A-P BMD values were negatively associated with the degree of restoration of the vertebral geometry (p < 0.01, r2 = 0.75, F < 0.05). No such association was found for the lateral BMD.

Table 1.

Specimen identification, vertebral bone properties, and the change in the vertebral anterior and posterior heights as a function of test condition.

Donor Level Age H/W BMD Vertebral body heights (mm)
(sex) (cm/kg) (g.cm2) HA_I HP_I VDI_I HA_F HP_F VDI_F HA_R HP_R VDI_R
22408 T12 62 (F) 158/56 0.37 22.5 25.4 11.4 20.8 24.4 14.8 21.9 24.8 11.7
121101 L1 78 (F) 147/52 0.21 29 27.8 − 4.3 23 23 0.0 24 24.5 2.0
1503 71 (F) 156/56 0.41 24.5 26.2 6.5 20 24.3 17.7 21.2 24.6 13.8
22408 0.35 27.8 30 7.3 22 28.6 23.1 21.5 25 14.0
121101 L2 0.17 24 26.6 9.8 18.6 22.5 17.3 20 24 16.7
1503 0.44 27 28 3.6 23 26.7 13.9 25 26.8 6.7
22408 0.35 28.3 28.8 1.7 22 25 12.0 24.4 27 9.6
1503 L3 0.44 28.3 26 8.8 21 24 12.5 23.5 24.9 5.6
22408 0.33 30 27 −11.1 23 25 8.0 23.5 25.3 7.1
51106 65 (F) 152/57 0.51 30.86 32.88 6.1 27.78 29.9 7.1 28 30.5 8.2
1503 0.46 29 25.5 −13.7 26 26.5 1.9 27.3 27.3 0.0
2003 66 (F) 163/59 0.34 28.7 29.6 3.0 22.3 28.8 22.6 25.3 29 12.8
22408 0.35 33 30.8 − 7.1 28.5 30 5.0
51106 0.49 31.2 32.8 4.9 24.7 29.4 16.0 27.6 30.3 8.9
1503 L5 0.64 29.6 24.7 − 19.8 21 22.3 5.8 25.2 22.6 − 11.5
2003 0.51 26.6 27.3 2.6 18.3 22.7 19.4 19.6 23 14.8
22408 0.50 32 31 − 3.2 28.8 29.3 1.7 28.8 30.3 5.0
51106 0.67 31.1 24 − 29.6 −24.2 25.3 4.3 26 27.5 5.5
Open in a new tab

HA_I, HP_I; HA_R, HP_R: Anterior and Posterior heights of the vertebral body in its Intact (pre-test) and post-Recovery; BMD: Bone Mineral Density. VDI: Vertebral Deformity Index (%).

Fig. 2.

Fig. 2.

Open in a new tab

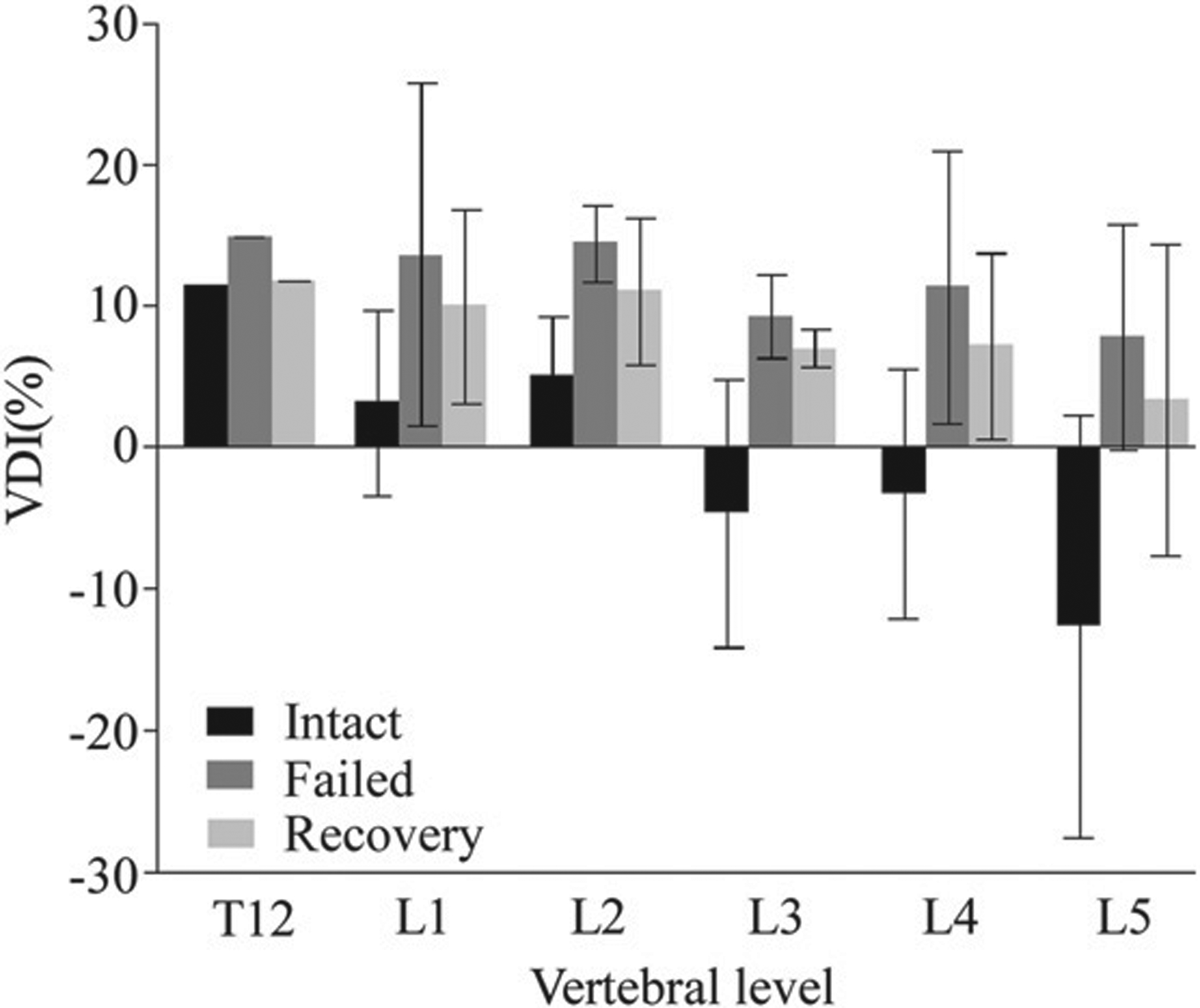
The change the geometry of the vertebral body, summarized using the computed vertebral deformity index (VDI), with failure and subsequent recovery as a function of vertebral levels. (Error bars indicate the standard deviation of the mean).

3.1. Mechanical tests

All of the vertebrae tested exhibited an anterior-flexion compressive failure. Fig. 3 illustrates the force [A] and moment [B] response curves for the intact and, once failed, L2 vertebra. Under increasing deformation, the intact vertebra exhibited several failure events experimentally observed to correspond to the buckling (Fig. 1 Suppl.) and fracture of the cortex around the defect (Region I). This fracture progressed by continual collapse of the defect until complete closure of the defect portal (Region II) followed by the deformation of the complete vertebra (Region III). The post-failure response of the vertebra, Regions (IV - V) is typical to that observed for osteoporotic vertebrae (Alkalay et al., 2008).

Fig. 3.

Fig. 3.

Open in a new tab

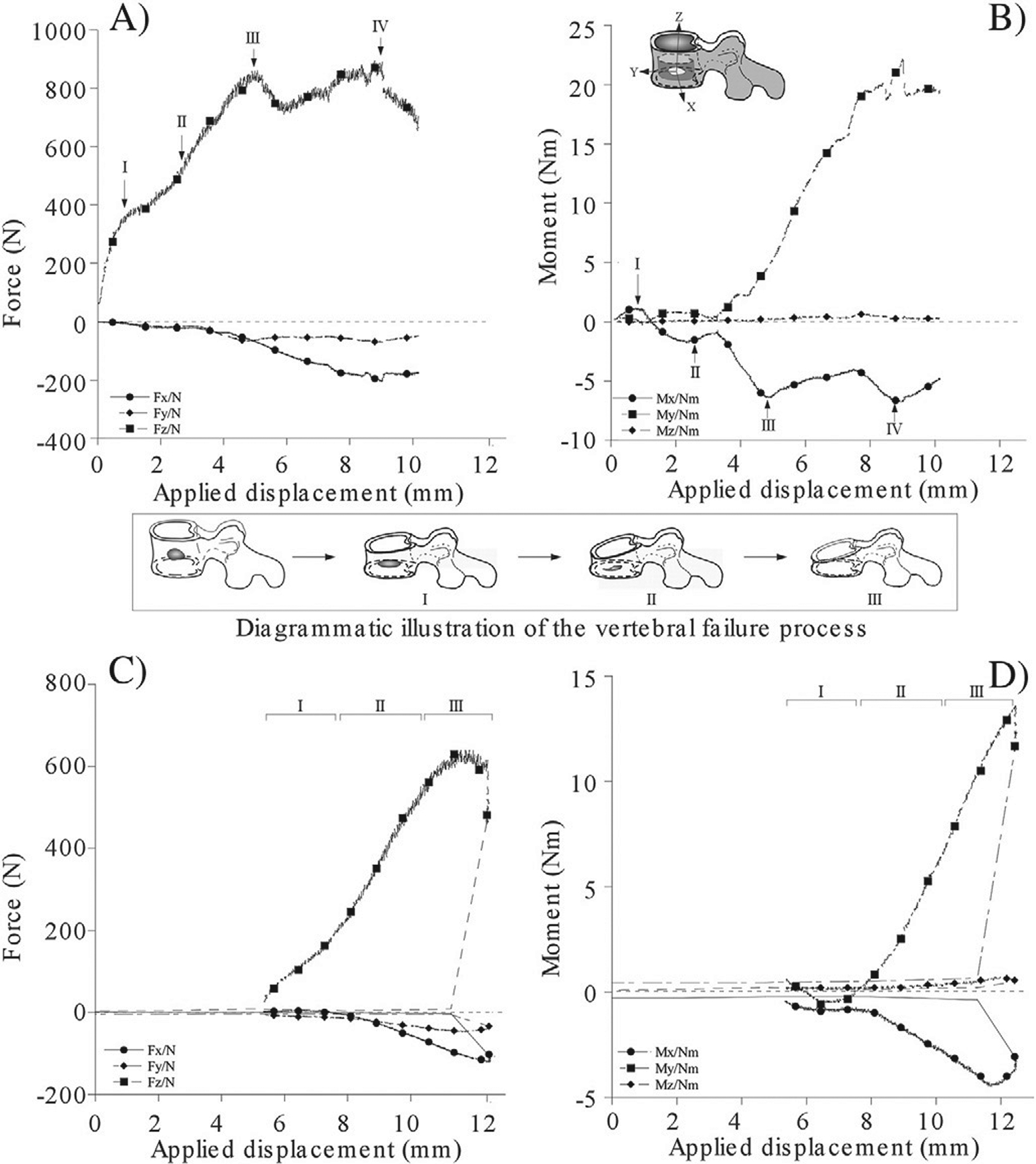
The force and moment displacement curves of an L2 vertebral specimen with lytic defect under increasing magnitude of combined axial compression and anterior flexion moment. The intact response is presented in subfigures (A and B), and the corresponding failed response in subfigures (C and D).

Table 2 summarizes the change in the ultimate strength and stiffness values of the intact and failed vertebrae. Compared to the intact vertebrae, the failed vertebrae exhibited significantly lower ultimate compressive strength [((1409.1(693.2) vs. 2246.3(897.0)) N, p < 0.001] and stiffness [((250.1(130.3) vs. 382.1(194.2)) Nm/mm, p < 0.05], Table 2. Similarly, the anterior-posterior shear strength [(308.6(195.8) vs. 502.3(278.4)) N, p < 0.01] and stiffness [(62.7(41.9) vs. 105.6(39.7)) N/mm, p < 0.01] and the ultimate strength in flexion [(62.7(26.3) vs. 36.9(21.4)) Nm, p < 0.01] and in lateral bending [(5.6 (5.3) vs. 13.1 (17.2))Nm, p < 0.05] were significantly reduced. Though lateral bending stiffness [(0.4 (1.7) vs. 0.9 (2.7))Nm/mm] and medial-lateral shear strength [0.2 (41.6) vs. 18.9 (33.8)]N were markedly lower, these differences were not statistically significant, (p > 0.05).

Table 2.

Comparison of the mechanical parameters associated with the load–displacement response of the intact and failed vertebrae.

Characteristic Parameter Intact Failed p (I-F)
Compression σU(N) 2246.3 (897.0) 1409.1 (693.2) < 0.001
S(N/mm) 382.1 (194.2) 250.1 (130.3) < 0.05
Flexion σU(Nm) 62.7 (26.3) 36.9 (21.4) < 0.01
S(Nm/mm) 11.4 (5.3) 9.2 (10.9) NS
A-P shear σU(N) 502.3 (278.4) 308.6 (195.8) < 0.01
S(N/mm) 105.6 (39.7) 62.7 (41.9) < 0.01
Lateral Bend σU(Nm) 13.1 (17.2) 5.6 (5.3) < 0.05
S(Nm/mm) 0.9 (2.7) 0.4 (1.7) NS
M-L shear σU(N) 18.9 (33.8) 0.2 (41.60 NS
S(N/mm) 0.9 (3.4) 2.0 (5.6) NS
Open in a new tab

A-P: along the Anterior-Posterior vertebral plane, M-L: along the transverse vertebral plane.

σy: Yield strength, σU: Ultimate strength. S: Stiffness. (I-F): Intact vs. Failed. Values presented in mean (SD). NS: p > 0.05.

Fig. 4 presents linear regression models employed to assess the effect of failure on the relationship between the yield strength and stiffness values, computed from the force and moment response curves of the intact and failed vertebrae. In the intact vertebrae, the increase in flexion strength was moderately correlated with the increase in stiffness (r2 = 0.63, p < 0.01). By contrast, yield strength values for axial compression, A-P shear and lateral bending were weakly correlated to their respective stiffness values, r2 = 0.24 and r2 = 0.31, (p > 0.05 respectively). Post-failure, strong correlations were found between the yield vs. stiffness values for axial compression (r2 = 0.91), flexion (r2 = 0.92) and the A-P shear (r2 = 0.86) responses (p < 0.001 for all three models). In contrast to the intact vertebrae, the failed vertebrae demonstrated negative association between the A-P shear and stiffness (Fig. 4). ANCOVA analysis of the model’s regression coefficients between the intact and the failed vertebrae, found the difference to be statistically significant (p = 0.028). Although the correlation between strength and stiffness for lateral bending was not statistically significant (r2 = 0.21, p > 0.05), similar to the A-P shear response, the association became negative with failure (Fig. 4.D). In the intact vertebrae, the increase in estimated BMD values was weakly correlated with either the increase in strength or in stiffness values associated with the compressive or flexion response (Fig. 2 Suppl.). By contrast, the estimated BMD values were strongly correlated with the failed vertebrae flexion and compressive strength (r2=0.71 and 0.77) and moderately to strongly correlated with the respective stiffness values (r2 = 0.54 and 0.70).

Fig. 4.

Fig. 4.

Open in a new tab

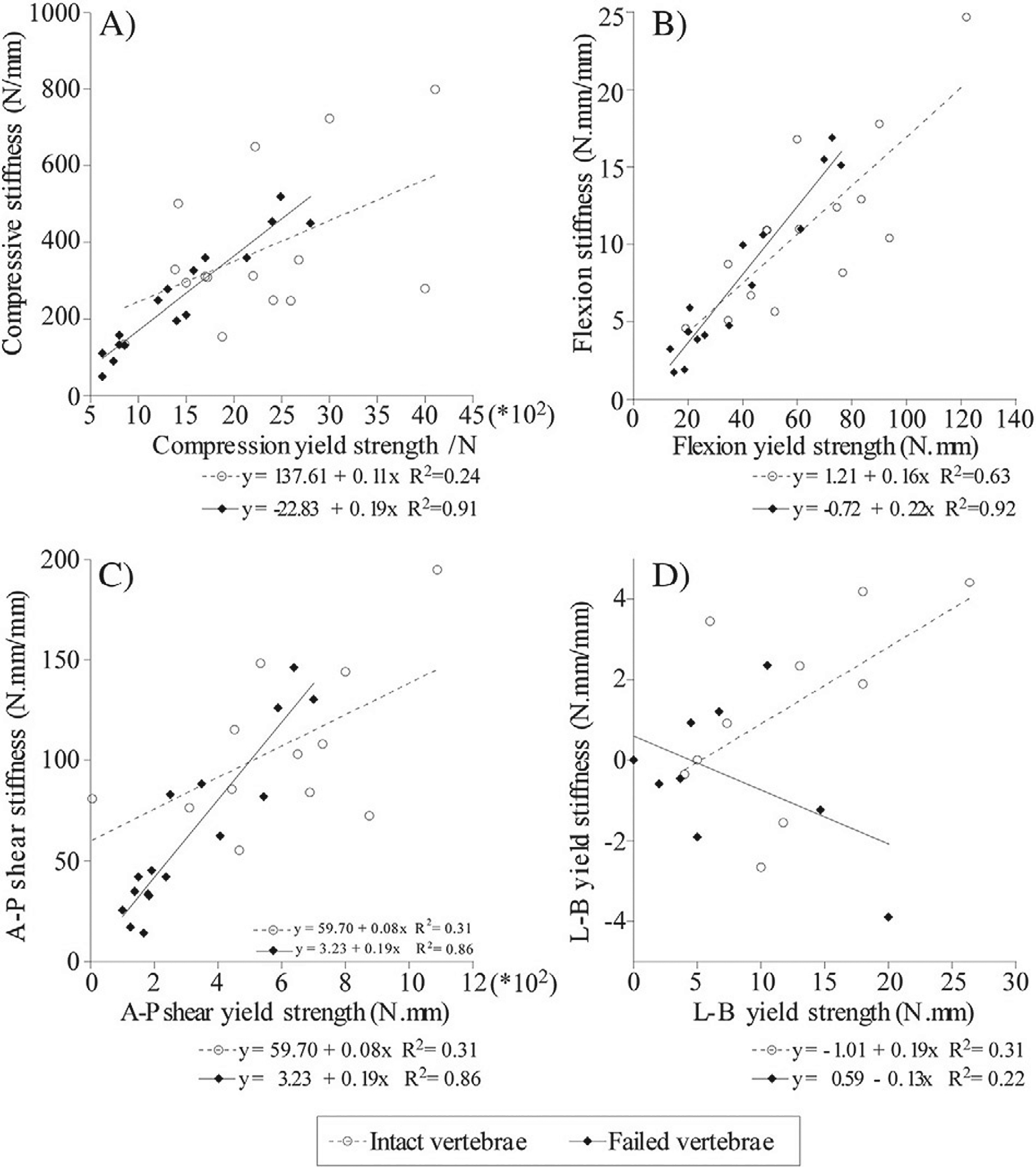
The effect of failure on the correlation between strength and stiffens parameters underlying the structural response of the vertebrae. The significant changes in the flexion yield strength of the failed vs. intact vertebrae, demonstrates the loss in the contribution of the cortex to the structural competence of the vertebrae.

4. Discussion

Retrospective (Taneichi et al., 1997) as well as experimental (Silva et al., 1993; Whealan et al., 2000) studies have found the involvement of the vertebral cortex to have a highly deleterious effect on the fracture risk of pathologic thoracolumbar vertebrae. In patients with existing PVF, selection of optimum treatment often requires an assessment of the “stability” of the involved vertebral level, i.e., the degree to which the failed vertebra will retain its geometrical and structural integrity under functional loads. The first part of this experimental study investigated the hypothesis that failure of the vertebral cortex in human vertebrae with a large, uncontained, osteolytic defect determines the initiation of vertebral failure. The second part investigated the post-failure structural response of the vertebrae and compared this response with their intact state. In particular, we explored the effects of failure on the interrelationships between the strength and stiffness parameters measured from the force and moment response of the vertebrae.

4.1. Effect of the uncontained lytic defect on the structural response of the vertebrae.

In response to applied compressive and flexion loading, the vertebrae exhibited a rapid onset of structural yield, observed via the sharp decrease in the flexion moments and, to a lesser extent, in the compressive force response (Fig. 3). The present study findings of the weak association between ultimate strength and stiffness parameters in compression and anterior-posterior shear, is in contrast to that reported for either single vertebra (Silva et al., 1993) and three level spines. In these studies, the trans-cortical defect explained 44 to 79% of the variance in the reduction of the vertebral axial compressive stiffness. However, the significant correlation between the ultimate flexion strength and stiffness is in close agreement to that reported for three-level spinal units with simulated lateral defects (r2 = 0.58) under combined compression and forward bending (Whealan et al., 2000). The differences in correlation between the axial and bending parameters could be explained from a mechanics of solids approach. In osteoporotic vertebrae, compressive strength was reported to explain 52 to 69% of the change in the compressive stiffness of the vertebrae (Buckley et al., 2009; Crawford and Keaveny, 2004; Crawford et al., 2003; Hou et al., 1998). However, marked destruction of the vertebral bone by the lytic lesion is likely to result in the transfer of the loading to the remaining bone within the vertebra and the surrounding vertebral cortex. Consequently, the vertebra’s axial rigidity undergoes a significant reduction, effectively degrading its ability to resist the applied compression. The higher correlation observed between bending strength and stiffness parameters, as well as the strong association between the compressive and flexion strength parameters, may reflect the role of the peripheral bone and the cortex in resisting the stresses conferred on the vertebral structure by the applied bending loads.

4.2. Failure of the cortex dominates the initiation and progression of vertebral failure.

The role of the vertebral cortex in effecting the structural response and failure of the vertebrae remain controversial (Chevalier et al., 2009; Christiansen et al., 2011; Crawford and Keaveny, 2004). The results of this study show the failure of the cortex to be the determining event in the initiation and progression of the failure process of the vertebrae (Fig. 3.B). The sharp decline in the ratio of applied displacement and the change in the sign, observed for both flexion and bending moment response (Fig. 3.B), is typical of a load–displacement response associated with the buckling of a shell structure under axial loading (Godoy, 2000). Once the cortex has undergone buckling, experimentally observed to initiate at the region of the breach within the cortex, a series of “localized” failure events ensued consisting of outward bulging plastic deformation of the cortex (regions II and III, Fig. 3) and the collapse of the vertebrae toward the defect site as demonstrated by the sharp increase in the lateral bending response (Fig. 3). Tschirhart et al., (Tschirhart et al., 2007) demonstrated the addition of a transcortical defect at either the anterior or lateral aspects of a vertebral body with an existing 20% lytic defect, to result in a 21% and 433% increase in the bulging of the vertebra respectively. Moreover, breaching the integrity of the cortex was reported to supersede the effect of either the location or the size (Tschirhart et al., 2004; Whyne et al., 2001) of the defect on the fracture risk of the vertebrae (Tschirhart et al., 2007). Once the vertebra has “consolidated”, observed as a marked deformation and loss of height of the vertebral body (Region III-IV, Fig. 3) the structural response of the vertebra was typical of a post-failure response of an osteoporotic vertebra (Kopperdahl et al., 2000; Lindahl, 1976; Mosekilde, 1993).

4.3. Effect of the lytic defect on the residual load carrying capacity of the vertebrae.

Demonstrated by the highly significant reduction in ultimate compressive strength and stiffness (59% and 53%, p < 0.001, Table 2) and statistically significant lower shear strength in flexion and anterior-posterior shear (70%, p < 0.01 and 75%, p < 0.05, Table 2), the failed vertebrae exhibited a sharp degradation in load carrying capacity (Table 2). In contrast to the intact vertebrae, the failed vertebrae’s ultimate compressive and flexion strengths, as well as the ultimate strength in A-P shear, were highly correlated with their respective stiffness parameters (r2 = 0.91 and r2 = 0.92, p < 0.001, and r2 = 0.86, p < 0.01, respectively, Fig. 4). The significant increase (ANCOVA, p = 0.028) in the correlation between strength and stiffness, an association typical to that reported for cancellous bone (Keaveny et al., 1994; Kopperdahl et al., 2000; Lindahl, 1976), suggests that the post-failure structural response of the vertebrae was determined exclusively by the response of the cancellous bone. Experimental (Andresen et al., 1998; Haidekker et al., 1999; McBroom et al., 1985) and computational (Crawford and Keaveny, 2004; Crawford et al., 2003; Roux et al., 2010) studies underlined the role of the vertebral cortex in affecting vertebral strength, energy absorption capacity and the onset of failure (Kopperdahl et al., 2000). These results, as well as the results of the current study, highlight the need to further elucidate the role of the cortex in supporting the structural response of the vertebrae both prior- and post-failure under single and more complex loading scenarios.

In assessing the finding of this study, several limitations must be considered. The vertebrae obtained for this study were from cadaveric donors with no evidence of metastatic spine disease. Measurements of bone density (BMD) for the L1 – L4 levels, combined (mean and standard deviation) value of 0.42 (0.13)g/cm2, indicated that these spines were osteoporotic (Lewiecki, 2005; Melton et al., 2005). These values are within the range reported for human vertebrae with lytic metastasis (Oakland et al., 2008). They reflect the low BMD values common in postmenopausal women with hormone receptor-positive breast cancer patients who have undergone treatment using aromatase inhibitors (Bruning et al., 1990;Maxwell and Viale, 2005). These are risk factors known to hasten fractures by approximately 10 years (Bruning et al., 1990; Coleman et al., 2010). At present, little is known about how metastases from different neoplasms affect the material and structural integrity of the bone and subsequent biomechanics of the vertebrae. Furthermore, the demarcated bone defect boundary created in this model cannot simulate the pattern of bone degradation that occurs due to neoplastic infiltration (Hipp et al., 1991, 1992; Walls et al., 1995; Whyne et al., 2000). In vertebrae with lytic metastases the defect contains tumor tissue, rather than being empty, as in our model. We elected not to attempt to simulate this soft tissue component (Whealan et al., 2000; Whyne et al., 2000), as it would likely have had little effect on the mechanical properties we measured. This model thus represents a condition in which the tumor has been fully ablated by radiation, mechanical or thermotherapy procedures (Masala et al., 2004) and thus the material properties of the lesion do not provide significant contribution to vertebral strength (Whyne et al., 2000).

The fracture model chosen for this study, an anterior wedge model with 50% collapse, results in significant structural damage to the vertebrae (Alkalay et al., 2008) and raises a risk of retropulsion of bone with spinal cord or cauda equina compression, thus reflecting a common clinical finding (Bostrom and Lane, 1997). Although the vertebral fracture patterns observed in this study are similar to that reported clinically (Ferguson and Allen, 1984; McAfee et al., 1983), the use of isolated vertebrae can only partially simulate the load transfer expected when the vertebra functions as part of complete functional spinal units. Furthermore, the loading conditions to which human vertebrae are exposed in vivo, and their effect on the resulting clinical pattern of fracture, are not well understood. Both static and instantaneous loads are likely to vary among patients in vivo and to contribute to vertebral failure. For this study, we have chosen an axial compression loading protocol, representing the simplest load pattern likely to be experienced by the spine during daily activities (Panjabi and A. A. W., 1990). This choice was largely driven by the effort to gain understanding of the vertebrae’s highly non-linear structural response prior to failure as well as once failed. The number of vertebrae included represents a relatively small sample size. The high standard deviation observed were the result of the highly non-linear structural response of the vertebrae, composed of a high degree of buckling and the occurrence of plastic deformation zones. This resulted in the vertebrae demonstrating multiple failure events during the failure process. To compensate for the relatively small sample size, we employed a repeated measure study design with the intact vertebrae acting as controls. This experimental design is able to partition the variability caused by individual differences yielding increased F-value due to a smaller sum of squares error term (JMP, SAS, NC). Power calculation (JMP) demonstrated the model to have β = 0.82 for the geometrical measurements and β = 0.84 for the mechanical tests. Hence, with the relatively small number of specimens and test conditions incomplete, i.e. single vertebra and limited applied load case, the regression models presented are not aimed at establishing causation but are solely aimed at highlighting the effect of failure on the change in structural response of the vertebrae.

Metastases vary in size, anatomy, and effects on vertebral strength. In vitro testing allows standardization of the lesion, control of the loading conditions and also permits consistent experimental conditions. Any model must simplify these factors. The study strengths is its experimental approach to investigate the effects of lytic destruction of the vertebral body and cortex on the load carrying capacity of an intact and then failed human vertebrae. In particular, the study quantified the effects of the defect on the relationship between the strength and stiffness parameters underlying the change in the structural response of the affected vertebra. Previous studies on the role of osteolytic defect were largely theoretical (Tschirhart et al., 2004, 2006, 2007; Whyne et al., 2001, 2003), whilst the study by Whealan et al., (Whealan et al., 2000) reported only the effects of the defect on the ultimate failure load of the vertebrae. To the best of our knowledge, this is the first study, either experimental or theoretical, to investigate the effects of osteolytic defect on the structural response of failed human vertebrae. It is also the first study to quantify the effect of failure on the degradation in residual load carrying capacity of vertebrae with simulated lytic defects. These insights into the effect of lytic defects on the structural response and failure patterns of human vertebrae represent substantial advances over current knowledge.

5. Conclusion

Inclusion of a large, solitary, uncontained lytic defect resulted in rapid failure of the vertebrae. The vertebrae exhibit a complex failure pattern that is initiated by the buckling of the vertebral cortex followed by increased involvement of the vertebral bone. Once failed, the vertebrae showed a highly significant degradation of their load carrying capacity with little or no recovery of vertebral geometry. The observed changes in the relationships between the strength to stiffness parameters further suggested the failure of vertebrae with osteolytic defects to significantly degrade their structural capacity.

Supplementary Material

Fig 2, suppl
Fig 1, suppl

Acknowledgment

The corresponding author gratefully acknowledges the financial support under NIH R01 grant 1R01AR055582-01A1 for this research.

Footnotes

Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.clinbiomech.2014.10.001.

References

  1. Alkalay RN, Stechow DV, Torres K, Hassan S, Sommerich R, Zurakowski D, 2008. The effect of cement augmentation on the geometry and structural response of recovered osteopenic vertebrae: an anterior-wedge fracture model. Spine 33, 1627–1636. [DOI] [PubMed] [Google Scholar]
  2. American-Cancer-Society, 2012. Cancer Facts and Figures. In: Society AC (Ed.), American Cancer Society, Atlanta, GA. [Google Scholar]
  3. Andresen R, Werner HJ, Schober HC, 1998. Contribution of the cortical shell of vertebrae to mechanical behaviour of the lumbar vertebrae with implications for predicting fracture risk. Br. J. Radiol. 71, 759–765. [DOI] [PubMed] [Google Scholar]
  4. Bostrom MP, Lane JM, 1997. Future directions. Augmentation of osteoporotic vertebral bodies. Spine 22, 38S–42S. [DOI] [PubMed] [Google Scholar]
  5. Bruning PF, Pit MJ, Jong-Bakker MD, Ende AVD, Hart A, Enk AV, 1990. Bone mineral density after adjuvant chemotherapy for premenopausal breast cancer. Br. J. Cancer 61, 308–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Buckley JM, Kuo CC, Cheng LC, Loo K, Motherway J, Slyfield C, et al. , 2009. Relative strength of thoracic vertebrae in axial compression versus flexion. Spine J. 9, 478–485. [DOI] [PubMed] [Google Scholar]
  7. Bunting REA, 1985. Pathologic fracture risk in rehabilitation of patients with bony metastases. Clin. Orthop. Relat. Res. 192, 222–227. [PubMed] [Google Scholar]
  8. Carlson K, Astrom G, Nyman R, Ahlstrom H, Simonsson B, 1995. MR imaging of multiple myeloma in tumour mass measurement at diagnosis and during treatment. Acta Radiol. 36, 9–14. [PubMed] [Google Scholar]
  9. Chevalier Y, Pahr D, Zysset PK, 2009. The role of cortical shell and trabecular fabric in finite element analysis of the human vertebral body. J. Biomech. Eng 131, 111003. [DOI] [PubMed] [Google Scholar]
  10. Christiansen BA, Kopperdahl DL, Kiel DP, Keaveny TM, Bouxsein ML, 2011. Mechanical contributions of the cortical and trabecular compartments contribute to differences in age-related changes in vertebral body strength in men and women assessed by QCT-based finite element analysis. J. Bone Miner. Res. 26, 974–983. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Coleman RE, 2001. Metastatic bone disease: clinical features, pathophysiology and treatment strategies. Cancer Treat. Rev 27, 165–176. [DOI] [PubMed] [Google Scholar]
  12. Coleman N, Stanley MA, 1994. Characterization and functional analysis of the expression of vascular adhesion molecules in human papillomavirus-related disease of the cervix. Cancer 74, 884–892. [DOI] [PubMed] [Google Scholar]
  13. Coleman RE, Banks LM, Girgis SI, Vrdoljak E, Fox J, Cawthorn SJ, et al. , 2010. Reversal of skeletal effects of endocrine treatments in the Intergroup Exemestane Study. Breast Cancer Res. Treat. 124, 153–161. [DOI] [PubMed] [Google Scholar]
  14. Crawford RP, Keaveny TM, 2004. Relationship between axial and bending behaviors of the human thoracolumbar vertebra. Spine 29, 2248–2255. [DOI] [PubMed] [Google Scholar]
  15. Crawford RP, Cann CE, Keaveny TM, 2003. Finite element models predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone 33, 744–750. [DOI] [PubMed] [Google Scholar]
  16. Falicov A, Fisher CG, Sparkes J, Boyd MC, Wing PC, Dvorak MF, 2006. Impact of surgical intervention on quality of life in patients with spinal metastases. Spine 31, 2849–2856. [DOI] [PubMed] [Google Scholar]
  17. Ferguson RL, Allen BL, 1984. A mechanistic classification of thoracolumbar spine fractures. Clin. Orthop. 189, 77–88. [PubMed] [Google Scholar]
  18. Fidler M, 1981. Incidence of fracture through metastases in long bones. Acta Orthop. Scand 52, 623–627. [DOI] [PubMed] [Google Scholar]
  19. Godoy LA, 2000. Theory of elastic stability: analysis and sensitivity. Taylor & Francis, Philadelphia. [Google Scholar]
  20. Haidekker MA, Andresen R, Werner HJ, 1999. Relationship between structural parameters, bone mineral density and fracture load in lumbar vertebrae, based on high-resolution computed tomography, quantitative computed tomography and compression tests. Osteoporos. Int 9, 433–440. [DOI] [PubMed] [Google Scholar]
  21. Hardisty MR, Akens MK, Hojjat SP, Yee A, Whyne CM, 2012. Quantification of the effect of osteolytic metastases on bone strain within whole vertebrae using image registration. J. Orthop. Res. 30, 1032–1039. [DOI] [PubMed] [Google Scholar]
  22. Hipp JA, Katz G, Hayes WC, 1991. Local demineralization as a model for bone strength reductions in lytic transcortical metastatic lesions. Invest. Radiol. 26, 934–938. [DOI] [PubMed] [Google Scholar]
  23. Hipp JA, Rosenberg AE, Hayes WC, 1992. Mechanical properties of trabecular bone within and adjacent to osseous metastases. J. Bone Miner. Res. 7, 1165–1171. [DOI] [PubMed] [Google Scholar]
  24. Hojjat SP, Hardisty MR, Whyne CM, 2010. Micro-computed tomography-based highly automated 3D segmentation of the rat spine for quantitative analysis of metastatic disease. J. Neurosurg. Spine 13, 367–370. [DOI] [PubMed] [Google Scholar]
  25. Hou FJ, Lang SM, Hoshaw SJ, Reimann DA, Fyhrie DP, 1998. Human vertebral body apparent and hard tissue stiffness. J. Biomech. 31, 1009–1015. [DOI] [PubMed] [Google Scholar]
  26. Keaveny TM, Wachtel EF, Ford CM, Hayes WC, 1994. Differences between the tensile and compressive strengths of bovine tibial trabecular bone depend on modulus. J. Biomech. 27, 1137–1146. [DOI] [PubMed] [Google Scholar]
  27. Kopperdahl DL, Pearlman JL, Keaveny TM, 2000. Biomechanical consequences of an isolated overload on the human vertebral body. J. Orthop. Res. 18, 685–690. [DOI] [PubMed] [Google Scholar]
  28. Lad SP, Patil CG, Lad EM, Boakye M, 2007. Trends in pathological vertebral fractures in the United States: 1993 to 2004. J. Neurosurg. Spine 7, 305–310. [DOI] [PubMed] [Google Scholar]
  29. Lewiecki EM, 2005. Clinical applications of bone density testing for osteoporosis. Minerva Med. 96, 317–330. [PubMed] [Google Scholar]
  30. Lindahl O, 1976. Mechanical properties of dried defatted spongy bone. Acta Orthop. Scand 47, 11–19. [DOI] [PubMed] [Google Scholar]
  31. Masala S, Roselli M, Massari F, Fiori R, 2004. Radiofrequency heat ablation and vertebroplasty in the treatment of neoplastic vertebral body fractures. Anticancer Res. 24, 3129–3133. [PubMed] [Google Scholar]
  32. Maxwell C, Viale PH, 2005. Cancer treatment-induced bone loss in patients with breast or prostate cancer. Oncol. Nurs. Forum 32, 589–603. [DOI] [PubMed] [Google Scholar]
  33. McAfee PC, Yuan HA, Fredrickson BE, Lubicky JP, 1983. The value of computed tomography in thoracolumbar fractures. J. Bone Joint Surg. 65-A, 461–473. [PubMed] [Google Scholar]
  34. McBroom RJ, Hayes WC, Edwards WT, Goldberg RP, White AA, 1985. Prediction of vertebral body compressive fracture using quantitative computed tomography. J. Bone Joint Surg. Am. 67, 1206–1214. [PubMed] [Google Scholar]
  35. Melton LJ, Looker A, Shepherd JA, O’Connor MK, Achenbach SL, Riggs BL, et al. , 2005. Osteoporosis assessment by whole body region vs. site-specific DXA. Osteoporos. Int. 16, 1558–1564. [DOI] [PubMed] [Google Scholar]
  36. Mosekilde L, 1993. Vertebral structure and strength in vivo and in vitro. Calcif. Tissue Int. 53, S121–S125. [DOI] [PubMed] [Google Scholar]
  37. Oakland RJ, Furtado NR, Timothy J, Hall RM, 2008. The biomechanics of vertebroplasty in multiple myeloma and metastatic bladder cancer: a preliminary cadaveric investigation. J. Neurosurg. Spine 9, 493–501. [DOI] [PubMed] [Google Scholar]
  38. Clinical Biomechanics of the Spine. In: Panjabi MM, A. AW III (Eds.), J. B. Lippincott Company, Philadelphia. [Google Scholar]
  39. Ratliff JK, Cooper PR, 2004. Metastatic spine tumors. South. Med. J. 97, 246–253. [DOI] [PubMed] [Google Scholar]
  40. Roth SE, Mousavi P, Finkelstein J, Chow E, Kreder H, Whyne CM, 2004. Metastatic burst fracture risk prediction using biomechanically based equations. Clin. Orthop 419. [DOI] [PubMed] [Google Scholar]
  41. Roux JP, Wegrzyn J, Arlot ME, Guyen O, Delmas PD, Chapurlat R, et al. , 2010. Contribution of trabecular and cortical components to biomechanical behavior of human vertebrae: an ex vivo study. J. Bone Miner. Res. 25, 356–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Silva MJ, Hipp JA, Mcgowan DP, Takeuchi T, Hayes WC, 1993. Strength reductions of thoracic vertebrae in the presence of transcortical osseous defects: Effects of defect location, pedicle disruption and defect size. Eur. Spine J 118–125. [DOI] [PubMed] [Google Scholar]
  43. Taneichi H, Kaneda K, Takeda N, Abumi K, Satoh S, 1997. Risk factors and probability of vertebral body collapse in metastases of the thoracic and lumbar spine. Spine 22, 239–245. [DOI] [PubMed] [Google Scholar]
  44. Tokuhashi Y, Matsuzaki H, Oda H, Oshima M, Ryu J, 2005. A revised scoring system for preoperative evaluation of metastatic spine tumor prognosis. Spine 30, 2186–2191. [DOI] [PubMed] [Google Scholar]
  45. Toma CD, Dominkus M, Nedelcu T, Abdolvahab F, Assadian O, Krepler P, et al. , 2007. Metastatic bone disease: a 36-year single centre trend-analysis of patients admitted to a tertiary orthopaedic surgical department. J. Surg. Oncol 96, 404–410. [DOI] [PubMed] [Google Scholar]
  46. Tschirhart CE, Nagpurkar A, Whyne CM, 2004. Effects of tumor location, shape and surface serration on burst fracture risk in the metastatic spine. J. Biomech. 37, 653–660. [DOI] [PubMed] [Google Scholar]
  47. Tschirhart CE, Finkelstein JA, Whyne CM, 2006. Optimization of tumor volume reduction and cement augmentation in percutaneous vertebroplasty for prophylactic treatment of spinal metastases. J. Spinal Disord. Tech. 19, 584–590. [DOI] [PubMed] [Google Scholar]
  48. Tschirhart CE, Finkelstein JA, Whyne CM, 2007. Biomechanics of vertebral level, geometry, and transcortical tumors in the metastatic spine. J. Biomech. 40, 46–54. [DOI] [PubMed] [Google Scholar]
  49. Walls J, Bundred N, Howell A, 1995. Hypercalcemia and bone resorption in malignancy. Clin. Orthop 312, 51–63. [PubMed] [Google Scholar]
  50. Weber MH, Burch S, Buckley J, Schmidt MH, Fehlings MG, Vrionis FD, et al. , 2011. Instability and impending instability of the thoracolumbar spine in patients with spinal metastases: a systematic review. Int. J. Oncol. 38, 5–12. [PubMed] [Google Scholar]
  51. Whealan KM, Kwak SD, Tedrow JR, Inoue K, Snyder BD, 2000. Noninvasive imaging predicts failure load of the spine with simulated osteolytic defects. J. Bone Joint Surg. Am. 82, 1240–1251. [DOI] [PubMed] [Google Scholar]
  52. White AP, 2006. Metastatic disease of the spine. J. Am. Acad. Orthop. Surg. 14, 587–598. [DOI] [PubMed] [Google Scholar]
  53. Whyne CM, Hu SS, Wolkman KL, Lotz JC, 2000. Biphasic material properties of lytic bone metastases. Ann. Biomed. Eng. 28. [DOI] [PubMed] [Google Scholar]
  54. Whyne CM, Hu SS, Lotz JC, 2001. Parametric finite element analysis of vertebral bodies affected by tumors. J. Biomech. 34, 1317–1324. [DOI] [PubMed] [Google Scholar]
  55. Whyne CM, Hu SS, Lotz JC, 2003. Biomechanically derived guideline equations for burst fracture risk prediction in the metastatically involved spine. J. Spinal Disord. Tech. 16, 180–185. [DOI] [PubMed] [Google Scholar]
  56. Windhagen HJ, Hipp JA, Silva MJ, Lipson SJ, Hayes WC, 1997. Predicting failure of thoracic vertebrae with simulated and actual metastatic defects. Clin. Orthop. Relat. Res. 344, 313–319. [PubMed] [Google Scholar]
  57. Windhagen H, Hipp JA, Hayes WC, 2000. Postfracture instability of vertebrae with simulated defects can be predicted from computed tomography data. Spine 25, 1775–1781. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Fig 2, suppl
NIHMS1811815-supplement-Fig_2__suppl.tif (2.6MB, tif)
Fig 1, suppl
NIHMS1811815-supplement-Fig_1__suppl.tif (1.8MB, tif)

RESOURCES