Machine Learning Can be Used to Predict Function but Not Pain After Surgery for Thumb Carpometacarpal Osteoarthritis

Abstract

Background

Surgery for thumb carpometacarpal osteoarthritis is offered to patients who do not benefit from nonoperative treatment. Although surgery is generally successful in reducing symptoms, not all patients benefit. Predicting clinical improvement after surgery could provide decision support and enhance preoperative patient selection.

Questions/purposes

This study aimed to develop and validate prediction models for clinically important improvement in (1) pain and (2) hand function 12 months after surgery for thumb carpometacarpal osteoarthritis.

Methods

Between November 2011 and June 2020, 2653 patients were surgically treated for thumb carpometacarpal osteoarthritis. Patient-reported outcome measures were used to preoperatively assess pain, hand function, and satisfaction with hand function, as well as the general mental health of patients and mindset toward their condition. Patient characteristics, medical history, patient-reported symptom severity, and patient-reported mindset were considered as possible predictors. Patients who had incomplete Michigan Hand outcomes Questionnaires at baseline or 12 months postsurgery were excluded, as these scores were used to determine clinical improvement. The Michigan Hand outcomes Questionnaire provides subscores for pain and hand function. Scores range from 0 to 100, with higher scores indicating less pain and better hand function. An improvement of at least the minimum clinically important difference (MCID) of 14.4 for the pain score and 11.7 for the function score were considered “clinically relevant.” These values were derived from previous reports that provided triangulated estimates of two anchor-based and one distribution-based MCID. Data collection resulted in a dataset of 1489 patients for the pain model and 1469 patients for the hand function model. The data were split into training (60%), validation (20%), and test (20%) dataset. The training dataset was used to select the predictive variables and to train our models. The performance of all models was evaluated in the validation dataset, after which one model was selected for further evaluation. Performance of this final model was evaluated on the test dataset. We trained the models using logistic regression, random forest, and gradient boosting machines and compared their performance. We chose these algorithms because of their relative simplicity, which makes them easier to implement and interpret. Model performance was assessed using discriminative ability and qualitative visual inspection of calibration curves. Discrimination was measured using area under the curve (AUC) and is a measure of how well the model can differentiate between the outcomes (improvement or no improvement), with an AUC of 0.5 being equal to chance. Calibration is a measure of the agreement between the predicted probabilities and the observed frequencies and was assessed by visual inspection of calibration curves. We selected the model with the most promising performance for clinical implementation (that is, good model performance and a low number of predictors) for further evaluation in the test dataset.

Results

For pain, the random forest model showed the most promising results based on discrimination, calibration, and number of predictors in the validation dataset. In the test dataset, this pain model had a poor AUC (0.59) and poor calibration. For function, the gradient boosting machine showed the most promising results in the validation dataset. This model had a good AUC (0.74) and good calibration in the test dataset. The baseline Michigan Hand outcomes Questionnaire hand function score was the only predictor in the model. For the hand function model, we made a web application that can be accessed via https://analyse.equipezorgbedrijven.nl/shiny/cmc1-prediction-model-Eng/.

Conclusion

We developed a promising model that may allow clinicians to predict the chance of functional improvement in an individual patient undergoing surgery for thumb carpometacarpal osteoarthritis, which would thereby help in the decision-making process. However, caution is warranted because our model has not been externally validated. Unfortunately, the performance of the prediction model for pain is insufficient for application in clinical practice.

Level of Evidence

Level III, therapeutic study.

Introduction

Thumb carpometacarpal (CMC1) osteoarthritis (OA) is common and increases in frequency with age. The symptomatic prevalence is 2% in men and 7% in women older than 50 years [20, 35, 46]. The disorder can lead to impaired hand function because of pain, weakness, loss of motion, and progressive deformity [3, 4]. Initial treatment options are nonsurgical, but surgical treatment might be indicated for a subset of patients who have persistent pain and disability. Although surgical treatment is generally successful in reducing symptoms, not all patients experience benefits from surgery, and some may not be satisfied with their treatment [3, 34, 48].

Pain reduction is generally the most important reason for patients seeking surgical treatment for CMC1 OA, followed by improving hand function [17]. Therefore, it would be useful to be able to accurately predict whether a patient will experience a clinically meaningful reduction in pain and improvement in hand function after surgery. This would help in the decision-making process, help manage patients’ expectations, and assist clinicians in determining which patients will benefit from surgery; this may lead to better preoperative patient selection and may improve the likelihood that patients will be pleased with their surgical results [34]. However, determining which patients will benefit from surgical treatment is challenging because many factors may influence outcomes, such as demographics, clinical characteristics, and psychosocial profiles [12, 26, 36, 47]. Thus, developing and implementing tools that accurately predict clinical improvement would be valuable. At present, there are no prediction models available to predict clinically meaningful improvement after the surgical treatment of CMC1 OA.

Machine learning is a type of artificial intelligence that is seeing wider use in healthcare and is increasingly being used to develop prediction models [9]. In a recent editorial, Clinical Orthopaedics and Related Research® highlighted the potential value of machine learning in clinical research [29]. Machine learning is based on algorithms that can build models that learn from sample data to make predictions without being explicitly programmed to do so [53]. The models are trained on a training dataset and then evaluated on one or two other datasets (validation and test datasets) [53]. Machine-learning methods can develop models based on large quantities of possible predictive variables and process large amounts of data [6]. Therefore, these algorithms may be better able to identify patterns in large datasets than traditional statistical methods, which may lead to better predictive performance [31].

We aimed to develop and validate two prediction models using machine-learning methods to forecast the probability of clinically meaningful improvement in (1) pain and (2) hand function of patients 12 months after surgery for CMC1 OA. More specifically, in separate models, we focused on predicting pain reduction and improvement in hand function. We trained and validated our models using different algorithms: one traditional statistical method and two commonly used machine-learning algorithms.

Patients and Methods

Study Population

We conducted a retrospective study using longitudinally maintained data from the Hand-Wrist Study Group, which is a collaboration between the Xpert Clinics Hand and Wrist Care and the Departments of Rehabilitation Medicine and Plastic and Reconstructive Surgery of Erasmus Medical Centre in Rotterdam, the Netherlands. The Xpert Clinics comprise 25 locations and 23 European board-certified (Federation of European Societies for Surgery of the Hand) hand surgeons. The cohort and data collection methods have been described in more detail elsewhere [41]. We used data collected between November 2011 and June 2020. All patients were asked to complete patient-reported outcome measures before surgery and 12 months after surgery as part of routine outcome measurements.

We included all patients who received surgery for CMC1 OA (trapeziectomy with ligament reconstruction and tendon interposition [LRTI] [8, 16, 42, 51]), and completed the Michigan Hand outcomes Questionnaire (MHQ) at baseline and 12 months after surgery. Patients with an incomplete MHQ were included if they had a complete MHQ pain score for the development of our pain model and a complete MHQ function score for the development of our hand function model. We excluded patients who underwent revision surgery and patients treated with a different surgical technique than trapeziectomy with LRTI because these procedures are not performed routinely in our clinics.

Diagnosis and Treatment

Diagnoses were made by European board-certified hand surgeons based on clinical symptoms and, when required, additional radiographs of the CMC1 joint. In general, surgery was recommended to patients who did not improve after at least 3 months of nonoperative treatment consisting of hand therapy and braces. In our clinics, this is about 15% of patients [45], and surgery generally consists of trapeziectomy with ligament reconstruction and tendon interposition. The choice of tendonplasty after trapeziectomy depended on the surgeon’s preference, which is most likely influenced by the location of residency. The most performed procedure in our clinics is the Weilby sling [51]. Given that the type of tendonplasty was not structurally recorded with sufficient detail in the dataset, we did not include this as possible predictor for our models. We did not expect this to influence our results because there is no evidence that one tendonplasty is superior regarding improvement in pain, hand function, and patient-reported outcome measures [48, 49].

Patients

During the data collection period, 2653 patients were surgically treated for CMC1 OA, excluding revision surgeries. Of those patients, 68% (1794) were treated with the Weilby sling procedure. After excluding patients who did not have complete MHQ score data for pain or function, 1489 patients were included in the prediction model development for pain and 1469 patients were included in the model development for hand function (Fig. 1). We performed two nonresponder analyses. One nonresponder analysis was conducted between all patients who were surgically treated for CMC1 OA and those who were included in our datasets for pain (Supplementary Table 1; http://links.lww.com/CORR/A709) and for function (Supplementary Table 2; http://links.lww.com/CORR/A710); the other was for patients with missing MHQ scores at 12 months for pain (Supplementary Table 3; http://links.lww.com/CORR/A711) and for function (Supplementary Table 4; http://links.lww.com/CORR/A712). Although we found differences in both analyses in symptom duration, second opinion (yes/no), and smoking, these were small effects with a maximum effect size of 0.12.

Fig. 1.

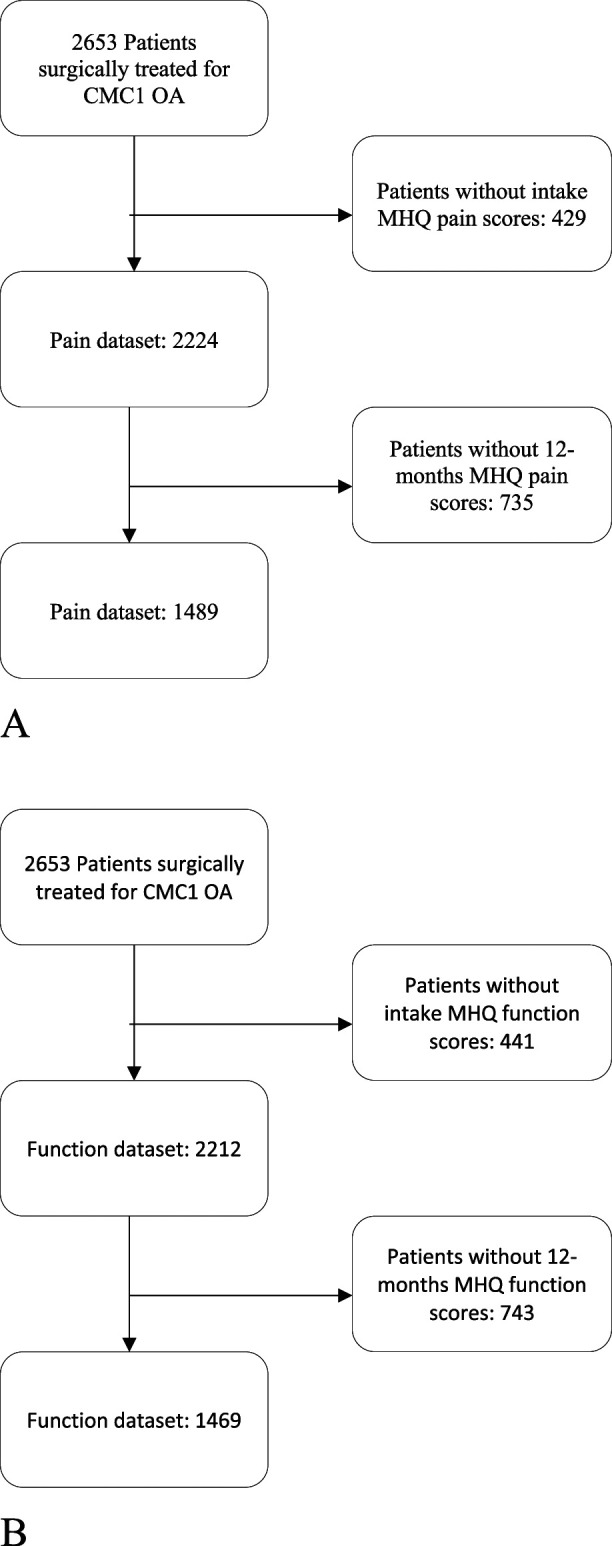
A-B Flow diagram of patient selection for the (A) pain dataset and (B) function dataset. During the inclusion period, 2653 patients were surgically treated with primary trapeziectomy with LRTI. Of these patients, 429 and 441 patients were excluded because they did not have baseline scores for MHQ pain and MHQ function, respectively; and 735 and 743 patients were excluded because of missing MHQ scores at 12 months.

In the dataset for pain, mean age was 61 ± 8 years and 79% (1178 of 1489) were women. Of these patients, 47% (704 of 1489) were unemployed. The average preoperative MHQ pain score was 34.3, and the average preoperative MHQ hand function score was 48.9. The most common comorbidities were other disorders of the locomotor system (23% [345 of 1489] of patients) and rheumatic disorders (17% [251 of 1489] of patients) (Table 1). Patient characteristics for the hand function model development were similar to those for the pain model (Table 2).

Table 1.

Characteristics of the patients in the training, validation, and test datasets for pain

Parameter	Complete dataset (n = 1489)	% missing	Training (n = 894)	Validation (n = 298)	Test (n = 297)
Age in years	61 ± 8	0	60.5 ± 8.2	60.9 ± 7.5	60.3 ± 7.9
Gender, women	79 (1178)		80 (718)	78 (231)	77 (229)
Duration of symptoms in months	37.2 ± 35.5	2	37.5 ± 35.0	35.9 ± 36.5	37.6 ± 36.0
Second opinion	89 (1325)	0	90 (805)	87 (259)	88 (261)
Hand dominance		0
Right	85 (1269)		85 (762)	85 (252)	86 (255)
Left	10 (143)		9 (83)	11 (33)	9 (27)
Both	5 (77)		5 (49)	4 (13)	5 (15)
Dominant hand treated	47 (695)	0	45 (405)	50 (149)	48 (141)
Occupational intensity		0
Not employed	47 (704)		46 (414)	52 (155)	45 (135)
Light	19 (278)		21 (184)	17 (52)	14 (42)
Moderate	22 (333)		21 (190)	20 (59)	28 (84)
Heavy	12 (174)		12 (106)	11 (32)	12 (36)
BMI in kg/m2	26.6 ± 3.9	35	26.7 ± 3.9	26.4 ± 3	26.7 ± 4.2
Smoking		45
Never	24 (358)		24 (214)	23 (69)	25 (75)
Disease severity
Preoperative MHQ pain score	34.3 ± 14.1	0	34.12 ± 13.98	34.95 ± 14.75	34.04 ± 13.61
Preoperative MHQ function Score	48.9 ± 17.0	0.6	48.41 ± 16.25	49.95 ± 18.28	49.51 ± 17.94
Medical history		35
Diabetes	4 (53)		3 (30)	2 (7)	5 (16)
Cardiovascular system	7 (104)		7 (60)	8 (24)	7 (20)
Thrombosis/vasculitis	1 (13)		1 (7)	1 (3)	1 (3)
Respiratory system	8 (119)		9 (82)	5 (15)	7 (22)
Liver/kidneys	1 (12)		1 (5)	2 (5)	1 (2)
Cranial nerves	2 (24)		2 (18)	1 (2)	1 (4)
Locomotor system	23 (345)		24 (215)	21 (63)	23 (67)
Rheumatic disorders	17 (251)		18 (157)	14 (41)	18 (53)
Hemorrhoids/varicosities	11 (166)		10 (87)	11 (33)	15 (46)
Allergies	17 (252)		17 (156)	14 (42)	18 (54)
Hematomas	3 (49)		3 (29)	3 (9)	4 (11)

Data presented as mean ± SD or % (n); the training dataset was used to select the predictive variables and to train our models; the performance of all models was evaluated in the validation dataset, after which one model was selected for further evaluation; performance of this final model was evaluated on the test data set.

Table 2.

Characteristics of the patients in the training, validation, and test datasets for function

Parameter	Complete dataset (n = 1469)	% missing	Training dataset (n = 883)	Validation dataset (n = 293)	Test dataset (n = 293)
Age in years	61 ± 8	0	61 ± 7	60 ± 8	61 ± 8
Gender, women	79 (1167)	0	78 (689)	81 (236)	83 (242)
Duration of symptoms in months	37 ± 46	2	38 ± 36	38 ± 36	34 ± 32
Second opinion	89 (1305)	0	89 (789)	88 (258)	88 (258)
Hand dominance		0
Right	85 (1251)		85 (748)	89 (260)	83 (243)
Left	10 (141)		10 (90)	7 (21)	10 (30)
Both	5 (77)		5 (45)	4 (12)	7 (20)
Dominant hand treated	47 (686)	0	49 (428)	46 (136)	42 (122)
Occupational intensity		0
Not employed	47 (691)		49 (428)	44 (130)	45 (133)
Light	19 (277)		18 (156)	20 (58)	22 (63)
Moderate	22 (329)		23 (199)	20 (58)	25 (72)
Heavy	12 (172)		11 (100)	16 (47)	9 (25)
BMI in kg/m2	26.6 ± 3.9	36	26.6 ± 4.0	26.4 ± 3.6	26.9 ± 3.9
Smoking		45
Never	24 (351)		25 (218)	20 (58)	26 (75)
Disease severity
Preoperative MHQ pain score	34.2 ± 14.0	0.3	33.8 ± 14.1	34.5 ± 14.0	35.3 ± 13.8
Preoperative MHQ function score	48.9 ± 17.0	0	49.1 ± 17.2	47.9 ± 16.1	49.2 ± 17.1
Medical history		36
Diabetes	3 (51)		3 (30)	3 (9)	4 (12)
Cardiovascular system	7 (104)		7 (62)	7 (20)	8 (22)
Thrombosis/vasculitis	1 (13)		1 (10)	0.3 (1)	1 (2)
Respiratory system	8 (118)		8 (70)	7 (21)	9 (27)
Liver/kidneys	1 (12)		1 (8)	1 (2)	1 (2)
Cranial nerves	2 (22)		2 (15)	2 (5)	1 (2)
Locomotor system	23 (337)		24 (208)	19 (55)	25 (74)
Rheumatic disorders	17 (243)		18 (158)	13 (37)	16 (48)
Hemorrhoids/varicosities	11 (162)		11 (101)	11 (33)	10 (28)
Allergies	17 (249)		17 (149)	16 (47)	18 (53)
Hematomas	3 (49)		3 (30)	4 (13)	2 (6)

Data presented as mean ± SD or % (n); the training dataset was used to select the predictive variables and to train our models; the performance of all models was evaluated in the validation dataset, after which one model was selected for further evaluation; performance of this final model was evaluated on the test data set.

Primary Outcome

To assess symptom relief after surgery, we used the difference in the MHQ scores between baseline and 12 months after surgery [11]. The MHQ is a self-reported questionnaire developed for all conditions of the hand. It provides a summary score and subscores for pain, hand function, ability to complete daily activities, work performance, aesthetics, and satisfaction separately. Scores range from 0 to 100, with higher scores indicating better health [11]. In this study, we focused on the pain and function scores of the MHQ. The Dutch-language version of the MHQ was used [11, 25].

We defined the threshold for a clinically meaningful improvement as having an increase of at least 14.4 and 11.7 points on the MHQ pain score and function score, respectively. These thresholds are based on the minimum clinically important differences (MCID). The MCIDs we used are triangulated estimates of three calculation methods: two anchor-based question methods and one statistical distribution method. They were calculated for patients with atraumatic hand and wrist conditions [32]. These MCIDs were chosen because determination of MCIDs based on triangulation of multiple calculation methods is recommended [40]. Furthermore, to our knowledge, there are currently no MCIDs available for the MHQ that are specifically determined for CMC1 OA [32]. We dichotomized each patient’s change in score between baseline and 12 months as threshold reached or threshold not reached. The prediction models were trained to predict whether a patient would reach the threshold and thus benefit from surgery. The outcome of each model represents the predicted probability of reaching the threshold for the individual patient.

We also included patients with an MHQ score at intake higher than 85.6 for pain and greater than 88.3 for hand function. These patients could not experience an improvement of 14.4 or 11.7, respectively, because of a ceiling effect. Therefore, the chance of these patients reaching the MCID after 12 months was, per definition, zero. However, to provide our model with the opportunity to also learn from these patients, we decided not to exclude them.

Measurements

We considered several baseline measurements as possible predictors for our models (Supplementary Table 5; http://links.lww.com/CORR/A713). Sociodemographic characteristics such as age, gender, BMI, and occupation as well as medical history, including comorbidities, were collected at intake.

Strength was measured at intake using a Biometrics E-link handgrip dynamometer (Biometrics Ltd). Strength measurements included grip strength, key pinch strength, and tip pinch strength. All measurements were performed according to the guidelines of the American Society of Hand Therapists [14].

Patient-reported outcome measure questionnaires were sent by email after consultation with the hand surgeon. The VAS was used to measure pain at rest and during loading, hand function, and satisfaction with hand function. Each subscale ranged from 0 to 100, with a higher score representing more pain but better hand function and greater satisfaction. The patient’s mindset toward their condition and treatment as well as their general mental health and quality of life were measured using several patient-reported outcome measures: the Brief Illness Perception Questionnaire, Credibility and Expectancy Questionnaire, the Patient Health Questionnaire-4, the Pain Catastrophizing Scale, and the Euro-QoL-5D-5L. The Dutch-language versions of all questionnaires were used [7, 13, 21, 27, 44]. We continue to improve our data collection and add new variables to the routine measurements. For example, the psychological questionnaires were added in September 2017. Therefore, only patients treated after September 2017 were invited to complete the psychological questionnaires. For the pain model, 248 patients were enrolled after September 2017 and for function 234 patients were enrolled.

Missing Data

There was a substantial proportion of missing data on mindset because only patients who were included between September 2017 and June 2020 were asked to complete these questionnaires. Furthermore, there was also a substantial number of nonresponders to the other measurements because these measures were collected as part of daily clinical practice. Therefore, we performed a nonresponder analysis by comparing baseline characteristics. We imputed data using the k-nearest-neighbor imputation implementation in the Caret package [28], as missingness is most likely missing completely at random or missing at random. Madley-Dowd et al. [33] reported that datasets with up to 90% of missing data can be reasonably imputed using multiple imputation.

Data Splitting and Measurements of Performance

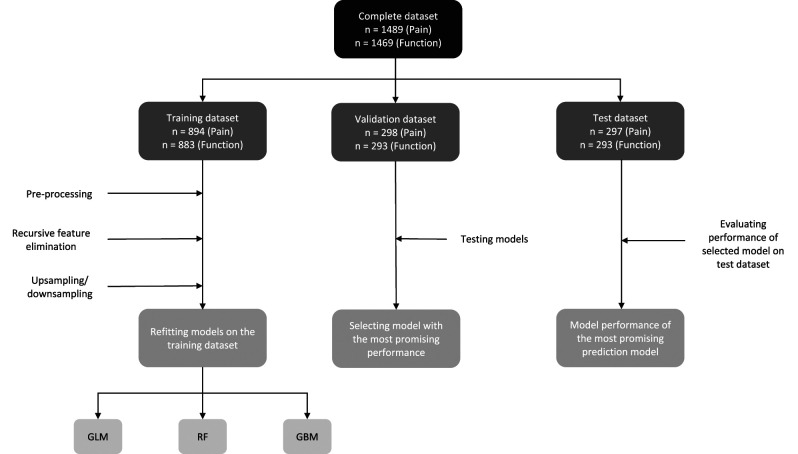
Patient-reported outcome measures, sociodemographic characteristics, and strength of the affected hand before surgery were considered as possible predictors in our models. To avoid overfitting and to base decisions for the most promising model(s) on, we split the resulting data into training (60%), validation (20%), and test datasets (20%) (Fig. 2). Both the validation dataset and test dataset refer to a sample of the dataset that is separate from the training dataset [53]. To select the algorithm for our final model, we applied all algorithms to the validation dataset and selected the one with the most promising performance in terms of (1) discrimination, (2) calibration, and (3) the number of predictors as our final model. We also took the number of predictors into account because we believe a low number of predictors will make the model easier to implement and use in daily practice. The test dataset was then used to evaluate the performance of this final model based on discrimination and calibration.

Fig. 2.

This flow diagram shows the selection of prediction models. The complete dataset was split into training (60%), validation (20%), and test (20%) datasets. The training set was used for feature elimination, resampling, and training of the prediction models. The best-performing models of each algorithm were evaluated in the validation dataset. The performance of the model with the best AUC and calibration in the validation dataset was further evaluated in the test dataset; GLM = generalized linear model; RF = random forest; GBM = gradient boosting machine; AUC = area under the curve.

The random split of the dataset for the pain model (1489) resulted in a training dataset of 894 patients, a validation dataset of 298 patients, and a test dataset of 297 patients. In the training dataset, 73% (653 of 894) of patients reached the MCID threshold of 14.4 points on the MHQ pain scale. In both the validation (218 of 298) and test (217 of 297) datasets, 73% of patients reached the MCID threshold.

The dataset for the hand function model (1469) was randomly split into a training dataset of 883 patients, a validation dataset of 293, and a test dataset of 293. In the training dataset, 56% (494 of 883) of patients reached the MCID threshold of 11.7 points on the MHQ function scale. In both the validation dataset and test dataset, 56% (164 of 293) of patients reached the MCID threshold.

For the dataset for the pain model development (Supplementary Table 6; http://links.lww.com/CORR/A714) and the dataset for the hand function development (Supplementary Table 7; http://links.lww.com/CORR/A715), there were no important differences in patient characteristics and preoperative patient-reported outcome measure values between the training, validation, and test datasets.

Ethical Approval

The medical ethics review board at Erasmus Medical Centre approved the study. This study was reported according to the guidelines of the Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis statement [37]. All patients provided written informed consent for their data to be used for research purposes.

Statistical Analysis and Machine Learning

After splitting the data, we standardized the data and imputed missing data. Standardization consisted of centering and scaling the data [53]. When standardization and imputation are performed before splitting the data, the validation and test dataset are not completely independent, which can result in a model performance that is too optimistic. Therefore, we performed standardization and imputation after splitting.

We compared three algorithms: logistic regression (generalized linear models), random forest, and gradient boosting machines. Logistic regression is a traditional regression-based statistical model. Random forest and gradient boosting machines are decision tree–based machine-learning models. We decided to use gradient boosting machine and random forest algorithms as our machine-learning algorithms for several reasons. First, they are relatively simple to implement, and because of their similarities with decision trees, they are easier to interpret than other, more complex algorithms [53]. Second, they are computationally less expensive and require less extensive datasets [6, 31, 53]. We selected variables for our models using recursive feature elimination with five repeats of 10-fold cross-validation in each training dataset (Fig. 2). Recursive feature elimination can be considered as backward selection of predictive variables. It starts by building a model that includes all variables as predictors. For each predictor, an importance score is computed, and predictors with the lowest score are removed. Then the model is rebuilt, and the process is repeated until model performance decreases by removing another variable [19].

Because the surgical treatment of CMC1 OA is generally successful [48], we expected more patients in the threshold-reached group than in the threshold-not-reached group. This was confirmed by a preliminary analysis for the MCID for pain, with 73% in the threshold-reached group and 27% of patients in the threshold-not-reached group. To account for this imbalance, we incorporated resampling in the feature elimination process. Thus, for our pain model, we performed recursive feature elimination three times for each machine-learning algorithm: without sampling, with up-sampling, and with down-sampling. With up-sampling, randomly selected patients are duplicated in the minority group, and with down-sampling, randomly selected patients are removed from the majority group. Because the resampling methods have disadvantages [10], we tested both. A preliminary analysis of the MCID for hand function showed the data were sufficiently balanced, with 56% in the threshold-reached group and 44% of patients in the threshold-not-reached group. Therefore, resampling was not needed in the function dataset. For each machine-learning algorithm for pain, the best-performing resampling method was selected based on area under the curve (AUC) values and the number of predictors. The AUC is a measure of the discriminative ability of a model; that is, the ability of the model to classify the two different groups correctly [23]. The models with the most promising performance were then used for further analysis.

The selected models, one from each machine-learning algorithm and with the predictive variables selected using recursive feature elimination, were trained in the original training set. After training the models, we analyzed performance in the validation set using AUC values and calibration. Calibration is a measure of the model’s fit and refers to the agreement between predicted probabilities and the observed frequency of the outcome [15]. In other words, this indicates whether, for example, out of 10 patients with a predicted probability to improve of 0.6, we observe that six patients actually improved. Calibration was visually assessed using calibration curves [15, 24, 38]. The model performs well on calibration when the calibration curve is close to the bisector. If the calibration curve lies above the bisector, it means the model underestimates the probability of the patient reaching the MCID; if the calibration curve lies under the bisector, the model overestimates the probability. The confidence belts represent the estimated degree of uncertainty of the calibration curve [15]. We then selected the algorithm with the best AUC and calibration. Additionally, we considered the number of predictors. This model was further evaluated in our test dataset using discriminative ability (AUC) and calibration (visual inspection of calibration curves). An AUC between 0.7 and 0.8 was considered acceptable discrimination, an AUC between 0.8 and 0.9 excellent, and an AUC above 0.9 outstanding [23]. Furthermore, we determined the sensitivity and specificity, positive predictive value, and negative predictive value.

The analysis was performed using R statistical programming, version 1.3.1073 (R Foundation). Prediction models were trained using the Caret package, version 6.0-86 [28]. A p value < 0.05 was considered statistically significant.

Results

Pain Model

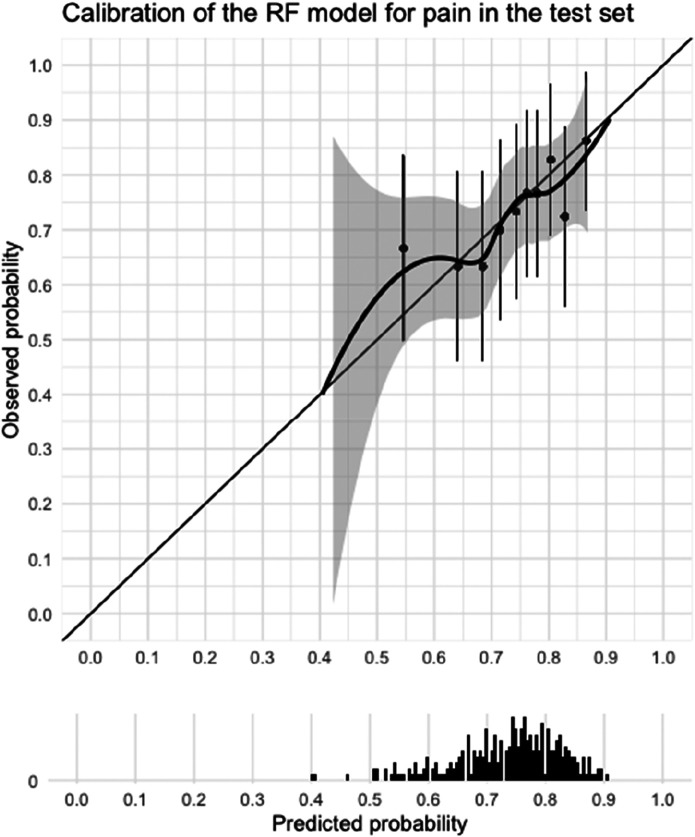
In the validation dataset, the random forest model with down-sampling showed the most promising performance in terms of discrimination, visual inspection of calibration curves (Supplementary Fig. 1A-C; http://links.lww.com/CORR/A716), and number of predictors (Supplementary Table 8; http://links.lww.com/CORR/A717). This model was evaluated further (Supplementary File 1; http://links.lww.com/CORR/A718). Unfortunately, in the test dataset, it performed poorly with an AUC of 0.59 (95% confidence interval 0.52 to 0.66), which is hardly better than chance. Sensitivity was 0.67 and specificity was 0.49 at a threshold of 0.72 (Table 3). In addition, a visual inspection of the calibration curve also indicated poor calibration (Fig. 3). We therefore believe this model should not be used in clinical practice.

Table 3.

Model properties in the test dataset of the selected prediction models for pain and function

Outcome	Training method		Results
	Algorithm	Sampling method	Number of variables	AUC in the test dataset	Sensitivity in the test dataset	Specificity in the test dataset	Positive predictive value	Negative predictive value	Threshold for improvement or no improvement
Pain	Random forest	Downsampling	27	0.59	0.67	0.49	0.78	0.35	0.72
Function	Gradient boosting machine	No sampling	1	0.74	0.62	0.72	0.73	0.60	0.62

Fig. 3.

This graph shows the calibration curve of the selected prediction model (random forest) for pain in the test dataset and a histogram of the distribution of the predicted probabilities of improvement. Calibration refers to agreement between the predicted probabilities and observed probabilities. In other words, if 10 people had a probability of improvement of 0.6, did six people actually improve? The model performs well on calibration when the calibration curve lies close to the bisector. Calibration for our pain model was insufficient because of the wide confidence interval and because the curve does not cover the lower probability range.

Function Model

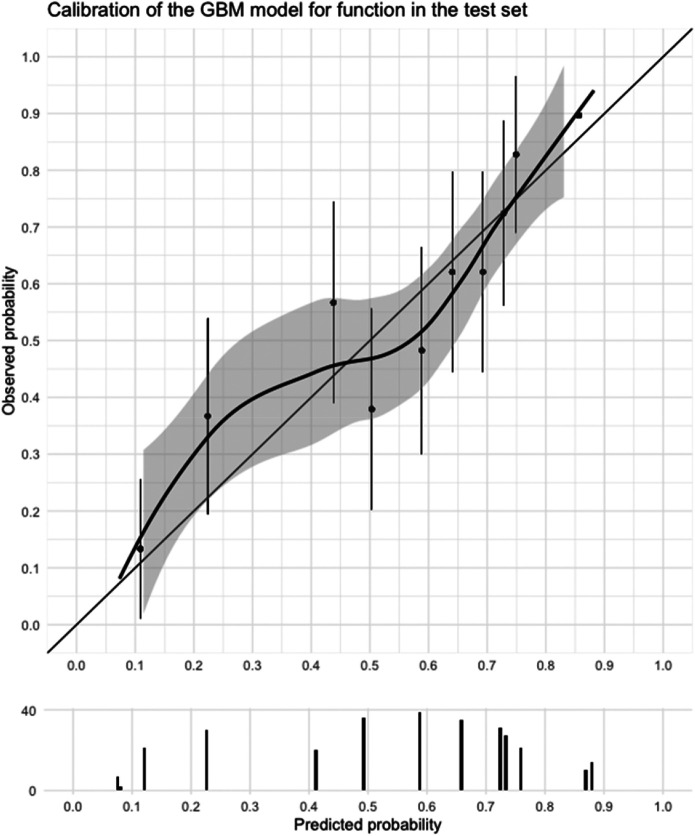
In the validation dataset, the gradient boosting machines model was selected for further evaluation because it showed the most promising performance in terms of discrimination, calibration (Supplementary Fig. 2A-C; http://links.lww.com/CORR/A719), and the fact that it required only a single predictor variable (Supplementary File 1; http://links.lww.com/CORR/A718): the MHQ function score at baseline (Supplementary Table 8; http://links.lww.com/CORR/A717). In the test dataset, it had a good discriminative ability, with an AUC of 0.74 (95% CI 0.69 to 0.80) (Table 3). Sensitivity was 0.62 and specificity was 0.72 at a threshold of 0.62 (Table 3). A visual inspection of the calibration curve showed good calibration (Fig. 4). We have made this model available as a web application. The model predicts the change of reaching the MCID for hand function for an individual patient 12 months after surgery, given the patient's preoperative MHQ hand function score (Supplementary Fig. 3; http://links.lww.com/CORR/A720).

Fig. 4.

This graph shows the calibration curve of the selected prediction model (gradient boosting machines) for function in the test dataset and a histogram of the distribution of the predicted probabilities of improvement. Calibration refers to agreement between the predicted probabilities and observed probabilities. In other words, if 10 people had a probability of improvement of 0.6, did six people actually improve? The model performs well on calibration when the calibration curve lies close to the bisector. Our model for function shows good calibration.

The final hand function model is presented as a Shiny internet application, accessible at https://analyse.equipezorgbedrijven.nl/shiny/cmc1-prediction-model-Eng/. The app currently does not have the Conformité Européenne (CE) mark and has not yet been externally validated; therefore, caution is warranted when using the application.

The R code of the models is available via GitHub [39]. Because of the poor predictive ability, we did not make an internet application for the pain model.

Discussion

Assessing the likelihood of success is an important part of the decision to undergo a certain treatment, especially when the treatment is invasive and elective in nature such as the surgical treatment of CMC1 OA. Thus, communicating the chance of a successful outcome can help the decision-making process. However, predicting which patients will improve in symptoms is difficult. Therefore, a model that predicts the probability of improvement for each patient might contribute to the shared decision-making process. It could also help manage patients’ expectations of the treatment outcome. This study aimed to develop prediction models for the probability of clinically meaningful improvement in pain and hand function 12 months after trapeziectomy with LRTI for CMC1 OA. Unfortunately, despite the relatively large dataset with many variables, we considered the performance of the pain model as insufficient for clinical practice. However, the hand function model had a good discriminative ability and good calibration in our test dataset. This model was a gradient boosting machines model with the baseline MHQ hand function score as the only predictor. We have made an internet application of our hand function model, which can be accessed via https://analyse.equipezorgbedrijven.nl/shiny/cmc1-prediction-model-Eng/. To calculate the prediction of an individual patient, the preoperative MHQ function score of the patient is submitted. The model then calculates the probability of improvement 12 months after surgery. If the MHQ function score of the patient is unknown, it can be calculated in the application by answering five questions.

Limitations

This study has some limitations. Although the models were internally validated in a separate test dataset, no external validation was performed. Evaluating predictive performance of these models in a prospective setting with new patients could be a valuable addition. The current models are generalizable to settings where patients with thumb base osteoarthritis are first treated nonsurgically, and trapeziectomy with LRTI is considered when symptoms are not sufficiently relieved. No distinction was made between different tendonplasties that can be considered as LRTI because they are very similar and there is little evidence for differences in patient-reported outcomes between these techniques [41, 49]. Before generalizing predictions from our model to other surgical treatment options than trapeziectomy with LRTI, such as arthrodesis and prosthetics, additional validation is needed.

Another important limitation is the relatively high proportion of missing data, which is inherent to the nature of the dataset, where all patients are invited to complete multiple patient-reported outcome measures as part as routine outcome measures. Specifically, there was a high proportion of missing data for the psychological variables, which have only been collected since September 2017. We have chosen to still include these because previous studies have shown that these are associated with treatment outcomes of thumb base osteoarthritis [18, 52]. Additionally, we compared patient characteristics and preoperative symptom severity to assess whether nonresponders differed from responders and found only small differences with negligible effect sizes. Missing data were imputed using k-nearest neighbors, but multiple imputation would be preferable. However, to our knowledge, this is currently not implemented in R. When this implementation is available, this may possibly result in better prediction models in the future.

Our models predict the probability that a patient will reach a clinically meaningful improvement, defined as reaching the MCID for the MHQ pain score and the MHQ function score [32]. These MCID scores were calculated for patients with atraumatic hand and wrist conditions, not specifically for patients with CMC1 OA. Additionally, the MCID threshold is determined for patient populations and may be less relevant for individual patients. Therefore, we believe it is important to clearly communicate our definition of improvement to clinicians and patients when using this model, emphasizing that this improvement is considered relevant for most patients but not all. Furthermore, we used random forest and gradient boosting as machine-learning algorithms in our study. It is, however, possible that more complex algorithms, such as artificial neural networks, have a better predictive performance. In our case, the relatively small dataset compared with other studies on machine learning limited our choice of algorithms. Further, the use of additional variables such as preoperative goniometric measurements, genetics, or comorbidities might have improved the performance of our prediction models [12, 22, 50]. However, we did not have sufficient data to evaluate these variables. In our opinion, the inclusion of variables such as genetics would make it harder to implement our model in daily clinical practice.

Finally, we judged that the AUC of the pain model (0.59) was insufficient since it was only slightly better than chance, and the AUC of the hand function model (0.74) was sufficient for application in clinical practice, given that it met the threshold for acceptable discrimination [23]. However, what is considered “sufficient” might be debatable and dependent on the action that will follow from the prediction on the model. We therefore strongly recommend that the model is only used as a decision aid that provides additional insight into the expected outcome of surgery.

Pain Model

The performance of our best-performing pain model was insufficient. The model performed poorly on both discrimination and calibration and should therefore not be used in clinical practice. This is in line with reports on surgery for OA of other joints [30, 43] and the finding that pain after total joint arthroplasty cannot accurately be predicted using clinical variables [5]. The nature of postoperative pain might be different from preoperative OA-related pain, and this is therefore more difficult to predict. In clinical practice, we have noticed that many patients indicate they still experience pain but not the familiar OA-related pain that was the surgical indication. Because there are indications that genetic factors play a role in chronic and neuropathic pain [22, 50], this may be a direction for further research into predicting postoperative pain.

Function Model

Our hand function model showed reasonable performance in terms of discrimination and calibration and required only one predictor. This model was used for the development of a web application that is publicly available online and can be used to help guide the decision-making process. However, since our model has not been externally validated, caution is warranted. The model was a gradient boosting machines algorithm.

In our study, machine-learning algorithms had a better predictive performance in both our datasets than the traditional statistical logistic regression model. Although the discriminative ability of the logistic regression model for hand function was only marginally worse than that of the gradient boosting machines model in the validation dataset, it required almost 80 variables as input, whereas the gradient boosting machines model only required one (Supplementary Table 8; http://links.lww.com/CORR/A717). Machine-learning algorithms might be better equipped to deal with the nonlinearities in datasets [1, 31] that are often present in real-world data. It might, however, be possible to fit these nonlinear effects using statistical methods such as generalized additive models or nonlinear effects in logistic regression.

Although some studies have reported prognostic factors influencing the outcome of surgical treatment of CMC1 OA [2, 12, 26, 36], the development of a prediction model is new. One study examined the prognostic value of preoperative patient-reported disability and psychological characteristics for early postoperative outcomes with a mean follow-up of 14 weeks [26]. The authors found that patients with greater preoperative disability experienced more improvement after surgery but did not find an association between psychological factors and outcomes. This is in line with the results of our hand function model, which only requires baseline function as a predictor. Another study evaluated the relationship between the duration of symptoms and surgical outcomes [2]. The authors found that patients with an increased duration of symptoms had a poorer postoperative outcome. Although the duration of symptoms was one of the variables in our dataset, this was not one of the predicting variables in our models. This indicates that in our dataset, the duration of symptoms did not have sufficient predictive power.

Conclusion

We developed a model to predict the probability of improvement in hand function 12 months after trapeziectomy and LRTI for CMC1 OA. The model had good discriminative ability and good calibration in our test dataset. Unfortunately, the performance of our pain model was insufficient for use in practice. The final model for hand function was used to develop an online application that can be used to estimate the chance of survival for an individual patient. However, our model does not have CE marking and has not been externally validated. By making our model available online, we encourage others to validate the model in their patient populations.

Group Authorship

Members of the Hand-Wrist Study include: R. Arjen M Blomme MD; Berbel J.R. Sluijter MD, PhD; Dirk-Jan J.C. van der Avoort MD; Alexander Kroeze MD; Jeroen Smit MD, PhD; Jan Debeij MD, PhD; Erik T. Walbeehm MD, PhD; Gijs M. van Couwelaar MD; Guus M. Vermeulen MD, PhD; Hans de Schipper MD; Hans Temming MD; Jeroen Hvan Uchelen MD, PhD; H. Luitzen deBoer MD; Nicoline de Haas MD; Kennard Harmsen MD; Oliver T. Zöphel MD, PhD; Reinier Feitz MD; Richard Koch MD; Steven E.R. Hovius MD, PhD; Thybout M. Moojen MD, PhD; Xander Smit MD, PhD; Rob van Huis PT; Pierre Y. Pennehouat PT; Karin Schoneveld PT, MSc; Yara E. van Kooij PT, MSc; Robbert M. Wouters PT, PhD; Paul Zagt PT; Folkert J. van Ewijk PT; Joris J. Veltkamp PT; Alexandra Fink PT; Willemijn A. de Ridder PT, MSc; Miguel C. Jansen MD, PhD; Mark J.W. van der Oest PhD; Pepijn O. Sun MD; Joris S. Teunissen BSc; Jak Dekker MSc; Marlies L. Jansen-Landheer MD, MSc; Marloes H.P. ter Stege MSc