Skip to main content
PMC home page
Applied and Environmental Microbiology logoLink to Applied and Environmental Microbiology
. 2000 Feb;66(2):869–873. doi: 10.1128/aem.66.2.869-873.2000

Survival of Bifidobacterium longum Immobilized in Calcium Alginate Beads in Simulated Gastric Juices and Bile Salt Solution

Ki-Yong Lee 1, Tae-Ryeon Heo 1,*
PMCID: PMC91913  PMID: 10653768

Abstract

Bifidobacterium longum KCTC 3128 and HLC 3742 were independently immobilized (entrapped) in calcium alginate beads containing 2, 3, and 4% sodium alginate. When the bifidobacteria entrapped in calcium alginate beads were exposed to simulated gastric juices and a bile salt solution, the death rate of the cells in the beads decreased proportionally with an increase in both the alginate gel concentration and bead size. The initial cell numbers in the beads affected the numbers of survivors after exposure to these solutions; however, the death rates of the viable cells were not affected. Accordingly, a mathematical model was formulated which expressed the influences of several parameters (gel concentration, bead size, and initial cell numbers) on the survival of entrapped bifidobacteria after sequential exposure to simulated gastric juices followed by a bile salt solution. The model proposed in this paper may be useful for estimating the survival of bifidobacteria in beads and establishing optimal entrapment conditions.

It has been reported that the microencapsulation of bifidobacteria can ensure greater survival in gastric and intestinal environments (18). Immobilized cells exhibit many advantages over free cells, including the maintenance of stable and active biocatalysts, high volumetric productivity, improved process control, the protection of cells against damage, and reduced susceptibility to contamination (12, 19). Recently, yogurt products containing encapsulated lactic acid bacteria have been distributed under the brand name Doctor-Capsule (Bingrae Co., Kyunggi-do, Korea) in Korea. Among the available techniques for immobilizing living cells, entrapment in Ca alginate beads has been frequently used for the immobilization of lactic acid bacteria (22). Alginate has the benefits of being nontoxic to the cells being immobilized, and it is an accepted food additive (17). This study used mathematical modelling to represent the influences of alginate concentration, bead size, and initial cell numbers on the survival rate of entrapped bifidobacteria against simulated gastric juices and bile salt solution.

Entrapment of bifidobacteria.

Bifidobacterium longum KCTC 3128 (ATCC 15707) was purchased in lyophilized form from the Korea Collection for Type Cultures (Genetic Resource Center, Taejon, Korea). B. longum HLC 3742 was screened from feces from a healthy Korean (14). These two types of bacteria were transferred twice in Trypticase-protease peptone-yeast extract (TPY) broth at 37°C. Cultivation was carried out in a 2.5-liter fermentor containing 1,000 ml of TPY broth. After cultivation for 20 h, cultures were collected by centrifugation (3,000 × g, 10 min), washed, and resuspended in a 0.85% NaCl saline solution to approximately 109 cells/ml. Sodium alginate (medium viscosity) obtained from Sigma Chemical Co. was used in this study. Various amounts of sodium alginate (5, 7.5, and 10 g) were autoclaved at 121°C for 15 min in powder and then individually dissolved in 250-ml resuspended cell solutions in aseptic vinyl bags. The solutions were thoroughly mixed with a Stomacher 400 (Seward Co., London, United Kingdom) laboratory blender. By using aseptic and compressed air, filtered by autoclaved 5-, 1-, and 0.22-μm-pore-size filters sequentially set in the compressor, the cell-alginate mixtures were ejected dropwise through a 20-gauge nozzle into a 0.1 M CaCl2 solution in a clean bench. Large, medium, and small beads (mean diameters, about 1.03, 1.75, and 2.62 mm, respectively) containing 2, 3, and 4% sodium alginate were obtained by controlling the compressed air pressure through a 20-gauge nozzle. The beads were made to be spherical and were prepared to be relatively uniform in size. The total viable numbers of untrapped bifidobacteria expressed as CFU were determined by the plate count method using TPY agar. To count the viable cell numbers in beads, 100 particles were washed with a sterile saline solution and dissolved for 10 min in 30 ml of a sterile 0.1 M sodium citrate solution with the aid of a Stomacher 400 (Seward Co.). The cultivation of bifidobacteria on a TPY agar plate was done anaerobically under N2 (75%), H2 (10%), and CO2 (5%) at 37°C for 48 h.

Survival of bifidobacteria in simulated gastric juices.

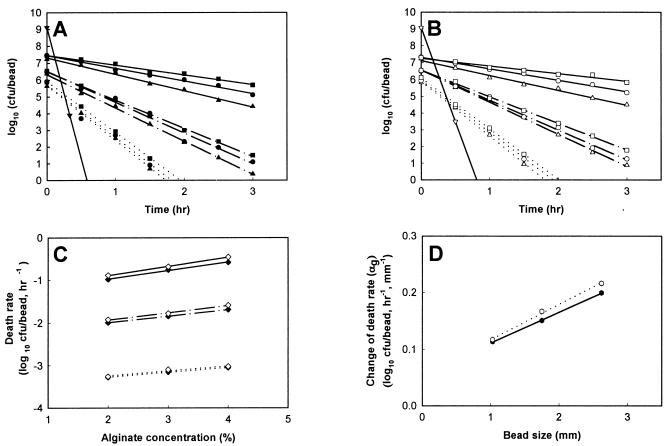
Simulated gastric juices without pepsin (0.08 M HCl containing 0.2% NaCl [pH 1.55]) were prepared by Rao et al. (18). One hundred single beads in each of six cap tubes containing 10 ml of simulated gastric juices were incubated anaerobically at 37°C for 3 h. At an interval of 30 min during incubation, all the beads from one cap tube sample were harvested, washed with physiological saline, and immediately assayed for cell enumeration. To prepare samples for untrapped bifidobacteria, 10-ml volumes of cultures were centrifuged (10 min, 3,000 × g). The pellets were resuspended in a 0.85% saline solution and collected by centrifugation. The supernatants were discarded, and 10 ml of simulated gastric juices was added to each cap tube containing the recovered cells. The cells were then lightly agitated, incubated at 37°C for the same time as described for the entrapped cells, and finally assayed for cell enumeration. Figure 1 shows that the log of the surviving cells decreased proportionally with the time that the entrapped bifidobacteria were exposed to simulated gastric juices. The death rate (slope of line) of B. longum KCTC 3128 and HLC 3742 entrapped in the beads decreased proportionally with increased bead size and alginate concentration (Fig. 1A and B). The viable cell numbers of untrapped B. longum KCTC 3128 and HLC 3742 rapidly decreased from 1.28 × 109 and 1.18 × 109 CFU/ml, respectively, to below 1 × 103 CFU/ml within 30 min. Therefore, the survival of entrapped bifidobacteria was higher than that of untrapped cells. In the presence of simulated gastric juices, the change of viable cell numbers in a bead (death rate) is given by dNg/dtg, where Ng is the log viable cell numbers and tg is the exposure time. Assuming that the beads have a constant cell density, the log viable cell numbers of bifidobacteria in a bead can be given by the following equation:

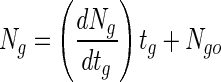graphic file with name M1.gif 1

where Ngo is the log viable cell numbers in a bead before exposure to simulated gastric juices. As shown in Fig. 1C, the absolute value of the cell death rate in beads decreased proportionally with increased alginate concentration in the beads. Therefore, the change in cell death rate in a bead after exposure to simulated gastric juices related to the change in alginate concentration can be expressed by:

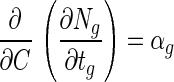graphic file with name M2.gif 2

where C is the alginate concentration of a bead and αg is the change in the cell death rate in a bead in relation to a change in alginate concentration of beads. In Fig. 1D, the value of αg increased proportionally with increased bead size. Therefore, the change in αg related to the change in bead size can be written as:

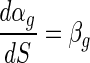graphic file with name M3.gif 3

where S is the bead size and βg is the change in αg in relation to a change in bead size. Accordingly, by using equations 1, 2, and 3, the viable cell numbers in a bead with a certain alginate concentration and bead size in the presence of simulated gastric juices can be expressed as follows:

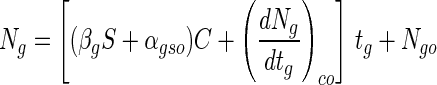graphic file with name M4.gif 4

where αgso is the slope of the cell death rate when S is zero, and (dNg/dtg)co is the change in viable cell numbers in beads when C is zero. These three values, including βg, were calculated from the experimental data. From the results shown in Fig. 1C, we know that (dNg/dtg)co was not a constant and increased proportionally with the increase in bead size (data not shown). This change is expressed by:

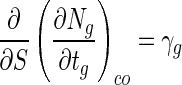graphic file with name M5.gif 5

where γg is the change in (dNg/dtg)co in relation to change in bead size. Equation 5 can be integrated as follows:

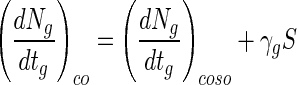graphic file with name M6.gif 6

where (dNg/dtg)coso is (dNg/dtg)co when S is zero. Therefore, equation 4 can be expressed as follows:

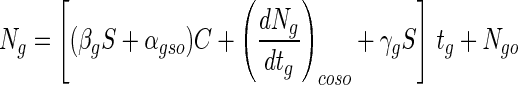graphic file with name M7.gif 7

To examine the effect of the initial cell loading in the beads on the survival of bifidobacteria, three 2.6-mm-diameter beads containing 3% alginate and different initial cell loads (approximately 108, 109, and 1010 cells/ml) were also tested by the same methods as described above. As expected, the death rates of the viable cells in all three different kinds of beads had the same values (data not shown). Accordingly, the initial cell numbers did not affect the death rates of the viable cells.

FIG. 1.

FIG. 1

Open in a new tab

Survival of entrapped bifidobacteria after exposure to simulated gastric juices at 37°C for 3 h. (A) Survival of B. longum KCTC 3128; (B) Survival of B. longum HLC 3742; (C) death rate of bifidobacteria in beads; (D) change in death rate of bifidobacteria in beads in relation to the change in bead size. Symbols: ▴ and ▵, 2% alginate beads; ● and ○, 3% alginate beads; ■ and □, 4% alginate beads; ···, small beads; — · —, medium beads; —, large beads; ⧫, death rate of B. longum KCTC 3128; ◊, death rate of B. longum HLC 3742; ···Inline graphic···, change in death rate of B. longum KCTC 3128; –Inline graphic–, change in death rate of B. longum HLC 3742; –▾–, untrapped B. longum KCTC 3128; –▿–, untrapped B. longum HLC 3742.

Survival of bifidobacteria in a bile salt solution.

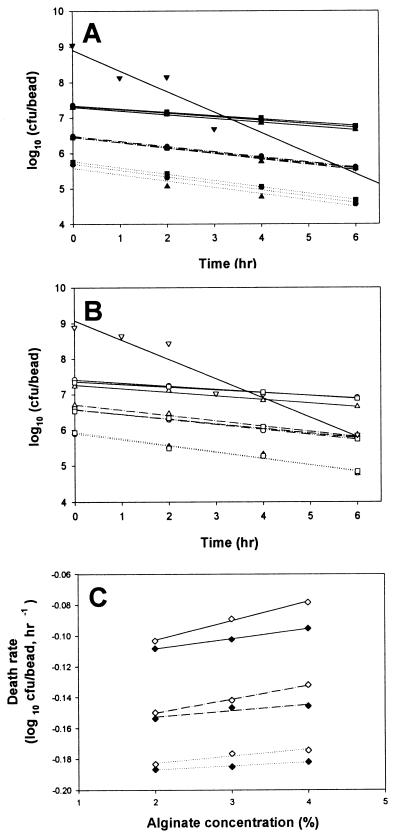
To determine the effect of bile salts on bifidobacteria survival, 100 single beads were separately put into each of three cap tubes containing 10 ml of a bile salt solution dissolved in 0.6% oxgall (Difco Co.) which had been sterilized by autoclaving at 121°C for 15 min and then incubated anaerobically at 37°C for 6 h. The influences of the entrapment parameters on the survival of the bifidobacteria exposed to bile salt solution were tested by the same methods as described for the simulated gastric juices. As expected, the log of the surviving cells in beads decreased proportionally with the exposed time as shown in Fig. 2. The alginate concentration had a mild effect on cell viability (Fig. 2A and B). However, the absolute value of the cell death rate in the beads decreased proportionally with increased alginate gel concentration and bead size (Fig. 2C). As with the pattern for survival of simulated gastric juices, the change in cell death rate in a bead after exposure to bile salt solution in relation to the change in alginate concentration (αb) increased proportionally with increased bead size (data not shown). Therefore, the survival of entrapped bifidobacteria in bile salt solution can be also expressed in the same manner with equation 7 and can be defined as follows:

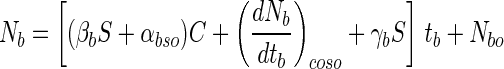graphic file with name M8.gif 8

where Nb is the log viable cell number in a bead with a certain alginate concentration and bead size in the presence of a bile salt solution and tb is the exposure time to a bile salt solution. Also, αb is the change in cell death rate in a bead after exposure to a bile salt solution in relation to a change in alginate concentration, and βb is the change in αb in relation to change in bead size. γb is the slope of (dNb/dtb)co in relation to change in bead size. βb, αbso, γb, Co, and Nbo were all calculated by using the experimental data.

FIG. 2.

FIG. 2

Open in a new tab

Survival of entrapped bifidobacteria after exposure to bile salt solution at 37°C for 6 h. (A) Survival of B. longum KCTC 3128; (B) Survival of B. longum HLC 3742; (C) death rate of bifidobacteria in beads. Symbols: ▴ and ▵, 2% alginate beads; ● and ○, 3% alginate beads; ■ and □, 4% alginate beads; ⋯, small beads; — · —, medium beads; —, large beads; ⧫, death rate of B. longum KCTC 3128; ◊, death rate of B. longum HLC 3742; –▾–, untrapped B. longum KCTC 3128; –▿–, untrapped B. longum HLC 3742.

However, in the case where some entrapped bifidobacteria are sequentially exposed to simulated gastric juices and a bile salt solution, the log viable cell numbers in a bead before exposure to a bile salt solution in equation 8 (Nbo) are the same as the log viable cell numbers in a bead after exposure to simulated gastric juices in equation 7 (Ng). Therefore, S, the bead size of equation 8, can be mismatched with the intrinsic bead size. The reduction in actual bead volume occupied by survivors with the exposure time to simulated gastric juices, given by −dV/dtg, is proportional to the death rate of log viable cell numbers in a bead, where V is the bead volume occupied by viable cells, tg is the exposure time to simulated gastric juices, and ρ is the cell density of a bead:

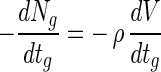graphic file with name M9.gif 9

Assuming that a bead has a complete spherical shape, it can be represented by:

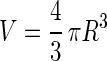graphic file with name M10.gif 10

where R is the radius of a bead. Accordingly, the substitution of equation 10 into equation 9 estimates the change in viable cell numbers in the beads. That is:

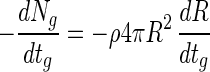graphic file with name M11.gif 11

Thus, equation 11 can be integrated to give a bead radius as a function of time, and it can be rearranged by:

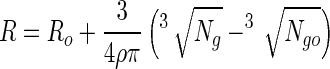graphic file with name M12.gif 12

where Ro is the initial radius of a bead before exposure to simulated gastric juices. Thus, the viable cell numbers in a calcium alginate bead after sequential exposure to simulated gastric juices followed by a bile salt solution can be expressed by using equations 7, 8, and 12. That is:

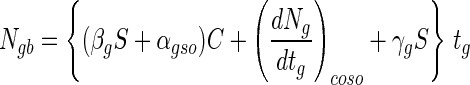graphic file with name M13.gif 13
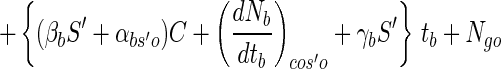graphic file with name M14.gif

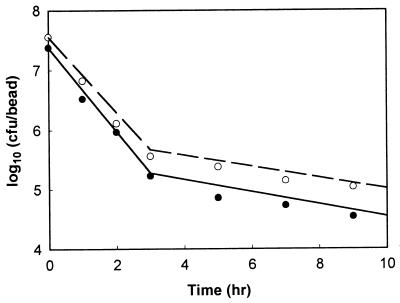
where S′ is the actual bead size occupied by viable cell numbers after exposure to simulated gastric juices, that is, 2R. One hundred single beads, 3% alginate beads with 2.62-mm diameters, were put separately into each of six cap tubes containing 10 ml of simulated gastric juice, and the cap tubes were incubated anaerobically at 37°C for 3 h. Every 1 h during incubation, all the beads from one cap tube sample were harvested, washed with physiological saline, and immediately assayed for cell enumeration. After 3 h, the solutions in the remaining three cap tubes were changed from simulated gastric juice to 10 ml of a bile salt solution and then incubation was continued for 6 h. Figure 3 shows that the number of survivors after sequential exposure to simulated gastric juices and a bile salt solution estimated from equation 13 (Ngb) is not in disagreement with the measured data; therefore, this equation has credibility. However, the experimental data were slightly lower than the calculated data, and there was some scatter in the measured data.

FIG. 3.

FIG. 3

Open in a new tab

Theoretical and experimental survival of bifidobacteria entrapped in 3% alginate beads containing three different initial cell numbers after sequential exposure to simulated gastric juices for 3 h followed by bile salt solution for 6 h. The lines   were calculated by using equation 13. The points marked by symbols (● and ○) are experimental data. Symbols: ●, the viable cell numbers of B. longum KCTC 3128; ○, the viable cell numbers of B. longum HLC 3742.

The influences of the entrapment parameters (alginate concentration, bead size, and initial cell number) on the survival of the bifidobacteria were quantitatively and systematically determined. Although some authors have studied the survival of bifidobacteria and lactic acid bacteria in the presence of gastric and/or intestinal juices (2, 5, 15, 16), this is the first report, as far as is known, to present a mathematical quantification of the survival of entrapped bifidobacteria when sequentially exposed to simulated gastric juices and a bile salt solution. The mathematical quantification described above was made possible by introducing a new entrapping procedure whereby alginate gel, containing bifidobacteria, was prepared by the addition of sterilized sodium alginate powder to a suspended cell solution. Prior to the experiment described above, another experiment had been conducted by the conventional entrapping procedures (4, 13, 17), with a cell suspension added to a sterile sodium alginate solution. However, the experimental results obtained from the conventional entrapping procedures did not provide sufficient information to study the survival characteristics of bifidobacteria entrapped in calcium alginate beads in simulated gastric juices and bile salt solution. It is thought that the nonuniform cell distribution in the gel beads resulted in the insufficient information. This phenomenon is related to mixing problems that result when the inoculum is added to the polymer solution during bead preparation, since this polymer solution has a very high viscosity and produces a nonuniform cell distribution in the gel beads (23). Sodium alginate concentrations from 2 to 4% were tested in this study. As expected, the higher the concentration of alginate in the beads, the lower the death rate of the cells in the beads (Fig. 1 and 2). It has been reported that the lower diffusion rate of glucose and ethanol in more-concentrated alginate gels is due to a decrease in the number and length of the pores rather than a decrease in the pore diameter (7). It was found that gel concentrations below 2% did not form spherically shaped beads. This result was in agreement with other investigations (9, 20). It has also been shown that low-viscosity droplets are less able to retain their spherical shape against drag forces upon collision with a solution. Yet, a high concentration of sodium alginate (5% or more) cannot form small droplets because of its physiological characteristics as a dough. Accordingly, cell entrapment is limited to the range of gel concentrations that form spherical beads.

In relation to bead size, the survival of cells in beads is higher with larger beads as shown in Fig. 1 and 2. Sheu et al. (21) indicated that larger bead diameters provided more protection for Lactobacillus bulgaricus in frozen desserts. Very large beads, however, can cause a coarseness of texture in live microbial feed supplements, and small beads cannot provide sufficient protection for the bacteria. Therefore, bifidobacteria should be entrapped within a limited range of bead sizes.

Two strains of B. longum (KCTC 3128 and HLC 3743), as used in this study, have a distinct value for each parameter in equation 13. Other bifidobacteria may have their distinct values. Species of Bifidobacterium have been reported to differ in their susceptibility to gastric acidity (2). In addition, they have a different tolerance of bile salts (6, 8). This suggests that the values of each parameter in equation 13 will be affected by the kind of bifidobacteria.

In order to survive and reach the colon in quantities large enough to facilitate colonization, a large number of initial cells must be entrapped in the beads. Hannoun and Stephanopoulos (7) reported that a larger cell load weakened the gel. Moreover, there is difficulty with high-concentration cultivation of bifidobacteria. Berrada et al. (2) demonstrated that not all commercial bifidobacterium-fermented milks can bring enough living bifidobacteria to the human intestine to ensure a health benefit. Accordingly, most researchers have chosen to use Bifidobacterium strains that are more resistant to gastric acid and bile salts (2, 6, 8, 10, 15, 16). As another effective way, Rao et al. (18) developed a preliminary procedure for the microencapsulation of Bifidobacterium pseudolongum with cellulose acetate phthalate by using phase separation-coacervation. Their results showed that microencapsulated bacteria were more resistant than unencapsulated bacteria against sequential stress in simulated gastric and intestinal juices. However, among the techniques for immobilizing living cells, gel entrapment using natural biopolymers is favored by most researchers for various reasons (1, 11), including nontoxicity of the matrix (crucial for food-related application), simplicity of immobilization technique, high viability, and productivity of the immobilized cells. Until now, most immobilization techniques for bifidobacteria or probiotic bacteria have been developed to test the hypothesis that immobilized cells survive better than nonimmobilized cells (3, 4, 18, 21, 22).

From this study, it was found that the survival of entrapped bifidobacteria was strongly dependent on various parameters, including alginate concentration, bead size, initial cell numbers, and bacterial species. The mathematical model outlined in this article should be useful in evaluating the influence of various parameters on the survival of entrapped bifidobacteria under sequential stress in the gastrointestinal tract and for establishing the optimal conditions for the entrapment of bifidobacteria. This model may have an important role in food processing and pharmaceutical preparations.

Acknowledgments

This work was supported by a grant (BK21 project) from the Ministry of Education, Korea.

REFERENCES

  • 1.Audet P, Paquin C, Lacroix C. Immobilized growing lactic acid bacteria with κ-carrageenan-locust bean gum gel. Appl Microbiol Biotechnol. 1988;29:11–18. [Google Scholar]
  • 2.Berrada N, Lemelan J F, Laroche G, Thouvenot P, Piaia M. Bifidobacterium from fermented milks: survival during gastric transit. J Dairy Sci. 1991;74:409–413. doi: 10.3168/jds.S0022-0302(91)78183-6. [DOI] [PubMed] [Google Scholar]
  • 3.Camelin I, Lacroix C, Paquin C, Prevost H, Cachon R, Divies C. Effect of chelatants on gellan gel rheological properties and setting temperature for immobilization of living bifidobacteria. Biotechnol Prog. 1993;9:291–297. doi: 10.1021/bp00021a008. [DOI] [PubMed] [Google Scholar]
  • 4.Champagne C P, Gaudy C, Poncelet D, Neufeld R J. Lactococcus lactis release from calcium alginate beads. Appl Environ Microbiol. 1992;58:1429–1434. doi: 10.1128/aem.58.5.1429-1434.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Conway P L, Gorbach S L, Goldin B R. Survival of lactic acid bacteria in the human stomach and adhesion to intestinal cells. J Dairy Sci. 1987;70:1–12. doi: 10.3168/jds.S0022-0302(87)79974-3. [DOI] [PubMed] [Google Scholar]
  • 6.Gopal A, Shah N P, Roginski J. Bile tolerance, taurocholate deconjugation and cholesterol removal by Lactobacillus acidophilus and Bifidobacterium spp. Milchwissenschaft. 1996;51:519–623. [Google Scholar]
  • 7.Hannoun B, Stephanopoulos G. Diffusion coefficients of glucose and ethanol in cell-free and cell-occupied calcium alginate membranes. Biotechnol Bioeng. 1986;28:829–835. doi: 10.1002/bit.260280609. [DOI] [PubMed] [Google Scholar]
  • 8.Ibrahim S A, Bezkorovainy A. Survival of bifidobacteria in the presence of bile salt. J Sci Food Agric. 1993;62:351–354. [Google Scholar]
  • 9.King G, Daugulis A, Goosen M, Faulkner P, Bayly D. Alginate concentration: a key factor in growth of temperature-sensitive baculovirus-infected cells in microcapsules. Biotechnol Bioeng. 1989;34:1085–1091. doi: 10.1002/bit.260340809. [DOI] [PubMed] [Google Scholar]
  • 10.Klaver F A M, Meer R. The assumed assimilation of cholesterol by lactobacilli and Bifidobacterium bifidum is due to their bile salt-deconjugating activity. Appl Environ Microbiol. 1993;59:1120–1124. doi: 10.1128/aem.59.4.1120-1124.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Klein J, Vorlop D. Immobilization technique—cells. In: Moo-Young M, editor. Comprehensive biotechnology. Vol. 2. Oxford, United Kingdom: Pergamon Press; 1985. pp. 203–224. [Google Scholar]
  • 12.Kolot F B. Immobilized cells for solvent production. Process Biochem. 1984;19:7–13. [Google Scholar]
  • 13.Lacroix C, Paquin C, Arnaud J P. Batch fermentation with entrapped growing cells of Lactobacillus casei. Appl Microbiol Biotechnol. 1990;32:403–408. [Google Scholar]
  • 14.Lee K Y, Heo T R. Identification of Bifidobacterium strains at the genus level by thin layer chromatographic determination of organic acids with culture broth of isolated bacteria strain from human feces. Food Biotechnol. 1998;7:95–99. [Google Scholar]
  • 15.Marteau P, Minekus M, Havenarr R, Huis Int Veld J H J. Survival of lactic acid bacteria in a dynamic model of the stomach and small intestine: validation and the effects of bile. J Dairy Sci. 1997;80:1031–1037. doi: 10.3168/jds.S0022-0302(97)76027-2. [DOI] [PubMed] [Google Scholar]
  • 16.Pochart P, Marteau P, Bouhnik T, Goderel I, Bourlioux P, Rambaud J. Survival of bifidobacteria ingested via fermented milk during their passage through the human small intestine: an in vivo study using intestinal perfusion. Am J Clin Nutr. 1992;55:78–80. doi: 10.1093/ajcn/55.1.78. [DOI] [PubMed] [Google Scholar]
  • 17.Prevost H, Divies C. Continuous pre-fermentation of milk by entrapped yoghurt bacteria. I. Development of the process. Milchwissenschaft. 1988;43:621–625. [Google Scholar]
  • 18.Rao A V, Shiwnarain N, Maharaj J. Survival of microencapsulated Bifidobacterium pseudolongum in simulated gastric and intestinal juices. Can Inst Food Sci Technol J. 1989;22:345–349. [Google Scholar]
  • 19.Scott C D. Immobilized cells: a review of recent literature. Enzyme Microb Technol. 1987;9:66–73. [Google Scholar]
  • 20.Seifert D, Phillips A. Production of small, monodispersed alginate beads for cell immobilization. Biotechnol Prog. 1997;13:562–568. [Google Scholar]
  • 21.Sheu T Y, Marshall R T, Heymann H. Improving survival of culture bacteria in frozen desserts by microentrapment. J Dairy Sci. 1993;76:1902–1907. doi: 10.3168/jds.S0022-0302(93)77523-2. [DOI] [PubMed] [Google Scholar]
  • 22.Sheu T Y, Marshall R T. Microentrapment of lactobacilli in calcium alginate gels. J Food Sci. 1993;54:557–561. [Google Scholar]
  • 23.Tanaka H, Matsumura M, Veliky I A. Diffusion characteristics of substrates in Ca-alginate gel beads. Biotechnol Bioeng. 1984;26:53–58. doi: 10.1002/bit.260260111. [DOI] [PubMed] [Google Scholar]

Articles from Applied and Environmental Microbiology are provided here courtesy of American Society for Microbiology (ASM)

RESOURCES