Unravelling the dynamics of the COVID-19 pandemic with the effect of vaccination, vertical transmission and hospitalization

Abstract

The coronavirus disease 2019 (COVID-19) is caused by a newly emerged virus known as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), transmitted through air droplets from an infected person. However, other transmission routes are reported, such as vertical transmission. Here, we propose an epidemic model that considers the combined effect of vertical transmission, vaccination and hospitalization to investigate the dynamics of the virus’s dissemination. Rigorous mathematical analysis of the model reveals that two equilibria exist: the disease-free equilibrium, which is locally asymptotically stable when the basic reproduction number (${\mathcal{R}}_0$) is less than 1 (unstable otherwise), and an endemic equilibrium, which is globally asymptotically stable when ${\mathcal{R}}_0>1$ under certain conditions, implying the plausibility of the disease to spread and cause large outbreaks in a community. Moreover, we fit the model using the Saudi Arabia cases scenario, which designates the incidence cases from the in-depth surveillance data as well as displays the epidemic trends in Saudi Arabia. Through Caputo fractional-order, simulation results are provided to show dynamics behaviour on the model parameters. Together with the non-integer order variant, the proposed model is considered to explain various dynamics features of the disease. Further numerical simulations are carried out using an efficient numerical technique to offer additional insight into the model’s dynamics and investigate the combined effect of vaccination, vertical transmission, and hospitalization. In addition, a sensitivity analysis is conducted on the model parameters against the ${\mathcal{R}}_0$ and infection attack rate to pinpoint the most crucial parameters that should be emphasized in controlling the pandemic effectively. Finally, the findings suggest that adequate vaccination coupled with basic non-pharmaceutical interventions are crucial in mitigating disease incidences and deaths.

Introduction

SARS-CoV-2, a newly emerged virus which emanated from China towards the end of 2019, has induced the current pandemic of COVID-19, as described by the World Health Organization (WHO) in early 2020 [1]. It was the first in the history of its kind from the coronavirus family to have caused a global pandemic [1], [2], [3], [4]. This pandemic has greatly derailed worldwide public health and the economy. As of 23 January 2022, there had been more than 318.6 million COVID-19 cases reported, including over 5.5 million deaths globally [5].

Interventions other than pharmaceuticals, such as face masks, remote schooling, social distancing, and border closure/travel restrictions have been the most crucial control measures in halting the effects of the pandemic, especially during the early stages [6], [7], [8]. Despite the crucial role played by the NPIs in slowing transmission and reducing the mortality rate, the pandemic continues to engulf and deteriorate global public health and the economy.

Consequently, pharmaceutical intervention measures, such as vaccines that are expected to come up with long-term or permanent shield against the SARS-CoV-2 infection, are currently the most efficient preventive measures, providing immunity against COVID-19 infection or protecting people from severe infection [8], [9], [10]. Owing to the efficiency of the COVID-19 vaccines in halting the pandemic’s effects, they are in high demand worldwide. Thus, it is imperative to employ a decision-making approach for the appropriate distribution of the vaccines, especially in vulnerable communities where the vaccine availability is still limited [8], [11], [12]. Interestingly, by 14 January 2022, more than 9.28 billion vaccine doses had been administered worldwide [5], [8], contributing significantly to the reduction in morbidity and fatality cases.

According to previous reports, infection with COVID-19 could be severe in pregnant women due to maternal physiological changes, which may raise the chance of acquiring a serious disease as a result of viral infections [13]. In addition, COVID-19 vertical transmission during pregnancy (primarily during the third trimester) has been reported in the literature [13], [14], [15], [16]. However, no previous coronaviruses have been reported to transmit from mother-to-child in the cause of pregnancy [13]. One of the epidemiological consequences of the SARS-CoV-2 infection from an infected mother to newborns during the pregnancy is that it increases the likelihood of more adverse effects, such as maternal depression, stillbirth, and maternal and neonatal mortality [14], [13].

However, diverse work must be done to explore the actual scenario of how the virus transmits vertically. Some reports also suggested that COVID-19 vertical transmission could be due to environmental exposure [13], [17], [18]. Moreover, the mode of delivery from COVID-19 infected mothers may not have an intense effect on the risk of newborn infection; therefore, it is insignificant to stop breastfeeding newborn babies [17], [18].

Since the pandemic’s beginning, many epidemiological studies have been conducted to investigate COVID-19 transmission dynamics. These studies include examining the disease’s clinical features [19], and estimating crucial epidemiological parameters, such as reproduction numbers, exponential growth, serial intervals and the infection fatality rate [2], [3], [7], [20], [21], [22], [23], [24], [25], [26], [27]. Moreover, studies have also assessed reinfection and reactivation [28], [29], [30], [31], the impact of declaring the disease a major public health crisis of international importance [4], [32], [33], the influence of public health awareness on COVID-19 dynamics [34], optimal control and cost-effectiveness [35], [36] and the effects of pharmaceutical and NPI measures [6], [37]. Some studies also adopted fractional calculus to analyse the COVID-19 dynamics to find the optimal control strategies [38], [39], [40].

Here, we proposed a new compartmental model to examine the dynamics of the virus’s transmission, taking into account the combined effects of vaccines, vertical transmission and early hospitalization. To our knowledge, no previous studies have employed an epidemiological model to investigate the transmission dynamics of SARS-CoV-2 with the combined effects of vaccination, vertical transmission and early hospitalization. The current research contributes additional insight into the existing knowledge on the epidemiological characteristics (e.g. transmission potential) of SARS-CoV-2 and provides suggestions for effective control measures.

The manuscript is arranged as follows. The model is formulated in Section “Formulation of the Conceptual Model” and analysed in Section “Analysis of the Conceptual Model”. Numerical results and sensitivity analysis are presented in Section “Numerical Simulations and Sensitivity Analysis”. Finally, a detailed discussion is presented in Section “Discussion and Conclusions”.

Formulation of the conceptual model

First, we obtained data on the number of COVID-19 cases in Saudi Arabia from the public domain of the WHO disease surveillance system (dashboard) [5]. To examine the dynamics behaviour of SARS-CoV-2 with the combined effects of vaccination, vertical transmission, and hospitalization, we designed a new deterministic model based on the standard susceptible–exposed–infectious–recovered (SEIR) type. This model assumes two different transmission scenarios: COVID-19 transmission through contact with an infected person (primarily by air droplets) and vertical transmission (mother-to-child infection during pregnancy).

The human population is denoted by $N\left(t\right)$ at time $t$ and is categorized into mutually exclusive compartments of unvaccinated susceptible $S\left(t\right)$, vaccinated susceptible $V\left(t\right)$, exposed $E\left(t\right)$ (epidemiologically, every infection from an infectious disease must pass through a latency period, the time interval between when a pathogen infects an individual or host and when the host becomes infectious), infectious $I\left(t\right)$ (comprising asymptomatically and symptomatically infected individuals, lumped together for computational convenience), hospitalized $H\left(t\right)$ (individuals receiving treatment for mild or severe COVID-19 cases) and recovered $R\left(t\right)$ humans. The parameters ${\theta }_i$ and ${\theta }_h$ denote the fraction of newly newborn babies infected with SARS-CoV-2 directly from COVID-19 infected mothers to the $I\left(t\right)$ and $H\left(t\right)$. Hence, we have

$$N\left(t\right)=S\left(t\right)+V\left(t\right)+E\left(t\right)+I\left(t\right)+H\left(t\right)+R\left(t\right).$$ (1)

Fig. 1 portrays model (2), while Table 1 classified the variables and parameters (all nonnegative). Therefore, using Fig. 1, we obtained the model equations, represented by (2), as follows:

$$\frac{\text{d}S}{\text{d}t}=\pi (1-{\theta }_{i}I-{\theta }_{h}H)+kR+\varphi V-\lambda S-(\eta +\mu )S,$$$$\frac{\text{d}V}{\text{d}t}=\eta S-(1-\epsilon )\lambda V-(\varphi +\mu )V,$$$$\frac{\text{d}E}{\text{d}t}=\lambda \left[S+(1-\epsilon )V\right]-(\sigma +\mu )E,$$$$\frac{\text{d}I}{\text{d}t}=\pi {\theta }_{i}I+\sigma E-({\tau }_i+{\delta }_i+\omega +\mu )I,$$$$\frac{\text{d}H}{\text{d}t}=\pi {\theta }_{h}H+\omega I-({\tau }_h+{\delta }_h+\mu )H,$$$$\frac{\text{d}R}{\text{d}t}={\tau }_{i}I+{\tau }_{h}H-(k+\mu )R.$$ (2)

In the model (2), the term $\lambda$, represent the force of infection, which reads

$$\lambda =\frac{{\beta }_{i}I+{\beta }_{h}H}{N}.$$ (3)

Fig. 1.

Diagrammatic representation of the COVID-19 model with vaccination and vertical transmission.

The parameters ${\beta }_i$ and ${\beta }_h$ represent the rate at which infectious (asymptomatic and symptomatic) and hospitalized humans transmit COVID-19 to susceptible humans, respectively. It is also assumed that ${\beta }_i\ne {\beta }_h$, implying that an infected individual from $I$ and $H$ have different transmission potentials. Epidemiologically, it is reasonable to assume that infectious humans can interact more with susceptible populations than hospitalized COVID-19-infected humans because the former are not isolated or quarantined. Thus, they are likely to have higher transmission ability, except if they are vaccinated and abide by the NPI control measures. Exposed humans progress out of the $E$ compartment at a rate of $\sigma$ ($\frac{1}{\sigma }$ is the intrinsic incubation period for COVID-19). Infectious humans can acquire the COVID-19 infection through vertical transmissions at a rate of $\pi {\theta }_i$ from $I$. Similarly, hospitalized humans can receive the COVID-19 infection through vertical transmission at a rate of $\pi {\theta }_h$ from $H$. The parameters ${\tau }_i$ and ${\tau }_h$ denote the recovery rate from $I$ and $H$, respectively. Individuals in the infectious ($I$) and hospitalized ($H$) compartments die of COVID-19 at rates ${\delta }_i$ and ${\delta }_h$, respectively. The vaccine efficacy $\epsilon$, at $0<\epsilon <1$, can provide up to 100% protection. Natural mortality occurs at a similar rate of $\mu$ in all epidemiological classes.

It is worth noting that one of the novelties of the proposed model over previous studies is that the current model aims to address the combined effects of vaccination, mother-to-child transmission as well as early hospitalization on the overall dynamics of SARS-CoV-2 transmission. We incorporated these measures/factors into the SEIR-typed model to assess their impact to find the optimum strategies for halting the pandemic impact in Saudi Arabia and beyond.

All model’s parameters are summarized and interpreted in Table 1.

Table 1.

Model’s variables and parameters explanation.

Variable	Interpretation
$N$	Total population of humans
$S$	Unvaccinated susceptible humans
$V$	Vaccinated susceptible humans
$E$	Exposed humans
$I$	infectious humans
$H$	Hospitalized humans
$R$	Recovered humans
Parameter
$\pi$	Recruitment rate
$\mu$	Natural death rate
$\eta$	Vaccination rate
$\varphi$	Vaccine waning rate
$\epsilon$	Infection reduction rate of vaccinated humans
${\beta }_i$	Transmission rate from $I$
${\beta }_h$	Transmission rate from $H$
$\sigma$	Progression rate
$\omega$	Hospitalization rate
${\delta }_i,{\delta }_h$	COVID-19 induced death rate
${\theta }_i,{\theta }_h$	Fraction of newly born babies who are infected with COVID-19
${\tau }_i,{\tau }_h$	Recovery rates
$k$	Loss of immunity rate

Basic properties

To analyse the transmission behaviour of the proposed model (2) qualitatively, we first study its fundamental properties by equating the sum of the systems (2) to $0$ (i.e. $\frac{dN\left(t\right)}{dt}=0$). So that

$$\frac{dN}{dt}=\pi -\mu N-({\delta }_{i}I+{\delta }_{h}H)\le \pi -\mu N.$$ (4)

For model (2) to be epidemiologically reasonable, the following biological feasible regions, given by $\Omega =\left\{(S,V,E,I,H,R)\in {\mathbb{R}}_{+}^6:N\le \frac{\pi }{\mu }\right\}$, are considered, solving for $N$ from the model (2). Thus, all solutions for (2) with initial data that are nonnegative maintain the region $\Omega$ for $t\ge 0$. Therefore, the biologically feasible region, $\Omega$, is invariant-positive and fascinating; thus, it suffices to compute solutions restricted to $\Omega$ in such a way that the continuation results, uniqueness, and existence hold for (2) only if the enclosed solutions in $\Omega$ are preserved [41].

Analysis of the conceptual model

Basic reproduction number and disease-free equilibrium

We rigorously analysed the qualitative dynamics features of the model (2). The model’s DFE is computed at a steady state. In this circumstance, there is no COVID-19 infection, so all infected compartments are assumed to be zero. Hence, the equation below,

$${\Xi }^0=(S^0,V^0,E^0,I^0,H^0,R^0)=\left(\frac{(\varphi +\mu )\pi }{\mu (\eta +\varphi +\mu )},\frac{\eta \pi }{\mu (\eta +\varphi +\mu )},0,0,0,0\right),$$ (5)

is always feasible.

One of the essential epidemiological variables to examine the control tactics and transmission dynamics of emerging diseases is the ${\mathcal{R}}_0$ [42]. The approach, called the next-generation matrix, was applied to scrutinize the asymptotic stability of the DFE and obtain the computation of ${\mathcal{R}}_0$ [42]. The notations $F_1$ and $F_2$, respectively, represent the associated NGM for the transition and the new infection stated as

$$F_1=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill a_1\hfill & \hfill a_2\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\text{and}{F}_2=\left[\begin{array}{ccc}\hfill N_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\sigma \hfill & \hfill b_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\omega \hfill & \hfill b_2\hfill \end{array}\right],$$ (6)

where, $N^0=\frac{\pi }{\mu }$, $a_1=\frac{{\beta }_i(M_2+M_3\eta )}{M_2+\eta }$, $a_2=\frac{{\beta }_h(M_2+M_3\eta )}{M_2+\eta }$, $b_1=-\pi {\theta }_i+N_2$, $b_2=-\pi {\theta }_h+N_3$, $M_1=\eta +\mu$, $M_2=\varphi +\mu$, $M_3=1-\epsilon$, $N_1=\sigma +\mu$, $N_2=\omega +{\delta }_i+{\tau }_i+\mu$, and $N_3={\delta }_h+{\tau }_h+\mu$, $N_4=\kappa +\mu$. Therefore, ${\mathcal{R}}_0=\rho F_1{F_2}^{-1}$ is computed below.

$${\mathcal{R}}_0={\mathcal{R}}_0^i+{\mathcal{R}}_0^h=\frac{\sigma a_1}{N_1{b}_1}+\frac{\sigma \omega a_2}{N_1{b}_1{b}_2}.$$ (7)

During the infectious time, the ${\mathcal{R}}_0$ evince the average number of secondary infections caused by normally infected people put in a totally susceptible population. It is represented by the sum of the component related to new infections generated by infectious (${\mathcal{R}}_0^i$) and hospitalized (${\mathcal{R}}_0^h$) humans.

The local asymptotic stability (LAS) of the DFE of (2) was analysed following Theorem 2 of [42].

Lemma 1

For model (2) , the LAS of the DFE, ${\Xi }^0$ , holds inside the region $\Omega$ if ${\mathcal{R}}_0<1$ and unstable when ${\mathcal{R}}_0>1$ .

Moreover, the results below are established following Theorem 2.2 in [43], and a similar approach was taken in [44], [45].

Theorem 2

For model (2) , if ${\mathcal{R}}_0\le 1$ , then the DFE, ${\Xi }^0$ , is GAS inside the region of attraction $\Omega$ .

Epidemiologically, the result above implies that a small inflow of COVID-19 infection does not cause an outbreak if ${\mathcal{R}}_0<1$. For epidemic model (2), the requirement for making ${\mathcal{R}}_0<1$ is only sufficient but not necessary for COVID-19 containment measures. Thus, the ailment is eradicated with time whenever ${\mathcal{R}}_0$ is alleviated to lower than unity, and the persistence is continuous for ${\mathcal{R}}_0>1$. Thus appropriate control measures should be emphasized before allowing the recruitment of susceptible people into a population that allows more chance for the disease to identify a suitable target, enhancing the transmission that continues to thrive in society [46], [47].

Endemic equilibrium and its stability

Existence of endemic equilibria

The steady-state solution of the model (2), which is attained by equating the right-hand side of (2) to $0$, which is known as the endemic equilibrium (EE) point. In this case, it is denoted by ${\Xi }^{\ast }$. It represents the phenomenon in which an ailment circulates and persists in a population. For the model (2), the EE points, ${\Xi }^{\ast }=(S^{\ast },V^{\ast },E^{\ast },I^{\ast },H^{\ast },R^{\ast })$, that is assumed to be the solution of the model (2). In terms of the $E$ and $\lambda$, the EE points are given by the following equations

$$S^{\ast }=\frac{M_2+M_3\lambda }{\eta }\times \left[\frac{\pi (1-{\theta }_i\left(\frac{\sigma E}{N_2-\pi {\theta }_i}\right)-{\theta }_h\left(\frac{\omega \sigma E}{(N_3-\pi {\theta }_h)(N_2-\pi {\theta }_i)}\right))+\kappa \left(\frac{((N_3-\pi {\theta }_h){\tau }_i+\omega {\tau }_h)\sigma E}{(N_2-\pi {\theta }_i)(N_3-\pi {\theta }_h)N_4}\right)}{\left(\frac{M_2+M_3\lambda }{\eta }\right)(M_1+\lambda )-\varphi }\right],$$$$V^{\ast }=\left[\frac{\pi (1-{\theta }_i\left(\frac{\sigma E}{N_2-\pi {\theta }_i}\right)-{\theta }_h\left(\frac{\omega \sigma E}{(N_3-\pi {\theta }_h)(N_2-\pi {\theta }_i)}\right))+\kappa \left(\frac{((N_3-\pi {\theta }_h){\tau }_i+\omega {\tau }_h)\sigma E}{(N_2-\pi {\theta }_i)(N_3-\pi {\theta }_h)N_4}\right)}{\left(\frac{M_2+M_3\lambda }{\eta }\right)(M_1+\lambda )-\varphi }\right],$$$$I^{\ast }=\frac{\sigma E}{N_2-\pi {\theta }_i},$$$$H^{\ast }=\frac{\omega \sigma E}{(N_3-\pi {\theta }_h)(N_2-\pi {\theta }_i)},\text{and}$$$$R^{\ast }=\frac{((N_3-\pi {\theta }_h){\tau }_i+\omega {\tau }_h)\sigma E}{(N_2-\pi {\theta }_i)(N_3-\pi {\theta }_h)N_4}.$$ (8)

Recall that, Eq. (3) described the incidence function of the model (2). So that, at the EE points, the force of infection (incidence rate) is now given by

$${\lambda }^{\ast }=\frac{{\beta }_i{I}^{\ast }+{\beta }_h{H}^{\ast }}{N^{\ast }}.$$ (9)

Also, in terms of the EE points, we have

$$N^{\ast }=S^{\ast }+V^{\ast }+E^{\ast }+I^{\ast }+H^{\ast }+R^{\ast }.$$ (10)

So that, Eq. (9) can be simplified as

$$S^{\ast }+V^{\ast }+E^{\ast }+(1-\frac{{\beta }_i}{{\lambda }^{\ast }})I^{\ast }+(1-\frac{{\beta }_h}{{\lambda }^{\ast }})H^{\ast }+R^{\ast }=0.$$ (11)

Substituting the right-hand sides of system (8) into (11), gives the following equation in terms of ${\lambda }^{\ast }$.

$$A_1{\lambda }^{\ast }2+A_2{\lambda }^{\ast }+A_3=0,$$

where

$$A_1=M_3\left(\left(\left(-\pi {\theta }_h+\omega +N_3\right)\sigma +\left(\pi {\theta }_i-N_2\right)\left(\pi {\theta }_h-N_3\right)\right)N_4\right)\left(-\sigma \left(\pi {\tau }_i{\theta }_h-\omega {\tau }_h-N_3{\tau }_i\right)\right),$$

$$A_2=\left(\eta +1\right)\left({\pi }^2{\theta }_h{\theta }_i\right)\left(+\left(\left(-N_2-\sigma \right){\theta }_h-N_3{\theta }_i\right)\pi +\left(N_2+\sigma \right)N_3+\omega \sigma \right)M_2{N}_4\left(M_3{N}_1\left(\pi {\theta }_h-N_3\right)\left(\pi {\theta }_i-N_2\right)\right)N_4-\sigma M_2\left(\eta +1\right)\left(\pi {\tau }_i{\theta }_h-\omega {\tau }_h-N_3{\tau }_i\right)+M_3\left(\pi {\beta }_a{\theta }_h-\omega {\beta }_b-N_3{\beta }_a\right)N_4\sigma ,\text{and}$$

$$A_3=N_1{N}_4\left(\eta +M_2\right)\left(\pi {\theta }_h-N_3\right)\left(\pi {\theta }_i-N_2\right)+\left(\eta +1\right)M_2{N}_4\sigma \left(\left(\pi {\theta }_h-N_3\right){\beta }_a-\omega {\beta }_b\right).$$

Hence, the endemic equilibria of system (2) correspond to positive solutions of the above equation, which is epidemiologically reasonable.

Following theorem 4.1 of [45], the result below can be easily constructed.

Theorem 3

The model (2) has a unique EE ${\Xi }^{\ast }$ , whenever ${\mathcal{R}}_0>1$ .

Global stability analysis of the endemic equilibrium

In this section, we show that all solutions in the viable region converge to the same unique EE ${\Xi }^{\ast }$ whenever ${\mathcal{R}}_0$ is greater than unity. Therefore, at the EE level, the disease spreads and persists in the community. We attained proof of global stability of ${\Xi }^{\ast }$ through constructing a global Lyapunov function. Mathematical modellers have used this technique extensively (e.g. [41], [45], [48], [49], [50], [51], [52] and the references therein).

Theorem 4

For the model (2) , if ${\mathcal{R}}_0>1$ and the following two conditions hold, i.e.,

• • (i) $\left(1-\frac{\lambda }{{\lambda }^{\ast }}\right)\left(1-\frac{I{\lambda }^{\ast }}{I^{\ast }\lambda }\right)\ge 0$ and
• • (ii) $\left(1-\frac{\lambda }{{\lambda }^{\ast }}\right)\left(1-\frac{H{\lambda }^{\ast }}{H^{\ast }\lambda }\right)\ge 0$ ,

then the EE ( ${\Xi }^{\ast }$ ) is globally-asymptotically stable (GAS) in the region of attraction, $\Omega$ .

Proof

Considering [48], [49], the Lyapunov function is defined as

$${\rm Y}\left(t\right)={\Delta }_1\left(S-S^{\ast }-S^{\ast }ln\frac{S}{S^{\ast }}\right)+{\Delta }_2\left(V-V^{\ast }-V^{\ast }ln\frac{V}{V^{\ast }}\right)+{\Delta }_3\left(E-E^{\ast }-E^{\ast }ln\frac{E}{E^{\ast }}\right)+$$$${\Delta }_4\left(I-I^{\ast }-I^{\ast }ln\frac{I}{I^{\ast }}\right)+{\Delta }_5\left(H-H^{\ast }-H^{\ast }ln\frac{H}{H^{\ast }}\right).$$ (12)

Then the derivative of the above Lyapunov function with respect to time ($t$) is given by

$$\dot{{\rm Y}}\left(t\right)={\Delta }_1\left(1-\frac{S^{\ast }}{S}\right)\dot{S}+{\Delta }_2\left(1-\frac{V^{\ast }}{V}\right)\dot{V}+{\Delta }_3\left(1-\frac{E^{\ast }}{E}\right)\dot{E}+{\Delta }_4\left(1-\frac{I^{\ast }}{I}\right)\dot{I}+{\Delta }_5\left(1-\frac{H^{\ast }}{H}\right)\dot{H}.$$ (13)

Computing each term of (13), we have

$${\Delta }_1\left(1-\frac{S^{\ast }}{S}\right)\dot{S}={\Delta }_1\left(1-\frac{S^{\ast }}{S}\right)\times \left(\pi (1-{\theta }_{i}I{\theta }_{h}H)+\kappa R+\varphi V-\lambda S-M_{1}S\right)={\Delta }_1\left(1-\frac{S^{\ast }}{S}\right)\left({\lambda }^{\ast }{S}^{\ast }+M_1{S}^{\ast }-\lambda S-M_{1}S\right)={\Delta }_1{\lambda }^{\ast }{S}^{\ast }\left(1-\frac{S^{\ast }}{S}\right)\left(1-\frac{\lambda S}{{\lambda }^{\ast }{S}^{\ast }}\right)-{\Delta }_1{M}_1\frac{{(S-S^{\ast })}^2}{S}\le {\Delta }_1{\lambda }^{\ast }{S}^{\ast }\left(1-\frac{\lambda S}{{\lambda }^{\ast }{S}^{\ast }}-\frac{S^{\ast }}{S}+\frac{\lambda }{{\lambda }^{\ast }}\right),$$ (14)

$${\Delta }_2\left(1-\frac{V^{\ast }}{V}\right)\dot{V}\le {\Delta }_2{M}_3{\lambda }^{\ast }{V}^{\ast }\left(1-\frac{\lambda V}{{\lambda }^{\ast }{V}^{\ast }}-\frac{V^{\ast }}{V}+\frac{\lambda }{{\lambda }^{\ast }}\right),$$ (15)

$${\Delta }_3\left(1-\frac{E^{\ast }}{E}\right)\dot{E}={\Delta }_3{\lambda }^{\ast }{S}^{\ast }\left(\frac{\lambda S}{{\lambda }^{\ast }{S}^{\ast }}-\frac{E}{E^{\ast }}-\frac{\lambda S{E}^{\ast }}{{\lambda }^{\ast }{S}^{\ast }E}+1\right)$$$$+{\Delta }_3{M}_3{\lambda }^{\ast }{V}^{\ast }\left(\frac{\lambda V}{{\lambda }^{\ast }{V}^{\ast }}-\frac{E}{E^{\ast }}-\frac{\lambda V{E}^{\ast }}{{\lambda }^{\ast }{V}^{\ast }E}+1\right),$$ (16)

$${\Delta }_4\left(1-\frac{I^{\ast }}{I}\right)\dot{I}={\Delta }_4\sigma E^{\ast }\left(\frac{E}{E^{\ast }}-\frac{I}{I^{\ast }}-\frac{I^{\ast }E}{I{E}^{\ast }}+1\right),$$ (17)

and,

$${\Delta }_5\left(1-\frac{H^{\ast }}{H}\right)\dot{H}={\Delta }_5\omega I^{\ast }\left(\frac{I}{I^{\ast }}-\frac{H}{H^{\ast }}-\frac{H^{\ast }I}{H{I}^{\ast }}+1\right).$$ (18)

After substituting the following terms ${\Delta }_1={\Delta }_2={\Delta }_3=1$, ${\Delta }_4=\frac{{\lambda }^{\ast }{S}^{\ast }}{\sigma E^{\ast }}$, and ${\Delta }_5=\frac{{\lambda }^{\ast }{M}_3{V}^{\ast }}{\omega I^{\ast }}$, and eqns (14)–(18) into eqns (13), we obtain

$$\dot{{\rm Y}}\left(t\right)\le {\lambda }^{\ast }{S}^{\ast }\left(2-\frac{S^{\ast }}{S}-\frac{E}{E^{\ast }}-\frac{\lambda S{E}^{\ast }}{{\lambda }^{\ast }{S}^{\ast }E}+\frac{\lambda }{{\lambda }^{\ast }}\right)+$$$$M_3{\lambda }^{\ast }{V}^{\ast }\left(2-\frac{V^{\ast }}{V}-\frac{E}{E^{\ast }}-\frac{\lambda V{E}^{\ast }}{{\lambda }^{\ast }{V}^{\ast }E}+\frac{\lambda }{{\lambda }^{\ast }}\right)+$$$${\lambda }^{\ast }{S}^{\ast }\left(\frac{E}{E^{\ast }}-\frac{I}{I^{\ast }}-\frac{I^{\ast }E}{I{E}^{\ast }}+1\right)+$$$$M_3{\lambda }^{\ast }{V}^{\ast }\left(\frac{I}{I^{\ast }}-\frac{H}{H^{\ast }}-\frac{H^{\ast }I}{H{I}^{\ast }}+1\right).$$ (19)

Following previous technique for the proof of GAS at EE [41], [45], [48], [49], [50], we first of all consider a function given by $\Im \left(\wp \right)=1-\wp +ln\wp$, so that, if $\wp >0$ implies that $\Im \left(\wp \right)\le 0$. Also, if $\wp =1$, implies $\Im \left(\wp \right)=0$. Hence, $\wp -1\ge ln\left(\wp \right)$ for any $\wp >0$. Using the above definition, previous computation from eqn (19), and conditions (i) and (ii) of Theorem 4, we have

$$\left(2-\frac{S^{\ast }}{S}-\frac{E}{E^{\ast }}-\frac{\lambda S{E}^{\ast }}{{\lambda }^{\ast }{S}^{\ast }E}+\frac{\lambda }{{\lambda }^{\ast }}\right)=\left(-(1-\frac{\lambda }{{\lambda }^{\ast }})(1-\frac{I{\lambda }^{\ast }}{I^{\ast }\lambda })+3-\frac{S^{\ast }}{S}-\frac{\lambda S{E}^{\ast }}{{\lambda }^{\ast }{S}^{\ast }E}-\frac{I{\lambda }^{\ast }}{I^{\ast }\lambda }-\frac{E}{E^{\ast }}+\frac{I}{I^{\ast }}\right)\le \left(-(\frac{S^{\ast }}{S}-1)-(\frac{\lambda S{E}^{\ast }}{{\lambda }^{\ast }{S}^{\ast }E}-1)-(\frac{I{\lambda }^{\ast }}{I^{\ast }\lambda }-1)-\frac{E}{E^{\ast }}+\frac{I}{I^{\ast }}\right)\le \left(-ln\left(\frac{S^{\ast }}{S}\frac{\lambda S{E}^{\ast }}{{\lambda }^{\ast }{S}^{\ast }E}\frac{I{\lambda }^{\ast }}{I^{\ast }\lambda }\right)-\frac{E}{E^{\ast }}+\frac{I}{I^{\ast }}\right)=\left(\frac{I}{I^{\ast }}-ln\left(\frac{I}{I^{\ast }}\right)+ln\left(\frac{E}{E^{\ast }}\right)-\frac{E}{E^{\ast }}\right).$$ (20)

Similarly,

$$\left(2-\frac{V^{\ast }}{V}-\frac{E}{E^{\ast }}-\frac{\lambda V{E}^{\ast }}{{\lambda }^{\ast }{V}^{\ast }E}+\frac{\lambda }{{\lambda }^{\ast }}\right)=\left(-(1-\frac{\lambda }{{\lambda }^{\ast }})(1-\frac{H{\lambda }^{\ast }}{H^{\ast }\lambda })+3-\frac{V^{\ast }}{V}-\frac{\lambda V{E}^{\ast }}{{\lambda }^{\ast }{V}^{\ast }E}-\frac{H{\lambda }^{\ast }}{H^{\ast }\lambda }-\frac{E}{E^{\ast }}+\frac{H}{H^{\ast }}\right)\le \left(-(\frac{V^{\ast }}{V}-1)-(\frac{\lambda V{E}^{\ast }}{{\lambda }^{\ast }{V}^{\ast }E}-1)-(\frac{H{\lambda }^{\ast }}{H^{\ast }\lambda }-1)-\frac{E}{E^{\ast }}+\frac{H}{H^{\ast }}\right)\le \left(-ln\left(\frac{V^{\ast }}{V}\frac{\lambda V{E}^{\ast }}{{\lambda }^{\ast }{V}^{\ast }E}\frac{H{\lambda }^{\ast }}{H^{\ast }\lambda }\right)-\frac{E}{E^{\ast }}+\frac{H}{H^{\ast }}\right)=\left(\frac{H}{H^{\ast }}-ln\left(\frac{H}{H^{\ast }}\right)+ln\left(\frac{E}{E^{\ast }}\right)-\frac{E}{E^{\ast }}\right).$$ (21)

Using eqn (19) again, we obtain

$$\frac{E}{E^{\ast }}-\frac{I}{I^{\ast }}-\frac{I^{\ast }E}{I{E}^{\ast }}+1=\left(u\left(\frac{I^{\ast }E}{I{E}^{\ast }}\right)+\frac{E}{E^{\ast }}-ln\left(\frac{E}{E^{\ast }}\right)-\frac{I}{I^{\ast }}+ln\left(\frac{I}{I^{\ast }}\right)\right)\le \frac{E}{E^{\ast }}-ln\left(\frac{E}{E^{\ast }}\right)+ln\left(\frac{I}{I^{\ast }}\right)-\frac{I}{I^{\ast }}.$$ (22)

Similarly,

$$\frac{I}{I^{\ast }}-\frac{H}{H^{\ast }}-\frac{H^{\ast }I}{H{I}^{\ast }}+1=\left(u\left(\frac{H^{\ast }I}{H{I}^{\ast }}\right)+\frac{I}{I^{\ast }}-ln\left(\frac{I}{I^{\ast }}\right)-\frac{H}{H^{\ast }}+ln\left(\frac{H}{H^{\ast }}\right)\right)\le \frac{I}{I^{\ast }}-ln\left(\frac{I}{I^{\ast }}\right)+ln\left(\frac{H}{H^{\ast }}\right)-\frac{H}{H^{\ast }}.$$ (23)

Thus,

$$\dot{{\rm Y}}\left(t\right)={\lambda }^{\ast }{S}^{\ast }\left(\frac{I}{I^{\ast }}-ln\left(\frac{I}{I^{\ast }}\right)+ln\left(\frac{E}{E^{\ast }}\right)-\frac{E}{E^{\ast }}\right)+$$$$M_3{\lambda }^{\ast }{V}^{\ast }\left(\frac{H}{H^{\ast }}-ln\left(\frac{H}{H^{\ast }}\right)+ln\left(\frac{E}{E^{\ast }}\right)-\frac{E}{E^{\ast }}\right)+$$$${\lambda }^{\ast }{S}^{\ast }\left(\frac{E}{E^{\ast }}-ln\left(\frac{E}{E^{\ast }}\right)+ln\left(\frac{I}{I^{\ast }}\right)-\frac{I}{I^{\ast }}\right)+$$$$M_3{\lambda }^{\ast }{V}^{\ast }\left(\frac{I}{I^{\ast }}-ln\left(\frac{I}{I^{\ast }}\right)+ln\left(\frac{H}{H^{\ast }}\right)-\frac{H}{H^{\ast }}\right).$$ (24)

Consequently, using eqns (14)–(24) and the LaSalle’s invariance principle [53], we have $\dot{{\rm Y}\left(t\right)}\le 0$. Therefore, $\frac{d{\rm Y}}{dt}=0$ true when $S=S^{\ast }$, $V=V^{\ast }$ $E=E^{\ast }$, $I=I^{\ast }$, and $H=H^{\ast }$. Hence, the EE points given in Eq. (8), is the only positively-invariant set for the model (2), which is contained in $\left\{(S,V,E,I,H)\in \Omega :S=S^{\ast },V=V^{\ast },E=E^{\ast },I=I^{\ast },H=H^{\ast }\right\}$. Thus, it implies every solutions of the system (13) with initial conditions converge to ${\Xi }^{\ast }$, as $t\to \infty$. Hence, the positive EE is GAS.

Model prediction

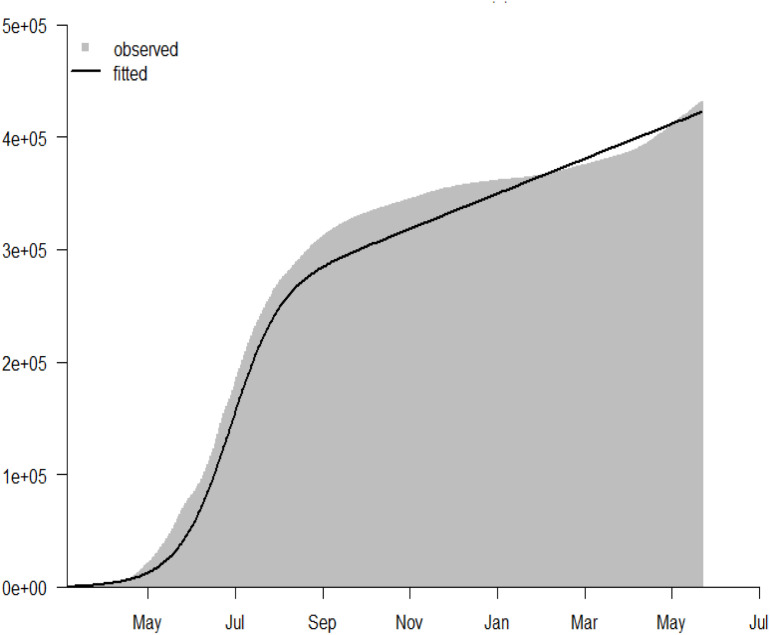
For the model-fitting procedure, we used least square sampling approach and Pearson’s chi-square using the $\mathbf{R}$ statistical software 3.4.1 version or above [41], [54]. This methods has been largely been adopted by previous studies for model fitting, validation or prediction, in order to testify the validity of outputs of epidemiological model with respect to the reasonable, realistic epidemic data of disease. The Eq. (2) was fitted epidemiologically well to the cumulative COVID-19 cases reported by the WHO for Saudi Arabia from 2 March 2020 to 15 May 2021. The model was simulated for 1000 random samples The WHO provided time-series of COVID-19 reported cases for Saudi Arabia. Dashboard for COVID-19, available from [5]. The population of Saudi Arabia was acquired from Worldometer [55], and demographic parameters were computed using the life expectancy data attained from [56]. The parameters are listed in Table 2, and the initial conditions for the model state variables provided by $S_0=30\times 10^6$, $V_0=0$, $E_0=85\times 10^3$, $I_0=5$, $H_0=2$, and $R_0=0$, with $\varphi =0.031$, ${\theta }_i=0$, and ${\theta }_h=0$. Fig. 2 illustrates the fitting outcomes for the (2) for the cumulative number of COVID-19 cases in Saudi Arabia. The results also reveal that the proposed model (2) captured the COVID-19 epidemic curves well for Saudi Arabia using the cumulative number of cases from 2 March 2020 to 15 May 2021.

Table 2.

Ranges of the parameters and their units used for the simulations.

Parameter	Value (Range)	Units/Remarks	Sources
$N_0$	34810000	per day	[68]
$\pi$	$1265.36(1000-4000)$	per day	estimated from [69]
$\mu$	$3.3635\times {10}^{-5}(0.00002-0.00006)$	per day	estimated from [69]
$\eta$	$2.{97\times 10}^{-4}(0.0001-0.05)$	per day	[70], [71]
$\varphi$	0	$\text{dimensionless}$	[72]
$\epsilon$	$0.70(0-1)$	$\text{dimensionless}$	[70]
${\beta }_i$	$1.2862(0.599-1.68)$	per day	fitted
${\beta }_h$	$0.7245(0.711360-0.739537)$	per day	fitted
$\sigma$	$0.243(0.05-0.275)$	per day	assumed
$\omega$	$0.5604(0.03-0.825)$	per day	fitted
${\delta }_i$	$0.000573(0.0000-0.002399)$	per day	[70]
${\delta }_h$	$0.01(0.00070-0.025)$	per day	assumed
${\theta }_i$	$0.00001(0-1)$	per day	assumed
${\theta }_h$	$0.000024(0-1)$	per day	assumed
${\tau }_i$	$1/1.5(1/30-1/8)$	per day	estimated from [6]
${\tau }_h$	$1/14(1/30-1/3)$	per day	[6]
$k$	$0.11(0-1)$	per day	estimated from [73]

Fig. 2.

The model fitting result using the reported COVID-19 cases in Saudi Arabia from 2 March 2020 to 15 May 2021. The grey bars represent the observed COVID-19 cases, and the black curve is the model prediction to the reported COVID-19 situation in Saudi Arabia. The result shows the cumulative number of COVID-19 scenario for Saudi Arabia. The initial conditions used for the fitting processes are: $S_0=30\times 10^6$, $V_0=0$, $E_0=85\times 10^3$, $I_0=5$, $H_0=2$, and $R_0=0$.

Numerical simulations and sensitivity analysis

Numerical results of the global stability of equilibria

Following previous works [45], [50], in this subsection, we carry out numerical simulations to depict the analytical results presented in earlier sections for the global stability of the COVID-19 dynamics using different initial conditions for each compartment. The numerical results presented in this section support the analytical results obtained for the global stability analyses of the model given in Section “Analysis of the Conceptual Model”. The technique is a simple time-series numerical framework using Maple statistical software to analyse the model numerically. The method was hugely used previously by mathematical epidemiologists to analyse the model numerically.

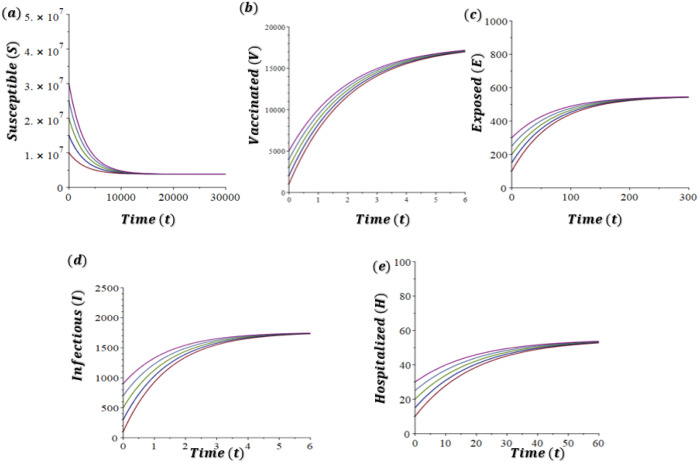
In Fig. 3(a)–(e), we take to account the dynamics of the model (2) when ${\mathcal{R}}_0=0.8492306<1$ for different initial conditions. The parameter values are the same as in the Table 2 except for ${\beta }_h=0.027245$, $\varphi =0.5$, $\sigma =0.0143$, and ${\tau }_i=1/7$. The dynamics of the model (2) with ${\mathcal{R}}_0<1$ is depicted in Figure 3 (a)–(e), which demonstrates the system (2) has a DFE and it is GAS whenever ${\mathcal{R}}_0\le 1$ underpinning the result presented in Theorem 2.

Fig. 3.

Time-series simulations results of the model (1) showing the global stability of the DFE (changes in COVID-19 dynamics at DFE), with varying initial conditions (denoted by different colours): (a) susceptible ($S$), (b) vaccinated ($V$), (c) exposed ($E$), (d) infectious ($I$), and (e) hospitalized ($H$), humans. Parameters values implemented are same in Table 2 with ${\beta }_h=0.027245$, $\varphi =0.5$, $\sigma =0.0143$, and ${\tau }_i=1/7$.

In Fig. 4, we take into account the dynamics of the model (2) when ${\mathcal{R}}_0=4.9466717>1$ for different initial conditions. All the parameter values are the same as in the Table 2 except for $\varphi =0.5$, $\sigma =0.0143$, and ${\tau }_i=1/7$. The dynamics of the model (2) with ${\mathcal{R}}_0>1$ is depicted in Fig. 4(a)–(e), which demonstrates the system (2) has EE, ${\Xi }^{\ast }$, which is GAS whenever ${\mathcal{R}}_0>1$ underpinning the result presented in Theorem 4.

Fig. 4.

Time series simulations results of the model (1) showing the global stability of the EE (changes in COVID-19 dynamics at EE), with varying initial conditions (denoted by different colours): (a) susceptible ($S$), (b) vaccinated ($V$), (c) exposed ($E$), (d) infectious ($I$), and (e) hospitalized ($H$), humans. Parameters values implemented are same in Table 2 with $\varphi =0.5$, $\sigma =0.0143$, and ${\tau }_i=1/7$.

Simulations on the general dynamics

Integer and non-integer order $\rho$, as well as several essential factors, can be used to show model dynamic behaviour via numerical methods. The numerical findings in [57], [58], [59], [60] were presented using first-order convergent numerical techniques. These are important numerical algorithms for solving non-integer order differential equations which gives accurate, conditionally stable, and convergent results.

Here, we utilized the framework used in [61] to carry out numerical simulations in order to show vital dynamics behaviour of the proposed model. The fractional model below was used to obtain the simulations results.

$${}^{\text{c}}{S}_{p+1}=S_0+\frac{h^{\rho }}{\Gamma (\rho +1)}\sum _{k=0}^p\left({(p-k+1)}^{\rho }-{(p-k)}^{\rho }\right)\times \left(\pi (1-{\theta }_{i}I-{\theta }_{h}H)+kR+\varphi V-\lambda S-(\eta +\mu )S\right),$$$${}^{\text{c}}{V}_{p+1}=V_0+\frac{h^{\rho }}{\Gamma (\rho +1)}\sum _{k=0}^p\left({(p-k+1)}^{\rho }-{(p-k)}^{\rho }\right)\times \left(\eta S-(1-\epsilon )\lambda V-(\varphi +\mu )V\right),$$$${}^{\text{c}}{E}_{p+1}=E_0+\frac{h^{\rho }}{\Gamma (\rho +1)}\sum _{k=0}^p\left({(p-k+1)}^{\rho }-{(p-k)}^{\rho }\right)\times \left(\lambda \left[S+(1-\epsilon )V\right]-(\sigma +\mu )E\right),$$$${}^{\text{c}}{I}_{p+1}=I_0+\frac{h^{\rho }}{\Gamma (\rho +1)}\sum _{k=0}^p\left({(p-k+1)}^{\rho }-{(p-k)}^{\rho }\right)\times \left(\pi {\theta }_{i}I+\sigma E-({\tau }_i+{\delta }_i+\omega +\mu )I\right),$$ (25)

$${}^{\text{c}}{H}_{p+1}=H_0+\frac{h^{\rho }}{\Gamma (\rho +1)}\sum _{k=0}^p\left({(p-k+1)}^{\rho }-{(p-k)}^{\rho }\right)\times \left(\pi {\theta }_{h}H+\omega I-({\tau }_h+{\delta }_h+\mu )H\right),$$

$${}^{\text{c}}{R}_{p+1}=R_0+\frac{h^{\rho }}{\Gamma (\rho +1)}\sum _{k=0}^p\left({(p-k+1)}^{\rho }-{(p-k)}^{\rho }\right)\times \left({\tau }_{i}I+{\tau }_{h}H-(k+\mu )R\right).$$

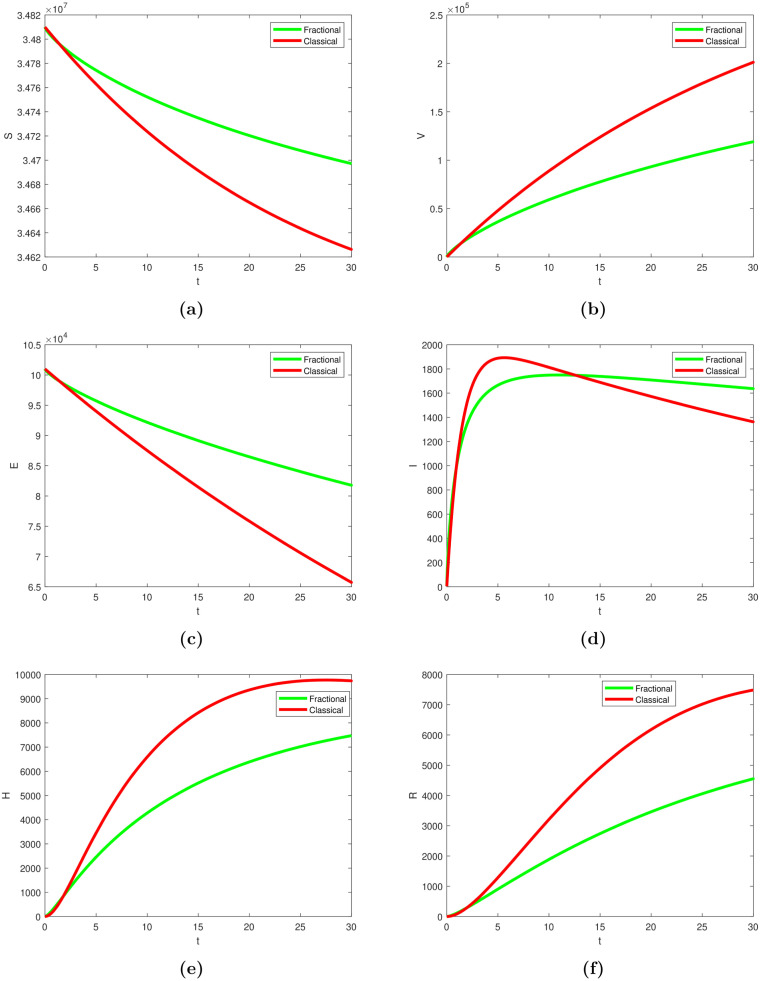
To explore the impact of each scenario on the overall dynamics, we utilized the above technique and simulated the model (using classical (1) and fractional (25) systems, respectively). Fig. 5, Fig. 6 shows the dynamics trends on each situation and their possible contribution on the general dynamics of the disease, thereby providing some suggestions for appropriate control strategies.

Fig. 5.

Simulation of the model showing the dynamics behaviour of COVID-19 transmission over time in panels (a)–(f) using fractional (green curve) and classical (red curve) variants. The parameters’ values used were given in Table 2. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

Time series simulation results of the model showing the dynamics behaviour of COVID-19 transmission using different fractional values in panels (a)–(f). The parameters’ values used were given in Table 2.

Assessing the effect of vaccination, vertical transmission and hospitalization

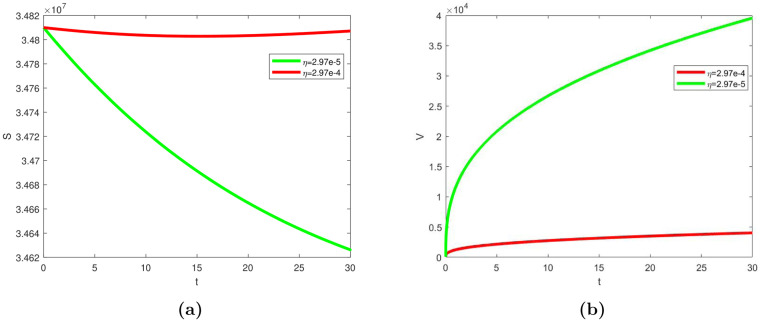
In this sub-section, we simulated the model (1) to assess the impact of the vaccination, vertical transmission and hospitalization on the overall dynamics. In Fig. 7, Fig. 8, as described on the dynamical system in Eq. (1), we conducted simple simulations considering multiple choices based on related/key parameters (i.e., $\eta$, ${\theta }_i$, ${\theta }_h$, and $\omega$) that drives the transmission, in this case. The results in Fig. 7 revealed that increasing vaccination rate, especially for the most vulnerable population, enhances the impact of vaccines as potential and effective strategy for mitigating COVID-19 pandemic. Also, our simulation result in Fig. 8 revealed how vertical transmission and early hospitalization affects infected individuals, which, in turn affects the overall transmission of the disease.

Fig. 7.

Model simulation showing the effect of vaccination rate, $\eta$, on (a) unvaccinated susceptible (b) vaccinated individuals. The parameters’ values used were given in Table 2.

Fig. 8.

Model simulation showing the effect of (a) vertical transmission, ${\theta }_i$, on infected individuals, (b) vertical transmission, ${\theta }_h$, on hospitalized individuals, and (a) hospitalized rate, $\omega$, on hospitalized individuals. The parameters’ values used were given in Table 2.

Sensitivity analysis

To investigate the impact of each parameter on the model (1), we utilized the partial ranked correlation coefficient (PRCC) technique [62], [63], [34], which is a standard approach for investigating the sensitivity analysis between the model outcomes and parameters. The results of the partial ranked correlation coefficient of the ${\mathcal{R}}_0$ and attack rate for the sensitivity analysis presented in Fig. 9 suggest that the most influential parameters for disease prevention and control are ${\theta }_i$, $\pi$ and ${\beta }_i$. The result demonstrates that the key parameters are consequentially linked with the disease infectivity and infection attack rate, and thus, priorities should given to them in controlling the COVID-19 pandemic efficaciously.

Fig. 9.

The partial rank correlation coefficients of ${\mathcal{R}}_0$ in panel (a), the infection attack rate (IAR) in panel (b) with respect to model parameters. The bars stand for the 95% confidence interval, and the dots are the estimated correlation. The parameter values utilized are presented in Table 1.

Discussion and conclusions

The COVID-19 pandemic has disproportionately affected all groups, including newborn babies. Considering the growing clinical evidence from the literature for mother-to-child infection of COVID-19 during pregnancy [13], [14], [16], it has become necessary for more efforts from researchers and public health practitioners to investigate this issue to contribute to the existing knowledge. Moreover, researchers need to elucidate the influence of vertical transmission and suggest control measures to policymakers for timely and effective prevention and control.

Although previous studies have revealed that most neonates infected with COVID-19 were delivered via a caesarean delivery [16], [64], this further indicates that the risk of mother-to-child infection does not heavily rely on the delivery route. Nevertheless, the short- or long-term adverse effects should be thoroughly analysed to prevent vulnerable newborns from being infected with COVID-19 during pregnancy. In addition, follow-up is necessary, especially for newborns already infected or with other comorbid conditions.

Early treatment for COVID-19 infected individuals and effective vaccines coupled with NPI measures are the most crucial means for effective control to provide long-term prevention to mitigate the pandemic. Nevertheless, based on the previous knowledge of other pandemics, disease mitigation is a complex phenomenon that typically requires a targeted multistrategy technique for timely and effective control [37], [65]. This technique could also be possible for the current pandemic, with elimination improbably attained in time and thus needing optimal global efforts. High uptake for COVID-19 vaccines helps reduce crucial epidemiological parameters, such as ${\mathcal{R}}_0$, the infection fatality and attack rates. However, sustaining other NPI measures is also necessary (at the moment) to continue to fight the pandemic effectively and reduce morbidity and mortality rates. Moreover, such strategies as testing, tracing, and isolating [66] are vital in keeping the infection fatality and attack rates at low levels and lowering the risk of vaccine escape [67]. Eventually, it is imperative to focus more on the long-term solution while reducing the effects of the current scenario to achieve the public health target.

This study employed an SEIR-type model designed by proposing a new deterministic model to investigate the dynamics of the COVID-19 pandemic. The formulated model incorporated vaccination, hospitalization and vertical or mother-to-child transmission of SARS-CoV-2 in the cause of pregnancy. The proposed model was rigorously analysed and revealed that the DFE is locally stable using existing differential and integral operators. We applied the technique to the governing model and generated simulations similar to real-world circumstances with some crossover behaviours, as can be seen in 6 $a$ and 6 $d$.

Different crucial parameter values have been tested in each scenario to show the dynamics features in both fractional and classic senses for the individual compartment using the model (1) and model (25), respectively. Simulation results showing the effect of the vaccination rate, $\eta$, on unvaccinated and vaccinated susceptible individuals given in Fig. 7, highlight that increasing the vaccination rate could significantly suppress the transmission rate of the disease and, in turn, reduce the morbidity and mortality rate in a population. Moreover, the model was simulated to show the impact of vertical transmission and early hospitalization of infected individuals, see Fig. 8. Based on the results, we suggest that vaccinating the most vulnerable population could help reduce the transmission of SARS-CoV-2 via vertical route by lowering the infection rate from pregnant women and preventing the onward spread of the disease. Thus, vaccination and early hospitalization are crucial measures in the fight to end the pandemic as well as to lower the transmissibility and likely increase the level of immunity in a population.

Finally, the sensitivity analysis results are illustrated in Fig. 9 divulged that the parameters ${\theta }_i$, $\pi$ and ${\beta }_i$, primarily associated with disease infectivity/transmission, are the most vital model parameters for effectively mitigating the pandemic. This study, like numerous others, is not free from limitations. We employed a single-strain model instead of an age-structured model, which might capture more dynamic features in investigating the combined effects of vaccination, vertical transmission and hospitalization. However, in the future, we plan to extend the current study by incorporating an aged-structured model and using different case scenarios to investigate and shed more light on the dynamics of COVID-19 transmission.

In conclusion, in this study, we proposed a new model to study the transmission of SARS-CoV-2, incorporating the combined effect of vaccination, hospitalization and vertical transmission. The results highlighted that maintaining basic NPI measures coupled with increased vaccine uptake, especially for the most the vulnerable population could greatly suppress the effects of the pandemic.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

I have shared the link to my data which is publicly available