Abstract
In this paper we propose a robust fuzzy clustering model, the STAR-based Fuzzy C-Medoids Clustering model with Noise Cluster, to define territorial partitions of the European regions (NUTS2) according to the workplaces mobility trends for places of work provided by Google with reference to the whole COVID-19 pandemic period. The clustering model takes into account both temporal and spatial information by means of the autoregressive temporal and spatial coefficients of the STAR model. The proposed clustering model through the noise cluster is capable of neutralizing the negative effects of noisy data. The main empirical results regard the expected direct relationship between the Community mobility trend and the lockdown periods, and a clear spatial interaction effect among neighboring regions.
Keywords: COVID-19 outbreak, STAR model, Fuzzy C-medoids clustering, Robust clustering, Google COVID-19 community mobility report, NUTS 2
1. Introduction
The COVID-19 pandemic has affected the dynamics of all social and economic variables, very often with the conditioning of policy actions dedicated to the attempt to stem the contagion. One of the variables mainly affected by these blocking policies actions has been mobility. These policies have encouraged work at home, thus reducing the number of commuters on the assumption that social distancing reduces the risk of infection for travelers and other people in their areas of residence and work (Francetic and Munford, 2021). So the most significant difference in behavior was staying at home and then working remotely (i.e. smart working). As a result, mobility for work purposes in many countries has been limited. Authorities continued to require their employees to work at home to avoid crowding of the roads and public transport networks (Lozzi et al., 2020). At the European level, the epidemic disease has produced a diversity of policy responses in the countries. These actions ranged from very drastic lockdown policies implemented in Southern Europe to less stringent approaches implemented elsewhere (e.g. Sweden) (Mendolia et al., 2020). On the other hand, it seems that the data on mobility do not follow the dynamics of contagion, with different behaviors among countries. This is what emerges from Google’s Mobility Report (Anon, 2021) relating to European countries, which highlights, for example, how the United Kingdom, Italy, most of Germany, the Netherlands show a net reduction in mobility due to local restriction rules, while Spain, many regions of France and Switzerland have an idiosyncratic behavior.
In the literature, recently, some interesting studies analyze the association between community mobility and COVID-19 outbreak (Cartenì et al., 2020, Saha et al., 2020, Ophir et al., 2021, Sulyok and Walker, 2020, Lapatinas, 2020).
An interesting aspect in the mobility dynamics is to understand if they are affected by spatial interactions due to the policy actions of the neighboring countries or the level of contagion of neighbors (also within the same country at a local regional level).
In this paper we propose to characterize the 451 European regions (NUTS2) identified by the classification ISO alpha 2 (ISO 3166) by the International Organization for Standardization with a set of coefficients derived from a simple Space–Time AutoRegressive (STAR) model, relative to both the time and space dimensions, and cluster the spatial units using a model-based fuzzy clustering algorithm. From a methodological point of view, this work belongs to the model-based clustering approach, generally adopted in a time series framework (see, D’Urso, 2016, Maharaj et al., 2019), in particular to the class of methods for panel data classification, where the clustering is based on two dimensions (space and time in our case), see Frühwirth-Schnatter (2011). The idea of this methodology is to compare the estimated coefficients of similar models referring to different series to verify which of them are characterized by the same data generating process. Starting from the AR distance for time series processes (Piccolo, 1990), several authors have proposed clustering algorithms for time series based on distance measure between coefficients (see, for example, Maharaj, 1999, Otranto, 2008, Otranto, 2010, D’Urso et al., 2013a, D’Urso et al., 2013b, D’Urso et al., 2015, D’Urso et al., 2016, D’Urso et al., 2017). Notice that, in the literature, other clustering approaches which manage the spatial–temporal information in a different manner have been proposed by Disegna et al., 2017, D’Urso et al., 2019, D’Urso and Vitale, 2020, D’Urso et al., 2021.
Considering the time series of the 451 European spatial units for the period from February 15, 2020 to April 18, 2021, we clustered them based on the STAR coefficients relative to each spatial unit and detecting spatial patterns with groups with similar coefficients, that can be considered as units with similar space–time dynamics. Moreover, we split the time span in four subsets to verify how the classification changes in different phases of the pandemic period.
In Section 2 we present the methodology adopted (model and clustering approach) to derive the proposed classification. In Section 3, after describing the dataset used in this analysis, the clustering results are presented; some final considerations conclude the paper.
2. Classification of spatial units: methodology
2.1. The space–time model
Our proposal consists in characterizing each spatial unit with a set of coefficients derived from a space–time model. The reference model is a classical STAR model (see, for example, Anselin, 1988) but with the properties of flexibility contained in Otranto and Mucciardi (2019). Their Flexible STAR (FSTAR) approach consists in the specification of a STAR model with the same coefficients for groups of spatial units; the final specification is obtained with a recursive procedure, which starts from an overparameterized model with different coefficients for each single spatial unit and converging toward a parsimonious model with a small set of parameters, obtained through statistical tests to verify the equality of coefficients of different spatial units.
Let us call (; ) the vector containing the variable of interest for each spatial unit; the general STAR model adopted is:
| (1) |
where , with for each , is the weight matrix representing the spatial connection between each pair of spatial units, is a vector of coefficients (one for each spatial unit) referred to the -th time lag, is the vector of spatial coefficients at time lag , represents the Hadamard (element-by-element) product. Not dealing with a forecasting framework, we consider the possibility that there is a simultaneous spatial dependence in the model ().
Each equation in (1) has the following form:
| (2) |
The set of equations (2) is the starting point of the Otranto and Mucciardi (2019) procedure to obtain a flexible but parsimonious STAR model. The particular structure of our dataset, with the number of spatial units largely greater than the number of time periods , can be analyzed unit by unit with univariate models as (2), whereas a simultaneous estimation, also considering groups of spatial units with the same and coefficients, as in model (1), is not feasible for collinearity problems.1 However, we can consider each spatial unit as characterized by the set of coefficients
with the () coefficients representing the dynamic behavior of the unit along time, and the () coefficients representing the spatial dependence elements of the same spatial unit.
Each set of coefficients can be used in a clustering algorithm to detect patterns of similar units in terms of space–time features. In our empirical application we identify and . Among the several possible alternative for the exogenous weighted matrix , we select the Gaussian kernel matrix (Otranto et al., 2016), where is obtained by row-standardizing the matrix with elements:
| (3) |
such that each row sums up to one; in (3), is the Euclidean distance between the centroids and of two regions identified by their spatial coordinates longitude and latitude and is the selected kernel bandwidth.2 We recall that varying the bandwidth results in a different exponential decay profile, which in turn produces weights that vary more or less rapidly over space. As a consequence the spatial weight matrix has the important property of being sensitive to topological transformations of the territory. The Arcgis 10 software was used to compute the matrix of the distances between the territorial barycentres of the European regions to derive the spatial weight matrix .
2.2. The STAR-based Fuzzy C-Medoids Clustering with Noise Cluster
STAR-based Fuzzy C-Medoids Clustering model with Noise Cluster (STAR-FCMdC-NC) deals with contaminating spatial time series units by introducing an “artificial” cluster, called noise cluster, in addition to the real clusters, that collects all objects distant from the prototypes of the groups.
Notice that the STAR-FCMdC-NC model is based on the Partitioning Around Medoids (PAM) approach: the partitioning process defines clusters in which the cluster prototypes, called medoids, are observed units, i.e. the actual objects in the cluster whose average dissimilarity to all the objects in the cluster is minimal. Medoids can provide more intuitive information about the dataset than the centroids (means) used in the Fuzzy C-Means clustering; in fact the centroids usually do not physically exist, meanwhile the medoids are the most (actual) representative objects in the dataset.
Given spatial time series of length , let be the matrix of model coefficients of dimension and let there be clusters, the -th representing the noise cluster (Davé, 1991); the STAR-FCMdC-NC model is, then, based on the minimization of the following objective function:
| (4) |
where represents the fuzzy membership of the th units in the th cluster while is the fuzziness parameter; the greater is its value, the higher is the fuzziness of the solution. The medoids are denoted by , …, .
The parameter is the noise distance whose role is that of giving, for higher values, more emphasis to the “noise component” in the objective function. A common setting for is
where may range between 0.05 and 0.5, even if the results are in general not very sensitive to its values (Davé, 1991).
The iterative solutions of are:
| (5) |
and
| (6) |
The computational steps of the proposed robust clustering model are described in Algorithm 1.
Summing up the proposed clustering model (??), we argue that it inherits different benefits by its structural features. Firstly, following the PAM (Partitioning Around Medoids) approach, the cluster prototypes (i.e., medoids) are not “fictious” units like “centroids” but observed ones (Bezdek, 1981) making clusters interpretation easier (Kaufman and Rousseeuw, 2005). Then, the fuzzy approach could be considered a more attractive and suitable solution when there are no clear boundaries among clusters (McBratney and Moore, 1985, Wedel and Kamakura, 2000); by the matrix of membership degrees, a second-best cluster almost as good as the best cluster could also be identified (Everitt et al., 2011). As stated in García-Escudero and Gordaliza (1999) and García-Escudero et al. (2010), since PAM procedure provides only a “timid robustification” of the C-Means clustering, the model formulation based on noise cluster, in a fuzzy context, allows to handle with outliers neutralizing their negative effects on groups structure.
Furthermore, in our model, we take into account both temporal and spatial information which have been embedded by means of autoregressive temporal coefficients and autoregressive spatial coefficients; in this manner, the spatio-temporal information is preserved considering only values instead of all time series observations leading to a sensible computational gain.
2.3. Validity measure
To choose the optimal number of groups, the Fuzzy Silhouette () index has been adopted, that is one of most well known internal validity criteria proposed by Campello and Hruschka (2006). It is based on the weighted average of the individual silhouettes width, , as follows:
| (7) |
where is the average distance of object to all other objects belonging to the same cluster (, …, ).3 If is the average distance of the object to all objects belonging to another cluster, say , with , then is the minimum average distance computed over the clusters: i.e. the dissimilarity of object to its closest neighboring cluster. is the weight of each , where and are the first and second largest elements of the th row of the fuzzy partition matrix , respectively; it implies that an object nearer to the cluster prototype is more important than a fuzzy one. is an optional user defined weighting coefficient that, when set equal to , reduces the FS to its crisp version.
Ranging from , the higher the value of FS, the better is the assignment of the units to the clusters implying that, simultaneously, the intra-cluster distance () is minimized while the inter-cluster distance () is maximized.
3. On clustering European regions in terms of community mobility and COVID-19 outbreak
3.1. Data description
Data on human mobility by country are drawn from the Google Community Mobility Reports (GCMR) released by Google for 133 countries. These reports are created with aggregated, anonymized sets of data from users’ mobile device and are classified into six location categories: retail and recreation, grocery and pharmacy, parks, public transports, workplaces and residential areas. The GCMR dataset shows how visitors to (or time spent in) categorized places change compared to baseline days (Anon, 2021). Data are provided as percentage variations in the number of visits or time spent in each category relative to a pre-COVID-19 baseline. The baseline day is the median value in the 5-week period from January 3rd to February 6th, 2020. However, it should be noted that the GCMR data does not represent a perfect random sample of the target population as users of Android smartphones and tablets may differ from the general population in terms of various demographic, social and economic characteristics. The time span we consider covers the period from February 15th, 2020 to April 21th, 2021 (429 daily data) and refer to 451 European regions. Moreover we consider four subperiods, chosen according to the main outbreak waves. The time windows considered are: First — from 02-15-2020 to 05-31-2020 (first wave of the pandemic); Second — from 06-01-2020 to 08-31-2020 (summer with a clear decrease of contagion); Third — from 09-01-2020 to 12-31-2020 (signals for a second wave of contagion); Fourth — from 01-01-2021 to 04-18-2021 (explosion of the second wave of the pandemic); Whole — from 02-15-2020 to 04-18-2021 (full dataset). Some European regions were not considered due to partial lack of data. To erase the presence of weekly seasonality patterns we transformed time series by moving averages of 7 terms.
Table 1 provides the descriptive statistics in the four subsets and for the whole period for workplace mobility category in Europe. The entries refer to the average values of each spatial units within the time span considered. The decrease in workplace mobility was on average around 28 percent with peaks of 33 percent in the first period. The great impact of the pandemic in the first subperiod, the attenuation of this effect in the second and third subperiod and a resurgence of the phenomenon in the fourth subperiod are evident. The greatest percentage decreases compared to the baseline (-92%) were recorded in the Lombardy region (Italy) and in the Community of Madrid (Spain) in April 2020. Specifically Fig. 1 shows the spatial distribution of workplace mobility in European regions at the beginning (first wave) of the COVID-19 pandemic (March 2020).
Table 1.
Descriptive statistics of mean percentage variations (change from baseline) of workplace mobility by time window.
| First | Second | Third | Fourth | Whole | |
|---|---|---|---|---|---|
| Mean | −32.69 | −27.54 | −23.81 | −29.56 | −28.30 |
| SD | 8.45 | 9.43 | 6.81 | 9.00 | 7.52 |
| Median | −34.45 | −27.39 | −22.98 | −27.91 | −26.88 |
| Min | −68.00 | −73.50 | −68.00 | −75.00 | −72.17 |
| Max | −11.00 | −2.56 | −9.53 | −13.38 | −15.03 |
Fig. 1.
Spatial distribution by decile range for the mean percentage variations (change from baseline) of workplace mobility in March 2020.
3.2. Clustering of the European regions
The proposed STAR-FCMdC-NC model has been applied to the matrix of model coefficients of dimension 451 × 3 (where and ), for different time windows. The identification of the orders and is based on the following procedure. We first identified, over the full time span, for each unit, the order P by comparing three alternative models with ; the comparison is made in terms of minimum BIC. In all the 451 spatial units the order was selected. Then we compared, for each unit, three models (2) with and ; in this case the result is a bit puzzling: BIC selects in 33.7% of units, in 26.6%, in 39.7%. However, repeating the same experiment for each sub-period, we see a clear preference for (see Table 2). For the sake of parsimony and to facilitate the interpretation and comparison of the models for clustering, we decide to fix for all models.
Table 2.
Percentage of spatial units with minimum BIC in correspondence of four different time spans and three different values of the order .
| Time Window | |||
|---|---|---|---|
| First | 63.2 | 22.4 | 14.4 |
| Second | 65.9 | 21.3 | 12.8 |
| Third | 59.0 | 22.8 | 18.2 |
| Fourth | 62.3 | 23.7 | 14.0 |
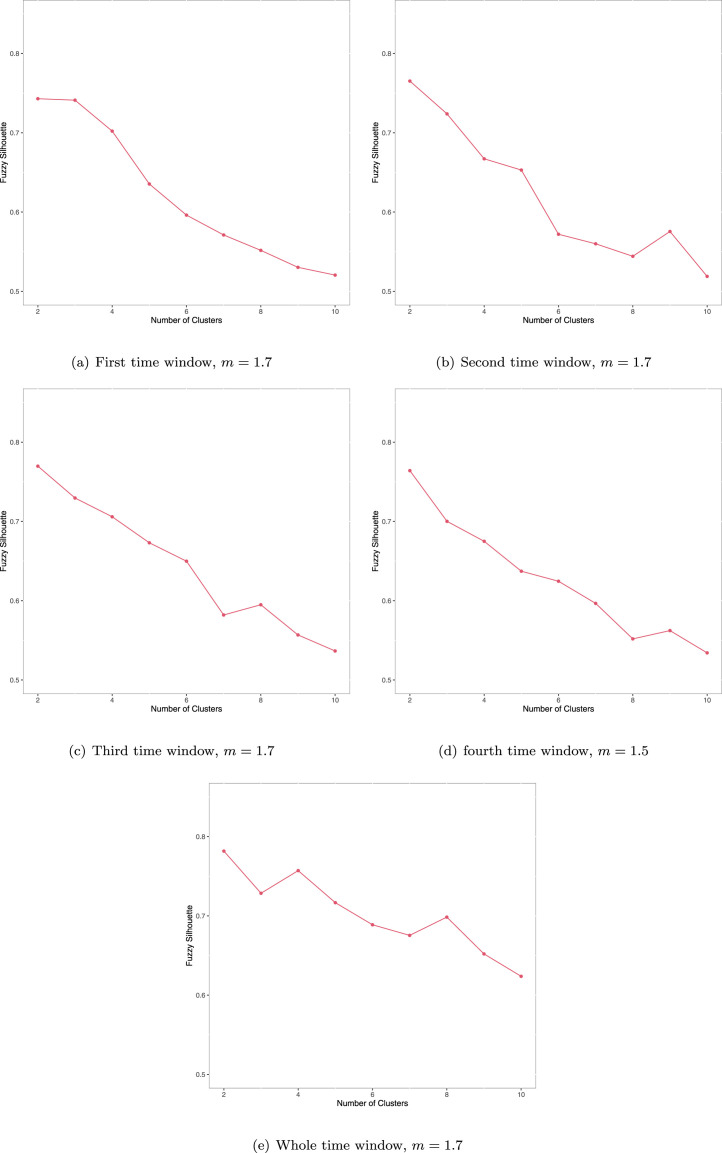
For each period, the number of groups has been chosen according to the combination of the and values that maximize the Fuzzy Silhouette (FS) index (Campello and Hruschka, 2006). To this purpose, the algorithm has been run for and leading to the solutions, for each time window, shown in Table 3.
Table 3.
The best combination of and based on the Fuzzy Silhouette (FS) index for each time window (Table includes also the Medoids of the two clusters).
| Time Window | Medoid Cluster 1 | Medoid Cluster 2 | |||
|---|---|---|---|---|---|
| First | 2 | 1.7 | 0.743 | Vwstra G taland county | LikaSenj county |
| Second | 2 | 1.7 | 0.765 | Aberdeen city | Community of Madrid |
| Third | 2 | 1.7 | 0.770 | Angus council | Vaud |
| Fourth | 2 | 1.5 | 0.764 | Kooice region | County Carlow |
| Whole | 2 | 1.7 | 0.781 | KomgromEsztergom | Geneva |
The FS values on varying have been shown in Fig. 2 for each time window. For each period, besides the noise cluster, two groups (whose medoids have been shown in Table 3) are always well identified as we can see by inspecting the membership degrees represented by means of the ternary plots of Fig. 3, Fig. 4. Indeed, most of units belongs to one of the two groups with high membership degree while lesser is the number of fuzzy units (distinguished among fuzzy units between the two natural clusters, fuzzy units between the first cluster and the noise one, fuzzy units between the second cluster and the noise one).
Fig. 2.
FS values on varying , for each time window.
Fig. 3.
Ternary plots of membership degrees for clustering results referred to the first, second and third time window.
Fig. 4.
Ternary plots of membership degrees for clustering results referred to the fourth time window and to the whole one.
To improve clusters interpretation, we assigned each region to a specific group setting a cut-off value according to the th time series is assigned to the th cluster if . Taking into account the obtained crisp partition, the multidimensional scaling projection on two dimensions of the model coefficients and their representation on the tridimensional space have been generated, as shown in Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9. By looking at these graphs, the structure in two separated groups becomes fairly evident together with the following important consideration, arisen above all from the 3D graph, i.e. groups have been mainly discriminated by the spatial coefficient. The violin plots of Fig. 10, Fig. 11, Fig. 12, Fig. 13, Fig. 14 strongly confirm this evidence. Indeed, looking at the kernel density of the model coefficients, we can conclude that the spatial component is the only one able to differentiate among observations, detecting a structure in two main groups while temporal autoregressive component has a very marginal role in the clustering process. On the other hand, we can argue that the spread of the distribution of the spatial coefficient is much wider than that of the temporal ones.
Fig. 5.
Muldidimensional scaling projection on two dimensions (on the left) and tridimensional representation (on the right) of the model coefficients by groups — First time window.
Fig. 6.
Multidimensional scaling projection on two dimensions (on the left) and tridimensional representation (on the right) of the model coefficients by groups — Second time window.
Fig. 7.
Multidimensional scaling projection on two dimensions (on the left) and tridimensional representation (on the right) of the model coefficients by groups — Third time window.
Fig. 8.
Multidimensional scaling projection on two dimensions (on the left) and tridimensional representation (on the right) of the model coefficients by groups — Fourth time window.
Fig. 9.
Multidimensional scaling projection on two dimensions (on the left) and tridimensional representation (on the right) of the model coefficients by groups — Whole time window.
Fig. 10.
Violin plots for Clusters 1 e 2 — First time window.
Fig. 11.
Violin plots for Clusters 1 e 2 — Second time window.
Fig. 12.
Violin plots for Clusters 1 e 2 — Third time window.
Fig. 13.
Violin plots for Clusters 1 e 2 — Fourth time window.
Fig. 14.
Violin plots for Clusters 1 e 2 — Whole time window.
In Table 4 we show the average of each coefficient within the detected two clusters and the different groups of fuzzy data (excluding the noise cluster, which contains extreme values, both small and high) for the entire period and each subperiod. It is confirmed that the time coefficients and do not seem to characterize the cluster, while some regularity can be seen in the spatial coefficient . In particular, it appears that these five groups can be interpreted in terms of the increasing level of spatial dependence in the following order: Fuzzy units cluster 2-Noise (very small spatial dependence), Cluster 2 (small), Fuzzy units Clusters 1–2 (medium), Cluster 1 (high), Fuzzy units Cluster 1-Noise (very high).
Table 4.
Clusters Centroids (the centroids have been computed also for the three groups of fuzzy units).
| Time Window | Cluster 1 | Cluster 2 | Fuzzy units clusters 1–2 | Fuzzy units clusters 1-Noise | Fuzzy units clusters 2-Noise | |
|---|---|---|---|---|---|---|
| First | 0.025 | 0.031 | 0.005 | 0.008 | 0.006 | |
| −0.077 | −0.130 | −0.106 | −0.103 | −0.152 | ||
| 1.450 | 0.680 | 1.072 | 2.127 | −0.019 | ||
| Second | 0.023 | 0.027 | 0.022 | 0.033 | 0.016 | |
| −0.082 | −0.147 | −0.119 | −0.034 | −0.150 | ||
| 1.355 | 0.545 | 0.979 | 2.037 | −0.097 | ||
| Third | 0.027 | 0.025 | 0.030 | 0.003 | 0.021 | |
| −0.087 | −0.122 | −0.071 | −0.108 | −0.156 | ||
| 1.408 | 0.593 | 1.018 | 2.097 | −0.074 | ||
| Fourth | 0.027 | 0.016 | 0.016 | −0.009 | 0.022 | |
| −0.084 | −0.143 | −0.093 | −0.097 | −0.148 | ||
| 1.334 | 0.557 | 0.954 | 2.053 | −0.147 | ||
| Whole | 0.031 | 0.021 | 0.034 | 0.018 | 0.017 | |
| −0.078 | −0.130 | −0.087 | −0.072 | −0.145 | ||
| 1.355 | 0.604 | 0.975 | 2.046 | −0.064 | ||
Given this interpretation, considering the entire period, we can see a low presence of very high spatial dependence (blue zones) and a high prevalence of dependence in Italy, a part of Spain, the United Kingdom and Eastern Europe (Fig. 15). By dividing the time span into the four subperiods, we note a general small spatial dependence during the first pandemic wave (Fig. 16), excluding parts of the United Kingdom and Northern Italy (where the European pandemic began). Probably the beginning of the COVID-19 pandemic in Lombardy (Italy) could have had an immediate impact on workplaces mobility trends in the surrounding European regions due to the strong economic, cultural and geographical links between these regions. The summer of 2020, with the hope of the end of the spread of the pandemic, is denoted by a sharp increase in the small spatial dependence (Fig. 17). This trend seems to be confirmed in the third period (Fig. 18) with a diffusion of violet areas, but also large areas characterized by noise. The second pandemic wave of 2021 is characterized by new increases in space dependence (Fig. 19), especially in Italy and in the Balkan regions, due to the new restrictions adopted in particular by these countries. In summary, space dependence appears to be directly related to the actions of pandemic waves and the protective measures adopted by European nations.
Fig. 15.
Map of clustering results — Whole time window.
Fig. 16.
Map of clustering results — First time window.
Fig. 17.
Map of clustering results — Second time window.
Fig. 18.
Map of clustering results — Third time window.
Fig. 19.
Map of clustering results — Fourth time window.
It might be interesting to link our results with some recent comments from the Spanish newspaper El Pais. In their purely descriptive analysis, they note that in 2021 the citizens of countries like Spain and France begun moving freely without taking into account the danger of contagion, while countries like Italy are blocked by internal restrictions. If we think of high spatial dependence as a uniformity of people’s behavior due to restrictions and low spatial dependence as idiosyncratic behavior of citizens, this picture is consistent with our analysis. It can be clearly seen how, in general (Fig. 15), Spain is characterized by a prevalence of gray areas (poor spatial relationship) with only a few black areas (high spatial dependence in the Center and North); France is clearly characterized by low spatial dependence (gray and purple zones); Northern Italy, where the European contagion started, is all black.
Also following the evolution over time (Fig. 16, Fig. 17, Fig. 18, Fig. 19) we note how Spain has increased its spatial dependence from the second to the third period (growth of black and blue areas), but in the fourth there is again the prevalence of gray areas.
In France, only Normandy has a certain degree of spatial dependence (perhaps due to its proximity to England which has shown high levels of mortality due to the pandemic), but the rest of the country always remains in the gray and purple zone, with some cases of noise.
To this purpose, it is worth mentioning the two French regions Hauts-de-France and Grand Est (the latter involved in the early diffusion of pandemic due to the cluster formed after the gathering of the Christian Open Door Church in February 2020 in the Mulhouse city), characterized by rates of positives and deaths amongst the highest in France and classified, in almost all partitions, as outliers, with a negative sign of their associated spatial coefficient. A possible explanation could be based on their geographic position. The Grand Est region is located in Northeastern France and can be seen as a “region gateway” being the only French region to border more than two countries. Indeed, it shares borders with the Wallonia region (Belgium), the Cantons of Esch-sur-Alzette and Remich (Luxembourg) on the North, with Germany on the East and Northeast and Switzerland on the Southeast. Within France, its neighbors are Bourgogne-Franche-Comté on the South, Île-de-France, seriously hit by pandemic on the West, and Hauts-de-France on the Northwest.
As far as Hauts-de-France is concerned, it is the Northernmost region of France and the second most densely populated in metropolitan France after its neighbor Île-de-France. It also borders Grand Est and Normandy. More important, outside France, it is connected to England via the Channel Tunnel sharing borders with the Flanders and Wallonia (Belgium), overlooking the North Sea to the North.
Therefore, the two regions are neighbors and have a strategic geographic position, sharing borders with regions belonging to other countries. They figure as outliers, with a negative spatial dependence, probably because of the effect of the lack of uniformity of restriction policies that varied in time and intensity across the European countries.
Northern Italy always remains black, reflecting the strong restrictions imposed in this country.
4. Concluding remarks
Social restrictions and local lockdowns have been implemented in many Europe countries to reduce viral transmission during the COVID-19 pandemic. Consequently these restrictions had a big impact in human mobility. Specifically to evaluate changes in workplace mobility we use GCMR data and propose an innovative strategy analysis. So we estimate a robust fuzzy partitioning around medoids model with noise cluster for clustering the European regions (NUTS2) -identified by the classification ISO alpha 2 (ISO 3166) by the International Organization for Standardization — considering spatial and temporal information and using community mobility during COVID-19 pandemic. In particular, considering the time series of the 451 European spatial units for the period from February 15th, 2020 to April 18th, 2021, we cluster them based on a set of estimated coefficients derived from a simple Space-Time AutoRegressive (STAR) model, relative to each spatial unit, and detecting spatial patterns with cluster with similar coefficients that can be considered as units with similar space–time dynamics. To cluster the European regions we proposed a model-based fuzzy clustering algorithm, i.e. the STAR-based Fuzzy C-Medoids Clustering model with Noise Cluster (STAR-FCMdC-NC). In addition, we split the time span in four subsets to verify how the classification changes in different phases of the COVID pandemic period. Clustering results are mainly influenced by spatial component that, in turn, as expected, seems to reflect the different regimes of restrictive measures adopted by the European Governments to face the outbreak waves. The effects of the total and local lockdowns across the different phases of pandemic and across regions translate into a spatial autocorrelation more than into a temporal one. The results seem consistent with the phases of the pandemic (first wave, illusion of the end of the pandemic, second wave), the blocking actions of European nations, the different times of spread of the pandemic among the European countries. To conclude, in this study we observed that there is a significant spatial dependence in workplace mobility reduction that relates with the incidence of the pandemic, demonstrating (with some exceptions) an impact of restrictions on mobility proportional to the epidemiological situation. We believe that the spatial–temporal approach of human mobility data can help to inform the European government in order to implement common policies capable of balancing the economic and social effects and controlling the spread of the pandemic. In the future, we will focus our attention on other possible methodological and empirical investigations connected to the territorial partitioning procedure based on complex data structures and, in particular, related to community mobility during the COVID-19 pandemic. In particular, from a methodological point of view, we will investigate the possibility to add another source of uncertainty in the partitioning process, i.e. the statistical uncertainty associated to the estimates of the temporal and spatial parameters of the STAR models; furthermore, we will define a weighting system for tuning in an objective manner the influence of the temporal and spatial information in the clustering process and we will explore other kinds of robust clustering procedures for spatial–temporal univariate and multivariate data.
In our empirical study we analyzed workplaces mobility trends for places of work. In the future, we will extend our empirical study adding in the dataset the Google mobility trends data related to other place categories; i.e. grocery & pharmacy (mobility trends for places like grocery markets, food warehouses, farmers markets, specialty food shops, drug stores, and pharmacies), parks (mobility trends for places like local parks, national parks, public beaches, marinas, dog parks, plazas, and public gardens), transit stations (mobility trends for places like public transport hubs such as subway, bus, and train stations), retail & recreation (mobility trends for places like restaurants, cafes, shopping centers, theme parks, museums, libraries, and movie theaters) and residential (mobility trends for places of residence) (Anon, 2021).
Acknowledgments
The authors thank the Editor and the referees for their useful comments and suggestions which helped to improve the quality and presentation of this manuscript.
Footnotes
When the number of spatial units is large we have problems of ill-conditioning of the covariance matrix of the estimators, with a near-to-zero determinant. See Otranto and Gallo (1994) for a simulation study to detect balanced space-to-time dimensions.
In this paper we set = 459 km. The Maxmin bandwidth is chosen in such a way that the following relationship is satisfied: where represents the minimum distance of the generic spatial unit with the other units (with ). As a consequence each spatial unit is connected to all the others (Mucciardi and Bertuccelli, 2012).
An object belongs to the th fuzzy cluster if its membership degree to this cluster, , is higher than the membership of this object to any other fuzzy cluster.
References
- Anon . 2021. Google COVID-19 community mobility reports. Retrieved from: https://www.google.com/covid19/mobility/april2021. [Google Scholar]
- Anselin L. Kluwer Academic; Dordrecht: 1988. Spatial Econometrics: Methods and Models. [Google Scholar]
- Bezdek J. Kluwer Academic; Norwell, MA, USA: 1981. Pattern Recognition with Fuzzy Objective Function Algorithms. [Google Scholar]
- Campello R.J.G.B., Hruschka E.R. A fuzzy extension of the silhouette width criterion for cluster analysis. Fuzzy Sets and Systems. 2006;157:2858–2875. [Google Scholar]
- Cartenì A., Di Francesco L., Martino M. How mobility habits influenced the spread of the COVID-19 pandemic: Results from the Italian case study. Sci. Total Environ. 2020;741 doi: 10.1016/j.scitotenv.2020.140489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davé R.N. Characterization and detection of noise in clustering. Pattern Recognit. Lett. 1991;12:657–664. [Google Scholar]
- Disegna M., D’Urso P., Durante F. Copula-based fuzzy clustering of spatial time series. Spatial Statist. 2017;21:209–225. [Google Scholar]
- D’Urso P. In: Handbook of Cluster Analysis. Hennig C., Meila M., Murtagh F., Rocci R., editors. Chapman and Hall; 2016. Fuzzy clustering; pp. 241–263. [Google Scholar]
- D’Urso P., De Giovanni L., Disegna M., Massari R. Fuzzy clustering with spatial–temporal information. Spatial Statist. 2019;30:71–102. [Google Scholar]
- D’Urso P., De Giovanni L., Massari R. Time series clustering by a robust autoregressive metric with application to air pollution. Chemometr. Intell. Lab. Syst. 2015;141:107–124. [Google Scholar]
- D’Urso P., De Giovanni L., Massari R. GARCH-based robust clustering of time series. Fuzzy Sets and Systems. 2016;305:1–28. [Google Scholar]
- D’Urso P., De Giovanni L., Massari R., Di Lallo D. Noise fuzzy clustering of time series by autoregressive metric. Metron. 2013;71(3):217–243. [Google Scholar]
- D’Urso P., De Giovanni L., Vitale V. Spatial robust fuzzy clustering of COVID 19 time series based on B-splines. Spatial Statist. 2021 doi: 10.1016/j.spasta.2021.100518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Urso P., Di Lallo D., Maharaj E.A. Autoregressive model-based fuzzy clustering and its application for detecting information redundancy in air pollution monitoring networks. Soft Comput. 2013;17(1):83–131. [Google Scholar]
- D’Urso P., Massari R., Cappelli C., De Giovanni L. Autoregressive metric-based trimmed fuzzy clustering with an application to PM10 time series. Chemometr. Intell. Lab. Syst. 2017;161:15–26. [Google Scholar]
- D’Urso P., Vitale V. A robust hierarchical clustering for georeferenced data. Spatial Statist. 2020;35 [Google Scholar]
- Everitt B., Landau S., Leese M., Stahl D. fifth ed. John Wiley & Sons, Ltd; London: 2011. Cluster Analysis. [Google Scholar]
- Francetic I., Munford L. Corona and coffee on your commute: a spatial analysis of COVID-19 mortality and commuting flows in England in 2020. Eur. J. Public Health. 2021:1–7. doi: 10.1093/eurpub/ckab072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frühwirth-Schnatter S. Panel data analysis: a survey on model–based clustering of time series. Adv. Data Anal. Classif. 2011;5:251–280. [Google Scholar]
- García-Escudero L.Á., Gordaliza A. Robustness properties of k means and trimmed k means. J. Amer. Statist. Assoc. 1999;94:956–969. [Google Scholar]
- García-Escudero L.A., Gordaliza A., Matrán C., Mayo-Iscar A. A review of robust clustering methods. Adv. Data Anal. Classif. 2010;4:89–109. [Google Scholar]
- Kaufman L., Rousseeuw P. WileyBlackwell; 2005. Finding Groups in Data: An Introduction to Cluster Analysis. [Google Scholar]
- Lapatinas A. Publications Office of the European Union; Luxemburg: 2020. The Effect of COVID-19 Confinement Policies on Community Mobility Trends in the EU, EUR 30258 EN. [Google Scholar]
- Lozzi G., Rodrigues M., Marcucci E., Teod T., Gatta V., Pacelli V. European Parliament. Policy Department for Structural and Cohesion Policies; Brussels: 2020. Research for TRAN Committee – COVID-19 and urban mobility: impacts and perspectives; pp. 1–24. [Google Scholar]
- Maharaj E.A. Comparison and classification of stationary multivariate time series. Pattern Recognit. 1999;32:1129–1138. [Google Scholar]
- Maharaj E.A., D’Urso P., Caiado J. Chapman and Hall; 2019. Time Series Clustering and Classification. [DOI] [Google Scholar]
- McBratney A., Moore A. Application of fuzzy sets to climatic classification. Agricult. Forest Meteorol. 1985;35(1–4):165–185. [Google Scholar]
- Mendolia, S., Stavrunova, O., Yerokhin, O., 2020. Determinants of the community mobility during the COVID-19 epidemic: The role of government regulations and information. Discussion Paper Series - IZA Institute of Labor Economics. pp. 1–27. [DOI] [PMC free article] [PubMed]
- Mucciardi M., Bertuccelli P. The impact of the weight matrix on the local indicators of spatial association: an application to per-capita value added in Italy. Int. J. Trade Glob. Mark. 2012;5:133–141. [Google Scholar]
- Ophir Y., Walter D., Arnon D., Lokmanoglu A., Tizzoni M., Carota J., D’Antiga L., Nicastro E. The framing of COVID-19 in Italian media and its relationship with community mobility: A mixed-method approach. J. Health Commun. 2021:1–13. doi: 10.1080/10810730.2021.1899344. [DOI] [PubMed] [Google Scholar]
- Otranto E. Clustering heteroskedastic time series by model-based procedures. Comput. Statist. Data Anal. 2008;52(10):4685–4698. [Google Scholar]
- Otranto E. Identifying financial time series with similar dynamic conditional correlation. Comput. Statist. Data Anal. 2010;54(1):1–15. [Google Scholar]
- Otranto E., Gallo G.M. Regression diagnostic techniques to detect space–to–time ratios in STARMA models. Metron. 1994;52:129–145. [Google Scholar]
- Otranto E., Mucciardi M. Clustering space-time series: FSTAR as a flexible STAR approach. Adv. Data Anal. Classif. 2019;13(1):175–199. [Google Scholar]
- Otranto E., Mucciardi M., Bertuccelli P. Spatial effects in dynamic conditional correlations. J. Appl. Stat. 2016;43:604–626. [Google Scholar]
- Piccolo D. A distance measure for classifying ARIMA models. J. Time Series Anal. 1990;11(2):153–164. [Google Scholar]
- Saha J., Barman B., Chouhan P. Lockdown for COVID-19 and its impact on community mobility in India: An analysis of the COVID-19 Community Mobility Reports, 2020. Child. Youth Serv. Rev. 2020;116 doi: 10.1016/j.childyouth.2020.105160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sulyok M., Walker M. Community movement and COVID-19: a global study using Google’s Community Mobility Reports. Epidemiol. Infect. 2020;148 doi: 10.1017/S0950268820002757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedel M., Kamakura W. Springer; 2000. Market Segmentation: Conceptual and Methodological Foundations, Vol. 8. [Google Scholar]