Knot selection for low-rank kriging models of spatial risk in case-control studies

Abstract

Many spatial analysis methods have been used to identify potential geographic clusters of disease in case-control studies. Low-rank kriging (LRK) models reduce the computational burden in generalized additive models by using a set of knot locations instead of the observed subject locations for estimating spatial risk. However, there is little guidance regarding selection of the number and location of the knots in case-control studies. We perform an extensive simulation study that compares a commonly-used method of knot selection in LRK models with two proposed methods and varies the number of knots. We find the commonly-used method is vastly outperformed by those that consider the locations of cases. We find that the Teitz and Bart heuristic allows the highest spatial sensitivity and power to detect zones of elevated risk, and recommend its use with a number of knots as close to the number of case locations as computation time will allow.

Introduction:

It is of great public health interest to create statistical analysis methods that are able to identify geographic areas of excess disease risk and spur geographically-informed interventions and policies. Examples abound in the literature of the use of such models, investigating a wide range of diseases that includes colorectal, lung, and lip cancers (Vieira et al.; Archer et al.; Wakefield). One effective and long-standing approach to analyze the distribution of spatial risk for disease is the use of case-control studies. Data collected from such studies can allow researchers to compare the spatial distributions of cases and population-based controls while accounting for the demographic, environmental, and lifestyle factors that may be associated with higher risk of disease. Case-control studies have been used to map the spatial distribution of disease risk and detect potential disease clusters of breast, bladder, and prostate cancers (Webster et al.; Jacquez et al.; Weichenthal et al.).

One advantage of case-control studies compared with ecological studies is they allow for precise detection of geographic areas of elevated risk. This can lessen the tendency to draw incorrect conclusions from areal disease mapping techniques, which are susceptible to unstable estimates based on low population counts and based on administrative boundaries that may be unrelated to public health (Openshaw; De Lepper set al.). A variety of methods have been developed to detect disease clusters with point-level data collected in case-control studies. One example is Kulldorff’s spatial scan statistic, which is implemented in the SaTScan software (Kulldorff). The scan statistic places circles of varying radii at each participant’s location and compares disease rates inside and outside of the circle with a likelihood ratio statistic. Another method is Jacquez’s focal Q-statistics (Jacquez et al.), which are designed to detect a cluster around a certain point, or focal source, counting the number of cases around the source among its k nearest neighbors. Finally, Besag and Newell’s test focuses on each case individually, testing whether its associated centroid defines the center of a cluster of a pre-specified size (Besag and Newell).

More comprehensive inference can be performed with spatial regression models, such as generalized additive models (GAMs) (Hastie and Tibshirani), which can adjust for covariates that may be associated with the outcome and provide estimates of uncertainty in quantities of interest, such as odds ratios. It is common in GAMs to use thin plate regression splines (S. N. Wood; S. Wood; David C. Wheeler et al.; David C Wheeler et al.) or lowess over spatial coordinates (Hastie and Hastie; Young et al.; Vieira et al.) to model the spatial variation in risk. GAMs have demonstrated better power to detect areas of elevated risk than Kulldorff’s scan statistic (Young et al.). In the Bayesian framework, it is straightforward to include spatial random effects with spatial correlation specified through prior distributions to model spatial risk. A common prior for spatial random effects is a zero-mean multivariate Gaussian, with a covariance matrix given by a parametric function of the distance between pairs of points and a parameter that controls the degree of spatial smoothing (Diggle et al.). The covariance matrix is of dimension equal to the sample size in the study. Though such an approach can accommodate models of increasing complexity, and can provide full posterior inference on any model parameter of interest, the Markov Chain Monte Carlo (MCMC) methods inherent in full Bayesian estimation require the inversion of this spatial covariance matrix at every iteration of the MCMC chain. Other approaches, such as spatial generalized linear mixed models for areal data, employ conditional autoregressive (CAR) random effects and work directly with the precision matrix, avoiding the need to invert the matrix at every iteration (Waller, Carlin, et al.). However, these models are typically used for count or continuous outcome variables collected over areal units, a spatial level that lacks the precision of residential point locations. The large size of modern case-control studies, combined with the requirement for regular matrix inversion, present a formidable computational challenge to fitting these models and suggest the need for methods that more efficiently enable model estimation.

Low-rank kriging (LRK) represents an effort to retain all the inferential benefits of a GAM while reducing the number of computations necessary in model fitting (Nychka et al.). LRK models simplify the representation of the spatial process into a lower dimension. This is accomplished using a vector of knots, which are points in space where the spatial random effects are estimated, and are of a dimension much less than the sample size, such that the spatial covariance matrix can be inverted. The LRK model has been used in the cancer literature to model prostate cancer risk (Nychka et al.; Gelfand et al.; French and Wand). When fitting LRK models, however, one must choose the number of knots, as well as their placement over the study region. This is akin to specifying how closely the knots approximate the full spatial process, as well as how the knots geographically represent study participant locations. LRK models have shown sensitivity to the selection of the number and position of knots (Kim et al.), and with few knots, the estimation of spatial dependence and parameters becomes more variable (Ruppert et al.).

Some studies have analyzed the effects of varying the number and location of knots in low-rank kriging models, though most have focused on modeling a continuous outcome variable with point-referenced data. For example, Kim et al. demonstrate a rapid decrease in the mean square error of prediction of observations generated on a Gaussian random field for the first several knots added, with little marginal benefit as the number of knots continued to increase beyond 35 to 40 (Kim et al.). Banerjee et al. find that more knots are often required in Gaussian predictive process modeling of a continuous outcome variable to preserve information about the spatial pattern, and particularly when spatial dependence occurs over a fine scale (Banerjee et al.). However, there has been little guidance given with respect to knot selection in case-control data. In such studies, the outcome variable is binary, not continuous, and the point locations are random variables that represent a spatial point process, as opposed to the point-referenced data which is more common with kriging models, that has fixed locations and random outcomes of a continuous outcome variable. Thus, the use of a low-rank kriging model for case-control data realized from a point process can allow the smoothing of spatial risk over the study region that is derived from a random sample of locations of cases and controls. The need is to consider the nature of study participant locations in the knot selection process.

A common method of knot placement in spatial analyses has been the space-filling coverage design algorithm (Johnson et al.), which has been implemented as an R function named “cover.design”. This algorithm was developed from the notions of “mini-max” and “maxi-min” distance sets, which are statistical designs – places to observe the variable of interest. The method was motivated by point-referenced data on a continuous outcome variable (a Gaussian process) and designed to predict responses at unmeasured locations. The design minimizes a geometric space-filling criterion and has been implemented widely (Wang and Ranalli; Roy and Stewart; Calder; Kim et al.; Crainiceanu et al.). But these objectives are not as relevant in a case-control study, in which the outcome variable is binary and locations arise from a marked point process. The discrepancy in the types of spatial design here may suggest that different methods are warranted to choose knots in LRK models of case-control data.

As alternatives to the space-filling algorithm, which effectively ignores the mark in the marked point process of case-control studies, we propose the use of two other methods that incorporate the mark. As the LRK model represents locations in space, the knots should be chosen in a principled way to represent the underlying spatial distribution of disease risk in the study region and to allow the identification of areas of significantly elevated risk. Because the prediction variance in kriging is greater with increasing distance between the predicted points and the data, there is potential for greater prediction error in regions that are far from sampled points (Zimmerman et al.). To avoid missing areas of elevated risk, we focus on the case locations in the proposed knot selection methods.

The first alternative is a simple modification of the space-filling algorithm in that it only operates on the spatial locations of cases. In this way, the algorithm will seek to efficiently fill space with respect to the case locations, and may better represent the spatial distribution of risk. The second alternative is Teitz and Bart’s location-allocation heuristic (Teitz and Bart), which has been used extensively in operations research problems to minimize distance between facilities and clients. Considering the knot locations to be the facilities and the clients to be the cases, this heuristic will seek to minimize the distance from cases to their closest knot location. As both of these alternatives are more aligned with the design of case-control studies, they may be more appropriate for analyzing such data.

To evaluate the hypothesis that the space-filling algorithm is suboptimal for knot selection in case-control studies, we evaluated its performance, along with our two proposed methods, in a simulation study. We accomplish this via an extensive series of simulation studies using many simulated populations distributed over a study region. The simulated populations vary in their risk of disease depending on their proximity to a zone of elevated risk. We compare spatial sensitivity, specificity, and spatial power between the different knot selection algorithms across a variety of scenarios and across a varying number of knots.

Methods:

Model Specification

We used a Bayesian LRK model to model the probability of being a case using a Bernoulli distribution for each subject. Specifically, for subject i, the probability of disease is distributed as Y_i ~ Bernoulli(p_i), where we modeled the log-odds of p_i as $log\left(\frac{p_i}{1-p_i}\right)={\beta }_0+{\sum }_{m=1}^{n_k}{\psi }_{m}C\left[\left|s_i-{\kappa }_m\right|/\rho \right]$. Here, $\left\{{\kappa }_1,\dots ,{\kappa }_{n_{\kappa }}\right\}$ are the n_κ knot locations that are a lower-dimensional representation of the locations of cases and controls and are chosen by some knot selection algorithm. The residential location for subject i is denoted by s_i, and the spatial correlation parameter is denoted by ρ. The term ψ_m is a spatially structured random effect, and the function C(·) is a member of the Matern family of covariance functions. Fixing parameters of the Matern family to values of m = 1 and ν = 3/2, the covariance function is given by $\left(1+\frac{d}{\rho }\right)e^{-\frac{d}{\rho }}$ Thus, while the model incorporated each subject’s residential location to estimate their spatial risk, it expressed the residential location indirectly, in terms of its model-specified covariance from the set of n_κ knot locations.

For priors in the Bayesian LRK model, the regression intercept had vague Normal priors β₀ ~ N(0, τ = 10⁻³), where τ denotes the precision, which is the reciprocal of the variance. The random effects ψ_m received a multivariate normal prior ψ ~ MVN(0, τ_RΩ⁻¹), where the precision matrix is given by Ω = [C[∥κ_m − κ_m′∥/ρ]], for 1 ≤ m, m′ ≤ n_κ, and ${\tau }_R=\frac{1}{{\sigma }_R^2}$ and σ_R ~ Unif(1, 10). The spatial correlation parameter, ρ, received a uniform prior on (0, 30).

Knot Selection

The specified model depends on a set of knots for estimating the spatial risk. We used three different methods to perform knot selection for the LRK model. The first method is the space-filling coverage design function, which has been described briefly above. The function seeks to minimize a geometric space-filling criterion. A random initial configuration of design points is chosen. For design points in set D and candidate points in set C, the criterion is given by $M(D,C)={\sum }_{c_i\in C}{\left[{\sum }_{d_i\in D}{\left({\left(r\left(c_i,d_i\right)\right)}^p\right)}^{q/p}\right]}^{1/q}$, where p is a parameter that affects how the distance from a point to a set of design points is calculated, q is a parameter that affects how distance from all points not in the design to those that are is averaged, and r(c_i, d_i) denotes a distance measure between these points. Default values of −20 and 20 for the p and q parameters, respectively, were used. The algorithm is guaranteed to converge but has exhibited sensitivity to the initial set of design points. So, we used three independent initial configurations and retained the solution that gave the smallest final coverage criterion. We used this method as a baseline for comparison due to its popularity in spatial analyses. The next two methods consist of our proposed approaches for knot selection in the low-rank kriging model.

The second method was a modification of the space-filling algorithm that only considered case locations, and not control locations. This minimizes the space-filling criterion over the case locations and better represents the spatial population distribution of cases, which may in turn better uncover areas that give rise to the processes that induce the population to become cases.

The third method was that of Teitz and Bart, which is an interchange heuristic that was designed to estimate the vertex median of a weighted graph (Teitz and Bart). The problem sought to choose the locations of destinations to balance the weighted demands of sources, where the amount of demand carried from source to destination was allowed either to vary, or to be constant as a special case. The latter aligned with our problem, where all cases carried an equal amount of demand. and controls carried zero demand. Teitz and Bart’s method was motivated as a better-performing and less variable alternative to the partition method of Maranzana (Maranzana), which successively found single-vertex medians of partitions of vertices to address the p-median problem. Here, the term median refers to a point that minimizes the summed distances to points in the sample, and p refers to the dimension of the median. Maranzana’s method began by finding single-vertex medians of p random subsets of demand points, where all points in the set of demand points were considered in the calculation ofthe same median. The method then reassigned demand points to different subsets, updated the location of the medians, and repeated until convergence (Maranzana). The Teitz and Bart heuristic begins with some initial configuration of knots and defines an objective function as the total distance from demand points (for our use, case locations) to facilities (knot locations). It moves the knots iteratively to candidate locations if doing so decreases value of the objective function. The process continues until no further interchange improves the distance criterion. This algorithm has been popular in operations research, particularly in producing an optimal set of facility locations with respect to the locations of clients (Owen and Daskin). We chose to use this algorithm because it was designed for an analogous problem – minimizing the distance from clients to facilities. As the spatial predictions of areas close in distance to the knots in the LRK model are more accurate than those areas farther in distance, we accomplish a similar goal by considering the cases to be the clients and the knots to be the facilities.

Simulation Study Design

Data-generating process.

We implemented a variety of scenarios to compare the performance of knot selection methods in the LRK model. The first factor that we varied in our simulations was the distribution of the population. We generated case and control locations over a study region, defined to be the tri-state area in New England (Maine, New Hampshire, and Vermont) for concreteness, to be either uniform or heterogeneous. Uniform density distributions were generated through a homogeneous Poisson point process, with intensity parameter λ = 0.0025, defined over the study region. Heterogeneous density distributions were generated by layering two additional Poisson point processes above the initial one, each with intensity parameter λ = 0.006, in coastal southern Maine and near the capital region (Augusta) in Maine. We considered heterogeneous distributions since they better resemble existing ones, as populations tend to cluster in certain areas, with other areas having low population density.

We assumed the residential location for each participant to be etiologically relevant for disease risk. This is reasonable when the disease under study has suspected environmental risk factors and when the population is residentially stable (i.e. not highly mobile). For this simulation study, for simplicity, we did not consider disease latency or allow for population mobility. In each scenario, we generated a zone of elevated risk for disease over the study region, varying the location for different scenarios. In different scenarios, participants living in the zone of elevated risk had odds ratios of being a case of 1.5, 2.0, and 2.5 relative to those who did not live in the zone. We also considered different locations for the zone. For the uniform density distribution scenarios, we placed the zone in southern Maine. For the heterogeneously-distributed populations, we placed the zone in southern Maine as well (Heterogeneous-Standard), which had a higher population density than other areas in the study region, and also in northern Maine, which had a lower population density (Heterogeneous-LPD). Using the odds ratios and locations of residences with respect to the zone, we randomly generated case-control status from a Bernoulli distribution with baseline probability of being a case p = 0.1 for those who did not live in the zone of elevated risk. For each scenario, we simulated D = 50 datasets using the data-generating process and fit models to the dataset using each of the three knot selection methods. A summary of the different scenarios is given in Table 1, which also lists the mean, minimum, and maximum proportion of cases in the generated study samples. We simulated case and control locations from populations with a low proportion of cases, and with a relatively small number of cases living in the zone of elevated risk, in order to reflect situations where the disease under study is rare, and detection of areas of elevated risk related to the disease is more challenging. Our choices led to the creation of simulated samples with case-control ratios of approximately 1:10. Such ratios accord with case-control studies with the resources to include a large number of controls. This setting could occur when case prevalence is relatively low in the general population. The cases are selected under the implicit assumption that all cases are observed. This assumption is reasonable when the disease outcome in question is severe and disease registries exist with mandatory reporting, such as with cancers. The controls are selected under the implicit assumption that they represent the spatial distribution of the at-risk population. If the Bayesian LRK models can detect zones of elevated risk with adequate sensitivity when the disease under study is rare, and there are not many disease cases in the true zone, then they will be likely to exhibit more than adequate performance in situations with stronger spatial signal. Maps of the different scenarios, showing the cases, controls, and zone of elevated risk, are given in Figure 1 for illustrative purposes.

Table 1.

Summary of simulation scenarios and average, minimum, and maximum proportion of cases across the simulated population samples.

Population	OR	Location	Mean	Min	Max
Uniform	1.5	Standard	0.102	0.072	0.134
	2.0		0.105	0.076	0.142
	2.5		0.107	0.078	0.142
Heterogeneous	1.5		0.103	0.072	0.132
	2.0		0.106	0.074	0.137
	2.5		0.110	0.084	0.139
	1.5	LPD	0.102	0.075	0.128
	2.0		0.103	0.075	0.130
	2.5		0.104	0.076	0.132

OR = Odds Ratio.

Figure 1.

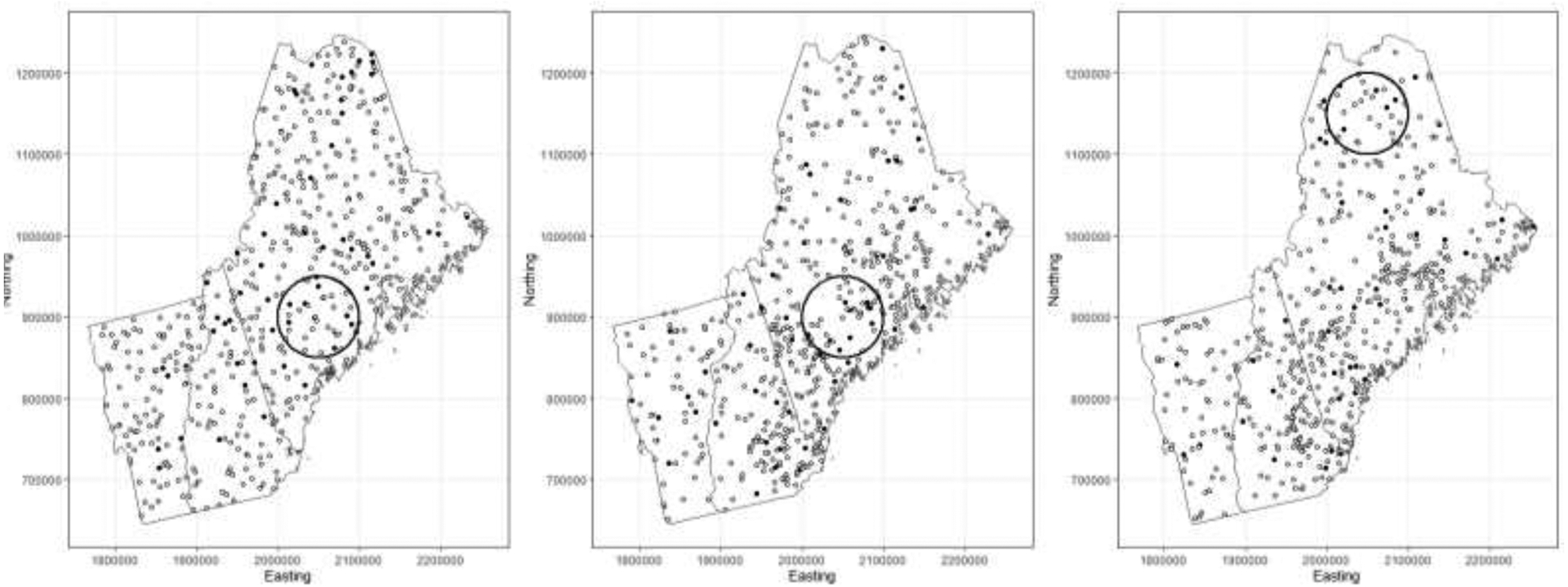
Illustrations of various simulation scenarios. From left to right, uniform population distribution, heterogeneous population distribution with zone in area of standard population density, heterogeneous population distribution with zone in area of lower population density. Cases and controls given by black and white circles, respectively.

Model Fitting.

We fitted a Bayesian LRK model to each simulated dataset, choosing knot locations with each specified knot selection method and varying the number of knots used. We began with n_κ = 35 knots, and then increased the number of knots to 70 and 105 for the best-performing models to examine the effect of number of knots on model performance.

We fit models in a Bayesian framework using Markov Chain Monte Carlo (MCMC) methods. For model estimation, we used Just Another Gibbs Sampler (JAGS) in R, using a burn-in period for 40,000 iterations and retaining 10,000 iterations for sampling from the joint posterior distribution (Plummer and others). We assessed convergence of model parameters using the Gelman-Rubin statistic, where a parameter was considered to have converged if its statistic was less than 1.2 (Gelman and Rubin). Using the posterior samples of ψ, and the covariance function, we predicted the spatial odds of disease to an approximately 6 kilometer by 6 kilometer grid covering the extent of the study region and assessed the significance of disease risk at each grid cell by determining whether its 95% credible interval excluded the null value of one.

Model Evaluation.

We compared model performance in several ways. The first metric is spatial sensitivity. Denoting the set of grid cells that are in the zone of elevated risk as S, the spatial sensitivity of a model for dataset d is given by $se{n}_d=\frac{1}{|S|}{\sum }_{s_i\in S}I\left(s_{iL}>1\right)$, where s_iL denotes the lower bound of the credible interval for grid cell s_i, and I(·) is an indicator function. The second metric is spatial specificity. Defining the set of grid cells that are not in the zone of elevated risk as NS, the specificity of a model for dataset d is given by $spe{c}_d=\frac{1}{|NS|}{\sum }_{n{s}_i\in NS}\left\{1-I\left(n{s}_{iL}>1\right)\right\}$. The spatial sensitivity and specificity will be averaged over the D datasets.

Finally, spatial power is calculated according to a sensitivity threshold of zero. Dataset d will be considered to have identified the zone of elevated risk if any of the grid cells defined to be of significantly elevated risk were identified as such. The spatial power is then calculated as $P=\frac{1}{D}{\sum }_{d=1}^{D}I\left(se{n}_d>0\right)$.

Evaluation of the Number of Knots.

In addition to the above simulation study, we evaluated the performance of the Teitz and Bart algorithm with the LRK model over a large and continuous range of knots for one dataset. The motivation for this was to determine if the objective function from the Teitz and Bart algorithm could be useful for selecting the number of knots to use in the LRK model. The study sample was one realization from a heterogeneous distribution, with the zone located in an area of higher population density, and with an odds ratio of 2.5 for participants living in the zone. For each number of knots in a sequence from 3 to 105 by 2, we fit LRK models using the Teitz and Bart method for knot selection. We recorded the final objective function value of the Teitz and Bart algorithm as well as the deviance, spatial sensitivity, and specificity from the resulting model fit.

Results:

A summary of the generated populations across all scenarios is shown in Table 1. This table also shows the mean, minimum, and maximum proportion of cases in each scenario. Though the proportion of cases increases with the odds ratio for each combination of population distribution and zone location, overall case proportions do not vary greatly across scenarios. This is attributable to the baseline probability of case membership and odds ratios in the zone used being relatively low, and relatively few people living in the zone of elevated risk. Therefore, while the distribution of cases and controls inside the zone varied, the overall distribution of these quantities changed little over the entire population. Additionally, a summary table of model performance is given in Table 2, showing model sensitivity, specificity, and power across the simulation scenarios, knot selection methods, and number of knots.

Table 2.

Simulation results comparing different knot selection techniques and numbers of knots.

Metric	Data Generation			Knot Selection and Number of Knots
	Population Distribution	OR in Zone	Location of Zone	CD-35	CD Cases-35	T-B-35	T-B-70	T-B-105
Sensitivity	Uniform	1.5	Standard	0.011	0.112	0.377	0.538	0.408
		2.0		0.014	0.124	0.467	0.608	0.459
		2.5		0.032	0.131	0.495	0.665	0.507
	Heterogeneous	1.5		0.000	0.118	0.372	0.576	0.398
		2.0		0.001	0.132	0.422	0.643	0.466
		2.5		0.014	0.149	0.455	0.726	0.447
		1.5	LPD	0.000	0.083	0.287	0.334	0.337
		2.0		0.000	0.093	0.312	0.383	0.306
		2.5		0.000	0.104	0.341	0.434	0.331
Specificity	Uniform	1.5	Standard	0.999	0.921	0.731	0.636	0.689
		2.0		0.999	0.922	0.722	0.634	0.683
		2.5		0.998	0.924	0.722	0.630	0.693
	Heterogeneous	1.5		1.000	0.926	0.745	0.673	0.760
		2.0		1.000	0.928	0.756	0.671	0.743
		2.5		0.999	0.930	0.770	0.669	0.790
		1.5	LPD	1.000	0.923	0.735	0.660	0.756
		2.0		1.000	0.924	0.734	0.659	0.770
		2.5		0.999	0.925	0.742	0.657	0.750
Power	Uniform	1.5	Standard	0.020	1.000	0.960	1.000	1.000
		2.0		0.060	1.000	0.980	1.000	0.980
		2.5		0.100	1.000	0.980	1.000	1.000
	Heterogeneous	1.5		0.000	1.000	1.000	1.000	0.920
		2.0		0.020	1.000	1.000	1.000	0.960
		2.5		0.080	1.000	1.000	1.000	0.940
		1.5	LPD	0.000	0.980	0.940	1.000	0.880
		2.0		0.000	0.980	0.940	1.000	0.840
		2.5		0.000	1.000	0.960	1.000	0.880

OR = Odds Ratio, LPD = Low Population Density, CD = cover.design(), CD Cases = cover.design() on case locations, T-B = Teitz and Bart.

Sensitivity.

A plot of model sensitivities is shown in Figure 2. There is a general trend of increasing sensitivity with respect to odds ratio in a given scenario, increasing with the spatial signal in the zone of elevated risk. For all scenarios, the space-filling algorithm on the cases demonstrated an improvement over the standard space-filling algorithm, but the Teitz and Bart method decidedly outperformed them both, doubling to tripling the sensitivity of the space-filling algorithm on the cases. The commonly-used space-filling method had a sensitivity close to zero in all scenarios, never detecting more than five percent of the zone of elevated risk on average.

Figure 2:

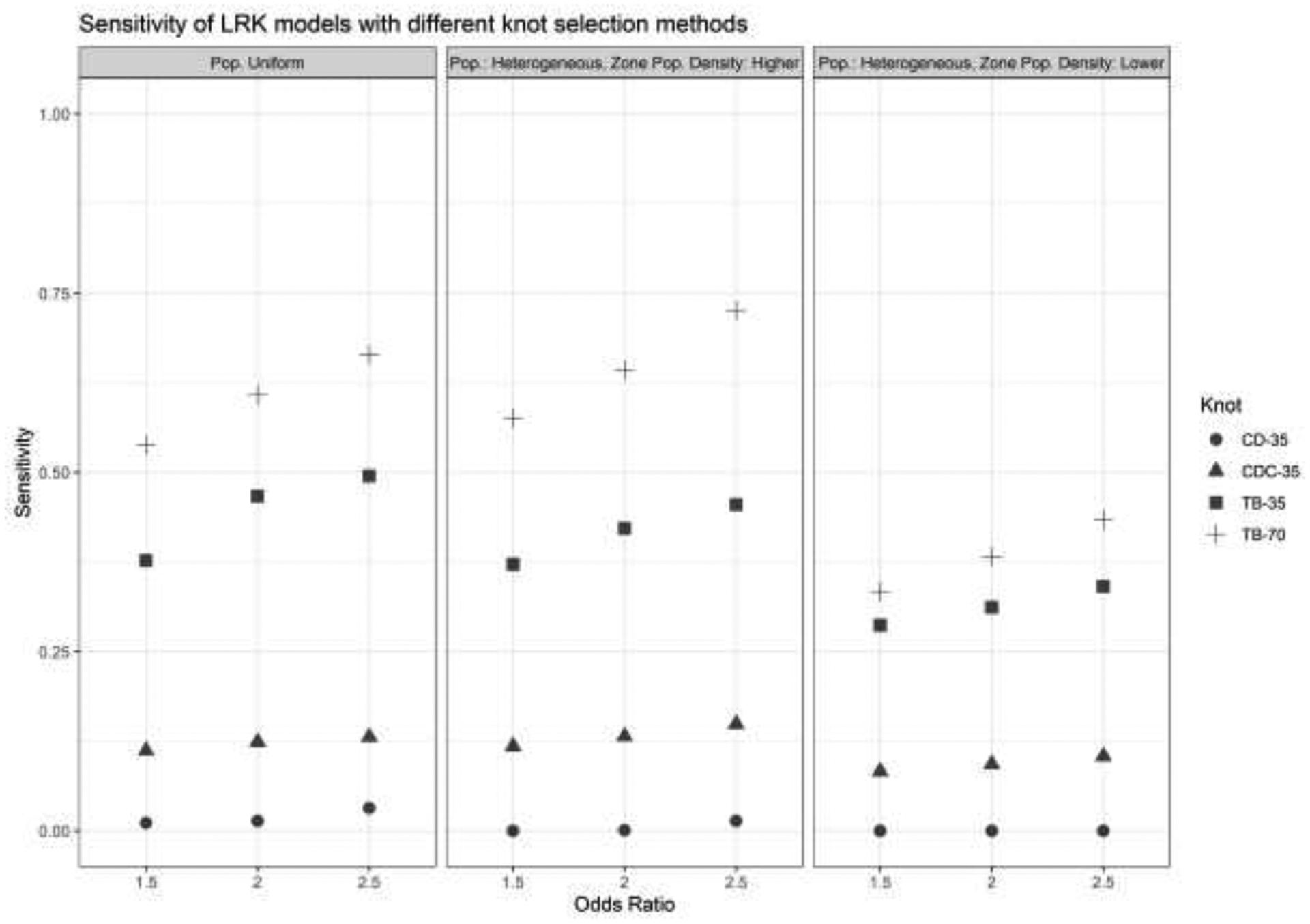
Sensitivity of LRK models with different knot selection methods and numbers of knots. OR = Odds Ratio, LPD = Low Population Density, CD = cover.design(), CD Cases = cover.design() on case locations, T-B = Teitz and Bart.

Using 70 knots chosen with the Teitz and Bart method demonstrated a further improvement in sensitivity over all scenarios. On average, this number of knots and method detected more than half of the grid cells in the zone of risk for the uniform population distribution and the heterogeneous distribution with the zone in an area of higher population density. It approached detecting half of the grid cells for the heterogeneous population and zone in an area of lower population density. The lower sensitivity values in this scenario reflect a low number of cases living in the area of elevated risk, but the general pattern in sensitivity between knot selection methods remained. Notably, methods that placed knots with respect to case locations decidedly outperformed the space-filling algorithm, which had a sensitivity close to zero.

Specificity.

A plot of model specificities is shown in Figure 3. A different and simpler pattern emerges when evaluating model specificity. In particular, the source of most of the variation in specificity appears to be the knot selection method used, and not the simulation scenario. The space-filling algorithm and its counterpart on the cases had high specificities, but this owed to the fact that they generally did not find many regions to have non-null risk in the first place, as demonstrated in Figure 2. The Teitz and Bart methods had lower specificities, but they were near approximately 0.75, and doubling the number of knots to the Teitz and Bart algorithm from 35 to 70 did not markedly decrease the specificity of the models.

Figure 3:

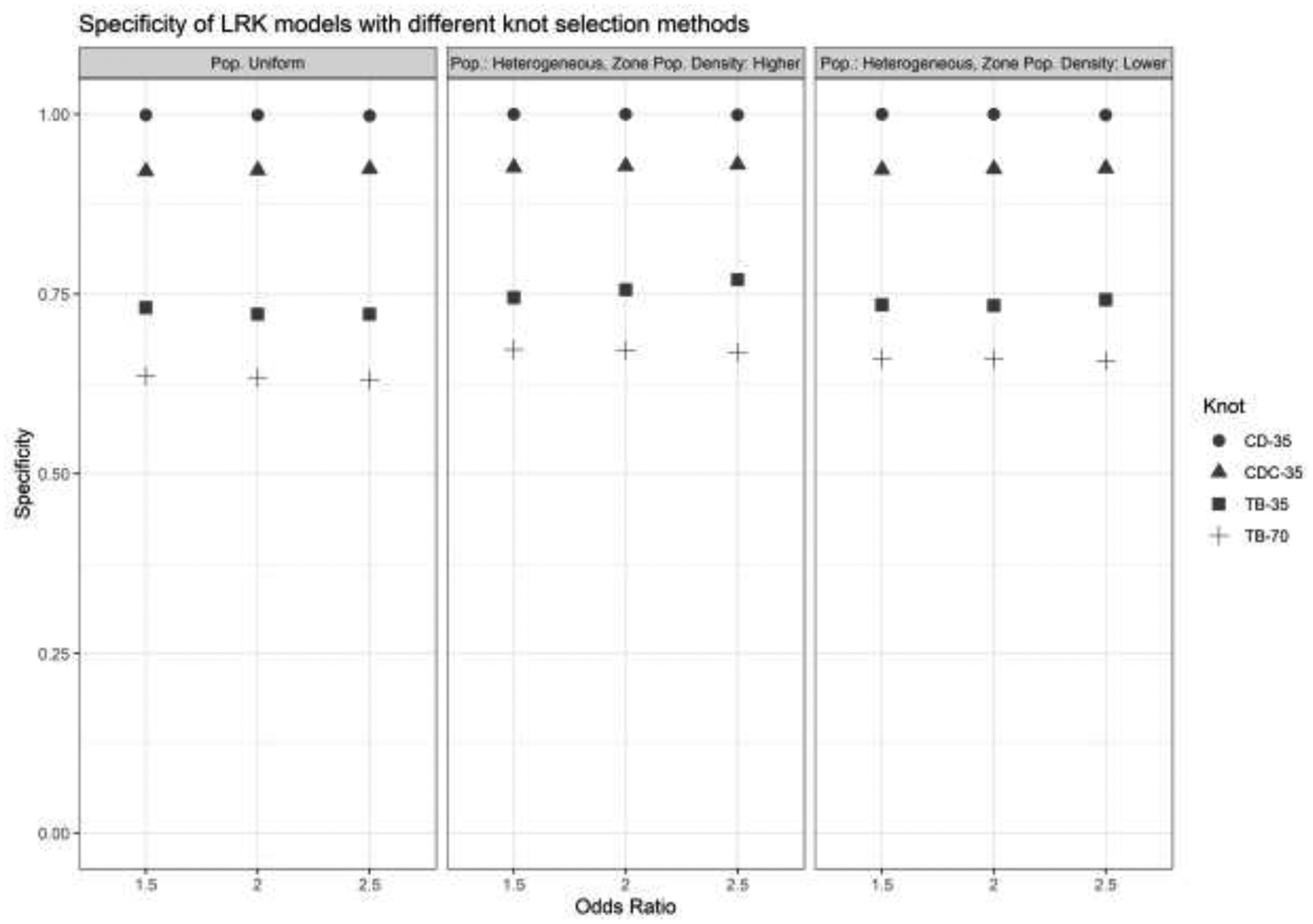
Specificity of LRK models with different knot selection methods and numbers of knots. OR = Odds Ratio, LPD = Low Population Density, CD = cover.design(), CD Cases = cover.design() on case locations, T-B = Teitz and Bart.

Power.

A plot of model power is shown in Figure 4 and illustrates the sharp contrast in performance between the space-filling algorithm and other methods. While any of the other methods detected some part of the zone almost all the time in every condition, having empirical power values very close to 1, the space-filling algorithm barely did so, with power between 0 and 0.1 depending on the scenario. Put another way, this method failed to detect the zone of elevated risk for disease in nearly all of the simulation conditions, but any of the other methods that placed knots with respect to case locations correctly identified at least one grid cell inthe zone in nearly all of the conditions.

Figure 4:

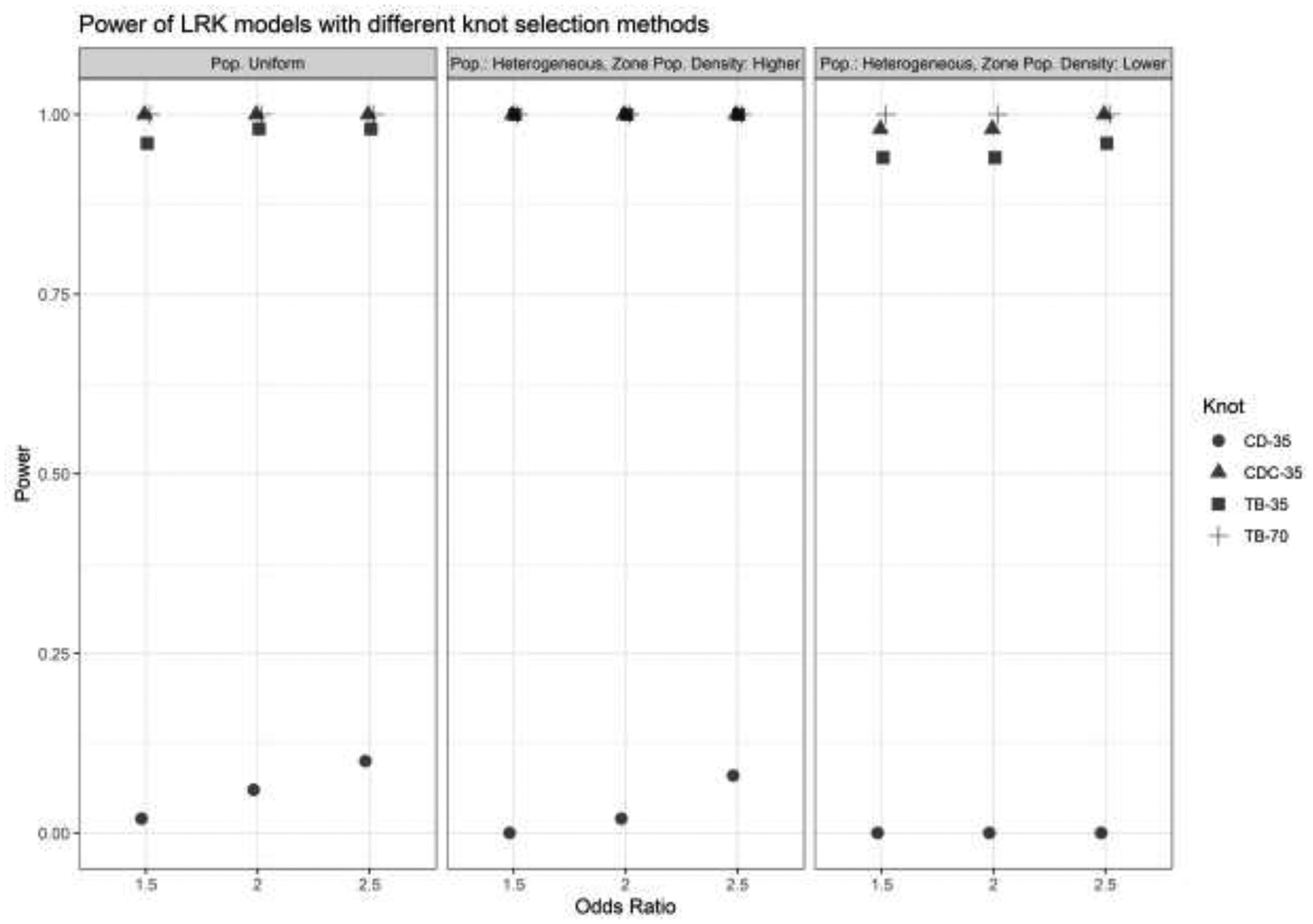
Power of LRK models with different knot selection methods and numbers of knots. OR = Odds Ratio, LPD = Low Population Density, CD = cover.design(), CD Cases = cover.design() on case locations, T-B = Teitz and Bart.

Comparison of the number of knots.

Results from the analysis of varying the number of knots used for Teitz and Bart knot selection are shown in Figure 5. Each metric improved as knots were added, until approximately the number of cases in the generated population (57) was reached. After this point, most metrics either did not improve or did so by a nominal amount, and for the highest numbers of knots, spatial sensitivity actually slightly decreased. For these high numbers of knots, candidate knot locations in the algorithm moved towards case locations quickly, leaving many of the remaining knots unchanged from their random initial configuration, which may have been in areas that did not provide value in model estimation. This suggests that placing knots very close to as many case locations as possible leads to improved model performance, but beyond this, false regions of elevated risk may be detected, and there is less value in increasing the number of knots.

Figure 5.

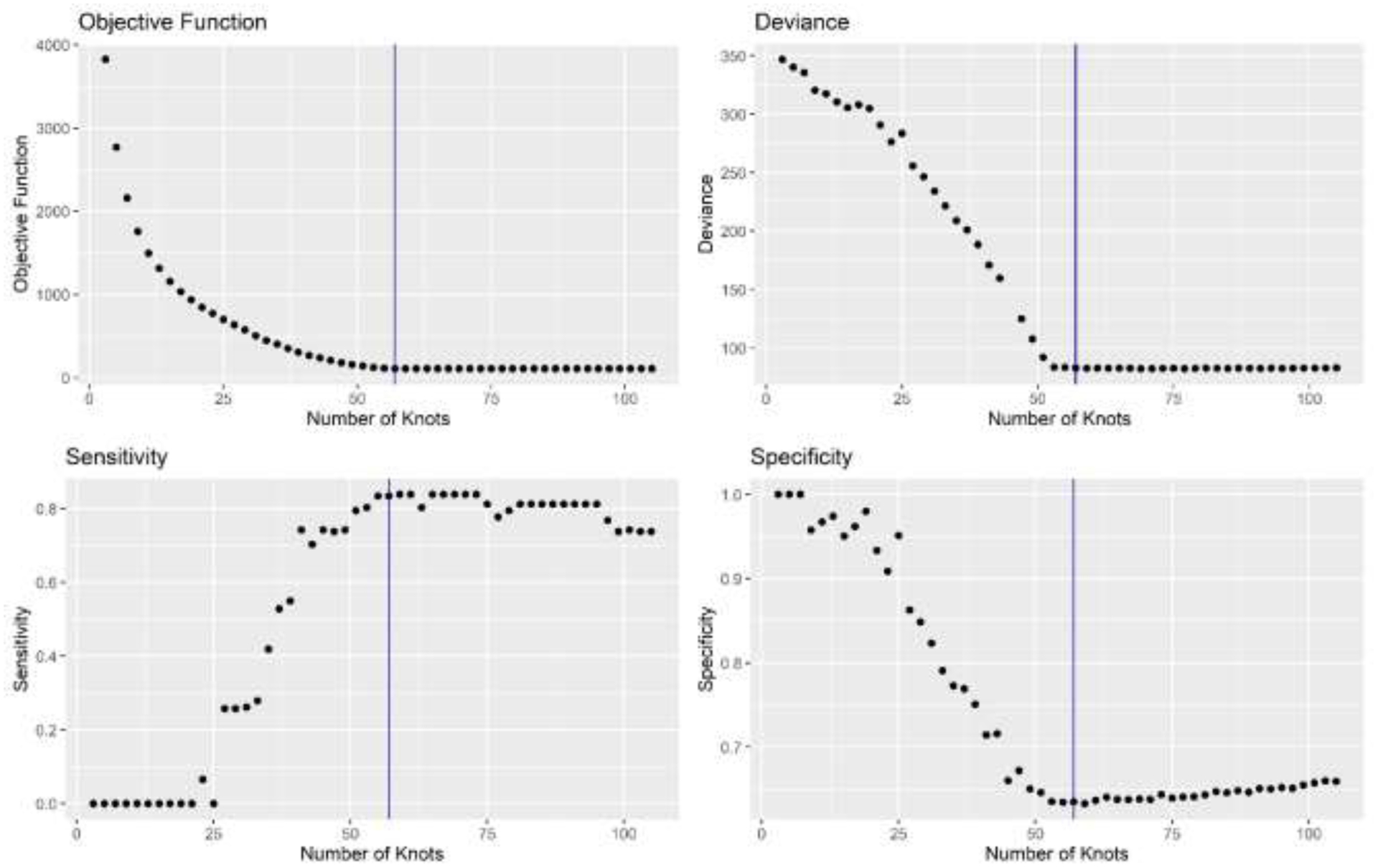
Varying the number of knots in one simulated population using the Teitz and Bart method of knot selection. Vertical line indicates the number of cases in the population.

Discussion:

In this study, we evaluated the adequacy of the commonly-used method of knot selection, the space-filling algorithm, in LRK models of disease risk for case-control data. Because this method was motivated for use with point-referenced data, predicting a continuous outcome variable, its performance in case-control studies had not been established. Through an extensive simulation study, generating many realizations of cases and control locations over a study region varying in population distribution and location of a zone of elevated spatial risk for disease, we found substantial evidence that the space-filling algorithm is suboptimal for case-control studies. It had extremely low sensitivity to detect zones of elevated risk and, correspondingly, very low power to detect any part of such zones. This has considerable implications for its use in future analyses of case-control data. Given such low power, the use of this method in such analyses likely prohibits the finding of significant disease clusters when they exist.

In contrast, use of either of the two proposed methods that considered case location in choosing knot locations provided a significant boost to spatial sensitivity and power. These methods, which included the simple modification to the space-filling algorithm of only considering case locations, and the Teitz and Bart heuristic, detected approximately half or more of the defined zone of elevated risk as such, which entailed finding a significant disease cluster that would warrant further follow-up in analyses of real data. Given the relative rarity of cases in our simulations, as well as the small odds ratios of case membership for those living in the zone of elevated risk, the performance of the LRK models with these methods is encouraging. For disease processes with a stronger spatial signal, results would likely improve further. The lowest-performing group of scenarios occurred when the cases and controls were generated from a heterogeneous population distribution, and the zone was located in a region of lower population density. This illustrates the challenges of finding significant disease clusters in low-density areas. Such difficulty of geographically varying power over a heterogeneous population distribution has been noted before (Waller, Hill, et al.), largely due to small local sample sizes to detect increases in spatial risk. The Teitz and Bart heuristic was the best-performing method of those considered, suggesting that the operations research problem of minimizing distance from clients to their closest facilities is analogous to that of accurately estimating spatial risk where it is more likely to exist by placing knot locations as close as possible to the spatial distribution of cases in the study. Thus, we recommend its use in analyses of case-control data, when LRK models are used and knot locations must be selected.

Model performance generally improved as the number of knots used in the LRK model increased, as evidenced by the overall simulation results as well as the analysis of varying the number of knots on one generated population. Once the number of knots was approximately equal to the number of cases in the study sample, however, performance did not increase. This suggests that, as computation time allows, one should choose a number of knots as close as possible to the number of case locations, but greater than the number of cases is not needed. This is distinct from other guidance regarding the number of knots, such as the 35 to 40 knots recommended to predict responses over a Gaussian random field (Kim et al.).

To our knowledge, this is the first study that analyzes knot selection in low-rank kriging models of case-control data. Our results demonstrate that, when using the low-rank kriging model, the knot selection method used should reflect the study design. The space-filling method has been used in several studies of point-referenced data modeling continuous outcome variables, including simulations over a grid (Kim et al.), measurements of mercury in estuarine environments (Wang and Ranalli), and measurements of lead in soil surrounding a river basin (Lee and Toscas). The fixed sample locations in these studies allowed the use of a spatially representative subset of the sample points. However, when the study design is different, specifically a marked point process here, the nature of the points differs with respect to case status. Thus, the space-filling algorithm, which treats all locations equally, should not be used. Rather, a method that considers the case status in choosing knot locations, such as either of our two proposed methods, should be used. These methods demonstrated an ability to detect zones of elevated risk underlying case status that the space-filling algorithm could not.

Three other important factors in the analysis of case-control data are covariates, disease latency, and the selection of cases and controls. First, if covariates are known or suspected to be associated with the outcome, they should be included in the spatial regression model. We did not focus on covariates in this study, instead assuming that the only factor associated with case membership was geographic proximity to a zone of elevated risk. Future research can investigate the effect of spatially structured and/or unstructured covariates on the performance of these models to detect disease clusters. Second, latency is relevant in case-control studies when individuals were exposed to processes that heighten risk for disease years before their inclusion in the study. In such cases, residential location at study entry may be a poor proxy for locations of high-intensity disease exposure, if populations are mobile and participants have moved locations between their exposure and the study entry. In future work, we will evaluate the ability of spatial models to estimate cumulative spatial risk that incorporate participants’ residential histories, not just their locations at one timepoint. Finally, our simulation study operated under the assumptions that all cases in the study region were observed and used in modeling, and that controls represented the at-risk population. Future research could investigate the effects on the accuracy of spatial risk estimates of differential probabilities of case reporting, as well as of the selection of controls in the sample that do not perfectly represent the spatial distribution of the at-risk population.

Highlights:

• Proposed two new approaches for knot selection in low-rank kriging models.

• Compared three knot selection approaches for low-rank kriging models.

• The commonly-used space-filling algorithm is suboptimal for case-control studies.

• Proposed methods increase the sensitivity and power to detect regions of risk.

• It is advised to use a number of knots approaching the number of cases in the study.