A Multi-Scale Spatial and Temporal Attention Network on Dynamic Connectivity to Localize The Eloquent Cortex in Brain Tumor Patients

Abstract

We present a deep neural network architecture that combines multi-scale spatial attention with temporal attention to simultaneously localize the language and motor areas of the eloquent cortex from dynamic functional connectivity data. Our multi-scale spatial attention operates on graph-based features extracted from the connectivity matrices, thus honing in on the inter-regional interactions that collectively define the eloquent cortex. At the same time, our temporal attention model selects the intervals during which these interactions are most pronounced. The final stage of our model employs multi-task learning to differentiate between the eloquent subsystems. Our training strategy enables us to handle missing eloquent class labels by freezing the weights in those branches while updating the rest of the network weights. We evaluate our method on resting-state fMRI data from one synthetic dataset and one in-house brain tumor dataset while using task fMRI activations as ground-truth labels for the eloquent cortex. Our model achieves higher localization accuracies than conventional deep learning approaches. It also produces interpretable spatial and temporal attention features which can provide further insights for presurgical planning. Thus, our model shows translational promise for improving the safety of brain tumor resections.

1. Introduction

The eloquent cortex consists of regions in the brain that are responsible for language and motor functionality. Neurosurgical procedures are carefully planned to avoid these regions in order to minimize postoperative deficits [1]. However, it can be difficult to accurately localize the eloquent cortex due to its varying anatomical boundaries across people [2]. The language network has especially high interindividual variability and can appear on one or both hemispheres [3]. The gold standard for preoperative mapping of the eloquent areas is intraoperative electrocortical stimulation (ECS) [1]. While reliable, ECS requires the patient to be awake and responsive during surgery and it carries much greater risk when performed on obese patients or individuals with respiratory problems [4]. For these reasons, task-fMRI (t-fMRI) has emerged as a noninvasive complement to ECS [5]. However, t-fMRI activations are unavailable for certain populations, like young children, the cognitively impaired, or aphasic patients, due to excessive head motion or an inability to perform the task protocol [6]. Resting-state fMRI (rs-fMRI) is an alternative modality that captures spontaneous fluctuations in the brain when the subject is awake and at rest. In contrast to t-fMRI paradigms, which are designed to activate an isolated cognitive region, rs-fMRI correlations can be used to simultaneously identify multiple cognitive systems [7]. Thus, rs-fMRI is an exciting alternative to t-fMRI activations for localizing sub-regions associated with the eloquent cortex [6,8,9].

Prior work that uses rs-fMRI for eloquent cortex localization can be broadly divided into three categories [10]. In the simplest case, a seed region of interest (ROI) is used to identify highly-correlated voxels in the eloquent cortex [11,12]. A more sophisticated method uses independent component analysis (ICA) to delineate functionally coherent systems in the brain, from which the eloquent networks can be identified [13,14]. While promising, these methods require expert intervention, either via the choice of seed ROI or the component selection. Furthermore, early studies are limited by the tremendous variability of rs-fMRI data. In fact, the works of [13,14] reveal highly variable accuracies across a large patient cohort (N > 50), particularly when mapping the language network.

The use of deep learning has fueled interest in end-to-end methods for eloquent cortex localization. For example, the work of [15] has proposed a multilayer perceptron that classifies voxels of the rs-fMRI data into one of seven functional systems based on seed correlation maps; this method was extended in [16] to handle tumor cases. While the perceptron has high sensitivity across several patients, its specificity is not quantified. Also, since the perceptron is trained on healthy subjects, it cannot account for neural plasticity effects from to the tumor. The authors of [8] propose the first end-to-end graph neural network (GNN) that leverages functional connectivity to localize a single eloquent subsystem. While the GNN outperforms a perceptron architecture, separate GNNs must be trained and evaluated for each eloquent area, which requires more data and longer training times. In addition, the GNN specificity is quite low, particularly for language. Finally, the work of [9] extends the original GNN to track dynamic connectivity changes associated with the eloquent cortex. However, the language localization accuracy and specificity are too low for clinical practice.

Recent work in the deep learning literature has introduced the idea of spatial attention, which mimics information processing in the human visual system. For example, a 2D spatial attention model learns where in the image to focus, thus improving the quality of the learned representations [17]. The notion of attention has been extended to the time domain in applications such as video processing [18]. In line with these works, we develop a spatiotemporal attention model to localize eloquent cortex from dynamic whole-brain rs-fMRI connectivity matrices. Unlike a 2D image, our “spatial” field corresponds to salient interactions in connectivity data, captured via graph-based convolutional filters. Our multi-scale spatial attention model pools three levels of granularity to amplify important interactions and suppress unnecessary ones. Then, our temporal attention mechanism selects key intervals of the dynamic input that are most relevant for either language or motor localization. Our model operates on a fine resolution parcellation and can handle missing training labels. We use t-fMRI activations as ground truth labels and validate our framework on rs-fMRI data from 100 subjects in the publicly available Human Connectome Project (HCP) [19] with artificially-inserted tumors as well as 60 subjects from an in-house dataset. Our model uniformly achieves higher localization accuracies than competing baselines. Our attention mechanisms learn interpretable feature maps, thus demonstrating the promise of our model for preoperative mapping.

2. A Multi-Scale Spatial and Temporal Attention Network to Localize the Eloquent Cortex

Our framework assumes that while the anatomical boundaries of the eloquent cortex may shift across individuals, its resting-state functional connectivity with the rest of the brain will be preserved [14]. Adding a layer of complexity, the eloquent cortex represents a relatively small portion of the brain. This is the motivation for our spatial attention mechanism, i.e., to zone in on the key connectivity patterns. Furthermore, the networks associated with the eloquent cortex will likely phase in and out of synchrony across the rs-fMRI scan [9]. Our temporal attention mechanism will track these changes. Fig. 1 shows our overall framework. As seen, we explictly model the tumor in our dynamic similarity graph construction and feed this input into a deep neural network which uses specialized convolutional layers designed to handle connectome data [20].

Fig. 1.

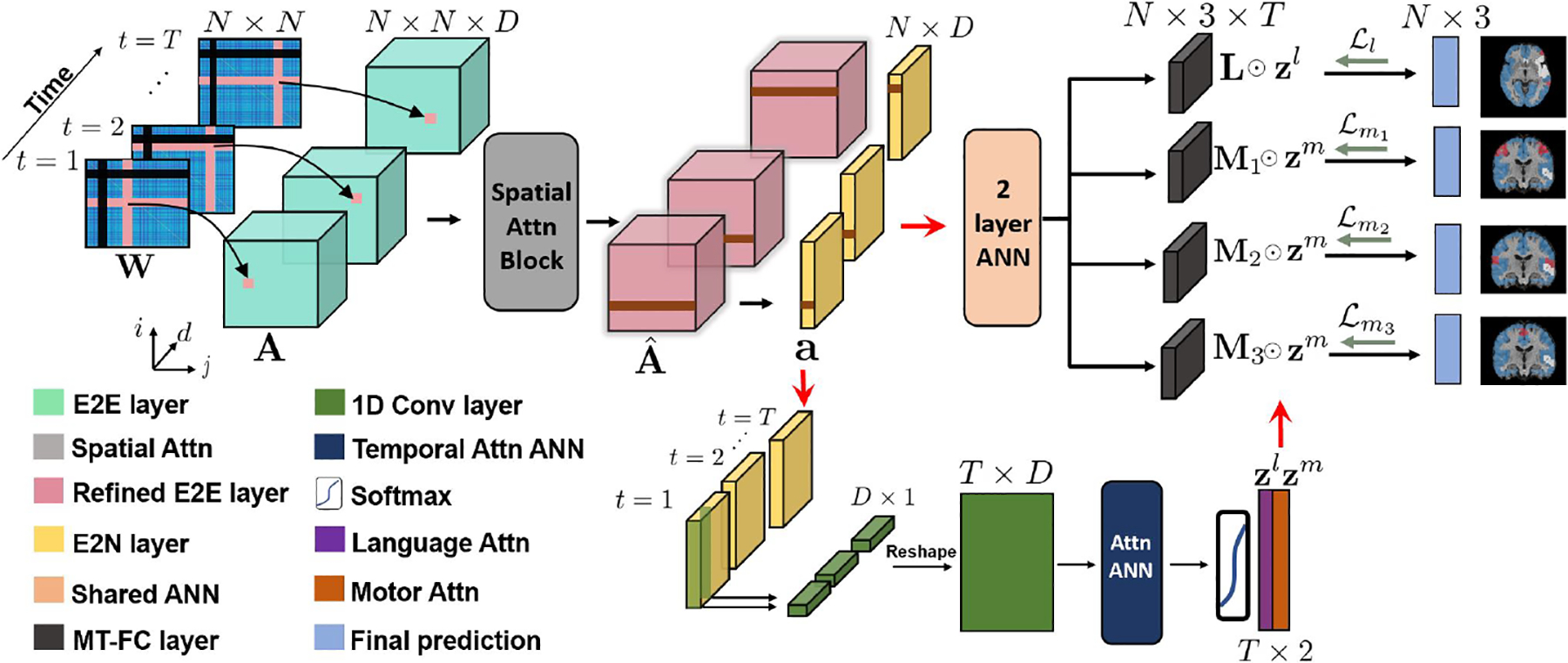
Top: Convolutional features extracted from dynamic connectivity are refined using a multi-scale spatial attention block. Bottom: The dynamic features are input to an ANN temporal attention network to learn weights z^l (language) and z^m (motor). Right: Multi-task learning to classify language (L), finger (M₁), tongue (M₂), and foot (M₃) subnetworks, where each subnetwork is a 3-class classification which is shown in red, white, and blue respectively on segmentation maps.

2.1. Input Dynamic Connectivity Matrices

We use the sliding window technique to construct our dynamic inputs [21]. Let N be the number of brain regions in our parcellation, T be the total number of sliding windows (i.e., time points in our model), and ${\left\{W^t\right\}}_{t=1}^T\in {ℝ}^{N\times N}$ be the dynamic similarity matrices. W^t is constructed from the normalized input time courses, ${\left\{X^t\right\}}_{t=1}^T\in {ℝ}^{G\times N}$ where each X^t is a segment of the rs-fMRI obtained with window size G. Formally, the input $W^t\in {ℝ}^{N\times N}$ is

$$W^t=\text{exp}\left[{\left(X^t\right)}^T{X}^t-1\right].$$ (1)

Our setup must also accomodate for the presence of brain tumors that vary across patients and are generally believed to represent non-functioning areas of the brain. Therefore, we follow the approach of [8,9] and treat the corresponding rows and columns of the simlarity matrix as “missing data” and fixing them to zero (shown by black bars in LHS of Fig. 1).

2.2. Multi-scale Spatial Attention on Convolutional Features

Our network leverages the specialized convolutional layers developed in [20] for feature extraction on each of the dynamic inputs. The edge-to-edge (E2E) filter (pink in Fig. 1) acts across rows and columns of the input matrix W^t. This cross-shaped receptive field can accommodate node reordering, and it mimics the computation of graph theoretic measures. Mathematically, let d ∈ {1,···,D} be the E2E filter index, $r^d\in {ℝ}^{1\times N}$ be the row filter d, $c^d\in {ℝ}^{N\times 1}$ be the column filter d, $b\in {ℝ}^{D\times 1}$ be the E2E bias, and φ(.) be the activation function. For each time point t the feature map $A^{d,t}\in {ℝ}^{N\times N}$ is computed as follows:

$$A_{i,j}^{d,t}=\varphi \left(W_{i,:}^t{\left(r^d\right)}^T+{\left(c^d\right)}^T{W}_{:,j}^t+b_d\right).$$ (2)

The E2E filter output $A_{\mathit{\text{ij}}}^{d,t}$ for edge (i, j) extracts information associated with the connectivity of node i and node j with the rest of the graph. We use the same D E2E filters {r^d, c^d} for each time point to standardize the feature computation.

Fig. 2 illustrates our multi-scale spatial attention model. The attention model acts on the E2E features and implicitly learns “where” informative connectivity hubs are located for maximum downstream class separation. The multi-scale setup uses filters of different receptive field sizes to capture various levels of connectivity profiles within the E2E features [22]. Following [17], we apply an average pooling and max pooling operation along the feature map axis and concatenate them to generate an efficient feature descriptor. Mathematically,

$$H_{\text{avg}}=\frac{1}{\mathit{\text{DT}}}\sum _{d=1}^D\sum _{t=1}^T{A}^{d,t}$$ (3)

is the N × N average pool features and

$$H_{\text{max}}^{i,j}=\underset{d,t}{\text{max}}{A}_{i,j}^{d,t}$$ (4)

is the N × N max pool features. Note that we extract the maximum and average activations across all feature maps and time points simultaneously. We then apply a multi-scale convolution to this feature descriptor, which implicitly identifies the deviation of the maximum activation from the neighborhood average, thus highlighting informative regions to aid in downstream tasks [23].

Fig. 2.

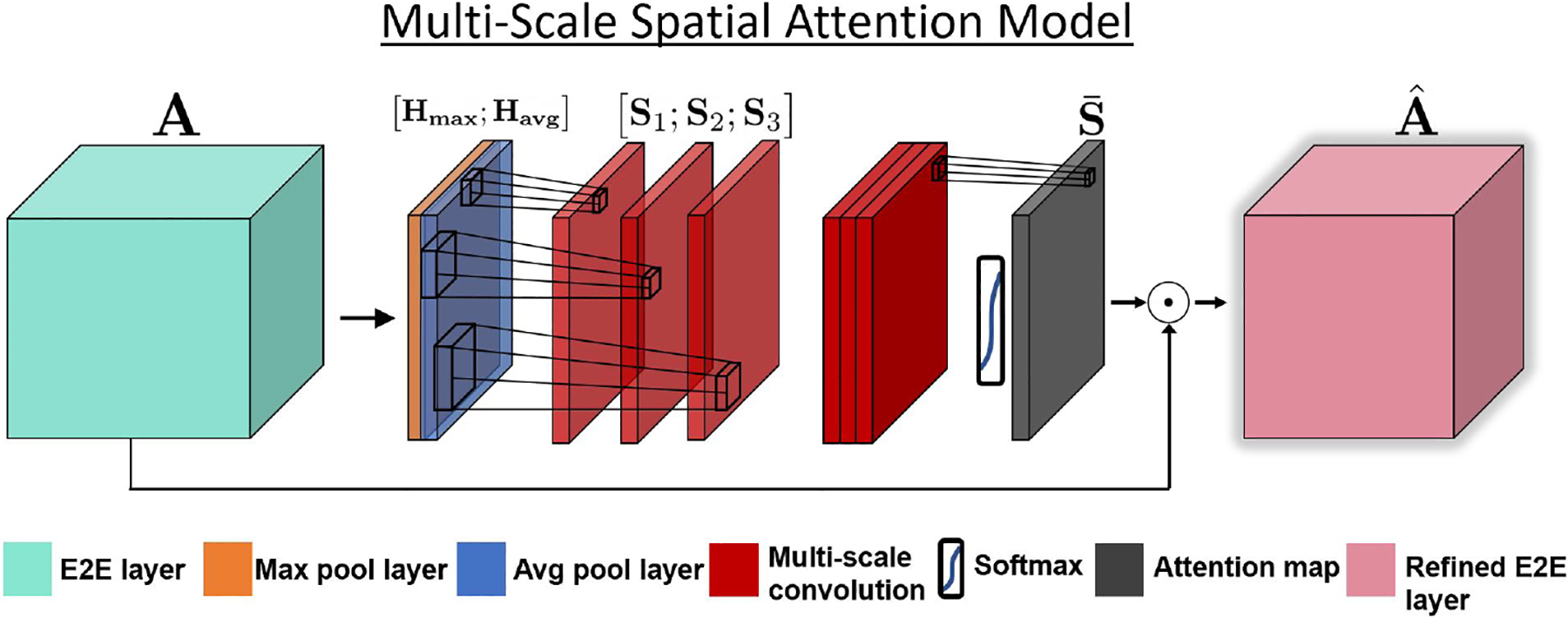
Our multi-scale spatial attention model extracts features from max pool and average pool features along the channel dimension. We use separate convolutional filters with increasing receptive field size to extract multi-scale features, and use a 1 × 1 convolution and softmax to obtain our spatial attention map $\overline{S}$. This map is element-wise multiplied along the channel dimension of the original E2E features.

We apply three separate convolutions with increasing filter sizes to the concatenated feature descriptor to obtain different scales of resolution of our analysis. The convolution outputs S₁, S₂ and $S_3\in {ℝ}^{N\times N}$ are computed using a 3 × 3, 7 × 7, and 11 × 11 kernel, respectively, on the concatenated maps [H_avg;H_max]. The convolutions include zero padding to maintain dimensionality. Each successive convolutional filter has an increasing receptive field size to help identify various connectivity hubs within the E2E layer. We obtain our spatial attention map $\overline{S}\in {ℝ}^{N\times N}$ with an element-wise softmax operation on the weighted summation, derived using a 1×1 convolution with bias b, across the three scales;

$$\overline{S}=\text{Softmax}\left(\sum _{i=1}^3{w}_i{S}_i+b\right).$$ (5)

This weighted combination is designed to highlight salient hubs in the network which appear across different spatial scales. The softmax transforms our attention into a gating operation, which we use to refine our convolutional features A^d,t by element-wise multiplication with $\overline{S}$. Let ☉ denote the Hadamard product. The refined features ${\widehat{A}}^{d,t}\in {ℝ}^{N\times N}$ are computed as

$${\widehat{A}}^{d,t}=A^{d,t}\odot \overline{S}.$$ (6)

Finally, we condense our representation along the column dimension by using the edge-to-node (E2N) filter [20]. Our E2N filter (brown in Fig. 1) performs a 1D convolution along the columns of each refined feature map to obtain region-wise representations. Mathematically, let $g^d\in {ℝ}^{N\times 1}$ be E2N filter d and $p\in {ℝ}^{D\times 1}$ be the E2N bias. The E2N output $a^{d,t}\in {ℝ}^{N\times 1}$ from input ${\widehat{A}}^{d,t}$ is computed as

$$a_i^{d,t}=\varphi \left({\widehat{A}}_{i,:}^{d,t}{g}_n^d+p_d\right).$$ (7)

Again, we apply the same E2N filters to each time point. At a high level, the E2N computation is similar to that of graph-theoretic features, such as node degree. The E2N outputs are fed into both the temporal attention model (bottom branch of Fig. 1) and the multi-task node classifier (right branch of Fig. 1).

2.3. Temporal Attention Model and Multi-task Learning

We use a 1D convolution to collapse the region-wise information into a low dimensional vector for our temporal attention network. Let $k^d\in {ℝ}^{N\times 1}$ be the weight vector for filter d and $j\in {ℝ}^{D\times 1}$ be the bias across all filters. A scalar output q^d,t for each input a^d,t is obtained

$$q^{d,t}=\varphi \left({\left(k^d\right)}^T{a}^{d,t}+j_d\right).$$ (8)

The resulting T × D matrix [q^d,t]^T is fed into a fully-connected layer of two perceptrons with size D to extract our temporal attention weights. We obtain one language network attention vector $z^l\in {ℝ}^{T\times 1}$ and one motor network attention vector $z^m\in {ℝ}^{T\times 1}$, which learn the time intervals during which the corresponding eloquent subnetwork is more identifiable. The FC attention model is more flexible than a recurrent architecture and can be easily trained on small clinical datasets (<100 subjects). We observed that the FC attention shows a good trade-off between representation and robustness to training with a limited sample size.

In parallel, the top branch of Fig. 1 applies a cascade of two FC layers to the E2N topological features for our downstream multi-task classification. In this work, we are interested in identifying four separate sub-regions of the eloquent cortex, as depicted by the multi-task FC (MT-FC) layers in Fig. 1. Let L^t, $M_1^t$, $M_2^t$, and $M_3^t\in {ℝ}^{N\times 3}$ be the output of the language, finger, foot, and tongue MT-FC layers, respectively, at time t. We consolidate information along the time axis using an element-wise multiplication with our temporal attention vectors, as shown in our loss function below. The N × 3 matrix represents the region-wise assignment into one of three classes; eloquent, tumor, and background, where the tumor class is introduced to disentangle the effect that the zero entries have on learning the eloquent class.

We use a weighted cross-entropy loss function which is designed to handle membership imbalance in multi-class problems. Let δ_c be the risk factor associated with class c. If δ_c is small, then we pay a smaller penalty for misclassifying samples that belong to class c (c = 1, 2, 3). Since the language network is generally smaller than the motor network, we set different values for the language class $\left\{{\delta }_c^l\right\}$ and motor classes $\left\{{\delta }_c^m\right\}$ respectively. Let Y^l, Y^m1, Y^m1, and $Y^{m_3}\in {ℝ}^{N\times 3}$ be one-hot encoding matrices for the ground-truth class labels of the language and motor subnetworks. Our loss function is the sum of four terms:

$$\begin{gathered} {\mathcal{L}}_{\Theta }\left({\left\{W^t\right\}}_{t=1}^T,Y\right)=\sum _{n=1}^N\sum _{c=1}^3[\underset{\text{Language}\text{Loss}{\mathcal{L}}_l}{\underbrace{-{\delta }_c^l\text{log}\left(\sigma \left(\sum _{t=1}^T{L}_{n,c}^t\cdot z^{l,t}\right)\right)Y_{n,c}^l}} \\ \underset{\text{Finger}\text{Loss}{\mathcal{L}}_{m_1}}{\underbrace{-{\delta }_c^m\text{log}\left(\sigma \left(\sum _{t=1}^T{M}_{1n,c}^t\cdot z^{m,t}\right)\right)Y_{n,c}^{m_1}}}\underset{\text{Foot}\text{Loss}{\mathcal{L}}_{m_2}}{\underbrace{-{\delta }_c^m\text{log}\left(\sigma \left(\sum _{t=1}^T{M}_{2n,c}^t\cdot z^{m,t}\right)\right)Y_{n,c}^{m_2}}} \\ \underset{\text{Tongue}\text{Loss}{\mathcal{L}}_{m_3}}{\underbrace{-{\delta }_c^m\text{log}\left(\sigma \left(\sum _{t=1}^T{M}_{3n,c}^t\cdot z^{m,t}\right)\right)Y_{n,c}^{m_3}]}} \end{gathered}$$ (9)

where σ(·) is the sigmoid function. Our loss in Eq. (12) allows us to handle missing patient training labels for the eloquent subsystems across patients. Specifically, we freeze the branches corresponding to missing data and backpropagate the known loss terms. This backpropagation technique will refine the shared layers prior to the MT-FC layer, thus maximizing the information used from our training data. Our model is flexible to handle any number of functional systems by changing the number of MT-FC layers and kernels in the temporal attention.

Implementation details.

We implement our network in PyTorch using the SGD optimizer with weight decay = 5 × 10⁻⁵ for parameter stability, and momentum = 0.9 to improve convergence. We train our model with learning rate = 0.005 and 140 epochs, which provides for reliable performance without over-fitting. We specified D = 50 feature maps in the convolutional branch. The LeakyReLU with slope = −0.1 was used for φ(.).

We compare the performance of our model against three baselines:

1. Random forest on dynamic connectivity matrices (RF)

2. A fully-connected network with temporal attention (FC-tANN)

3. Same as proposed without spatial attention (w/o sp. attn.)

The first baseline is a traditional machine learning RF approach to our problem. The FC-tANN maintains the same number of parameters as our model but has fully-connected layers instead of convolutional layers. Finally, we compare against our same architecture without spatial attention to observe the performance gain of focusing on different neighborhoods. To avoid biasing performance, we selected the hyperparameters using a development set of 100 subjects downloaded from the Human Connectome Project (HCP). The final settings are: δ^m = (1.48, 0.44, 0.18), δ^l = (2.16, 0.44, 0.18) for proposed, δ^m = (1.57, 0.42, 0.22), δ^l = (2.31, 0.42, 0.22) for FC-tANN and δ^m = (1.51, 0.46, 0.19), δ^l = (2.22, 0.46, 0.19) for w/o sp. attn.

3. Experimental Results

3.1. Dataset and Preprocessing

We evaluate the methods on rs-fMRI data from an additional HCP cohort [19] in which we artificially insert “fake tumors” by zeroing out entries of the connectivity matrix, and an in-house brain tumor dataset. All subjects underwent t-fMRI scanning, which we use to derive pseudo ground-truth labels for the language, finger, tongue and foot subnetworks. Fig. 3 shows each of the cognitive networks of interest. Details on the acquisition paramters, sequencing, and preprocessing of the HCP dataset can be found in [19].

Fig. 3.

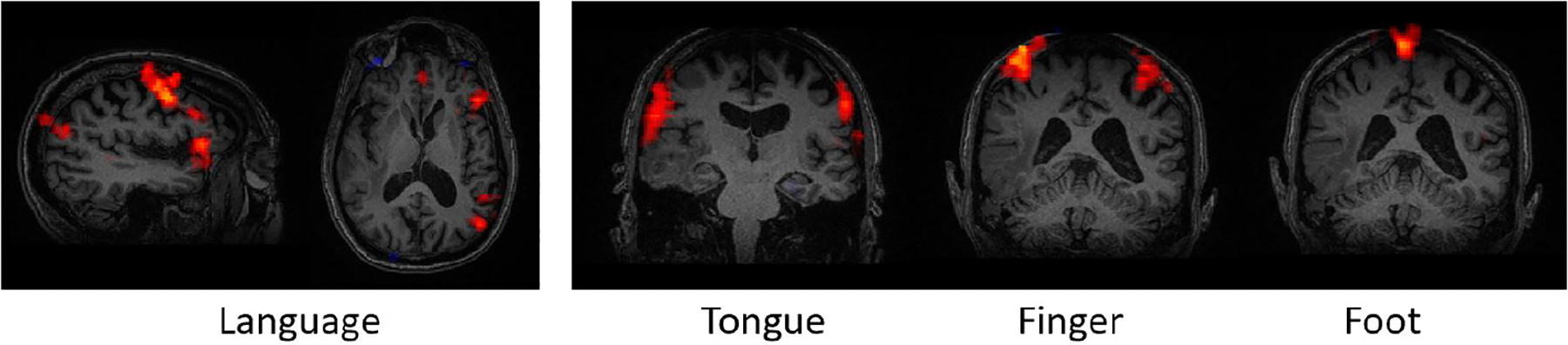
Left: One sagital and axial view of a language network. Right: Coronal views of the motor sub-networks for one patient.

Our in-house tumor dataset contains 60 patients. Since the t-fMRI data was acquired for clinical purposes, not all patients in the in-house dataset performed each task. The number of subjects that performed the tasks are displayed in the left column of Table 1. The fMRI data was acquired using a 3.0 T Siemens Trio Tim (TR = 2000 ms, TE = 30 ms, FOV = 24 cm, res = 3.59 × 3.59 × 5 mm). Preprocessing steps include slice timing correction, motion correction and registration to the MNI-152 template. The rs-fMRI was further bandpass filtered from 0.01 to 0.1 Hz, spatially smoothed with a 6 mm FWHM Gaussian kernel, scrubbed using the ArtRepair toolbox [24] in SPM8, linearly detrended, and underwent nuisance regression using the CompCor package [25]. A general linear model implemented in SPM8 was used to obtain t-fMRI activation maps.

Table 1.

Overall accuracy, and ROC statistics. The number in the second column indicates number of patients who performed the task.

Dataset	Task	Method	Accuracy	Sens.	Spec.	F1	AUC
HCP	Language (100)	RF	0.58	0.32	0.55	0.42	0.5
		FC-tANN	0.65	0.61	0.58	0.59	0.64
		w/o Sp. Attn.	0.77	0.73	0.68	0.69	0.72
		Proposed	0.83	0.79	0.81	0.82	0.80
	Finger (100)	RF	0.70	0.53	0.67	0.64	0.56
		FC-tANN	0.76	0.70	0.72	0.73	0.72
		w/o Sp. Attn.	0.87	0.83	0.78	0.80	0.86
		Proposed	0.91	0.86	0.85	0.85	0.88
	Foot (100)	RF	0.67	0.48	0.65	0.62	0.53
		FC-tANN	0.79	0.77	0.69	0.73	0.76
		w/o Sp. Attn.	0.86	0.86	0.83	0.84	0.85
		Proposed	0.90	0.87	0.86	0.86	0.88
	Tongue (100)	RF	0.70	0.46	0.68	0.63	0.53
		FC-tANN	0.75	0.72	0.68	0.72	0.73
		w/o Sp. Attn.	0.81	0.83	0.80	0.81	0.81
		Proposed	0.89	0.87	0.85	0.85	0.86
In-house	Language (60)	RF	0.65	0.40	0.66	0.59	0.53
		FC-tANN	0.78	0.76	0.70	0.71	0.73
		w/o Sp. Attn.	0.84	0.85	0.74	0.79	0.82
		Proposed	0.93	0.91	0.85	0.87	0.91
	Finger (36)	RF	0.67	0.43	0.67	0.61	0.55
		FC-tANN	0.76	0.75	0.69	0.71	0.77
		w/o Sp. Attn.	0.88	0.88	0.79	0.82	0.85
		Proposed	0.91	0.88	0.85	0.84	0.89
	Foot (17)	RF	0.68	0.49	0.65	0.60	0.56
		FC-tANN	0.79	0.73	0.68	0.72	0.75
		w/o Sp. Attn.	0.86	0.86	0.78	0.80	0.82
		Proposed	0.89	0.87	0.83	0.84	0.86
	Tongue (39)	RF	0.69	0.38	0.70	0.64	0.52
		FC-tANN	0.79	0.78	0.71	0.74	0.76
		w/o Sp. Attn.	0.86	0.85	0.77	0.81	0.84
		Proposed	0.90	0.87	0.82	0.84	0.87

We used the Schaefer atlas to obtain N = 1000 brain regions [26], which is on par with the resolution of eloquent areas we are trying to detect. Tumor boundaries for each patient were manually delineated by a medical fellow using the MIPAV software package [27]. The fake tumors added to the HCP dataset are randomly positioned but created to be spatially continuous with the same size as the real tumor segmentations we obtained from the in-house dataset. An ROI was determined as belonging to the eloquent class if a majority of its voxel membership coincided with that of the t-fMRI activation map. Tumor labels were determined in a similar fashion according to the MIPAV segmentations.

3.2. Localization Results

We use 10-fold cross-validation to evaluate each method. Table 1 shows the performance metrics for detecting the eloquent class. In the second column, the number next to the task refers to the number of subjects whom we have training labels. As highlighted in bold, our proposed method outperforms the baseline algorithms in nearly all cases. We observe that the spatial attention model improves the specificity by improving the ratio of true negatives to false positives. Our performance gains are most notable regarding the language network, which is arguably the most challenging rea to localize during preoperative mapping. Fig. 4 shows the ground truth (blue) and predicted (yellow) for all four systems in a challenging bilateral language subject, with both the proposed and w/o spatial attention methods. The model without spatial attention overpredicts the right-hemipshere language nodes, and misses various parts of the motor strip. Our model can localize functional regions right on the tumor boundary that the baseline method misses as well, which is relevant for clinical practice.

Fig. 4.

Ground truth (blue) and predicted (yellow) for a bilateral language subject.

3.3. Feature Analysis

To better understand how the attention models improve the localization performance, Fig. 5 illustrates the spatial attention (left) and temporal attention weights (right) for our in-house dataset. These plots are generated by summing across the rows of the attention map $\overline{S}$ and plotting the top ten nodes in one unilateral language and one bilateral language case. The spatial attention model is accurately able to capture right hemisphere activation in the bilateral case while correctly omitting this region in the unilateral case. This lateralization ability may be why localization performance increases for the language network. On the right-hand side of Fig. 5, we show the temporal attention weights for both language and motor networks across all patients and time. The language and motor networks phase in and out at different times, which improves localization by identifying important time intervals within the scan for each network.

Fig. 5.

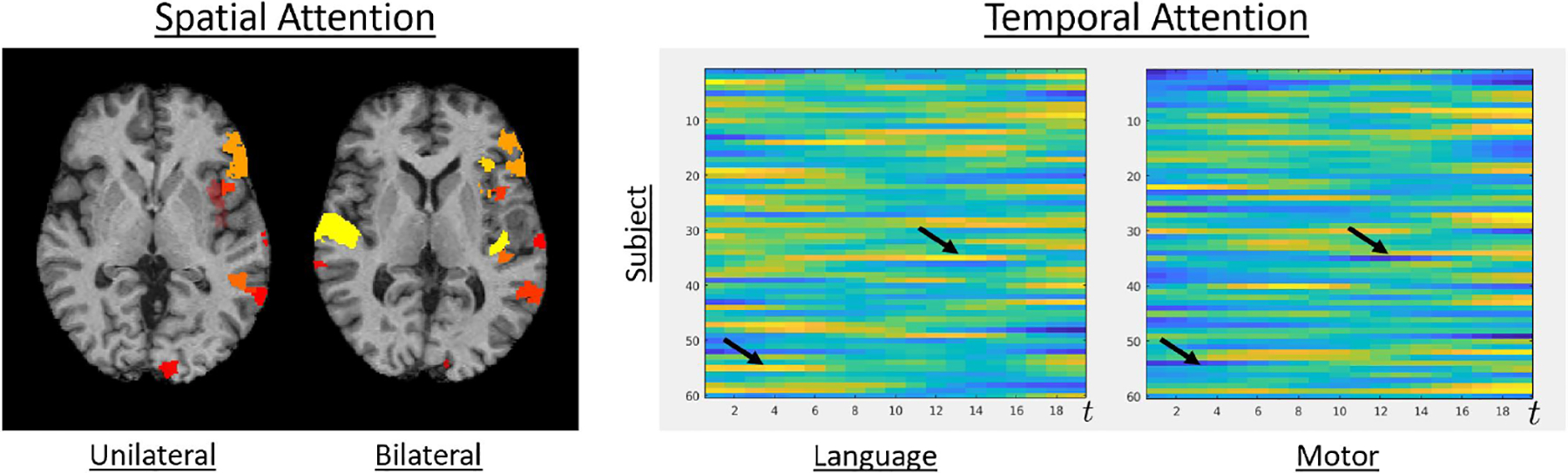
Left: Heat map for the nodes with highest total spatial attention for a unilateral and a bilateral language subject. Right: Temporal attention weights for language and motor networks. The black arrows indicate networks phasing in and out with each other.

4. Conclusion

We present a novel deep learning framework that leverages specialized convolutional layers, multi-scale spatial attention, temporal attention, and multi-task learning to identify critcal regions of the eloquent cortex in tumor patients using dynamic resting-state connectivity. We validate our method on a real in-house dataset and a synthetic dataset to show generalizability of our method. We outperform machine and deep learning baselines by a large margin. Finally, we show the spatial and temporal attention features, which can be important biomarkers for simultaneous language and motor network identification. Future work includes exploring different pooling operations to improve atlas selection. Taken together, our results show promise for using rs-fMRI for presurgical planning of resection procedures.