Delta Machine Learning to Improve Scoring-Ranking-Screening Performances of Protein-Ligand Scoring Functions

Abstract

Protein-ligand scoring functions are widely used in structure-based drug design for fast evaluation of protein-ligand interactions, and there is of strong interest to develop scoring functions with machine learning approaches. In this work, by expanding the training set, developing physically meaningful features, employing our recently developed linear empirical scoring function Lin_F9 (J. Chem. Inf. Model. 2021, 61, 4630 – 4644) as the baseline, and applying extreme gradient boosting (XGBoost) with $\mathrm{\Delta }$-machine learning, we have further improved robustness and applicability of machine-learning scoring functions. Besides the top performances for scoring-ranking-screening power tests of CASF-2016 benchmark, the new scoring function ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ also achieves superior scoring and ranking performances in different structure types that mimic real docking applications. The scoring power of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ for locally optimized poses, flexible re-docked poses and ensemble docked poses of CASF-2016 core set achieve Pearson’s correlation coefficient (R) of 0.853, 0.839 and 0.813, respectively. In addition, large-scale docking-based virtual screening test on LIT-PCBA dataset demonstrates the reliability and robustness of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ in virtual screening application. The ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ scoring function and its code are freely available on the web at: (https://yzhang.hpc.nyu.edu/Delta_LinF9_XGB)

Graphical Abstract

INTRODUCTION

Molecular docking is one of widely utilized computational tools for structure-based drug discovery that attempts to predict the ligand binding pose and provide an estimate of binding affinity for protein-ligand complex.^1–3 The most critical component of docking is the scoring function, and a robust scoring function should perform well across a variety of applications.^4–11 In recent years, a variety of machine-learning (ML) scoring functions^12–25 have been developed and outperformed classical scoring functions at retrospective benchmarks, and some scoring functions also performed well on prospective structure-based virtual screening (SBVS) application, such as AtomNet²⁶ and vScreenML.^{27, 28} Wallach et al introduced AtomNet, the first CNN-based scoring function incorporating 3D structural information, and they applied AtomNet in several VS campaigns.^{26, 29–31} Adeshina et al proposed the vScreenML and used it for prospective SBVS against human acetylcholinesterase (AChE).²⁷ Besides the generic scoring functions, target-specific ML scoring functions have been developed to focus on certain protein target or family,^{20, 21, 32, 33} which can outperform other models on that particular target case. However, the target specific scoring function approach will not be applicable for a novel target with little experimental data available. Thus, it is of significant interest to develop robust ML scoring functions.

Several key metrics^5–9 have been developed to assess performance of scoring function for different tasks, including: (I) scoring, which assesses the linear correlation between predicted and experimental measured binding affinities; (II) ranking, which evaluates the ranking ability of a scoring function to rank the known ligands for a certain target protein by predicted binding affinities; (III) docking, which evaluates the ability of a scoring function to identify native binding site and binding mode of ligand among computer generated decoys; (IV) screening, which assesses the ability to identify true binders for a given target from random molecule libraries. Extensive retrospective and comparative studies^{1, 5–9, 34–42} demonstrate that some widely used classical scoring functions, such as GlideScore^{43, 44} and Autodock Vina⁴⁵, perform relatively well in docking and screening tasks, but their scoring power are less satisfactory. Many ML scoring functions have achieved significantly better scoring power on crystal structures.^{17–19, 25, 33, 46–63} However, more extensive evaluations indicate that this enhancement in scoring performance accompany with significant under-performance in docking and screening power tests compared to classical scoring functions.^{64, 65} It remains a challenge for the scoring function development to not only improve scoring power, but also perform well for docking and screening tasks.

To tackle the challenge, recently we have employed the $\mathrm{\Delta }$-machine learning approach,^{66, 67} in which a correction term to the Vina scoring function is parametrized with machine learning, to develop two successive scoring functions, ${\mathrm{\Delta }}_{\text{vina}}{\text{RF}}_{20}$⁶⁶ and ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$,⁶⁷ achieving top performances for all metrics of CASF-2016 benchmark compared to 33 classical scoring functions. On the other hand, based on a small high-quality training data, we have developed a linear empirical scoring function, Lin_F9, which achieves better scoring and ranking powers than Vina on different structure types, including crystal pose, local optimized pose and docked pose.⁶⁸ Lin_F9 has been successfully applied to virtual screening and rational design of SARS-Cov-2 main protease inhibitors.⁶⁹

A major motivation for the current work is to use Lin_F9 as the new baseline scoring function and incorporate $\mathrm{\Delta }$-Learning machine learning approach to further enhance scoring and ranking performances on different structure types. Here, $\mathrm{\Delta }$-Lin_F9 machine learning strategy via eXreme Gradient Boosting (XGBoost)⁷⁰ have been explored. The training set is enlarged to include more experimental measured weak binders. One is crystal structures with weak binding affinities obtained from updated PDBbind database^{71, 72}. The other is to use computer-generated decoys with weak binding affinities obtained from BindingDB database^{73, 74}. In addition, in order to learn from docked poses, top 1 docked poses from end-to-end (E2E) docking are also included in the training set. More details of E2E docking protocol are described in Methods. For feature exploration, the previous used Vina 58 features in ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$ is replaced by a specialized Vina 48 features, in which polar-polar, polar-nonpolar, nonpolar-nonpolar, hydrogen bond and metal-ligand interactions in different distance ranges are described using a series of gauss functions. The overall feature set consists of 76 protein-ligand features and 16 ligand-specific features.

In this article, we described the development of a new state-of-the-art scoring function ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$. The overall evaluation indicates that ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ can not only perform consistently among the top compared to classical scoring functions in CASF-2016 benchmark, but also achieve superior prediction accuracy on different structure types, including docked poses that mimic real docking applications. In addition, we evaluated the screening performance of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on LIT-PCBA dataset,⁷⁵ which consists of 15 diverse target proteins with large-scale experiment-verified actives/decoys. The ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ scoring function and its code are freely available on the web at: (https://yzhang.hpc.nyu.edu/Delta_LinF9_XGB).

METHODS

Data Preparation

Training Set

The main component of our training set is inherited from the previous ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$’s training set, which is based on PDBbind (v2016) database⁷¹ and CSAR decoy set^{76, 77}. The details of this component can refer to the paper.⁶⁷ We cleaned the data by removing 3 covalent ligands and by removing previous constructed PDBbind decoys. The afterward cleaned data consists of 6816 PDBbind binders and 6321 CSAR decoys. In terms of binder set, 1556 weak binders (pK_d < 6) and 510 strong binders (pK_d > 9) were selected from PDBbind (v2018) general set⁷¹ and added to our binder set. It should be noted that the binder set have both with water (receptor-bound waters) and without water structures. All these binders come from PDBbind database and meet the requirements: (I) should be K_d/K_i binding data; (II) local optimized pose with RMSD <=2 Å from crystal pose; (III) Noncovalent ligand. Furthermore, in order to add more strong binder poses, 235 docked poses obtained by flexible re-docking (pK_d > 9 and RMSD <= 1 Å from crystal pose) were selected and added to the binder set. As shown in Table S1, the overall binder subset of training set has 9117 complex structures with Lin_F9 local optimized ligand poses used to generate features, and the experimental measured binding affinities (pK_d(exp)) are the labels.

In terms of decoy set 1 (see Table S1), which serves as a negative control of binding pose and binding affinity in the whole training set, a total of 7111 structures with estimated binding affinities (pK_d(est)) are constructed using CSAR^{76, 77} decoy set and BindingDB^{73, 74} weak binders. For 6321 CSAR decoys inherited from ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$ training set⁶⁷, the (pK_d(est)) for each decoy is determined by comparing the RMSD between decoy and crystal pose, as well as by comparing the Lin_F9 predicted binding affinity (pK_d(Lin_F9)) and pK_d(exp) of crystal pose: if the RMSD is no larger than 1 Å, which means the decoy is similar as crystal pose, pK_d(est) is assigned as the pK_d(exp) of crystal pose; else, for RMSD larger than 1 Å, pK_d(Lin_F9) is calculated and compared with pK_d(exp): if the pK_d(Lin_F9) is less than the pK_d(exp), the pK_d(est) is assigned as pK_d(Lin_F9); otherwise, pK_d(est) is assigned as the maximum value between pK_d(exp) – 0.5×(RMSD-1) and 0.5×pK_d(exp). So, the pK_d(est) is smaller when RMSD is larger, but not smaller than half of pK_d(exp). In addition, 790 decoys were obtained from top 1 docked poses of very weak binders (pK_d < 3) in BindingDB using E2E flexible docking. As these weak binders do not have crystal protein-ligand structures, the above pK_d(est) protocol is not applicable. For these BindingDB decoys, the pK_d(est) is determined by only comparing the pK_d(Lin_F9) and pK_d(exp): if the pK_d(Lin_F9) is less than the pK_d(exp), the pK_d(est) is assigned as pK_d(Lin_F9), otherwise, pK_d(est) is assigned as pK_d(exp).

In addition, in order to learn from flexible docked poses of complexes, we construct a decoy set 2 (see Table S1), in which top 1 docked poses are generated from the above binder set using E2E docking protocol that combines ligand conformer generation and flexible docking: starting with ligand 2D SDF file, a maximum of 10 conformers per ligand are first generated with OpenBabel 2.4.1 version using genetic algorithm, and then are docked to the target protein by flexible ligand docking using Lin_F9 scoring function. The top 1 scored pose is used to construct decoy set 2. Next, we only select top 1 docked pose that is diverse from its crystal pose, but the predicted pK_d(Lin_F9) is not different too much with pK_d(exp). It meets the requirements: (I) RMSD between top 1 docked pose and crystal pose, minus RMSD between its locally optimize pose and crystal pose, should larger than 0.5 Å. (II) The difference between pK_d(exp) and pK_d(Lin_F9) is smaller than 3. The decoy set 2 consists of 5715 E2E top1 docked poses.

Overall, our training set consists of 21,943 complexes, including 9,117 crystal structures (locally optimized near native poses) and 12,826 docked structures, which have no overlap with the following validation and test sets. Based on the UniProt ID, these 21,943 complexes come from 1366 target proteins (with UniProt ID) and 42 antibody proteins (without UniProt ID). There are 7,493 structures with waters and 14,450 structures without waters in the training set, and the latter includes 6,321 docked decoys obtained from CSAR decoy set.

Validation Set

The binder subset of validation set is same as the previous ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$’s validation set⁶⁷, which included 316 complexes with three different structure types: crystal pose, local optimized pose without water and local optimized pose with receptor-bound waters. In addition, we also construct a decoy set (see Table S1) that consists of E2E top 1 docked poses of these 316 complexes in both dry and water environments. The overall validation set consists of 1578 complexes. This validation set is used to (1) conduct the early stopping in model training to avoid the overfitting of XGBoost on training set; (2) select a model that can perform well on different structure types.

Test Set

CASF-2016 benchmark⁹ is used to evaluate the performance of our scoring function. Besides the standard assessment of four different powers (scoring power, ranking power, docking power and screening power) defined in CASF-2016 benchmark, we have also assessed scoring power and ranking power of our scoring function on locally optimized poses (LocalOpt) of CASF-2016 core set, in which ligand crystal poses have been locally optimized with Lin_F9.

Feature Generation

Table S2 summarizes all features employed in our scoring function development. The feature set consists of 28 buried solvent accessible surface area (bSASA) features, 48 Vina features, 3 bridge water features, 2 Beta-cluster features, one ligand efficiency (using Lin_F9 score divided by number of heavy atoms) and 10 ligand descriptors computed using RDKit version 2020.09.4. For bSASA features, same as ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, a total of 30 bSASA features are computed regarding to three different structures (complex, ligand, and protein). Each structure comprises of one total bSASA term and nine pharmacophore-based bSASA terms where pharmacophore types are characterized based on SYBYL⁷⁸ atom types and DOCK⁷⁹ neighboring atoms. MSMS⁸⁰ program is employed to calculate the atomic SASA with a 1.0 Å probe radius and the $\text{bSASA}={\text{SASA}}_{\text{unbound}}- {\text{SASA}}_{\text{bound}}$. As the halogen atoms are only presented in ligand molecules, we kept only halogen-based bSASA complex term to avoid zero variance of halogen-based bSASA protein term and avoid redundancy with halogen-based bSASA ligand term. This resulted in 28 bSASA terms in our feature set.

Different from Vina 58 features⁸¹ used in ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$,⁶⁷ there are 48 Vina features employed in our scoring function. As shown in Table S2 and Figure S1, polar-polar, polar-nonpolar and nonpolar-nonpolar interactions in different distance ranges are described using a series of gauss functions, in which the defined polar and nonpolar atoms are based on X-Score atom types⁸² (same as in Vina⁴⁵). Also, anti-hydrogen bond, hydrogen bond and metal-ligand terms in different distances are described using a series of gauss functions as well. The anti-hydrogen bond terms describe polar-polar atoms that can’t possibly be hydrogen bond. The metal-ligand terms describe metal-ligand interactions in protein-ligand complexes. There are 37 gauss functions to describe the above interactions (see Figure S1). In addition, 6 ligand specific terms and 5 interaction terms (1 repulsion and 2 desolvation and 2 electrostatic terms) from the Vina 58 features⁸¹ are employed as well (see Table S2). This resulted in 48 Vina terms in our feature set.

In addition, 3 bridge water features (number of bridge waters, the Lin_F9 score between bridge water and protein, the Lin_F9 score between bridge water and ligand), which are inherited from the previous ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, are added to our feature set. Co-crystallized waters that involve in protein-ligand interactions are considered as bridge water molecules based on the following criteria: (1) contact with both ligand and protein, the distance between oxygen atom of water and polar atoms of protein-ligand should within the range of 2.0 and 3.5 Å; (2) likely to form hydrogen bond networks, the angles between polar atoms in ligand, oxygen atom of bridge water, and polar atoms in protein are no less than 60 degrees; (3) favorable for protein-ligand binding, Lin_F9 score for bridge water is negative value when using protein or ligand as receptor.

Moreover, our feature set contains two Beta-cluster⁸³ features (ligand BetaScore and ligand coverage), which compute ligand and Beta-cluster overlaps in order to describe potential ligand-pocket complementarity.^{83, 84} Beta cluster is a pseudo-molecular representation of fragment-centric pockets detected by AlphaSpace2.0⁸³. It mimics the shape as well as atomic details of potential molecular binders. Ligand BetaScore is obtained by summing of the best Lin_F9 score of each beta-atom overlapping with ligand heavy atoms (atom distance < 1.6 Å means overlapping), this feature describes the occupied pocket ligandability. Ligand coverage is calculated by number of overlapped ligand heavy atoms divided by total number of heavy atoms. This feature describes the percentage of ligand atoms occupying the pocket.

Furthermore, 10 ligand descriptors (shown in Table S2), such as molecular logP and topological polar surface area (TPSA), are computed for each ligand using RDKit version 2020.09.4 and added to our feature set. In our above Vina 48 features, there are 6 ligand-specific terms. Thus, our feature set consists of 16 ligand-specific features and 76 protein-ligand features.

Lin_F9 Scoring Function

Lin_F9⁶⁸ is a newly developed linear scoring function that employs 9 empirical terms, including 5 Vina empirical terms (Gauss₁, Repulsion, Hydrophobic, Hydrogen Bond, Number of torsions), as well as 4 new empirical terms (two new Gauss terms, one metal bond term, one new torsion penalty term). The details of each term and Lin_F9 scoring function development can refer to this paper.⁶⁸ For the CASF-2016 benchmark scoring test, Lin_F9 performs best among 34 classical scoring functions with Pearson’s correlation coefficient (R) of 0.680. We have implemented Lin_F9 in a fork of Smina docking suite as an optional built-in scoring function for protein-ligand docking. Lin_F9 is accessible through: https://yzhang.hpc.nyu.edu/Lin_F9/. Recently, Lin_F9 has been applied to the prospective virtual screening and rational inhibitor design to target SARS-Cov-2 main protease.⁶⁹

∆-Lin_F9 XGBoost Strategy

Similar as previous ∆-Vina strategy,^{66, 67} the difference between Lin_F9 score and experimental binding affinity is used to parameterize a correction term by using XGBoost, and our ∆-Lin_F9 scoring function in term of pK_d has the following formula:

$$\text{p}{K}_{\text{d}}\left({\mathrm{\Delta }}_{\text{Lin}\_\text{F}9}\text{XGB}\right)=\text{ p}{K}_{\text{d}}\left(\text{Lin}\_\text{F}9\right)+\mathrm{\Delta }\text{p}{K}_{\text{d}}\left(\text{XGBoost}\right)$$ 1

Given a training sample i with input feature vector $x_i=\left(x_{i\_1},x_{i\_2},\dots ,x_{i\_p}\right)$, K additive trees are parameterized to predict the output $y_i$, in which each new tree corrects the difference between target and predictions made by all of the previous trees, as the equation shown below:

$${\widehat{y}}_i^{\left(K\right)}= {\sum }_{k=1}^K{f}_k\left(x_i\right)= {\widehat{y}}_i^{\left(K-1\right)}+f_K\left(x_i\right).$$ 2

Here, ${\widehat{y}}_i^{\left(K-1\right)}$ is the prediction from previous K-1 trees and $f_K\left(x_i\right)$ is the K-th tree model. The objective function consists of loss function $\left(l\left(y_i, {\widehat{y}}_i\right)\right)$ and regularization term $\left(\text{Ω}\left(f_k\right)\right)$ for tree complexity as follows:

$$\mathcal{L}\left(f_k\right)= {\sum }_{i=1}^{N}l\left(y_i, {\widehat{y}}_i\right)+ {\sum }_{i=1}^k\text{Ω}\left(f_i\right)= {\sum }_{i=1}^{N}l\left(y_i, {\widehat{y}}_i^{\left(k-1\right)}+f_k\left(x_i\right)\right)+\text{Ω}\left(f_k\right)+constant$$ 3

$$\text{Ω}\left(f_k\right)= \gamma T+\frac{1}{2}\lambda {\omega }^2$$ 4

Here, mean squared error (MSE) is used as our loss function and the regularization term $\mathrm{\Omega }$ is used to control the model complexity in which T and $\omega$ refer the number of leaves and the scores on leaves in $f_k$ respectively. To reduce correlations among trees, only a random subset of features is chosen for splitting in each tree development.

In our development of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$, we use the $\mathrm{\Delta }\text{p}{K}_{\text{d}}$ as the label y and employ the XGBoost package (version 1.20) in Python 3.7 to build the XGBoost model. The input feature vector x has p = 92 features. The hyper-parameters utilized in our model are n_estimators = 800, learning_rate = 0.04, subsample = 0.6, colsample_bytree = 0.8, min_child_weight = 2, max_depth = 12, and loss function (regression type) = “reg: squarederror”. By using the validation set, the early stopping round with 50 steps is applied to reduce overfitting of training data. Considering the high variance of XGBoost models, the final scoring prediction is the average of ten XGBoost models initialized with different random seeds.

Evaluation Methods

CASF 2016 Benchmark

The comparative assessment of scoring functions (CASF) benchmark^5–9 provides four different powers (scoring power, ranking power, docking power and screening power) for evaluation of scoring function’s performance. CASF-2016⁹ is the latest version of CASF benchmark, which has tested more than 30 prevailing scoring. Pearson’s correlation coefficient (R) between predicted binding affinity and experimental measured binding affinity is used to evaluate scoring power. The CASF-2016 benchmark includes 57 targets and 5 known ligands for each target. The Spearman’s rank correlation coefficient $\left(\rho \right)$ is used as the quantitative indicator of ranking power by averaging over 57 targets. Docking power is evaluated by the success rate of top scored poses having RMSD less than 2 Å in comparison with the crystal pose. Screening power, which refers the ability of a scoring function to identify true binders among a pool of molecules, is evaluated by two quantitative indicators: one is the success rate of identifying the highest-affinity binder among the 1%, 5% and 10% top-ranked ligands over all 57 targets, and the other is the enhancement factor (EF) computed with the following formula:

$${\text{EF}}_{\alpha }=\frac{NT{B}_{\alpha }}{NT{B}_{total}\cdot \alpha }$$ 5

Here, $NT{B}_{\alpha }$ is the number of true binders among top $\alpha$ ranked candidates (e.g. $\alpha =1\%,5\%,10\%$) based on predicted binding affinities. $NT{B}_{total}$ is the total number of true known binders for a given target. The final ${\text{EF}}_{\alpha }$ is also the average over all 57 targets.

Extended Docking-Scoring tests of CASF-2016 core set

Besides standard assessment, we also carried out extended tests of scoring and ranking performances with various structure types of protein-ligand complexes that are generated by several flexible docking protocols as which have first been introduced in tests of Lin_F9. They are summarized in Table 1, including: (i) flexible re-docking, (ii) E2E docking, (iii) ensemble docking using all 5 protein structures and (iv) ensemble docking using 4 non-native protein structures. All these docking experiments are conducted using a fork of Smina docking suite with Lin_F9 scoring function. Both dry environment (protein without water) and water environment (protein with receptor-bound waters) are evaluated for these docking-scoring tests. For each docking-scoring test, after docking, the top 5 docked poses are selected for re-scoring using ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$, and the best-scored pose from re-scoring is used for scoring, ranking and docking performances evaluation. In term of docking performance evaluation, the symmetry corrected RMSD between the best-scored pose and crystal pose is calculated by open source tool DockRMSD.⁸⁵

Table 1.

Different docking-scoring tests of CASF-2016 benchmark. The details are described in Ref. 68.

Name	Ligand conformation for each ligand	Protein conformation for each ligand	Docking method
flexible re-docking	native ligand pose	native protein structure	flexible ligand docking
E2E docking	Computer-generated maximum 10 conformersa	native protein structure	flexible ligand docking
ensemble (E5) docking	Computer-generated maximum 10 conformers	5 protein structures (include native protein structure)	flexible ligand docking
ensemble (E4) docking	Computer-generated maximum 10 conformers	4 non-native protein structures	flexible ligand docking

^aComputer-generated maximum 10 conformers per ligand using OpenBabel.

D3R GC4 Datasets

Drug Design Data Resource (D3R)^86–89 Grand Challenge 4 (GC4)⁸⁶ consist of two sub-challenges: one is BACE1 Sub-challenge for pose prediction of 20 macrocyclic BACE inhibitors and affinity ranking of 154 macrocyclic BACE inhibitors, and the other is CatS Sub-challenge for affinity ranking of 459 CatS inhibitors. Our group has participated in GC4 BACE1 Sub-challenge, and the pose prediction of our submitted model achieved an average RMSD of 1.01 Å. In further exploration after competition, the average RMSD can be decreased to 0.74 Å using a similarity-based constraint docking method³². Similar as in the work of Lin_F9, our latest predicted poses of whole BACE1 dataset are used to test the affinity ranking performances of our scoring function and Vina (as comparison); for the CatS dataset (459 inhibitors), predicted poses obtained from Top submitter’s model (Max Totrov group, receipt id: x4svd) in D3R website⁸⁶ are used. It should be noted that, before re-scoring, all the poses are local optimized by Vina or Lin_F9.

LIT-PCBA Dataset

LIT-PCBA is an unbiased data set designed for benchmarking virtual screening (VS) and machine-learning, and it can be directly used for the evaluation of screening performance of scoring functions.^{75, 90} LIT-PCBA dataset consists of 15 diverse target sets, 8020 true actives and 2,675,399 true inactive compounds. The high imbalance between actives and inactives is intended to mimic the real-life screening tasks, which makes it quite challenging for computational screening methods, thereby offering an opportunity to estimate performance of virtual screening protocols in practical applications.

For each of the 15 targets in LIT-PCBA, several PDB templates are available (no more than 15 crystal complexes) as input receptor files for docking. In order to save the CPU cost, we only used a limit number of PDB templates for targets with more than 100,000 compounds. For each target, only one ligand binding site was considered for docking. For example, there are 2 different structures (HAT domain and BRD domain structures) in KAT2A target, we only selected HAT domain structure as the receptor for docking. RDKit 2020.09.4 version^{91, 92} was used to read SMILES string and add hydrogens and generate initial 3D conformer for each compound. The following docking protocol was same as the E2E docking described above. After docking, for each compound, top 5 docked poses were selected for re-scoring using ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ and the best-score from re-scoring was used to rank the compound in the library. The EF at top 1% was used as the quantitative indicator to evaluate the screening power.

RESULTS AND DISCUSSION

CASF-2016 Benchmark Assessment

The scoring-ranking-docking-screening performance of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ was tested on standard CASF-2016 benchmark and compared with other traditional scoring functions (Figure 1). Meanwhile, scoring power comparison with several recently developed machine learning scoring functions has been carried out, as shown in Figure 2 and Table 2. In addition, based on CASF-2016 benchmark, the ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$’s scoring and ranking performances on locally optimized poses, which are obtained by Lin_F9 local optimization of crystal poses, were also tested.

Figure 1.

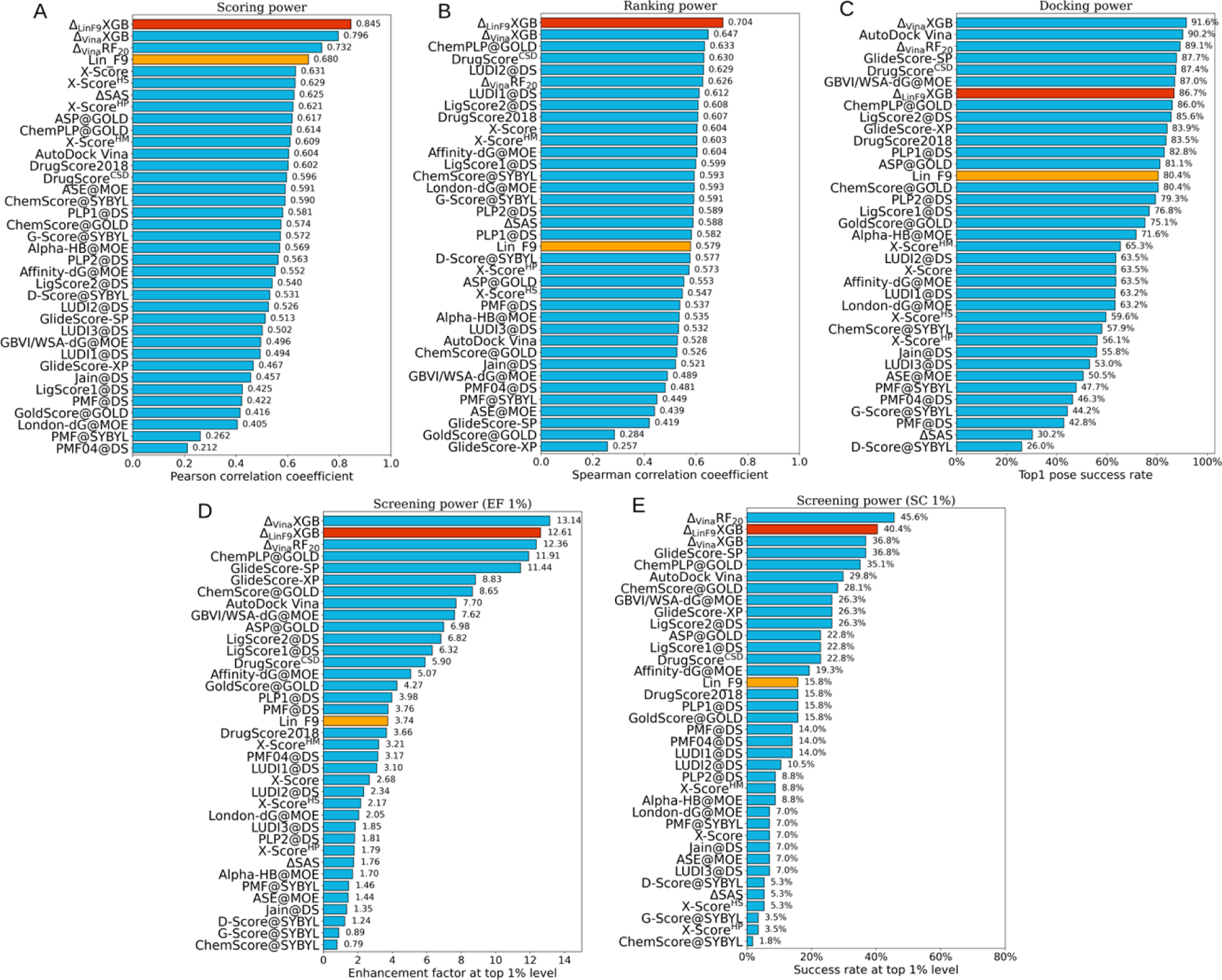
Performances of scoring functions on CASF-2016 benchmark. (A) Scoring power evaluated by Pearson correlation coefficient, (B) ranking power measured by Spearman correlation coefficient, (C) docking power calculated by success rate for top1 poses (include crystal structures), screening power measured by (D) enhancement factor and (E) success rate at top 1% level. Performances of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are colored red, performances of Lin_F9 are colored orange and all other scoring functions are colored cyan. All scoring functions are ranked in a descending order.

Figure 2.

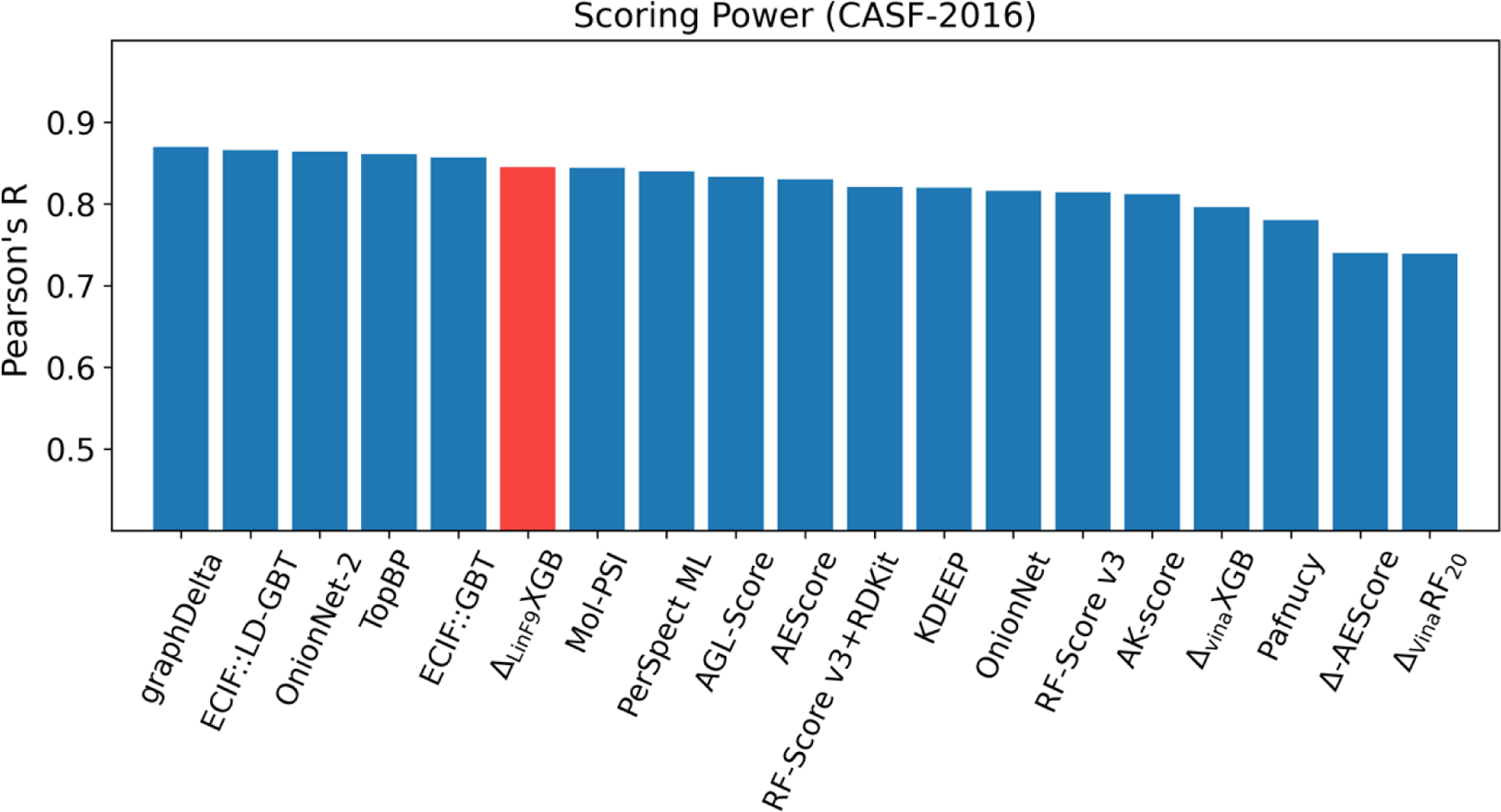
Scoring power comparison of several state-of-the-art ML scoring functions on CASF-2016 benchmark. The Pearson correlation coefficients of other ML scoring functions are taken from refs 12–19, 22–24, 66–67, 95–96.

Table 2.

CASF-2016 benchmark test results for several ML scoring functions. (The highest values of each column are shown in bold)

Model	CASF-2016 Metrics
	Scoring	Ranking	Docking	Screening
	Pearson R	Spearman $\rho$	Success Rate at top1 pose	EF at top 1%	Success Rate at top 1%
${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$ 66	0.739	0.635	89.1%	12.36	45.6%
${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$ 67	0.796	0.647	91.6%	13.14	36.8%
${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$	0.845	0.704	86.7%	12.61	40.4%
$\mathrm{\Delta }-$ AEScore93	0.740	0.590	85.6%	6.16	19.3%
AEScore93	0.830	0.640	35.8%	–	–
AK-score (ensemble)94	0.812	0.670	36.0%	–	–
DeepDock95	–	–	87.0%	16.41	43.9%

Standard Assessment

In Figure 1, ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ is compared with three scoring functions, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$ and Lin_F9, previously developed in our group,^{66, 67} as well as 33 traditional scoring functions that have been evaluated by Su et al.⁹ Our evaluation results show that ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ achieves Top 1 performances on scoring power and ranking power, it also achieves Top 2 performances on both the enhancement factor at top 1% (EF_1%) and success rate at top 1% (SC_1%) of screening power tasks. For the scoring power, the Pearson’s correlation coefficient (R) and the Root-Mean-Square-Error (RMSE) of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are 0.845 and 1.240, which are better than our previous best result (R = 0.796 and RMSE=1.327 for ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$), as shown in Figure 1A. For the ranking power comparison, Figure 1B shows that ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ achieves the best ranking power with the average Spearman’s rank correlation coefficient $\rho =0.704$, which is also much better than our previous best result ($\rho =0.647$ for ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$). In addition, Kendall correlation coefficient $\left(\tau \right)$ ranking performance of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ is evaluated as well, with $\tau =0.625$. For the docking power assessment, 86.7% of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ predicted best-scored pose is considered to be successfully docked if 2.0 Å RMSD threshold is used in comparison with the crystal pose. In Figure 1C, the docking power of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ is ranked at the 7^th place among all 37 scoring functions. Enhancement factor and success rate at top 1% level are computed as the indicators for the screening power, which evaluates the ability of a scoring function to identify true binders from random compounds. As shown in Figure 1D and 1E, the screening power is ranked at the 2^nd place among all 37 scoring functions. EF_1% and SC_1% of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are 12.61 and 40.4%. When computing the success rate at the top 5% level (SC_5%) and at the top 10% level (SC_10%), ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ achieves 59.6% and 68.4%, which are much better than previous ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$’s performance (see Table S3 in Supporting Info).

In addition, in Figure 2, we compared with several advanced ML scoring functions for the scoring power of CASF-2016 benchmark test, since these ML scoring functions are mainly developed for protein-ligand binding affinity prediction. As can be seen, our ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ model ranks at the 6^th position among these start-of-the-art models. The top 5 performers are graphDelta¹⁷ (graph-convolutional neural network model, Pearson’s R = 0.87), ECIF::LD-GBT¹⁸ (gradient boosting tree model incorporating extended connectivity interaction features and RDKit ligand features, Pearson’ R = 0.866), OnionNet-2¹⁵ (convolutional neural network model with inputs based on rotation-free specific contacts between protein and ligand in different shells, Pearson’s R = 0.864), TopBP¹² (a consensus model incorporating different ML methods and with inputs based on algebraic topology for characterizing biomolecular complexes, Pearson’s R = 0.861), ECIF::GBT¹⁸ (gradient boosting tree model incorporating only extended connectivity interaction features, Pearson’s R = 0.857). Other methods, such as persistent spectral based ML models (Mol-PSI¹³ and PerSpect ML¹⁴), algebraic graph theory-based model (AGL-Score¹⁹) and usage of diverse ligand-based features in previous ML model (RF-Score v3+RDKit²²), also show very good scoring power in CASF-2016 test. All these methods enrich the methodology for ML scoring function development, and our ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ also achieves state-of-the-art scoring performance among these methods. It should be noted that, although all the ML scoring functions presented in Figure 2 use PDBbind dataset for their training and validation, the differences in PDBbind versions (v2007, v2010, v2014 and v2016) as well as the choice of using PDBbind refined set or general set, will also affect the scoring performance test on CASF-2016 benchmark.

Moreover, we also compared with several ML scoring functions that have been evaluated with at least three different metrics for CASF-2016 benchmark. Many other ML scoring functions that only presented scoring power in their original paper are not summarized in Table 2. As can be seen,${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ shows best scoring and ranking powers among these scoring functions. AEScore,⁹³ a deep neural network model, also has very good scoring power (R = 0.830), but its docking power is very low (success rate = 35.8%). This low success rate is also observed with AK-score (ensemble),⁹⁴ a CNN-based scoring function, reporting a success rate of 36.0%. A similar scoring function that employed $\mathrm{\Delta }$-Learning to retain docking power is $\mathrm{\Delta }$-AEScore,⁹³ which reports a success rate of 85.6%. But its screening power is far less satisfying (EF_1% = 6.16), worse than the Vina (EF_1% = 7.70). Recently, Wegner et al proposed DeepDock,⁹⁵ a method based on geometric deep learning to predict the ligand binding poses using distance potential, achieving very good docking power (success rate = 87.0%) and screening power (EF_1% = 16.41). Scoring and ranking powers are not evaluated since DeepDock is not trained to predict binding affinities. Their study inspired us to train a native pose identification model in our future work to further improve the screening power. Standard assessment shows that ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ is already a very robust and competitive protein-ligand scoring function for different tasks.

Locally Optimized Poses Assessment

Based on the crystal structure of CASF-2016 core set, we also evaluated scoring power and ranking power of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on its locally optimized (LocalOpt) pose, which is locally optimized from crystal pose using Lin_F9 scoring function. Both LocalOpt pose in dry environment $\left({\text{C}}_{\text{o}}\right)$ and LocalOpt pose in water environment $\left({\text{C}}_{\text{o}}^{\text{rw}}\right)$ are evaluated. Figure 3A, B illustrate the scoring power and ranking power on LocalOpt (${\text{C}}_{\text{o}}$ and ${\text{C}}_{\text{o}}^{\text{rw}}$), together with performance on crystal structure without local optimization (C). Compared with ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, Lin_F9 and Vina, our new developed ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ achieves much better scoring and ranking power on both ${\text{C}}_{\text{o}}$ and ${\text{C}}_{\text{o}}^{\text{rw}}$. For the scoring power, the Pearson’s R of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{o}}$$$ and ${\text{C}}_{\text{o}}^{\text{rw}}$ are 0.853 and 0.834. The RMSE of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{o}}$ and ${\text{C}}_{\text{o}}^{\text{rw}}$ are 1.162 and 1.205. For the ranking power, the Spearman’s $\rho$ of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{o}}$ and ${\text{C}}_{\text{o}}^{\text{rw}}$ are 0.693 and 0.700, respectively. A scatter plot of experimental pK_d vs predicted pK_d for LocalOpt pose $\left({\text{C}}_{\text{o}}\right)$ is shown in Figure 4B. The results indicate that ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ performs consistently well on the near native poses.

Figure 3.

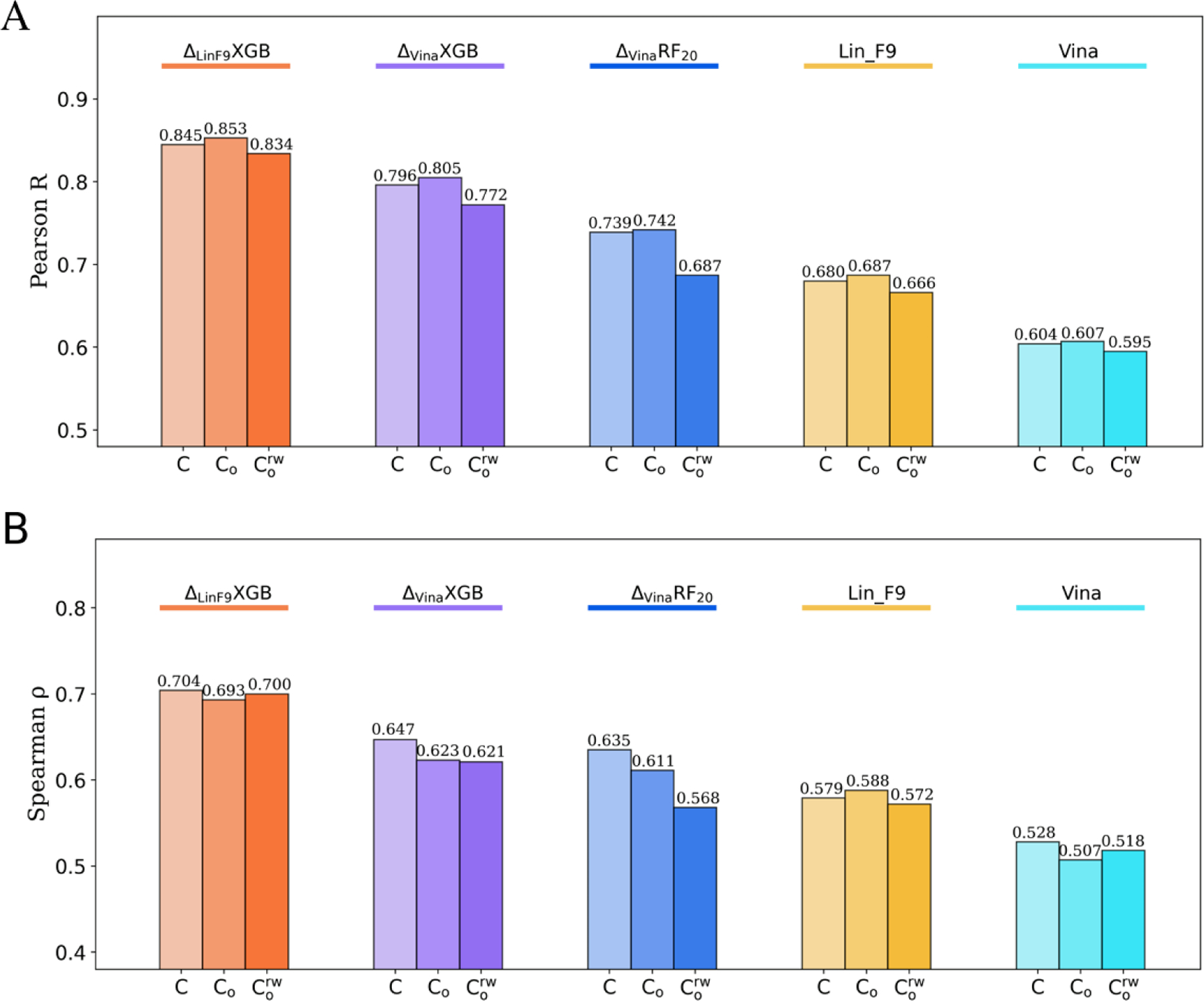
Scoring and ranking performances of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, Lin_F9 and Vina on LocalOpt pose, as well as crystal pose. (A) Pearson correlation coefficient used to measure scoring power. (B) Spearman correlation coefficient used for ranking power. Performances of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, Lin_F9 and Vina are colored red, purple, blue, orange and cyan, respectively. For each scoring function, performance on crystal pose (C), LocalOpt pose (C_o), and local optimized pose with receptor-bound water molecules $\left({\text{C}}_{\text{o}}^{\text{rw}}\right)$ are displayed from left to right with gradually changed color.

Figure 4.

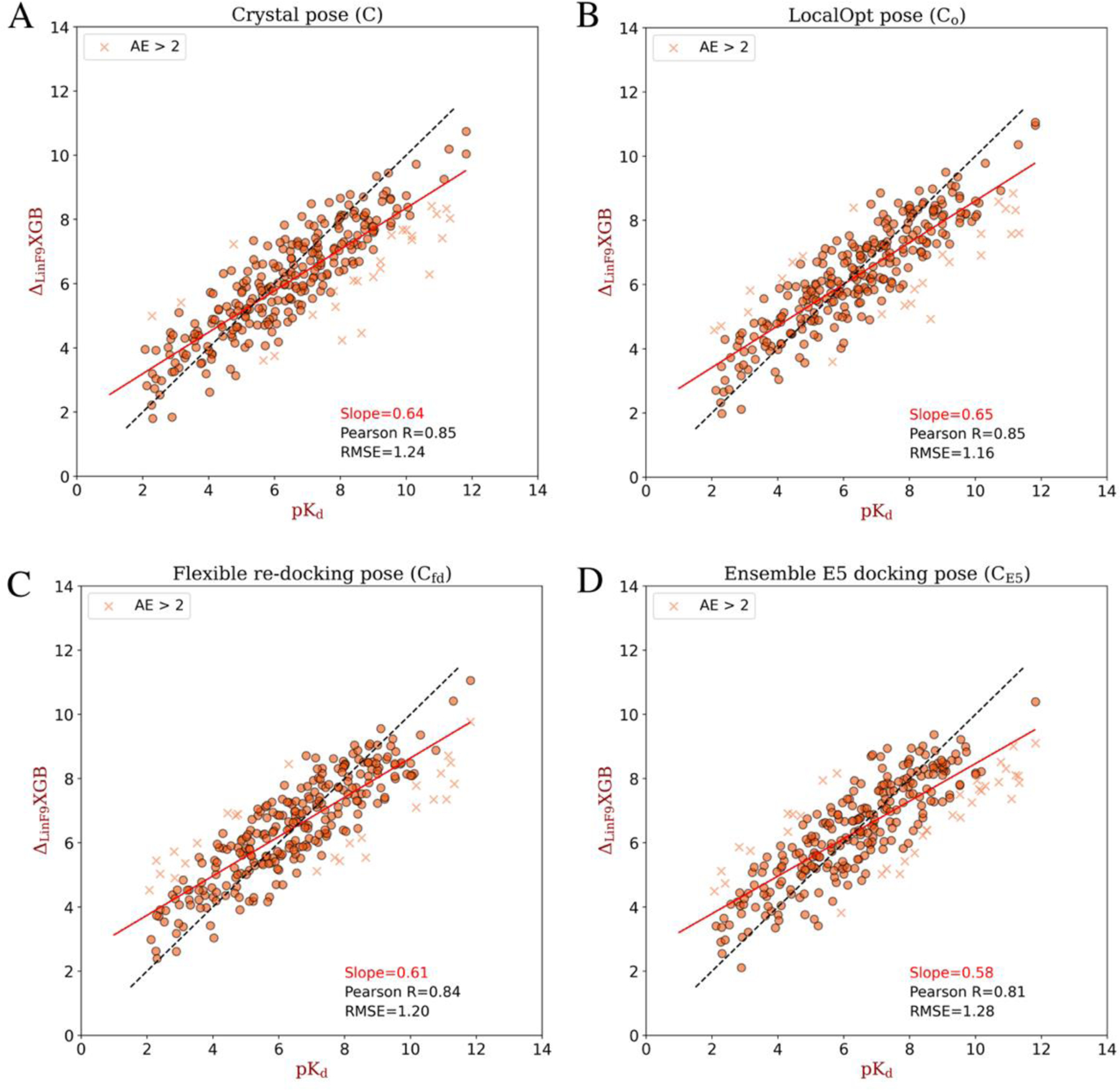
Scatter plots between experimental pK_d and predicted pK_d of different poses re-scored by ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$. (A) Crystal pose, (B) locally optimized pose, (C) flexible re-docking pose and (D) ensemble E5 docking pose. The absolute error (AE) in pK_d larger than 2 are plotted with marker “x”, and others are plotted with marker “o”. Pearson correlation coefficient (R) and root-mean-square error (RMSE) between predicted pK_d and experimental pK_d are shown for each plot. The solid red line for each plot corresponds to the linear fit between predicted pK_d and experimental pK_d, the slope value for this linear fit is shown in the plot.

Docking Tests of CASF-2016 Core Set

In order to further test the scoring, ranking and docking performances for real docking application, we enlarged the evaluation category from re-scoring of crystal pose and LocalOpt pose to re-scoring of docking poses. Several docking tests on CASF-2016 core set (illustrated in Table 1) are carried out, and the docked poses are re-scored by ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ to select the best-scored pose for scoring, ranking and docking evaluations.

Flexible re-docking test

In docking preparation of flexible re-docking, both the ligand conformer and protein conformation come from the corresponding crystal protein-ligand complex. After docking, the top 5 docked poses for each complex were selected and then re-scored by ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$. Similar as LocalOpt pose, both docked poses without water $\left({\text{C}}_{\text{fd}}\right)$ and with water molecules $\left({\text{C}}_{\text{fd}}^{\text{rw}}\right)$ are evaluated. In the evaluation process, the best-scored pose from re-scoring is used for assessment, and the performance is compared with its baseline Lin_F9, as well as ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$ and Vina.

Figure 5A, B illustrate the scoring power and ranking power on ${\text{C}}_{\text{fd}}$ and ${\text{C}}_{\text{fd}}^{\text{rw}}$. The baseline Lin_F9 achieves much better scoring and ranking performances than Vina on both ${\text{C}}_{\text{fd}}$ and ${\text{C}}_{\text{fd}}^{\text{rw}}$, which has been discussed in our previous paper. Then, ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ is used to re-score the top 5 docked poses, and the best-scored pose from re-scoring further improved the scoring and ranking performances a lot. The Pearson’s R of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{fd}}$ and ${\text{C}}_{\text{fd}}^{\text{rw}}$ are 0.839 and 0.826, respectively. The RMSE of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{fd}}$ and ${\text{C}}_{\text{fd}}^{\text{rw}}$ are 1.204 and 1.238. For the ranking power, the Spearman’s $\rho$ of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{fd}}$ and ${\text{C}}_{\text{fd}}^{\text{rw}}$ are 0.712 and 0.723, respectively. A scatter plot of experimental pK_d vs predicted pK_d for flexible re-docking pose $\left({\text{C}}_{\text{fd}}\right)$ is shown in Figure 4C. As far as we know, the scoring and ranking performances for flexible re-docking of CASF-2016 core set are better than existing ML scoring functions. In addition, docking success rates of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on both ${\text{C}}_{\text{fd}}$ and ${\text{C}}_{\text{fd}}^{\text{rw}}$ are computed to assess the ability of scoring function to identify near-native pose, as shown in Figure 5C. Vina achieves highest docking success rate on both ${\text{C}}_{\text{fd}}$ and ${\text{C}}_{\text{fd}}^{\text{rw}}$. At a 2 Å RMSD threshold, the docking success rates for Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{fd}}$ are 69.1%, 67.0%, 64.9%, 57.9% and 57.9%, respectively. For ${\text{C}}_{\text{fd}}^{\text{rw}}$, the docking success rates for Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are 84.6%, 83.9%, 80.0%, 80.0% and 79.3%, respectively. All scoring function’s performances improved a lot after keeping receptor-bound water, which demonstrates the importance of explicit water molecules for molecular docking. The difference of docking success rates between Vina and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ decreases from around 11.2% to 5.3% when water molecules are included. It is observed that scoring and ranking powers of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are significantly better than Vina on both ${\text{C}}_{\text{fd}}$ and ${\text{C}}_{\text{fd}}^{\text{rw}}$, while the docking success rate of Vina is higher. This trend is consistent for other docking tests (see Figure 5C).

Figure 5.

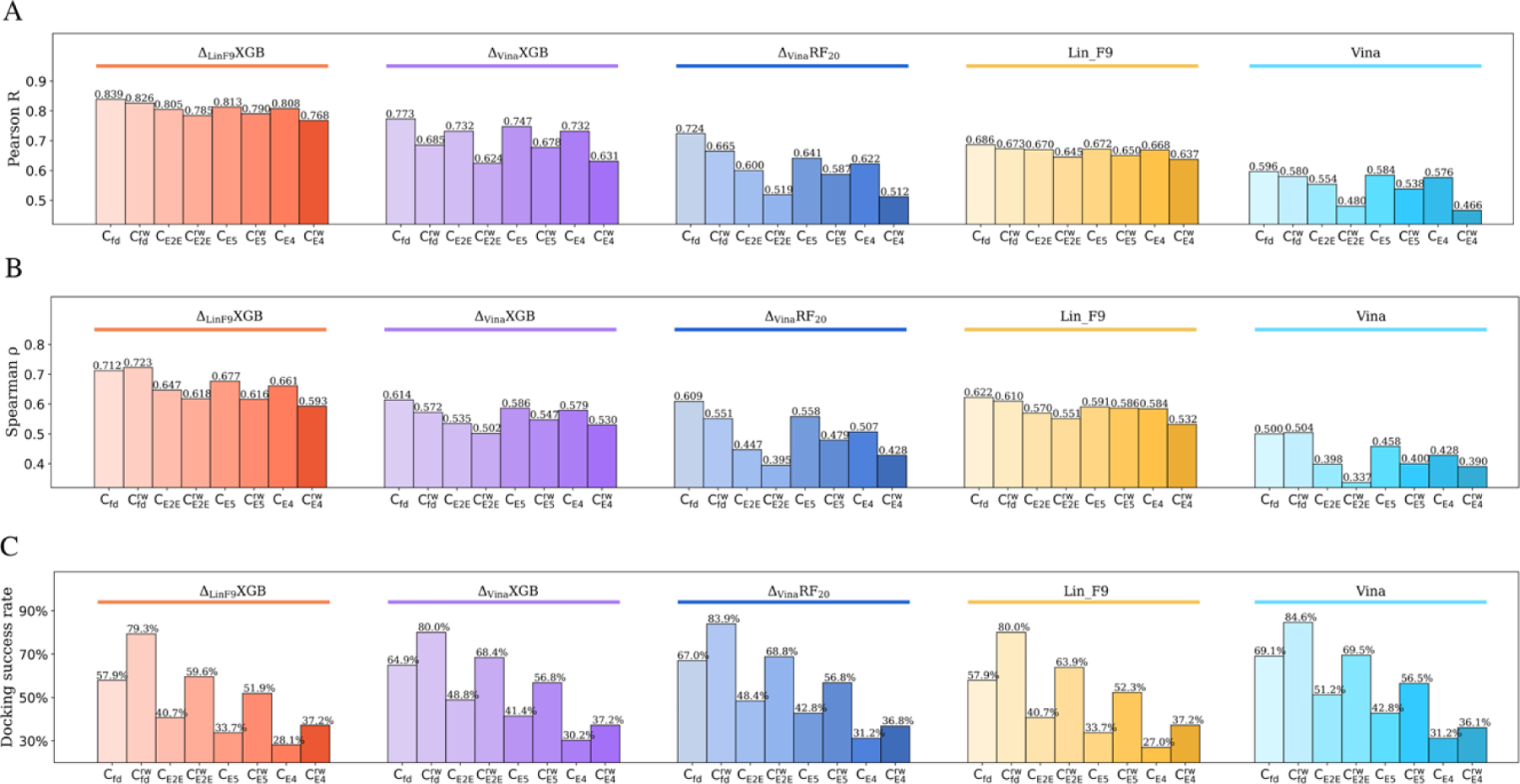
Scoring, ranking and docking powers of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, Lin_F9 and Vina for different docking tests on CASF-2016 core set. (A) Pearson correlation coefficient used to measure the scoring power. (B) Spearman correlation coefficient for ranking power. (C) Docking power measured by success rate of best-scored pose (RMSD < 2 Å). Performances of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, Lin_F9 and Vina are colored red, purple, blue, orange and cyan, respectively. For each scoring function, performances on flexible re-docking poses (${\text{C}}_{\text{fd}}$ and ${\text{C}}_{\text{fd}}^{\text{rw}}$), E2E docking poses (${\text{C}}_{\text{E}2\text{E}}$ and ${\text{C}}_{\text{E}2\text{E}}^{\text{rw}}$), ensemble (E5) docking poses (${\text{C}}_{\text{E}5}$ and ${\text{C}}_{\text{E}5}^{\text{rw}}$), ensemble (E4) docking poses (${\text{C}}_{\text{E}4}$ and ${\text{C}}_{\text{E}4}^{\text{rw}}$) are displayed from left to right with gradually changed color.

End-to-End Docking Test

Here we evaluated the flexible docking on CASF-2016 core set in an end-to-end (E2E) protocol, in which ligand conformer generation and flexible docking are combined. For this E2E docking protocol, maximum 10 conformers were generated for each small molecule, and all these conformers were docked to the target protein. After docking, the top 5 docked poses were re-scored using ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$, and the best-scored pose from re-scoring was used to assess the performance of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ model.

Figure 5A, B illustrate the scoring power and ranking power on E2E docked pose in dry environment $\left({\text{C}}_{\text{E}2\text{E}}\right)$ and in water environment $\left({\text{C}}_{\text{E}2\text{E}}^{\text{rw}}\right)$. The baseline Lin_F9 achieves much better scoring and ranking performances than ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$ and Vina on both ${\text{C}}_{\text{E}2\text{E}}$ and ${\text{C}}_{\text{E}2\text{E}}^{\text{rw}}$. Similar as above flexible re-docking results, the best-scored pose from re-scoring by ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ further improved the performance. For the scoring power, the Pearson’s R of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}2\text{E}}$ and ${\text{C}}_{\text{E}2\text{E}}^{\text{rw}}$ are 0.805 and 0.785, respectively. The RMSE of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}2\text{E}}$ and ${\text{C}}_{\text{E}2\text{E}}^{\text{rw}}$ are 1.314 and 1.356. For the ranking power, the Spearman’s $\rho$ of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}2\text{E}}$ and ${\text{C}}_{\text{E}2\text{E}}^{\text{rw}}$ are 0.647 and 0.618. For the docking power, the docking success rates of best-scored pose for Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are shown in Figure 5C. Once again, Vina achieves highest docking success rate on both ${\text{C}}_{\text{E}2\text{E}}$ and ${\text{C}}_{\text{E}2\text{E}}^{\text{rw}}$. At a 2 Å RMSD threshold, the docking success rates for Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}2\text{E}}^{\text{rw}}$ are 69.5%, 68.8%, 68.4%, 63.9% and 59.6%, respectively. Though the docking power of Vina is better, its scoring and ranking performances are less satisfied. Overall, our ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ achieves much better scoring and ranking performances for this E2E docking test.

Ensemble (E5 and E4) docking tests

Ensemble docking is a practically useful approach to account for protein flexibility in docking applications by docking a ligand into a selected ensemble of protein structures. The CASF-2016 core set can be used to evaluate the performance of ensemble docking, as it includes 57 targets and 5 protein structures for each target. For each ligand in CASF-2016 core set, it can be docked into 5 protein structures with the E2E docking protocol. After docking, the top 5 docked poses for each protein structure were selected and re-scored by ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$. The best-scored pose from re-scoring was selected to calculate scoring- ranking-docking performances of our scoring function.

From Figure 5A and 5B, we can see that in comparison with the other four scoring functions, ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ achieves much better scoring and ranking powers for this ensemble E5 docking test. For the scoring power, the Pearson’s R of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}5}$ and ${\text{C}}_{\text{E}5}^{\text{rw}}$ are 0.813 and 0.790, respectively. The RMSE of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}5}$ and ${\text{C}}_{\text{E}5}^{\text{rw}}$ are 1.283 and 1.343. For the ranking power, the Spearman’s $\rho$ of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}5}$ and ${\text{C}}_{\text{E}5}^{\text{rw}}$ are 0.677 and 0.616. Both the scoring power and ranking power of ensemble E5 docking are slightly better than the above E2E docking with native protein structure. This suggests that, for ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$, ensemble docking can improve the scoring and ranking performances than docking with a single structure. At a 2 Å RMSD threshold, docking success rates for Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9, ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}5}^{\text{rw}}$ are 56.5%, 56.8%, 56.8%, 52.3% and 51.9%, respectively.

A more stringent test for ensemble docking is to exclude the native protein structure for each ligand from the ensemble. The docked poses without water (${\text{C}}_{\text{E}4}$, in which E4 represents 4 ensemble protein structures used) and with water molecules $\left({\text{C}}_{\text{E}4}^{\text{rw}}\right)$ were assessed. As shown in Figure 5, for the scoring power, the Pearson’s R of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}4}$ and ${\text{C}}_{\text{E}4}^{\text{rw}}$ are 0.808 and 0.768, respectively. The RMSE of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}4}$ and ${\text{C}}_{\text{E}4}^{\text{rw}}$ are 1.309 and 1.418. For the ranking power, the Spearman’s $\rho$ of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}4}$ and ${\text{C}}_{\text{E}4}^{\text{rw}}$ are 0.661 and 0.593. At a 2 Å RMSD threshold for the best-scored pose, docking success rates for Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9, ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on ${\text{C}}_{\text{E}4}^{\text{rw}}$ are 36.1%, 36.8%, 37.2%, 37.2% and 37.2%, respectively.

Altogether, in term of (i) flexible-redocking, (ii) E2E docking, (iii) ensemble docking test including native protein structure and (iv) ensemble docking test excluding native protein structure, the scoring and ranking performances of our new developed ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ achieves consistently superior prediction accuracy on these real docking tests.

Case Studies of D3R GC4 Datasets

Here we evaluated affinity ranking performances of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on two D3R GC4 challenge datasets ⁸⁶ regarding beta secretase 1 (BACE1) and Cathepsin S (CatS) respectively. Both targets are of significant pharmaceutical interests.^96–101 The structure-based ranking protocol depends on the protein-ligand complex structures. However, both BACE1 and CatS datasets are very challenge for pose prediction using traditional docking program (such as Smina) and ligand conformer generation method (such as RDKit).^{32, 87, 102–104} For BACE1 dataset, we used a similarity-based constraint docking method to generate the near-native poses. The method uses similar co-crystal macrocycle ring with BACE1 structure as reference in the sampling process and has achieved very good pose prediction performance (see Figure S6). For the CatS dataset, the poses were obtained from Max Totrov group’s submitted data (receipt ID: x4svd) on D3R website, since they have achieved top2 pose prediction in previous GC3 CatS competition.⁸⁷

BACE1 macrocyclic inhibitor dataset.

The BACE1 dataset encompasses 154 small molecules inhibitors, in which 151 of 154 ligands have macrocycle rings.⁸⁶ The measured binding affinities of the dataset span over five orders of magnitude range of IC₅₀ (pIC₅₀ range from 4.2 to 9.3). The macrocycle ring size ranges from 14 to 17, and conformation of these macrocycle rings are hard to properly generated due to the limitation of ligand conformational sampling methods.^{105, 106} Here, we evaluated the ranking powers of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on whole 154 ligands, in which the poses were predicted using our similarity-based constraint docking method (see Figure S6). Table 3 illustrates the ranking powers of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on LocalOpt pose. For the ranking power, the Spearman’s $\rho$ of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are 0.332, 0.299, 0.307, 0.439 and 0.481, respectively. The Kendall’s $\tau$ of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are 0.222, 0.201, 0.211, 0.311 and 0.349. The baseline Lin_F9 achieves better ranking power when compared with Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$ and ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$. ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ further improved the ranking power, which achieves the Top 3 place when compared with top 20 submissions on D3R website (the best performer in D3R achieves $\rho =0.54$ and $\tau =0.39$),^{86, 102, 103, 107–109} as can be seen in Figure 6. It should be noted that our ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ is a general scoring function evaluated for this target-specific challenging case. The scoring power is consistently improved by ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ since the Pearson’s R and RMSE of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are better in general.

Table 3.

Scoring and ranking performances of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9, ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on BACE1 dataset.

Scoring functions	Pearson R	Spearman $\rho$	Kendall $\tau$	RMSE
Vina	0.334	0.332	0.222	1.842
${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$	0.293	0.299	0.201	2.441
${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$	0.345	0.307	0.211	1.790
Lin_F9	0.481	0.439	0.311	1.950
${\text{Δ}}_{\mathbf{L}\mathbf{i}\mathbf{n}\mathbf{\_}\mathbf{F}9}\mathbf{X}\mathbf{G}\mathbf{B}$	0.517	0.481	0.349	1.518

Figure 6.

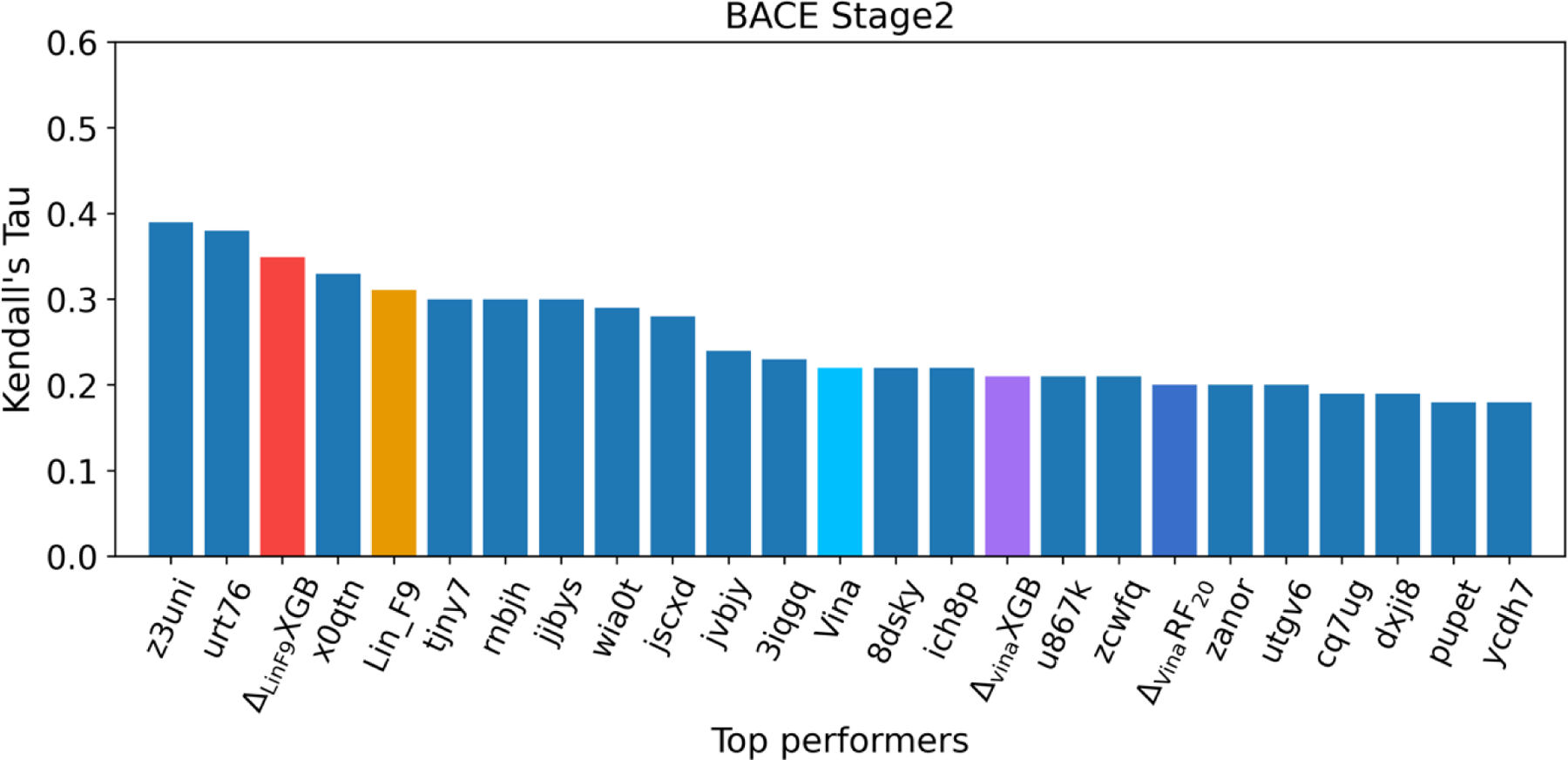
Affinity ranking performances of top 20 performers in D3R GC4 as well as five scoring functions (Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9,${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$) for the BACE1 Stage 2. Ranking power is evaluated by Kendall rank correlation coefficient.

CatS dataset

The GC4 CatS dataset is composed of 459 small molecule inhibitors with measured binding affinities spanning over three orders of magnitude range of IC₅₀ (pIC₅₀ range from 5.0 to 8.2).⁸⁶ The challenge for ranking these CatS inhibitors might come from their large size, high flexibility and similar chemical structures. The D3R organizers observed an obvious improvement in participant performance for CaS between GC3 and GC4, which may come from the use of GC3 CatS data or other CatS data from ChemBL^110–112 to develop target-specific machine learning models.^{86, 87} Similarly, we evaluated the ranking performance of five general scoring functions: Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on GC4 CatS dataset. The poses were obtained from Max Totrov group’s submitted data on D3R website.¹⁰⁷ They have participated in both GC3 and GC4 CatS Sub-challenges with available predicted pose structures, and their submitted data performs very well on pose prediction (Top 2 pose prediction in GC3⁸⁷). Based on their predicted poses for 459 CatS inhibitors, Table 4 illustrates the scoring and ranking powers of the five scoring functions on LocalOpt pose. For the ranking power comparison, Spearman’s $\rho$ of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are 0.430, 0.430, 0.399, 0.446 and 0.457, respectively. The Kendall’s $\tau$ of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are 0.293, 0.296, 0.275, 0.304 and 0.309. The improvement of ranking power for CatS is not as significant as the above BACE1. This could be attributed to either limitation of general scoring function for CatS or narrow binding affinities range of the dataset (only three orders of magnitude range for 459 CatS inhibitors). In Figure 7, we also compared with top 20 submissions on D3R website,^{86, 107, 108} ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ only ranks at the 15^th place. The top 2 performers in D3R GC4 CatS used target-specific 3D-QSAR model¹⁰⁷ and target-specific ligand-based deep neural network model (unpublished yet).

Table 4.

Scoring and ranking performances of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9, ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on CatS dataset.

Scoring functions	Pearson R	Spearman $\rho$	Kendall $\tau$	RMSE
Vina	0.427	0.430	0.293	0.841
${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$	0.455	0.430	0.296	0.621
${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$	0.441	0.399	0.275	0.657
Lin_F9	0.451	0.446	0.304	0.680
${\text{Δ}}_{\mathbf{L}\mathbf{i}\mathbf{n}\mathbf{\_}\mathbf{F}9}\mathbf{X}\mathbf{G}\mathbf{B}$	0.464	0.457	0.309	0.611

Figure 7.

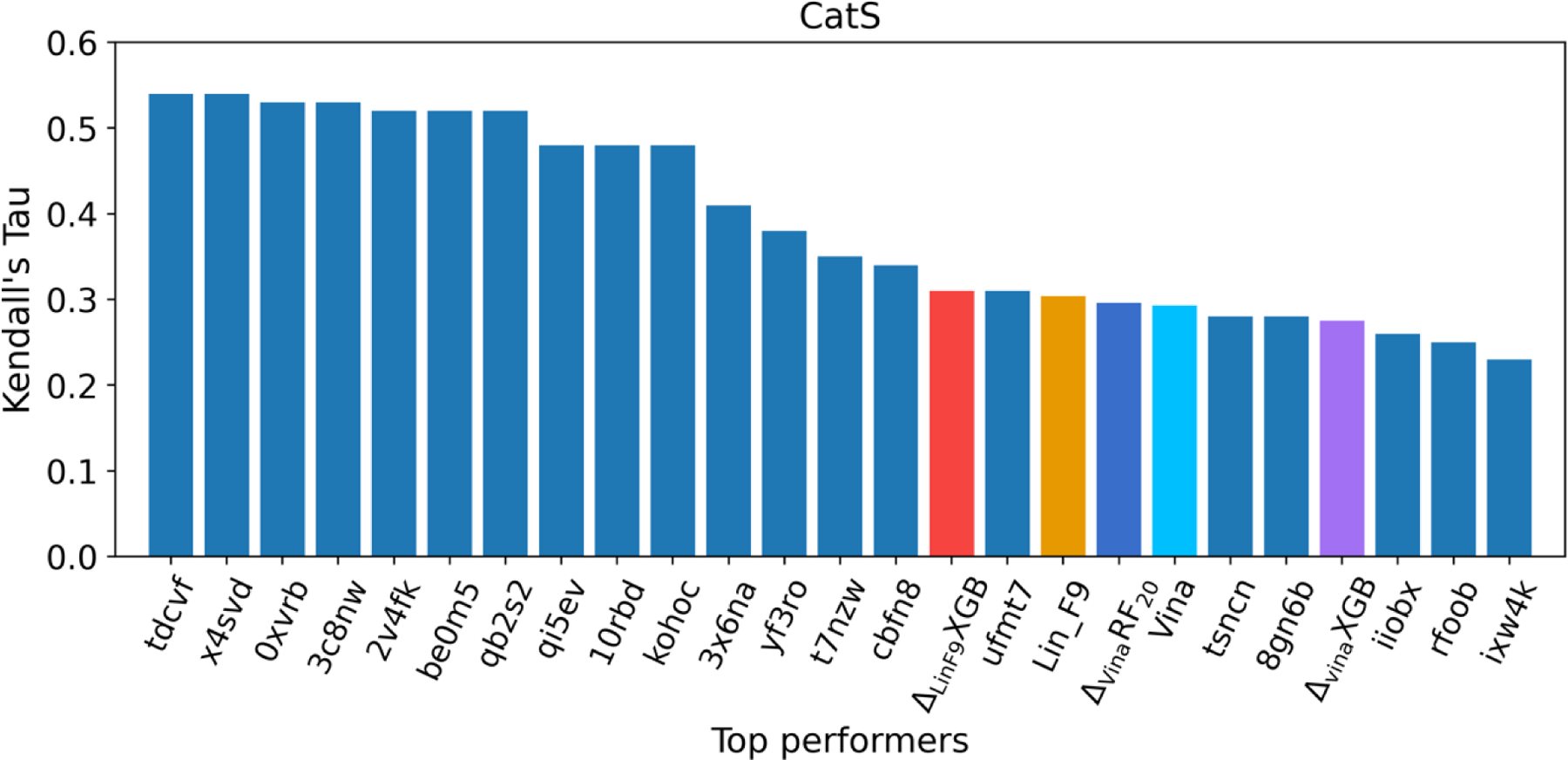
Affinity ranking performances of top 20 performers in D3R GC4 as well as five scoring functions (Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, Lin_F9,${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$) for the CatS dataset. Ranking power is evaluated by Kendall rank correlation coefficient.

Assessment of Screening Power on LIT-PCBA Dataset

Many previous studies evaluated virtual screening methods based on the Directory of Useful Decoys (DUD)¹¹³ and its successor DUD-E¹¹⁴, in which most of the presumed decoys have not been experimentally verified. To overcome this drawback, recently Tran-Nguyen and co-workers proposed LIT-PCBA,⁷⁵ a dataset derived from dose-response assays in the PubChem BioAssay database.^{115, 116} All the actives and inactives in LIT-PCBA were taken from the experimental data under homogeneous conditions. Preliminary virtual screening (VS) experiments indicated that LIT-PCBA is very challenging, due to the (I) high imbalance active/inactive compounds to mimic the real screening hit rate, (II) common molecular properties shared between active and inactive compounds, (III) weak potencies of the active compounds. One main limitation of LIT-PCBA dataset is that, more than half of the primary assays (8 of 15 targets) are cell-based phenotypic assays, so many actives are not validated against their putative target. Structure-based virtual screening tests on this benchmark may have some issues, nevertheless, LIT-PCBA still provide valuable clues for evaluation of scoring functions in large-scale VS.

Here, VS experiments on all 15 targets in LIT-PCBA were carried out using the E2E docking protocol as described above in CASF-2016 docking test. It should be noted that, in order to save the CPU cost, the PDB templates of some targets (targets with more than 100,000 compounds) used for docking experiments are less than the original LIT-PCBA provided. In addition, some targets in LIT-PCBA, such as ALDH1, IDH1 and KAT2A, have more than one ligand binding site in the PDB templates (shown in Figure S7). Based on the assay description and co-crystal ligand type, we only selected one docking site for each target. Also, previous ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$ is excluded in this VS evaluation since it needs to calculate the time-consuming ligand stability features using RDKit (need to generate maximum 1000 conformers per ligand).

As shown in Table 5, the EF_1% metric is used as the quantitative indicator to evaluate the screening performances of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on LIT-PCBA dataset. The average EF_1% metric of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ over all 15 targets is 5.55, which clearly outperforms Vina (average EF_1% = 2.78), ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$(average EF_1% = 3.18) and Lin_F9 (average EF_1% = 2.21). Similar with the previous virtual screening results from Tran-Nguyen et al,⁹⁰ the average EF_1% values range from 2 to 6, indicating the challenge of the dataset. In addition, counting number of targets that satisfy the increasing thresholds (2, 5, and 10) of EF_1% values, serves as a comprehensive metric to evaluate the generalization ability of scoring function on diverse targets. As can be seen, ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ achieves the best screening performance among these four scoring functions. At EF_1% > 2, EF_1% >5, and EF_1% >10, number of satisfied targets for ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ are 13, 8 and 2, respectively. Vina only have 6 satisfied targets at EF_1% > 2 threshold, limiting its applicability in real virtual screening. Two target sets (TP53 and VDR) are really challenging for ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ since it yields EF_1% < 2. These two challenge cases were also observed by Tran-Nguyen et al,⁹⁰ and they mentioned the main reason for this failure is the weak potencies of the actives. Overall, the results indicate that ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ has the top early hit enrichment ability among these four scoring functions for this challenging LIT-PCBA dataset.

Table 5.

Screening performance comparison of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on LIT-PCBA dataset.^a

Target set	Scoring Function				PDB Templates	Number of Actives	Number of Inactives
	Vina	${\text{Δ}}_{\text{Vina}}\text{R}{\text{F}}_{\text{20}}$	Lin_F9	${\text{Δ}}_{\text{Lin\_F9}}\text{XGB}$
ADRB2*	0	0	0	11.76	4	17	312,433
ALDH1	1.49	1.66	1.58	6.46	2	7167	137,822
ESR1-ago*	15.38	15.38	0	7.69	15	13	5,582
ESR1-ant*	3.92	2.94	2.94	3.92	15	102	4,947
FEN1	0.54	0.81	1.90	2.17	1	369	355,323
GBA	4.82	6.63	7.23	9.64	3	166	294,202
IDH1	0	0	2.56	5.13	10	39	361,691
KAT2A	0.52	0.52	2.06	7.73	1	194	348,257
MAPK1*	2.92	1.95	1.62	2.60	15	308	62,522
MTORC1*	2.06	3.09	2.06	2.06	11	97	32,972
OPRK1*	0	0	4.17	12.5	1	24	269,776
PKM2	1.65	2.93	0.73	2.56	2	546	245,485
PPARG*	7.41	11.11	3.70	7.41	15	27	5,210
TP53*	0	0	2.53	1.27	6	79	4,168
VDR	1.02	0.68	0.11	0.34	1	882	355,094
Average	2.78	3.18	2.21	5.55
EF1% > 2	6	6	8	13
EF1% > 5	2	3	1	8
EF1% > 10	1	2	0	2

^aEnrichment factor at top 1% (EF1%) is used as the quantitative indicator to evaluate the screening performance for each target set. The average EF1% over all 15 targets are highlighted in bold. PDB templates same as the original benchmark used are highlighted in green color. The 8 targets using cell-based phenotypic assays are marked with *.

In addition, we compared the ROC curves and AUC values (in the Table S5, Figure S8 and S9 of the Supporting Information) in this evaluation. The average AUC values of Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$, Lin_F9 and ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ on LIT-PCBA benchmark are 0.571, 0.560, 0.586 and 0.603, respectively. The AUC results are quite different from the EF_1% results, since ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ only shows slightly better performance based on AUC values. It is due to the reason that EF_1% metric focuses on the early hit enrichment. The ROC curves in Figure S9 also show that, compared with Vina, ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$ and Lin_F9, actives in 7 of 15 targets (ADRB2, ALDH1, GBA, IDH1, KAT2A, OPRK1 and PPARG) can be earlier enriched by ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$.

In Table 6, we also collected LIT-PCBA benchmark test results from three other groups. Tran-Nguyen et al⁹⁰ evaluated 5 scoring functions (Surflex,¹¹⁷ Pafnucy,^{24${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$},⁶⁶ IFP¹¹⁸ and GRIM¹¹⁹) where the IFP achieved the best performance (average EF_1%= 7.46). They used Surflex-Dock to generate top 20 poses for each ligand and other 4 scoring functions were used to re-scoring these poses. For targets with several PDB templates, the highest score value for each compound was used to evaluate the early hit enrichment performance (for IFP and GRIM, the score for each compound is the highest similarity between the templates and the docking poses). Compared with original Surflex-Dock, all re-scoring methods improved the screening performance a lot, and the re-scoring based on simple interaction fingerprints (IFP) or interaction graphs (GRIM) outperforms ML scoring functions. It should be noted that the performance of IFM and GRIM are highly dependent on the PDB template: choosing one that is not well represented in the dataset can lead to much worse results. Zhou et al¹²⁰ reported the test results of their template-based virtual screening models (FINDSITE^comb2.0 and FRAGSITE), which also showed comparable screening performance (FRAGSITE’s average EF_1%= 4.78). Sunseri et al¹²¹ assessed the built-in CNN models of GNINA¹²² compared to 4 other scoring functions (RFScore-4,¹²³ RFScore-VS,⁴⁹ Vina,⁴⁵ Vinardo¹²⁴). Their CNN default (Affinity) also achieved comparable performance (average EF_1%= 4.64). It is interesting to note that, the early enrichment performance of Vina (average EF_1%= 2.78) in our test is better than their Vina result (average EF_1%= 1.71), despite the average AUC values of Vina are the same (average AUC = 0.57 in both our and their tests). We find that the docking protocols are somewhat different: (I) they used one conformer per ligand for docking, while we used maximum 10 conformers per ligand for docking; (II) they used --autobox_add 16 to define docking box, while we used the default --autobox_add 4; (III) they used all the PDB templates for docking, while we used less PDB templates for some targets. One comparable target is ESR1_ago, since all 15 PDB templates are used in our docking. Our Vina test result is 15.38, while their Vina test result is 7.69. This target could contribute most of the Vina performance difference. The results suggest that LIT-PCBA benchmark early hit enrichment performance is not only dependent on the protein-ligand scoring function, but also is influenced by docking protocols and parameters.

Table 6.

Collected LIT-PCBA benchmark test results from different groups.

Model	Average EF1%	Number of Targets (EF1% > 2)	Number of Targets (EF1% > 5)	Number of Targets (EF1% > 10)	References
FINDSITEcomb2.0	3.04	5	4	1	Zhou et al120
FRAGSITE	4.78	11	5	1
RFScore-4	1.67	4	1	0	Sunseri et al121
RFScore-VS	1.75	5	2	0
Vina	1.71	6	1	0
Vinardo	1.70	4	2	0
CNN Default (Affinity)	4.64	6	6	2
Surflex	2.51	6	3	0	Tran-Nguyen et al90
Pafnucy	5.32	9	7	3
${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$	5.38	10	7	3
IFP	7.46	11	9	4
GRIM	6.87	12	8	5
Vina	2.78	6	2	1	Our test
${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$	3.18	6	3	2
Lin_F9	2.21	8	1	0
${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$	5.55	13	8	2

Moreover, target-specific scoring functions developed based on LIT-PCBA dataset (split into training set and validation set with ratio 3:1) show better performance over the generic scoring functions summarized in Table 6. Shen et al¹²⁵ reported their finding that ligand-based target-specific models (2D fingerprint-based QSAR models, best model performance EF_1% = 14.59) and structure-based target-specific models (descriptor-based XGBoost models, best model performance EF_1% = 8.93) outperform classical scoring function (Glide SP, EF_1% = 3.37) on 7 targets of LIT-PCBA validation set. With the abundant specific target training samples, target-specific scoring functions (both ligand-based and structure-based) can outperform current generic ML scoring functions as a promising alternative. However, it should be noted that the target-specific scoring function approach will not be applicable for a novel target with little experimental data available.

CONCLUSION

In order to develop a robust protein-ligand scoring function that can perform well for a variety of docking tasks, we have explored our previous developed Lin_F9 scoring function as the baseline and via $\mathrm{\Delta }$-Learning XGBoost approach to correct Lin_F9 score. The training set is enlarged to include docked poses, and physically meaningful features are explored. Our new scoring function ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ can not only perform consistently among the top compared to traditional scoring functions for scoring-ranking-screening powers of CASF-2016 benchmark, but also achieves superior scoring and ranking powers on real docked poses, including flexible re-docking, E2E docking and ensemble docking. Also, compared with Vina and ${\mathrm{\Delta }}_{\text{Vina}}{\text{RF}}_{20}$ and ${\mathrm{\Delta }}_{\text{Vina}}\text{XGB}$, ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ achieves better ranking power for target-specific cases (BACE1 and CatS) of D3R GC4. Large-scale docking-based virtual screening test on LIT-PCBA dataset demonstrates the reliability and robustness of ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ in virtual screening application. In summary, although there remains substantial room for virtual screening performance improvement, our extensive test results suggest that ${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ has improved both robustness and applicability of machine-learning scoring functions in real docking application, and can serve as a very useful re-scoring tool for structure-based inhibitor design.

DATA AND SOFTWARE AVAILABILITY

${\mathrm{\Delta }}_{\text{Lin\_F}9}\text{XGB}$ is accessible through: https://yzhang.hpc.nyu.edu/Delta_LinF9_XGB. RDKit 2020.09.4 version^{91, 92} is used to read SMILES string and add hydrogens and generate initial 3D conformer for each compound. OpenBabel 2.4.1 version¹²⁶ is used to generate multiple conformations based on RMSD. MGLTools 1.5.4 version¹²⁷ is used for preparing PDBQT files of protein and ligand. DockRMSD⁸⁵ is used for the calculation of RMSD between docking pose and original crystal pose of the same ligand molecule.