Multi-functional topology optimization of Victoria cruziana veins

Abstract

The growth and development of biological tissues and organs strongly depend on the requirements of their multiple functions. Plant veins yield efficient nutrient transport and withstand various external loads. Victoria cruziana, a tropical species of the Nymphaeaceae family of water lilies, has evolved a network of three-dimensional and rugged veins, which yields a superior load-bearing capacity. However, it remains elusive how biological and mechanical factors affect their unique vein layout. In this paper, we propose a multi-functional and large-scale topology optimization method to investigate the morphomechanics of Victoria cruziana veins, which optimizes both the structural stiffness and nutrient transport efficiency. Our results suggest that increasing the branching order of radial veins improves the efficiency of nutrient delivery, and the gradient variation of circumferential vein sizes significantly contributes to the stiffness of the leaf. In the present method, we also consider the optimization of the wall thickness and the maximum layout distance of circumferential veins. Furthermore, biomimetic leaves are fabricated by using the three-dimensional printing technique to verify our theoretical findings. This work not only gains insights into the morphomechanics of Victoria cruziana veins, but also helps the design of, for example, rib-reinforced shells, slabs and dome skeletons.

1. Introduction

Morphomechanics of biological tissues and organs has attracted much attention in recent years, with the aim to decode the interrelation of the geometric structures, chemical compositions, mechanical properties and biological functions of living systems. For instance, the elegant cellular architecture in plant tissues can effectively lower the stress magnitude in cell walls at the microscopic scale [1]. The active mechanical forces generated by their internal cells are crucial for the development of organoids and tissues at the macroscopic scale [2,3]. Recently, Yang et al. [4] studied the functions of highly porous bones of cuttlefishes and found that the functionally graded walls of the bones can enhance both their specific stiffness and energy absorption capacity. Fernandes et al. [5,6] reported that the double-diagonal and checkboard-like square morphology endows the skeleton of deep-sea glass sponges with outstanding strength robustness and buckling resistance.

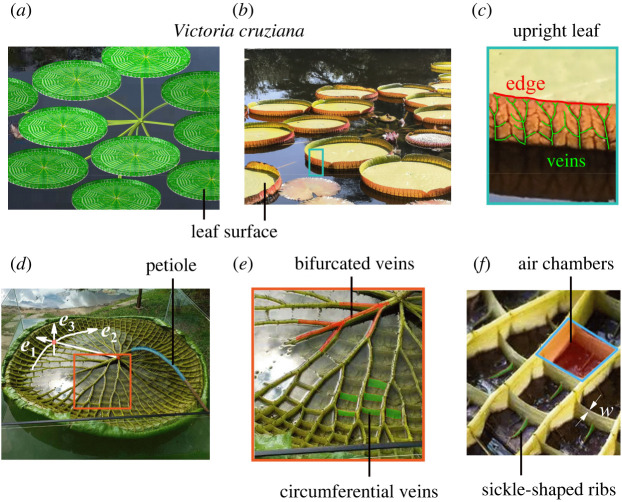
Veins are widely observed in animal and plant tissues, and they usually possess a complex fractal topology. Veins can not only transport nutrients and promote the exchange of matters between different tissues, but also bear mechanical forces from the environment. The morphomechanics of veins is of significance for understanding the growth and development of biological tissues [7–11]. In plants such as Victoria cruziana (figure 1a,b), the vein networks can greatly improve the stiffness of leaves. Since its discovery in 1801 in the Amazon, Victoria cruziana has attracted extensive attention from both scientists and engineers [12–14]. It has the largest leaves among almost all aquatic plants, with a diameter of up to 3 m [15,16], rendering superior photosynthesis, such that it can survive in the tropical rainforest. Besides, Victoria cruziana leaves exhibit an excellent load-bearing capacity. A mature leaf could withstand a compressive force of up to 500 N [13]. Victoria cruziana veins have porous sponge microstructures, which form numerous air chambers at the bottom of the leaves and endow the leaves with a large buoyancy [13,14]. Though the biological functions of Victoria cruziana veins have been recognized, it remains unclear how their optimal topology is influenced by biomechanical factors.

Figure 1.

(a,b) Leaves of Victoria cruziana. (c) Bifurcated veins on an upright leaf. (d) The vein network on the bottom of the leaf with the radial direction e₁ and the circumferential direction e₂. The normal direction of the leaf is e₃. (e) The bifurcated radial veins (red colours) and circumferential veins (green walls). (f) Magnified photo of the air chambers and sickle-shaped ribs, where w denotes the wall thickness of the circumferential veins. Photo (b) was taken at Beijing Botanical Garden, China, and photo (d) was taken at Yuanmingyuan Park, China.

The optimal design of free-form, rib-reinforced shell structures is of technologically significant interest in many engineering fields [17–23]. Attempts have been made to attain the optimized layout of ribs that can maximize the stiffness and strength of the structures [20,21,23–26]. In these previous studies, however, the functions of the ribs, such as heat conduction [27] and mass transport, have not been taken into account in the topological optimization of structures. The coupling effects of structural stiffness and nutrient transport on the layout of leaf veins were studied by using the theory of thin plates or shells [28–31]. To date, however, there is still a lack of an efficient topological optimization approach to investigate the three-dimensional hierarchical and multi-functional vein networks.

In this work, we investigate the three-dimensional and multi-functional vein network in Victoria cruziana leaves (figure 1c,d) by using a topology optimization method [32,33], in which both the mechanical performance and nutrient transport of veins are considered. This method can well reproduce the hierarchical vein networks in Victoria cruziana leaves, each of which has radial veins with gradient cross-sections and perpendicular to the leaf surface.

It is found that the vein network is optimal in the functions of both nutrient transport and load-bearing. Especially, the branching order, the non-uniform pressure, and component sizes of the network play important roles in the circumferential vein developments. Our findings also reveal that a better layout and morphology of the circumferential veins make a great contribution to the leaf stiffness, endowing the leaf with an excellent load-bearing capacity. In addition, artificial leaves fabricated by the Polyjet three-dimensional printing method [34] are used to verify our theoretical findings.

2. Material and methods

During the growth of a Victoria cruziana leaf, veins evolve on its lower surface to construct a network structure that can achieve its multiple biomechanical functions with high robustness [10,11]. Topology optimization [33,35–37] provides an efficient tool to design engineering structures with better properties and functions and to mimic the growth processes of biological structures. In the past few decades, some optimization techniques have been established, e.g. the model of solid isotropic material with penalization (SIMP) interpolation [33,36], the level set function [37], the moving morphable component [35] and the ground structure [38]. Optimization problems can be solved by using different approaches such as the optimality criteria (OC) method [33,36], the sequential linear/integer programming method [33,39], the method of moving asymptotes [40], and the non-gradient method [41–43]. These methods have been used in diverse fields of, for example, additive manufacturing [44,45], metamaterials [46–49], bionics [32,48,50,51], medical devices [52], flexible electronics [53], soft robotics [54,55] and aerospace [22,27,56].

In this work, the SIMP topology optimization method combined with the OC algorithm is applied to study the structural design of Victoria cruziana leaves. Particular attention is paid to the topological optimization of the veins on the lower surface of the leaf. The three-dimensional vein network, rather than the leaf surface itself, is the design domain of optimization (figure 1). The mathematical programming of the compliance minimization problem is formulated as [32,33,36]

$$\begin{array}{rl}\underset{\mathbf{x}}{min}:\hspace{0.17em}J=& \hspace{0.17em}{\mathbf{F}}^{\mathrm{T}}\mathit{u}\\ \mathrm{subject}\hspace{0.17em}\mathrm{to}:\hspace{0.17em}\mathbf{K}(\mathbf{x})\mathbf{u}=& \hspace{0.17em}\mathbf{F},\\ V(\mathbf{x})/V_0\le & \hspace{0.17em}{f}^{\ast },\\ G(\mathbf{x})\le & \hspace{0.17em}{R}_{max},\\ 0\le x_i\le & \hspace{0.17em}1,(i=1,2,\cdots ,n),\end{array}$$ 2.1

where the compliance J denotes the external work under a specified load, u and F are the global displacement and force vectors, respectively, K(x) is the global stiffness matrix, x (x_i, i = 1, 2, …, n) is the vector of design variables, n is the total number of elements in the design domain, $V(\mathbf{x})={\sum }_{i\in \mathrm{\Omega }}{x}_i{v}_i$ and $V_0={\sum }_{i\in \mathrm{\Omega }}{v}_i$ are the material volume during the optimization process and the volume of the design domain, respectively; v_i is the volume of the ith element. f =$V(\mathbf{x})/V_0$ and f* are the material volume fraction and the prescribed volume fraction. The geometric constraint $G(\mathbf{x})$ [50,57,58] could be added to equation (2.1) by tuning the maximum component size R_max for the local material layout in the optimization module of the software Abaqus. Assume that the veins and leaves are composed of the same material. The elastic modulus of element i can be described as

$$E({\rho }_i)=E_{min}+(E_{\hspace{0.17em}\mathrm{b}}-E_{\hspace{0.17em}min})\rho {\hspace{0.17em}}_i^{{\eta }_{\hspace{0.17em}1}},\hspace{0.17em}{\rho }_{\hspace{0.17em}i}\in [0,1],$$ 2.2

where E_b is Young's modulus of the material, E_min = 10⁻⁹E_b is a small Young's modulus assigned to the void regions to avoid numerical singularity [33,36], and η₁ is a penalty factor (typically, η₁ is about 3.0) introduced to obtain the black-and-white results. To accelerate the convergence, we take η₁ = 4.0 [32,59], which does not interfere with the objective value of optimization. Let ρ_i(i = 1, 2,…, n) denote the physical density of the ith element. To avoid the checkboard problem [33,36,60,61], we define

$${\rho }_i={\displaystyle \frac{{\sum }_{\hspace{0.17em}j\in N_i}w({\mathit{r}}_i,{\mathit{r}}_j)v_j{x}_j}{{\sum }_{\hspace{0.17em}j\in N_i}w({\mathit{r}}_i,{\mathit{r}}_j)v_j},}$$ 2.3

where $N_i=\{\hspace{0.17em}j\hspace{0.17em}=|||{\mathit{r}}_i-{\mathit{r}}_j||\le R\hspace{0.17em}\}$, and R is the filtering radius of the ith element. The elements located in this circle region all make contributions to the stiffness of the ith element. Besides, R may approximately control the minimal size of the optimized struts [33,36], r_i and r_j are the position vectors of element i and j (j ∈ N_i), respectively, w(r_i, r_j)= max(0, R-$||$r_i − r_j$||$) is the weight factor, and v_j is the volume of element j (j ∈ N_i). For the minimum size control in topology optimization, the reader may refer to previous studies [57,62]. A smaller J indicates that the structure has a higher capacity to resist deformation under the specified load.

In this study, we also consider the efficiency of nutrient transport in the optimization of the vein network. The Victoria cruziana leaf has radial bifurcated or fractal veins similar to those in Hedera canariens leaf [63], as shown in figure 1d,e. Therefore, a two-dimensional model is used to analyse nutrient transport. The steady nutrient transport equation is written as [28,30,33,64,65]

$${\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(\kappa {\displaystyle \frac{\mathrm{\partial }\xi }{\mathrm{\partial }x}}\right)+{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }y}\left(\kappa {\displaystyle \frac{\mathrm{\partial }\xi }{\mathrm{\partial }y}}\right)=-Q,}}$$ 2.4

where ξ is the concentration of the nutrient matter, κ is the isotropic nutrient transport coefficient, and Q is the nutrient generating rate. The transport efficiency maximization problem [28,30,65] is expressed as

$$\begin{array}{rl}\underset{\mathbf{x}}{min}:\hspace{0.17em}{C}_{\hspace{0.17em}\mathrm{H}}=& \hspace{0.17em}{\xi }^{\mathrm{T}}{\mathbf{K}}_{\mathrm{H}}\xi \\ \mathrm{subject}\hspace{0.17em}\mathrm{to}\hspace{0.17em}:\hspace{0.17em}{\mathbf{K}}_{\mathrm{H}}(\mathbf{x})\xi =& \hspace{0.17em}{\mathbf{F}}_{\mathrm{H}},\\ V(\mathbf{x})/V_0\le & \hspace{0.17em}{f}^{\ast },\\ 0\le x_i\le & \hspace{0.17em}1,\hspace{0.17em}(i=1,\hspace{0.17em}2,\dots ,\hspace{0.17em}n),\end{array}$$ 2.5

where C_H is the objective function and denotes the generalized work driven by nutrient concentration $\mathit{\xi }$, K_H is the global matrix of nutrients in the leaf (figure 1a,b), and F_H is the vector of the nutrient transport from petiole (figure 1d). The nutrient transport coefficient κ in the ith element is [33,64]

$$\kappa ({\rho }_i)={\kappa }_{min}+({\kappa }_{\mathrm{b}}-{\kappa }_{min}){\rho }_i^{{\eta }_{\hspace{0.17em}2}},$$ 2.6

where κ_b denotes the normalized transport coefficient, κ_min is a small transport coefficient assigned to the void regions to avoid the numerical singularity [30], and η₂ is a penalty factor. In the following simulations, we set κ_b = 1.0, κ_min = 10⁻⁴κ_b, and η₂ = 4.0. The smaller the value of C_H, the more efficient the nutrient transport. To verify the effectiveness of this method, we provide two benchmark examples, with a square and a rectangular domain, respectively (electronic supplementary material, figure S1).

In this study, the optimization of the three-dimensional vein network is viewed as a synergetic process dictated by both its load-bearing capacity and nutrient transport efficiency, though many other factors may influence its growth. As observed in figure 1, the generation of the bifurcated veins in the radial direction e₁ prominently promotes the nutrient transport efficiency [28,30,31]. The circumferential veins have a smaller wall thickness w than the radial veins (figure 1f). Therefore, it is emphasized that the circumferential veins in a Victoria cruziana leaf are optimized to sustain a balance of the nutrient transport efficiency and the overall stiffness of the leaf. Therefore, we divide the synergetic optimization process into two main steps. In §3.1, we first use the nutrient transport model to analyse the morphology of bifurcated veins in the radial direction, and in §3.2, we use the maximum stiffness model to elucidate the generation of circumferential veins.

3. Results

3.1. Radial veins

A Victoria cruziana leaf [12,13,18,66,67] has a circular and flat disc, surrounded by an upright leaf of several centimetres in height along the direction e₃ (figure 1c,d). Complex and rugged veins are distributed on the lower surface of the disc (figure 1d), rather than embedded in the disc [8–11]. Along the radial direction e₁ (figure 1d), the radial veins have hierarchical or fractal branches, with a decreasing height in the upward direction e₃.

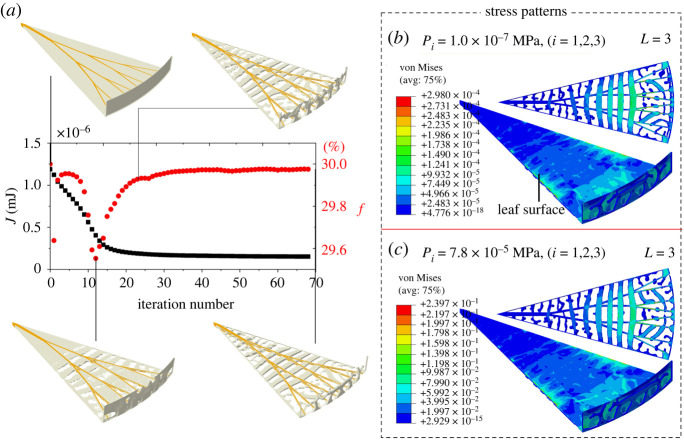
In the analysis of nutrient transport in a Victoria cruziana leaf, a nutrient resource is assumed at the centre (highlighted in red) of the circular design domain (figure 2 and electronic supplementary material, figure S2). The discretized design domain is composed of the uniform linear square 4-node elements with a dimensionless unit edge length (electronic supplementary material, figure S2). Using the method presented in §2, the optimized structures of radial bifurcated veins are generated by setting two key parameters, i.e. the target material volume fraction f* and the filtering size R. For example, R = 3 denotes that the filtering radius is three times the uniform square mesh size. In figure 2a, as f* increases, the branching order L (figure 2b) becomes larger and the value C_H becomes smaller, indicating a higher efficacy of nutrient transport. Besides, as the filtering radius R decreases and the branching order L increases, the sizes of the optimized veins decrease remarkably (figure 2a). This means that the structure containing a smaller branching order L features a lower capacity for nutrient transport (figure 2c,d), which motivates us to make a comparative analysis of the branching order in §3.2. Besides, the obtained bifurcated topology can transport nutrients efficiently from the radial veins to the external edges (figure 2e) of the upright leaf.

Figure 2.

(a) Optimized and bifurcated veins for f* = 20% and 30%, where we take different values of filtering radius R. (b) The nutrient delivery versus the branching order L. (c) Convergence of the objective function C_H. (d) Relation between the objective function C_H and the filtering radius R. (e) Veins in the upright leaves. The red, yellow, and green colours represent nutrient resources, optimized radial veins, and leaf, respectively.

3.2. Circumferential veins

The superior load-bearing capacity of a mature Victoria cruziana leaf originates from numerous air chambers enclosed by the radial and circumferential veins. These air chambers (figure 1f) endow the leaf with astonishing buoyancy [13,18,68]. Besides, the plate-like veins in the circumferential direction (figure 1e,f) connect the radial veins. The circumferential and radial veins work synergistically as a network to stiffen the leaf structure. Here, instead of considering the maximal buoyancy as the objective of optimization [60,69,70], we apply mechanical pressures and wind loads on the leaf surface (figures 1a,b and 3, and electronic supplementary material, figure S3) to mimic the natural environment of Victoria cruziana leaves.

Figure 3.

Numerical result of an optimized three-dimensional vein network, including the radial bifurcated veins (yellow colour) and optimized veins (grey colour). The veins consist of the circumferential structures, veins in the upright leaf, and the sickle-shaped ribs. The sickle-shaped ribs are along the radial direction (purple arrow). The pressures and wind load are P₁ = P₂ = P₃ = 1.0 × 10⁻⁷ MPa and P_W = 1.0 × 10⁻⁸ MPa, respectively, which are applied on the upper surface of the leaf (green colour region). The target volume fraction of material is f* = 30%, and the maximum size is R_max = 4 mm. The details of the design domain are given in electronic supplementary material, figure S4. l denotes the distance measured from the petiole to the marked red point. A larger l indicates a wider layout of the optimized circumferential veins.

In §3.1, we have studied the influence of the branching order L on the nutrient transport efficiency, and now we further address its influence on the load-bearing capacity. For illustration, we compare the parametrized and bifurcated vein networks with L = 3 and L = 2 (electronic supplementary material, figure S3, and figure 2b). In the first example, we consider a radial vein with L = 3, as shown in electronic supplementary material, figure S4. The three-dimensional optimization model consists of three parts, including the leaf with a small thickness (green region, electronic supplementary material, figure S4a), the radial vein (yellow region, electronic supplementary material, figure S4b), and the pre-designed domain for optimizing the circumferential veins (grey regions, electronic supplementary material, figure S4b). All geometric parameters are shown in electronic supplementary material, figure S4c, where the thickness decreases from $t_{\hspace{0.17em}1}^{\hspace{0.17em}(d)}$ = 2.0 mm to $t_{\hspace{0.17em}2}^{\hspace{0.17em}(d)}=$ 0.6 mm along the radial direction e₁. The radius and thickness of the leaf are r = 100.0 mm and t^(s) = 1.0 mm, respectively. The height of the upright leaf is set as h = 9.6 mm. To reduce the computational cost, we analyse only one representative part of the sector domain (electronic supplementary material, figure S4a), with a central angle of θ = π/6, as shown in figure 3 and electronic supplementary material, figure S4a.

The applied pressure is uniformly distributed on the three regions of the upper leaf surface (figure 3) with ${\mathbf{P}}_1={\mathbf{P}}_2={\mathbf{P}}_3$, and the uniform wind load ${\mathbf{P}}_{\mathrm{w}}$ is normally applied on the surface of the upright leaf (figure 3 and electronic supplementary material, figure S4a). The loads keep constant during the optimization process. In the stiffness maximization problem, the Young's modulus and Poisson's ratio of the basal material are taken as E_b = 10 MPa and ν = 0.3, respectively [12].

The model (electronic supplementary material, figure S4a) is discretized into 0.31 million 8-node linear brick, reduced integration elements (C3D8R), and the maximum element size is 0.2 mm (electronic supplementary material, figure S4d). This large-scale optimization problem [32,51] is performed by the commercial software Abaqus, where we make use of its parallel computation platform. The optimization problem is solved by the OC algorithm [33,36]. The target volume fraction f* of material is set as 20% or 30% in different cases. By changing the maximum geometric size R_max defined in equation (2.1), the local accumulation of material can be avoided [50,57,58].

It was reported that a Victoria cruziana leaf with a diameter of 3 m can bear a load of about 500 N (https://www.52zzl.com/wanglian/4181.html), which induces a pressure of 7.07 × 10⁻⁵ MPa. This value is close to our experimental test result of 6.4 × 10⁻⁵ MPa, which will be described in §4. It is worth mentioning that due to the small thickness of the leaf, a larger pressure may cause distortions of the three-dimensional elements, which may cause an unexpected stop of iteration (electronic supplementary material, figure S4d). To overcome this difficulty, we specify the pressure on the leaf surface with a smaller value P₁ = P₂ = P₃ = 1.0 × 10⁻⁷ MPa in figure 3, and the hypothetical wind load P_W = 1.0 × 10⁻⁸ MPa. Linear elastic finite-element analysis is made in the optimization process. The leaf edges (electronic supplementary material, figure S4a) and all freedoms in the Euclidean space of the petiole are fixed. In the design domain, the target volume fraction of material is set as f* = 30%.

Figure 3 shows the optimized structure with J = 1.55 × 10⁻⁷ mJ, which features a complex three-dimensional vein network. Its circumferential structures connect the bifurcated veins. This kind of layout not only promotes the transport of nutrients but also more importantly enhances the stiffness of the whole leaf. Numerous air chambers separated by the veins (figure 3) endow the leaf with an outstanding buoyancy. It is seen that the distribution of the circumferential veins is approximately isometric along the radial direction e₁. However, due to the coupled effects of wind loads and pressures, the veins near the edge evolve complex morphologies (figure 3).

In addition, there are many auxiliary ribs along the radial direction e₁ (figure 3), which can increase the flexural stiffness of the circumferential veins. As shown in figure 1f, due to the gradient thickness of the veins in the direction e₃, a big pressure difference could be generated by the captured air between the adjacent air chambers (figure 1f). This helps understand why the Victoria cruziana leaf evolves these kinds of ribs to support the circumferential veins.

The history of the objective function J and the volume fraction f of the material (figure 4a) show that the optimization algorithm is effective and stable. A lower stress is uniformly distributed over the middle part of the leaf surface (figure 4b), while higher stress concentration occurs on the leaf edges because of the boundary condition. Besides, a high-tension stress field occurs on the circumferential veins (figure 4b), suggesting that the compressive force applied on the leaf surface induces the tensile deformation of the circumferential veins. This deformation mechanism ensures the superior load-bearing capability of the Victoria cruziana leaves. Further, we simulate two more cases, which undergo higher pressures of 6.4 × 10⁻⁵ MPa (electronic supplementary material, figure S5) and 7.8 × 10⁻⁵ MPa (figure 4c), respectively. The stress fields show a similar pattern, as shown in figure 4b. In the following analysis, therefore, we will assume a smaller pressure of 1.0 × 10⁻⁷ MPa to study the design of circumferential veins.

Figure 4.

Iteration history and stress analysis. (a) History of the objective function J and the volume fraction f of material. The yellow and grey colours are the bifurcated veins and the design domain for the circumferential veins, while the leaf surface (green colour in figure 3) is hidden for clear illustration of the optimized veins. (b,c) The von Mises stress fields under uniform pressures of 1.0 × 10⁻⁷ MPa and 7.8 × 10⁻⁵ MPa, respectively, showing that the pressure amplitude has little influence on the optimization results of the vein topologies and stress patterns. The corresponding objective function values are J = 1.55 × 10⁻⁷ mJ and J = 0.096 mJ, respectively.

3.3. Effects of branching order and non-uniform pressure

Now we investigate the effects of the branching order of radial veins on the structural stiffness of the Victoria cruziana leaf. As concluded in §3.1, under a fixed material dosage, a vein network with a smaller L yields a lower nutrient delivery.

Further, we examine the effect of non-uniform pressure on the optimized architecture of veins. Figure 5 shows the optimization results of 12 representative examples under different pressures and branching orders. In these examples, we take the same optimization conditions, with the maximum component thickness R_max = 4 mm, the wind load P_W = 1.0 × 10⁻⁸ MPa and the element size being 0.2 mm. These examples are classified into the following four groups:

• (1) Group I: This group contains the cases a–c, which have a uniform pressure P₁ = P₂ = P₃ = 1.0 × 10⁻⁷ MPa and bifurcated radial veins with L = 2.
• (2) Group II: This group, including cases d–f, have radial veins with L = 2 and a hypothetic gradient pressure with P₂ = 3/5P₁, P₃ = 2/5P₁ and P₁ = 1.0 × 10⁻⁷ MPa.
• (3) Group III: This group (cases g–i) has the branching order L = 3, and the same uniform pressure as that in group I.
• (4) Group IV: In this group (cases j–l), the branching order is L = 3, and the pressure is the same as that in group II.

Figure 5.

Optimization results under different values of L and pressure. (a) Optimized veins in the 12 cases, which are divided into four groups. (b,c) The iteration histories of J in all cases. Under a specified value of f*, the stiffness of the optimized structure with L = 3 has a slight difference from that with L = 2. (d) Stress distributions in cases b and h. It is seen that increasing the branching order can make the stress distribution in the veins more uniform and thus enhance the load-bearing capacity of the leaf.

Besides, the three cases in each group have the target volume fractions f* = 20%, 25% and 30%, respectively.

As can be seen from the simulation results in figure 5b, the histories of the objective function J in these examples decrease smoothly in the logarithmic coordinate system. Figure 5c reveals that a higher material usage will enhance the stiffness of the leaf and converge to a smaller value of J. It is also seen from figure 5c that, under a specified value of f*, the stiffness of the optimized structure with L = 3 has a slight difference from that with L = 2. For example, the optimized J of cases a and g are 2.21 × 10⁻⁷ mJ and 2.24 × 10⁻⁷ mJ, respectively. However, increasing the branching order can make the stress distribution in the veins more uniform, thus enhancing its load-bearing capacity (figure 5d).

Now we compare the values of the parameters w, l and σ in the 12 cases, which quantify the morphological features of the circumferential vein networks. Here, $\sigma =\sqrt{{\sum }_i^n{(w_i-\tilde{w})}^2/N}$ defines the standard error of the wall thicknesses w_i of the circumferential veins, where N is the counted number of the circumferential veins, which are highlighted with red symbols in figure 5a, and $\tilde{w}={\sum }_i^N(w_i)/N$ is the averaged value of w_i (more details are given in electronic supplementary material, tables S1–S5). A small σ indicates that the wall thicknesses of the circumferential veins at different radial positions are close to each other. Due to the thickness variations of the veins, we measure twice to obtain the average values of these parameters, denoted as $\overline{w}=({\tilde{w}}_1+{\tilde{w}}_2)/2$, $\overline{l}$ and $\overline{\sigma }$.

Figure 6 gives the statistical average wall thickness $\overline{w}$, the maximum layout distance $\overline{l}$, and the standard error $\overline{\sigma }$ in all 12 cases (figure 5a). In figure 6a, it is found that a larger branching order L promotes a larger $\overline{w}$ under the same material dosage. For example, the radial veins with L = 2 are thicker than those with L = 3, as shown in figure 5a (cases a and g), which both have f* = 20%. Therefore, the optimized leaf in case g needs a larger $\overline{w}$ for the circumferential veins to compensate for the loss of its stiffness compared to case a. This finding is also verified by the cases under non-uniform pressures (e.g. cases d and j).

Figure 6.

(a) The average wall thickness w̅ of the circumferential veins. (b) The maximum layout distance l̅ from the red point to the petiole (figure 5a). (c) The uniform standard error σ̅ of the wall thicknesses of the circumferential veins along the direction e₁. (d) The phase diagram in the l̅ –σ̅ space. Quadrants I and IV indicate the optimized veins with non-uniform wall thickness. The optimized structures in quadrant III have a smaller layout distance. In region II, the circumferential veins have a relatively more uniform wall thickness and larger layout.

In addition, the result in figure 6b reveals that the maximum circumferential vein layout distance $\overline{l}$ has a remarkable increase in the case with a larger L. This finding can also be observed in the vein network of Victoria cruziana (figure 1), where its circumferential veins extend to the leaf edge.

As shown in figure 6c, the vein networks with a larger branching order have a smaller $\overline{\sigma }$. This tendency becomes more obvious as the material volume increases. When a non-uniform pressure is also applied to the leaf, $\overline{\sigma }$ is considerably reduced for the veins with a branching order of L = 2.

To further investigate the combined effects of the branching order and non-uniform pressure on the optimal morphology of circumferential veins, we give the $\overline{l}$ versus $\overline{\sigma }$ relations for all the 12 cases in figure 6d. The coordinate origin is set at the centre of $\overline{l}$–$\overline{\sigma }$, and the examples in quadrant II have a similar vein morphology and nutrient delivery capacity to the real veins of Victoria cruziana. The highlighted points in this region, including cases h, i, k and l, have a lower $\overline{\sigma }$ and a higher $\overline{l}$, because of the contributions of the larger branching order L = 3 and non-uniform pressure. By contrast, the radial veins of L = 2 have a larger $\overline{\sigma }$ and a smaller $\overline{l}$ in quadrant IV.

3.4. Size and morphology variations of circumferential veins

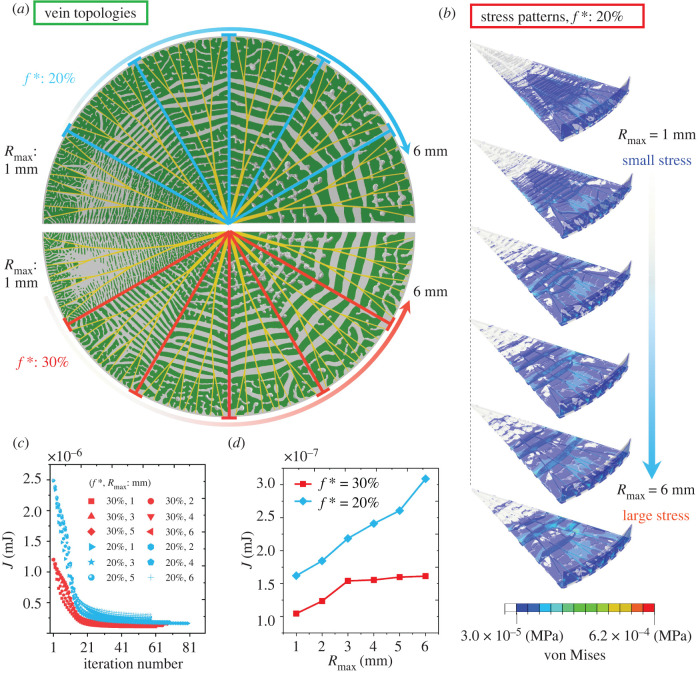
In the simulations, we set the maximal component thickness R_max in order to avoid material build-up in the circumferential veins during optimization. For example, R_max = 3.0 mm means that the wall thicknesses w of all circumferential veins are limited to be smaller than 3.0 mm (electronic supplementary material, tables S6–10). In this section, a finer grid is used to discretize the three-dimensional design domain, where the largest element size is 0.14 mm, with a total of 0.57 million three-dimensional elements. We take cases g and i (figure 5a) to uncover the effect of R_max on the leaf stiffness and vein morphology, with the target volume fraction of 20% and 30%, respectively (figure 7a). The two examples have a radial vein with L = 3 (electronic supplementary material, figure S3b). For each case, the value R_max ranges from 1 mm to 6 mm (figures 7a and 8a). Similarly, as discussed in §3.3, the parameters $\overline{l}$, $\overline{w}$ and $\overline{\sigma }$ are all calculated to examine the structural variations as shown in figure 8 with respect to R_max (electronic supplementary material, tables S6 and S10).

Figure 7.

Effects of R_max on the leaf stiffness and vein morphologies. (a) Optimized leaves of all cases. (b) Stress patterns with respect to R_max. (c,d) Histories of the objective function J with R_max. It is found that with increasing R_max, the maximal stress in the veins increases with R_max while the leaf stiffness decreases.

Figure 8.

Varying vein features with respect to R_max. (a) Optimized upright leaves. (b) The average wall thickness of the optimized circumferential veins. (c) The counted number and (d) the maximum layout distance of the circumferential veins. (e) The standard error of the wall thickness in circumferential veins. (f) The phase diagram of J in the l̅ –σ̅ space. Three highlighted points are located in the upper-left region, indicating that the vein networks can yield a high stiffness and load-bearing capacity of the leaf.

In figure 8b, the average wall thickness $\overline{w}$ increases with respect to R_max, which leads to a decrease in the number of circumferential veins N (figures 7b and 8c). Thus, the stress in the optimized veins gradually increases (figure 7b), resulting in a decrease in the leaf stiffness with increasing R_max (figure 7c,d).

In figure 8d,e, with increasing R_max, $\overline{l}$ decreases but $\overline{\sigma }$ increases. In the phase diagram of $\overline{l}$–$\overline{\sigma }$ (figure 8f), three highlighted points are located in the upper-left region, where the vein networks can yield a high stiffness and load-bearing capacity of the leaf. By contrast, one example is located at the left-bottom corner, which has smaller $\overline{l}$ and N, indicating a poor vein topology in the leaf. The size R_max plays a signficant role in the optimization of the vein net work and the mechanical behaviour of the leaf.

4. Experiments

To qualitatively verify the optimization results (figure 5a), we fabricate biomimetic leaves by using the Polyjet three-dimensional printing technique [34]. Three samples (I, II and III) are made, as shown in figure 9b, corresponding to the cases c, f and i (figures 5a and 9a), respectively. The minimum printing size of Objet 30 prime made by Stratasys is 16 μm, and the printing and supporting materials are polypropylene (material density: 9.2 × 10² kg m⁻³) and SUP705, respectively. The supporting material SUP705 is dissolved in water and can be easily removed by a high-pressure water jet. The experimental equipment is given in electronic supplementary material, figure S6. We adhere a layer of cling film with glue (electronic supplementary material, figure S7c), which helps improve the quality of the printed samples (electronic supplementary material, figure S7). The weights of glue and film can be ignored.

Figure 9.

Artificial leaves fabricated by three-dimensional printing technique and their load-bearing capacities. (a) Numerical results for the optimized structures of leaves, corresponding to cases c, f and i in figure 5a. (b) Three-dimensional printed leaves, fabricated according to the numerical optimization results. (c) Measurement of the load-bearing capabilities of the artificial leaves. Leaves II (case f) and III (case i), which are in the second quadrant (figure 6d), have better vein topology and higher load-bearing capacity than leaf I (case c), which is located in the fourth quadrant.

The optimized results obtained from our numerical simulations using Abaqus are generated and used in the input data of the software Rhino for the three-dimensional printing fabrication. Then three artificial leaf specimens are made, corresponding to the numerical examples described above. As can be seen in figure 9b, the printed biomimetic leaves can capture the prominent geometric features of the smaller struts because of the higher printing resolution. The weights of the three samples are 11.6 g, 11.8 g and 11.0 g, respectively. Due to the limitations of the printing condition, all printed leaves are scaled to 0.7 times the initial optimized results (cases c, f and i in figure 9a). In addition, the scaled leaves still have an identical stress pattern to the simulation results (figure 4b,c) because the symmetry in the boundary conditions and loads is not broken.

We use weights to mimic the external loads, which are placed at the centre of the leaf. The loads are 110 g, 120 g and 120 g for the cases c, f and i, respectively. Several tests have been made for each case, and the results are averaged. After removing the supporting material, the printed leaf surface becomes hard several hours later, which endows the leaf with a considerable stiffness. This enhanced surface ensures that the forces generated by the weight can be uniformly distributed to all veins.

According to the weight, the uniform load-bearing pressures are calculated as 1.1 N (P₁ = 6.5 × 10⁻⁵ MPa), 1.2 N (P₁ = 7.8 × 10⁻⁵ MPa), and 1.2 N (figure 9c) for the printed leaves I, II, and III, respectively. As aforementioned in figure 6d, leaves II (case f) and III (case i) are in the second quadrant, in which they have a better vein topology to enhance their load-bearing capacity than that of leaf I located in the fourth quadrant.

5. Conclusion

The outstanding load-bearing capacity of Victoria cruziana leaves results mainly from their peculiar hierarchical vein network structure. A multi-functional optimization method is proposed in this paper to investigate the biomechanical mechanisms in the three-dimensional topological morphology of the veins. The structural optimization of the connected radial and circumferential veins is dictated by the balance of the nutrient transport efficiency and the load-bearing capacity of the leaf. Our simulations show that radial veins with a large branching order L not only have a higher efficiency of nutrient delivery, but also are beneficial for the developmental morphologies and layouts of circumferential veins. The load transfer mechanism between the leaf surface and vein is uncovered through the stress pattern analysis. Besides, the experiments of three-dimensional printed artificial leaves also provide a support for our theoretical findings.

Finally, it is noticed that, in the water lily family Nymphaeaceae, apart from Victoria cruziana [12–15,17,68,71], the leaf of Euryale ferox Salisb. [72–74] also evolves a strong three-dimensional vein network. The multi-functional optimization method proposed in this paper may be extended to understand the possible mechanisms of their morphogenesis by introducing more possible influencing factors. The effects of the intrinsic active mechanisms associated with, for example, cells [2,75], genes [76–78], and biochemical signals on the topological evolution of plant or animal tissues deserve further theoretical and experimental efforts.

Data accessibility

All data needed to evaluate the conclusions in the paper are present in the paper and/or the electronic supplementary material [79]. Electronic supplementary material supporting this article is available online.

The custom codes for modelling and simulation are available from the corresponding author upon reasonable request.

Data have been included in the main paper and electronic supplementary material. The code for the first part of the calculation is available as electronic supplementary material. The second part of the calculation was conducted using Abaqus. This is commercial software which we are unable to share.

Authors' contributions

H.-K.Z.: data curation, investigation, methodology, software, validation, writing—original draft; J.Y.Z.: data curation, investigation, writing—original draft; W.F.: data curation, investigation, writing—original draft; H.C.Z.: funding acquisition, supervision, writing—review and editing; X.D.C.: methodology, writing—original draft; Z.-L.Z.: methodology, writing—review and editing; H.-P.Z.: validation, writing—original draft, writing—review and editing; X.-Q.F.: conceptualization, funding acquisition, methodology, project administration, resources, supervision, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

The authors declare no competing interests.

Funding

Support from the National Natural Science Foundation of China (grant nos. 11921002 and 11872232) is acknowledged.