Abstract
Intervertebral disc degeneration is a common disease that is often related to impaired mechanical function, herniations and chronic back pain. The degenerative process induces alterations of the disc’s shape, composition and structure that can be visualized in vivo using magnetic resonance imaging (MRI). Numerical tools such as finite element analysis (FEA) have the potential to relate MRI-based information to the altered mechanical behavior of the disc. However, in terms of geometry, composition and fiber architecture, current FE models rely on observations made on healthy discs and might therefore not be well suited to study the degeneration process. To address the issue, we propose a new, more realistic FE methodology based on diffusion tensor imaging (DTI). For this study, a human disc joint was imaged in a high-field MR scanner with proton-density weighted (PD) and DTI sequences. The PD image was segmented and an anatomy-specific mesh was generated. Assuming accordance between local principal diffusion direction and local mean collagen fiber alignment, corresponding fiber angles were assigned to each element. Those element-wise fiber directions and PD intensities allowed the homogenized model to smoothly account for composition and fibrous structure of the disc. The disc’s in vitro mechanical behavior was quantified under tension, compression, flexion, extension, lateral bending and rotation. The six resulting load-displacement curves could be replicated by the FE model, which supports our approach as a first proof of concept towards patient-specific disc modeling.
Keywords: Intervertebral disc, Diffusion tensor imaging, Magnetic resonance imaging, in vitro testing, Finite element modeling
1. Introduction
Intervertebral disc (IVD) degeneration is an aberrant cell-mediated response to progressive structural failure which leads to disc hernia- tions and chronic back pain (Adams and Roughley, 2006). In the United States and Switzerland, low back and neck pain are the number one causes of disabilities (IHME, 2016). In the healthy disc, compressive forces are transmitted through the gel-like nucleus pulposus (NP) which is restrained by the annulus fibrosus (AF). With increased degeneration, the IVD hydration level decreases followed by a reduction in disc height. The AF starts to act like a fibrous solid and resists compression directly (Adams and Roughley, 2006). The ensuing structural defects such as radial fissures, ingrowth of innervated fibrous tissue and inflammation (Setton and Chen, 2006) may cause disc herniations or discogenic pain (Brisby, 2006; Yang et al., 2015). From a mechanical point of view, disc degeneration generally increases joint laxity and stiffness (Ellingson et al., 2013). The clinical assessment of IVD pathology (e.g. Pfirrmann scale (Pfirrmann et al., 2001)) is mainly based on MRI and relies on the evidence of gross morphological disruptions (Griffith et al., 2007) and the signal intensity of T2 weighted images (Watanabe et al., 2007).
Finite element (FE) models can help bridging MRI data and disc mechanics (Schmidt et al., 2013). However, current FE models generally employ assumptions about the disc’s composition and the fiber orientation distribution within the AF. These modeling choices result in idealized disc models that are not appropriate when studying disc de- generation. Future FE models will need to integrate the structure and composition of each disc to understand the etiology of disc herniation and back pain. To address the limitations of the current state-of-the-art, we propose a new FE methodology that incorporates a more realistic fibrillar structure and an accurate tissue composition (NP/AF transition). The diffusion of water molecules in a porous media highly depends on its underlying microstructure (Boss and Stejskal, 1965). Based on this principle, MR diffusion tensor imaging (DTI) allows quantitative measurements of the spatial orientation distribution of anisotropic tissues (Le Bihan et al., 2001; Basser and Jones, 2002). In a previous study, Hsu and colleagues could demonstrate correspondence between principal MR diffusion directions and tissue orientations for AF explants (Hsu and Setton, 1999).
As a very first step, this work aimed to develop and illustrate an MRI-based methodology to create an FE model with specific shape, composition and fiber orientation distribution that can predict the multiaxial compliance of the human IVD (Fig. 1). To avoid excessive complexity, only the reversible, time-independent, quasi-static behavior of the IVD was considered.
Fig. 1.
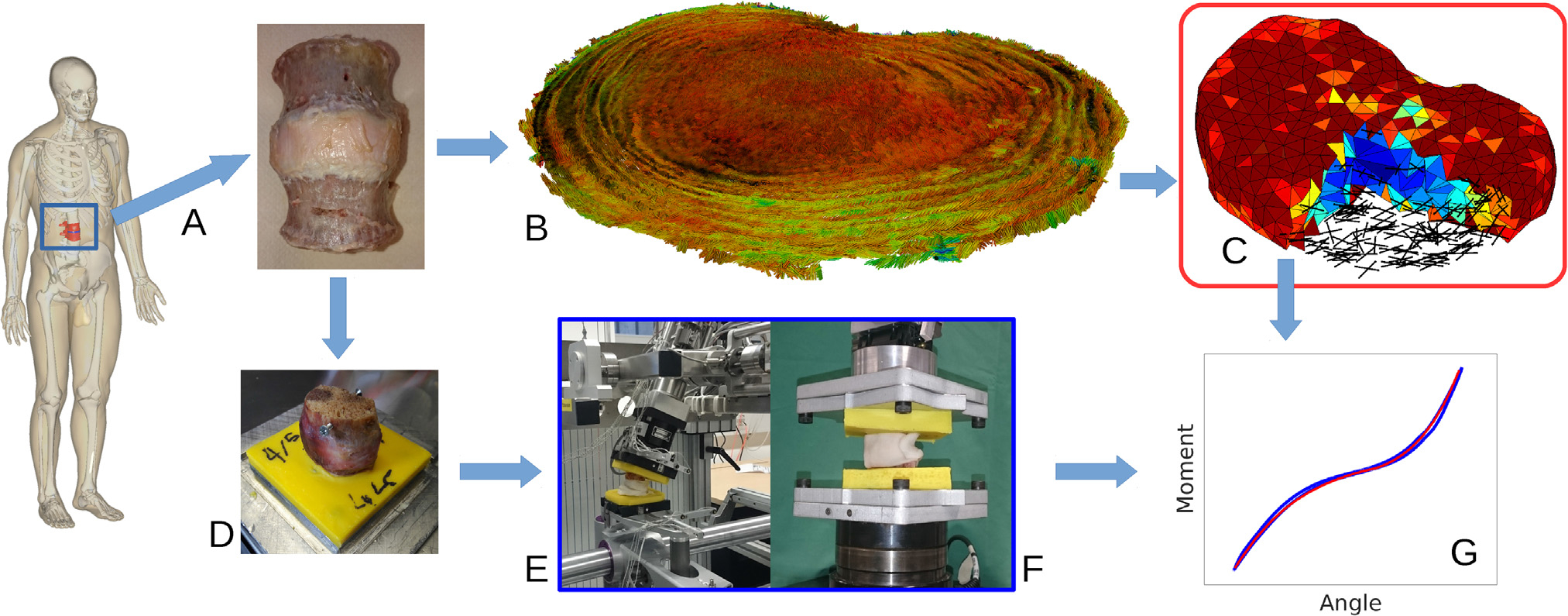
Study overview: A) A human L2-L3 functional spinal unit was prepared and scanned in a 9.4 T MR scanner. Proton-density weighted and B) diffusion tensor images were acquired and processed to generate C) a fully MRI-based finite element model (geometry, composition and anisotropy). D) The sample was embedded and in vitro mechanical tests in E) lateral bending, axial rotation, flexion, extension and F) tension and compression were conducted on the sample. G) Using the acquired load-displacement curves, the material parameters were calibrated and the performance of the model was evaluated.
2. Materials and methods
2.1. Specimen
A fresh-frozen L2-L3 functional spinal unit was obtained from a 60 years old male donor through an Anatomy Gifts Registry (Hanover, MD). An orthopedic surgeon classified the degeneration grade of the sample as Pfirrmann grade two. With the specimen frozen, the posterior processes, the ligaments and muscular tissues were dissected followed by the transverse sectioning of the cranial and caudal vertebral bodies at mid-body height to isolate the disc joint. The disc joint was wrapped in saline soaked gauze and stored at −20 °C in a double plastic bag.
2.2. MR Imaging
The disc was thawed for four hours at room temperature and was placed in a custom-made imaging chamber. To decrease susceptibility effects at the tissue’s surface (Benveniste et al., 2000) and prevent de- hydration, the chamber was filled with Fomblin Y (Sigma-Aldrich Co., St. Louis, MO), a perfluoropolyether-based lubricant that does not in- duce any MR-signal and was reported to cause no damage to tissues (Miller et al., 2011). Using a 72 mm birdcage coil (Bruker Biospin MRI GmbH, Ettlingen, Germany), the disc was imaged in a 9.4 T horizontal bore magnet (BioSpec, Bruker Biospin MRI GmbH, Ettlingen, Germany) with the disc’s cranial-caudal axis aligned along the axis of the magnet. Axial images (slice thickness: 0.5 mm, in-plane resolution: 0.2 mm, matrix: 270×290, 96 Slices) were acquired using the following proto- cols (Alkalay et al., 2015):
Proton-density weighted (PD) FLASH sequence (TE: 5.5 ms, TR: 1755 ms, flip angle: 60°).
Echo-planar DTI sequence (TE: 29 ms, TR 500 ms, b-value: 700 s/mm2, averages: 3). Diffusion gradients were applied at 30 uniformly distributed, non-collinear directions, generating 31 diffusion-weighted images (one per direction plus one baseline image). The measurement was performed at room temperature and lasted 10 h.
2.3. Mechanical testing
With the scans completed, the cranial and caudal vertebral bodies were embedded in polymethylmethacrylate cement (Technovit 3040, Heraeus Kulzer, Hanau, Germany). The sample was kept moist during the embedding process as well as during all following mechanical testing procedures.
Angular testing:
The embedded disc was secured to a custom six degrees of freedom (DOF), computer-controlled spine testing system (Gédet et al., 2007; Maquer et al., 2014). Under displacement control (0.5°/s), the disc was exposed to pure moments (up to 5 Nm) in flexion, extension, right lateral bending and right axial rotation. Each loading scenario was repeated five times with disc allowed to freely deform about the remaining five DOF thanks to a friction-free air-bearing system. An active optical tracking system (Optotrak Certus, Northern Digital, Canada) was used to record the six DOF motion of the disc. Forces and torques were measured using a six-axis load cell (MC3A, AMTI, U.S.A.).
Compression/tension testing:
A hydraulic testing system (858 Mini Bionix II, MTS, Eden Prairie, MN) was used for the axial loading scenarios. First, five compressive load cycles up to 350 N at a rate of 10 N/s were performed. The disc was then held at 0 N for 15 min (the time equivalent to the loading time) to allow recovery to its original height and an equivalent test was conducted in tension with a maximal load set to 200 N (this force was reduced to prevent the sample from sliding out of the PMMA end-caps). For both tests, the cranial vertebra was allowed to freely translate in the disc’s transversal plane with rotational motions constrained. For each test, applied load and resulted dis- placement were recorded using the MTS built-in sensors (load cell: model 662.20D-04 and LVDT displacement sensor).
2.4. Image processing
A pipeline, developed in Matlab (V.15, Mathworks, USA) was used for segmentation, mesh generation and processing the DTI-based fiber data (Fig. 2).
Fig. 2.
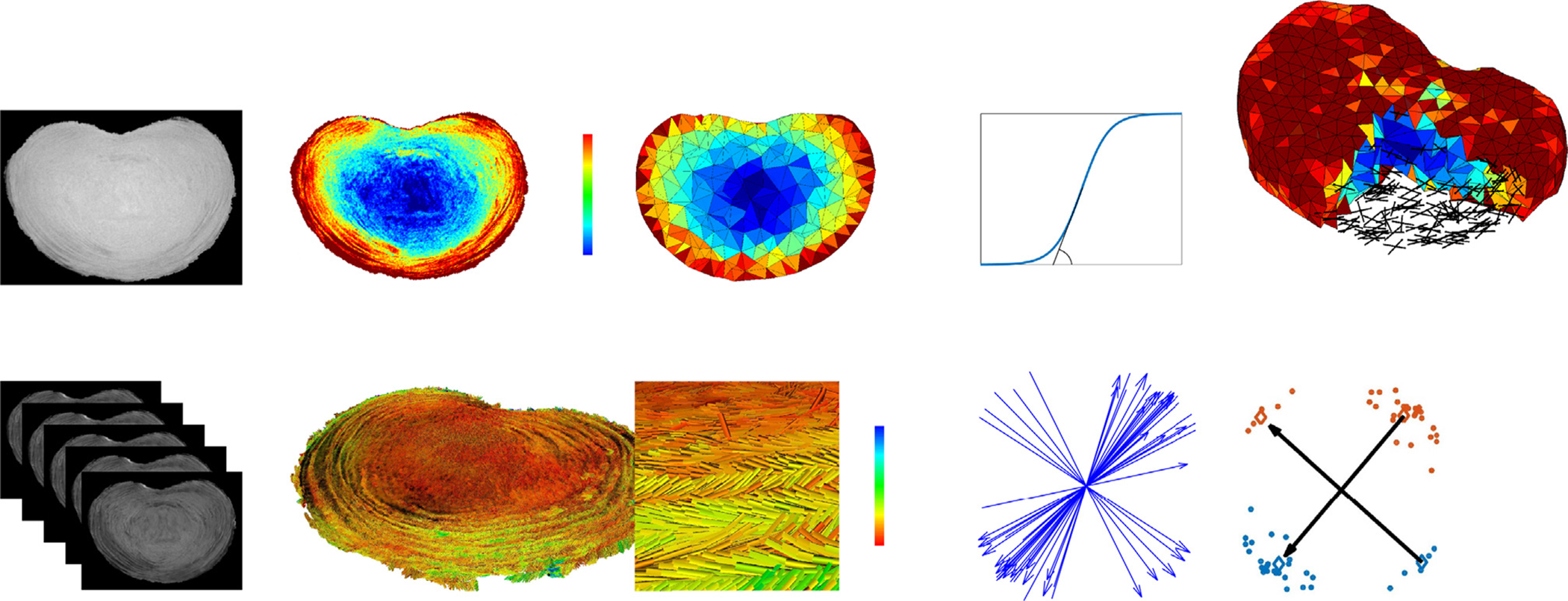
Proton-density weighted images were acquired, normalized to the highest signal intensity found within the annulus fibrosus (AF), segmented and the disc volume converted into a tetrahedral mesh. The normalized voxel values, λ, were assigned to each of the tetrahedrons and used to smoothly distinguish the material properties of the inner nucleus pulposus (NP) and the surrounding AF using a sigmoid function characterized by α and β Diffusion tensors (DTI) were estimated from the DWI images, with only the eigenvectors corresponding to the largest eigenvalues retained and colored by fraction anisotropy (FA). From the computed DTI eigenvector data, and for each tetrahedron, a k-mean clustering algorithm was used to compute and assign the main fiber directions (a4 and a6).
Disc geometry and tissue characterization:
The values of the PD MR images were highest at the highly hydrated inner NP. Using the assumption that for a given sub-region, the amount of collagen fibers is inversely proportional to the amount of water, the PD images were inverted and normalized, leading to a new voxel value (λ). These new voxel values were later used to scale the contribution of the collagen fibers for each finite element. The geometry of the disc was segmented using an Otsu threshold-based algorithm (Otsu, 1979).
DTI-based fiber orientations:
The DTI data set (31 diffusion-weighted images) was processed to yield a single diffusion tensor per voxel. To prevent negative eigenvalues, DTI tensors were computed using an iterative method proposed by Niethammer and colleagues (Niethammer et al., 2006). The fundamental assumption of this work is that this principal eigenvector directly corresponds to the local mean fiber orientation (Hsu and Setton, 1999). Hence, a spectral decomposition was conducted on each tensor with only the eigenvector corresponding to the largest eigenvalue (direction of highest diffusion) retained for fur- ther processing. Fraction anisotropy (FA), a scalar measure describing the degree of anisotropy of a diffusion process (FA = 0 = isotropic diffusion, FA = 1 = highly oriented diffusion) (Le Bihan et al., 2001), was computed from the resulting eigenvalues.
2.5. Finite element modeling
Using the ISO2MESH toolbox (Fang and Boas, 2009), a tetrahedral mesh (quadratic C3D10 tetrahedrons, mean edge length=2.5 mm) was generated from the segmented disc geometry. Instead of simulating individual collagen fiber bundles, a homogenization approach (Hill, 1963) was used. Each homogenized element represents the average mechanical behavior of the underlying structure. The contribution of the individual annular fibers is implicitly accounted for by the model’s constitutive law. Considering a small sub-volume of the AF, in- dependent of the number of collagen fiber layers included, reveals that two main directions of collagen fibers have to be defined for each finite element. For this purpose, a spherical sub-volume was defined at the center of gravity of each tetrahedron. For each sphere, all DTI eigen- vectors located within were selected and a k-mean clustering algorithm applied. This clustering algorithm regrouped all start- and end-points of the eigenvectors into four point-clouds. Finally, the centers of gravity of opposite clouds were connected with two vectors. These vectors (a4 and a6) represent the mean fiber orientations for the given sub-volume (Fig. 2).
To catch both principal directions, this sub-volume has to include at least two adjacent collagen fiber layers. The diameters for these layers were reported to vary between 0.1 mm and 0.5 mm, depending on age and position within the disc (Marchand and Ahmed, 1990). A sensitivity study was performed to define the size of this sub-volume. While too small volumes are prone to outliers, too large volumes reduce the local sensitivity of the method. Values between 0.6 mm and 1 mm were found to yield stable, yet qualitatively and quantitatively correct results (the resulting vectors followed the circumferential shape of the AF, and the angles with respect to the transversal were within the previously reported range). Taking the mean value of this stable range, the final radius was set to 0.8 mm.
To scale the local amount of collagen fibers and the compressibility of each finite element, the average value of the normalized PD image, λ, within the same spherical sub-volume was computed. Finally, the specific values of λ, a4 and a6 were assigned to the corresponding tetrahedral element.
The low sensitivity of the FE model to the mesh size was verified by varying the size of the tetrahedrons (2–3 mm mean edge length).
Based on the Holzapfel-Gasser-Odgen model for simulating anisotropic hyperelastic fiber-reinforced materials (Holzapfel et al., 2000; Eberlein et al., 2001), we implemented a time-independent constitutive law with a free energy function (Eq. (1)). The law incorporates a separate isotropic term, corresponding to the ground substance (Eq. (2)), and an anisotropic term with two normalized vectors (a4 and a6), corresponding to the two main fiber directions (Eq. (3)). The main difference to previous models lies in the fact, that a4 and a6 are not defined based on assumptions, but originate directly from MR images. Furthermore, the full anisotropic invariants (Eq. (7)) were used as highlighted by Nolan and colleagues (Nolan et al., 2014).
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
k1 corresponds to the stiffness of the fibers and k2 to their non-linearity. The deformations and reorientations of the fibers are given by the invariantsI4 and I6 which are derived from the deformation gradient F. At the material level, the fibers are only active under tension (ψfibers4,6 = 0 if I4,6 < 1). κ is the resistance against volumetric deformations (bulk modulus), μ the resistance against isochoric deformations (shear modulus). As in-plane shear deformations are prevented by the fibers, the shear term in the isotropic energy equation could be simplified, reducing the number of material parameters. However, this caused numerical instability at the beginning of the loading cycle, especially in compression, as the fibers become only active when stretched. To avoid this, μ was manually set to a low value (0.05 MPa) for all elements. Κ and k1 are not material parameters per se, but are scaled using the MRI based λ value of each element and a smooth sigmoid function characterized by α and β (Eqs. (8) and (9)). α determines how quickly κ andk1 change from minimal to maximal values (NP values to AF values or vice versa), corresponding to the size of the transition zone between NP and AF. β defines the ratio between NP and AF. The time-independent constitutive law was implemented as an Abaqus (6.13 Dassault Systems, France) user material (UMAT), with the simulation’s boundary conditions defined precisely as the experimental test conditions.
2.6. Calibration
All simulations were performed in Abaqus (6.13 Dassault Systems, France). As the disc’s time-depended response was not simulated, the measured load-displacement curves were further processed prior to their use for the calibration process. For flexion, extension, lateral bending and axial rotation loading scenarios, the mean curves of the measured hysteresis were used. For axial compression and tension, the drift caused by the disc’s time-dependent deformation was subtracted from each cycle, with each cycle shifted to the origin. A mean curve was then computed from the combined hysteresis loops. The limit values of κ (κAF, κNP ), k1 (k1AF, k1NP ) as well as k2 (for which the same value was assigned to all elements), α and β were determined upon calibration of the FE model vs. the experimental data. For this purpose, a Particle Swarm Optimization (PSO) (Clerc and Kennedy, 2002) was used to minimize the difference between the experimental and simulated data curves to allow calibration of the tissues material parameters (Maquer et al., 2015). The optimization lasted 12 h using four CPUs. Once completed, the obtained load-displacement curves were compared to the experimental load-displacement data.
3. Results
3.1. MRI-derived disc structure
Computation of the diffusion tensors revealed a disorganized distribution of fibers with almost isotropic diffusivity at the center of the NP (FA < 0.2). Extending outwards towards the outer portion of the AF showed a clear increase in organization, revealing a layer-based arrangement with the diffusion tensors becoming increasingly anisotropic (FA reaching up to 0.5) (Fig. 2). The final fiber angles assigned to the elements ranged from 25° to 50° with respect to the transverse plane. Although having no physical units, λ values computed from the normalization of the PD images accounted for the varying composition of the sample (Fig. 3).
Fig. 3.
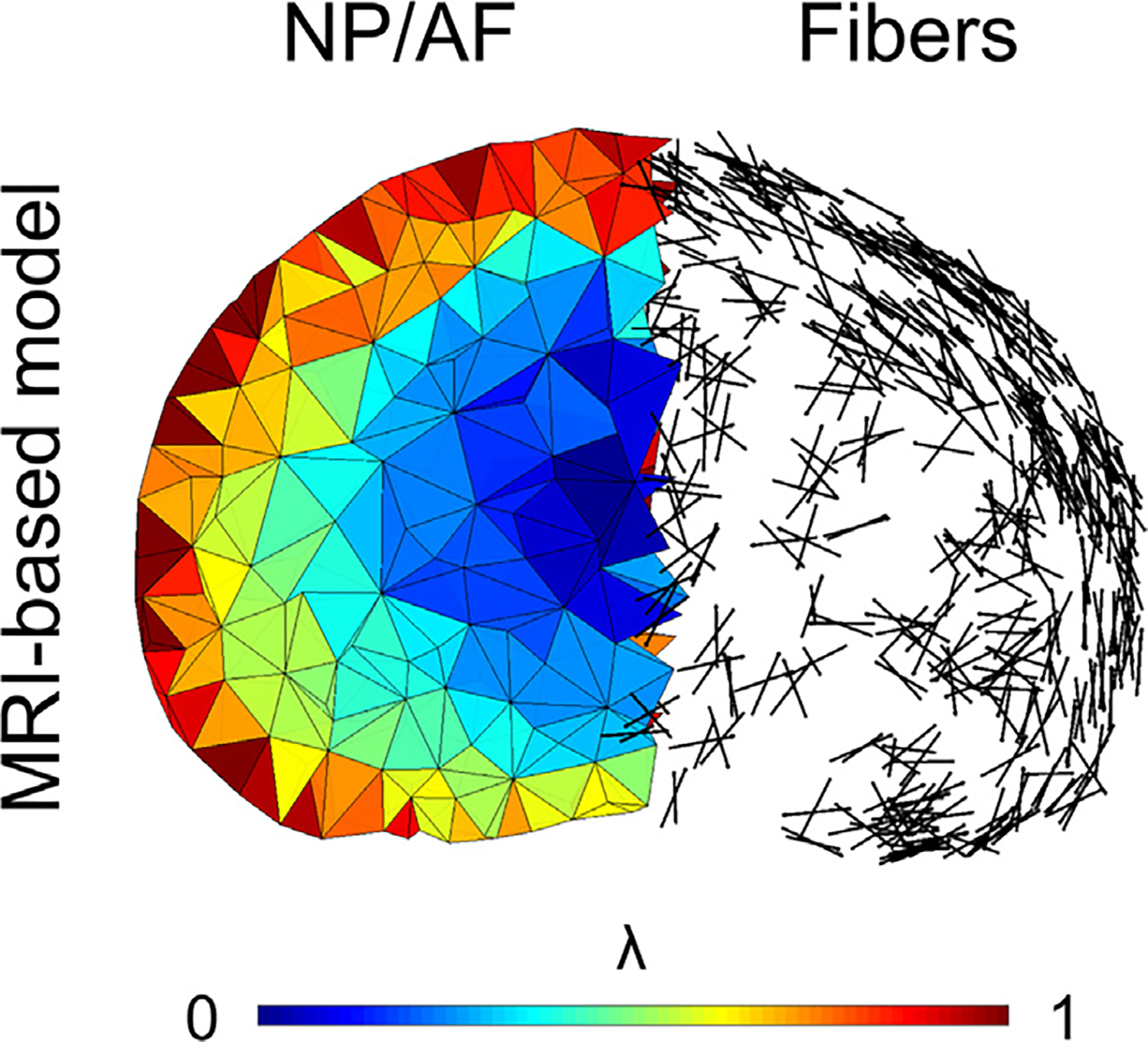
The fully MRI-based model accounts for the smooth transition between nucleus pulposus (NP) and annulus fibrosus (AF). The presentation of the fibers demonstrates the clear distinction between the outer AF, showing spatially organized fibers, becoming increasingly disorganized towards the inner NP.
3.2. Finite element predictions
Fig. 4 presents the experimental and FE predicted moment-angle and force-displacement response of the disc joint. Generally, the FE model agrees with the in vitro load-displacement curves of all loading cases. A high fiber stiffness (k1) and a relatively soft ground substance (κ) were found to provide the best agreement with all the in vitro load cases. To verify that the fibers were the main contributor to the disc’s compliance, the fiber term was switched off, leaving the model solely relying on its ground substance (Fig. 4: MRI-based model w/o fibers). In this case, the model lost most of its stiffness in all directions.
Fig. 4.
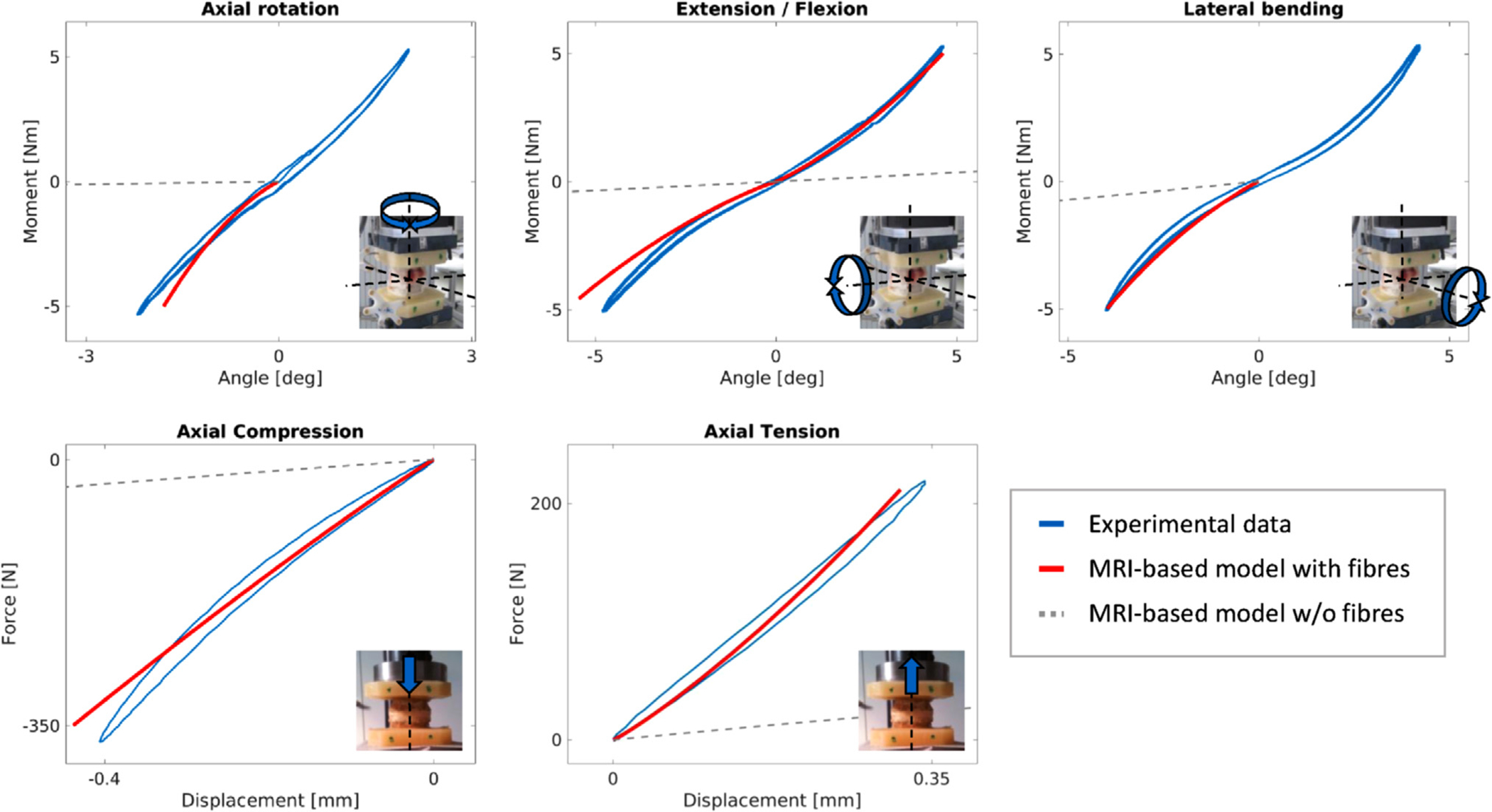
The DTI MR-based model replicates the in vitro load-displacement curves. The gray curves show the compliance of the model if the contribution of the fibers is switched off.
4. Discussion
This work aimed to demonstrate the potential of diffusion tensor MRI in FE modeling of the human IVD. A PD sequence was used to generate a mesh based on the disc’s geometry and to map its composition to the model, while the change in local fiber orientation within each element was directly computed from DTI measurements. With disc’s composition and fiber architecture treated as a continuum, the outcome of such a model may depend on the homogenization procedure (Hill, 1963). Accordingly, the model’s low sensitivity to mesh size and material mapping sub-volume was verified. Independent of the underlying tissue structure, the generation of such homogenized FE models can be fully automatized, which constitutes a distinct advantage for high-throughput in vitro studies or potential clinical applications. The MRI-based model successfully reproduced the six different loading scenarios despite the simple constitutive law. The presented methodology was applied to one single sample, which constitutes its biggest limitation. A direct comparison to idealized FE models was not undertaken as this would require a more substantial number of samples. The proposed model is based on high-field MRI images. To be considered for potential clinical applications, the methodology will have to be adapted to clinical MRI scanners. The lower field strength of clinical MR scanners will lead to a reduced image resolution. Considering the alignment of the collagen fiber bundles, this will not induce major changes for the circumferential angle of the fibers, as this angle remains relatively constant in a given sub-region. However, because of the angle alterations between adjacent collagen layers, the angle of the fibers with respect to the transversal plane will suffer from a decreased image resolution, and eventually reach a point where adjacent layers cannot be distinguished. In this case, the angles from each layer will cancel each other and a mean direction of approximately 0° will be measured. We confirmed on the 9.4 T scanner that the fibers families can be distinguished on images at a resolution of 0.5 mm, corresponding to the resolution of a clinical 3T scanner. Nevertheless, further work is necessary to implement the methodology on a 3T scanner. If unsuccessful, the methodology could be implemented on a 7T scanner. Although a previous study suggested that main diffusion directions correspond to the collagen fiber orientations (Hsu and Setton, 1999), hard evidence proving this is currently lacking. However, the lamellar criss-cross organization (Fig. 2) and angular range (25–50°) of the main diffusion directions compare favorably with histological observations (Marchand and Ahmed, 1990). Nevertheless, future work should compare DTI directions to in vitro 3D histology (Adam et al., 2015). In its current state, the model neglected all time-dependent effects and a reversible, quasi-static behavior was assumed. The sample was prevented from drying out by keeping it moist during mechanical testing. No visible loss of water content or disc height could be observed, however, these variables were not measured. Ex vivo mechanical tests were performed with similarly low rates in all loading modes to minimize time-dependent effects. The loading curves in tension and compression (loading modes with the highest volumetric strains) were high-pass filtered to subtract drifts caused by poroelasticity before using them as input for the material parameter calibration. We acknowledge that this did not completely remove all time-dependent effects in our measurements. However, adding anisotropic and heterogeneous poroviscoelasticity to our newly developed MRI-based model was clearly beyond the scope of this study (Table 1). Patient-specific FE models of the degenerating IVD could be useful to better understand the degeneration process and estimate the risk of herniation or instability-related back-pain, but this perspective will require a more systematic validation of the methodology with clinical MRI images.
Table 1.
Material parameters resulting from the calibration of the models with the in vitro load-displacement data
| μ [MPa] | κNP [MPa] | κAF [MPa] |
k1NP [MPa] |
k1AF [MPa] |
k2 [-] | α [-] | β [-] |
|---|---|---|---|---|---|---|---|
| 0.05 | 24.3 | 3.1 | 580 | 2219 | 1.2 | 68 | 0.28 |
Acknowledgments
We thank Dr. Sven Hoppe for the clinical classification of the sample. The research reported in this publication was supported by the Swiss National Science Foundation, grant number 147153 (Prof. Zysset) and the National Institutes of Health under award number R21AR066916 (Dr. Alkalay).
Footnotes
Conflict of interest
The authors have no conflict of interest to declare.
References
- Adam C, Rouch P, Skalli W, 2015. Inter-lamellar shear resistance confers compressive stiffness in the intervertebral disc: an image-based modelling study on the bovine caudal disc. J. Biomech 48 (16), 4303–4308. 〈http://www.sciencedirect.com/science/article/pii/S0021929015005898〉. [DOI] [PubMed] [Google Scholar]
- Adams MA, Roughley PJ, 2006. What is intervertebral disc degeneration, and what causes it? Spine 31 (18), 2151–2161. http://content.wkhealth.com/linkback/openurl?sid=WKPTLP:landingpage&an=00007632-200608150-00024〉〈https://s3.amazonaws.com/academia.edu.documents/41169523/What_is_Intervertebral_Disc_Degeneration20160114-8623-1jqmevl.pdf?AWSAccessKeyId=AKIAIWOWYYGZ2Y53UL3A&〉. [DOI] [PubMed] [Google Scholar]
- Alkalay RN, Westin C. f., Meier D, Hackney DB, 2015. Diffusion Tensor Imaging Detects The Spatial Variation In Fiber Angle and Lamellar Number In Intact Human Disc Joint. In: ORS 2015 Annual Meeting: Poster No: 1564. ORS 2015 Annual Meeting. 〈http://www.ors.org/Transactions/61/1564.pdf〉. [Google Scholar]
- Basser PJ, Jones DK, 2002. Diffusion-tensor MRI: theory, experimental design and data analysis - A technical review. NMR Biomed. 15 (7–8), 456–467. 〈 10.1002/nbm.783/full〉〈http://www.ncbi.nlm.nih.gov/pubmed/12489095〉. [DOI] [PubMed] [Google Scholar]
- Benveniste H, Kim K, Zhang L, Johnson GA, 2000. Magnetic resonance microscopy of the C57BL mouse brain. NeuroImage 11 (6), 601–611. 〈http://www.ncbi.nlm.nih.gov/pubmed/10860789〉. [DOI] [PubMed] [Google Scholar]
- Boss BD, Stejskal EO, 1965. Anisotropic diffusion in hydrated vermiculite. J. Chem. Phys 43 (3), 1068. 〈http://link.aip.org/link/JCPSA6/v43/i3/p1068/s1&Agg=doi〉. [Google Scholar]
- Brisby H, 2006. Pathology and possible mechanisms of nervous system response to disc degeneration. J. Bone Jt. Surg. Am 88 (Suppl (2)), S68–S71. 〈http://www.ncbi.nlm.nih.gov/pubmed/16595447〉. [DOI] [PubMed] [Google Scholar]
- Clerc M, Kennedy J, 2002. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evolut. Comput 6 (1), 58–73. 〈http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=985692〉 〈http://ieeexplore.ieee.org/document/985692/〉. [Google Scholar]
- Eberlein R, Holzapfel GA, Schulze-Bauer CA, 2001. An anisotropic model for annulus tissue and enhanced finite element analyses of intact lumbar disc bodies. Comput. Methods Biomech. Biomed. Eng 4 (3), 209–229. 〈 10.1080/10255840108908005〉. [DOI] [Google Scholar]
- Ellingson AM, Mehta H, Polly DW, Ellermann J, Nuckley DJ, 2013. Disc degeneration assessed by quantitative T2* (T2 Star) correlated with functional lumbar mechanics. Spine 38 (24), E1533–40. 〈http://www.ncbi.nlm.nih.gov/pubmed/23921323〉〈http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC3830665〉. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang Q, Boas DA, 2009. Tetrahedral mesh generation from volumetric binary and grayscale images. In: Proceedings of the 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, ISBI 2009, 1142–1145. 〈http://ieeexplore.ieee.org/abstract/document/5193259/〉. [Google Scholar]
- Gédet P, Thistlethwaite PA, Ferguson SJ, 2007. Minimizing errors during in vitro testing of multisegmental spine specimens: considerations for component selection and kinematic measurement. J. Biomech 40 (8), 1881–1885. 〈http://www.sciencedirect.com/science/article/pii/S0021929006002934〉. [DOI] [PubMed] [Google Scholar]
- Griffith JF, Wang Y-XJ, Antonio GE, Choi KC, Yu A, Ahuja AT, Leung PC, 2007. Modified Pfirrmann grading system for lumbar intervertebral disc degeneration. Spine 32 (24), E708–E712. 〈http://content.wkhealth.com/linkback/openurl?sid=WKPTLP:landingpage&an=00007632-200711150-00028〉. [DOI] [PubMed] [Google Scholar]
- Hill R, 1963. Elastic properties of reinforced solids: some theoretical principles. J. Mech. Phys. Solids 11, 357–372. 〈http://www.sciencedirect.com/science/article/pii/002250966390036X〉. [Google Scholar]
- Holzapfel GA, Gasser TC, Ogden RW, 2000. A new constitutive framework for ar- terial wall mechanics and a comparative study of material models. J. Elast 61 (1–3), 1–48. [Google Scholar]
- Hsu EW, Setton LA, 1999. Diffusion tensor microscopy of the intervertebral disc an- ulus fibrosus. Magn. Reson. Med 41 (5), 992–999. 〈http://www.ncbi.nlm.nih.gov/pubmed/10332883〉〈〉. [DOI] [PubMed] [Google Scholar]
- IHME, 2016. Switzerland: Institute for Health Metrics and Evaluation. 〈http://www.ealthdata.org/switzerland〉. [Google Scholar]
- Le Bihan D, Mangin J-F, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H, 2001. Diffusion tensor imaging: concepts and applications. J. Magn. Reson. Imaging 13 (4), 534–546. 〈 10.1002/jmri.1076〉. [DOI] [PubMed] [Google Scholar]
- Maquer G, Brandejsky V, Benneker LM, Watanabe A, Vermathen P, Zysset PK, 2014. Human intervertebral disc stiffness correlates better with the Otsu threshold computed from axial T2 map of its posterior annulus fibrosus than with clinical classifications. Med. Eng. Phys 36 (2), 219–225. 〈http://www.sciencedirect.com/science/article/pii/S1350453313002506〉. [DOI] [PubMed] [Google Scholar]
- Maquer G, Schwiedrzik J, Huber G, Morlock MM, Zysset PK, 2015. Compressive strength of elderly vertebrae is reduced by disc degeneration and additional flexion. J. Mech. Behav. Biomed. Mater 42 (325230), 54–66. 〈http://www.ncbi.nlm.nih.gov/pubmed/25460926〉〈http://www.sciencedirect.com/science/article/pii/S1751616114003415〉. [DOI] [PubMed] [Google Scholar]
- Marchand F, Ahmed AM, 1990. Investigation of the laminate structure of lumbar disc anulus fibrosus. Spine 15 (5), 402–410. 〈http://content.wkhealth.com/linkback/openurl?sid=WKPTLP:landingpage&an=00007632-199005000-00011〉. [DOI] [PubMed] [Google Scholar]
- Miller KL, Stagg CJ, Douaud G, Jbabdi S, Smith SM, Behrens TEJ, Jenkinson M, Chance SA, Esiri MM, Voets NL, Jenkinson N, Aziz TZ, Turner MR, Johansen-Berg H, McNab JA, 2011. Diffusion imaging of whole, post-mortem human brains on a clinical MRI scanner. NeuroImage 57 (1), 167–181. 〈http://www.sciencedirect.com/science/article/pii/S1053811911003491〉. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niethammer M, Estepar RSJ, Bouix S, Shenton M, Westin CF, 2006. On diffusion tensor estimation. In: Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology. pp. 2622–2625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nolan DR, Gower AL, Destrade M, Ogden RW, McGarry JP, 2014. A robust an- isotropic hyperelastic formulation for the modelling of soft tissue. J. Mech. Behav. Biomed. Mater 39, 48–60. 〈http://linkinghub.elsevier.com/retrieve/pii/S1751616114001805〉. [DOI] [PubMed] [Google Scholar]
- Otsu N, 1979. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst., Man, Cybern 9 (1), 62–66. 〈http://ieeexplore.ieee.org/document/4310076/〉. [Google Scholar]
- Pfirrmann CWA, Metzdorf A, Zanetti M, Hodler J, Boos N, 2001. Magnetic re- sonance classification of lumbar intervertebral disc degeneration. Spine 26 (17), 1873–1878. 〈http://content.wkhealth.com/linkback/openurl?sid=WKPTLP:landingpage&an=00007632-200109010-00011〉. [DOI] [PubMed] [Google Scholar]
- Schmidt H, Galbusera F, Rohlmann A, Shirazi-Adl A, 2013. What have we learned from finite element model studies of lumbar intervertebral discs in the past four decades? J. Biomech 46 (4), 2342–2355. 〈http://www.sciencedirect.com/science/article/pii/S0021929013003394〉. [DOI] [PubMed] [Google Scholar]
- Setton L.a., Chen J, 2006. Mechanobiology of the intervertebral disc and relevance to disc degeneration. J. Bone Jt. Surg. Am Vol. 88 (Suppl (2)), S52–S57. 〈https://scholar.google.ch/scholar?q=Setton+LA%2C+Chen+J.+Mechanobiology+of+the+intervertebral+disc+and+relevance+to+disc+degeneration.+J+Bone+Joint+Surg+Am.+2006%3B88%28suppl+2%29%3A52-7&btnG=&hl=de&as_sdt=0%2C5〉. [DOI] [PubMed] [Google Scholar]
- Watanabe A, Benneker LLM, Boesch C, Watanabe T, Obata T, Anderson SE, 2007. Classification of intervertebral disk degeneration with axial T2 mapping. Am. J. Roentgenol 189 (4), 936–942. 〈 10.2214/ajr.07.2142〉. [DOI] [PubMed] [Google Scholar]
- Yang H, Liu H, Li Z, Zhang K, Wang J, Wang H, Zheng Z, 2015. Low back pain associated with lumbar disc herniation: role of moderately degenerative disc and annulus fibrous tears. Int. J. Clin. Exp. Med 8 (2), 1634–1644. 〈https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4402739/〉. [PMC free article] [PubMed] [Google Scholar]


