Muscle active force-length curve explained by an electrophysical model of interfilament spacing

Abstract

The active isometric force-length relation (FLR) of striated muscle sarcomeres is central to understanding and modeling muscle function. The mechanistic basis of the descending arm of the FLR is well explained by the decreasing thin:thick filament overlap that occurs at long sarcomere lengths. The mechanistic basis of the ascending arm of the FLR (the decrease in force that occurs at short sarcomere lengths), alternatively, has never been well explained. Because muscle is a constant-volume system, interfilament lattice distances must increase as sarcomere length shortens. This increase would decrease thin and thick-filament electrostatic interactions independently of thin:thick filament overlap. To examine this effect, we present here a fundamental, physics-based model of the sarcomere that includes filament molecular properties, calcium binding, sarcomere geometry including both thin:thick filament overlap and interfilament radial distance, and electrostatics. The model gives extremely good fits to existing FLR data from a large number of different muscles across their entire range of measured activity levels, with the optimized parameter values in all cases lying within anatomically and physically reasonable ranges. A local first-order sensitivity analysis (varying individual parameters while holding the values of all others constant) shows that model output is most sensitive to a subset of model parameters, most of which are related to sarcomere geometry, with model output being most sensitive to interfilament radial distance. This conclusion is supported by re-running the fits with only this parameter subset being allowed to vary, which increases fit errors only moderately. These results show that the model well reproduces existing experimental data, and indicate that changes in interfilament spacing play as central a role as changes in filament overlap in determining the FLR, particularly on its ascending arm.

Significance

The entire force-length-activity relation (FLAR) of skeletal muscle sarcomeres is mechanistically explained for the first time. The key addition is that interfilament spacing, as well as filament overlap, must change as sarcomere length changes. Our classical-physics model, utilizing volume constancy and electrostatic interaction, well reproduces the FLARs of multiple muscles. The model explains the rightward shift of lengths at which maximum force occurs with decreasing activity (calcium concentration). Consistent with interfilament spacing changing as sarcomere length changes, the model output is most sensitive to changes in geometric parameters.

Introduction

The active force-length relation (FLR) is a very important and well-investigated property of striated muscle. Its general form has been known for over a century (1, p.93) (2, 3, 4): 1) at very short lengths, muscle fibers exert no force upon activation; 2) over a range of longer lengths, active force increases with length (the ascending arm); 3) over a range of still longer lengths, force is more or less constant (the “plateau”); 4) with further lengthening, force decreases, eventually to zero (the descending arm). Gordon et al. (1966) (5) proposed a geometric explanation of the descending arm and plateau based on the sliding filament hypothesis of muscle contraction: the descending arm arising from decreasing thin- and thick-filament overlap as length increases, and the plateau being the length range where the leading portions of the thin filaments are in the thick-filament central bare zone, and length changes thus do not alter thin-filament overlap with the myosin head-bearing portion of the thick filaments (see Fig. 1).

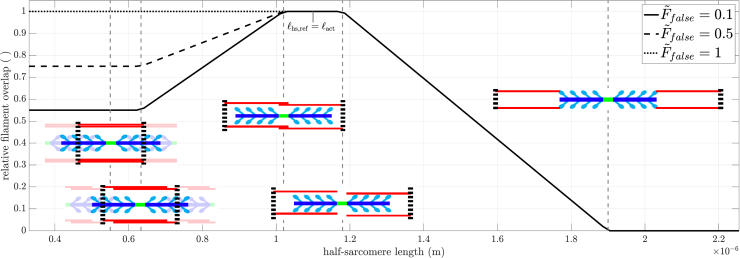
Figure 1.

Relative filament overlap versus half-sarcomere length for the case that false cross-bridges produce a marginal amount of (${\tilde{F}}_{\text{false}}=0.1$, solid line), half of (${\tilde{F}}_{\text{false}}=0.5$, dashed line), or the full (${\tilde{F}}_{\text{false}}=1$, dotted line) force of a proper cross-bridge. Full (not half-) sarcomere sketches shown for clarity. Note that actin (red) and myosin (blue-cyan) filament radial spacing decreases at longer lengths (insets). To see this figure in color, go online.

This explanation provided no geometrical reason for the ascending arm. At these short lengths, the thin filaments have crossed to the far side of the thick-filament central bare zone. Gordon et al. (1966) “identified” two linear regions of different slope in the ascending arm. They hypothesized that one corresponded to lengths over which the thin filaments from the two half-sarcomeres overlap, and the other to lengths where the thick-filament ends reach and become increasingly “squeezed” against the Z disk (an “overlap/collision” mechanism). Most textbooks consequently depict the ascending arm as two linear regions with different slopes as in (5, Fig. 5). However, Gordon et al. (1966) actually used the word “linearly” only when referring to prior and their work on the descending arm; their summary Fig. 12 shows two linear regions connected by a smooth, not discontinuous, slope change; continuous functions (see below) fit as well the ascending arm data in their Fig. 5; and later experiments (e.g., (6, Fig. 4), and (7)) confirmed the absence of kinks on the ascending arm.

Perhaps the most compelling evidence against the overlap/collision mechanism, however, was provided only 3 years after Gordon et al. (1966) by Rack and Westbury (1969) (8), who showed that the FLR maximum shifted to longer lengths (moved rightward) with decreasing muscle activation, i.e., reduced calcium-induced cross-bridge formation, an observation confirmed since multiple times (9, 10, 11, 12, 13, 14, 15, 16, 17, 18). The overlap/collision mechanism cannot explain this rightward shift, since calcium concentration should not affect filament overlap or when thick filaments reach the Z disk. This shift of the FLR peak with decreased activity shows that both FLR shape and amplitude depend on muscle activation. We therefore use here the term force-length-activity relation (FLAR) instead of FLR.

In considering these issues, we realized that prior hypotheses did not consider the implications of muscle being a constant-volume system. Length decreases will therefore increase radial interfilament spacing. This increase will decrease the likelihood of interfilament electrostatic interactions, and thus force, at short muscle lengths, and hence explain why the ascending arm of the FLAR exists at all. Although not as intuitively obvious why, these changes could possibly also result in the FLAR peak shifting right with decreasing activation.

Testing these hypotheses required considering not only sarcomere geometry but also the fundamental physics of the system, electrostatics (Debye-Hückel theory), statistical physics (Boltzmann statistics), and thermodynamics (reaction kinetics). We present here such a fundamentally based model, and show it reproduced very well FLAR experimental data of a large number (12) of muscles. A local first-order sensitivity analysis (measuring the change of model output induced by changing each parameter individually while holding the others constant) of the model showed that model output was highly sensitive to only half the model’s 16 free parameters. The model was most sensitive to interfilament spacing, and most of the seven other most important parameters also involved interfilament electrostatic interactions. Re-fitting the data with only these eight most sensitive parameters being allowed to vary increased model error, but it remained small relative to the amplitudes present in the data. These results suggest that the ascending arm of the FLAR, and the rightward shift of the FLAR peak with decreasing muscle activation, arise from the increased interfilament lattice spacing that occurs as muscle fiber length decreases.

Current explanations of the ascending arm of the FLR

The mechanistic basis of the ascending arm is typically addressed only vaguely in contemporary textbooks. As a rule, a two-piece-wise linear ascending arm is shown, accompanied with phrases like “The decrease in tension at sarcomere lengths below 2.05 μm is due to actin filaments poking into the other half of the sarcomere.” (19, p.11), “As the muscle shortens, the cross-bridges overlap and the active tension is […] reduced.”(20, p.380), or “Several theories addressing the force reduction at lengths shorter than optimal are suggested. Detailed discussion of the theories is beyond the scope of this book.” (21, p.175). Even in the primary literature, concrete explanations for the ascending arm are not provided (e.g., (22, p.1447)), and we are unaware of a source that reviews this issue. The following topic organization is therefore only our idiosyncratic summary of the explanations we have found in the literature.

Assertion 1: The ascending arm of the FLAR is a piece-wise linear function

In their Fig. 5, Gordon et al. (5) fit their ascending arm data with two linear segments with different slopes. Their using linear functions is understandable because, in the 1960s, non-linear fitting techniques were difficult to apply. Even though the data were known to be sigmoidal, in this era enzyme kinetic data were also commonly analyzed with linearizing methods (Eadie-Hofstee diagrams, Lineweaver-Burk plots, or Hanes-Woolf plots (23)). With present computing abilities, however, the Gordon et al. (1966) ascending arm data are as well or better fit with non-linear functions (24, p.329, Fig. 1). Subsequent experimental data also challenge the existence of a slope discontinuity in the ascending arm (6,7). The assertion that the ascending arm is a two-piece linear function is thus very unlikely. This belief is supported by examining the ascending arm FLAR data shown in the results (section “optimization of parameters to fit experimental FLAR”), in which two-piece linear ascending arms are not visually apparent for many of the muscles, and which are well fitted for all muscles with continuous sigmoidal-like functions.

Assertion 2: Internal extending forces occur at short lengths

Some papers (5,22) cite early (1940) work (4) showing that non-stimulated muscle fibers initially held at a short length and then lengthened tend to lengthen further to support the conclusion that “there must exist a force tending to extend the fiber” (5, p.187). However, Ramsey and Street (4) state that 1) the fibers still contained some pieces of connective tissue (p.12), 2) the resting fiber “hung in a large loop” (p.23), and 3) a fiber “shorten[ed] below 65% of its resting length … no longer relaxed after cessation of the tetanic stimulus but remained shortened at the length it was allowed to shorten to” (p.24). These remarks suggest that gravity or parallel elastic forces could have served as extending forces in this particular experiment. Given the alternative explanations for these results provided by points 1) and 2) above; that any internal extending forces would have to increase as length shortened, not cease as in point 3); and the lack, to our knowledge, of replication of this work, we believe this single article is insufficient to demonstrate the existence of intrinsic extending forces that continually increase as length decreases so as to give rise to the ascending arm.

Assertion 3: Force falls because thin filaments from opposite Z disks overlap on the far side of the M-line

This argument is found in many textbooks and research articles, e.g., (5, p.187, Fig. 14), (25, p.1466), (26, p.3), (19, p.11), (27, p.122). However, no mechanistic explanation is provided of why or how doubling the number of thin filaments around each thick filament would decrease force production. Gordon et al. (1966) (5, p.187) hypothesize that the “invading” actin filaments would have repelling “collisions” with the original half-sarcomere thin filaments. In the above references, only (26) refers to primary literature, namely, Trombitas and Tigyi-Sebes (1989) (28). These workers stretched glycerinated insect flight muscle in rigor solution to detach the actin filaments from the Z disk. Upon addition of ATP, some detached filaments (asymmetrically broken filaments) slid through the M-line into the adjoining “intact” half-sarcomere while others (symmetrically broken filaments) gathered at the M-line, only half-way penetrating the adjoining half-sarcomere, in each case forming a zone of actin filament double overlap. The authors concluded from these data that “only … bridges … located in the normal overlap zone can generate effective force”. However, this interpretation assumed that myosin does not generate force on wrongly oriented actin filaments. Later work disproved this assumption (29, 30, 31), see also assertion 4, thus throwing the (28) conclusions into question. As to the more general idea, we know of no experimental evidence or mechanistic explanations that thin-filament double overlap should reduce force production or have repelling interactions.

Assertion 4: Oppositely polarized cross-bridges push the actin back

A recent attempt by (26) to explain the shape of the ascending arm made several assumptions about the nature of properly and oppositely polarized (“swiveled”) cross-bridges (see also Fig. 1 and its surrounding text). One assumption was that, in oppositely polarized cross-bridges, the myosin head pushes actin back to its own half-sarcomere, with half the force magnitude of properly polarized cross-bridges. On closer inspection, flaws become evident in this estimation of a swiveled cross-bridge’s force. First, part of its estimation was made from work by Kaya and Higuchi (32), who pulled and pushed a single myosin S2 within an optical trap in order to estimate its direction-dependent passive stiffness response. Hence, nothing can be immediately learned from this experiment about internally generated forces of an active myosin head.

Second, as they themselves acknowledge (26, Fig. 4), the S2 part of the myosin molecule, which connects the myosin head to the molecule’s backbone, is two orders of magnitude more compliant, and thus prone to buckle, when the head would exert a push (32, Fig. 1 c). Consequently, even presuming a head can push back, the force and movement it would transmit to the thin filament cannot be calculated from present data. Moreover, when different portions of a single thin filament are exposed to different forces, the intervening portion of the thin-filament loops, bends, and curls (29, Fig. 3 c), (33, Fig. 1 a), and (31, Fig. 2 d). Thin filaments thus have rope-like rather than rod-like mechanical properties, particularly in the activated state when tropomyosin is moved aside (34), and thus could not in any case transmit a localized push back from myosin to the entirety of the thin filament.

Third, and most important, as already mentioned in assertion 3, actin polarization, not myosin head orientation, dictates movement direction (33) (a reference included in (26)). As such, thin-filament portions that have crossed the bare zone are not pushed by the thick filament in the opposite direction, but instead continue to be pulled in the same direction as if they were located on their original side of the central bare zone. This fact is also shown in (26, Fig. 4 c).

Conclusively, actin that crosses over the thick-filament central bare zone is not pushed back by the myosin on that side, and thin filaments are in any case too compliant to transmit pushes. We believe assertion 4 is therefore untenable.

Assertion 5: The myosin filament folds upon collision with the Z disk

Sketches of sarcomere geometries next to the piece-wise linear FLR usually suggest the steeper force decrease at very short lengths arises from a “collision of ends of thick filaments with the Z lines. This would be expected to cause added resistance to shortening” (5, p.187). This explanation assumes that the Z disk is impenetrable. However, the Z disk is actually a loose net (35,36) that widens to a lattice spacing of approximately 26 nm when the half-sarcomere is shortened to the length of the myosin backbone (37, Fig. 2), wide enough to allow thick-filament penetration (38). We are also unaware of any verification of such a collision state in imaging work. Taken together, the plausibility of this assertion is therefore poor.

Assertion 6: It has something to do with lattice spacing

In the sarcomere cross-section, myosin and actin filaments are ordered in a regular two-dimensional finite lattice. In vertebrate skeletal muscle, the filaments form a hexagonal lattice in which the myosins themselves form a coarse hexagonal lattice and the actins fill the remaining two triangular lattices. In invertebrates, a wide variety of lattices is present, cf. (39, Fig. 10), which will not be considered here (the stick insect muscles are likely to have arrangements similar to vertebrate skeletal muscles). Center-to-center distances between actin and myosin filaments, the lattice spacing, can be determined by crystallographic measurements, e.g., X-ray diffraction. As expected from the volume constancy of muscles (40, 41, 42, 43, 44, 45, 46, 47, 48, 49), lattice spacing changes when muscle length changes (44,50,51). It has been argued that these changes in lattice spacing affect actin-myosin interactions (52, 53, 54). However, unlike the hypothesis we present here, this work assumes that the changes in force with changing lattice spacing are due to the angular orientations of the S1 parts in the cross-bridges systematically shifting with lattice spacing. Schoenberg et al. (1980) (52) consider the FLR at only plateau and longer sarcomere lengths (descending arm), and is thus not relevant here. The model calculations in (54) may suffer from three faults. First, if the presentation of the mechanical core of their model, the force equilibria according to Fig. S1(c) in their supplementary material, correctly reflects their model code, then an erroneous sign of the contribution of the driving cross-bridge torque makes the quantitative predictions of the FLR in (54, Fig. 2) unreliable. Second, the rationale in the caption of their Fig. S1(c) about the axial force acting at the M-line is confusing, leaving doubt about which force is plotted in the figure. Third, their idea of the lever geometry, particularly where the driving torque is generated within a cross-bridge, is odd. They assume the drive’s pivot to be on or close to the myosin backbone. The angular head orientation at attachment is, therefore, altered with spacing, and the lever arm (distance between pivot axis and the attachment point on the actin) correspondingly increases with spacing, see (53, Fig. 1 B) and (54, Suppl., Fig. S1(c)). However, it seems established that the torque-driving pivot in a cross-bridge is located in the S1 part of the myosin head, at the connection between the S1’s catalytic domain (CD), which attaches to the actin, and the S1’s light chain domain (LCD), which acts as an 11–14-nm-long, deformable (55) lever arm (56, Fig. 2), (57, Fig. 1), and (58, Figs. 1, 2, and 4). At its pivot-opposite terminal, the LCD connects to the myosin filament backbone via its S2 part, with the LCD making a hinge connection (59) with S2, and S2 potentially acting as an almost frictionless swing-out cantilever (60, Fig. 2).

Regardless, another very important characteristic of the ascending arm, the rightward shift of the peak of the FLAR with decreasing activity, is not explainable by the spacing affecting lever geometry interaction of the myosin head and actin. A further difficulty with much of this work is the use of the polysaccharide dextran to reverse the swelling of skinned fibers by increasing the osmotic pressure on the lattice (40). Although dextran-induced alteration of lattice spacing alters isometric force production (51), the evidence is contradictory on whether (61, Fig. 1) or not (62, Fig. 4) dextran affects calcium sensitivity (see also section “calcium sensitivity”). Dextran also alters sarcomere physiological properties; e.g., it induces inverted changes in spacing when ATP is removed to generate transitions from the relaxed to the rigor state (63). This is not a surprising effect as dextran replaces the water in the muscle and thus changes the physical properties of the muscle cytoplasm.

Thus, although it is plausible that assertion 6 plays some role in the ascending arm, it has not yet been used to develop a convincing mechanistic FLR model, much less a mechanistic explanation of the entire FLAR.

Assertion 7: It has something to do with electrostatic forces

Electrostatic forces unambiguously play a crucial role in actin-myosin interactions (64), stabilizing the filament lattice (65, 66, 67), modulating actin affinity for myosin heads and the subsequent ATPase reaction, varying with changes in cytoplasm ionic strength (68), and generating the driving force for the work stroke of the myosin head (60,69, 70, 71), although the exact mechanism of electrostatic force action in the work stroke remains unresolved (69, 70, 71). Electrostatic mechanisms have also been used (60) to explain contractile steady states and to reproduce the hyperbolic force-velocity relation (72) as well as non-steady-state responses to rapid steps in length or force. Other electrostatics-based models of muscle contraction have been proposed, but, as with the above, either no predictions about the FLR were made (73), or cross-bridge interactions and volume constancy (i.e., spacing effects) were not taken into account (74).

Thus, similar to assertion 6, it is very likely that assertion 7 plays a role in the ascending arm of the FLAR. However, again, a convincing explanatory model of the FLAR using electrostatics alone has not been advanced. In the following, we present a model combining aspects of assertion 6 and assertion 7 that does so.

Materials and methods: Muscle datasets and model parameter estimation procedure

Muscle datasets

Finding data in the literature that simultaneously covered wide ranges of both sarcomere length and activity was difficult. With respect to calcium activity, typically only a few sarcomere lengths are examined (75, 76, 77, 78). With respect to FLR calcium dependency, typically only one FLR sub-region, i.e., ascending arm (79, 80, 81, 82, 83), plateau (84,85), or descending arm (86), are examined. Table 1 summarizes datasets we identified that fulfilled all the following criteria:

• 1)At least three activity levels were considered (exception: (5))
• 2)Sufficient (at least the number of parameters plus the number of activity levels) data points were available to perform the optimization (exception: (9), see below)
• 3)Length changes of more than 50% were present
• 4)Data from both the ascending and descending arms were available

Table 1.

Overview of muscle data used in fits, Fig. 8

First author name	Source	Number of data points	Species	Muscle	Fiber preparation	Temperature	Stimulus application	Sarcomere reference length	Maximum tension of preparation	CSA of preparation	Remarks
Balnave	(9), Fig. 2	20	mouse	flexor brevis	intact	22°C	electrical	≈2.85 μm	≈344 kPa	≈1000 μm2	10 mM caffeine
Brown	(10), Fig. 3 c	25	cat	caudofemoralis	whole muscle	37°C	electrical	2.4–2.5 μm	not given	not given	–
deBeer	(11), Fig. 6 b	21	rabbit	gracilis	skinned	20°C	calcium	≈2.4 μm	≈100 kPa	≈3300 μm2	I ≈ 0.16 M
deBrito	(12), Fig. 3	100	human	vastus lateralis	in vivo muscle	37°C	voluntary (EMG)	not given	not given	not given	–
Gordon	(5), Figs. 2, 3, 5	66	frog	semitendinosus	intact	20°C	electrical	≈2.1 μm	≈265 kPa	not given	max contraction
Guschlbauer (a) and (b)	(13), Fig. 9 a/b	65/84	stick insect	extensor tibiae	whole muscle	20°C –22°C	electrical	not given	≈96 kPa	1.9 mm2	extreme examples
Morgan	(14), Fig. 1	24	cat	soleus	whole muscle	38°C	electrical	≈2.45 μm	34 N/CSA	not given	–
Roszek	(15, Fig. 3)	70	rat	gastrocnemius medialis	intact	27°C	electrical	≈2.3 μm	≈10 N/CSA	not given	–
Stephenson	(16), Fig. 3	40	rat	extensor digitorum longus	skinned	22°C –25°C	calcium	2.5–2.6 μm	not given	not given	I ≈ 0.23 M
Stienen	(17), Fig. 4	28	frog	ileofibularis	skinned	5°C	calcium	<2 μm	0.8 mN/CSA	not given	I ≈ 0.16 M
Zuurbier	(18), Fig. 2	76	rat	gastrocnemius medialis	intact	27°C	electrical	≈2.3 μm	≈307 kPa	not given

Vertebrate muscles were from frog (two) (5,17), mouse (9), rat (three) (15,16,18), rabbit (11), cat (two) (10,14), and human (12). Data from a striated insect leg muscle (13) were also used. Data points were extracted from the figures given in Table 1 by a graph digitizer software, cf. (24). Table 1 lists species, muscle type and preparation, temperature, activity measure, estimated optimal sarcomere length, maximum tension of the specimen, its cross-sectional area, and, for skinned fibers, the ionic strength of the bathing saline.

Parameter estimation procedure

We aimed to find, individually for each muscle dataset, starting always from the same set ω₀ of initial parameter values, parameter values that optimally reproduced the data (see section “results”). For each literature source (LS), we define the tuple of extracted force-length-activity data as $\left({\mathbf{F}}_{\text{LS}},{\ell }_{\text{hs},\text{LS}}\right)$. The bold notation emphasizes the two-dimensional nature of the data, as the FL curves were extracted at $n_{\ell }$ different lengths and for n_c different activation levels. The optimization problem was posed in a least-squares sense to find for each LS the optimized parameter set ω^∗ and the corresponding vector of optimized values of the initially unspecified activity levels ${\tilde{C}}^{\text{∗}}:=\left({\tilde{c}}_1^{\text{∗}},\dots ,{\tilde{c}}_{n_C}^{\text{∗}}\right)$ that minimized the deviation of the data from the model output $\mathfrak{F}$ (see results)

$$\left({\omega }^{\text{∗}},{\tilde{C}}^{\text{∗}}\right)=\underset{\omega \in \text{Ω},\tilde{C}\in {\left[\mathrm{0,1}\right]}^{n_c}}{\mathrm{argmin}}{\Vert \mathfrak{F}\left({\ell }_{\text{hs},\text{LS}},\tilde{C},\omega \right)-{\mathbf{F}}_{\text{LS}}\Vert }_2^2.$$ (1)

Optimization was performed in MatLab (version R2021b, The MathWorks, Natick, MA, USA) using the pre-implemented routine lsqcurvefit, which deploys a trust-region reflective algorithm (87). Advantages of this method are the derivative-free initialization and the ability to set bounds on parameter values. Disadvantages include the need for at least as many equations (data points) as there are parameters and non-insurance of global optima (88). In the case of the data from (9), for example, we had to count the maximum force data points twice to “artificially” obtain sufficient (number of parameters plus number of activity levels: 17 + 4 = 21) equations. Algorithms for finding global optima (simulated annealing, particle swarm, Bayesian optimization) were generally found not to produce better results. The residual, i.e., the least-squares error (LSE), at the optimal parameter set was defined as

$$\text{LSE}=\left|\right|\mathfrak{F}\left({\ell }_{\text{hs},\text{LS}},{\tilde{C}}^{\text{∗}},{\omega }^{\text{∗}}\right)-{\mathbf{F}}_{\text{LS}}|{|}_2^2$$ (2)

and, for better comparison, divided by the number of data points in the experiment, $n_{\ell }\cdot n_c$, to give the relative residual $\widetilde{\text{LSE}}$.

Results

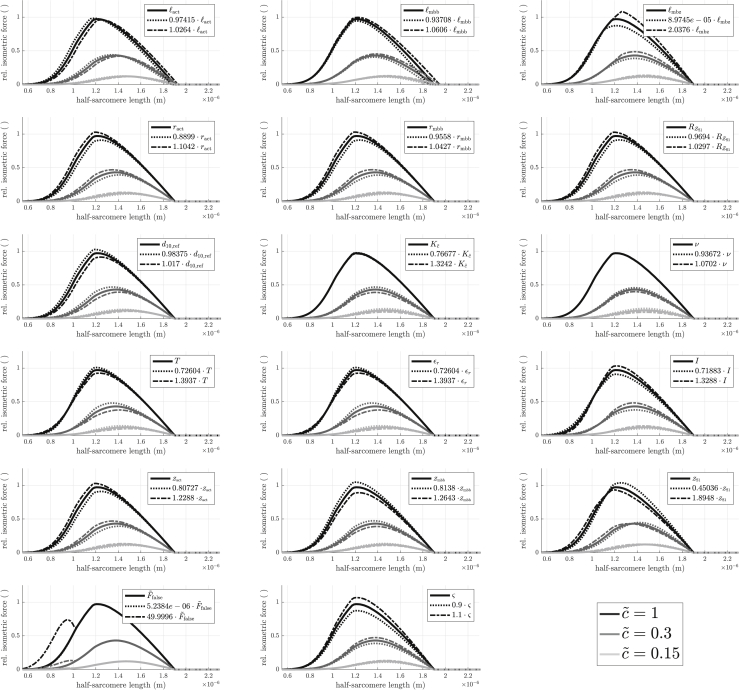
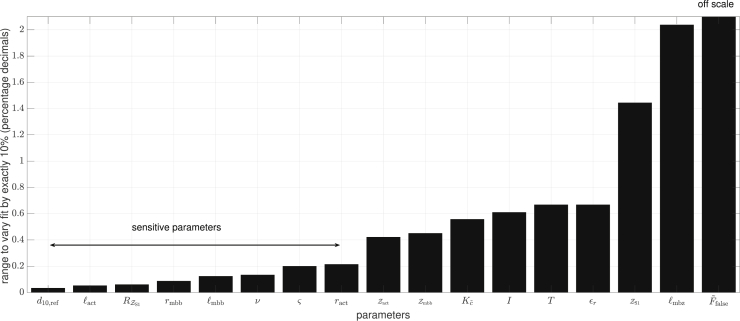
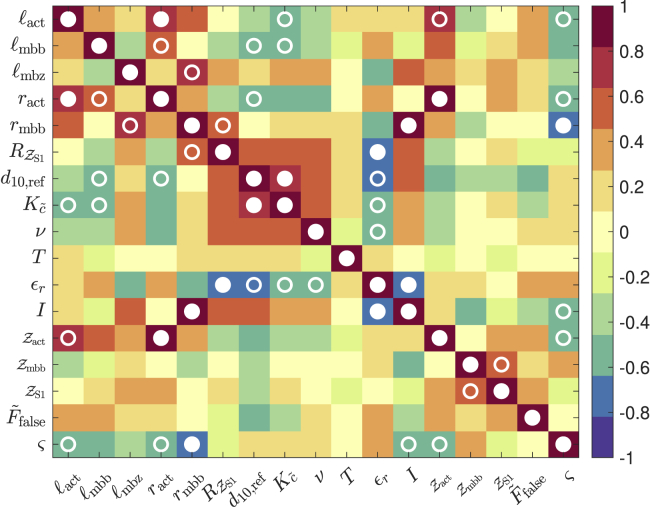
We describe here the model (section “model introduction”), show that it well fits multiple experimental datasets (section “optimization of parameters to fit experimental FLAR”), and present a simplified, five-parameter model that retains the central intellectual components of the model and reproduces the real muscle data as well or better than the original model, with its larger (17) number of fitted parameters (section “a simpler descriptive model that fits as well as the complete model”). In the appendices, we use very simple functions to give an intuitive understanding of how the model reproduces the rightward FLAR shifts that occur in real data as activity (calcium concentration) decreases (Appendix A), perform a sensitivity analysis to identify which parameters are most important for model output, and confirm this analysis by showing that, when the fits are limited to these most important parameters, the model still gives very to moderately good fits (Appendix B), elaborate on the role of physical parameters (Appendix C), and finally test for correlation among the model parameters (Appendix D).

Model introduction

Our aim was to derive a reductionist yet mechanistic model $\mathfrak{F}$ based on filament geometry, chemical reaction kinetics, and myosin-actin electrostatic interactions that well reproduced real muscle FLARs. To form a cross-bridge and produce force, a myosin head needs an active actin site within its reach. This requires simultaneously fulfilling three conditions: 1) Axially, both filaments have to overlap. 2) Radially, the head and an active actin site have to be located close enough for the head to be (electrostatically) attracted to the actin site. 3) For a myosin head to be attracted, the actin site has to be cleared from tropomyosin, i.e., be available (active), which depends on [Ca²⁺]. These conditions multiply to give the following product,

$$\mathfrak{F}\left(\text{input}\right)=\frac{\mathrm{s}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{c}\mathrm{e}}{\max \mathrm{s}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{c}\mathrm{e}}=\varsigma \cdot P_{\text{ovl}}\cdot P_{\text{aas}}\cdot P_{\text{esa}}.$$ (3)

The proportionality factor ς and the probabilities of existing filament overlap (P_ovl, Eq. (5)), of active sites being available (P_aas, Eq. (6)), and of sufficient electrostatic attraction occurring (P_esa, Eq. (14)) are derived and explained in detail below, together with the required states, controls, and parameters of the model $\mathfrak{F}$. The end result is a model of the striated muscle FLAR based on sarcomere geometry and physico-chemical considerations that maps the control states (half-sarcomere length ${\ell }_{\text{hs}}$ and relative calcium ion concentration $\tilde{c}$), together with the set $\omega \in \text{Ω}\subset {\mathbb{R}}_{+}^{17}$ of the model’s 17 parameters, to the corresponding relative isometric half-sarcomere force ${\tilde{F}}_{\text{hs}}$:

$$\mathfrak{F}:{\mathbb{R}}_{+}\times \left[\mathrm{0,1}\right]\times \text{Ω}\to \left[\mathrm{0,1}\right],\text{with }\left({\ell }_{\text{hs}},\tilde{c},\omega \right)\mapsto {\tilde{F}}_{\text{hs}}.$$ (4)

Note that the model is formulated in terms of normalized rather than absolute sarcomere force, as the number of myosin heads, and thus the maximum exertable force per half-sarcomere, varies across muscles and species.

Model parameters and parameter initial values

Table 2 lists the model’s 17 parameters, grouped by whether they involve anatomical constraints (${\ell }_{\text{act}},{\ell }_{\text{mbb}},{\ell }_{\text{mbz}}$, r_act, r_mbb, $R_{{\mathcal{Z}}_{\text{S}1}}$, d_10,ref), calcium kinetics ($K_{\tilde{c}},\nu$), physical boundary conditions (T,ϵ_r, $I,\left|{\mathcal{Z}}_{\text{act}}\right|,\left|{\mathcal{Z}}_{\text{mbb}}\right|,\left|{\mathcal{Z}}_{\text{S}1}\right|$), or cross-bridge dynamics (${\tilde{F}}_{\text{false}},\varsigma$). Table 2 also lists the basis set ω₀ of initial parameter values used by the optimizer. To our knowledge, values of all these parameters have never been simultaneously measured for any individual muscle. The ω₀ values were therefore extracted from multiple literature sources on striated muscle from different animals. We nonetheless believe these values are likely reasonably representative, as vertebrate striated muscle sarcomeres do not show the large variety in filament geometry (89) present in some invertebrates, particularly molluscs (90). The one set of invertebrate data we use, stick insect leg tibia extensor, are not in one of these anomalous groups. That the ω₀ values are not extreme is shown by the model giving normal-appearing FLAR curves with ω₀ (see Fig. 7). Furthermore, ω₀ was used only as the optimizer initial condition. It thus needed only to be well enough situated in the optimizer fitness landscape that routes to low error parameter sets for a wide range of real data existed. The ability of the optimizer to do so (see Fig. 8) demonstrates that ω₀ fulfills this requirement.

Table 2.

Symbols and meaning for occurring model parameters

Part	Symbol	Unit	Initial guess value	Source	Meaning
Actin filament	${\ell }_{\text{act}}$	[μm]	1.1	(91)	length of actin (half) filament
	ract	[nm]	5.5	(92)	radius of actin filament
	${\varrho }_{\text{act}}$	[nm]	5.5	(91)	repetition of active sites
	${\varrho }_{\text{TnC}}$	[nm]	37.5	(91)	repetition of TnC terminals
	nTnC	[ ]	$4\cdot {\ell }_{\text{act}}/{\varrho }_{\text{TnC}}=117$	–	number of TnC terminals per half-sarcomere primitive (two actin filaments and two tropomyosin helices)
	nact	[ ]	7 ⋅ nTnC≈820	–	number of active sites per half-sarcomere primitive
Myosin filament	${\ell }_{\text{mbb}}$	[μm]	0.8	(91)	length of half-myosin filament (backbone)
	${\ell }_{\text{mbz}}$	[μm]	$0.1\cdot {\ell }_{\text{mbb}}=0.08$	(91)	half-myosin bare zone width
	rmbb	[nm]	7.5	(19)	inner myosin backbone (rod) radius
	$R_{{\mathcal{Z}}_{\text{S}1}}$	[nm]	13	(60)	charge location on myosin head
	${\varrho }_{\text{S}1}$	[nm]	14.3	(91)	repetition of myosin crowns (each three double-heads)
	nS1	[ ]	$3\cdot \left({\ell }_{\text{mbb}}-{\ell }_{\text{mbz}}\right)/{\varrho }_{\text{S}1}\approx 150$	–	number of myosin double-heads per half-sarcomere
	χact,mbb	[ ]	2:1	–	ratio actin to myosin filaments
	ncb,max	[ ]	$1/\varsigma \cdot n_M\approx 100$	(93,94)	maximum number of possible cross-bridges
	ς	[ ]	1.8	(93,94)	reciprocal of ratio of maximally formed cross-bridges
	${\tilde{F}}_{\text{false}}$	[ ]	0.1	(95), Table 1	ratio of force between false and proper cross-bridges
Hill equation	$\tilde{c}$	[ ]	state [0 … 1]	–	relative concentration of calcium ions
	ν	[ ]	2.5	(96)	Hill exponent
	$K_{\tilde{c}}$	[ ]	1/40	(96)	Hill coefficient
Half-sarcomere geometry (all values here for hexagonal lattice)	${\ell }_{\text{hs}}$	[μm]	state [0.4 … 2.2]	–	half-sarcomere length
	${\ell }_{\text{hs},\text{ref}}$	[μm]	${\ell }_{\text{act}}=1.1$	–	half-sarcomere reference length
	κ10	[ ]	$2/\sqrt{3}$	–	lattice constant
	$d_{10}\left({\ell }_{\text{hs}}\right)$	[nm]	$2/3\cdot \sqrt{d_{10,\text{ref}}^2\cdot {\ell }_{\text{hs},\text{ref}}/{\ell }_{\text{hs}}}$	(50)	lattice spacing as function of ${\ell }_{\text{hs}}$
	d10,ref	[nm]	37	(51), Table 1	lattice spacing at ${\ell }_{\text{hs},\text{ref}}$
	$d_{\text{act},\text{act}}\left({\ell }_{\text{hs}}\right)$	[nm]	$\frac{2}{3}\cdot d_{10}\left({\ell }_{\text{hs}}\right)$	–	(center) distance actin-to-actin filament
	$d_{\text{act},\text{mbb}}\left({\ell }_{\text{hs}}\right)$	[nm]	$d_{\text{act},\text{act}}\left({\ell }_{\text{hs}}\right)$	–	(center) distance actin-to-myosin backbone
	$d_{\text{mbb},\text{mbb}}\left({\ell }_{\text{hs}}\right)$	[nm]	${\kappa }_{10}\cdot d_{10}\left({\ell }_{\text{hs}}\right)$	–	(center) distance myosin-to-myosin backbone
	${\hat{d}}_{\text{act},\text{mbb}}\left({\ell }_{\text{hs}}\right)$	[nm]	$d_{\text{act},\text{mbb}}\left({\ell }_{\text{hs}}\right)-r_{\text{act}}-r_{\text{mbb}}$	–	surface distance actin-to-myosin backbone
	CSAhsp$\left({\ell }_{\text{hs}}\right)$	[μm2]	$d_{\text{mbb},\text{mbb}}\left({\ell }_{\text{hs}}\right)\cdot d_{10}\left({\ell }_{\text{hs}}\right)$	–	cross-sectional area of half-sarcomere primitive
	CSAhsp,ref	[μm2]	${\kappa }_{10}\cdot d_{10,\text{ref}}^2=1.6\cdot {10}^{-3}$	–	reference cross-sectional area of half-sarcomere primitive
	$V_{\text{hsp}}\left({\ell }_{\text{hs}}\right)$	[μm3]	$\text{CS}{\text{A}}_{\text{sp}}\left({\ell }_{\text{hs}}\right)\cdot {\ell }_{\text{hs}}=V_{\text{hsp},\text{ref}}$	–	constant half-sarcomere primitive volume
	Vhsp,ref	[μm3]	${\text{CSA}}_{\text{sp},\text{ref}}\cdot {\ell }_{\text{hs},\text{ref}}=1.7\cdot {10}^{-3}$	–	half-sarcomere primitive reference volume
Electrostatics, Debye-Hückel theory	T	[K]	280 … 310	–	temperature of 7 … 37°C
	kB	[N ⋅ m ⋅ K−1]	1.381 ⋅ 10−23	–	Boltzmann constant
	e0	[C]	1.602 ⋅ 10−19		elementary charge
	${\mathcal{Z}}_i$	[ ]	integer	–	charge number (valence) of ion i
	${\mathcal{Z}}_{\text{act}},{\mathcal{Z}}_{\text{mbb}},{\mathcal{Z}}_{\text{S}1}$	[ ]	integer	–	charges on actin/myosin backbone and the head (S1)
	qi	[C]	$\left|{\mathcal{Z}}_i\right|\cdot e_0$	–	absolute electric charge of ion i
	ci	[mol/L]	solution-dependent	–	molar concentration of ion i
	I	[mol/L]	$\frac{1}{2}\sum _{i=1}^n{c}_i\cdot {\mathcal{Z}}_i^2\approx 0.17$	(97)	ionic strength of a solution with n sorts of ions
	NA	[mol−1]	6.02214 ⋅ 1023	–	Avogadro constant
	λ	[nm]	$\sqrt{\frac{{ϵ}_0\cdot {ϵ}_r\cdot k_B\cdot T}{2\cdot {10}^3\cdot N_A\cdot e_0^2\cdot I}}$	(19,98)	Debye length in electrolyte solution
	ϵ0	[C2 · N−1 · m−2]	8.854 ⋅ 10−12	–	vacuum permittivity
	ϵr	[ ]	≈80 for water	(99)	dielectric constant (relative permittivity) of the solvent
	K0(x),K1(x)	[ ]	function	–	modified Bessel functions of second kind
	${\text{Φ}}_{DH\text{cyl}}\left(d\right)$	[J]	$-\frac{q_i\cdot q_j\cdot \lambda \cdot K_0\left(d/\lambda \right)}{2\cdot \pi \cdot R_c\cdot {\ell }_c\cdot {ϵ}_0\cdot {ϵ}_r\cdot K_1\left(R_c/\lambda \right)}$	(100,101)	Debye-Hückel potential energy of cylindrical ion i of radius Rc and length ${\ell }_c$, attracting charge qj
	FDHcyl(d)	[N]	$\frac{q_i\cdot q_j\cdot K_1\left(d/\lambda \right)}{2\cdot \pi \cdot R_c\cdot {\ell }_c\cdot {ϵ}_0\cdot {ϵ}_r\cdot K_1\left(R_c/\lambda \right)}$	–	Debye-Hückel force of cylindrical ions

Which of these are optimizer-fitted parameters is given in Table 3. Activation $\tilde{c}$ and half-sarcomere length ${\ell }_{\text{hs}}$ are state variables. T was set to the temperature at which the experiment was performed. The other entries are either physical constants or auxiliary values/functions.

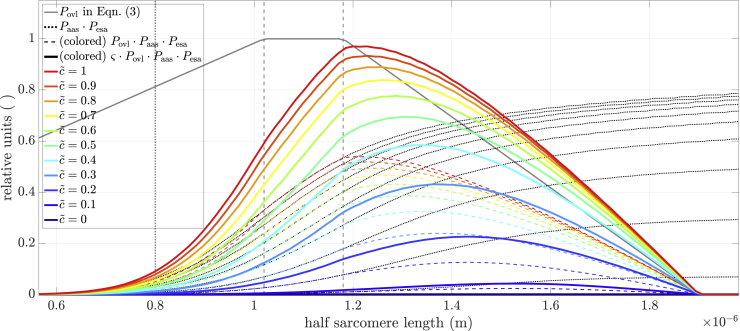
Figure 7.

Final result of Eq. (3). Filament overlap (P_ovl, solid gray line) times the product of the amount of cleared active sites and myosin binding (P_aas ⋅ P_esa, black dotted lines) is shown for several relative calcium concentrations (colored dashed lines). The scaled version of this amount ($\varsigma \cdot P_{\text{ovl}}\cdot P_{\text{aas}}\cdot P_{\text{esa}}$) is shown by the correspondingly colored solid lines and represents the relative active force-length relation (FLAR) of the half-sarcomere. The dashed vertical lines show the edges of the Gordon et al. (1966) plateau region (see text). The dotted vertical line at 0.8 nm is the initial (half-)myosin filament length. To see this figure in color, go online.

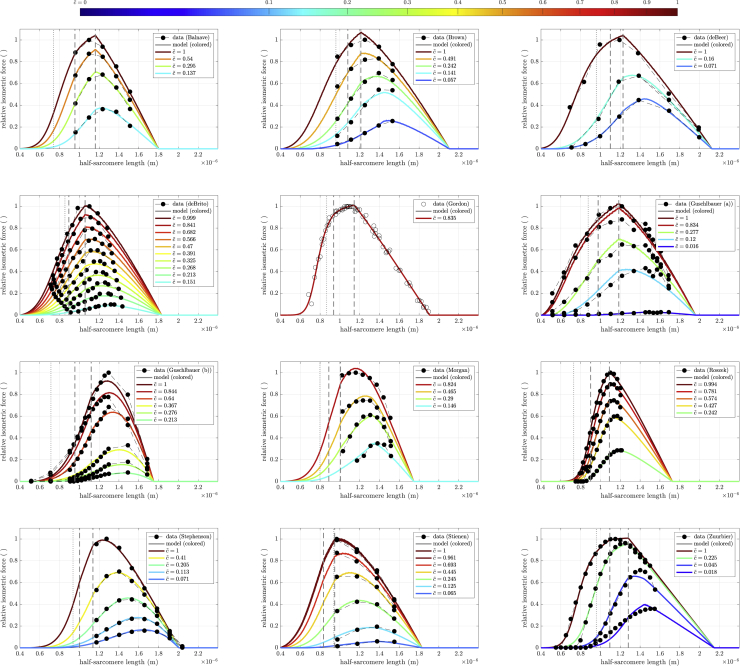
Figure 8.

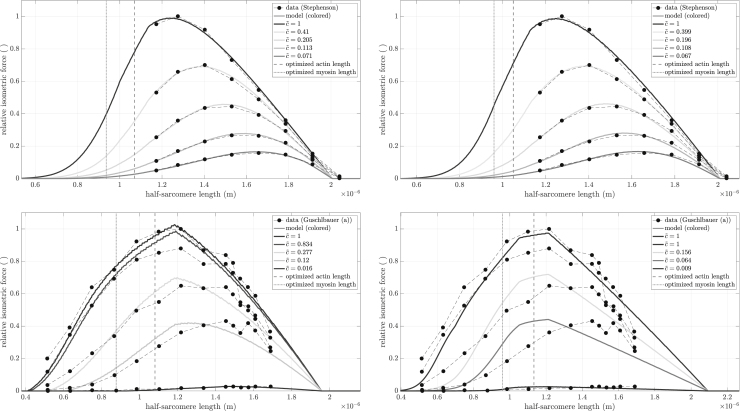
Optimal fit of model $\mathfrak{F}$ to the available datasets, see section “muscle datasets.” The dashed vertical lines in each panel show the edges of the Gordon et al. (1966) plateau region. The dotted vertical line in each panel is myosin filament length, at which the ends of the thick filament would reach the Z disk.

Filament overlap

Effective filament overlap, P_ovl in Eq. (3), was quantified by a dimensionless number between zero and one. The number of myosin heads in a half-sarcomere that see an active site in a radial direction were counted, weighted by their force-generating efficacy, and divided by the total number of heads anatomically present.

In detail: half-sarcomere reference configuration was defined as the ${\ell }_{\text{hs}}$ where the actin filaments just touched the M-line (${\ell }_{\text{hs}}={\ell }_{\text{hs},\text{ref}}={\ell }_{\text{act}}$; ${\ell }_{\text{hs}}$, half-sarcomere length; ${\ell }_{\text{hs},\text{ref}}$, half-sarcomere reference length; ${\ell }_{\text{act}}$, length of actin half filament) (${\ell }_{\text{hs}}$ equal to 1.1 micrometer in Fig. 1), and hence all myosin heads having an active site in their neighborhood. Around ${\ell }_{\text{hs},\text{ref}}$, there existed a plateau region where filament overlap does not change due to the myosin bare zone length ${\ell }_{\text{mbz}}$ on each side of the M-line. When ${\ell }_{\text{hs}}$ exceeded ${\ell }_{\text{hs},\text{ref}}$ by more than ${\ell }_{\text{mbz}}$, filament overlap decreased linearly with length reaching zero at length ${\ell }_{\text{act}}+{\ell }_{\text{mbb}}$. Since isometric force monotonically decreases with decreasing overlap (5), this ${\ell }_{\text{hs}}$ range gives rise to the descending arm. For lengths smaller than ${\ell }_{\text{hs},\text{ref}}$, the number of myosin heads that saw an active site in a radial direction was always the total number of heads anatomically present. Consequently, at these shorter lengths, a myosin head could attach to an oppositely polarized actin filament, one originating from the Z disk of the adjacent half-sarcomere. Such “false” cross-bridges nevertheless pull the oppositely polarized actin in the proper direction (i.e., the actin filament’s Z disk toward the head’s M-line) (29,30,33), but more slowly (31, Fig. 3). As the fraction of false cross-bridges rose with further shortening, half-sarcomere force dropped until ${\ell }_{\text{hs}}=\frac{1}{3}\left({\ell }_{\text{act}}+{\ell }_{\text{mbb}}\right)$ was reached, where the number of false and proper cross-bridges were equal, cf. (26, l₅ in their Eq. (A.2)). The force generated by a false cross-bridge has been measured only once, with a value one-tenth that of a proper cross-bridge (95, Table 1). Because of this value being measured only once, we introduced a parameter $0\le {\tilde{F}}_{\text{false}}\le 1$, the ratio of forces exerted by a false and a proper cross-bridge, to allow us to vary false cross-bridge force. We thus ended up with the following continuous but not differentiable effective filament overlap function ${\tilde{F}}_{\text{ovl}}\left({\ell }_{\text{hs}}\right)$, plotted in Fig. 1.

$$\begin{array}{l}{P}_{\text{ovl}}\left({\ell }_{\text{hs}}\right)={\tilde{F}}_{\text{ovl}}\left({\ell }_{\text{hs}}\right)=\\ \{\begin{array}{cc}\frac{1+{\tilde{F}}_{\text{false}}}{2}& ,\text{ if }{\ell }_{\text{hs}}\le \frac{1}{3}\left({\ell }_{\text{act}}+{\ell }_{\text{mbb}}\right)\\ \frac{1+{\tilde{F}}_{\text{false}}}{2}+\frac{1-\frac{1+{\tilde{F}}_{\text{false}}}{2}}{{\ell }_{\text{act}}-{\ell }_{\text{mbz}}-\frac{1}{3}\left({\ell }_{\text{act}}+{\ell }_{\text{mbb}}\right)}\cdot \left({\ell }_{\text{hs}}-\frac{1}{3}\left({\ell }_{\text{act}}+{\ell }_{\text{mbb}}\right)\right)& ,\text{ if }\frac{1}{3}\left({\ell }_{\text{act}}+{\ell }_{\text{mbb}}\right)<{\ell }_{\text{hs}}\le {\ell }_{\text{act}}-{\ell }_{\text{mbz}}\\ 1& ,\text{ if }{\ell }_{\text{act}}-{\ell }_{\text{mbz}}<{\ell }_{\text{hs}}\le {\ell }_{\text{act}}+{\ell }_{\text{mbz}}\\ 1-\frac{1}{{\ell }_{\text{mbb}}-{\ell }_{\text{mbz}}}\cdot \left({\ell }_{\text{hs}}-\left({\ell }_{\text{act}}+{\ell }_{\text{mbz}}\right)\right)& ,\text{ if }{\ell }_{\text{act}}+{\ell }_{\text{mbz}}<{\ell }_{\text{hs}}\le {\ell }_{\text{act}}+{\ell }_{\text{mbb}}\\ 0& ,\text{ if }{\ell }_{\text{act}}+{\ell }_{\text{mbb}}<{\ell }_{\text{hs}}\end{array}\end{array}$$ (5)

Availability of active sites: kinetics of calcium binding to troponin

After being released from the sarcoplasmic reticulum as the consequence of a muscle action potential, calcium binds to troponin C (TnC), resulting in tropomyosin moving to expose the active sites on the actin filament ($P_{\text{aas}}$ in Eq. (3)). The higher the calcium concentration, the more active sites are exposed, and the higher the force. In the model, the number of TnC terminals (n_TnC) on an active filament, and hence the maximum concentration of non-occupied terminals ([TnC]_max), was fixed at 117 TnC terminals per half-sarcomere primitive (two actin filaments each with two tropomyosin molecules spaced at a repetition distance of 37.5 nm (91)). Normalizing to the constant volume of the half-sarcomere primitive gave ${\left[\text{TnC}\right]}_{\text{max}}\equiv n_{\text{TnC}}/V_{\text{hsp},\text{ref}}\approx 120\mu \text{mol/L}$, the amount estimated from physiological measurements (102, Table 1).

Calcium concentration (muscle activation) was an experimenter-set model state parameter. Constant electrical stimulation of intact fibers or bathing skinned fibers with constant pCa = −log([Ca²⁺]) solutions yields an equilibrium concentration of free Ca²⁺ in the muscle cell cytoplasm. Rockenfeller and Günther (2017) (103) estimated a maximum concentration of free Ca²⁺ ([Ca²⁺]_max) as approximately 13 μmol/L, a pCa of approximately 4.9, based on experiments with frog skinned fibers (17). This value agrees well with a ${\left[{\text{Ca}}^{2+}\right]}_{\text{max}}\approx 17\mu \text{mol}/\text{L}$ from a recent model by (104). However, since Ca²⁺ binding sites, e.g., on TnC or ATP, make muscle cytoplasm a calcium buffer (105), the total amount of Ca²⁺ will be substantially higher, 500–1000 μmol/L (106, p.311). To account for the different calcium concentrations and dynamics among species (107), fiber types (108), and preparations (81), we introduced a relative calcium concentration parameter, $\tilde{c}=:\left[{\text{Ca}}^{2+}\right]/{\left[{\text{Ca}}^{2+}\right]}_{\text{max}}$, as a dimensionless measure of calcium saturation.

In more detail, the kinetic equilibrium equation between free TnC terminals and free calcium was

$$\nu \cdot {\text{Ca}}^{2+}+\text{TnC}\underset{k_a}{\overset{k_b}{\rightleftharpoons }}\text{TnC}-\text{Ca},$$

where TnC-Ca is a calcium-bound TnC terminal and ν is the average number of Ca²⁺ ions bound per terminal. The reaction rate constants k_a and k_b allowed calculating the equilibrium constant K_Ca:

$$K_{\text{Ca}}=\frac{k_a}{k_b}=\frac{{\left[{\text{Ca}}^{2+}\right]}^{\nu }\cdot \left[\text{TnC}\right]}{[\text{TnC}-\text{Ca}]}\iff [\text{TnC}-\text{Ca}]=\frac{{\left[{\text{Ca}}^{2+}\right]}^{\nu }\cdot \left[\text{TnC}\right]}{K_{\text{Ca}}}.$$

Since $\left[\text{TnC}\right]+[\text{TnC}-\text{Ca}]={\left[\text{TnC}\right]}_{\text{max}}$ is a constant, [TnC] could be replaced in the above equation, yielding a sigmoidal Hill equation (109) relating calcium and calcium-bound TnC:

$$[\text{TnC}-\text{Ca}]=\frac{{\left[{\text{Ca}}^{2+}\right]}^{\nu }\cdot \left({\left[\text{TnC}\right]}_{\text{max}}-[\text{TnC}-\text{Ca}]\right)}{K_{\text{Ca}}}\iff \frac{[\text{TnC}-\text{Ca}]}{{\left[\text{TnC}\right]}_{\text{max}}}=\frac{{\left[{\text{Ca}}^{2+}\right]}^{\nu }}{K_{\text{Ca}}+{\left[{\text{Ca}}^{2+}\right]}^{\nu }}=\frac{{\tilde{c}}^{\nu }}{K_{\tilde{c}}+{\tilde{c}}^{\nu }}=:P_{\text{aas}}\left({\ell }_{\text{hs}}\right),$$ (6)

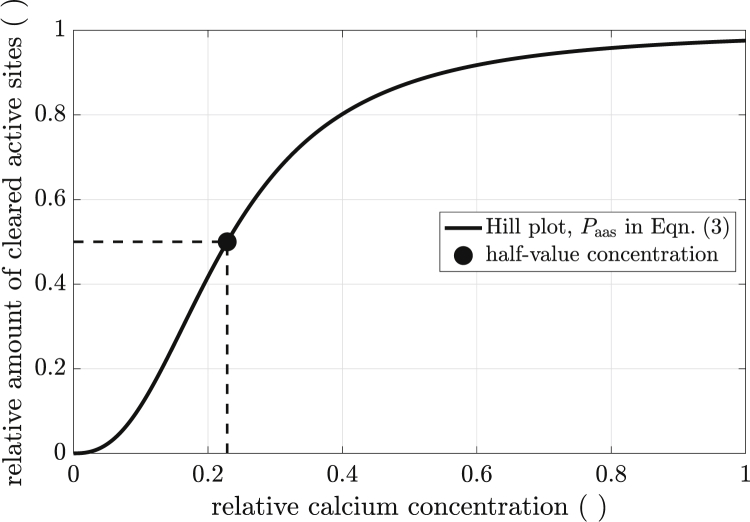
where $K_{\tilde{c}}:=K_{\text{Ca}}/{\left[{\text{Ca}}^{2+}\right]}_{\text{max}}$ denotes the normalized equilibrium constant. Hence, the quotient $[\text{TnC}-\text{Ca}]/{\left[\text{TnC}\right]}_{\text{max}}$, the probability of an active site being available (P_aas), could be directly calculated from the relative calcium concentration $\tilde{c}$. Note that ν can be interpreted not only as the number of calcium ions bound to TnC but also as a degree of cooperativity of calcium binding; see (110, 111, 112, 113) for reviews. Fig. 2 shows a Hill plot with parameters ν = 2.5 and $K_{\tilde{c}}=1/40$ (17,103). Note that $K_{\tilde{c}}={\tilde{c}}_{50}^{\nu }$, where ${\tilde{c}}_{50}$ marks the relative calcium concentration at which half the actin sites are cleared, and thus active (available for myosin head binding). Assuming [Ca²⁺]_max = 13 μmol/L, a ${\tilde{c}}_{50}$ of $1/{40}^{\left(1/2.5\right)}\approx 0.23$ corresponded to approximately 2.97 μmol/L or a pCa of around 5.7.

Figure 2.

Hill plot: probability of an actin site to be available for myosin head binding (active) (black line) versus relative calcium concentration. At $\tilde{c}={\tilde{c}}_{50}\approx 0.23$, the probability of an actin site to be active was already 50% (black dot). For explanation and parameters, see text.

Volume constancy and geometric consequences

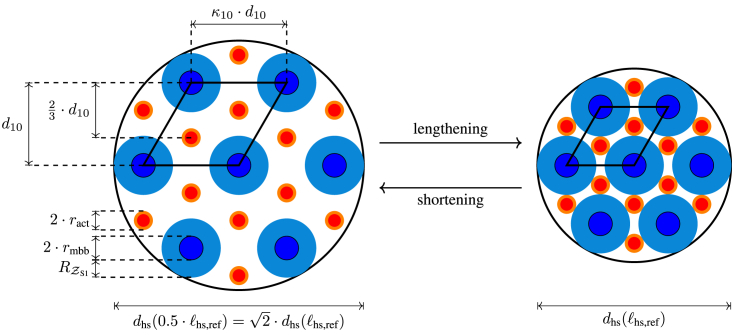
Because of muscle volume constancy (43,51), the thin and thick filaments move radially apart as muscles shorten, reducing the probability of myosin heads attaching to available active sites on the actin filaments (see section “availability of active sites: kinetics of calcium binding to troponin,”), and thus force generation. The cross-sectional area (CSA_hsp) of a single, constant-volume ($V_{\text{hsp}}\equiv V_{\text{hsp},\text{ref}}$), hexagonally arranged lattice (39) half-sarcomere primitive cell (index: hsp) changes as follows as sarcomere length changes:

$$V_{\text{hsp}}\left({\ell }_{\text{hs}}\right)\equiv V_{\text{hsp},\text{ref}}={\text{CSA}}_{\text{hsp}}\cdot {\ell }_{\text{hs}}={\kappa }_{10}\cdot d_{10}^2\left({\ell }_{\text{hs}}\right)\cdot {\ell }_{\text{hs}}={\kappa }_{10}\cdot d_{10,\text{ref}}^2\cdot {\ell }_{\text{hs},\text{ref}}={\text{CSA}}_{\text{hsp},\text{ref}}\cdot {\ell }_{\text{hs},\text{ref}}\approx 1.7\cdot {10}^{-3}\mu {\text{m}}^3$$ (7)

where the final number was obtained by substituting the following Miller-indexed vertebrate sarcomere parameter values: ${\ell }_{\text{hs},\text{ref}}=1.1\mu$m, ${\kappa }_{10}=2/\sqrt{3}$, and $d_{10,\text{ref}}=d_{10}\left({\ell }_{\text{hs},\text{ref}}\right)=37$ nm (51, Table 1). Rearranging the middle equation in Eq. (7), gives an inversely proportional relation between lattice constant $d_{10}^2$ and half-sarcomere length ${\ell }_{\text{hs}}$:

$$d_{10}^2\left({\ell }_{\text{hs}}\right)=\frac{{\ell }_{\text{hs},\text{ref}}\cdot d_{10,\text{ref}}^2}{{\ell }_{\text{hs}}}\propto \frac{1}{{\ell }_{\text{hs}}}.$$ (8)

To show the effect of length changes on lattice spacing (Fig. 3), we used these lattice parameter values to calculate the actin and myosin filament surface-to-surface distances for a 50% change in sarcomere length (${\hat{d}}_{\text{act},\text{mbb}}$):

$$\begin{array}{l}{\hat{d}}_{\text{act},\text{mbb}}\left({\ell }_{\text{hs},\text{ref}}\right)=\frac{2}{3}\cdot d_{10,\text{ref}}-r_{\text{act}}-r_{\text{mbb}}=\frac{2}{3}\cdot 37\text{nm}-5.5\text{nm}-7.5\text{ nm}=11.7\text{nm}\\ {\hat{d}}_{\text{act},\text{mbb}}\left(0.5\cdot {\ell }_{\text{hs},\text{ref}}\right)=\frac{2}{3}\cdot \frac{37}{\sqrt{0.5}}-5.5-7.5=21.9\text{nm}\\ {\hat{d}}_{\text{act},\text{mbb}}\left(1.5\cdot {\ell }_{\text{hs},\text{ref}}\right)=\frac{2}{3}\cdot \frac{37}{\sqrt{1.5}}-5.5-7.5=7.1\text{nm},\end{array}$$

with the factor $\frac{2}{3}$ arising from the actin filament being the barycenter of an equilateral triangle formed by the myosin filaments around it. Hence, in the physiological range of ${\ell }_{\text{hs}}\in \left[\mathrm{0.44...1.76}\right]\mu$m, the distance between the actin and myosin surfaces, which the myosin head must bridge, varies over a considerable range.

Figure 3.

Cross-sectional view of sarcomere lattice. A double triangular lattice of actin filaments (red-orange circles: red, actin; orange, tropomyosin) and hexagonal lattice of myosin filaments (blue-cyan circle: blue, myosin back bone (mbb); cyan, myosin heads (S1)), with each filament located in the center of six actin filaments. As the sarcomere lengthened from $\approx 1/2\cdot {\ell }_{\text{hs},\text{ref}}$ (left) to twice this length ($\approx {\ell }_{\text{hs},\text{ref}}$, right), cross-sectional area CSA_hsp halved. Black rhombus shows one possible half-sarcomere primitive cell. Every myosin lies on the vertex of a rhombus and is thus shared by four primitive cells, for a total of one myosin per cell. The two interior actin filaments are not shared and hence count fully, resulting in an actin:myosin ratio of 2:1. For parameter meanings see text or Table 2. To see this figure in color, go online.

Attraction (cross-bridge formation): Modeling electrostatics-induced actin-myosin binding

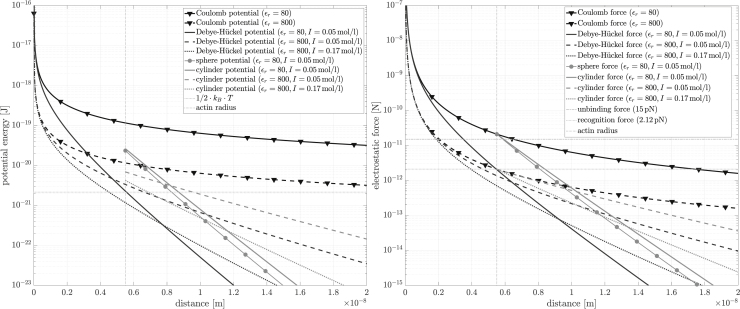
Electrostatic forces on the molecular level have been assumed to stabilize the actin-myosin lattice (67), underlie the tilting mechanics of the myosin head during force generation (60,69, 70, 71), and found experimentally (98) as well as theoretically (64) to account for crucial mechanical interactions between a myosin head and actin. We used these data to calculate the binding probability of a myosin head to the actin filament, based on the electrostatic potential of two negatively charged cylinders (actin and myosin backbones) and the (net) positively charged myosin head (S1 region).

Our interest was calculating the probability of the position of the myosin head in the summed potential field produced by the cylinders. This required calculating the potential energy of the head (Fig. 4) in the field. The cylindrical (100,101) Debye-Hückel formulation of Nakajima et al. ((98), see also Appendix C) gives the general equation for the potential energy of a charged entity in a potential field:

$${\text{Ψ}}_{DH\text{cyl}}\left(d\right)=\frac{|{\mathcal{Z}}_i\cdot {\mathcal{Z}}_j|\cdot e_0^2\cdot \lambda \cdot K_0\left(d/\lambda \right)}{2\cdot \pi \cdot R_c\cdot {\ell }_c\cdot {ϵ}_0\cdot {ϵ}_r\cdot K_1\left(R_c/\lambda \right)},$$ (9)

where ${\mathcal{Z}}_i$ and ${\mathcal{Z}}_j$ are the total number of charges on the whole cylinder and the attracted object, respectively; K₀ and K₁ modified Bessel functions of second kind; d center-to-center distance between the cylinder’s and object’s charges; R_c and l_c radius and the length of the cylinder, respectively; λ Debye length; and ϵ₀ and ϵ_r absolute permittivity of the vacuum and the dielectric constant of the matter near the object (muscle cytoplasm as well as head material), respectively.

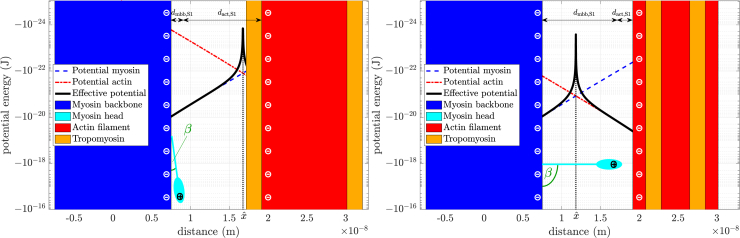
Figure 4.

Change of the potential energy function of the myosin head with sarcomere activity. (Left) Actin inactive state. The actin (red) charges are blocked by tropomyosin (orange) and the potential energy of the myosin head due to the actin electrostatic field is therefore orders of magnitude smaller than the potential energy due to the myosin backbone field (blue). The myosin head (cyan) remains near the backbone at the most negative potential energy value. Black line, the difference between the potential energies of the myosin head due to each cylinder; red line, due to actin; blue line, due to myosin. (Right) Activated state. The tropomyosin has moved aside and the actin charges are no longer blocked. The potential energy of the myosin head due to the activated actin field has become much more negative (its magnitude has increased), and the myosin head therefore orients more toward the actin surface. In both states, myosin surface charge remains unchanged (≈9 zJ potential energy at the surface). A myosin to actin center-to-center distance of approximately 25 nm was chosen, corresponding to the situation at ${\ell }_{\text{hs},\text{ref}}$. Myosin and actin radii were 7.5 nm and 5.5 nm, respectively (92). Myosin and actin charge densities were −12 e₀ and −4 e₀ per nm, respectively (101). To see this figure in color, go online.

Fig. 4 shows the situation present in muscle: two negatively charged cylinders (the myosin backbone and actin filament), and the myosin head attached to the myosin backbone by a rod (cyan head and rod attached to blue myosin backbone). Taking into account how myosin head (charge position at S1) distance to the myosin backbone and actin filament depends on the head/rod orientation β ($d_{\text{mbb},\text{S}1}=d_{\text{mbb},\text{S}1}\left(\beta \right)$ to the myosin backbone, and $d_{\text{act},\text{S}1}=d_{\text{act},\text{S}1}\left(\beta ,{\ell }_{\text{hs}}\right)$ to the actin filament), and that the myosin head is believed to carry a charge of +5 e₀, Eq. (9), allowed calculating the potential energy functions of the myosin head in the myosin backbone and actin filament electrostatic fields, respectively,

$${\text{Ψ}}_{DH\text{cyl},\text{mbb}}\left(d_{\text{mbb},\text{S}1}\right)=\frac{|{\mathcal{Z}}_{\text{mbb}}\cdot {\mathcal{Z}}_{\text{S}1}|\cdot e_0^2\cdot \lambda \cdot K_0\left(d_{\text{mbb},\text{S}1}/\lambda \right)}{2\cdot \pi \cdot r_{\text{mbb}}\cdot {\ell }_{\text{mbb}}\cdot {ϵ}_0\cdot {ϵ}_r\cdot K_1\left(r_{\text{mbb}}/\lambda \right)}$$ (10)

and

$${\text{Ψ}}_{DH\text{cyl},\text{act}}\left(d_{\text{act},\text{S}1}\right)=\frac{|{\mathcal{Z}}_{\text{act}}\cdot \tilde{c}\cdot {\mathcal{Z}}_{\text{S}1}|\cdot e_0^2\cdot \lambda \cdot K_0\left(d_{\text{act},\text{S}1}/\lambda \right)}{2\cdot \pi \cdot r_{\text{act}}\cdot {\ell }_{\text{act}}\cdot {ϵ}_0\cdot {ϵ}_r\cdot K_1\left(r_{\text{act}}/\lambda \right)}.$$ (11)

In each panel of Fig. 4, the potential energy of the head due to the myosin electrostatic field alone is shown by the blue line and that due to the actin filament alone by the red line. Note that the ordinate is logarithmic, and thus the lines are oppositely oriented; the field of the myosin backbone pulls a positive charge toward the myosin backbone, the field of the actin filament toward the actin filament. Potentials appear as almost straight lines because K₀(x) equals −log(x) to a first approximation. The black line shows the magnitude of the difference between the two potential energy functions (the difference being taken because of their opposite orientations), the actual potential energy of the myosin head in the two cylinder case.

The magnitude of the potential energy produced by the actin cylinder varies as a function of activity $\tilde{c}$ (Eq. (11)). In the inactive state (Fig. 4, left panel, $\tilde{c}=0.01$), all actin surface charges are shielded by tropomyosin, and the potential energy of the myosin head due to the actin field is, at most distances between the cylinders, much less than the potential energy of the head due to the myosin field. As a result, the most negative potential energy of the head between the two cylinders is located at the surface of the myosin backbone. Ignoring random (Brownian) movements (see below), the myosin head would orient to lie on the myosin filament backbone.

In a fully activated state (Fig. 4, right panel, $\tilde{c}=1$), all actin surface charges are unshielded. The potential energy of the myosin head in the actin electrostatic field is, at all distances, therefore much more negative (has a greater magnitude). This increase is sufficient that the most negative potential energy of the myosin head is now located at the surface of the actin filament. In the model, this effect is achieved by linearly scaling the number of “visible,” that is, unshielded, actin charges with calcium concentration ($\tilde{c}$ in Eq. (11)). Again ignoring random movements, the myosin head would orient toward the actin filament.

The description to now has assumed that the myosin head and rod were macroscopic objects. However, they are actually molecules surrounded by a fluid, and are therefore constantly randomly moving (Brownian motion) to some extent. To determine if the myosin head potential energies shown in Fig. 4 are large enough to substantially affect head position, we must compare the magnitudes of the head Brownian kinetic and electrostatic potential energies. The head is composed of a very large number of atoms (approximately 115,000 atomic units (114)) connected by covalent bonds, the proteins that comprise it, which themselves form a tertiary structure due to ionic and van der Waals forces. Each of these atoms are moving among their (temperature-dependent) degrees of freedom, and the entire ensemble is embedded in a solution composed of much smaller particles (mostly only a few atomic units) that are also moving among their temperature-dependent degrees of freedom. Determining the head Brownian kinetic energies from first principles is thus clearly difficult. However, we show now that doing so is unnecessary to demonstrate that head Brownian kinetic energies are much too small to prevent the heads from responding to the cylinder electrostatic potential energies shown in Fig. 4.

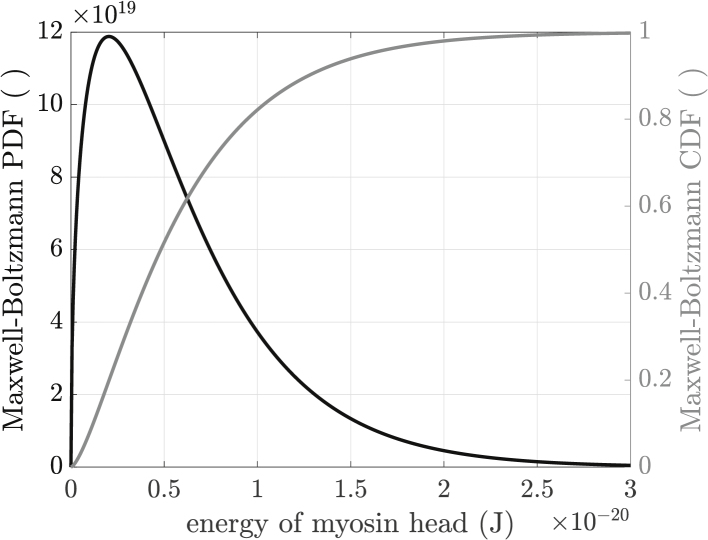
For an ideal gas, the kinetic energy distribution of its constituent entities can be calculated from the Maxwell-Boltzmann equation (Fig. 5), which describes the distribution of kinetic energies (E_kin) of three-degree-of-freedom particles by the probability density function (PDF in Fig. 5, f_MB in equations below) and the corresponding cumulative distribution function (CDF in Fig. 5, F_MB in equations below):

$$f_{MB}\left(E_{\text{kin}}\right)=2\cdot \sqrt{\frac{E_{\text{kin}}}{\pi \cdot {\left(k_B\cdot T\right)}^3}}\cdot \text{exp}\left(\frac{-E_{\text{kin}}}{k_B\cdot T}\right)$$ (12)

$$F_{MB}\left(E_{\text{kin}}\right)=\text{erf}\left(\sqrt{\frac{E_{\text{kin}}}{k_B\cdot T}}\right)-k_B\cdot T\cdot f_{MB}\left(E_{\text{kin}}\right)$$ (13)

where k_B is the Boltzmann constant and T temperature.

Figure 5.

Maxwell-Boltzmann distribution: probability density function (PDF) (black) and cumulative distribution function (CDF) (gray).

Mathematically, the Maxwell-Boltzmann distribution of the kinetic energy is equivalent to a chi (not chi-square) distribution with three degrees of freedom, or a gamma distribution with shape parameters $k_{\text{shape}}=\frac{3}{2}$ and ${\theta }_{\text{shape}}=k_B\cdot T$, respectively. Physically, the Maxwell-Boltzmann distribution describes the kinetic energy distribution of homogeneous gaseous particles under a maximum entropy condition, not the situation described above for the myosin heads. That these considerations result in a great overestimation of the myosin head Maxwell-Boltzmann velocity can be appreciated by noting that the peak E_kin (approximately 2 zJ) shown in Fig. 5 would imply a head velocity around $v=\sqrt{E_{\text{kin}}/m}\approx 3$ m/s, roughly five orders of magnitude higher than the 20 μm/s estimated work stroke velocities of myosin heads after having been rapidly and entirely unloaded, cf. (115, Fig. 7e, f) and (116, Fig. 3 a).

The curves in Fig. 5 should thus be interpreted as an upper limit below which the actual myosin head kinetic energy distribution exists. The black line shows that some 80% of the particles in a Maxwell-Boltzmann distribution at near-physiological temperatures (T was set to 298 K) have kinetic energies with magnitudes less than the 10⁻²⁰ J myosin head potential energy maximum magnitude in the right panel of Fig. 4, and all have kinetic energy magnitudes less than the 10⁻¹⁹ J myosin head potential energy maximum magnitude in the actin activated (left panel) state. Given that actual myosin head kinetic energy distribution is certain to be less, likely much less, than that in Fig. 5, these arguments show that the electrostatic potential energies in Fig. 4 are sufficient, at physiological temperatures, to drive large percentages or all of the myosin heads to the orientations shown in Fig. 4.

The next step is to combine the knowledge of the electrostatic potential energy of a myosin head as a function of distance between an actin filament and myosin backbone (Fig. 4), and the kinetic energy distribution of the myosin heads, to quantify the probability of a head becoming attached. As explained above, we have only an upper bound of the kinetic energy distribution of the heads. However, because even this upper bound kinetic energy distribution gives head kinetic energies of which the large majority or all are less than the electrostatic potential energies, we can use F_MB with little loss of accuracy in these calculations (reducing the head energy distribution by moving the energy distribution shown in Fig. 5 leftward induced negligible changes in Fig. 6). Technically, we thus replace the kinetic energy E_kin in Eq. (13) by the potential energy ${\text{Ψ}}_{DH\text{cyl}}\left(x\right):={\text{Ψ}}_{DH\text{cyl},\text{mbb}}\left(x\right)+{\text{Ψ}}_{DH\text{cyl},\text{act}}\left(x\right)$, see Eqs. (10) and (11).

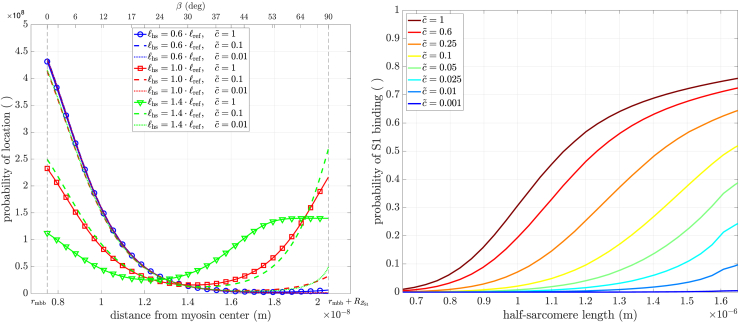
Figure 6.

(Left) Probability of location (f_pos(x)) of the tip of the myosin head (S1) at different half-sarcomere lengths ${\ell }_{\text{hs}}$ and relative calcium ion concentrations $\tilde{c}$. Note how, for short lengths, the calcium concentration did not influence the probability (solid, dashed, and dotted blue lines). The same holds for the change of lengths from short to reference length at low calcium (blue, red dotted lines). Increasing calcium concentration or sarcomere length shifted the probability in favor of the head being arranged toward the actin filament, as increasing calcium increases the visible charges on actin and increasing length decreases the lattice spacing and thus shifts the potential energy function of actin closer toward the head. (Right) The probability of myosin binding, i.e., of a head being “caught” by available actin (P_aas ⋅ P_esa in Eq. (3)), calculated by the integral of the location’s distribution from the minimum of the potential energy function to the tip of the swung-out head (Eq. (14)). The sigmoidal curves shifted right as calcium concentration decreased. To see this figure in color, go online.

For this, let x denote an arbitrary point on the (one-dimensional) line segment L of length $R_{{\mathcal{Z}}_{\text{S}1}}$ between the surface of the myosin backbone and the tip of the myosin head when fully swung out. Hence, $L=[r_{\text{mbb}},r_{\text{mbb}}+R_{{\mathcal{Z}}_{\text{S}1}}]$ represents the entirety of possible radial positions x of a head. For every $x\in L$, the evaluation $F_{MB}\left({\text{Ψ}}_{DH\text{cyl}}\left(x\right)\right)$ in Eq.(13) gives the fraction of heads whose kinetic energy is smaller than or equal to ${\text{Ψ}}_{DH\text{cyl}}\left(x\right)$. By normalizing this fraction by the integral over L, i.e., ${\int }_{x=r_{\text{mbb}}}^{r_{\text{mbb}}+R_{{\mathcal{Z}}_{\text{S}1}}}{F}_{MB}\left({\text{Ψ}}_{DH\text{cyl}}\left(x\right)\right)\text{d}x$, we obtain a probability distribution function $f_{\text{pos}}\left(x\right)$ of head position. Since the sum of the two potential energy functions in Fig. 4 (black line) has exactly one root $\hat{x}\in L$, its integral (colored lines in Fig. 6, left) has exactly one minimum. We assume that heads positioned on either side of the potential’s root are attracted toward the corresponding cylinder. The relative amount of heads aligned to the myosin backbone can therefore be calculated by integrating the distribution from the backbone’s surface to the distribution’s minimum, ${\int }_{r_{\text{mbb}}}^{\hat{x}}{f}_{\text{pos}}\left(x\right)\text{d}x$, and the relative amount of heads potentially attachable to actin can be calculated by integrating from the minimum to the tip of the swung-out head, i.e., the net probability of a head being electrostatically attracted by the actin filament instead of the myosin backbone (P_esa from Eq. (3)):

$$P_{\text{esa}}\left(\tilde{c},{\ell }_{\text{hs}}\right)=\stackrel{r_{\text{mbb}}+R_{{\mathcal{Z}}_{\text{S}1}}}{\underset{\hat{x}}{\int }}{f}_{\text{pos}}\left(x\right)\text{d}x=\frac{{\int }_{\hat{x}}^{r_{\text{mbb}}+R_{{\mathcal{Z}}_{\text{S}1}}}{F}_{MB}\left({\text{Ψ}}_{DH\text{cyl}}\left(x\right)\right)\text{d}x}{{\int }_{r_{\text{mbb}}}^{r_{\text{mbb}}+R_{{\mathcal{Z}}_{\text{S}1}}}{F}_{MB}\left({\text{Ψ}}_{DH\text{cyl}}\left(x\right)\right)\text{d}x}.$$ (14)

Fig. 6, left, sketches this scenario for several lengths and calcium levels. Myosin heads positioned left of the minimum of f_pos(x) may be associated with the so-called super-relaxed state (117), in which the heads align closely with, and are well ordered on, the myosin backbone (Fig. 4, left). Myosin heads positioned right of the minimum may be associated with the “disordered-relaxed state” (118), in which the heads move freely in the interfilament space. This distinction should, however, not be considered sharp, as heads near the myosin filament could also be disordered; i.e., not align perfectly with the backbone. Nevertheless, only disordered heads near the actin filament have a chance of becoming “attached” to an available active site and produce force. In the (practically) deactivated ($\tilde{c}=0.01$; left, dotted lines) state, most heads were near the myosin filament (super-relaxed), in accordance with experimental findings on myosin head orientation (119, Fig. 3). There is also evidence that this distribution is length dependent (120, Fig. 1 b). For lengths ${\ell }_{\text{hs}}\ge {\ell }_{\text{hs},\text{ref}}$ (Fig. 6 left, red, green), in the fully activated state ($\tilde{c}=1$, solid lines), most heads were swung out (disordered) and occupied the angular range of a myosin head’s work stroke ($\approx 60°$) (60, Fig. 2), (56, Fig. 2), (57, Fig. 1).

Fig. 6, right, shows the probability of a myosin head attaching to the actin filament as a function of half-sarcomere length at various calcium concentrations. These curves had different magnitudes and shifted progressively left as $\tilde{c}$ increased. Much of both these changes is undoubtedly due to the presence of $\tilde{c}$ in Eq. (11) for the myosin head potential in the actin filament electrostatic field. However, their shapes also changed; i.e., they are not simply differently scaled and translocated versions of a single curve. Given the complexity of the derivation of these curves, it is difficult to associate their differences to parameters of the model other than $\tilde{c}$. Presumably, the changing interfilament distances, and consequent non-linear changes in the summed electrostatic field between the two filaments, play a central role in these differences.

Scaling factor

Because of the charges on the myosin backbone, even at full activity, not all the heads can escape the myosin attraction. A total of $n_M=3\cdot \left({\ell }_{\text{mbb}}-{\ell }_{\text{mbz}}\right)/{\varrho }_M\approx 150$ S2 regions, each with a double head, are available per myosin filament within the half-sarcomere. Either head can form a force-generating cross-bridge (121). A maximum of ≈100 cross-bridges contribute to measured isometric tension ((93), Fig. 3 D). Thus, approximately two-thirds of theoretically possible cross-bridges account for 100% of measured force. Eq. (3) therefore contains the scale parameter $\varsigma \approx 1.5$ (a model parameter to be found by optimization; Eq. (3)), by which the relative amount of bound heads (cross-bridges) was multiplied to obtain 100% of relative force (maximum: 1).

Model initial conditions output

Fig. 7 shows model FLAR’s at multiple calcium concentrations using the parameter set ω₀ (Table 3). These data were generated, as explained above, by multiplying in Eq. (3) the terms of the length-dependent effective overlap function (Eq. (5), Fig. 1), the calcium-dependent probability of an active site being available (Eq. (6), Fig. 2), the length-calcium-dependent electrostatic binding of the head (Eq. (14), Fig. 6), and scaling the result by ς (1.8 in ω₀; from experimental data, expected to be about 1.5, see section “scaling factor”). These curves were then re-scaled to give a final model output (solid colored lines) with a peak of approximately 1 for the largest curve. The model gives smooth FLAR curves without any sign of piece-wise linear ascending arms. FLAR curve maxima decrease and shift right (toward longer lengths) with decreasing calcium concentration. The model thus reproduced all qualitative aspects of experimental FLAR curves.

Table 3.

Initial parameter guesses for model $\mathfrak{F}$ and optimizer lower and upper bounds

Parameter	Unit	Sensitive	Initial guess ω0	Lower bound		Upper bound
				Factor	Value	Factor	Value
${\ell }_{\text{act}}$	[μm]	✓	1.1	0.8	0.88	1.2	1.32
${\ell }_{\text{mbb}}$	[μm]	✓	0.8	0.8	0.64	1.2	0.96
${\ell }_{\text{mbz}}$	[μm]	✗	0.08	0.7	0.056	1.3	0.104
ract	[nm]	✓	5.5	0.8	4.4	1.2	6.6
rmbb	[nm]	✓	7.5	0.8	6	1.2	9
$R_{{\mathcal{Z}}_{\text{S}1}}$	[nm]	✓	13	0.8	10.4	1.2	15.6
d10,ref	[nm]	✓	37	0.9	33.3	1.1	40.7
$K_{\tilde{c}}$	[ ]	✗	0.025	0.2	0.005	5	0.125
ν	[ ]	✓	2.5	0.5	1.25	2	5
T	[K]	✗	exp.	1	exp.	1	exp.
ϵr	[ ]	✗	800	0.8	640	1.2	960
I	[mol/L]	✗	0.17	0.5	0.085	2	0.34
$\left|{\mathcal{Z}}_{\text{act}}\right|$	[ ]	✗	4400	0.5	2200	2	8800
$\left|{\mathcal{Z}}_{\text{mbb}}\right|$	[ ]	✗	9600	0.5	4800	2	19,200
${\mathcal{Z}}_{\text{S}1}$	[ ]	✗	5	0.2	1	2	10
${\tilde{F}}_{\text{false}}$	[ ]	✗	0.2	0.2	0.04	5	1
ς	[ ]	✓	1.8	0.5	0.9	1.5	2.7

Factors are given for clarity. Column three shows whether the parameters were sensitive (✓) or not (✗), see Appendix B. Temperature values were directly taken from experiments.

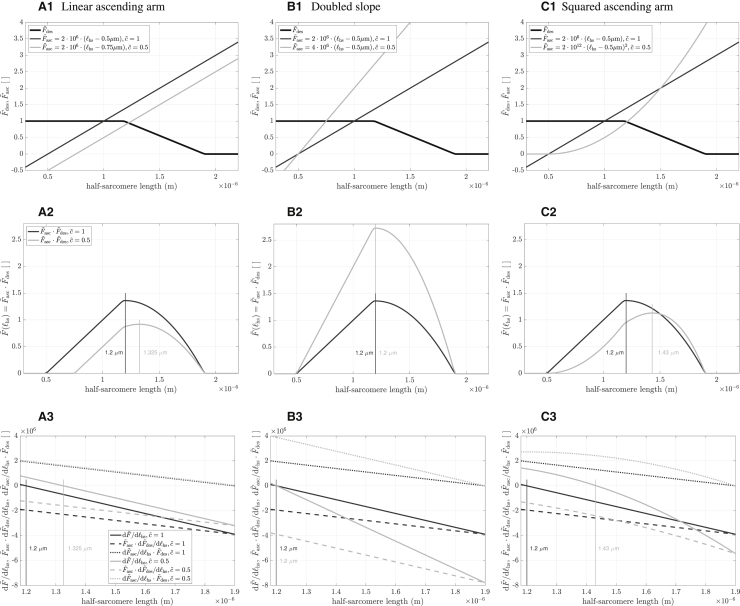
There are several important points to make about this figure. First, although the FLAR curve maxima correctly shifted right with decreasing calcium concentration, there is no obvious explanation of why they do so in the constituent parts of Eq. (3) plotted in Fig. 7, P_ovl (solid gray line) and the product of the P_aas and P_esa terms (dotted lines). That is, across the range of half-sarcomere lengths where the maxima occur, P_ovl is a simple straight line with negative slope. P_aas ⋅ P_esa are a series of smooth, sigmoid-like curves whose maxima, and maximum slopes, smoothly increase with increased calcium concentration, but there is no discontinuity or other special characteristic of the curves at the lengths where the FLAR peaks occur. The peaks instead shift due to a non-intuitive property of multiplying each P_aas ⋅ P_esa curve with P_ovl, with the position of the peak being determined by the particular slopes and magnitudes of each P_aas ⋅ P_esa curve and magnitude of P_ovl as half-sarcomere length changes. Appendix A uses simple functions analogous to the P_aas ⋅ P_esa curves to demonstrate how this non-intuitive multiplicative process can give rise to shifting FLAR peaks.

Second, the vertical dashed lines show the edges of the Gordon et al. (1966) plateau (see Fig. 1). The right vertical dashed line is the longest half-sarcomere length at which all myosin heads can be attached to an actin (thin) filament. The left vertical dashed line is the half-sarcomere length at which the actin filaments arising from the two Z disks begin to overlap. As such, in the Gordon et al. (1966) model, force would be constant between these two lines. What is actually seen is that, for all $\tilde{c}$, force continues to rise from the left to the right dashed lines. This rise is what would be expected from our model, as in it interfilament distances decrease, and thus myosin head binding probability increases, with increases in half-sarcomere length at all sarcomere lengths. For FLAR above $\tilde{c}=0.7$, a kink, i.e., a slope discontinuity, is seen at the right dashed line (the beginning of the descending arm), consistent with the Gordon et al. (1966) model. However, at lower $\tilde{c}$, no kinks are present and force begins to decline at longer and longer lengths, much longer than those predicted by Gordon et al. (1966). This again is consistent with our model. At high $\tilde{c}$, with the associated very high percentage of attached myosin heads, the effects of decreased thin:thick-filament overlap could understandably be the primary determinant of when force begins to decline. For lower $\tilde{c}$, the increased interfilament electrostatic interactions that will occur at longer half-sarcomere lengths could become more important than how many myosin heads are attached, and thus move the peaks rightward.

This trade-off between interfilament spacing decreasing (and hence acting to increase force) and thin:thick-filament overlap decreasing (and hence acting to decrease force) is also seen in two other aspects of the peak and descending arm portions of the FLAR curves. For FLAR above $\tilde{c}=0.7$, a plateau is visible, well outside the Gordon et al. (1966) half-sarcomere length at which a plateau should occur. For these $\tilde{c}$ and half-sarcomere lengths, the increased force due to decreasing interfilament spacing (P_aas ⋅ P_esa), and the decreased force due to decreasing thin:thick-filament overlap (P_ovl), just balance each other, keeping force constant. Further down the descending arm, this balance is broken as the constant negative slope of P_ovl increasingly exceeds the positive slope of the sigmoidal P_aas ⋅ P_esa. This interplay of changing force by changing spacing and overlap thus explains why the model descending arms are not linear, as they appear in Gordon et al. (1966).

Third, the left dashed line is the half-sarcomere length where opposing thin filaments begin to overlap, and thus a length at which, according to Gordon et al. (1966), a kink should occur. It is apparent that no noticeable kink is present for any $\tilde{c}$ at this half-sarcomere length.

Fourth, the vertical dotted line, myosin filament length, is the half-sarcomere length at which the myosin filaments would reach the Z line, and then become increasingly squeezed with further half-sarcomere shortening. Again, no kink is associated with this important state change of Gordon et al. (1966).

Optimization of parameters to fit experimental FLAR

Initial optimizations showed that the values of some parameters would “run away” and assume non-physiological values. Bounds were therefore set for each parameter. Table 3 gives the initial values (ω₀) plus the allowed bounds, both as absolute values and as a multiplicative factor of each parameter’s ω₀ value, and whether the model output was sensitive to the parameter in the sensitivity analysis (Appendix B). Temperature was set to the temperature at which each experiment was performed. Relative calcium concentrations, $\left({\tilde{c}}_1,\dots ,{\tilde{c}}_{n_c}\right)$ were all assumed to be greater than zero and less than or equal to one, without any hierarchical boundary conditions (e.g., ${\tilde{c}}_1<{\tilde{c}}_2$ or the like). If n_c denotes the number of different activation levels, the Cartesian product of these boundary intervals forms a hyperrectangle $\text{Ω}\subset {\mathbb{R}}_{+}^{17+n_c}$ in which all feasible parameter sets for any striated muscle are assumed to be found.

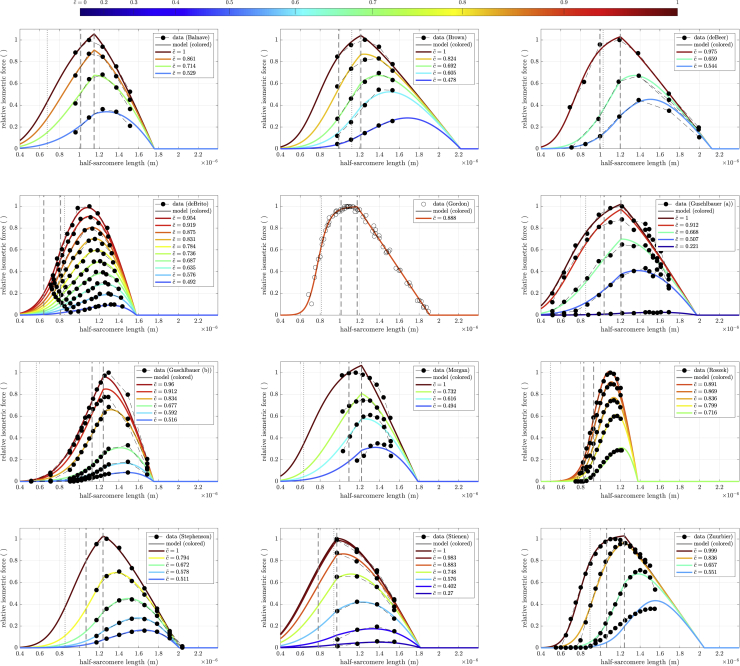
Fig. 8 shows the fits (Eq. (1)) for each of the 12 datasets (Table 1). Optimized calcium levels are indicated in the figure insets with consistent coloring according to the superimposed color bar. Note that values are ordered between full relaxation ($\tilde{c}=0$, blue) and full activity ($\tilde{c}=1$, red) in a square-root fashion to account for the non-linear activity-calcium relation (Eq. (6)). Hence, for example, $\tilde{c}=0.25={0.5}^2$ (green) is at the middle of the color spectrum. Data points are shown as black circles, with each activity level connected by a dashed line. Optimized parameter values are shown in Table 4 along with each fit’s calculated Debye length $\lambda =\sqrt{\frac{{ϵ}_0\cdot {ϵ}_r\cdot k_B\cdot T}{2\cdot {10}^3\cdot N_A\cdot e_0^2\cdot I}}$, LSE, and $\widetilde{\text{LSE}}$.

Table 4.

Optimized parameters for each data fit in Fig. 8

Dataset	${\ell }_{\text{act}}$ [μm]	${\ell }_{\text{mbb}}$ [μm]	${\ell }_{\text{mbz}}$ [μm]	ract [nm]	rmbb [nm]	$R_{{\mathcal{Z}}_{\text{S}1}}$ [nm]	d10,ref [nm]	$K_{\tilde{c}}$ [ ]	ν [ ]	T [K]	ϵr [ ]	I [mol/L]	${\mathcal{Z}}_{\text{act}}$ [ ]	${\mathcal{Z}}_{\text{mbb}}$ [ ]	${\mathcal{Z}}_{\text{S}1}$ [ ]	${\tilde{F}}_{\text{false}}$ [ ]	ς [ ]	λ [nm]	LSE ⋅ 103 [ ]	$\widetilde{\text{LSE}}$ ⋅ 103 [ ]
Balnave	1.06	0.739	0.103∗	5.69	8.01	14	35.2	0.0345	1.64	295	895	0.15	−4960	−9300	+4.26	0.514	1.44	2.64	2.77	0.111
Brown	1.15	0.96∗	0.0659	5.8	7.71	13.4	35.3	0.00506	1.44	310	960∗	0.0852∗	−5450	−8630	+4.65	0.995∗	1.59	3.72	19.3	0.77
deBeer	1.16	0.96∗	0.064	6.25	7.8	13	34.5	0.00593	1.35	293	958∗	0.103	−6780	−5580	+4.73	0.924	1.28	3.28	14.8	0.707
deBrito	0.976	0.854	0.0823	5.62	7.71	13.1	36.6	0.104	2.08	310	960∗	0.1	−5120	−8340	+4.79	0.958	1.75	3.43	52.7	0.527
Gordon	1.04	0.866	0.104∗	5.55	8.72	14.7	37	0.0627	3.07	293	644∗	0.34∗	−4970	−8020	+4.1	0.764	1.24	1.48	54.1	0.819
Guschlbauer (a)	1.08	0.877	0.104∗	6.59∗	7.64	11.9	33.6	0.0182	1.38	294	960∗	0.0864	−8620	−12900	+9.37	0.973	1.62	3.59	206	2.95
Guschlbauer (b)	1.04	0.713	0.0825	5.3	7.17	12.3	37.9	0.0435	2.7	294	960∗	0.115	−4110	−7190	+1.03	0.999∗	2.39	3.11	94.2	1.05
Morgan	0.947	0.799	0.0588	5.35	7.44	13.1	36.1	0.0373	1.25∗	311	960∗	0.116	−3510	−10800	+1.5	0.2	2.21	3.19	50.3	1.57
Roszek	0.995	0.729	0.0946	5.52	8.2	14.5	40.7∗	0.125∗	1.97	300	643∗	0.334	−5130	−6280	+4.57	0.0401∗	1.42	1.51	15	0.215
Stephenson	1.07	0.936	0.0675	6.01	7.37	11.4	37.1	0.015	1.36	297	922	0.148	−5510	−5370	+1∗	0.2	1.51	2.71	3.32	0.0831
Stienen	0.891	0.938	0.0567	5.5	6.98	11.8	34.7	0.0376	1.75	278	926	0.086	−4860	−9040	+5.29	0.614	1.87	3.44	6.85	0.245
Zuurbier	1.19	0.96∗	0.0934	6.56∗	8.67	12.1	34.2	0.005∗	1.25∗	300	960∗	0.307	−8650	−4870	+1∗	0.653	1.03	1.93	67.1	0.883

Debye length, absolute error (LSE), and normalized (thousandfold) error ($\widetilde{\text{LSE}}$) shown in last three columns. Optimal parameters within a 1% neighborhood of optimizer boundaries (Table 3) are indicated by asterisks. All numbers given to three significant digits.

Description of fits

The model extremely well reproduced the experimental data across a wide range of muscles, capturing both the variations in FLAR peak values and, where such data were available, the rightward shift of the peak as calcium concentration changed. Normalized LSE values (Table 4) were extremely good, with a maximum LSE of 0.2, and a mean LSE of 0.0489 in data running from 0 to 1. Some of this error is also clearly due to experimental flaws. In the data with the greatest LSE (Guschlbauer (a)), the $\tilde{c}=0.12$ data had two peaks and the maximum activity data line crossed lower activity data lines. Similarly, in the data with the second greatest LSE (Guschlbauer (b)), the second-most-activated data line crossed the third-most-activated data line.

As with the theoretical FLAR curves in Fig. 7, the curves showed multiple differences from Gordon et al.’s (1966) predictions (all conventions in Fig. 8 are the same as in Fig. 7). At high $\tilde{c}$, many curves did show a kink (Balnave, Brown, deBeer, deBrito, Gordon, Guschlbauer (a), Roszek, Stienen, Zuurbier), at the end of the Gordon et al. (1966) plateau (right vertical dashed line, the beginning of not all myosin heads being bound, the classic beginning of the descending arm), with the Zuurbier fit actually showing a true plateau, although this was just the flattening of a clearly sigmoidal function. In almost all cases (Guschlbauer (a) being an exception), this kink disappeared at lower $\tilde{c}$. In no cases except our Gordon fit were the left edge of the plateau (the beginning of opposing thin-filament overlap) or the half-sarcomere length at which the thick-filament ends would reach the Z disk (dotted vertical line) associated with any noticeable kink in the FLAR ascending arm. A notable observation was that for many fits (Brown, deBeer, deBrito, Gordon, Guschlbauer (a), Stienen, Zuurbier) the half-sarcomere length at which the ends of the thick filaments would reach the Z disk were at large force values on the ascending arms, suggesting that, if these fits are valid, thick-filament penetrations of rather than collisions with the Z disk (assertion 5) occur in the muscle. With respect to descending arm linearity, both Gordon et al. (1966)-like completely linear arms were present (deBeer, Gordon, and Zuurbier) and descending arms in which only the end portions appeared nearly linear, as in Fig. 7.

We now describe the parameter values found in the fits, grouping the parameters as in section “model parameters and parameter initial values.”

Anatomical parameters

Optimized actin lengths all settled well within the bounds, with a minimum of 0.891 μm (Stienen) and a maximum of 1.19 μm (Zuurbier). Myosin lengths, alternatively, showed large variation, ranging from a minimum of 0.713 μm (Guschlbauer (b)) and reaching the upper bound of 0.96 μm for three muscles (Brown, deBeer, Zuurbier). Real myosin lengths vary less than actin lengths (89,122). We show in Appendix B that the sensitivity of $\mathfrak{F}$ was greater to actin length than myosin length, possibly explaining the wider variation of model myosin values. Myosin bare zone length was also highly variable, ranging from 0.0567 μm (Stienen) to the upper bound 0.104 μm (Balnave, Gordon, Guschlbauer (a)). Bare zone to backbone ratio also varied substantially, between 6.6% (deBeer) and 14% (Balnave). Since absolute forces were not considered, we do not assess the absolute number of possible cross-bridges, which decrease with a higher ${\ell }_{\text{mbz}}/{\ell }_{\text{mbb}}$ ratio or shorter ${\ell }_{\text{mbb}}$.

Radial sarcomere geometry remained close to our initial guesses: actin radius varied from 5.3 nm (Guschlbauer (b)) to 6.59 nm (Guschlbauer (a)) and myosin backbone radius from 7.17 nm (Guschlbauer (b)) to 8.72 nm (Gordon). The reference lattice constant d_10,ref was predominantly below our initial guess, ranging from 33.6 nm (Guschlbauer (a)) to 40.7 nm (Roszek).

Hill parameters

$K_{\tilde{c}}$ settled mainly within the bounds, although Zuurbier again reached the lower bound of 0.005 and Roszek the upper bound of 0.125. Assuming a maximum calcium concentration of $13\mu$mol/L, these values give half-activity pCas of 6.7 and 5.3, respectively. ν almost always decreased, with the lower bound of 1.25 reached twice (Morgan, Zuurbier), and only Guschlbauer (b) increasing (to 2.7). The Gordon data gave a ν of 3.07, but this value is not reliable as only fully activated data were available for this muscle. Further reducing ν’s lower bound to 1 did not improve the residuals.

Electrostatic parameters

We here only summarize these parameters; see Appendix C for detailed discussion. The optimizer tended to increase Debye length (last column, Table 4) from the initial value of ≈0.76 nm, settling between 1.48 nm (Gordon) and 3.72 nm (Brown). Debye length depends, in part, on ϵ_r and ionic strength (Table 2). The changes in Debye length in the model were achieved by simultaneous increases in ϵ_r (from 644 for Gordon to 960 for Brown and others) and decreases in ionic strength (from 0.0852 mol/L for Brown to 0.34 mol/L for Gordon). Charge number on the actin filament and the myosin backbone did not reach the bounds for any muscle. Actin charges always increased (from 3510 e₀ for Morgan to 8620 e₀ for Guschlbauer (a)). Myosin backbone charges showed more variability (from 4870 e₀ for Zuurbier to 12,900 e₀ for Guschlbauer (a)). These values correspond to charge densities between 3.7 e₀/nm and 8 e₀/nm (actin) and 5.1 e₀/nm and 14.9 e₀/nm (myosin). The actin-to-myosin charge ratio consequently varied from 0.3 (Morgan) to 1.8 (Zuurbier). The number of charges on the head showed no strong correlation with the number of charges on either filament (see Appendix D). Values between the lower bound of 1 e₀ (Stephenson, and Zuurbier) and the upper value of 9.37 e₀ (Guschlbauer (a)) were found, with a mean of approximately 3.86 e₀. Using this value, the total number of charges engaged in binding one myosin head to a 10-nm length of actin filament (approximately two active sites) was $3.86e_0\cdot 6e_0/\text{nm}\cdot 10\text{nm}\approx 232e_0^2$, which compares well with the 200 $e_0^2$ found by (98).

Cross-bridge dynamics parameters

The sensitivity analysis presented in Appendix B shows that the value of the false to proper cross-bridge force ratio either had no measurable effect on model output, or, at extreme values, caused the model to fail (introducing two peaks in the FLAR at high [Ca²⁺] levels). This low sensitivity is presumably a reason for the wide variety of false cross-bridge force values found by the optimizer: for Morgan and Stephenson, ${\tilde{F}}_{\text{false}}=0.2$ remained unaltered; in Roszek, ${\tilde{F}}_{\text{false}}$ was diminished to 0.04; and in almost half of the cases (Brown, deBeer, deBrito, Guschlbauer (a) and (b)), it reached values above 0.9; i.e., false cross-bridges were exerting a force almost equal to proper ones.

The scale factor ς

The parameter ς ranged from 1.03 (Zuurbier) to 2.39 (Guschlbauer (b)), corresponding to 98% and 42%, respectively, of maximally possible cross-bridges simultaneously binding to produce force. These values can directly be related to the variable actin-to-myosin charge ratios above; i.e., the more charges on actin compared to myosin, the more likely the heads will form cross-bridges. Although it would not make sense physiologically, ς was mathematically allowed to reach values less than one. That no optimization gave values less than one is consistent with the model being intrinsically physiologically plausible.

Residuals

The Stephenson data had the overall best fit with a relative residual $\widetilde{\text{LSE}}$ (LSE per data point) of 8.31 ⋅ 10⁻⁵. Most of the other fits had $\widetilde{\text{LSE}}$ between 1.11 ⋅ 10⁻⁴ (Balnave) and 8.83 ⋅ 10⁻⁴ (Zuurbier). Three fits had $\widetilde{\text{LSE}}$ above 10⁻³ (Morgan, Guschlbauer (a) and (b)). As noted in section “description of fits,” the high residual for Guschlbauer (a) and (b) is likely partially explained by experimental errors. It is important to stress that all fits were conducted using the same initial guess, bounds, and algorithm. Varying these for individual muscles might have improved the LSE of that individual muscle, but would have likely worsened the LSE of others. It is beyond the scope (and would contradict the general applicability claim) of this modeling paper to identify the best initial guess, boundaries, and optimization procedure for each dataset individually.

A simpler descriptive model that fits as well as the complete model

Rockenfeller and Günther (2018) argued in earlier work (96) that calcium density within a fixed cross-sectional area in the neighborhood of the TnC terminals varies with sarcomere length. Unfortunately, this explanation is wrong; calcium concentration [Ca²⁺] per unit volume does not change with length. Experiments have also not provided any evidence of a length-dependent change in TnC calcium affinity (123,124). Despite the constancy of [Ca²⁺] as length changes, there is an effective dependence on length of the ability of a given [Ca²⁺] to produce force, due to the length-dependent changes in interfilament distance and thus the probability of a myosin head to bind (Fig. 6, right), see sections “availability of active sites: kinetics of calcium binding to troponin,” “volume constancy and geometric consequences,” “attraction (cross-bridge formation): modeling electrostatics-induced actin-myosin binding,” and “scaling factor”. We use here this effective length dependency to present a very reduced, descriptive FLAR model. Rockenfeller and Günther (96) used the following equation to describe a calcium and length-dependent force replacing the P_esa · P_aas product in Eq. (3).

$${\tilde{F}}_{\text{asc}}\left(\tilde{c},{\ell }_{\text{hs}}\right)=\frac{{\left({\varpi }_{\text{asc}}·\tilde{c}·{\ell }_{\text{hs}}/{\ell }_{\text{hs},\text{ref}}\right)}^{{\nu }_{\text{asc}}}}{1+{\left({\varpi }_{\text{asc}}·\tilde{c}·{\ell }_{\text{hs}}/{\ell }_{\text{hs},\text{ref}}\right)}^{{\nu }_{\text{asc}}}}.$$ (15)

This equation continually increases with ${\ell }_{\text{hs}}$ (that is, does not include the effects of decreasing filament overlap at large ${\ell }_{\text{hs}}$). Because the FLAR is essentially insensitive to false cross-bridges (Appendix B), we used the following simplified version of Eq. (5), in which false cross-bridges are omitted, for P_ovl in Eq. (3).

$${\tilde{F}}_{\text{des}}\left({\ell }_{\text{hs}}\right)=\{\begin{array}{cc}1& ,\text{ if }{\ell }_{\text{hs}}\le {\ell }_{\text{act}}+{\ell }_{\text{mbz}}\\ 1-\frac{1}{{\ell }_{\text{mbb}}-{\ell }_{\text{mbz}}}\cdot \left({\ell }_{\text{hs}}-\left({\ell }_{\text{act}}+{\ell }_{\text{mbz}}\right)\right)& ,\text{ if }{\ell }_{\text{act}}+{\ell }_{\text{mbz}}<{\ell }_{\text{hs}}\le {\ell }_{\text{act}}+{\ell }_{\text{mbb}}\\ 0& ,\text{ if }{\ell }_{\text{act}}+{\ell }_{\text{mbb}}<{\ell }_{\text{hs}}\end{array}.$$ (16)

Assuming that the myosin bare zone length is always 10% of the myosin backbone length (${\ell }_{\text{mbz}}=0.1\cdot {\ell }_{\text{mbb}}$), we ended up with a very compact five-parameter model approximation ${\mathfrak{F}}_{\text{simple}}$ of the complete FLAR:

$${\mathfrak{F}}_{\text{simple}}\left(\tilde{c},{\ell }_{\text{hs}}\right)=\varsigma \cdot {\tilde{F}}_{\text{asc}}\left(\tilde{c},{\ell }_{\text{hs}}\right)\cdot {\tilde{F}}_{\text{des}}\left({\ell }_{\text{hs}}\right).$$ (17)

Fig. 9 and Table 5 show the ability of ${\mathfrak{F}}_{\text{simple}}$ to fit the 12 muscle datasets (sections “muscle datasets” and “optimization of parameters to fit experimental FLAR”), again using the optimizer described by Eq. (1). In this example, all boundaries were chosen so as not to be reached during optimization. Remarkably, for some data (deBrito, Gordon, Guschlbauer (a), Stephenson, and Stienen), ${\mathfrak{F}}_{\text{simple}}$ gave better absolute residuals than $\mathfrak{F}$. This result may suggest that finding mathematically possible solutions in the complete model $\mathfrak{F}$ might have been impeded by physical boundary conditions. That is, limiting some of the parameters to certain ranges may have prevented the optimizer, starting from the initial parameter guess ω₀, from being able to find better fitness maxima. For cases where errors are unbearably large, that might indicate that changing ω₀, the boundaries imposed on the optimizer, or revising the physically based $\mathfrak{F}$ model, is required. A drawback to the simple model is that the parameter values obtained by it can often not be meaningfully interpreted, see for example ${\ell }_{\text{act}}=0.73\mu \text{m}$ (deBrito), ${\ell }_{\text{mbb}}<0.6\mu \text{m}$ (Guschlbauer (b), Roszek), ν_asc > 10 (Gordon, Roszek) or $\varsigma >2$ (deBrito, Roszek). Hence, the model simplification definitely hinders mechanistic understanding of the physical system. For this reason, although we show the edges of the Gordon et al. (1966) predicted plateau (dashed vertical lines) and the half-sarcomere length at which the ends of the thick filaments would reach the Z disk (dotted lines), we do not describe them here. However, if the goal is a computationally cheap model for describing the full FLAR, model ${\mathfrak{F}}_{\text{simple}}$ is highly suitable. Finally, we note that the number of state variables (currently two: $\tilde{c}$ and ${\ell }_{\text{hs}}$) in both models (${\mathfrak{F}}_{\text{simple}}$ and $\mathfrak{F}$) can be extended in a straight forward way to include other physiological processes; e.g., ATP dynamics (125).

Figure 9.

Optimal fit of model ${\mathfrak{F}}_{\text{simple}}$ to the available datasets, see section “muscle datasets.” Note that the color bar differs from Fig. 8 due to inherently different Hill exponents. The dashed vertical lines show the edges of the Gordon et al. (1966) plateau region. The dotted vertical line is myosin filament length, the sarcomere length at which the ends of the thick filament would reach the Z disk.

Table 5.

Comparison of optimized parameters, including initial guess and bounds, from each data fit of ${\mathfrak{F}}_{\text{Simple}}$, cf. Fig. 9

Parameter/dataset	${\ell }_{\text{act}}$ [μm]	${\ell }_{\text{mbb}}$ [μm]	${\varpi }_{\text{asc}}$ [ ]	νasc [ ]	ς [ ]	LSE ⋅ 103 [ ]	$\widetilde{\text{LSE}}$ ⋅ 103 [ ]
Initial guess	1.1	0.8	1.5	5	1.5
Lower bound	0.66	0.48	0.3	2.5	0.45
Upper bound	1.54	1.12	7.5	15	3
Balnave	1.08	0.676	1.33	3.93	1.33	12.3	0.491
Brown	1.1	1.11	1.33	5.84	1.15	11.7	0.469∗
deBeer	1.1	1.03	1.45	6.36	1.09	15.7	0.747
deBrito	0.726	0.851	0.758	5.49	2.54	29.7	0.297∗
Gordon	1.09	0.815	1.58	14	0.999	53.2	0.805∗
Guschlbauer (a)	1.12	0.851	1.55	4.24	1.14	135	1.93∗
Guschlbauer (b)	1.19	0.566	1.07	5.96	1.6	78.5	0.873∗
Morgan	1.15	0.634	1.53	4.93	1.17	76.3	2.39
Roszek	0.882	0.496	0.956	10.9	2.46	48.8	0.697
Stephenson	1.15	0.856	1.18	6.38	1.25	1.77	0.0442∗
Stienen	0.875	0.939	1.11	3.5	1.49	8.47	0.303
Zuurbier	1.15	0.895	1.45	9.82	1.04	95.6	1.26

Corresponding absolute (LSE) and relative ($\widetilde{\text{LSE}}$) errors (thousandfold) shown in the last two columns. Relative errors indicated by asterisks indicate better residuals than the ones obtained with model $\mathfrak{F}$, cf. Table 2. Numbers given to three significant digits.

Discussion

We presented here an FLAR muscle model based on fundamental physical properties. The model well reproduced experimental data from a large number of muscles. The key addition to prior models was including the changes in interfilament spacing that occur as sarcomere length changes, something that, to our knowledge, prior muscle models lack. This addition naturally and intuitively explains the ascending arm of the FLAR without resort to “hand-waving” arguments about filament collisions or thick-filament compression. Although not as intuitively obvious, the combination of 1) the force decrease due to decreased filament overlap and 2) the contemporaneous increase in force due to decreased filament spacing naturally leads (Fig. 7) to the ubiquitous observation that FLAR peaks move to longer sarcomere lengths as muscle activity ([Ca²⁺]) decreases (see also Appendix A). The combination of extremely good fits and a mechanistic explanation of the ascending arms and shifting force maxima of real FLAR curves makes us believe the proposed model constitutes a substantial advance in muscle models. We also provide a simpler descriptive model that reproduces experimental data as well or better than the complete model, and which may therefore be advantageous for “everyday” computational modeling in practice.

Potential limitations/flaws in model approach

Most aspects of the model are a direct application of geometric constraints, physical laws, and well-described biochemical processes (e.g., Hill-curves), and thus unlikely to be flawed. One concern is the calculation of the myosin head binding in section “attraction (cross-bridge formation): modeling electrostatics-induced actin-myosin binding.” We model this process solely on the basis of the potential energy of the myosin head in the summed potential field produced by the myosin backbone and actin filament. Although this approach likely well approximates myosin head position between the filaments, myosin head binding to the actin filament depends on the amino acid sequences of the myosin head and actin binding sites. Our model assumes that these atomic-specific interactions do not need to be specifically modeled, but occur “automatically” provided the myosin head and open actin binding site are sufficiently close. We are unaware of data that contradict this assumption. The good fits the model produces also suggest that including this level of detail is not required to produce extremely accurate FLAR models.

Alamo et al. (126) estimated a 60:40 ratio of super-relaxed to disordered-relaxed myosin heads in low calcium mouse heart muscle. In our model, at short sarcomere lengths and low calcium, essentially 100% of the heads are in what we presume might be the super-relaxed state (blue lines, Fig. 6, left). At longer sarcomere lengths (red, green lines, Fig. 6, left), our super-relaxed and disordered-relaxed ratios are comparable with those in (126). To our knowledge, the dependence of the super-relaxed/disordered-relaxed ratio on sarcomere length has not been explicitly reported, although it is visible in the data of (119, Fig. 3). If the Alamo et al. (126) data are from short sarcomeres, our model ratios may thus agree with existing data. If not, one explanation could be the molecular differences between heart and skeletal muscle myosins. Another explanation could be that tropomyosin does not perfectly shield the actin filament, which would increase the effect of the actin potential energy in the inactive state, and hence the number of disordered-relaxed heads. A final explanation could be that we have not considered the effect dissolved entities in the cytoplasm between the two filaments would have on myosin head movement or attraction. For example, such entities reduce the effective volume in which proteins can move (excluded volume effects (127)), which might hinder the formation of super-relaxed heads. Also, the physical properties of such entities in the cytoplasm, or the cytoplasm itself, may well affect the dielectric constant (relative permittivity) ϵ_r, similar to how charged particles in a fluid determine ionic strength I.

Another model limitation is that it explains the FLAR, which describes muscle activity at steady state. In its present form, it is thus not immediately applicable for modeling the temporal evolution of muscle contraction. A time-dependent model could be developed in future work by allowing calcium concentration to change over time, the muscle to shorten in response by including equations predicting how much filament movement should result from each head attachment, and feeding the contractile response back to the existing P_ovl, P_esa, and P_ass equations. These changes would allow P_ovl, P_esa, and P_ass to be continuously updated, and hence predict dynamic contractions in response to varying muscle activity and boundary (load) conditions.

The simple model and further simplifications

The simple model (section “a simpler descriptive model that fits as well as the complete model”) emphasizes many of the issues raised above. The model gave very good performance, but reduced understanding of which parameters were being altered to achieve the fits. Given the unimportance of false cross-bridges demonstrated here, an obvious simplification of both $\mathfrak{F}$ and ${\mathfrak{F}}_{\text{simple}}$ is replacing the piece-wise linear ${\tilde{F}}_{\text{des}}\left({\ell }_{\text{hs}}\right)$ function used here with single, often continuously differentiable, functions, e.g., sigmoid (103, Appendix F) or hyperbolic tangent ($\frac{1}{2}\text{tanh}\left(slope\cdot \left(position-{\ell }_{\text{hs}}\right)\right)+\frac{1}{2}$, where the two shape parameters slope and position lie in the magnitude of approximately 3 μm⁻¹ and 1.5 μm).

Calcium sensitivity

The term calcium sensitivity is used in multiple ways in the muscle contraction literature (e.g., (17,80,81,86,128, 129, 130)) and consequently, at least to a mathematician, is not well defined. For instance, calcium sensitivity is defined as both “the term that is used to express the fact that force at a given [Ca]²⁺ can vary” (131, p.222) and “a concept used by researchers to simplify the complex, dynamic process of […] contraction […] into a relationship between the concentration of free calcium ions available for binding to TnC and the amount of force generated by the muscle” (132, p.2). It is unclear from these descriptions whether calcium sensitivity refers to changes in output (e.g., force) as a function of input state variables (e.g., length), where [Ca²⁺] is an additional state variable, or to changes of an additional state or boundary condition (e.g., length or pH), with these changes being performed at a fixed [Ca²⁺], which is then varied systematically.

Furthermore, the term sensitivity has different meanings in different fields. In mathematics, sensitivity is a differential measure, quantifying the changes in output that correspond to changes in the input when only a single parameter is changed with the others held constant (see Appendix B). This meaning is also present in the muscle literature in such uses such as “Ca-sensitivity […] was lost” (133, p.713) or “there is little Ca²⁺ sensitivity” (134, p.4910). In physiology, alternatively, sensitivity commonly is an absolute measure, describing the minimum value of an input required for any system response (system threshold), or to achieve a certain system output (e.g., 50% of maximum response). This sense is also (although often only implicitly) used in the muscle literature when describing system output relative to a characteristic pCa₅₀ value (e.g., the pCa at which half the maximum output state value is attained), cf. (135, p.4195), (19, p.337), and (136, p.114).

A particular problem with the physiological definition arises when describing force-pCa curves (Hill plots) by means of their inflection point (pCa₅₀) and slope (ν): the Hill exponent ν can be expressed as the derivative of the force with respect to pCa at pCa₅₀, and thus in a mathematical sense as the local sensitivity of force with respect to calcium around pCa₅₀. Presumably to prevent confusion for having pCa₅₀ already named calcium sensitivity instead of, e.g., “half-maximal effective calcium concentration” (137), we find compensatory designations of ν in the physiological literature, e.g., “cooperativity” (138) or even “ultrasensitivity” (139). Similar conceptual and terminological ambiguities also occur regarding normalized sensitivity, i.e., percentage change in output per percentage change in input. This quantity can also be found under the names elasticity (coefficient) or response coefficient, cf. (140), which could easily be confused with material properties (fiber elasticity) or enzyme kinetics (the dependence of a system variable on an external parameter).

Biological implications

Using actin:myosin filament interaction to generate force first evolved in eukaryotes to power cell division (141,142), only later being co-opted (perhaps more than once (143,144)) to generate tissue contraction (originally in combined neuromuscular cells; for a brief review, see (145)). Given this evolutionary history, it is not surprising that, when examined across Animalia, a great variety of actin:myosin contraction systems exist (90), particularly with respect to myosin thick-filament structure. The relative constancy in vertebrate striated muscle design, e.g., myosin length and diameter, a marked exception to this rule, is perhaps due to vertebrates being, species wise, so small (less than 5%) a portion of animals.

All these muscles work well enough to fulfill their many and varied functions. That does not mean they are optimal at doing so. Evolution works on what is available, which may preclude finding best, or even close to best, solutions (human knees and backs, derived from those of four-legged ancestors, being prime examples). Moreover, optimal is environment dependent, and thus evolution to optimal states requires constant environment over evolutionary times scales, something likely often not available. Contemporary muscles should thus be considered just good enough solutions in that they allow species continuation, not entities that optimally perform the tasks they are set (146). The variations in FLAR curves in Fig. 8 should thus not be interpreted as necessarily being best adaptations of the muscles to function.

Nonetheless, however arisen, these variations are specific to the muscles examined. Muscle models must reproduce these variations. They should do so, moreover, in terms of mechanistic and comprehensible foundations and also offer the possibility of physiologically interpretable and reasonable parameter variations. Our model, being physically based, meets the first requirement. Table 4 shows that, to fit the experimental data, many model parameters showed wide variations. Some of these variations (e.g., myosin length) are presumably spurious, as the sensitivity analysis in Appendix B shows their parameters had little effect on muscle output.

Others, however, presumably represent biologically relevant variation. Relevant to this issue, all the parameters to which model output is most sensitive ($d_{10,\text{ref}},{\ell }_{\text{act}},R_{{\mathcal{Z}}_{\text{S}1}},r_{\text{mbb}},{\ell }_{\text{mbb}},\nu ,\varsigma$, and r_act) are explicitly biological, having to do with filament and lattice geometry, charge location on the myosin head, the dependence of actin active site clearance on [Ca²⁺], and how many myosin heads have to be activated to achieve maximum muscle force. That these parameters are biological suggests that the variations in them were evolutionarily selected. Greater confidence in this conclusion could be obtained were data from muscles with a wider variety of these parameters available.

It is time to discard the overlap/collision hypothesis of the ascending arm

In Fig. 5 of Gordon et al. (1966) (5), the authors imposed on the ascending arm a two-piece-wise linear fit to data that, to modern eyes, could clearly be fitted with a variety of continuous functions. In their mechanistic explanation Fig. 12, they follow the ascending arm with a constant amplitude plateau and a linear descending arm. They then relate the plateau and the descending arm with changes in thin:thick-filament overlap (with which we do not disagree, although changing interfilament spacing on the descending arm will make it somewhat non-linear; see our fits in Fig. 8).

As mentioned several times before, their explanation of the ascending arm is not based on filament overlap considerations but arguments that thin-filament overlap and thick-filament collision with the Z disks will reduce force. These hypotheses were reasonable at the time. What is striking is that they have remained the accepted explanation since then, particularly given the demonstration a mere three years later that FLR peaks shifted with changes in calcium concentration (8), something not explainable by the Gordon et al. (1966) (5) hypothesis for the ascending arm, and the lack, in general, of any clear kink in the ascending arm in later work on other muscles, see again Fig. 8.

We assume that the Gordon et al. (1966) (5) hypothesis for the ascending arm still being the accepted explanation is due to their certainly true explanation of the plateau and descending arm (a penumbra effect). This history is nonetheless a compelling example of how a hypothesis that is true in part (plateau, descending arm) can be accepted in whole (the ascending arm) despite the accumulation of many examples (see references in second part of section “introduction”) contrary to its predictions. And it is also true that the overlap/collision hypothesis is intuitively attractive and easy to understand. Nonetheless, the continuing use of this hypothesis to explain the ascending arm, in the light of the large body of contrary evidence that has since been obtained, is clearly inappropriate.

We provide here an alternative explanatory mechanism for the ascending arm, that it arises from increases in lattice spacing as sarcomere length decreases. Except the Gordon data, we chose the datasets in Fig. 8 on the basis of them having force-length curves over a large range of [Ca²⁺] values. We cannot thus state that they are representative of muscle force-length curves across the entire muscle literature. Nonetheless, the goodness of fits of the ascending arm that the interfilament spacing hypothesis model gives, and its mechanistic likelihood, intuitive attraction, and ease of understanding, suggest it is, for now, a better explanation of the ascending arm.

Author contributions

The manuscript is a joint work of all three authors, who contributed as follows: initial idea for the study, R.R., M.G., and S.L.H.; model development, R.R. and M.G.; calculations and coding, R.R.; sensitivity analysis, R.R., M.G., and S.L.H.; data collection, R.R.; main writing, R.R.; editing, M.G. and S.L.H.; figures, R.R., with feedback/suggestions from M.G. and S.L.H.; discussion, R.R., M.G., and S.L.H..

Declaration of interests

The authors declare no competing interests.

Editor: Samantha Harris.

Appendix A. Explanation with simple functions of rightward shift of FLAR peaks with decreasing [Ca²⁺]

A striking property of FLAR curves is the rightward shift of their peaks with decreasing activity (decreased [Ca²⁺], Fig. 8) (8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18). Finding a mechanistic explanation for this shift was a driving force to begin the work presented here. The resulting model well reproduces the rightward shifts with decreasing activity (Fig. 8). It does so by, in a muscle-specific manner, finding model parameter values that alter the changes in force due to changes in filament overlap (solid gray line in Fig. 7), and how changes in [Ca²⁺] alter the force being generated by the myosin heads (black dotted lines in Fig. 7) at any filament overlap (any ${\ell }_{\text{hs}}$). Only the force generated by the myosin heads depends on [Ca²⁺]. Nonetheless, because each [Ca²⁺]’s black dotted curve is multiplied by the gray curve (and ς) to give that [Ca²⁺]’s FLAR (the solid colored lines in Fig. 7), the optimizer alters both types of curves in the fitting procedure. The black dotted curves in turn arise from an interaction of the Hill equation (Fig. 2) and the changes in intra-filament spacing described in section “attraction (cross-bridge formation): modeling electrostatics-induced actin-myosin binding” (note that the final equation in that section, Eq. (14), implicitly depends on [Ca²⁺]). Given this complex dependence of model output on [Ca²⁺] and number of parameters in the model, obtaining an intuitive understanding of how the rightward shifts occur in the model is difficult. We attempt here to provide such an understanding.

A word explanation of this difficulty follows. Calcium binding to TnC unmasks actin filament charges, increasing actin’s electrostatic attraction of the myosin head (Fig. 4). Length increases increase the likelihood of myosin head binding by decreasing lattice spacing. The consequence is that, at a lower [Ca²⁺], the sarcomere has to be longer to give an equivalent overall head binding probability (an equivalent force) than it does at a higher [Ca²⁺]. This (rightward) shift might seem a sufficient explanation for the FLAR peak moving right with decreased [Ca²⁺]. However, as length increases beyond a certain length, force decreases with length because how many cross-bridges can occur at any activity decreases as filament overlap decreases (Eq. (5)). It is this interaction between how sarcomere lengthening increases the ability of calcium to induce force (due to decreased interfilament spacing) and decrease the amount of force that a given [Ca²⁺] induces (due to decreased filament overlap) that makes understanding why the FLAR peak moves right with decreasing [Ca²⁺] so non-intuitive.

Increased understanding of how these shifts occur can be obtained using very simple functions (Fig. A10). The black trace in Fig. A10 A1 shows a filament overlap force dependency. This dependency does not depend on [Ca²⁺], and is therefore the same in panels (A1) –(C1). This curve is identical to that shown in Fig. 1, with false cross-bridges developing no force. It therefore consists of an initial portion (${\ell }_{\text{hs}}$ from 0.3 to 1.18 μm) with a value of 1, a linear portion from 1.18 to 1.9 μm over which filament overlap decreases, reaching 0 at 1.9 μm, at which there is no filament overlap, and having a value of 0 at all longer lengths. The blue trace in Fig. A10 A1 is the myosin force generated at a constant [Ca²⁺] as ${\ell }_{\text{hs}}$ changes. As was explained in section “attraction (cross-bridge formation): modeling electrostatics-induced actin-myosin binding,” as ${\ell }_{\text{hs}}$ increases, interfilament spacing decreases, and myosin force therefore increases. In this simple example, we model this length dependency as being linear (the curve becoming negative at very short lengths is immaterial to the explanation being provided here). For ease of explanation, we from here refer to the black, filament overlap curve, as ${\tilde{F}}_{\text{des}}$, and the blue, change in myosin head force generation curve, as ${\tilde{F}}_{\text{asc}}$.

Figure A. 10.

Conceptual explanation of FLAR rightward shift with decreasing [Ca²⁺]. Some changes (rightward translocation, column A; squaring, column C) in the myosin force generation curve (${\tilde{F}}_{\text{asc}}$, top row) result in rightward shifts of the FLAR peak (middle row). Changing ${\tilde{F}}_{\text{asc}}$ slope, alternatively, does not (column B). An understanding of these different responses of the FLAR peak to changes in ${\tilde{F}}_{\text{asc}}$ can be obtained by considering how these changes affect the equation that gives rise to the FLAR, $\tilde{F}\left({\ell }_{\text{hs}}\right)={\tilde{F}}_{\text{asc}}\cdot {\tilde{F}}_{\text{des}}$ (bottom row). See text for detailed explanation. Keys in (A2) and (A3) apply to all other panels in same row. To see this figure in color, go online.

Because we are here concerned only with the FLAR peak position, not amplitude, we ignore the scaling factor ς. Thus, in this simple model, muscle force as a function of ${\ell }_{\text{hs}}$ is given simply by $\tilde{F}\left({\ell }_{\text{hs}}\right)={\tilde{F}}_{\text{asc}}\cdot {\tilde{F}}_{\text{des}}$. The blue trace in Fig. A10 A2 shows this multiplication. The thin blue line shows that the FLAR peak occurs at 1.2 μm. Our task is to try to understand why the peak occurs at this length. The peak corresponds to the ${\ell }_{\text{hs}}$ at which $\text{d}\tilde{F}\left({\ell }_{\text{hs}}\right)/\text{d}{\ell }_{\text{hs}}$ equals zero. Applying the chain rule to $\tilde{F}\left({\ell }_{\text{hs}}\right)$ gives $\text{d}\tilde{F}\left({\ell }_{\text{hs}}\right)/\text{d}{\ell }_{\text{hs}}={\tilde{F}}_{\text{asc}}\cdot \text{d}{\tilde{F}}_{\text{des}}/\text{d}{\ell }_{\text{hs}}+\text{d}{\tilde{F}}_{\text{asc}}/\text{d}{\ell }_{\text{hs}}\cdot {\tilde{F}}_{\text{des}}$. We can therefore examine how the two products in the sum add to zero at the ${\ell }_{\text{hs}}$ they do. Fig. A10 A3 shows the individual products (dashed blue line, ${\tilde{F}}_{\text{asc}}\cdot \text{d}{\tilde{F}}_{\text{des}}/\text{d}{\ell }_{\text{hs}}$; dotted blue line (overlying with dotted green line, see next paragraph), $\text{d}{\tilde{F}}_{\text{asc}}/\text{d}{\ell }_{\text{hs}}\cdot {\tilde{F}}_{\text{des}}$) and their sum (solid blue line, $\text{d}\tilde{F}\left({\ell }_{\text{hs}}\right)/\text{d}{\ell }_{\text{hs}}$) for the blue lines in Fig. A10 A2 between ${\ell }_{\text{hs}}$ values of 1.18 and 1.9 μm (the only relevant portion of ${\ell }_{\text{hs}}$, as it is over this range that ${\tilde{F}}_{\text{des}}$ is not constant). ${\tilde{F}}_{\text{asc}}\cdot {\tilde{F}}_{\text{des}}/\text{d}{\ell }_{\text{hs}}$ decreases with ${\ell }_{\text{hs}}$, and is negative over this ${\ell }_{\text{hs}}$ range. d ${\tilde{F}}_{\text{asc}}/\text{d}{\ell }_{\text{hs}}\cdot {\tilde{F}}_{\text{des}}$ also decreases with ${\ell }_{\text{hs}}$, but is positive over the ${\ell }_{\text{hs}}$ range. The curves are such that they sum to zero at ${\ell }_{\text{hs}}=1.2\mu \text{m}$, consistent with the FLAR peak in Fig. A10 A2.

We can now examine how changes in the ${\tilde{F}}_{\text{asc}}$ curve (in the model, arising from changes in [Ca²⁺]) affect FLAR peak position. With the linear ${\tilde{F}}_{\text{asc}}$ curve used here, only a limited number of changes are possible. One is to shift the curve right by changing its zero value from 0.5 to 0.75 μm (green line in Fig. A10 A1). Multiplication of this ${\tilde{F}}_{\text{asc}}$ by the (unchanged) ${\tilde{F}}_{\text{des}}$ gives the green FLAR in Fig. A10 A2. It is apparent that, if decreasing [Ca²⁺] induced this shift in ${\tilde{F}}_{\text{asc}}$, the FLAR peak would shift right, to a value of 1.325 μm. The reason for this shift can be understood by considering the green ($\tilde{c}=0.5$) lines in Fig. A10 A3. For both [Ca²⁺], the $\text{d}{\tilde{F}}_{\text{asc}}/\text{d}{\ell }_{\text{hs}}\cdot {\tilde{F}}_{\text{des}}$ curves are identical, since shifting ${\tilde{F}}_{\text{asc}}$ right does not alter its derivative. The term ${\tilde{F}}_{\text{asc}}\cdot \text{d}{\tilde{F}}_{\text{des}}/\text{d}{\ell }_{\text{hs}}$, alternatively, is altered by shifting ${\tilde{F}}_{\text{asc}}$ rightward, since this shift alters ${\tilde{F}}_{\text{asc}}$’s value at each ${\ell }_{\text{hs}}$. The effect is to increase the value of ${\tilde{F}}_{\text{asc}}\cdot \text{d}{\tilde{F}}_{\text{des}}/\text{d}{\ell }_{\text{hs}}$ at each ${\ell }_{\text{hs}}$ (to shift the curve upward). The sum of the $\text{d}{\tilde{F}}_{\text{asc}}/\text{d}{\ell }_{\text{hs}}\cdot {\tilde{F}}_{\text{des}}$ and ${\tilde{F}}_{\text{asc}}\cdot \text{d}{\tilde{F}}_{\text{des}}/\text{d}{\ell }_{\text{hs}}$ curves therefore reaches zero at a larger ${\ell }_{\text{hs}}$, 1.325 μm, matching the peak of the green FLAR in Fig. A10 A2.

Another possible change in ${\tilde{F}}_{\text{asc}}$ is to change its slope, here by a factor of two (Fig. A10 B1, green curve). Multiplying the blue and green ${\tilde{F}}_{\text{asc}}$ curves by ${\tilde{F}}_{\text{des}}$ gives the FLAR curves in Fig. A10 B2. The amplitude of the FLAR peak (as also occurs in Fig. A10 B1) is altered by the increase in ${\tilde{F}}_{\text{asc}}$ slope, but its position, 1.2 μm, is not. The reason for this maintenance of FLAR peak position can be understood by examining Fig. A10 B3. Changing ${\tilde{F}}_{\text{asc}}$ slope changed both $\text{d}{\tilde{F}}_{\text{asc}}/\text{d}{\ell }_{\text{hs}}\cdot {\tilde{F}}_{\text{des}}$ (compare the dotted blue, $\tilde{c}=1$, and green, $\tilde{c}=0.5$ lines) and ${\tilde{F}}_{\text{asc}}\cdot \text{d}{\tilde{F}}_{\text{des}}/\text{d}{\ell }_{\text{hs}}$ (compare the dashed blue, $\tilde{c}=1$, and green, $\tilde{c}=0.5$ lines). In both cases, the slopes of the product curves increased. However, the effects on the amplitude of the two product curves differ. For the dotted curves, the green $\tilde{c}=0.5$ curve is greater than the blue $\tilde{c}=1$ curve at all relevant ${\ell }_{\text{hs}}$ values. For the dashed curves, the $\tilde{c}=0.5$ curve is less than the $\tilde{c}=1$ curve at all relevant ${\ell }_{\text{hs}}$ values. These changes are such that the sum of the product curves (blue and green solid line) continue to add to zero at the same length of 1.2 μm. That this will occur for any multiplication of the ${\tilde{F}}_{\text{asc}}$ curve can be shown as follows: define ${\tilde{F}}_{\text{asc}}=m\cdot \left({\ell }_{\text{hs}}-\hat{\ell }\right)$. Its derivative $\text{d}{\tilde{F}}_{\text{asc}}/\text{d}{\ell }_{\text{hs}}$ is therefore m, and so $\text{d}{\tilde{F}}_{\text{asc}}/\text{d}{\ell }_{\text{hs}}\cdot {\tilde{F}}_{\text{des}}=m\cdot {\tilde{F}}_{\text{des}}$ and ${\tilde{F}}_{\text{asc}}\cdot \text{d}{\tilde{F}}_{\text{des}}/\text{d}{\ell }_{\text{hs}}=m\cdot \left({\ell }_{\text{hs}}-\hat{\ell }\right)\cdot \text{d}{\tilde{F}}_{\text{des}}/\text{d}{\ell }_{\text{hs}}$. Summing the products gives $m\cdot {\tilde{F}}_{\text{des}}+m\cdot \left({\ell }_{\text{hs}}-\hat{\ell }\right)\cdot \text{d}{\tilde{F}}_{\text{des}}/\text{d}{\ell }_{\text{hs}}$. When solving this sum for the value of ${\ell }_{\text{hs}}$ that gives zero, the common m terms are divided out, and thus changes in m cannot affect the ${\ell }_{\text{hs}}$ value at which the sum of the products are zero.

Although not obvious as written, the ${\tilde{F}}_{\text{asc}}$ curve $m\cdot \left({\ell }_{\text{hs}}-\hat{\ell }\right)$ has one more parameter, the power to which the $\left({\ell }_{\text{hs}}-\hat{\ell }\right)$ term is raised. Fig. A10 C1 shows ${\tilde{F}}_{\text{asc}}$ with $\left({\ell }_{\text{hs}}-0.5\right)$ squared, resulting in ${\tilde{F}}_{\text{asc}}$ being a parabola. We use here only the values of the parabola greater than ${\ell }_{\text{hs}}=0.5\mu \text{m}$ (where $\left({\ell }_{\text{hs}}-0.5\right)=0$), and fix ${\tilde{F}}_{\text{asc}}$ at zero for smaller ${\ell }_{\text{hs}}$. Multiplying ${\tilde{F}}_{\text{des}}$ with the two ${\tilde{F}}_{\text{asc}}$ again gives FLARs with different peak positions (in this case, shifting the low [Ca²⁺] FLAR peak to 1.43 μm, Fig. A10 C2). Consideration of Fig. A10 C3 again allows this shift to be understood. The change in ${\tilde{F}}_{\text{asc}}$ by lowering [Ca²⁺] caused the $\text{d}{\tilde{F}}_{\text{asc}}/\text{d}{\ell }_{\text{hs}}\cdot {\tilde{F}}_{\text{des}}$ product curve (green dotted line) to become rightward curved (concave), rather than straight, and increased its values for all ${\ell }_{\text{hs}}$. The change in ${\tilde{F}}_{\text{asc}}$ likewise caused the ${\tilde{F}}_{\text{asc}}\cdot \text{d}{\tilde{F}}_{\text{des}}/\text{d}{\ell }_{\text{hs}}$ curve (green dashed line) to become concave, but changed its amplitude such that the curve is greater than the $\tilde{c}=1$ line for values of ${\ell }_{\text{hs}}$ less than about 1.5 μm and less than the $\tilde{c}=1$ line for longer ${\ell }_{\text{hs}}$ values. These changes in the two product curves necessarily move where their sum equals zero to a longer ${\ell }_{\text{hs}}$, namely 1.43 μm.

Despite the simplicity of the functions used here, the explanation of how the FLAR peaks move to longer lengths as [Ca²⁺] decreases is analogous to the situation occurring in Fig. 7, with ${\tilde{F}}_{\text{des}}$ being analogous to the P_ovl curve and ${\tilde{F}}_{\text{asc}}$ being analogous to the P_aas ⋅ P_esa curves. In Fig. 7, each P_aas ⋅ P_esa curve has different magnitudes and maximum slopes. The “top” four P_aas ⋅ P_esa curves, corresponding to $\tilde{c}$ values between 0.7 and 1, have very similar shapes and primarily differ because of rightward shifts as $\tilde{c}$ decreases (i.e., they would essentially overlap if translocated to lie over each other). The shifts in FLAR peak for these $\tilde{c}$ is thus similar to that shown in Fig. A10 column A. For lower $\tilde{c}$, the P_aas ⋅ P_esa curves both effectively shift right and have increasingly different shapes. The shifts in FLAR peak for these $\tilde{c}$ are thus similar to a combination of the explanations shown in columns A and C of Fig. A10. In Fig. 7, performing a differential-based explanation of why the FLAR peaks move as was done in Fig. A10 is difficult because of the complexity of the equations giving rise to the P_aas ⋅ P_esa curves. Nonetheless, it is clear from Fig. A10 how the changes in the P_aas ⋅ P_esa curves could result in the shifts in the FLAR peak positions.

Appendix B. Sensitivity analysis

The complex interactions of the model parameters make it difficult to assess how changes in their values alter model output. To examine this issue, we performed a local first-order sensitivity analysis, in which each parameter is varied alone while the others remain fixed at their ω₀ values. For each parameter, we first varied the parameter to values less and greater than the parameter’s ω₀ value at three activity ([Ca²⁺]) levels, finding value bounds for the parameter for which the total mean deviation about all three curves was exactly 10% (Fig. B11).

Figure B. 11.

Sensitivity analysis. The factors in front of the parameters indicate the lower (dotted) and upper (dash-dotted) bound at which the mean deviation D_r from the three solid curves is exactly 10%. The metric, i.e., distance, of a function g(x) from the solid curves r(x) was therefore defined by $D_r:=\underset{{\ell }_{\text{hs}}}{\int }|r\left(x\right)-g\left(x\right)|\text{d}x/\underset{{\ell }_{\text{hs}}}{\int }r\left(x\right)\text{d}x$.

We then plotted the total range of each parameter in Fig. B11 in increasing order (Fig. B12). The parameters clearly fell into three groups. The first (d_10,ref to r_act) were eight parameters to which model output was highly sensitive. The second (z_act to ϵ_r) was a group to which model output was moderately sensitive. The third was a group to which the model was largely insensitive (${\mathcal{Z}}_{\text{S}1}$ to ${\tilde{F}}_{\text{false}}$). The highly sensitive parameters include d_10,ref, ${\ell }_{\text{act}}$, r_mbb, ${\ell }_{\text{mbb}}$, and r_act; all geometric constraints, with the model being most sensitive to d_10,ref. The sensitivity to these geometric parameters is presumably due to the effective electrostatic potential (black line in Fig. 4) decaying in essence exponentially with distance. This conclusion is further supported by one of the remaining sensitive parameters being $R_{{\mathcal{Z}}_{\text{S}1}}$, the charge location on the myosin head, which would also strongly affect myosin head response to changes in the electric field between the actin and myosin filaments. In the insensitive group, it is notable that ${\tilde{F}}_{\text{false}}$ has extremely little effect on model output, further supporting the arguments made in the introduction that myosin push-back is unlikely to play a substantial role in the genesis of the ascending arm.

Figure B. 12.

Range over which each parameter in Fig. B11 varied, arranged by increasing magnitude. Two clear breaks are apparent, one between r_act and ${\mathcal{Z}}_{\text{act}}$ and the another between ϵ_r and ${\mathcal{Z}}_{\text{S}1}$. We identified the first eight parameters as being sensitive parameters (see Table 3). Note that the bar for ${\tilde{F}}_{\text{false}}$ is truncated.

These sensitivity considerations led us to re-perform the fits with the optimizer being allowed to alter only the parameters in the most sensitive group. In all cases, this increased fit error, in some cases as much as fivefold (Table B1). However, the original errors were so small that, in most cases, the increased error was visually small. Fig. B13 shows the best (Stephenson) and worst (Guschlbauer (a)) fits with the sensitive parameters as the only free parameters (right column) and the fits with all parameters free (left column). Not surprisingly, the two Stephenson fits are essentially equally good. The Guschlbauer sensitive-only fit is substantially worse than the all-fit case, with the fits to the most- and second-most-activated data being identical, and the fits to the third- and fourth-most-activated data having peaks in the wrong positions. These data had substantial experimental difficulties, with the most-activated data overlapping with the second- and third-most-activated data on the descending arm. It is thus perhaps not surprising that fitting these data would be most sensitive to reductions in allowed parameter number. The optimizer was nonetheless able to find calcium concentrations that varied appropriately as muscle activity decreased, and peaks that had approximately the correct amplitude. This ability was true for all the fits with relatively high errors in the sensitive-only fits (Brown, deBeer, Zuurbier), confirming the importance of the parameters identified as sensitive in Fig. B12.

Table B1.

Comparison of residuals with boundaries from Table 4 and optimization with non-sensitive parameters fixed, cf. Fig. B12

Dataset	Balnave	Brown	deBeer	deBrito	Gordon	Guschl (a)	Guschl (b)	Morgan	Roszek	Stephenson	Stienen	Zuurbier
${10}^3\cdot \widetilde{\text{LSE}}$Table 4	0.111	0.77	0.707	0.527	0.819	2.95	1.05	1.57	0.215	0.0831	0.245	0.883
${10}^3\cdot \widetilde{\text{LSE}}$ (fixed params)	0.161	2.09	4.06	1.06	1.33	5.91	1.19	1.77	0.811	0.148	0.316	4.35

Figure B. 13.

Best (Stephenson, upper row) and worst (Guschlbauer (a), lower row) examples of fixing non-sensitive parameters. Left column shows results from the parameter fit with bounds from Table 4. Right column shows the optimal fit after fixing the nine most insensitive parameters. Note that for Guschlbauer (a), the fits to the two highest activation FLAR datasets were identical (both found $\tilde{c}=1$). For residuals, see Table B1. To see this figure in color, go online.

Appendix C. The electrostatic parameters

The parameter ϵ_r markedly differed from the initial guess of 80, the relative permittivity of water, reaching a minimum of 643 and the upper bound of 960 seven times (Table 4; Brown, deBeer, deBrito, Guschlbauer (a) and (b), Morgan, Zuurbier). These high values are close to that found in a theoretical study (147) but are 12 times water’s relative permittivity, which is commonly assumed to apply to the sarcoplasm (19, p.222). We are unaware of direct measurements of cytoplasm ϵ_r. High ϵ_r values would either indicate a highly viscous, net-like structure of molecular dipoles in muscle cytoplasm or layers of dipoles (not only elementary charges as in Debye-Hückel theory) on or closely under the surfaces of the myosin head and the filament backbones. The latter mechanism would provide “dipole shielding” of central elementary charges in the head and the backbones analogous to the ion-induced shielding in Debye-Hückel theory. Optimized values of ionic strength I reached both the lower (Brown) and upper (Gordon) bounds. However, these values are comparable with literature values of 0.1–0.2 mol/L (19, p.30). The Debye length corresponding to the optimized ϵ_r and I values varied from 3.59 nm for Guschlbauer (a) to 1.48 nm for Gordon, all well above textbook values of 0.7–0.8 nm (19, p.30). The number of charges on the actin filament, myosin backbone, and head varied 2.1-fold (${\mathcal{Z}}_{\text{act}}$), 2.6-fold (${\mathcal{Z}}_{\text{mbb}}$), and 9.4-fold (${\mathcal{Z}}_{\text{S}1}$), respectively. The first two are parameters to which model output was only moderately sensitive and the last a parameter to which model output showed low sensitivity (Fig. B12), which may also have contributed to these wide ranges. We are unaware of experimental data with which to compare these results.

We used Debye-Hückel theory rather than “naked” coulomb interaction because of a sophisticated experiment in which recognition distance and unbinding force between a single myosin molecule and an activated actin filament were determined (98). Because this experiment contained near-physiological boundary conditions and the data were well explained by Debye-Hückel theory alone, we did not consider other particle-particle interactions (e.g., van der Waals forces, Brownian motion, Casimir forces, Donnan potential) (66,148, 149, 150). In this approach, the electrostatic potential energy functions between two charges q_i and q_j, with charge numbers ${\mathcal{Z}}_i$ and ${\mathcal{Z}}_j$, respectively, must be carefully chosen. Following original Debye-Hückel theory (151), Nakajima et al. (1997) (98) used point charges and assumed ionic shielding by the surrounding solution. The potential energy of the central charge therefore did not decrease with the first power of the distance between the charges, but with a dominating superposed negative exponential term. In our work, we assumed the charges were homogeneously distributed along an actin filament backbone of finite cylinder shape (100). Table C1 summarizes the coulomb and original and two refined Debye-Hückel potential energy functions, each including the factor $A:=\frac{|{\mathcal{Z}}_{\text{act}}\cdot {\mathcal{Z}}_{\text{S}1}|\cdot e_0^2}{4\cdot \pi \cdot {ϵ}_0\cdot {ϵ}_r}$ (unit: N ⋅ m²) representing a generalized coulomb constant.

Table C1.

Possible formulations of electrostatic potential energy functions assuming point charges (coulomb and Debye-Hückel) or charges homogeneously distributed on surfaces (sphere or cylinder with radius r_act)

Formulation	Coulomb	Debye-Hückel/Nakajima	Sphere (radius ract)	Cylinder (radius ract, length ${\ell }_c$)
Potential $\text{Ψ}$ [J]	${\text{Ψ}}_C\left(d\right)=-\frac{A}{d}$	${\text{Ψ}}_{DH}\left(d\right)=-A\cdot \frac{\text{exp}\left(-d/\lambda \right)}{d}$	${\text{Ψ}}_{DH\text{sph}}\left(d\right)=-A\cdot \frac{\text{exp}\left(-\left(d-r_{\text{act}}\right)/\lambda \right)}{\left(1+r_{\text{act}}/\lambda \right)\cdot d}$	${\text{Ψ}}_{DH\text{cyl}}\left(d\right)=-A\cdot \frac{2\cdot \lambda \cdot K_0\left(d/\lambda \right)}{r_{\text{act}}\cdot {\ell }_c\cdot K_1\left(r_{\text{act}}/\lambda \right)}$
Force F [N]	$F_C\left(d\right)=\frac{A}{d^2}$	$F_{DH}\left(d\right)=A\cdot \frac{\text{exp}\left(-d/\lambda \right)\cdot \left(\lambda +d\right)}{\lambda \cdot d^2}$	$F_{DH\text{sph}}\left(d\right)=A\cdot \frac{\text{exp}\left(-\left(d-r_{\text{act}}\right)/\lambda \right)\cdot \left(\lambda +d\right)}{\left(\lambda +r_{\text{act}}\right)\cdot d^2}$	$F_{DH\text{cyl}}\left(d\right)=A\cdot \frac{2\cdot K_1\left(d/\lambda \right)}{r_{\text{act}}\cdot {\ell }_c\cdot K_1\left(r_{\text{act}}/\lambda \right)}$

Regarding the forces, we note that, for equal ϵ_r and I values, $F_C\left(r_{\text{act}}\right)=F_{DH\text{sph}}\left(r_{\text{act}}\right)=F_{DH\text{cyl}}\left(r_{\text{act}}\right)=A\cdot r_{\text{act}}^{-2}$, where the latter equation requires ${\ell }_c=2\cdot r_{\text{act}}$ (as chosen here).

Based on inferred (98) values of attraction force (2.12 pN) and distance (5.3 nm) between the surfaces of a single myosin molecule and an activated actin filament, Nakajima et al. (1997) determined A ≈ 590 pN ⋅ nm². Note that the “recognition force” value of 2.12 pN lay below the uncertainty threshold of their measuring device (3 pN). In calculating the number of involved charges, they omitted a factor of 4 ⋅ π (confirmed by personal communication with T. Ando), therefore calculating $|{\mathcal{Z}}_{\text{act}}\cdot {\mathcal{Z}}_{\text{mbb}}|\approx 16.3$ (98, p.181) instead of the correct value $|{\mathcal{Z}}_{\text{act}}\cdot {\mathcal{Z}}_{\text{mbb}}|\approx 205$. Calculations were made assuming $I\approx 0.05$ mol/L, ϵ_r = 80, and T = 298 K, yielding a Debye length of $\lambda \approx 1.36$ nm. They further calculated a “recognition distance” (similar to the Bjerrum length) from the energy condition ${\text{Ψ}}_D\left(d\right)=-\frac{1}{2}\cdot k_B\cdot T$, which yielded a recognition distance and force of 5.4 nm and 1.9 pN, respectively. An unbinding (yank-off) force of the myosin molecule was measured to be approximately 15 pN, which, using the original Debye-Hückel theory, would correspond to a charge distance of 3.3 nm (see Fig. C14, right). The unbinding force was similar to prior measurements (152), while the charge distance was shorter than the actin radius.

Figure C. 14.

Electrostatic potential (left) and force (right) resulting from different model approaches (Table C1; black, blue, lilac, green) under different conditions (solid, dashed, dotted). Experimental conditions as in (98), ϵ_r = 80 and I = 0.05 mol/L, are used as reference against increased permittivity and increased ionic strength, respectively. The solid blue lines represent the corresponding reference case Debye-Hückel proposed by Nakajima et al. (1997). Reference values of the potential (gray dotted line) and force (gray dotted and dash-dotted line) taken from (98) given for orientation. The actin radius r_act (red dotted line) marks the start of the cylinder and sphere formulations. To see this figure in color, go online.

Using the directly measured Nakajima et al. (1997) unbinding force of 15 pN and applying the refined Debye-Hückel formulation with the shielding charges (on actin) distributed on a spherical surface, we can set up a three-parameter equation system to estimate the actin radius r_act, the surface-to-surface distance ${\hat{d}}_{\text{jump}}$ between actin and myosin head at “jump-in,” and the constant A:

$$F_{DH\text{sph}}\left(r_{\text{act}}+{\hat{d}}_{\text{jump}}\right)=A\cdot \frac{\text{exp}\left(-{\hat{d}}_{\text{jump}}/\lambda \right)\cdot \left(\lambda +r_{\text{act}}+{\hat{d}}_{\text{jump}}\right)}{\left(\lambda +r_{\text{act}}\right)\cdot {\left(r_{\text{act}}+{\hat{d}}_{\text{jump}}\right)}^2}=\left(6.3\cdot {10}^{-9}\text{m}-{\hat{d}}_{\text{jump}}\right)\cdot 2.09\cdot {10}^{-3}{\text{N m}}^{-1}$$ (C.1a)

$$F_{DH\text{sph}}\left(r_{\text{act}}\right)=A\cdot \frac{1}{r_{\text{act}}^2}=15\cdot {10}^{-12}\text{N}$$ (C.1b)

$$\frac{F_{DH\text{sph}}\left(r_{\text{act}}+{\hat{d}}_{\text{jump}}\right)}{\frac{\text{d}}{\text{d}d}{F}_{DH\text{sph}}\left(r_{\text{act}}+{\hat{d}}_{\text{jump}}\right)}\approx -\lambda \cdot \left(1-\frac{\lambda }{r_{\text{act}}+{\hat{d}}_{\text{jump}}}\right)={\hat{d}}_{\text{jump}}-6.3\cdot {10}^{-9}\text{m}.$$ (C.1c)

Numerically solving system (C.1) yields r_act ≈ 5.51 nm, ${\hat{d}}_{\text{jump}}\approx 6.27$ nm, and $A\approx 456$ pN ⋅ nm². Our re-calculation of Nakajima et al. parameter values thus strengthens their conclusion favoring a Debye-Hückel potential as a physical model for explaining actin-myosin attachment. In particular, the value r_act ≈ 5.5 nm being the revised prediction of the lower boundary of the myosin head charges to approach actin is close to the actin filament radii predicted (Table 4) from our fits to FLARs.

We now consider the effects on the potential energy function of altering ϵ_r or I. For this, we compare our optimally fitted model $\mathfrak{F}$ parameter predictions based on the cylinder-based version of the Debye-Hückel potential with the other three electrostatic potential formulations shown in Table C1. Coulomb potential and force both decrease with increasing ϵ_r, if properties of a surrounding solvent, i.e., ionic strength I, are not taken into account. Alternatively, two opposite effects occur for Debye-Hückel potential (and force): with increasing ϵ_r, the pre-factor A is diminished, but the Debye length $\lambda =\sqrt{\frac{{ϵ}_0\cdot {ϵ}_r\cdot k_B\cdot T}{2\cdot {10}^3\cdot N_A\cdot e_0^2\cdot I}}$ is increased, resulting in a generally weaker potential (and force) that in turn penetrates further into the sarcoplasm. With increasing I, only λ decreases, resulting in stronger shielding of the head and backbone charges, and a steeper decrease of potential (and force). Fig. C14 compares alterations in ϵ_r and I on the potential energy and force of a single myosin head with a total charge of +5e₀ located next to a part of the actin filament with r_act = 5.5 nm, length ${\ell }_c=11$ nm (approximately two monomers), and a total of 40 negative elementary charges (−e₀). Two solvent permittivities were considered: 1) that of water, ϵ_r = 80, resulting in $A\approx 577\cdot {10}^{-30}$ N ⋅ m²; and 2) the mean of our optimized (Table 4) values, ϵ_r ≈ 800, resulting in A ≈ 577 ⋅ 10⁻³¹ N ⋅ m². For ϵ_r = 80, two ionic strengths were used: 1) I = 0.05 as in (98), resulting in a Debye length of λ ≈ 1.4 nm; and 2) I = 0.17, as assumed for in vivo muscle (97), resulting in a Debye length of λ ≈ 0.76 nm. Fig. C14 shows the potential energies (left) and forces (right) under these conditions. While coulomb and Debye-Hückel potential energy (and force) asymptotically start from infinity, the spherical and cylindrical potential (and force) were bound to the finite extent of the hypothetical actin filament. Under similar physical conditions, the cylinder and sphere potentials lie between the coulomb and the Debye-Hückel potentials. The recognition distance of approx. 5.4 nm, corresponding in Nakajima et al. (1997) to the energy of $\frac{1}{2}\cdot k_B\cdot T$, agrees well with the assumed actin radius.

In interpreting these results, it is important to note that distance has different meanings in the original Debye-Hückel model (as applied by Nakajima et al. (1997)) and when modeling a sphere or cylinder with charges distributed on the surface, in which distances d from the origin (d = 0) are offset by r_act. r_act is the distance from the origin (the center of the actin filament) below which the attracted (myosin head) charges cannot move closer (the head can only “feel” the potential at d > r_act). Alternatively, in (98), d was treated as in the original Debye-Hückel formulation, in which distance is measured from a singularity in the origin where the central (actin) charge is assumed to be located. Unfortunately, in (98), there seems to be an inconsistency between the meaning of d in their analysis of the experimental data (in which d = 0 represents actin-head contact) and in their theoretical Debye-Hückel analysis (98, Eq. 2). Regardless, using our corrected re-calculation, for a sphere charged at its surface, the jump-in distance is 6.27 nm, away from the sphere/actin surface, compared with about 5.3 … 5.4 nm from the origin in (98) (see Fig. C14). Taken together, this re-analysis of Nakajima et al. (1997) shows that our fitting data are consistent with the experimental data in (98), and support their, and our, use of the Debye-Hückel formulation to model myosin head attachment to active sites on actin.

Permittivity ϵ_r, ionic strength I, and the numbers of the central charges (on actin) and the attracted charges (on the myosin head) contribute to the extended Debye-Hückel cylinder formulation that is a basis of our FLAR model $\mathfrak{F}$ (Eq. (3)). Unfortunately, the values of these parameters are presently not well known. Given their importance to our model, more evidence that electrostatics-based models of myosin head attachment to actin are sufficient to predict head binding is very important. Repeating the pioneering experiments of Nakajima et al. (1997) with the modern technology could provide such data. For example, repeating them with a 10-fold force resolution enhancement (by use of a more sensitive cantilever sensor) would allow the FLR of the almost certainly Debye-Hückel-like actin-head attraction potential to be followed over a much longer distance along the head approach to actin, as opposed to detecting only the jump-in condition as was possible in 1997. Present techniques may also allow better fixation of the end of the actin filament, removing the need to include a deformation degree of freedom of actin “lift” in the analyses. Independent of technological improvements, simply repeating the experiments with saline of varying the ionic strength is clearly possible, and would greatly help characterize the nature of the attraction between actin and myosin head.

Appendix D. Parameter correlations

The model has 16 free parameters, many of which interact, often in non-linear ways, in creating model output. Some parameters may therefore be correlated, either due to the mathematical structure of the model or physical or biological properties of the real system. Fig. D15 shows a correlation matrix among all 17 parameters for which numerical entries were made. However, only 16 of these were free, as temperature was entered as a fixed value for each experiment. We identify both correlations with p ≤ 0.05 (open white circles) and ≤0.01 (solid white circles). Given the large number of comparisons made, we describe only correlations with p ≤ 0.01.

Figure D15.

Correlation coefficients between each pair of optimized model parameters, see Table 4. White closed and open circles are α = 0.01 and α = 0.05 deviations of the correlation coefficient ρ from zero, respectively. The test statistic was calculated as $t=\frac{\rho \cdot \sqrt{n-2}}{\sqrt{1-{\rho }^2}}$ (153) and compared against the corresponding quantile of the Student’s t-distribution with n − 2 degrees of freedom (two-sided test), where n = 12 is the number of available datasets.

Several model parameters were strongly correlated: positive correlations between l_act and r_act, r_act and z_act, and r_mbb and I and negative correlations between r_mbb and ς and $R_{{\mathcal{Z}}_{\text{S}1}}$ and ϵ_r. r_act is well maintained across muscles. Thus the l_act and r_act, as well as r_act and z_act, correlations are unlikely due to these parameters co-varying in real muscle, and instead likely arise from the mathematical structure of the model. It is similarly doubtful that muscle cytoplasm ionic strength (I) or dielectric constant (ϵ_r) show large across-species variation, particularly in vertebrates, from which most of the experimental data were obtained. However, they may well do so because of varying experimental conditions. The r_mbb and I, and $R_{{\mathcal{Z}}_{\text{S}1}}$ and ϵ_r, correlations therefore also likely arise from model-specific character of the electrostatic interactions between the parameter-associated structures. The highly successful performance of the simple model (section “a simpler descriptive model that fits as well as the complete model”) is consistent with this conclusion. The myosin backbone radius r_mbb and the fraction $1/\varsigma$ of total cross-bridges needed to be formed to produce maximum muscle force could well be evolutionarily selected. However, all the data used here are from vertebrate muscles in which r_mbb shows small, if any, variation. In the present dataset, this correlation thus also likely arises not from a biological correlation but the structure of the mathematical model.

Myosin backbone radius (r_mbb) and other myosin filament and half-sarcomere properties show much greater variation in some invertebrates, particularly molluscs (90). Invertebrates’ muscles may also show greater variation in I and ϵ_r, given that some invertebrates do not maintain hemolymph ion concentrations within the narrow ranges common in vertebrates. It would thus be of interest to examine the correlations between these model parameters in muscles with such enlarged biological parameter ranges.