Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 May 31;62(11):2846–2856. doi: 10.1021/acs.jcim.1c01532

Modified Hamiltonian in FEP Calculations for Reducing the Computational Cost of Electrostatic Interactions

Hiraku Oshima †, Yuji Sugita †,‡,§,*
PMCID: PMC9199518  PMID: 35639709

Abstract

graphic file with name ci1c01532_0009.jpg

The free-energy perturbation (FEP) method predicts relative and absolute free-energy changes of biomolecules in solvation and binding with other molecules. FEP is, therefore, one of the most essential tools in in silico drug design. In conventional FEP, to smoothly connect two thermodynamic states, the potential energy is modified as a linear combination of the end-state potential energies by introducing scaling factors. When the particle mesh Ewald is used for electrostatic calculations, conventional FEP requires two reciprocal-space calculations per time step, which largely decreases the computational performance. To overcome this problem, we propose a new FEP scheme by introducing a modified Hamiltonian instead of interpolation of the end-state potential energies. The scheme introduces nonuniform scaling into the electrostatic potential as used in Replica Exchange with Solute Tempering 2 (REST2) and does not require additional reciprocal-space calculations. We tested this modified Hamiltonian in FEP calculations in several biomolecular systems. In all cases, the calculated free-energy changes with the current scheme are in good agreement with those from conventional FEP. The modified Hamiltonian in FEP greatly improves the computational performance, which is particularly marked for large biomolecular systems whose reciprocal-space calculations are the major bottleneck of total computational time.

1. Introduction

Fast and accurate predictions of protein–ligand binding affinities are desired in in silico drug design to reduce the total cost and time required for drug development.1−6 The alchemical free-energy perturbation (FEP) method based on the all-atom molecular dynamics (MD) simulation is one of the most essential tools to predict the binding affinity and solubility of ligands with high accuracy.7−11 FEP includes all degrees of freedom relevant to protein–ligand binding, for instance, atomistic interactions between protein and ligand, protein conformational flexibility, solvent effects, and so on. Therefore, the prediction of absolute/relative free-energy changes via FEP is considered more reliable than binding affinity predictions based on rigid-body docking or other empirical approaches. Nowadays, most of the major MD packages support FEP calculations (and/or thermodynamic integration (TI)).12−14 To improve the conformational sampling during the simulation, FEP is combined with Replica Exchange with Solute Tempering 2 (REST2) or other enhanced sampling methods.12,14−18 FEP is often used for the virtual optimization of lead compounds in drug discovery.19−21

The dual-topology approach in FEP is often used in the alchemical calculations of the relative binding free-energy differences of two ligands. In the approach, each ligand is considered as an end state (states A and B) and the atoms in the system are decomposed into three groups: the commonly existing atoms, those only in state A, and those only in state B. The last two groups represent the different atoms between the two ligands. To interpolate the two end states, the scaling factors (λA and λB) are multiplied by the nonbonded energies of the groups. This scheme is referred to as energy interpolation (EI).7,22 The potential energies of the two end states can be connected smoothly by changing λA and λB from 0 to 1. Since the dual-topology approach focuses only on the differences between two ligands, the perturbation can be limited to a small region in the target system, leading to fast convergences in the free-energy calculation.

However, in conventional FEP, to evaluate λ-scaled interactions, the above decomposition requires the calculations of potential energies of both two end states per time step. When the particle mesh Ewald (PME) method23,24 is used, the long-range parts of electrostatic interactions are computed in the reciprocal space using the fast Fourier transformation (FFT),25 whose computational time increases as O(N log N), where N is the number of degrees of freedom in the system. At least two PME calculations must be performed (i.e., FFT calculations are necessary twice) at each energy evaluation per time step, which largely decreases the computational performance of the alchemical calculation and hampers the applicability of FEP to large chemical or biological systems.

Parameter interpolation (PI) has been also used to perform alchemical calculations.26−28 In PI, the force field parameters are scaled by λA and λB, and nonbonded energies are evaluated with the scaled parameters like normal MD simulation. Since PI does not require two PME calculations at each energy evaluation, the computational cost can be largely reduced compared to EI. PI has been combined with FEP, Bennett acceptance ratio (BAR), and multistate BAR (MBAR) for the single-topology approach in a variety of MD software packages (BOSS,29 Tinker-OpenMM,30 etc.). Recently, AMBER developers have combined PI with TI for the dual-topology approach.28 In the PI–TI method, no modification of the MD code is required to perform the dynamics, which is the advantage in graphics processing unit (GPU) acceleration, because GPU code is much complicated compared to central processing unit (CPU) code. The soft-core method is often used in EI to avoid end-point catastrophe, but it is not employed in the PI–TI method. Recently, some methods have been proposed to avoid the catastrophe without introducing the soft-core potentials, which reduces costs for FEP-specified coding or additional computation for the soft-core method.31,32

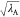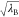In this study, we propose a scheme for evaluation of electrostatic interactions in the combination of FEP with PI to avoid additional reciprocal-space calculations. In our proposed scheme, the total long-range interaction of the electrostatic potential is computed by scaling partial charges by Inline graphic and Inline graphic. The potential energy is nonuniformly scaled, which is similar to that used in Replica Exchange with Solute Tempering 2 (REST2).33 To suppress instability of alchemical calculations near end points, we apply the soft-core method to Lennard-Jones (LJ) and electrostatic interactions. In PI, energy differences between adjacent λ points should be evaluated for the BAR estimator, which requires the cost of postprocessing, such as recalculation of energies from obtained trajectories. To minimize the postprocessing cost, energy differences are evaluated on the fly with low frequency during FEP simulations. In this method, we combined the modified Hamiltonian, the soft-core method, and on-the-fly energy evaluation to reduce the computational cost in FEP calculations compared to the conventional FEP with EI.

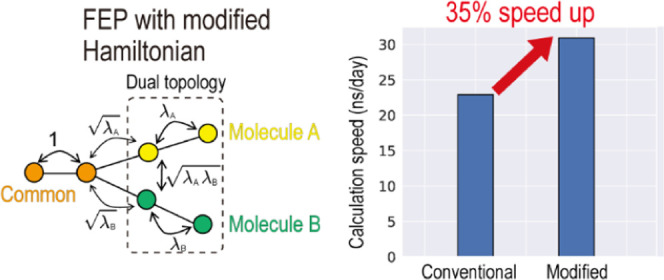
We have implemented this method in GENESIS software package34,35 and tested it by employing several systems, such as the relative and absolute solvation free-energy changes of amino-acid side-chain analogues and the relative binding free-energy changes in a barnase–barstar complex upon the Y29A mutation in barnase. In all cases, the calculated free-energy changes with the current method are in good agreement with those from conventional FEP, although the alchemical calculation paths used in the FEP methods are different. The new FEP with PI in GENESIS greatly improves the computational performances in particular for the hybrid CPU + GPU computation: more than 30% faster than conventional FEP. This method is expected to be particularly useful when it is applied to large biomolecular systems, such as membrane or crowding systems, whose reciprocal-space calculations are the major bottleneck of total computational time.

2. Methods

2.1. Conventional FEP with the Dual-Topology Approach

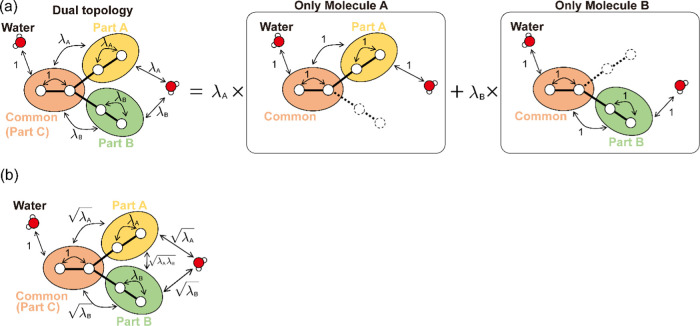
We assume that two ligands (ligands A and B) have a common chemical core structure.36,37 The dual topology of the hybrid ligands consists of three parts: the commonly existing atoms (part C), those only in ligand A (part A), and those only in ligand B (part B) (Figure 1a). In FEP, the potential energy of part C (UC in eq 1) does not change its functional form. In contrast, the potential energies involving part A or B (UA or UB in eq 1) are changed with scaling factors of λA or λB, respectively. In FEP based on the dual-topology approach, the nonbonded potential energy is decomposed into three terms

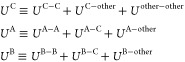2.1. 1

where C, A, B, and “other” represent part C, part A, part B, and the other molecules including solvent molecules, proteins, or other ligands, respectively, and UA–C represents the interactions between atoms in part A and those in part C, for example. For clarity, we distinguish atoms labeled as “C” and “other”, but there is essentially no difference in nonbonded potentials. In the conventional FEP method, the total nonbonded potential of the intermediate state between ligands A and B is described as

2.1. 2

At the initial state (λA = 1 and λB = 0), eq 2 corresponds to the potential energy of the system containing only ligand A. As λA and λB change to 0 and 1, respectively, ligand A gradually disappears, whereas ligand B appears. At the final state (λA = 0 and λB = 1), eq 2 becomes the potential energy containing only ligand B. From eq 2, the Lennard-Jones interactions, ULJ, and the short-range parts of electrostatic interactions, Uelec,sr, in the PME method23,24 can be evaluated by calculating each energy term (ULJA, ULJ, ULJC, Uelec,sr, Uelec,srB, and Uelec,sr).

Figure 1.

Figure 1

Open in a new tab

(a) Scheme for the calculation of the long-range electrostatic interactions in conventional FEP. The system is decomposed into two subsystems (including only molecule A or B). The total potential energy is evaluated, after calculating the potential energy of each system, multiplying by the respective λ value, and calculating their sum. (b) Proposed scheme based on the partial charge scaling for the long-range electrostatic interactions. The decomposition into two subsystems is no longer required, while three types of scaling factors are used.

The above decomposition is not applicable in the evaluation of long-range electrostatic interactions, Uelec,lr, when the PME method is used. In the PME method, the long-range parts of electrostatic interactions are computed in the reciprocal space using FFT.25 The reciprocal-space calculation cannot be decomposed into those for parts of the system such as part A, B, or C, which means that Uelec,lrA, Uelec,lr, or Uelec,lrC in eq 2 cannot be separately calculated. In the EI with the dual-topology approach, instead of the decomposition, two systems are considered: one excludes only part B and the other excludes only part A (see the right-hand side of Figure 1a), which are referred to as AC and BC, respectively. The long-range interaction of the electrostatic potential of each system, Uelec,lr (=Uelec,lrA + Uelec,lr) or Uelec,lrBC (=Uelec,lr + Uelec,lrC), is calculated individually. The total long-range electrostatic potential of the intermediate state between ligands A and B is obtained as follows

2.1. 3

In eq 3, at least two PME reciprocal-space calculations must be performed (i.e., FFT calculations are necessary twice) at each energy evaluation for both AC and BC systems. This type of calculation is computationally expensive, in particular, for large chemical or biological systems, because the computational time of the FFT calculation increases as O(N log N), where N is the number of degrees of freedom in the system.

2.2. Modified Hamiltonian in FEP with the Dual-Topology Approach

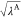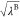
To avoid additional FFT calculations, we propose a PI in FEP for the evaluation of electrostatic interactions more efficiently. In this scheme, the point charge of atom i, qi, which is involved in the perturbed parts (parts A or B), is scaled by Inline graphic or Inline graphic

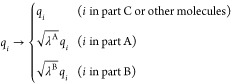2.2. 4

The electrostatic interactions involving the atoms in part A become dependent on λA

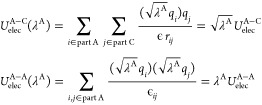2.2. 5

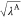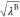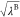where UelecA–other, Uelec, UelecB–B, and Uelec are also scaled by Inline graphic, Inline graphic, λB, and Inline graphic, respectively. Therefore, the total long-range interaction of the electrostatic potential is computed using the following modified potential energy function

2.2. 6

In the conventional method as described in eq 3, all of the electrostatic interactions including part A, UA–A, UA–C, and UA–other, are multiplied by the same scaling factor, λA, while those including part B are scaled with λB. In our proposed scheme, three types of scaling factors, namely, (i) 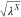Inline graphic, (ii) λX, and (iii) 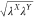Inline graphic, are included, where X, Y = A or B. Importantly, the modified potential energy in eq 6 can be calculated only by substituting the scaled parameters in eq 4 into the original energy function, implying that the reciprocal-space calculations in PME are computed only once at every energy evaluation in FEP. The potential energy scaling in eq 6 is similar to that used in REST2.33 We referred to this scheme as the modified Hamiltonian hereafter. At (λA, λB) = (1, 0) and (0, 1) (i.e., state A and state B), eq 6 corresponds to eq 3. By gradually changing λA and λB, states A and B can be connected smoothly. In the intermediate λ values, eqs 3 and 6 are different, but the free-energy changes should correspond to the end states because the free-energy changes depend only on the two end-point states and not on the calculation path.

This formula is applicable not only to the long-range electrostatic interactions but also in the calculation of the short-range interactions

2.2. 7

We note that the last term in eq 6, which is not included in the conventional method, is excluded in eq 7. This cross term might cause numerical troubles in the calculation of short-range interactions. At the end point of the alchemical FEP calculations, the LJ interactions of part A (or part B) appear, while those of part B (or part A) vanish. Then, atoms in part A can overlap with those in part B, leading to the extremely large value of Uelec,srA–B in the electrostatic interactions. Since the short-range part of electrostatic interaction is pairwise additive in the real-space calculation, the cross term can be separately removed from the energy evaluation during the FEP simulation.

In contrast to the short-range part, the cross term in eq 6 cannot be removed because the PME reciprocal-space calculation includes all pair interactions involving A–B interactions. The effect of the cross term disappears at the end states (λA = 0 or λB = 0). However, at intermediate λ points, eq 6 is not consistent with eq 7. From this inconsistency, the free-energy changes at intermediate points might depend on simulation settings, such as the real-space cutoff. A simple solution to remove the effect of the cross term is always to keep λAλB equal to zero, by setting either λA or λB to zero. The free-energy change from state A to state B can be realized by following the procedure: First, the atoms in part A are decharged. The LJ interactions are changed from part A to part B. Finally, the atoms in part B are recharged. This procedure is referred to the three-step procedure. This, however, limits possible alchemical pathways in FEP.

In contrast to the three-step procedure, there is another way to treat the cross term. In the PME method, the long-range part of the electrostatic interaction always has a small value even if atoms in part A overlap with those in part B, and its gradient does not become infinite. The calculation of Uelec,lrA–B never causes numerical troubles. The cross term might be not important in free-energy calculations so that alchemical pathways can be freely selected. For example, λA or λB for the electrostatic and LJ interactions are simultaneously and linearly changed. This procedure is referred to be the one-step procedure. We compare two procedures in Section 3.1.

In this study, the LJ interactions in FEP for dual topology are the same as those in conventional FEP. PI can be also applied to the LJ interactions.28

2.3. Energy Evaluation

The free-energy change upon the mutation can be calculated by gradually switching the interactions of the dual-topology part from molecule A (state A) to molecule B (state B). At state A, only part-A atoms exist in the dual-topology part, while part-B atoms do not interact with the other atoms in the system. During the alchemical transformation, interactions of part-A atoms gradually disappear, whereas interactions of part-B atoms gradually appear. At state B, only part-B atoms exist in the dual-topology part and interact with the other atoms. In the conventional method, the nonbonded potential energy is modified to connect smoothly state A to state B by introducing λLJ and λelec

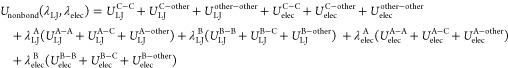2.3. 8

where “C”, “A”, “B”, and “other”, respectively, represent atoms in part C, atoms in part A, atoms in part B, and the other molecules including solvent molecules, proteins, or other ligands. For example, ULJC–A represents the LJ interactions between common atoms and part-A atoms. The potential energy at (λLJ, λelecA, λLJ, λelecB) = (1,1,0,0) corresponds to that of state A, while the energy at (λLJ, λelecA, λLJ, λelecB) = (0,0,1,1) corresponds to that of state B. By gradually changing (λLJ, λelecA, λLJ, λelecB), states A and B can be connected smoothly. In the current method, only λelec(UelecA–A + Uelec + UelecA–other) + λelec(UelecB–B + Uelec + UelecB–other) is modified as described in Section 2.2.

Close to the end point of alchemical calculations (λ = 0 or 1), overlaps between perturbed atoms or between perturbed and nonperturbed atoms can cause large energy changes. Due to the overlap, the system becomes unstable, and the simulations might crash, a situation referred to as the end-point catastrophe. To avoid the catastrophe, soft-core treatment is introduced to the LJ and electrostatic potentials38,39

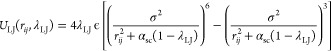2.3. 9
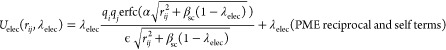2.3. 10

where αsc and βsc are the parameters for the soft-core potentials. In the LJ potential, rij2 is shifted to αsc(1 – λLJ), which weakens the repulsive part in the LJ potential when λLJ approaches 0. In the electrostatic potential, rij is shifted to βsc(1 – λelec) like the LJ soft-core potential, which softens disruptions due to overlaps of point charges. The soft-core treatment is not applied to the reciprocal-space calculation in PME and the self-term. Since the soft-core potential corresponds to the original potentials at the end points (λLJ, λelec) = (1, 1) or (0, 0), the soft-core modification in the potentials does not affect the result of the free-energy calculation.

Energy differences between adjacent windows (i and j) are required to calculate free-energy differences between windows i and j, ΔGij = −kBT ln⟨exp[−βΔUij]⟩i, where the subscript i represents the ensemble average at window i. ΔUij is the energy difference between windows i and j evaluated by window i, ΔUij = Unonbond(λLJj, λelec) – Unonbond(λLJi, λelec). To evaluate ΔUij, Unonbond (λLJi, λelec) and Unonbond(λLJj, λelec) must be calculated using the same configuration at window i, which means that the cost of energy calculation becomes at least twice. However, the evaluation of ΔUij is not needed at each time step to obtain the free-energy change.40 For example, it is sufficient to evaluate ΔUij once every 500 time steps, which has little effect on the computational performance.

We have implemented the conventional and modified FEP methods and the soft-core potentials into GENESIS software package.34,35 The FEP calculations in GENESIS are available in both CPU and hybrid CPU + GPU platforms. In the hybrid CPU + GPU scheme, the reciprocal-space component in PME (i.e., FFT) is computed using CPU, while the real-space component is computed using a graphics processing unit (GPU).41 The FFT calculation often constitutes the bottleneck in the whole computation because the CPU computation is slower than that on GPU. Since the modified FEP alleviates the bottleneck by reducing the number of FFT calculations, it should make the hybrid CPU + GPU computation more efficient.

2.4. System Setup, Simulation Protocol, and Analysis

We tested the modified FEP by employing the relative and absolute solvation free-energy changes of amino-acid side-chain analogues and the relative binding free-energy changes in a barnase–barstar complex upon the Y29A mutation in barnase. We performed all simulations using the development version of GENESIS.34,35 We used the CHARMM36 force field42 and the TIP3P model43 for protein and water molecules, respectively. Long-range electrostatic interactions were evaluated using smooth particle mesh Ewald (PME) summation, while Lennard-Jones interactions were truncated at a cutoff distance of 12 Å with a force switch function. All systems were equilibrated in the NPT ensemble at 300 K and 1 bar using the Bussi thermostat and barostat.44 All bonds involving hydrogen atoms were kept rigid using SHAKE45 and SETTLE46 algorithms.

For the absolute solvation free-energy calculation of amino-acid side-chain analogues, initial structures of chemical compounds corresponding to amino-acid side-chain analogues were taken from the ChemSpider and PubChem databases (e.g., the analogue of Ser is methanol). We modified some force field parameters, namely, changing β-carbon parameters and adding one hydrogen atom to the β carbon.47 For each analogue, we calculated ΔGwater and ΔGvacuum, which are the free-energy changes upon annihilating interactions of the analogue in water and in vacuum, respectively, and then obtained the solvation free energy, ΔGsolv = ΔGvacuum – ΔGwater. For the water system, each analogue was solvated within a rectangular box containing approximately 4000 water molecules. In FEP calculations, the electrostatic and Lennard-Jones (LJ) interactions of the ligand are decoupled from the system by λelec and λLJ, respectively (λ = 1 for full interaction and λ = 0 for no interaction). The 27 windows were used with different coupling parameters (see the Supporting Information). In each calculation, the simulation was run for 3 ns per window, and trajectories from 2 to 3 ns were used for analysis. For the vacuum system, instead of using PME, nonbonded interactions were truncated at a cutoff distance of 1000 Å. We employed the same λ parameters that were used in the water system. We did not include a long-range van der Waals correction.47 The correction is not essential for comparison of the conventional and modified methods.

For the relative solvation free-energy calculation of amino-acid side-chain analogues, we used the same initial structures and modified force field parameters as used for calculations of absolute solvation free energies. To construct dual topologies of mutants, we first decomposed two analogues into common atoms (part C) and others (part A and part B), and then connected part A and part B to part C. For each mutation, we calculated ΔGmutwater and ΔGmut, which are free-energy changes upon changing from one analogue to another analogue in water and in vacuum, respectively, and then obtained the relative solvation free energy, ΔΔGmut = ΔGmutwater – ΔGmut. The setup of the water and vacuum systems and the length of the FEP simulations were the same as for absolute solvation. In FEP simulations, the 21 windows were used for the three-step procedure, while the 12 windows were used for the one-step procedure (see the Supporting Information).

For the relative binding free-energy changes in the barnase–barstar complex, initial structures of the barnase–barstar complexes were obtained from the crystal structure (PDB ID 1BRS(48)). Missing side-chain atoms were added using MODELLER.49 We used the HSE configuration for all histidine residues because we assumed excluding H102 their tautomer states do not largely affect interactions within proteins. For H102 which is located in the protein–protein interface, the HSE configuration stabilizes the protein–protein interaction. From the thermodynamic cycle, the change in the binding free energy, ΔΔG = ΔGbindY29A – ΔGbindwt, can be calculated from the free-energy changes of the mutation in the complex and in the monomer (i.e., ΔΔG = ΔGmut – ΔGmutmonomer). We calculated ΔGmut and ΔGmutmonomer, which are free-energy changes upon changing from the wild type (wt) to the mutant in the complex and in the monomer, respectively. Each system was solvated within a rectangular box containing approximately 16,000 water molecules. Na+ ions were added to neutralize the system. Each simulation system was first minimized using the steepest descent algorithm. 100 ps heating and another 100 ps NPT equilibration were subsequently performed with harmonic positional restraints on the heavy atoms of the proteins. Then, 20 ns equilibration run in the NPT ensemble at 300 K was performed without the restraints. We conducted FEP simulations from the equilibrated structures. For FEP simulations, we used 31 windows (see the Supporting Information). In each calculation, the simulation was carried out for 20 ns per window, and trajectories from 10 to 20 ns were used for the free-energy analysis.

For evaluation of free-energy changes, we used the Bennett’s acceptance ratio (BAR) method.50 The obtained trajectories were decomposed into three blocks. The mean and the standard error were calculated using the block averages.

2.5. Performance Measurements

We employed the mutation from Leu to Phe as a benchmark system for estimating the performance. The λ values used were λelecA = 0.75, λelec = 0, λLJA = 1, and λLJ = 0. We prepared four systems with different box sizes by increasing the number of water molecules. The systems consist of 27k, 55k, 109k, and 219k atoms. We measured the calculation time or speed of FEP simulations on a CPU + GPU cluster. Each node of the cluster has two CPUs and two GPUs. The CPU used was Intel Xeon Gold 6142 which has 16 cores with a 2.6 GHz clock speed, while the GPU was GeForce RTX 2080 Ti. The nodes in the cluster are interconnected by InfiniBand.

3. Results

3.1. Solvation Free Energies of Amino-Acid Side-Chain Analogues

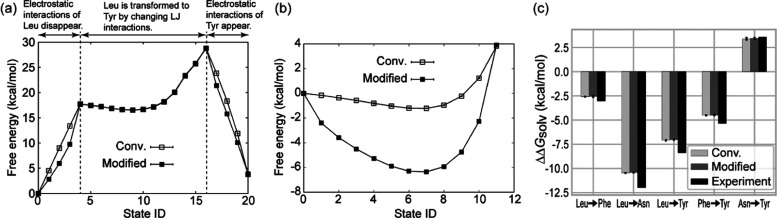
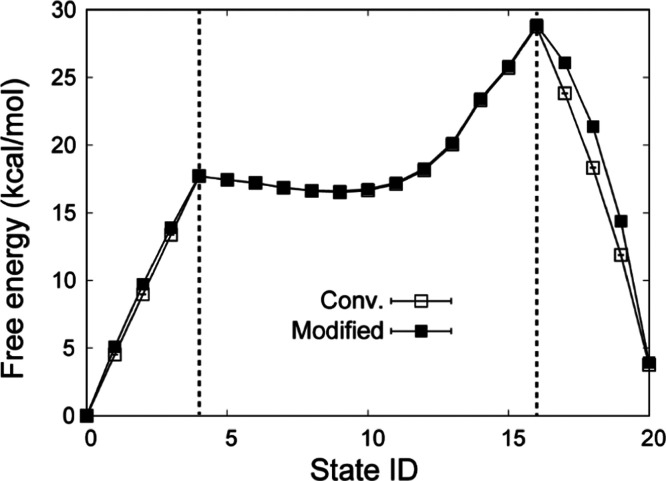
To test the free-energy calculations using the modified Hamiltonian, we calculated the free-energy change along the mutation of the side-chain analogue from Leu to Tyr in water (Figure 2a). The free-energy change at each state ID is compared between the conventional (eq 3) and the current methods (eq 4). Due to the restriction in the latter method, we employed a three-step procedure: the atoms in Leu are decharged (state IDs 0 to 4), the LJ interactions are changed from Leu to Tyr (state IDs 5 to 15), and the atoms in Tyr are recharged (state IDs 16 to 20). λTyr and λLeu in the electrostatic term should be zero at state IDs 0 to 16 and 4 to 20, respectively. Since the alchemical pathways at the state IDs 0 to 4 and 16 to 20 are different between the two methods, the intermediate states have different free-energy changes. However, the free-energy changes in the current method correspond to those in the conventional method at the end points in the electrostatic FEP calculations (at state ID 4, 16, or 20) because the free-energy changes depend only on the two end-point states and not on the calculation path. At state IDs 4 to 16, the two FEP methods produce the same free-energy changes upon switching the LJ interactions from Leu to Tyr. For the LJ interaction in FEP, we just applied the conventional method (eq 2) in both methods. The free-energy calculations for conventional and the current schemes converge within 3 ns FEP simulations (Figure S1). Also, for both methods, the distributions of the energy difference between adjacent windows sufficiently overlap (Figures S2 and S3), implying that the result of the current scheme is as reliable as that of conventional FEP.

Figure 2.

Figure 2

Open in a new tab

(a) Free-energy changes at each state ID using the three-step procedure. At state IDs 0 to 4, the electrostatic interactions of Leu are gradually vanished. At state IDs 4 to 16, the LJ interactions of Leu are vanished, while those of Tyr appear. At state IDs 16 to 20, the electrostatic interactions of Tyr appear. (b) Free-energy changes using the one-step procedure. At state IDs 0 to 11, λelecA and λLJ are linearly changed from 1 to 0 at state IDs 0 to 11, while λelecB and λLJ are linearly changed from 0 to 1. (c) Relative solvation free energies between four amino-acid side-chain analogues. All values of the relative solvation free energies are shown in Table S1.

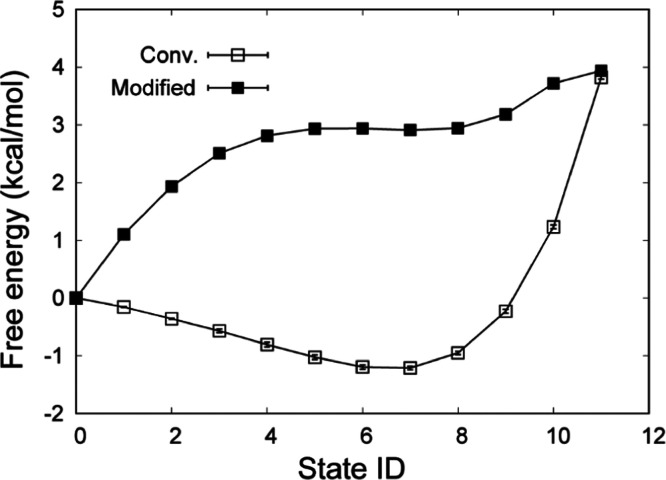
The three-step procedure can remove the effect of the cross term in eq 6. However, as described in Section 2.2, the calculation of Uelec,lrA–B may not cause numerical instability and may not affect the free-energy change. To check the effect of the cross term, we calculated the free-energy change from Leu to Tyr using the one-step procedure, in which LJ and electrostatic interactions are simultaneously and linearly changed. We employed the 12 windows (see the Supporting Information). The free-energy changes at intermediate λelec values are largely different between the conventional and modified methods (Figure 2b). At the end states (state IDs 0 and 11), the free energies of the modified method are in good agreement with those of conventional FEP: 3.82 ± 0.04 kcal/mol for conventional FEP and 3.91 ± 0.04 kcal/mol for the modified method. The effect of the cross term is negligible, and the three-step procedure is not essential for the modified method. Even for the one-step procedure, the distributions of the energy difference between adjacent windows sufficiently overlap (Figures S4 and S5). We note that one-step procedure requires the soft-core potential for the electrostatic interactions because the electrostatic interactions sometimes become very large when the repulsive interaction in LJ is weakened (i.e., the distance between two atoms can be too short).

Using the one-step procedure, we calculated the relative solvation free energies upon five mutations in amino-acid side-chain analogues (from Leu to Phe, from Leu to Asn, from Leu to Tyr, from Phe to Tyr, and from Asn to Tyr), all of which involve a change from a hydrophobic side chain to a hydrophilic side chain. The methyl group is treated as the common part, while the remaining parts are treated as perturbed parts (Figure S6). In Figure 2c, we show the relative solvation free energies calculated using the conventional FEP and that with the modified Hamiltonian. The two FEP calculations agree with each other within statistical errors.

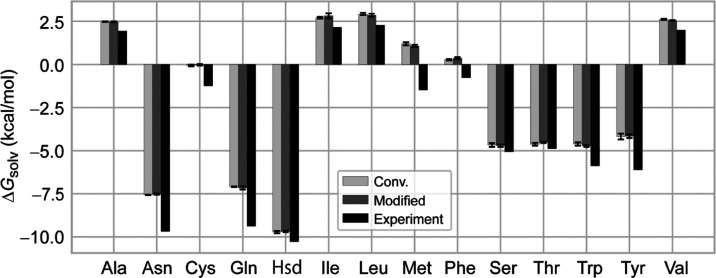
The absolute solvation free energies of 14 side-chain analogues of noncharged amino acids (Figure S7) were also computed using the conventional and the modified methods. In the absolute solvation free-energy calculations, the dual topology is not required. Part A corresponds to an amino-acid analogue, while part B and part C do not exist in eq 4, which is simplified to 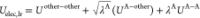Inline graphic. In Figure 3, we compare the absolute solvation free energies obtained by the conventional and the modified methods. The results of the modified method are in good agreement with those of the conventional method within statistical errors. Both methods well reproduce the trend of the experimental data, but FEP underestimates experimental results for some analogues. The underestimations are also observed in previous FEP calculations,47,51,52 suggesting that there is still some room for improving the force field used in the FEP calculations.

Figure 3.

Figure 3

Open in a new tab

Absolute solvation free energies of 14 amino-acid side-chain analogues in water. Experimental data are taken from ref (53). All values of the absolute solvation free energies are shown in Table S2.

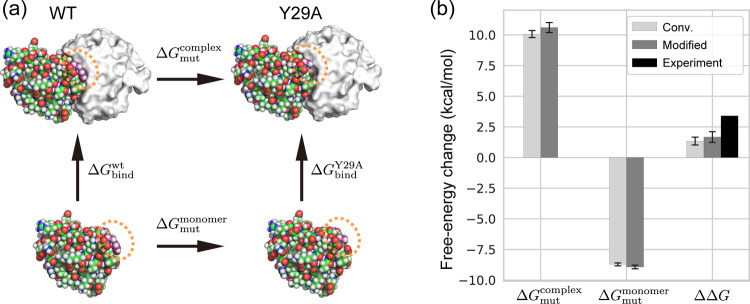
3.2. Binding Free-Energy Changes of Barnase–Barstar Complex

Next, we applied the FEP with the modified Hamiltonian to the calculation of binding free-energy changes of barstar–barnase complexes. Experimentally, the Y29A mutation in barnase (Y29A) is known to decrease the binding affinity with barstar compared to the wild type (wt).54 The relative binding free-energy changes of the complex between wt and Y29A are experimentally obtained using the relationship, ΔΔG = ΔGbindY29A – ΔGbind, where ΔGbindwt and ΔGbind are binding free energies of wt barnase and its Y29A, respectively. Direct calculations of the absolute binding free energies, ΔGbindwt and ΔGbind, have large computational costs.55 In alchemical FEP, it is common to use the thermodynamic cycle in Figure 4a and estimate ΔΔG from the mutation free-energy changes from Y29 to Ala in the barster–barnase complex and in barnase, ΔGmutcomplex and ΔGmut, respectively. The free-energy changes calculated using the modified method are in good agreement with those calculated using the conventional method (Figure 4b). The modified and the conventional methods yield ΔΔG values of 1.67 and 1.34 kcal/mol, respectively. However, these results largely differ from the known experimental result (3.4 kcal/mol54). An earlier study suggested that the CHARMM force field might underestimate the barnase–barstar binding free energy.55

Figure 4.

Figure 4

Open in a new tab

(a) Thermodynamic cycle of the barnase–barstar binding in wild type (wt) and the Y29A mutant barnase (Y29A). Structures of barstar and barnase are shown in sphere and surface representations in white and color, respectively. The mutated residue (Y29) is marked by the orange dashed circle. (b) Relative free-energy changes of the barnase-barster binding between wt and Y29A. The experimental result is taken from ref (54). All values are shown in Table S3.

3.3. Computational Performance of the Modified FEP

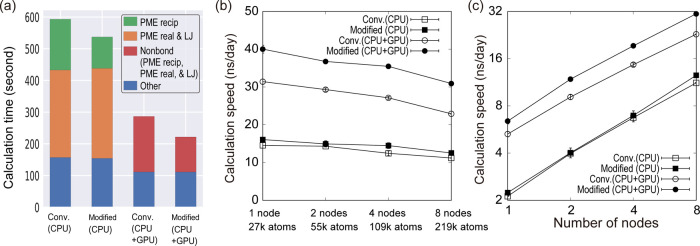
Finally, the computational speed of the modified method is compared with the conventional method. We employ the mutation free-energy calculation of an amino-acid side-chain analogue from Leu to Phe with λelecA = 0.75, λelec = 0, λLJA = 1, and λLJ = 0. We tested not only CPU-based computers but also hybrid CPU + GPU computers using the velocity Verlet integrator with a 2 fs time step. In Figure 5a, we decompose the total calculation time into components of real- and reciprocal-space calculations in PME and other calculations. In the hybrid CPU + GPU computation using GENESIS, the computational time of the non-bonded-energy calculations cannot be decomposed because PME real- and reciprocal-space calculations are simultaneously performed on CPU and GPU, respectively. In the CPU-only computation, the PME reciprocal-space calculation using the modified method is 38% faster than the conventional method. In the hybrid CPU + GPU computation, the total time of the non-bonded-energy calculations decreases by 37% in the modified method. The modified method can speed up the total calculation by 10 and 23% for CPU-only and hybrid computations, respectively. The speed-up in the computation time results from the reduction of the number of PME reciprocal-space calculations in FEP.

Figure 5.

Figure 5

Open in a new tab

(a) Computational times of 100 ps FEP simulations for a system consisting of 27k atoms on a single node. The PME reciprocal-space calculations are colored in green, while the PME real-space calculation and the LJ interactions are colored in orange. Times for other calculations are colored blue. In the CPU + GPU hybrid computation, the nonbonded interactions are colored in red. (b) Performance of FEP calculations while fixing the number of atoms per processor. (c) Strong scaling of FEP calculations for the large system (219k atoms). In all cases, mutation free-energy calculation of an amino-acid side-chain analogue from Leu to Phe with λelecA = 0.75, λelec = 0, λLJA = 1, and λLJ = 0 was used. All values are shown in Tables S4 and S5.

To test the scalability of the modified method, we performed the same mutation free-energy calculations while changing the number of water molecules (from 27k to 219k atoms) in periodic boundary boxes of different sizes. We measured the calculation speed by changing the number of processors while fixing the number of atoms per processor. Figure 5b shows that the performance of the modified method is better than the conventional method in both CPU-only and hybrid computations. The modified method is 12% faster on CPU for the largest system, while it is 35% faster in hybrid computations.

We examined the strong scaling of the modified method using the largest system (219k atoms) (Figure 5c). The difference between the modified and conventional methods becomes larger as the number of computer nodes increases. This speed-up effect is mainly due to the reduction of internode communication in the modified method. In GENESIS SPDYN, the simulation space is divided into subdomains, and the calculations in each domain are assigned to different MPI processes. When multiple nodes are used during the simulation, FFT calculations require extensive communication between MPI processes in different nodes to obtain information of all atoms. As the number of nodes increases, the cost of the communication becomes larger, which decreases the speed of reciprocal-space calculations in PME. The modified method reduces the communication cost by decreasing the number of FFT calculations. The reduction of the communication is more effective in the hybrid CPU + GPU computations because the FFT calculation on CPU is the main bottleneck in the non-bonded-energy calculation.

The computational speed of FEP using the r-RESPA integrator with 2.5 and 5.0 fs time steps of fast and slow motions, respectively, was also examined. Since the PME reciprocal-space calculation is performed once every two time steps in r-RESPA, the number of FFT calculations decreases, which reduces the total computation cost. Although the speed-up by the modified method is weakened using the r-RESPA integrator, the total calculation time becomes 4 and 14% faster on CPU and the hybrid CPU + GPU computations, respectively (Figure S8). Also, the strong scaling of the modified method is better than that of the conventional method in the r-RESPA integrator (Figure S8 and Tables S6 and S7).

The speeding-up by the modified FEP is relevant only for the windows, in which electrostatic interactions are changed. For example, the modified FEP decreases the calculation times in decharging and recharging processes (8 windows) in Figure 2a, but it does not affect 13 windows. However, if 21 windows are independently calculated (e.g., embarrassingly parallel computation), the total calculation time depends on the calculation time for the slowest windows (i.e., decharging or recharging windows). The modified Hamiltonian in FEP can decrease the total calculation time by reducing the time of the slowest windows. Also, if the replica-exchange FEP is used, the slowest replicas become the bottleneck. The modified method also increases the total computational performance by reducing the time of the slowest replicas.

4. Discussion

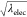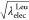In Section 3.1, for the three-step procedure, we changed λelecLeu and λelec values linearly (λelecLeu = 1, 0.75, 0.5, 0.25, and 0 or λelec = 0, 0.25, 0.5, 0.75, and 1), but this alchemical pathway might not be the best for the modified method because eqs 6 and 7 include not only λelec but also Inline graphic. We checked how the choice of λelec values affects the free energy in the modified method. 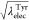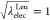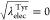We calculated the free-energy change along the mutation of the side-chain analogue from Leu to Tyr by changing λelecLeu and λelec values as Inline graphic and Inline graphic vary linearly (Figure 6): Inline graphic, 0.75, 0.5, 0.25, and 0 at the state IDs 0 to 4, or Inline graphic, 0.25, 0.5, 0.75, and 1 at the state IDs 16 to 20. 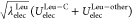At the state IDs 0 to 4, the free energy in the modified method increases linearly almost the same as conventional FEP, which suggests that Inline graphic largely contributes to the total energy compared to λelecLeuUelec. On the other hand, at the state IDs 16 to 20, the free energy in the modified method decreases nonlinearly. This might come from the large contribution of λelecTyrUelec due to nonlinear change in λelecTyr.

Figure 6.

Figure 6

Open in a new tab

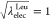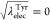Free-energy changes of the mutation of the side-chain analogue from Leu to Tyr. In the modified method,Inline graphic, 0.75, 0.5, 0.25, and 0 at the state IDs 0 to 4, or Inline graphic, 0.25, 0.5, 0.75, and 1 at the state IDs 16 to 20. The free-energy changes of conventional FEP are the same as shown in Figure 2a.

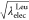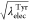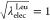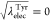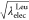For the one-step procedure, we also linearly changed the values of Inline graphic and Inline graphic for the modified FEP: Inline graphic, 0.909, 0.818, 0.727, 0.636, 0.545, 0.455, 0.364, 0.273, 0.182, 0.091, and 0 and Inline graphic, 0.091, 0.182, 0.273, 0.364, 0.455, 0.545, 0.636, 0.727, 0.818, 0.909, and 1 at the state IDs 0 to 11. When the values of λelecLeu and λelec are linearly changed, the free-energy profile in the modified method largely changes through the alchemical path (Figure 2b): after decreasing to −6 kcal/mol at the state ID 7, the free energy increases to 4 kcal/mol at the state ID 11. In particular, the free-energy change from the state ID 10 to the state ID 11 is 6 kcal/mol. 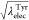On the other hand, when the values of Inline graphic and Inline graphic are linearly changed, the free-energy profile mildly changes from the initial state to the final state (Figure 7). The free-energy differences between two adjacent windows are within about 1 kcal/mol. For the modified method, one should choose appropriate λelec values for good statistics. The choice of the free-energy path might affect the convergence efficiency.40,56 Potentially the alternative path might lead to more efficient free-energy calculations. The best alchemical path for the modified FEP method should be elucidated in the future work.

Figure 7.

Figure 7

Open in a new tab

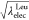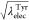Free-energy changes of the mutation of the side-chain analogue from Leu to Tyr. In the modified method,Inline graphic and Inline graphic are linearly changed. The free-energy changes of conventional FEP are the same as shown in Figure 2b.

We implemented the modified Hamiltonian in FEP calculations into GENESIS and tested the method using GENESIS. However, in the modified method, the partial charges are just scaled by λ values, which does not require any special treatment in MD software. This method can be easily implemented in any MD software.

5. Conclusions

In the present study, we introduce a new scaling method in the FEP calculation of electrostatic interactions. The new method reduces the number of PME reciprocal-space calculations using the nonuniform scaling of electrostatic potential terms like the scheme used in REST2. By calculating the solvation free energies of amino-acid side-chain analogues and the barnase–barstar binding free energy, we show that our scaling method reproduces the results obtained by the conventional scaling method. The reduction of PME reciprocal-space calculations greatly improves the computational performance, in particular in the CPU + GPU hybrid computation. The improvement would become more significant for large biomolecular systems, such as membranes or crowded systems, because calculation time for PME reciprocal-space calculations increases with O(N log N) and constitutes the bottleneck in the total calculation cost. We believe that our method could help the free-energy calculations for a large variety of biosystems.

Acknowledgments

The authors thank Dr. Ai Shinobu for her critical reading of the manuscript. They used the computational resources provided by the HPCI System Research Project (Project ID: hp160207, hp170254, hp180201, hp190181, hp200129, hp200135, hp210172, and hp210177) and those in RIKEN Advanced Center for Computing and Communication (HOKUSAI BigWaterfall). This work was supported by MEXT/JSPS KAKENHI Grant Number 19H05645 (to Y.S.) and 20K06582 (to H.O.), RIKEN pioneering projects in “Biology of Intracellular Environment”, “Dynamic Structural Biology” and “Glycolipidlogue” (to Y.S.), and MEXT “Program for Promoting Research on the Supercomputer Fugaku (Biomolecular dynamics in a living cell/MD-driven Precision Medicine)”.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.1c01532.

  • Convergence of FEP calculations; distributions of energy differences between λ windows; chemical structures of the amino-acid side-chain analogues; computational performance for the r-RESPA integrator; all values of the solvation free-energy changes of amino-acid side-chain analogues and the binding free-energy changes of barnase–barstar complex; and λ values for FEP simulations (PDF)

Author Contributions

H.O. and Y.S. designed the research; H.O. performed the simulations and analyzed the data; and H.O. and Y.S. wrote the manuscript.

The authors declare no competing financial interest.

Notes

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supplementary Material

ci1c01532_si_001.pdf (2.7MB, pdf)

References

  1. De Vivo M.; Masetti M.; Bottegoni G.; Cavalli A. Role of Molecular Dynamics and Related Methods in Drug Discovery. J. Med. Chem. 2016, 59, 4035–4061. 10.1021/acs.jmedchem.5b01684. [DOI] [PubMed] [Google Scholar]
  2. Mobley D. L.; Gilson M. K. Predicting Binding Free Energies: Frontiers and Benchmarks. Annu. Rev. Biophys. 2017, 46, 531–558. 10.1146/annurev-biophys-070816-033654. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Cournia Z.; Allen B. K.; Beuming T.; Pearlman D. A.; Radak B. K.; Sherman W. Rigorous Free Energy Simulations in Virtual Screening. J. Chem. Inf. Model. 2020, 60, 4153–4169. 10.1021/acs.jcim.0c00116. [DOI] [PubMed] [Google Scholar]
  4. Decherchi S.; Cavalli A. Thermodynamics and Kinetics of Drug-Target Binding by Molecular Simulation. Chem. Rev. 2020, 120, 12788–12833. 10.1021/acs.chemrev.0c00534. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Śledź P.; Caflisch A. Protein Structure-Based Drug Design: From Docking to Molecular Dynamics. Curr. Opin. Struct. Biol. 2018, 48, 93–102. 10.1016/j.sbi.2017.10.010. [DOI] [PubMed] [Google Scholar]
  6. Gallicchio E.; Lapelosa M.; Levy R. M. Binding Energy Distribution Analysis Method (BEDAM) for Estimation of Protein–Ligand Binding Affinities. J. Chem. Theory Comput. 2010, 6, 2961–2977. 10.1021/ct1002913. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Jorgensen W. L.; Thomas L. L. Perspective on Free-Energy Perturbation Calculations for Chemical Equilibria. J. Chem. Theory Comput. 2008, 4, 869–876. 10.1021/ct800011m. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Gilson M. K.; Given J. A.; Bush B. L.; McCammon J. A. The Statistical-Thermodynamic Basis for Computation of Binding Affinities: A Critical Review. Biophys. J. 1997, 72, 1047–1069. 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Deng Y.; Roux B. Computations of Standard Binding Free Energies with Molecular Dynamics Simulations. J. Phys. Chem. B 2009, 113, 2234–2246. 10.1021/jp807701h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Boresch S.; Tettinger F.; Leitgeb M.; Karplus M. Absolute Binding Free Energies: A Quantitative Approach for Their Calculation. J. Phys. Chem. B 2003, 107, 9535–9551. 10.1021/jp0217839. [DOI] [Google Scholar]
  11. Fujitani H.; Tanida Y.; Matsuura A. Massively Parallel Computation of Absolute Binding Free Energy with Well-Equilibrated States. Phys. Rev. E 2009, 79, 021914 10.1103/PhysRevE.79.021914. [DOI] [PubMed] [Google Scholar]
  12. Pronk S.; Páll S.; Schulz R.; Larsson P.; Bjelkmar P.; Apostolov R.; Shirts M. R.; Smith J. C.; Kasson P. M.; van der Spoel D.; Hess B.; Lindahl E. GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Jiang W.; Chipot C.; Roux B. Computing Relative Binding Affinity of Ligands to Receptor: An Effective Hybrid Single-Dual-Topology Free-Energy Perturbation Approach in NAMD. J. Chem. Inf. Model. 2019, 59, 3794–3802. 10.1021/acs.jcim.9b00362. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Lee T.-S.; Allen B. K.; Giese T. J.; Guo Z.; Li P.; Lin C.; McGee T. D.; Pearlman D. A.; Radak B. K.; Tao Y.; Tsai H.-C.; Xu H.; Sherman W.; York D. M. Alchemical Binding Free Energy Calculations in AMBER20: Advances and Best Practices for Drug Discovery. J. Chem. Inf. Model. 2020, 60, 5595–5623. 10.1021/acs.jcim.0c00613. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Phillips J. C.; Hardy D. J.; Maia J. D. C.; Stone J. E.; Ribeiro J. V.; Bernardi R. C.; Buch R.; Fiorin G.; Hénin J.; Jiang W.; McGreevy R.; Melo M. C. R.; Radak B. K.; Skeel R. D.; Singharoy A.; Wang Y.; Roux B.; Aksimentiev A.; Luthey-Schulten Z.; Kalé L. V.; Schulten K.; Chipot C.; Tajkhorshid E. Scalable Molecular Dynamics on CPU and GPU Architectures with NAMD. J. Chem. Phys. 2020, 153, 044130 10.1063/5.0014475. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Wang L.; Wu Y.; Deng Y.; Kim B.; Pierce L.; Krilov G.; Lupyan D.; Robinson S.; Dahlgren M. K.; Greenwood J.; Romero D. L.; Masse C.; Knight J. L.; Steinbrecher T.; Beuming T.; Damm W.; Harder E.; Sherman W.; Brewer M.; Wester R.; Murcko M.; Frye L.; Farid R.; Lin T.; Mobley D. L.; Jorgensen W. L.; Berne B. J.; Friesner R. A.; Abel R. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. J. Am. Chem. Soc. 2015, 137, 2695–2703. 10.1021/ja512751q. [DOI] [PubMed] [Google Scholar]
  17. Kim S.; Oshima H.; Zhang H.; Kern N. R.; Re S.; Lee J.; Roux B.; Sugita Y.; Jiang W.; Im W. CHARMM-GUI Free Energy Calculator for Absolute and Relative Ligand Solvation and Binding Free Energy Simulations. J. Chem. Theory Comput. 2020, 16, 7207–7218. 10.1021/acs.jctc.0c00884. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Oshima H.; Re S.; Sugita Y. Prediction of Protein–Ligand Binding Pose and Affinity Using the GREST+FEP Method. J. Chem. Inf. Model. 2020, 60, 5382–5394. 10.1021/acs.jcim.0c00338. [DOI] [PubMed] [Google Scholar]
  19. Jorgensen W. L. Efficient Drug Lead Discovery and Optimization. Acc. Chem. Res. 2009, 42, 724–733. 10.1021/ar800236t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Homeyer N.; Stoll F.; Hillisch A.; Gohlke H. Binding Free Energy Calculations for Lead Optimization: Assessment of Their Accuracy in an Industrial Drug Design Context. J. Chem. Theory Comput. 2014, 10, 3331–3344. 10.1021/ct5000296. [DOI] [PubMed] [Google Scholar]
  21. Liu S.; Wu Y.; Lin T.; Abel R.; Redmann J. P.; Summa C. M.; Jaber V. R.; Lim N. M.; Mobley D. L. Lead Optimization Mapper: Automating Free Energy Calculations for Lead Optimization. J. Comput.-Aided Mol. Des. 2013, 27, 755–770. 10.1007/s10822-013-9678-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kirkwood J. G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. 10.1063/1.1749657. [DOI] [Google Scholar]
  23. Darden T.; York D.; Pedersen L. Particle Mesh Ewald: An N ·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
  24. Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
  25. Frigo M.; Johnson S. G. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. 10.1109/JPROC.2004.840301. [DOI] [Google Scholar]
  26. Jorgensen W. L.; Ravimohan C. Monte Carlo Simulation of Differences in Free Energies of Hydration. J. Chem. Phys. 1985, 83, 3050–3054. 10.1063/1.449208. [DOI] [Google Scholar]
  27. Mezei M.; Beveridge D. L. Computer Simulation of Chemical and Biomolecular Systems. Ann. N. Y. Acad. Sci. 1986, 482, 1–307. [PubMed] [Google Scholar]
  28. Giese T. J.; York D. M. A GPU-Accelerated Parameter Interpolation Thermodynamic Integration Free Energy Method. J. Chem. Theory Comput. 2018, 14, 1564–1582. 10.1021/acs.jctc.7b01175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Jorgensen W. L.; Tirado-Rives J. Molecular Modeling of Organic and Biomolecular Systems UsingBOSS AndMCPRO. J. Comput. Chem. 2005, 26, 1689–1700. 10.1002/jcc.20297. [DOI] [PubMed] [Google Scholar]
  30. Harger M.; Li D.; Wang Z.; Dalby K.; Lagardère L.; Piquemal J.; Ponder J.; Ren P. Tinker-OpenMM: Absolute and Relative Alchemical Free Energies Using AMOEBA on GPUs. J. Comput. Chem. 2017, 38, 2047–2055. 10.1002/jcc.24853. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Boresch S.; Bruckner S. Avoiding the van Der Waals Endpoint Problem Using Serial Atomic Insertion. J. Comput. Chem. 2011, 32, 2449–2458. 10.1002/jcc.21829. [DOI] [PubMed] [Google Scholar]
  32. König G.; Glaser N.; Schroeder B.; Kubincová A.; Hünenberger P. H.; Riniker S. An Alternative to Conventional λ-Intermediate States in Alchemical Free Energy Calculations: λ-Enveloping Distribution Sampling. J. Chem. Inf. Model. 2020, 60, 5407–5423. 10.1021/acs.jcim.0c00520. [DOI] [PubMed] [Google Scholar]
  33. Wang L.; Friesner R. A.; Berne B. J. Replica Exchange with Solute Scaling: A More Efficient Version of Replica Exchange with Solute Tempering (REST2). J. Phys. Chem. B 2011, 115, 9431–9438. 10.1021/jp204407d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Jung J.; Mori T.; Kobayashi C.; Matsunaga Y.; Yoda T.; Feig M.; Sugita Y. GENESIS: A Hybrid-Parallel and Multi-Scale Molecular Dynamics Simulator with Enhanced Sampling Algorithms for Biomolecular and Cellular Simulations. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2015, 5, 310–323. 10.1002/wcms.1220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Kobayashi C.; Jung J.; Matsunaga Y.; Mori T.; Ando T.; Tamura K.; Kamiya M.; Sugita Y. GENESIS 1.1: A Hybrid-Parallel Molecular Dynamics Simulator with Enhanced Sampling Algorithms on Multiple Computational Platforms. J. Comput. Chem. 2017, 38, 2193–2206. 10.1002/jcc.24874. [DOI] [PubMed] [Google Scholar]
  36. Pearlman D. A. A Comparison of Alternative Approaches to Free Energy Calculations. J. Phys. Chem. A 1994, 98, 1487–1493. 10.1021/j100056a020. [DOI] [Google Scholar]
  37. Hénin J.; Chipot C. Overcoming Free Energy Barriers Using Unconstrained Molecular Dynamics Simulations. J. Chem. Phys. 2004, 121, 2904–2914. 10.1063/1.1773132. [DOI] [PubMed] [Google Scholar]
  38. Zacharias M.; Straatsma T. P.; McCammon J. A. Separation-shifted Scaling, a New Scaling Method for Lennard-Jones Interactions in Thermodynamic Integration. J. Chem. Phys. 1994, 100, 9025–9031. 10.1063/1.466707. [DOI] [Google Scholar]
  39. Steinbrecher T.; Joung I.; Case D. A. Soft-Core Potentials in Thermodynamic Integration: Comparing One- and Two-Step Transformations. J. Comput. Chem. 2011, 32, 3253–3263. 10.1002/jcc.21909. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. de Ruiter A.; Oostenbrink C. Extended Thermodynamic Integration: Efficient Prediction of Lambda Derivatives at Nonsimulated Points. J. Chem. Theory Comput. 2016, 12, 4476–4486. 10.1021/acs.jctc.6b00458. [DOI] [PubMed] [Google Scholar]
  41. Jung J.; Naurse A.; Kobayashi C.; Sugita Y. Graphics Processing Unit Acceleration and Parallelization of GENESIS for Large-Scale Molecular Dynamics Simulations. J. Chem. Theory Comput. 2016, 12, 4947–4958. 10.1021/acs.jctc.6b00241. [DOI] [PubMed] [Google Scholar]
  42. Huang J.; MacKerell A. D. CHARMM36 All-Atom Additive Protein Force Field: Validation Based on Comparison to NMR Data. J. Comput. Chem. 2013, 34, 2135–2145. 10.1002/jcc.23354. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  44. Bussi G.; Zykova-Timan T.; Parrinello M. Isothermal-Isobaric Molecular Dynamics Using Stochastic Velocity Rescaling. J. Chem. Phys. 2009, 130, 074101 10.1063/1.3073889. [DOI] [PubMed] [Google Scholar]
  45. Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
  46. Miyamoto S.; Kollman P. A. Settle: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13, 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
  47. Shirts M. R.; Pitera J. W.; Swope W. C.; Pande V. S. Extremely Precise Free Energy Calculations of Amino Acid Side Chain Analogs: Comparison of Common Molecular Mechanics Force Fields for Proteins. J. Chem. Phys. 2003, 119, 5740–5761. 10.1063/1.1587119. [DOI] [Google Scholar]
  48. Buckle A. M.; Schreiber G.; Fersht A. R. Protein-Protein Recognition: Crystal Structural Analysis of a Barnase-Barstar Complex at 2.0-.ANG. Resolution. Biochemistry 1994, 33, 8878–8889. 10.1021/bi00196a004. [DOI] [PubMed] [Google Scholar]
  49. Šali A.; Blundell T. L. Comparative Protein Modelling by Satisfaction of Spatial Restraints. J. Mol. Biol. 1993, 234, 779–815. 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
  50. Bennett C. H. Efficient Estimation of Free Energy Differences from Monte Carlo Data. J. Comput. Phys. 1976, 22, 245–268. 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
  51. Deng Y.; Roux B. Hydration of Amino Acid Side Chains: Nonpolar and Electrostatic Contributions Calculated from Staged Molecular Dynamics Free Energy Simulations with Explicit Water Molecules. J. Phys. Chem. B 2004, 108, 16567–16576. 10.1021/jp048502c. [DOI] [Google Scholar]
  52. Karino Y.; Fedorov M. V.; Matubayasi N. End-Point Calculation of Solvation Free Energy of Amino-Acid Analogs by Molecular Theories of Solution. Chem. Phys. Lett. 2010, 496, 351–355. 10.1016/j.cplett.2010.07.054. [DOI] [Google Scholar]
  53. Wolfenden R.; Andersson L.; Cullis P. M.; Southgate C. C. B. Affinities of Amino Acid Side Chains for Solvent Water. Biochemistry 1981, 20, 849–855. 10.1021/bi00507a030. [DOI] [PubMed] [Google Scholar]
  54. Schreiber G.; Fersht A. R. Energetics of Protein-Protein Interactions: Analysis of the Barnase-Barstar Interface by Single Mutations and Double Mutant Cycles. J. Mol. Biol. 1995, 248, 478–486. 10.1016/S0022-2836(95)80064-6. [DOI] [PubMed] [Google Scholar]
  55. Suh D.; Jo S.; Jiang W.; Chipot C.; Roux B. String Method for Protein–Protein Binding Free-Energy Calculations. J. Chem. Theory Comput. 2019, 15, 5829–5844. 10.1021/acs.jctc.9b00499. [DOI] [PubMed] [Google Scholar]
  56. de Ruiter A.; Petrov D.; Oostenbrink C. Optimization of Alchemical Pathways Using Extended Thermodynamic Integration. J. Chem. Theory Comput. 2021, 17, 56–65. 10.1021/acs.jctc.0c01170. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ci1c01532_si_001.pdf (2.7MB, pdf)

Articles from Journal of Chemical Information and Modeling are provided here courtesy of American Chemical Society

RESOURCES