Abstract
The second quantum revolution harnesses exquisite quantum control for a slate of diverse applications including sensing, communication, and computation. Of the many candidates for building quantum systems, molecules offer both tunability and specificity, but the principles to enable high temperature operation are not well established. Spin–lattice relaxation, represented by the time constant T1, is the primary factor dictating the high temperature performance of quantum bits (qubits), and serves as the upper limit on qubit coherence times (T2). For molecular qubits at elevated temperatures (>100 K), molecular vibrations facilitate rapid spin–lattice relaxation which limits T2 to well below operational minimums for certain quantum technologies. Here we identify the effects of controlling orbital angular momentum through metal coordination geometry and ligand rigidity via π-conjugation on T1 relaxation in three four-coordinate Cu2+S = ½ qubit candidates: bis(N,N′-dimethyl-4-amino-3-penten-2-imine) copper(ii) (Me2Nac)2 (1), bis(acetylacetone)ethylenediamine copper(ii) Cu(acacen) (2), and tetramethyltetraazaannulene copper(ii) Cu(tmtaa) (3). We obtain significant T1 improvement upon changing from tetrahedral to square planar geometries through changes in orbital angular momentum. T1 is further improved with greater π-conjugation in the ligand framework. Our electronic structure calculations reveal that the reduced motion of low energy vibrations in the primary coordination sphere slows relaxation and increases T1. These principles enable us to report a new molecular qubit candidate with room temperature T2 = 0.43 μs, and establishes guidelines for designing novel qubit candidates operating above 100 K.
Elucidating the role of specific vibrational modes in spin lattice relaxation is a key step to designing room temperature qubits. We executed an experimental and theoretical study on a series of Cu2+ qubits to increase their operating temperature.
Introduction
The second quantum revolution is transforming our world with technological advances in many fields ranging from quantum computation, quantum communication, and quantum sensing.1–5 Progress in quantum information science (QIS) is driven by improvements in its foundational unit of information – the quantum bit (qubit). A qubit is a two-level system that exists in either of its two states or in an arbitrary superposition of them.2 Potential qubit candidates cover a wide range of materials, and take advantage of a myriad of quantum particles1 including Cooper pairs in superconductors,6–8 the nuclear states of trapped ions,9,10 and the polarization of photons.11,12 Electronic spins have demonstrated great promise as qubits for quantum sensing applications,13–16 because they combine strong coupling to the local environment with spatial precision to enable high resolution and high precision microscopy and metrology.17–21 Solid-state defect systems such as the anionic nitrogen-vacancy center are widely studied, owing in part to their long coherence times (described by the parameter T2) that persist to room temperature.22 In recent years, molecular electronic spins have emerged as a novel platform with atom-by-atom, bottom-up control over qubit structure and the local spin environment, allowing for direct control over qubit properties. The power of designer qubits has advanced molecular QIS on many fronts including: direct synthetic control over coherence times,23–26 scaling into multiqubit arrays,27–30 and incorporation of a designable optical interface.31 These studies paved the way for creating new molecular qubit candidates with millisecond coherence times, and approaches to integrate molecular qubits with device architectures for sensing.14,15 Historically, these results are primarily limited to low temperatures (<5 K). The coherence of few qubit candidates have maintained operationally useful coherence times (>0.2 μs) at elevated temperatures, with T2 falling off as temperature increases.32,33
This low temperature limitation prevents the investigation of molecular qubits in technologies they are otherwise well suited for, such as in vivo biological quantum sensors. In these devices, the high sensitivity of the electron coupled with atom-by-atom design of spin arrays would enable high precision detection of dangerous toxic agents, and nanoscale mapping of 3D protein structure.34–39 Unfortunately, few transition metal qubits remain measurable above 200 K, with substantially fewer remaining operable out to physiological temperatures.13,25,40–42 While T2 is largely considered temperature insensitive, it begins to decrease at higher temperatures due to a second parameter – the spin–lattice relaxation time T1. T1 represents the relaxation of a spin population from an excited state, such as a superposition state, back to thermal equilibrium.43,44 Since coherence cannot exist out of the superposition state, this places a fundamental limit on T2 where 2T1 ≥ T2.23 Unlike T2, T1 is strongly temperature dependent – decreasing as high coupling vibrational modes become more occupied at higher temperature.45–47 All quantum systems eventually reach the limit where 2T1 = T2 and T2 decreases with decreasing T1. Maximizing T2 at high temperatures requires maximizing T1.
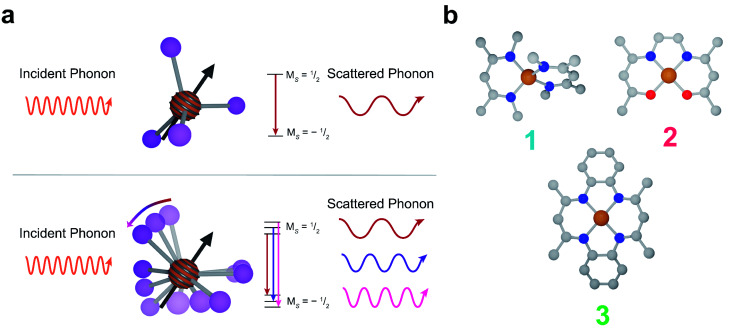
Spin–lattice relaxation arises from vibrational modes in the system facilitating the release of energy from a non-equilibrium spin population to return the system to equilibrium.48 Under standard experimental conditions, the energy gap between spin sublevels is less than 10 GHz (0.3 cm−1). The only pathway available for molecular systems to release such small energy quanta are low energy lattice modes called phonons. At low temperatures, phonons relax molecular spins through a scattering process where an incident phonon scatters off the spin, facilitating the release of energy. At higher temperatures, local molecular vibrations become thermally populated and distort the molecular geometry. This distortion increases electron spin relaxation by modulating Zeeman splitting (Fig. 1a).43,49–51
Fig. 1. (a) (Top) A representation of the phonon interactions in the Raman process. (bottom) A representation of phonon interactions in the local modes process. (b) Molecular structures of 1, 2, and 3. Grey, blue, red, and orange represent carbon, nitrogen, oxygen and copper, respectively. Hydrogen atoms are omitted for clarity. 1 is best described as pseudo-tetrahedral, whereas 2 and 3 are square planar.
Above the temperatures where molecular vibrations are thermally occupied, they are the predominant pathway for spin–lattice relaxation. The T1-limited regime of coherence for S = 1/2 systems typically occurs under local mode dominated relaxation. The impact of modifying vibrational modes, therefore, is felt most strongly at high temperatures. Restricting or modifying vibrations which cause relaxation allows us to control relaxation rates at these temperatures. In molecular qubits, our enhanced control over metal-coordination geometry and ligand structure gives us a direct method for controlling these local vibrational modes. Previous work has investigated the role of metal coordination geometry in V4+ electronic spin qubits.52,53 These studies found strong correlations between coordination complex geometry and spin–lattice relaxation rates. However, due to the localization of the unpaired electron in V+4 to a nominally nonbonding orbital (minimizing the spin delocalization onto the ligand),40,54 these studies were unable to address the role of ligand structure in relaxation rates.
In this report, we demonstrate deliberate control of the molecular vibrations in three molecular systems: bis(N,N′-dimethyl-4-amino-3-penten-2-imine) copper(ii) (Cu(Me2Nac)2 (1)),55,56 bis(acetylacetone)ethylenediamine copper(ii) (Cu(acacen) (2)),57 and tetramethyltetraazaannulene copper(ii) (Cu(tmtaa) (3))58–60 (Fig. 1b). Both 1 and 3 can be viewed as chemical modifications to 2. In 1, the breaking of an ethylene linker, as well as additional steric interaction through the presence of N-methyl groups enforces a distorted tetrahedral geometry. In contrast, 2 and 3 are locally square planar complexes. 3 maintains the same general structure of 2, but with additional rigidity imparted by increased π-conjugation and complete cyclization of the ligand. Additionally, by changing the spin active metal to Cu2+, we significantly increase the ligand delocalization of our electronic spin, allowing us to directly interrogate the role of ligand structure on relaxation.
Results and discussion
We first quantify the geometry of each complex through the τ4′ parameter, which represents the distortion of a four coordinate metal complex on a scale from 0 (square planar) to 1 (tetrahedral).61 The τ4′ value of 1 shows that it is pseudo-tetrahedral (τ4′ = 0.62). 2 and 3 are nearly perfectly square planar (τ4′ = 0.066 and 0.052 respectively). The relative rigidity of the molecules from weakest to strongest is 1 < 2 < 3 (Fig. S1†). The different geometries result in a weaker (less covalent) metal–ligand interaction and a lower energy singly occupied molecular orbital (SOMO) in 1 relative to 2 and 3 (Tables S8–S10†).62 The lower covalency in 1 compared to 2 and 3 is also reflected in their Cu–N bond lengths. 1 has an average Cu–N bond length of 1.955 Å, compared to the Cu–N bond length of 1.924 Å in 2 and 1.930 Å in 3. The decreased π rigidity, as well as the lack of a tethering functional group makes 1 the least rigid qubit candidate. 2 is more flexible than 1 due to a combination of stronger bonding and its tethering ethylene group. 3 is the most rigid of the three molecules due to rigidity from its π-conjugated ligand (Fig. S1†).
Next, we probed the magnetic structures of the three complexes using continuous-wave electron paramagnetic resonance (CW-EPR) spectroscopy. EPR spectroscopy tells us not only the energy of the Zeeman interaction, but also gives us important information about the strength of spin–orbit coupling (SOC) and orbital angular momentum (OAM) – two critical factors in determining how both lattice and molecular vibrations interact with a spin. SOC allows orbital perturbations (such as lattice phonons and molecular vibrations) to impact the spin moment. In the limit of zero SOC, orbital perturbations do not influence spins, and therefore vibrations cannot cause relaxation. The spin–orbit interaction is described by the term λ(Ŝ·L̂). In a crystal field, the d orbitals split in energy, and in the absence of OAM, L̂ is zero. In real molecular systems, second order OAM is recovered through the interaction between the molecular ground state with low energy excited states, allowing for a non-zero spin–orbit interaction. An in-depth understanding of how these systems should relax, therefore, necessitates an understanding of these parameters.
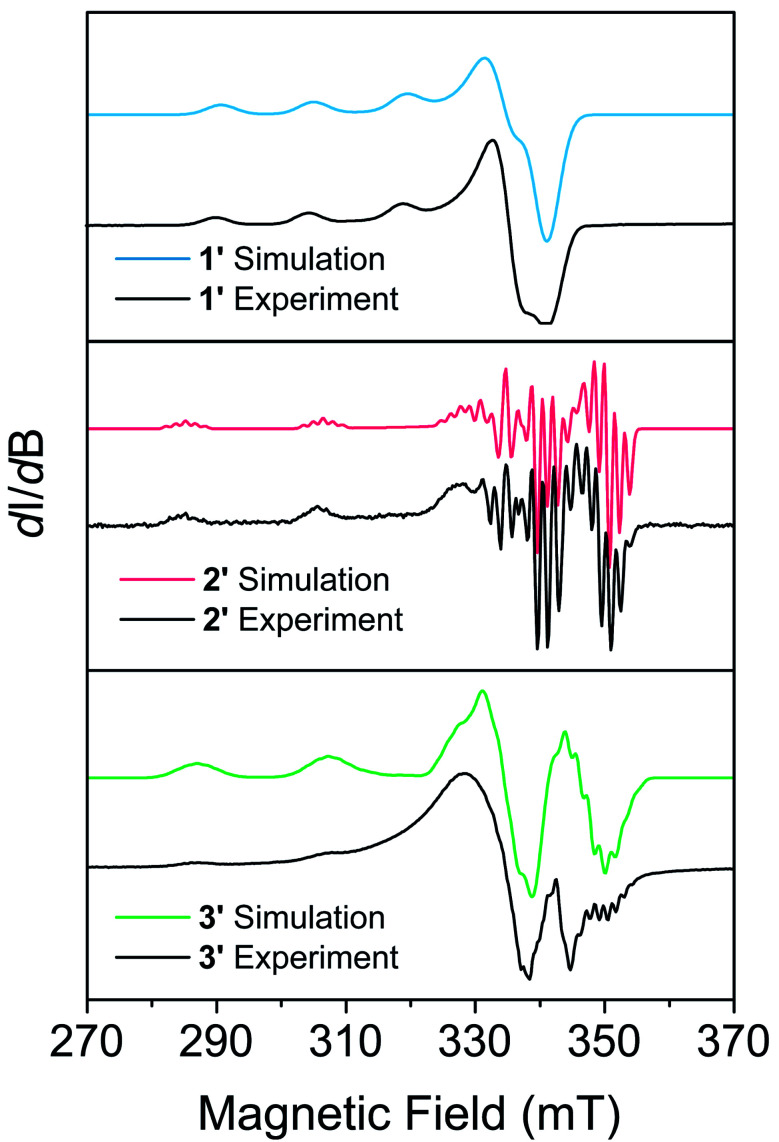
EPR measurements were performed on powder samples of 1–3 diluted to 1% by weight in a diamagnetic analogue (Zn(Me2Nac)2 (4) for 1, Ni(acacen) (5) for 2, and Ni(tmtaa) (6) for 3), denoted 1′–3′ respectively. Fig. 2 shows the CW-EPR spectra of 1′–3′ at 10 K. Simulations of all spectra were performed using a spin Hamiltonian Ĥ = gμBBS + IAS, where g is the g-tensor for the spin, μB is the Bohr magneton, B is the magnetic field, S is the electronic spin, I is a matrix with the nuclear spin of the metal and the atoms directly bound to the metal, and A is the nuclear hyperfine tensor, respectively, using the program Easyspin.63 Table S11† provides the parameters which best simulate the spectra for 1′–3′. Additional details on simulating CW-EPR spectra, and comments on the effects of broadening in our spectra, can be found in the ESI.† All three complexes are best simulated as axial copper systems such that gx = gy ≠ gz (for axial systems the equivalent gx = gy pair is termed g⊥ and the gz component is termed g∥) with hyperfine interactions from the copper and the nitrogen atoms. The parameters we obtain are comparable to other four-coordinate copper complexes in similar geometries.27,41,43 We see a clear dependence of g∥ on the geometry of our complexes: the square planar 2′ and 3′ are within simulation error (g∥ = 2.17(1) and g∥ = 2.175(1) respectively) and pseudo-tetrahedral 1′ is greater (g∥ = 2.205(5)). We attribute this to OAM contributions arising from a spin–orbit coupling effect that allows mixing with low-lying excited states.43 The aforementioned lower-lying excited states in 1′ mix more strongly, recovering more OAM and causing a greater deviation from the free electron g value. Coupled with the decreased rigidity around the metal center, we would expect 1′ to have more rapid spin–lattice relaxation (i.e. a shorter T1) than 2′ or 3′. 2′ and 3′ have similar OAM contributions, but the slightly increased rigidity of 3 makes it likely relax slower.25
Fig. 2. CW-EPR spectra of 1′–3′ taken at X-band (∼9.5 GHz), 10 K.
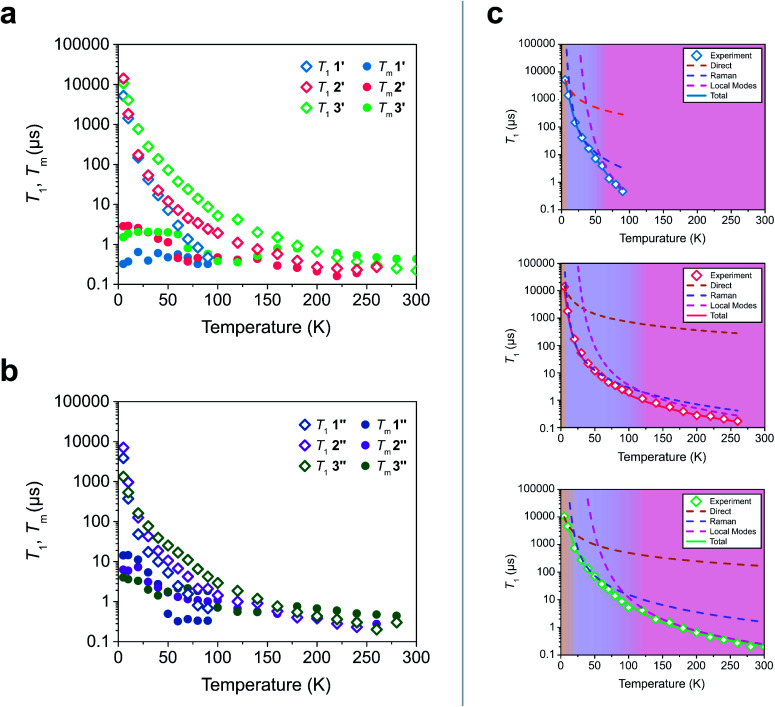
To test these hypotheses, we directly measured the relaxation dynamics of the three systems with pulse-EPR spectroscopy. We pulsed each system at its peak of maximum intensity in their echo-detected field swept EPR spectra (Fig. S10–S12†). As these measurements were performed on ensembles where each electron spin is not isolated from additional magnetic interactions (such as nearby electronic spins), measurement of an intrinsic T2 is not possible. We instead measure the phase memory time Tm, which is the decay constant for all sources of dephasing, not just spin–spin interactions.48 We wish to highlight that the previously described relationships between T1 and T2 are approximately true for T1 and Tm (namely Tm < 2T1). The T1 and Tm relaxation times across temperature for 1′–3′ are given in Fig. 3. As previously discussed, local vibrations and lattice vibrations both contribute to T1 relaxation. In order to deconvolute the impact of local vibrations and lattice vibrations, we compared all measurements performed on 1′–3′ to analogous systems made through dissolution in the room temperature glass ortho-terphenyl (OTP) denoted 1′′–3′′. A further discussion on the role the matrix plays in deconvoluting matrix effects can be found in the ESI.†
Fig. 3. (a and b) Relaxation time constants extracted from pulse-EPR spectroscopy for complexes diluted in a diamagnetic analogue (1′–3′) and in OTP (1′′–3′′). T1 was obtained through saturation recovery, wherein a train of short microwave pulses saturates the transition and the return to equilibrium is monitored. Tm was obtained through a two-pulse Hahn echo experiment, wherein coherence loss in the superposition state is monitored. (c) Fits of the T1 relaxation data for 1′–3′ to eqn (1). The shaded regions correspond to the process which is dominant in that temperature regime.
At low temperatures, trends in T1 depend most strongly on the matrix. The T1 of the crystalline solids (1′–3′) are all larger than the low temperature T1 of their amorphous glass analogues (1′′–3′′). Glasses have a higher density of low energy phonons, which have a better energy match to the Zeeman transition of the spin center and therefore promote faster relaxation in the phonon-dominated temperature regime.68–70 As temperature increases, the discrepancy between the matrices decreases, with the behaviour of each complex in both matrices hitting a near coalescence point (around 50 K for 1 and 2, and around 200 K for 3). The eventual near identical relaxation behaviour highlights the importance of the different types of vibrations in different temperature regimes: at low temperatures, the phonon modes of the matrix dominate relaxation behaviour. At high temperature, relaxation becomes dominated by molecular vibrations. Above 60 K, the T1 relaxation of 1′ and 1′′ becomes much faster than the relaxation of 2′–3′ or 2′′–3′′. By 80 K the T1 of 1′ and 1′′ are less than 1 μs whereas the T1 of 2′ and 2′′ are approximately 3.5 μs and the T1 of 3′ and 3′′ are both greater than 6 μs. By 100 K, the T1 of 1′ is undetectably fast (<0.15 μs). The T1 of 2′ and 2′′ remain measurable out to 260 K (T1 = 0.27 μs and T1 = 0.20 μs respectively). Similar to what was noted for Tm, the T1 of 3′′ remains measurable out to 280 K (T1 = 0.3 μs) but was undetectable at higher temperatures and the T1 of 3′ was measurable at room temperature (T1 = 0.22 μs). We note that in all six measured systems, the highest temperature at which coherence is measurable is limited by the T1 time of the system, as we would expect from the fundamental T2 < 2T1 limit, now applied to Tm.
Although 1 was the fastest relaxing qubit, as predicted from the recovered OAM, the large difference between 2 and 3 could not be understood from orbital momentum alone. As discussed previously, molecular vibrations provide additional mechanisms to relax the spin, but are only operative at high temperatures. The difference in the high temperature relaxation of 2 and 3 must then originate from these molecular vibrations. To gain insight into these high temperature dynamics, we modelled the temperature dependence of T1 to account for contributions from three relaxation processes: (1) the direct process, corresponding to single phonon emission, (2) the Raman process where an incident phonon scatters off of a spin center to facilitate relaxation, and (3) a local mode mediated process that occurs via modulation of magnetic parameters.71 In the literature, the terms “phonon” and “molecular vibration” are frequently used interchangeably. In order to better contextualize our discussion, we use the terms “phonon” and “lattice mode” to exclusively refer to lattice vibrations, whereas “molecular vibration” and “local mode” will exclusively refer to local molecular distortions. Understanding the different temperature regimes and energy scales of these two processes is imperative to understanding their role in relaxation. Molecular vibrations involved in the local modes process are specifically modulations of these phonon interactions. Therefore, we fit the relaxation data with the standard Debye model derived equation as follows:
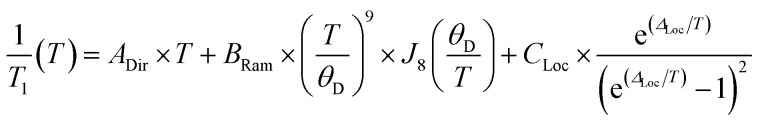 |
1 |
where ADir, BRam, and CLoc are the coefficients of the direct, Raman, and local modes processes, and are interpreted as weighting coefficients to represent the number of relaxation events caused by the process per unit time. Additional details of T1 fitting are provided in the ESI.†
Although ADir, BRam, and CLoc are best fit parameters, molecular correlations have been attributed to changes in these parameters as follows: ADir is associated with the low energy phonon density-of-states for a compound.48 Both Bram and CLoc arise from SOC interactions and second-order orbital momentum.48,72CLoc is additionally weighted by the spin–phonon coupling (SPC) of the various local vibrational modes.49 Since each local mode uniquely distorts the molecular geometry, each mode has a unique SPC coefficient representing its impact on spin relaxation. To prevent overparameterization of the system, we used a generalized local modes term, which is an average of all modes in the system weighted by their SPC (ΔLoc), and a generalized CLoc coefficient representing the average impact of all modes in ΔLoc.48,49ΔLoc is highly correlated with the rigidity of the metal–ligand bond, as well as ligand rigidity from π-conjugation.40,73ΘD is the Debye temperature of the matrix for the spin center, and scales the Raman process by the phonon energy of the matrix.44 In molecular systems, ΘD is not a true Debye temperature; it is better understood as a proxy for lattice phonon energy of the molecular crystal. Fits to the relaxation data for 1′–3′ are shown in Fig. 3c, and the fit parameters for these fits are given in Table 1 (fits and parameters for 1′′–3′′ can be found in the ESI† as well as a complete discussion on the differences in fit parameters between matrices). We limit the following discussion to the crystalline solids 1′–3′, but note that all discussed trends are also observed in 1′′–3′′.
Debye Model Fit Parameters for 1′–3′.
| 1′ | 2′ | 3′ | |
|---|---|---|---|
| A Dir | 39(4) | 13.8(4) | 18(1) |
| B Ram | 15(5) | 7(2) | 2.7(2) |
| Θ D | 75(10) | 63(8) | 81(4) |
| C Loc | 18.5(9) | 0.6(1) | 1.1(1) |
| Δ Loc | 290(40) | 213(25) | 328(15) |
Eqn (1) provides an excellent fit for the temperature-dependent relaxation of 1′, 2′, and 3′, as seen in Fig. 3. The Bram coefficients also reflect the information extracted from their CW-EPR spectra. 1′ experiences more second-order OAM from low lying excited states relative to 2′ and 3′, so it has a higher BRam. The BRam of 2′ and 3′ are similar, suggesting each exhibit similar OAM. This follows the expected trend based on ligand field strengths in the two complexes (Table S8–S10†). We find a similar trend in CLoc where CLoc of 1′ is significantly greater than 2′ and 3′ by one to two orders of magnitude (18.5 × 107 s−1 in 1′versus 0.6 × 107 s−1 in 2′ and 1.1 × 107 s−1 in 3′), also suggesting increased OAM.
Surprisingly, the ΔLoc parameter of 1′ (ΔLoc = 290 cm−1) is higher than that of 2′ (ΔLoc = 213 cm−1), despite 1 being the less rigid molecule. This implies that the rapid relaxation of 1′ is not driven by an abundance of low energy vibrational modes, but instead must be driven by the large OAM of 1′ driving inherently faster relaxation. The significant difference in high temperature relaxation between 1′ and 2′–3′ is then an effect of OAM by similar logic. The difference in relaxation between 2′ and 3′ cannot be explained through OAM, but it can be attributed to differences in molecular rigidity. The ΔLoc parameter of 3′ is the largest of the three complexes (328 cm−1), whereas the ΔLoc of 2 is the smallest (213 cm−1). This suggests that because 2 is more flexible than 3, the vibrations which cause relaxation are lower in energy. Therefore, they are thermally occupied at lower temperatures, and drive faster local mode mediated relaxation. Because the low energy of vibrational modes in 2 does not drive its relaxation to be faster than 1, but does drive its relaxation to be faster than 3, we conclude that OAM effects are the primary factor dictating molecular relaxation – a molecule with less OAM will tend to relax slower, independent of its vibrational mode energy. Vibrational mode energy, then, is a secondary factor in determining relaxation rates. Between two systems with competitive OAM values, the one with the larger vibrational mode energy will tend to have longer T1 times out to higher temperatures.
Though the preceding analysis gives us the ability to qualitatively describe the effects of the changes to molecular structure on relaxation, it is unable to give us any information about the specific vibrations which relax electronic spins. In order to gain insight into the individual and collective impact of the vibrational modes in each complex, we performed density-functional theory calculations from which we quantify SPC through changes in the g and A tensor from excitation of each vibrational mode.33,49,74 Although full ab initio calculation of T1 been demonstrated,49,75–78 we use a proxy that does not include the computationally expensive single phonon correlation function that is included in these more complex models to understand the mode dependencies. Our proxy is defined as a sum of the derivatives of each component of the g-tensor squared with respect to each normal mode weighted by their Bose–Einstein occupation integrated over the relevant temperature range from experiment as:
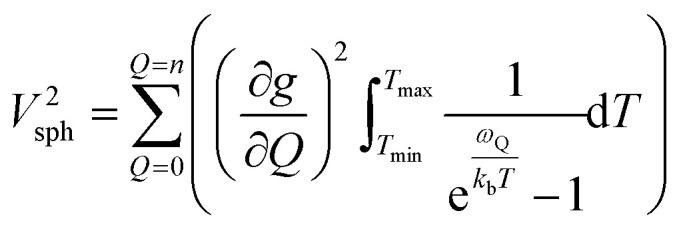 |
2 |
V 2 accounts for the impact of SPC by each mode using the thermodynamic occupancy of the mode at a given temperature. We emphasize that these calculations are performed on isolated single molecules. Therefore, the results of these calculations exclusively give us information about the modulation of relaxation rate from local mode distortions (i.e., relaxation from the local modes process).
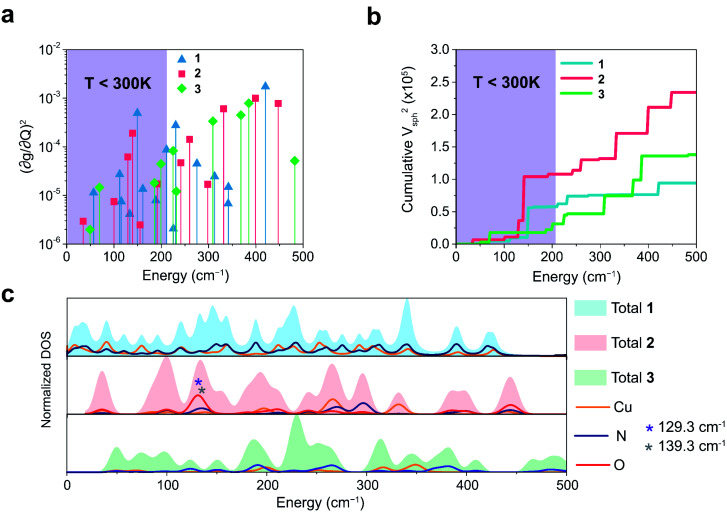
We plot both the SPC coefficient 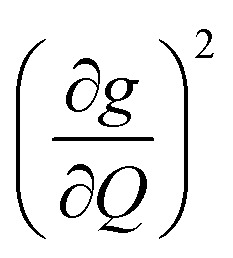 of each mode and the cumulative, thermally weighted SPC (V2sph) as a function of energy in Fig. 4a and b. We first note that these calculations support previous conclusions that local mode relaxation is driven primarily by a small number of very highly coupled vibrational modes (Fig. S25†).25,73,79 The vast majority of vibrational modes have little to no impact on relaxation (a near zero
of each mode and the cumulative, thermally weighted SPC (V2sph) as a function of energy in Fig. 4a and b. We first note that these calculations support previous conclusions that local mode relaxation is driven primarily by a small number of very highly coupled vibrational modes (Fig. S25†).25,73,79 The vast majority of vibrational modes have little to no impact on relaxation (a near zero 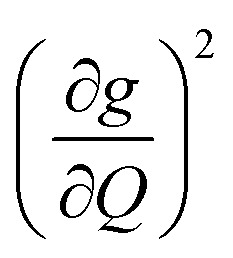 . In the energy range considered, each molecule has between three and four vibrational modes with
. In the energy range considered, each molecule has between three and four vibrational modes with 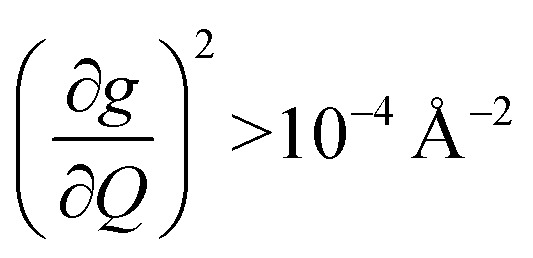 , and significantly more vibrations with orders of magnitude weaker coupling. Importantly, 3 has no thermally occupied vibrations above this cutoff by 300 K, whereas 1 and 2 both have a highly coupled mode in this low energy regime (in 1, 149.5 cm−1,
, and significantly more vibrations with orders of magnitude weaker coupling. Importantly, 3 has no thermally occupied vibrations above this cutoff by 300 K, whereas 1 and 2 both have a highly coupled mode in this low energy regime (in 1, 149.5 cm−1, 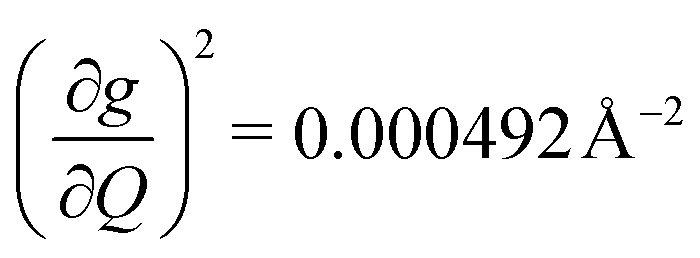 and in 2, 139.3 cm−1
and in 2, 139.3 cm−1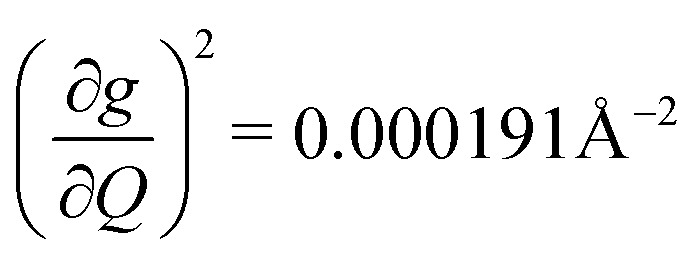 ). We find that 2 has the largest V2sph of all three complexes above 120 K, despite having measurable coherence out to significantly higher temperatures than 1. Additionally, two of the four most strongly coupled modes in 2 (399.1 cm−1,
). We find that 2 has the largest V2sph of all three complexes above 120 K, despite having measurable coherence out to significantly higher temperatures than 1. Additionally, two of the four most strongly coupled modes in 2 (399.1 cm−1, 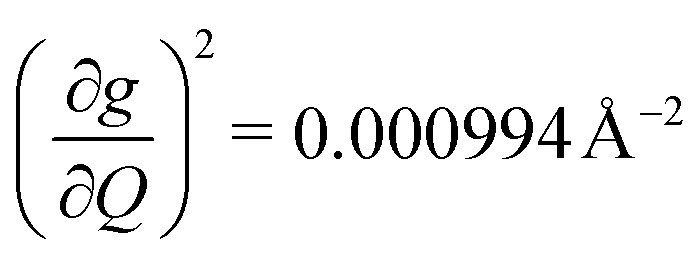 and 447.2 cm−1,
and 447.2 cm−1, 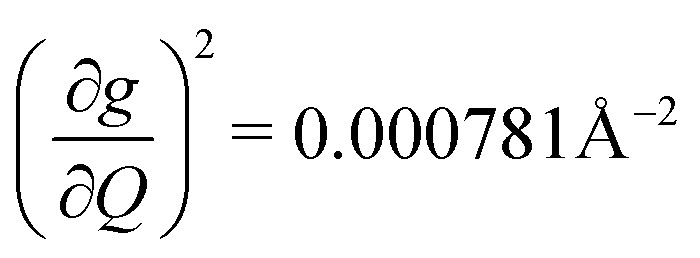 ) are higher in energy than the most coupled mode in 3 (385.0 cm−1,
) are higher in energy than the most coupled mode in 3 (385.0 cm−1, 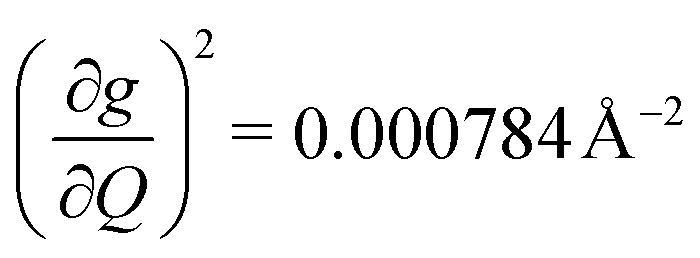 ). Rapid relaxation in 2, then, is likely driven by the lower energy modes with large SPC constants: 129.3 cm−1, and 139.3 cm−1,
). Rapid relaxation in 2, then, is likely driven by the lower energy modes with large SPC constants: 129.3 cm−1, and 139.3 cm−1, 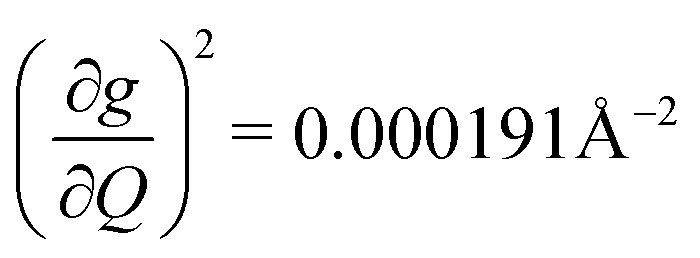 . These highly coupled low-energy modes are thermally occupied at much lower temperatures than the highly coupled modes in 3. These modes may also be responsible for the low ΔLoc of 2 – low energy vibrations with significant SPC contribute to relaxation at a lower temperature, and are therefore more impactful to relaxation than low thermal occupancy modes with slightly higher SPC coefficients. By extension, the observed slow relaxation in 3 is result of having no thermally occupied modes with significant coupling at 300 K.
. These highly coupled low-energy modes are thermally occupied at much lower temperatures than the highly coupled modes in 3. These modes may also be responsible for the low ΔLoc of 2 – low energy vibrations with significant SPC contribute to relaxation at a lower temperature, and are therefore more impactful to relaxation than low thermal occupancy modes with slightly higher SPC coefficients. By extension, the observed slow relaxation in 3 is result of having no thermally occupied modes with significant coupling at 300 K.
Fig. 4. (a) Spin–phonon coupling decomposed by vibrational mode into spin–phonon-coupling coefficient 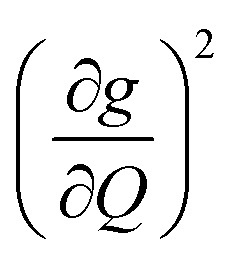 between 0 and 500 cm−1 (modes with
between 0 and 500 cm−1 (modes with 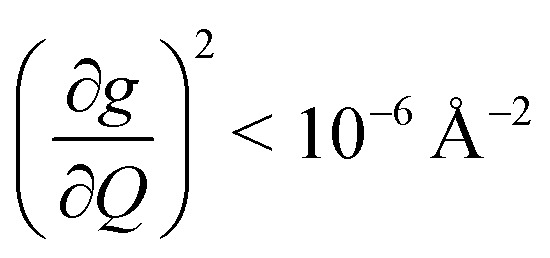 are omitted for clarity). Values are expressed in units of Å−2 (b) total SPC (cumulative) of all modes with increasing energy. Large increases in SPC generally occur stepwise, with single highly coupled modes contributing heavily to SPC. Values are expressed in units of Å−2. In both (a) and (b), the energy range below 300 K (208.5 cm−1) corresponding to modes thermally occupied at room temperature, is highlighted in purple (c) atom-resolved vibrational density-of-states (DOS) for 1–3.
are omitted for clarity). Values are expressed in units of Å−2 (b) total SPC (cumulative) of all modes with increasing energy. Large increases in SPC generally occur stepwise, with single highly coupled modes contributing heavily to SPC. Values are expressed in units of Å−2. In both (a) and (b), the energy range below 300 K (208.5 cm−1) corresponding to modes thermally occupied at room temperature, is highlighted in purple (c) atom-resolved vibrational density-of-states (DOS) for 1–3.
These results raise the question of why are there low energy modes in 2 to drive relaxation, but not in 3. To more deeply investigate this, we examined the atom-resolved partial vibrational density-of-states (PDOS) of 1–3 (Fig. 4c, more information can be found in the ESI†). These calculations decompose vibrational modes into the sum of atomic motion that comprises them and plots the amplitude of motion for each element in the molecule as a function of energy. The amplitude of each element's contribution to a mode then represents how much those atoms move during that particular vibration. For both 2 and 3, modes with large SPC coefficients also contain noticeably greater displacement of the primary coordination sphere (Cu, N, and O – represented by larger percentages of the DOS comprising these atomic motions) than other atoms in these complexes, with motions of the donor atoms (N and O) more strongly affected than the spin-bearing atom. Notably, the strongly coupled low-energy modes in 2 at 129.3 cm−1 and 139.3 cm−1 (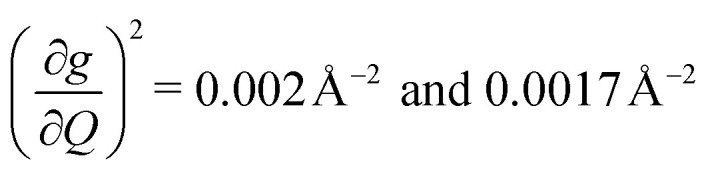 , respectively) mainly consist of motion in the untethered oxygen donor. This lack of tethering clearly allows a greater range of motion in the oxygen atoms (Fig. S29†), perturbing the local spin environment more, and resulting in faster relaxation. These two modes also appear to be responsible for the significant increase in V2sph, which also occurs at approximately 130 cm−1 (Fig. 4b).
, respectively) mainly consist of motion in the untethered oxygen donor. This lack of tethering clearly allows a greater range of motion in the oxygen atoms (Fig. S29†), perturbing the local spin environment more, and resulting in faster relaxation. These two modes also appear to be responsible for the significant increase in V2sph, which also occurs at approximately 130 cm−1 (Fig. 4b).
The increased π rigidity of 3 appears to be reflected in both shifting modes involving the primary coordination sphere to higher energy, as well as reducing the involvement of those atoms in the mode. In other words, the chemical rigidity “stiffens” the atoms involved in the mode, increasing the energy required to activate them and reducing the motion of the atoms when they do vibrate. The importance we place on modes involving the primary coordination sphere is well captured by viewing the modes in each complex with the highest 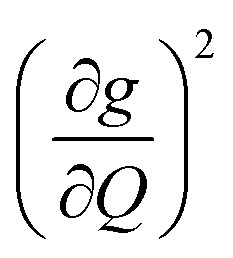 term (Fig. S30†). In each mode, we see distortions which heavily involve moving donor atoms and the copper spin center.
term (Fig. S30†). In each mode, we see distortions which heavily involve moving donor atoms and the copper spin center.
We continued these studies by probing Tm to gain insight into the coherence properties of these systems. Tm was measured with a Hahn echo decay sequence. In all systems, Tm relaxation is impacted by additional decohering effects from the nuclear spins in the local environment. We note that for all three complexes, Tm is longer in OTP solution than in the crystalline solid. In 2 and 3, these differences are relatively small, with the 5 K Tm of 2 increasing from 2.82 μs in 2′ to 6.20 μs in 2′′, and the 5 K Tm increasing from 1.49 μs in 3′ to 3.98 μs in 3′′. These slight improvements are in line with the low nuclear spin density of OTP.64 The Tm improvement in 1 between the two matrices is significantly larger, with the 5 K Tm of 1′ (0.32 μs) being nearly 2 orders of magnitude smaller than the 5 K Tm of 1′′ (14.1 μs). We attribute this to the large number of protons on the Me2Nac ligand, leading to a nuclear spin rich spin environment (Fig. S8†). In OTP solution, the space between Me2Nac molecules becomes significantly larger, and the nearest protons are rather found on the solvent phenyl groups as opposed to the methyl groups of nearby Me2Nac units, dramatically increasing Tm at low temperatures.65 Beginning at 40 K, the Tm of 1′′ approaches the relaxation rate of 1′, with the two time constants being effectively equal by 50 K, likely as a result of the thermal activation of methyl rotation.66 The Tm of 1′ has already been significantly restrained by the high nuclear spin density of its local environment, so the additional decohering effect of methyl rotation is only weakly felt. In 1′′ however, methyl rotation becomes the strongest decohering effect, drastically shortening Tm until it approaches the Tm of 1′. The effects of methyl rotation are also observed in 2′–3′ and 2′′–3′′.
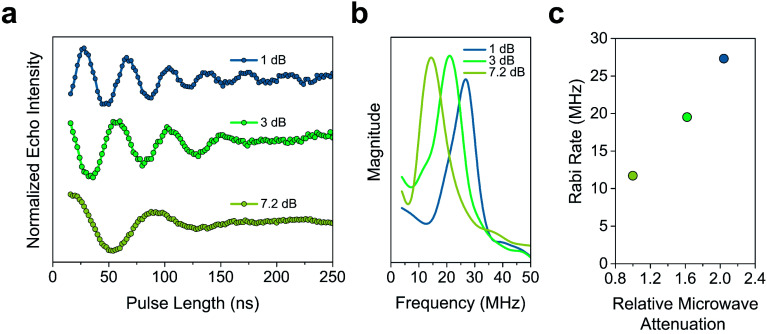
The Tm of 2′ and 2′′ begins to decrease around 40 K and continues to decrease until it becomes too short to measure at 240 K (Tm = 0.16 μs) and 260 K (Tm = 0.27 μs), respectively. In 3′ and 3′′ we observe the onset of methyl rotation beginning at 80 K. We believe the higher temperature onset of rotation in 3 is a result of the steric interaction between the methyl group and the ortho-proton on the phenyl ring.59 Interestingly, we observe a slight recovery of Tm beginning at 120 K (Tm = 0.36 μs and 0.55 μs respectively), until 160 K (Tm = 0.79 μs and 0.75 μs respectively), where relaxation becomes T1 limited and Tm decreases with decreasing T1. We attribute the recovery of Tm to methyl rotation becoming so rapid, that on the time scale of Tm for the electron spin, it begins to average out into background nuclear spin noise.48,53,67 Though the Tm of 3′′ is unmeasurable above 280 K (Tm = 0.44 μs), we were able to measure the Tm of 3′ up to 300 K (Tm = 0.43 μs). We also observed power dependent Rabi oscillations at 300 K (Fig. 5) – a hallmark of qubit operation demonstrating the superposition state of 3 can be manipulated at room temperature. Room temperature measurement of Tm in 3′ makes it one of a paucity of known transition metal coordination complexes with detectable coherence at these temperatures.13,25,29,40–42,67
Fig. 5. (a) Rabi oscillations of 3′ observed at 300 K at 3 different microwave attenuations. This hallmark of qubit behaviour demonstrates the continued operability of 3′, even at these high temperatures (b) Fourier transform of the 300 K Rabi oscillation in 3′. (c) Dependence of the Rabi rate of 3′ on the relative microwave attenuation at 300 K. The relative microwave attenuation is calculated relative to the weakest microwave power examined (7.2 dB).
Conclusions
These results demonstrate a framework to design and modify molecular qubit candidates for high temperature operation. Contrary to the discussion of ligand rigidity in the field previously, we find that π-rigidity provides only small improvements in T1. Instead, the largest improvements in T1 come from reduction of OAM through tuning geometry. The molecular geometry determines the energy of the molecular orbitals in the complex, with lower energy excited states reintroducing more OAM via the spin–orbit interaction. The extent of recovered OAM controls the strength of the interaction between the spin and the lattice and therefore the relaxation rate. Constraining the primary coordination sphere of the complex reduces the relaxation rate, but the net effect on relaxation is much smaller. While some of this is provided through increased π-rigidity, larger improvements are found from cyclizing the ligand. This implies there may be a wholly unexplored field of macrocyclic qubits that have previously been ignored by the field due to their lack of π-bonding. Design of future qubits for high temperature operation should focus on limiting OAM and SOC as their primary goal. Although 3 is a room temperature qubit candidate its T1 is still an order of magnitude below other known candidates, some of which display T1 > 1 μs out to room temperature.40,80 We hypothesize the comparatively shorter T1 of 3 may be the result of small differences in OAM at the metal center, offering a potential handle for future improvements. Synthetic chemistry provides us with the tools to manipulate the ligand field with the incredible precision to create the next generation of qubits based on this theoretical insight.
Notably the systems described herein are primed for integration with future qubit technologies. All three complexes are neutral, allowing for surface assembly via monolayer sublimation and potential investigation via STM-ESR.81,82 The long high temperature coherence times of 3 make it incredibly attractive to interface with a variety of different substrates to investigate the effects surface phonon modes have on relaxing molecular systems.83 This study lays the groundwork for these important future directions in the field.
Data availability
Crystallographic information can be found in the ICSD. The structures of optimized molecules used in density-functional theory calculations can be found at: https://github.com/MTD-group/Molecular_Qubit_Structures
Author contributions
Conceptualization: M. J. A., J. M. R., and D. E. F.; investigation and formal analysis: M. J. A., K. R. M., M. J. W., D. P. and M. K.W.; resources: L. S. and P. H. O.; visualization: M. J. A. and M. J. W.; supervision: D. E. F. and J. R. M.; all authors contributed to writing the manuscript.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
We are grateful for the intellectual discussions and scientific guidance provided by H. Mao, M. Krzyaniak, Drs K. Collins, M. Fataftah, S. Coste and S. v. Kugelgen. We thank H. Park for assistance with Raman spectroscopy. This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under award DE-SC0019356. M. J. A. thanks QISE-NET for support of the collaboration with Argonne National Laboratory. Mass spectrometry, NMR spectroscopy, and crystallography made use of the IMSERC at Northwestern University, which has received support from the NSF (CHE-1048773), Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF ECCS-1542205), the state of Illinois, and the International Institute for Nanotechnology (IIN). The Caltech EPR facility acknowledges support from the NSF (MRI grant 1531940) and the Dow Next Generation Educator Fund. This work used resources at the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Argonne National Laboratory's contribution is based upon work supported by Laboratory Directed Research and Development (LDRD) funding from Argonne National Laboratory, provided by the Director, Office of Science, of the U.S. Department of Energy under Contract No. DE-AC02-06CH11357.
Electronic supplementary information (ESI) available: Full experimental details, synthetic procedures, UV-Vis spectroscopy, IR spectroscopy, ESI mass spectrometry data, EPR spectroscopic details, X-ray crystallographic details, full computational details, and additional computational analysis. CCDC [2103567, 2103568, 2103569 and 2103570]. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d1sc06130e
References
- Degen C. L. Reinhard F. Cappellaro P. Quantum Sensing. Rev. Mod. Phys. 2017;89:1–39. doi: 10.1103/RevModPhys.89.035002. [DOI] [Google Scholar]
- DiVincenzo D. P. The Physical Implementation of Quantum Computation. Fortschr. Phys. 2000;48:771–783. doi: 10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E. [DOI] [Google Scholar]
- Liu X. Hersam M. C. 2D Materials for Quantum Information Science. Nat. Rev. Mater. 2019;4:669–684. doi: 10.1038/s41578-019-0136-x. [DOI] [Google Scholar]
- Morton J. J. L. Bertet P. Storing Quantum Information in Spins and High-Sensitivity ESR. J. Magn. Reson. 2018;287:128–139. doi: 10.1016/j.jmr.2017.11.015. [DOI] [PubMed] [Google Scholar]
- Ferrando-Soria J. Moreno Pineda E. Chiesa A. Fernandez A. Magee S. A. Carretta S. Santini P. Vitorica-Yrezabal I. J. Tuna F. Timco G. A. McInnes E. J. L. Winpenny R. E. P. A Modular Design of Molecular Qubits to Implement Universal Quantum Gates. Nat. Commun. 2016;7:1–10. doi: 10.1038/ncomms11377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gambetta J. M. Chow J. M. Steffen M. Building Logical Qubits in a Superconducting Quantum Computing System. Npj Quantum Inf. 2017;3:1–7. doi: 10.1038/s41534-016-0002-2. [DOI] [Google Scholar]
- Clarke J. Wilhelm F. K. Superconducting Quantum Bits. Nature. 2008;453:1031–1042. doi: 10.1038/nature07128. [DOI] [PubMed] [Google Scholar]
- Plantenberg J. H. De Groot P. C. Harmans C. J. P. M. Mooij J. E. Demonstration of Controlled-NOT Quantum Gates on a Pair of Superconducting Quantum Bits. Nature. 2007;447:836–839. doi: 10.1038/nature05896. [DOI] [PubMed] [Google Scholar]
- Monroe C. Kim J. Scaling the Ion Trap Quantum Processor. Science. 2013;339:1164–1169. doi: 10.1126/science.1231298. [DOI] [PubMed] [Google Scholar]
- Harty T. P. Allcock D. T. C. Ballance C. J. Guidoni L. Janacek H. A. Linke N. M. Stacey D. N. Lucas D. M. High-Fidelity Preparation, Gates, Memory, and Readout of a Trapped-Ion Quantum Bit. Phys. Rev. Lett. 2014;113:1–5. doi: 10.1103/PhysRevLett.113.220501. [DOI] [PubMed] [Google Scholar]
- Kok P. Munro W. J. Nemoto K. Ralph T. C. Dowling J. P. Milburn G. J. Linear Optical Quantum Computing with Photonic Qubits. Rev. Mod. Phys. 2007;79:135–173. doi: 10.1103/RevModPhys.79.135. [DOI] [Google Scholar]
- Slussarenko S. Pryde G. J. Photonic Quantum Information Processing: A Concise Review. Appl. Phys. Rev. 2019;6:1–19. [Google Scholar]
- Atzori M. Tesi L. Morra E. Chiesa M. Sorace L. Sessoli R. Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits. J. Am. Chem. Soc. 2016;138:2154–2157. doi: 10.1021/jacs.5b13408. [DOI] [PubMed] [Google Scholar]
- Moreno-Pineda E. Godfrin C. Balestro F. Wernsdorfer W. Ruben M. Molecular Spin Qudits for Quantum Algorithms. Chem. Soc. Rev. 2018;47:501–513. doi: 10.1039/C5CS00933B. [DOI] [PubMed] [Google Scholar]
- Bader K. Winkler M. Van Slageren J. Tuning of Molecular Qubits: Very Long Coherence and Spin–Lattice Relaxation Times. Chem. Commun. 2016;52:3623–3626. doi: 10.1039/C6CC00300A. [DOI] [PubMed] [Google Scholar]
- Perunicic V. S. Hill C. D. Hall L. T. Hollenberg L. C. L. A Quantum Spin-Probe Molecular Microscope. Nat. Commun. 2016;7:1–10. doi: 10.1038/ncomms12667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong S. Grinolds M. S. Pham L. M. Le Sage D. Luan L. Walsworth R. L. Yacoby A. Nanoscale Magnetometry with NV Centers in Diamond. MRS Bull. 2013;38:155–161. doi: 10.1557/mrs.2013.23. [DOI] [Google Scholar]
- Degen C. L. Scanning Magnetic Field Microscope with a Diamond Single-Spin Sensor. Appl. Phys. Lett. 2008;92:1–3. doi: 10.1063/1.2943282. [DOI] [Google Scholar]
- Balasubramanian G. Chan I. Y. Kolesov R. Al-Hmoud M. Tisler J. Shin C. Kim C. Wojcik A. Hemmer P. R. Krueger A. Hanke T. Leitenstorfer A. Bratschitsch R. Jelezko F. Wrachtrup J. Nanoscale Imaging Magnetometry with Diamond Spins under Ambient Conditions. Nature. 2008;455:648–651. doi: 10.1038/nature07278. [DOI] [PubMed] [Google Scholar]
- Fu C. C. Lee H. Y. Chen K. Lim T. S. Wu H. Y. Lin P. K. Wei P. K. Tsao P. H. Chang H. C. Fann W. Characterization and Application of Single Fluorescent Nanodiamonds as Cellular Biomarkers. Proc. Natl. Acad. Sci. U. S. A. 2007;104:727–732. doi: 10.1073/pnas.0605409104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thiel L. Wang Z. Tschudin M. A. Rohner D. Gutiérrez-Lezama I. Ubrig N. Gibertini M. Giannini E. Morpurgo A. F. Maletinsky P. Probing Magnetism in 2D Materials at the Nanoscale with Single-Spin Microscopy. Science. 2019;364:973–976. doi: 10.1126/science.aav6926. [DOI] [PubMed] [Google Scholar]
- Kennedy T. A. Colton J. S. Butler J. E. Linares R. C. Doering P. J. Long Coherence Times at 300 K for Nitrogen-Vacancy Center Spins in Diamond Grown by Chemical Vapor Deposition. Appl. Phys. Lett. 2003;83:4190–4192. doi: 10.1063/1.1626791. [DOI] [Google Scholar]
- Zadrozny J. M. Freedman D. E. Qubit Control Limited by Spin-Lattice Relaxation in a Nuclear Spin-Free Iron(III) Complex. Inorg. Chem. 2015;54:12027–12031. doi: 10.1021/acs.inorgchem.5b02429. [DOI] [PubMed] [Google Scholar]
- McInnes E. J. L. Timco G. A. Whitehead G. F. S. Winpenny R. E. P. Heterometallic Rings: Their Physics and Use as Supramolecular Building Blocks. Angew. Chem., Int. Ed. 2015;54:14244–14269. doi: 10.1002/anie.201502730. [DOI] [PubMed] [Google Scholar]
- Ariciu A. M. Woen D. H. Huh D. N. Nodaraki L. E. Kostopoulos A. K. Goodwin C. A. P. Chilton N. F. McInnes E. J. L. Winpenny R. E. P. Evans W. J. Tuna F. Engineering Electronic Structure to Prolong Relaxation Times in Molecular Qubits by Minimising Orbital Angular Momentum. Nat. Commun. 2019;10:1–8. doi: 10.1038/s41467-018-07882-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson J. N. Zhang J. Zhou J. Rugg B. K. Krzyaniak M. D. Wasielewski M. R. Effect of Electron-Nuclear Hyperfine Interactions on Multiple-Quantum Coherences in Photogenerated Covalent Radical (Qubit) Pairs. J. Phys. Chem. A. 2018;122:9392–9402. doi: 10.1021/acs.jpca.8b07556. [DOI] [PubMed] [Google Scholar]
- Yu C. J. Krzyaniak M. D. Fataftah M. S. Wasielewski M. R. Freedman D. E. A Concentrated Array of Copper Porphyrin Candidate Qubits. Chem. Sci. 2019;10:1702–1708. doi: 10.1039/C8SC04435J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zadrozny J. M. Gallagher A. T. Harris T. D. Freedman D. E. A Porous Array of Clock Qubits. J. Am. Chem. Soc. 2017;139:7089–7094. doi: 10.1021/jacs.7b03123. [DOI] [PubMed] [Google Scholar]
- Urtizberea A. Natividad E. Alonso P. J. Pérez-Martínez L. Andrés M. A. Gascón I. Gimeno I. Luis F. Roubeau O. Vanadyl Spin Qubit 2D Arrays and Their Integration on Superconducting Resonators. Mater. Horiz. 2020;7:885–897. doi: 10.1039/C9MH01594A. [DOI] [Google Scholar]
- Ardavan A. Bowen A. M. Fernandez A. Fielding A. J. Kaminski D. Moro F. Muryn C. A. Wise M. D. Ruggi A. McInnes E. J. L. Severin K. Timco G. A. Timmel C. R. Tuna F. Whitehead G. F. S. Winpenny R. E. P. Engineering Coherent Interactions in Molecular Nanomagnet Dimers. Npj Quantum Inf. 2015;1:1–7. [Google Scholar]
- Bayliss S. L. Laorenza D. W. Mintun P. J. Kovos B. D. Freedman D. E. Awschalom D. D. Optically Addressable Molecular Spins for Quantum Information Processing. Science. 2020;370:1309–1312. doi: 10.1126/science.abb9352. [DOI] [PubMed] [Google Scholar]
- Atzori M. Tesi L. Morra E. Chiesa M. Sorace L. Sessoli R. Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits. J. Am. Chem. Soc. 2016;138:2154–2157. doi: 10.1021/jacs.5b13408. [DOI] [PubMed] [Google Scholar]
- Mirzoyan R. Hadt R. G. The Dynamic Ligand Field of a Molecular Qubit: Decoherence through Spin-Phonon Coupling. Phys. Chem. Chem. Phys. 2020;22:11249–11265. doi: 10.1039/D0CP00852D. [DOI] [PubMed] [Google Scholar]
- Barry J. F. Turner M. J. Schloss J. M. Glenn D. R. Song Y. Lukin M. D. Park H. Walsworth R. L. Optical Magnetic Detection of Single-Neuron Action Potentials Using Quantum Defects in Diamond. Proc. Natl. Acad. Sci. U. S. A. 2016;113:14133–14138. doi: 10.1073/pnas.1601513113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucsko G. Maurer P. C. Yao N. Y. Kubo M. Noh H. J. Lo P. K. Park H. Lukin M. D. Nanometre-Scale Thermometry in a Living Cell. Nature. 2013;500:54–58. doi: 10.1038/nature12373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devience S. J. Pham L. M. Lovchinsky I. Sushkov A. O. Bar-Gill N. Belthangady C. Casola F. Corbett M. Zhang H. Lukin M. Park H. Yacoby A. Walsworth R. L. Nanoscale NMR Spectroscopy and Imaging of Multiple Nuclear Species. Nat. Nanotechnol. 2015;10:129–134. doi: 10.1038/nnano.2014.313. [DOI] [PubMed] [Google Scholar]
- Price J. C. Levett S. J. Radu V. Simpson D. A. Barcons A. M. Adams C. F. Mather M. L. Quantum Sensing in a Physiological-Like Cell Niche Using Fluorescent Nanodiamonds Embedded in Electrospun Polymer Nanofibers. Small. 2019;15:1–11. doi: 10.1002/smll.201900455. [DOI] [PubMed] [Google Scholar]
- Yu C. J. Von Kugelgen S. Laorenza D. W. Freedman D. E. A Molecular Approach to Quantum Sensing. ACS Cent. Sci. 2021;7:712–723. doi: 10.1021/acscentsci.0c00737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottscholl A. Diez M. Soltamov V. Kasper C. Sperlich A. Kianinia M. Bradac C. Aharonovich I. Dyakonov V. Room Temperature Coherent Control of Spin Defects in Hexagonal Boron Nitride. Sci. Adv. 2021;7(14):eabf3630. doi: 10.1126/sciadv.abf3630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fataftah M. S. Krzyaniak M. D. Vlaisavljevich B. Wasielewski M. R. Zadrozny J. M. Freedman D. E. Metal-Ligand Covalency Enables Room Temperature Molecular Qubit Candidates. Chem. Sci. 2019;10:6707–6714. doi: 10.1039/C9SC00074G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jing-Long D. U. Eaton G. R. Eaton S. S. Electron Spin Relaxation in Vanadyl, Copper(II), and Silver(II) Porphyrins in Glassy Solvents and Doped Solids. J. Magn. Reson., Ser. A. 1996;119:240–246. doi: 10.1006/jmra.1996.0079. [DOI] [Google Scholar]
- Bader K. Dengler D. Lenz S. Endeward B. Jiang S. Da. Neugebauer P. Van Slageren J. Room Temperature Quantum Coherence in a Potential Molecular Qubit. Nat. Commun. 2014;5:1–5. doi: 10.1038/ncomms6304. [DOI] [PubMed] [Google Scholar]
- Fielding A. J. Fox S. Millhauser G. L. Chattopadhyay M. Kroneck P. M. H. Fritz G. Eaton G. R. Eaton S. S. Electron Spin Relaxation of Copper(II) Complexes in Glassy Solution between 10 and 120 K. J. Magn. Reson. 2006;179:92–104. doi: 10.1016/j.jmr.2005.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann S. K. Lijewski S. Raman Electron Spin-Lattice Relaxation with the Debye-Type and with Real Phonon Spectra in Crystals. J. Magn. Reson. 2013;227:51–56. doi: 10.1016/j.jmr.2012.11.026. [DOI] [PubMed] [Google Scholar]
- Follmer A. H. Ribson R. D. Oyala P. H. Chen G. Y. Hadt R. G. Understanding Covalent versus Spin–Orbit Coupling Contributions to Temperature-Dependent Electron Spin Relaxation in Cupric and Vanadyl Phthalocyanines. J. Phys. Chem. A. 2020;124:9252–9260. doi: 10.1021/acs.jpca.0c07860. [DOI] [PubMed] [Google Scholar]
- Abragam A. and Bleaney B., Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, 1970 [Google Scholar]
- Lunghi A. Totti F. Sanvito S. Sessoli R. Intra-Molecular Origin of the Spin-Phonon Coupling in Slow-Relaxing Molecular Magnets. Chem. Sci. 2017;8:6051–6059. doi: 10.1039/C7SC02832F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eaton G. R. and Eaton S. S., Biological Magnetic Resonance, ed. Berliner L., Kluwer Academic Publishers, 2000, vol. 19 [Google Scholar]
- Escalera-Moreno L. Suaud N. Gaita-Ariño A. Coronado E. Determining Key Local Vibrations in the Relaxation of Molecular Spin Qubits and Single-Molecule Magnets. J. Phys. Chem. Lett. 2017;8:1695–1700. doi: 10.1021/acs.jpclett.7b00479. [DOI] [PubMed] [Google Scholar]
- Escalera-Moreno L. Baldoví J. J. Gaita-Ariño A. Coronado E. Spin States, Vibrations and Spin Relaxation in Molecular Nanomagnets and Spin Qubits: A Critical Perspective. Chem. Sci. 2018;9:3265–3275. doi: 10.1039/C7SC05464E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lunghi A. Sanvito S. How Do Phonons Relax Molecular Spins? Sci. Adv. 2019;5:1–8. doi: 10.1126/sciadv.aax7163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atzori M. Benci S. Morra E. Tesi L. Chiesa M. Torre R. Sorace L. Sessoli R. Structural Effects on the Spin Dynamics of Potential Molecular Qubits. Inorg. Chem. 2018;57:731–740. doi: 10.1021/acs.inorgchem.7b02616. [DOI] [PubMed] [Google Scholar]
- Yu C. J. Graham M. J. Zadrozny J. M. Niklas J. Krzyaniak M. D. Wasielewski M. R. Poluektov O. G. Freedman D. E. Long Coherence Times in Nuclear Spin-Free Vanadyl Qubits. J. Am. Chem. Soc. 2016;138:14678–14685. doi: 10.1021/jacs.6b08467. [DOI] [PubMed] [Google Scholar]
- Bechlars B. D'Alessandro D. M. Jenkins D. M. Iavarone A. T. Glover S. D. Kubiak C. P. Long J. R. High-Spin Ground States via Electron Delocalization in Mixed-Valence Imidazolate-Bridged Divanadium Complexes. Nat. Chem. 2010;2:362–368. doi: 10.1038/nchem.585. [DOI] [PubMed] [Google Scholar]
- Park K. H. Marshall W. J. Remarkably Volatile Copper(II) Complexes of N,N′-Unsymmetrically Substituted 1,3-Diketimines as Precursors for Cu Metal Deposition via CVD or ALD. J. Am. Chem. Soc. 2005;127:9330–9331. doi: 10.1021/ja051158s. [DOI] [PubMed] [Google Scholar]
- El-Zoghbi I. Ased A. Oguadinma P. O. Tchirioua E. Schaper F. One-Pot Synthesis of β-Diketimine Ligands. Can. J. Chem. 2010;88:1040–1045. doi: 10.1139/V10-109. [DOI] [Google Scholar]
- Tomažin U. Grošelj U. Počkaj M. Požgan F. Štefane B. Svete J. Combinatorial Synthesis of Acacen-Type Ligands and Their Coordination Compounds. ACS Comb. Sci. 2017;19:386–396. doi: 10.1021/acscombsci.7b00027. [DOI] [PubMed] [Google Scholar]
- Kim D. I. Kim E. H. Bae Z. U. Na H. G. Choi J. H. Park Y. C. Synthesis and Characterization of Nickel(II) and Copper(II) Complexes with Non-Symmetric Tetraaza[14]Annulene Derivatives. X-Ray Crystal Structure of Copper(II) Complex. J. Inclusion Phenom. 2004;49:107–113. doi: 10.1023/B:JIPH.0000031122.02399.c7. [DOI] [Google Scholar]
- Mountford P. Dibenzotetraaza[14]Annulenes: Versatile Ligands for Transition and Main Group Metal Chemistry. Chem. Soc. Rev. 1998;27:105–115. doi: 10.1039/A827105Z. [DOI] [Google Scholar]
- Andrews P. C. Atwood J. L. Barbour L. J. Croucher P. D. Nichols P. J. Smith N. O. Skelton B. W. White A. H. Raston C. L. Supramolecular Confinement of C60, S8, P4Se3 and Toluene by Metal(II) Macrocyclic Complexes. J. Chem. Soc., Dalton Trans. 1999;17:2927–2932. doi: 10.1039/A903669E. [DOI] [Google Scholar]
- Okuniewski A. Rosiak D. Chojnacki J. Becker B. Coordination Polymers and Molecular Structures among Complexes of Mercury(II) Halides with Selected 1-Benzoylthioureas. Polyhedron. 2015;90:47–57. doi: 10.1016/j.poly.2015.01.035. [DOI] [Google Scholar]
- Figgis B. and Hitchman M., Ligand Field Theory and Its Applications, Wiley-VHC, New York, 2000 [Google Scholar]
- Stoll S. Schweiger A. EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR. J. Magn. Reson. 2006;178:42–55. doi: 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
- Lin C. Y. Ngendahimana T. Eaton G. R. Eaton S. S. Zadrozny J. M. Counterion Influence on Dynamic Spin Properties in a V(IV) Complex. Chem. Sci. 2019;10:548–555. doi: 10.1039/C8SC04122A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graham M. J. Krzyaniak M. D. Wasielewski M. R. Freedman D. E. Probing Nuclear Spin Effects on Electronic Spin Coherence via EPR Measurements of Vanadium(IV) Complexes. Inorg. Chem. 2017;56:8106–8113. doi: 10.1021/acs.inorgchem.7b00794. [DOI] [PubMed] [Google Scholar]
- Tancredo A. Pizani P. S. Mendonca C. Farach H. A. Poole C. P. Ellis P. D. Byrd R. A. Spin-Rotation Relaxation Times at Different Temperatures for Methyl Compounds with Hindrance Barriers. J. Magn. Reson. 1978;32:227–231. [Google Scholar]
- Du J. L. Eaton G. R. Eaton S. S. Temperature and Orientation Dependence of Electron-Spin Relaxation Rates for Bis(Diethyldithiocarbamato)Copper(II) J. Magn. Reson., Ser. A. 1995;117:67–72. doi: 10.1006/jmra.1995.9971. [DOI] [Google Scholar]
- Takeno S. Gôda M. A Theory of Phonons in Amorphous Solids and Its Implications to Collective Motion in Simple Liquids. Prog. Theor. Phys. 2005;45:331–352. doi: 10.1143/PTP.45.331. [DOI] [Google Scholar]
- Huber D. L. Raman Contribution to the Homogeneous Optical Linewidth of Impurity Ions in Vitreous Silica. J. Lumin. 1987;36:327–329. doi: 10.1016/0022-2313(87)90206-7. [DOI] [Google Scholar]
- Huber D. L. Reassessment of the Raman Mechanism for Homogeneous Linewidths in Glasses. J. Non-Cryst. Solids. 1982;51:241–244. doi: 10.1016/0022-3093(82)90008-4. [DOI] [Google Scholar]
- Eaton S. S. Eaton G. R. Relaxation Mechanisms. eMagRes. 2016;5:1543–1556. [Google Scholar]
- Fielding A. J. Fox S. Millhauser G. L. Chattopadhyay M. Kroneck P. M. H. Fritz G. Eaton G. R. Eaton S. S. Electron Spin Relaxation of Copper(II) Complexes in Glassy Solution between 10 and 120 K. J. Magn. Reson. 2006;179:92–104. doi: 10.1016/j.jmr.2005.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atzori M. Benci S. Morra E. Tesi L. Chiesa M. Torre R. Sorace L. Sessoli R. Structural Effects on the Spin Dynamics of Potential Molecular Qubits. Inorg. Chem. 2018;57:731–740. doi: 10.1021/acs.inorgchem.7b02616. [DOI] [PubMed] [Google Scholar]
- Kazmierczak N. P. Mirzoyan R. Hadt R. G. The Impact of Ligand Field Symmetry on Molecular Qubit Coherence. J. Am. Chem. Soc. 2021;143:17305–17315. doi: 10.1021/jacs.1c04605. [DOI] [PubMed] [Google Scholar]
- Albino A. Benci S. Tesi L. Atzori M. Torre R. Sanvito S. Sessoli R. Lunghi A. First-Principles Investigation of Spin-Phonon Coupling in Vanadium-Based Molecular Spin Quantum Bits. Inorg. Chem. 2019;58:10260–10268. doi: 10.1021/acs.inorgchem.9b01407. [DOI] [PubMed] [Google Scholar]
- Reta D. Kragskow J. G. C. Chilton N. F. Ab Initio Prediction of High-Temperature Magnetic Relaxation Rates in Single-Molecule Magnets. J. Am. Chem. Soc. 2021;143:5943–5950. doi: 10.1021/jacs.1c01410. [DOI] [PubMed] [Google Scholar]
- Garlatti E. Chiesa A. Bonfà P. Macaluso E. Onuorah I. J. Parmar V. S. Ding Y. S. Zheng Y. Z. Giansiracusa M. J. Reta D. Pavarini E. Guidi T. Mills D. P. Chilton N. F. Winpenny R. E. P. Santini P. Carretta S. A Cost-Effective Semi-Ab Initio Approach to Model Relaxation in Rare-Earth Single-Molecule Magnets. J. Phys. Chem. Lett. 2021;12:8826–8832. doi: 10.1021/acs.jpclett.1c02367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briganti M. Santanni F. Tesi L. Totti F. Sessoli R. Lunghi A. A Complete Ab Initio View of Orbach and Raman Spin-Lattice Relaxation in a Dysprosium Coordination Compound. J. Am. Chem. Soc. 2021;143:13633–13645. doi: 10.1021/jacs.1c05068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warner M. Din S. Tupitsyn I. S. Morley G. W. Stoneham A. M. Gardener J. A. Wu Z. Fisher A. J. Heutz S. Kay C. W. M. Aeppli G. Potential for Spin-Based Information Processing in a Thin-Film Molecular Semiconductor. Nature. 2013;503:504–508. doi: 10.1038/nature12597. [DOI] [PubMed] [Google Scholar]
- Atzori M. Morra E. Tesi L. Albino A. Chiesa M. Sorace L. Sessoli R. Quantum Coherence Times Enhancement in Vanadium(IV)-Based Potential Molecular Qubits: The Key Role of the Vanadyl Moiety. J. Am. Chem. Soc. 2016;138:11234–11244. doi: 10.1021/jacs.6b05574. [DOI] [PubMed] [Google Scholar]
- Manassen Y. Averbukh M. Jbara M. Siebenhofer B. Shnirman A. Horovitz B. Fingerprints of Single Nuclear Spin Energy Levels Using STM – ENDOR. J. Magn. Reson. 2018;289:107–112. doi: 10.1016/j.jmr.2018.02.005. [DOI] [PubMed] [Google Scholar]
- Balatsky A. V. Nishijima M. Manassen Y. Electron Spin Resonance-Scanning Tunneling Microscopy. Adv. Phys. 2012;61:117–152. doi: 10.1080/00018732.2012.668775. [DOI] [Google Scholar]
- Hu L. Zhang L. Hu M. Wang J. S. Li B. Keblinski P. Phonon Interference at Self-Assembled Monolayer Interfaces: Molecular Dynamics Simulations. Phys. Rev. B: Condens. Matter Mater. Phys. 2010;81:1–5. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Crystallographic information can be found in the ICSD. The structures of optimized molecules used in density-functional theory calculations can be found at: https://github.com/MTD-group/Molecular_Qubit_Structures