Wide-Field Calcium Imaging of Dynamic Cortical Networks during Locomotion

Abstract

Motor behavior results in complex exchanges of motor and sensory information across cortical regions. Therefore, fully understanding the cerebral cortex’s role in motor behavior requires a mesoscopic-level description of the cortical regions engaged, their functional interactions, and how these functional interactions change with behavioral state. Mesoscopic Ca²⁺ imaging through transparent polymer skulls in mice reveals elevated activation of the dorsal cerebral cortex during locomotion_. Using the correlations between the time series of Ca²⁺ fluorescence from 28 regions (nodes) obtained using spatial independent component analysis (sICA), we examined the changes in functional connectivity of the cortex from rest to locomotion with a goal of understanding the changes to the cortical functional state that facilitate locomotion. Both the transitions from rest to locomotion and from locomotion to rest show marked increases in correlation among most nodes. However, once a steady state of continued locomotion is reached, many nodes, including primary motor and somatosensory nodes, show decreases in correlations, while retrosplenial and the most anterior nodes of the secondary motor cortex show increases. These results highlight the changes in functional connectivity in the cerebral cortex, representing a series of changes in the cortical state from rest to locomotion and on return to rest.

Introduction

Locomotion is one of the most fundamental classes of behavior in the animal kingdom. While much of the cyclic pattern of locomotion is generated by the central pattern generators in the spinal cord, the cerebral cortex plays a critical role in monitoring the constantly changing external world and adjusting the output of central pattern generators accordingly (for reviews, see Rossignol et al. 2006; Grillner and El Marina 2020). Motor and parietal cortical areas adjust locomotion in response to obstacles and sensory stimuli (Drew and Marigold 2015), while primary sensory cortical computations are altered, presumably to interpret relevant stimuli more effectively during locomotion (Schneider 2020). This suggests that the exchange of information between cortical regions is altered during locomotion, creating a distinct cortical functional state from rest. Indeed, new wide-field Ca²⁺ imaging techniques show that discrete movements cause widespread activation across the cerebral cortex, including regions not directly involved in motor control (Musall et al. 2019; Steinmetz et al. 2019), and this widespread activity contains mixed representations of sensory, motor, and behavioral states (Li 2015; Kauvar et al. 2020). This activation occurs in a wide range of contexts, including in instructed and uninstructed discrete movements, in locomotion, and across measurement modalities (Makino et al. 2017; Clancy et al. 2019; Musall et al. 2019; Kauvar et al. 2020). Clearly, no cerebral cortical region functions independently during movement (Harris 2005; Buzsaki 2010; Carrillo-Reid et al. 2016; Allen et al. 2017; Steinmetz et al. 2019; Musall et al. 2019).

As noted above, primary motor cortex (M1) plays a crucial role in the accurate placement of limbs during locomotion. M1 acts as the motor output for the cerebral cortex’s sensory and navigational computations by enacting required changes in gait. Lesioning M1 or the corticospinal tract produces locomotor deficits, including hypermetria and abnormalities in limb trajectory and intralimb coordination (Liddell and Phillips 1944). Pyramidal neuronal firing in M1 correlates with individual muscle activity during visually guiding locomotion (Drew, Andujar, et al. 2008a; Drew, Kalaska, et al. 2008b; Drew and Marigold 2015) and modulates when the subject maneuvers around an obstacle (Stout et al. 2015; Yakovenko and Drew 2015). Moreover, M1 layer V pyramidal neuron firing is modulated by the level of visual information available (Armer et al. 2013), emphasizing the importance of incoming sensory information in even motor output calculations. Much of this sensory information is integrated and relayed to M1 by the posterior parietal cortex (PPC). During locomotion, PPC is thought to integrate sensory information from multiple modalities (Beloozerova and Sirota 2003), aid in navigation (Shelley and Nitz 2021), and engage in movement planning (Mao et al. 2020). PPC is necessary for storing information of an upcoming obstacle (Marigold et al. 2011; Drew and Marigold 2015; Takakusaki 2017), and in the mouse, the homologous retrosplenial cortex shows increased correlation with sensory cortical regions during locomotion (Clancy et al. 2019). In discrete movements, PPC transforms both movement to sensory information and sensory to movement information (Buneo and Andersen 2006). PPC therefore appears to be a necessary player in the exchange of information in the cortex during locomotion.

Locomotion also involves the delivery of motor information to primary sensory regions to inform sensory neural processing. Spontaneous activity in somatosensory cortex increases during locomotion (Chapin and Woodward 1982; Favorov et al. 2015; Ayaz et al. 2019), while primary visual cortex increases in both spontaneous activity and in response to stimuli (Niell and Stryker 2010; Saleem et al. 2013; Lee et al. 2014; Dadarlat and Stryker 2017; Dipoppa et al. 2018). In contrast, primary auditory cortex decreases in activity (Schneider et al. 2014; Zhou et al. 2014; McGinley et al. 2015; Schneider and Mooney 2018). Notably, these changes in activity occur even in absence of a change in sensory stimuli (see Schneider 2020), and are independent of arousal level (Vinck et al. 2015), suggesting they are internally driven by the motor state (see Schneider 2020). It is likely these modulations reflect the brain’s reprioritizing of incoming stimuli to emphasize sensory modes that provide the most useful information to an animal in motion, since performance on visual and auditory discrimination tasks increases and decreases, respectively (Schneider et al. 2018; Tang and Higley 2020). Supporting this, pyramidal neurons in visual cortex that are driven by locomotion do so most strongly by unexpected stimuli (Keller et al. 2012). In the rodent, these modulations may come via direct connections from M1 (Zagha et al. 2013) and from upstream motor regions, including the secondary motor cortex (M2) (Schneider et al. 2014; Nelson and Mooney 2016; Leinweber et al. 2017).

In contrast to M1, PPC, and the primary sensory cortices, comparatively little is known about the functions of upstream motor cortical regions in locomotion (Drew and Marigold 2015). Activity in the human supplementary motor cortex is associated with postural changes that precede gait initiation, consistent with a role in locomotion initiation (Jacobs et al. 2009; Richard et al. 2017; Tsuru et al. 2020). In the cat, neurons in the premotor cortex discharge in response to an upcoming obstacle several steps before the obstacle is reached, indicative of planning gait modifications during locomotion (Nakajima et al. 2019). More is known about upstream motor cortical regions during discrete movements. Multimodal neurons in the nonhuman primate premotor cortex encode sensory stimuli occurring close to the body, which is then used to plan discrete movement trajectories executed by the primary motor cortex (Serino et al. 2011; Avenanti et al. 2012; Di Pellegrino and Ladavas 2015). This suggests upstream motor regions play an important role in utilizing sensory information to augment motor control, perhaps as an intermediate step between PPC and M1. In addition, since sensory regions may receive modulation from M2 (see above), upstream motor regions may also contribute to the reverse phenomenon, in which motor activity augments sensory processing. Interestingly, it has been found that M2 develops causal influence over activity in much of the cortex after a mouse learns a discrete motor task (Makino et al. 2017), and inactivation of M2 reduces cortical responses to sensory stimuli (Allen et al. 2017). This suggests M2 may have influence over nonmotor areas across the cerebral cortex. In rodents, M2 encompasses several subregions, such as the anterior lateral motor area, rostral forelimb area, and medial secondary motor cortex (Neafsey and Sievert 1982; Hira et al. 2013; Inagaki et al. 2018; Yang and Kwan 2020). The functions and boundaries of these subregions in locomotion are not well established.

Therefore, complex exchanges of information occur across the cerebral cortex during locomotion, both from sensory to motor regions and from motor to sensory regions. Fully categorizing the nature and organization of these information flows requires simultaneous monitoring of neuronal activity across the cortex. While developed only in the last decade, mesoscopic Ca²⁺ imaging is a powerful tool to simultaneously investigate the interactions among brain regions (for reviews, see Cardin et al. 2020; Ren and Komiyama 2021). Here, we examine the interactions among different cortical areas during the transition from rest to continued, steady-state locomotion using mesoscopic Ca²⁺ imaging across the entire dorsal cerebral cortex in head-fixed mice during spontaneous locomotion on a treadmill. We found that global increases in activity occur at initiation and then stabilize to a lower, but still elevated, level when the mouse reaches steady-state (continued) locomotion. Treadmill velocity accounts for up to 50% of the fluorescence modulation in individual regions. Analysis of the fluorescence activity between regions at different time periods, from rest to locomotion and back to rest, reveals an evolution in the patterns of cortical functional connectivity, as measured by correlation, centrality, and Granger causality. While not a measure of anatomical connectivity, functional connectivity is used widely to understand how brain regions interact during different behaviors (for reviews, see Bullmore and Sporns 2009; Damoiseaux and Greicius 2009; Hutchison et al. 2013; Bastos and Schoffelen 2015; Lurie et al. 2020). We found that steady-state locomotion is characterized by region-specific changes in region-to-region functional connectivity as compared with rest. In this state, premotor and retrosplenial regions increase in correlation and centrality, while primary motor, somatosensory, and parietal regions decrease. This steady-state pattern is bracketed by a distinct transition state at the start and termination of locomotion, in which most regions increase in functional connectivity before readjusting to the lower connectivity levels of the ongoing locomotion or rest state. During locomotion, the anterior regions in M2 alone show increases in outward Granger causality to many other regions, indicating they may play a role in facilitating motor and sensory computations across the cerebral cortex.

Materials and Methods

All animal studies were approved by and conducted in conformity with the Institutional Animal Care and Use Committee of the University of Minnesota.

Animals and Surgical Procedures

Eight (five male, three female) transgenic mice expressing GCaMP6f primarily in layers II/III and V excitatory pyramidal neurons of the cerebral cortex (C57BL/6J, Thy1-GCaMP6f Jackson Laboratories JAX 024339) were used (Dana et al. 2014). To obtain optical access to a large region of the dorsal cerebral cortex, we implanted morphologically conformant windows made from transparent polymer (Ghanbari et al. 2019). Prior to surgery, animals were administered slow-release buprenorphine (2 mg/kg, subcutaneous injection) and then anesthetized with isoflurane (5% induction, 0.5–3% maintenance). The head was shaved and mounted in a stereotaxic frame that did not damage the auditory meatus. Depth of anesthesia was monitored by toe pinch response every 15 min. Isoflurane levels were adjusted with respiration rate or if a response to pain was registered. Body temperature was maintained (37°C) using a feedback-controlled heating pad, and the corneas were protected with eye ointment. The surgical procedure began with excision of the scalp, followed by removal of the fascia so that the positions of lambda and bregma could be recorded. High-resolution images with a reference scale were captured both before and after securing the implant to the skull using a digital microscope camera (S01-0801A, Science Supply) attached to the surgical microscope to identify bregma after removing the skull. A manual craniotomy removed a flap of skull that matched the geometry of the implant window, leaving the dura intact. The implant was aligned to the craniotomy and fixed to the skull using a bone screw (F000CE094, Morris Precision Screws and Parts) placed 2–3 mm posterior to lambda. The implant periphery was glued to the skull (Vetbond, 3M) and cemented in place with dental cement (S380 S&B Metabond, Parkell Inc.). Following the cure of the cement, a custom, head-fixing titanium frame was fastened to the implant using three screws (3/32″ flat head 0–80). A second application of dental cement enclosed the fastening screws. After surgery, the mice recovered to an ambulatory state on a heating pad and then were returned to a clean home cage. Mice were administered meloxicam (2 mg/kg, s.c.) for three days and allowed a minimum of seven days to recover before any experimental procedures were initiated.

Behavioral Setup

Mice were housed in a reversed light–dark (12 h–12 h) room with experiments performed during the dark period, which is the normal waking and high activity phase of the circadian cycle in mice. After recovery from surgery, polymer window-implanted mice were habituated to the behavioral setup in increasing time increments (5 min, 15 min, 40 min, 1 h) before experiments began. For the behavioral setup, mice were head-fixed on a low-friction, horizontal disk treadmill that allowed for natural movements such as walking and grooming (Fig. 1A). Once habituated, animals alternated between periods of awake quiescence (i.e., rest) and spontaneous walking, which were used for spontaneous locomotion analysis. To offset any potential effects created by the mildly curved path of the disk treadmill, a subset (22 of 62) of experimental sessions were recorded with the mouse head-fixed to the disk pointing in the opposite direction. A high-speed, IR-sensitive CMOS camera (Flea3, Point Grey) recorded the limb and body movements at 40 Hz throughout a session, under diffuse infrared light that did not interfere with the Ca²⁺ imaging. Behavioral videos were recorded using Spinnaker SDK software (FLIR Systems).

Figure 1.

Mesoscopic cortical recording setup and activity during locomotion. (A) Experimental setup for behavioral and Ca²⁺ fluorescence imaging of head-fixed mice. (B) Approximate cortical regions, as defined by the Allen Brain Atlas Common Coordinate Framework (Allen Institute for Brain Science 2015), observable through the polymer skull (inset) by epifluorescence microscopy. Scale bar = 1 mm. Common Framework colors correspond to cortical regions defined in key. (C) Treadmill velocity (bottom, blue line) is plotted for an example of spontaneous locomotion in a single mouse. Preprocessed maps of cortical activity (top) shown as mean subtracted % change in fluorescence (∆F/F). For visualization only, frames were spatially filtered with a 3 × 3 moving mean and averaged across five frames. Gray dashed lines link maps of cortical Ca²⁺ fluorescence with time points prior to, during, and after locomotion. (D) Markers used to track paw positions during periods of rest and locomotion for this example data. Blue, front left paw (FL); red, front right paw (FR); orange, hind left paw (HL). (E) Horizontal (top) and vertical (bottom) paw displacements versus time during rest. (F) Horizontal (top) and vertical (bottom) paw displacements versus time during locomotion. Maximum displacement of each paw (inset, arrows) shows stereotypic, repeating step-cycles.

Locomotion kinematics were calculated from the treadmill angular displacement as measured by a high-resolution rotary encoder and recorded by an Arduino Uno microcontroller (Arduino) at 1 kHz. Velocity was determined and smoothed using a sliding average (100 ms window, 1-ms step size). Locomotion was defined as periods of movement in which the wheel reached a velocity of 0.25 cm/s or greater. Working back from 0.25 cm/s, movement onset was then defined as the time wheel velocity first exceeded 0 cm/s, and movement offset was defined as the time velocity returned to 0 cm/s. Periods in which velocity remained between −0.25 and 0.05 cm/s were labeled as rest, while all remaining periods were discarded as “fidgeting” or backwards walking. During rest, visual observation confirmed that the mice were awake but quiet. The horizontal and vertical positions of all four paws were tracked and extracted from the behavioral camera recordings using DeepLabCut behavior tracking software (Mathis et al. 2018). The position of the left forepaw was chosen for further analysis as it was the most visible in the behavioral camera’s field of view and most accurately tracked. The other paws were not included in the final results because of lower quality tracking data and because their movements are highly correlated to the left forepaw, therefore not providing additional information to the regression analysis of the fluorescence data with forepaw velocity (see below). Paw position was only included in further analysis if the DeepLabCut tracking was of high quality (confidence >70%). The horizontal and vertical velocities were calculated as the absolute change in pixels over time and down sampled to 20 fps to align with fluorescence data. Total paw velocity was calculated as the magnitude of the vector sum of the horizontal and vertical velocities. Note that as the view of the infrared camera was not perfectly parallel to the main axis of paw motion, this measure of velocity will not be exact and should be considered an estimate of paw velocity.

Fluorescence Imaging

Head-fixed mice were placed on the treadmill beneath a Nikon AZ-100 microscope (Fig. 1A). Single-photon fluorescence imaging was performed using a high-speed, electron multiplying CCD (Andor, iXon3) controlled with MetaMorph (Molecular Devices Inc.). A filter set with 480/20 nm excitation, 505 nm dichroic, and 535/25 nm emission filters was used (Chroma). Using the variable magnification function, the field-of-view was adjusted to image the exposed dorsal cortical surface (6.2 mm × 6.2 mm) with a spatial resolution of 256 × 256 pixels (pixel size of ~24.2 μm × 24.2 μm). Images were acquired at 20 Hz, 20 ms exposure, for 5 min (6000 frames), and 12 imaging trials were obtained in a session (i.e., the number of trials obtained in 1 day). Time between imaging trials ranged between 1 and 5 min. As the imaging modality was single-photon, the Ca²⁺ fluorescence signals are primarily from the excitatory neuronal activity in layers II/III (Yizhar et al. 2011; Ma et al. 2016; Waters 2020).

Fluorescence Imaging Analysis

The Ca²⁺ fluorescence data from each imaging session was spatially registered using affine transformations. Consistent points on the visible blood vessels in the brain were manually selected and aligned using the built-in MATLAB function, fitgeotrans, with the “affine” method selected. All sessions were registered to the same representative session for a mouse. To remove motion artifacts within trials, all frames were registered to subpixel precision using the dftregistration MATLAB function (Guizar-Sicairos et al. 2008). To remove artifacts potentially introduced through increased overall fluorescence or through blood flow and blood vessel constriction or dilation, masks were drawn over representative sections of background and blood vessels. The mean activity was taken from each of these masks, and the activity of each pixel was regressed against these traces. Only the residuals from these regressions were kept for further analysis, thus removing from the fluorescence signals contributions of background fluorescence and blood flow.

To reduce the dimensions of the data to a manageable level and decrease noise, we performed spatial independent component analysis (sICA) to identify a catalog of functionally relevant cortical regions. For each mouse, images from all trials were concatenated and compressed using singular value decomposition (SVD). Only the first 200 singular values were used to recreate the spatial dimension of the data (Musall et al. 2019). We computed the first 50 spatial independent components (ICs) using the Joint Approximation Diagonalization of Eigenmatrices (JADE) algorithm that decomposes mixed signals into ICs by minimizing the mutual information with a series of Givens rotations (Cardoso 1999; Makino et al. 2017; Sahonero-Alvarez and Calderon 2017). This method provides a blind segmentation of the cerebral cortex based only on statistical properties of the Ca²⁺ activity and does not use any prior assumptions regarding cerebral function or architecture. Masks of ICs were made by setting intensity values below 3.5 equal to 0. Masks covering less than 150 contiguous pixels or that, upon visual inspection, corresponded to artifacts not associated with cortical activity were discarded. This included vascular artifacts that survived the regression step above. An IC that included multiple discontinuous areas, such as homotopic cortical regions, was separated into individual ICs, and these individual ICs were used in subsequent analyses. All remaining IC masks were visually inspected, and any remaining area corresponding to blood vessels that were not separated from cortical activity were manually identified and removed. To group data across animals, ICs in each mouse catalog were manually assigned to 1 of 28 nodes of interest (14 per hemisphere) that were present in the majority of mice and corresponded, approximately, to known cortical regions based on the Common Coordinate Framework (Fig. 2) (Allen Institute for Brain Science 2015).

Figure 2.

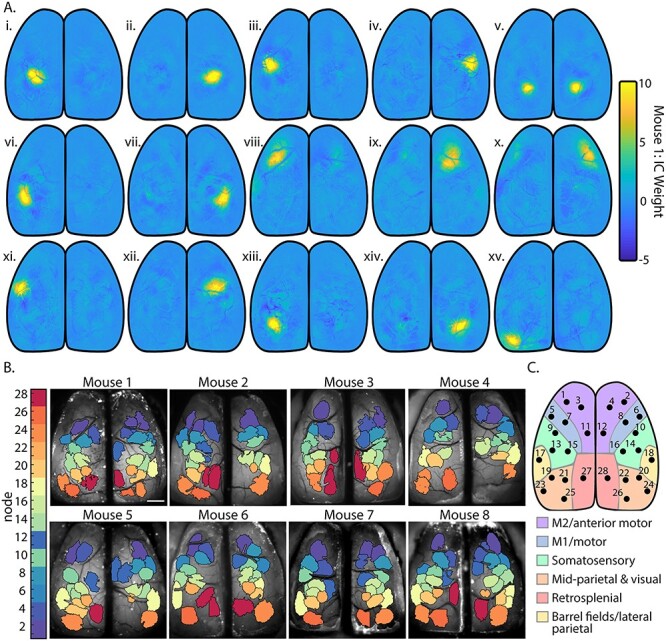
Spatial segmentation of the dorsal cerebral cortex using sICA. (A) Fifteen ICs representing cortical activity from mouse 1 calculated using JADE ICA, before thresholding and manual artifact removal. (B) IC catalogs of each mouse after thresholding and manual artifact removal. Color corresponds to the node identity assigned to each one of the 28 common ICs found across mice as shown in C. (C) Locations of the 28 common ICs that define the network nodes observed across mice mapped onto the Common Coordinate Framework (Allen Institute for Brain Science 2015).

Behavior Periods

Recordings were divided into six behavior periods, each 3 s in duration, as defined by treadmill velocity (see Figs 3B and 4A): 1) rest (see definition above); 2) prelocomotion (rest just prior to locomotion onset; “prep.”); 3) initiation of locomotion (locomotion just after locomotion onset; “init.”); 4) continued locomotion (periods of steady-state, continued locomotion outside of transition periods; “cont.”); 5) termination of locomotion (locomotion just prior to locomotion offset; “term.”); and 6) postlocomotion (rest just after locomotion offset; “after”). Periods of rest or continued locomotion that lasted longer than 3 s were divided into multiple 3-s segments, and remainder data at the end of the period was removed. Periods less than 3 s were also removed. We chose 3-s periods (60 time points) because this provides sufficient data to calculate robust Pearson correlations on the associated fluorescence time series for the functional connectivity analysis (see below). For the subsequent analyses (linear regression, functional connectivity, and Granger causality) of the fluorescence signals, all computations are based on the data from the individual 3-s periods, followed by averaging of the results for each behavior period.

Figure 3.

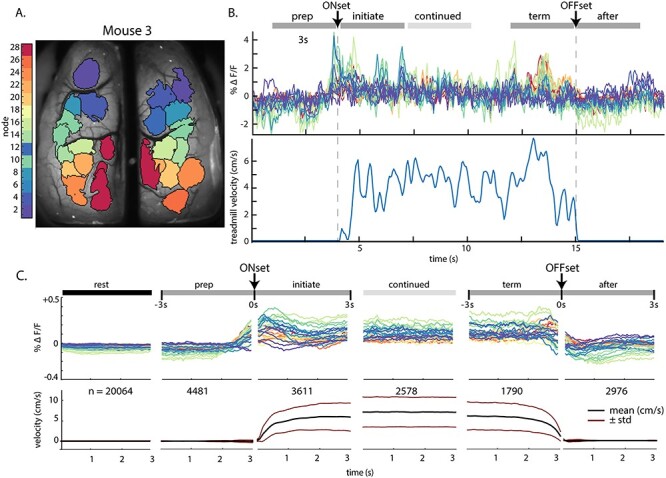
Fluorescence activity (∆F/F) within ICs across behavior periods. (A) IC catalog of mouse 3, as shown in Figure 2B. (B) Top: Example fluorescence time series from each IC for a single bout of locomotion in mouse 3, with the timeline of five of the six behavior periods on top. Bottom: corresponding treadmill activity. (C) Top: Fluorescence activity from the common set of 28 nodes averaged over all mice and across all instances of each 3-s behavior period (n = number of periods averaged). Abbreviations: pre., prelocomotion; initiate., initiation of locomotion; continued, continued locomotion; term., termination of locomotion; after, after locomotion. Bottom: Mean (black lines) and SD (red lines) of treadmill velocity across each behavior time period for all mice.

Figure 4.

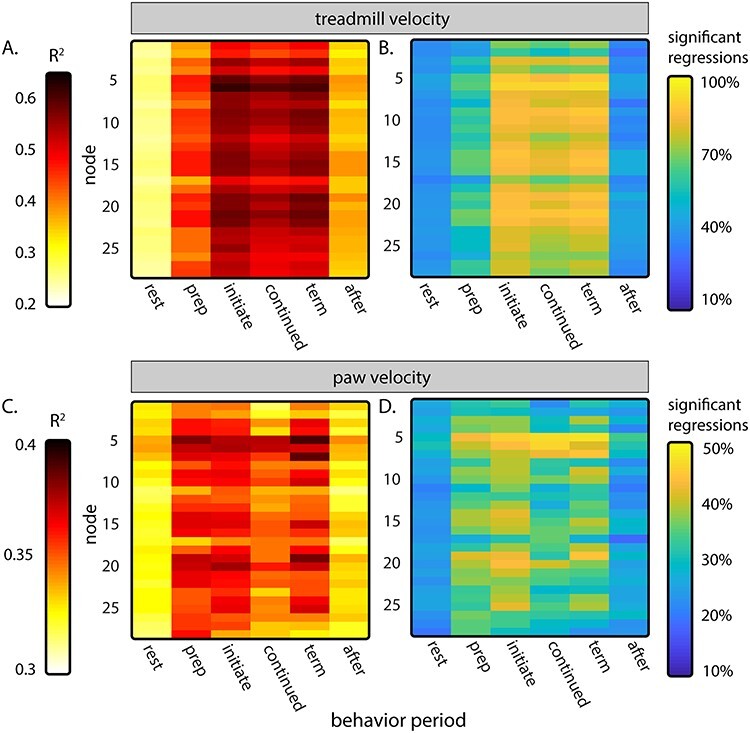
Average results of node fluorescence activity regressions against treadmill velocity (A and B) and velocity of the left front paw (C and D). (A) Average R² of regressions of fluorescence activity against treadmill velocity for each behavior period. (B) Percent of regressions preformed for each 3-s period in A that reach significance. (C) Average R² of fluorescence regressions activity against the velocity of the front left paw in each behavior period. (D) Percent of regressions in C that reach significance.

Regression of Fluorescence Activity against Treadmill and Paw Velocity

The masks from the IC catalog for each mouse were used to extract mean fluorescence time series (based on the preprocessed series of image data) for each 5-min trials. The resulting time series were linearly detrended and divided into individual 3-s behavior periods. To determine how fluorescence activity in each node modulated with the parameters of locomotion, linear models were used to regress the fluorescence activity of each node to the treadmill velocity and to the velocity of the left forepaw. Because brain activity and behavior are not necessarily aligned in time, the velocity of the treadmill and left paw were shifted in time relative to the fluorescence activity and included in the regression models as independent predictors (see Fig. 4). Shifts in time (“lags”) extended from 500 ms before fluorescence activity to 1.0 s after, in intervals of 100 ms, for a total of 16 predictors in a regression, plus an intercept predictor. Note that, since the fluorescence activity is assigned to a specific 3-s behavior period and does not vary in time, velocity from before or after the behavior period is included in the regression (i.e., the preparation period fluorescence will be regressed to treadmill velocity from up to 1.0 s of the initiation period). Separate regressions were also performed for each lag individually (Supplementary Fig. 1) to clarify how fluorescence activity and behavior are related in time. The R² values and statistical significance (F-test, α < 0.05) were calculated for each instance of a behavior. The R² values were averaged for each behavior period over all trials and then across animals. All regressions were calculated using the MATLAB built-in regress function.

Functional Connectivity Analysis

For each 3-s period, the correlation coefficients (ρ) were calculated between the time series from all catalog ICs to generate a correlation (i.e., adjacency) matrix, and the matrices obtained from each 3-s period were averaged to create mean adjacency matrices for each behavior period per mouse. To combine data across animals, the averaged correlations were assigned to the appropriate corresponding node. If more than one catalog IC had been assigned to a node, then the correlation values of those catalog ICs were averaged. The mean adjacency matrices were then averaged across the subjects. For each pair of regions, the significant change in correlation of activity between behavior periods was calculated using custom MATLAB code. The difference in correlation was compared with a null distribution of differences from 500 reshufflings of the correlations across behavior. Significance was determined by α < 0.05 corrected with the false discovery rate (Genovese et al. 2002).

To further quantify the functional relationships between brain regions during locomotion, the network centrality of ICs was calculated on 3-s correlation matrices using MATLAB code from the Brain Connectivity Toolbox (Rubinov and Sporns 2010). The eigenvector centrality was calculated from the correlation adjacency matrices for each 3-s period and averaged within each mouse before being averaged across mice. Similar to the comparisons among the correlations between regions, the difference in eigenvector centrality for each region from one period to another was compared with a null distribution of differences from 500 reshufflings of the centralities across behavior. Again, significance was determined by α < 0.05 corrected with the false discovery rate.

Since it is possible that large, global increases or decreases in fluorescence activity could increase correlation coefficients between nodes and obscure more subtle changes in connectivity, an additional analysis was performed in which low-frequency changes in fluorescence activity were removed using a 5^th order high-pass Butterworth filter with a cutoff filter of 2 Hz. The filter was applied to the mean fluorescence time series extracted from the IC masks for each mouse. Correlation and eigenvector centrality calculations were repeated on the filtered data as described above.

Granger Causality Analysis

Granger causality among the nodes was determined as a measure of the directional influence between cortical regions during different behavior periods. We used the Multivariate Granger Causality MATLAB Toolbox (Barnett and Seth 2014), with the ordinary least squares model estimation and regression information criteria and the Akaike information criterion (AIC) model order. The model was limited to a maximum of 20 lags. For each animal, the time series from all instances of a 3-s behavior period were inputted to the algorithm as separate trials to generate a single, multivariate causality adjacency matrix for each mouse. These individual adjacency matrices were averaged across mice as described above. Granger causality estimates the causality between time series in both directions. In order to have a single directional value representing the net relationship between two regions, a “total causality” value was calculated based on the difference in magnitude of the corresponding causalities. In adjacency matrices, total causality direction is indicated as a positive or negative value. Significant changes in causality between behavior periods were determined similar to the approach used for significant changes in correlation and centrality. The difference in causality and total causality from one period to another between each pair of ICs was compared with a null distribution of differences from 500 reshufflings of the causalities across behavior. Significance was determined by α < 0.05 corrected with the false discovery rate.

Hemodynamic Correction

Blood flow increases with neuronal activation, and oxygenated blood absorbs light with peak absorption at ~530 nm, decreasing the duration of the increased GCaMP fluorescence (Ma et al. 2016). Therefore, additional experiments were performed to evaluate the effects of hemodynamics and other Ca²⁺-independent fluorescence changes such as flavoprotein autofluorescence (Vanni and Murphy 2014; Jacobs et al. 2020), using three mice (one from the original cohort and two additional). Data were collected in 5-min stacks, similar to the primary dataset. Data were collected in 36 stacks across 3 recording days for mouse #8, 35 stacks across 8 days for mouse #9, and 68 stacks across 12 days for mouse #10, for a total of 11.58 hours of data. We used dual-wavelength illumination to capture both Ca²⁺-dependent (470 nm, blue light) and Ca²⁺-independent (405 nm, violet light) GCaMP6f signals on consecutive frames using a Cairn OptoLED driver (Cairn OptoLED, P1110/002/000; P1105/405/LED, P1105/470/LED) (Ma et al. 2016; Allen et al. 2017; Jacobs et al. 2020; Musall et al. 2019; MacDowell and Buschman 2020). An excitation filter (ET480/40, Chroma) was placed in front of the 470 nm LED and then both light sources were combined into the parallel light path of a Nikon AZ100M macroscope through a dichroic mirror (425 nm, Chroma T425lpxr), which was reflected off a second dichroic (505 nm, Chroma T505pxl) to the brain. Cortical GCaMP6f emissions then passed back through the second dichroic into an sCMOS camera (Andor Zyla 4.2 Oxford Instruments). Exposure times for each frame were 18 ms, synced via TTL pulses from a Cambridge Electronics 1401 (Cambridge Electronic Design Limited) acquisition system that controlled both LEDs and the external trigger of the Andor Zyla 4.2. Frames were captured at 40 Hz (20 Hz per channel) at 256 × 256 pixels per image.

Using a previously described correction method (Ma et al. 2016; Jacobs et al. 2020; MacDowell and Buschman 2020), the Ca²⁺-independent signals were removed by first calculating the per-pixel average intensity in both channels and then scaling the 405-nm channel to a similar level of the 470-nm channel by multiplying by the ratio of the per-pixel averages. The scaled 405-nm signal was then subtracted from the 470-nm signal and the resulting signal was then normalized by dividing by the scaled 405-nm signal. All subsequent processing, including sICA, functional connectivity, and network measures, was identical to that preformed on the mono-wavelength, uncorrected data.

All MATLAB analysis codes for sICA segmentation of mesoscale Ca²⁺ imaging, eigenvector centrality, and hemodynamic correction are available upon request.

Results

Database

We collected imaging data from eight Thy1-GCaMP6f transgenic mice. Eight imaging sessions were performed on seven of the animals, while six imaging sessions were performed on the remaining animal, resulting in a total of 62 sessions. During each imaging session, we obtained 60 min of data (12 trials × 5 min each), resulting in 480 min of imaging in seven mice and 360 min in one mouse. Mice spent an average of 75.7 ± 10.5% of recording time at rest, 21.3 ± 10.4% locomoting, 2.2 ± 0.9% fidgeting, and 0.9 ± 0.4% of recording time moving backwards. Across the eight mice, we fully analyzed a total of 2743 min of rest and 776 min of spontaneous locomotion.

Changes in Ca²⁺ Fluorescence during Behavior

Mice were head-fixed over a disk treadmill that allowed for spontaneous locomotion (Fig. 1A), and wide-field Ca²⁺ imaging was performed through an implanted polymer skull (Ghanbari et al. 2019) (Fig. 1B). Regions across the dorsal cerebral cortex show dynamic changes activity as the mouse transitions from rest to locomotion and back to rest (Fig. 1C). For each animal, spontaneous locomotion exhibits an alternating and rhythmic step-cycle typical of coordinated walking (Fig. 1D–F).

Functional Segmentation of the Cortex

We segmented cortical activity into functionally distinct regions based on changes in Ca²⁺ fluorescence using sICA, a blind source separation tool commonly used in fMRI studies (Cardoso 1999; Makino et al. 2017; Sahonero-Alvarez and Calderon 2017). By minimizing the mutual information between regions to segment the cortex, sICA does not make assumptions about the underlying neuroanatomy of individual animals. The processed fluorescence datasets yield 22–31 spatial ICs per mouse, with 28 ICs in common across mice. As an example, 15 individual ICs from a single mouse are shown in Figure 2B. The entire, thresholded IC catalogs for each animal are shown in Figure 2C. Across the IC catalogs, 28 ICs were the most consistent and approximately equivalent across the majority of the 8 mice (Fig. 2B,C). These 28 common ICs were mapped onto the Common Coordinate Framework (Fig. 2C) and are the nodes in the following cortical network analyses. Though there are considerable similarities in the IC catalogs across the eight mice, individual differences in functional anatomy are preserved with this method.

Fluorescence Activity during Behavioral Transitions

To analyze the functional connectivity of the cortex during the transitions between rest and locomotion, we extracted the average of the fluorescence time series from each IC in relation to the six behavioral periods (see Materials and Methods), as shown for an individual bout of walking in a mouse (Fig. 3A, B) and for the average data across all animals (Fig. 3C). At the transition from rest to walking, most nodes exhibit an increase in activity prior to locomotion that peaks around locomotion onset (Fig. 3C). The increases in fluorescence include nodes in primary motor regions, primary sensory areas (including somatosensory and visual cortices), and throughout posterior parietal and retrosplenial areas. This agrees with previous reports of motor, somatosensory, parietal, auditory, retrosplenial, and visual cortical engagement during locomotion (Drew, Kalaska, et al. 2008b; Niell and Stryker 2010; Petersen et al. 2012; Saleem et al. 2013; Favorov et al. 2015; Drew and Marigold 2015; Schneider and Mooney 2018; Clancy et al. 2019) and highlights the involvement of multiple cerebral cortical regions in processing and integrating information related to locomotion. In all regions except the most anterior nodes, this increase begins 784 ± 201 ms before the onset of locomotion by an increase greater than the mean + 2.5 SD of the fluorescence at rest. Nodes 1 and 2, in contrast, decrease in mean fluorescence. Throughout locomotion, average neural activity remains elevated compared with rest and decreases to baseline levels on return to rest (Fig. 3C). This pattern of fluorescence changes was present in all mice.

Regressions of Fluorescence Activity to Parameters of Locomotion

To quantify the degree to which the parameters of locomotion are represented in the Ca²⁺ signals, the fluorescence activity of each node was regressed to treadmill velocity and to the velocity of the left forepaw, revealing widespread encoding of these parameters across the cerebral cortex (Fig. 4). Treadmill velocity explains a large amount of the variability in fluorescence activity in all nodes during the preparation, initiation, continued, and termination periods (Fig. 4A). The strongest correlations occur during the initiation and termination periods, with somewhat smaller average R² values during the continued period. Nodes 5 and 6 (in approximately the lateral primary motor cortex) have the strongest relationship to treadmill velocity (reaching average R² > 0.60 during initiation and termination), while the average R² of secondary motor cortical nodes 1 and 2 remain somewhat lower than most other nodes (average R² < 0.50 during initiation, continued, and termination periods). The percent of the total number of regressions that reached significance was highest for the initiation, continued, and termination periods (F(16, 58) > 1.82, α < 0.05, Fig. 4B). Regressions against individual time lags of treadmill velocity confirm these findings (F(1, 58) > 4.01, α < 0.05, Supplementary Fig. 1A,B). In the preparation period, fluorescence activity in most nodes is significantly correlated with treadmill velocity, leading by 300–600 ms (reflecting the large increase in fluorescence 200–300 ms before the increase in treadmill velocity shown in Fig. 3C). This continues through the initiation period before, interestingly, decreasing during the continued period.

The R² again rises across the cortex in the termination period, with fluorescence leading the treadmill velocity by 200–500 ms. Nodes 1 and 2 as well as nodes 17 and 18 have somewhat lower R² than others.

The velocity of the left forepaw explains some of the variability of the fluorescence activity during walking, but less than the overall treadmill velocity, with a smaller percentage of the regressions reaching significance (F(16, 58) > 1.82, α < 0.05; Fig. 4C,D; note the different color axis range compared with A and B). Like treadmill velocity, there is significant correlation in the preparation, initiation, and termination periods, with less during continued locomotion. As expected, nodes 5 and 6 show some of the strongest correlation to paw velocity. Regressions against individual time lags show only weak relationships between fluorescence activity and paw velocity, with the strongest R² occurring during the preparation and termination periods (F(1, 58) > 4.01, α < 0.05; Supplementary Fig. 1C,D). Regressions were also performed with the addition of the right forepaw velocity, but there was no notable improvement over the left paw only in average R² or in percent significant regressions (data not shown). While the low R² values and fraction of periods with significant modulation in relation to forepaw velocity are not unexpected, given the slow time course of Ca²⁺ signal relative to the step-cycle, the results provide evidence for widespread step-cycle modulation. We acknowledge that parameters potentially correlated with locomotion, for example, effort, are not disambiguated in these analyses and could contribute to the regression results. Still, these regression findings highlight that across much of the dorsal cerebral cortex Ca²⁺ fluorescence activity modulates with specific aspects of locomotion.

Correlations between Nodes

To understand the functional coupling among the ICs during these transitions, we defined six behavioral periods related to locomotion, each 3 s in length: 1) rest, 2) prelocomotion, 3) initiation of locomotion, 4) continued locomotion, 5) locomotion prior to termination, and 6) rest after termination of locomotion (see Materials and Methods and Fig. 3B,C). As stated earlier, functional connectivity is a widely used approach across neural recording modalities to understand the interactions among regions within the nervous system but does not directly imply structural connectivity (Bullmore and Sporns 2009; Damoiseaux and Greicius 2009; Greicius et al. 2009; Hutchison et al. 2013; Bastos and Schoffelen 2015; Lurie et al. 2020). Within each 3-s behavior period for a mouse, the Pearson correlation (ρ), as commonly used in determining functional connectivity, was calculated between the fluorescence time series for each possible pair of ICs. The resulting correlation coefficients were averaged across all instances of the behavior period in that mouse and then averaged across mice using the 28 common nodes. Each node’s mapping to the Common Coordinate Framework is shown again in Figure 5A. The average correlation coefficients between nodes were plotted as both correlation matrices and network graphs (Fig. 5B). Across behavior periods, there is a prominent intrahemispheric effect, in which nodes of the same hemisphere are more strongly correlated with each other than with nodes in the opposite hemisphere (note the “checkerboard” pattern of the correlation matrices). In addition, nodes that are anatomically adjacent tend to show high correlation. For example, nodes located in the parietal cortex (9–22) exhibit especially high connectivity, except for nodes 17 and 18 in the lateral parietal area that are approximately equivalent to the barrel fields. Similarly, the nodes in the premotor, primary motor, and visual cortices have high internal functional connectivity within and across hemispheres. Qualitatively, there is a general decrease in functional connectivity during movement initiation that persists through the termination of locomotion, followed by an increase in correlations after movement.

Figure 6.

Significant changes in correlations between nodes across behavior periods. (A) Matrix of significant changes in correlation between nodes comparing rest to continued locomotion (α < 0.05, permutation test with false discovery rate correction). (B) Significant increases (left) and decreases (right) from rest to continued locomotion shown in graph representations, superimposed on the cortical surface. The size of each node reflects the magnitude of significant increases or decreases, respectively, for that region. (C) Significant changes in correlations across sequential behavior periods, calculated and displayed as in A and B. Directly above each correlation matrix, the gray bracket indicates the adjacent behavior periods being compared (i–vi).

Figure 5.

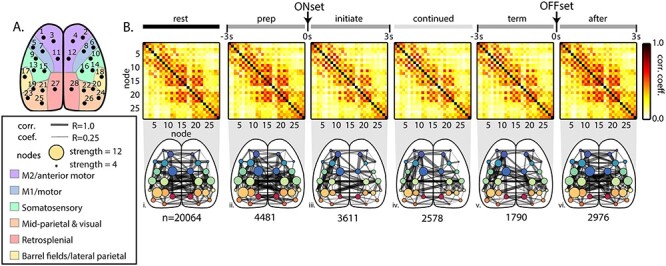
Functional connectivity among the common cortical nodes during behavior periods across all mice. (A) Diagram of nodes common to the catalog ICs across mice mapped onto the Common Coordinate Framework (Allen Institute for Brain Science 2015). (B) Top: Averaged correlation matrices between nodes across all mice. Bottom: Graphical representation of the correlation matrices shown above superimposed on the dorsal cortical surface. Width of connecting edges indicates the Pearson correlation coefficient (ρ ≥ 0.25). The size of the node reflects the strength; that is, the sum of all correlations with that node. n = number of 3-s time periods included in each behavior period across animals.

We used a permutation test with false discovery rate correction to evaluate the significant changes in mean correlations between nodes, both increases and decreases, between behavior periods (Fig. 6). Compared with rest, continued locomotion exhibits general decreases in correlation with important exceptions (Fig. 6A,B). Unexpectedly, nodes within M1 (5–10) decrease in correlation with most other regions including with homologous nodes in the contralateral hemisphere (82 of a possible 162 connections). However, there are some increases in correlation among nodes within M1 (12 of a possible 30 connections) between intrahemispheric nodes. Also, nodes within the primary somatosensory cortex exhibit decreases in correlations widely. There are two prominent patterns of increased functional connectivity. First, nodes (1–4) in M2 show increases in connectivity with visual and retrosplenial regions as well as increases with other parietal regions (49 of 108 possible connections). Second, retrosplenial nodes 27 and 28 exhibit large increases with regions across the cortex (35 of 54 possible connections). Other than for nodes in M1, the changes in correlation tend to be similar both within and across hemispheres.

Next, we evaluated the significant changes in correlations across sequential behavior periods. From rest to the prelocomotion period, functional connectivity increases between many nodes, with large increases in the nodes located in visual and somatosensory regions to those in other regions, with the strongest increases involving the retrosplenial nodes (Fig. 6Ci). In contrast, correlations between the anterior M2 nodes and many other nodes significantly decrease (18 of 54 possible connections). Nodes within M1 (5 and 6) show decreases in correlation with somatosensory nodes (9, 10, and 13–16; 8 of 12 possible connections). During initiation of locomotion compared with prelocomotion, correlations increase between the two most anterior nodes (1 and 2) in the M2 region and nodes in nearly all other regions (Fig. 6Cii; 32 of 54 possible connections). However, the correlations between anterior M2 nodes (1 and 2) and primary motor nodes (5–10) significantly decrease (8 of 12 possible connections). Correlations decrease between nodes in most other regions, with primary motor, somatosensory, and parietal nodes exhibiting large decreases. As the animal transitions from the initiation of locomotion to continued locomotion, correlations across much of the dorsal cortex continue to decrease (Fig. 6Ciii). These patterns reverse as the animal progresses through the termination of locomotion and postlocomotion periods to rest (Fig. 6Civ–vi), with striking increases in functional connectivity across the dorsal cortex with the termination of locomotion and a widespread decrease as the animal returns to rest. A similar pattern of significant changes in network correlations across behavior periods was observed in individual animals, as shown for two example mice in Supplementary Figure 2. Again, except for M1 nodes, the changes in correlation tend to be similar both within and across hemispheres.

It is possible that the large shift in overall fluorescence activity occurring during different behavior periods (Fig. 3C, top) may be the main contributor to the changes in correlations between nodes and may obscure more subtle changes in connectivity. To investigate this possibility, we removed these low-frequency fluorescence shifts by applying a high-pass filter with a 2Hz cutoff frequency to the average IC time series extracted from the fluorescence images from each individual trial (Supplementary Fig. 3). Filtering eliminates the large magnitude changes in fluorescence at the start and the termination of locomotion, as shown for a single instance of walking (Supplementary Fig. 3A; the same instance of walking shown unfiltered in Fig. 3B) and in the averaged fluorescence time series across all instances of each behavior period (Supplementary Fig. 3B). Notably, the patterns of changes in correlations across behavior periods remain intact, as observed in the adjacency matrices and network diagrams (Supplementary Fig. 3C–F), both for the comparison of rest versus continued locomotion (Supplementary Fig. 3C,E) and for comparisons between adjacent behavior periods (Supplementary Fig. 3D,F). Therefore, global changes in fluorescence amplitude do not dictate the dynamic patterns of functional connectivity that occur from rest to locomotion and with return to rest.

Eigenvector Centrality during Behavioral Transitions

To further characterize the changes in network structure, we calculated the mean eigenvector centrality of nodes within each behavior period and compared how centrality changed across periods. Eigenvector centrality provides a measure of how tightly connected the behavior of a node is to all other nodes in the network (Rubinov and Sporns 2010). The average eigenvector centrality across all mice, for each node and behavioral period (Fig. 7A), shows the overall importance of different nodes. For example, somatosensory and parietal nodes show high centrality during rest, preparation, and after periods. During locomotion periods, the centrality of these regions generally decreases with other nodes increasing in importance. Therefore, we determined the significant changes in centrality from rest to continued locomotion and between adjacent period by calculating a permutation distribution with false discovery rate correction.

Figure 7.

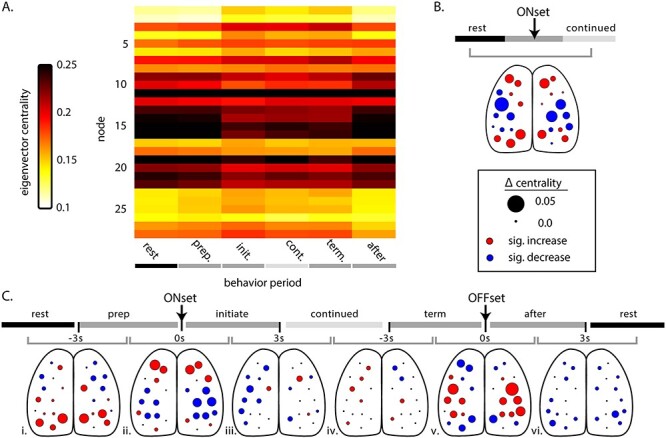
Eigenvector centrality across behavior periods. (A) Average eigenvector centrality for each node during the behavior periods, across mice. (B) Significant change in centrality comparing rest to continued locomotion across all mice. Size of circles indicate magnitude of the change, while circle color depicts the direction of significant change (red = increase, blue = decrease, black = not significant; α < 0.05, permutation distribution with false discovery rate). (C) Significant change in centrality across sequential behavior periods (shaded timeline on top). As in Figure 6, gray bracket indicates the adjacent behavior periods being compared (i–vi). Color and size of circles as described in B.

Comparing rest with continued locomotion (Fig. 7B) reveals robust changes in centrality that confirm the changes observed in the correlations (Fig. 6B). In M2, nodes 1–4, 11, and 12 increase in eigenvector centrality, with the largest in nodes 1–4. Nodes 5–8 in M1 exhibit a mixture of smaller increases and larger decreases. Centrality decreases in somatosensory and more posterior parietal nodes (9–22), with the largest decreases occurring in somatosensory cortex nodes (9, 15, 10, and 16). Nodes 23–25 in the visual areas and 27–28 in retrosplenial areas increase in centrality when comparing rest to continued locomotion.

Comparing adjacent behavior periods, there are significant increases in centrality of visual and retrosplenial nodes as the animal transitions from rest to prelocomotion (Fig. 7Ci). Meanwhile, increases in premotor nodes (1–4) and decreases in somatosensory and middle parietal nodes (9–22) do not occur until the initiation of locomotion (Fig. 7Cii). The centrality changes reverse during the transition from the termination of locomotion to postlocomotion with large increases in somatosensory and parietal nodes and decreases in premotor, retrosplenial, and visual nodes (Fig. 7Cv). This is followed by more general decreases in centrality as the animal returns to rest (Fig. 7Cvi). As observed for significant changes in correlation, the changes in eigenvector centrality are also preserved following high-pass filtering (Supplementary Fig. 3F,G) and demonstrate centrality is independent of the large fluorescence shifts that occur during locomotion. These changes in network centrality highlight the dynamic roles played by different functional regions and their interactions between behavior periods.

Granger Causality

The Granger causalities between all nodes were calculated to estimate the directionality of the functional connectivity during different behavior periods (Fig. 8A). Granger causality was calculated for each direction of every possible pair of nodes (i.e., time series X Granger causing time series Y as well as time series Y Granger causing time series X), plotting the resultant causality in both directions (Fig. 8A). There is a tendency for certain nodes, for example, 1 and 4 in the premotor region and 26 in the visual region, to causally impact several other nodes in the cortex. Conversely, some nodes receive input from many others. Qualitatively, causality increases from rest to prelocomotion, continues to increase during continued locomotion and increases even further at the termination of locomotion (Fig. 8A).

Figure 8.

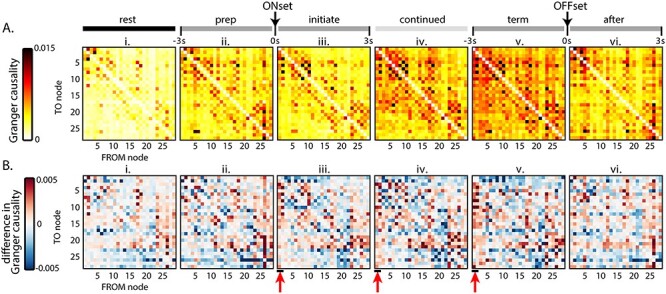
Granger causality between nodes during the behavior periods. In these plots, rows represent the TO node Granger causality, and columns represent the FROM node causality. (A) Average Grainger causality between nodes in both directions for each period, across all mice. (B) Total Granger causality between nodes determined by subtracting the upper triangle of the matrix from the lower triangle. Red arrows highlight the outward causality of anterior M2 nodes (nodes 1–2) during locomotion.

To simplify, we determined a single total causality vector between pairs by summing the causalities between each pair of nodes. The magnitude and direction (positive or negative) of the total Granger causality “to” and “from” each node is shown in Figure 8B. During all behavior periods, visual nodes (23–26) exert greater Granger causality (positive values) on other nodes than others exert back on visual nodes (Fig. 8Bi–vi). A similar pattern is observed for nodes 17 and 18, which correspond approximately to the barrel fields, suggesting these two sensory systems exert net positive Granger causality on many other cortical areas. Most notably, however, nodes 1 and 2 in the anterior M2 area exert Granger causality on many other nodes beginning at the initiation of locomotion (Fig. 8Biii, 44 of 54 possible connections) and persisting through continued (44 of 54 possible connections) and termination (47 of 54 possible connections, Fig. 8Biv,v), suggesting the premotor cortices play causal roles from the start to end of locomotion (see red arrows in Fig. 8Biii–v).

We calculated the significant change in Granger causality between adjacent behavior periods for both directed (Fig. 9A) and total causality (Fig. 9B). Comparing rest to locomotion, the changes include scattered increased influence among nodes located in premotor, primary motor, and somatosensory regions (Fig. 9A,C). Most of the significant changes between behavior periods occur across locomotion onset and across locomotion offset. The most prominent changes in Granger causality are increases from the anterior M2 nodes, from preparation to initiation of locomotion (Fig. 9C,D; 10 of 54 possible connections in C, 19 of 54 in D; see red arrows). This finding supports the average causalities (Fig. 8A) as well as the increases in correlation (Fig. 6Cii) and centrality (Fig. 7Cii) and suggests that anterior M2 nodes begin exerting a causal influence on other cerebral cortical regions at the start of locomotion and continue to do so until locomotion ends.

Figure 9.

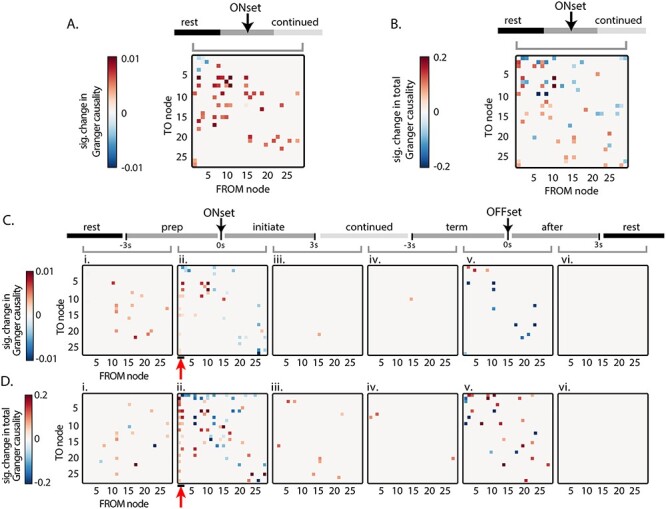
Significant changes in Granger causality between nodes across behavior periods. In these plots, rows represent the TO node Granger causality, and columns represent the FROM node causality. (A) Significant change in Granger causality in both possible directions from rest to continued locomotion. (B) Significant change in total Granger causality, as shown in Figure 8B, from rest to continued locomotion. (C) Significant change in Granger causality across sequential behavior periods. (D) Significant change in total Granger causality across sequential behavior periods. (Significance based on α < 0.05 using permutation distribution with false discovery rate). Red arrows highlight the significant increase in outward causality of anterior M2 nodes (nodes 1–2) at the onset of locomotion. Gray bracket indicates the adjacent behavior periods being compared (i–vi) in C and D.

Hemodynamic Contributions

We imaged three mice using dual-wavelength imaging to correct for Ca²⁺-independent changes in fluorescence to remove the hemodynamic component from the GCaMP signal (see Materials and Methods). The IC catalogs were similar to those in the uncorrected dataset and were grouped into the same 28 common nodes (Supplementary Fig. 4A,B). The overall patterns of changes in fluorescence across the behavior periods (Supplementary Fig. 4C) were similar to those observed in the original eight mice (see Fig. 3C). Because less data were used, these catalogs included fewer ICs than were found in the primary dataset, although all but node 11 were represented in the three mice at least once. As in the primary dataset, anterior M2 nodes increased in correlation with the majority of more posterior nodes comparing rest to continued locomotion (Supplementary Fig. 4D,F, left). These increases occurred at the onset of locomotion, from the preparation to initiation periods (Supplementary Fig. 4Eii,Gii), and then the correlations decreased to rest levels at the offset of locomotion, from termination to after periods (Supplementary Fig. 4Ev). These changes in correlation were confirmed in the changes in centrality (Supplementary Fig. 4G). These data demonstrate that the blood flow had minimal effects on the sICA segmentation and network connectivity during the transitions between rest and locomotion.

Discussion

We performed wide-field Ca²⁺ imaging of the mouse cerebral cortex during locomotion and studied the functional connectivity between cortical regions. The results confirm previous studies demonstrating that locomotion activates many regions in the cerebral cortex (Niell and Stryker 2010; Ghose 2015; Dadarlat and Stryker 2017). Four key findings resulted from this study. First, the cerebral cortex enters a new state during locomotion characterized by a distinct pattern of interregional functional correlations and elevated activity compared with rest. This locomotion state is bracketed by transition states that occur at both locomotion onset and offset. Second, correlations and centrality of nodes in the primary motor and somatosensory cortices decrease during locomotion compared with rest. Third, there is an increase in correlations and centrality of the retrosplenial cortex during locomotion. Fourth, the correlations, centrality, and the outward causality of nodes in the anterior M2 region increase at the onset of locomotion. Notably these changes occur in this relatively simple locomotion task that does not overtly require the specialized functions of the motor or retrosplenial cortices, such as spatial navigation, precise limb placement, or obstacle avoidance. However, others have also reported activation changes in primary sensory cortices in similarly simple walking tasks (Niell and Stryker 2010; Dadarlat and Stryker 2017; Tang and Higley 2020).

Results Are Limited to Layers II/III

As the recordings are based on single-photon, mesoscopic imaging in this line of transgenic GCaMP6f mice, the functional connectivity patterns primarily reflect excitatory neuronal activity in cortical layers II/III. Cortical layers II/III provide intrahemispheric projections throughout the cortex and interhemispheric projection via callosal axons to equivalent locations in the contralateral cortex (Wahl et al. 2007; Wahl et al. 2009). Therefore, the Ca²⁺ signals recorded are excellent candidates to assess cortico-cortical interactions. However, the results do not provide insights into the pattern of connectivity or cortical state present in deeper layer V. Studies suggest layer-specific modulation, for example, locomotion-induced firing in V1 occurs in all cortical layers, while retrosplenial locomotion-induced firing may be limited to more superficial layers (Clancy et al. 2019). In M1, layer II/III may show distinct activation patterns from layer V during visually guided locomotion (Heindorf et al. 2018). Additional work is needed to fully understand how connectivity and cortical state vary with cortical layers.

Cortical Segmentation with sICA

We assumed that the cerebral cortex is composed of modules or clusters of functionally similar neurons, that these modules are functionally connected in an ordered manner to other modules, and that they have a relatively specific role in behavior. In the present study, sICA uncovered 22–31 independent spatial regions per mouse that we used to functionally segment the cerebral cortex into independent functional modules and characterize the changes in Ca²⁺ epifluorescence. A previous implementation of sICA using JADE (Makino et al. 2017) obtained 16 ICs of approximately similar size and locations across the dorsal cerebral cortex. Our greater number of ICs can likely be attributed to the higher sensitivity of imaging through transparent polymer windows as opposed to thinned bone, as well as differences in data collection and analyses. The minimization of mutual information between regions by sICA provides a complementary approach to that provided by the Common Coordinate Framework (Allen Institute for Brain Science 2015). Here, we elected to determine the ICs independently and then align the ICs with the major cortical divisions in the mouse. Our implementation of sICA was performed over all available data from a given mouse, which allowed for determination of the ICs over a large data base (432 000–576 000 images). Other segmentation approaches used with wide-field Ca²⁺ imaging include seed-based correlation (Vanni et al. 2017), seed-correlation colocalized with tract-tracing (Mohajerani et al. 2013), spike-triggered mapping (Xiao et al. 2017), and nonnegative matrix factorization (MacDowell and Buschman 2020). While there have been few direct comparisons of these methods in Ca²⁺ imaging, different analytical approaches will likely provide complementary information.

Hemodynamic Correction

While the analysis removed as much blood flow contribution to the signal as possible by regressing out fluorescence activity correlated with blood vessels, some fluorescence changes resulting from hemodynamic activity may have remained. In a group of three animals, we determined the influence of increased blood flow on the spatial ICs and the functional connectivity network, using dual-wavelength imaging (470 and 405 nm) to remove Ca²⁺-independent changes (Vanni and Murphy 2014; Jacobs et al. 2020). Removing the Ca²⁺-independent signal produced IC catalogs similar to the catalogs produced from the uncorrected signal. Furthermore, the functional connectivity analyses on hemodynamic corrected signals revealed connectivity changes across behavior periods similar to those found with uncorrected signals. Therefore, the additional dual-wavelength results agree with previous reports that the hemodynamic contribution to GCaMP6 Ca²⁺ response is limited (Vanni and Murphy 2014; Makino et al. 2017; Allen et al. 2017; Jacobs et al. 2020; Musall et al. 2019).

Modulation with Treadmill Velocity and Step-Cycle

The fluorescence activity is significantly modulated with treadmill velocity, with the strongest modulation during the initiation and termination of locomotion. While nodes in the primary motor cortex exhibit the highest R² values, we would emphasize that treadmill velocity is widely represented across the dorsal cerebral cortex. The regression results reveal similar, although less robust, modulation with paw velocity. The modulation with treadmill velocity and forepaw step-cycle demonstrates locomotion-specific cerebral cortical neuronal activity. That locomotion speed contributes more to the variation in Ca²⁺ fluorescence signal than the movement of individual limbs is due, in part, to the slow temporal dynamics of the Ca²⁺ signal, which will not be able to reflect the faster dynamics of the step-cycle. However, our results match well with studies showing strong correlation between overall locomotion speed and the firing rate of individual V1 neurons (Vinck et al. 2015; Clancy et al. 2019).

Continued Locomotion Is Characterized by a Distinct Cortical State

Continued locomotion shows elevated fluorescence activity and a distinct state of cerebral cortical activity and functional connectivity as compared with rest. In addition, there exists a transition state from rest to locomotion as well as from locomotion back to rest that shows a generalized increase in cortical activity and functional connectivity. This pattern of overall activation is similar to the pattern shown by the firing rate of V1 and retrosplenial neurons in locomotion (Vinck et al. 2015; Clancy et al. 2019). The intracortical functional connectivity features of these states as compared with rest are discussed below. While our techniques do not differentiate between individual aspects of locomotor behavior, such as step-cycle, whisking, and arousal, we suggest that all these aspects are components of the natural locomotor state.

These results have implications for how locomotion can be disrupted in disease. Freezing of gait is a disabling symptom of severe Parkinson’s disease, in which patients are suddenly and briefly unable to take a step during walking (for review, see Nutt et al. 2011). Freezing most often occurs when a patient initiates walking or when gait must be altered in response to an external cue and is less likely when the patient is walking continuously. The transient nature of these episodes suggests a temporary disruption to the communication dynamics of the locomotion circuitry (Nutt et al. 2011) that is specific to adjusting gait but not continued locomotion. In Parkinson patients, freezing may be precipitated by sudden disruptions to locomotion network connectivity, including between cortical motor areas and subcortical regions (Fling et al. 2014; Pozzi et al. 2019). In the context of the present results, the human studies reinforce that the transition states observed at locomotion onset and offset are distinct from the continued locomotion cortical state and suggest that disruption of these transition states manifests as freezing of gait.

Decrease in Connectivity of Primary Motor and Somatosensory Regions

Primary motor and somatosensory nodes decrease in Pearson correlation (ρ) with nodes in other regions, both at the onset and throughout locomotion. These nodes show increased connectivity to other M1 nodes in the same hemisphere, but not to those in the contralateral M1. These M1 nodes show somewhat higher correlation with treadmill and paw velocity than other nodes (Fig. 4), suggesting some of the decrease in functional connectivity is due to limb –movement–related activity. It would have been reasonable to expect an increased connectivity in M1 nodes to other regions, since gait modulation inherently requires receiving upstream sensory inputs of those obstacles (Drew and Marigold 2015). Further complicating this finding, the results of two-photon Ca²⁺ imaging of M1 layers II/III suggest these neurons integrate sensory information from other cortical regions to send to layer V (Heindorf et al. 2018), which does not agree with the decrease in correlation with sensory regions found here. Additional investigation into the role of layers II/III of M1 in locomotion is needed to clarify these seemingly conflicting findings.

Lesioning the corticospinal tract or M1 produces locomotor deficits, including hypermetria and abnormalities in limb trajectory and intralimb coordination (Liddell and Phillips 1944). Pyramidal neuronal firing in M1 correlates with individual muscle activity during locomotion (Drew, Andujar, et al. 2008a; Drew, Kalaska, et al. 2008b; Drew and Marigold 2015) and modulates when the subject maneuvers around an obstacle, suggesting M1 directly controls locomotion and influences the central motor pattern. Interestingly, the decrease in connectivity seen here begins before the onset of locomotion, which agrees with the long-known finding that M1 is activated during movement preparation (Tanji and Evarts 1976; Georgopoulos et al. 1989; Churchland et al. 2010).

Increase in Connectivity of Retrosplenial Regions

In contrast to primary motor cortical nodes, retrosplenial nodes display increased functional connectivity with the majority of the dorsal cerebral cortex and across both hemispheres. These increases in connectivity occur when comparing rest with preparation and rest with continued locomotion and agree with previous findings showing increased retrosplenial connectivity during locomotion (Clancy et al. 2019). This corroborates previous evidence that the retrosplenial region is approximately equivalent to PPC in carnivores and primates and is engaged in integrating the sensory and spatial information needed to accurately and safely navigate the environment during locomotion (Drew and Marigold 2015; Takakusaki 2017). For example, animals with lesioned PPCs are unable to retain information of obstacles once the obstacle passes out of the visual field (Lajoie et al. 2010). The largest increase occurs before the onset of locomotion, as would be expected if the retrosplenial region is tasked with assessing the environment for navigational routes or potential obstacles at the start of locomotion. As there was no change in the magnitude or direction of Granger causality, the ratio of information being sent and received by retrosplenial nodes does not change from rest to locomotion.

Increase in Connectivity and Outward Causality of Anterior M2 Regions

Our final and perhaps most notable finding is the increase in functional connectivity of the most anterior nodes of M2. The increase first occurs at the onset of locomotion and remains elevated through the offset. These anterior M2 nodes increase in correlation with somatosensory, parietal, visual, and retrosplenial regions of both hemispheres during locomotion and show a significant increase in outward Granger causality to these regions. While we acknowledge that Granger causality is not a direct measure of cause-and-effect, it is a valuable tool for estimating directed connectivity between brain regions (Seth et al. 2015; Barnett et al. 2018). Our results corroborate the observed increases in correlation between V1 and M2 during locomotion in the mouse (Clancy et al. 2019) and suggest the more rostral regions of the premotor cortex provide an organizing signal to the rest of the cerebral cortex during locomotion. This agrees with previous studies that show the premotor cortex modulates individual primary sensory regions (Schneider et al. 2014; Nelson and Mooney 2016; Leinweber et al. 2017).

The function of the premotor cortex in locomotion is not well understood (Drew and Marigold 2015), but it is known to be essential in several discrete motor behaviors. In mice, these behaviors include licking (Allen et al. 2017; Chen et al. 2017; Inagaki et al. 2018) and lever pressing (Makino et al. 2017). In such tasks, M2 activity can be used to causally predict activity in other dorsal cortical regions during movement (Makino et al. 2017), and inactivation of M2 represses cortex-wide responses to sensory stimuli (Allen et al. 2017), suggesting M2 has widespread influence over the activity of the cerebral cortex. Furthermore, premotor cortex is widely anatomically connected, receiving inputs from the somatosensory, auditory, posterior parietal, and orbital cortices, and projecting to primary motor, somatosensory, parietal, and retrosplenial areas (Yamawaki et al. 2016; Zhang et al. 2016; Leinweber et al. 2017; Lin et al. 2018). During locomotion, M2 may provide cortical sensory regions signals needed for proper processing of sensory inputs. While subcortical structures, such as the basal forebrain, contribute activating inputs to sensory regions via cholinergic projections (Fu et al. 2014; Lee et al. 2014; Nelson and Mooney 2016), modulation in visual and auditory cortices occurs most strongly in pyramidal neurons of layers II/III, suggesting a cortical origin of motor-driven changes (Polack et al. 2013; Zhou et al. 2014). In rodents, this modulation may come directly from M2 efferents (Schneider et al. 2014; Nelson and Mooney 2016; Leinweber et al. 2017).

In the primate, the premotor cortex is involved in transforming sensory information for movement planning in discrete movements (Di Pellegrino and Ladavas 2015). Multimodal neurons in the ventral premotor cortex map visual and auditory stimuli in spatial relation to the space immediately surrounding the body, or “peripersonal space” (Rizzolatti et al. 1981a, 1981b; Graziano et al. 1994; Fogassi et al. 1996). Peripersonal space is important for both motor and cognitive computations (Serino 2019), and inhibiting the premotor cortex impairs reaction times to stimuli in peripersonal space (Serino et al. 2011). Stimuli within peripersonal space modulate the motor system, including decreasing the excitability of M1 (Makin et al. 2009; Serino et al. 2009), and the premotor cortex is necessary for this modulation (Avenanti et al. 2012). During locomotion, the representation of physical distance from the body expands during walking, even when other sensory cues are stationary (Noel et al. 2015). Moreover, locomotive behavior is facilitated when salient stimuli appear far away rather than up close (Di Marco et al. 2019). These effects likely improve obstacle avoidance during locomotion (Noel et al. 2015) and/or promote movement toward a salient stimulus (Di Marco et al. 2019).

Funding

National Institutes of Health (R01 NS111028 and P30 DA04872 to S.B.K. and T.J.E., R61/R33 NS115089 to T.J.E., and T32-MH115688 to S.L.W.); University of Minnesota Informatics Institute, which includes support from the University of Minnesota’s MnDRIVE Initiative (to S.L.W).

Notes

We would like to thank Lijuan Zhuo for her assistance in animal surgeries. The Minnesota Supercomputing Institute provided high-processing computing, and the University of Minnesota University Imaging Centers (UIC, SCR_020997) provided 3D printing services of the cortical implants. Conflict of Interest: The authors declare no competing financial interests.