Abstract

High-energy materials containing azole and furazan have revealed numerous properties; however, the underlying optical properties need to be solved. Meanwhile, the uncertainty for the choice of fluorescent matrix materials and the flexible situational conditions prompted us to estimate the optical and fluorescent properties of 5,5′-dinitro-2H,2H′-3,3′-bi-1,2,4-triazole (DNBT), 4,4′-dinitroazolefurazan (DNAF), and 4,4′-dinitro-3,3′-4,3′-ter-1,2,5-oxadiazole (DNTO). The first-principles calculation with improved dispersion correction terms and time-dependent density functional theory were utilized to calculate the absorbance and excitation energy of DNBT, DNAF, and DNTO, as well as characterization for their crystal structure, electronic structure, molecular orbitals, and so forth, synchronously. In this work, the absorbance anisotropy of DNBT and DNTO is stronger than that of DNAF. The absorbance for each of the (0,0,1) crystal planes in the three compounds is greater than that of the other two crystal planes. Moreover, DNBT has the maximum absorbance on the (0,0,1) crystal plane. The N–N–H from DNBT and N–O–N from DNTO and DNAF are responsible for these results, while N=N in DNAF weakens the performance of N–O–N. UV–vis spectra show that the maximum absorption wavelengths λmax for DNBT, DNAF, and DNTO are 225, 228, and 201 nm, respectively. The number of five-membered rings and the coplanarity of groups in the intermolecular non-conjugation interaction potentially improve this ability due to the results from the crystal diffraction analysis. In addition, the polarization rate DNBT > DNTO > DNAF based on the molecular orbital analysis and the electrostatic potential calculation implies that the excitation energy of DNBT is less than DNTO, and the excitation energy of DNTO is less than DNAF. This work is beneficial to the expansion of energetic materials into the optical field and the accelerated application process of the related industry.
Introduction
The traditional nitro-compounds such as trinitrotoluene (TNT), 1,3,5-trinitroperhydro-1,3,5-triazine (RDX), and 1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane (HMX) have been revealed so many properties since they were first utilized because of their unique structures.1−3 Numerous scholars have made great efforts in the study of material composition, especially dedicated to discover the relationship between properties and structure.4−7 The structural mechanism of fluorescent materials and the interpretation of specific structures of optical materials currently involved in many fields, such as single-molecule fluorescent probes in proteins8,9 and small molecule fluorescent chemical sensors,10−12 have also been given to a series of possible conformational interpretations have been proposed. It provides a valuable implementation method for the structural identification of materials in the search for matrix materials with low excited states. However, these materials must possess specific properties, which significantly narrows the range of new target materials that can be pursued. As an ingredient with simple structure and active chemical properties, a series of energetic materials (EMs) with high conjugation properties were prospectively demonstrated to have potential optical properties, such as TNT and picric acid (PA).13,14 Unfortunately, these materials have fallen out of favor for optical applications due to poor thermal stability and toxic factors that are detrimental to environmental concerns, especially being potential carcinogens and inducing long-term damage to liver function.15 With these unfavorable factors, turning attention to the furazans and oxidazoles that have similar effects but are innocuous and harmless has become a potential opportunity worth exploring and revealing.
From a long-term perspective, the continuous improvement of the computer level, especially the popularity of applications in the field of computational chemistry, the first principles and density functional theory (DFT) have become a reliable, accurate core theory to reveal the structure and property laws of materials. In particular, during these similar compounds containing N conjugated structures, Zaier and Ayachi16 designed a D−π–A−π–D type cyclopentadithiophene (CPDT)–diketopyrrolopyrrole (DPP) using mixed functional B3LYP combined with the 6-311g(d,p) basis set for optimizing and investigating its geometric shapes, electronic structural, photo-physical, optical, and intramolecular charge transfer properties, which achieved good results in the final open-circuit voltage testing. Irfan, Chaudhry, and Al-Sehemi17 studied four amine derivatives of 1,3-diphenyl-1H-pyrazolo[3,4-b] quinolone (DPPQ) and several pyridine compounds using the time-dependent DFT (TD-DFT) and hybrid functional method, respectively. Moreover, the calculations are carried out on the basis of ionization potential, hole extraction potential, electron affinity, recombination energy, transfer integral, refractive index, reflectivity, and intrinsic mobility. Except that, Latosińska, Tomczak, and Medycki18 explored the HMR spectra of triclosan 5-chloro-2-(2′,4′-dichlorophenoxy)-phenol (CDP) by employing hybrid functional with modified long-range interactions. Dorotíková and Dvoranová et al.19 performed conformational analysis of potential antibacterial fluoroquinolone 3-fluoroanilino-ethylene (FAE) and its derivatives, from which they accurately verified vibrational frequencies, electron transitions, as well as nuclear magnetic resonance (NMR) spectra are analyzed with respect to conformational analysis. Arulaabaranam, Muthu, Mani, and Irfan20 predicted the molecular geometry, conformational stability, and corresponding molecular orbitals of methyl-2-pyrazinecarboxylate (M2PC) optimized by B3LYP/6-311++G(d,p) while using water as the medium solution using TD computational UV–vis spectral projection simulations. Overall, the exploration of the structure and properties of materials using first-principles and DFT methods not only has objectively feasible significance but also facilitates the initiation of revelations.
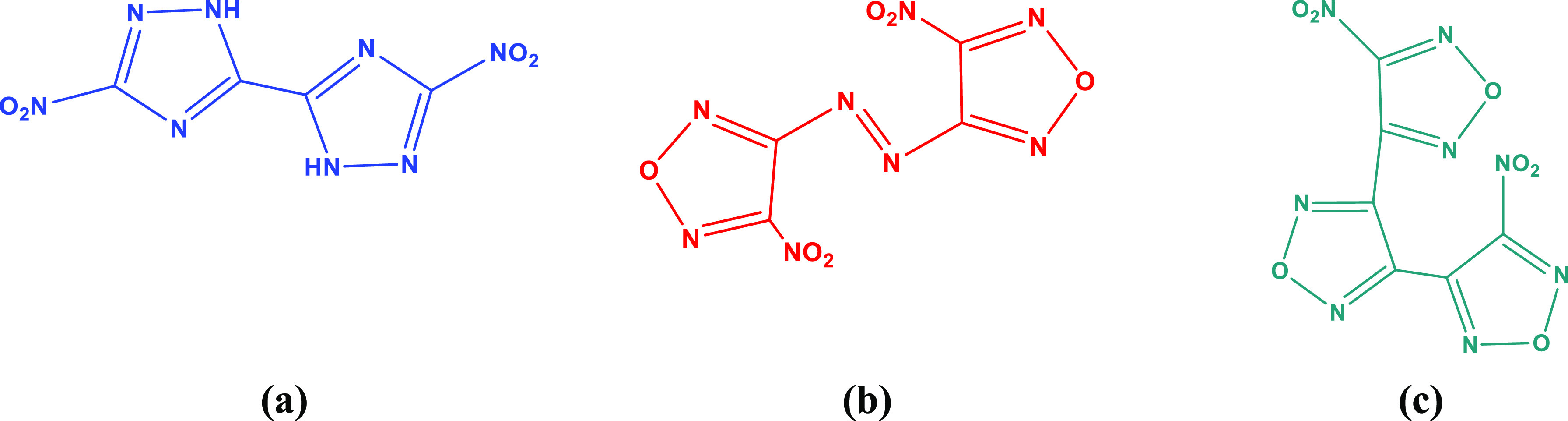
Recently, exploration for fluorescent material which consists of nitro groups has developed a series of hot spots for its remarkable performance and reliable stability in the field of EMs. Moreover, a traditional high-energy-density-material21 which consist of nitro-compounds especially composed by the furazan and oxidazole rings have been a previous interesting point for its safety, toxic free, and industrial processes. 5,5′-Dinitro-2H,2H′-3,3′-bi-1,2,4-triazole(DNBT)21,22 is a secondary potential explosive that can be synthesized in two steps starting from aminoguanidinium carbonate and oxalic acid, which has a high density (1.903 g cm–3), high heat of formation (285 kJ mol–1), and formidable detonation velocity (8413 m s–1). 4,4′-Dinitroazolefurazan (DNAF) and 4,4′-dinitro-3,3′-4,3′-ter-1,2,5-oxadiazole (DNTO) both are also excellent nitro-compounds whose densities are 1.856 and 1.875 g cm–3, and the high heat of formation values are 267 and 245 kJ mol–1, respectively21,23−26 ((Scheme 1, Supporting Information, Text S1). A sufficient evidence shows that the high positive heats of formation considered from the N–N and N–C bond.25,26 Notably, nitro-compound such as azole and furazan have already been investigated remarkably from high decomposition function and outstanding energetic properties, but their structural characteristics still need to be continuously built up and verified. Several further fundamental learning procedures containing co-crystal cell structure and thermal stability for DNBT were validated during the time 2015 and 2018.27,28 Due to the uniqueness of the 2-N atoms for the azole structure, DNBT can apply on ions such as Fe, Ni, and Cu combined layer-style frameworks composed to metal coordinate nitro salts by Seth and Matzger,29 whose works provide a lot of possibilities that the structural anisotropy of DNBT has an impact on the packing mode. Therefore, as a derivation and extension, it is worth exploring and discussing whether the furazan structure has a similar performance in structure and properties with feasible and worthy of tracking and follow up the consideration to analyze the optical properties and fluorescence characteristics of these nitro-compounds from the perspective of crystal structure and electronic energy state.
Scheme 1. Structures of 5,5′-Dinitro-2H,2H′-3,3′-bi-1,2,4-triazole (a), 4,4′-Dinitroazolefurazan (b), and 4,4′-Dinitro-3,3′-4,3′-ter-1,2,5-oxadiazole (c).
Lack of understanding of the optical mechanism and potential fluorescent excitation characteristics of the nitroazole compound and nitrofurazan compound push up previous works to carry out more discoveries. Our works rely on a free-combination for TD-DFT and quantum chemical methods with first-principles calculation based on the plane-waves pseudopotential to have a carving for quenching the mysteries of these three potential compounds. More significant and interesting pieces of information were found. Orbit-energy relationship of DNBT, DNAF, and DNTO was provided; characterization of the electronic structure and calculation of electronic localization function; statistics for the influence of absorbance and anisotropy of the three compounds; in order to select suitable conditions, we have performed UV–vis spectrum calculations, highest occupied molecular orbitals (HOMOs), and lowest unoccupied molecular orbitals (LUMOs). In addition, corresponding electronic crystal structures for DNBT, DNAF, and DNTO were also analyzed and discussed.
Methodologies
The optical simulations are performed using the CASTEP30 code based on the exchange correlation functional with the TD-DFT,31,32 the functional form used is the Perdew–Burke–Ernzerhof33 form under the generalized gradient approximation (GGA–PBE), combined with the modified DFT-D correction term, for the crystal structure optimization and ground state energy calculation of the compounds in this work. We choose the Tkatchenko–Scheffler34 method as the basic tuning parameters with the Koeling–Hamon relativistic treatment applied in the norm-conserving pseudopotentials. The energy cutoff is 1080 eV. The geometry optimization is calculated according to a Quasi–Newton algorithm with BFGS minimizer35 for both lattice parameter and atomic coordinates. The UV–vis was calculated by the Gaussian 1636 software package using the functional/basis set combination of TD-B3LYP/6-311++G(d,p) under the condition of singlet spin hybridization. The detailed explanatory for simulation settings and strategies are described in Supporting Information, Table S1.
Results and Discussion
Non-covalent forces, such as hydrogen bonding and van der Waals (vdW) interactions, are crucial for the formation, stability, and function of molecules and materials. At present, ubiquitous vdW interactions can only be accounted for properly by high-level quantum-chemical wavefunctions or by the quantum Monte Carlo method.37 In contrast, the correct long-range interaction tail (e.g. for separated molecules) is absent from all popular local-density or gradient corrected exchange–correlation functionals of density-functional theory, as well as from the Hartree–Fock approximation.38 Therefore, it is extremely significant to select an appropriate functional to describe the non-covalent interaction.
| 1 |
| 2 |
 |
3 |
In order to capture
a more ideal description of the interaction
between atoms, a measurement and adjustment for dispersion correction
were proposed before the orbital analyzing process of DNBT, DNAF, and DNTO. Hence, we picked up the
three potential compounds and calculate the local energy for each
unit cell by eqs 1 and 2, where En(k) describes the dispersion of the given
band and the integral determination over the Brillouin zone, and an
alternative representation of the density states is based on NndE is proportional
to the number of allowed wave vectors in the energy range E to E + dE. Etotal is the overall energy situation for the combination
of DNBT, DNAF, and DNTO, EDFT shows the ground state energy which calculated
by the DFT method under the way in ab initio algorithm, represents
the standard DFT total energy and the sum goes over all N atoms in the system, where si terms means different coefficients for each atom in each molecule
of crystals got accounted by the potential and 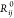 is the vdW radii for the free atom. Short-ranged
damping function is represented by a Fermi function
is the vdW radii for the free atom. Short-ranged
damping function is represented by a Fermi function 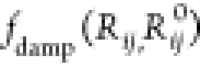 in eq 2, which is due
to the distance between the molecule and the
vdW radii, where d is the steepness for the damping
function. In a semi-empirical dispersion-correction way, missing dispersion
contribution to the inter-atomic interaction is approximated by a
simple isotropic potential. At long range, this potential is given
by Lennard-Jones (L-J potential) and
in eq 2, which is due
to the distance between the molecule and the
vdW radii, where d is the steepness for the damping
function. In a semi-empirical dispersion-correction way, missing dispersion
contribution to the inter-atomic interaction is approximated by a
simple isotropic potential. At long range, this potential is given
by Lennard-Jones (L-J potential) and  term, where the C6,ij coefficient is atomic
specific;39,40 meanwhile, the dispersion coefficient taken
into account by suitable
modification of the corrected term was adjusted through the free parameters SR and dumping factor ϵdamp.
term, where the C6,ij coefficient is atomic
specific;39,40 meanwhile, the dispersion coefficient taken
into account by suitable
modification of the corrected term was adjusted through the free parameters SR and dumping factor ϵdamp.
Because the addition of the DFT dispersion correction term can more accurately describe the long-range weak interactions between atoms, and the scheme is directly implemented in computation, the description of this semi-empirical dispersion correction also requires intramolecular transferable parameters. Therefore, for the same or different elements within a molecule, most problems are dealt with around substantial changes in properties between effective atoms.41−43 Actually, on the basis of neglecting hybridization and effective polarizability, molecular orbitals from each compound could be severed for the crystal surface, and hence, we can reflect directive values for energies and reduced dispersion coefficient of atoms in deeper layers in the substrate. According to this method, we have fitted all the information and completed the corresponding adjustment of the interaction potential including the atom distance parameters, long-range interaction parameters, and atomic potential coefficient, which are under the comparison with the results of Wu and Yang.44 and Tkatchenko and Scheffler,45 and the detail parameters have been fitted, which are described in Supporting Information, Table S1. We also made statistics on the bond relationship and evaluation for the potential, and further details can be learned from Supporting Information, Tables S2–S5 and Figure S1.
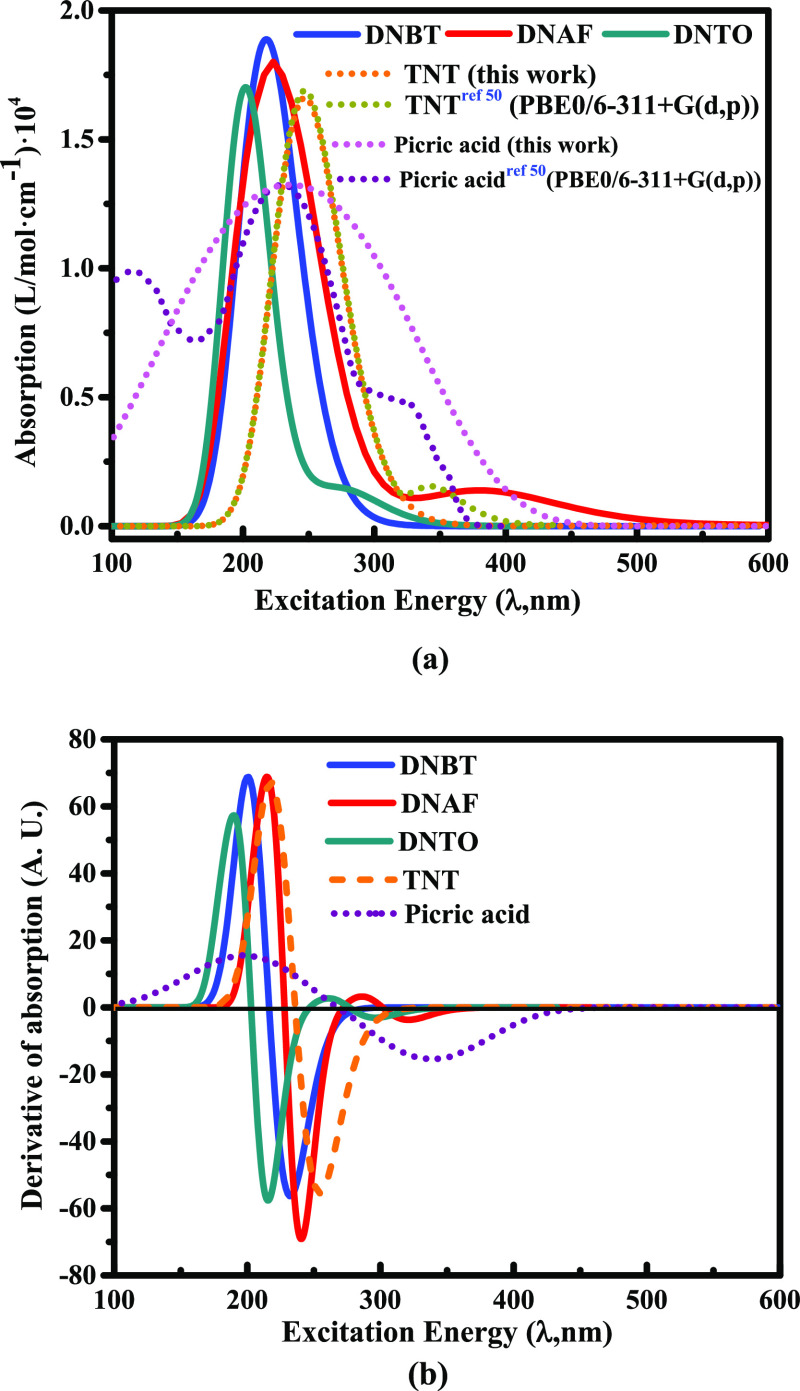
As shown in Figure 1a–c, the evolution of light absorption can be understood as four modes. According to these four modes, we have divided the regions from I to IV, which are as follows: (I) light high-frequency absorption zone; (II) interference cancellation zone; (III) secondary light zone; and (IV) absorbed vibration overlapping and disappearing zone. From the perspective of the three crystal plane directions, the high-frequency absorption zone I and the secondary light generating zone III on the (0,0,1) crystal plane of DNBT have one of the three maximum absorbance peaks in DNBT and are 3.75 and 1.25 cm–1/10–5, respectively. However, DNBT also has the lowest absorbance among the three on the (0,0,1) crystal plane and the bottom value is 0.15 cm–1/10–5. The maximum absorbance of the high-frequency absorption zone I and the maximum absorbance of the secondary light zone III in DNAF on the (0,1,0) crystal plane are 2.27 and 0.65 cm–1/10–5, respectively, which are the lowest level among the three compounds on the three crystal planes. However, in the interference cancellation zone II on the (0,0,1) crystal plane, the absorbance change of DNAF is so complicated that even affects the region III with more multiple secondary light phenomena. Besides that, there is no obvious secondary light phenomena for TNT and PA(13,14) found in zones II and III.
Figure 1.
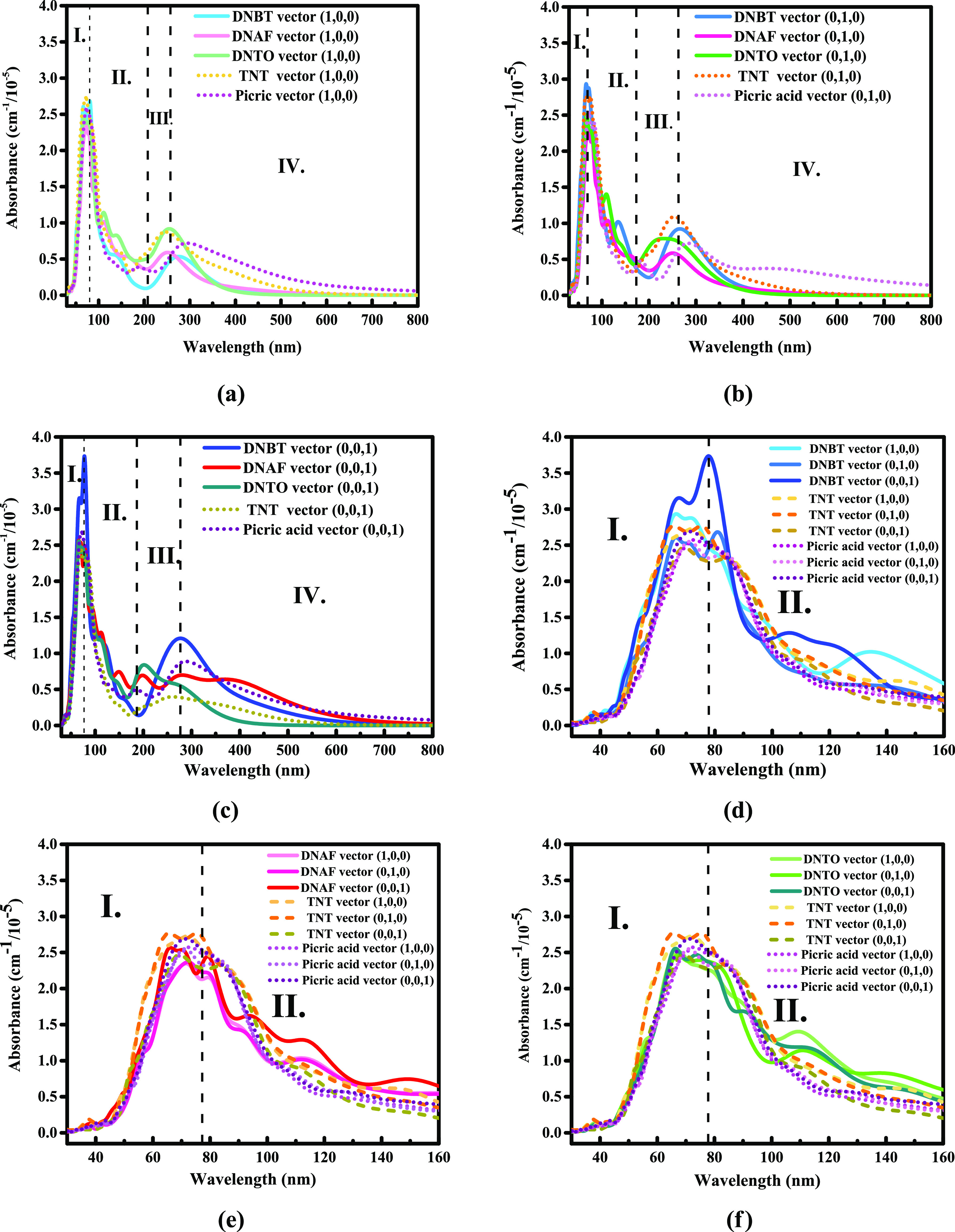
Figures (a–c) represent the calculated results of absorbance in the range of 0–800 nm (visible light) for DNBT, DNAF, and DNTO, respectively. Figures (d–f) represent the calculated absorbance results of DNBT, DNAF, and DNTO in the range of 0–160 nm (short-frequency ultraviolet light), respectively. DNBT is identified as blue series, DNAF is identified as red series, DNTO is identified as green series, and it is compared with TNT(13) (orange series) and PA(14) (purple series).The (1, 0, 0) crystal plane, the (0, 1, 0) crystal plane, and the (0, 0, 1) crystal plane are presented in light to dark colors.
According to the signs reflected in the curve, the average absorbance of DNTO between zone II and zone III is greater than DNBT and DNAF on the three crystal planes, and the secondary light effect of DNTO is the most obvious on the (1,0,0) crystal plane. Therefore, we can find that the overall absorbance of DNBT is stronger than that of DNAF and DNTO, and the interference cancellation phenomenon enhances the overall absorbance level of DNTO and DNAF to a certain extent. Moreover, the generation of secondary light has the greatest impact on the absorbance of DNBT on the (0,1,0) and (0,0,1) crystal planes, and it also has the greatest impact on the absorbance of DNTO on the (1,0,0) crystal plane. Learning from zone IV, among the three crystal planes, the overlapping and evanescent effects of the vibrations of the three compounds on the (0,0,1) crystal plane make the absorbance gradually tend to the same level. Furthermore, as shown in Figure 1d–f, there are differences between DNBT, DNAF, and DNTO on the three crystal planes, that is, the existence of anisotropy also affects the light absorption. The absorbance values of (0,0,1) crystal planes of DNBT, DNAF, and DNTO are significantly greater than (1,0,0) crystal planes and (0,1,0) crystal planes. It is shown that the (0,1,0) crystal plane of DNBT and the (1,0,0) crystal plane of DNTO have the weakest absorbance level, while the (1,0,0) crystal plane and (0,1,0) crystal plane of DNAF have the same absorbance contribution.
Because the generation of secondary light largely depends on the interference destruction effect and the influence of the crystal structure of the target irradiated object, and the stacking form inside the crystal is related to the superposition of light, there are considerable differences in the absorbance of different crystal planes. In addition, as substances of different compositions respond differently to light of various frequencies, the frequency range of the secondary light phenomenon will also be different, and the dominant frequency of the reflected and scattered light formed by superimposing with the incident light will be different, which causes a large difference in absorbance. The positions and angles of molecules in DNBT, DNAF, and DNTO unit cells are many. When the light source is concentrated, the superposition and interference cancellation effects of incident photo-electrons are different. We speculate that the absorption of DNBT is greater than that of DNAF and DNTO, which is also determined by the large difference in the structure. The π–π stacking structure formed by the conjugated ring structure in DNBT is stable and directional, which is one of the reasons why DNBT is more anisotropic than DNAF and DNTO. The N=N conjugation of furazan and DNAF weakens the electron-withdrawing ability on N–O–N; nevertheless, the nitro group strengthens the electric-absorbing effect, thus maintaining the relatively stable absorption of photo-electrons.
Because the generation of secondary light largely depends on the interference destruction effect and the influence of the crystal structure of the target irradiated object,46 and the crystal packing form also affects the absorption of incident light, there are considerable differences in the absorbance of different crystal planes. In addition, as substances of different compositions respond differently to light of various frequencies, the frequency range of the secondary light phenomenon will be different, and the dominant frequency of the reflected and scattered light formed by superimposing with the incident light will be different, which also causes a large difference in absorbance. The positions and angles of molecules in DNBT, DNAF, and DNTO unit cells are many. When the light source is concentrated, the superposition and interference cancellation effects of incident photo-electrons are different. We speculate that the absorption of DNBT is greater than that of DNAF and DNTO, which is also determined by the large difference in the structure. The π–π stacking structure formed by the conjugated ring structure in DNBT is stable and directional,47,48 which is one of the reasons why DNBT is more anisotropic than DNAF and DNTO; thus, the maximum absorbance of DNBT is the highest among the three compounds. Apart from these, the N=N conjugation of DNAF weakens the electron-withdrawing ability on N–O–N; nevertheless, the nitro group strengthens the electric-absorbing effect,49 maintaining the relatively stable absorption of photo-electrons.
According to the vibration simulation of the ultraviolet–visible (UV–vis) absorption spectrum as shown in Figure 2a, the three compounds have no obvious absorption phenomenon in the far ultraviolet region (0–200 nm), and the absorption phenomenon is mainly concentrated in the ultraviolet region (200–400 nm). The calculation results show that among the three compounds, DNBT has a maximum absorption value of 1.853 L/mol cm–1 at 225 nm, while the maximum absorption peaks of DNAF and DNTO are 1.582 and 1.321 L/mol cm–1, respectively. What is more interesting is that DNAF and DNTO both have a small absorption peak after the maximum absorption peak, and the two small peaks have a tendency to move in the direction of the long-wave range (red shift trend). With the iteration and optimization of relaxation calculations for DNBT, DNAF, and DNTO, there is no longer an effective UV–vis absorption capacity in the visible region beyond 500 nm. From the perspective of the absorbance derivative function, as shown in Figure 2b, the corresponding absorption wavelengths (excitation energy) at the zero point of the absorbance derivative functions of DNBT, DNAF, and DNTO are 225, 228, and 201 nm, which are the maximum wavelength λmax for the three compounds under the maximum absorption. The calculation results show that the excitation energy levels of these three compounds are generally lower than those of TNT and PA.50 Therefore, the order of the three compounds according to the maximum absorption capacity is AbsorpDNBT > AbsorpDNAF > AbsorpDNTO, and the order of maximum absorption wavelength is λDNAF> λDNBT> λDNTO.
Figure 2.
Calculation of UV–vis absorption spectra of DNBT, DNAF, and DNTO. TNT and PA in figure (a) are compared with related work. Figure (b) shows the calculated derivative of UV–vis absorption.
Analyzed from the calculation results of the UV–vis spectrum, because the wavelength distribution of the spectrum is supported by the transition energy level difference of the generated band, this is also the basis for describing the internal energy level distribution and qualitative of the three compounds. The intensity of the absorption band has a great relationship with the change of the molecular dipole moment and the transition probability.51 There are effective structures inside DNBT, DNAF, and DNTO that provide favorable conditions for energy level transitions; in particular, the large conjugated ring structure in DNTO enables a large number of π–π* transitions to be realized, so the absorption peak is the strongest, while the N=N bond in DNAF as the furazan connection is a very effective chromophore.52,53 There are not only π–π* transitions but also n−π* transitions inside DNAF, and because the n-orbital energy level is the highest, this is also an important factor that λmax for DNAF is greater than DNBT and DNTO. The nitro group, as a strong absorption band auxochrome caused by the n−π* jump, provides strong evidence for the red shift of the small absorption peak where next to the maximum absorption peak of DNAF and DNTO.54−57 Additionally, because each compound has a maximum absorption rate at specific wavelengths of 225, 228, and 201 nm, it can be predicted that there will be ultraviolet absorption in the secondary light region (region III in Figure 1) and exhibit potential possibility of fluorescence excited state.
As shown in Figure 3, the orbital energy for the crystal structure of the three compounds was calculated. The minimum orbital energies for N atoms of DNBT, DNAF, and DNTO are −24.521, −25.075, and −24.215 eV, respectively. The maximum orbital energy is −0.003, −0.082, and −0.011 eV, respectively. We found that the energy levels for nitrogen atoms of DNBT in all orbits are all higher than that of DNAF and DNTO. According to statistical analysis, the average orbital energy of DNBT is higher than the average orbital energy of DNAF by 2.193357 eV, the average orbital energy of DNBT is higher than the average orbital energy of DNTO by 4.20714 eV (except the first N atom). Because the triazole ring structure in DNBT belongs to a plane conjugated structure with a π–π stacking form, its structure is stable, and the electrons are delocalized and have a higher orbital energy level. In contrast to DNTO, there is a tri-furazan structure in a single molecule with no conjugation in the DNTO system. Not only that, the series distribution of the N–O–N structure on the five-membered ring of DNTO expands the moving range of electrons to a certain extent; thus, the average orbital energy is the lowest. By observing the orbital energy of DNAF, the average orbital energy of DNAF is higher than that of DNTO. However, there are several orbitals where the orbital energy of DNTO is greater than that of DNAF (Figure 3a,b is shown by the orange dotted line). According to our analysis, the N=N bond in DNAF and should be jointly responsible from the orbital energy of N5 and N10. Under these conditions, when the electron orbit extends outward with the increase in energy, the electron on the external orbital is enhanced by the N–O–N structure, and weakened by the N=N bond in DNAF. In addition, from the perspective of the total energy orbital distribution, DNBT, DNAF, and DNTO have different energies under the same orbital for N atoms, and the orbitals for N atoms under the same energy are also different.
Figure 3.
Evaluation of orbital analysis for nitrogen atoms. (a) Lowest value of the energy of the orbital for N at any k-point. (b) Highest value of the energy of the orbital for N at any k-point.
As shown in Figure 4, we have given nine kinds of DNBT, DNAF, and DNTO electric local function (ELF) [(1,0,0) direction, (0,1,0) direction, and (0,0,1) direction], the electronic localization range is defined in the range of 5 × 10–5 to 9 × 10–1, and their performance on the three crystal planes is different. The electrons on the molecular structure in the DNBT unit cell are highly dense. From Figure 4a,b, we can find that the electron density around the carbon atoms in the ring is generally low, while a large number of electrons are distributed around the nitrogen atoms and a certain density of surrounding electron bands are formed, showing strong localization, and this phenomenon is also reflected in the nitro group. In addition, the main molecular structure on these planes is also affected by the weaker electronic localization of atoms from other molecules in the other directions. In particular, it could not be neglected that the N–N–H located on the ring structure of DNBT from the (0,0,1) crystal plane direction shows stronger localization. As proved by Figure 4d–f, a localization phenomenon of N–O–N is exhibited through the information reflected by the ELF intensity. The localization phenomenon in the (0,1,0) direction is even stronger than the contribution of the nitro group, and the N=N conjugation that we are concerned about also has a good electronic localization effect in the (0,0,1) direction, which can maintain the same level with the N–O–N structure. Even though the electronic localization range of DNTO is smaller than that of DNBT and DNAF, a similar phenomenon also occurs on DNTO, that is, there is no localized electron band around the carbon atoms of DNTO, and the main localization effect58 is still caused by N–O–N and nitro groups, simultaneously, both have the similar ELF intensity levels.
Figure 4.
Electronic local function of DNBT (a–c), DNAF (d–f), and DNTO (g–i). The atoms on the ring structure are represented by black fonts, and the atoms on the nitro group are represented by white fonts. Where (a,d,g) are the (1,0,0) crystal plane direction, (b,e,h) are the (0,1,0) crystal plane direction, and (c,f,i) are (0,0,1) crystal plane direction.
On the one hand, the nitro groups, as a supposedly strong current-absorbing group, exhibits a strong degree of electronic localization in the molecular structure, which significantly increases the electronic density in the unit cell and enhance the ability of electronic localization; on the other hand, the manifestation of conjugation can also be demonstrated by ELF analysis, that is, the stable electronic localization in the azole ring from the structure of DNBT, information about the electron density and electronic localized provided by N=N in DNAF. Moreover, the twisting of the group involved in each molecule of the crystal unit and the tightening-relaxation of the ring structure of these compounds will have a certain degree of influence on the change of the ELF value. In particular, superfluous orbital hybridization may be formed on N–O–N; thus, from the perspective of the number of N–O–N, this is one of the reasons why DNAF and DNTO have the same ring structure but different electronic localization capabilities.59 Moreover, the ELF model of each of these compounds does not clearly show the distribution of electrons between adjacent molecules, so these effects are only for the inside of the molecule. Hence, we can use this to extend the insights of electronic structure and optical phenomenon for the target compound.
Because Raman spectroscopy is used to study vibration, rotation, and other low-frequency modes in the system, which is based on the Raman effect of inelastic scattering of monochromatic light. Therefore, this interaction with the molecular vibrations in the crystal causes the energy of the incident photon to move up or down. Moreover, our calculation is to calculate the polarization of each displacement by using the linear response form and numerically calculate the spatial derivative of the macroscopic polarization along the eigenvector of each Raman active phonon mode. Once these derivatives are known, the Raman cross-section can be calculated directly through appropriate spatial averaging. The Raman activity defined by Porezag and Pederson60−62 characterizes the contribution of the phonon mode to the peak intensity of the Raman spectrum. Therefore, when a certain room temperature or a certain range of incident light wavelength is specified, the internal structural properties of the material can be reflected appropriately.45,61
According to the Raman spectrum calculation results of Figure 5a, DNBT, DNAF, and DNTO all have similar high-intensity characteristic peaks in the Raman shift range of 0 to 200 and 1500 to 1600 cm–1, which provides an effective proof for the appearance of nitro groups (including torsion forms). However, the characteristic peaks of the three compounds are significantly different in the range of 200–1500 cm–1. DNBT and DNTO have continuous characteristic peaks in the range of 900–1400 cm–1 except DNAF. It could be attributed to the planar conjugation of DNBT playing a leading role, and coplanar for the intermediate furazan ring of DNTO. These signs indicate that the N=N bond effect of DNAF is weaker than that of DNBT, and the number of furazan rings affects the effect of diffraction. In order to further distinguish the internal structure relationship between DNBT, DNAF, and DNTO, we evaluated the relationship between the internal atomic distance and diffraction angle of the three compounds through crystal structure diffraction simulation. As shown in Figure 5b, the maximum diffraction angles of DNBT, DNAF, and DNTO are 160, 137, and 121°, respectively. Comparing the atomic distance among the three compounds, DNBT is the smallest and DNAF is the largest when diffracting at the same angle. The inner space for the crystal of DNBT is tightest, and the inner space of DNAF is the most relaxed. Therefore, it is not difficult to consider that when light of a specific wavelength is incident on the three compounds, the scattering ability of DNBT is the weakest, and thus, the gathering ability is the strongest. In contrast, DNBT is more difficult to interfere with cancellation, which ideally explains that the maximum absorbance of DNBT is higher than that of DNAF and DNTO. On the basis of these works, we also performed NMR calculations for the structures of DNBT, DNAF, and DNTO (see Supporting Information, Figures S3–S5).
Figure 5.

Raman spectrum analysis of the crystal structure of DNBT, DNAF, and DNTO, evaluation of atomic distance-diffraction angle.
As an effective means to measure the optical and electrical properties of materials and evaluate their chemical stability, according to the frontier molecular orbital theory (FMOT),63−66 we calculated the HOMO and the LUMO for DNBT, DNAF, and DNTO, as demonstrated in Figure 6a and Table 1. The HOMO values of DNBT, DNAF, and DNTO are −6.32026, −6.52151, and −6.62419 eV, respectively, and the LUMO values are −8.18347, −8.87160, and −8.62744 eV, respectively. Besides that, according to the coverage of the positive and negative isosurfaces, the N site and C–N site on the azole ring of DNBT, the N=N site from DNAF, and the two five-membered furazan ring structures from DNTO have obvious molecular orbital (MO) wavefunction phase values, which are beneficial to their intramolecular charge transfer. Furthermore, as both contain the furazan structure, the N=N bond of DNAF is stronger than the furazan ring and the nitro group, and the furazan ring of DNTO is stronger than the nitro group, which indirectly reveals that the role of the N=N bond provides a weakening of the electrophilic ability for the furazan ring in DNAF. These results strongly support the electron-donating ability of title compounds. It can also be considered from the electrostatic potential (ESP) calculation results in Figure 6b. The nitro group is easier to attract electrons, reflecting that it is more electrophilic than other regions in DNBT,27DNAF, and DNTO. In contrast, the N–H region on the azole ring in DNBT and the furazan ring region of DNTO are more nucleophilic than other regions. Thus, from the depth of the color showed in Figure 6b. The electrophilicity of DNAF is weaker than DNBT and DNTO.
Figure 6.
HOMO–LUMO calculation and ESP analysis of DNBT, DNAF, and DNTO. (a) The green color represents the positive isosurface, and the pink color represents the negative isosurface. (a,b) The red, blue, gray, and white spheres represent oxygen atoms, nitrogen atoms, carbon atoms, and hydrogen atoms, respectively.
Table 1. Molecular Orbital Energy Calculation for DNBT, DNAF, and DNTOa.
|
DNBT |
DNAF |
DNTO |
||||
|---|---|---|---|---|---|---|
| MO(s) | E (eV) | ΔE(Gap) (eV) | E (eV) | ΔE(Gap) (eV) | E (eV) | ΔE(Gap) (eV) |
| HOMO | –8.18347 | 1.86321 | –8.87160 | 2.35009 | –8.62744 | 2.00325 |
| LUMO | –6.32026 | –6.52151 | –6.62419 | |||
| HOMO – 1 | –8.68331 | 2.66216 | –8.99001 | 2.74889 | –8.88110 | 2.65769 |
| HOMO + 1 | –6.02115 | –6.24112 | –6.22341 | |||
| HOMO – 2 | –9.01324 | 3.03223 | –9.05440 | 3.04439 | –8.98104 | 2.97229 |
| LUMO + 2 | –5.98101 | –6.01001 | –6.00875 | |||
E (eV), energy; ΔE(Gap) (eV) = ELUMO – EHOMO; MO, molecular orbital.
In addition, it can be comprehensive from the expression of polarizability that one term in the denominator is excitation energy, which is related to the energy difference between the two orbitals excited by the dominant electron.67,68 This can be understood from the perspective of a complete state summation formula (see Supporting Information, Text S2 for details). The narrower the HOMO–LUMO gap, the smaller the overall energy difference between the occupied orbital and the non-occupied orbital, which tends to make the excitation energy to be lower, thus the polarization rate tends to be larger. Therefore, we infer that the excitation energy of DNBT is potentially smaller than DNTO, and the potential excitation energy of DNTO is less than DNAF, which means that DNAF is the most stable among the three compounds.
Conclusions
On the basis of modifying the DFT dispersion correction, we performed absorbance analysis, UV–vis calculations, and electronic structure analysis for DNBT, DNAF, and DNTO. The absorbance performance of DNBT, DNAF, and DNTO on the (0,0,1) crystal plane is better than the other two crystal planes, and the maximum absorbance for each of them is overall higher than that of TNT and picric acid. The generation of secondary light has the greatest impact on the absorbance of DNBT on the (0,1,0) and (0,0,1) crystal planes, of DNTO on the (1,0,0) crystal plane. DNBT has the most pronounced absorbance anisotropy. UV–vis spectra show that the maximum absorption wavelengths λmax are 225, 228, and 201 nm, respectively, which are smaller than TNT and PA. The contribution of planar conjugation and π–π stacking is stronger than that of inter-atomic conjugation and non-conjugation due to the orbital analysis for N atoms. The N–N–H structure from DNBT on the (0,0,1) crystal plane, the N–O–N and N=N structure from DNAF on the (0,0,1) crystal plane, and the N–O–N structure from DNTO on all the three crystal planes could be the main contribution for the absorbance of (0,0,1) crystal plane is higher than the other crystal plane. Besides that, the number of five-membered rings for DNTO and DNAF, and the non-conjugation between molecules but the coplanarity is also responsible. Calculations for HOMO and LUMO infer that DNAF is the most stable among the three compounds. Additionally, the nucleophilic direction tended to be on the five-membered ring of DNBT, DNAF, and DNTO. These results should be helpful in the design and optimization of explosives detection methods utilizing optical sensing, meanwhile, broadening people’s horizons of material selection for fluorescent probes.
Finally, as the fourth paradigm of science, data-driven methods have the potential to guide experimenters in the discovery and development of new high-performance materials. The theoretical issue of more efficient machine learning that people have high hopes for is still being extended and expanded; however, such as the design of organic solar cells,69−71 the investigation of the structure of organic optoelectronic components and light-emitting diodes,72 a series of favorable evidence have made certain breakthroughs and accumulations. Therefore, the expansion of these similar methods based on EMs in military and industrial fields is also thought-provoking.
Acknowledgments
The work was supported by the National Natural Science Foundation of China (no. 51874255) and the Opening Project of Oil & Gas Field Applied Chemistry Laboratory of Sichuan Province (YQKF202102). The referees who provided valuable references and suggestions for this work.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c01438.
Computation details and simulation settings; parameter fitting; bonding statistics; evaluation and comparison of dispersion correction; calculations for frequency–absorbance, reflectivity, and refractive index; NMR calculations; equation of the polarization rate; and corresponding reference (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- a Klapötke T. M.Chemistry of High-Energy Materials; De Gruyter: Berlin, 2011. [Google Scholar]; b Bachmann W. E.; Sheehan J. C. A New Method of Preparing the High Explosive RDX. J. Am. Chem. Soc. 1949, 71, 1842–1845. 10.1021/ja01173a092. [DOI] [Google Scholar]
- Pagoria P. F.; Lee G. S.; Mitchell A. R.; Schmidt R. D. A review of Energetic Materials Synthesis. Thermochim. Acta 2002, 384, 187–204. 10.1016/s0040-6031(01)00805-x. [DOI] [Google Scholar]
- Dippold A. A.; Klapötke T. M.; Winter N. Insensitive Nitrogen-Rich Energetic Compounds Based on the 5,5′-Dinitro-3,3′-bi-1,2,4-triazol-2-ide Anion. Eur. J. Inorg. Chem. 2012, 3474–3484. 10.1002/ejic.201200221. [DOI] [Google Scholar]
- Jones F. T.; White L. M. The Composition, Optical and Crystallographic Properties of Two Calcium Oxalate-Chloride Double Salts. J. Am. Chem. Soc. 1946, 68, 1339–1342. 10.1021/ja01211a075. [DOI] [PubMed] [Google Scholar]
- Calabrese J. C.; Cheng L. T.; Green J. C.; Marder S. R.; Tam W. Molecular Second-order Optical Nonlinearities of Metallocenes. J. Am. Chem. Soc. 1991, 113, 7227–7232. 10.1021/ja00019a020. [DOI] [Google Scholar]
- Sifain A. E.; Tadesse L. F.; Bjorgaard J. A.; et al. Cooperative Enhancement of the Nonlinear Optical Response in Conjugated energetic materials: A TD-DFT study. J. Chem. Phys. 2017, 146, 114308. 10.1063/1.4978579. [DOI] [PubMed] [Google Scholar]
- Jharapla P. K.; Vaitheeswaran G.; Gupta M.; Mittal R. Comparative Study of Electronic structure, Optical properties, Lattice Dynamics and Thermal Expansion Behaviour of Energetic Ammonium and Potassium Dinitramide salts. Mater. Chem. Phys. 2021, 267, 124645. 10.1016/j.matchemphys.2021.124645. [DOI] [Google Scholar]
- Guo L.; Tian M.; Feng R.; Zhang G.; Zhang R.; Li X.; Liu Z.; He X.; Sun J. Z.; Yu X. Interface-Targeting Strategy Enables Two-Photon Fluorescent Lipid Droplet Probes for High-Fidelity Imaging of Turbid Tissues and Detecting Fatty Liver. ACS Appl. Mater. Interfaces 2018, 10, 10706–10717. 10.1021/acsami.8b00278. [DOI] [PubMed] [Google Scholar]
- Mozziconacci O.; Subelzu N.; Schöneich C.; Liu Y.; Abend A.; Wuelfing W. P. Probing Protein Conformation Destabilization in Sterile Liquid Formulations through the Formation of 3,4-Dihydroxyphenylalanine. Mol. Pharm. 2020, 17, 3783–3793. 10.1021/acs.molpharmaceut.0c00554. [DOI] [PubMed] [Google Scholar]
- Shiraishi Y.; Nakamura M.; Yamamoto K.; Hirai T. Rapid. Selective, and Sensitive Fluorometric Detection of Cyanide Anions Inaqueous Media by Cyanine Dyes with Indolium-coumarin Linkages. Chem. Commun. 2014, 50, 11583–11586. 10.1039/c4cc05412a. [DOI] [PubMed] [Google Scholar]
- Wu M.-Y.; Li K.; Hou J.-T.; Huang Z.; Yu X.-Q. A Selectivecolorimetric and Ratiometric Fluorescent Probe for Hydrogen Sulfide. Org. Biomol. Chem. 2012, 10, 8342–8347. 10.1039/c2ob26235e. [DOI] [PubMed] [Google Scholar]
- Sun S.-L.; Sun X.-Y.; Sun Q.; Gao E.-Q. Highly Efficient Fluorescent Chemosensor for Nitro Antibiotic Detection Based on Luminescent Coordination Polymers with 2,6-di(4-carboxyphenyl)pyrazine. CrystEngComm 2021, 23, 3167–3174. 10.1039/d1ce00245g. [DOI] [Google Scholar]
- Chu F. Experimental Study of Plastic Optical Fiber TNT Sensor Based on Evanescence Absorption. Opt. Eng. 2012, 51, 054403. 10.1117/1.oe.51.5.054403. [DOI] [Google Scholar]
- Senapati S.; Nanda K. K. MgO Nanocubes as a Self-calibrating Optical Probes for Efficient Ratiometric Detection of the Picric Acid in Solid State. ACS Sustain. Chem. Eng. 2018, 6, 13719–13729. 10.1021/acssuschemeng.8b01330. [DOI] [Google Scholar]
- Sohn H.; Calhoun R. M.; Sailor M. J.; Trogler W. C. Detection of TNT and Picric Acid on Surfaces and in Seawater by Using Photoluminescent Polysiloles. Angew. Chem. 2001, 40, 2104–2105. . [DOI] [PubMed] [Google Scholar]
- Zaier R.; Ayachi S. DFT Molecular Modeling Studies of D-π-A-π-D Type Cyclopentadithiophene- Diketopyrrolopyrrole based Small Molecules Donor Materials for Organic Photovoltaic Cells. Optik 2021, 239, 166787. 10.1016/j.ijleo.2021.166787. [DOI] [Google Scholar]
- Irfan A.; Rasool Chaudhry A.; Al-Sehemi A. G. Electron Donating Effect of Amine Groups on Charge Transfer and Photophysical Properties of 1,3-Diphenyl-1H-Pyrazolo[3,4-b]Quinolone at Molecular and Solid State Bulk Levels. Optik 2020, 208, 164009. 10.1016/j.ijleo.2019.164009. [DOI] [Google Scholar]
- Latosińska J. N.; Latosińska M.; Tomczak M. A.; Medycki W. Conformational Stability and Thermal Pathways of Relaxation in Triclosan (Antibacterial/Excipient/Contaminant) in Solid-State: Combined Spectroscopic (1H NMR) and Computational (Periodic DFT) Study. J. Phys. Chem. A 2015, 119, 4864–4874. 10.1021/acs.jpca.5b02393. [DOI] [PubMed] [Google Scholar]
- Dorotíková S.; Plevová K.; Bučinský L.; Malček M.; Herich P.; Kucková L.; Bobeničová M.; Šoralová S.; Kožíšek J.; Fronc M.; Milata V.; Dvoranová D. Conformational, Spectroscopic, and Molecular Dynamics DFT Study of Precursors for New Potential Antibacterial Fluoroquinolone Drugs. J. Phys. Chem. A 2014, 118, 9540–9551. 10.1021/jp506355f. [DOI] [PubMed] [Google Scholar]
- Arulaabaranam K.; Muthu S.; Mani G.; Irfan A. Conformational Study, FT-IR, FT-Raman, Solvent Effect on UV–Vis, Charge Transfer and Protein–Ligand Interactions of Methyl-2-Pyrazinecarboxylate. J. Mol. Liq. 2021, 341, 116934. 10.1016/j.molliq.2021.116934. [DOI] [Google Scholar]
- O’Sullivan O. T.; Zdilla M. J. Properties and Promise of Catenated Nitrogen Systems As High–Energy– Density Materials. Chem. Rev. 2020, 120, 5682–5744. 10.1021/acs.chemrev.9b00804. [DOI] [PubMed] [Google Scholar]
- Dippold A. A.; Klapötke T. M.; Winter N. Insensitive Nitrogen–Rich Energetic Compounds Based on the 5,5′-Dinitro-3,3′-bi-1,2,4-triazole-2-ide Anion. Eur. J. Inorg. Chem. 2012, 3474–3484. 10.1002/ejic.201200221. [DOI] [Google Scholar]
- Zelenin A. K.; Trudell M. L.; Gilardi R. D. Synthesis and Structure of Dinitroazofurazan. J. Heterocyclic Chem. 1998, 35, 151. 10.1002/jhet.5570350128. [DOI] [Google Scholar]
- Sheremetev A. B.; Kulagina V. O.; Aleksandrova N. S.; Dmitriev D. E.; Strelenko Y. A.; Lebedev V. P.; Matyushin Y. N. Dinitro Trifurazans with Oxy, Azo, and Azoxy Bridges. Propellants, Explos. Pyrotech. 2015, 23, 142–149. . [DOI] [Google Scholar]
- Aldoshin S. M.; Aliev Z. G.; Astrat’ev A. A.; Goncharov T. K.; Dashko D. V.; Milekhin Y. M.; Stepanov I.; Shishov N. I. Crystal Structure of 4,4″-Dinitro-[3,3′,4′,3″]-tris-[1,2,5]-oxadiazole. J. Struct. Chem. 2013, 54, 462. 10.1134/s0022476613020285. [DOI] [Google Scholar]
- Kazakov A. I.; Dashko D. V.; Nabatova A. V.; Stepanov A. I.; Lempert D. B. Thermochemical and Energy Characteristics of DNTF and DNFF. Combust. Explos. Shock Waves 2018, 54, 147–157. 10.1134/s001050821802003x. [DOI] [Google Scholar]
- Bennion J. C.; McBain A.; Son S. F.; Matzger A. J. Design and Synthesis of a Series of Nitrogen-Rich Energetic Cocrystals of 5,5′-Dinitro-2H,2H′-3,3′-bi-1,2,4-triazole (DNBT). Cryst. Growth Des. 2015, 15, 2545–2549. 10.1021/acs.cgd.5b00336. [DOI] [Google Scholar]
- Wiscons R. A.; Bellas M. K.; Bennion J. C.; Matzger A. J. Detonation Performance of Ten Forms of 5,5′-Dinitro-2H,2H′-3,3′-bi-1,2,4-triazole (DNBT). Cryst. Growth Des. 2018, 18, 7701–7707. 10.1021/acs.cgd.8b01583. [DOI] [Google Scholar]
- Seth S.; Matzger A. J. Coordination Polymerization of 5, 5′-Dinitro-2H, 2H′-3, 3′-bi-1, 2, 4-triazole Leads to a Dense Explosive with High Thermal Stability. Inorg. Chem. 2017, 56, 561–565. 10.1021/acs.inorgchem.6b02383. [DOI] [PubMed] [Google Scholar]
- Clark S. J.; Segall M. D.; Pickard C. J.; Hasnip P. J.; Probert M. I. J.; Refson K.; Payne M. C. First Principles Methods using CASTEP. Z. für Kristallogr.-Cryst. Mater. 2005, 220, 567. 10.1524/zkri.220.5.567.65075. [DOI] [Google Scholar]
- Hutter J. Excited State Nuclear Forces from the Tamm–Dancoff Approximation to Time-dependent Density Functional Theory within the Plane Wave Basis Set Framework. J. Chem. Phys. 2003, 118, 3928. 10.1063/1.1540109. [DOI] [Google Scholar]
- Colmenero F.; Escribano R. Thermodynamic, Raman Spectroscopic, and UV–Visible Optical Characterization of the Deltic, Squaric, and Croconic Cyclic Oxocarbon Acids. J. Phys. Chem. A 2019, 123, 4241–4261. 10.1021/acs.jpca.9b01354. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
- Tkatchenko A.; DiStasio R. A. Jr.; Car R.; Scheffler M. Accurate and Efficient Method for Many-Body van der Waals Interactions. Phys. Rev. Lett. 2012, 108, 236402. 10.1103/physrevlett.108.236402. [DOI] [PubMed] [Google Scholar]
- Pfrommer B. G.; Côté M.; Louie S. G.; Cohen M. L. Relaxation of Crystals with the Quasi-Newton Method. J. Comput. Phys. 1997, 131, 233–240. 10.1006/jcph.1996.5612. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J.; Scalmani R. G.; Barone V.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Marenich A.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers K. N.; Kudin V. N.; Staroverov T.; Kobayashi K.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16, Revision C. 01; Gaussian, Inc.: Wallingford CT, 2016.
- Bennett C. H. Efficient Estimation of Free Energy Differences from Monte Carlo Data. J. Comput. Phys. 1976, 22, 245–268. 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
- Mizokawa T.; Fujimori A. Electronic Structure and Orbital Ordering in Perovskite-type 3d Transition-metal Oxides Studied by Hartree-Fock Band-structure Calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 5368–5380. 10.1103/physrevb.54.5368. [DOI] [PubMed] [Google Scholar]
- Jhanwar B. L.; Meath W. J. Dipole Oscillator Strength Distributions, Sums, and Dispersion Energy Coefficients for CO and CO2. Chem. Phys. 1982, 67, 185–199. 10.1016/0301-0104(82)85033-7. [DOI] [Google Scholar]
- Chechin G.; Lapina V. Static Structures of Strained Carbon Chains: DFT-Modeling vs Classical Modeling of the Chain with Lennard-Jones Potential. Mater. Lett. 2019, 9, 151. 10.22226/2410-3535-2019-2-151-156. [DOI] [Google Scholar]
- Heath D. F.; Linnett J. W. Intramolecular Forces between Non-Bonded Atoms. J. Chem. Phys. 1950, 18, 147. 10.1063/1.1747438. [DOI] [Google Scholar]
- Smedarchina Z.; Siebrand W.; Wildman T. A. Intramolecular tunneling exchange of the inner hydrogen atoms in free-base porphyrins. Chem. Phys. Lett. 1988, 143, 395–399. 10.1016/0009-2614(88)87054-4. [DOI] [Google Scholar]
- Ungerer P.; Beauvais C.; Delhommelle J.; Boutin A.; Rousseau B.; Fuchs A. H. Optimization of the Anisotropic United Atoms Intermolecular Potential for n-alkanes. J. Chem. Phys. 2000, 12, 5499–5510. 10.1063/1.481116. [DOI] [PubMed] [Google Scholar]
- Wu Q.; Yang W. Empirical Correction to Density Functional Theory for van der Waals Interactions. J. Chem. Phys. 2002, 116, 515. 10.1063/1.1424928. [DOI] [Google Scholar]
- Tkatchenko A.; Scheffler M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. 10.1103/physrevlett.102.073005. [DOI] [PubMed] [Google Scholar]
- Merkes J. M.; Lammers T.; Kancherla R.; Rueping M.; Kiessling F.; Banala S. Tuning Optical Properties of BODIPY Dyes by Pyrrole Conjugation for Photoacoustic Imaging. Adv. Opt. Mater. 2020, 8, 1902115. 10.1002/adom.201902115. [DOI] [Google Scholar]
- Zhang C.; Li X.; Wang Y.; An M.; Sun Z. A hydrazone organic optical modulator with a π electronic system for ultrafast photonics. J. Mater. Chem. C 2021, 9, 11306–11313. 10.1039/d1tc02434e. [DOI] [Google Scholar]
- Tonami T.; Nagami T.; Okada K.; Yoshida W.; Miyamoto H.; Nakano M. Quantum Design for Singlet-fission-induced Nonlinear Optical Systems: Effects of π Conjugation Length and Molecular Packing of Butterfly-shaped Acenes. J. Chem. Phys. 2020, 153, 084304. 10.1063/5.0013985. [DOI] [PubMed] [Google Scholar]
- Vogt A.; Schwer F.; Förtsch S.; Lorenz C.; Mena-Osteritz E.; Aubele A.; Kraus T.; Bäuerle P. Broadly Applicable Synthesis of Arylated Dithieno[3,2-b:2’,3’-d]pyrroles as Building Blocks for Organic Electronic Material. Chem.—Eur. J. 2021, 48, 12362–12370. 10.1002/chem.202101478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper J. K.; Grant C. D.; Zhang J. Z. Experimental and TD-DFT Study of Optical Absorption of Six Explosive Molecules: RDX, HMX, PETN, TNT, TATP, and HMTD. J. Phys. Chem. A 2013, 117, 6043–6051. 10.1021/jp312492v. [DOI] [PubMed] [Google Scholar]
- Sadlej-Sosnowska N. The Response of Electronic and Energetic Properties of Conjugated vs Aromatic Molecules to an External Uniform Electric Field. Struct. Chem. 2019, 30, 1407–1413. 10.1007/s11224-019-01345-6. [DOI] [Google Scholar]
- Gentili P. L.; Mugnai M.; Bussotti L.; Righini R.; Foggi P.; Cicchi S.; Ghini G.; Viviani S.; Brandi A. The Ultrafast Energy Transfer Process in Naphtole-nitrobenzofurazan Bichromophoric Molecular Systems: A study by Femtosecond UV-vis Pump-probe Spectroscopy. J. Photochem. Photobiol., A 2007, 187, 209–221. 10.1016/j.jphotochem.2006.10.020. [DOI] [Google Scholar]
- Buscemi S.; Vivona N.; Caronna T. Photoinduced Molecular Rearrangements. Some Investigations of the Photochemical Behavior of 3-(Acylamino)-1,2,5-Oxadiazoles (Furazans). J. Org. Chem. 1995, 60, 4096–4101. 10.1021/jo00118a028. [DOI] [Google Scholar]
- Mansø M.; Kilde M. D.; Singh S. K.; Erhart P.; Moth-Poulsen K.; Nielsen M. B. Dithiafulvene Derivatized Donor-acceptor Norbornadienes with Redshifted Absorption. Phys. Chem. Chem. Phys. 2019, 21, 3092–3097. 10.1039/c8cp07744d. [DOI] [PubMed] [Google Scholar]
- Peng S.-H.; Wang L. L.; Cai S. S.; Xiao H. Q.; Zhao X. T.; Wang H.; Liu H. Y. UV, FL and IR Spectroscopic Analysis of N-Confusedmeso-Tetra(methoxyphenyl)porphyrins. J. Porphyr. Phthalocyanines 2022, 26, 195–202. 10.1142/s1088424622500031. [DOI] [Google Scholar]
- Zhao W.; Li B.; Xu S. Y.; Zhao Q. DFT/TD-DFT Study of the Structural and Spectral Properties of Two Forms of Rhodamine B. J. Theor. Comput. Chem. 2015, 14, 1550030. 10.1142/s0219633615500303. [DOI] [Google Scholar]
- Suomivuori C.-M.; Fliegl H.; Starikov E. B.; Balaban T. S.; Kaila V. R. I.; Sundholm D. Absorption Shifts of Diastereotopically Ligated Chlorophyll Dimers of Photosystem I. Phys. Chem. Chem. Phys. 2019, 21, 6851–6858. 10.1039/c9cp00616h. [DOI] [PubMed] [Google Scholar]
- Rincón L.; Alvarellosb J. E.; Almeida R. An Analysis of Two Local Measures of the Electronic Localization: a Comparison with the ELF and the Exchange-correlation Density Results. Phys. Chem. Chem. Phys. 2011, 13, 9498–9506. 10.1039/c0cp02711a. [DOI] [PubMed] [Google Scholar]
- Costa S. N.; Sales F. A. M.; Freire V. N.; Maia F. F. Jr.; Caetano E. W. S.; Ladeira L. O.; Albuquerque E. L.; Fulco U. L. L-Serine Anhydrous Crystals: Structural, Electronic, and Optical Properties by First-Principles Calculations, and Optical Absorption Measurement. Cryst. Growth Des. 2013, 13, 2793–2802. 10.1021/cg400111w. [DOI] [Google Scholar]
- Porezag D.; Pederson M. R. Infrared Intensities and Raman-scattering Activities within Density-Functional Theory. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 7830. 10.1103/physrevb.54.7830. [DOI] [PubMed] [Google Scholar]
- Patton D. C.; Porezag D. V.; Pederson M. R. Simplified Generalized-gradient Approximation and Anharmonicity: Benchmark Calculations on Molecules. Phys. Rev. B: Condens. Matter Mater. Phys. 1997, 55, 7454. 10.1103/physrevb.55.7454. [DOI] [Google Scholar]
- Porezag D.; Pederson M. R.; Liu A. Y. Importance of Nonlinear Core Corrections for Density-functional based Pseudopotential Calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 60, 14132–14139. 10.1103/physrevb.60.14132. [DOI] [Google Scholar]
- Javed I.; Khurshid A.; Arshad M. N.; Wang Y. Photophysical and Electrochemical Properties and Temperature Dependent Geometrical Isomerism in Alkyl Quinacridonediimines. New J. Chem. 2014, 38, 752–761. 10.1039/c3nj00477e. [DOI] [Google Scholar]
- Ali A.; Khalid M.; Tahir M. N.; Imran M.; Ashfaq M.; Hussain R.; Assiri M. A.; Khan I. Synthesis of Diaminopyrimidine Sulfonate Derivatives and Exploration of Their Structural and Quantum Chemical Insights via SC-XRD and the DFT Approach. ACS Omega 2021, 6, 7047–7057. 10.1021/acsomega.0c06323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srnec M.; Solomon E. I. Frontier Molecular Orbital Contributions to Chlorination Versus Hydroxylation Selectivity in the Non-heme Iron Halogenase SyrB2. J. Am. Chem. Soc. 2017, 139, 2396–2407. 10.1021/jacs.6b11995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adeel M.; Braga A. A. C.; Tahir M. N.; Haq F.; Khalid M.; Halim M. A. Synthesis Crystallographic, X-ray Spectroscopic and Computational Studies of Aminothiazole Derivatives. J. Mol. Struct. 2017, 1131, 136–148. 10.1016/j.molstruc.2016.11.046. [DOI] [Google Scholar]
- Ziparo C.; Colognesi D.; Giannasi A.; Zoppi M. Raman Spectra of Ammonia Borane: Low Frequency Lattice Modes. J. Phys. Chem. A 2012, 116, 8827–8832. 10.1021/jp303968p. [DOI] [PubMed] [Google Scholar]
- Vivas M. G.; Barboza C. A.; Germino J. C.; Fonseca R. D.; Silva D. L.; Vazquez P. A. M.; Atvars T. D. Z.; Mendonça C. R.; De Boni L. Molecular Structure–Optical Property Relationship of Salicylidene Derivatives: A Study on the First-Order Hyperpolarizability. J. Phys. Chem. A 2021, 125, 99–105. 10.1021/acs.jpca.0c08530. [DOI] [PubMed] [Google Scholar]
- Mahmood A.; Wang J.-L. Machine Learning for High Performance Organic Solar Cells: Current Scenario and Future Prospective. Energy Environ. Sci. 2021, 14, 90–105. 10.1039/d0ee02838j. [DOI] [Google Scholar]
- Mahmood A.; Irfan A.; Wang J. L. Developing Efficient Small Molecule Acceptors with sp2-Hybridized Nitrogen at Different Positions by Density Functional Theory Calculations, Molecular Dynamics Simulations and Machine Learning. Chem.—Eur. J. 2022, 28, e202103712 10.1002/chem.202103712. [DOI] [PubMed] [Google Scholar]
- Mahmood A.; Irfan A.; Wang J. L. Machine Learning and Molecular Dynamics Simulation-assisted Evolutionary Design and Discovery Pipeline to Screen Efficient Small Molecule Acceptors for PTB7-Th-based Organic Solar Cells with over 15% Efficiency. J. Mater. Chem. A 2022, 10, 4170–4180. 10.1039/d1ta09762h. [DOI] [Google Scholar]
- Ha J.; Kim S. C.; Jung M.; Lee J. Y. Rational Design of Blocking Groups for High Triplet Energy n-type Host Materials. J. Mater. Chem. C 2022, 10, 5962–5969. 10.1039/d1tc06083j. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.