Seamless phase I/II design for novel anti-cancer agents with competing disease progression

Abstract

Molecularly-targeted agents and immunotherapies have prolonged administration and complicated toxicity and efficacy profiles requiring longer toxicity observation windows and the inclusion of efficacy information to identify the optimal dose. Methods have been proposed to either jointly model toxicity and efficacy, or for prolonged observation windows. However, it is inappropriate to address these issues individually in the setting of dose-finding because longer toxicity windows increase the risk of patients experiencing disease progression and discontinuing the trial, with progression defining a competing event to toxicity, and progression free survival being a commonly used efficacy endpoint. No method has been proposed to address this issue in a competing risk framework. We propose a seamless phase I/II design, namely the competing risks continual reassessment method (CR-CRM). Given an observation window, the objective is to recommend doses that minimizes the progression probability, among a set of tolerable doses in terms of toxicity risk. In toxicity-centered stage of the design, doses are assigned based on toxicity alone, and in optimization stage of the design, doses are assigned integrating both toxicity and progression information. Design operating characteristics were examined in a simulation study compared to benchmark performances, including sensitivity to time-varying hazards and correlated events. The method performs well in selecting doses with acceptable toxicity risk and minimum progression risk across a wide range of scenarios.

1. Introduction

New classes of anti-cancer agents, such as molecularly-targeted agents (MTAs) and immunotherapy, have brought challenges to the development of new oncology drugs, particularly in the setting of dose-finding trials, because designs have long relied on assumptions based on the cytotoxic chemotherapy paradigm [1; 2; 3; 4]. The mechanism of action of these new classes of drugs differs from cytotoxic chemotherapy, leading to prolonged administration and different toxicity and efficacy profiles [3; 5]. The longer periods of administration have been associated with late-onset toxicities. Thus, longer toxicity observation windows have been advocated for dose-finding trials of these agents [1; 4; 6; 7; 8; 9; 10]. Moreover, while monotone increasing dose-efficacy relationships are assumed with cytotoxic agents, MTAs and immunotherapies can potentially exhibit non monotone dose-efficacy relationships. Therefore, the paradigm of selecting the highest dose that can be tolerated in the hope of achieving maximum efficacy, namely the Maximum Tolerated Dose (MTD), has been questioned, and the choice of a so-called optimal dose has been advocated [1; 11; 12]. While methods have been proposed to address these issues individually, they are closely related given that subjects enrolled in oncology dose-finding trials generally are those with poor prognosis, and longer toxicity windows are associated with a greater risk of patients experiencing disease progression. Disease progression or progression free survival is indeed a relevant efficacy endpoint that has been frequently used in phase II trials, and has recently gained interest in phase I/II trials for novel agents in oncology [13]. In the conduct of trials, for ethical reasons, study protocols usually allow treatment discontinuation after progression to propose alternative therapies if available. Similarly, patients who experience toxicity are generally dose reduced or discontinued and are inconsistently followed for efficacy or progression. Therefore, toxicity and progression are mutually exclusive, since both result in trial or treatment discontinuation. While this is a common issue in planning and managing oncology dose-finding trials, it has been traditionally handled in an ad-hoc manner and has been scarcely addressed in the literature.

Most dose-finding designs rely on the full observation of a binary toxicity endpoint in all patients (3+3 design, Continual Reassessment Method [14], escalation with overdose control (EWOC)[15], modified toxicity probability interval design (mTPI)[16], Bayesian Optimal Interval design (BOIN[17])). Therefore, progression with subsequent trial discontinuation within the toxicity window results in mandatory patient replacement. Time-to-event designs, such as the time to event CRM (TITE-CRM), allow for partial observations to be used for sequential MTD estimation and dose assignments during the trial [18]. This leaves room to some practical strategies to handle discontinued partial observations due to progression and to avoid excluding them altogether [19]. However, we showed that the operating characteristics of the design remain impacted to some extent, with decreased performances in correctly selecting the MTD and limiting overdose selection, while progression is considered as an independent censoring event with no use made of this efficacy information [19]. We found that accounting for any discontinuation event as informative censoring, using the cumulative incidence of dose-limiting toxicities (DLT) in a survival CRM setting improved the design operating characteristics compared to the binomial TITE-CRM [20].

Phase I/II designs have been proposed incorporating efficacy to toxicity for dose finding, with binary or continuous endpoints [21; 22; 23] and time-to-event endpoints [24]. These designs mostly assume that both toxicity and efficacy can be observed within the time frame of the trial. However, in the context of these novel agents, it may not be possible to accommodate this requirement due to the lack of a reliable surrogate efficacy endpoints or the short time to progression relative to the toxicity observation window [25]. Nevertheless, as we discussed above, progression and toxicity usually result in trial discontinuation and informative censoring of one another, reciprocally. Overall, patients’ outcomes within the trial are: DLT, disease progression, or completed observation window without DLT nor progression. As we were finalizing our method, Zhang et al. [26] recently proposed a dose finding phase I/II design in this setting, relying on a multinomial distribution for these outcomes, combined with piecewise cause-specific hazards for DLT and progression, imputation of incomplete observations during the trial and a utility function for identifying the optimal dose. A comprehensive method for incorporating competing toxicity and progression as censored time-to-event outcomes has not been proposed.

In this paper, we propose a novel seamless phase I/II design which we call competing risks continual reassessment method (CR-CRM), that can estimate a dose or a set of doses that satisfies traditional toxicity thresholds while minimizing time to progression under the more realistic competing risk framework for time to events endpoints whereby both toxicity and progression can lead to treatment or trial discontinuation and only one of them is observed. This work was motivated by a phase I trial in unresectable sarcoma or malignant peripheral nerve sheath tumors, which is further discussed below.

2. Motivating example

The present work was motivated by a dose-finding trial in patients with unresectable sarcoma or malignant peripheral nerve sheath tumors that was recently completed at Columbia University Irving Medical Center (Clinical Trials Identifier: NCT02584647). The goal of the trial was to identify the maximum tolerated dose (MTD) out of five doses of interest. The trial was designed as a phase I trial, using the time-to-event CRM (TITE-CRM) [18] with a sample size of 24 patients and a pre-specified target DLT probability of 0.25. DLT was defined as any grade 3 or higher non-hematologic toxicity or grade 4 or higher hematologic toxicity in the first two cycles of treatment (i.e. 8 weeks). The TITE-CRM was selected to allow for enrollment before fully observed outcomes at the end of 8 weeks. However, given a median progression-free survival (PFS) of 6 weeks under standard of care [27], we expected almost 50% of discontinuation due to progression by the end of the 8-week toxicity observation window. Ad-hoc rules were used to handle progression events that occurred during DLT window using the TITE-CRM design [19]. Moreover, a phase II trial is currently on-going, directly following the phase I trial, to evaluate the drug efficacy, using progression-free survival as the main endpoint (Clinical Trials Identifier: NCT02584647). A seamless phase I/II design that selects the dose with the minimum progression risk while satisfying a pre-specified toxicity threshold would have been ideal in this setting.

3. Methods

We consider dose-finding trials where patients are followed through an observation window [0, t^⋆] defined for safety assessment by observation of DLTs, and where there is a non negligible risk of disease progression, resulting in treatment discontinuation in this window and therefore precluding complete safety assessment. Disease progression, in the same manner as DLTs, can be defined in the trial protocol, as an aggravation of the patient status, related to the progression of the malignancy, which results in trial discontinuation, so that the patient can be proposed alternative therapy, for ethical reasons. At the same time, we assume that the occurrence of a DLT also results in treatment discontinuation or dose reduction, rendering the assessment of progression challenging and hence to assign a given dose level. In other words, DLT and progression under treatment are mutually exclusive events within [0, t^⋆]. By time t^⋆, a patient may have one and only one of the 3 different states or outcomes: DLT under treatment, progression under treatment, treated with neither DLT nor progression.

These considerations lead us to consider a competing risks framework in the dose-finding setting [28]. Additionally, we propose using a time-to-event approach which allows accommodating a longer follow-up time t* and straightforwardly handling right-censored observations, including those at interim dose-assignment analyses during the trial.

3.1. General notations for censored data

For a patient in a dose-finding trial, let t^⋆ be the prespecified DLT follow-up time. Treatment with a particular drug dose will usually be discontinued or altered (treatment failure) following the occurrence of two events: DLT or disease progression (or non-toxicity-related death). For simplicity, given the framework of oncology dose-finding trials, we will assume no other cause of treatment discontinuation and no censoring due to lost-to-follow-up, since, generally, patients are followed very closely.

Let K indicate the cause of failures, with K = 1 failure due to DLT and K = 2 failure due to progression. Following notations in Putter et al. (2006)[28], let T be the time to failure and define

$$h_k(t)=\underset{\Delta t\to 0}{\text{lim}}\frac{\text{Prob}(t\le T<t+\Delta t,K=k\mid T\ge t)}{\Delta t},$$

the cause-specific hazard of failing from a given cause k = 1 or 2, and

$$H_k(t)={\int }_0^t{h}_k(s)ds,$$

the cause-specific cumulative hazard. The event-free survival at time t can then be defined as follows

$$S(t)=\text{exp}\left\{-\sum _{k=1}^2{H}_k(t)\right\},$$

which is the probability of not having experienced a failure from any cause at time t, that is, in our setting, remaining on treatment without DLT or disease progression. The cumulative incidence function of cause k, p_k(t), is the probability Prob(T ≤ t, K = k), which can be estimated from the cause-specific hazards as

$$p_k(t)={\int }_0^t{h}_k(s)S(s)ds.$$ (1)

Of note, we see that p_k(t) depends on all underlying competing process through S(t), not only on cause k and that p_k(t) is an improper probability distribution, for p_k(∞) = Prob(K = k) < 1.

For any given set of cumulative incidences p_k(t) resulting from k competing processes, cause-specific hazards can be estimated from the observed data under the hypothesis of independence between the competing events and censoring processes [28; 29; 30].

Consider a dose-finding trial with N patients. For each included patient i, i = 1, …, N, we observe the data (U_i, Y_i), where U_i = min{T_i, t^⋆}, Y_i = K_iI(T_i ≤ t^⋆). Here I(·) is the indicator function.

3.2. Objective

With immunotherapies and other anti-cancer agents, which may not have a monotone dose-efficacy profile, the aim of a dose finding trial will be to identify a dose which optimizes efficacy outcomes among tolerable doses. In our setting, optimizing the efficacy outcome corresponds to maximizing the time to progression or progression-free survival (death usually included as a disease progression event).

Define F_k(t, d) = 1 − exp{−H_k(t, d)} the cause-specific cumulative distribution of event k at time t with dose d. Under the assumption that events are independent conditional on the drug dose, F_k(t, d) can be interpreted as the marginal or “potential” [30] probability of event k at time t, in the hypothetical situation where there is no competing event(s) [28]. We propose to use probabilities F_k(t, d) for dose finding, under the working assumption that toxicity and progression are independent consistent with previous work [13; 31]. The appropriateness of this assumption is evaluated in simulations.

First, we define tolerable doses as those with a marginal probability of DLT by time t^⋆, F₁(t^⋆, d), no more than a pre-specified threshold π_DLT (e.g., 0.25), defining maximum tolerable toxicity risk. The set of tolerable doses is:

$$\mathcal{A}=\left\{d:F_1\left(t^{\star },d\right)\le {\pi }_{\text{DLT}}\right\}.$$ (2)

Then, we incorporate information on the time to progression to identify the most desirable dose. Among set $\mathcal{A}$, we rely on F₂(t^⋆, d), the marginal probability of progression by time t^⋆, to identify the best dose(s), d_ν, as the one(s) with minimum progression risk:

$$d_{\nu }=\underset{d\in \mathcal{A}}{\text{arg\hspace{0.17em}min}}\left\{F_2\left(t^{\star },d\right)\right\}.$$ (3)

In some situations, with non-monotone or flat dose-progression relationships, and given the limited sample size of phase I/II trials, the definition of best dose may be too stringent. We therefore define a set D_ν of good doses, as those among tolerable set $\mathcal{A}$ which are sufficiently close to the minimum progression risk:

$${\mathcal{D}}_{\nu }=\left\{d\in \mathcal{A}:F_2\left(t^{\star },d\right)-F_2\left(t^{\star },d_{\nu }\right)\le {\delta }_P,{\delta }_P\ge 0\right\},$$ (4)

where δ_P is a fixed known parameter that can be tuned based on clinical considerations related to the progression risk under standard of care, and depending on the planned trial sample size.

3.3. Working models

Let D be a drug dose assigned to a patient, and $\mathcal{D}=\left\{d_1,\dots ,d_J\right\}$ be the set of doses that are investigated in the trial. We introduce the drug dose as a covariate in the competing risk framework presented above. Both events, DLT and progression, may depend on the drug dose and we propose to model the corresponding cause-specific hazards as functions of D. For simplicity, we model both competing event processes with constant hazard exponential distributions [32; 33].

Let h₁(D) be the cause-specific hazard for DLT and h₂(t, D) the cause-specific hazard for progression. We assume a monotone increasing dose-toxicity relationship on the cause-specific hazard

$$h_1(t,D)=\text{exp}\left({\beta }_{1}D\right).$$ (5)

In the setting of immunotherapy and MTA, we allow for a non monotone dose-progression relationship on the cause-specific hazard h₂ and we define

$$h_2(t,D)=h_2(D)=\text{exp}\left({\beta }_{20}+{\beta }_{21}D+{\beta }_{22}{D}^2\right).$$ (6)

Of note, exp(β₂₀) represents the cause-specific hazard for progression under standard-of-care. Given θ = (β₁, β₂₀, β₂₁, β₂₂) and N included patients, the model likelihood can be written as

$$L(\theta \mid U,Y,D)=\prod _{i=1}^N{f}_1{\left(U_i\mid \theta ,D_i\right)}^{I\left(Y_i=1\right)}{f}_2{\left(U_i\mid \theta ,D_i\right)}^{I\left(Y_i=2\right)}S{\left(U_i\mid \theta ,D_i\right)}^{I\left(Y_i=0\right)},$$

where f_k(t|θ, D) = dp_k(t|θ, D)/dt = h_k(θ^(k), D)S(t|θ, D) are potentially improper density functions in the competing risk framework[33]. The likelihood therefore reduces to

$$L(\theta \mid U,Y,D)=\prod _{i=1}^N{h}_1{\left({\theta }^{(1)},D_i\right)}^{I\left(Y_i=1\right)}{h}_2{\left({\theta }^{(2)},D_i\right)}^{I\left(Y_i=2\right)}S\left(U_i\mid \theta ,D_i\right).$$

Inference on cause-specific hazards can be performed separately for toxicity and progression, from the log-likelihood which factors into 2 distinct pieces. Defining the cause specific parameters vectors, θ⁽¹⁾ = β₁ and θ⁽²⁾ = (β₂₀, β₂₁, β₂₂), h₁(θ⁽¹⁾, D) and h₂(θ⁽²⁾, D) can be estimated separately [28; 32; 33].

3.4. Dose-finding algorithm

The proposed design, CR-CRM, is conducted in three stages: trial initiation, toxicity-centered stage, optimization stage. The first two stages aim at identifying safe doses (equation 2), while allowing accumulating data; the last stage incorporates information on the dose-progression relationship to find the best dose among those which are safe (equation 3). Throughout the trial, patients are dose-assigned in cohorts of size m.

3.4.1. Trial initiation

Initially, doses are assigned in a ruled-based fashion until at least one DLT has been observed, with cohort size m = 1. Given that patient i was assigned dose $d_j\in \mathcal{D}$, patient i + 1 is assigned as follows:

1. dose level d_j, if patient i experienced neither DLT nor progression by t^⋆;

2. dose level d_{min{J, j+1}}, if patient i experienced progression before t^⋆;

3. if patient i experienced a DLT, the trial moves to the next stage and the dose for patient i + 1 is assigned according to the toxicity working model (see next section).

The initial stage requires completion of the observation window for a given patient, unless an event occurs, T_i ≤ t^⋆.

In case the first patient experiences a DLT, the design transitions directly to the next stage, the survival exponential working model allowing maximum likelihood estimation and model-based dose-assignment for the next patient.

3.4.2. Toxicity-centered stage

At that early point in the trial, at least one DLT has been observed (nevertheless, information may not be sufficient to estimate the dose-progression relationship within our model in equation (6)). This model-based stage therefore relies on the toxicity working model (5) only. During this stage, we allocate an upcoming cohort of patients (i + 1)th similarly to the CRM algorithm [34], in the following manner:

$$d_j^{i+1}=\underset{d\in \mathcal{D}}{\text{arg\hspace{0.17em}min}}|{\widehat{F}}_1\left(t^{\star },d\right)-{\pi }_{\text{DLT}}|.$$

This working model is used exclusively until a fraction r of the total planned sample size N has been included, that is up to n₁ = rN included patients. At the extremes, setting r = 1 defines a toxicity-centered design, similar to the TITE-CRM [18]. Setting r = 0 skips the toxicity-centered stage and directly includes the progression endpoint in dose-finding; it is not recommended as information is very limited at beginning of the trial which precludes robust estimation of progression working model (equation 6).

3.4.3. Optimization stage

Starting from the (rN+1)th patient, where r ∈ (0, 1) is a design parameter to be prespecified on planning the trial, we incorporate information on the dose-progression relationship in the dose-assignment process.

After the ith patient being included, i ≥ rN, we define the estimated set of acceptable doses as:

$${\mathcal{A}}_i^{\star }=\{d_j\in \mathcal{D}:d_j\le \underset{d\in \mathcal{D}}{\text{arg\hspace{0.17em}min}}|{\widehat{F}}_1\left(t^{\star },d\right)-{\pi }_{\text{DLT}}|\}.$$

The dose $d_j^{i+1}$ for patient i+1 (or cohort) is assigned based the minimization of the progression risk among the set ${\mathcal{A}}_i^{\star }$. Given the uncertainty on the dose-progression relationship in the setting of sparse data, we use adaptive randomization for dose assignment at this stage [13; 22; 23; 35]. Among the set ${\mathcal{A}}_i^{\star }$ of tolerable doses, a randomization probability R_j of each tolerable dose, $d_j\in {\mathcal{A}}_i^{\star }$, is computed based on the estimate risk of progression, ${\widehat{F}}_2\left(t^{\star },d_j\right)$, as follows:

$$R_j=\frac{1-{\widehat{F}}_2\left(t^{\star },d_j\right)}{{\sum }_{d_j\in {\mathcal{A}}_i^{\star }}1-{\widehat{F}}_2\left(t^{\star },d_j\right)}$$

3.4.4. Trial termination

When the maximum sample size N has been reached and the follow-up completed for every patient, the final estimate of the tolerable set, ${\mathcal{A}}_N^{\star }$, is identified.

We obtain the estimated best dose(s) ${\widehat{d}}_{\nu }$ as the dose(s) associated with the minimum progression marginal risk, among ${\mathcal{A}}_N^{\star }$:

$${\widehat{d}}_{\nu }=\underset{d\in {\mathcal{A}}_N^{\star }}{\text{arg\hspace{0.17em}min}}\left\{{\widehat{F}}_2\left(t^{\star },d\right)\right\}.$$ (7)

In most cases, a unique best dose is estimated, given the progression working model (equation 6). The estimate of the good doses set ${\mathcal{D}}_{\nu }$ is then estimated as the dose levels among ${\mathcal{A}}_N^{\star }$ which are associated with an estimated marginal progression probability ${\widehat{F}}_2\left(t^{\star }\right)$ lying within a range δ_P of the minimum estimated:

$${\widehat{\mathcal{D}}}_{\nu }=\left\{d\in {\mathcal{A}}_N^{\star }:{\widehat{F}}_2\left(t^{\star },d\right)-{\widehat{F}}_2\left(t^{\star },{\widehat{d}}_{\nu }\right)\le {\delta }_P\right\}.$$ (8)

4. Simulation study

4.1. Setting

We conducted a simulation study in this setting to evaluate the operating characteristics of the proposed CR-CRM, in comparison with benchmark performances, in the setting of our motivating example. The observation window was t^⋆ = 8 weeks (with day-level precision) and we considered a setting with K = 5 candidate dose levels, a target maximum tolerable probability of DLT by t^⋆: π_DLT = 0.25, and a threshold δ_P = 0.10 to define the good doses close to the minimum progression risk.

Simulated trials were initiated with the first dose level. The cohort size was 1 patient and no dose skipping was allowed during dose-escalation. We compared total sample sizes of included patients N = (50, 70), for the proposed phase I/II CR-CRM design, consistently with current practice in planning oncology early phase trials [36].

4.2. Calibration of model parameters

The CR-CRM design was calibrated both on the dose skeleton and on the sample size n₁ for the toxicity stage of the design. Both aspects impact the design performance and require tuning.

The dose skeleton was calibrated using the indifference interval approach [37]. We applied this approach to the toxicity working model, which estimates the marginal cumulative incidence of toxicity at the end of the observation window, t^⋆, for each dose: $F_1\left(d,{\beta }_1\right)=1-\text{exp}\left\{-t^{\star }\text{\hspace{0.17em}exp}\left(e^{{\beta }_1}d\right)\right\}$.

Given π_DLT the target probability of toxicity at t^⋆, we define Θ = [b₁, b_J+1] the parameter space for the working model (parameter β₁), and the intervals θ₁ = [b₁, b₂), θ_j = (b_j, b_j+1), for j = 2,…,J − 1, such as b_j verifies F₁(t^⋆, d_j−1; b_j) + F₁(t^⋆, d_j; b_j) = 2π_DLT. In case the MTD coincides with the dose with minimal progression risk among tolerable doses, the desired d_ν can be obtained using backward substitution: $d_{\nu }=F_1^{-1}\left(t^{\star },d_{\nu };{\beta }_0\right)={\pi }_{\text{DLT}}$ with F₁(t^⋆, d_ν; β₀) = π_DLT, where β₀ denotes the prior mean of β₁. If an indifference interval of length 2δ is desired, dose levels d_ν−1 and d_ν+1 can be obtained from the following equations:

$$F_1\left(t^{\star },d_{\nu -1};b_{\nu }\right)+F_1\left(t^{\star },d_{\nu };b_{\nu }\right)=2{\pi }_{\text{DLT}},F_1\left(t^{\star },d_{\nu };b_{\nu +1}\right)+F_1\left(t^{\star },d_{\nu +1};b_{\nu +1}\right)=2{\pi }_{\text{DLT}},$$

$$F_1\left(t^{\star },d_{\nu -1};b_{\nu }\right)={\pi }_{\text{DLT}}-\delta \text{\hspace{1em}and\hspace{1em}}{F}_1\left(t^{\star },d_{\nu +1};b_{\nu +1}\right)={\pi }_{\text{DLT}}+\delta .$$

To compute the initial guesses of the probabilities of toxicity by dose, $\left({\tilde{p}}_1,\dots ,{\tilde{p}}_J\right)$, with F₁(t^⋆, d; β₀) our exponential working model, we used the following equations:

$$d_{j-1}=\text{log}\left[\frac{-\text{log}\left\{1-\left({\pi }_{\text{DLT}}-\delta \right)\right\}}{t^{\star }}\right]\times \frac{1}{e^{b_j}},$$

for j = ν, …, J – 1

$$d_{j+1}=\text{log}\left[\frac{-\text{log}\left(1-\left({\pi }_{DLT}+\delta \right)\right)}{t^{\star }}\right]\times \frac{1}{e^{b_{j+1}}}$$

for j = 1, …, ν, with ${\tilde{p}}_j=1-\text{exp}\left\{-\text{exp}\left(e^{{\beta }_1}{d}_j\right)t^{\star }\right\}$, for j = 1, …, J.

We implemented the algorithm described in Lee and Cheung (2009) [37] to calibrate the width of the indifference intervals in our trial setting, with J = 5 dose levels, and target toxicity probability π_DLT = 0.25. The probability of correct selection (PCS) with the CR-CRM design was estimated over a range of candidate widths of indifference intervals defining the dose skeleton, and over simulation scenarios, by total sample size N = (50, 70).

We also calibrated the design on the size of stage 1, n₁, given N. Specifically, for N = 70, we evaluated n₁ = (20, 25, 30, 35, 40), and for N = 50, n₁ = (15, 20, 25, 30). For each tuning combination (indifference interval width and n₁), 2000 simulated trials were performed.

Overall, in our settings, the optimal length of the indifference interval was .06 and optimal n₁ corresponded to 0.5N, respectively 25 and 35, for total N of 50 and 70. Detailed results of calibration are reported in Supporting Web Materials.

4.3. Simulation scenarios

The design was evaluated in different toxicity scenarios defined by the MTD location assuming accrual was of a rate of 2 patients per observation window. Different scenarios of dose-progression relationship were also considered, covering possible configurations of relationship between the dose-toxicity curve and the dose-progression curve, including monotone decreasing dose-progression relationship, plateau and U-shape. Overall, we performed simulations in 12 scenarios, combining the various dose-toxicity and dose-progression relationships (Figure 1). We describe scenarios by the latent marginal cause-specific cumulative incidences of toxicity and progression at t^⋆, F₁(t^⋆, d) and F₂(t^⋆, d) respectively. Corresponding observed cumulative incidences p_k(t) can be obtained following (1). The progression probability F₂(t^⋆, d) ranged from 0.60 to 0.27, depending on dose, corresponding to an improvement in progression-free survival (PFS) from a median of 6 weeks to 18 weeks at best. As a sensitivity analysis, we also evaluated scenarios with a smaller effect size in progression risk, with F₂(t^⋆, d) ranging from 0.60 to 0.37, the latter corresponding to a median PFS of 12 weeks (Supporting Web materials, figure S4).

Figure 1:

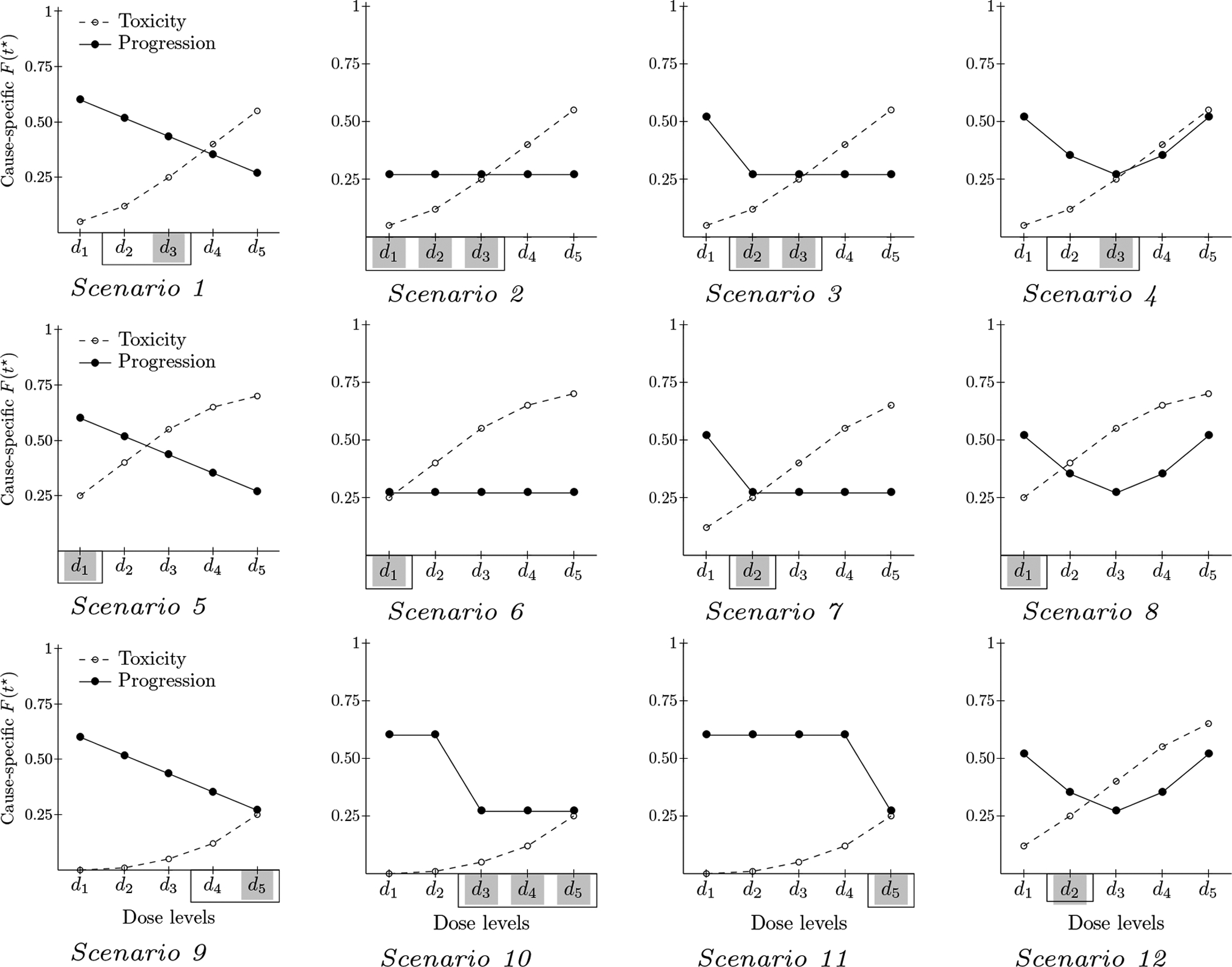
Simulations scenarios: Marginal probability of DLT (dashed line) and progression (solid line) at time t^⋆ by dose. Simulated trials included J = 5 candidate dose levels. For each scenario, the best dose is shaded in gray and the good doses are framed with a solid black line

As per the design objective, the best dose level was that with minimal progression risk among doses with tolerable toxicity risk (Equation 3); the good doses were those with minimal or close to (δ_P = 0.10) minimal progression risk among doses with tolerable toxicity risk (Equation 4).

For data generation, the instantaneous cause-specific hazards of both events, at each dose level, h₁(t) and h₂(t), were back computed from the marginal cumulative incidence values, under the assumptions of independence between events and time-constant hazards, and using exponentially-distributed event times. Following Beyersmann et al. (2009)[38] for competing risks data simulations, observations were then sampled from an exponential model for the time to the first event T (event-free survival), with all-cause hazard h_1k(t) + h_2k(t) and event cause at the sampled time T_i determined by a random draw from a Bernoulli distribution with probability $\frac{h_1\left(T_i\right)}{h_1\left(T_i\right)+h_2\left(T_i\right)}$ for toxicity (otherwise progression), which is constant over time in the case of exponentially-distributed event times. Last, administrative censoring was applied at t^⋆ = 8 to mimic the trial observation window.

To assess the robustness of our proposed method, sensitivity simulations were also conducted using different approaches to generate observations. First, we used time-dependent hazards, using Weibull distributions. Given t^⋆ = 8, we set the Weibull shape parameter at 0.3 or 3, to simulate time-decreasing or increasing hazard respectively (Supplementary material, table 1 and figure S5). In each scenario, the scale parameter was then obtained based on the shape parameter and the marginal event incidence values at t^⋆ = 8. Observations were then generated following the procedure described above [38]. We examined the different combinations of time-decreasing or increasing hazards for toxicity and progression. Furthermore, we also evaluated our method in the case of correlated time-to-events, using Clayton’s model for time-to-event data [24]. Details are available in Supporting Web Materials.

Table 1:

Simulation results: percent of selecting good, best or toxic dose, for the proposed CR-CRM design compared to benchmark performances and Wages and Tait’s design (W&T). Simulated trials with targeted maximum toxicity = 25% and N = 35 + 35. (n/a : not applicable)

					Probability of picking (percent)
Scenario	MTD	Good	Best	Method	Good dose	Best dose	Toxic dose
S1	3	2,3	3	CR-CRM	82	63	10
				Benchmark	90	81	10
				W&T	72	39	3
S2	3	1,2,3	1,2,3	CR-CRM	94	94	6
				Benchmark	99	99	1
				W&T	99	99	1
S3	3	2,3	2,3	CR-CRM	92	92	6
				Benchmark	98	98	2
				W&T	86	86	2
S4	3	2,3	3	CR-CRM	93	69	4
				Benchmark	100	91	0
				W&T	83	42	1
S5	1	1	1	CR-CRM	91	91	9
				Benchmark	87	87	13
				W&T	56	56	4
S6	1	1	1	CR-CRM	95	95	5
				Benchmark	97	97	3
				W&T	80	80	2
S7	2	2	2	CR-CRM	76	76	8
				Benchmark	89	89	3
				W&T	73	73	3
S8	1	1	1	CR-CRM	91	91	9
				Benchmark	90	90	10
				W&T	70	70	6
S9	5	4,5	5	CR-CRM	93	72	n/a
				Benchmark	100	91	n/a
				W&T	40	18	n/a
S10	5	3,4,5	3,4,5	CR-CRM	100	100	n/a
				Benchmark	100	100	n/a
				W&T	77	77	n/a
S11	5	5	5	CR-CRM	80	80	n/a
				Benchmark	93	93	n/a
				W&T	25	25	n/a
S12	2	2	2	CR-CRM	71	71	9
				Benchmark	83	83	8
				W&T	63	63	5

For each scenario, we performed 10000 simulations and estimated: the probability of correct selection as the best dose, the probability of correct selection as good dose, the probability of DLT and progression per trial, the probability of allocation per dose level. Trial algorithm and computations were implemented using R statistical platform, with the L-BFGS-B optimizer for the dose-progression model maximum likelihood estimation. Code for the proposed design and methods is available on GitHub platform: https://github.com/luciebiard.

4.4. Alternative methods

As an indicator of the difficulty of the scenario, given the sample size and our trial objective, we computed benchmark performances in selecting best and good doses using an optimal benchmark non parametric approach for dose finding [39]. Specifically, since our trial objective relied on two endpoints (toxicity and progression), we used an approach similar to that of Cheung (2014)[40] for complex designs, also accounting for the time to event outcomes [41]. While trial designs only use observed outcomes under the doses assigned during the trial, the benchmark uses complete information on patients’ outcomes under each dose, hence providing an optimal performance for the dose-finding objective [39].

Basically, for a given sample size, we first generated the complete outcome for each patient under each dose. Then we estimated the marginal cumulative incidence of toxicity and progression by dose using the non parametric Kaplan-Meier estimator using the complete data and applied the trial objective to determine the best dose (equation (7)). Details of the benchmark approach we applied to our setting are provided in Supporting Web Material.

For comparative purposes in dose selection performances, we also implemented the simulation scenarios with Wages and Tait (2015)’s design [22]. Since the design considers toxicity and activity as binary endpoints, both evaluable within the trial timeframe t^⋆, marginal latent probabilities of toxicity and activity (absence of progression) at time t^⋆ were used for scenarios definition (figure 1). In line with our motivating example, the target DLT rate was 25% and the minimum acceptable activity rate was 40% based on an expected 60% rate of progression within 8 weeks under standard of care (see section 2). The cohort size was 1, the maximum sample size was 70 and we did not implement any stopping rule based on the number of patients treated at one dose. A safety stopping rule relied on the exact binomial 95% confidence interval of the probability of toxicity at dose level 1: if the lower bound of the interval exceeded the target toxicity rate π_DLT, the trial was stopped. Similarly, in the maximization phase of the design, a futility stopping rule defined that the trial was stopped if the upper bound of the 95% exact binomial confidence interval of activity probability was lower than the target activity rate for the estimated optimal dose level [22]. The starting dose level was level 1. We used the available online RShiny application (http://uvatrapps.uvadcos.io/wtdesign/) to obtain simulations results. We ran 5000 replicates simulations for each scenario.

4.5. Operating characteristics

Table 1 summarizes the dose finding performance with a total sample size of 70 patients (first stage n₁ = 0.5N = 35) and constant hazards of events. For each scenario, 1 to 12, the table reports the probability of selecting a good dose, the probability of correctly selecting the best dose (PCS) and the probability of selecting a toxic dose (probability of overdose selection, POS), estimated over simulated trials implementing the proposed CR-CRM design and the benchmark approach.

In these settings, CR-CRM correctly selected the best dose in more than 60% of cases in all scenarios. The design’s performance was consistent with the difficulty of scenarios as assessed by the benchmark. The PCS for the CR-CRM ranged from 63.1 to 99.6%, while the benchmark PCS ranged from 81.0 to 100%. In cytotoxic scenarios (monotone decreasing dose-progression, scenarios 1, 5 and 9), the CR-CRM performed slightly better when the MTD was at the extremes of the dose range: 63.1% in scenario 1 when the MTD is dose level is 3 versus 90.7% and 72.4% in scenarios 5 and 9 when the MTD is dose level 1 and 5 respectively. In plateau scenarios (3, 7, 10 and 11), our design selected the best dose in more than 75% of cases, wherever the location of the true MTD. In U-shape progression scenarios (4, 8 and 12), the PCS for the CR-CRM ranged from 68.6% to 90.7%. The CR-CRM outperformed the W&T design except in scenario 2.

The CR-CRM correctly picked a good dose in more than 70% of cases, ranging from more than 94% in scenarios 2 and 10 with three good doses to 71.4% in scenario 12 with a single good dose, while the benchmark ranged from 100% to 83.4%. The CR-CRM performed slightly better than the benchmark in scenarios 5 and 8 when the MTD is at dose level 1, combined with decreasing progression risk from dose level 1 to 3.

In terms of risk to the patient, the probability of selecting a toxic dose at the end of the trial was lower than 10.23% across all scenarios for the CR-CRM (Table 2). During the trial, the probability of treating a patient with a toxic dose was lower than 20.5% and the probability of a DLT ranged from 13.86 (scenario 10) to 24.2% (scenario 6). The probability of progression during the trial ranged from 23.2 to 50.3% which remained lower than the assumed reference probability of progression without the evaluated drug.

Table 2:

Simulation results: average percent of DLT or progression per trial, of patients treated at toxic doses with the proposed CR-CRM design. Simulated trials with targeted maximum toxicity = 25% and N = 35 + 35. (n/a : not applicable)

					Average percent per trial of
Scenario	MTD	Good	Best	DLT	Progression	Toxic assignment
S1	3	2,3	3	18	41	18
S2	3	1,2,3	1,2,3	17	24	14
S3	3	2,3	2,3	19	26	15
S4	3	2,3	3	18	30	15
S5	1	1	1	20	50	20
S6	1	1	1	24	23	17
S7	2	2	2	21	30	18
S8	1	1	1	22	42	20
S9	5	4,5	5	15	31	n/a
S10	5	3,4,5	3,4,5	14	28	n/a
S11	5	5	5	15	37	n/a
S12	2	2	2	20	35	18

With a smaller total sample size N = 50, the probability of selecting the best dose was slightly impaired but remained greater than 50% in all scenarios (Web figure S6). In the case of a smaller effect size of the drug, decreasing from 60% to 37% (instead of 27%) in the marginal probability of progression at 8 weeks, results were similar. The PCS slightly decreased (less than 10%) compared to the scenarios in table 1, except in scenarios 5, 6 and 8 where the design performed slightly better (Web figure S7).

Results of sensitivity analyses on observations with time-varying hazards or correlated events are available in Supporting Web Materials (figures S8 and S9). In case of late-onset events (increasing hazards), the PCS was maintained, but the POS increased. In case of early onset events (decreasing hazards), while POS was consistently improved compared to constant hazards, PCS decreased except in scenarios with a flat dose-progression relationship (scenarios 2 and 3) or when the true MTD is dose level 1 (scenarios 5, 6, 8). PCS was mostly robust to data generated with correlated times to toxicity and progression, but POS increased.

Of note, in case patients safety is a major concern, the CR-CRM can be modified. The CRM algorithm chooses for dose assignment the dose level with the closest DLT probability to the target π_DLT with the motivation to avoid treating patients at low and inefficacious dose levels [14; 34], which we similarly applied in the CR-CRM to define the tolerable set. Nevertheless, our method can be modified to restrict the tolerable set to dose levels with DLT probability lower than or equal to the target π_DLT. Performances of such a modified CR-CRM (mCR-CRM) are shown in table S2 in Supporting Web Material; this lead to more conservative dose selection, closer to W&T design. The mCR-CRM was even more conservative in scenarios 7 and 12, choosing safer dose level 1 more frequently.

5. Discussion

In this paper, we propose a seamless phase I/II design named competing risks CRM (CR-CRM) for novel anti-cancer drugs such as immunotherapies, with the purpose to identify doses with acceptable toxicity risk and minimum progression risk. This design is particularly useful for immunotherapy dose-finding trials whereby there is a non negligible risk of disease progression during the desired toxicity observation window. Using a competing risks framework with cause-specific time-to-event working models for the dose-toxicity and dose-progression relationships, the design accounts for the practical fact that disease progression and DLT are mutually exclusive events in a trial, since both usually result in treatment discontinuation, while making use of the progression information in the dose-finding setting, rather than handling it as non-informative censoring and replacing patients. A competing risks time-to-event framework also allows continuous enrollment of patients, prolonged observation windows and the inclusion of progression as an efficacy endpoint.

The CR-CRM design performs well in selecting an optimal dose, as well as selecting a set of tolerable good doses within a small range of the dose with the minimum progression risk, particularly in cases with non-monotone dose-progression relationship, where conventional dose-finding designs relying on toxicity only may not apply. The design also offers some flexibility by allowing for the specification of a threshold to define the selection of doses sufficiently close to the minimum progression risk, and the sample sizes split between the toxicity centered and optimization stage. The progression threshold should be specified based on clinical considerations of a clinically meaningful effect size. Based on our simulations, the sample size for toxicity centered stage should be similar to that of the optimization stage.

The proposed CR-CRM outperformed the benchmark in some scenarios, in terms of dose selection. In fact, this has been observed previously for the benchmark approach with a binary endpoint as compared to the original CRM [34]. In sparse settings such as phase I clinical trials, parametric working models may outperform the non parametric benchmark in capturing the dose-response relationship(s) since they allow sharing information across dose levels. The CR-CRM also outperformed the W&T design in most of the selected scenarios, in terms of dose selection. Moreover, via the use of right-censored endpoints, the CR-CRM allows continuous enrollment of patients, contrary to W&T design and other designs relying on binary endpoints which require complete observation of a cohort before including the next one. However, it should be noted that the definition of tolerable doses differs slightly between the designs. For the W&T design, the tolerable set comprises of dose levels with probability of DLT strictly lower than the target threshold [22], whereas the CR-CRM includes dose levels with DLT probability lower, as well as, closer to the target rate, to avoid overly conservative dose-assignments as the CRM [34]. Therefore, as expected the W&T design has lower rates of overdose selection and performs better in scenarios with toxic dose level(s) and flat dose-progression relationship, such as our scenario 2. In case safety of patients is a major concern, the CR-CRM can be modified to accommodate the more conservative definition of the tolerable set. Similarly, the designs differ in the definition of acceptable doses in efficacy. While the W&T design sets a minimum acceptable activity threshold and rely on candidate efficacy skeletons to identify the dose-efficacy relationship, the CR-CRM targets the dose level with maximum efficacy (minimum progression) and allows the specification of a tolerance below (above) it. Therefore, using our definition, poorer performances in selecting good doses are to be expected using the W&T design.

We compared the CR-CRM to the W&T design because it was closer to our design, which targets the marginal latent incidences of events (toxicity and progression). Conversely, Zhang et al.’s recently proposed design targets the observed incidence of outcomes and has therefore a different dose-finding objective [26]. We believe our objective is closer to the current practice in dose finding and more realistic. However, there are pros and cons to either approach defining the dose-finding target, and a formal comparison is difficult, given the different targets.

Sensitivity simulations showed that the CR-CRM performances were mostly robust to time-varying hazards or correlated events. The probability of overdose selection tended to increase in case of late-onset events, especially when the MTD was among the lower dose levels while the dose-progression relationship favoured higher levels. Rules for early trial termination for safety could be defined for practical implementation of the design to limit overdose exposure and selection. Moreover, the proposed working model uses exponential distributions for the cause-specific hazards of toxicity and progression, with time-independent effect of the dose. This allows limiting the number of parameters to be estimated. While these simplified models assume constant and proportional hazards, they support our aim in dose-finding which is to identify the optimal dose, rather than meticulously modeling the dose-response relationships. More complex models might perform better in the setting of time-varying hazards, although their operating characteristics would need further evaluation, in comparison with parsimonious working models.

While the design is proposed along with a calibration procedure for the dose skeleton and a benchmark performance evaluation, both were adapted from existing methods to the present setting of censored endpoints, toxicity and progression. The calibration procedure relied on the toxicity working model to obtain working dose levels. The procedure could therefore be further adapted to more comprehensively account for progression in the calibration of the design. Furthermore, we have proposed the design in a likelihood framework with stages based on the heterogeneity of the outcome data. The implementation of the proposed design using a Bayesian estimation approach would allow for fewer stages and is the subject of further research.

With the increasing number of early stage clinical trials evaluating immunotherapies and MTAs, it is important to start incorporating both late-onset toxicities and efficacy information which are often collected as mutually exclusive events into the identification of optimal doses. This paper is a first attempt at using a comprehensive competing risk framework to solve this complex issue in the context of dose-finding clinical trials.

Supplementary Material

Supplementary Materials

Figure S1. Average PCS across Set 1 scenarios, by calibration interval width, with N = 25 + 25 and N = 35 + 35 patients.

Figure S2. Average PCS in Set 1 scenarios with total sample sizes N = 50 and N = 70 with various sizes n₁ for stage 1.

Figure S3. PCS by interval width and by progression scenario, with N = 70 and various sizes n₁ for stage 1 (Set 1 scenarios: progression probability ranging from 0.60 to 0.27).

Figure S4. Simulation scenarios: Set 2, with progression cause-specific incidence ranging from 0.60 to 0.37 across doses.

Figure S5. Simulated Weibull hazard functions h(t) (left panel) and corresponding cumulative distribution F(t) (right panel) over the observation window t^⋆ = 8: constant (shape=1) or time-varying (decreasing (shape=0.3), increasing (shape=3), with pre-specified F(t^⋆) = 0.25.

Figure S6. PCS by total sample size: N = 35 + 35 or N = 25 + 25, in Set 1 scenarios.

Figure S7. PCS by progression scenario, Set 1 or 2, with N = 35 + 35.

Figure S8. Sensitivity analysis: PCS by type of true hazards, in Set 1 scenarios, with N = 35 + 35.

Figure S9. Sensitivity analysis: POS by type of true hazards, in Set 1 scenarios, with N = 35 + 35.

Table S1. Time-to-event simulations with competing toxicity and progression: example of Weibull parameters by dose level in Scenario 1, with constant (shape=1), decreasing (shape=0.3) or increasing hazard (shape=3), and t^⋆ = 8.

Table S2. Simulation results with the modified CR-CRM algorithm (mCR-CRM), with modified definition of the tolerable set: percent of selecting good, best or toxic dose

Data availability statement

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.