Conformational heterogeneity of UCAAUC RNA oligonucleotide from molecular dynamics simulations, SAXS, and NMR experiments

Abstract

We describe the conformational ensemble of the single-stranded r(UCAAUC) oligonucleotide obtained using extensive molecular dynamics (MD) simulations and Rosetta's FARFAR2 algorithm. The conformations observed in MD consist of A-form-like structures and variations thereof. These structures are not present in the pool generated using FARFAR2. By comparing with available nuclear magnetic resonance (NMR) measurements, we show that the presence of both A-form-like and other extended conformations is necessary to quantitatively explain experimental data. To further validate our results, we measure solution X-ray scattering (SAXS) data on the RNA hexamer and find that simulations result in more compact structures than observed from these experiments. The integration of simulations with NMR via a maximum entropy approach shows that small modifications to the MD ensemble lead to an improved description of the conformational ensemble. Nevertheless, we identify persisting discrepancies in matching experimental SAXS data.

INTRODUCTION

An important step forward in understanding RNA structure is the consideration of ensembles as the best descriptors of flexible systems (Plumridge et al. 2019; Liu et al. 2021). Folding behavior and intermolecular interactions of single-strand RNA molecules have implications in biopharmaceutical drug development, including rational design and predicting delivery properties (Costales et al. 2020), as single stranded antisense oligonucleotides (ASOs) have been approved as drug products starting in 1998 (de Smet et al. 1999). To predict pharmacokinetic properties of native versus modified single stranded RNAs, advanced potential functions and molecular dynamics can be used in conjunction with a variety of biophysical characterization methods.

To this end, solution state nuclear magnetic resonance (NMR) spectroscopy provides an important tool to monitor the dynamics experienced by single-stranded RNAs. A key step in the interpretation of the NMR data is the site-specific resonance assignment, forming the basis of structural analysis. However, the determination of the single-stranded RNA structure, as well as its NMR spectral assignment utilizing nuclear Overhauser effect (NOE) connectivities, is complicated by the fact that oligonucleotides can adopt a variety of conformations which can be difficult to decouple into independent structure contributions to an ensemble (Tubbs et al. 2013; Condon et al. 2015).

Molecular dynamics has been used to aid the interpretation of experimental NMR data into structures and ensembles. Given an adequate amount of experimental data, or a more structured helical system, structure prediction yields good agreement with experimental observables (Bergonzo and Grishaev 2019). Though known to have limited accuracy in predicting complete Boltzmann weighted ensembles of structures (Sponer et al. 2018), MD simulations can be used to effectively explore conformational space and generate accurate structural predictions for well-described free energy minima (Roe et al. 2014).

The accuracy of MD ensembles can be improved by including experimental data in simulations, either a posteriori, as in reweighting or selection schemes, or during simulations (Ward et al. 2013; Hummer and Köfinger 2015; Bonomi et al. 2017). For flexible systems, it is crucial to consider experimental measurements as averages over multiple conformational states, and this should hold true in simulations as well.

Previous studies have shown how to obtain conformational ensembles of dynamic RNA by integrating solution NMR data with extensive MD simulations using maximum entropy approaches (Borkar et al. 2017; Reißer et al. 2020). Furthermore, through the use of this reweighting technique, it has been possible to identify inaccuracies both in the force field and in the experimental data (Bottaro et al. 2018). Force field improvements can be achieved by investigating systems that are large enough to display a high degree of structural complexity, yet simple enough to be amenable to extensive, converged simulations (Bottaro and Lindorff-Larsen 2018). To expand the repertoire of such systems, here we provide an atomic-level detailed structural description of the UCAAUC RNA hexamer oligonucleotide using extensive MD simulations in combination with available NMR (Zhao et al. 2020) and newly measured solution X-ray scattering (SAXS) experimental data. First, we find that two recent MD force fields, namely AMBER FFLJbb (Bergonzo and Cheatham 2015) with OPC water (Izadi et al. 2014) and ROC-RNA (Aytenfisu et al. 2017) with TIP3P water, both produce ensembles containing single-stranded, A-form-like structures but with different conformational preferences. Both ensembles share almost no overlap with the structures generated using Rosetta's FARFAR2 algorithm (Watkins et al. 2020). Second, we compare the computational results with solution experiments, including chemical shifts, ³J scalar couplings, NOE, and SAXS data. We examine the complementary roles played by these experimental data types and show that MD force fields provide a more accurate description of the structure ensemble compared to FARFAR2. Finally, we integrate NMR data into simulations a posteriori using Bayesian maximum entropy reweighting, and describe a conformational ensemble that agrees with all available experimental data.

RESULTS

FFLJbb, ROC-RNA, and FARFAR2 produce different conformational ensembles

We compare three conformational ensembles of the UCAAUC RNA hexanucleotide obtained by extensive MD simulations using the FFLJbb (Bergonzo and Cheatham 2015) and ROC-RNA (Aytenfisu et al. 2017) force fields (see Materials and Methods), and using Rosetta's FARFAR2 (Watkins et al. 2020) algorithm. MD simulations of r(UCAAUC) with the widely used FFOL3 force field (Zgarbová et al. 2011) and TIP3P water have been shown to be less accurate compared to ROC-RNA (Zhao et al. 2020) and are thus not included in this study. MD ensembles were generated using multidimensional replica exchange MD, where temperature and biased dihedral force constant scaling were combined (Bergonzo et al. 2014). Two simulations were initiated from either A-form or extended linear structures, and throughout the manuscript we show results from each independent simulation. Convergence was analyzed by comparing the top five principal components as well as the results of cluster analysis and indicate that the independent simulations are sampling highly similar conformational populations (Supplemental Information 1 and 2).

FFLJbb populates conformations very close to the canonical A-form, as well as distant ones as judged by the histogram in Figure 1A. The structural dissimilarity is here evaluated using a nucleic acid-specific distance called ellipsoidal root-mean-square distance (eRMSD) that only considers the relative arrangements between nucleobases in a molecule (Bottaro et al. 2014). For ROC-RNA, we observe one large peak around eRMSD = 0.75, indicating this ensemble to be less heterogeneous compared to FFLJbb. In FARFAR2, instead, all structures are distant from A-form. The distribution of the radii of gyration (Fig. 1B) shows that FFLJbb is more extended compared to ROC-RNA and FARFAR2, and all three ensembles are on average more compact with respect to the ideal A-form (dashed line in Fig. 1B). To evaluate the degree of overlap between the ensembles, we show in Figure 1C a uMAP projection (McInnes et al. 2018) obtained by aggregating all samples. While FFLJbb and ROC-RNA partially overlap, FARFAR2 samples are located in a different region of this plane. By cluster analysis and visual inspection, we identified in the MD samples A-form-like structures (Aform), C6-inverted (C6-I) (Zhao et al. 2020), C6-bulged (C6-B), U5-bulged (U5-B), C2-bulged (C2-B), and U1-bulged (U1-B) conformations. These structures represent altogether ≈50% of the FFLJbb ensemble, with the remainder being intermediate or other lowly populated conformations. C6 inverted conformations are highly populated (75%) in ROC-RNA ensembles (Fig. 1D); A-form and C6 bulged structures are observed as well, but with lower populations. FARFAR2 ensemble, instead, is composed by a diverse set of compact structures with several intra-molecular interactions, none of them being similar to A-form-like structures (Supplemental Information 3).

FIGURE 1.

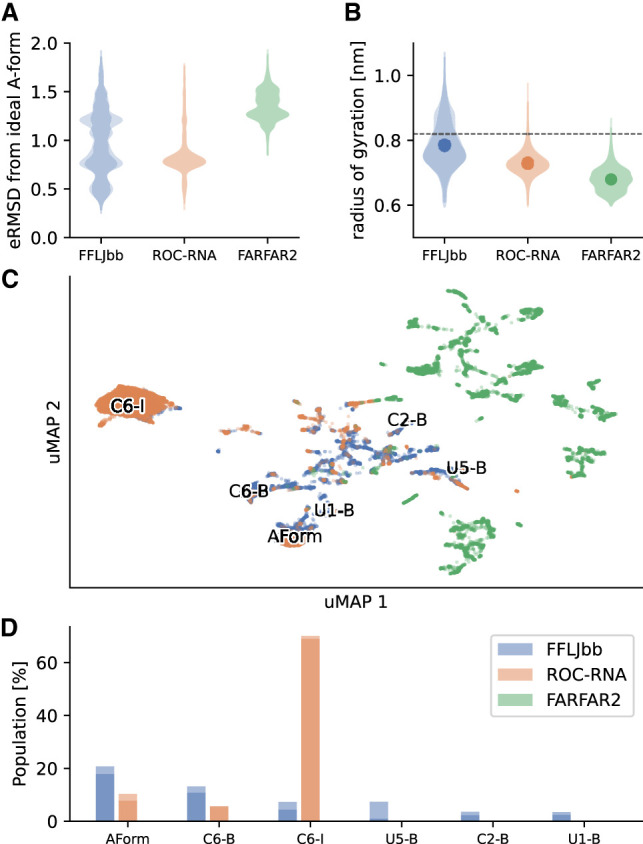
Structural analysis of r(UCAAUC) simulations. (A) eRMSD from ideal A-form histograms. For each ensemble, the distributions calculated for two replicates are shown in shade. (B) Radii of gyration distributions of the three ensembles, as labeled. Averages are shown as dots, and the horizontal dashed line indicates the radius of gyration of an ideal A-form structure. (C) MD simulations and FARFAR2 samples projected onto a uMAP 1/uMAP2 plane. The color scheme follows panels A and B: FFLJbb in blue, ROC-RNA in orange, and FARFAR2 in green. The structures discussed in the main text are labeled on the plane: A-form-like structures (Aform), C6-inverted (C6-I), C6-bulged (C6-B), U5-bulged (U5-B), C2-bulged (C2-B), and U1-bulged (U1-B) structures. (D) Population of different clusters, as labeled. The populations in FARFAR2 ensembles are zero for all clusters.

MD simulations better agree with NMR and SAXS measurements compared to FARFAR2

The conformational ensemble from MD simulations is in qualitative agreement with NMR data that suggest a dominant A-form state in equilibrium with C6-inverted, C6 bulged, and C2-bulged conformations (Zhao et al. 2020). These structures are observed in the FFLJbb ensemble (Fig. 1C,D), and to a lesser extent in ROC-RNA as well. To quantify this agreement, we compare experimental data with ensemble averages calculated for different data sets: chemical shifts (CS), NOE, ³J scalar couplings, unobserved NOE (uNOE), ambiguous NOE (ambNOE) (Zhao et al. 2020), and SAXS. For each data type, we report the ${\mathcal{X}}^2$ calculated for two independent simulations in Figure 2 (see Materials and Methods section). Since ${\mathcal{X}}^2$ is defined as the average squared difference between calculated and experimental measurements normalized by the experimental errors (see Equation 3 in Materials and Methods), values below one are typically considered acceptable (Gull and Daniell 1978). Scatter plots showing experimental versus calculated averages for NMR data are shown in Supplemental Information 4–8. We find that FFLJbb is in better agreement with NOEs, scalar couplings, and SAXS data compared to ROC-RNA and FARFAR2, and that ROC-RNA better agrees with ambiguous and unobserved NOEs. Note also that the sensitivity, positive predictive values, and accuracy calculated from NMR data also suggest FFLJbb to be more accurate compared to ROC-RNA and FARFAR2, as shown in Table 1 (Zhao et al. 2020).

FIGURE 2.

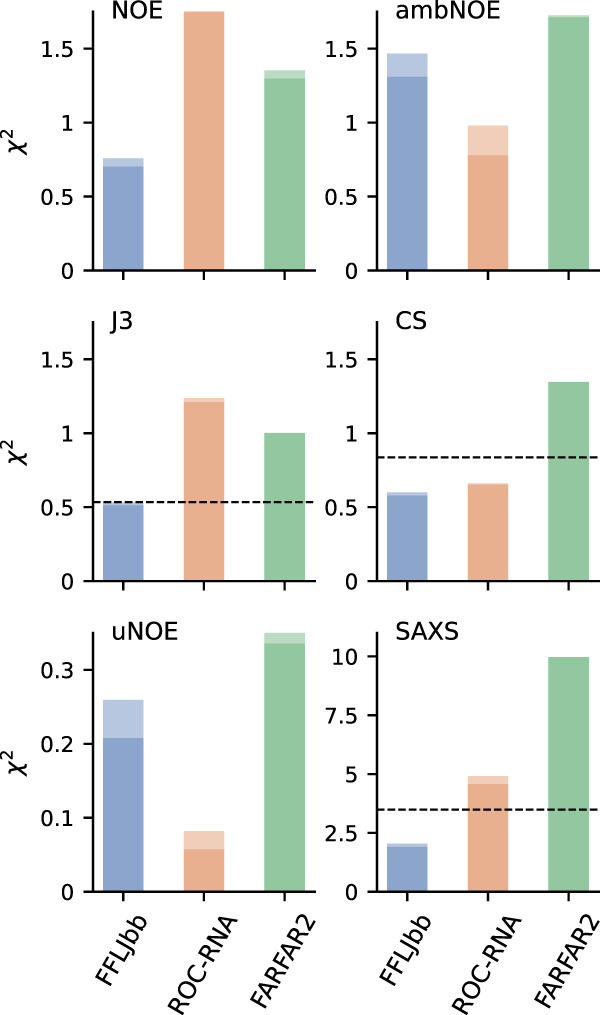
Agreement between NOE, ³J scalar couplings, unobserved NOE (uNOE), chemical shifts (CS), ambiguous NOE (ambNOE), and SAXS data, as labeled. As a reference, the ${\mathcal{X}}^2$ relative to the ideal A-form structure are 6.13 (NOE), 0.02 (uNOE), and 4.82 (ambNOE), while the values for CS, J3, and SAXS are shown as dashed lines. The two bars show the statistics calculated on two independent runs.

TABLE 1.

Sensitivity, positive predictive value (PPV), and accuracy for different ensembles as defined in Zhao et al. (2020)

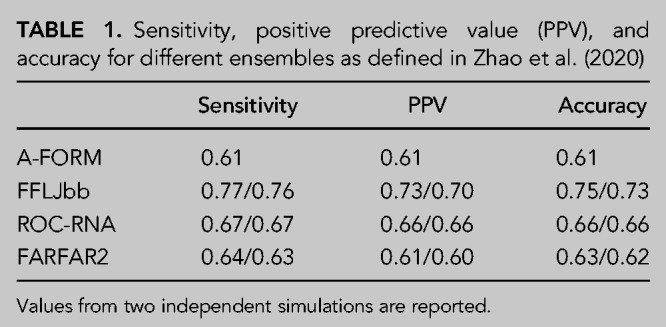
Note that a single, ideal A-form structure is in poor agreement with experimental data, except for unobserved NOEs. These results show that (i) a single A-form structure could not explain the NMR data, as previously described (Zhao et al. 2020) and (ii) at least a fraction of conformations in the computational ensembles do violate unobserved NOEs, indicating the presence of structures not compatible with experimental evidence.

FARFAR2 is a widely used RNA structure prediction algorithm that has been recently used to perform ensemble refinement of flexible regions with improved results compared to MD (Shi et al. 2020). While the agreement between FARFAR2 and experiments is poorer compared to FFLJbb and ROC-RNA, ${\mathcal{X}}^2$ do not significantly exceed unity for all NMR measurements. This is to some extent surprising, as A-form structures are completely absent from the FARFAR2 ensemble (Fig. 1A,C,D; Supplemental Information 3). We observe even larger deviations for SAXS data in the FARFAR2 ensemble, in agreement with the high degree of compaction of FARFAR2 structures (Fig. 1B). Note that here we are using FARFAR2 outside its original scope, as it has been designed to predict the structure of large molecules, and not to sample the equilibrium distribution of a flexible single-stranded RNA. Nonetheless, common applications of FARFAR2 include regions of possible conformational heterogeneity such as loops and bulges, which strongly affect the long-range RNA structure. Our observation of overcompactness, consistent with exaggerated formation of intra-RNA interactions, suggests the need for better validation of conformations generated via this approach.

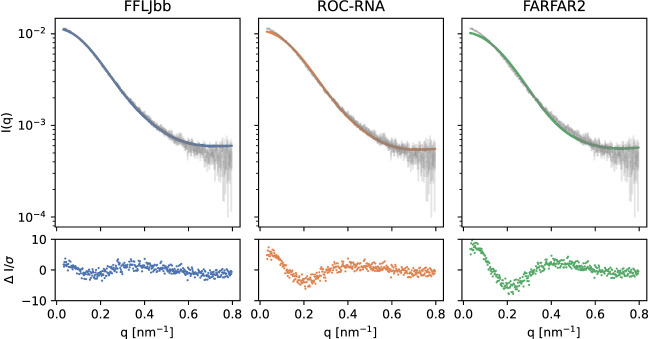
Figure 3 shows the experimental and calculated SAXS intensities for the three ensembles. We find persistent discrepancies between the ensemble-predicted and measured data, particularly at the lowest scattering angles, suggesting the structures sampled in simulations to be overly compact. This result is consistent with previous computational studies (Tan et al. 2018).

FIGURE 3.

(Top panels) Experimental SAXS curve (gray) and average intensities calculated from the ensembles, as labeled. The normalized difference between the two is shown in the bottom panels.

Ensemble-averaged SAXS profiles calculated via FoXS (Schneidman-Duhovny et al. 2010), one of the most popular data modeling methods, exhibit differences with the measured data throughout the entire experimental resolution range, but particularly pronounced at lowest q values. Indeed, the calculated radius of gyration (0.79 nm) is smaller than the experimental one (0.88 nm). SAXS-reported radii of gyration are affected by both the RNA coordinates and the structure of the surface solvent layer. With FoXS placing surface solvent directly on top of the surface-facing atoms rather than offset from them, its use could lead to underestimation of the predicted radii of gyration. To investigate this issue, we repeated SAXS data prediction via two additional techniques, both of which position surface solvent layer outside the volume occupied by the RNA—Crysol (Svergun et al. 1995) and AXES (Grishaev et al. 2010). Crysol uses a layer of uniform electron density to represent the surface solvent implicitly, while AXES uses all-atom molecular representation via frames from an MD simulation of a water-filled volume, with solvent represented explicitly. We find the agreement between the measured and ensemble-predicted data improving from FoXS to Crysol to AXES, with ${\mathcal{X}}^2$ values decreasing by factors of 2.2, and 1.9, respectively. Since AXES leads to the best agreement between the measured and model-predicted data, we use it throughout the manuscript. The impact of the effects such as the distribution of the surface counter ions on the low-angle scattering data is minor as the differences between the SAXS-extracted radii of gyration for the buffers containing 150 mmol/L and 75 mmol/L NaCl do not exceed 0.01 nm.

Conformational ensemble of r(UCAAUC) by integrating MD and NMR

The agreement with experimental data can be further improved by using reweighting techniques. In such approaches, the weight of each sampled set of coordinates is adjusted so that the resulting ensemble averages more closely match experimental measurements compared to the original ensemble. In previous studies, we have used the BME approach (Bottaro et al. 2020a) to provide an accurate description of structure and conformational heterogeneity of RNA tetranucleotides and tetraloops (Bottaro et al. 2018, 2020b). We use a similar approach here and integrate experimental data with simulations. In BME, as in many optimization procedures, the user needs to set the value of a regularization parameter (θ). Small values of θ correspond to a better fit (small ${\mathcal{X}}^2$), whereas in the limit of large θ one approaches the ${\mathcal{X}}^2$ obtained using the original ensemble. At the same time, it is possible to monitor the ${\mathcal{X}}^2$ relative to data that were not used for reweighting (i.e., a validation set): by doing so it is usually possible to identify a range of θ values that provide a trade-off between overfitting and underfitting.

What we observe here is that when we reweight using NMR data, the ${\mathcal{X}}^2$ relative to SAXS (not used for reweighting) is marginally affected (Supplemental Information 9). This observation holds across a wide range of θ values and for all ensembles, indicating that SAXS data are sensitive to the detailed structural information contained in NMR measurements to a small extent.

Conversely, fitting to SAXS data results in a sharp increase of ${\mathcal{X}}^2$ relative to NMR data for small values of θ. By inspecting the structural properties of SAXS-reweighted MD ensembles, we observe that large weights are associated with extended non-A-form structures. Taken together, these results indicate that at least a fraction of the samples in MD simulations are correct on a local scale, but they all possess a degree of compaction that is not fully compatible with SAXS measurements.

This inherent limitation of all computational ensembles makes it difficult to combine both NMR and SAXS data at the same time. Therefore, we proceed by describing the conformational ensemble obtained by reweighting the ensemble that best agrees with all available data (FFLJbb) using only NMR data (Fig. 4).

FIGURE 4.

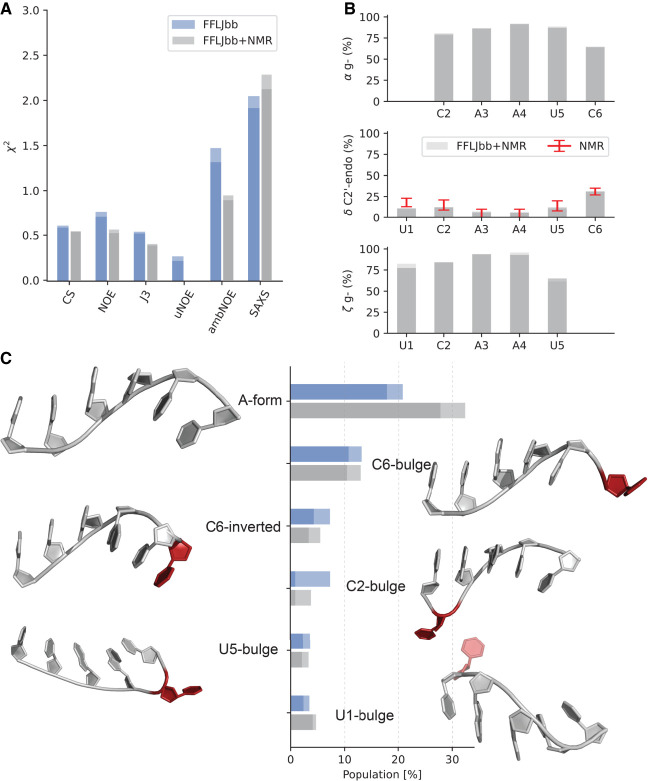
FFLJbb MD ensemble reweighted using NMR data. (A) Agreement with experimental data measured as ${\mathcal{X}}^2$ before (blue bars) and after reweighting (gray bars). (B) Population of rotameric states for each residue: α gauche⁻, δ in C2′-endo, and ζ in gauche⁻ conformation, as indicated. (C) Cluster populations before and after NMR reweighting. The two bars in all panels indicate averages calculated over two independent simulations. Representative three-dimensional structures are shown next to each bar. Nucleotides that deviate from the canonical A-form conformations are shown in red.

By construction, the agreement with chemical shifts, NOE, and scalar couplings improve in the reweighted ensemble. The most significant improvement is observed for uNOE, and the ${\mathcal{X}}^2$ goes to zero, meaning that no uNOE violations are present in the reweighted ensemble. Ideally, we would expect the ${\mathcal{X}}^2$ for SAXS data (not used for reweighting) to become smaller. Instead, it increases by a small amount, likely consistent with the previously noted complementarity between the global long-range SAXS data and local short-range NMR restraints such as NOEs, scalar couplings and chemical shifts.

The weights obtained from integrating FFLJbb and NMR can be used to calculate any observable of choice. As an example, in Figure 4B we report the population of the most variable torsion angles. Residues U1 to U5 are compatible with A-form-like conformations, where pucker angles are predominantly in C3′-endo conformation and α/ζ in gauche⁻. C6 shows a higher degree of flexibility, both around the phosphate group as well as in the sugar. From the FFLJbb + NMR ensemble, we estimate a population of C2′-endo in C6 of 32%. Note that this percentage is compatible with the estimate obtained from ³J scalar couplings alone (31% ± 5%) (Zhao et al. 2020). We note the presence of structures with $\mathcal{X}$ angles in high-anti-conformations (>270°) that have been described in previous simulation studies as possible force field artifacts (Mlynsky et al. 2010; Chen and García 2013; Bergonzo et al. 2015). The presence of high-anti-rotameric states in FFLJbb is below 5% for pyrimidines and in the range 10%–15% for A3 and A4. Since their population is marginally smaller in the reweighted ensembles, we conclude that these high-anti-states might be force-field artifacts, but their presence could not be ruled out completely given the available experimental and simulation data.

We report in Figure 4C NMR-adjusted cluster populations (see also Fig. 1D). The inclusion of NMR data brings the population of A-form structures between 27.8% and 32.4% (≈+11% with respect to the original FFLJbb ensemble). The population of C6 inverted conformations is 3.4%–6%, in agreement with the NOE-based estimate of 6% (Zhao et al. 2020), while the populations of other clusters are below 5% and are essentially unchanged upon NMR reweighting.

The weighted average radius of gyration is 0.78 nm, unchanged or marginally smaller compared to the original FFLJbb ensemble. Note that this value is smaller than the experimental value of 0.89 nm ± 0.01 nm obtained by SAXS measurements, and that both ROC-RNA and FARFAR2 provide more compact structures (Fig. 1B).

DISCUSSION

We started this work as an exercise in calculating the structure ensemble for an RNA hexamer that was reported to have a more complicated composition than a single A-form conformation (Zhao et al. 2020). Through calculating a highly converged ensemble using enhanced sampling, we hypothesized that any errors with respect to the experimental NMR data could be used to quantify errors by the force field. Due to the diversity of the available experimental data including NOEs, chemical shifts, ³J coupling constants, we expected to correlate deviations from forward predictions based on the complete structure ensemble to specific force field terms, i.e., matching ³J coupling constants to limitations in specific torsions, or chemical shifts to balance electrostatic interactions between RNA and water. What we found was that the current FFLJbb force field, used with the OPC water model, reproduced experimental observables from NMR to a high degree—in fact, reweighting only minimally changed the ensemble. By running better converged simulations of the ROC-RNA force field, we were able to confirm the overstabilization of C6 bulged and inverted structures, resulting in a much more homogenous ensemble compared to FFLJbb.

A key result here, that has been recorded elsewhere as well (Zhao et al. 2020), is that a single conformer description of these short and seemingly simple oligonucleotides is insufficient. It is incorrect to describe even these short RNAs as “a structure,” when they are an ensemble that contributes to a whole. A single ideal A-form structure deviated from the experimental NOEs including ambiguous as well as chemical shifts, lacking the structure diversity to fit these observables.

We tried to generate other ensembles to test whether or not having an accurate force field made a difference, versus a non-MD-based functional in Rosetta, FARFAR2, which has been used recently to predict nucleotide bulge conformations via a sample-and-select scheme (Shi et al. 2020). In summary, the results tell us that simply using any ensemble is insufficient—ensembles better matching experimental data are generated using FFLJbb. While the FARFAR2 ensemble tends to fit the NOEs relatively well, there are slight deviations from experiment for ³J coupling constants and more so for the chemical shifts and SAXS data.

This result suggests that multiple, independent experimental observables are important to assess the accuracy of heterogeneous structural ensembles. Furthermore, it is essential to sample the “correct” structures in order for reweighting to be accurate (Rangan et al. 2018).

We find that residual discrepancies with respect to the SAXS data cannot be accounted for by systematic errors of SAXS curve prediction from the RNA coordinates, which may be reflecting a degree of imbalance between the intra-RNA and RNA-solvent interactions carried by the force fields tested here (Salsbury and Lemkul 2021). More work needs to be done to correct for these effects before SAXS data can be used to reweight conformationally heterogeneous ensembles in combination with the NMR data (Plumridge et al. 2017; Bernetti et al. 2021).

MATERIALS AND METHODS

MD simulation setup

An initial RNA structure was built linearly from the sequence (U5 C A A U C3) using tLEaP in Amber18. The A-form RNA was built using the NAB functionality in Amber18 (Case et al. 2018), specifying an A-RNA helix and deleting the complementary strand. The force field used, abbreviated FFLJbb (Bergonzo and Cheatham 2015), combines modified phosphate oxygen van der Waals parameters (Steinbrecher et al. 2012) with previous revisions to FF99 (Wang et al. 2000; Pérez et al. 2007; Zgarbová et al. 2011). The RNA built with FFLJbb was solvated with 3000 OPC water molecules (Izadi et al. 2014). The RNA built with ROC-RNA was solvated with 3000 TIP3P water (Jorgensen et al. 1983). A truncated octahedron box with 1.2 nm buffer from the nucleic acid atoms was used, and five Na⁺ ions were added to neutralize the RNA hexamer's charge, with the addition of six Na⁺ ions and Cl⁻ ions to yield a concentration of 80 mmol/L, where Joung–Cheatham (Joung and Cheatham 2008) monovalent ion parameters were used. A canonical ensemble was implemented with a Langevin thermostat to regulate temperature, with a collision frequency of 5 psec⁻¹ (Loncharich et al. 1992). Exchange between neighboring replicas was attempted every 1 psec. Cutoff for calculating direct space electrostatic interactions was 0.9 nm. SHAKE was used to constrain bonds to hydrogens (Ryckaert et al. 1977), and hydrogen mass repartitioning was implemented, increasing the mass of each solute hydrogen to 3.02 Da and decreasing the mass of the heavy atom to which each solute hydrogen atom is bonded by the same amount, allowing a 4 fsec time step (Hopkins et al. 2015). Two 1 microsecond multidimensional replica exchange MD (M-REMD) (Bergonzo et al. 2014) simulations were performed, starting from each of the initial configurations described above. The temperature range used was as follows, in Kelvin: 277, 279.98, 282.98, 286.01, 289.07, 292.15, 295.26, 298.39, 301.55, 304.77, 307.99, 311.23, 314.5, 317.8, 321.13, 324.48, 327.86, 331.28, 334.72, 338.19, 341.69, 345.21, 348.77, 352.36. The range was calculated using an online generator (Patriksson and van der Spoel 2008). The dihedral force constant bias (Bergonzo et al. 2015) was used over the following range: 1.000 0.971 0.942 0.912 0.883 0.854 0.825 0.796 0.766 0.737 0.708 0.679 0.650 0.620 0.591 0.562 0.533 0.504 0.474 0.445 0.416 0.387 0.358 0.328.

NMR data and forward models

We compare the results of our MD simulations with previously published NMR data (Zhao et al. 2020). Specifically, we consider 64 NOE measurements, 577 unobserved NOEs, 94 chemical shifts and 39 ³J scalar couplings. NOEs are calculated from 5000 evenly spaced frames from the last half of each simulated trajectory (total 10,000 frames) as

$${\mathrm{NOE}}_{\mathrm{CALC}}={\left[\sum _j^n{w}_j{r}_j^{-6}\right]}^{{\displaystyle -\frac{1}{6}}}.$$ (1)

The index j runs over the n frames/models with associated weight W_j, and r is the proton–proton distance. The original data set contains 13 ambiguous NOEs that are calculated by summing the contribution from both nuclei pairs (Zhao et al. 2020):

$$\mathrm{ambNO}{\mathrm{E}}_{\mathrm{CALC}}{\left[\sum _j^n{w}_j(r{1}_j^{-6}+r{2}_j^{-6})\right]}^{{\displaystyle -\frac{1}{6}}}.$$ (2)

We use Larmor D (Frank et al. 2014) to calculate hydrogen and carbon chemical shifts from simulations, while scalar couplings are computed using Karplus equations as defined in the software package BaRNAba (Davies 1978; Lankhorst et al. 1984; Ippel et al. 1996; Marino et al. 1999; Condon et al. 2015; Bottaro et al. 2019).

Bayesian/maximum entropy (MaxEnt) ensemble refinement

The MD simulation ensemble is refined a posteriori by including experimental information into the simulation's ensemble. The refinement is obtained by assigning a new weight to each MD frame, in such a way that the averages calculated with these new weights match more closely a set of input (or “training”) experimental data within a given error. This is achieved by minimizing the following function of the weights W = W₁ …W_n (Hummer and Köfinger 2015):

$$\mathrm{T}\left(\mathit{w}\right)=x^2\left(\mathit{w}\right)-\theta S_{REL}\left(\mathit{w}\right)$$

$$\begin{array}{r}\mathrm{T}(\mathit{w})={\displaystyle \frac{1}{\mathrm{m}}\sum _{\mathrm{i}}^{\mathrm{m}}{\displaystyle \frac{{\left(<F{\left(x\right)>}_i-F_i^{EXP}\right)}^2}{{\sigma }_{\mathrm{i}}^2}+\theta \sum _{i=1}^N{\mathrm{w}}_{\mathrm{i}}\log \left({\displaystyle \frac{w_i}{w_i^0}}\right).}}\end{array}$$ (3)

This corresponds to minimizing the deviation from the experimental measurements (${\mathcal{X}}^2$) with an entropic regularization term (S_REL). The index i runs over m experimental measurements F^EXP_i with associated uncertainty σ_i, while <F(x)>_i indicates the calculated measurement averaged over the ensemble. The initial weights W⁰_i are set to 1/N ∀ i. In the present work, we perform the ensemble refinement using the Bayesian/MaxEnt (BME) code (Bottaro et al. 2020a). The regularization parameter θ was chosen using a k-fold cross-validation procedure.

SAXS

The r(UCAAUC) hexamer was ordered from Integrated DNA Technologies and purified using high-performance liquid chromatography. It was dialyzed into buffers containing 50 mmol/L tris(hydroxymetyl) aminomethane (TRIS), 0.1 mmol/L ethylenediaminetetraacetic acid (EDTA), and either 75 mmol/L NaCl or 150 mmol/L NaCl at pH 6.2 to a final concentration of 2.4 mg/mL. Data were collected at 283K and 298K for RNA concentrations of 0.6 mg/mL, 1.2 mg/mL, and 2.4 mg/mL using MOLMEX Ganesha instrument at IBBR with the sample to a detector distance of 355 mm. As data collected at two lowest concentrations were completely consistent, buffer-subtracted scattering intensity profiles at 1.2 mg/mL RNA were used for further analysis. Theoretical SAXS profiles were predicted from the coordinates of the MD trajectories using FoXS (Schneidman-Duhovny et al. 2010), Crysol (Svergun et al. 1995), and AXES (Grishaev et al. 2010). Ensemble averages were fitted by linear regression to the experimental profile. The fitting parameters were used to scale and shift the calculated average to the experimental profile before calculating the ${\mathcal{X}}^2$ as defined in Equation 3 (Gull and Daniell 1978).

FARFAR2

The FARFAR2 program in Rosetta was used to generate the “FARFAR2” ensemble. 10,000 structures were generated based on the six-residue sequence, and later refined with the high-resolution Rosetta potential (Watkins et al. 2020).

Cluster analysis

Cluster analysis was performed based on similarity, using the heavy atom root mean square deviation (RMSD) of all residues. The last half (500 nsec) of each M-REMD simulation was used. K-means clustering was used to generate eleven clusters, after optimization of the Davies–Bouldin index and pseudo F clustering metrics (see Supplemental Information). The initial set of points chosen was randomized.

uMAP

The low-dimensional uMAP projection (McInnes et al. 2018) was performed using the uMAP Python package version 0.5.1 with nneighbors = 60 and using the collection of G-vectors (Bottaro et al. 2014) as input features. Cluster members were defined as all structures with eRMSD < 0.6 from one of the reference structures described in Figures 1 and 4.

DATA DEPOSITION

MD and FARFAR2 structure ensembles and experimental data in tabular format are hosted on github (https://github.com/sbottaro/UCAAUC).

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.

MEET THE FIRST AUTHOR

Christina Bergonzo.

Meet the First Author(s) is a new editorial feature within RNA, in which the first author(s) of research-based papers in each issue have the opportunity to introduce themselves and their work to readers of RNA and the RNA research community. Christina Bergonzo is the first author of this paper, “Conformational heterogeneity of UCAAUC RNA oligonucleotide from molecular dynamics simulations, SAXS, and NMR experiments.” Christina is a research chemist in the Biomolecular Measurement Division at the National Institute of Standards and Technology.

What are the major results described in your paper and how do they impact this branch of the field?

Multiple, independent experimental observables are necessary to assess the accuracy of heterogeneous RNA, which is best described as an ensemble instead of a single structure. The impact of these results to the field details how to generate and assess these ensembles, telling us that molecular dynamics (MD) simulations yield more descriptive ensembles versus non-MD-based functionals.

What led you to study RNA or this aspect of RNA science?

RNA is more interesting than just what's going on in its helical/ordered regions. The questions of how to represent something inherently flexible, so we can understand it better, has always interested me. MD simulations make a great tool for investigating the dynamics of RNA.

During the course of these experiments, were there any surprising results or particular difficulties that altered your thinking and subsequent focus?

The surprising results were from the Rosetta FARFAR2 predicted ensemble. While the ensemble “fits” the NOE data, that is really because the NOE data tells us less about different conformations than it does about intra-residue distances, which are all pretty fixed. It helped reinforce that we should be comparing to multiple experiments, and a robust MD force field will do a good job approximating all of them.

Are there specific individuals or groups who have influenced your philosophy or approach to science?

Professor Cheatham, who advised my postdoctoral research, is a big influence on my approach to science—it should be open, shared, and communicated in good faith.