Dual-consistency semi-supervision combined with self-supervision for vessel segmentation in retinal OCTA images

Abstract

Optical coherence tomography angiography(OCTA) is an advanced noninvasive vascular imaging technique that has important implications in many vision-related diseases. The automatic segmentation of retinal vessels in OCTA is understudied, and the existing segmentation methods require large-scale pixel-level annotated images. However, manually annotating labels is time-consuming and labor-intensive. Therefore, we propose a dual-consistency semi-supervised segmentation network incorporating multi-scale self-supervised puzzle subtasks(DCSS-Net) to tackle the challenge of limited annotations. First, we adopt a novel self-supervised task in assisting semi-supervised networks in training to learn better feature representations. Second, we propose a dual-consistency regularization strategy that imposed data-based and feature-based perturbation to effectively utilize a large number of unlabeled data, alleviate the overfitting of the model, and generate more accurate segmentation predictions. Experimental results on two OCTA retina datasets validate the effectiveness of our DCSS-Net. With very little labeled data, the performance of our method is comparable with fully supervised methods trained on the entire labeled dataset.

1. Introduction

Abnormalities in the retinal microvasculature often indicate the presence of diseases, such as early-stage glaucomatous optic neuropathy, diabetic retinopathy, and age-related macular degeneration [1–4]. In recent years, several studies have shown that the microvascular morphological changes revealed by OCTA are associated with Alzheimer’s disease and mild cognitive impairment [5,6]. Therefore, the automatic segmentation and quantitative analysis of blood vessels in OCTA images are valuable for the early diagnosis of blood vessel-related diseases affecting the retinal circulation and the assessment of disease progression. However, studies on automatic segmentation of blood vessels in retinal OCTA images are few.

Only a few methods based on fully automatic thresholding schemes have been developed to segment the retinal vessels from OCTA images, such as the method proposed in [7,8]. Several deep learning-based methods for vessel segmentation in OCTA images have been developed recently. Ma et al. [9] proposed an OCTA vessel segmentation network based on coarse-fine two-stage. Mou et al. [10] proposed a segmentation network based on channel and spatial attention. This segmentation network segments large, small, and microvessels into uniform widths and could not obtain an accurate retinal vascular network. Li et al. [11] proposed an end-to-end image projection network that can achieve 3D to 2D image segmentation in OCTA images. The network can input 3D OCTA data and output 2D segmentation results for retinal vessel segmentation. The above methods segment the blood vessels of the retina in OCTA images. They are all based on fully supervised learning, which requires a large number of annotated images to guarantee the accuracy and robustness of the network. Such pixel-level annotation in medical images is laborious and difficult to obtain, particularly for retinal OCTA vessel images, and relies heavily on experienced ophthalmologists.

Training methods with limited supervision are investigated in the present study to address the issues mentioned. These methods, such as self-supervised learning and semi-supervised learning, are dedicated to learning from unlabeled data.

Self-supervised learning methods are trained by defining pretext tasks that can be constructed using only unlabeled data. At present, self-supervised techniques [12–14] are widely used in computer vision. Zhang et al. [15] propose to use grayscale image colorization as a proxy task in self-supervised learning. Spyros et al. [16] predicted the angle of the rotation transformation applied to the input image. In addition to the above methods using image-level losses, some self-supervised techniques using patch-based networks exist. These techniques are similar to real-world jigsaw puzzles. Doersch et al. [17] proposed training a model to predict the relative position of two randomly sampled nonoverlapping image patches. Follow-up works [18,19] generalized this idea to predict the permutation of multiple randomly sampled and permuted patches.

Semi-supervised learning aims to learn from a small number of labeled data and a large number of unlabeled data. Current deep learning-based semi-supervised segmentation methods can be roughly divided into two categories. The first category is pseudo-label-based methods [20–22], which takes the prediction result of the model on the unlabeled image as the pseudo-label, and adds the pseudo-label to the ground truth set for training. However, the segmentation results of these methods are easily affected because of the uneven quality of the predicted pseudo labels. The second category comprises the semi-supervised segmentation methods based on consistency regularization, which encourages consistent segmentation predictions for the same input under different perturbations. A typical example is $\mathrm{\Pi }$ -Model [23], which regularizes the model by adding perturbations to the input data and minimizes the distance between the results of two forward passes. Li et al. [24] introduced other data perturbation and model perturbation on the basis of the average teacher model to improve the regularization effect further and achieved good results.

Inspired by the success of semi-supervised learning and self-supervised learning, we propose in this study a dual-consistency semi-supervised segmentation network that combines multi-scale self-supervised puzzle subtasks(DCSS-Net). We use the self-supervised proxy task in promoting the semi-supervised model to learn better feature representations to improve the model’s segmentation ability. For vessel segmentation, we design a multi-scale self-supervised puzzle prediction proxy task by using two scales of puzzles to tile at different positions, avoiding the network ignoring the connectivity of the blood vessels at the edge of the tile. Then, we propose a dual-consistency training strategy for unlabeled data. Different from the existing extensive data perturbation-based consistency networks, an additional feature perturbation-based consistency regularization is introduced. Regularization can effectively avoid network overfitting and further improve network performance. We evaluated DCSS-Net on both ROSE-1 [9] and private OCTA datasets. The results show that DCSS-Net considerably improves over supervised baselines and outperforms other semi-supervised segmentation methods. The following are the main contributions of this study:

• 1)We propose a semi-supervised segmentation method for vessel segmentation in OCTA. This method only needs to use a small amount of label data to achieve comparable performance to fully supervised methods, thus alleviating the difficulty of vessel labeling in OCTA images and the lack of images with accurate vessel labels. We experiments on two OCTA datasets to demonstrate the effectiveness of our method over other methods.
• 2)A multi-scale self-supervised puzzle subtask is designed. It is used to improve the network performance by assisting the semi-supervised network in learning good feature representations.
• 3)A dual-consistency training strategy based on data perturbation and feature perturbation is proposed to make full use of unlabeled data by further improving the effect of regularization and producing accurate segmentation predictions.

2. Methods

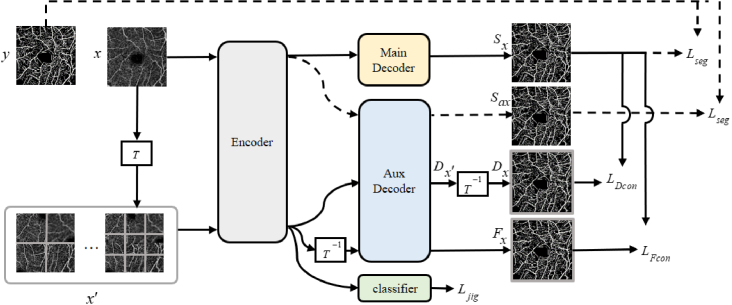
The proposed DCSS-Net framework is shown in Fig. 1. The training set of our framework consists of labeled and unlabeled data. The framework involves four losses (i.e., ${\mathcal{L}}_{jig}$ , ${\mathcal{L}}_{Dcon}$ , ${\mathcal{L}}_{seg}$ , and ${\mathcal{L}}_{Fcon}$ ). Pixel-level supervised loss ${\mathcal{L}}_{seg}$ is used for labeled images to ensure the segmentation capability of the network. Self-supervised loss ${\mathcal{L}}_{jig}$ is used for all images to exploit the rich information in the original data. Feature consistency loss ${\mathcal{L}}_{Fcon}$ and data consistency loss $L_{Dcon}$ are used for unlabeled images to constrain unlabeled data and imporove segmentation performance.

Fig. 1.

Overview of DCSS-Net. The proposed framework optimizes the network by solving self-supervised learning tasks (i.e. supervised by ${\mathcal{L}}_{jig}$ ). The self-supervised task is trained using both labeled and unlabeled images. For labeled images, the supervised loss ${\mathcal{L}}_{seg}$ (dashed path) is calculated using the image label $y$ and the segmentation results $S_x$ and $S_{ax}$ of the two decoders, respectively. A dual-consistency training strategy based on data perturbation and feature perturbation is proposed for unlabeled images. The consistency based on data disturbance is composed of the prediction $S_x$ of the main decoder and the prediction $D_x$ of the auxiliary decoder after inverse transformation. Based on the consistency of feature perturbation, the encoded features are directly inversely transformed. Then they are input to the auxiliary decoder to obtain the result $F_x$ and the prediction $S_x$ of the main decoder to calculate the consistency loss. $T$ refers to the transformation of the puzzle subtask of this study, including operations, such as shuffling image tiles and flipping and rotating.

2.1. Multiscale puzzle subtask

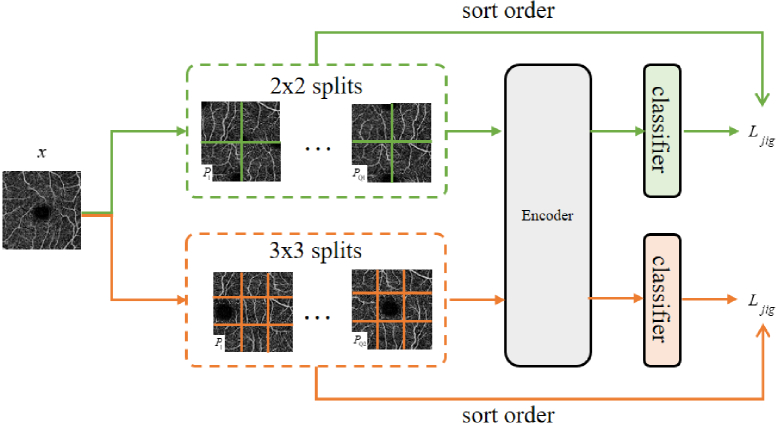
The multi-scale puzzle subtask is inspired by self-supervised learning, as shown in Fig. 2. Self-supervision can mine image information from unlabeled images using various pretexts, such as rotation prediction and coloring. In this study, we use a multi-scale puzzle consisting of flip and rotation transformations as a self-supervised subtask to assist a semi-supervised segmentation network. We divide the image into equal pieces, e.g. 9 pieces represent a 3 $\times$ 3 piece, similar to a standard jigsaw puzzle. We use the method proposed by [18] to form the jigsaw puzzle task by selecting $Q$ permutations with the largest Hamming distance from all permutations to form a subset, selecting one permutation in this subset every time, and using the classifier to predict which permutation is selected in the subset. This method involves a classification task containing $Q$ categories. Therefore, the cross-entropy loss function is used as ${\mathcal{L}}_{jig}$ to supervise this subtask.

Fig. 2.

Multiscale Puzzle Subtask.

To integrate the Jigsaw puzzles task into our semi-supervised framework, we assemble the shuffled tiles into the original size image instead of using a shared-weight neural network for each tile as in the classic self-supervised approach [18]. Then, it is fed into the network for classification. We chooses 2 $\times$ 2 and 3 $\times$ 3 scales for the scale of puzzle segmentation. The subset size $Q$ of the 2 $\times$ 2 scale is set to 20, and the subset size of the 3 $\times$ 3 scale is set to 100. During training, a permutation is selected from the permutation set of 2 $\times$ 2 scale and 3 $\times$ 3 scale respectively, and the image is shuffled, flipped, and rotated randomly. Then, the input network is reassembled for training.

The two scales are combined to consider the continuity of blood vessels in our segmentation task. Using a single-scale transformation often cuts blood vessels at the same location. This scenario is not conducive to the continuity of blood vessels, thereby hindering and misleading the model’s learning of features, such as blood vessel topology and length. Therefore, we use two different scale transformations by dividing tiles at different positions to prevent the network from ignoring the continuity of the blood vessels at the edge of the tile and make up for the lack of information caused by the edge of the tile.

2.2. Dual-consistency learning

DCSS-Net adopts consistency training widely used in semi-supervised learning. However, it differs from the existing methods by having both data perturbation-based and feature perturbation-based dual-consistency regularization without modifying the network structure.

First, we introduce the consistency based on data perturbation. The inherent advantage of our method is that the jigsaw-transformed images can be directly used as perturbed images without additional data perturbation. As shown in Fig. 1, the images $x$ of the self-supervised subtask is shuffled in tiles, rotated and flipped to obtain $x^{\prime }$ . After inverting the transformation of the segmentation results $D_{x^{\prime }}$ obtained by the input network, the final segmentation result $D_x$ is obtained. Consistency loss ${\mathcal{L}}_{Dcon}$ can be constructed with segmentation results $S_x$ of the original image:

$${\mathcal{L}}_{Dcon}=\frac{1}{|{\mathcal{D}}_u|}\sum _{x\in {\mathcal{D}}_u}{d}_{mse}(S_x,D_x)$$ (1)

where $d_{mse}(S_x,D_x)$ represents the mean square error of $S_x$ and $D_x$ , and ${\mathcal{D}}_u$ represents unlabeled training data.

Then, we introduce feature perturbation-based consistency regularization to take full advantage of the unlabeled data and avoid overfitting. The network structure of this study is based on the structure of encoding and decoding. The jigsaw-transformed image $x^{\prime }$ is input into the encoder to obtain the encoded features, and the features are inversely transformed. Then, these features are input to the auxiliary decoder to obtain the blood vessel segmentation result $F_x$ . Consistency loss ${\mathcal{L}}_{Fcon}$ based on feature perturbation is still measured using mean square error:

$${\mathcal{L}}_{Fcon}=\frac{1}{|{\mathcal{D}}_u|}\sum _{x\in {\mathcal{D}}_u}{d}_{mse}(S_x,F_x)$$ (2)

2.3. Loss function

For the OCTA image vessel segmentation task, the overall loss function of the DCSS-Net network proposed in this topic is mainly composed of three parts, as shown in formula (3):

$$\mathcal{L}={\mathcal{L}}_{seg}+w_{ss}\ast {\mathcal{L}}_{jig}+w_{con}\ast {\mathcal{L}}_{Dcon}+w_{con}\ast {\mathcal{L}}_{Fcon}$$ (3)

Among them, $w_{con}$ is unsupervised weight ramp-up function to avoid using the raw noise prediction of the main decoder. $w_{ss}$ is the classification loss weight of the puzzle sub-task. ${\mathcal{L}}_{seg}$ is a supervised loss for labeled images, which uses cross-entropy loss as the loss function. ${\mathcal{L}}_{Dcon}$ and ${\mathcal{L}}_{Fcon}$ are data perturbation-based and feature perturbation-based consistency losses, respectively, which measure the difference between the output of the main decoder and the auxiliary decoder. ${\mathcal{L}}_{jig}$ is the classification loss for the puzzle subtask of all training images, which uses the cross-entropy loss as the loss function.

3. Experiments

3.1. Dataset

In this work, our proposed DCSS-Net is evaluated on two retinal OCTA image datasets. One is the public dataset ROSE-1, and the other is our private dataset.

The ROSE-1 dataset [9] is a public OCTA dataset, which contains a total of 117 images at three levels of SVC, DVC, and SVC+DVC of 39 subjects, and the size of each image is 304 $\times$ 304 pixels. We use blood vessel-rich SVC images for experiments, including 39 images, of which 30 constitute the training set and 9 are the test set. This dataset also contains images with vessel centerline annotations and pixel-level annotations. In this study, we use pixel-level annotations for experiments.

We also collected 62 superficial OCTA blood vessel images from Changsha Aier Eye Hospital, of which 40 were used as the training set and 22 were used as the test set. All used images, with the size of 400 $\times$ 400 pixels, were captured by Optovue OCTA device in the 6 $\times$ 6-mm scan area centered on the fovea. Blood vessels are annotated pixel-wise by an ophthalmologist with five years of experience.

3.2. Evaluation metrics

We use the dice coefficient (DI), jaccard index (JA), pixel-wise accuracy (ACC), area under curve(AUC), and false discovery rate (FDR) as metrics to evaluate the segmentation performance of the DCSS-Net comprehensively and objectively. These evaluation metrics are calculated as follows:

$$\begin{array}{c}DI=\frac{2\times TP}{FP+FN+2\times TP}\\ ACC=\frac{TP+TN}{TP+TN+FP+FN}\\ JA=\frac{TP}{TP+FN+FP}FDR=\frac{FP}{FP+TP}\end{array}$$ (4)

where $TP$ , $TN$ , $FP$ , and $FN$ refer to the number of true positives, true negatives, false positives, and false negatives, respectively.

3.3. Implementation detail

DCSS-Net is a general framework, any segmentation network with encoder-decoder architecture can be used in DCSS-Net. The UNet structure commonly used in the field of medical images is mainly used in the experiments in this paper. We use Pytorch to implement DCSS-Net and train it on an NVIDIA GTX TITAN V GPU. Data augmentation using random rotations and random flips, trained for 200 epochs. Adam is used as optimizer, with the initial learning rate of 1e-2, batch size of 1, and weight decay of 5e-5. In the experiment, we set the classification loss weight $w_{ss}$ to 0.1. The unsupervised weight ramp-up function $w_{con}=10\ast \exp (-5\ast {(1-epoch/N)}^2)$ , and $N$ is set to 400.

3.4. Performance comparison and analysis

3.4.1. Experiments on the ROSE-1 dataset

3.4.1.1. Quantitative and visual results of 3.3 $\mathrm{\%}$ labeled data

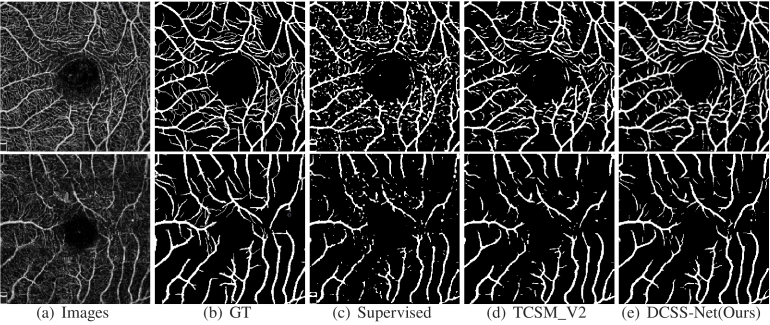
This paper reports the performance of the method trained with 3.3 $\mathrm{\%}$ labeled images and 96.7 $\mathrm{\%}$ unlabeled images, in other words, using only 1 labeled data and 29 unlabeled data. Table 1 shows the experiments using the supervised method and our DCSS-Net on the validation dataset. The supervised method adopts the classic UNet network. Table 1 shows that our DCSS-Net outperforms the supervised method on all evaluation metrics, with considerable improvements of 8.58 $\mathrm{\%}$ and 6.86 $\mathrm{\%}$ on JA and DI, respectively. Our DCSS-Net achieves good performance improvement through unlabeled images. Figure 3 presents the segmentation results of the supervised method and DCSS-Net. The small vessel segmentation results of DCSS-Net are better than the segmentation results obtained by the supervised method. The experimental results show that DCSS-Net is effective compared with supervised learning methods.

Table 1. Comparison of supervised and semi-supervised learning on the validation set of the ROSE-1 (SVC) dataset (3.3 $\mathrm{\%}$ labeled / 96.7 $\mathrm{\%}$ unlabeled).

Metric	Supervised	DCSS-Net
DI	0.6926	0.7612
JA	0.5306	0.6164
ACC	0.8929	0.9135
AUC	0.7922	0.8359
FDR	0.2196	0.1733

Fig. 3.

Vessel segmentation results of different methods on the ROSE-1 dataset.

3.4.1.2. Ablation experiments for model effectiveness

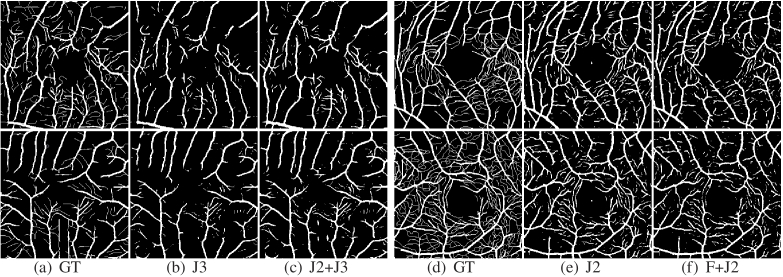
Ablation experiments are performed on ROSE-1 on multi-scale jigsaws and dual-consistency to demonstrate the effectiveness of DCSS-Net. The results are shown in Table 2. In the supervised setting, only 3.3 $\mathrm{\%}$ of the labeled data are used to train the network. The results in Table 2 show that the multi-scale puzzle is good because the multi-scale jigsaw segments the image tiles at different positions to avoid decreased vascular connectivity caused by fixed position segmentation. Dual-consistency also remarkably improves segmentation. The performance can be further improved when dual-consistency is used in conjunction with multi-scale jigsaw puzzles. In Fig. 4, the multi-scale jigsaw segmentation results extract small capillaries, which have good continuity and integrity. The addition of consistency regularization based on feature perturbation alleviates the overfitting problem and allows the model to gain the antinoise ability, suppressing the response in avascular regions.

Table 2. Ablation experiments on the ROSE-1 (SVC) dataset. "J2" represents a 2x2 tiled puzzle, "J3" represents a 3x3 tiled, and "F" represents the use of feature-based consistency.

Setting	DI	JA	ACC	AUC	FDR
F	0.7561	0.6098	0.9134	0.8294	0.1599
J3	0.7526	0.6051	0.9117	0.8290	0.1670
F+J3	0.7584	0.6128	0.9122	0.8346	0.1774
J2	0.7555	0.6089	0.9110	0.8337	0.1798
F+J2	0.7582	0.6123	0.9126	0.8337	0.1743
J2+J3	0.7597	0.6145	0.9133	0.8332	0.1655
F+J2+J3	0.7612	0.6164	0.9135	0.8359	0.1733

Fig. 4.

Vessel segmentation results for ablation experiments.

3.4.1.3. Comparison with other segmentation methods

We compare DCSS-Net with the following recent methods. The first group is fully supervised learning methods. We list some recent state-of-the-art methods, such as CE-Net [25] and OCTA-Net [9], on ROSE-1 using all data as training. Then, we compare our method with many classical and state-of-the-art semi-supervised learning methods.For example, MT [26]and MixMatch [27] are classical semi-supervised methods based on consistency and mixed data augmentation, respectively, which are extended to segmentation for comparison. Self-loop [28] adopts the training method of the pseudo label, TCSM $\mathrm{\_}$ v2 [24] is an advanced semi-supervised segmentation method based on consistency. Partially [29] adopts the idea of partial supervision, which is the most advanced methods at present. The Ratio column indicates the proportion of the labeled data used by the method in the training set. Table 3 shows the performance of different methods on the validation set. Compared with other methods, our method achieves the best results, indicating its effectiveness. Figure 3 shows some visual segmentation results. We can see that our method better guarantees vascular connectivity.

Table 3. Performance comparison on ROSE-1 (SVC) dataset.

Methods	Ratio	Dice	ACC	FDR
CE-Net	100%	0.7511	0.9121	0.1997
OCTA-Net	100%	0.7697	0.9182	0.1775
MT	3.30%	0.6658	0.8827	0.2896
TCSM	3.30%	0.7308	0.9053	0.1827
MixMatch	3.30%	0.7299	0.9079	0.2313
Self-loop	3.30%	0.7416	0.9017	0.2362
TCSM_v2	3.30%	0.7348	0.9070	0.1749
Partially	3.30%	0.7483	0.9119	0.2008
DCSS-Net	3.30%	0.7612	0.9135	0.1733
	6.60%	0.7665	0.9157	0.1613

3.4.1.4. Results under different numbers of labeled data

Table 4 shows the vessel segmentation results of our method (trained with labeled data and unlabeled data) and the supervised method (trained with labeled data only) under different numbers of labeled images. We plot the resulting JA scores in Fig. 5. The results show that DCSS-Net consistently outperform supervised methods in different proportions of labeled data, indicating that DCSS-Net effectively utilizes unlabeled data and brings performance gains. As expected, the performance of supervised training improves when more labeled training images are available(see orange line in Fig. 5). The higher the number of labeled images is, the better the segmentation performance of the semi-supervised learning is(see the red line). The performance gap between supervised training and semi-supervised learning narrows as large numbers of labeled samples become available. This observation is in line with our expectations. When the number of labeled data is small, our method can effectively utilize considerable information in the unlabeled data, and our method can achieve great improvements. By contrast, the improvement becomes limited as the number of labeled data increases.

Table 4. Validation set results of DCSS-Net under different amounts of labeled data.

Ratio	Metric	Supervised	DCSS-Net
3.30%	DI	0.6926	0.7612
	JA	0.5306	0.6164
	ACC	0.8929	0.9135
	AUC	0.7922	0.8359
10.00%	DI	0.7232	0.7669
	JA	0.5677	0.6241
	ACC	0.9002	0.9162
	AUC	0.8144	0.8375
30.00%	DI	0.7501	0.7704
	JA	0.6018	0.6287
	ACC	0.9100	0.9169
	AUC	0.8288	0.8409

Fig. 5.

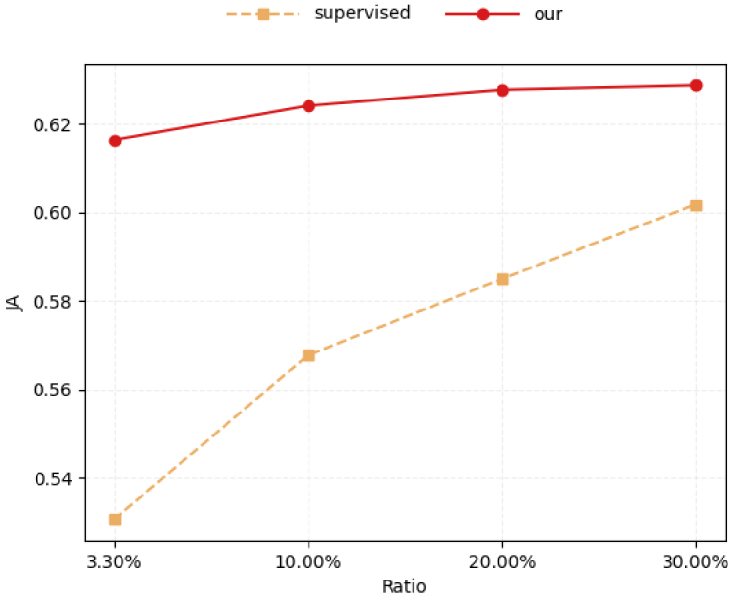
Results on the validation set of the ROSE-1 dataset with different amounts of labeled data.

3.4.2. Experiments on private OCTA datasets

3.4.2.1. Comparison with other semi-supervised segmentation methods

We also conduct experiments on the private OCTA dataset. Table 5 shows the experimental results. With only 2.5 $\mathrm{\%}$ and 5 $\mathrm{\%}$ of the annotated data, our method can still perform well on this dataset. Compared with semi-supervised methods, our method can achieve high performance on the metrics under the same scale of labeled data.

Table 5. Performance comparison on private OCTA dataset.

Methods	Ratio	DI	JA	ACC	AUC	FDR
Supervised	100%	0.8870	0.7970	0.8857	0.8852	0.1197
	2.50%	0.8654	0.7628	0.8626	0.8619	0.1481
MT	2.50%	0.8750	0.7780	0.8794	0.8791	0.0891
TCSM	2.50%	0.8713	0.7720	0.8702	0.8693	0.1328
Self-loop	2.50%	0.8756	0.7789	0.8795	0.8778	0.1282
TCSM_v2	2.50%	0.8781	0.7828	0.8775	0.8769	0.1233
DCSS-Net	2.50%	0.8896	0.8013	0.8870	0.8882	0.1146
	5.00%	0.9055	0.8274	0.9041	0.9037	0.1033

3.4.2.2. Results with different numbers of labeled data

Table 6 shows the experimental results of the ablation of our method on private datasets with respect to the number of labeled data. The results are consistent with the results on the ROSE dataset. Our method consistently outperforms the supervised methods in different proportions of the labeled data, fully demonstrating that our method effectively utilizes unlabeled data and brings performance gains.

Table 6. Validation set results of our method on different amounts of labeled data.

Ratio	Metric	Supervised	DCSS-Net
2.50%	DI	0.8654	0.8896
	JA	0.7628	0.8013
	ACC	0.8626	0.8870
	AUC	0.8619	0.8882
10.00%	DI	0.8773	0.9117
	JA	0.7814	0.8378
	ACC	0.8752	0.9105
	AUC	0.8745	0.9101
30.00%	DI	0.8812	0.9146
	JA	0.7877	0.8427
	ACC	0.8805	0.9139
	AUC	0.8800	0.9135

4. Conclusion

In this study, we propose a dual-consistency semi-supervised segmentation method incorporating the multi-scale self-supervised jigsaw subtask for the OCTA vessel segmentation task. In addition to the segmentation task, a self-supervised puzzle prediction task, which uses the self-supervised task to learn good feature representations, is introduced. The method also uses a combination of two scales to improve the connectivity of the blood vessels at the edge of the tile. We also propose a dual-consistency regularization strategy based on data perturbation and feature perturbation to make full use of unlabeled data and avoid method overfitting, allowing the model to learn information as accurately as possible. Experiments are conducted on two OCTA datasets. The experimental results demonstrate the feasibility and superiority of our method.

Funding

National Natural Science Foundation of China10.13039/501100001809 (61672542, 61972419); Natural Science Foundation of Hunan Province10.13039/501100004735 (2020JJ4120, 2021JJ30865, 2021JJ30879).

Disclosures

The authors declare no conflicts of interest.

Data availability

ROSE-1 datasets underlying the results presented in this paper are available at [9]. The private dataset underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.