Abstract
We present a novel optical coherence elastography (OCE) method to characterize mechanical hysteresis of soft tissues based on transient (milliseconds), low-pressure (<20 Pa) non-contact microliter air-pulse stimulation and micrometer-scale sample displacements. The energy dissipation rate (sample hysteresis) was quantified for soft-tissue phantoms (0.8% to 2.0% agar) and beef shank samples under different loading forces and displacement amplitudes. Sample hysteresis was defined as the loss ratio (hysteresis loop area divided by the total loading energy). The loss ratio was primarily driven by the sample unloading response which decreased as loading energy increased. Samples were distinguishable based on their loss ratio responses as a function loading energy or displacement amplitude. Finite element analysis and mechanical testing methods were used to validate these observations. We further performed the OCE measurements on a beef shank tissue sample to distinguish the muscle and connective tissue components based on the displacement and hysteresis features. This novel, noninvasive OCE approach has the potential to differentiate soft tissues by quantifying their viscoelasticity using micron-scale transient tissue displacement dynamics. Focal tissue hysteresis measurements could provide additional clinically useful metrics for guiding disease diagnosis and tissue treatment responses.
1. Introduction
Soft tissue biomechanical properties (e.g., stiffness, elasticity, and viscosity) are directly associated with tissue structure, health, aging, and function. Pathological tissue changes such as tumors, swelling, or inflammation, are often accompanied by changes in the mechanical properties at organ-, tissue-, or cellular- levels [1–3]. Changes affecting tissue mechanical properties have become a hallmark for the diagnosis of many human diseases. For example, liver fibrosis is associated with cirrhosis [4]; arterial wall stiffness is related to systemic inflammation and atherosclerosis in hypertension [5]; and breast tissue fibrosis or tumor formations have altered stiffness that can be differentiated from normal or benign tissue formations [6].
Tissue elasticity is usually defined as a static property in response to an immediate deformation force or mechanical stress, which arises from the tensile characteristics of the tissue architecture. Analogous to manual palpation, modern elastography methods, such as ultrasound elastography [7–9] and magnetic resonance elastography [10,11], were developed to provide objective and quantitative information of tissue stiffness by imaging the tissue response under a mechanical load [12,13]. Optical coherence elastography (OCE) [14]—based on optical coherence tomography (OCT) imaging [15]—provides micron-scale resolution in both the axial and lateral directions, exceeding the resolution of ultrasound or magnetic resonance elastography. Phase-sensitive imaging techniques [16–18] enable the detection of sub-nanometer scale dynamic tissue displacements [19,20]. More recently, OCE methods have been used to characterize the biomechanical properties of delicate tissues, such as the human cornea in vivo using shear-wave propagation [21,22], local [23] or global tissue displacements [24–26], and corneal mechanical resonance frequency [20].
Tissue viscoelasticity is a time-dependent mechanical property due to osmotic diffusion or molecular rearrangement in response to the application of a mechanical load [27]. Most soft tissues are composed of cells, extracellular matrix proteins, polysaccharides, interstitial fluids that exist in extracellular matrixes, as well as intravascular fluids [28] and exhibit nonlinear viscoelastic behaviors under a mechanical load [29]. Current OCE applications are primarily based on the strain [30] or shear-wave propagation speed measurements [31] to estimate tissue stiffness or Young’s modulus that rely on linear elasticity assumptions. Studies on tissue nonlinear elasticity, viscosity, or viscoelasticity are less common [32–34]. Nevertheless, typical soft tissues are viscoelastic, where neglecting nonlinear elasticity and viscosity can lead to inaccurate measurement results [35]. We hypothesize that a comprehensive characterization of tissue elasticity and viscosity may be helpful to understand the effects of disease better and serve as useful markers for disease [36]. Furthermore, viscoelasticity imaging techniques could provide additional useful diagnostic insights as compared to elasticity imaging alone.
The aim of this study is to develop an OCE method for characterizing tissue viscoelasticity based on hysteresis measurements from micron-scale transient tissue displacements. Hysteresis is defined as the difference between the strain energy required to generate given stress in an object and the elastic energy of the object at that stress [27]. In physics and material science, a tested material may exhibit a unique stress-strain path during the loading period and a different path during the unloading period. Energy loss is caused by internal friction (or heat) in a material during mechanical testing (loading and unloading periods), and the area of the loop between the two paths (i.e., hysteresis loop) can represent the extent of energy dissipation. In tissue biomechanics, hysteresis can infer tissue viscoelasticity at low mechanical frequencies [37]. Generally, a softer and more viscous tissue tends to display greater hysteresis values than a more rigid and less viscous tissue [37,38]. The value of hysteresis measurements in mechanical testing is well recognized for determining the viscoelastic behavior of tissues. Mechanical hysteresis measurements have been used to characterize organ function such as heart (e.g., left ventricle) [39,40], lung [41], bladder [42] and gallbladder [43]. For example, lung tissue hysteresis was significantly larger in patients with pulmonary tuberculosis than in normal lungs, and its value was related to the extent of the lesion present and to the severity of dyspnea [41]. Previous studies clearly demonstrate that tissue structure and composition can be distinguished through mechanical assessments, including viscoelasticity (Fig. 11 in [44]). Studies involving ligaments, tendons, smooth muscle, and cardiovascular tissues each have different (detectable) viscoelastic characteristics related to their physiological state (normal and diseased). For example, blood vessel walls which are composed of smooth muscle, elastin, and collagen undergo a structural transformation in atherosclerotic cardiovascular disease [45]. These changes include inflammatory cell accumulation, cellular and interstitial lipid aggregations, and eventual plaque calcification. Each of these stages may result in detectable changes in tissue mechanical properties (e.g., viscoelasticity or hysteresis) that may be targetable as a quantifiable marker for disease staging or provide a specific basis for treatment selection. More recently, corneal hysteresis has been proposed as a basis for keratoconus detection and for refractive surgery patient selection. The air-puff based Ocular Response Analyzer (Reichert Inc. Buffalo, NY) was the first clinical instrument designed to measure corneal hysteresis by comparing the deformation force required to applanate the cornea during a loading and unloading response [46]. This corneal hysteresis estimate is based upon two applanation moments and does not provide a full characterization of corneal deformation dynamics. Other systems combine similar millimeter-scale deformation forces with high-speed Scheimpfug imaging [47] (the CorVis ST [48]) or an OCT system (air-puff OCE system [25,49]) to observe the entire dynamic process of corneal applanation, thereby characterizing the entire corneal hysteresis loop. However, these air-puff based modalities utilize large-amplitude forces (up to 60 mmHg) for corneal applanations at relatively large diameters and displacements (several millimeters) which can result in global corneal deformation, ocular motion, and aqueous fluid displacement, as well as globe retraction and rotation [50,51]. When these factors are coupled with the measurements of ocular biomechanics (hysteresis included), it is difficult to spatially resolve the corneal biomechanics that indicates minute variations in spatial stiffness caused by ocular diseases or treatments [52].
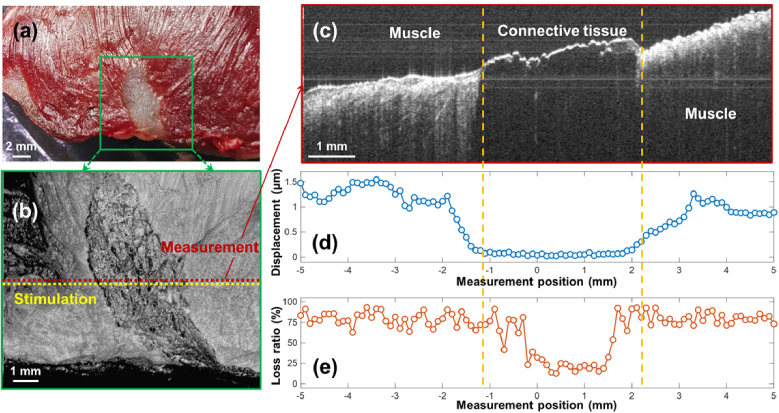
Fig. 11.
Assessment of tissue hysteresis for a beef shank sample. (a) Top view photo of a beef shank sample. The window shows the region (10×10 mm2) for the optical coherence tomography (OCT) structural imaging, which includes a mixture of connective tissue centered between muscle fibers on both sides. (b) En face OCT imaging. (c) Cross-sectional OCT imaging for the measured positions. (d) and (e) are the displacement and hysteresis loss ratio values along the measurement portions (total 101 points in 10 mm length).
The present study proposes a novel OCE-based method to characterize the hysteresis property of tissue-mimicking phantom samples and beef shank samples from micron-scale, transient displacements. The surface displacements are induced by microliter air-pulse stimulation (< 20 Pa [0.15 mmHg]) [53] perpendicular to the sample and are detected by a sub-nanometer resolution phase-sensitive common-path OCT system [19] in an M-mode imaging protocol (repeated A-scan acquisitions over time at the same measurement location). The temporal profiles of the air pressure are measured and calibrated independently by a pressure sensor. We combine the pressure and displacement profiles by removing the time factor, construct the hysteresis loop, and quantify the hysteresis dynamic behavior for different agar phantoms under different stimulation loads. We perform finite element analysis (FEA) and mechanical tests to verify this OCE approach and to predict the estimated sample hysteresis as functions of air-pulse pressure, analyzed location, and sample viscosity. We further perform OCE measurement on a heterogeneous beef shank sample to evaluate the correspondence between hysteresis values and the regional variations in tissue components (i.e., muscle and connective tissue). We aim to provide an alternative OCE approach that can provide both the elastic and the viscous information of the tissue using the hysteresis measurement method.
2. Methods
2.1. Samples
Agar tissue-mimicking phantoms were used to illustrate and verify the OCE hysteresis characterization method. The agar phantoms were made from a mixture of agar powder (Biowest agarose 111860) and water following the procedures described previously [19,34]. We prepared agar phantoms of two different sizes. The first type of phantom (concentrations: 1%, 1.4%, 1.8%) was 60 mm in diameter, 26 g in weight, and has a thickness of 9.81−10.85 mm. The second type (concentrations: 0.8%, 1.5%, 2.0%) was 35 mm in diameter, 10 g in weight, with a thickness of 11.10−12.31 mm. Phantom densities were derived from the volumes and weights and were in the range of 847 to 937 kg/m3 for the 0.8−2.0% agar phantoms. A beef shank sample was bought from a local market, which was selected to contain muscle and connective tissues for hysteresis measurements.
2.2. Hysteresis and loss ratio
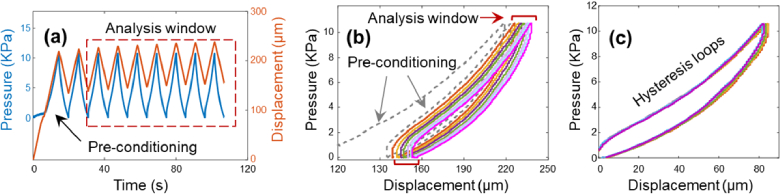
Most soft tissues are viscoelastic with both elasticity and viscous responses to loading forces. Young’s modulus (E) is used to describe the elasticity of a material and is defined by an immediate deformation response between the stress (σ, force per unit area) and strain (ɛ, proportional deformation). For an ideal elastic sample, Young’s modulus is equal to the slope of the stress–strain curve (σ/ɛ) for uniaxial deformation. However, for a viscoelastic sample, the mechanical response is time-dependent [54], and part of the energy can be lost during the loading and unloading process. The hysteresis property represents the energy loss value during the loading and unloading periods and is defined as the difference between the strain energy required to generate given stress in the sample and the elastic energy at that stress [27], as demonstrated in Fig. 1. Here, we used the loss ratio to describe the energy dissipation rate under different loading forces (stresses) and displacement amplitudes (strains). The loss ratio is defined as the result of the hysteresis loop area (yellow area) divided by the energy loading area (dotted area). The loss ratio is in the range of 0–1, wherein loss ratio = 0 indicates an ideal elastic material and loss ratio = 1 indicates an ideal viscous material. Since the loss ratio is a normalized hysteresis value, it remains constant whether the hysteresis is reconstructed based on the stress–strain relation or the force (or pressure)–displacement relation.
Fig. 1.
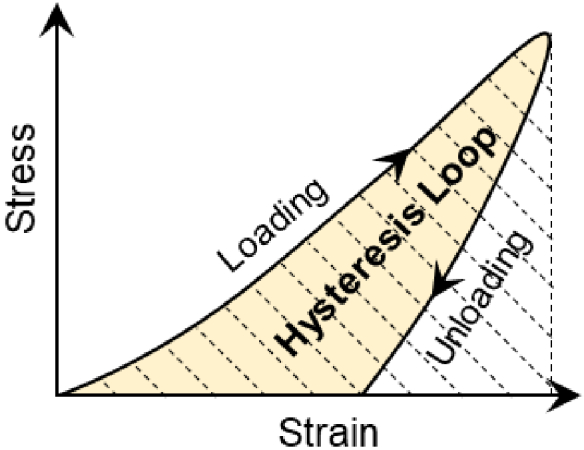
Hysteresis represents the energy loss during the loading and unloading periods and is defined as the difference between the strain energy required to generate given stress in the sample and the elastic energy at that stress. The hysteresis loss ratio is defined by the hysteresis loop area (yellow area) divided by the energy loading area (dotted area).
2.3. OCE setup
We recently constructed a dynamic OCE system based on a 1300-nm linear-wavenumber spectral domain OCT platform [55]. The layout of this OCE system is shown in Fig. 2. A microliter air-pulse stimulation system was added into this OCT platform to deliver perpendicular air-pulse to the tissue through a solenoid valve attached to an air cannula. The tip of the air cannula was inserted into an opening hole of the reference plate in the OCT system to provide focused (150 µm in diameter), low-pressure (0–60 Pa), and short duration (as small as ∼1 ms) stimulation force to the sample tissue and to produce transient mechanical waves and sample displacements in micro-scale magnitudes. The OCT system [55] was synchronized to the stimulation system to record the dynamic response of the tested sample. The minimum measurable lateral distance by the OCT system was 0.15 mm from the stimulation point, which was used for hysteresis characterization in this study.
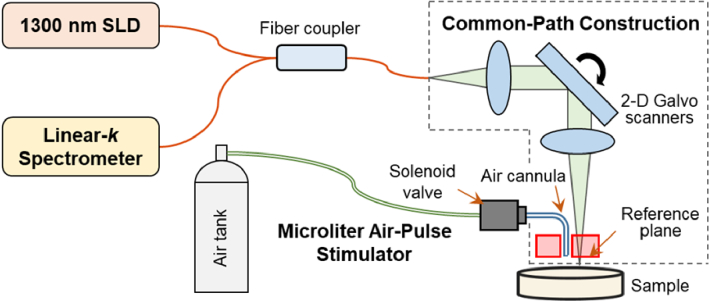
Fig. 2.
The optical coherence elastography (OCE) system comprises a microliter air pulse stimulator to induce mechanical waves in the sample and a common-path OCT imaging system to track the resulting dynamics of elastic wave propagation. The distance between the stimulation and measurement points was 0.15 mm. SLD: a 1290 ± 40-nm superluminescent laser diode. Common-path construction was formed using an acrylic reference plate, 4 mm thick, to provide a reference plane so that both the sample and the reference arms shared the same optical path [19]. Linear-k spectrometer was formed by a grating and a prism to disperse the interference spectrum optically in the k domain so that the interference signals can be processed directly (without any digital interpolation) via Fourier transform to acquire the depth profiles (A-scans) [55,57,58].
The light source was a superluminescent diode (SLD, IPSDS1307C-1311, Inphenix Inc., Livermore, CA, USA) with a central wavelength of 1290 nm and a 3-dB bandwidth of ± 40 nm. The light emitted from the SLD was split by a 50:50 fiber coupler (TW1300R5A2, Thorlabs, Inc., Newton, NJ, USA) into two arms, where one arm was blocked, and the other arm was used to construct the common-path configuration [19], using a 4-mm-thick acrylic reference plate to provide a reference plane (the optical surface proximal to the sample), so that both the sample and the reference arms shared the same optical path. This common-path construction can effectively reduce the amplitude of the background phase instability to a sub-nanometer level and improve phase stability and detection sensitivity for the phase-sensitive OCE imaging [19]. In the common light path, the light beam was collimated by a reflective collimator (RC04APC-P01, Thorlabs, Inc., Newton, NJ, USA) with a beam diameter of 4 mm. It was scanned by 2D scanning galvo mirrors (GVS102, Thorlabs Inc., Newton, NJ, USA) and then focused by a telecentric scan objective (LSM54-1310, Thorlabs Inc., Newton, NJ, USA) with a focal length of 54 mm and a large field of view (18.8 × 18.8 mm2 maximally). The maximum output power in the common light path is ∼1.8 mW. Specifically, a linear-wavenumber (k) spectrometer (PSLKS1300-001-GL, Pharostek, Rochester, Minnesota, USA) was used to record the interference spectrum generated from the common light path. This spectrometer was equipped with an InGaAs line scan camera (GL2048L-10A-ENC-STD-210, Sensors Unlimited, Inc., Princeton, NJ, USA) at a maximum line rate of 76 kHz. By comparison, a conventional spectrometer in an SD-OCT system disperses the light spectrum evenly in wavelength, and requires additional digital rescaling in the k domain and results in decreased signals in deeper regions [56]; while the linear-k spectrometer disperses the spectrum optically in the k domain by an optimized combination of a grating and a prism so that the signal-to-noise ratio (SNR) can be improved for deeper tissue, and the computing time to generate the OCT images can be reduced. The details for designing such a linear-k spectrometer are explained by previous studies [57,58]. Thus, the interference signals were transported through a frame grabber (PCIE-1433, National Instruments Corp., Austin, Texas, USA) into a computer and were then processed directly (without any digital interpolation) via Fourier transform to acquire the depth profiles (A-scans) using code written in the LabVIEW language.
2.4. Hysteresis characterization using OCE
The present study used the pressure-displacement curves at a single spatial point location of the sample surface to describe the hysteresis loop during the loading and unloading periods. The applied pressures were in a range of pascals to tens of pascals. The induced displacement magnitudes were in the micron-scale and the time duration for hysteresis measurement was milliseconds. The classic approach to characterizing sample hysteresis relies on analysis of stress-strain curves, but adapting this method to and air-pulse-based OCE system is complex and not straightforward. This is because the microliter air pulse stimulation is a local stimulation method (150 µm diameter) and causes uneven distributions of the stress and strain in the radial and axial directions of the tested phantom. To simplify the calculation, we assessed the pressure-displacement relationship to describe the hysteresis loop like previously published elastography studies [48,59–49], and we acquired the pressure-displacement relationship using separate measurements of the air-pulse pressures and the surface displacements in the time domain. Figure 3 demonstrates the workflow of the hysteresis characterization method and a sample calculation with a 2% agar phantom, an air pressure of 8 Pa, and the maximum induced sample surface displacement of 1.84 µm.
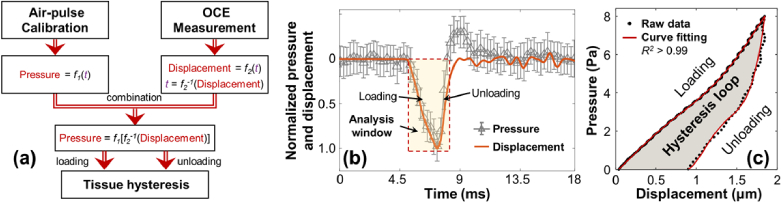
Fig. 3.
Hysteresis characterization method using OCE. (a) Workflow of the hysteresis characterization method based on the separate measurements of the air-pulse and surface displacement profiles. (b) and (c) are based on a hysteresis characterization example, where (b) shows the normalized air pressure (mean ± SD) and surface displacement profiles in the time domain and (c) demonstrates the hysteresis loop based on the measurement of the pressure-displacement relations in the loading and unloading periods. In this example, the sample was a 2% agar phantom, the air pressure was 8 Pa, and the maximum induced surface displacement was 1.84 µm at a measurement distance of 0.15 mm from the stimulation center.
Figure 3(a) shows the procedures for tissue hysteresis estimation using the OCE method, which were based on the independent measurements of pressure profiles and deformation profiles during the loading-unloading periods. We defined the time (t)-dependent air pressure profiles as f1(t) and the surface displacement profiles as f2(t). Each profile was fit as a second-order Fourier curve as shown in Eq. (1):
| (1) |
where y represents the pressures or displacement during either a loading or unloading period, a0 to a4 are the fitting coefficients, and ω is the angular frequency for the Fourier curve. We interpolated the pressure and displacement profiles to the same time scale and acquired the pressure-displacement correlation curves by removing the time factor t for both the loading and unloading periods [Pressure = f1(f2−1(Displacement)]. The pressure-displacement correlation curves between the loading-unloading periods were then constructed as the hysteresis loop.
During the pressure calibration procedure, the air pressure was released through a two-stage pressure regulator that was connected to a high-speed solenoid valve by a rigid plastic tube. The solenoid valve controlled the delivery of transient air pulses to the sample via the cannula. Under a certain input air-source pressure, the output air-pulse pressure from the cannula was measured at a sampling rate of 4000 Hz and was repeatedly measured 50 times using a pressure transducer sensing system (STS ATM.1ST Precision Pressure Transmitter, PMC Engineering, Danbury, CT, US) and a data acquisition system (PowerLab 8/35, AD Instruments Inc., Colorado Springs, CO, US). Based on these measurements, the relation between the output air pulse and the input air source pressure was established. The air-pulse profile of each pressure was then assumed as a triangle wave characterized by slopes (k1, k2) and times (t1, t2) for the loading and unloading periods. The air-pulse parameters (k1, k2, t1, t2) were then calibrated as functions of the output air-pulse pressures based on the measurements. We then used the mathematical expressions to predict the temporal air-pulse profile with any pressure in the measurement range.
In the displacement measurement procedure, the induced surface displacements were measured using the phase-sensitive common-path OCE system [19]. In each M-mode elastic imaging, the unwrapped phase change Δφ (tj-t0) at the time tj relative to the time t0 in successive A-scan signals can be converted to the surface displacement Δz (tj–t0) using Eq. (2):
| (2) |
where λ0 is the center wavelength. Since the displacement measurements were performed at the phantom surface, there was no need for the physical rescaling due to the refractive index or the correction of the surface motion and refractive index mismatch error [61].
An example is shown in Fig. 3(b) and Fig. 3(c), for which the sample was a 2% agar phantom, the output air-pulse pressure was 8 Pa, and a maximum induced surface displacement was 1.84 µm at a measured distance of 0.15 mm from the stimulation center. The normalized air pressure (mean ± SD) and surface displacement profiles are represented in Fig. 3(b). In the loading period, both the pressure and displacement curves nearly overlapped, indicating that the displacements happened nearly simultaneously with the transient force applied to the sample. In the unloading period, however, there was an apparent time-lag between the pressure and displacement curves so that the sample returned to its equilibrium position slower than the pressure release, which was primarily due to sample viscosity. We set a time window for hysteresis analysis that started when the loading pressure was applied and ended when the unloading pressure decreased to zero. The loading displacement magnitude ranged from zero to 1.84 µm and remained at a residual displacement of 0.87 µm when the loading pressure reduced to 0 and the analysis window was ended. The average air-pulse pressure and the displacement data in the analysis window were used to construct the hysteresis loop, illustrated in Fig. 3(c). The R2 fit was larger than 0.99 for both the loading and the unloading periods. The hysteresis loss ratio is the ratio of the area attributed to the hysteresis loop divided by the total energy loading area, and was calculated as 53.6%.
2.5. Hysteresis characterization using FEA method
FEA was performed to simulate the transient surface displacements of phantoms under the air-pulse stimulations using the ANSYS 18.0 software (Canonsburg, PA, US). Damping forces and spring forces are applied parallel to the node elements, similar to a Voigt model, as shown in Fig. 4(a), where F(t) is the driving force in time, k is the spring stiffness coefficient, c is the viscous damping coefficient, and m is mass. The dynamic equation of a particular node for the Voigt model can be described as
| (3) |
where u(t) is the time-dependent displacement. The dynamics for the whole finite element structure can be described using a matrix function [62]
| (4) |
where M is the global mass matrix, C is the global damping coefficient matrix, and K is the global stiffness matrix. F(t) is the load vector, and u(t) is the node displacement vector. Each node of the finite elements is in a force equilibrium condition among the inertial force, damping force, elastic force, and the external load. The damping coefficient matrix C can be expressed in a typical Rayleigh damping equation of C = αM + βK, where α and β are the mass- and stiffness-proportional damping coefficients, respectively [62]. In general, the αM contributes more in the lowest damping modes, and the βK contributes more in the highest damping modes. The damping ratio (ξf) is dependent upon the frequency (f), and can be expressed as in the following equation [62]
| (5) |
Generally, the α damping (or mass damping) represents the friction damping and can be ignored [63]. Hence, in many finite analysis models of viscoelastic bio-tissues, α damping is set to 0 s-1, and β damping is used to represent the material structure damping [64–67]. In this situation, the damping ratio formula [Eq. (5)] can be then simplified as ξf = πfβ.
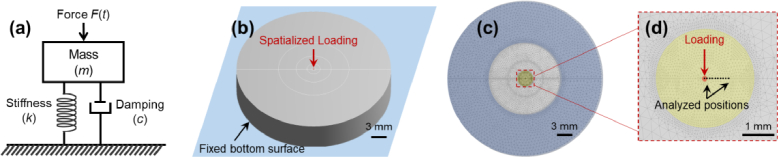
Fig. 4.
Finite element analysis (FEA) model for the phantom. (a) Schematic of a Voigt spring-mass-damper model. F(t) is the force, k is the spring stiffness coefficient, c is the viscous damping coefficient, and m is the mass. (b) Schematic of the phantom geometry and boundary conditions. (c) and (d) show the global view and local view of the FEA model, respectively. The stimulation was applied in the center of the phantom, and the dynamic response was analyzed at seven selected points at the top surface of the phantom at distances of 0–0.5 mm from the center.
Figure 4(b) shows the general geometry and boundary conditions of the finite element phantom model which was built on the elastic parameters of the 2% agar tissue phantom used in our previous work [19,34]. The agar tissue phantom had a cylindrical geometry with 35-mm diameter, 7.1-mm height, and 6.7-g weight. The density of this material was 985 kg/m3, Young’s modulus was 117.8 kPa, and the Poisson ratio was 0.499. The natural frequency of the dominant modal response was simulated as 440 Hz. The α value was set to 0 s-1, and the β values in the dynamic simulations were 0 s, 2×10−5 s, 4×10−5 s, 8×10−5 s, 1.6×10−4 s, 4×10−4 s, and 8×10−4 s. Because the damping ratio ξf is frequency-dependent, we defined the modal damping ratios (ξ) as the damping ratio at the dominant modal natural frequency (440 Hz), which were calculated as 0.0, 0.03, 0.06, 0.11, 0.22, 0.55, and 1.11, respectively.
The model bottom surface was fixed, while the top surface was divided into six concentric zones: a circular zone (of 0.15-mm diameter) in the center and five annulus zones around the center. A Gaussian-shape loading force was applied in the central circular zone to mimic the air-pulse stimulation of the OCE method. The force magnitude and Full width at half maximum (FWHM) values were adjusted to match the OCE measured displacement values of 2% agar phantom in our previous results [19]. Fig. 4 (c, d) show the global and local view of the top surface of the FEA model, respectively. In the ANSYS simulation, we made irregular meshes of the FEA model using 123,300 SOLID187 elements. Each element is a 10-node, 3-D structure and has three degrees of freedom. The sizes of elements were from 0.08 mm to 0.6 mm, increasing from the center to the peripheral areas. The loading pressures applied ranged from 3.6 Pa to 38.9 Pa, and the responses of seven selected points at the top surface of the phantom were analyzed. The distances from the analyzing points to the stimulation point were 0.0 mm, 0.08 mm, 0.15 mm, 0.22 mm, 0.28 mm, 0.36 mm, and 0.5 mm.
We then performed a transient structural analysis to characterize the dynamic response in the time domain and performed a harmonic analysis to evaluate the dominant resonant frequencies in the frequency domain. The sample surface displacement responses and the hysteresis were then simulated and compared as functions of the modal damping ratios ξ (0–1.11), air-pulse pressures (3.6–38.9 Pa), and analyzed locations (0–0.5 mm).
2.6. Hysteresis measurement using a mechanical test
Typical cyclic uniaxial mechanical measurements [68] were performed using a TH-8203A testing instrument (Wane Testing Equipment Co., Ltd, Suzhou, Jiangsu, China). A contact plate with the same diameter as the sample phantom (i.e., 35 mm or 60 mm) was used to compress the whole sample during the loading and unloading periods. A force sensor recorded the applied forces during the measurement, and a position sensor recorded the induced sample displacements. A phenomenon of pre-conditioning has been known in a typical cyclic mechanical test procedure for the soft biological tissue, which means that the hysteresis loop tends to increase in strain values as the cycles increased, and the hysteresis loops are becoming more and more consistent as the cycles increased [54]. Because of the pre-conditioning phenomenon, several loading and unloading cycles are performed before the measurement to better quantify the soft tissue hysteresis [54].
Figure 5 demonstrates an example of cyclic mechanical tests to measure hysteresis for a 2% agar phantom. We increased the pressure from 0 to 10 kPa at a speed of 8 µm/s and then decreased the pressure to zero at the same speed. The test was repeated for 9 cycles. It was seen in Fig. 5(a, b) that the first cycle was deviated from the following cycles in the loading and unloading periods due to the existence of the pre-conditioning phenomenon, and the third to ninth cycles had repeatable and consistent features. We used these cycles to measure the hysteresis for this agar phantom, as shown in Fig. 5(c). The hysteresis loss ratios were 36.0% ± 1.4% (mean ± SD, coefficient of variation: 3.9%).
Fig. 5.
Hysteresis measurement using the cyclic mechanical test method. These representative data were acquired from a 2% agar phantom. Maximum loading pressure was 10 kPa, and loading/unloading speed was 8 µm/s. The pre-conditioning phenomenon was clearly seen for the first cycle in both the overlayed force and displacement profiles of the time domain (a) and the force-displacement relation profiles (b). The third to ninth cycles had repeatable and consistent loading-unloading features and were used to describe the hysteresis curves in (c). The hysteresis loss ratios were 36.0% ± 1.4% (mean ± SD).
3. Results
3.1. Air-pulse calibration
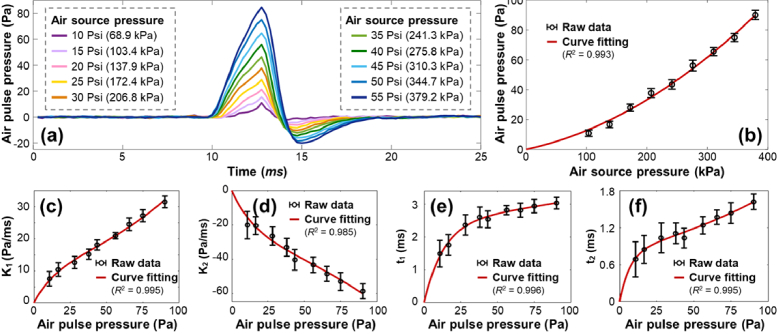
The measured and calibrated air-pulse profiles are shown in Fig. 6. The input air-source pressures were increased from 10 Psi (68.9 kPa) to 55 Psi (379.2 kPa) with an increment of 5 Psi (34.5 kPa) for each step, and the output air-pulse pressures from the cannula were measured from 7.9 Pa to 89.9 Pa. There was more than a 1000-fold difference between the supply and output pressure. This output pressure reduction was produced by the combination of a narrow port diameter (150 µm) and a brief temporal air pulse duration which was controlled by a high-speed solenoid valve (millisecond time-scale).
Fig. 6.
The measured and calibrated air-pulse profiles (n = 50 repeated measurements for each pressure). (a) The measured air-pulse profiles in the time domain. The input air source pressures were controlled in the range of 10–55 Psi (color series). Each profile is the average value of 50 measurements. (b) The relation between the output air-pulse pressure and the input air-pulse pressure was fit by a second-order polynomial curve. Panels (c–f) show the calibrated air-pulse parameters (k1, k2, t1, t2) in relation to the air-pulse pressures, where k1 and k2 are the slops, and t1 and t2 are the time durations of the air-pulse profile. The relations between the air-pulse parameters (k1, k2, t1, t2) and the air-pulse pressures were fit to second-order exponential curves based on Eq. (6).
Figure 6(a) illustrates the average air-pulse profile for 50 measurements at each pressure. Figure 6(b) shows the measured output air-pulse pressures in relation to the input air-pulse pressures. The output air-pulse pressures increased as the air-source pressures increased, and their relation was fit to a second-order polynomial curve (y = 3.96×10−4×2 + 8.70×10−2x, R2 = 0.993).
Figures 6(c–f) show the calibrated air-pulse parameters k1, k2, t1, and t2, respectively, in relation to the air-pulse pressures. The relations between the air-pulse parameters (k1, k2, t1, t2) and the air-pulse pressures were all fit to second-order exponential curves as
| (6) |
where A, B, and C are the fitting coefficients. In Fig. 6(c), A = 10.59, B = 0.0123, C = -0.0687, and R2 = 0.995. In Fig. 6(d), A = -26.15, B = 0.0093, C = -0.0631, and R2 = 0.985. In Fig. 6(e), A = 2.456, B = 0.0024, C = -0.0744, and R2 = 0.996. In Fig. 6(f), A = 0.8065, B = 0.0078, C = -0.1416, and R2 = 0.995. The loading and unloading slopes (speeds) were in the range of pascals to tens of pascals per millisecond, and the loading and unloading duration times were in the range of milliseconds.
3.2. FEA results
FEA was performed to simulate and evaluate the OCE-based sample hysteresis quantification method. The air-pulse profile was set as a triangle wave, which was consistent with the air-pulse calibration results in Section 3.1. The air-pulse pressure was increased from 3.6 Pa to 38.9 Pa, the ranges of air-pulse parameters were 2.80 Pa/ms to 16.37 Pa/ms for k1, −6.20 Pa/ms to −35.29 Pa/ms for k2, 0.60 ms to 2.56 ms for t1, and 0.34 ms to 1.09 ms for t2. The sample hysteresis and loss ratios were predicted as functions of air-pulse pressures, phantom modal damping ratios ξ (0–1.11), and analyzed locations (0–0.5 mm).
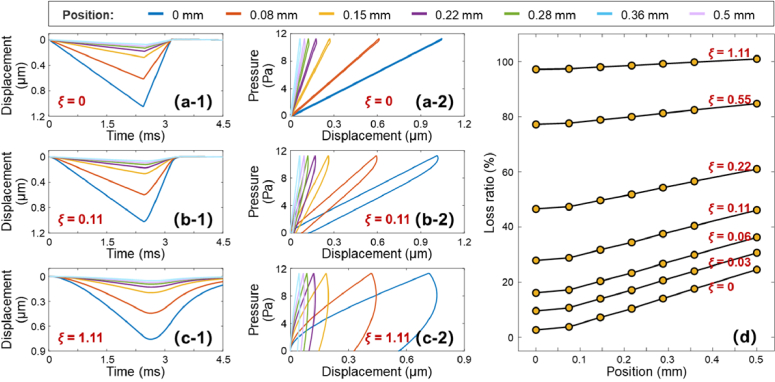
Figure 7 shows the FEA results of the predicted sample hysteresis as a function of analyzed locations (0–0.5 mm). The excitation pressure was set to 11.3 Pa. Figures 7(a-1), (b-1), and (c-1) display the temporal surface displacement profiles for the phantoms with the ξ values of 0, 0.11, and 1.11, respectively; and their hysteresis profiles are shown in Fig. 7(a-2), (b-2), and (c-2) correspondingly. The maximum displacement amplitudes decreased as the analyzed position changed from 0 mm to 0.5 mm, indicating the attenuation of the mechanical wave magnitudes during wave propagation [34,69]. As the sample viscosities (ξ values) increased, the surface displacement peak shifted from a peaked shape to a rounded shape, indicating an increase in the time lag (hysteresis) between the pressure and the displacement, and the phenomenon of time lag was more obvious during unloading than during loading. The hysteresis was more obvious in a more viscous sample, as expected. Using the FEA method, Fig. 7(d) shows the estimated hysteresis loss ratios trends. Noticeably, the loss ratio increased with the increase in the modal damping ratio (ξ) and in the measurement distance. In addition, the slopes (between the analyzed position and hysteresis) shifted from steep to flat as ξ increased from 0 to 1.11. It means the difference in loss ratio between the OCE measurement position (0.15 mm) and the ideal measurement position (0 mm) decreased as the value of ξ increased.
Fig. 7.
Finite element analysis (FEA) results of the predicted sample hysteresis at different measurement locations (0–0.5 mm). The phantoms had different modal damping ratios (ξ) of 0–1.11. Panels (a-1), (b-1), and (c-1) demonstrate the displacement profiles of phantoms with ξ values of 0, 0.11, and 1.11 respectively. Panels (a-2), (b-2), and (c-2) demonstrate the corresponding hysteresis profiles. Panel (d): comparison of the hysteresis loss ratio for all the measurement positions. The hysteresis loss ratio increased as the measurement position increased. The difference in loss ratio between 0 mm (ideal measurement position) and 0.15 mm (OCE measurement position) decreased as the value of ξ increased.
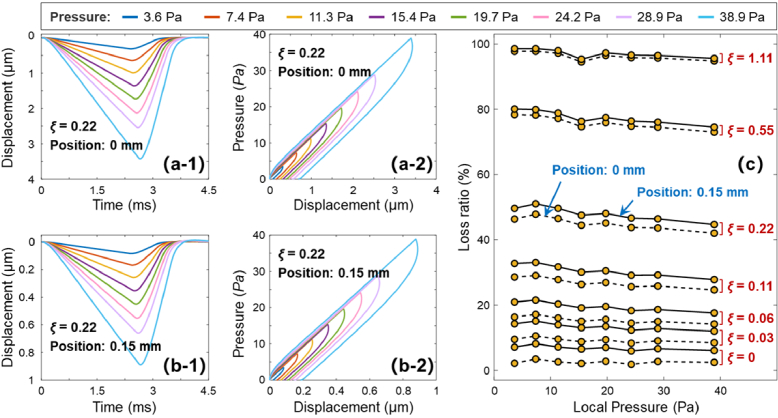
Figure 8 shows the FEA results of the predicted sample hysteresis as a function of air excitation pressures (3.6–38.9 Pa). Figures 8(a-1) and (b-1) show the examples of the induced displacements of the model phantom (ξ = 0.22) at the measurement positions of 0 mm and 0.15 mm, respectively, in response to air excitation pressures (3.6–38.9 Pa). As expected, the displacement magnitudes were obviously larger at the 0-mm position than those at the 0.15-mm position, while the deformation shapes resembled each other despite the differences in magnitude. The similarity features are also seen in Fig. 8(a-2) and (b-2), which are the hysteresis profiles of this model phantom (ξ = 0.22) at these two measurement locations. The loss ratios were 44.9 ± 1.9% (0-mm) and 47.9 ± 2.1% (0.15-mm). Figure 8(c) shows the trends of the estimated hysteresis loss ratios using the FEA method. In general, the hysteresis loss ratio decreased as the loading force increased. For example, the loss ratio decreased from 46.4% (3.6 Pa) to 42.0% (38.9 Pa) for the model phantom (ξ = 0.22) at the 0-mm measurement position. The difference in loss ratio between the OCE measurement position (0.15 mm) and the ideal position (0 mm) also decreased as the value of ξ increased over this air pressure range (3.6–38.9 Pa). For example, the difference was 4.3 ± 0.4% when ξ = 0, 3.7 ± 0.3% when ξ =0.11, 3.0 ± 0.2% when ξ = 0.22, and 0.8 ± 0.02% when ξ =1.11.
Fig. 8.
Finite element analysis (FEA) results of the predicted sample hysteresis features under different air excitation pressures (3.6–38.9 Pa). Panels (a-1, a-2, b-1, and b-2) demonstrate the surface displacement and hysteresis profiles of a model phantom (ξ = 0.22) at measurement positions of 0 mm and 0.15 mm. Panel (c) comparison of the hysteresis loss ratio for phantoms with different modal damping ratios (ξ) of 0–1.11 at the analyzed positions of 0 mm (dash line) and 0.15 mm (solid line). In general, the hysteresis loss ratio decreased as the loading force increased.
In summary, the FEA results from Fig. 7 and 8 predicted the trends of the OCE-measured sample hysteresis loss ratios as functions of phantom modal damping ratios (ξ), air-pulse pressures, and analyzed locations. First, the loss ratio increased dramatically with the modal damping ratio (ξ) increase from 0 to 1.11. Second, the loss ratio decreased as the loading force increased from 3.6 Pa to 38.9 Pa. Third, the loss ratio increased as the measurement distance increased from 0 mm to 0.5 mm, and the slopes (between the analyzed position and hysteresis) shifted from steep to flat as ξ increased from 0 to 1.11. It can be concluded that the estimated hysteresis loss ratios were very close at the location (i.e., 0.15 mm) near the stimulation point for a sample that is viscoelastic (e.g., ξ > 0.1). The change in loss ratio values between the OCE measurement position (0.15 mm) and the ideal position (0 mm) was reduced as the viscosities (e.g., ξ) increased.
3.3. Comparison between the OCE measurement and mechanical tests
We performed the OCE measurements and mechanical tests on agar samples and compared the measured hysteresis loss ratios in two sets of experiments. During OCE measurements, the transient microliter air pulse was applied locally in the center of the sample, and the measurement distance from the stimulation point was 0.15 mm. The measurement was conducted and repeated five times for each phantom after a pre-test of two air stimulations. During mechanical tests, the global, step-wise forces were applied at the sample surface. A total of seven cycles of loading and unloading were performed on each phantom, and the last five cycles were used to calculate the hysteresis of that phantom.
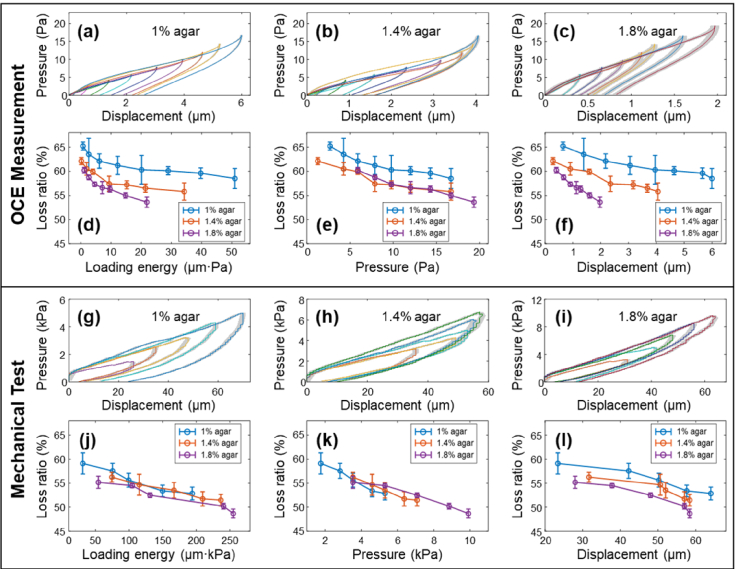
The first set of experiments was performed on 60-mm-diameter agar phantoms with concentrations of 1%, 1.4%, and 1.8%. A series of stimulation pressures were set for both the OCE measurements (1.2 Pa to 19.4 Pa) and the mechanical tests (1.7 kPa to 9.9 kPa, the increase/decrease speed was 8 µm/s). Hysteresis loss ratios were estimated with respect to the loading energy, pressure, and displacement, as shown in Fig. 9. The hysteresis loops of the 1%, 1.4%, and 1.8% agar phantoms are characterized in Fig. 9(a−c) by OCE measurements and in Fig. 9(g–i) by mechanical tests. It was clearly observed that softer samples (e.g., 1% agar phantom) deformed more than stiffer samples (e.g., 1.8% agar phantom) under the same loading pressure. For example, the surface displacement magnitudes were 6.00 ± 0.01 µm (1%), 4.05 ± 0.02 µm (1.4%), and 1.60 ± 0.03 (1.8%) under a 17-Pa stimulation pressure in OCE measurements, and were 64.0 ± 1.1 µm (1%), 52.1 ± 1.1 µm (1.4%), and 37.8 ± 1.0 µm (1.8%) under a 5.3-kPa stimulation pressure in mechanical tests. These results were consistent with our previous measurements on agar phantoms [19,34]. Figure 9(d) and (j) compare the measured loss ratio in relation to the loading energy. In both measurements, the loss ratio decreased as the loading energy increased, and the agar phantoms of different concentrations (i.e., 1%, 1.4%, and 1.8%) were distinguishable by OCE measurements, but not distinguishable by mechanical tests. We further decomposed the loading energy into the applied pressure and displacement domains. Figures 9(e) and (k) show the measured loss ratio in relation to the applied pressure. Neither the OCE measurement nor the mechanical test can distinguish 1-1.8% agar phantoms from the loss ratio and pressure relation. Figures 9(f) and (l) show the measured loss ratio in relation to sample surface displacement. The 1%, 1.4%, and 1.8% agar phantoms were clearly distinguishable by the change in loss ratio in relation to the surface displacements, using both the OCE method (f) and the mechanical testing method (l). By comparison, the use of loss ratio was most effective in relation to the displacement domain, and least effective in the pressure domain for distinguishing of 1%, 1.4% and 1.8% agar phantoms.
Fig. 9.
Quantification of the hysteresis loss ratio in relation to the loading energy, applied pressure and the surface displacement using OCE and the mechanical test methods. The samples were 60-mm-diameter agar phantoms (concentration: 1%, 1.4%, and 1.8%). (a–c) Hysteresis loops for 1–1.8% agar phantoms by OCE measurements (1.2–19.4 Pa stimulation pressures: color series). (d–f) show the relation between the OCE measured loss ratio with the loading energy, applied pressure, and surface displacement, respectively. (g–i) Hysteresis loops for 1–1.8% agar phantoms by mechanical tests (1.7–9.9 kPa compression pressure: color series). (i–l) show the relation between the mechanical testing results for the loss ratio with the loading energy, applied pressure and surface displacement, respectively. Noticeably, the 1%, 1.4% and 1.8% agar phantoms were more distinguishable from the loss ratio features in relation to the surface displacement using both the OCE method (f) and the mechanical testing method (l).
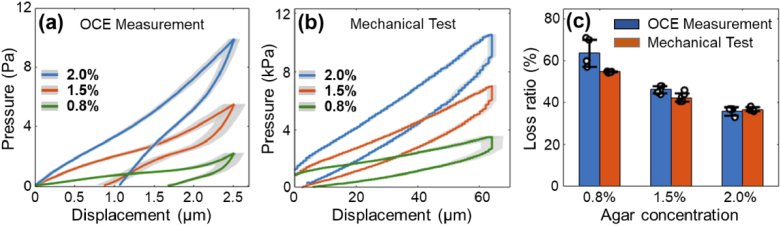
We performed a second set of experiments to verify whether the agar phantoms (diameter: 35 mm; concentrations: 0.8%, 1.5%, and 2%) could be distinguishable based on the same induced displacement magnitudes. During the OCE measurement, the applied air-pulse pressures were 2.2 Pa (0.8%), 5.5 Pa (1.5%), and 9.9 Pa (2%) to achieve a displacement value of 2.5 µm. During the mechanical test, the applied compression pressures were 3.5 kPa (0.8%), 7.1 kPa (1.5%), and 10.6 kPa (2%) to achieve a displacement value of 65 µm. The measurements were repeated 5 times for each test. Figures 10(a) and (b) show the quantified hysteresis loops by OCE measurements and mechanical tests, respectively. Figure 10(c) shows the measured hysteresis loss ratios (mean ± SD) of different phantoms under the two methods. The hysteresis loss ratio values measured by OCE were 0.636 ± 0.064 (0.8%), 0.462 ± 0.017 (1.5%), and 0.360 ± 0.020 (2%). The measured mechanical hysteresis values were 0.547 ± 0.002 (0.8%), 0.424 ± 0.022 (1.5%), and 0.368 ± 0.009 (2%). These two quantification methods show consistent results on agar hysteresis measurements. The loss ratios decreased as agar concentrations increased, indicating that a phantom with a lower concentration (e.g., 0.8%) was more viscous than a phantom with a higher concentration (e.g., 2%).
Fig. 10.
Distinguishment of agar phantoms (diameter: 35 mm; concentrations: 0.8%, 1.5%, and 2%) using sample hysteresis at the same induced displacement magnitudes (OCE: 2.5 µm; Mechanical test: 65 µm). The measurements were repeated 5 times for each test. (a) Hysteresis loops by OCE measurements. (b) Hysteresis loops by mechanical tests. The shadow areas in (a) and (b) were in the range of ± SD. (c) Comparison of the calculated hysteresis loss ratios for the agar phantoms (mean ± SD).
3.4. Variation of hysteresis in heterogeneous tissue sample
We performed OCE measurements in a heterogeneous beef shank sample, which included connective tissue in the center of the tested region and muscle fibers on both sides (see the top view photo in Fig. 11(a)). Figure 11(b) shows an en face OCT imaging that covered a 10×10 mm2 area. The yellow and red dots demonstrate the stimulation and measurement locations, respectively. During OCE measurement, the stimulation pressure was 60 Pa, the distance between each stimulation and measurement points was 0.15 mm, and the beef sample was moved using a translation stage to cover a measurement length of ±5 mm at 101 points with a sampling length of 0.1 mm. The cross-sectional features in the measurement location are demonstrated in Fig. 11 (c). Connective tissue was identified in the central region from -1.1 mm to 1.8 mm in the OCT structural imaging, and muscle tissues were on both sides.
Figures 11(d) and (e) show the OCE measurement results for the surface displacements and the loss ratios, respectively. Connective and muscle tissues were distinguishable based on OCE displacement and hysteresis measurements. In Fig. 11 (d); connective tissue has much smaller displacement values (mean ± SD: mm, position: 0.07 ± 0.03 µm; position: -1.1 to 1.8 mm) than the displacements in the muscle regions (mean ± SD: 1.16 ± 0.21 µm; positions: -5.0 to -1.9 mm and 3.3 to 5.0 mm). In Fig. 11(e), connective tissue has much smaller loss ratios (mean ± SD: 22.2 ± 6.7%, location: -0.2 to 1.4 mm) than the loss ratios measured in muscle regions (mean ± SD: 79.5 ± 7.8%, location: -5 mm to -1.1 mm, and 1.8 mm to 5.0 mm). Notably, mechanical detection of the tissue boundaries by OCE measurements were less clearly defined than that they were by structural OCT imaging. Displacement measurement slightly overestimated the connective tissue region size and defined by a gradient edge. Hysteresis measurements slightly underestimated the size of the connective tissue region and had more sharply defined boundaries. This may be a product of our instrument design which had a 0.15 mm distance between the stimulation and measurement positions. It may also be the product of a more complex sample response in the boundary regions where sample stiffness and hysteresis are confounded by the heterogenous tissues at these locations. The tissue components (especially in a heterogeneous tissue) within the wave propagation path from stimulation to measurement positions can affect the temporal displacement profiles of the mechanical waves thereby influencing the displacements and hysteresis measurements.
4. Conclusions and discussion
In this study, we introduce a transient OCE approach to characterize soft tissue viscoelasticity using micron-scale hysteresis features and employ both an FEA method and mechanical tests to validate the OCE method. In the OCE measurement method, the loading and unloading periods of the hysteresis loop were characterized by independent measurements of the stimulation pressure and surface displacement profiles and hysteresis loss ratio values were primarily driven by the unloading response. Although the hysteresis loss ratios decreased as the loading pressures increased, agar phantoms of different concentrations (e.g., 0.8–2%) were distinguishable based on the relation between loss ratio and sample displacement, or based on loss ratio values at a common displacement amplitude. The FEA simulation, mechanical test, and OCE measurements on agar phantoms have consistently shown that the hysteresis loss ratios measured adjacent to the stimulation point can reflect the viscoelasticity of soft tissue. In addition, we performed OCE measurements on a heterogeneous beef shank sample and distinguished the connective and muscle tissues based on their displacement and hysteresis features. This novel OCE approach has the potential to quantify and distinguish tissues with different viscosities and elasticities using small-amplitude tissue displacement features that were induced and observed using the OCE imaging techniques. In future studies we will investigate whether this noninvasive novel OCE method can provide viscoelasticity measurements that are clinically useful for guiding disease diagnosis or characterizing treatment responses for delicate and viscous tissues, such as the human eye.
The hysteresis loss ratio is calculated as the dissipation energy (hysteresis loop area) divided by the loading energy (Fig. 1). By definition, it would be more direct to estimate tissue hysteresis by inducing the same loading energy for each sample. However, this concept is not straightforward to implement, especially for clinical measurements, for several reasons. While it is possible to apply a common pressure, the resulting tissue displacement is the product of a more complex interaction between the load (its dynamic and geometric parameters) and the sample response (its deformation dynamics and geometry). It would be more convenient to distinguish tissue viscosity (hysteresis) using fixed pressure or displacement parameters if possible. Our results from Fig. 9 show that loss ratio could separate our samples using a common displacement paradigm, while a common stimulus pressure was less effective for distinguishing 1%, 1.4% and 1.8% agar phantoms. These differences in loss ratio-displacement curves partly reflects the non-linear force required to produce similar displacements for stiffer vs. softer agar phantoms. In Fig. 10, results from additional experiments show the separability of agar phantoms using a common displacement magnitude strategy and these results are consistent with our results shown in Fig. 9.
Although some recent work has demonstrated the feasibility of using OCE systems to assess the strain rate-, frequency-, or time-dependent tissue viscosities [32–34], these methods have some limitations. Han et al. provided a modified Rayleigh-Lamb frequency equation to quantify Young’s moduli and shear viscosities of porcine corneas from OCE measurements [32]. Wu et al. provided a kinematic model to distinguish the viscoelastic properties of young and mature rabbit crystalline lenses from the tissue relaxation response [33]. These two analytical models are based on tissue displacement profiles but ignore the time dependent spatial force (or stress) profiles that could also affect the temporospatial features of tissue displacement where viscosity is calculated. In addition, both methods are based on a first-order assumption that the tissue is isotropic, homogenous, can be geometrically complex (curved, thin plate, etc.), and simplified boundary conditions. Lan et al. presented a single degree of freedom analytical method to quantify the natural frequency and damping ratio from a free oscillation period where the oscillation amplitudes ranged from sub-micrometer to sub-nanometer scales [34], and demonstrated its use in resolving local variations in heterogeneous tissues [70] and in showing highly repeatable corneal natural frequency identifications in vivo [20]. This single degree of freedom method is also an approximation and simplification method describing the dominant oscillation frequency and the frequency-dependent viscosity (damping ratio) while ignoring other frequencies and other damping ratio values that can vary by tissue viscosity. By comparison, the present study is based on both the stimulation and response features, and uses them to directly measure the sample hysteresis value, which can represent sample viscoelasticity without any modeling or assumption.
There are also some limitations of this OCE approach for hysteresis characterization. First, although the OCE system has a high resolution for displacement measurements, the measurement of air-pulse pressures is still limited (see large error bars in Fig. 3 and Fig. 6), especially for low pressures. Due to this limitation, we currently used an average of 50 repeated measurements for air-pulse force calibrations. Second, the air-pulse pressure and displacement were measured separately. If we could measure the low-pressure air-pulse profiles more reliably, we can develop an OCE system that simultaneously measures pressure and displacement, suggesting a direction for further developing our OCE system. Third, we used pressure-displacement curves for hysteresis characterization instead of the classic response relation between the stress (force per unit area) and strain (proportional deformation). In a typical mechanical test, the compressive or extensive force is usually applied evenly onto the sample surface so that the relation of the stress and strain can be quickly and accurately acquired. In the OCE measurement, the actual values of stress and strain were hard to determine due to the complexity of the transient, local air-pulse stimulation method. We adopted previous elastography methods to solve this problem, which use the force-displacement features to determine the hysteresis values [48,59–49] during the loading and unloading periods. By comparison, compression OCE consisting of a translucent compliant stress sensor sandwiched between the glass window and sample [30,71] can map the stress and strain behaviors during elastography imaging. The use of compression OCE can aid tissue hysteresis measurements by providing additional volumetric details about a sample’s stress-strain relation. Because the air-pulse stimulation is a non-contact method, we do not yet have stress sensors to measure the force directly. In addition, we had to make the OCE measurement at a lateral distance of 0.15 mm from the stimulation point instead of the actual point under the excitation of the air pulse due to the spatial constraint between the air-cannula and the OCT imaging beam (as shown in Fig. 2). Consequently, the current OCE hysteresis estimation method is subjected to wave propagation and attenuation effects that occur between the stimulation and measurement positions. As waves propagate between stimulation and measurement points, wave displacement magnitude decreases with traveling distance and high-frequency waves are attenuated faster [72]. The waveform measured at 0.15 mm had more low-frequency wave components and less high-frequency wave components, compared with the original. We have quantified the estimation errors using the FEA simulation, shown in Fig. 7 and 8, due to this spatial constraint. The FEA results have shown that the difference in the estimated hysteresis loss ratio values between the 0.15 mm and 0 mm measurement positions is reduced as ξ increased, and their differences could be very small for a viscoelastic sample (e.g., ξ > 0.1). Therefore, this hysteresis OCE approach can be used for characterizing both the elastic and viscous materials. Further modification of this method is needed to better interpret the sample biomechanical property by compensating for the effect of wave attenuation in traveling distance.
Important methodological differences should be noted between OCE and mechanical testing methods for hysteresis characterization. The OCE approach uses a fast (millisecond scale), highly-localized (150 µm diameter), and low-pressure (0–60 Pa) air-pulse stimulation method to induce transient, micro-scale, and local sample displacements, while the mechanical testing method uses a step-wise, slower (8 µm/s), global compression loading-unloading method to induce sample displacements with larger magnitudes. Differences between these two methods include the speed at which the sample is loaded, the displacement magnitude, the loading area, and the influence of boundary conditions (sample and stimulation geometry). Moreover, these test methods assess samples over different regions of the stress-strain curve. While estimates of Young’s modulus for soft tissues (especially cornea) reportedly vary over several orders of magnitude (e.g., estimation of Young’s modulus of rabbit cornea ranged from kPa [73] to MPa [74]), these results show that normalized hysteresis values based on measurements of viscoelastic responses are comparable between transient OCE and global compression measurement methods. Although the OCE measurement has shown higher estimated hysteresis loss ratios than the mechanical testing method (shown in Fig. 9 and 10), the predicted hysteresis trends were consistent between these two methods, in which the hysteresis loss ratios decreased as the loading force increased and agar phantoms of different concentrations (e.g., 0.8%–2%) were distinguishable based on the relation between the loss ratios and the sample displacements (Fig. 9).
The microliter air-pulse stimulator used in the current OCE set-up has far less mechanical stimulation pressure (10-60 Pa), stimulation diameter (150 µm), and duration time (< 4 ms) compared to these parameters (70–300 kPa; ∼3 mm; 10–30 ms) in clinical air-puff based instruments (i.e., ORA and CorVis ST). Similarly, we may expect different hysteresis values but similar hysteresis measurement trends among these elastography modalities for ocular biomechanics measurement. We aim to apply this microliter air-pulse OCE system to corneal hysteresis measurements. In the next step, we will also perform a comparison study between our OCE method with the existing clinical instruments on ocular biomechanics (hysteresis included) characterization in the future. In addition, detecting local differences in ocular biomechanics is essential for diagnosing the effects of injuries, pathological degenerations, surgical, or medical treatments [70]. Clinical ORA and CorVis ST devices are currently unable to evaluate the local properties of the cornea due to their global stimulation and measurement strategy. Transient OCE measurement methods have shown clinical potential to spatially quantify corneal mechanical wave propagation [21,69] and natural frequency distributions [20]. However, the local and spatial assessment of corneal hysteresis using transient OCE methods is not yet fully developed due to the cornea’s complex architecture. Previous work has shown that the cornea is spatially inhomogeneous, and anisotropic in its response to mechanical loading [75,76]. As a first step, we have performed a preliminary study using a hysteresis OCE method to distinguish local variations in tissue components (connective tissue and muscle) in a beef sample (Fig. 11). In future studies, we will perform OCE hysteresis measurements in tissues with more complex structure, compositions, and components, including corneal tissues ex vivo and in vivo.
Acknowledgments
The authors thank Dr. Yanping Huang and Dr. Jingjiang Xu for the helpful discussions.
Funding
National Natural Science Foundation of China10.13039/501100001809 (61975030); Basic and Applied Basic Research Foundation of Guangdong Province10.13039/501100021171 (2021A1515011981); Department of Education of Guangdong Province10.13039/501100010226 (2020KTSCX130); Guangdong Provincial Pearl River Talents Program10.13039/100016691 (2019ZT08Y105); Guangdong-Hong Kong-Macao Intelligent Micro-Nano Optoelectronic Technology Joint Laboratory (2020B1212030010); Hubei University of Science and Technology10.13039/501100017590 (BK202019); National Eye Institute10.13039/100000053 (P30EY003039, P30EY07551, R01-EY022362).
Disclosures
The authors declare no conflicts of interest.
Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
References
- 1.Guillot C., Lecuit T., “Mechanics of epithelial tissue homeostasis and morphogenesis,” Science 340(6137), 1185–1189 (2013). 10.1126/science.1235249 [DOI] [PubMed] [Google Scholar]
- 2.Butcher D. T., Alliston T., Weaver V. M., “A tense situation: forcing tumour progression,” Nat. Rev. Cancer 9(2), 108–122 (2009). 10.1038/nrc2544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wu P. H., Aroush D. R. B., Asnacios A., Chen W. C., Dokukin M. E., Doss B. L., Durand Smet P., Ekpenyong A., Guck J., Guz N. V., “A comparison of methods to assess cell mechanical properties,” Nat. Methods 15(7), 491–498 (2018). 10.1038/s41592-018-0015-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.De Lédinghen V., Vergniol J., Barthe C., Foucher J., Chermak F., Le Bail B., Merrouche W., Bernard P. H., “Non-invasive tests for fibrosis and liver stiffness predict 5-year survival of patients chronically infected with hepatitis B virus,” Aliment. Pharmacol. Ther. 37(10), 979–988 (2013). 10.1111/apt.12307 [DOI] [PubMed] [Google Scholar]
- 5.Mahmud A., Feely J., “Arterial stiffness is related to systemic inflammation in essential hypertension,” Hypertension 46(5), 1118–1122 (2005). 10.1161/01.HYP.0000185463.27209.b0 [DOI] [PubMed] [Google Scholar]
- 6.Samani A., Zubovits J., Plewes D., “Elastic moduli of normal and pathological human breast tissues: an inversion-technique-based investigation of 169 samples,” Phys. Med. Biol. 52(6), 1565–1576 (2007). 10.1088/0031-9155/52/6/002 [DOI] [PubMed] [Google Scholar]
- 7.Ophir J., Cespedes I., Ponnekanti H., Yazdi Y., Li X., “Elastography: a quantitative method for imaging the elasticity of biological tissues,” Ultrason Imaging 13(2), 111–134 (1991). 10.1177/016173469101300201 [DOI] [PubMed] [Google Scholar]
- 8.de Korte C. L., van der Steen A. F., Cespedes E. I., Pasterkamp G., “Intravascular ultrasound elastography in human arteries: initial experience in vitro,” Ultrasound Med Biol 24(3), 401–408 (1998). 10.1016/S0301-5629(97)00280-9 [DOI] [PubMed] [Google Scholar]
- 9.Nightingale K., McAleavey S., Trahey G., “Shear-wave generation using acoustic radiation force: in vivo and ex vivo results,” Ultrasound Med Biol 29(12), 1715–1723 (2003). 10.1016/j.ultrasmedbio.2003.08.008 [DOI] [PubMed] [Google Scholar]
- 10.Muthupillai R., Lomas D. J., Rossman P. J., Greenleaf J. F., Manduca A., Ehman R. L., “Magnetic resonance elastography by direct visualization of propagating acoustic strain waves,” Science 269(5232), 1854–1857 (1995). 10.1126/science.7569924 [DOI] [PubMed] [Google Scholar]
- 11.Manduca A., Oliphant T. E., Dresner M. A., Mahowald J. L., Kruse S. A., Amromin E., Felmlee J. P., Greenleaf J. F., Ehman R. L., “Magnetic resonance elastography: non-invasive mapping of tissue elasticity,” Med. Image Anal. 5(4), 237–254 (2001). 10.1016/S1361-8415(00)00039-6 [DOI] [PubMed] [Google Scholar]
- 12.Greenleaf J. F., Fatemi M., Insana M., “Selected methods for imaging elastic properties of biological tissues,” Annu. Rev. Biomed. Eng. 5(1), 57–78 (2003). 10.1146/annurev.bioeng.5.040202.121623 [DOI] [PubMed] [Google Scholar]
- 13.Sarvazyan A., Hall T. J., Urban M. W., Fatemi M., Aglyamov S. R., Garra B. S., “An overview of elastography - an emerging branch of medical imaging,” Curr. Med. Imaging Rev. 7(4), 255–282 (2011). 10.2174/157340511798038684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schmitt J., “OCT elastography: imaging microscopic deformation and strain of tissue,” Opt. Express 3(6), 199–211 (1998). 10.1364/OE.3.000199 [DOI] [PubMed] [Google Scholar]
- 15.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhao Y., Chen Z., Saxer C., Xiang S., de Boer J. F., Nelson J. S., “Phase-resolved optical coherence tomography and optical Doppler tomography for imaging blood flow in human skin with fast scanning speed and high velocity sensitivity,” Opt. Lett. 25(2), 114–116 (2000). 10.1364/OL.25.000114 [DOI] [PubMed] [Google Scholar]
- 17.Sticker M., Hitzenberger C. K., Leitgeb R., Fercher A. F., “Quantitative differential phase measurement and imaging in transparent and turbid media by optical coherence tomography,” Opt. Lett. 26(8), 518–520 (2001). 10.1364/OL.26.000518 [DOI] [PubMed] [Google Scholar]
- 18.Kirkpatrick S. J., Wang R. K., Duncan D. D., “OCT-based elastography for large and small deformations,” Opt. Express 14(24), 11585–11597 (2006). 10.1364/OE.14.011585 [DOI] [PubMed] [Google Scholar]
- 19.Lan G., Singh M., Larin K. V., Twa M. D., “Common-path phase-sensitive optical coherence tomography provides enhanced phase stability and detection sensitivity for dynamic elastography,” Biomed. Opt. Express 8(11), 5253–5266 (2017). 10.1364/BOE.8.005253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lan G., Aglyamov S., Larin K. V., Twa M. D., “In vivo human corneal natural frequency quantification using dynamic optical coherence elastography: repeatability and reproducibility,” J. Biomech. 121, 110427 (2021). 10.1016/j.jbiomech.2021.110427 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lan G., Aglyamov S. R., Larin K. V., Twa M. D., “In vivo human corneal shear-wave optical coherence elastography,” Optom. Vis. Sci. 98(1), 58–63 (2021). 10.1097/OPX.0000000000001633 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ramier A., Eltony A. M., Chen Y., Clouser F., Birkenfeld J. S., Watts A., Yun S. H., “In vivo measurement of shear modulus of the human cornea using optical coherence elastography,” Sci. Rep. 10(1), 17366 (2020). 10.1038/s41598-020-74383-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lan G., Gu B., Larin K. V., Twa M. D., “Clinical corneal optical coherence elastography measurement precision: effect of heartbeat and respiration,” Transl. Vis. Sci. Technol. 9(5), 3 (2020). 10.1167/tvst.9.5.3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Curatolo A., Birkenfeld J. S., Martinez-Enriquez E., Germann J. A., Muralidharan G., Palací J., Pascual D., Eliasy A., Abass A., Solarski J., “Multi-meridian corneal imaging of air-puff induced deformation for improved detection of biomechanical abnormalities,” Biomed. Opt. Express 11(11), 6337–6355 (2020). 10.1364/BOE.402402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Maczynska E., Rzeszewska-Zamiara J., Villar A. J., Wojtkowski M., Kaluzny B. J., Grulkowski I., “Air-puff-induced dynamics of ocular components measured with optical biometry,” Invest. Ophthalmol. Visual Sci. 60(6), 1979–1986 (2019). 10.1167/iovs.19-26681 [DOI] [PubMed] [Google Scholar]
- 26.Chen S., Jin Z., Zheng G., Ye S., Wang Y., Wang W., Wang Y., Zhu D., Shen M., Lu F., “Diurnal variation of corneal elasticity in healthy young human using air-puff optical coherence elastography,” J. Biophotonics 14(8), e202000440 (2021). 10.1002/jbio.202000440 [DOI] [PubMed] [Google Scholar]
- 27.Huston R. L., Fundamentals Of Biomechanics (Springer US, 2007). [Google Scholar]
- 28.Wang Y., “ Soft tissue viscoelastic properties: measurements, models and interpretation ,” dissertation (University of Illinois at Urbana-Champaign, 2016). [Google Scholar]
- 29.Lakes R. S., “Viscoelastic measurement techniques,” Rev. Sci. Instrum. 75(4), 797–810 (2004). 10.1063/1.1651639 [DOI] [Google Scholar]
- 30.Kennedy K. M., Es’haghian S., Chin L., McLaughlin R. A., Sampson D. D., Kennedy B. F., “Optical palpation: optical coherence tomography-based tactile imaging using a compliant sensor,” Opt. Lett. 39(10), 3014–3017 (2014). 10.1364/OL.39.003014 [DOI] [PubMed] [Google Scholar]
- 31.Song S., Huang Z., Nguyen T. M., Wong E. Y., Arnal B., O’Donnell M., Wang R. K., “Shear modulus imaging by direct visualization of propagating shear waves with phase-sensitive optical coherence tomography,” J. Biomed. Opt. 18, 121509 (2013). 10.1117/1.JBO.18.12.121509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Han Z., Aglyamov S. R., Li J., Singh M., Wang S., Vantipalli S., Wu C., Liu C., Twa M. D., Larin K. V., “Quantitative assessment of corneal viscoelasticity using optical coherence elastography and a modified Rayleigh–Lamb equation,” J. Biomed. Opt. 20(2), 020501 (2015). 10.1117/1.JBO.20.2.020501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wu C., Han Z., Wang S., Li J., Singh M., Liu C., Aglyamov S., Emelianov S., Manns F., Larin K. V., “Assessing age-related changes in the biomechanical properties of rabbit lens using a coaligned ultrasound and optical coherence elastography system,” Invest. Ophthalmol. Visual Sci. 56(2), 1292–1300 (2015). 10.1167/iovs.14-15654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lan G., Larin K. V., Aglyamov S., Twa M. D., “Characterization of natural frequencies from nanoscale tissue oscillations using dynamic optical coherence elastography,” Biomed. Opt. Express 11(6), 3301–3318 (2020). 10.1364/BOE.391324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nitta N., Shiina T., “Estimation of nonlinear elasticity parameter of tissues by ultrasound,” Jpn. J. Appl. Phys. 41(Part 1, No. 5B), 3572–3578 (2002). 10.1143/JJAP.41.3572 [DOI] [Google Scholar]
- 36.Voorhees A. P., Ho L. C., Jan N. J., Tran H., Yolandi V. D. M., Chan K., Sigal I. A., “Whole-globe biomechanics using high-field MRI,” Exp. Eye Res. 160, 85–95 (2017). 10.1016/j.exer.2017.05.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kirby M. A., Pelivanov I., Song S. Z., Ambrozinski L., Yoon S. J., Gao L., Li D., Shen T. T., Wang R. K. K., O’Donnell M., “Optical coherence elastography in ophthalmology,” J. Biomed. Opt. 22(12), 1–28 (2017). 10.1117/1.JBO.22.12.121720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cristina L., Penelope D. S. M., Giuseppe L., Marco L., Craig B., “Understanding of the viscoelastic response of the human corneal stroma induced by riboflavin/uv-a cross-linking at the nano level,” PLoS One 10, e0122868 (2015). 10.1371/journal.pone.0122868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rankin J. S., Arentzen C. E., McHale P. A., Ling D., Anderson R. W., “Viscoelastic properties of the diastolic left ventricle in the conscious dog,” Circ. Res. 41(1), 37–45 (1977). 10.1161/01.RES.41.1.37 [DOI] [PubMed] [Google Scholar]
- 40.Starc V., Yellin E. L., Nikolic S. D., “Viscoelastic behavior of the isolated guinea pig left ventricle in diastole,” Am. J. Physiol.-heart C. 271(4), H1314–H1324 (1996). 10.1152/ajpheart.1996.271.4.H1314 [DOI] [PubMed] [Google Scholar]
- 41.Lourenço R. V., Castellanos D., “Lung tissue hysteresis in pulmonary tuberculosis,” Am. Rev. Respir. Dis. 103, 49–56 (1971). [DOI] [PubMed] [Google Scholar]
- 42.Remington J., Alexander R., “Stretch behavior of the bladder as an approach to vascular distensibility,” Am. J. Physiol. 181(2), 240–248 (1955). 10.1152/ajplegacy.1955.181.2.240 [DOI] [PubMed] [Google Scholar]
- 43.Li W., “Modelling of viscoelasticity in pressure-volume curve of an intact gallbladder,” Mech. Soft Mater. 2(1), 1–16 (2020). 10.1007/s42558-019-0016-y [DOI] [Google Scholar]
- 44.Azuma T., Hasegawa M., “A rheological approach to the archtecture of arterial walls,” Jpn. J. Physiol. 21(1), 27–47 (1971). 10.2170/jjphysiol.21.27 [DOI] [PubMed] [Google Scholar]
- 45.Wang Z., Lakes R. S., Golob M., Eickhoff J. C., Chesler N. C., “Changes in large pulmonary arterial viscoelasticity in chronic pulmonary hypertension,” PLoS One 8(11), e78569 (2013). 10.1371/journal.pone.0078569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Luce D. A., “Determining in vivo biomechanical properties of the cornea with an ocular response analyzer,” J. Cataract Refractive Surg. 31(1), 156–162 (2005). 10.1016/j.jcrs.2004.10.044 [DOI] [PubMed] [Google Scholar]
- 47.Hon Y., Lam A. K. C., “Corneal deformation measurement using scheimpflug noncontact tonometry,” Optom. Vis. Sci 90(1), E1–E8 (2013). 10.1097/OPX.0b013e318279eb87 [DOI] [PubMed] [Google Scholar]
- 48.Qin X., Tian L., Zhang H., Chen X., Li L., “Evaluation of corneal elastic modulus based on corneal visualization scheimpflug technology,” Biomed. eng. online 18(1), 42 (2019). 10.1186/s12938-019-0662-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Maczynska E., Karnowski K., Szulzycki K., Malinowska M., Dolezyczek H., Cichanski A., Wojtkowski M., Kaluzny B., Grulkowski I., “Assessment of the influence of viscoelasticity of cornea in animal ex vivo model using air-puff optical coherence tomography and corneal hysteresis,” J. Biophotonics 12(2), e201800154 (2019). 10.1002/jbio.201800154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jiménez-villar A., Mączyńska E., Cichański A., Wojtkowski M., Kałużny B. J., Grulkowski I., “High-speed OCT-based ocular biometer combined with an air-puff system for determination of induced retraction-free eye dynamics,” Biomed. Opt. Express 10(7), 3663–3680 (2019). 10.1364/BOE.10.003663 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Boszczyk A., Kasprzak H., Jóźwik A. J. O., Optics P., “Eye retraction and rotation during Corvis ST ‘air puff’intraocular pressure measurement and its quantitative analysis,” Ophthal. Physl. Opt. 37(3), 253–262 (2017). 10.1111/opo.12383 [DOI] [PubMed] [Google Scholar]
- 52.Singh M., Li J., Vantipalli S., Han Z., Larin K. V., Twa M. D., “Optical coherence elastography for evaluating customized riboflavin/UV-A corneal collagen crosslinking,” J. Biomed. Opt 22(9), 091504 (2017). 10.1117/1.JBO.22.9.091504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wang S., Larin K. V., Li J., Vantipalli S., Manapuram R. K., Aglyamov S., Emelianov S., Twa M. D., “A focused air-pulse system for optical-coherence-tomography-based measurements of tissue elasticity,” Laser Phys. Lett. 10(7), 075605 (2013). 10.1088/1612-2011/10/7/075605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Huang Y., Zheng Y., Measurement of Soft Tissue Elasticity In Vivo: Techniques and Applications (CRC Press, 2015). [Google Scholar]
- 55.Lan G., Xu J., Hu Z., Huang Y., Wei Y., Yuan X., Liu H., Qin J., Wang Y., Shi Q., Zeng J., Shi Y., Feng J., Tan H., An L., Wei X., “Design of 1300-nm spectral domain optical coherence tomography angiography system for iris microvascular imaging,” J. Phys. D: Appl. Phys. 54(26), 264002 (2021). 10.1088/1361-6463/abf577 [DOI] [Google Scholar]
- 56.Dorrer C., Belabas N., Likforman J.-P., Joffre M., “Spectral resolution and sampling issues in Fourier-transform spectral interferometry,” J. Opt. Soc. Am. B 17(10), 1795–1802 (2000). 10.1364/JOSAB.17.001795 [DOI] [Google Scholar]
- 57.Hu Z., Rollins A. M., “Fourier domain optical coherence tomography with a linear-in-wavenumber spectrometer,” Opt. Lett. 32(24), 3525–3527 (2007). 10.1364/OL.32.003525 [DOI] [PubMed] [Google Scholar]
- 58.Lan G., Li G., “Design of a k-space spectrometer for ultra-broad waveband spectral domain optical coherence tomography,” Sci. Rep. 7(1), 42353 (2017). 10.1038/srep42353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kato Y., Nakakura S., Asaoka R., Matsuya K., Kiuchi Y., “Cataract surgery causes biomechanical alterations to the eye detectable by Corvis ST tonometry,” PLoS One 12, e0171941 (2017). 10.1371/journal.pone.0171941 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kotaro Ishii M. D., Saito K., Kameda T., Tetsuro Oshika M. D. J. C., Ophthalmology E., “Elastic hysteresis in human eyes is an age-dependent value,” Clin. Exp. Optom. 41(1), 6–11 (2013). 10.1111/j.1442-9071.2012.02830.x [DOI] [PubMed] [Google Scholar]
- 61.Song S., Huang Z., Wang R. K., “Tracking mechanical wave propagation within tissue using phase-sensitive optical coherence tomography: motion artifact and its compensation,” J. Biomed. Opt. 18(12), 121505 (2013). 10.1117/1.JBO.18.12.121505 [DOI] [PubMed] [Google Scholar]
- 62.Cook R. D., Concepts and Applications of Finite Element Analysis (John wiley & sons, 2007). [Google Scholar]
- 63.Cai C., Zheng H., Khan M., Hung K., “Modeling of material damping properties in ANSYS,” in CADFEM Users’ Meeting & ANSYS Conference, 2002, 9–11. [Google Scholar]
- 64.Lee C.-F., Hsu L.-P., Chen P.-R., Chou Y.-F., Chen J.-H., Liu T.-C., “Biomechanical modeling and design optimization of cartilage myringoplasty using finite element analysis,” Audiol. Neuro-Otol. 11(6), 380–388 (2006). 10.1159/000095900 [DOI] [PubMed] [Google Scholar]
- 65.Ferris P., Prendergast P., “Middle-ear dynamics before and after ossicular replacement,” J. Biomech. 33(5), 581–590 (2000). 10.1016/S0021-9290(99)00213-4 [DOI] [PubMed] [Google Scholar]
- 66.Prendergast P. J., Ferris P., Rice H. J., Blayney A. W., “Vibro-acoustic modelling of the outer and middle ear using the finite-element method,” Audiol. Neurootol. 4(3-4), 185–191 (1999). 10.1159/000013839 [DOI] [PubMed] [Google Scholar]
- 67.Schoemaker I., Hoefnagel P. P., Mastenbroek T. J., Kolff C. F., Schutte S., van der Helm F. C., Picken S. J., Gerritsen A. F., Wielopolski P. A., Spekreijse H., “Elasticity, viscosity, and deformation of orbital fat,” Invest. Ophthalmol. Visual Sci. 47(11), 4819–4826 (2006). 10.1167/iovs.05-1497 [DOI] [PubMed] [Google Scholar]
- 68.and Y M. GOTO, Kimoto, “Hysteresis and stress-relaxation of the blood vessels studied by a universal tensile tes ing instrument,” Jpn. J. Physiol. 16(2), 169–184 (1966). 10.2170/jjphysiol.16.169 [DOI] [PubMed] [Google Scholar]
- 69.Twa M. D., Li J., Vantipalli S., Singh M., Aglyamov S., Emelianov S., Larin K. V., “Spatial characterization of corneal biomechanical properties with optical coherence elastography after UV cross-linking,” Biomed. Opt. Express 5(5), 1419–1427 (2014). 10.1364/BOE.5.001419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Lan G., Shi Q., Wang Y., Ma G., Cai J., Feng J., Huang Y., Gu B., An L., Xu J., Qin J., Twa M. D., “Spatial assessment of heterogeneous tissue natural frequency using micro-force optical coherence elastography,” Front. Bioeng. Biotechnol. 10, 851094 (2022). 10.3389/fbioe.2022.851094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Kennedy K. M., Chin L., McLaughlin R. A., Latham B., Saunders C. M., Sampson D. D., Kennedy B. F., “Quantitative micro-elastography: imaging of tissue elasticity using compression optical coherence elastography,” Sci. Rep. 5(1), 15538 (2015). 10.1038/srep15538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Lakes R. S., Viscoelastic Solids (CRC Press, 2017). [Google Scholar]
- 73.Thomasy S. M., Raghunathan V. K., Winkler M., Reilly C. M., Sadeli A. R., Russell P., Jester J. V., Murphy C. J., “Elastic modulus and collagen organization of the rabbit cornea: Epithelium to endothelium,” Acta Biomater. 10(2), 785–791 (2014). 10.1016/j.actbio.2013.09.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Wollensak G., Iomdina E., “Long-term biomechanical properties of rabbit cornea after photodynamic collagen crosslinking,” Acta Ophthalmol. 87(1), 48–51 (2009). 10.1111/j.1755-3768.2008.01190.x [DOI] [PubMed] [Google Scholar]
- 75.Meek K. M., “Corneal collagen—its role in maintaining corneal shape and transparency,” Biophys. Rev. 1(2), 83–93 (2009). 10.1007/s12551-009-0011-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Chong J., Dupps W. J., “Corneal biomechanics: Measurement and structural correlations,” Exp. Eye Res. 205, 108508 (2021). 10.1016/j.exer.2021.108508 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.