Abstract
The predictive synthesis of metal nanocrystals with desired structures relies on the precise control of the crystal formation process. Using a capping ligand is an effective method to affect the reduction of metal ions and the formation of nanocrystals. However, predictively synthesizing nanostructures has been difficult to achieve using conventional capping ligands. DNA, as a class of the promising biomolecular capping ligands, has been used to generate sequence-specific morphologies in various metal nanocrystals. However, mechanistic insight into the DNA-mediated nanocrystal formation remains elusive due to the lack of quantitative experimental evidence. Herein, we quantitatively analyzed the precise control of DNA over Ag+ reduction and the structures of resulting Au–Ag core–shell nanocrystals. We derived the equilibrium binding constants between DNA and Ag+, the kinetic rate constants of sequence-specific Ag+ reduction pathways, and the percentage of active surface sites remaining on the nanocrystals after DNA passivation. These three synergistic factors influence the nucleation and growth process both thermodynamically and kinetically, which contributed to the morphological evolution of Au–Ag nanocrystals synthesized with different DNA sequences. This study demonstrates the potential of using functional DNA sequences as a versatile and tunable capping ligand system for the predictable synthesis of metal nanostructures.
Graphical Abstract
INTRODUCTION
Metal nanocrystals have found wide applications in catalysis,1 electronics,2 sensing,3 imaging,4 and medicine.5 The structures of nanocrystals play important roles in determining their physical and chemical properties, which dictate their functions.6–11 The predictive synthesis of metal nanocrystals toward desired structures thus holds the key to successful applications of nanomaterials. Despite the promise, predictive control over the structures of nanomaterials in solution-based synthesis is challenging. In a typical wet chemical synthesis, ion precursors are reduced by reductants to yield metal atoms to form nanocrystals. The choice of reagents and experimental conditions are largely empirical because it is difficult to quantify the outcome for each synthetic protocol. To achieve predictable synthesis of metal nanocrystals with desired structures, it is essential to attain quantitative understanding and then control the metal ion reduction process at the molecular level. Among various strategies, using a capping ligand is a versatile and proven method. Capping ligands may affect metal ion reduction in two different ways. On the one hand, the ligands can interact with the metal ion precursors through metal-ion–ligand complexation,12,13 which directly alters the electronic structure of the metal ion and changes their reduction potentials and kinetics.14 On the other hand, the ligands may interact with the surface of the crystals, altering the deposition and diffusion rate of adatoms, which changes the growth rates of different facets.15–17 Despite many studies that explored different conditions, we are still far from comprehensive understanding of the role of the capping ligands in nanocrystal formation. Systematically tunable capping ligands that have predictable interactions with both the precursor and the surface of the nanocrystals18 are indispensable for precisely controlling metal ion reduction and nanocrystal formation.
DNA is an especially promising class of capping ligands because of its well-defined molecular structures and conformations that are predictable from the sequences composed of the four-letter genetic codes. Single stranded DNA (ssDNA) with the same nucleotides or mixed nucleotides have been used in the synthesis of Au,19–22 Ag,23 and Pd–Au bimetallic nanocrystals.24 Nanocrystals with different morphologies formed when different DNA molecules were applied to the synthesis. To realize the full potential of DNA in the predictive synthesis of nanostructures, one needs to understand the mechanism for DNA-controlled metal ion reduction and nanocrystal formation process.21,22,24 There is, however, a general lack of quantitative experimental data, which is crucial in parameterizing the nanocrystal formation process. Quantitative description of the nanocrystal formation is challenging in not only DNA-mediated but also peptide-mediated and other biomolecule-mediated processes.25,26 Such a challenge is largely due to the complexity of the interactions between biomolecules and nanocrystals, as well as the limited characterization techniques available for probing the kinetic and thermodynamic parameters of the biomolecular–inorganic interface.8,18,27 Therefore, quantitative experimental data and the corresponding theoretical frameworks are crucial in interpreting the mechanisms for the biomolecule-controlled formation of nanocrystals.
DNA interacts with metal ions in definable binding modes. Metal cations generally interact with DNA either through electrostatic interaction of the negatively charged phosphodiester backbone or the nitrogen and oxygen atoms on the nucleo bases.28,29 Ag+ is one of the few metal ions that interact with DNA exclusively through the nucleobases.30–33 Therefore, DNA-controlled Ag+ reduction and nanocrystal formation is an ideal model system to achieve quantitative understanding, because it eliminates possible interferences from the non-specific interactions with the phosphodiester backbones. Therefore, by using the DNA-controlled formation of Au–Ag core–shell nanocrystals as a model system, we report herein quantitative analysis of the interaction between DNA and Ag+ precursors, the reduction pathways of Ag+, and the interaction between DNA and nanocrystal surfaces. We used the mechanistic insight of DNA-controlled Ag+ reduction kinetics to elucidate the morphological evolution of the resulting nanocrystals. This study demonstrated the predictive power of DNA-sequence-specific control on the formation of metal nanocrystals.
RESULTS AND DISCUSSION
To understand the DNA-mediated growth of silver on gold nanoparticles (Au NPs) and their effects on the resulting morphologies, we chose to use Au decahedra with an average diameter of 74.8 ± 3.4 nm (Figure S1) as the seed, on the basis of a protocol reported previously.34 There are several advantages of selecting Au decahedra as the seed crystals. First, Au atoms have minimal lattice mismatch with that of Ag atoms.35 Therefore, using Au NPs as the seed avoided lattice strain, which could result in complications in elucidating the mechanism of seed-mediated growth. Second, Au and Ag exhibit a large contrast under transmission electron microscopy (TEM), making it easier to differentiate between the Au core and Ag shell of the hybrid or core–shell NPs. Finally, decahedra has a unique penta-twinned structure36 that is expected to produce interesting defect-induced morphologies.37
To elucidate the effect of DNA molecules on the morphological growth of the NPs, ssDNA made of 20 units of all four nucleotides (C20, A20, T20, and G20) were used in the synthesis of Au–Ag core–shell NPs, while ascorbic acid was employed as the reducing agent and silver acetate (AgOAc) as the silver precursor. An overgrowth of Ag shells was found when C20, A20, or T20 was used as the DNA capping ligand, whereas no obvious overgrowth of the Ag shell was detected when G20 was used (Figure S2), which could be due to the effect of Ag+ sequestering by a G-quadruplex.23
Figure 1 shows the scanning electron microscope (SEM) images and TEM micrographs of Au–Ag core–shell nanostructures synthesized with different DNA sequences. The SEM image shows uniform Ag shells grown on the decahedral Au seeds in the presence of C20 (Figure 1a). The TEM images of Au–Ag NPs at representative time points were taken by sampling the NPs by centrifugation to analyze their morphological evolution. The morphological evolution of the Ag shell grown with C20 followed the same shape as that of the Au decahedra core at all sampling time points (Figure 1 b–e), which resulted in a decahedral shell that shared a common 5-fold symmetrical axis with the core in the final structure (Figure 1e). A20-mediated Ag+ reduction generated a 5-fold symmetrical face protruded structure (Figure 1f). The 10 {111} facets of the decahedra core were symmetrically deposited with Ag, whereas the lateral growth along the equatorial plane was mostly restricted (Figure S3). The overgrowth of the Ag shell in the presence of A20 initially took place on all five domains of the decahedron structure (Figure 1g,h), followed by a protrusion of each face (Figure 1i), which resulted in the rounded particle morphology as viewed from the 5-fold symmetrical axis (Figure 1j). More interestingly, the T20-mediated growth of Au–Ag NPs exhibited asymmetrical protrusions (Figure 1k). The time-dependent TEM showed that the T20-mediated growth of the Ag shell selectively favored one of the five domains of the 5-fold twin structure inherited from the Au decahedra seed (Figure 1l–n), which led to the asymmetrical protrusion in the final structure (Figure 1o). The automatic symmetry breaking in the T20-mediated nanostructure has rarely been reported previously.
Figure 1.
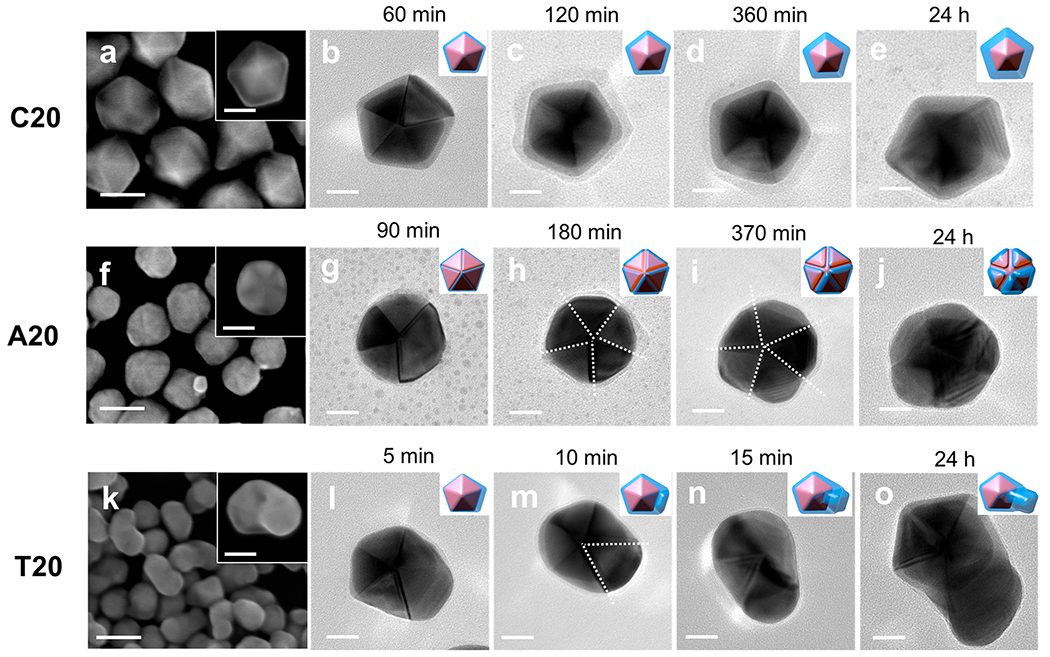
SEM images and TEM micrographs of Au–Ag core–shell NPs formed at different time points in the presence of (a–e) C20, (f–j) A20, and (k–o) T20, respectively. The insets in the SEM images are enlarged single particles. The white dashed lines in the TEM images highlight the twin boundary along which the Ag shells selectively grew. Scale bars are 50 nm in SEM (a, f, and k) images and 20 nm in TEM micrographs (b–e, g–j, and i–o).
To elucidate the role of DNA in controlling the growth of the Au–Ag NPs toward different morphologies, we investigated these systems from three aspects. We first studied the interaction between DNA and Ag+ precursors by quantifying the complexation between Ag+ and DNA using electrochemical analysis. We then quantitatively analyzed the reduction of Ag+ in the presence of DNA and derived the rate equations for different reduction pathways. Finally, we characterized the percentage of active surface sites remaining on the nanocrystals after DNA passivation. Our quantitative analyses suggest that DNA molecules of different sequences directly affect the kinetics and thermodynamics of Ag+ reduction and nanocrystal formation processes, which lead to the sequence-specific atom deposition and NP formation that result in different morphologies.
Interaction between DNA and the Ag Precursor.
Silver cation binds to the DNA nucleobases mostly by bridging two bases to function similarly to the hydrogen bonding interaction in a Watson–Crick base pair.32,38–41 The silver-mediated bridging of base pairs can also take place in the presence of ssDNA containing the same nucleobases, particularly C–C.42 Herein, the interaction between Ag+ and the nucleobases in ssDNA can be described using a one-to-two binding model:
| (1) |
The reduction of Ag+ in the presence of DNA could be described in the context of a metal–ligand equilibrium 2,43 followed by a reduction reaction 3.44 We propose that the Ag+ reduction went through the following reaction steps:
| (2) |
| (3) |
The reduction of Ag+ in the reaction 3 can be described using the Nernst equation:
| (4) |
An effect of a metal–ligand complexation from reaction 2 is to decrease the effective concentration of [Ag+] in eq 4. Thus, the potential (E) of Ag+ in eq 4 is lower than that without the perturbation from DNA.44
To test the proposed model, we added solutions of A20, C20, and T20, respectively, into a 20 μM AgOAc solution and measured its open circuit potential (OCP) as an indicator of E in eq. 4 using a polycrystalline Ag working electrode (Figure 2). The addition for each sequence was repeated three times, and the error bar represents the standard deviation of the triplicated experiments. The final concentration of the DNA strands was 20 μM. The concentration of the DNA nucleobases was 400 μM, because each DNA strand contains 20 nucleobases. The concentration of nucleobases was in large excess (20 times) compared with that of the AgOAc solution. As shown in Figure 2, the OCP in the presence of C20 dropped the most significantly (276 +− 8 mV). A20 also caused a drop of the OCP by 148 +− 8 mV, whereas the OCP only dropped by 3 +− 1 mV in the presence of the T20 sequence.
Figure 2.
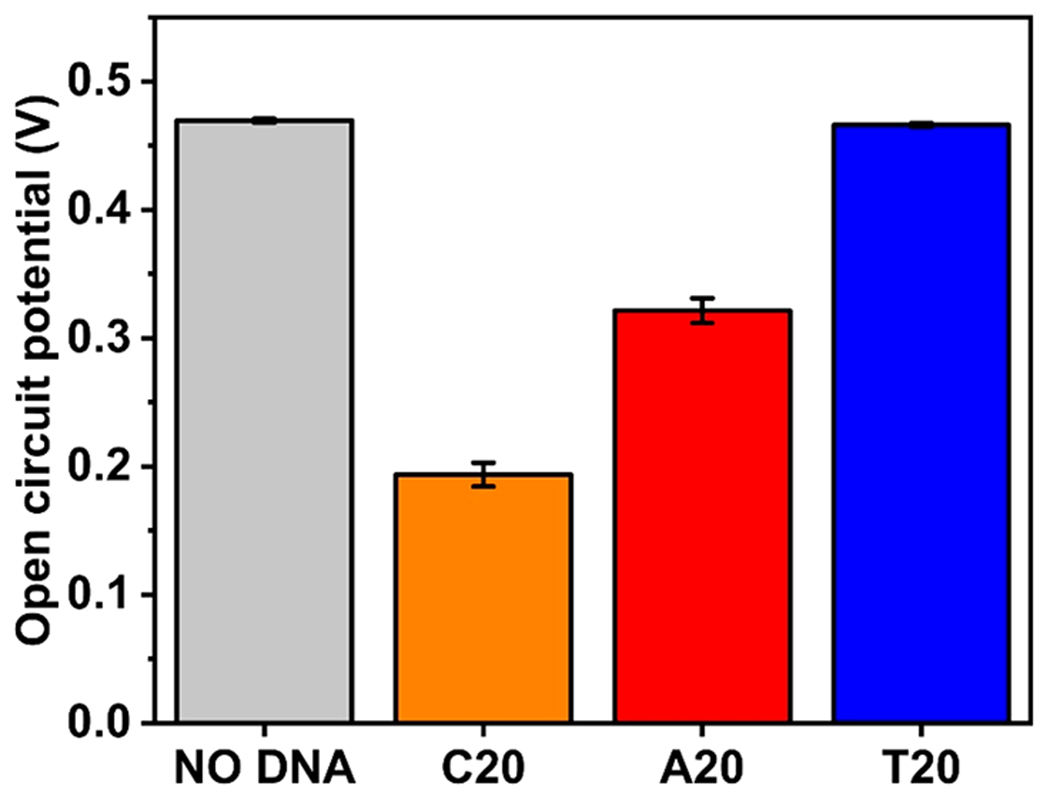
Open circuit potential of Ag+ solution versus Ag/AgCl reference without and with adding DNA solutions of different sequences.
The drop in the E of the Ag+/Ag0 redox pair strongly suggests the complexation between Ag+ and bases equilibrium 2. The degree of complexation varied between the DNA molecules of different sequences, which could be ascribed to the different binding abilities between DNA nucleotides and Ag+.32,41,42 Furthermore, the OCP could be converted into the concentration of Co using the following Nernst equation:
| (5) |
where CAg+free is the effective concentration of Ag+ (unbound Ag+) participating in the redox reaction and was determined experimentally using the OCP of 20 μM AgOAc solution without DNA. Using eq 5, the calculated Ag+ concentrations after DNA complexation were 4.37 × 10−4 μM for C20, 6.36 × 10−2 μM for A20, and 17.8 μM for T20. Because the total Ag+ concentration in the solution was 20 μM, the remaining unbound Ag+ concentration indicated that A20 and C20 sequestered more Ag+ than T20 did. If we assume that the concentration of free Ag+ equals the equilibrium concentration of Ag+ ([Ag+]eq), the equilibrium constants between Ag+ and DNA molecules of different sequences could be calculated as Keq (C20) = 0.286 μM−2, Keq (A20) = 0.195 μM−2, and Keq (T20) = 7.72 × 10−7 μM−2 (see the Supporting Information (SI), Note 4 for details of calculation). The Keq for T20 is 6 orders of magnitude smaller than those of A20 and C20, which indicates a weak binding between thymine and Ag+.42 An assumption of our model is that if the oxidized form of a redox couple is stabilized by a ligand, the free energy of the initial state of the reduction reaction is lowered; hence, the metal–ligand complex becomes difficult to be reduced. We also assumed that the DNA adsorption on the silver metal did not significantly affect the reduction potential of the Ag+. We treated the DNA-complexed Ag+ reduction as the dissociation of the complex and release of unbound Ag+ followed by the reduction of the free Ag+, which might not be the exact case if a concerted reduction of the DNA–Ag+ complex to free DNA and Ag0 occurs. However, because the model only concerns the thermodynamic driving force of the reaction, the exact mechanistic path does not affect the conclusions drawn from the experimental result.44
DNA-Mediated Ag+ Reduction Pathways.
The pathways of metal ion reduction determine the site and rate for metal atom generation and deposition. Hence, studying the reduction pathways of precursors is essential in a mechanistic understanding of the growth pattern of metal nanocrystals. In seed-mediated synthesis, metal ion precursors could be reduced in two different pathways.45 In the solution reduction pathway, metal ions are directly reduced by the reductant molecules in the solution. The corresponding reaction equation and rate expression of Ag+ reduced by the reductant (Red), ascorbic acid, are as follows (SI Note 2):
| (6) |
| (7) |
where k1 is the rate constant for the solution reduction.
In the surface reduction pathway, metal ions are first adsorbed onto the surface of the growing crystals and then reduced.45–47
| (8) |
| (9) |
where k2 is the rate constant for surface reduction and Agn0 is the concentration of surface atoms on the nanocrystals. The total rate for Ag+ reduction should include the contribution from both pathways:
| (10) |
As shown in the previous section, DNA binds to Ag+ in a sequence-specific manner, thus certainly affecting the reduction kinetics by changing [Ag+] in the rate expression.
| (11) |
Herein, the rate expression for the DNA-controlled Ag+ reduction reaction could be modified into the following equation:
| (12) |
To follow the DNA-mediated Ag+ reduction kinetics, we used a UV–vis spectroscopy-based method45,47 to monitor the concentration of the reductant remaining in the solution at different time points (see Figures S4 and S5 and SI Note 1 for experimental details). We conducted two parallel experiments in both the absence and presence of preformed seed nanocrystals. While we focused on seed-mediated synthesis in this work, reduction kinetics without the preformed seeds provide important information on the solution reduction pathway, because without the preexisting surface of the seeds, the solution reduction is dominant.45,46 Furthermore, the sequence-specific reduction pathways in response to the absence and presence of seed also shed light on the interaction between DNA ligands and the surface of the crystals.
Kinetic Analyses of the DNA-Mediated Ag+ Reduction Pathways in the Absence of Presynthesized Seed.
Parts a, c, and e of Figure 3 show the remaining concentration of the reductant during the Ag+ reduction process without seeds. The reduction reaction in the presence of T20 (Figure 3a) proceeded much faster than those with A20 (Figure 3c) and C20 (Figure 3e). Moreover, only the curve with T20 exhibited a self-catalyzed behavior.46
Figure 3.
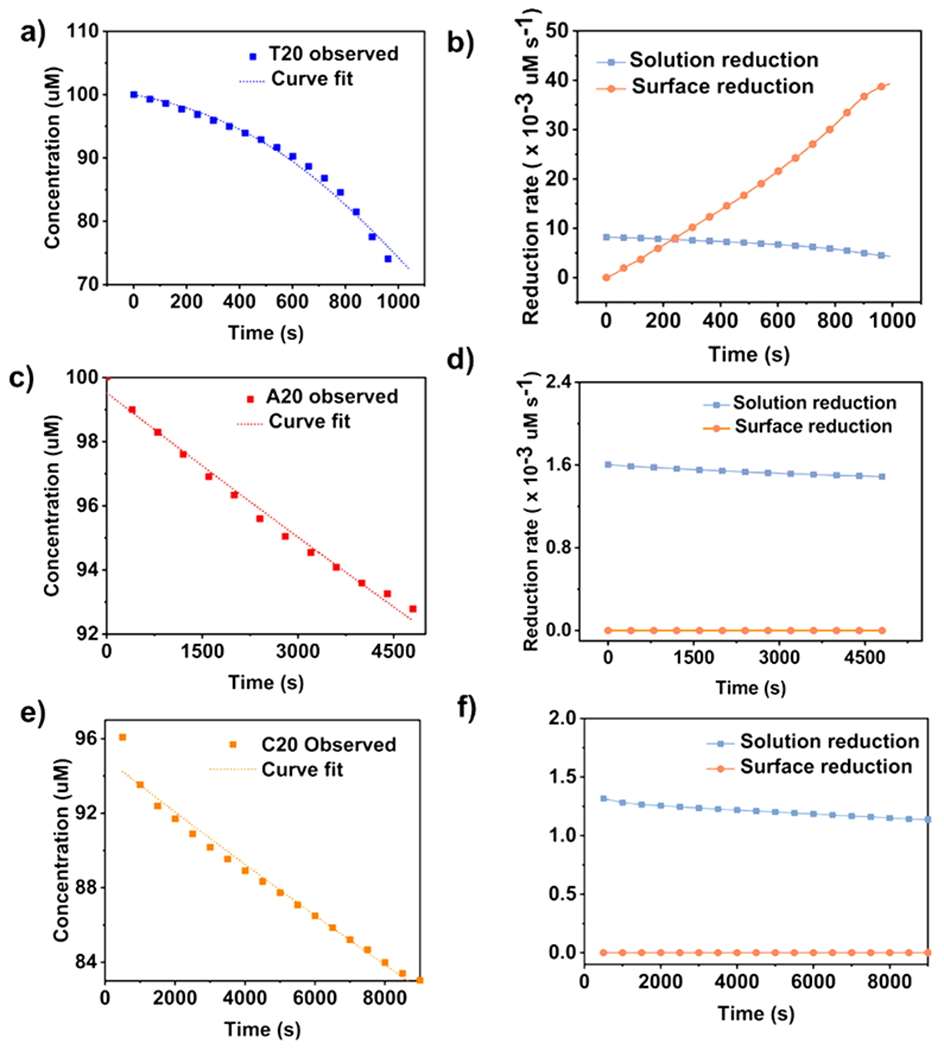
Quantitative analysis of the reduction of Ag precursor by ascorbic acid without seeds in the presence of (a and b) T20, (c and d) A20, and (e and f) C20. (a, c, and e) Concentrations of ascorbic acid in the reaction solution, and (b, d, and f) rates of solution reduction and surface reduction as a function of time in the presence of the three DNA sequences.
On the basis of the above analyses, the model for the T20-mediated Ag+ reduction without preformed seeds could be described using a two-step model (SI Note 3):
| (13) |
| (14) |
| (15) |
| (16) |
Equation 13 describes the solution reduction, and eq 15 describes the autocatalytic surface reduction45–47 on the formed nuclei (Agn0 represents the concentration of surface atoms on the just-formed nuclei). The homogeneous nucleation step (eq 14) was excluded when considering the reduction rate of Ag0 because the process is much faster compared with the rate for Ag+ reduction.48
This model was used to analyze the growth curve with T20 (Figure 3a) (see SI Note 3 for derivation of the equations). The rate constants k1′ and k2′ were derived from the fitting to be 4.02 × 10−7 s−1 μM−1 and 6.96 × 10−8 s−1 μM−2, respectively. On the basis of these kinetic parameters, we came up the rates for solution reduction and surface reduction as a function of time. As shown in Figure 3b, the rate for surface reduction was slower than that of solution reduction in the first 200 s, which could be ascribed to the limited surface sites on the newly generated nucleus (Agn0). As the reaction progressed, the rate for surface reduction increased until it surpassed the rate for solution reduction.
The kinetic model needs to be further developed to be applied to A20- and C20-mediated Ag+ reduction reactions, because these two DNA strands bind stronger to Ag+ than T20. By using the Keq derived from the OCP measurements, we calculated the concentrations of unbound [Ag+] at given times during the reduction process (see SI Note 4). The average concentrations of unbound [Ag+] were 0.57 μM ± 0.46% with C20 and 6.83 μM ± 1.65% with A20 within the time scale of the investigation. These values were 2–3 orders of magnitude lower than that with T20 (164.00 μM ± 7.26%), which was consistent with the observations that A20 and C20 bound strongly with Ag+. The DNA molecules whose sequences bound more strongly to Ag+ shifted the equilibrium toward the DNA–Ag+ complex, resulting in a low supersaturation of the metal ion precursor throughout the reduction process. Consequently, the solution reduction became the rate-limiting step because the surface reduction relied on Agn0 generated from solution reduction. The whole process thus can be approximated as a first order reaction where only the solution reduction of Ag+ is considered:12
| (17) |
| (18) |
| (19) |
To test this hypothesis, we fitted the kinetic curve in the presence of A20 and C20 with both one- and two-step models (see SI Note 5 for derivations of the equation and additional discussion). As shown in Figure S6, the two-step model significantly deviated from the experimental data (R2 values are 0.79 for A20 and 0.26 for C20), whereas the one-step model matched well with the kinetic results with R2 values of 0.99 for A20 and 0.95 for C20. The rate constants k1′ derived from the one-step model were 1.53 × 10−5 s−1 μM−1 for A20 and 1.37 × 10−5 s−1 μM−1 for C20. Compared with the two-step model, the one step-model for A20- and C20-mediated reduction kinetics did not involve the surface reduction. We calculated further the reduction rates in the presence of A20 and C20 using the kinetic parameters derived from the fitting (Figure 3d,f). Our results showed that the solution reduction dominated the A20-mediated (Figure 3d) and C20-mediated (Figure 3f) Ag+ reductions. In contrast, in the presence of T20, surface reduction became the dominate reduction pathway over time (Figure 3b). The reduction rate with T20 was also much larger than those with A20 and C20. Table 1 lists all the kinetic parameters derived from the fitting.
Table 1.
Kinetic Parameters for Ag+ Reduction with Different DNA Sequences in the Absence of Seed Crystalsa
| solution reduction |
surface reduction |
|||||||
|---|---|---|---|---|---|---|---|---|
| DNA sequence | k1′ (×10−5) | k1 (×−6) (s−1 μM−1) | percentages | absolute rate (× 10−3) (s−1 μM) | k2′ (×10−8) (s−1 μM−2) | k2 (× 10−8) (s−1 μM−2) | percentages | absolute rate (× 10−3) (s−1 μM) |
| T20 | 0.0402 ± 0.0020 s−1 μM−1 | 0.444 ± 0.002 | 59.0 | 7.26 ± 0.35 | 6.96 ± 0.28 | 7.79 ± 0.31 | 41.0 | 12.6 ± 0.05 |
| A20 | 1.53 ± 0.11 s−1 | 2.24 ± 0.16 | 100.0 | 1.45 ± 0.10 | 0 | |||
| C20 | 1.37 ± 0.02 s−1 | 24.0 ± 3.50 | 100.0 | 1.30 ± 0.02 | 0 | |||
Contribution of two-reduction pathways and absolute rate were calculated for the initial stage when the first 5% of ascorbic acid (Red) was consumed.
There was a clear correlation between the DNA–Ag+ interactions and reduction pathways of Ag+ on the basis of the above quantitative analyses, particularly in two aspects. Macroscopically, the solution and surface reductions were two consecutive steps when Ag+ was reduced without seeds. The product of the solution reduction (Agn0) became the reactant for the surface reduction. The strong binding of Ag+ with A20 and C20 limited the concentration of free Ag+, thus the product (Agn0) generated from the solution reduction. In the corresponding rate expression, the solution reduction became the rate-limiting step that dominated the reduction process. From a molecular perspective, the surface reduction required at least a termolecular collision (eq 15), which was unlikely to happen unless the concentrations of the reactants were extremely high.49 Such conditions could however be achieved by tuning the reaction parameters, as have been demonstrated previously in cases where the reductant was in large excess compared with the precursor.45,46 In the case of T20 in this work, free Ag+ concentration did not significantly decrease because of the weak DNA binding. In the two-step T20-mediated growth, concentrations of both Ag+ and the reductant were high enough for the termolecular collision to take place in the microenvironment near the surface of nuclei. However, in the presence of A20 and C20, the possibility for termolecular collision was low because of the limited amount of Ag+. As a result, the solution reduction dominated the A20- and C20-mediated reductions because this reaction only required bimolecular collision (eq 17). In other words, even though the rate for autocatalytic surface reduction was much faster than that of solution reduction,45–47 the surface reduction did not contribute significantly to the overall reduction rate in the presence of A20 and C20 because it was a rare event.
Kinetic Analyses of the DNA-Mediated Ag+ Reduction Pathways in the Presence of Presynthesized Seed.
Having analyzed the kinetics in the absence of presynthesized seed, we extended the kinetic study to the reduction of Ag+ in the presence of seeds. Similar to the curve fitting in the absence of seeds, the kinetic curve of Ag+ reduction in the presence of T20 and the Au decahedra was fitted to the two-step model (Figure 4a).
Figure 4.
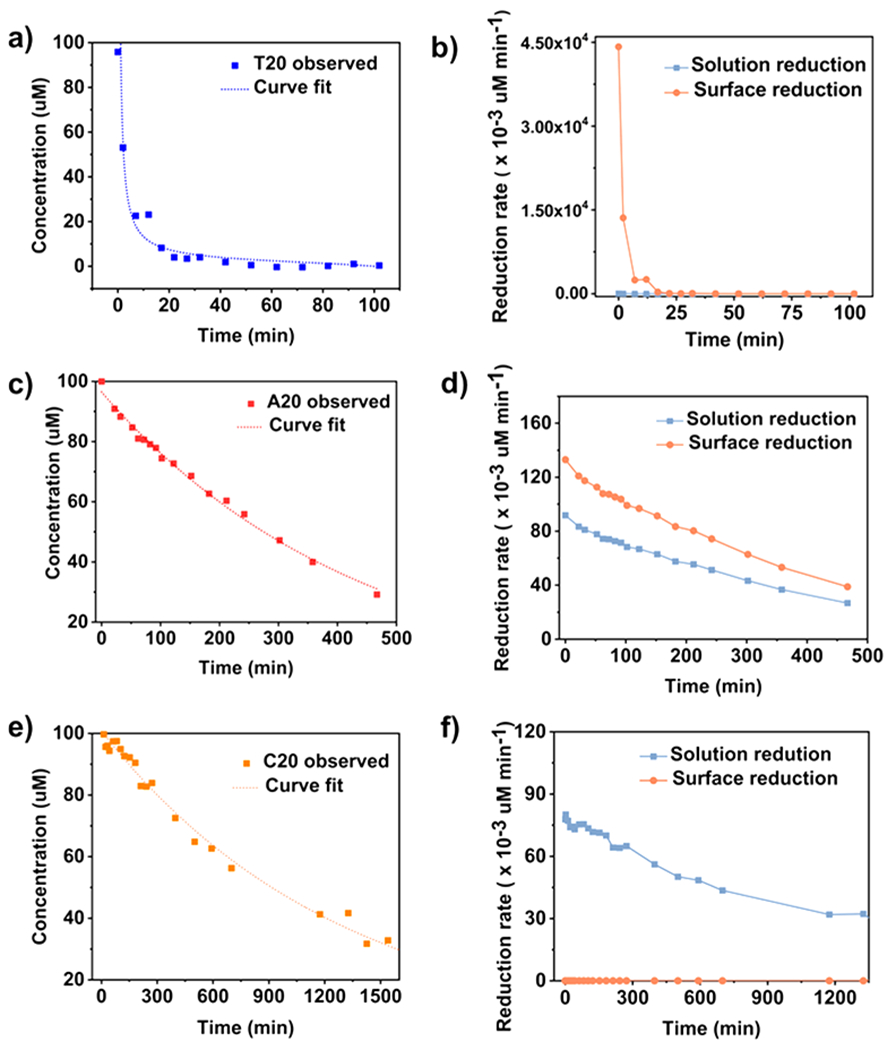
Quantitative analysis of the reduction of Ag precursor by ascorbic acid with Au decahedra seeds in the presence of (a and b) T20, (c and d) A20, and (e and f) C20. (a, c, and e) Concentrations of ascorbic acid in the reaction solution, and (b, d, and f) rates of solution reduction and surface reduction as a function of time in the presence of the three DNA sequences.
To use the model developed, we made one modification to replace the concentration of surface atoms of nuclei (Agn0 in eq 8) with the concentration of surface atoms of the preformed seeds (Agn0 (seed) in the following equations:
| (20) |
| (21) |
| (22) |
| (23) |
On the basis of this analysis, the rate constant for surface reduction k2′ was determined to be 8.96 × 10−6 s−1 μM−2 assuming that the observed rate constant for solution reduction (k1′) was the same as that in the reduction kinetic without seeds (see SI Note 6 for derivations of the equation).45 The reduction rate with T20 was then calculated using the obtained rate constant (Figure 4b). The rate for surface reduction was the highest at the early stage of the reaction, because of the abundant seeds in the solution, and quickly dropped due to the depletion of the reagents. Overall, surface reduction had a much higher rate than solution reduction in T20-mediated Ag+ reduction with the seeds.
In the presence of A20 and C20, the seed-mediated growth was no longer a simple one step as in the case without seeds. In the one-step growth, the solution reduction was the rate-limiting step because the concentrations of the precursor, reductant, and reactive surface sites were limited. However, when seeds were introduced, the concentration of the surface sites available for the reductive adsorption of Ag+ was greatly increased. Moreover, the solution and surface reductions occurred simultaneously with seeds instead of consecutively as without the seeds. The solution reaction and surface reaction were no longer interdependent because the surface reduction also took place on the seeds rather than just the nuclei. Therefore, in the presence of the seeds, the A20- and C20-mediated reactions should be analyzed using the two-step models.
We used the two-step model to fit the kinetic curve with A20 (see SI Note 7 for derivation of the equation and additional discussions). The fitted curve was in excellent agreement with the experimental data (Figure 4a, R2 = 0.99). The rate constant for surface reduction k2′ was determined to be 6.93 × 10−6 s−1 μM−2. We also calculated the reduction rate for the A20-mediated reaction kinetic as a function of time. As shown in Figure 4d, both solution and surface reduction pathways were present in A20-mediated reaction, with the surface reduction pathway contributed more significantly in the overall reduction rate.
Similarly, the two-step model was used to analyze the kinetics in the presence of C20. The rate constant for solution reduction k1′ derived from fitting was 1.29 × 10−5 s−1 (Figure 4e, R2 = 0.99), which was strikingly consistent to the k1′ in the absence of seeds (5.8% difference), suggesting the absence of the surface reduction as in the one-step growth mechanism (SI Note 8). Therefore, the one-step model was a better fit for C20. Unlike with A20, introducing seeds did not alter the reduction pathway in the C20-coupled growth. We also calculated the reduction rate using the kinetic parameter derived from the one-step model (Figure 4f). A summary of all the kinetic parameters obtained from the above analyses is listed in Table 2.
Table 2.
Kinetic Parameters for Ag+ Reduction with Different DNA Sequences in the Presence of Preformed Seeda
| solution reduction |
surface reduction |
|||||||
|---|---|---|---|---|---|---|---|---|
| DNA sequence | k1′ (× 10−5) | k1 (× 10−6) (s−1 μM−1) | contribution (%) | absolute rate (× 10−3) (s−1 μM) | k2′ (× 10−6) | k2 (× 10−5) (s−1 μM−2) | contribution (%) | absolute rate (× 10−3) (s−1 μM) |
| T20 | 0.0402 ± 0.0020 s−1 μM−1 | 0.444 ± 0.022 | 0.01 | 7.26 ± 0.36 | 8.96 ± 0.89 s−1 μM−2 | 1.00 ± 0.01 | 99.9 | 359 ± 35.5 |
| A20 | 1.53 ± 0.11 s−1 | 2.24 ± 0.16 | 40.3 | 1.45 ± 0.10 | 5.28 ± 0.18 s−1 μM−1 | 0.77 ± 0.03 | 59.7 | 2.16 ± 0.07 |
| C20 | 1.29 ± 0.05 s−1 | 1.26 ± 0.05 | 100 | 1.23 ± 0.15 | 0 | |||
Contribution of two reduction pathways and absolute rate were calculated when first 5% of ascorbic acid (Red) was consumed.
To compare the reduction pathways of DNA with all three sequences, we calculated the percentage of solution and surface reductions by integrating the reaction rates over time (Figure 5a, Tables 1 and 2). For C20, the solution reduction accounted for 100% of the particle formation with or without the seeds. Similarly, the solution reduction dominated the seedless reduction kinetic in the case of A20. However, when the seeds were introduced, surface reductions (59.7%) became the dominate reduction pathway. On the contrary, when using T20, both solution (59.0%) and surface reductions (41.0%) contributed to the crystal growth in the absence of seeds, whereas the surface reduction (99.9%) dominated with the seeds.
Figure 5.
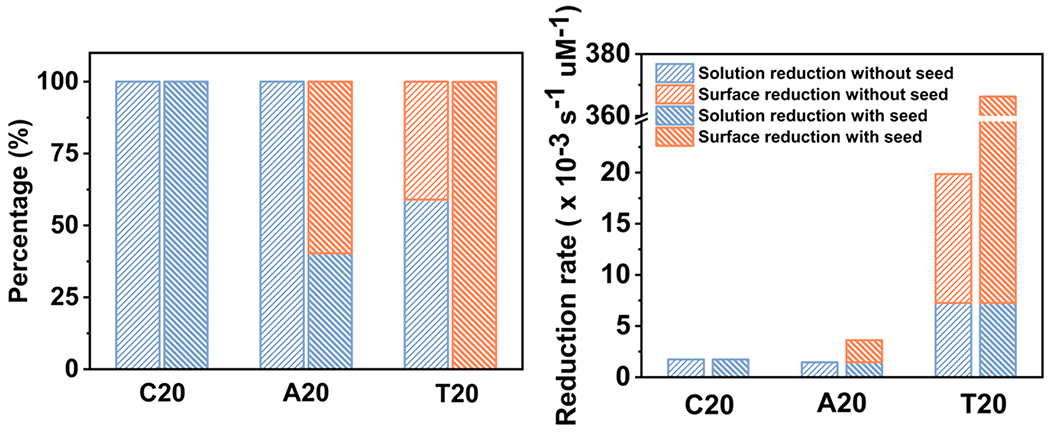
(a) Percentages and (b) corresponding rates of solution and surface reductions with and without seeds when 5% of AA is reacted.
We further analyzed the absolute reduction rates for all three sequences for the initial period of the reaction, that was, until 5% of ascorbic acid was consumed (Figure 5b, Tables 1 and 2). The rates for solution reduction was comparable between A20 (1.45 × 10−3 s−1 μM) and C20 (1.23 × 10−3 s−1 μM) but 5–9 times higher for that with T20 (7.26 × 10−3 s−1 μM). Moreover, the rate for surface reduction when using T20 without seeds reached 1.26 × 10−2 s−1 μM, while there was no observable surface reduction for A20 and C20. More significantly, the rate for the surface reduction for T20 with seeds (3.59 × 10−1 s−1 μM) was almost 2 orders of magnitude higher than that of A20 (2.16 × 10−3 s−1 μM).
Interactions between DNA and the Surface of Nanocrystals.
Unlike A20, surface reduction did not become the dominate reduction pathway when we introduced the preformed seeds in the C20-mediated Ag+ reduction. What caused the difference in the sequence-specific reduction pathways in the presence of the seed? Besides the difference in the DNA–Ag+ binding, could DNA sequences also interact differently with the surface of the nanocrystals? We hypothesize that C20 might have passivated the surface of the nanocrystals more than A20 did, which prevented the active sites on the surface from participating in the surface reduction. To test this hypothesis, we designed a mercaptoethanol (ME) replacement assay to test the relative binding affinity of DNA to the surface of nanocrystals. Previously, Demers et al. developed a method to use ME to replace thiolated DNA on the surface of Au nanocrystals for DNA quantification.50 However, unlike the DNA conjugated onto the nanocrystals through thiol–metal bonding, the DNA attached on the surface of nanocrystals during the synthesis could not be completely removed by the ME replacement, even if it did not have the thiol modification.19,23 On the basis of these observations, we reasoned that ME could be used as a reference for binding affinity of DNA toward the surface of nanocrystals. Upon exchange with ME, the DNA whose sequences have a high affinity toward the surface of the crystals should be replaced to a lesser extent than the ones with a low affinity.
Using a modified fluorescence-based DNA quantification method (see SI Note 9 for experimental details and additional discussions), we quantified the percentage of DNA strands being replaced (%Re) after the ME exchange and obtained 93.77 ± 1.27% for C20, 95.63 ± 0.31% for A20, and 98.71 ± 0.40% for T20. The concentration of available surface sites ([Agn0 (seed)]available) for Ag atom deposition was less than the total concentration of surface atoms ([Agn0 (seed)]) due to DNA passivation. The percentage of DNA strands being replaced (%Re) after the ME exchange indicated the remaining active sites on the nanocrystal surfaces. Therefore, the active surface sites on the nanocrystals in the presence of DNA were described by the following equation:
| (24) |
The above quantitative analysis was further incorporated into the kinetic models in the previous sections. The rate constants for surface reduction in the presence of seed (k2) could be derived as 1.03 × 10−5 s−1 μM−2 for A20-mediated and 1.00 × 10−5 s−1 μM−2 for T20-mediated growth. The derived rate constants are summarized in Table 2.
We used ME as a reference for binding affinity to quantify the active sites on nanocrystals that have not been permanently blocked by the DNA binding. A variety of capping ligands have been proposed to bind to the surface of the nanocrystals.51–53 If the binding is weak, the ligands can then dynamically adsorb and desorb from the surface, which might not prevent the adatom from incorporating into the nanocrystals. However, capping ligands that bound strongly to the surface could irreversibly passivate the reactive sites and reduce the accessibility of the surface. Mercaptoethanol forms covalent bonds with Au and Ag surfaces though its S atom.54,55 Therefore, we used ME to estimate the extent by which the DNA irreversibly bound the surface-active sites, though we recognize there exists an uncertainty of using the affinity of ME to the surface as a reference and the number of surface sites occupied by each DNA strand could be hard to determine. Despite the limitations, such an essay provides important insights for studying the binding of the capping ligand to nanocrystal surfaces.
Proposed Mechanism for Morphology Evolution.
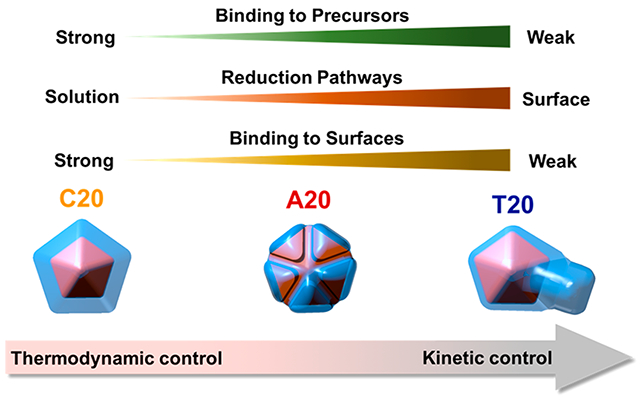
On the basis of the above quantitative analysis, we analyzed the effects of the DNA molecules on the precursor complexation, reduction pathways, and surface passivation. All three factors synergistically affected the atom deposition and diffusion on the growing nanocrystals, which resulted in different morphologies. Specifically, the binding between the DNA and Ag+ precursor determined the supersaturation level of Ag+ available for reduction; the corresponding reduction pathways of Ag+ dictated the location and rate for Ag0 generation and deposition, and the interactions between DNA and the surfaces of nanocrystals determined the diffusion pattern of adatoms. On the basis of these insights gained from quantitative analysis, we propose the following mechanisms for DNA-mediated Ag+ reduction pathways and morphological evolution of Au–Ag NPs (Scheme 1).
Scheme 1.
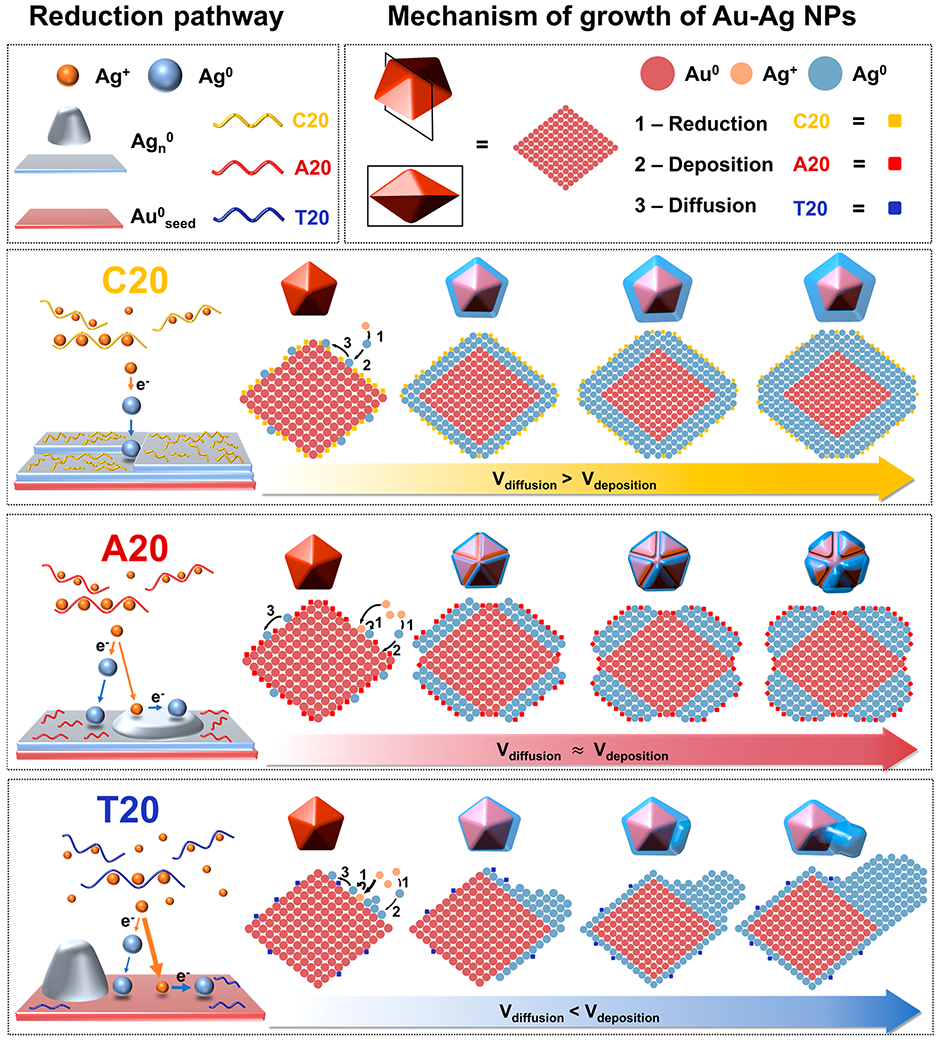
Proposed Mechanism of the Ag+ Reduction Pathway and Morphology Evolution of Au–Ag Core–Shell NPs Influenced by Different DNA Sequences
First, the strong binding between C20 and Ag+ limited the free Ag+ for reduction, while a slow solution reduction dominated under this C20-mediated Ag+ reduction pathway. Both factors resulted in the slow rate of Ag0 deposition (Vdep). C20 also passivated the surface the most among the three sequences, which reduced the rate for atom diffusion on the nanocrystals (Vdif). However, the reduced Vdif was still larger than Vdep, resulting in adatoms to migrate to low surface energy sites. The corresponding morphological evolution of the Au–Ag structure synthesized with C20 exhibited well-controlled epitaxial deposition on the decahedral core. The final structures exhibited primarily {111} facets, which are thermodynamically favorable. The growth kinetics and resulting structures indicate that the growth process of C20 was likely to be thermodynamically controlled. Besides, the stabilization of {111} facets by C20 might have also contributed to the exposure of {111} facets in the final structures. Stabilization of {111} facets by C20 was also reported previously in the synthesis of Ag nanocrystals.23
A20 had a weaker Ag+ binding affinity than C20. As a result, A20-mediated Ag+ reduction went through a mixed reduction pathway with the surface reduction being the dominant. The weaker Ag+ binding affinity and surface reduction dominated pathway resulted in a higher Vdep for A20-mediated Ag+ reduction than that of C20. In the meantime, A20 also occupied less surface-active sites on the nanocrystal surfaces, leading to a higher Vdif than that of C20. The morphology of nanocrystals synthesized with A20 maintained the 5-fold symmetric structures that retained the thermodynamically favorable {111} facets, while exhibiting grooves and ridges along the twin edges. The A20-mediated structures were likely the result of a mixed thermodynamic and kinetic controlled growth. Reentrant grooves appeared during the growth of penta-twinned structures due to the lattice strain stemmed from the symmetrical axis.56 If Vdif is much larger than Vdep, those high-energy grooves and ridges would be filled by the adatoms moving over from other regions of the surface. However, when Vdif is comparable with Vdep, the reentrant grooves are preserved. Under this mode of formation, the crystals grew along the direction parallel to the central axis to minimize the increase of lattice strain. The observation of partially preserved {111} facets suggests A20-mediated structure was the result of the mixed thermodynamically and kinetically controlled growth. Besides, A20 might also preferentially bind to the high-index facets in the grooves and ridges. Previously, it was reported that A30 was used to stabilize the high-index facets of Au prisms, preferentially localized in the reentrant grooves around the twin plan.22 This prior result agrees with the growth trends using A20 in this study.
Among the three DNA sequences, T20 had the weakest interaction with Ag+, which resulted in the highest supersaturation level of the precursor. Meanwhile, T20-mediated reduction pathways were dominated by surface reduction. Even though there were more surface sites due to the weak passivation of T20, Vdep was still significantly higher than Vdif. When T20 was used to control the morphology evolution of Au–Ag structures, we observed an automatic symmetry breaking and selective deposition on certain domains, which was likely the result of a kinetically controlled process. The selectivity of the domain that was primarily grown might have either been completely random or dictated by the uneven distribution of the strain in the decahedra seed.56 Furthermore, the weak binding affinity of T20 toward the NPs also facilitated the disappearance of {111} facets in the final structures.
CONCLUSIONS AND PERSPECTIVE
In summary, we have quantitatively analyzed the effects of DNA on the formation of Au–Ag nanocrystals in a sequence-specific manner. Three major factors contributed to the sequence-specific controlled growth of Au–Ag core–shell nanocrystals. First, the complexation between the DNA and Ag+ precursor modified the supersaturation level of the ion precursors. Second, the DNA-mediated Ag+ reduction pathways determined the sites and rates for the generation and deposition of Ag atoms. Finally, the passivation of DNA toward the surface determined the diffusion of the adatoms on the nanocrystal surface. The synergistic effect from these three factors controls the thermodynamics and kinetics of the growth process, which led to sequence-specific morphologies.
The analyses of the growth mechanism and morphology evolution of the penta-twinned decahedra-derived structures have furthered our understanding for the growth process of nanocrystals with complex structures and demonstrate the possibility to use DNA-based crystallization mechanisms to predict the final structure of the nanocrystals. The rules we have learned from this DNA ligand-based study should be applicable in identifying and understanding other biomolecular ligands for nanocrystal synthesis. Moreover, the findings from this study can also facilitate precise thermodynamic and kinetic controls by rational design of metal–ligand interactions. Finally, the methods developed in this study for the interaction between DNA sequences with the precursor and the surface of nanocrystals are suited for other ligands and other types of nanomaterials, which helps moving toward the goal of predictable synthesis of nanomaterials.
EXPERIMENTAL SECTION
Chemicals and Materials.
All single stranded DNA sequences were purchased from Integrated DNA Technologies (Coralville, IA) with standard desalting and without further purification. Gold(III) chloride trihydrate (≥99.9% trace metals basis), benzyldimethylhexadecyl-ammonium chloride (BDAC, cationic surfactant), sodium borohydride (99.99% trace metals basis), silver acetate (AgOAc, 99.99% trace metals basis), l-ascorbic acid (≥99%), 2-mercaptoethanol (≥99%), cetyltrimethylammonium chloride (CTAC), and citric acid were purchased from Sigma-Aldrich. Deionized water (18.2 MΩ) was used to dissolve all chemicals.
Preparation of Au Decahedra NPs.
Au decahedra NPs were synthesized using a previously published seed-mediated procedure.34 The seed for Au decahedra was synthesized by reducing HAuCl4 (10 mL, 0.25 mM) with NaBH4 (0.25 mL, 25 mM) in the presence of CTAC (50 mM) and citric acid (5 mM) under vigorous stirring at room temperature. The seed solution was then heated in an oil bath at 80 °C for 90 min under gentle stirring. Gold seeds (45 μL) were added to a growth solution containing BDAC (12.5 mL, 100 mM), HAuCl4 (125 μL, 50 mM), and ascorbic acid (93.75 μL, 100 mM) at 30 °C. The mixture was left undisturbed at 30 °C for 30 min.
DNA-Mediated Synthesis of Au–Ag Core–Shell NPs.
The Au decahedra seed was washed by centrifugation (6000 rpm, 5 min) three times to remove as much BDAC as possible (SI Note 10). The washed decahedra solution was diluted with DI water until the absorbance at 557 nm reached 0.7. The concentration of Au decahedra was calculated to be 3.27 × 109 particles/mL on the basis of the Au concentration determined by inductively coupled plasma mass spectrometry (ICP-MS). The diluted solution (97 μL) was incubated with 20 μM single stranded DNA (C20, A20, and T20) for 15 min. Then, 1 μL of 10 mM ascorbic acid solution and 2 μL of 10 mM AgOAc solution were added, followed by vortex of the solution. Then, the reaction was left to completion.
Measurement of Open Circuit Potential of AgOAc Solution with Different DNA Sequences.
The open circuit potential was measured on a CHI 760 potentiostat. A polycrystalline silver wire was used as the working electrode and Ag/AgCl as the reference electrode. The reference was separated from solution via an agar–0.1 M NaClO4 salt bridge to prevent chloride crossover into the working solution. Twenty microliters of 1 mM single stranded DNA solution of a certain sequence (C20, A20, and T20) was added into 1 mL of 20 μM AgOAc solution. The solution was left undisturbed for 30 min to reach equilibrium. Each experiment was repeated three times with different batches of DNA solution to ensure reproducibility. No supporting electrolyte was added during the titration.
Instrumentation and Characterization.
The synthesized nanostructures were analyzed using a JEOL 2100 cryo TEM operated at 200 kV or a Hitachi S4800 SEM at 10 kV and 10 μA. UV–vis spectroscopy was performed on an HP 8453 UV–vis spectrometer.
Supplementary Material
ACKNOWLEDGMENTS
SEM and TEM were carried out at the Materials Research Laboratory Central Research Facilities, University of Illinois. The authors would like to thank Dr. Satyavolu for valuable discussions and support. The authors would also like to thank Dr. Grzelczak for suggestions in the synthetic protocol.
Funding
Research reported in this publication was supported by National Institute of General Medical Sciences of the National Institutes of Health under award number GM124316 (to Y.L.).
Footnotes
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c08604.
Figures of SEM images, UV–vis absorbances, calibration curves, concentration of ascorbic acid solution in air as a function of time, one-step and two-step model fittings, and ζ potential, discussions of spectroscopic measurement of ascorbic acid concentration, effect of oxidation of ascorbic acid by oxygen, reaction steps, analysis of T20-mediated Ag+ reduction, calculations of Keq, [Ag+]eq, and [base]eq, A20- and C20-mediated Ag+ reductions, and fluorescence-based DNA quantification method using ME replacement, and tables of average values of [Ag+]eq and [base]eq in the Ag+ reduction processes with different DNA sequences and percentage of DNA on both Ag shells and Ag cores replaced by ME (PDF)
Complete contact information is available at: https://pubs.acs.org/10.1021/jacs.0c08604
The authors declare no competing financial interest.
Contributor Information
Yiming Wang, Department of Chemistry, University of Illinois at Urbana–Champaign, Urbana, Illinois 61801, United States.
Michael J. Counihan, Department of Chemistry, University of Illinois at Urbana–Champaign, Urbana, Illinois 61801, United States
Jeffrey Wayjer Lin, Department of Chemistry, University of Illinois at Urbana–Champaign, Urbana, Illinois 61801, United States.
Joaquín Rodríguez-López, Department of Chemistry, University of Illinois at Urbana–Champaign, Urbana, Illinois 61801, United States.
Hong Yang, Department of Chemistry and Department of Chemical and Biomolecular Engineering, University of Illinois at Urbana–Champaign, Urbana, Illinois 61801, United States.
Yi Lu, Department of Chemistry, University of Illinois at Urbana–Champaign, Urbana, Illinois 61801, United States.
REFERENCES
- (1).Stamenkovic VR; Fowler B; Mun BS; Wang G; Ross PN; Lucas CA; Markovic NM Improved Oxygen Reduction Activity on Pt3Ni(111) via Increased Surface Site Availability. Science 2007, 315 (5811), 493–497. [DOI] [PubMed] [Google Scholar]
- (2).Leenders SHAM; Gramage-Doria R; de Bruin B; Reek JNH Transition metal catalysis in confined spaces. Chem. Soc. Rev 2015, 44 (2), 433–448. [DOI] [PubMed] [Google Scholar]
- (3).Bogart LK; Pourroy G; Murphy CJ; Puntes V; Pellegrino T; Rosenblum D; Peer D; Lévy R Nanoparticles for Imaging, Sensing, and Therapeutic Intervention. ACS Nano 2014, 8 (4), 3107–3122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Smith BR; Gambhir SS Nanomaterials for In Vivo Imaging. Chem. Rev 2017, 117 (3), 901–986. [DOI] [PubMed] [Google Scholar]
- (5).Giljohann DA; Seferos DS; Daniel WL; Massich MD; Patel PC; Mirkin CA Gold Nanoparticles for Biology and Medicine. Angew. Chem., Int. Ed 2010, 49 (19), 3280–3294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Xia Y; Xiong Y; Lim B; Skrabalak SE Shape-controlled synthesis of metal nanocrystals: simple chemistry meets complex physics? Angew. Chem., Int. Ed 2009, 48 (1), 60–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Gu J; Zhang Y-W; Tao F Shape control of bimetallic nanocatalysts through well-designed colloidal chemistry approaches. Chem. Soc. Rev 2012, 41 (24), 8050–8065. [DOI] [PubMed] [Google Scholar]
- (8).Xia Y; Xia X; Peng H-C Shape-Controlled Synthesis of Colloidal Metal Nanocrystals: Thermodynamic versus Kinetic Products. J. Am. Chem. Soc 2015, 137 (25), 7947–7966. [DOI] [PubMed] [Google Scholar]
- (9).Xia YN; Gilroy KD; Peng HC; Xia XH Seed-Mediated Growth of Colloidal Metal Nanocrystals. Angew. Chem., Int. Ed 2017, 56 (1), 60–95. [DOI] [PubMed] [Google Scholar]
- (10).Zhan G; Zeng HC Smart Nanocatalysts with Streamline Shapes. ACS Cent. Sci 2017, 3 (7), 794–799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Zheng K; Loh KY; Wang Y; Chen Q; Fan J; Jung T; Nam SH; Suh YD; Liu X Recent advances in upconversion nanocrystals: Expanding the kaleidoscopic toolbox for emerging applications. Nano Today 2019, 29, 100797. [Google Scholar]
- (12).Yin X; Shi M; Wu J; Pan YT; Gray DL; Bertke JA; Yang H Quantitative Analysis of Different Formation Modes of Platinum Nanocrystals Controlled by Ligand Chemistry. Nano Lett. 2017, 17 (10), 6146–6150. [DOI] [PubMed] [Google Scholar]
- (13).Ortiz N; Skrabalak SE On the Dual Roles of Ligands in the Synthesis of Colloidal Metal Nanostructures. Langmuir 2014, 30 (23), 6649–6659. [DOI] [PubMed] [Google Scholar]
- (14).Langille MR; Personick ML; Zhang J; Mirkin CA Defining Rules for the Shape Evolution of Gold Nanoparticles. J. Am. Chem. Soc 2012, 134 (35), 14542–14554. [DOI] [PubMed] [Google Scholar]
- (15).Murphy CJ; Jana NR Controlling the Aspect Ratio of Inorganic Nanorods and Nanowires. Adv. Mater 2002, 14 (1), 80–82. [Google Scholar]
- (16).Burrows ND; Vartanian AM; Abadeer NS; Grzincic EM; Jacob LM; Lin W; Li J; Dennison JM; Hinman JG; Murphy CJ Anisotropic Nanoparticles and Anisotropic Surface Chemistry. J. Phys. Chem. Lett 2016, 7 (4), 632–641. [DOI] [PubMed] [Google Scholar]
- (17).Xia X; Xie S; Liu M; Peng H-C; Lu N; Wang J; Kim MJ; Xia Y On the role of surface diffusion in determining the shape or morphology of noble-metal nanocrystals. Proc. Natl. Acad. Sci. U. S. A 2013, 110 (17), 6669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Wang Y; Reddy Satyavolu NS; Lu Y Sequence-specific control of inorganic nanomaterials morphologies by biomolecules. Curr. Opin. Colloid Interface Sci 2018, 38, 158–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Wang Z; Zhang J; Ekman JM; Kenis PJA; Lu Y DNA-Mediated Control of Metal Nanoparticle Shape: One-Pot Synthesis and Cellular Uptake of Highly Stable and Functional Gold Nanoflowers. Nano Lett. 2010, 10 (5), 1886–1891. [DOI] [PubMed] [Google Scholar]
- (20).Wang Z; Tang L; Tan LH; Li J; Lu Y Discovery of the DNA “Genetic Code” for Abiological Gold Nanoparticle Morphologies. Angew. Chem., Int. Ed 2012, 51 (36), 9078–9082. [DOI] [PubMed] [Google Scholar]
- (21).Song T; Tang L; Tan LH; Wang X; Satyavolu NSR; Xing H; Wang Z; Li J; Liang H; Lu Y DNA-Encoded Tuning of Geometric and Plasmonic Properties of Nanoparticles Growing from Gold Nanorod Seeds. Angew. Chem., Int. Ed 2015, 54 (28), 8114–8118. [DOI] [PubMed] [Google Scholar]
- (22).Tan LH; Yue Y; Satyavolu NSR; Ali AS; Wang Z; Wu Y; Lu Y Mechanistic Insight into DNA-Guided Control of Nanoparticle Morphologies. J. Am. Chem. Soc 2015, 137 (45), 14456–14464. [DOI] [PubMed] [Google Scholar]
- (23).Wu J; Tan LH; Hwang K; Xing H; Wu P; Li W; Lu Y DNA Sequence-Dependent Morphological Evolution of Silver Nanoparticles and Their Optical and Hybridization Properties. J. Am. Chem. Soc 2014, 136 (43), 15195–15202. [DOI] [PubMed] [Google Scholar]
- (24).Satyavolu NSR; Tan LH; Lu Y DNA-Mediated Morphological Control of Pd-Au Bimetallic Nanoparticles. J. Am. Chem. Soc 2016, 138 (50), 16542–16548. [DOI] [PubMed] [Google Scholar]
- (25).Chiu C-Y; Ruan L; Huang Y Biomolecular specificity controlled nanomaterial synthesis. Chem. Soc. Rev 2013, 42 (7), 2512–2527. [DOI] [PubMed] [Google Scholar]
- (26).Walsh TR; Knecht MR Biointerface Structural Effects on the Properties and Applications of Bioinspired Peptide-Based Nanomaterials. Chem. Rev 2017, 117 (20), 12641–12704. [DOI] [PubMed] [Google Scholar]
- (27).Walsh TR Pathways to Structure-Property Relationships of Peptide-Materials Interfaces: Challenges in Predicting Molecular Structures. Acc. Chem. Res 2017, 50 (7), 1617–1624. [DOI] [PubMed] [Google Scholar]
- (28).Chen Z; Liu C; Cao F; Ren J; Qu X DNA metallization: principles, methods, structures, and applications. Chem. Soc. Rev 2018, 47 (11), 4017–4072. [DOI] [PubMed] [Google Scholar]
- (29).Pu F; Ren J; Qu X Nucleobases, nucleosides, and nucleotides: versatile biomolecules for generating functional nanomaterials. Chem. Soc. Rev 2018, 47 (4), 1285–1306. [DOI] [PubMed] [Google Scholar]
- (30).Yamane T; Davidson N On the complexing of deoxyribonucleic acid by silver(I). Biochim. Biophys. Acta, Spec. Sect. Nucleic Acids Relat. Subj 1962, 55 (5), 609–621. [DOI] [PubMed] [Google Scholar]
- (31).Berti L; Burley GA Nucleic acid and nucleotide-mediated synthesis of inorganic nanoparticles. Nat. Nanotechnol 2008, 3, 81. [DOI] [PubMed] [Google Scholar]
- (32).Kondo J; Tada Y; Dairaku T; Hattori Y; Saneyoshi H; Ono A; Tanaka Y A metallo-DNA nanowire with uninterrupted one-dimensional silver array. Nat. Chem 2017, 9, 956. [DOI] [PubMed] [Google Scholar]
- (33).Izatt RM; Christensen JJ; Rytting JH Sites and thermodynamic quantities associated with proton and metal ion interaction with ribonucleic acid, deoxyribonucleic acid, and their constituent bases, nucleosides, and and nucleotides. Chem. Rev 1971, 71 (5), 439–481. [DOI] [PubMed] [Google Scholar]
- (34).Sanchez-Iglesias A; Winckelmans N; Altantzis T; Bals S; Grzelczak M; Liz-Marzan LM High-Yield Seeded Growth of Monodisperse Pentatwinned Gold Nanoparticles through Thermally Induced Seed Twinning. J. Am. Chem. Soc 2017, 139 (1), 107–110. [DOI] [PubMed] [Google Scholar]
- (35).Davey WP Precision Measurements of the Lattice Constants of Twelve Common Metals. Phys. Rev 1925, 25 (6), 753–761. [Google Scholar]
- (36).Zhou S; Zhao M; Yang T-H; Xia Y Decahedral nanocrystals of noble metals: Synthesis, characterization, and applications. Mater. Today 2019, 22, 108–131. [Google Scholar]
- (37).Xia Y; Gilroy KD; Peng H-C; Xia X Seed-Mediated Growth of Colloidal Metal Nanocrystals. Angew. Chem., Int. Ed 2017, 56 (1), 60–95. [DOI] [PubMed] [Google Scholar]
- (38).Clever GH; Kaul C; Carell T DNA-Metal Base Pairs. Angew. Chem., Int. Ed 2007, 46 (33), 6226–6236. [DOI] [PubMed] [Google Scholar]
- (39).Ono A; Cao S; Togashi H; Tashiro M; Fujimoto T; Machinami T; Oda S; Miyake Y; Okamoto I; Tanaka Y Specific interactions between silver(i) ions and cytosine-cytosine pairs in DNA duplexes. Chem. Commun 2008, No. 39, 4825–4827. [DOI] [PubMed] [Google Scholar]
- (40).Ono A; Torigoe H; Tanaka Y; Okamoto I Binding of metal ions by pyrimidine base pairs in DNA duplexes. Chem. Soc. Rev 2011, 40 (12), 5855–5866. [DOI] [PubMed] [Google Scholar]
- (41).Takezawa Y; Shionoya M Metal-Mediated DNA Base Pairing: Alternatives to Hydrogen-Bonded Watson-Crick Base Pairs. Acc. Chem. Res 2012, 45 (12), 2066–2076. [DOI] [PubMed] [Google Scholar]
- (42).Swasey SM; Leal LE; Lopez-Acevedo O; Pavlovich J; Gwinn EG Silver (I) as DNA glue: Ag+-mediated guanine pairing revealed by removing Watson-Crick constraints. Sci. Rep 2015, 5, 10163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).DeFord DD; Hume DN The Determination of Consecutive Formation Constants of Complex Ions from Polaro-graphic Data. J. Am. Chem. Soc 1951, 73 (11), 5321–5322. [Google Scholar]
- (44).Bard AJ; Faulkner LR; Leddy J; Zoski CG Electrochemical methods: fundamentals and applications; Wiley: New York, 1980; Vol. 2. [Google Scholar]
- (45).Yang TH; Peng HC; Zhou S; Lee CT; Bao S; Lee YH; Wu JM; Xia Y Toward a Quantitative Understanding of the Reduction Pathways of a Salt Precursor in the Synthesis of Metal Nanocrystals. Nano Lett. 2017, 17 (1), 334–340. [DOI] [PubMed] [Google Scholar]
- (46).Watzky MA; Finke RG Transition Metal Nanocluster Formation Kinetic and Mechanistic Studies. A New Mechanism When Hydrogen Is the Reductant: Slow, Continuous Nucleation and Fast Autocatalytic Surface Growth. J. Am. Chem. Soc 1997, 119 (43), 10382–10400. [Google Scholar]
- (47).Yang TH; Zhou S; Gilroy KD; Figueroa-Cosme L; Lee YH; Wu JM; Xia Y Autocatalytic surface reduction and its role in controlling seed-mediated growth of colloidal metal nanocrystals. Proc. Natl. Acad. Sci. U. S. A 2017, 114 (52), 13619–13624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Yang T-H; Peng H-C; Zhou S; Lee C-T; Bao S; Lee YH; Wu J-M; Xia Y Toward a Quantitative Understanding of the Reduction Pathways of a Salt Precursor in the Synthesis of Metal Nanocrystals. Nano Lett. 2017, 17 (1), 334–340. [DOI] [PubMed] [Google Scholar]
- (49).Ingold CK Structure and mechanism in organic chemistry; Cornell University Press: Ithaca, New York, 1953. [Google Scholar]
- (50).Demers LM; Mirkin CA; Mucic RC; Reynolds RA; Letsinger RL; Elghanian R; Viswanadham G A Fluorescence-Based Method for Determining the Surface Coverage and Hybridization Efficiency of Thiol-Capped Oligonucleotides Bound to Gold Thin Films and Nanoparticles. Anal. Chem 2000, 72 (22), 5535–5541. [DOI] [PubMed] [Google Scholar]
- (51).Sun Y; Mayers B; Herricks T; Xia Y Polyol Synthesis of Uniform Silver Nanowires: A Plausible Growth Mechanism and the Supporting Evidence. Nano Lett. 2003, 3 (7), 955–960. [Google Scholar]
- (52).Feng J; Pandey RB; Berry RJ; Farmer BL; Naik RR; Heinz H Adsorption mechanism of single amino acid and surfactant molecules to Au {111} surfaces in aqueous solution: design rules for metal-binding molecules. Soft Matter 2011, 7 (5), 2113–2120. [Google Scholar]
- (53).Park J-W; Shumaker-Parry JS Structural Study of Citrate Layers on Gold Nanoparticles: Role of Intermolecular Interactions in Stabilizing Nanoparticles. J. Am. Chem. Soc 2014, 136 (5), 1907–1921. [DOI] [PubMed] [Google Scholar]
- (54).Jadzinsky PD; Calero G; Ackerson CJ; Bushnell DA; Kornberg RD Structure of a Thiol Monolayer-Protected Gold Nanoparticle at 1.1 A Resolution. Science 2007, 318 (5849), 430. [DOI] [PubMed] [Google Scholar]
- (55).Battocchio C; Meneghini C; Fratoddi I; Venditti I; Russo MV; Aquilanti G; Maurizio C; Bondino F; Matassa R; Rossi M; Mobilio S; Polzonetti G Silver Nanoparticles Stabilized with Thiols: A Close Look at the Local Chemistry and Chemical Structure. J. Phys. Chem. C 2012, 116 (36), 19571–19578. [Google Scholar]
- (56).Lofton C; Sigmund W Mechanisms Controlling Crystal Habits of Gold and Silver Colloids. Adv. Funct. Mater 2005, 15 (7), 1197–1208. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


