Significance of Inoculum Size in the Lag Time of Listeria monocytogenes

Abstract

The lag time of Listeria monocytogenes growing under suboptimal conditions (low nutrient concentrations, pH 6, and 6.5°C) was extended when the inoculum was severely stressed by starvation and the inoculum size was very small. Predictive microbiology should deal with bacterial stress and stochastic approaches to improve its value for the agro-food industry.

In predictive microbiology, it is commonly assumed that inoculum size has no effect on subsequent microbial growth, and some studies (8, 9, 10) have confirmed this for growth of Listeria monocytogenes. However, Gay et al. (12) observed that inoculum size could have an effect on the duration of the lag phase of L. monocytogenes under particular conditions simulating soft cheese ripening. This observation could challenge the validity of predictive models because growth modelling is usually done with initial concentrations of bacteria higher than 10³ CFU · ml⁻¹, even though foods are usually contaminated with lower numbers of cells.

It has been shown with other bacteria, like Bacillus (19), Achromobacter delmarvae, Micrococcus luteus (see reference 16 for review), and Salmonella (26), that the duration of the lag phase depends inversely on the size of the inoculum. This phenomenon was observed only under a restricted range of conditions, for example, in poor but not in rich media, with starved cells (16), or with heat-injured cells (26). The aim of this work was to study the effect of inoculum size on the lag phase of L. monocytogenes growing in a poor medium, i.e., broth, containing only 1 g of Bacto Peptone (Difco Laboratories, Detroit, Mich.) per liter plus 0.85% sodium chloride (Prolabo, Paris, France) (TS), under suboptimal conditions: pH 6 and 6.5°C and with cells stressed by starvation.

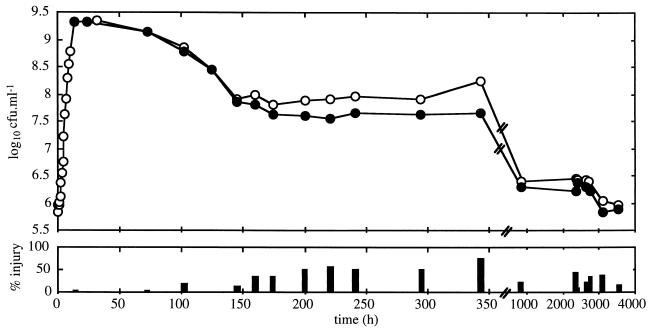
L. monocytogenes Scott A maintained on tryptone-soya agar (Oxoid, Unipath, Ltd., Basingstoke, Hampshire, England) at 4°C was subcultured onto tryptone-soya agar (Oxoid) plus 0.6% yeast extract (AES, Combourg, France) (TSYE) at 37°C for 24 h, and five colonies were transferred into TSYE broth and incubated at 30°C for 24 h. This culture was used to inoculate TSYE broth to prepare inocula at 30°C. The change in viable count of L. monocytogenes in TSYE broth at 30°C determined on nonselective TSYE agar and selective Palcam (Oxoid) agar is shown in Fig. 1. The percentage of injured cells was determined by differential counts on selective and nonselective media (24). Inocula were prepared at 30°C for 14, 160, and 840 h to obtain cells in late log phase, early stationary phase after a decrease in cell viability of 96.8% viable cells and 35% injured cells and late stationary phase with a loss of viability of 99.9% and 21% injured cells (Fig. 1). Samples were prepared by filtering 10 ml of culture through a 0.45-μm-pore-size sterile filter (Schleicher & Schuell, Dassel, Federal Republic of Germany). Cells were washed three times with 10 ml of sterile TS and removed from the membrane with 10 ml of TS.

FIG. 1.

Viable counts on TSYE agar (○) and Palcam agar (●) of L. monocytogenes incubated in TSYE broth at 30°C.

TS agar (100 ml) with pH adjusted to 6.0 with 1 M HCl in 250-ml flasks was inoculated with 1 ml of a 10- or 100-fold dilution of filtered cells and incubated at 6.5°C. Initial bacterial concentrations for cells in late log and early and late stationary phases ranged from 10⁴ to 10⁻², 10² to 10⁻², and 10⁴ to 10⁰ CFU · ml⁻¹, respectively. The cultures were grown once, except for cells in late log phase with initial concentrations of 10¹ and 10⁻² CFU · ml⁻¹, which were grown in triplicate. Flasks containing high bacterial concentrations (more than 30 CFU · ml⁻¹) were enumerated by performing plate counts on TSYE agar incubated at 37°C for 24 h. Flasks containing low bacterial concentrations (<30 CFU · ml⁻¹) were enumerated by the most-probable-number technique used by Gay et al. (12).

Growth curves were fitted using the logistic equation with delay, i.e., with a breakpoint at the transition between the lag and the exponential phase (3, 18, 24):

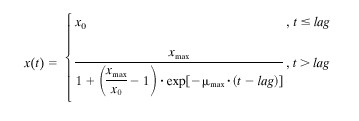where x(t) is the bacterial concentration (CFU per milliliter) at time t (in hours), x₀ is the initial bacterial concentration, x_max is the maximum bacterial concentration, lag is the duration of the lag phase (in hours), and μ_max is the maximum specific growth rate (per hour).

Fits were performed by nonlinear regression using the weighted-least-squares criterion (5) by minimizing the sum of the weighted squared residuals (SWSR). SWSR is defined as follows:

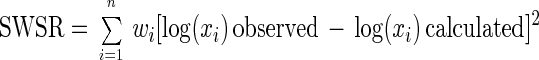where n is the number of datum points and w_i is the reciprocal of the variance of log(x_i) observed. These variances were estimated from replicates when they were available or were theoretically calculated from the variances of the numbers of microorganisms per sample (11) and from dilution and plating errors (15). The minimum SWSR values were computed with the NLINFIT subroutine of MATLAB 5.2 software (The Math Works Inc., Natick, Mass.), modified for weighted method of least squares.

Maximum specific growth rates and lag times obtained for growth of L. monocytogenes in TS agar at 6.5°C are shown in Table 1. Confidence regions for parameter estimations were defined as parameter values checking Beale's inequality (4, 20):

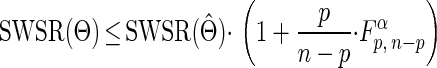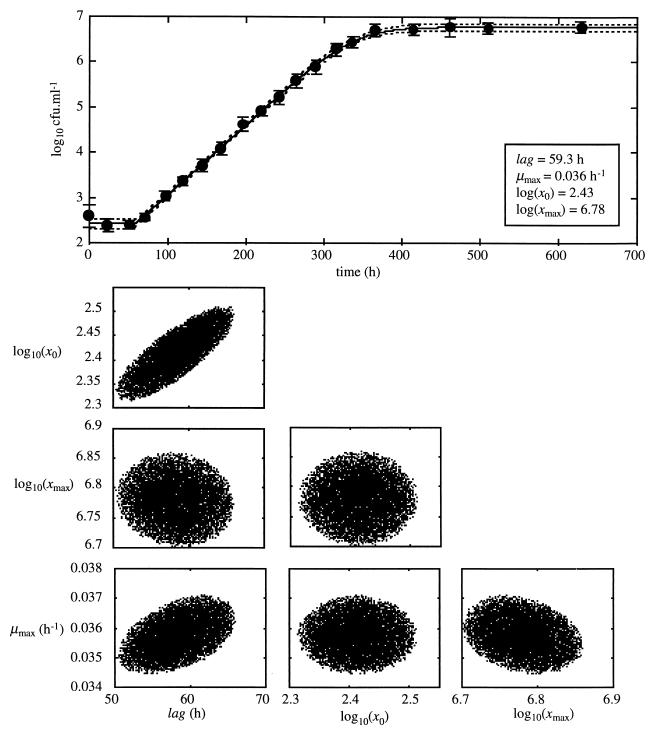
where Θ is the vector of parameter values, Θ̂ is the vector of weighted-least-squares-estimated parameters, n is the number of datum points, p is the number of parameters, and F_p, n-p^α is the α quantile for Fisher's F distribution with p and n - p degrees of freedom. Random sampling in the parameter space of points whose SWSR value checked the inequality was made with MATLAB software. Confidence limits for parameter values were determined by projecting these points in each of the parameter planes (Fig. 2). No significant effect of inoculum size or duration of storage at 30°C in TSYE broth was observed on maximum specific growth rates (Table 1) or on lag time with storage of 14 h, and an average lag time of 40.6 ± 13.4 h (standard deviation [SD]) was obtained.

TABLE 1.

Growth parameters of L. monocytogenes in TS, pH 6, at 6.5°C after different durations of storage at 30°C^a

Duration of storage (h)	log10(x0)	Duration of log phase (h)	μmax (h−1)
14	4.30 (4.22, 4.39)	61.6 (28.3, 75.8)	0.068 (0.038, 0.103)
	3.32 (3.23, 3.41)	24.7 (16.9, 40.9)	0.040 (0.036, 0.048)
	2.38 (2.26, 2.47)	32.6 (21.9, 43.9)	0.048 (0.045, 0.052)
	1.32 (1.20, 1.45)	26.6 (8.19, 78.7)	0.044 (0.035, 0.105)
	0.39 (0.24, 0.53)	44.2 (31.6, 56.1)	0.057 (0.053, 0.062)
	−0.68 (−1.05, −0.32)	50.9 (34.0, 69.1)	0.055 (0.053, 0.057)
	−1.66 (−Infb, −1.14)	43.6 (−Inf, 101)	0.046 (0.039, 0.055)
160	2.43 (2.32, 2.51)	59.3 (50.4, 65.9)	0.036 (0.034, 0.037)
	1.41 (1.10, 1.70)	79.1 (55.6, 98.4)	0.037 (0.035, 0.040)
	0.54 (0.15, 1.00)	93.1 (66.0, 126)	0.035 (0.034, 0.037)
	−0.41 (−1.08, 0.28)	95.1 (47.4, 139)	0.035 (0.034, 0.039)
	−1.41 (−2.50, −0.34)	98.8 (32.9, 160)	0.041 (0.038, 0.044)
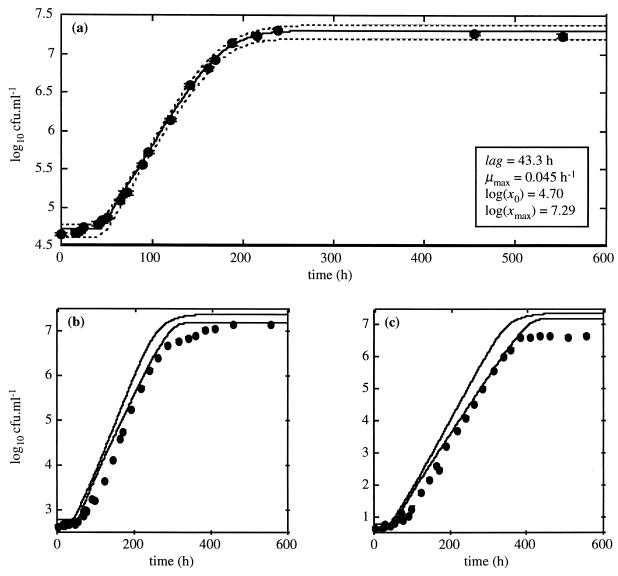
840	4.70 (4.61, 4.78)	43.3 (35.2, 51.9)	0.045 (0.041, 0.051)
	2.68 (2.64, 2.75)	56.8 (50.7, 60.7)	0.043 (0.038, 0.045)
	0.74 (0.59, 0.89)	66.6 (56.7, 79.8)	0.046 (0.044, 0.049)

^aIn parentheses are the 95% confidence limits. 

^bInf, infinity. 

FIG. 2.

Growth curve of L. monocytogenes grown in TS, pH 6, at 6.5°C after storage at 30°C for 160 h. The solid line is the best fit of the growth model to the data, and the dotted lines define the 95% confidence region for the growth curve. Vertical bars indicate 1 SD of the bacterial cell count. At the bottom are the 95% confidence regions of estimated growth parameters.

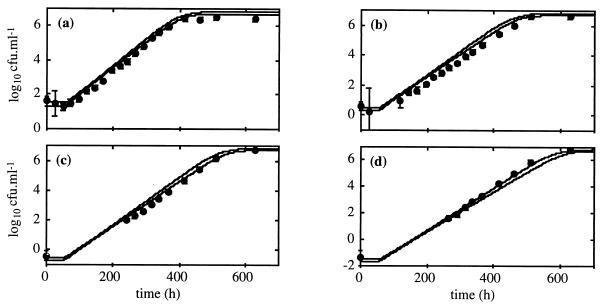
Increasing lag time was observed with storage for 160 h when the inoculum size was decreased from 10² to 10⁰ CFU · ml⁻¹ (Table 1). Because large 95% confidence regions were obtained for these estimated lag times, this increase was not significant. The growth curve with an initial bacterial concentration of 10² CFU · ml⁻¹ was used to derive growth parameters with their confidence regions (Fig. 2) and to predict confidence regions of growth curves for smaller inoculum sizes (Fig. 3). Because the growth model is a monotonous function for each parameter, confidence regions (α = 0.05) for the predicted growth curves were constructed by determining the minimum and the maximum of the function when the parameter values belong to the confidence regions (13). Longer lag times were observed for inoculum sizes of 10¹ to 10⁻¹ CFU · ml⁻¹ but not with the inoculum size of 10⁻² CFU · ml⁻¹. The effect of inoculum size on lag time was considered not significant given the available datum sets. The average lag time for the cells stored for 160 h at 30°C was 85.1 ± 16.2 h (SD).

FIG. 3.

Predicted growth curves and observed bacterial cell counts of L. monocytogenes in TS, pH 6, at 6.5°C after storage for 160 h at 30°C for suspensions with initial bacterial concentrations of 10¹ (a), 10⁰ (b), 10⁻¹ (c), and 10⁻² (d) CFU · ml⁻¹. The solid lines define the 95% confidence regions of the predicted growth curves from the parameters estimated with the initial bacterial concentration of 10² CFU · ml⁻¹. Vertical bars indicate 1 SD.

A uniform increase in lag time with decreased inoculum size was observed for storage for 840 h, and the difference between lag times obtained for initial concentrations of 10⁴ and 10⁰ CFU · ml⁻¹ was significant, as 95% confidence regions did not overlap (Table 1). By using the growth curve with an initial bacterial concentration of 10⁴ CFU · ml⁻¹ to predict 95% confidence regions for growth curves with smaller inoculum sizes (Fig. 4), discrepancies between predicted growth regions and observed growth curves were found for initial bacterial concentrations of 10² and 10⁰ CFU · ml⁻¹.

FIG. 4.

Growth curve of L. monocytogenes in TS, pH 6, at 6.5°C after storage for 840 h at 30°C for the suspension with initial bacterial count of 10⁴ CFU · ml⁻¹ (a) and predicted growth curves and observed bacterial cell counts for suspensions with initial bacterial concentrations of 10² (b) and 10⁰ (c) CFU · ml⁻¹. In panel a, the solid line is the best fit of the growth model to the data and the dotted lines define the 95% confidence region for the growth curve. In panels b and c, the solid lines define the 95% confidence regions of the predicted growth curves. Vertical bars indicate 1 SD of the bacterial cell count.

The change from an inoculum of approximately 10² CFU · ml⁻¹ maintained at 30°C for 14 h to an inoculum of about 1 CFU · ml⁻¹ starved for 840 h at 30°C led to an increase in lag time from 32.6 to 66.6 h. The extension of lag phase with physical injury of cells has been frequently reported (14, 17, 21, 22), and models describing the effect of heat injury on subsequent lag period have been published for L. monocytogenes (6, 7, 23). Albertson et al. (1) also observed a uniform increase in lag time with increasing starvation time for a Vibrio sp., but no models have been published.

The inoculum size effect, observed only with cells severely stressed by starvation, could be explained by an increase in the variation of individual cells' lag time when cells are stressed (2, 26). Predictive microbiology should deal with stochastic models for the prediction of the growth of the small populations typically encountered in foods, especially when microbial cells have been subject to injury.