Terahertz wave emission from the trigonal layered PtBi₂

Summary

In this work, broadband terahertz (THz) wave emissions have been detected from the trigonal layered PtBi₂ on the excitation of the femtosecond laser pulses. Such THz generation is found to arise from the dominated linear photogalvanic effect, which is further discovered to strongly depend on the unique electronic structures of PtBi₂. Furthermore, an effective nonlinear susceptibility of PtBi₂ is also obtained and is nearly two orders of magnitude larger than that of the traditional nonlinear crystal for THz generation.

Graphical abstract

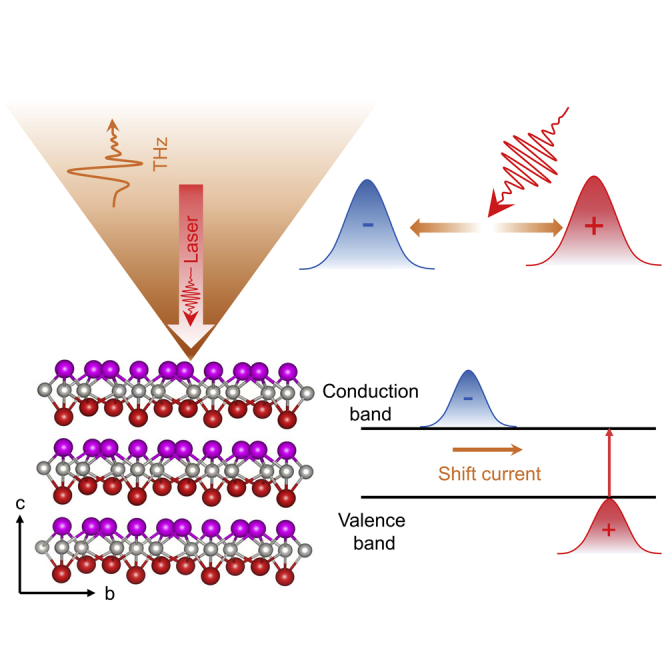
Highlights

• •Terahertz (THz) wave emission, topological semimetal, ultrafast photocurrent

Transport property of condensed matter; Radiation physics; Nanomaterials

Introduction

Topological materials (TMs) are a new class of quantum materials with nontrivial topological band structures (Qi and Zhang, 2011; Hasan and Kane, 2010; Weng et al., 2016; Armitage et al., 2018; Burkov, 2016). Typical examples include the topological insulators and topological semimetals (e.g. Dirac and Weyl semimetals), which have common features characterized by some band(s) with linear dispersion in k-space near the Fermi level (Weng et al., 2016; Armitage et al., 2018). Owing to the exotic electronic structures in TMs, giant nonlinear responses can be usually expected, such as second harmonic generation (Wu et al., 2017; Patankar et al., 2018; Hamh et al., 2016), nonlinear Hall effect (Ma et al., 2019), and photogalvanic effect (PGE) (Guan et al., 2017; Li et al., 2017). Particularly, on the excitation of the femtosecond (fs) laser pulses, the ultrafast photocurrents and the associated electromagnetic wave emission in the terahertz (THz) regime have attracted enormous attention recently in TMs (Sirica et al., 2019; Gao et al., 2020; Rees et al., 2020; Ni et al., 2021; Braun et al., 2016). Among the variety of origins triggering the ultrafast currents, those mechanisms associated with the crystal symmetry and topology of TMs have recently attracted intense attention (Sirica et al., 2019; Gao et al., 2020; Rees et al., 2020; Ni et al., 2021; Braun et al., 2016; Luo et al., 2021; Ma et al., 2021), such as PGE (Guan et al., 2017; Li et al., 2017) and photon drag effect (Shi et al., 2021; Karch et al., 2010). In addition, owing to the spin-momentum locking property emerging in TMs (Qi and Zhang, 2011; Hasan and Kane, 2010; Weng et al., 2016; Armitage et al., 2018), the charge current involving the bands with spin-nondegeneracy can be naturally spin-polarized and hence enables TMs to be a potential candidate in the spintronic applications. Clearly, the THz emission spectroscopy provides us with an excellent way to study the nonlinear emerging properties in TMs.

The trigonal layered PtBi, owing to the absence of spatial inversion symmetry, was predicted to host a triply-degenerate point near the Fermi level (Gao et al., 2018) and have a giant anisotropic Rashba-like spin-splitting along three momentum directions (3D Rashba-like spin-splitting) with a helical spin-polarization around the M points in the Brillouin zone (Feng et al., 2020). Meanwhile, PtBi₂ is also proposed to be the three-dimensional topological semimetal by several studies (Gao et al., 2018; Nie et al., 2020; Xing et al., 2020). Therefore, it will be very interesting to investigate if any unusual nonlinear and dynamic properties can emerge in PtBi₂ owing to its unique electronic structures. However, no ultrafast nonlinear spectroscopy research has been reported on this material, which limits our further understanding and its potential applications.

Here, we report the studies of ultrafast broadband THz wave emission from the PtBi₂ single crystal on the excitation of the fs optical pulses for the first time. The mechanism behind is identified to be dominated by the linear photogalvanic effect (LPGE), while no clear circular photogalvanic effect (CPGE) has been observed. The ultrafast photocurrent inducing the THz emission originates from the giant anisotropic bands, which are manifested by the strong photon-energy-dependent THz wave signals that can be attributed to various optical transitions related to the anisotropic electronic structures in PtBi₂.

Results and discussion

Terahertz emission from PtBi₂

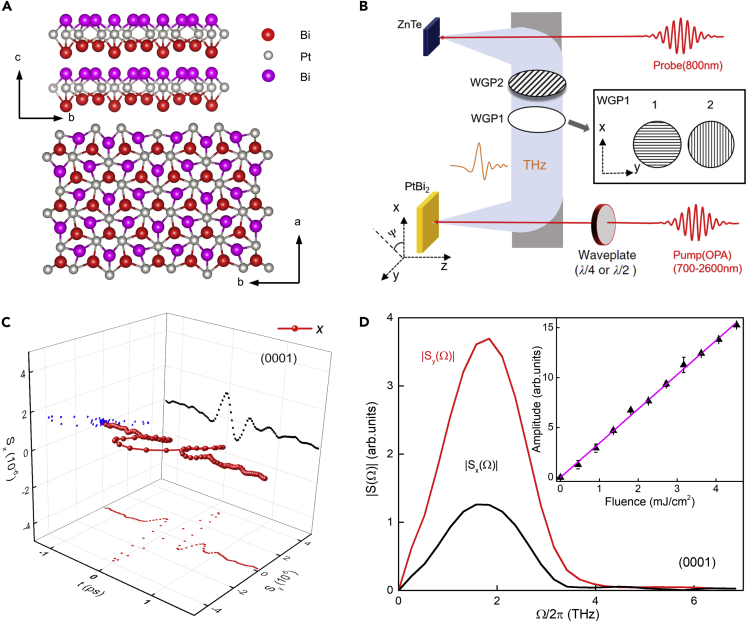
The trigonal layered PtBi₂ is a van der Waals material, with space group P31m (No.157) (Gao et al., 2018), made of two metallic elements both with strong spin-orbit couplings (Gao et al., 2018; Feng et al., 2020; Xu et al., 2016; Yao et al., 2016; Thirupathaiah et al., 2018). The crystal structure of trigonal layered PtBi₂ is shown in Figure 1A and represented in lattice coordinate. In our experiments, the incident pump laser beam is normal to the a-b plane of the crystal or along the [0001] direction (c-axis), which is perpendicular to the layered structure. Owing to the inequivalent Bi atoms in a monolayer, such a layered stacking is lack the space-inversion symmetry (as shown in Figure 1A).

Figure 1.

THz wave emission from the trigonal layered PtBi₂ (0001) single crystal

(A) The crystal structure of trigonal layered PtBi₂.

(B) Experimental setup of the THz emission spectroscopy.

(C) The far-field EO signals $\overrightarrow{S}\left(t\right)$$[=S_x\left(t\right)\hat{x}+S_y\left(t\right)\hat{y}]$ with x-polarized pump light. (For clarity, the error bars are not shown here, which is about 4×10⁻⁷).

(D) The Fourier transform spectra $\left|S_y\left(\text{Ω}\right)\right|$ and $\left|S_x\left(\text{Ω}\right)\right|$ corresponding to the time-domain THz waveforms in (C). The inset is the peak value of S(t) (at t=0 ps) as a function of the pump fluence, and the purple solid line is a linear fit. The error bars in the inset are the standard deviation of the experimental data.

The schematic of our experimental setup is shown in Figure 1B, where the fs-laser pulses are employed to generate the ultrafast photocurrents that induce the THz wave emission afterward. The laser light is divided into pump and probe beams to excite the sample and detect the THz radiation, respectively. The pump pulses are directly from a Ti:sapphire amplifier (1-kHz repetition rate, 80-fs duration, 800-nm wavelength) or from an optical parametric amplifier. In our measurements, the pump wavelength could be tuned in the near- and mid-infrared region (700–2600 nm), and the polarization state of the pump pulse is controlled by a quarter-wave plate (QWP) or a half-wave plate (HWP). Typical results shown here are for 800 nm unless noted in the text. As seen in Figure 1B, the pump beam is perpendicular to the a-b plane (x-y plane in lab coordinate) of the crystal, and the sample azimuthal angle (Ψ) could be tuned around the z axis (or c-axis). The beam is focused onto the sample with a ∼1.5-mm diameter, and the pump fluence is about 1.36 mJ/cm², which is below the damage threshold (∼5.9 mJ/cm²). The generated THz waves along x- and y axis (S_x and S_y) are measured individually, with two wire-grid polarizer (WGP1 and WGP2) placed between the two off-axis parabolic mirrors. To keep the responses of THz wave detection the same for different components, the polarization angle of WGP2 is set to 45° in the lab coordinate, and the WGP1 is with angle 0° and 90° for detecting S_x and S_y, respectively (as seen in the inset of Figure 1B). The THz electric field was detected by the electric-optic(EO) sampling with a 0.5-mm thick ZnTe(110) crystal. All the measurements were performed at room temperature in a dry-air environment with relative humidity <5% to avoid the absorption of water vapor.

Figure 1C shows the THz emission wave components (S_x(t),S_y(t)) from the sample on the excitation of the x-polarized light (along the x-axis). Clearly, $\overrightarrow{S}\left(t\right)$ displays very good linear polarization. Besides, the Fourier transform spectra, $\left|S_y\left(\text{Ω}\right)\right|$ and $\left|S_x\left(\text{Ω}\right)\right|$, reveal the THz waves have broadband property (see Figure 1D). The center frequency is ∼1.9 THz and the frequency upper limit goes to ∼4 THz. In particular, we observe a linear dependence of the peak value in the THz time-domain signal S(t) (t = 0 ps) on the fluence (the inset of Figure 1D). Such observation strongly suggests that the detected THz waves should arise from some effect having quadratic-like nonlinear optical response (Morimoto and Nagaosa., 2016; Okumura et al., 2021).

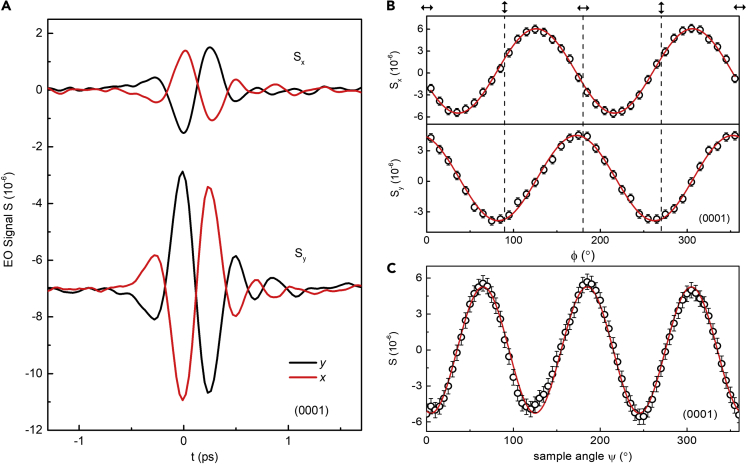
Polarization dependence of the terahertz wave signals

Generally, the ultrafast photocurrent and accompanying THz emission are usually dependent on the polarization states of pump laser, whose relevant measurements can reveal the intrinsic symmetry of the materials and their interactions with the light. Therefore, to clarify the mechanism behind our observations, we performed the measurement under a different linear-polarization state of the pump light, characterized by the angle ϕ. Figure 2A shows the time-domain THz far-field EO signals S_x(t) and S_y(t) under the excitation of the x-polarized pump light. We noticed that there is a slight difference in the THz waveform under two different pump polarizations in Figure 2A, which might arise from: (1) incident pump light cannot be perfectly normal to the sample surface, and (2) the polarization of the incident pump light cannot be perfectly x-polarized or y-polarized. Dependence of the peak values of S_x(t) and S_y(t) on the linear-polarization angle ϕ is shown in Figure 2B. Clearly, both the magnitude and phase of the THz waveform (S_x(t) or S_y(t)) depend strongly on the polarization state. This is consistent with the fact that the THz wave emission is closely related to the nonlinear optical effect evidenced by the pump-power-dependent measurement shown above (Hebling et al., 2008; Zhai et al., 2021). On the other hand, a 3-fold symmetry is found in the dependence of THz wave magnitude on the sample azimuthal angle, Ψ (Figure 2C). In fact, based on the quadratic nonlinear optical process and the symmetry of [0001]-oriented PtBi₂ crystal, we can derive the phenomenological equations as a function of ϕ and Ψ to describe the THz waves along the x- and y axes (see the STAR Methods of symmetry analysis for details) (Boyd, 2003):

$$S_x\left(\text{Ψ},\varphi \right)\propto E_0^2{\xi }_{xxx}cos\left(3\text{Ψ}-2\varphi \right)$$ (Equation 1)

$$S_y\left(\text{Ψ},\varphi \right)\propto E_0^2{\xi }_{xxx}sin\left(3\text{Ψ}-2\varphi \right)$$ (Equation 2)

Figure 2.

The THz EO signals obtained by rotating the HWP

(A) Typical THz EO-signal components S_x(t) and S_y(t) along the x- and y axes were measured at various pump polarization state via rotating the HWP, characterized by the angle ϕ, which stands for the linear-polarization state with respect to the y-polarized light (ϕ = 0°). (For clarity, the error bars are not shown here, which is about 4×10⁻⁷).

(B) The peak value of S_x(t) and S_y (t) (at t=0 ps) as functions of ϕ, respectively. The red solid curves show the fitting based on Equations (1) and (2).

(C) The azimuthal angle-dependent (Ψ-dependent) amplitude of emitted THz waves with linearly polarized pump pulses. The red solid curves show the fitted results. The error bars in B and C are the standard deviation of the experimental data.

Here E₀ is the electric field intensity and ${\xi }_{xxx}$ is an element of the second-order nonlinear susceptibility of PtBi₂. Using the above equations, we can fit the data in Figures 2B and 2C extremely well (see red curves). In addition, the derived equations demonstrate that the x- and y-components are in phase, and leads to the emitted THz waves being linearly polarized. This agrees well with our observation in Figure 1C.

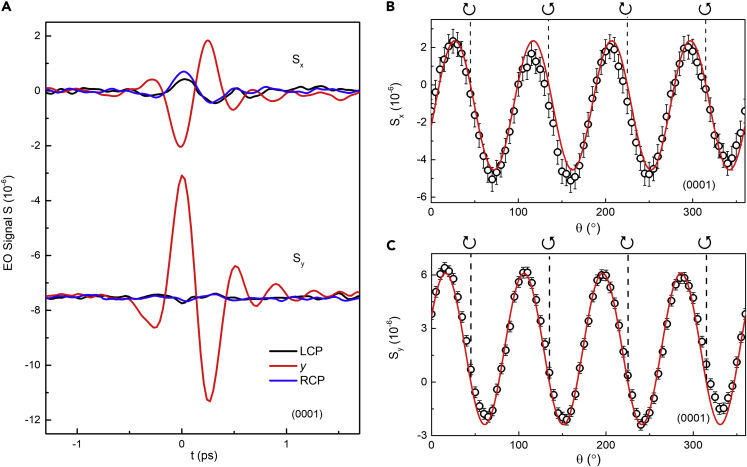
We also measured the dependence of S_x(t) and S_y(t) on the helicity of the pump light, which is controlled by rotating a QWP, characterized by the angle θ (Figure 3). The time-domain signals are shown in Figure 3A, where we can see that the magnitude of emitted THz waves induced by the circularly polarized pump light is much smaller than that generated by the linearly polarized light. Also, considering the accuracy of our measurements, there is a negligible difference between the results for pump light with left- and right-circular polarization. More detailed magnitude dependence on the QWP angle is shown in Figures 3B and 3C. Similar to the previous case of the linearly polarized pump, we can also derive the THz wave emission as a function of θ and Ψ based on the quadratic nonlinear optical process (see STAR Methods of symmetry analysis for details):

$$S_x\left(\text{Ψ},\theta \right)\propto \frac{1}{2}{E}_0^2{\xi }_{xxx}\left[cos3\text{Ψ}+cos\left(3\text{Ψ}-4\theta \right)\right]$$ (Equation 3)

$$S_y\left(\text{Ψ},\theta \right)\propto \frac{1}{2}{E}_0^2{\xi }_{xxx}\left[sin3\text{Ψ}+sin\left(3\text{Ψ}-4\theta \right)\right]$$ (Equation 4)

Figure 3.

The THz EO signals obtained by rotating the QWP

(A) Typical EO signal S_x(t) and S_y(t) were measured at various pump helicity via rotating the QWP, characterized by the angle θ. Here, y(θ = 0°), LCP (θ = 45°), and RCP (θ = 135°) represent the y-direction, left-handed, and right-handed circularly polarized light, respectively. (For clarity, the error bars are not shown here, which is about 4×10⁻⁷).

(B and C) The peak value of S_x(t) and S_y(t) (at t = 0 ps) as functions of θ. The red solid curves show the fitting based on Equations (3) and (4). The error bars in B and C are the standard deviation of the experimental data.

Clearly, the results in Figures 3B and 3C can be well reproduced by the above equations (see the red curves in the figures). We note that according to our experimental data and analysis, the dependence of THz wave emission on helicity should mainly come from the contribution of the linear polarization. This result is quite different from some other TMs, such as TaAs (Gao et al., 2020; Sun et al., 2017; Ma et al., 2017), where the THz emission from TaAs under fs-laser pump is helicity-dependent. Such helicity-dependence could be explained by the photocurrent generated from the optical transitions involving the Weyl cones in TaAs (Gao et al., 2020; Sun et al., 2017; Ma et al., 2017). Although it is quite different in PtBi₂ as there are no spin/chirality related optical transitions and hence the optical transitions involved with different helicity (left- and right-circular polarization) contribute equally to the photocurrent. As a result, no helicity-dependent THz emission is observed. Phenomenologically, as the helicity-dependent second-order optical nonlinear response is only related to the imaginary part of the second-order susceptibility (Ganichev and Prettl, 2003), the value of ${\xi }_{\lambda \mu \nu }$ of PtBi₂ should be almost real, which is different from TaAs as well.

In addition, the helicity-dependent THz emission is also measured for pump photon energy of 0.9 and 0.7 eV, respectively. The results are consistent with Equations (3) and (4), as shown in Figures S6 and S7 in the supplemental information. Moreover, the dependence of THz wave emission from PtBi₂ on linear polarization with pump photon energy of 0.9 eV (Figure S5 in supplemental information) is also similar to that in Figure 2. This further proves that the pump polarization dependence of the emitted THz is mainly related to the crystal symmetry of PtBi₂, and suggests that such symmetry is independent of the photon energy or wavelength. More discussions on the pump wavelength dependence of THz emission from PtBi₂ will be discussed in the next section.

Ultrafast photocurrent

Observation of THz wave emission arises from the ultrafast photocurrent J(t). Based on the discussion above, we arrive at excitation of the linearly polarized light producing the THz radiation from the PtBi₂ single crystal, i.e. the LPGE plays the dominant role, while the CPGE can be negligible.

Phenomenologically, the non-local transient ultrafast photocurrent j in the frequency domain owing to the LPGE can be described by (Braun et al., 2016; Ganichev and Prettl, 2003; Kampfrath et al., 2013; Mills, 2012),

$$j_{\lambda }\left(\overrightarrow{r},\text{Ω}\right)=2\sum _{\mu \nu }{\int }_{\omega >0}d\omega {\xi }_{\lambda \mu \nu }\left(\overrightarrow{r};\omega +\text{Ω},\omega \right)F_{\mu }{f}_{\nu }^{\text{∗}}$$ (Equation 5)

where λ, μ, and ν stand for the Cartesian coordinates $\hat{x}$, $\hat{y}$ and $\hat{z}$. ${\xi }_{\lambda \mu \nu }$ is the third-rank pseudo-tensor. $\overrightarrow{F}$ and $\overrightarrow{f}$ are the complex-valued pump-field amplitudes at frequencies $\omega +\text{Ω}$ and ω originating from the fs optical pump pulse. Owing to $\omega \gg \text{Ω}$, $\left|\overrightarrow{F}\left(\omega +\text{Ω}\right)\right|\simeq \left|\overrightarrow{f}\left(\omega \right)\right|$. For PtBi₂ with inversion symmetry broken, there are five independent nonvanishing elements of ${\xi }_{\lambda \mu \nu }$ (Boyd, 2003): ${\xi }_{zzz}$ , ${\xi }_{yzy}={\xi }_{xzx}$ and ${\xi }_{yyz}={\xi }_{xxz}$ , ${\xi }_{zyy}={\xi }_{zxx}$ and ${\xi }_{xxx}={\xi }_{-xyy}={\xi }_{-yyx}={\xi }_{-yxy}$. They are defined in the coordinates for (0001) face, where x, y, and z are parallel to the unit cell axes a, b, and c, respectively. Equation (5) evidently reveals why the THz signals varying with Ψ, ϕ, and θ can be described by the (Equation 1), (Equation 2), (Equation 3), (Equation 4).

Quantitatively, we can extract the photocurrent J(t) via the THz signal S(t) (see Figure S4). The peak value of ∼18.4 ± 0.5 A/m is obtained for 800 nm pump light. Hence, the effective third-rank pseudo-tensor in Equation (5) can be obtained as ξ_xxx∼339 ± 8 pm/V, which is almost two orders of magnitude larger than that of the typical THz nonlinear crystal, such as ZnTe (Planken et al., 2009). The direct comparison of THz wave emission between 0.5-mm-thick ZnTe and PtBi₂ under the same pump fluence is shown in Figure S4. Considering the penetration depth of 800-nm light in PtBi₂ is only 21.3 nm obtained from FTIR data (Figure S3), the THz emission efficiency per length of PtBi₂ is more than 150 times larger than ZnTe in our experimental conditions. This result could be closely related to the non-trial topology of band structures in PtBi₂ (Gao et al., 2018).

Microscopically, optical excitation is able to generate the charge current which is associated with the anisotropic processes of photoexcitation, scattering, or recombination of carriers in the crystal. The LPGE occurs when the electron density distribution of the excited state is spatially shifted with respect to the initial states during the optical transitions in real space or carrier shifting via excitation of the anisotropic bands in momentum space. Therefore, the induced charge current is also called the shift current (Ganichev and Prettl, 2003; Osterhoudt et al., 2019). This effect not only depends on the crystal symmetry but also on the linear polarization state of the light. As a quadratic nonlinear optical effect, LPGE is absent for systems with inversion symmetry (Ganichev and Prettl, 2003) and is also referred to the bulk photovoltaic effect (Osterhoudt et al., 2019).

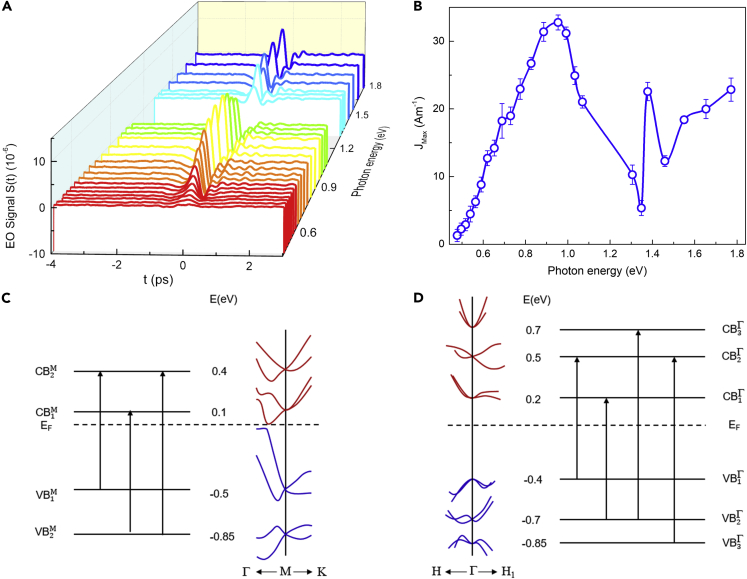
As mentioned above, the photocurrent in LPGE and its subsequent THz wave generation is dependent on the optical transitions, and hence should be sensitive to the pump photon energy. Therefore, we performed the THz emission measurements as a function of the pump wavelength to further explore the underneath mechanism. As seen in Figure 4A, the magnitude of THz waveform emitted from PtBi₂ is highly dependent on the pump photon energy, while the shape (or spectrum shown in Figure S9) remains almost the same, which suggests the similar time evolution and mechanism of the photocurrent under excitation with different photon energies in the range of our experimental conditions. As demonstrated in Figure 4B, the peak current density shows a maximum at ∼0.9 eV, below which it decreases continuously. Although in the range 0.95–1.77 eV (1300-700 nm), as the photon energy increases, there is a dip plus a sharp peak at 1.38 eV (900 nm).

Figure 4.

Dependence of the emitted THz waves on the photon energy of pump light

(A) THz EO signals S(t) under excitation of linearly polarized light at different wavelengths.

(B) The peak value of photocurrent J_Max (at t = 0 ps) as a function of the excitation photon energy. The error bars in B are the standard deviation of the experimental data.

(C and D) Schematic band diagram near M and Γ points.

First, the number of excited carriers can affect the magnitude of photocurrent. To clarify it, we thus measured the complex refractive index as a function of the photon energy using the Fourier transform infrared spectroscopy(FTIR) (see Figure S3 in the supplemental information). Based on our measurements, there are no clear abrupt changes in the extinction coefficient k (or absorption coefficient) emerging in our covered energy range. Therefore, excited carrier population should not be considered the main factor. Instead, the band anisotropy or band topology involved in the related optical transitions could play the key role here (Ganichev and Prettl, 2003). Possible transitions elucidating the features observed in the photon-energy-dependent measurements rely on the band structures of PtBi₂ (Gao et al., 2018; Shipunov et al., 2020), as schematically shown in Figures 4C and 4D.

According to our previous work (Gao et al., 2020), optical transitions involving the tilted anisotropy Weyl or Dirac cones with linear dispersion might initiate large photocurrent in the TMs. This aspect can be ignored in PtBi₂ because no obvious tilt and anisotropy is found for the bands around the Dirac nodes above the Fermi level (Gao et al., 2018). Instead, near M point, colossal anisotropic Rashba spin-splitting bands have been reported in the valence bands of PtBi₂ (Feng et al., 2020). Therefore, based on the energy scales, the optical transitions ${\text{VB}}_2^M\to {\text{CB}}_1^M$ and ${\text{VB}}_1^M\to {\text{CB}}_2^M$, shown in Figure 4C, may contribute to the maximum signals around 0.9 eV, while the peak at ∼1.38eV probably derived from ${\text{VB}}_2^M\to {\text{CB}}_2^M$ of the optical transition. Owing to the Rashba-Edelstein effect (Shao et al., 2016), ultrafast spin-polarized current might appear in this material.

Similarly, giant anisotropies are also observed for bands near the $\text{Γ}$ point (Gao et al., 2018). In specific, the optical transitions from the ${\text{VB}}_1^{\text{Γ}}\to {\text{CB}}_2^{\text{Γ}}$ and ${\text{VB}}_2^{\text{Γ}}\to {\text{CB}}_1^{\text{Γ}}$ can contribute to the main peak at ∼0.9 eV. The second peak at ∼1.38 eV might be owing to the transitions from ${\text{VB}}_2^{\text{Γ}}\to {\text{CB}}_3^{\text{Γ}}$ and ${\text{VB}}_3^{\text{Γ}}\to {\text{CB}}_2^{\text{Γ}}$. We note that there are only a few transitions listed here for demonstration (see Figures 4C and 4D). In the investigated photon-energy range there could also exist many other irrelevant optical transitions, where anisotropy of the involved bands is possibly small and hence the photoinduced currents nearly cancel each other in the conduction and valence bands. As a result, these irrelevant transitions play a minor role in the experimental data. Nonetheless, our simple analysis qualitatively explains the photon-energy-dependent behavior. We need more accurate theoretical calculations and analysis to clarify the detailed electronic structures contributing to the LPGE-induced photocurrent in the future.

Additionally, we noticed that the pulse duration of pump laser may also influence the experimental data, e.g. the amplitude and spectrum of the THz emission waveform. According to the THz spectrum in the frequency domain shown in Figure S9, we can see that the central frequency and the spectral distribution of the THz emission under different wavelengths are nearly the same. This suggests that the pulse duration of the laser pulses from OPA in our covered photon energy range does not change too much, and ensures the accuracy of our measurements.

Conclusions

In summary, we experimentally discovered that the trigonal layered PtBi₂ is an effective material for generating the broadband THz waves, and revealed the LPGE plays the dominant role behind the THz wave emission. The nonlinear suscepibility of PtBi₂ is obtained as ∼339 ± 8 pm/V, which is very large compared to frequently used THz crystal, i.e. ZnTe, suggesting its potential applications in the THz technology. Utilizing the crystal symmetry and nonlinear LPGE, we can easily manipulate the linear polarization state of the emitted THz waves. The ultrafast photocurrent intensity and its associated THz wave emission were found to maximize around 0.9 eV, which may be caused by the strongly anisotropic bands in this material.

Limitations of the study

In our work, owing to the limitation of EO sampling applied in THz detection, the spectral width in our measurements is only up to ∼4 THz. Therefore, the high-frequency information of emitted THz in radiation is not detectable.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
Origin 2016	Originlab	http://www.originlab.com/
MATLAB R2016a	Mathworks	http://www.mathworks.com/
Other
NIR power meter	Newport	843-R

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Prof. Jingbo Qi jbqi@uestc.edu.cn.

Materials availability

This study did not generate new unique reagents.

Experimental model and subjiect details

Our study does not use experimental models.

Method details

Materials details

The single crystals of PtBi₂ were grown by flux method (Nie et al., 2020). A mixture of Pt (slice, 99.99%) and Bi (piece, 99.999 %) in a molar ratio of 1:4 were placed in an alumina crucible and sealed in an evacuated quartz tube. The tube was then heated up to 1073 K for 10 h and slowly cooled down to 723 K, where the samples were separated from the Biflux by a centrifuge. The dimension of the sample is approximately 4 × 5 × 0.1 mm³. The sample is confirmed to be with trigonal layered PtBi₂ by XRD measurement, which is shown in Figure S8.

Symmetry analysis

In the description of second-order nonlinear optical effects, the thrid-rank tensor ${\xi }_{\lambda \mu \nu }$ can be non-zero only in the crystal without inversion symmetry. According to the P31m crystal symmetry of PtBi₂, there are five independent nonvanishing tensor elements (Boyd, 2003): ${\xi }_{zzz}$ , ${\xi }_{yzy}={\xi }_{xzx}$ and ${\xi }_{yyz}={\xi }_{xxz}$ , ${\xi }_{zyy}={\xi }_{zxx}$ and ${\xi }_{xxx}={\xi }_{-xyy}={\xi }_{-yyx}={\xi }_{-yxy}$.

According to our experimental configurations, the second-order response could be derived as following:

(1) For half-wave plate case (polarization angle-dependence):

The electric field of incident light in lab-frame, $E={\left(E_x,E_y\right)}^T$ could be written as:

$$\left(\begin{array}{l}{E}_x\\ E_y\end{array}\right)=\left(\begin{array}{l}{E}_{0}cos\varphi \\ E_{0}sin\varphi \end{array}\right)$$ (Equation 6)

In the frame of crystal, the electric field of incident light is converted with a rotational matrix that determined by the sample azimuthal angle $\text{Ψ}$:

$$\left(\begin{array}{l}{E_x}^{\prime }\hfill \\ {E_y}^{\prime }\hfill \end{array}\right)=\left(\begin{array}{ll}cos\text{Ψ}\hfill & sin\text{Ψ}\hfill \\ -sin\text{Ψ}\hfill & cos\text{Ψ}\hfill \end{array}\right)\left(\begin{array}{l}{E}_x\hfill \\ E_y\hfill \end{array}\right)$$ (Equation 7)

Considering the non-zero tensor elements, the second-order response in crystal frame is:

$${P_x}^{\prime }={\xi }_{xxx}{E_x}^{\prime }{E_x}^{\prime }+{\xi }_{xyy}{E_y}^{\prime }{E_y}^{\prime }$$ (Equation 8)

$${P_y}^{\prime }={\xi }_{yxy}{E_x}^{\prime }{E_y}^{\prime }+{\xi }_{yyx}{E_y}^{\prime }{E_x}^{\prime }$$ (Equation 9)

Then we can convert it to the lab frame according to:

$$\left(\begin{array}{l}{P}_x\hfill \\ P_y\hfill \end{array}\right)={\left(\begin{array}{ll}cos\text{Ψ}\hfill & sin\text{Ψ}\hfill \\ -sin\text{Ψ}\hfill & cos\text{Ψ}\hfill \end{array}\right)}^{-1}\left(\begin{array}{l}{P_x}^{\prime }\hfill \\ {P_y}^{\prime }\hfill \end{array}\right)$$ (Equation 10)

Finally, we have:

$$P_x=E_0^2{\xi }_{xxx}cos\left(3\text{Ψ}-2\varphi \right)$$ (Equation 11)

$$P_y=E_0^2{\xi }_{xxx}sin\left(3\text{Ψ}-2\varphi \right)$$ (Equation 12)

Therefore, considering that the EO signal is proportional to P, we obtain the relationship between the THz emission signal and pump polarization angle (and sample azimuthal angle):

$$S_x\left(\text{Ψ},\varphi \right)\propto P=E_0^2{\xi }_{xxx}cos\left(3\text{Ψ}-2\varphi \right)$$ (Equation 13)

$$S_y\left(\text{Ψ},\varphi \right)\propto P=E_0^2{\xi }_{xxx}sin\left(3\text{Ψ}-2\varphi \right)$$ (Equation 14)

(2) For quarter-wave plate case (helicity-dependence):

The electric field of incident light in lab-frame (after the quarter-wave plate), $E={\left(E_x,E_y\right)}^T$ could be written as:

$$\left(\begin{array}{l}{E}_x\hfill \\ E_y\hfill \end{array}\right)=e^{\frac{-i\pi }{4}}\left(\begin{array}{ll}co{s}^2\theta +isi{n}^2\theta \hfill & \left(1-i\right)sin\theta cos\theta \hfill \\ \left(1-i\right)sin\theta cos\theta \hfill & si{n}^2\theta +ico{s}^2\theta \hfill \end{array}\right)E_0\left(\begin{array}{l}1\hfill \\ \mathrm{0}\hfill \end{array}\right)$$ (Equation 15)

$$\left(\begin{array}{l}{E}_x\hfill \\ E_y\hfill \end{array}\right)=\frac{\sqrt{2}}{2i}{E}_0\left(\begin{array}{l}i+cos2\theta \hfill \\ sin2\theta \hfill \end{array}\right)$$ (Equation 16)

In the frame of crystal, the electric field of incident light is converted with a rotational matrix that determined by the sample azimuthal angle $\text{Ψ}$:

$$\left(\begin{array}{l}{E_x}^{\prime }\hfill \\ {E_y}^{\prime }\hfill \end{array}\right)=\left(\begin{array}{ll}cos\text{Ψ}\hfill & sin\text{Ψ}\hfill \\ -sin\text{Ψ}\hfill & cos\text{Ψ}\hfill \end{array}\right)\left(\begin{array}{l}{E}_x\hfill \\ E_y\hfill \end{array}\right)$$ (Equation 17)

Considering the non-zero tensor elements, the second-order response in crystal frame could be written as:

$${P_x}^{\prime }={\xi }_{xxx}{E_x}^{\prime }{E_x}^{\prime }+{\xi }_{xyy}{E_y}^{\prime }{E_y}^{\prime }$$ (Equation 18)

$${P_y}^{\prime }={\xi }_{yxy}{E_x}^{\prime }{E_y}^{\prime }+{\xi }_{yyx}{E_y}^{\prime }{E_x}^{\prime }$$ (Equation 19)

Then we can convert it to the lab frame according to:

$$\left(\begin{array}{l}{P}_x\hfill \\ P_y\hfill \end{array}\right)={\left(\begin{array}{ll}cos\text{Ψ}\hfill & sin\text{Ψ}\hfill \\ -sin\text{Ψ}\hfill & cos\text{Ψ}\hfill \end{array}\right)}^{-1}\left(\begin{array}{l}{P_x}^{\prime }\hfill \\ {P_y}^{\prime }\hfill \end{array}\right)$$ (Equation 20)

Finally, we have:

$$P_x=\frac{1}{2}{E}_0^2{\xi }_{xxx}\left(cos\left(3\text{Ψ}\right)+cos\left(3\text{Ψ}-4\theta \right)\right)$$ (Equation 21)

$$P_y=\frac{1}{2}{E}_0^2{\xi }_{xxx}\left(sin\left(3\text{Ψ}\right)+sin\left(3\text{Ψ}-4\theta \right)\right)$$ (Equation 22)

Therefore, considering that the EO signal is proportional to P, we obtain the relationship between the THz emission signal and QWP angle (and sample azimuthal angle):

$$S_x\left(\text{Ψ},\theta \right)\propto P=\frac{1}{2}{E}_0^2{\xi }_{xxx}\left[cos3\text{Ψ}+cos\left(3\text{Ψ}-4\theta \right)\right]$$ (Equation 23)

$$S_y\left(\text{Ψ},\theta \right)\propto P=\frac{1}{2}{E}_0^2{\xi }_{xxx}\left[sin3\text{Ψ}+sin\left(3\text{Ψ}-4\theta \right)\right]$$ (Equation 24)

Ultrafast photocurrent calculation and refractive index data

In order to obtain the sheet current density J(t), we need to extract the emitted THz electric field E(t) from the measured EO signal S(t). There is a linear relation between these two quantities in frequency domain. The THz electric field E(Ω) and the corresponding EO signal S(Ω) are related by the function h(Ω) through the simple multiplication (Kampfrath et al., 2007, 2013; Kuzel et al., 1999)

$$S\left(\text{Ω}\right)=h\left(\text{Ω}\right)E\left(\text{Ω}\right)$$ (Equation 25)

where $h\left(\text{Ω}\right)=h_{det}\left(\text{Ω}\right)h_{prop}\left(\text{Ω}\right)$ includes the detector response function $h_{det}\left(\text{Ω}\right)$ and the transfer function $h_{prop}\left(\text{Ω}\right)$. Here $h_{det}\left(\text{Ω}\right)$ describes the response of EO crystal under THz radiation, and $h_{prop}\left(\text{Ω}\right)$ represents for the transport factor of THz wave from the sample to the detection crystal. Then we can use the following generalized Ohm’s law to calculate the sheet current: (Braun et al., 2016; Gao et al., 2020; Shan and Heinz, 2004).

$$E\left(\text{Ω}\right)=-\frac{Z_0}{cos\text{Θ}+\sqrt{\left(n^2-si{n}^2\text{Θ}\right)}}J\left(\text{Ω}\right)$$ (Equation 26)

Here, $\text{Ω}$ is the THz frequency, Z₀ (≃377 Ohm) is the vacuum impedance, n is the refractive index of PtBi₂ at THz frequency, and $\text{Θ}$ (=0) is the angle of incidence. In our calculation, the refractive index n of PtBi₂ in THz regime is measured by FTIR, and shown in Figure S1. Eventually, the ultrafast photocurrent could be obtained which is displayed in Figure S2.

Here we also measured the complex refractive index as a function of the photon energy in the regime of our pump laser wavelength by using the FTIR, which is shown in Figure S3. This data for comparing the THz emission signal with different pump photon energy.

Fluence dependence of THz emission signal

According to the fluence-dependent measurements, THz emission from PtBi₂ shows very good linear relation (the inset of Figure 1D in the main text). Such linearity indicates that the pump fluence applied is far from saturation absorption region, and the carrier generation mechanism in THz emission should be uniform in the fluence range of our work. Furthermore, since the recombination process emerges very late in the time domain, it cannot be related to the THz generation with 1 ps timescale induced by the shift current mechanism in our observations. Therefore, the THz emission mechanism does not change in the fluence range we covered.

Quantification and statistical analysis

During the measurements, the fluctuation of humidity and electronic noise of our instruments may induce some noise or error in our data. To minimize the unexpected noise, the data shown in our work are the averaged values, and each error bar obtained from at least 16 sets of measurement under the same experimental conditions. Some error bars are estimated using the error propagation calculation (Taylor, 1982).

Published: July 15, 2022

Data and code availability

Data reported in this paper will be shared by the lead contact upon request.

Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.