Dynamics of absolute and relative disparity processing in human visual cortex

Abstract

Cortical processing of binocular disparity is believed to begin in V1 where cells are sensitive to absolute disparity, followed by the extraction of relative disparity in higher visual areas. While much is known about the cortical distribution and spatial tuning of disparity-selective neurons, the relationship between their spatial and temporal properties is less well understood. Here, we use steady-state Visual Evoked Potentials and dynamic random dot stereograms to characterize the temporal dynamics of spatial mechanisms in human visual cortex that are primarily sensitive to either absolute or relative disparity. Stereograms alternated between disparate and non-disparate states at 2 Hz. By varying the disparity-defined spatial frequency content of the stereograms from a planar surface to corrugated ones, we biased responses towards absolute vs. relative disparities. Reliable Components Analysis was used to derive two dominant sources from the 128 channel EEG records. The first component (RC1) was maximal over the occipital pole. In RC1, first harmonic responses were sustained, tuned for corrugation frequency, and sensitive to the presence of disparity references, consistent with prior psychophysical sensitivity measurements. By contrast, the second harmonic, associated with transient processing, was not spatially tuned and was indifferent to references, consistent with it being generated by an absolute disparity mechanism. Thus, our results reveal a duplex coding strategy in the disparity domain, where relative disparities are computed via sustained mechanisms and absolute disparities are computed via transient mechanisms.

1. Introduction

In the perceptual and oculomotor literatures, at least four functional dichotomies have been proposed to underly the percept of depth from disparity. These include processes common to other visual modalities, such as local or global processing, (Julesz, 1971), coarse or fine mechanisms (Wilcox and Allison, 2009), first-order vs. second-order processing (Hess and Wilcox, 1994), and temporally transient or sustained mechanisms (Edwards et al., 1998; Jones, 1980; Mitchell, 1970; Westheimer and Mitchell, 1969). Other stimulus-based dichotomies specific to stereopsis include absolute vs. relative disparity, crossed vs. uncrossed disparities, and horizontal vs. vertical disparities.

It is likely that some of these functional and stimulus-based dichotomies are inter-related, sharing a common set of neural resources. It is therefore desirable to identify a smaller number of component processes that can be mapped onto underlying neural mechanisms. In this study, we aim to identify neural processes underlying the spatial stimulus constructs of absolute and relative disparity, and to unify them with the temporal functional constructs of transient and sustained mechanisms.

Absolute and relative disparity are computationally distinct and appear to be processed by different mechanisms. Absolute disparity is the difference in angle subtended on the left and right retina of an object in space and gives an estimate of the depth of that object to the observer. Relative disparity is the comparative depth between two objects in space and arises when there are two or more depth planes present in the image. Perceptually, depth judgements are dominated by relative disparity – observers can discriminate smaller changes in disparity in the presence of a reference than in its absence (Andrews et al., 2001; Kumar and Glaser, 1991; McKee et al., 1990; Westheimer, 1979). Stereoacuity, a relative disparity task, improves with increasing exposure duration up to several seconds (Harwerth and Rawlings, 1977; Ogle and Weil, 1958), suggesting that it is subserved by neural mechanisms that are sustained.

Studies of the vergence system have implicated both transient and sustained disparity-tuned processes. Vergence can be initiated by disparate, but non-fusible targets that vary in their absolute disparity, but only fusible targets allow for a sustained vergence response (Jones, 1980; Mitchell, 1970; Westheimer and Mitchell, 1969). While changes in absolute disparity over time provide a strong cue for vergence eye movements, they lead to weak percepts of motion-in-depth (Cottereau et al., 2012a; Erkelens and Collewijn, 1985a, 1985b; Regan et al., 1986).

Thus, behavioural evidence would predict that perceptual mechanisms linked to the extraction of relative disparities are associated with sustained neural responses. Vergence eye movements, on the other hand, are strongly driven by absolute disparities and are associated with transient responses, especially for the initiation of vergence. These lines of evidence suggest functional associations between transient neural mechanisms and absolute disparities, and sustained mechanisms and relative disparities.

To our knowledge, there are no comparative studies that directly test the dynamics of disparity sensitive cells, whilst also explicitly distinguishing between absolute and relative disparity. One study measured responses from absolute disparity sensitive cells in macaque V1, and suggested, on the basis of a model and of human psychophysics, that these cells have a sustained temporal profile (Nienborg et al., 2005). This finding is surprising given the context of the oculomotor literature, and raises the question as to how transient vergence responses arise from a disparity signal that is fundamentally sustained. Furthermore, Nienborg’s study focussed only on the early stages of disparity processing in V1. It is unknown whether their findings are generally true throughout cortex.

In this study, we test the generality of Nienborg’s results by measuring EEG responses to modulating dynamic random-dot (DRDS) stimuli that evoke a steady-state response (SSVEP) and that isolate either absolute or relative disparity cues. In addition to its wide field of view over multiple cortical areas, a key advantage of our approach is that the temporal resolution of the EEG grants direct access to underlying neural dynamics. By contrast, previous behavioural studies have depended on a range of stimulus-based manipulations to make inferences about the underlying neural processes. Indeed, the terms ‘transient’ and ‘sustained’ have been used to refer to properties of the stimulus and the resulting visual percept, as well as the underlying neural mechanisms (Gheorghiu and Erkelens, 2005). Here, by measuring response dynamics, per se, we do not need to manipulate the monocular image content of the stimulus. In a first experiment, we vary the availability of disparity references and illustrate how a Fourier filtering approach to the SSVEP separates transient versus sustained neural processes (McKeefry et al., 1996).

In the main experiment, we varied the availability and nature of disparity references by varying the corrugation frequency of DRDS stimuli. Our stimuli generated a percept of a horizontally oriented, sinusoidal, depth-defined grating, where the grating was only visible after binocular fusion of the half-images and where the ‘corrugation frequency’ described the variation in depth across space. In the absolute disparity case, the corrugation frequency was 0, whilst relative disparity stimuli varied between 0.1 and 2 cycles per degree (cpd).

In line with the behavioural literature on disparity sensitivity as a function of stimulus duration, we would expect the sustained response component to be linked to perceptual phenomena. Because perceptual sensitivity to relative disparity depends on the corrugation frequency of disparity grating stimuli (Tyler, 1973), we expected the amplitude of the sustained response component to vary as a function of the corrugation frequency in a manner similar to that for perception.

Using a spatial filtering approach (Dmochowski et al., 2015), we identify a neural source over early visual cortex whose sustained response component is highly sensitive to disparity references and is strongly tuned for corrugation frequency, but whose transient component is not. We conclude that there is a dominant sustained channel that is tuned for corrugation frequency and thus relative disparity, whilst the transient channel is best driven by absolute disparity.

2. Methods

2.1. Participants

All participants were recruited from the Stanford community and were screened for normal or corrected-to-normal vision, ocular diseases and neurological conditions. Visual acuity was measured using a Log-MAR chart (Precision Vision, Woodstock, IL, USA) and was better than 0.1 in each eye with less than 0.3 acuity difference between the eyes. Stereoacuity was measured with the RANDOT stereoacuity test (Stereo Optical Company, Inc., Chicago, IL, USA) with a pass score of 50 arcsec or better. In the control experiment, 22 participants (13 female, 9 male, mean age 31 years) were recruited. Data from one participant were excluded for technical issues during the recording, and data from a second participant were excluded for a low signal-to-noise ratio in the EEG response component indexing low-level luminance changes (dot update response occurring at 20 Hz, see Methods: Visual Display for more detail). In the main experiment, 30 participants (15 female, 15 male, mean age 34 years) were recruited. Of these, five were excluded from analysis, two due to ocular and other chronic diseases that met the exclusion criteria and two for technical issues arising during the recording. One participant was excluded for a low signal-to-noise ratio in the dot update response. Data from 25 participants were retained for analysis. Informed written and verbal consent was obtained from all participants prior to participation under a protocol approved by the Institutional Review Board of Stanford University.

2.2. Visual display

Stimuli were displayed on a SeeFront 32” autostereoscopic 3D monitor running at a refresh rate of 60 Hz. The SeeFront display comprises a TFT LCD panel with an integrated lenticular system that interdigitates separate images for the left and right eyes on alternate columns of the 3840 × 3160 native display resolution. In 3D mode, the effective resolution is 1920 × 1080 pixels per eye. Mean luminance was 50 cd/m² as requested by the stimulus generation software after in-house calibration and gamma linearization. The viewing distance was 70 cm which is within the optimal range for the adult average of a 65 mm inter-pupillary distance, as per the manufacturer’s specifications. At this distance, the total field of view in degrees of visual angle was 53.8° × 31.5°. The SeeFront device monitors the participants’ head position via an integrated pupil location tracker and shifts the two eyes’ views to compensate for motion, thus ensuring that the images are projected separately into each eye. Head positioning was checked periodically for each participant by asking them to report on the separate visibility of the nonius lines.

The stimulus comprised dynamic random-dot stereograms (DRDS) whose frames were generated in MATLAB using Psychtoolbox-3 (Brainard, 1997; Kleiner et al., 2007; Pelli, 1997). These frames were presented via a custom Objective C application with no jitter or frame dropping. The general layout of each stimulus condition is illustrated in Fig. 1, Panel A. The DRDS were viewed through a circular aperture (28.5° diameter) embedded within a square 39.5° by 39.5° 1/f noise fusion lock that was used to control eye gaze and vergence angle. The fusion lock was at zero disparity (identical images in left and right eyes). A ring of binocularly uncorrelated dots that was 1.2° wide was placed in between the edge of the DRDS and the fusion lock to reduce the availability of relative disparity cues arising from the edge of the zero-disparity fusion lock and the DRDS (Cottereau et al., 2012b). These uncorrelated dots were identical to the stimulus dots in size, density, and contrast but their positions did not update, and they were static during each stimulus trial. To minimize the appearance of a contour between the edge of the DRDS and the uncorrelated dot ring, the luminance of dots falling on the edge was blended with a cosine ramp. The visible diameter of the DRDS stimulus was 27.3°. To control the eye position of participants, and to aid stable binocular fusion, nonius lines were placed at central fixation where the length of each line was 1° with 0.3° separation between upper and lower lines.

Fig. 1.

Stimulus details. Panel A shows the general layout common to all stimulus conditions. Stimuli were viewed through a circular aperture embedded within a peripheral 1/f noise fusion lock (1). A ring of decorrelated dots (2) separated the edge of the stimulus. The stimulus was a dynamic random dot stereogram (DRDS, 3) where the corrugation frequency was disparity-defined and followed a sine-wave profile, except in the absolute disparity condition where it was a flat plane. Central nonius lines helped control eye gaze (4). Panel B shows screenshots of the stimulus as viewed by the left and right eyes. Note that in the monocular half-images, the decorrelated dots around the edge are indistinguishable from the DRDS, until they are fused and convey no depth information. Panel B is cross-fusible to reveal a sinusoidal disparity grating. Panel C illustrates the stimulus alternation between a corrugated surface and a flat, zero-disparity plane. The modulation rate was 2 Hz and generated the fundamental frequency in the steady-state visual evoked potential.

Dots within the DRDS were 6 arcmin in diameter and were presented at a density of 15 dots/degree². The placement of the dots was pseudo-random, and to avoid dot overlap we introduced a dot spacing criterion where dots were separated by at least 1.5 x their width. The dot update rate was 20 Hz, and dots were regenerated in new positions every 3rd video frame. Because the frequency of the dot update rate is detectable on the Fourier spectrum of the EEG, we were able to use this as an exclusion criterion against participants who showed weak overall visual evoked responses to the stimulus.

We manipulated the disparity-defined corrugation frequency of the DRDS in 8 separate stimulus conditions for the corrugation tuning experiment, ranging in seven roughly log-spaced steps between 0.1 cpd and 2 cpd with an additional 0 cpd (absolute disparity) condition. Throughout this paper, we will refer to our corrugated stimuli as “grating” conditions, and our 0 cpd stimulus as the “plane” condition. By definition, the grating stimuli contain both absolute and relative disparities, whilst the plane stimulus was designed to contain only absolute disparities, with minimal availability of relative disparity information. At our 70 cm viewing distance each display pixel subtended 10.8 arcsec. Dots in our DRDS stimuli were drawn in OpenGL using anti-aliasing, allowing us to present disparities at sub-pixel resolution. The upper limit for resolving a disparity-defined grating is constrained physically by the resolution limit of the monitor and the size of the dots and biologically by the disparity gradient (Burt and Julesz, 1980; Filippini and Banks, 2009) and underlying receptive field size properties (Banks et al., 2004; Nienborg et al., 2004). The upper limit for the corrugation frequency was near the limit of what could be achieved on our system, given the dot size and spacing constraints that determined the sampling of the disparity surface. Above 2 cpd, the rendering of the dots in the monocular half-image began to look irregular.

The corrugation frequency of the grating was defined in the following manner. First, the DRDS was split into bars of alternating ‘zero-disparity’ and ‘crossed-disparity’ pairs, such that an integer number of bar pairs was viewed though the aperture to achieve a desired corrugation frequency. Second, the overall bar pattern was smoothed to generate sine-wave, rather than square-wave, modulation in depth. This was done by multiplying the magnitude of the dot shift between left and right eye dot pairs that generate the disparity cue with a sine-wave function. The resultant stimulus looks like a 3D wave viewed from above (Fig. 1, panel B). The peak of the sine-wave fell in the centre of the crossed-disparity bar, whilst the trough of the sine wave fell in the centre of the zero-disparity bar.

The stimulus alternated in time between a crossed-disparity corrugated surface, and a flat zero-disparity plane (Fig. 1, panel C) or in the case of the absolute disparity condition between a flat disparate surface and a zero-disparity surface. The alternation rate was 2 Hz.

The peak-to-trough disparity amplitude of the grating was “swept” in 10 equal log steps over each 10 s stimulus presentation. The stimulus completed two disparate/non-disparate cycles at each step in the disparity sweep. Because disparity sensitivity varies as a function of corrugation frequency, two different sweep ranges were chosen. For ‘low sensitivity’ corrugation frequencies, disparity amplitude was swept between 0.5 and 8 arcmin, whereas for ‘high sensitivity’ conditions the disparity amplitude was swept between 0.2 and 6 arcmin. Low sensitivity conditions were absolute disparity (0 cpd), 0.1 cpd, 1.21 cpd, and 2.00 cpd. High sensitivity conditions were 0.16 cpd, 0.27 cpd, 0.45 cpd, and 0.74 cpd (for an overview of disparity sensitivity at different temporal and spatial frequencies, (see Kane et al. 2014)). Optimal sweep ranges were chosen on the basis of pilot experiments, such that the disparity response emerged from the noise in the first half of the sweep and did not saturate towards the end.

2.3. Procedure

For all experiments, trials began with a 1 s prelude in which the display presented the first 60 frames of the upcoming disparity sweep, allowing the EEG and the adaptive filter to reach a steady state. This prelude was followed seamlessly by the 10 s stimulus presentation period, during which disparity amplitude was the swept parameter. The trial ended with a 1 s postlude, recycling the last 60 frames of the stimulus. There was a 2 s gap between subsequent trials, during which participants were instructed to blink as needed. In the control experiment, participants viewed the plane stimulus with two different tasks superimposed on the disparity modulation in two separate stimulus conditions (see below, ‘Fixation Tasks’). Participants completed 20 trials of each condition, split into presentation blocks of 10 trials each and where each block contained stimuli from one condition. The order of blocks was randomised between participants and breaks were permitted between each block. In total, 20 × 10 s trials were acquired for each of the 2 fixation tasks, per participant. In the main experiment, participants completed 20 trials of each condition, split into blocks of 10 trials each where each block contained stimuli from one of the 8 corrugation frequency conditions. The order of blocks was randomised between participants and breaks were permitted between each block. In total, 20 × 10 s trials were acquired for each of the 8 corrugation frequencies, per participant.

2.4. Fixation tasks

During stimulus trials, participants were asked to attend to a change at central fixation and press a button to indicate when the change had occurred. The purpose of the task was to encourage fixation at the centre of the screen, allowing convergence on the plane of the display, and to monitor the attentional state of the participants. In the first experiment, we compared responses recorded with two different fixation tasks that varied the availability of a disparity cue from the fixation target. In the first task, a binocularly viewed letter (either an X or an O) was presented at zero disparity between two nonius lines. The vertically separated nonius lines were presented to the left and right eyes individually and thus did not convey a disparity cue. Participants pressed a button when the X changed to an O. In the second task, the nonius lines themselves changed colour from blue to red and the binocular letters were not presented. Data recorded during the nonius colour task was compared to that obtained in the X-O task in the first experiment and only the nonius task was used in the main experiment. The initial duration of the letter or colour change was 0.5 s and was varied on a staircase that maintained an 82% correct level of performance.

2.5. EEG acquisition and pre-processing

High-density, 128-channel electroencephalograms (EEG) were recorded using HydroCell electrode arrays and an Electrical Geodesics Net Amps 400 (Electrical Geodesics, Inc., Eugene, OR, USA) amplifier. The EEG was sampled natively at 500 Hz and then resampled at 420 Hz, giving 7 data samples per video frame. The display software provided a digital trigger indicating the start of the trial with millisecond accuracy. The data were filtered using a 0.3–50 Hz bandpass filter upon export of the data to custom signal processing software. Artifact rejection was performed in two steps. First, the continuous filtered data were evaluated according to a sample-by-sample thresholding procedure to locate consistently noisy sensors. These channels were replaced by the average of their six nearest spatial neighbours. Once noisy channels were interpolated in this fashion, the EEG was re-referenced from the Cz reference used during the recording to the common average of all sensors. Finally, 1 s EEG epochs that contained a large percentage of data samples exceeding threshold (30–80 μV) were excluded on a sensor-by-sensor basis.

2.6. Fourier decomposition and filtering

The steady-state VEP (SSVEP) amplitude and phase at the first four harmonics of the disparity update frequency (2 Hz) were calculated by a Recursive Least Squares (RLS) adaptive filter (Tang and Norcia, 1995). The RLS filter consisted of two weights – one for the imaginary and the other for the real coefficient of each frequency of interest. Weights were adjusted to minimise the squared estimation error between the reference and the recorded signal. The memory-length of the filter was 1 s, such that the learned coefficients were averaged over an exponential forgetting function that was equivalent to the duration of one bin of the disparity sweep. Background EEG levels during the recording were derived from the same analysis and were calculated at frequencies 1 Hz above and below the response frequency, e.g., at 1 and 3 Hz for the 2 Hz fundamental. Finally, the Hotelling’s T² statistic (Victor and Mast, 1991) was used to test whether the VEP response was significantly different from zero.

2.7. Dimension reduction via reliable component analysis

Reliable Components Analysis (RCA) was used to reduce the dimensionality of the sensor data into interpretable, physiologically plausible linear components (Dmochowski et al., 2015). This technique optimizes the weighting of individual electrodes to maximize trial-to-trial consistency of the phase-locked SSVEPs. Components were learned on RLS-filtered complex value data, and were learned on the 1F1, 2F1, 3F1 and 4F1 responses across all trials, all participants, and all conditions. The Rayleigh quotient of the cross-trial covariance matrix divided by the within-trial covariance matrix was decomposed into a small number of maximally reliable components by solving a generalised eigenvalue problem. Each component can be visualised as a topographic map by weighting the filter weights by a forward model (Dmochowski et al., 2015; Haufe et al., 2014) and yields a complex-valued response spectrum for that component.

Participant-level sensor-space data were weighted by the two most reliable spatial filters, RC1 and RC2. Group-level amplitude and phase estimates for signal (1F1 and 2F1) and noise (side bands of the 1F1 and 2F1 harmonics, respectively) frequencies were calculated by first taking the vector mean across real and imaginary components, across all trials within the same condition. Amplitude was calculated by taking the square root of the sum of the squared real and the squared imaginary components. Phase was calculated by taking the inverse tangent of the real and imaginary components. These vector-averaged amplitude and phase estimates were used to derive neural thresholds (see section below, ‘Estimating neural thresholds’).

For visualizing sweep data, for extracting suprathreshold responses, and for further statistical analyses, we determined the magnitude of the projection of each participant’s response vector on to the group vector average (Hou et al., 2009). Each individual response vector amplitude was multiplied by the cosine of the phase difference between it and the mean vector (Hou et al., 2009). The magnitude of these projections was then used to calculate the group mean projected amplitude and we calculated the scalar standard error of the mean of the projected amplitudes. This procedure yields a group mean amplitude that is very close to the group vector mean but is advantageous as it converts the vector data to scalar data so that conventional univariate and multi-variate statistics can be used while retaining the improvement in the group-level signal-to-noise ratio when the SSVEP is phase consistent across subjects. The measure also minimizes error estimates that are non-normally distributed.

2.8. Estimating neural thresholds

Because 1F responses increase linearly with log disparity amplitude (Norcia et al., 1985b) a linear function was fit to the group-level disparity response functions to estimate a neural threshold for each corrugation frequency as the zero-amplitude intercept (Campbell and Maffei, 1970; Norcia et al., 1985a; Wesemann et al., 1987). Our fitting function searched for a range of at least two consecutive 1 s bins where amplitude was both monotonically increasing and likely dominated by signal and thus usable for extrapolation to zero amplitude. The range was established on the basis of the following criteria. First, to avoid fitting spikes in the record caused by artifacts, the amplitude at the noise frequencies in a bin could not exceed 70% of the amplitude of the signal in a bin. Second, the p value of a the Hotelling’s T² test was below 0.160 (at least 1.5 standard deviations from zero). Third, the noise in the frequency side bands did not exceed 30% of the signal in the same bin. Fourth, the phase difference compared to the previous bin was between −100 and +80, minimizing fitting over non-physiological data where the response phase lags with increasing visibility. Fifth, the amplitude was monotonically increasing, and the signal was larger than that measured in the previous bin. Finally, the SNR of the signal was greater than 1.5. Bins that satisfied these criteria were deemed likely to contain meaningful signals, and a linear function was fit to consecutive bins that satisfied these conditions. On spontaneous EEG, these criteria yield a false-positive rate of spuriously fitting a regression line of < 5% for 42 applications of the algorithm (Pei et al., 2007). Here we apply the fit 16 times.

The x-axis intercept was taken as the neural threshold – the disparity at which the cortical response would have been zero in the absence of additive EEG noise. In some cases, especially when amplitudes were low and changes in amplitude from bin-to-bin were small, the slope of the fit was shallow resulting in an over-extrapolated threshold. This was deemed to be the case when there were more than two bins between the first bin used to fit the function, and the estimated threshold. When this occurred, the threshold was set to the disparity value at the bin prior to the first bin containing measurable signal. This occurred in one instance, for the neural threshold of the 1F1 response in RC1, in the 0.10 cpd condition. An example of the scoring procedure is shown in Fig. 5, panel B.

Fig. 5.

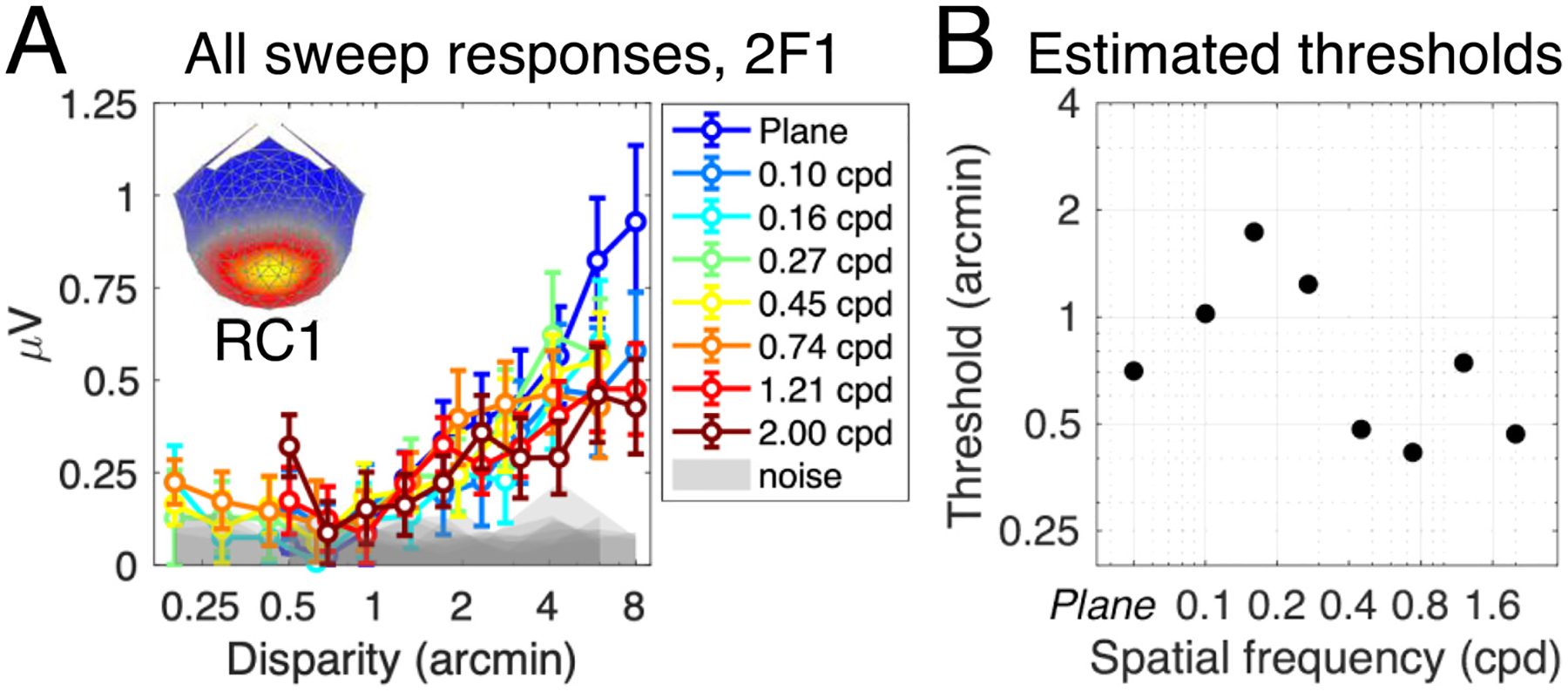
Results from the 2F1 response to disparity in RC1. Responses to gratings at different corrugation frequencies are plotted in Panel A, where the signal increased in amplitude as the peak-to-trough disparity in the grating increased. Neural thresholds were extracted by fitting a linear function to each curve in A. The value of the x-axis intercept was taken as the threshold, and is plotted in Panel B. Both panels indicate no systematic tuning to corrugation frequency, in contrast to the 1F1 response which was strongly tuned. Note the sensitivity of the 2F1 response to the 0 cpd, plane stimulus, expressed as a large signal amplitude in Panel A (dark blue curve) and a relatively low threshold in Panel B (leftmost point on the plot).

We constructed a Disparity Sensitivity Function (DSF) from the estimated neural thresholds. To compare the shape of the ‘neural DSF’ against the DSF measured in a range of psychophysical studies (Fig. 5, Panel D: (Bradshaw et al., 2006; Bradshaw and Rogers, 1999; Didyk et al., 2011; Hess et al., 1999; Hogervorst et al., 2000; Kane et al., 2014; Lankheet and Lennie, 1996; Lee and Rogers, 1997; Peterzell et al., 2017; Pulliam, 1982; Rogers and Graham, 1982; Schumer and Ganz, 1979; Serrano-Pedraza and Read, 2010; Tyler, 1973; Tyler and Kontsevich, 2001)), we extracted reported data using WebPlotDigitizer (software freely available at https://automeris.io/WebPlotDigitizer/) and normalised by dividing each threshold against the lowest threshold in each dataset, forcing each DSF to bottom out at 1. Where both upper and lower limits of disparity sensitivity were measured, the upper limit datapoints were excluded.

2.9. Suprathreshold disparity tuning functions

Disparity tuning functions were also estimated from the projected amplitude data from suprathreshold disparities to maximize the signal to noise ratio and to allow comparisons to be made across different conditions using conventional scalar-valued statistics. Because different sweep ranges and different disparity-step values were used in different corrugation frequency conditions, we used linear interpolation to estimate signal amplitude at 6 and 2 arcmin. Estimates were generated for each participant using their mean projected amplitudes calculated across all trials, giving a sweep function from which the amplitudes at the two disparity levels were estimated.

2.10. Statistical analyses

Suprathreshold data were analysed using repeated measures analysis of variance (ANOVA) in R, using functions from the rstatix package (in particular, anova_test which is a wrapper for car∷Anova). Data were assessed for normality using the Shapiro-Wilk test and visual inspection of QQ plots. Sphericity was assessed using Mauchly’s test. Where sphericity was violated, the Greenhouse-Geisser correction was applied. The generalised effect size (Olejnik and Algina, 2003), which estimates the proportion of variability explained by the within-subjects factor, is reported with each F test. Qualitative descriptors of effect size are consistent with Cohen’s benchmarks, with small, medium and large effects ascribed to effect sizes of 0.2, 0.5 and 0.8, respectively (Olejnik and Algina, 2003). Pairwise t-tests were used to interrogate main effects and interactions and reported p-values are adjusted for multiple comparisons using the Bonferroni correction.

3. Results

We measured steady-state VEPs in response to DRDS stimuli. In the control experiment, we aimed to generate a ‘pure’ absolute disparity response to the plane stimulus by eliminating refence effects caused by the fixation task. In the main experiment, we varied the corrugation frequency of the disparity grating stimulus and assessed the tuning properties of the 1F1 and 2F1 signals. Results are focussed on the most reliable component, RC1, which was maximal over midline occipital electrodes. The topography of RC1 was reproduced in both the control and the main experiment. Results from a second neural source over right-lateralised occipito-temporal electrodes, RC2, mirrored the results in RC1 and are described in the Supplement.

3.1. Minimizing reference effects in the plane stimulus

Fixation targets can create unwanted reference effects when trying to estimate responses to absolute disparity, in essence turning a notionally absolute disparity stimulus into a relative disparity stimulus. The absence of binocular references is therefore critical for generating a ‘pure’ absolute disparity stimulus. In a control experiment, we measured the reference effects arising from the fixation task embedded in the plane stimulus. The task was either on a binocular central fixation mark that created a relative disparity reference, or on dichoptic nonius lines at fixation that did not. In the former case, a binocularly viewed changing letter was presented centrally at zero disparity. For the dichoptic fixation task, the nonius lines themselves changed colour and the only references available were from the peripheral fusion-lock (which we disrupted, see Methods) and monitor bezel. Both tasks served to stabilize vergence.

The effect of the presence of a binocular, relative disparity reference is in shown in Fig. 2. In RC1, there was a robust 1F1 response to the disparity change when there was a binocular reference at fixation (panel A). However, there was a marked reduction in the amplitude of the 1F1 response when the task was switched to the nonius colour-change task which did not create a relative disparity reference. The amplitudes of the responses between conditions were compared using paired-samples t-tests at each bin, and bins where this difference was significant (p <. 050, adjusted for multiple comparisons) are marked in Fig. 2.

Fig. 2.

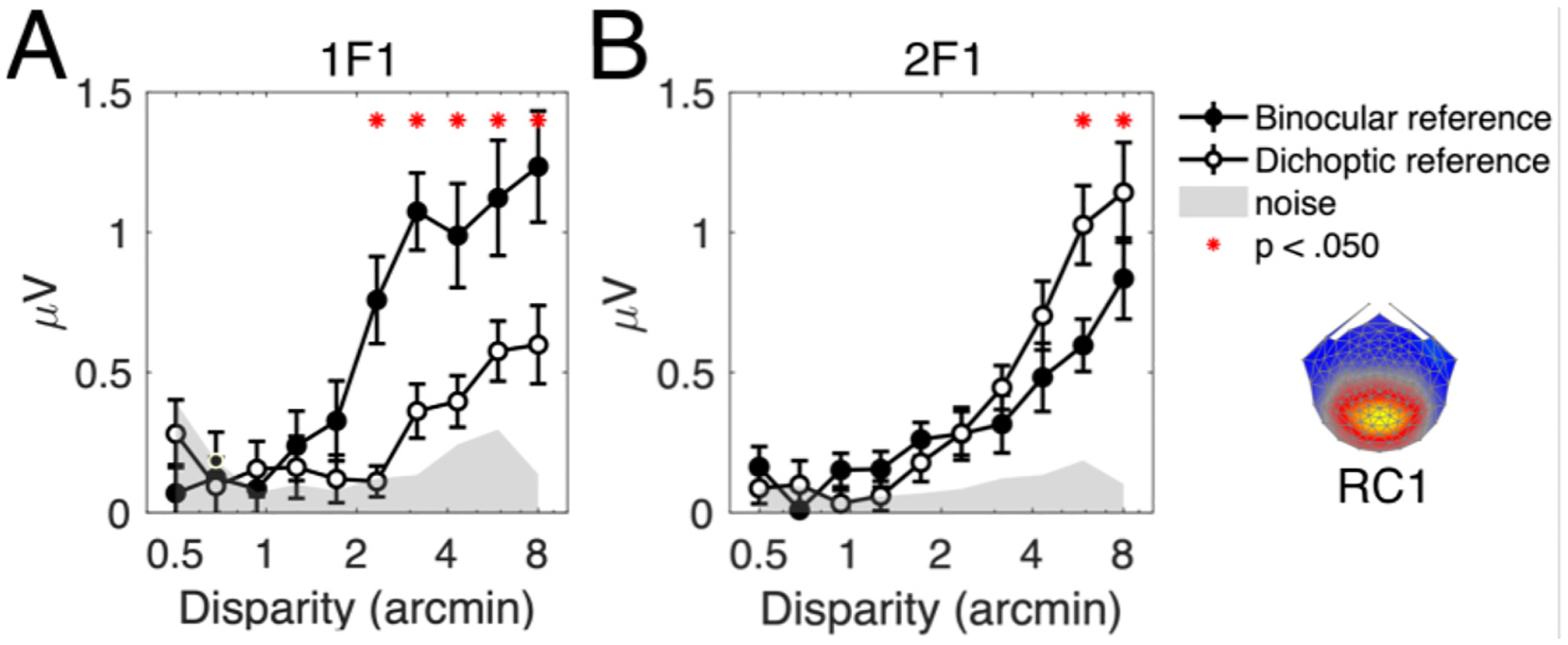
Effect of a central fixation task on the 1F1 and 2F1 response amplitudes. Responses were evoked by a plane stimulus oscillating between zero disparity and crossed disparity. Participants performed an attention task placed on the nonius lines (‘dichoptic reference’, open circles) or a letter change task (‘binocular reference’, filled circles). The introduction of a binocular reference adds a zero-disparity signal to the foveated part of the stimulus. Both 1F1 and 2F1 are sensitive to the change in fixation task, where the 1F1 response is significantly greater when the task is binocular. The 2F1 responses show the opposite trend, where the response is weaker when the task is binocular. The noise floor (light grey) is the mean signal amplitude in the frequency side-bands, at each disparity level, and averaged across both conditions.

In addition to the change in amplitude at 1F1, we also observed a shift in threshold where a larger disparity was required to evoke a response during the dichoptic task condition. This residual 1F1 response may be due to some relative disparity leakage arising from imperfect separation of the edge of the changing disparity region and the static zero-disparity fusion lock or monitor bezel. Alternatively, a functional explanation could be that the 1F1 signal is driven by asymmetries in the preferred direction of motion in depth (Cottereau et al., 2011).

The sensitivity of the VEP to a binocular reference at fixation demonstrates that the asymmetric 1F1 response is highly sensitive to the presence of more than one disparity in the stimulus. This result is consistent with previous results (Cottereau et al., 2012a) where the dynamic nature of the changing disparity stimulus also resulted in ‘making and breaking’ of a disparity plane defined by a binocular zero disparity reference. Thus, the 1F1 response is a strong readout for relative disparity mechanisms.

The 2F1 response in the dichoptic condition (panel B), on the other hand, was the same at small disparities but larger than the response in the binocular reference condition at larger disparities. Thresholds were similar in both task conditions. Notably, for the dichoptic task, the threshold was lower for the in the 2F1 response than in the residual 1F1 response. We therefore suggest that the 2F1 response is dominated by mean changes in absolute disparity, and that it is somewhat suppressed by the introduction of a small reference disparity at fixation.

3.2. Dissociating transient and sustained mechanisms via fourier analysis

To distinguish temporal response components that are reflective of transient vs. sustained mechanisms, we used a spectral analysis approach previously introduced for the study of contrast evoked potentials (McKeefry et al., 1996). McKeefry et al. used simulations to argue that sustained responses like those we observe for the stereo grating will manifest in the first harmonic of the SSVEP, whereas transient mechanisms manifest in the even harmonics.

This approach applied to our disparity-driven responses is illustrated in Fig. 3, which shows spectra (panels A and D) and time courses (panels B, C, E and F) of the responses to a flat plane with nonius lines at fixation (top row) vs. the binocular fixation task (bottom row). Data are taken from the control experiment, and are single-cycle group averages across a cluster of midline occipital electrodes that underlie RC1 (71, 72, and 76). Red and black lines in the spectra indicate odd harmonics and even harmonics used to selectively reconstruct response time courses.

Fig. 3.

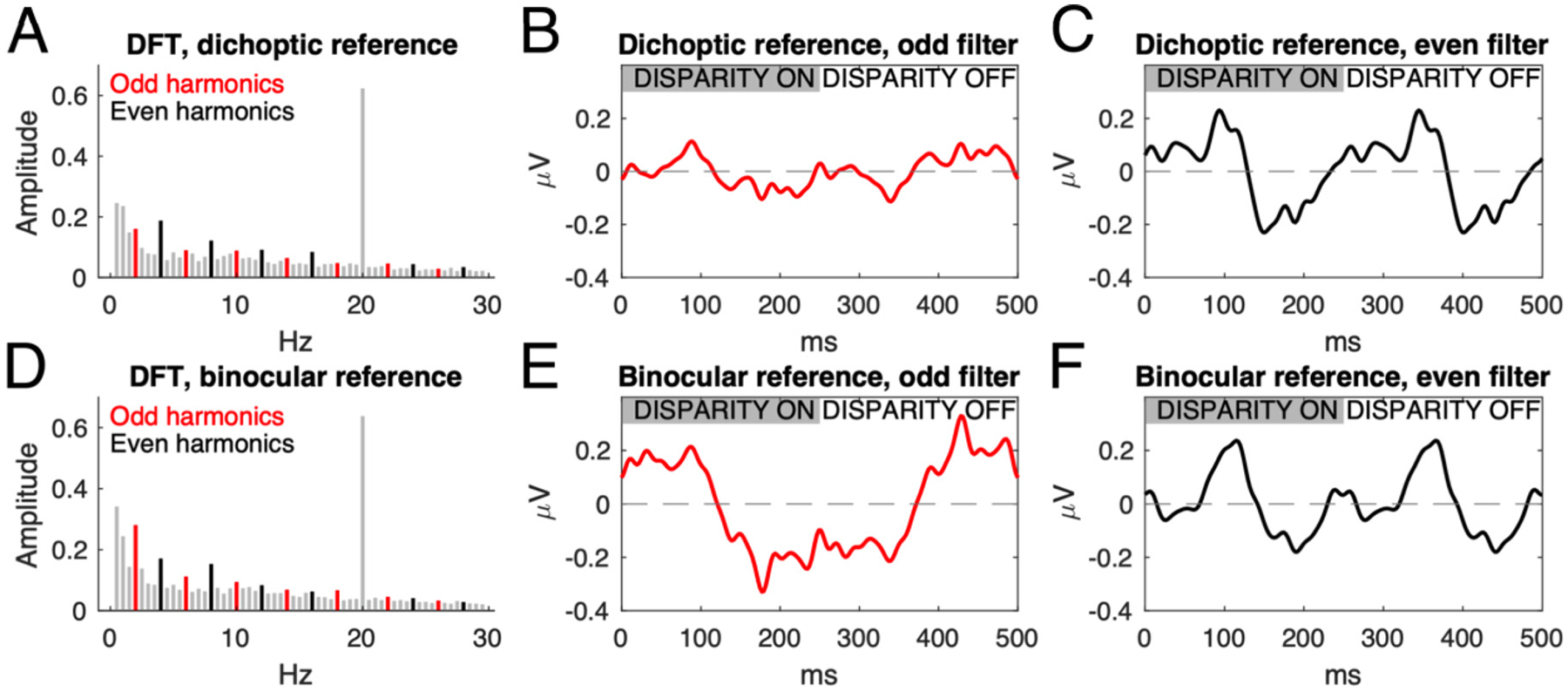
Fourier transform-based filtering approaches reveal the sustained and transient response components of the SSVEP. Participants viewed a disparity plane alternating between crossed disparity (first 150 ms, indicated by grey bar in middle and right columns) and zero disparity. Fixation was encouraged using nonius lines (dichoptic reference, no relative disparity signals) or an X-O task at fixation (binocular reference, inducing relative disparity cues). Filtering on the odd (in red, panels B and E) or even (in black, panels C and F) harmonics reveals sustained (panel E) and transient (panels C and F) response components in the reconstructed waveforms. Gray bars in the discrete Fourier transforms (panels A and D) are frequencies that are nulled by the filtering – the large 20 Hz dot update response has also been removed. The introduction of a binocular reference point at fixation results in a sustained negative-going potential, shifted ~120 ms relative to stimulus onset, that is revealed by the odd filter (panel E), which is absent in the dichoptic reference condition (panel B) where only nonius lines are present. Both conditions have transient response components revealed by the even filter (panels C and F). Data are group-level averages of single-cycle responses across all trials, for a cluster of midline occipital electrodes.

Reconstructing the response waveform from only the odd-harmonics yields a very small response in the dichoptic reference condition (Fig. 3 B), but a much larger, nearly square-wave response in the binocular foveal reference condition (Fig. 3 E). The nearly square-wave waveform indicates a sustained response is present in the odd harmonics. Reconstructing the response from the dichoptic reference condition using only the even harmonics (2F1, 4F1, 6F1 and so on) yields a brief, biphasic response after both onset and offset of the stimulus for both fixation conditions (Fig. 3, C and F), consistent with transient processing. In practice, odd and even harmonic responses above the 1^st and 2^nd harmonics are small and difficult to measure over a wide range of stimulus conditions, so in the remainder we focus on 1F1 and 2F1 as correlates of sustained and transient activity.

3.3. 1F1 response is tuned for corrugation frequency and mirrors perception

If the sustained 1F1 response is an indicator of relative disparity processing, it should be tuned for corrugation frequency. In particular, the response to disparity gratings should differ from responses to a disparity plane. In our main experiment, we thus measured evoked responses while sweeping the amplitude of disparity-defined gratings that varied in their corrugation frequency. Because the stimulus modulated between zero disparity and crossed disparity, evoked responses locked to changing disparity could be generated in two ways: first, from the local change in disparity within a single temporal stimulus cycle (e.g., from changes in local, absolute disparity) or secondly, from the change from a flat plane at fixation, to a corrugated surface in depth (relative disparity).

The magnitude of the 1F1 response was found to increase with the disparity amplitude. We analysed this sweep response in the most reliable component (RC1). Sweep responses for all stimulus conditions are overlaid on the same axis in Fig. 4, panel A. The lateral shift in the responses along the x-axis implies that sensitivity to disparity changes as a function of corrugation frequency. Note that the conditions with the earliest, and largest, responses above the noise floor lie in the mid-ranges of the corrugation frequencies we tested. Least sensitive are the responses to very high or very low corrugation frequencies. The weakest response was to the 0 cpd, plane stimulus, where the signal emerged from the noise only late in the sweep and the response was more than a factor of three weaker as compared to more sensitive conditions.

Fig. 4.

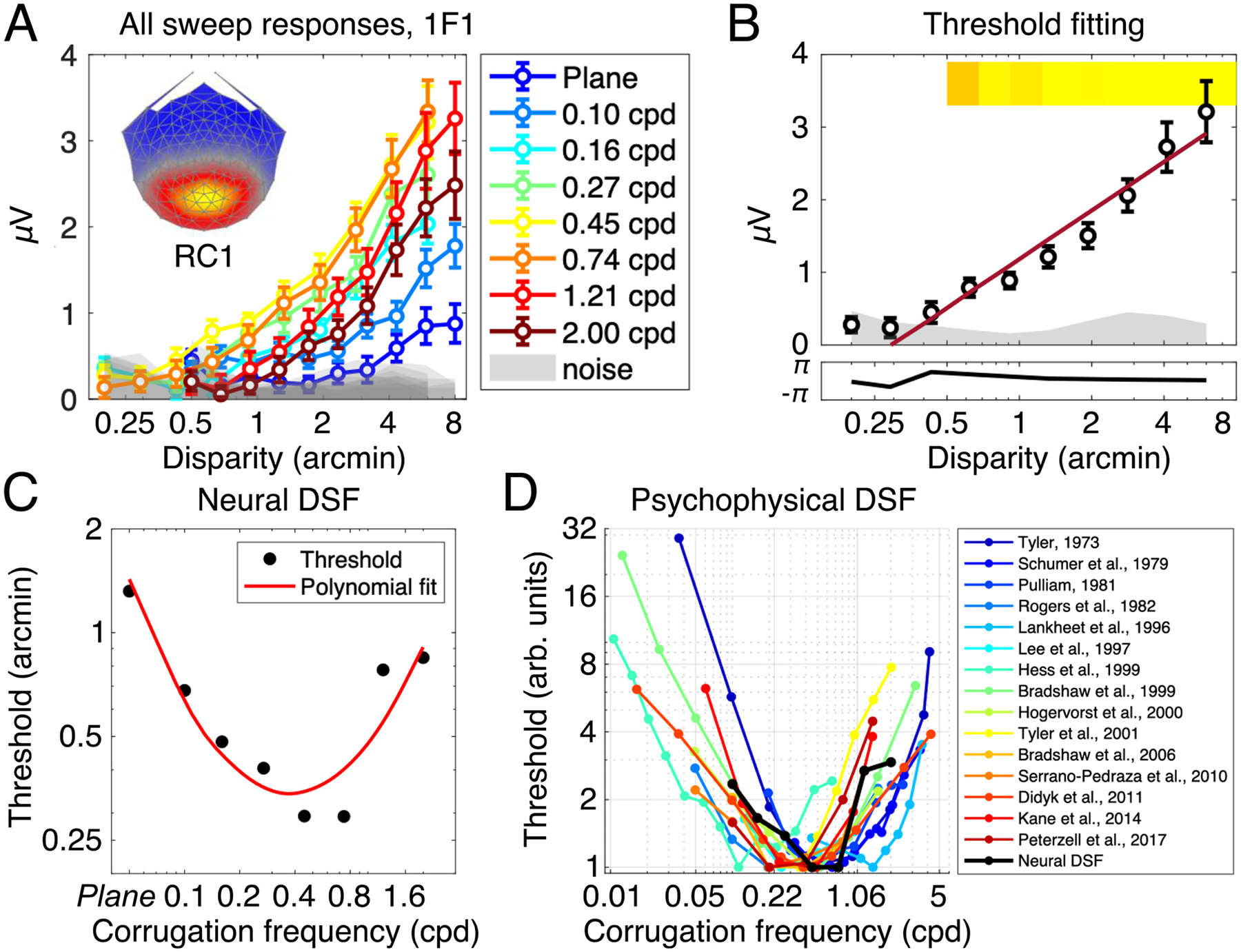
Results from the 1F1 response in RC1 showing dependence on corrugation frequency. Panel A shows all sweep responses, plotted as the amplitude of the 1F1 response against the peak-to-trough disparity amplitude of the grating. Different colours denote different corrugation frequency conditions, and all error bars are ± 1SEM. The shaded area is the mean noise amplitude in the frequency side bands, for each condition. Weightings for RC1 at each electrode are shown in the topographical map insert. Panel B shows an example of the neural threshold estimation, here, data from the 0.45 cpd condition are shown. A linear trend (in red) is fit against bins that fulfil a set of criteria (see Methods for more details). The intersection of the linear trend with the x-axis is taken as the estimated neural threshold. Thresholds for each condition are plotted in Panel C and demonstrate U-shaped corrugation frequency sensitivity. The corrugation tuning in C is consistent with previous psychophysical measurements of the disparity sensitivity function, shown in Panel D (y-axis is normalised, with the best threshold measured for each study being set to 1. ‘Plane’ condition in Neural DSF data omitted for consistency on the x-axis).

Because the magnitude of the disparity amplitude increases monotonically and is approximately linear, it is possible to estimate a neural threshold by regression to zero amplitude of the disparity response function (Norcia et al., 1985a). The value at which the linear function crosses the x-axis is taken as the neural threshold and is indicative of the smallest disparity required to elicit a neural response. An example of this process is illustrated in Fig. 4, panel B.

We extracted neural thresholds for all corrugation frequency conditions and found that they form a U-shaped function of corrugation frequency tuning (Fig. 5, panel C; for a non-normalised version of this plot, see Fig. S1, Supplementary Materials). In both our measurements and previous psychophysical ones (Fig. 5, panel D), disparity sensitivity is maximal between ~ 0.5 and 0.75 cpd. In the limiting case (0 cpd plane condition), the threshold we measure is on the ~ 4 times higher than at peak sensitivity. Our monitor resolution and rendering capabilities limited the maximum usable corrugation frequency to 2 cpd where the threshold (0.85 arcmin) was ~ 3 times higher than that measured at peak sensitivity.

Taken together, these results demonstrate that the sustained, 1F1 response is strongly tuned for corrugation frequency. Our measurement can reproduce the psychophysical Disparity Sensitivity Function, linking our direct neural readout to behaviour and implying that the 1F1 response is associated with the perception of relative disparities.

3.4. 2F1 is untuned for corrugation frequency

By contrast, transient, biphasic responses illustrated in the “even” filter in Fig. 3 are dominated by the 2F1 component, which is a response that is the same at the onset and the offset of the change in disparity, irrespective the direction of the disparity change. All 2F1 sweep responses in RC1 are plotted in Fig. 5, Panel A. We measured reliable sweep responses in all conditions, however, as opposed to the 1F1 responses, many of these overlapped across different corrugation frequency conditions. Notably, the response to the plane stimulus was the largest by about a factor of 2, where for the 1F1 response it was the weakest. Thus, we observe little evidence for corrugation frequency tuning in the 2F1 responses, and we note its response to the plane stimulus is particularly robust.

We also estimated 2F1 neural thresholds in RC1 for each corrugation frequency condition using the same method as for the 1F1 responses. Results are plotted in Fig. 5, Panel B. The 2F1 response did not show the same systematic tuning to corrugation frequency as the 1F1 response, where thresholds followed the U-shaped function of the DSF. Instead, the estimated 2F1 thresholds are irregularly scattered between 0.4 and 1.7 arcmin, indicating little tuning to corrugation frequency.

The extracted threshold for the 2F1 plane condition was ~2 times lower than for the simultaneously recorded 1F1 response in the same condition (0.70 vs. 1.32, respectively) and a factor of ~ 2.5 times higher than the best grating condition threshold at 1F1 (0.29 arcmin). Whilst the 2F1 response in RC1 is not particularly sensitive to corrugation frequency – and therefore to relative disparity – it does appear to be a stronger readout for the absolute disparity mechanism.

Together, these findings indicate that the transient, 2F1 disparity response is insensitive to disparity and to the spatial structure of disparity in the stimulus, as would be the case if it were driven by absolute disparity detectors that are sensitive to mean changes in disparity. In line with this, the response to the plane condition is strongest.

3.5. Corrugation tuning at suprathreshold: 1F1

Another way to reveal the corrugation tuning of disparity mechanisms is to examine suprathreshold responses at different levels of disparity. To do this, we extract the response amplitude at 2 and 6 arcmin, and plot results as a function of corrugation frequency in Fig. 6, where results for the 1F1 response is shown in Panel A.

Fig. 6.

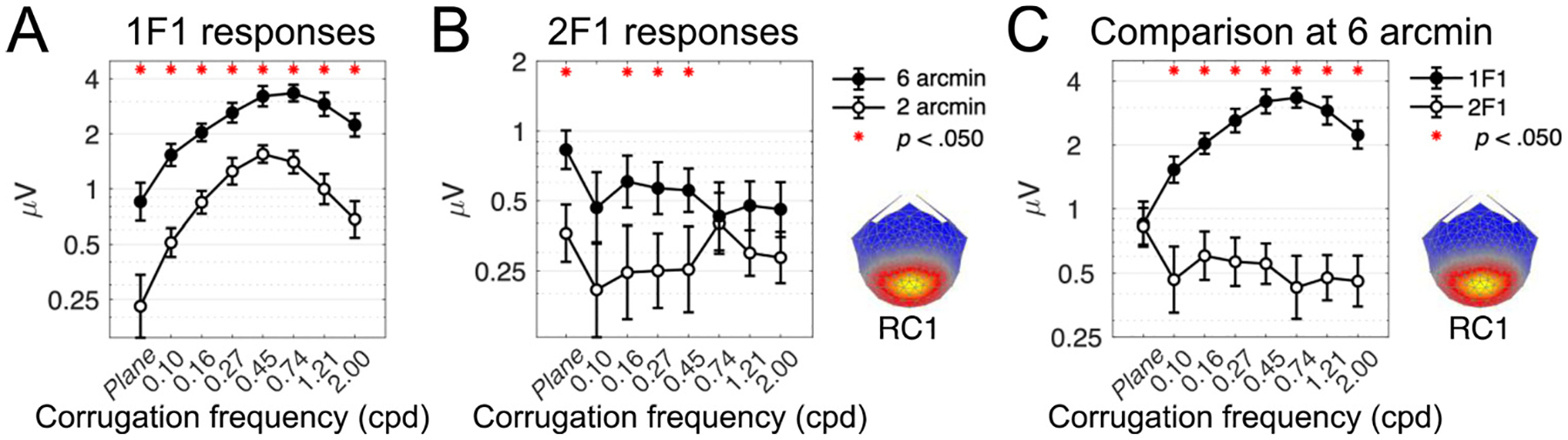
Suprathreshold response amplitudes for 1F1 and 2F1 in RC1. Panels A and B show tuning functions measured at 2 and 6 arcmin of disparity, for 1F1 and 2F1, respectively. Overlaying the 1F1 and 2F1 responses on the same axes in panel C clearly reveals their differences in tuning, where 1F1 is highly sensitive to the spatial structure of the stimulus. 2F1 is untuned and responses are similar across all corrugation frequencies, except for at 0 cpd (plane stimulus) where the response is higher and matches the 1F1 response. Red asterisks in each panel mark pairwise comparisons at each corrugation frequency where amplitudes are significantly different (Bonferroni corrected for multiple comparisons). Error bars are ± 1 SEM and the y-axes are log-scaled.

Qualitatively, suprathreshold tuning mimics the tuning observed at threshold at both levels of disparity, though the shapes of the functions are inverted. The largest responses are evoked by the 0.45 and 0.74 corrugation frequencies. We asked whether the tuning is identical across different disparity levels and compared the 2 arcmin and 6 arcmin functions using a repeated measures ANOVA testing for main effects of disparity level and corrugation frequency. The majority of the variance was captured by the main effect of disparity level (F (1, 24) = 63.59, p <. 001, generalised effect size (η²_G) = 0.23) where the mean amplitude of the responses at 6 arcmin was significantly larger than the mean amplitude at 2 arcmin. The main effect of corrugation frequency was also highly significant F (2.57, 61.61) = 17.93, p <. 001, η²_G = 0.18, with Greenhouse-Geisser correction), indicating that the amplitude of the 1F1 response component was dependent on the corrugation frequency of the DRDS stimulus.

The interaction between disparity level and corrugation frequency was significant (F (3.93, 94.29) = 6.16, p <. 001, η²_G = 0.03, with Greenhouse-Geisser correction), which would indicate differences between the tuning functions and 2 and 6 arcmin. This is driven by the slight shift in the peak of the function as well as the more exaggerated U-shape at 2 arcmin, where the amplitude of the response increased almost seven-fold (as opposed to four-fold at 6 arcmin) from 0 cpd to the peak of the function. However, we think it unlikely that the neural sources of the 1F1 response are different at these two disparity levels, as the two functions are highly correlated (R(14) = .94, p <. 001) and the effect size of the interaction is small.

3.6. Lack of corrugation tuning at suprathreshold: 2F1

The same analysis was carried out for the 2F1 responses, which showed no evidence of corrugation frequency tuning at threshold. Results are plotted in Fig. 6, panel B. Again, the amplitude of the response to the 0 cpd plane stimulus is large compared to all other corrugation frequencies.

Similar to the 1F1 response, there was a main effect of disparity level though the effect size was modest (F (1, 24) = 11.04, p = .003, η²_G = 0.04) showing that the amplitude of the 2F1 signal scales with disparity. Pairwise comparisons revealed that the amplitude of the response at 6 arcmin was greater than at 4 arcmin at 0 cpd, 0.16 cpd, 0.27 cpd and 0.45 cpd, but nowhere else (adjusted p = .003, .004, .007 and .017, respectively, Bonferroni corrected for multiple comparisons). The lack of significant differences at the high corrugation frequencies implies weaker scaling with disparity here.

Replicating the patterns observed in the sweep functions and neural thresholds, there was no effect of corrugation frequency (F (7, 168) = 1.40, p = .210, η²_G = 0.01). This lack of corrugation tuning at 2F1 reflects a deviation from the responses measured at 1F1, and implies that the neural mechanisms and their functional significance are different. The interaction between disparity level and corrugation frequency was also nonsignificant, indicating that the lack of tuning was consistent across both disparity levels (F (3.93, 94.29) = 6.16, p <. 001, η²_G = 0.01).

Together, the suprathreshold tuning functions measured at 2F1 replicate the patterns seen in the neural threshold data, showing an insensitivity to the corrugation frequency of the stimulus. The response for the plane stimulus was elevated.

3.7. Comparisons between 1F1 and 2F1 at suprathreshold

To compare across our two harmonics of interest, we draw on the greater signal to noise ratio in responses extracted at 6 arcmin disparity. At this disparity amplitude, both 1F1 and 2F1 signals are significantly above the noise floor. Suprathreshold responses as a function of corrugation frequency are plotted in Fig. 6, panel C.

The suprathreshold 1F1 response is U-shaped, mirroring the disparity tuning function extracted via neural thresholds. In contrast, the 2F1 response is flat across all corrugation frequencies. A notable exception is the response to the plane stimulus, which is ~ 2 x larger than the other 2F1 responses and reaches a similar amplitude to the 1F1 response, which overall has a higher SNR.

We used a two-way repeated measures ANOVA to quantify the effects of harmonic and corrugation frequency on suprathreshold response amplitudes, and measured a significant main effect of harmonic (F (1, 24) = 78.65, p <. 001, generalised effect size (η²_G) = 0.34) and a smaller significant effect of corrugation frequency (F (2.61, 62.57) = 11.80, p <. 001, η²_G = 0.08, with Greenhouse-Geisser correction for sphericity as assessed by Mauchly’s test (W = 0.01, p <. 001)).

The most telling result was the interaction between harmonic and corrugation frequency, which was significant (F (2.74, 65.70) = 16.65, p <. 001, η²_G = 0.11, with Greenhouse-Geisser correction for sphericity as assessed by Mauchly’s test (W = 0.02, p <. 001)). This implies that the tuning functions are different between 1F1 and 2F1, where 1F1 shows a dependence on corrugation frequency whereas the 2F1 response does not.

Furthermore, pairwise comparisons showed that the 1F1 response amplitude was greater than the 2F1 response amplitude at all corrugation frequencies except 0 cpd, after Bonferroni correction for multiple comparisons (adjusted p values were. 932, and <. 001 for absolute disparity and all other corrugation frequencies). This echoes the observation that the 2F1 response to the plane stimulus is particularly large.

4. Discussion

Here we show using the SSVEP, that human disparity processing is subserved by multiple mechanisms differing in their corrugation frequency tuning, response dynamics, and cortical distribution. We used harmonic analysis of the evoked response to gain access to underlying temporal channel dynamics without depending on ‘transient’ or ‘sustained’ stimulus presentation profiles. Our results suggest links between harmonics of the evoked response and relative disparity processing via sustained mechanisms (e.g. 1F responses) versus the processing of absolute disparity information by mechanisms with dominantly transient response dynamics (e.g 2F responses). Reliable Components Analysis suggests the identified spatio-temporal disparity channels have different cortical distributions, given the observed component topographies.

4.1. Relative disparity mechanisms drive the 1F1 response

Behaviourally, stereopsis is strongly dependent on the presence of references in the visual field and is optimal for a certain range of corrugation frequencies. We find that that the first harmonic of the changing disparity SSVEP shares these features at electrodes over early visual cortex (RC1). Adding binocular disparity information to a small fixation target amplified the first harmonic in our control experiment, both increasing the evoked response and lowering the threshold. This is reminiscent of the classic effects of adding references to stereograms, which results in an improvement in perceptual depth sensitivity (Andrews et al., 2001; Kumar and Glaser, 1991; McKee et al., 1990; Westheimer, 1979).

The first harmonic response was also strongly tuned for corrugation frequency at both threshold and suprathreshold levels. Psychophysical disparity sensitivity also varies as a function of corrugation frequency as illustrated by the wide range of studies shown in Fig. 4, panel D. Our neural data closely match the shape of the behavioural Disparity Sensitivity Function. The neural thresholds we measure are in the hyper-acuity range (Westheimer, 1979), being well under 0.5 arcmin under optimal conditions (0.29 arcmin at 0.45 and 0.74 cpd). Perceptual thresholds measured across behavioural studies vary between around 0.05 arcmin (Bradshaw and Rogers, 1999) and 0.5 arcmin (Pulliam, 1982) at the minimum of each DSF (see Fig. S1, Supplementary Materials). The smallest neural threshold we measure sits within this range at 0.29 arcmin, suggesting that our measurements at 1F1 can be used as a proxy for behavioural thresholds (Kohler et al., 2018; Norcia and Tyler, 1985). Given these results, SSVEP threshold estimation provides a means for linking behavioural phenomena with neural dynamics.

4.2. Absolute disparity mechanisms and the 2F1 response

The evoked response also contains activity at the second harmonic. Here, we find that the dependence of the second harmonic on references and corrugation frequency is less prominent than at the first harmonic – 2F1 threshold-level amplitudes were unaffected by the availability of binocular disparity at the fixation target and 2F corrugation tuning was flat. These features imply that the 2F1 response is driven by an absolute disparity signal, which is by its nature insensitive to the spatial structure of the stimulus.

Regarding the lack of corrugation tuning of the 2F response, prior work has shown that the mean response of disparity-tuned cells in V1 of macaque is independent of corrugation frequency, as is the output of the binocular energy model of disparity tuning (Bredfeldt et al., 2009; Nienborg et al., 2004). Our stimuli, whose mean disparity is modulated between zero and non-zero values may thus modulate the population response via changes in the summed activity of cells sensitive to absolute disparity whose mean level of activity is changing. By contrast, the modulated component of the same V1 disparity tuned cells recorded by Nienborg et al., is strongly dependent on corrugation frequency. It is possible that the tuning of the 1F response inherits this limitation, as has been suggested for perception (Banks et al., 2004). This would presumably happen at a later stage of disparity processing, beginning in V2 and V3 where relative disparity tuning emerges.

Also consistent with 2F1 receiving a dominant contribution from cells tuned for absolute disparity is our observation that 2F1 amplitude was largest for the 0 cpd, plane condition in the corrugation frequency tuning experiment. During the plane condition, every dot pair in the DRDS was at the same disparity during the disparate portion of the stimulus cycle. In the grating condition however, the disparity amplitude varied across the field of view and thus the average disparity was only at one-half the disparity amplitude as compared to the plane condition. The boost in response amplitude during the plane condition thus suggests that 2F1 is being driven by the local mean disparity, as would be the case if it were dominated by a contribution from cells’ responses to absolute disparity. The binocular energy model of disparity processing exhibits the same behaviour (Bredfeldt et al., 2009; Nienborg et al., 2004), where the response is driven by the weighted mean of the disparities within the receptive field (Bredfeldt et al., 2009).

A well-known feature of the perception of absolute disparity is that observers are several orders of magnitude less sensitive to it than to relative disparity (Andrews et al., 2001; Kumar and Glaser, 1991; McKee et al., 1990; Westheimer, 1979). The estimated thresholds we extract, from both grating and plane stimuli, follow this pattern and provide additional evidence that the 2F1 response indexes absolute disparity mechanisms. Generally, estimated neural thresholds for our disparity grating stimuli were higher at 2F1 than at 1F1 and did not vary systematically with the corrugation frequency. Importantly, the 2F1 plane stimulus threshold was ~2.5 times higher than the best grating stimulus thresholds measured at 1F1, consistent with psychophysics. Our threshold estimates therefore illustrate an overall lower sensitivity to absolute disparity that is manifest in the 2F1 response – a response pattern that can be extracted whether the driving stimulus is purely absolute or also contains relative disparities.

We find a small, but measurable 1F response to the plane condition in the dichoptic nonius fixation condition. This condition was designed to minimize the availability of relative disparity information, but this may not have been fully successful, leading to a weakened but not absent relative disparity response. Alternatively, this response could arise from asymmetries in the population response to absolute disparity for the direction of disparity change.

It should be noted that our stereograms were comprised of relatively small dots and small disparities. The relative weighting of first and second harmonic responses in our system might be shifted by varying scale of the monocular half-images, or the disparity amplitude. Experiments with a larger sweep range extending into coarse disparity mechanisms could confirm whether this is the case.

4.3. Sustained and transient mechanisms in stereopsis

The relationship between sustained mechanisms and relative disparity has repeatedly been shown in psychophysical data, where longer stimulus durations result in lower depth detection thresholds (Harwerth and Rawlings, 1977; Ogle and Weil, 1958; Westheimer and Pettet, 1990). Manipulations of the contrast corrugation frequency content of disparity stimuli have linked relative disparity processing with sustained activity in the parvocellular pathway (Edwards et al., 1998; Gheorghiu and Erkelens, 2005; Kontsevich and Tyler, 2000; Lee et al., 2007; Schor et al., 1984).

Transient disparity mechanisms have been implicated by studies of vergence eye movements (Jones, 1980; Mitchell, 1970) where non-fusable disparate target can initiate brief, directionally appropriate vergence (Erkelens and Collewijn, 1985a, 1985b; Jones, 1980). Consistent with this, depth sensations can be conveyed by very brief presentations of anticorrelated stimuli (Edwards et al., 1998; Pope et al., 1999; Schor et al., 1998), implicating a transient disparity system using correlation-based computations that do not depend on binocular feature matching (Doi et al., 2013). Behavioural lines of evidence thus dove-tail with our results, implying a division of labour between a transient, absolute disparity channel, and a sustained, relative disparity channel. The apparent sensitivity of the 2F response to changes in mean disparity makes this signal a possible substrate for vergence eye-movement control, in that it would provide an input that tracks changes in mean disparity.

The temporal dynamics of disparity tuned cells in V1 of macaque, by contrast, have been modelled by a single channel model comprising a bandpass linear monocular temporal kernel, followed by a rectifying non-linear binocular energy computation (Nienborg et al., 2005). This energy computation renders the temporal kernel of the disparity response monophasic and thus temporally low-pass, with the implication being that the response to disparity should have a lower high temporal frequency cut-off than the monocular kernel. This was observed in both single cells and their human psychophysical observers (see also Beverley and Regan 1974, Gray and Regan 1996, Norcia and Tyler 1984 Regan and Beverley 1973, Richards 1972).

A second implication of the Nienborg et al. model is that sensitivity to low temporal frequency disparity modulations should not fall off relative to moderate temporal frequencies. However, in three of four of their human observers, sensitivity was lower at 0.5 Hz than at 1–1.5 Hz, consistent with previous studies (Gray and Regan, 1996; Lages et al., 2003; Richards, 1972; Tyler, 1971). Nienborg et al.’s cellular measurements did not extend to 0.5 Hz, so the model prediction was not fully tested on the low-frequency range. Their model raises the question where the transient disparity responses measured in the oculomotor and behavioural literatures, and observed in own our VEP data, are purported to arise.

In our system, these predictions could be tested by measuring the temporal frequency tuning of the first and second harmonic response components. If the first harmonic reflects sustained processes, it should exhibit little low temporal frequency roll-off. Conversely, if the second harmonic response reflects a transient mechanism, its temporal tuning should be bandpass. The presence or absence of disparity references should also determine which component dominates.

4.4. Purpose of duplex coding strategies in the disparity domain

Integration over long periods of time, say to increase acuity by averaging over noisy inputs, precludes detection of rapid changes that occur over shorter timescales. Sensory systems may solve this resolution/integration paradox through duplex coding systems that involve both transient and sustained mechanisms (Abraira and Ginty, 2013; Ikeda and Wright, 1972; Shiramatsu et al., 2016). In the visual system, transient and sustained channels originate in outputs of retinal ganglion cells (Cleland et al., 1971; Fukuda, 1971; Ikeda and Wright, 1972) that are segregated in the LGN and the input layers of V1, but converge there-after (Nassi and Callaway, 2009).

These channels have been associated with distinct functional roles. As part of the magnocellular pathway, cells with transient response profiles support fixation and orientation behaviours, whilst cells with sustained response profiles in the parvocellular pathway support accurate registration of corrugation characteristics of the stimulus (Kaplan and Benardete, 2001; Lee, 2011; Van Essen and Gallant, 1994). In our experiments, the outputs of these channels do not vary over the stimulus conditions we employ because all of our monocular half-images are of identical spatiotemporal content. Despite this, we observe frequency domain responses originating purely from binocular signals that are consistent with transient and sustained temporal integration. Thus, a duplex coding strategy is recapitulated in the disparity domain itself, rather than being simply inherited from the monocular inputs.

4.5. Topography of disparity responses

The approximate localisation of the disparity signals we measure can be inferred from the topographies provided by Reliable Components Analysis. The midline occipital RC1 source is likely driven by signals in early visual areas including V1, V2 and V3, which contain cells tuned for absolute and/or relative disparity (Anzai et al., 2011; Cumming and Parker, 1999; Thomas et al., 2002). The proximity of V3B and its substantive contribution to form-from-disparity mechanisms (Kohler et al., 2019) is also likely to contribute to RC1. We also measured disparity responses in a secondary, right-lateralised response component. In RC2, data followed roughly the same pattern as in RC1 and results are presented in the supplement. Thus, disparity responses are by no means limited to early visual areas – transient and sustained response components can also be measured in extrastriate cortex (Norcia et al., 2017).

Conclusions

Our data suggest a duplex coding strategy for disparity in which a sustained channel processes the corrugation structure of the depth map, coupled with a transient channel in early visual cortex processing local, absolute disparity.

Data and code availability

Data and code used in the analyses will be made freely available on the Open Science Framework.