Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 May 11;9(6):1926–1935. doi: 10.1021/acsphotonics.1c01651

Numerical Optimization of a Nanophotonic Cavity by Machine Learning for Near-Unity Photon Indistinguishability at Room Temperature

J Guimbao †,*, L Sanchis †, L Weituschat †, J Manuel Llorens †,*, M Song ‡, J Cardenas ‡, P Aitor Postigo †,‡
PMCID: PMC9205277  PMID: 35726240

Abstract

graphic file with name ph1c01651_0006.jpg

Room-temperature (RT), on-chip deterministic generation of indistinguishable photons coupled to photonic integrated circuits is key for quantum photonic applications. Nevertheless, high indistinguishability (I) at RT is difficult to obtain due to the intrinsic dephasing of most deterministic single-photon sources (SPS). Here, we present a numerical demonstration of the design and optimization of a hybrid slot-Bragg nanophotonic cavity that achieves a theoretical near-unity I and a high coupling efficiency (β) at RT for a variety of single-photon emitters. Our numerical simulations predict modal volumes in the order of 10–3(λ/2n)3, allowing for strong coupling of quantum photonic emitters that can be heterogeneously integrated. We show that high I and β should be possible by fine-tuning the quality factor (Q) depending on the intrinsic properties of the single-photon emitter. Furthermore, we perform a machine learning optimization based on the combination of a deep neural network and a genetic algorithm (GA) to further decrease the modal volume by almost 3 times while relaxing the tight dimensions of the slot width required for strong coupling. The optimized device has a slot width of 20 nm. The design requires fabrication resolution in the limit of the current state-of-the-art technology. Also, the condition for high I and β requires a positioning accuracy of the quantum emitter at the nanometer level. Although the proposal is not a scalable technology, it can be suitable for experimental demonstration of single-photon operation.

Keywords: single-photon, neural network, genetic algorithm, nanophotonics, nanocavity

Introduction

Indistinguishable single photons are the leading candidates for quantum communication and quantum information processing technologies. They play a central role in a range of proposed schemes, including quantum simulation,1 quantum walks,2 boson sampling,3 quantum teleportation,4 and quantum networks.5 However, the complex mesoscopic environment of solid-state sources entails fundamental barriers that restrict the operation to cryogenic temperature (T).6 Trying to overcome the thermal restrictions of quantum devices remains a challenge for the development of on-chip, on-demand single-photon sources (SPS). A feasible approach for achieving efficient indistinguishable photon emission from a solid-state emitter consists of maximizing the emitter–field coupling (g) through the effective confinement of light in an ultrasmall cavity-mode volume (Veff) and reaching the strong coupling regime.7 In this regime, the transfer rate between the emitter and the cavity field exceeds the dephasing rate of the emitter, and the emitted photons are able to leave the cavity before being affected by decoherence.7 Plasmonic cavities with subnanometer gaps between dimers like Au spheres,8 Ag nanowires,9 and surface plasmon-polariton systems10 or metallic bowties with CdSe/ZnS quantum dots11 produce the highest g value up to 200 meV11 and the lowest quality factors (Q ∼ 10).9 There are different proposals to improve Q and β in these systems, some of them involving dielectric-core/metal-shell schemes for Q(10,12) or hybrid FP-nanoantenna cavities for β.13,14 However, using plasmonic cavities faces two obstacles:15 (i) the placement of the emitter in the point with the strongest cavity field can be challenging and (ii) ohmic and quenching losses can be very high. The use of dielectric cavities can avoid the latter limitation, and strong coupling can happen using strategies to decrease the modal volume, like slotted photonic crystals. Discrete slotted nanobeams16,17 lead to volumes in the order of 10–3(λ/2n)3 while keeping high Q. However, because introducing a finite slot causes a large perturbation to the optical mode, β values remain low. Continuous-slot designs improve β and Q,18 and more recently, slot–antislot concatenations in 1D-PC19,20 have shown record Q/Veff ratios with PC cavities. Also, designs based on cascaded cavities schemes have shown promising results with dielectric structures.21 According to those works, a slotted dielectric cavity can provide a sufficient small modal volume for strong coupling, thus a high I, avoiding at the same time the losses inherent to plasmonic cavities. However, for highly dissipative emitters, the dependence of I with g at RT is highly nontrivial.7 With high g, there is a high population transfer rate between the emitter and the cavity field, so the emitted photons must leave the cavity before getting dephased by the emitter. This can be accomplished by setting the right Q. As we will show, this trade-off between different rates (i.e., dephasing rate, g, and Q) translates into a complex dependence of I with the cavity figures of merit.

In this work, we show that achieving a high I at RT requires tuning of Q together with a small modal volume. That does not translate to a high Q but a specific Q threshold depending on the emitter’s intrinsic properties and the modal volume. From our calculations, none of the previously mentioned dielectric cavities can provide a high I for strong dissipative emitters despite achieving small modal volumes. Furthermore, the implementation of machine learning algorithms for the geometrical optimization of the cavity modal volume and Q has shown promising results in recent works.22−25 Here, we present a numerical demonstration of a design strategy for high indistinguishable SPS at RT strongly coupled to a hybrid slot-Bragg waveguide cavity. We vary the geometrical parameters of the waveguide cavity (i.e., the waveguide width, slot width, number of periods), and we obtain a theoretical estimation of the cavity performance for I, β, and the Purcell enhancement. We explore different types of promising SPS (InGaAs26 and GaAs27 quantum dots, single molecules,28 localized excitons in transition metal dichalcogenides transition-metal dichalcogenide (TMDC) monolayers,29 and diamond color centers30), and we obtain theoretical near-unity I and high β simultaneously by parameter optimization. Finally, we develop a hybrid deep neural network-genetic algorithm (GA) scheme that further reduces the modal volume for achieving near-unity I with a slot width of 20 nm. The optimized device presents strong challenges for current fabrication and quantum emitter (QE) positioning techniques. In this regard, we have developed a comparison of the design requirements with the state-of-the-art demonstrations.

Methods

We can compute the value of I for a QE with radiative decay rate γ and pure dephasing rate γ* coupled to a photonic cavity (with decay rate κ and electromagnetic coupling constant g) from the Lindblad equation and applying the quantum nonregression theorem. For each (g, κ, γ, γ*), we have:7

graphic file with name ph1c01651_m001.jpg 1

where ↠and â are the creation and annihilation operators of the cavity mode, respectively. Details of the calculation can be found in the Supporting Information. The values of g and κ are linked to Q and Veff by κ ∼ 1/Q and g ∼ 1/√Veff.

Figure 1e shows the value of I for photons emitted by a high dissipative QE with γ* = 104 γ as a function of g and κ normalized to γ in the coherent strong-coupling regime (i.e., g > γ* + γ). In this regime, the rate of photon transfer from the emitter to the cavity is R = 4g2/κ,7 which exceeds the pure dephasing rate (R > γ*) for certain values of κ. For a high I, the photon must escape out of the cavity before the emitter dephases it. In other words, κ > γ*, which means that a small Q is needed. Specifically, for a QE with γ* = 104γ, one needs a value of κ/γ above 2 × 104 for I > 0.9. The region of high I in Figure 1e has a shape and area that depend on T through γ*. For a QE at RT, γ*∼ 104 γ7 and the minimum value of g/γ to achieve I > 0.9 is (g/γ)min ∼ 104. As γ*/γ decreases, the area of high I grows and (g/γ)min decreases.

Figure 1.

Figure 1

Open in a new tab

(a) |E|2 field profile in the y–z plane. (b) Variation of the ratio (g/γ)min with T for I > 0.9 and different SPS: GaAs (red), S.molecules (green), two-dimensional (2D) materials (blue), InAs (yellow). (c) |E|2 field profile of the cavity mode in the x–y plane. (d) Layout of the proposed structure, where ωh is the width of each waveguide, ωs is the slot width, L is the cavity length, and Λ is the grating period. (e) Color map of I as a function of g/γ and κ/γ for photons emitted by a high dissipative QE with γ* = 104γ. (f) SEM image of the center of the cavity. (g) Contour map of regions with I > 0.9 for different dephasing values (γ* = 20γ, 50γ, 80γ, 102γ, 2 × 102γ, 4 × 102γ, 8 × 102γ, 103γ, 5 × 103γ, and 104γ). (h) Transmission spectrum of the structure for a different number of periods, the full width at half maximum (FWHM) of the resonance scales exponentially with #p. (i) Q versus number of periods.

Figure 1g shows the contour maps of the region with a high I (I > 0.9) as γ* changes. For moderate dissipative emitters (γ* ∼ 102 γ), the minimum g/γ necessary for I > 0.9 is (g/γ)min = 1 03. As γ* increases (g/γ)min grows monotonously, reaching 104 for γ* ∼ 104 γ. Similarly, the minimum (κ/γ)min increases from 103 for γ* ∼ 102, to 2 × 104 for γ* ∼ 104 γ. We can use this color map to plot the cavities mentioned before, according to its performance for I. Plasmonic cavities8−10 can achieve I > 0.9 even for high dissipative emitters with γ* ∼ 104 γ. On the other hand, slotted dielectric cavities16−18 can achieve I > 0.9 for emitters with γ* between ∼102 to ∼2 × 102 γ and slot–antislot concatenations in 1D-PC19 for emitters with γ* ∼ 2 × 102 γ to γ* ∼ 4 × 102 γ. The cavity shown in ref (20) is the only one, in the group of dielectric structures, that can reach I > 0.9 when γ* > 2 × 103 γ. According to our calculations, those dielectric cavities can potentially achieve the region with I > 0.9 for high dissipative emitters (i.e., QE at RT) just by increasing its cavity decay rate κ (i.e., deteriorating its quality factor Q). Figure 1b shows the dependence of the value (g/γ)min with T for I > 0.9, calculated for quantum dots of GaAs31 and InAs,32 organic molecules,33,34 and defects in 2D materials.35 The evolution of (g/γ)min with T shows a proportional increase with a different trend that depends on γ*. We can obtain the (g/γ)min needed for I > 0.9 for a QE at a specific T from Figure 1g. It is interesting to observe that for the technologically relevant T of liquid nitrogen (77 K), the same value (g/γ)min = 490 works for InAs and GaAs QDs and 2D materials.

Therefore, our goal is to keep the κ/g ratio inside the region with a high I by increasing g and adjusting Q. Moreover, we look for an on-chip cavity that can be CMOS-compatible with photonic integrated circuits (PICs) used in silicon photonics. Slotted one-dimensional dielectric photonic crystal cavities16−20 have been shown to fulfill most of our requirements in terms of compatibility and small modal volume. Nevertheless, to efficiently control Q, we choose a hybrid slot-Bragg cavity, where Q changes by the number of periods of the Bragg reflector section. Figure 1d shows a layout of our hybrid slot-Bragg photonic cavity aiming to achieve a near-unity I and a high β simultaneously; ωh is the width of each waveguide, ωs is the slot width, and #p is the number of periods. While this structure has been explored for sensing applications,36−38 it has never been proposed for SPS operation, as far as we know, nor its performance is calculated in terms of the figures of merit (I, β). It consists of a phase-shifted corrugated Bragg grating situated at the sides of a Si3N4 (n1 = 2) deposited on top of a SiO2 substrate (n2 = 1.4). The cavity length L corresponds to the central section between the two periodic regions and matches the wavelength of the zero-order Fabry–Perot mode for the target wavelength λ. The Si3N4 thickness (t) is set for optimum field enhancement at the slot for the target λ. Each of the periodic regions behaves like a mirror with an effective reflectivity that depends on the number of periods (#p), creating a Fabry–Perot structure. The grating period Λ matches the central frequency of the photonic bandgap at the target λ. To get information about the physical behavior of the device, we will set first λ = 801 nm to perform a general evaluation of the performance. After that, for each type of emitter, the geometrical parameters of the device (i.e., t, L, and Λ) are set to match the specific emission wavelength λ: (λ, t, L, Λ) = (915, 900, 263, 263 nm) for InGaAs,26 (916, 900, 263, 263 nm) for GaAs,27 (728, 710, 210, 210 nm) for TMDC,28 (785, 770, 225, 225 nm) for S.molecules,29 and (685, 680, 195, 195 nm) for diamond color centers.30Figure 1a shows how the slotted cross section of the cavity enhances the field of the zero-order TE mode in the gap showing an evanescent tail in the top of the waveguide. This field distribution provides advantages related to the coupling of the source when it is heterogeneously integrated on top. The cavity provides strong coupling if the slot width is sufficiently small, and it also provides advantages in extraction efficiency (β) since (i) cavity and output waveguide share the same cross section, so the modes are perfectly matched; (ii) the integration of the QE (for example colloidal QDs) can be done by direct deposition on top of the cavity, which avoids interferences by total internal reflection and enhances β; and (iii) the slot mode has the field maxima at the edges of the slot, which matches well with the region of maximum probability of having SPS in 2D materials deposited on top of waveguides.39 Finally, the cavity modal volumes are in the order of 10–3(λ/2n)3 along with the whole slot, increasing the probability of having one or several QE strongly coupled to the cavity mode. As a proof of concept, we have fabricated a specific design valid for diamond color center requirements. We selected (ωs, #p) = (38 nm, 50) and added vertical grating couplers to the structure to collect the input and output light beams. Figure 1f shows an SEM image of the cavity fabricated by e-beam lithography (EBL) and reactive-ion etching on a layer of 130 nm thick Si3N4 deposited on top of a SiO2 layer (1 μm thick) by plasma-enhanced chemical vapor deposition (PECVD). The obtained slot width is ωs = 54 nm, and the grating period is 204 nm, with less than 5% of the error to the initial design for the grating period and 30% for ωs. According to our simulations, the wider slot translates into a modal volume increase, Veff ∼ 6 × 10–2(λ/2n)3, which slightly reduces the indistinguishability to I = 0.81. This issue can be solved by further optimization by machine learning, as we will show later. We can obtain the transmission spectrum T(λ) shown in Figure 1h and the field profile (Figure 1c) of the cavity mode for a set (ωs, ωh, #p) using a fully vectorial, bidirectional, frequency-domain model for solving Maxwell’s equation (3D-FD).40 We obtain Q from T(λ) by 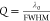Inline graphic and the cavity decay rate from κ = ω/2Q. Details of the model appear in the Supporting Information. There is a different effective index for each set (ωs, ωh, #p), so the values of Λ and L are changed to keep the cavity resonance at 801 nm. The volume of the cavity-mode Veff is41

graphic file with name ph1c01651_m003.jpg 2

The value of g, when the QE is placed at the maximum cavity field and perfectly matches the polarization, is42

graphic file with name ph1c01651_m004.jpg 3

where μeg is the electric dipole moment of the excitonic transition, ω is the frequency of the transition, e is the electron charge, εM is the dielectric constant in the source region, ℏ is the reduced Planck constant, meff is the exciton effective mass, and f is the oscillator strength. Once we have g and κ, we obtain I according to the procedure outlined in Figure 2a. For the computation of the Purcell enhancement (Γp) and the coupling efficiency β, we perform three-dimensional-finite difference time domain (3D-FDTD) simulations40 by placing a dipole point source emitting at 801 nm with position x0, y0 at the center of the slot and z0 4 nm above the top of the waveguides. We obtain Γp by integrating the power P emitted by the source and normalizing it to the power inside a homogeneous environment P0.(43) Finally, we calculate β by measuring the fraction of light coupled to guided modes at the output waveguide. Details of the simulations appear in the Supporting Information.

Figure 2.

Figure 2

Open in a new tab

(a) Outline of the computation algorithm for the calculation of I. (b) Parametrization of the Bragg corrugations for machine learning optimization. Each ωi represents the width of the corresponding Bragg corrugation. (c) Routine for the hybrid NN-GA optimization of the Bragg corrugations.

Our design strategy can be further enhanced using machine learning techniques, especially to keep critical fabrication parameters, like the slot width ωs, experimentally accessible and far from too narrow and unrealistic values. Recently, the optimization of nanophotonic structures by deep learning techniques has been reported.22−25 The two main advantages are: (i) further improved performance beyond the time-consuming method of sweeping the (ωs, ωh, #p) parameters and (ii) we can introduce a vast number of new parameters for the optimization, such as the width of each of the Bragg corrugations, as shown in Figure 2b.

For that purpose, we can use a vector ω = (ω1, ω2, ω3,...,ωn), where each entry ωi with i = 1,...,20 represents the width of each Bragg corrugation. For each configuration ω, we obtain I using the two-step method described in Figure 2c. We use a GA to create a random vector ω and the fitness function obtains I from the 3D-FD simulation (Figure 2a). Through the iteration of crossover and mutation, the GA should find the optimal configuration for maximizing I after a certain number of generations. Details of the code appear in the Supporting Information. However, this procedure faces a critical issue. Typically, in a GA optimization, one needs to generate about 105 pairs (ω, I) and the generation of each pair (ω, I) involves a 3D-FD simulation that may take several minutes, making the whole optimization process unfeasible in terms of time and computational resources. To solve this issue, we take a different approach: (i) we generate 5000 pairs (ω, I) through 3D-FD simulations; (ii) with these data, we train a deep neural network (NN) which learns to estimate the outcome of I for any possible ω. Now we can use the NN to calculate I for the fitness function of the GA optimization. In this way, the calculation of the fitness function for each ω takes just a few seconds; (iii) We perform the GA optimization by calculating the fitness function for each individual of the population through the NN. With this scheme, we reduce by 2 orders of magnitude the number of actual numerical simulations for the dataset from 105 to 103 with the aid of the NN.

Results and Discussion

We first assess the performance of the cavity by sweeping the main geometrical parameters and setting a target λ = 801 nm; t, L, and Λ are set to (t, L, Λ) = (800, 230, 230 nm), respectively. Figure 3 shows how I changes with (ωs, ωh) and #p when γ* = 104 γ (a typical ratio for many QE at RT as we have seen before). Figure 3a shows I versus ωh and ωs for #p = 10 with ωs varying between 10–50 nm and ωh between 150–220 nm (required for single-mode operation). With #p fixed, Q remains constant (Q = 50), while the field profile of the cavity mode varies for each (ωh, ωs). Therefore, the variation of I follows the variation of g with ωh and ωs. As ωs increase, the cavity mode spreads out from the slot and gets confined at each waveguide core separately. That results in an exponential decay of the field intensity in the slot region,44 increasing Veff exponentially with ωs. Since g ∼ 1/√Veff, g decreases, driving the system to the weak coupling regime (i.e., going downward in Figure 1a) and inducing an exponential decay of I. For a small enough ωs (<20 nm), the system remains in the strong-coupling regime and I becomes independent of g.7 Therefore, we can observe that for ωs < 20 nm, I shows a weak variation with ωh. When ωs > 20 nm, the cavity starts to perform away from the strong coupling regime and I shows an evident change with ωh, which we will further analyze later. A slot width ωs <10 nm produces a maximum value of I = 0.96, decaying with ωs at a rate of 5 × 10–3 nm–1. Figure 3d shows the dependence of I with #p, with #p in the range of 10–100 and fixed ωh = 140 nm and ωs = 15 nm so we keep the strong coupling regime. As #p increases, the effective reflectivity also increases and the Q factor grows exponentially (see Figure 1i). Consequently, κ decreases exponentially with #p. Therefore, the time that the photon stays in the cavity increases exponentially with #p, and when κ < γ*, the photon is dephased by the emitter (i.e., going in the left direction in Figure 1a). The result is that I decreases with #p giving I = 0.4 for #p = 100. Figure 3b shows Γp versus (ωs, ωh) when #p = 10, ωs in the range 10–100 nm, and ωh between 110 and 600 nm. Since Γp ∼ 1/Veff, Γp changes with ωs in a similar way to I. As the slot mode spreads over the waveguide cores, the field’s intensity at the source’s position decreases and Γp shows an exponential decay. The change with ωh displays a more complex structure, shown more clearly in Figure 3e. For ωs = 15 nm and ωh = 80, Γp increases monotonically as the zero-order cosine/even45 slot mode gets more efficiently confined in the waveguide. Γp is maximum (Γp = 11) when ωh = 125 nm, and the strongest light confinement in the waveguide happens. For a higher ωh, the mode spreads over the structure producing a decay of the overlapping with the source that scales with 1/ωh. The decay interrupts abruptly when the zero-order sin-type/odd mode cutoff is reached at ωh = 155 nm. From there, the same pattern reproduces until the activation of the subsequent mode, and so on. The same behavior happens for ωs. However, as ωs increase the dependence of Γp with ωh shifts to lower values of ωh. This is because the ωh cutoff value of the zero-order sine mode/odd decreases monotonically with ωs.45 Therefore, the activation of the second mode shifts to lower values of ωh as ωs increases.

Figure 3.

Figure 3

Open in a new tab

(a) Cavity-induced I when γ/γ* = 104 versus waveguide width (ωh) and slot width (ωs) for #p = 10. (b) Purcell enhancement (Γp) versus waveguide width (ωh) and slot width (ωs). (c) Coupling efficiency (β) versus waveguide width (ωh) and slot width (ωs) for #p = 10. (d) I versus number of grating periods (#p) for (ωs, ωh) = (5 nm, 140 nm). (e) Γp versus ωh for three ωs (green, ωs = 15 nm; blue, ωs = 20 nm; yellow, ωs = 25 nm). (f) Γ versus source position y0 along the y-axis.

Figure 3c shows β versus ωs and ωh for the same values of #p, ωs and ωh used in Figure 3b. While Γp is a measure of the field enhancement due to the overlapping of all available modes, β accounts just for the overlapping with guided modes. Therefore, we expect a similar dependence and, in fact, β shows an exponential decay with ωs similarly to I and Γp. The dependence with ωh shows the same “mode jumps” found for Γp, giving a maximum β = 75% at ωh = 128 nm. In this case, the regions of high β become bigger for higher values of ωh, as the number of available modes increases with ωh.

The position of the QE inside the cavity plays a relevant role.46 To explore the effect of the position of the QE in Γp, we have performed 3D-FDTD simulations changing the position (y0) of the QE along the cavity cross section (y-axis) at z0 = 4 nm above the top of the cavity. Figure 3f shows Γp versus y0 varying from −225 to +225 nm when ωh = 200 nm, ωs = 30 nm, and #p = 10. Since Γp is proportional to the field of the available modes for each spatial position, the plot reproduces the field profile of the zero-order mode of the slot waveguide. The maximum Γp happens in the region inside the slot, with maxima at the edges of the waveguides. The enhancement falls abruptly inside the waveguide, with values reduced by 1 order of magnitude. For a QE located away from the outer edges of the waveguide cores, the evanescent coupling increases the enhancement slightly. In summary, even for a strong dissipative emitter with γ* = 104γ, we can achieve I > 0.9 by adjusting the number of periods and reducing the slot width ωs below 10 nm. At the same time, a high Purcell enhancement (Γp = 45) and a good extraction efficiency (β = 0.7) can be obtained for the same ωs. On the other hand, we need an accurate positioning of the emitter inside the slot region.

We further explore the performance of the device and the design requirements for different types of QE with different dephasing rates. For each type of emitter, the geometrical parameters of the device (i.e., t, L, and Λ) are set to match the specific emission wavelength λ. Table 1 shows the values of the pairs (ωs, #p) needed for I > 0.9 for five different γ*/γ values corresponding to each emitter. The values of the oscillation strengths are extracted from InGaAs,47 GaAs,48 TMDC,49,50 single molecules,28,51 and diamond.52 We observe that as γ* increases (i.e., T increases), the cavity demands smaller ωs (i.e., narrower slot). For the highest oscillator strength (∼5 in InGaAs QD and diamond color centers), (g/γ)min is easily reached when ωs < 44 nm and γ* = 102γ. A TMDC QE with oscillator strength ∼ 0.1 demands ωs < 38 nm on the opposite side. In an intermediate situation, the oscillation strength of the GaAs QD (∼1) gives ωs < 42 nm. From this, we can find the optimal design for each emitter at a high T. InGaAs at 300 K has a pure dephasing of 600γ,53 so (ωs, #p) = (36 nm, 50) are needed for I > 0.9. GaAs at 300 K has 1450γ54 and needs the same values (ωs, #p) = (36, 50). High dissipative emitters with dephasing of ∼104γ at 300 K, like TMDC55 and single molecules, demand narrower slot widths (ωs, #p) = (5 nm, 10). For color centers in diamond, with γ* = 103γ at room T,56 the optimal configuration is (ωs, #p) = (38 nm, 50).

Table 1. Maximum (ωs (nm), #p) for I > 0.9 Using InGaAs QD, GaAs QD, TMDCs, and Single Molecules as QE.

  γ* = 102γ γ* = 103γ γ* = 104γ
InGaAs (43,100) (36,50) (15,10)
GaAs (41,100) (30,50) (9,10)
TMDC (36,120) (25,60) (5,12)
S.molecules (40,120) (28,60) (8,12)
Diamond (45,100) (38,50) (15,10)
Open in a new tab

As we have shown, for high dissipative emitters with γ* = 104γ, the width of the cavity slot must be ωs < 10 nm for I > 0.9. Similarly, ωs < 10 nm is needed for β > 0.7. At the same time, the emitter’s position plays a critical role, giving very low coupling when the emitter is outside the slot region. These requirements make complex both the fabrication and the emitter integration. Achieving slot widths below 10 nm is beyond the state of the art of almost any fabrication technology, and deterministic deposition of a QD with that accuracy can be complicated. To reduce those limitations, we need to optimize the geometry of the cavity further. We have performed a hybrid GA-NN optimization of the Bragg corrugation geometry. The GA-NN optimization must deal with the trade-off between reducing the cavity modal volume (to increase g) and maintaining the appropriate Q to achieve I > 0.9 with γ* = 104γ. With this aim, we set ωs = 20 nm and the number of periods to #p = 20. The structure without optimization has a modal volume of about 10–2(λ/2n)3, which gives I = 0.82 with γ* = 104γ. Figure 4a shows the GA-NN optimized geometry. Somehow surprisingly to us, the GA-NN found that it is enough to change the widths of the most external Bragg corrugations, leaving the others unperturbed. This geometry provides the best confinement of the cavity mode in the center of the structure, significantly reducing the modal volume while maintaining the correct Q.

Figure 4.

Figure 4

Open in a new tab

(a) Optimized structure for fixed (ωs, #p) = (20,20). Cavity-mode field profile in the XY plane inside the cavity region for (b) cavity mode profiles of the nonoptimized structure (top) and optimized structure (bottom). Transmission spectra for (c) structure without optimization and (d) GA-NN optimized structure.

Figure 4b–d shows the cavity-mode profile and the transmission spectrum for the structure with and without optimization. It is easy to appreciate how the cavity mode is significantly more confined in the central region of the optimized cavity. The modification of the widths of the external Bragg corrugations creates a tapered section that connects the cavity with the input/output slot waveguides and increases the confinement of the cavity mode. The modal volume is reduced from 7 × 10–3(λ/2n)3 to 2.5 × 10–3(λ/2n)3, a factor of 2.8. At the same time, FWHM has been increased to Q = 50, keeping the system in the region of high I. The reduction in the modal volume and the Q adjustment improve the indistinguishability from I = 0.82 to 0.91. In conclusion, we obtain that for the optimized structure, we can achieve I > 0.9 for γ* = 104γ with a slot width of ωs = 20 nm, relaxing the tight requirements for the fabrication of the slot to more realistic values. The resulting transmission spectra of the optimized device reveal that there is a 7 nm shift of the resonance wavelength. This results from the discontinuous alteration of the periodicity of the Bragg reflectors. The λ-Bragg condition for total reflection changes along the corrugations, giving rise to a small modification of the spectra. This resonance displacement could be reduced through a second optimization process involving the maximization of I together with the minimization of the λ-shift, which will be covered in future works.

Although simulation results show a promising device performance, potential difficulties related to fabrication have to be considered according to CMOS-compatible processes. Realization of vertical slot widths below 80 nm can be difficult with standard lithography techniques. For emitters with γ* = 102γ, slots between 36 and 45 nm are needed (see Table 1). Despite that achieving these widths can be challenging, there are many experimental demonstrations reporting the fabrication of sub-100 nm slots (between 30 and 80 nm) using e-beam lithography (EBL).57−64 On the other hand, strong dissipative emitters with γ* = 104γ require slot widths between 5 and 15 nm. Defining sub-10 nm structures with EBL is a great challenge, requiring simultaneous control of several factors like resist contrast, beam diameter, resist development mechanics, and limitations in metrology.65 A novel fabrication procedure with EBL was reported,65 which allows us to achieve slot widths down to 8 nm in Si substrates. Also, recent works66 experimentally demonstrate a different fabrication approach achieving slots with 10 nm width in Si waveguides. In this context, the relaxation up to 20 nm width achieved through the ML optimization is especially relevant since it reduces the fabrication requirements from the limit of the technology (5 nm) to a more accessible value (20 nm). Still, we must emphasize that achieving such ultranarrow slots presents a significant challenge, which requires top-state-of-the-art resolution technology.

Another key aspect to consider for the experimental realization is the nanoscale positioning approach for the deposition of the QE in the 20 nm slot region of the cavity. Recently, several nanoscale positioning techniques compatible with nanofabrication processes have shown promising results, achieving positioning accuracy at the nanometer level.67 Atomic force microscopy-based positioning approaches with 30 nm positioning accuracy have been reported with GaAs QDs strongly coupled to a nanocavity.68 Confocal micro-photoluminescence techniques also showed 10 nm positioning accuracy with GaAs QDs inside a photonic structure.69 Bichromatic photoluminescence approaches with 5 nm position accuracy were recently achieved through a novel image analysis software implementation in the positioning setup.70 Also, in situ lithographic techniques, where the QD position extraction and the nanostructure definition are developed in the same setup, have improved position accuracy down to 30 nm.71 Pick-and-place techniques, which are the most suitable approach for our specific structure, have also shown significant progress.72 Recently, Si vacancy centers were transferred to AIN waveguides achieving 98% coupling efficiency,73 the placement mean error was about 38 nm. According to this, for a pick-and-place deposition, assuming a normal distribution, we would have a standard deviation of 38 nm with a target of 20 nm, which leads to 34% probability of successful deposition. Therefore, the positioning accuracy required for our structure lies close to the limit of the technology depending on the positioning approach. An experimental realization of a QE coupling requires fabricating many devices and looking for good candidates one by one. This approach allows the experimental demonstration of certain quantum effects for quantum information applications, but is still far from a scalable technology.

Conclusions

We explored a hybrid slot-Bragg nanophotonic cavity for the generation of indistinguishable photons at RT from various quantum emitters through a combination of numerical methods. We obtain the values of the theoretical indistinguishability, efficiency, and Purcell enhancement for each configuration (i.e., waveguide width, slot width, number of periods). We obtained theoretical near-unity indistinguishability and high efficiency simultaneously by parameter sweep optimization. To relax the fabrication requirements (slot width) for near-unity indistinguishability, we have developed a machine learning algorithm that provides the optimal geometry of the cavity. According to our simulations, the optimized structure shows high indistinguishability (I > 0.9) with slot widths of about 20 nm. The geometrical features of the optimized design present significant challenges from the perspective of fabrication process. Although the device may be far from a real scalable technology, it can be suitable for experimental demonstration of single-photon operation. Also, the developed ML approach may provide insights for the optimization of different photonic structures for quantum information applications.

Acknowledgments

The authors gratefully acknowledge financial support from the European Union’s Horizon 2020 research and innovation program under grant agreement no. 820423 (S2QUIP) and CSIC Quantum Technology Platform PT-001. J.M.L. acknowledges the Agencia Estatal de Investigación (AEI) grant PID2019-106088RB-C31.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.1c01651.

  • Computation of the indistinguishability; numerical simulation; machine learning algorithm; and fabrication process (PDF)

This work was funded by the European Union’s Horizon 2020 research and innovation program under grant agreement no. 820423 (S2QUIP).

The authors declare no competing financial interest.

Notes

Details underlying the results presented in this paper are available in the Supplement 1 file.

Supplementary Material

ph1c01651_si_001.pdf (256.6KB, pdf)

References

  1. Aspuru-Guzik A.; Walther P. Photonic quantum simulators. Nat. Phys. 2012, 8, 285–291. 10.1038/nphys2253. [DOI] [Google Scholar]
  2. Aharonov D.; Ambainis A.; Kempe J.; Vazirani U. In Quantum Walks on Graphs, Proceedings of the 33rd ACM Symposium on Theory of Computing, 2001.
  3. Broome M. A.; Fedrizzi A.; Rahimi-Keshari S.; Dove J.; Aaronson S.; Ralph T. C.; White A. G. Photonic boson sampling in a tunable circuit. Science 2013, 339, 794–798. 10.1126/science.1231440. [DOI] [PubMed] [Google Scholar]
  4. Fattal D.; Diamanti E.; Inoue K.; Yamamoto Y. Quantum teleportation with a quantum dot single photon source. Phys. Rev. Lett. 2004, 92, 037904 10.1103/PhysRevLett.92.037904. [DOI] [PubMed] [Google Scholar]
  5. Kimble H. J. The quantum internet. Nature 2008, 453, 1023–1030. 10.1038/nature07127. [DOI] [PubMed] [Google Scholar]
  6. Aharonovich I.; Englund D.; Toth M. Solid-state single-photon emitters. Nat. Photonics 2016, 10, 631–641. 10.1038/nphoton.2016.186. [DOI] [Google Scholar]
  7. Grange T.; Hornecker G.; Hunger D.; Poizat J. P.; Gérard J. M.; Similar P.; Affixes A. Cavity-funneled generation of indistinguishable single photons from strongly dissipative quantum emitters. Phys. Rev. Lett. 2015, 114, 193601 10.1103/PhysRevLett.114.193601. [DOI] [PubMed] [Google Scholar]
  8. Chikara R.; De Nibs B.; Benz F.; Barrow S. J.; Sucherman O. A.; Rosa E.; Blumberg J. J. Single-molecule strong coupling at room T in plasmonic nanocavities. Nature 2016, 535, 127–130. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Russell K. J.; Hu E. L. Gap-mode plasmonic nanocavity. Appl. Phys. Lett. 2010, 97, 163115 10.1063/1.3505154. [DOI] [Google Scholar]
  10. Seo M. K.; Kwon S. H.; Ee H. S.; Park H. G. Full three-dimensional subwavelength high-Q surface-plasmon-polariton cavity. Nano Lett. 2009, 9, 4078–4082. 10.1021/nl902274m. [DOI] [PubMed] [Google Scholar]
  11. Santhosh K.; Button O.; Chitonid L.; Haran G. Vacuum Rabi splitting in a plasmonic cavity at the single quantum emitter limit. Nat. Commun. 2016, 7, 11823 10.1038/ncomms11823. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kang J. H.; No Y. S.; Kwon S. H.; Park H. G. Ultrasmall subwavelength nanorod plasmonic cavity. Opt. Lett. 2011, 36, 2011–2013. 10.1364/OL.36.002011. [DOI] [PubMed] [Google Scholar]
  13. Peng P.; Liu Y. C.; Xu D.; Cao Q. T.; Lu G.; Gong Q.; Xiao Y. F. Enhancing coherent light-matter interactions through microcavity-engineered plasmonic resonances. Phys. Rev. Lett. 2017, 119, 233901 10.1103/PhysRevLett.119.233901. [DOI] [PubMed] [Google Scholar]
  14. Gurlek B.; Sandoghdar V.; Martín-Cano D. Manipulation of quenching in nanoantenna–emitter systems enabled by external detuned cavities: a path to enhance strong-coupling. ACS Photonics 2018, 5, 456–461. 10.1021/acsphotonics.7b00953. [DOI] [Google Scholar]
  15. Hugall J. T.; Singh A.; van Hulst N. F. Plasmonic cavity coupling. ACS Photonics 2018, 5, 43–53. 10.1021/acsphotonics.7b01139. [DOI] [Google Scholar]
  16. Robinson J. T.; Manolatou C.; Chen L.; Lipson M. Ultrasmall mode volumes in dielectric optical microcavities. Phys. Rev. Lett. 2005, 95, 143901 10.1103/PhysRevLett.95.143901. [DOI] [PubMed] [Google Scholar]
  17. Seidler P.; Lister K.; Drechsler U.; Hofrichter J.; Stöferle T. Slotted photonic crystal nanobeam cavity with an ultrahigh quality factor-to-mode volume ratio. Opt. Express 2013, 21, 32468–32483. 10.1364/OE.21.032468. [DOI] [PubMed] [Google Scholar]
  18. Ryckman J. D.; Weiss S. M. Low mode volume slotted photonic crystal single nanobeam cavity. Appl. Phys. Lett. 2012, 101, 071104 10.1063/1.4742749. [DOI] [Google Scholar]
  19. Hu S.; Weiss S. M. Design of photonic crystal cavities for extreme light concentration. ACS Photonics 2016, 3, 1647–1653. 10.1021/acsphotonics.6b00219. [DOI] [Google Scholar]
  20. Choi H.; Heuck M.; Englund D. Self-similar nanocavity design with ultrasmall mode volume for single-photon nonlinearities. Phys. Rev. Lett. 2017, 118, 223605 10.1103/PhysRevLett.118.223605. [DOI] [PubMed] [Google Scholar]
  21. Saxena A.; Chen Y.; Ryou A.; Sevilla C. G.; Xu P.; Majumdar A. Improving indistinguishability of single photons from colloidal quantum dots using nanocavities. ACS Photonics 2019, 6, 3166–3173. 10.1021/acsphotonics.9b01481. [DOI] [Google Scholar]
  22. Sanchis L.; Cryan M. J.; Pozo J.; Craddock I. J.; Rarity J. G. Ultrahigh Purcell factor in photonic crystal slab microcavities. Phys. Rev. B 2007, 76, 045118 10.1103/PhysRevB.76.045118. [DOI] [Google Scholar]
  23. Sanchis L.; Håkansson A.; López-Zanón D.; Bravo-Abad J.; Sánchez-Dehesa J. Integrated optical devices design by genetic algorithm. Appl. Phys. Lett. 2004, 84, 4460–4462. 10.1063/1.1738931. [DOI] [Google Scholar]
  24. Morgado-León A.; Escuín A.; Guerrero E.; Yáñez A.; Galindo P. L.; Sanchis L.. Genetic Algorithms Applied to the Design of 3D Photonic Crystals. In International Work-Conference on Artificial Neural Networks; Springer: Berlin, Heidelberg, 2011; pp 291–298. [Google Scholar]
  25. Marqués-Hueso J.; Sanchis L.; Cluzel B.; de Fornel F.; Martínez-Pastor J. P. Genetic algorithm designed silicon integrated photonic lens operating at 1550 nm. Appl. Phys. Lett. 2010, 97, 071115 10.1063/1.3479046. [DOI] [Google Scholar]
  26. Tomm N.; Javadi A.; Antoniadis N. O.; Najer D.; Löbl M. C.; Korsch A. R.; Warburton R. J.; et al. A bright and fast source of coherent single photons. Nat. Nanotechnol. 2021, 16, 399–403. 10.1038/s41565-020-00831-x. [DOI] [PubMed] [Google Scholar]
  27. Schnauber P.; Singh A.; Schall J.; Park S. I.; Song J. D.; Rodt S.; Davanco M.; et al. Indistinguishable photons from deterministically integrated single quantum dots in heterogeneous GaAs/Si3N4 quantum photonic circuits. Nano Lett. 2019, 19, 7164–7172. 10.1021/acs.nanolett.9b02758. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Iff O.; Buchinger Q.; Moczała-Dusanowska M.; Kamp M.; Betzold S.; Davanco M.; Schneider C.; et al. Purcell-enhanced single photon source based on a deterministically placed WSe2 monolayer quantum dot in a circular Bragg grating cavity. Nano Lett. 2021, 21, 4715–4720. 10.1021/acs.nanolett.1c00978. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Toninelli C.; Gerhardt I.; Clark A. S.; Reserbat-Plantey A.; Götzinger S.; Ristanović Z.; Orrit M. A. J. G.; et al. Single organic molecules for photonic quantum technologies. Nat. Mater. 2021, 20, 1615–1628. 10.1038/s41563-021-00987-4. [DOI] [PubMed] [Google Scholar]
  30. Dolan P. R.; Adekanye S.; Trichet A. A. P.; Johnson S.; Flatten L. C.; Chen Y. C.; Smith J. M.; et al. Robust, tunable, and high purity triggered single photon source at room temperature using a nitrogen-vacancy defect in diamond in an open microcavity. Opt. Express 2018, 26, 7056–7065. 10.1364/OE.26.007056. [DOI] [PubMed] [Google Scholar]
  31. Fan X.; Takagahara T.; Cunningham J. E.; Wang H. Pure dephasing induced by exciton–phonon interactions in narrow GaAs quantum wells. Solid State Commun. 1998, 108, 857–861. 10.1016/S0038-1098(98)00461-X. [DOI] [Google Scholar]
  32. Jakubczyk T.; Delmonte V.; Fischbach S.; Wigger D.; Reiter D. E.; Mermillod Q.; Rodt S.; et al. Impact of phonons on dephasing of individual excitons in deterministic quantum dot microlenses. ACS Photonics 2016, 3, 2461–2466. 10.1021/acsphotonics.6b00707. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Kummer S.; Basche T. Measurement of optical dephasing of a single terrylene molecule with nanosecond time resolution. J. Phys. Chem. A 1995, 99, 17078–17081. 10.1021/j100047a005. [DOI] [Google Scholar]
  34. Hesselink W. H.; Wiersma D. A. Optical dephasing and vibronic relaxation in molecular mixed crystals: A picosecond photon echo and optical study of pentacene in naphthalene and p-terphenyl. J. Chem. Phys. 1980, 73, 648–663. 10.1063/1.440167. [DOI] [Google Scholar]
  35. Moody G.; Dass C. K.; Hao K.; Chen C. H.; Li L. J.; Singh A.; Li X.; et al. Intrinsic homogeneous linewidth and broadening mechanisms of excitons in monolayer transition metal dichalcogenides. Nat. Commun. 2015, 6, 8315 10.1038/ncomms9315. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wang X.; Grist S.; Flueckiger J.; Jaeger N. A.; Chrostowski L. Silicon photonic slot waveguide Bragg gratings and resonators. Opt. Express 2013, 21, 19029–19039. 10.1364/OE.21.019029. [DOI] [PubMed] [Google Scholar]
  37. Bera A.; Kuittinen M.; Honkanen S.; Roussey M. Silicon slot waveguide Fano resonator. Opt. Lett. 2018, 43, 3489–3492. 10.1364/OL.43.003489. [DOI] [PubMed] [Google Scholar]
  38. Wang X.; Flueckiger J.; Schmidt S.; Grist S.; Fard S. T.; Kirk J.; Chrostowski L.; et al. A silicon photonic biosensor using phase-shifted Bragg gratings in slot waveguide. J. Biophotonics 2013, 6, 821–828. 10.1002/jbio.201300012. [DOI] [PubMed] [Google Scholar]
  39. Errando-Herranz C.; Schöll E.; Picard R.; Laini M.; Gyger S.; Elshaari A. W.; Jöns K. D.. On-Chip Single Photon Emission from a Waveguide-Coupled Two-Dimensional Semiconductor. In Quantum Nanophotonic Materials, Devices, and Systems 2020; International Society for Optics and Photonics, 2020; Vol. 11471, p 1147105. [Google Scholar]
  40. Lumerical Inc. https://www.lumerical.com/products/ (accessed February 21, 2022).
  41. Kristensen T.; Van Vlack C.; Hughes S. Effective mode volumes and purcell factors for leaky optical cavities. 2011-7-22. Opt. Lett. 2011, 37, 1649–1651. [DOI] [PubMed] [Google Scholar]
  42. Vuckovic J.Quantum Optics and Cavity QED with Quantum Dots in Photonic Crystals. In Quantum Optics and Nanophotonics; Oxford University Press, 2017. [Google Scholar]
  43. Novotny L.; Hecht B.. Principles of Nano-Optics; Cambridge University Press, 2012. [Google Scholar]
  44. Almeida V. R.; Xu Q.; Barrios C. A.; Lipson M. Guiding and confining light in void nanostructure. Opt. Lett. 2004, 29, 1209–1211. 10.1364/OL.29.001209. [DOI] [PubMed] [Google Scholar]
  45. Liu Y.; Kong M.; Jiang Y. Transverse magnetic modes in planar slot waveguides. J. Opt. Soc. Am. B 2015, 32, 2052–2060. 10.1364/JOSAB.32.002052. [DOI] [Google Scholar]
  46. Guimbao J.; Weituschat L. M.; Montolio J. L.; Postigo P. A. Enhancement of the indistinguishability of single photon emitters coupled to photonic waveguides. Opt. Express 2021, 29, 21160–21173. 10.1364/OE.422023. [DOI] [PubMed] [Google Scholar]
  47. Stoleru V. G.; Towe E. Oscillator strength for intraband transitions in (In, Ga) As/GaAs quantum dots. Appl. Phys. Lett. 2003, 83, 5026–5028. 10.1063/1.1631740. [DOI] [Google Scholar]
  48. Hatami F.; Grundmann M.; Ledentsov N. N.; Heinrichsdorff F.; Heitz R.; Böhrer J.; Kop’ev P. S.; et al. Carrier dynamics in type-II GaSb/GaAs quantum dots. Phys. Rev. B 1998, 57, 4635 10.1103/PhysRevB.57.4635. [DOI] [Google Scholar]
  49. Schneider C.; Glazov M. M.; Korn T.; Höfling S.; Urbaszek B. Two-dimensional semiconductors in the regime of strong light-matter coupling. Nat. Commun. 2018, 9, 2695 10.1038/s41467-018-04866-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Lundt N.; Maryński A.; Cherotchenko E.; Pant A.; Fan X.; Tongay S.; Schneider C. Monolayered MoSe2: a candidate for room T polaritonics. 2D Mater. 2016, 4, 015006 10.1088/2053-1583/4/1/015006. [DOI] [Google Scholar]
  51. Zhao H.; Zhao Y.; Song Y.; Zhou M.; Lv W.; Tao L.; Wang X.; et al. Strong optical response and light emission from a monolayer molecular crystal. Nat. Commun. 2019, 10, 5589 10.1038/s41467-019-13581-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Heidari Saani M.; Vesaghi M. A.; Esfarjani K. Oscillator strength calculations in color centers of diamond and the role of spin. Eur. Phys. J. B 2004, 39, 441–446. 10.1140/epjb/e2004-00215-9. [DOI] [Google Scholar]
  53. Borri P.; Langbein W.; Schneider S.; Woggon U.; Sellin R. L.; Ouyang D.; Bimberg D. Ultralong dephasing time in InGaAs quantum dots. Phys. Rev. Lett. 2001, 87, 157401 10.1103/PhysRevLett.87.157401. [DOI] [PubMed] [Google Scholar]
  54. Bayer M.; Forchel A. Temperature dependence of the exciton homogeneous linewidth in In 0.60 Ga 0.40 As/GaAs self-assembled quantum dots. Phys. Rev. B 2002, 65, 041308 10.1103/PhysRevB.65.041308. [DOI] [Google Scholar]
  55. Huang L.; Krasnok A.; Alu A.; Yu Y.; Neshev D.; Miroshnichenko A. Enhanced Light-Matter Interaction in Two-Dimensional Transition Metal Dichalcogenides. Rep. Prog. Phys. 2022, 85, 046401. [DOI] [PubMed] [Google Scholar]
  56. Albrecht R.; Bommer A.; Deutsch C.; Reichel J.; Becher C. Coupling of a single nitrogen-vacancy center in diamond to a fiber-based microcavity. Phys. Rev. Lett. 2013, 110, 243602 10.1103/PhysRevLett.110.243602. [DOI] [PubMed] [Google Scholar]
  57. Häyrinen M.; Roussey M.; Säynätjoki A.; Kuittinen M.; Honkanen S. Titanium dioxide slot waveguides for visible wavelengths. Appl. Opt. 2015, 54, 2653–2657. 10.1364/AO.54.002653. [DOI] [PubMed] [Google Scholar]
  58. Raza A.; Van Daele M.; Wuytens P.; Dendooven J.; Detavernier C.; Clemmen S.; Baets R.. E-beam-Lithography Free Plasmonic Slot Waveguides for On-Chip Raman Spectroscopy. In CLEO: Science and Innovations; Optical Society of America, 2018; p SW3L-6. [Google Scholar]
  59. Wang Y.; He S.; Gao X.; Ye P.; Lei L.; Dong W.; Zhang X.; Xu P. Enhanced optical nonlinearity in a silicon–organic hybrid slot waveguide for all-optical signal processing. Photonics Res. 2022, 10, 50–58. 10.1364/PRJ.439251. [DOI] [Google Scholar]
  60. Lin S.; Hu J.; Crozier K. B. Ultracompact, broadband slot waveguide polarization splitter. Appl. Phys. Lett. 2011, 98, 151101 10.1063/1.3579243. [DOI] [Google Scholar]
  61. Hochberg M.; Baehr-Jones T.; Wang G.; Huang J.; Sullivan P.; Dalton L.; Scherer A. Towards a millivolt optical modulator with nano-slot waveguides. Opt. Express 2007, 15, 8401–8410. 10.1364/OE.15.008401. [DOI] [PubMed] [Google Scholar]
  62. Wang J.; Cheng Z.; Chen Z.; Wan X.; Zhu B.; Tsang H. K.; Shu C.; Xu J. High-responsivity graphene-on-silicon slot waveguide photodetectors. Nanoscale 2016, 8, 13206–13211. 10.1039/C6NR03122F. [DOI] [PubMed] [Google Scholar]
  63. Lin C. Y.; Wang X.; Chakravarty S.; Lee B. S.; Lai W.; Luo J.; Jen A. Y.; Chen R. T. Electro-optic polymer infiltrated silicon photonic crystal slot waveguide modulator with 23 dB slow light enhancement. Appl. Phys. Lett. 2010, 97, 194 10.1063/1.3486225. [DOI] [Google Scholar]
  64. Zhang H.; Zhang J.; Chen S.; Song J.; Kee J. S.; Yu M.; Lo G. Q. CMOS-compatible fabrication of silicon-based sub-100-nm slot waveguide with efficient channel-slot coupler. IEEE Photonics Technol. Lett. 2012, 24, 10–12. 10.1109/LPT.2011.2171936. [DOI] [Google Scholar]
  65. Cord B. M.Achieving sub-10-nm Resolution Using Scanning Electron Beam Lithography. Doctoral Dissertation, Massachusetts Institute of Technology, 2009. [Google Scholar]
  66. Debnath K.; Khokhar A. Z.; Reed G. T.; Saito S. Fabrication of arbitrarily narrow vertical dielectric slots in silicon waveguides. IEEE Photonics Technol. Lett. 2017, 29, 1269–1272. 10.1109/LPT.2017.2722003. [DOI] [Google Scholar]
  67. Liu S.; Srinivasan K.; Liu J. Nanoscale Positioning Approaches for Integrating Single Solid-State Quantum Emitters with Photonic Nanostructures. Laser Photonics Rev. 2021, 15, 2100223 10.1002/lpor.202100223. [DOI] [Google Scholar]
  68. Hennessy K.; Badolato A.; Winger M.; Gerace D.; Atatüre M.; Gulde S.; Imamoğlu A.; et al. Quantum nature of a strongly coupled single quantum dot–cavity system. Nature 2007, 445, 896–899. 10.1038/nature05586. [DOI] [PubMed] [Google Scholar]
  69. Thon S. M.; Rakher M. T.; Kim H.; Gudat J.; Irvine W. T.; Petroff P. M.; Bouwmeester D. Strong coupling through optical positioning of a quantum dot in a photonic crystal cavity. Appl. Phys. Lett. 2009, 94, 111115 10.1063/1.3103885. [DOI] [Google Scholar]
  70. Liu J.; Davanço M. I.; Sapienza L.; Konthasinghe K.; De Miranda Cardoso J. V.; Song J. D.; Badolato A.; Srinivasan K. Cryogenic photoluminescence imaging system for nanoscale positioning of single quantum emitters. Rev. Sci. Instrum. 2017, 88, 023116 10.1063/1.4976578. [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Gschrey M.; Schmidt R.; Schulze J. H.; Strittmatter A.; Rodt S.; Reitzenstein S. Resolution and alignment accuracy of low-temperature in situ electron beam lithography for nanophotonic device fabrication. J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom. 2015, 33, 021603 10.1116/1.4914914. [DOI] [Google Scholar]
  72. Elshaari A. W.; Pernice W.; Srinivasan K.; Benson O.; Zwiller V. Hybrid integrated quantum photonic circuits. Nat. Photonics 2020, 14, 285–298. 10.1038/s41566-020-0609-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Wang J.; Sciarrino F.; Laing A.; Thompson M. G. Integrated photonic quantum technologies. Nat. Photonics 2020, 14, 273–284. 10.1038/s41566-019-0532-1. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ph1c01651_si_001.pdf (256.6KB, pdf)

Articles from ACS Photonics are provided here courtesy of American Chemical Society

RESOURCES