Unique Features of Stimulus-Based Probabilistic Reversal Learning

Abstract

Reversal learning paradigms are widely used assays of behavioral flexibility with their probabilistic versions being more amenable to studying integration of reward outcomes over time. Prior research suggests differences between initial and reversal learning, including higher learning rates, a greater need for inhibitory control, and more perseveration after reversals. However, it is not well-understood what aspects of stimulus-based reversal learning are unique to reversals, and whether and how observed differences depend on reward probability. Here, we used a visual probabilistic discrimination and reversal learning paradigm where male and female rats selected between a pair of stimuli associated with different reward probabilities. We compared accuracy, rewards collected, omissions, latencies, win-stay/lose-shift strategies, and indices of perseveration across two different reward probability schedules. We found that discrimination and reversal learning are behaviorally more unique than similar: Fit of choice behavior using reinforcement learning models revealed a lower sensitivity to the difference in subjective reward values (greater exploration) and higher learning rates for the reversal phase. We also found latencies to choose the better option were greater in females than males, but only for the reversal phase. Further, animals employed more win-stay strategies during early discrimination and increased perseveration during early reversal learning. Interestingly, a consistent reward probability group difference emerged with a richer environment associated with longer reward collection latencies than a leaner environment. Future studies should systematically compare the neural correlates of fine-grained behavioral measures to reveal possible dissociations in how the circuitry is recruited in each phase.

A critical feature of goal directed, instrumental behavior is the ability to discriminate stimuli that predict reward from those that do not, and further, to flexibly update the response to those stimuli if predictions become inaccurate. Discrimination learning paradigms in rodents often involve pairing of an action (e.g., lever pressing, digging in a bowl, nosepoking stimuli on a touchscreen, or displacing an object) with an outcome (e.g., a desirable food reward). In typical paradigms, two or more stimuli are presented concurrently and the subject learns about the features of the stimuli that bring about reward and those that do not (e.g., nosepoking S_A results in a better probability of reward than S_B; pressing left lever yields better payout than right lever; scent A is more rewarded than scent B; Alvarez & Eichenbaum, 2002; Dalton et al., 2016; Eichenbaum et al., 1986; Izquierdo et al., 2013; Schoenbaum et al., 2000, 2002). With training, subjects become increasingly proficient at discrimination, in line with the associative rules imposed by the experimenter. The stimulus-reward rules can be deterministic (e.g., S_A results in a sucrose pellet reward and S_B does not) or probabilistic (e.g., S_A results in a better probability of reward over S_B), with deterministic and probabilistic schedules of reinforcement producing marked dissociations in the neural circuitry recruited (Averbeck & Costa, 2017; Costa et al., 2016).

In reversal learning paradigms (Izquierdo et al., 2017; Izquierdo & Jentsch, 2012), after either reaching a discrimination learning criterion for accuracy (Brushfield et al., 2008; Izquierdo et al., 2013; Stolyarova et al., 2019), a number of consecutive correct responses (Dalton et al., 2014, 2016), or a fixed block length of trials (Farashahi et al., 2017; Soltani & Izquierdo, 2019), the stimulus-reward contingencies are reversed. At reversal, the trained response no longer results in a better probability of reward, though it usually remains the more frequently chosen option because of initial discrimination training. Indeed, usually reversals are acquired more slowly than the original discrimination, and younger subjects are quicker to learn than older ones (Brushfield et al., 2008; Schoenbaum et al., 2006). Perhaps partly due to this difference with original learning, reversal learning is considered unique in its requirement of flexibility, because it involves the subject inhibiting the prepotent response and, instead, responding to stimuli that were previously irrelevant. Other popular views are that discrimination and reversal learning phases occupy different task “spaces” (Wilson et al., 2014) and that the phases differ in the likelihood that changes in contingencies will occur (Jang et al., 2015). Importantly, probabilistic learning and reversal paradigms, in particular, are more amenable to the application of reinforcement learning (RL) models that can estimate parameters for choice behavior based on the integration of previous rewarded and nonrewarded trials (Lee et al., 2012). Despite various favored accounts, it is not well-understood how behaviorally unique reversal learning is compared to original (initial discrimination) learning. For example, latency measures can be used to dissociate attention, decision speed, and motivation via analyses of the time taken to initiate trials, choose a stimulus, and collect reward, respectively (Aguirre et al., 2020). Here, we explored if such detailed trial-by-trial measures of latencies and omissions differ across learning phases. Further, we probed if there are differences between reward probability schedules on these various measures by comparing the ability of separate cohorts of animals tested on different reward probability schedules to discriminate between the better and worse options, which were rewarded with a probability of .90 versus .30, compared to .70 versus .30. We also analyzed win-stay and lose-shift strategies, and perseveration and repetition metrics in each learning phase. Finally, we investigated if RL models fit these learning phases differently. We studied this in both male and female animals.

We found a higher perseveration index and reduced use of win-stay strategies unique to early reversal compared to discrimination learning, which was expected. However, more surprisingly, we found consistent differences across discrimination and reversal learning phases to be limited to latencies to choose the better option (greater in females than males, only in the reversal) and to collect reward (greater in the higher reward probability group). These two metrics are proxies for decision speed and motivation, respectively. As for RL models, we found a lower sensitivity to the difference in subjective reward values and higher learning rates during reversal than initial discrimination. The sex differences, particularly in reversal learning, support previous findings using this paradigm. Interestingly, the only consistent probability group difference we observed across discrimination and reversal learning phases was in motivation (i.e., a richer environment was associated with longer reward collection latencies than a leaner environment). Collectively, our fine-grained analyses suggest that trial-by-trial behavioral measures of latencies and strategies may be particularly sensitive metrics to pair with neural correlate data in reversal learning. These measures may also be revealing in uncovering the unique substrates of flexible learning.

Method

Subject

Subjects were N = 25 adult male (n = 13) and female (n = 12) Long-Evans rats (Charles River Laboratories) aged > postnatal-day (PND) 60 at the start of testing. Rats arrived to the vivarium between PND 40 and 60. The rats included in this report served as controls for two different experiments: One was a cohort of water (H₂O)-only drinking (n = 8 female and n = 8 male) rats that served as controls in an ethanol study (see Two-Bottle Choice section) and the other was a cohort of rats (n = 5 female and n = 4 male) that experienced surgical procedures (see Surgery section), serving as controls for a study targeting the orbitofrontal cortex (OFC) with Designer Receptors Exclusively Activated by Designer Drugs (DREADDs). Importantly, all rats were the same age (PND 140–155) when pretraining commenced, and further, all rats were part of experiments that ran in parallel, minimizing differences between cohorts.

Before any treatment, all rats underwent a 3-day acclimation period during which they were pair-housed and given food and water ad libitum, and remained in cages with no experimenter interference. Following this 3-day acclimation period, animals were handled for 10 min per animal for 5 consecutive days. During the handling period, the animals were also provided food and water ad libitum. After the handling period, animals were individually housed under standard housing conditions (room temperature 22–24 °C) with a standard 12 hr light/dark cycle (lights on at 6 a.m.). Following either two-bottle choice or surgery, rats were tested on probabilistic discrimination and reversal learning, as below. All procedures were conducted in accordance with the recommendations in the Guide for the Care and Use of Laboratory Animals of the National Institutes of Health and the Chancellor’s Animal Research Committee at the University of California, Los Angeles.

Two-Bottle Choice

Home cages were modified to allow for the placement of two bottles for drinking, whereas standard housing allows for only one bottle. Rats (n = 16; 8 male and 8 female) included in this analysis were singly housed and given access to two H₂O bottles simultaneously (no ethanol) for 10 weeks, the same duration that experimental animals were provided the choice of ethanol versus H₂O. Weight of bottles was measured three times per week to measure consumption amounts, compared to a control cage placed on the same rack to account for leakage. Rats were not monitored for weight during this time.

Surgery

Viral Constructs

Rats (n = 9; 4 male and 5 female) included in the present comparison were singly housed and allowed to express DREADDs or Green Fluorescent Protein (eGFP) in OFC for 6 weeks, the same duration experimental animals that were treated with clozapine-N-oxide (CNO) were allowed to express DREADDs. An adeno-associated virus AAV8 driving the hM4Di-mCherry sequence under the CaMKIIa promoter was used to express DREADDs on OFC neurons (AAV8-CaMKIIa-hM4D(Gi)-mCherry, packaged by Addgene) (Addgene, viral prep #50477-AAV8). A virus lacking the hM4Di DREADD gene and only containing the green fluorescent tag eGFP (AAV8-CaMKIIa-EGFP, packaged by Addgene) was also infused into OFC in separate cohorts of animals as a null virus control. Altogether the animals included in these sets of analyses served as control cohorts for a larger experiment in which they were given subcutaneous injections of either CNO or a saline vehicle (VEH) prior to reversal learning. The animals included here were five animals prepared with hM4Di DREADDs in OFC who received VEH, two animals prepared with eGFP in OFC who received VEH, and two animals prepared with eGFP in OFC, who received CNO during reversal learning. Importantly, although these animals received virus in OFC, the DREADDs were not activated. Further, we provide analyses to show these cohorts did not differ, and could be combined.

Surgical Procedure

Infusion of AAV virus-containing DREADD or eGFP (n = 9) in OFC was performed using aseptic stereotaxic techniques under isoflurane gas (1%–5% in O₂) anesthesia prior to any behavioral testing experience. Before surgeries were completed, all animals were administered 5 mg/kg s.c. carprofen (NADA #141–199, Pfizer, Inc., Drug Labeler Code: 000069) and 1 cc saline. After being placed in the stereotaxic apparatus (David Kopf; model 306041), the scalp was incised and retracted. The skull was leveled to ensure that bregma and lambda were in the same horizontal plane. Small burr holes were drilled in the skull above the infusion target. Virus was bilaterally infused at a rate of 0.02 μL/min for a total volume of 0.2 μL per hemisphere into OFC (anterior-posterior [AP] = +3.7; medial-lateral [ML] = ±2.0; dorsal-ventral [DV] = −4.6, relative to bregma). After each infusion, 10 min elapsed before the syringe was pulled up.

Food Restriction

Five days prior to any behavioral testing, rats were placed on food restriction with females on average maintained 12–14 g/day and males given 16–18 g/day of chow. Food restriction level remained unchanged throughout behavioral testing, provided animals completed testing sessions. Water remained freely available in the home cage. Animals were weighed every other day and monitored closely to not fall below 85% of their maximum, free-feeding weight.

Learning

Pretraining

Behavioral testing was conducted in operant conditioning chambers outfitted with an LCD touchscreen opposing the sugar pellet dispenser. All chamber equipment was controlled by customized ABET II TOUCH software.

The pretraining protocol, adapted from established procedures (Stolyarova & Izquierdo, 2017), consisted of a series of phases: Habituation, Initiation Touch to Center Training (ITCT), Immediate Reward Training (IMT), designed to train rats to nosepoke, initiate a trial, and select a stimulus to obtain a reward (i.e., sucrose pellet). During habituation, rats were required to eat five pellets out of the pellet dispenser inside the chambers within 15 min before exposure to any stimuli on the touchscreen. ITCT began with the display of white graphic stimuli on the black background of the touchscreen. During this stage, a trial could be terminated for one of two reasons: If a rat touched the displayed image and received a reward, or if the image display time (40 s) ended, after which the stimulus disappeared, a black background was displayed, and a 10 s intertrial interval (ITI) ensued. If the rat did not touch within 40 s this was scored as an initiation omission. IMT began in the same way as ITCT, but the disappearance of the white graphic stimulus was now paired with the onset of a target image immediately to the left or right of the stimulus (i.e., forced choice). During this stage, a trial could be terminated for one of three reasons. First, if a rat touched the center display (i.e., white graphic stimulus) and touched the image displayed on either side, after which there was a dispensation of one sucrose pellet and illumination of the tray light. Second, if the rat failed to touch the center white graphic stimulus after the display time ended (40 s), after which the stimulus disappeared, a black background was displayed, and a 10 s ITI ensued, scored as an initiation omission. Third, if the image display time (60 s) ended, after which the stimulus disappeared, a black background was displayed, and a 10 s ITI ensued, scored as a choice omission. Rats could also fail to respond to the center stimulus within 40 s during this phase (i.e., initiation omission, as in the previous phase). For habituation pretraining, the criterion for advancement was collection of all five sucrose pellets. For ITCT, the criterion to the next stage was set to 60 rewards consumed in 45 min. The criterion for IMT was set to 60 rewards consumed in 45 min across 2 consecutive days.

Probabilistic Discrimination Learning

After completion of all pretraining schedules, rats were advanced to the discrimination (initial) phase of the probabilistic reversal learning (PRL) task, in which they would initiate a trial by touching the white graphic stimulus in the center screen (displayed for 40 s), and choose between two visual stimuli presented on the left and right side of the screen (displayed for 60 s) counterbalanced between trials, assigned as the better or worse options, with a reward (i.e., sucrose pellet) probability of either p_R(B)=.90 or .70 (i.e., better option) or p_R(W)=.30 (i.e., worse option). If a trial was not initiated within 40 s, it was scored as an initiation omission. If a stimulus was not chosen, it was scored as a choice omission, and a 10 s ITI ensued. If a trial was not rewarded, a 5 s time-out would follow, subsequently followed by a 10 s ITI. Finally, if a trial was rewarded, a 10 s ITI would follow after the reward was collected (Figure 1). The criterion was set to 60 or more rewards consumed and selection of the better option in 70% of the trials or higher during a 60-min session across 2 consecutive days. After reaching the criterion for the discrimination phase, the rats advanced to the reversal phase beginning on the next session. Notably, one animal in the 90–30 group and five animals in the 70–30 group did not meet discrimination criteria and were forced reversed after 25+ days.

Figure 1. Task Design.

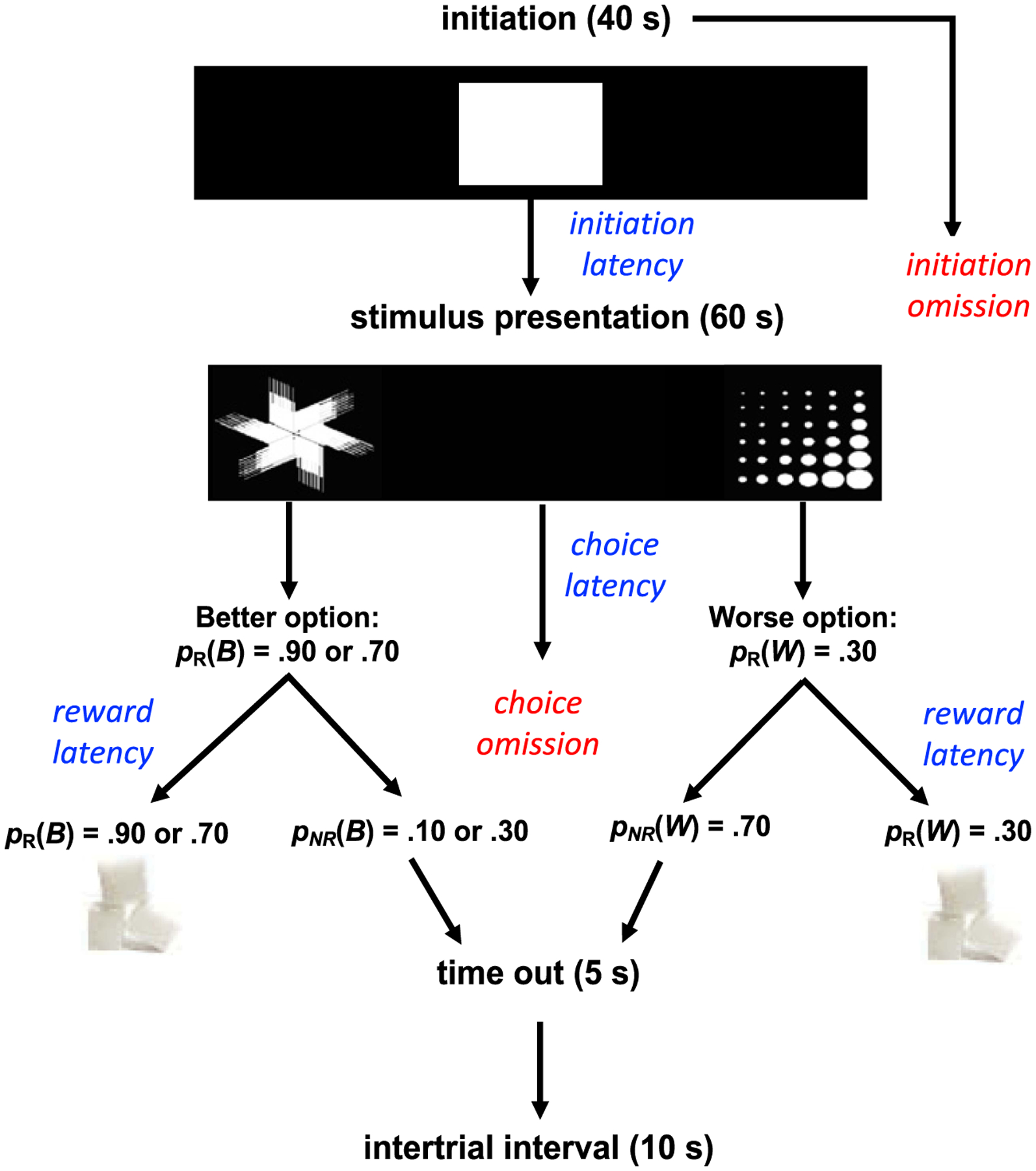
Note. Schematic of probabilistic learning task. Rats initiated a trial by nosepoking the center stimulus (displayed for 40 s) and then selected between two visual stimuli pseudorandomly that were presented on either the left and right side of the screen (displayed for 60 s), Assigned as the better (B) and worse (W) options. Correct nosepokes were rewarded with a sucrose pellet with probability p_R(B) = .90 or .70 versus p_R(W) = .30. If a trial was not rewarded [p_NR(B) or p_NR(W)], a 5 s time-out would commence. If a stimulus was not chosen, it was considered a choice omission and a 10 s ITI would commence. Rats could also fail to initiate a trial, in which case, it was scored as an initiation omission. If a trial was rewarded, a 10 s ITI would follow reward collection. Other prominent measures collected on a trial-by-trial basis were trial initiation latency (time to nosepoke the center white square), choice latency (time to select between the two stimuli), and reward latency (time to collect reward in the pellet magazine).

Probabilistic Reversal Learning

After the discrimination phase, the rats advanced to the reversal phase during which rats were required to remap stimulus-reward contingencies and adapt to reversals in the reward probabilities. The stimuli associated with the p_R(B) = .90 or .70 probability (i.e., better option), would now be associated with a p_R(W) = .30 probability of being rewarded (i.e., worse option). Consistent with prior literature showing freely behaving rodents exhibit slow learning on probabilistic reversals with visual stimuli (Aguirre et al., 2020), most animals from either cohort did not meet a 70% criterion before the termination of the study, so we limited our analyses to the first seven sessions of discrimination and reversal phases for all animals.

Data Analyses and Computational Modeling

MATLAB (MathWorks, Natick, Massachusetts; Version R2019b) was used for all statistical analyses and figure preparation. Data were analyzed with a series of mixed-effects General Linear Models (GLM); omnibus analyses across discrimination and reversal phases in early learning (operationally defined as the first seven sessions), and then individual analyses within each phase separately if justified by a phase interaction. We and others have analyzed early learning in previous work, as it may be particularly informative to revealing sensitivity to reward feedback and perseveration (Izquierdo et al., 2010; Jones & Mishkin, 1972; Stolyarova et al., 2014, 2019), measured using touchscreen response methods (Izquierdo et al., 2006). In the individual analyses for the reversal learning phase, we first ran an unadjusted model which only included the main factors (i.e., day, group, and sex) and their interactions for our main behavioral outcome measures (i.e., probability of choosing the better option, number of rewards, omissions, and latencies) for which a phase interaction was obtained. This was followed by an adjusted model, which included discrimination sessions to criterion as a covariate. The adjusted model was generated to ensure that differences between discrimination and reversal measures were not due to training differences between groups or within individual animals.

Learning data were analyzed with GLM (fitglme function; Statistics and Machine Learning Toolbox; MathWorks, Natick, Massachusetts; Version R2017a), with learning phase (discrimination vs. reversal), probability group (90–30 vs. 70–30), and sex (male vs. female) as fixed factors, and individual rat as random factor. All Bonferroni post hoc tests were corrected for number of comparisons. Statistical significance was noted when p values were less than .05, and p values between .05 and .07 were reported as a trend, or marginally significant. Major dependent variables include: probability correct, number of rewards (sucrose pellets earned), total initiation omissions (failure to initiate a trial), total choice omissions (failure to select a stimulus), and median latencies (to initiate a trial, to nosepoke the correct stimulus, to nosepoke the incorrect stimulus, and to collect reward). The latter we refer to as initiation-, correct-, incorrect-, and reward latencies, respectively.

Each trial was classified as a win if an animal received a sucrose pellet, and as a loss if no reward was delivered. Decisions were classified as better if the animal chose the more rewarding stimulus (stimulus with the larger probability of reward) and worse if it chose the less rewarding stimulus. We classified decisions as Stays when a rat chose the same stimulus on the subsequent trial and as Shifts when it switched to the other alternative. From these first-order measures, we were able to construct win-stay, the probability of choosing the same stimulus on the following trial after being rewarded, and lose-shift, the probability of choosing the alternative stimulus after not receiving a reward. These were further parsed into better or worse win-stay or lose-shift, depending on whether the win-stay/lose-shift followed selection of the better option or the worse option. Because we were primarily interested in the differences between the initial phases of discrimination and reversal learning, only the first seven sessions (i.e., early phase learning) for each animal were included in our analysis on response to reward feedback.

Metrics of Repetition and Perseveration

We also used two additional higher order measures: repetition index and perseveration index. We calculated repetition index (Soltani et al., 2013) as the difference between the actual probability of staying and the chance level of staying (Equation 1):

$$\text{RI}=p(\text{ stay })-(p(\text{ better })\times p(\text{ better })+p(\text{ worse })\times i(\text{ worse })),$$ (1)

where p(stay) is the actual probability of staying equal to the joint probability of choosing the option on two consecutive trials, p(better) is the probability of choosing the more rewarded stimulus, and p(worse) is the probability of choosing the less rewarded stimulus. We further parsed repetition index into RI_B and RI_W, which accounts for differing tendency to stay on better and worse options (Equations 2 and 3):

$${\text{RI}}_{\text{B}}=p(\text{ stay, better })-(p(\text{ better })\times p(\text{ better })),$$ (2)

$${\text{RI}}_{\text{W}}=p(\text{ stay, worse })-(p(\text{ worse })\times p(\text{ worse })).$$ (3)

Additionally, we introduced a perseverative index, analogous to the perseverative index defined in Brigman et al. (2008, 2010) as the number of same stimulus choices following a loss divided by the number of such “runs,” or the ratio of first-presentation stimulus errors to consecutive errors.

We used these two measures, in addition to the probability of staying, to analyze repetitive behavior. As above, we only used the first seven sessions in calculating repetition measures.

Reinforcement Learning Model

We utilized two simple reinforcement learning models to capture animals’ learning and choice behavior across all sessions during discrimination and reversal. In each model, the estimated subjective reward value of a choice (V) was determined by prior choices and corresponding reward feedback. Specifically, subjective reward values were updated based on reward prediction error, the discrepancy between actual and expected reward. For each observed choice, we updated the subjective reward value of the corresponding option. Accordingly, if the more rewarded stimulus was chosen then V = V_better, and if the less rewarded stimulus was selected V = V_worse, where V was the option subjective reward value. We used the following learning rules to update V.

RL1: Model With a Single-Learning Rate

On a given trial t, the subjective reward value of the chosen stimulus is updated using the following function (Equation 4):

$$V(t+1)=V(t)+(r(t)-V(t)),$$ (4)

where V(t) is the subjective reward value on trial t, r(t) is 1 (0) if trial t is rewarded (not rewarded), and α is the single-learning rate.

RL2: Model With Separate Learning Rates for Rewarded and Unrewarded Trials

On a trial t, the following learning rule was used (Equation 5):

$$V(t+1)=\{\begin{array}{l}V(t)+{\alpha }_{\text{Rew }}(1-V(t)),r(t)=1\hfill \\ V(t)-{\alpha }_{\text{Unrew }}V(t)),r(t)=0\hfill \end{array},$$ (5)

where α_Rew and α_Unrew are the learning rates for rewarded and unrewarded trials, respectively.

We then applied the following decision rule to determine the probability of selecting the better option on trial t (Equation 6):

$$P_{\text{better }}(t)=\frac{1}{1+\text{exp}\left(-\sigma \left(V_{\text{better }}-V_{\text{worse }}\right)\right)},$$ (6)

where α is the inverse temperature parameter or sensitivity to the difference in subjective reward values.

We fit each model’s parameters to minimize the negative log likelihood (LL) of observed responses. The learning rate parameters (α, α_Rew, and α_Unrew) were restricted to values between 0 and 1, and σ was constrained to values greater than 0. Learning rate parameters were passed through a sigmoid function to avoid local minima at very low learning rates. Initial parameter values were selected from this range, then fit using MATLAB’s fmincon function. For each set of trials, we performed 20 iterations with different initial, randomly selected parameter values to avoid local minima, and the best fit was selected from the iteration with the lowest negative LL. Additionally, we also calculated the Bayesian information criterion (BIC) for each fit, defined as (Equation 7):

$$\text{BIC}=k\text{ln}(n)-2(\text{LL}),$$ (7)

where k is the number of parameters (two in RL1, and three in RL2) and n is the number of trials.

We used two methods to examine the relationship between the learning rates and sensitivity to the difference in subjective reward values. First, we calculated the Pearson correlation coefficient between the estimated learning rate and inverse temperature across animals. That is, after estimating parameters for both groups during discrimination and reversal, we calculated the correlation between sets of learning rates and inverse temperatures across groups during each phase. Second, we examined the parameter correlation derived from our parameter fitting procedure. More specifically, for each animal in each phase, we used the inverse of the Hessian matrix output by fmincon to estimate parameter covariance. From this covariance matrix, we calculated the correlation matrix. This allowed us to obtain analytic estimates of the correlation between parameters for each animal in each phase (Bishop, 2006; Daw, 2011).

Result

Comparisons of Sessions to Criterion, Omnibus Measures

90–30 Reward Probability Control Cohorts

We first conducted statistical analyses to ensure the surgical control cohorts (c-cohort) [i.e., DREADD/VEH, eGFP (CNO + VEH)] that constituted the 90–30 reward probability group did not differ significantly on omnibus measures: number of sessions to criterion (to 70% accuracy), probability of choosing the better option, and number of rewards collected during discrimination and reversal learning (i.e., first 7 days of learning common to all rats). There was no effect of surgical control cohort (GLM: β _c-cohort = 4.17, t(5) = 0.79, p = .46) or sex (GLM: β_sex = 8.17, t(5) = 1.55, p = .18) on sessions to reach criterion, probability correct (GLM: β_c-cohort = 0.004, t(54) = 0.05, p = .96; GLM: β_sex = 0.06, t(54) = 0.98, p = .33), or number of rewards collected (GLM: β_c-cohort = −6.39, t(54) = −0.27, p = .78; GLM: β_sex = 2.80, t(54) = 0.09, p = .93) for discrimination learning. Similarly, for reversal learning, we did not find any effect of surgical control group (GLM: β_c-cohort = −0.17, t(5) = −0.05, p = .96) or sex (GLM: β_sex = −2.67, t(5) = −0.76, p = .48) on sessions to reach criterion, probability correct (GLM: β_c-cohort = 0.02, t(53) = 0.37, p = .72; GLM: β_sex = 0.10, t(53) = 1.24, p = .22), or number of rewards collected (GLM: β_s-group = −18.52, t(53) = −1.19, p = .24; GLM: β_sex = −7.81, t(53) = −0.40, p = .69). Given the lack of differences between surgical control cohorts within the 90–30 reward probability group, we collapsed data across these cohorts for further analyses.

Number of Sessions

In total, the 70–30 probability group performed a total of 847 sessions, 417 during the discrimination phase and 430 during reversal (an average of 26.1 ± 3.1 during the discrimination phase and 26.9 ± 1.71 during the reversal phase). The 90–30 probability group performed 270 sessions, 118 during discrimination and 152 during reversal (an average of 13.1 ± 2.6 during discrimination and 16.9 ± 1.65 reversal), Figure 2B and D. For discrimination learning, we found no effect of group (p = 0.24), sex (p = 0.21), or significant Group × Sex interaction (p = 0.49) on sessions to reach criterion. The 90–30 reward probability group required an average of 11.56 ± 2.56 (M ± SEM) sessions while the 70–30 reward probability group required an average of 21.13 ± 3.26 sessions to reach a 70% criterion; females required an average of 11.92 ± 2.47 sessions, while males required an average of 23.92 ± 3.59 sessions. For reversal learning, there was a significant effect of group (GLM: β_group = 8.28, t(21) = 2.63, p = 0.02), with the 90–30 reward probability group requiring fewer sessions to reach criterion on average (17.44 ± 1.68) than the 70–30 reward probability (23.50 ± 1.95). However, there was no effect of sex (p = 0.20), with males (17.67 ± 1.97) and females (24.69 ± 1.80) requiring a comparable number of sessions to reach criterion for reversal learning, and no significant Group × Sex interaction (p = 0.41). As differing rates of acquisition during discrimination learning could be attributed to differences in performance in the reversal learning phase, discrimination sessions to criterion were included as a covariate in reversal learning analyses (whenever a phase interaction justified analysis of each phase separately), specifically on the main behavioral outcome measures for which those interactions were found. As a preview, the pattern of results was largely consistent with those obtained without the covariate in the model.

Figure 2. Greater Number of Completed Sessions for the 70–30 Reward Probability Group in Both Discrimination and Reversal Learning.

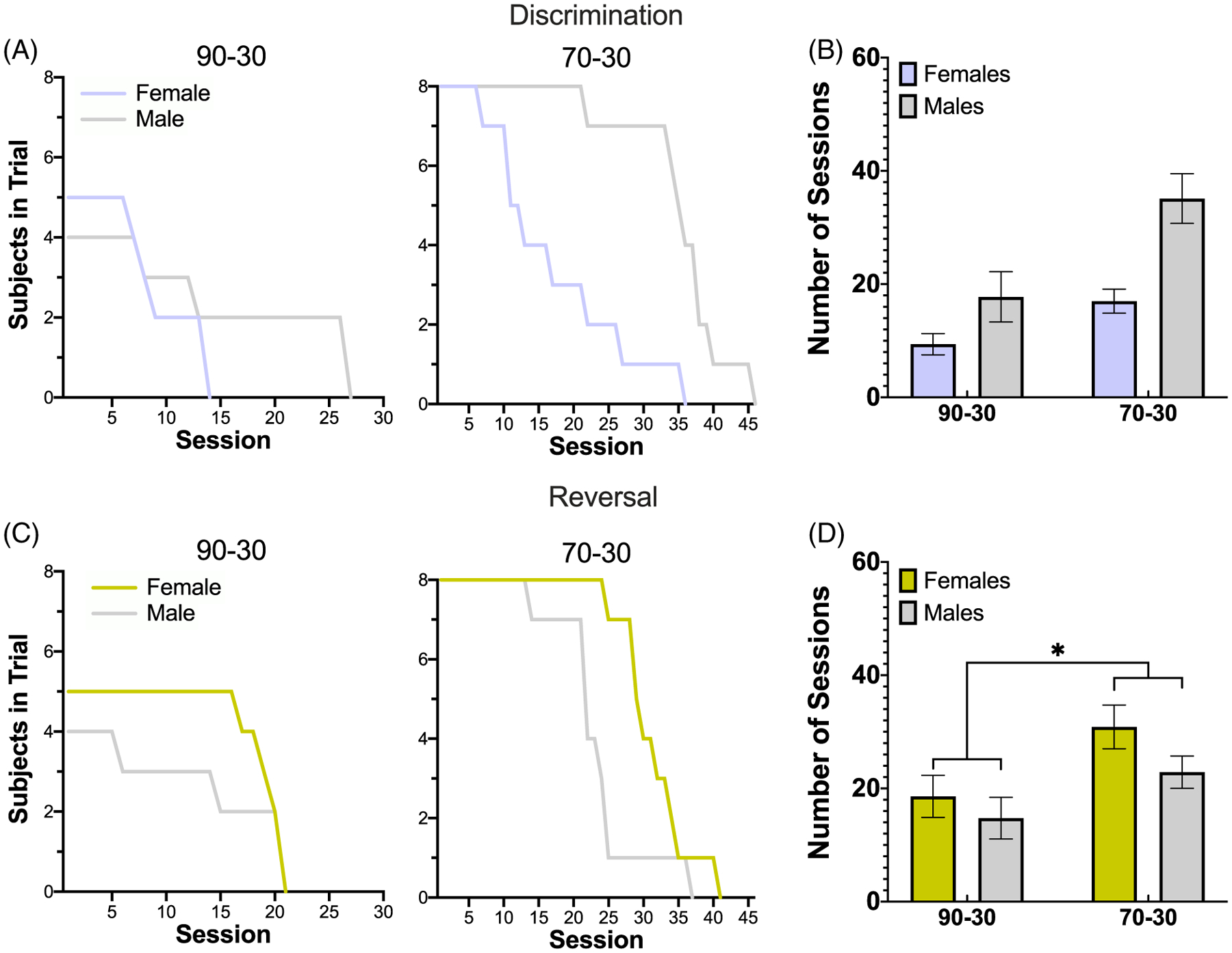
Note. (A and B) Plotted are the number of subjects per session (A) and the number of sessions to criterion (B) during the discrimination (prereversal) phase. The 70–30 reward probability group completes significantly more sessions during discrimination than the 90–30 group. (C and D) The same as (A) and (B) but during reversal learning. The 70–30 reward probability group again completes significantly more sessions than the 90–30 group. Bars indicate ±SEM.

* p ≤ .05.

Comparisons of Accuracy and Rewards Collected

Comparisons Between Early Discrimination and Reversal Learning

We fitted GLMs that combined analysis of the first 7 days of learning across both phases (discrimination and reversal). For probability of choosing the better option (Table 1), we found that all rats exhibited learning by demonstrating an increase in choosing the better option across days (Figure 3). Overall animals chose the better option more in the discrimination phase than the reversal phase. For the number of rewards (Table 2), all rats increased their number of rewards collected across days for both learning phases. There were no difference between reward probability group, or learning phase, nor were there any factor interactions on probability correct or number of rewards. As there were no significant phase interactions, we were not justified to analyze the learning phases separately for these measures.

Table 1.

Probability of Choosing the Better Option During Early Discrimination and Reversal Learning

Early discrimination and reversal learning γ = probability of choosing the better option
Formula Coefficients	γ ~ [1 + Phase × Group × Sex × Day + (1|rats)]
	β	SE	tStat	df	P	CIL	CIU
Intercept	0.4479	0.0463	9.6847	328	<.0001	0.3570	0.5389
Phase	−0.2293	0.0758	−3.0271	328	.0027	−0.3783	−0.0803
Group	0.0070	0.0535	0.1314	328	.8955	−0.0982	0.1122
Sex	0.0433	0.0763	0.5667	328	.5713	−0.1069	0.1934
Day	0.0462	0.0104	4.4607	328	<.0001	0.0258	0.0666
Sex:group	−0.0270	0.0848	−0.3189	328	.7500	−0.1938	0.1398
Sex:phase	0.0836	0.1000	0.8357	328	.4039	−0.1132	0.2804
Group:phase	−0.0270	0.0831	−0.3251	328	.7453	−0.1905	0.1365
Sex:day	−0.0270	0.0228	−1.1846	328	.2370	−0.0719	0.0179
Group:day	−0.0157	0.0142	−1.1069	328	.2692	−0.0435	0.0122
Phase:day	−0.0040	0.0157	−0.2532	328	.8003	−0.0348	0.0269
Sex:group:phase	0.0134	0.1138	0.1175	328	.9065	−0.2105	0.2372
Sex:group:day	0.0152	0.0254	0.5979	328	.5503	−0.0348	0.0652
Sex:phase:day	0.0086	0.0247	0.3474	328	.7285	−0.0400	0.0572
Group:phase:day	0.0070	0.0193	0.3611	328	.7183	−0.0310	0.0449

Note. Bold values indicates p < 0.05.

Figure 3. Both Reward Probability Groups and Both Sexes Increase Their Collected Rewards Over Time but Animals Choose the Better Option More Often in the Discrimination Phase.

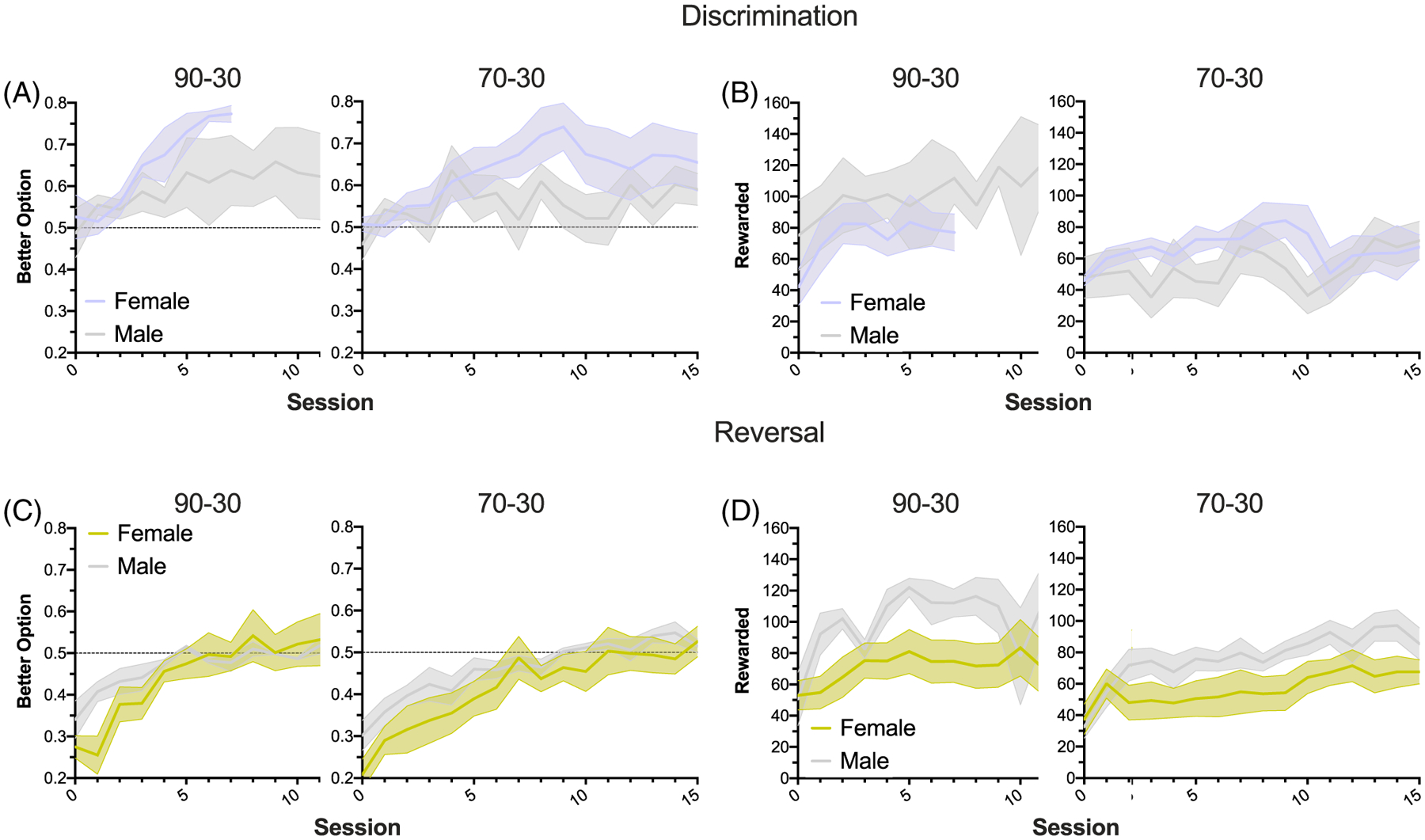
Note. (A and B) Proportion of better option selections (A) and number of rewards in a session (B) in the discrimination (prereversal) phase, showing the first 10 and 15 trials. Both groups increase selection of the better option and receive more rewards per session over time, with no significant differences between reward probability groups or sex. (C and D) Same as (A) and (B), but in the reversal phase. Again, animals in both reward probability groups improve accuracy and collected rewards over time, with no differences by group or sex. Notably, there was significant phase difference on choice of the better option, with the discrimination > reversal phase.

Table 2.

Total Number of Rewards Collected During Early Discrimination and Reversal Learning

Early discrimination and reversal learning γ = number of rewards
Formula Coefficients	γ ~ [1 + Phase × Group × Sex × Day + (1|rats)]
	β	SE	tStat	df	P	CIL	CIU
Intercept	50.727	10.730	4.7278	328	<.0001	29.620	71.835
Phase	−0.6417	11.562	−0.0555	328	.9558	−23.387	22.103
Group	−2.1959	12.206	−0.1799	328	.8573	−26.207	21.815
Sex	29.130	17.266	1.6871	328	.0925	−4.8371	63.097
Day	5.9808	2.0728	2.8854	328	.0042	1.9031	10.058
Sex:group	−27.929	21.903	−1.2751	328	.2032	−71.018	15.160
Sex:phase	−21.182	29.708	−0.7130	328	.4764	−79.624	37.260
Group:phase	−5.3005	15.352	−0.3453	328	.7301	−35.502	24.901
Sex:day	−2.4540	5.8143	−0.4221	328	.6733	−13.892	8.9840
Group:day	−2.1913	2.4551	−0.8925	328	.3728	−7.0211	2.6386
Phase:day	−1.4236	2.2873	−0.6224	328	.5341	−5.9233	3.0760
Sex:group:phase	23.830	33.182	0.7182	328	.4732	−41.446	89.106
Sex:group:day	−2.0186	6.094	−0.3312	328	.7407	−14.007	9.9698
Sex:phase:day	0.0086	0.0247	0.3474	328	.7285	−0.0400	0.0572
Group:phase:day	0.0070	0.0193	0.3611	328	.7183	−0.0310	0.0449

Note. Bold values indicates p < 0.05.

Summary

The omnibus comparison across phases of early discrimination and reversal learning revealed that all animals demonstrated an increase in accuracy (i.e., probability of choosing the better option) and an increase in the number of rewards collected across days, regardless of reward probability group or sex. However, animals chose the better option more often in the discrimination phase, compared to reversal as expected.

Comparisons of Omissions and Latencies

Comparisons Between Early Discrimination and Reversal Learning

Similar to above, we fitted GLMs that combined analysis of the first 7 days of learning across both phases (discrimination and reversal), Table 3. For total number of initiation omissions, there was a significant Phase × Group × Sex interaction, with post hoc comparisons revealing 70–30 males exhibited more initiation omissions in the discrimination phase than the reversal phase (p = .01). There was also a significant Group × Sex interaction on this measure, but post hoc tests were not significant after accounting for the number of comparisons. There was no effect of phase, reward probability group, or sex, and no significant Phase × Group, or Phase × Sex interactions on this measure. For total number of choice omissions, there was no effect of phase, reward probability group, or sex, and no significant Phase × Group, Phase × Sex, Group × Sex, or Phase × Group × Sex interactions.

Table 3.

Initiation and Choice Omissions During Early Discrimination and Reversal Learning

Coefficients	Early discrimination and reversal learning Formula: γ ~ [1 + Phase × Group × Sex + (1|rats)]
	β	SE	tStat	df	P	CIL	CIU
γ = initiation omissions
Intercept	138.40	40.087	3.4524	42	.0013	57.500	219.30
Phase	−18.600	17.622	−1.0555	42	.2972	−54.162	16.962
Group	−27.900	44.500	−0.6270	42	.5341	−117.71	61.906
Sex	−58.650	51.131	−1.147	42	.2579	−161.84	44.538
Phase:group	69.350	48.505	1.4298	42	.1602	−28.537	167.24
Phase:sex	1.1000	28.122	0.0391	42	.9690	−55.652	57.852
Group:sex	164.90	70.480	2.3397	42	.0241	22.665	307.13
Phase:group:sex	−158.10	61.395	−2.5751	42	.0136	−282.00	−34.200
γ = choice omissions
Intercept	1.000	0.2828	3.5355	42	.0010	0.4292	1.5708
Phase	0.200	0.3347	0.5976	42	.5533	−0.4754	0.8754
Group	0.625	0.8003	0.7809	42	.4392	−0.9902	2.2402
Sex	3.750	2.7390	1.3691	42	1.3691	−1.7774	9.2774
Phase:group	−0.700	0.5751	−1.2172	42	.2303	−1.8606	0.4606
Phase:sex	−2.450	2.0085	−1.2198	42	.2293	−6.5032	1.6032
Group:sex	−4.625	2.8545	−1.6202	42	.1127	−10.386	1.1357
Phase:group:sex	2.575	2.0843	1.2354	42	.2235	−1.6313	6.7813

Note. Bold values indicates p < 0.05.

Next we analyzed median initiation and better choice latencies (Table 4), as well as worse choice and reward collection latencies (Table 5). For initiation latencies, we found a marginal Group × Sex interaction, but no effect phase, or reward probability group, and no significant Phase × Group, Phase × Sex, Group × Sex, or Phase × Group × Sex interactions. For better choice latencies, there was a significant Phase × Sex interaction, with males exhibiting longer choice latencies for the better option in the discrimination phase compared to the reversal phase (p = .01), but no effect of phase, reward probability group, or sex, and no significant Phase × Group, Group × Sex, or Phase × Group × Sex interactions. For worse choice latencies, there was a significant effect of phase, with animals in the reversal phase exhibiting longer latencies than in the discrimination phase, but no effect of reward probability group, sex, or significant Phase × Group, Phase × Sex, Group × Sex, Phase × Group × Sex interactions. For reward collection latencies, we found a significant effect of reward probability group, with the 90–30 group taking longer to collect reward than the 70–30 group, but no effect of phase or sex. There was a significant Phase × Sex interaction, with females exhibiting longer latencies than males in the reversal phase (p = .01), and a Phase × Group × Sex interaction, with 90–30 males in the discrimination phase than 90–30 males in the reversal phase, but no significant Phase × Group or Group × Sex interaction.

Table 4.

Initiation and Better Choice Latency During Early Discrimination and Reversal Learning

Coefficients	Early discrimination and reversal learning Formula: γ ~ [1 + Phase × Group × Sex + (1|rats)]
	β	SE	tStat	df	P	CIL	CIU
γ = initiation latency
Intercept	4.5118	0.8013	5.6307	42	<.0001	2.8947	6.1289
Phase	−0.8195	0.4883	−1.6782	42	.1007	−1.8049	0.1660
Group	−0.2730	0.9112	−0.2996	42	.7660	−2.1118	1.5658
Sex	−1.1703	1.0509	−1.1136	42	.2718	−3.2911	0.9505
Phase:group	1.0286	0.9268	1.1098	42	.2734	−0.8418	2.8991
Phase:sex	−0.5760	0.9377	−0.6143	42	.5423	−2.4683	1.3163
Group:sex	3.3462	1.7256	1.9392	42	.0592	−0.1362	6.8287
Phase:group: sex	−2.4249	1.7569	−1.3802	42	.1748	−5.9706	1.1207
γ = better choice latency
Intercept	0.9025	0.0704	12.818	42	<.0001	0.7604	1.0446
Phase	0.0332	0.0737	0.4503	42	.6548	−0.1156	0.1820
Group	0.1099	0.1540	0.7138	42	.4793	−0.2009	0.4208
Sex	−0.1401	0.1273	−1.1005	42	.2774	−0.3971	0.1169
Phase:group	−0.2615	0.1338	−1.9537	42	.0574	−0.5315	0.0086
Phase:sex	−0.2118	0.0785	−2.6991	42	.0100	−0.3702	−0.0534
Group:sex	−0.0796	0.2092	−0.3804	42	.7056	−0.5017	0.3426
Phase:group:sex	0.2999	0.1648	1.8193	42	.0760	−0.0328	0.6325

Note. Bold values indicates p < 0.05.

Table 5.

Worse Choice and Reward Latency During Early Discrimination and Reversal Learning

Coefficients	Early discrimination and reversal learning Formula: γ ~ [1 + Phase × Group × Sex + (1|rats)]
	β	SE	tStat	df	P	CIL	CIU
γ = worse choice latency
Intercept	0.8044	0.0824	9.7582	42	<.0001	0.6380	0.9708
Phase	0.0965	0.0312	3.0977	42	.0035	0.0336	0.1594
Group	0.0885	0.1358	0.6519	42	.5181	−0.1856	0.3627
Sex	−0.1177	0.1553	−0.7575	42	.4530	−0.4311	0.1958
Phase:group	−0.1059	0.0919	−1.1521	42	.2558	−0.2913	0.0796
Phase:sex	−0.1543	0.0828	−1.8636	42	.0694	−0.3213	0.0128
Group:sex	−0.0308	0.2051	−0.1502	42	.8814	−0.4446	0.3830
Phase:group:sex	0.0965	0.1379	0.6999	42	.4879	−0.1818	0.3748
γ = reward collection latency
Intercept	1.9392	0.1232	15.737	42	<.0001	1.6905	2.1879
Phase	−0.0482	0.0677	−0.7120	42	.4804	−0.1848	0.0884
Group	−0.5845	0.1387	−4.2155	42	.0001	−0.8643	−0.3047
Sex	−0.1688	0.2034	−0.8300	42	.4113	−0.5793	0.2417
Phase:group	0.0313	0.0781	0.4001	42	.6911	−0.1264	0.1890
Phase:sex	−0.2257	0.0906	−2.4909	42	.0168	−0.4085	−0.0428
Group:sex	0.2706	0.2202	1.2288	42	.2260	−0.1738	0.7151
Phase:group:sex	0.2924	0.1188	2.4604	42	.0181	0.0526	0.5322

Note. Bold values indicates p < 0.05.

Comparisons Within Discrimination Learning

Because we found phase interactions on initiation omissions, better choice latencies, and reward collection latencies, we used GLMs to analyze these variables for the discrimination phase separately (Table 6). For total number of initiation omissions, there were no significant effects of reward probability group, sex, or Group × Sex interaction (Figure 4A). For better choice latencies, there was also no effect of reward probability group or sex, or Group × Sex interaction, despite a phase by sex interaction found during early learning (Figures 4B, S1A, and S1B). However, for reward collection latencies, there was a significant effect of reward probability group with the 90–30 group taking longer to collect reward than the 70–30 group, but no effect of sex and no Group × Sex interaction (Figures 4C, S1C, and S1D).

Table 6.

Initiation Omissions, Better Choice Latency, and Reward Collection Latency During Discrimination Learning

Coefficients	Discrimination learning Formula: γ ~ [1 + Group × Sex]
	β	SE	tStat	df	P	CIL	CIU
γ = initiation omissions
Intercept	236.00	145.72	1.6195	21	.1203	−67.05	539.05
Group	76.125	185.76	0.4098	21	.6861	−310.19	462.44
Sex	−11.000	218.59	−0.0503	21	.9603	−465.58	443.58
Group:sex	462.88	272.63	1.6978	21	.1043	−104.08	1029.8
γ = better choice latency
Intercept	0.9173	0.1052	8.7342	21	<.0001	0.6989	1.1357
Group	0.0555	0.1339	0.4147	21	.6826	−0.2229	0.3339
Sex	−0.0619	0.1575	−0.3931	21	.6982	−0.3895	0.2657
Group:sex	−0.1631	0.1965	−0.8303	21	.4157	−0.5717	0.2455
γ = reward collection latency
ntercept	1.9705	0.1200	16.42	21	<.0001	1.7209	2.2201
Group	−0.6006	0.1530	−3.9258	21	.0008	−0.9187	−0.2824
Sex	−0.2429	0.1800	−1.3492	21	.1916	−0.6172	0.1315
Group:sex	0.3960	0.2245	1.7638	21	.0923	−0.0709	0.8629

Note. Bold values indicates p < 0.05.

Figure 4. Patterns of Latencies by Sex and Reward Probability Group During Discrimination and Reversal Learning.

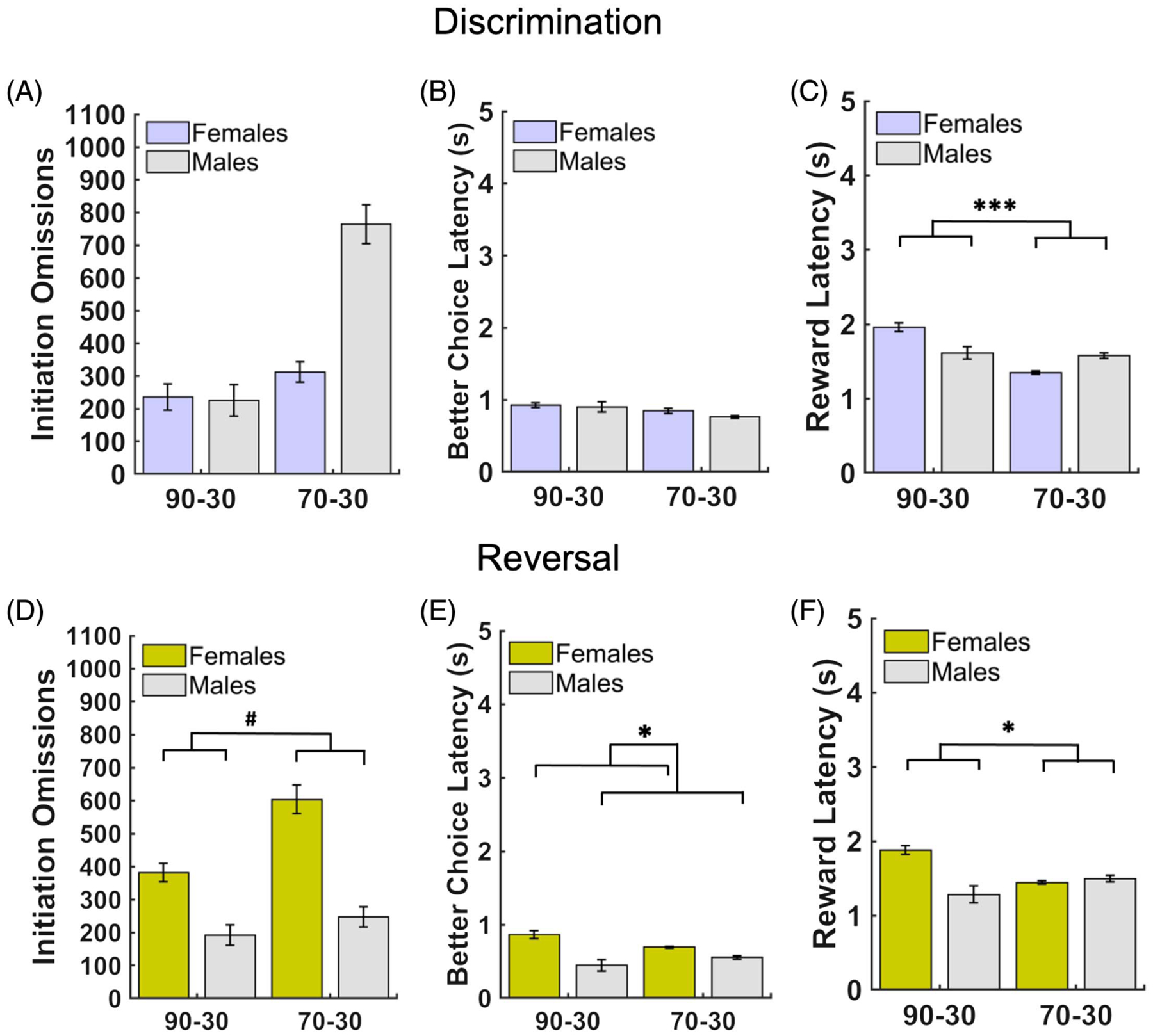
Note. (A) There were no group or sex differences in initiation omissions in discrimination. (B) There were no group or sex differences in better choice latencies in discrimination. (C) There were significant probability group differences in reward collection latencies in discrimination, with the 90–30 reward probability group exhibiting longer latencies than the 70–30 reward probability group. (D) There were no group or sex differences in initiation omissions in reversal. (E) There were sex differences in better choice latencies in the reversal phase, with females taking longer to make a choice of the better option than males (with and without controlling for the number of discrimination sessions to criterion). (F) There were significant probability group differences in reward collection latencies in the reversal phase, with the 90–30 reward probability group exhibiting longer latencies than the 70–30 reward probability group (with and without controlling for the number of discrimination sessions to criterion). Bars indicate ±SEM.

^# p = .07. * p ≤ .05. *** p ≤ .001.

Comparisons Within Reversal Learning

As above, because we found phase interactions on initiation omissions, better choice latencies, and reward collection latencies, we used GLMs to analyze these variables for the reversal phase separately. We ran two models for the reversal learning phase: an unadjusted model which included only the main factors (i.e., group and sex) and an adjusted model with the number of discrimination sessions to criterion added as a covariate (Tables 7 and 8). For total number of initiation omissions, we found a marginal effect of reward probability group (p = .07) in the adjusted model, but did not find a significant sex, or Group × Sex interaction with either model (Figure 4D). For better choice latencies, there was an effect of sex in both the unadjusted and adjusted model, with females exhibiting longer choice latencies than males when choosing the better option. No significant group or Group × Sex interactions were found for either model (Figures 4E, S1E, and S1F). For reward collection latencies, there was a significant effect of reward probability group, with the 90–30 group taking longer to collect reward than the 70–30 group, in both the unadjusted and adjusted model, but no significant sex or Group × Sex interaction was observed (Figures 4F, S1G, and S1H).

Table 7.

Initiation Omissions, Better Choice Latency, and Reward Collection Latency During Reversal Learning

Coefficients	Reversal learning Formula: γ ~ [1 + Group × Sex]
	β	SE	tStat	df	P	CIL	CIU
γ = initiation omissions
Intercept	381.80	113.35	3.3682	21	.0029	146.07	617.53
Group	222.08	144.50	1.5369	21	.1393	−78.426	522.58
Sex	−189.30	170.03	−1.1133	21	.2782	−542.90	164.30
Group:sex	−167.08	212.07	−0.7878	21	.4396	−608.09	273.94
γ = better choice latency
Intercept	0.8899	0.0930	9.5727	21	<.0001	0.6966	1.0832
Group	−0.1766	0.1185	−1.4901	21	.1511	−0.4230	0.0699
Sex	−0.3229	0.1394	−2.3156	21	.0308	−0.6129	−0.0329
Group:sex	0.2153	0.1739	1.2382	21	.2293	−0.1463	0.5770
γ = reward collection latency
Intercept	1.8941	0.1442	13.139	21	<.0001	1.5943	2.1939
Group	−0.4881	0.1838	−2.6560	21	.0148	−0.8703	−0.1059
Sex	−0.3879	0.2163	−1.7936	21	.0873	−0.8376	0.0619
Group:sex	0.4887	0.2697	1.8121	21	.0843	−0.0722	1.0496

Note. Bold values indicates p < 0.05.

Table 8.

Initiation Omissions, Better Choice Latency, and Reward Collection Latency During Reversal Learning With Discrimination Sessions to Criterion (dis_stc) as a Covariate

Coefficients	Reversal learning (covariate: discrimination sessions to criterion) Formula: γ ~ [1 + Group × Sex + dis_stc]
	β	SE	tStat	df	P	CIL	CIU
γ = initiation omissions
Intercept	445.62	116.21	3.8344	20	.0010	203.2	688.04
Group	272.93	142.18	1.9197	20	.0693	−23.643	569.50
Sex	−125.48	167.93	−0.7472	20	.4636	−475.77	224.81
dis_stc	−7.9773	5.2301	−1.5253	20	.1428	−18.887	2.9325
Group:sex	−123.20	204.87	−0.6014	20	.5544	−550.55	304.15
γ = better choice latency
Intercept	0.8958	0.0996	8.9951	20	<.0001	0.6881	1.1036
Group	−0.1719	0.1218	−1.4106	20	.1737	−0.4260	0.0823
Sex	−0.3170	0.1439	−2.2026	20	.0395	−0.6172	−0.0168
dis_stc	−0.0007	0.0045	−0.1653	20	.8570	−0.0101	0.0086
Group:sex	0.2194	0.1756	1.2498	20	.2258	0.1468	0.5856
γ = reward collection latency
Intercept	1.8448	0.1521	12.131	20	<.0001	1.5275	2.162
Group	−0.5274	0.1861	−2.8348	20	.0102	−0.9155	−0.1393
Sex	−0.4372	0.2198	−1.9894	20	.0605	−0.8956	0.0212
dis_stc	0.0062	0.0068	0.9009	20	.3784	−0.0081	0.0204
Group:sex	0.4548	0.2681	1.6965	20	.1053	−0.1044	1.014

Note. Bold values indicates p < 0.05.

Summary

After controlling for the number of discrimination sessions to criterion in reversal learning, we observed the same pattern of effects as that obtained with the original model: Female animals exhibited longer choice latencies for the better option than males (this pattern was not observed for the discrimination phase). Additionally, we found longer reward collection latencies in animals learning the 90–30 reward probabilities, compared to animals in the 70–30 group. This effect was observed in both the discrimination and reversal phases. Finally, though we initially found a phase interaction for initiation omissions in early learning, follow-up analyses yielded only a marginal effect of group, but no sex, or group by sex interactions when the phases were analyzed separately. In sum, we determined that latencies, and not omissions, are among the more sensitive measures of performance; certainly beyond omnibus measures of accuracy and cached rewards that are typically reported in the literature.

Comparisons of Response to Reward Feedback

Comparisons Between Early Discrimination and Reversal Learning

We analyzed win-stay and lose-shift strategies during early discrimination and reversal learning (Table 9). For win-stay, we found a marginally significant effect of phase on employing the win-stay strategy, with animals using this strategy more in the discrimination phase than in the reversal phase, a significant effect of reward probability group, with animals in the 90–30 reward probability group using this strategy more than those in the 70–30 reward probability group, but no effect of sex. There was also a significant Phase × Group interaction, with animals in the 90–30 reward probability group using this strategy more in the discrimination phase than the reversal phase (p = .001), but no significant Phase × Sex, Group × Sex, or Phase × Group × Sex interactions. For lose-shift, there was a significant effect of phase, with animals employing this strategy more in the discrimination learning phase than the reversal phase, a significant effect of reward probability group, with the 90–30 group using the lose-shift strategy more than the 70–30 group. Finally, there was also an effect of sex, with males employing this strategy more than females, but no significant Phase × Group, Phase × Sex, Group × Sex, Phase × Group × Sex interactions.

Table 9.

Win-Stay and Lose-Shift During Early Discrimination and Reversal Learning

Coefficients	Early discrimination and reversal learning Formula: γ ~ [1 + Phase × Group × Sex + (1|rats)]
	β	SE	tStat	df	P	CIL	CIU
γ = win-stay
Intercept	0.5941	0.0122	48.508	42	<.0001	0.5694	0.6188
Phase	−0.1269	0.0290	−4.3795	42	.0001	−0.1853	−0.0684
Group	−0.0746	0.0344	−2.1708	42	.0357	−0.1440	−0.0052
Sex	−0.0876	0.0551	−1.5900	42	.1193	−0.1988	0.0236
Phase:group	0.1068	0.0512	2.0834	42	.0433	0.0033	0.2102
Phase:sex	0.0442	0.0621	0.7118	42	.4805	−0.0811	0.1695
Group:sex	0.0403	0.0667	0.6036	42	.5494	−0.0944	0.1750
Phase:group:sex	−0.0328	0.0782	−0.4196	42	.6769	−0.1907	0.1251
γ = lose-switch
Intercept	0.5721	0.0156	36.586	42	<.0001	0.5405	0.6036
Phase	−0.1572	0.0370	−4.2478	42	.0001	−0.2318	−0.0825
Group	−0.0634	0.0192	−3.3082	42	.0019	−0.1020	−0.0247
Sex	0.0398	0.0186	2.1392	42	.0383	0.0023	0.0773
Phase:group	0.0345	0.0487	0.7082	42	.4827	−0.0638	0.1328
Phase:sex	0.0325	0.0409	0.7942	42	.4316	−0.0501	0.1150
Group:sex	−0.0321	0.0253	−1.2661	42	.2124	−0.0832	0.0191
Phase:group:sex	0.0368	0.0561	0.6564	42	.5152	−0.0763	0.1499

Note. Bold values indicates p < 0.05.

Comparisons Within Discrimination Learning

Because we found phase interactions on win-stay, we were justified to analyze potential differences in win-stay strategies on stimulus responses employed by each reward probability group and by sex, in the discrimination phase separately (Table 10). For win-stay, there was an effect of reward probability group, but no effect of sex, and no Group × Sex interaction (Figure 5A). When we considered win-stay on the better option (win-stay|better), we found a marginally significant effect of reward probability group, with the 90–30 group employing this strategy more, but no effect of sex or significant Group × Sex interaction (Figure 5B). When we analyzed win-stay on the worse option (win-stay|worse), we found no significant effect of reward probability group, sex, or Group × Sex interaction (Figure 5C).

Table 10.

Win-Stay, Win-Stay|Better, and Win-Stay|Worse During Discrimination Learning

Coefficients	Discrimination learning Formula: γ ~ [1 + Group × Sex + (1|rats)]
	β	SE	tStat	df	P	CIL	CIU
γ = win-stay
Intercept	0.5941	0.0122	48.508	21	<.0001	0.5686	0.6196
Group	−0.0746	0.0344	−2.1708	21	.0416	−0.1461	−0.0031
Sex	−0.0876	0.0551	−1.5900	21	.1268	−0.2022	0.0270
Group:sex	0.0403	0.0667	0.6036	21	.5526	−0.0985	0.1791
γ = win-stay|better
Intercept	0.6349	0.0145	43.817	21	<.0001	0.6047	0.6650
Group	−0.0857	0.0412	−2.0801	21	.0500	−0.1714	<.0001
Sex	−0.0971	0.0619	−1.5674	21	.1320	−0.2258	0.0317
Group:sex	0.0288	0.0779	0.3699	21	.7152	−0.1332	0.1908
γ = win-stay|worse
Intercept	0.3791	0.0220	17.266	21	<.0001	0.3334	0.4247
Group	0.0034	0.0360	0.0957	21	.9247	−0.0715	0.0784
Sex	−0.0402	0.0350	−1.1481	21	.2638	−0.1131	0.0326
Group:sex	0.0853	0.0574	1.4858	21	.1522	−0.0341	0.2046

Note. Bold values indicates p < 0.05.

Figure 5. Greater Overall Win-Stay and Win-Stay on the Better Option in the 90–30 Group During Discrimination.

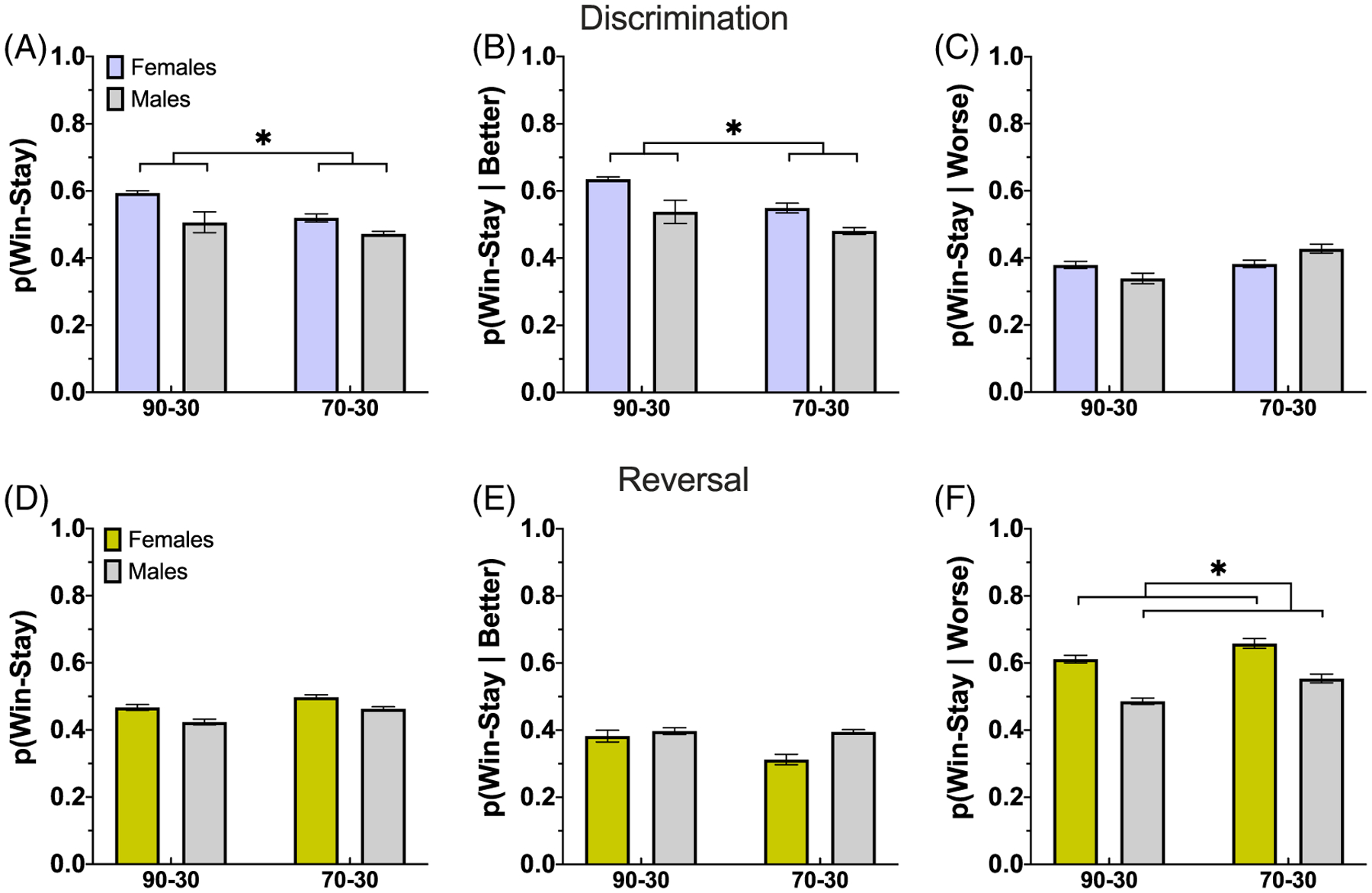
Note. (A–C) Plotted are proportion of win-stay responses overall (A), after choosing the better option (B), and after choosing the worse option (C) during discrimination. Overall win-stay and win-stay on the better option is used more often in the 90–30 group than the 70–30 group. (D–f) The same as (A)–(C) but for reversal. We find no significant effects on overall win-stay and win-stay on the better option, but do find females are more likely to apply a win-stay strategy after choosing the worse option than males. Bars indicate ±SEM.

* p ≤ .05.

Comparisons Within Reversal Learning

Per the phase interactions, we were permitted to analyze win-stay (Table 11) strategies on stimulus responses employed during the reversal phase, separately. We found males were less likely to employ a win-stay strategy (Figure 5D), but no effect of reward probability group, or Group × Sex interaction. We found no significant group or sex differences, and no Group × Sex interaction for win-stay|better (Figure 5E). We did, however, find a significant effect of sex on win-stay|worse, with males less likely to employ the strategy than females, but no reward probability group effect or Group × Sex interaction (Figure 5F).

Table 11.

Win-Stay, Win-Stay|Better, and Win-Stay|Worse During Reversal Learning

Coefficients	Reversal learning Formula: γ ~ [1 + Group × Sex + (1|rats)]
	β	SE	tStat	df	P	CIL	CIU
γ = win-stay
Intercept	0.4672	0.0174	26.850	21	<.0001	0.4311	0.5034
Group	0.0304	0.0256	1.1878	21	.2482	−0.0228	0.0836
Sex	−0.0434	0.0228	−1.9004	21	.0712	−0.0909	0.0041
Group:sex	0.0092	0.0333	0.2771	21	.7844	−0.0600	0.0784
γ = win-stay|better
Intercept	0.3822	0.0351	10.901	21	<.0001	0.3093	0.4552
Group	−0.0696	0.0542	−1.2843	21	.2130	−0.1822	0.0431
Sex	0.0147	0.0392	0.3744	21	.7119	−0.0668	0.0962
Group:sex	0.0671	0.0597	1.1238	21	.2738	−0.0571	0.1913
γ = win-stay|worse
Intercept	0.6115	0.0232	26.313	21	<.0001	0.5632	0.6598
Group	0.0468	0.0450	1.0390	21	.3106	−0.0469	0.1404
Sex	−0.1253	0.0285	−4.4024	21	.0002	−0.1844	−0.0661
Group:sex	0.0208	0.0593	0.3505	21	.7294	−0.1026	0.1442

Note. Bold values indicates p < 0.05.

Summary

Win-stay and win-stay|better strategies were employed more often during early discrimination learning compared to early reversal learning. Further, the 90–30 reward probability group used both win-stay and win-stay|better strategies more in discrimination learning than the 70–30 group. Lastly, female animals were more likely to apply a win-stay|worse strategy in the reversal phase compared to males.

Comparisons of Repetition Measures

Comparisons Between Early Discrimination and Reversal Learning

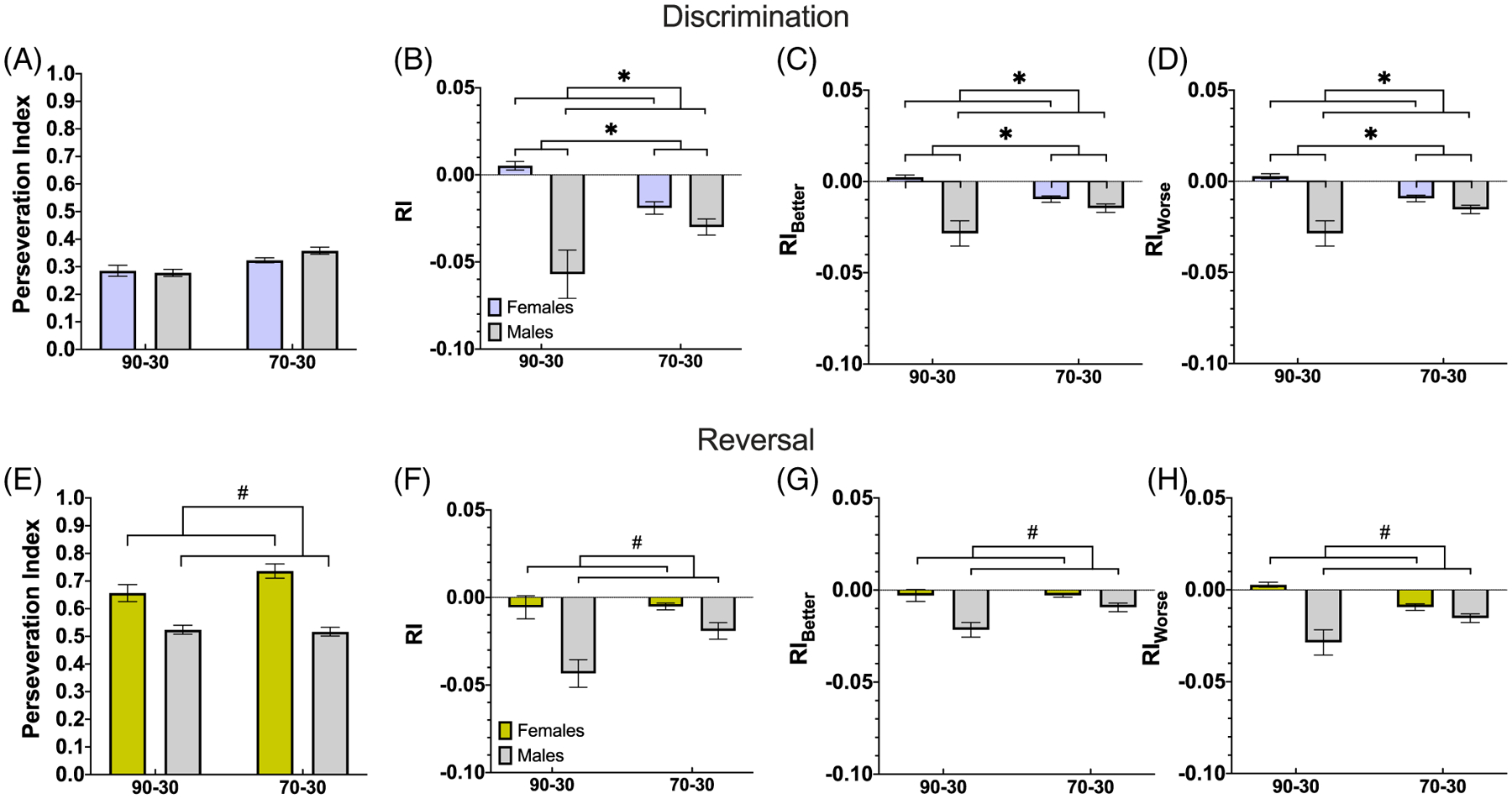
We next fitted GLMs to examine the effects of different factors on repetition in choice behavior. We did not find any significant effect of phase, group, sex, or any significant interaction of those factors on overall p(stay), p(stay|better), or p(stay|worse) (Table 12). However, there was an increased perseveration index in the reversal phase relative to discrimination (Figure 6A and E), regardless of reward probability group or sex (Table 13). For RI, we found a significantly lower value in the 70–30 group and in males, but no significant effects of phase, Phase × Group, Phase × Sex, Group × Sex, or Phase × Group × Sex interaction (Figure 6B and F). Similarly, for RI_B (Table 14) we observed lower values in the 70–30 group and in males, but no significant difference by phase, Phase × Group, Phase × Sex, Group × Sex, or Phase × Group × Sex interaction (Figure 6C and G). This pattern holds for RI_W as well, with a lower RI_W in the 70–30 group and males, and no significant effects of phase, Phase × Group, Phase × Sex, Group × Sex, or Group × Phase × Sex interaction (Figure 6D and H). As we observed no phase interactions, we were not justified in further analyses of discrimination and reversal phases, separately.

Table 12.

p(Stay), p(Stay|Better), and p(Stay|Worse) During Early Discrimination and Reversal Learning

Coefficients		Early discrimination and reversal learning γ ~ [1 + Phase × Group × Sex + (1|rats)]
		β	SE		tStat	df	P	CIL		CIU
γ = p(Stay)
Intercept	0.5420		0.0054	100.37		42	<.0001	0.5311	0.5529
Phase	−0.0172		0.0174	−0.9867		42	.3295	−0.0523	0.0179
Group	−0.0335		0.0234	−1.4321		42	.1595	−0.0806	0.0137
Sex	−0.0727		0.0426	−1.7066		42	.0953	−0.1587	0.0133
Phase: group	0.0738		0.0405	1.8211		42	.0757	−0.0080	0.1556
Phase: sex	0.0110		0.0469	0.2351		42	.8152	−0.0836	0.1057
Group:sex	0.0434		0.0505	0.8590		42	.3952	−0.0585	0.1453
Phase:group:sex	−0.0437		0.0623	−0.7008		42	.4873	−0.1695	0.0821
γ = p(Stay|better)
Intercept	0.6346		0.0143	44.351		42	<.0001	0.6058	0.6635
Phase	−0.2521		0.0472	−5.3433		42	<.0001	−0.3473	−0.1569
Group	−0.0766		0.0397	−1.9307		42	.0603	−0.1566	0.0035
Sex	−0.1078		0.0637	−1.6919		42	.0981	−0.2363	0.0208
Phase:group	0.0172		0.0791	0.2172		42	.8291	−0.1424	0.1768
Phase:sex	0.1202		0.0834	1.4414		42	.1569	−0.0481	0.2886
Group:sex	0.0493		0.0784	0.6281		42	.5333	−0.1090	0.2075
Phase:group:sex	0.0086		0.1088	0.0787		42	.9376	−0.2109	0.2281
γ = p(Stay|worse)
Intercept	0.3761		0.0219	17.134		42	<.0001	0.3318	0.4204
Phase	0.2285		0.0434	5.2692		42	<.0001	0.1410	0.3160
Group	0.0295		0.0333	0.8868		42	.3802	−0.0377	0.0968
Sex	−0.0157		0.0268	−0.5869		42	.5604	−0.0697	0.0383
Phase:group	0.0267		0.0637	0.4200		42	.6766	−0.1018	0.1553
Phase:sex	−0.0718		0.0497	−1.4435		42	.1563	−0.1721	0.0286
Group:sex	0.0501		0.0437	1.1464		42	.2581	−0.0381	0.1383
Phase:group:sex	−0.0548		0.0754	−0.7274		42	.4710	−0.2069	0.0973

Figure 6. Greater Perseveration During Reversal and Lower Repetition Index Measures for Males as Compared to Females in Both Phases, and for the 70–30 Group as Compared to the 90–30 Group in the Discrimination Phase.

Note. Plotted is the perseveration index (A), overall repetition index (B), repetition index for the better option (C), and repetition index for the worse option (D) in the discrimination phase. Though we find no significant differences in perseveration index, the 70–30 group shows a significantly lower RI and RI_B, and marginally significantly lower RI_W. Additionally, males have significantly lower values for all three repetition index measures. (E–H) Same as (A)–(D), but for reversal. We observe a significantly lower perseveration index and a marginally significant lower RI, RI_B, and RI_W in males than females. Bars indicate ± SEM.

^# p = .06. * p ≤ .05.

Table 13.

Perseveration Index and Repetition Index (RI) During Early Discrimination and Reversal Learning

Coefficients	Early discrimination and reversal learning γ ~ [1 + Phase × Group × Sex + (1|rats)]
	β	SE	tStat	df	P	CIL	CIU
γ = perseveration index
Intercept	0.2855	0.0398	7.1683	42	<.0001	0.2052	0.3659
Phase	0.3710	0.0836	4.4373	42	.0001	0.2023	0.5398
Group	0.0379	0.0461	0.8232	42	.4151	−0.0551	0.1309
Sex	−0.0078	0.0456	−0.1707	42	.8653	−0.0998	0.0842
Phase:group	0.0412	0.1101	0.3745	42	.7099	−0.1810	0.2635
Phase:sex	−0.1251	0.0936	−1.3369	42	.1885	−0.3139	0.0637
Group:sex	0.0424	0.0620	0.6838	42	.4978	−0.0828	0.1676
Phase:group:sex	−0.1286	0.1296	−0.9924	42	.3267	−0.3902	0.1330
γ = RI
Intercept	0.0052	0.0049	1.0620	42	.2943	−0.0047	0.0152
Phase	−0.0109	0.0130	−0.8370	42	.4074	−0.0371	0.0153
Group	−0.0243	0.0106	−2.2810	42	.0277	−0.0457	−0.0028
Sex	−0.0623	0.0245	−2.5417	42	.0148	−0.1117	−0.0128
Phase:group	0.0247	0.0185	1.3372	42	.1883	−0.0126	0.0621
Phase:sex	0.0245	0.0306	0.8026	42	.4267	−0.0372	0.0862
Group:sex	0.0513	0.0290	1.7718	42	.0837	−0.0071	0.1098
Phase:group:sex	−0.0275	0.0365	−0.7531	42	.4556	−0.1012	0.0462

Note. Bold values indicates p < 0.05.

Table 14.

Repetition Index on the Better Option (RI_B) and Repetition Index on the Worse Option (RI_W) During Early Discrimination and Reversal Learning

Coefficients	Early discrimination and reversal learning γ ~ [1 + Phase × Group × Sex + (1|rats)]
	β	SE	tStat	df	P	CIl	CIU
γ = RIb
Intercept	0.0024	0.0023	1.0606	42	.2949	−0.0022	0.0070
Phase	−0.0054	0.0064	−0.8437	42	.4036	−0.0182	0.0075
Group	−0.0121	0.0052	−2.3252	42	.0250	−0.0225	−0.0016
Sex	−0.0308	0.0122	−2.5192	42	.0157	−0.0555	−0.0061
Phase:group	0.0122	0.0092	1.3214	42	.1935	−0.0064	0.0308
Phase:sex	0.0122	0.0152	0.8033	42	.4263	−0.0185	0.0429
Group:sex	0.0259	0.0145	1.7912	42	.0805	−0.0033	0.0551
Phase:group:sex	−0.0139	0.0182	−0.7607	42	.4511	−0.0506	0.0229
γ = RIW
Intercept	0.0028	0.0027	1.0606	42	.2949	−0.0025	0.0082
Phase	−0.0055	0.0066	−0.8296	42	.4115	−0.0189	0.0079
Group	−0.0122	0.0055	−2.2351	42	.0308	−0.0232	−0.0012
Sex	−0.0314	0.0123	−2.5632	42	.0140	−0.0562	−0.0067
Phase:group	0.0126	0.0093	1.3515	42	.1838	−0.0062	0.0313
Phase:sex	0.0123	0.0154	0.8016	42	.4273	−0.0187	0.0433
Group:sex	0.0254	0.0145	1.7514	42	.0872	−0.0039	0.0547
Phase:group:sex	−0.0136	0.0183	−0.7451	42	.4604	−0.0506	0.0233

Note. Bold values indicates p < 0.05.

Summary

We found more perseveration during early reversal learning, compared to the discrimination phase. This indicates animals continued to perform according to contingencies learned in discrimination. When using the RI measure, we observed less repetition (lower RI, particularly RI_W) in the 70–30 reward probability group and in males, suggesting probability group and sex have an effect on repetitive behavior that is not due to differences in the propensity to be rewarded.

Comparisons of Estimated Parameters Based on Fit of Choice Behavior With RL Models

Comparisons Between Discrimination and Reversal Learning

To gain more insight into learning and decision-making, we next estimated model parameters (learning rate, α and sensitivity to difference in subjective reward values, σ) based on two RL models across groups in each of the two phases. Unlike our analyses of response to reward feedback and repetition measures, we include all sessions in our RL analysis rather than the first seven to capture learning over a longer time period. We found that the single-learning rate model, RL1, fit the choice data significantly better, as shown by the lower BIC value (difference in BIC between RL1 and RL2 = −7.78, pairwise t test: t(49) = −75.8, p < .0001). For this reason, only results for RL1 are presented below.

Comparison of estimated parameters from RL1 revealed that the average learning rate was significantly higher during reversal than discrimination phase (difference in α = 0.28; two-sample t test: t(48) = −5.48, p < .0001) and at the same time, sensitivity to subjective reward values was significantly lower (difference in σ = −0.77; two-sample t test: t(48) = 8.18, p < .00001), which corresponds to enhanced exploration. Additionally, to better explore the relationship between learning rate and sensitivity to difference in reward values, we calculated the correlation coefficients between parameters across groups. We found a significant negative correlation between learning rate and sensitivity to difference in reward values during reversal (r = −.76, p = .0028) but not discrimination learning (r = −.42, p = .0762). We also calculated the correlation between model parameters using the inverse Hessian at the ML estimate (see Method section). However, we did not find any evidence that the correlations between model parameters of the RL1 model to be significantly different from 0 during discrimination (r = −.16 ± .20, t(24) = −0.82, p = .42) or reversal learning (r = 0.017 ± .14, t(24) = 0.12, p = .90). These results suggest that the observed simultaneous increase in learning rates and decrease in sensitivity to subjective reward value in the reversal relative to the discrimination phase was not due to our fitting procedure and, instead, happened due to independent mechanisms.

Comparisons Within Discrimination Learning

Using estimated parameters based on RL1, we found that the 90–30 reward probability group had a learning rate α = 0.038 ± 0.017, sensitivity to difference in reward values σ = 0.91 ± 0.12 and fit of BIC = 2,227 ± 600 (Figure 7A). The 70–30 reward probability group had a learning rate α = 0.032 ± 0.031, sensitivity to difference in reward values σ = 0.86 ± 0.12 and fit of BIC = 4,234 ± 622. We found no significant differences between reward probability groups in terms of α (two-sample t test: t(23) = 0.74, p = .47) or σ (two-sample t test; t(23) = −0.32; p = .76).

Figure 7. Higher Learning Rate and Lower Sensitivity to Difference in Subjective Reward Values in Reversal Compared to Discrimination Learning.

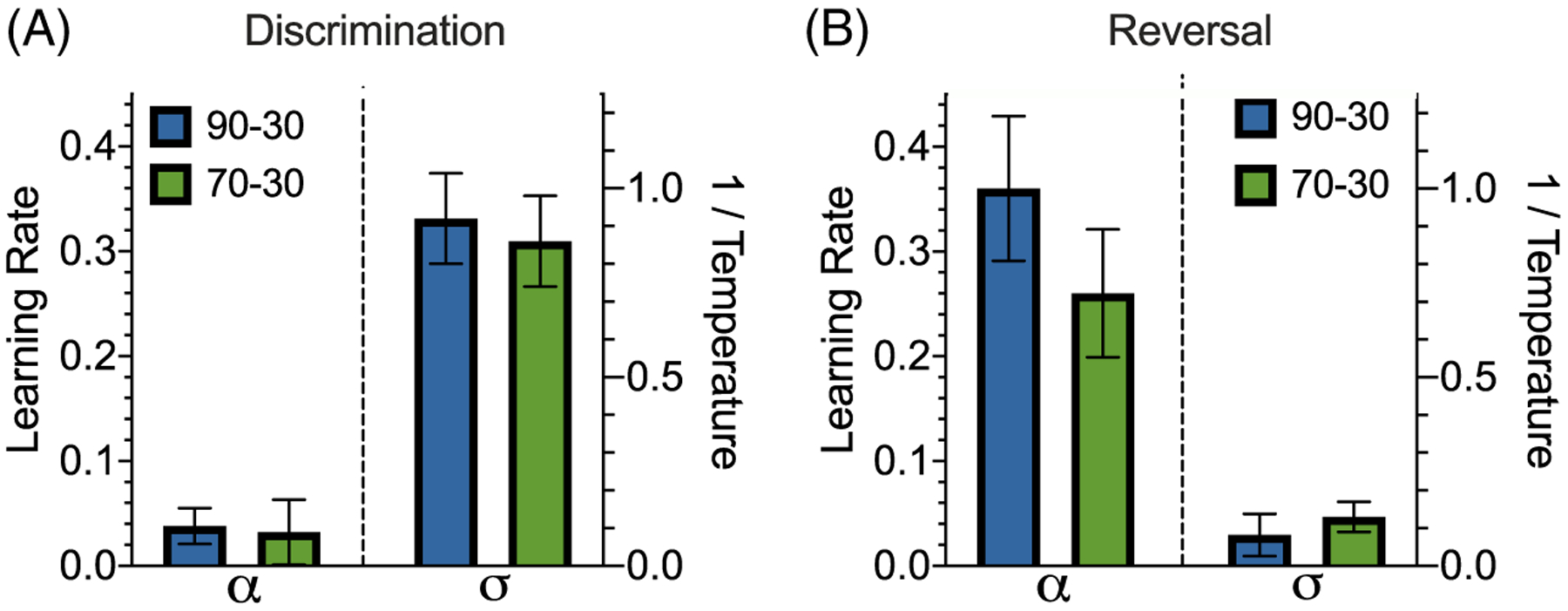
Note. (A and B) Learning parameters and sensitivity to difference in reward values for the single-learning rate model during the discrimination (A) and reversal (B) phases. We find no significant difference in parameter values between reward probability groups during discrimination or reversal. However, we do find significantly higher learning rates and significantly lower sensitivity to difference in reward values parameters following reversal.

Comparisons Within Reversal Learning

As in the discrimination phase, we again fit choice behavior for each subject in the reversal phase using RL1 (Figure 7B). We found that the 90–30 reward probability group had a learning rate α = 0.36 ± .069, sensitivity to difference in reward values σ = 0.082 ± 0.056 and fit of BIC = 3,167 ± 390. The 70–30 reward probability group had a learning rate α = 0.26 ± 0.061, sensitivity to difference in reward values σ = 0.13 ± 0.04 and fit of BIC = 5,262 ± 396. We found no significant difference between the α (two-sample t test; t(23) = −0.96; p = .35) or σ (two-sample t test; t(23) = 0.70; p = .49) parameters between groups.

Summary

In analyses across discrimination and reversal phases, we found that sensitivity to difference in reward values was lower during reversal than discrimination, and learning rate(s) were higher (the single-learning rate for RL1, and both learning rates for RL2) during reversal relative to the discrimination phase. These results indicate that reversal caused faster learning and more exploration at the same time. However, within each phase of learning, the estimated model parameters were not significantly different between probability groups in either phase. We also found no sex-dependent differences. This suggests the slight increased probability of reward corresponding to the better option in the 90–30 reward probability group, as compared to the 70–30 group, was not large enough to induce significantly different learning or, alternatively, this effect could not be captured by our RL models.

Discussion

Here, we used a stimulus-based probabilistic discrimination and reversal paradigm with different probabilities of reward (i.e., 90/30, 70/30) to test learning and performance on several measures (i.e., probability of choosing the better option, initiation and choice omissions and latencies, perseveration and repetition measures, and win-stay/lose-shift strategies). We also examined whether fit of choice data using RL models would reveal differences between the two learning phases, and tested for potential differences in learning rates (single, separate) and explore/exploit behavior. We found higher learning rates in the reversal than discrimination phase, which mirror recent reports (described in more detail below). Animals also exhibited decreased sensitivity to the difference in subjective reward values of the two options during the reversal learning phase compared to discrimination, indicative of greater exploration. Further, we found increased perseveration in early reversal compared to early discrimination learning. Finally, we found that differences in reward collection latencies depended on the richness of the environment (90% vs. 70% reward). Notably, the only pronounced sex difference was in longer latencies to choose the better option during reversal learning (females taking longer than males), which is generally consistent with the pattern of effects of a recent study by our group (Aguirre et al., 2020). We elaborate on these findings in the context of the broader literature below.

Learning Rates

We found that the learning rate was higher in reversal than discrimination learning. The general trend of increased learning rates following reversal and decreased sensitivity to the difference in subjective reward values is consistent with existing literature (Costa et al., 2015; Massi et al., 2018). The increased learning rate suggests a more rapid integration of reward feedback, while the lower sensitivity to difference in reward values indicates rats choose the higher valued option less consistently, corresponding to greater exploration. These changes may reflect response to increased environmental volatility following the reversal in terms of both faster learning and more exploration. Bathellier et al. (2013) accounted for a similar change in learning rate in mice by assuming slower initial learning during discrimination due to weaker initial synaptic weights, and much faster learning during reversal due to the same synapses being activated, but at a state where synaptic weights are stronger than they were in discrimination. Future modeling studies are needed to explain how a single reversal can induce both higher learning rates and decreased sensitivity to subjective values.

Latencies to Collect Reward and Choose the Better Option

Probability group differences across both learning phases were found for reward collection latencies, with the 90–30 group exhibiting longer reward collection times than the 70–30 group, suggesting the 90–30 group may experience attenuated motivation by comparison. Latency to collect reward is commonly used as a measure of motivation, whereas stimulus-response latency (i.e., latency to choose the better option) is often used as a measure of processing or decision-making speed in the Five-Choice Serial Reaction Time Task (5CSRTT; Amitai & Markou, 2010; Asinof & Paine, 2014; Bari et al., 2008; Bushnell & Strupp, 2009; Chudasama et al., 2003; Remmelink et al., 2017; Robbins, 2002; Robinson et al., 2009). One interpretation of this finding is that animals may have been more motivated to confirm whether they had received a reward under higher uncertainty (i.e., when the probability for the better option was lower), and conversely, were more confident in their decision with a higher reward probability associated with choosing the better option. Another related explanation is that animals exert more effort and display more vigor when in leaner and more uncertain reward environments (Amsel, 1967; McNamara et al., 2013), which in our experiments was directly tied to the differences in reward probabilities associated with the better option. Because there was greater reward uncertainty associated with the better option for the 70–30 group, rats may have exerted more effort to retrieve rewards compared to the 90–30 group. Interestingly, although animals generally increased their choice of the better option across days during discrimination learning, this was actually not as much the case for reversal learning where this measure over time was relatively flat. Despite the reward collection latency differences, we found no difference in the number of cached rewards between the probability groups, so these differences are likely not due to satiety per se, but instead, an effect of an experience with overall reward rate over time.

A final consideration related to our consistent probability group difference is a recent report (Song & Lee, 2020) providing evidence for differential neural recruitment in environments that require different “resource allocations.” Agents (or in our case, rats) learn over time to assign resources to certain stimuli, and make adjustments as stimuli gain more reward-predictive value. The leaner reward schedule (70–30) may actually promote a more adjustable, flexible resource allocation than the more profitable schedule (90–30). Empirically testing how midbrain dopamine interacts with cortical structures to support flexible resource allocation is an interesting line of future inquiry. To probe this, different reward probability schedules could be compared.

Perseveration and Win-Stay Strategies

All animals exhibited more perseveration during early reversal learning than early discrimination learning. This finding supports those by Verharen et al. (2020) in which they simulated data of thousands of probabilistic reversal learning sessions using a Q-learning model consisting of separate learning rates for learning from positive (i.e., rewarded) and negative (i.e., nonrewarded) feedback, a beta parameter, and a stickiness parameter indicative of perseveration. They found that a greater number of reversals occurred when the stickiness parameter value was high (i.e., greater perseveration), but only when both learning rates were also high (Verharen et al., 2020). Interestingly, we found reward probability group differences for perseveration, with the 90–30 group exhibiting greater perseveration than the 70–30 group. This finding implies that more consistent reward feedback (i.e., higher reward probability associated with the better option) in the 90–30 group promoted perseverative responding in early learning. Furthermore, males demonstrated greater exploratory behavior (i.e., lower perseveration) during discrimination learning, in line with previous research showing greater impulsivity in male rats (Lukkes et al., 2016; Palanza et al., 2001).

Greater perseveration during early reversal is consistent with the long-standing idea that reversal learning is a measure of inhibitory control, such that the inability to disengage from previously rewarding behavior after a change in contingency may be reflective of compulsive and even impulsive response tendencies, commonly associated with drug dependence (Izquierdo & Jentsch, 2012). Indeed, there is evidence that inflexible responding in reversal learning may be genetically related to impulsivity (Crews & Boettiger, 2009; Fineberg et al., 2010; Franken et al., 2008; Groman et al., 2009; Groman & Jentsch, 2013; Jentsch et al., 2014). However, greater perseveration can also be explained by slower updating of model-free learning in which animals are not benefiting as much from trial-by-trial feedback, or (just as likely) failing to detect task transitions, especially in early reversal (Izquierdo et al., 2017). It is particularly interesting that we show here stimulus perseveration, aside from spatial- or response-based perseveration, which we control for here by pseudorandomly presenting the stimuli on the left versus right sides of the screen.

A related observation we report here is that animals more often used reward-dependent choice strategies (i.e., win-stay and win-stay|better) in the early discrimination phase compared to the reversal phase, and adopted an opposing pattern after reversal (i.e., win-stay|worse as more prevalent). Importantly, as above, this strategy is stimulus-dependent and not location-dependent, which is more often probed in lever-based (left vs. right) tasks. Indeed, animals exhibited less consistent response to reward feedback during the reversal compared to the discrimination phase, indicative of noisier behavior or equivalently more exploration.

Sex Differences

Females exhibited longer latencies to choose the better option than males, and this was only observed during the reversal learning phase. Measures of decision speed in rodents vary, but can include latencies to nosepoke (i.e., time to make a response before the end of the trial), as well as the percentage of correct responses (i.e., accuracy), usually on the 5CSRTT as described above. Our data support the interpretation that females exhibit greater response demands (and consequently slower performance) than males in the reversal phase. This adds to a growing literature on sex differences in reversal learning (Aarde et al., 2020; Bissonette et al., 2012; Branch et al., 2020; LaClair & Lacreuse, 2016).

Conclusion

The present results suggest that certain measures of decision speed (i.e., choice latencies) and motivation (i.e., reward collection latencies) should be used as more than auxiliary measures to study reversal learning. Indeed, latencies, and not omissions, are more sensitive measures than omnibus measures of accuracy and cached rewards that are typically reported in the literature. Some of the measures we studied here are likely correlated with others and it would be interesting in follow-up experiments to pinpoint the most predictive factors in discriminating the two types of learning using a much larger data set. Future studies should probe the neural correlates of these fine-grained behavioral measures, as these have been underutilized and may reveal marked dissociations in how the circuitry is recruited in each phase.