Distance-Independent Cross-Correlated Relaxation and Isotropic Chemical Shift Modulation in Protein Dynamics Studies

Abstract

Cross-correlated relaxation (CCR) in multiple-quantum coherences differs from other relaxation phenomena in its theoretical ability to be mediated across an infinite distance. The two interfering relaxation mechanisms may be dipolar interactions, chemical shift anisotropies, chemical shift modulations or quadrupolar interactions. These properties make multiple-quantum CCR an attractive probe for structure and dynamics of biomacromolecules not accessible from other measurements. Here, we review the use of multiple-quantum CCR measurements in dynamics studies of proteins. We compile a list of all experiments proposed for CCR rate measurements, provide an overview of the theory with a focus on protein dynamics, and present applications to various protein systems.

Graphical Abstract

Cross-correlated relaxation (CCR) in multiple-quantum coherences can theoretically be mediated across an infinite distance. This property makes multiple-quantum CCR an attractive probe for structure and dynamics of biomacromolecules not accessible from other measurements.

• We compile a list of all experiments proposed for long-range multiple-quantum cross-correlated relaxation rate measurements on proteins

• We provide an overview of the theory with a focus on protein dynamics

• We present applications to various protein systems

1. Introduction

Owing to its quantum physical nature, nuclear magnetic resonance (NMR) spectroscopy has its own ‘spooky action at a distance’.^[1] Cross-correlation effects in multiple-quantum (MQ) relaxation offer a tool to observe the interference of two spatially separated events in multi-spin systems.^[2–5] These effects are fundamentally different from the better known autorelaxation, which is responsible for the return of magnetization to the equilibrium state after excitation by radio-frequency pulses. Because cross-correlated relaxation rates constants may be both positive or negative, cross-correlation can enhance or counteract autorelaxation. A brilliant use of this feature is made by so-called TROSY experiments:^[6,7] Spectral peaks that are split by scalar couplings can have autorelaxation rates that are affected in opposite ways by cross-correlated relaxation. TROSY then selects only the component with the narrower lineshape which relaxes slower, thus enabling experiments with substantially larger tumbling times.^[6,7] On the one hand, cross-correlated relaxation between two rank-two relaxation mechanisms including dipole-dipole interaction, chemical shift anisotropy and quadrupolar interaction depends on the relative orientation of the two relevant interaction axes or tensors.^[8–14] As the interactions are modulated by the overall tumbling of the molecule and its internal dynamics with respect to an external polarizing magnetic field, the relaxation rates ultimately report on the temporal correlation of these relative orientations and are sensitive to motion on all time scales.^[15–19] On the other hand, correlated modulation of two rank-zero isotropic chemical shifts provides insight into concerted changes of the electronic environment of two spins.^[2,3,20] In order to be observable in MQ relaxation, this modulation must occur on the slow motion time scale, yet be sufficiently fast to average the chemical shifts of the exchanging spins (setting the limit to μs-ms).

In this review, we focus on the extraction of information on protein dynamics from cross-correlated relaxation (CCR) between two mechanisms that do not share any spin (Figure 1). These types of CCR are usually referred to as ‘remote’ CCR.^[14] Measurement of such CCR rates allows quantification of correlated motions in proteins that may have implication for their functions. We note that CCR also occurs between interactions that share common spins.

Figure 1.

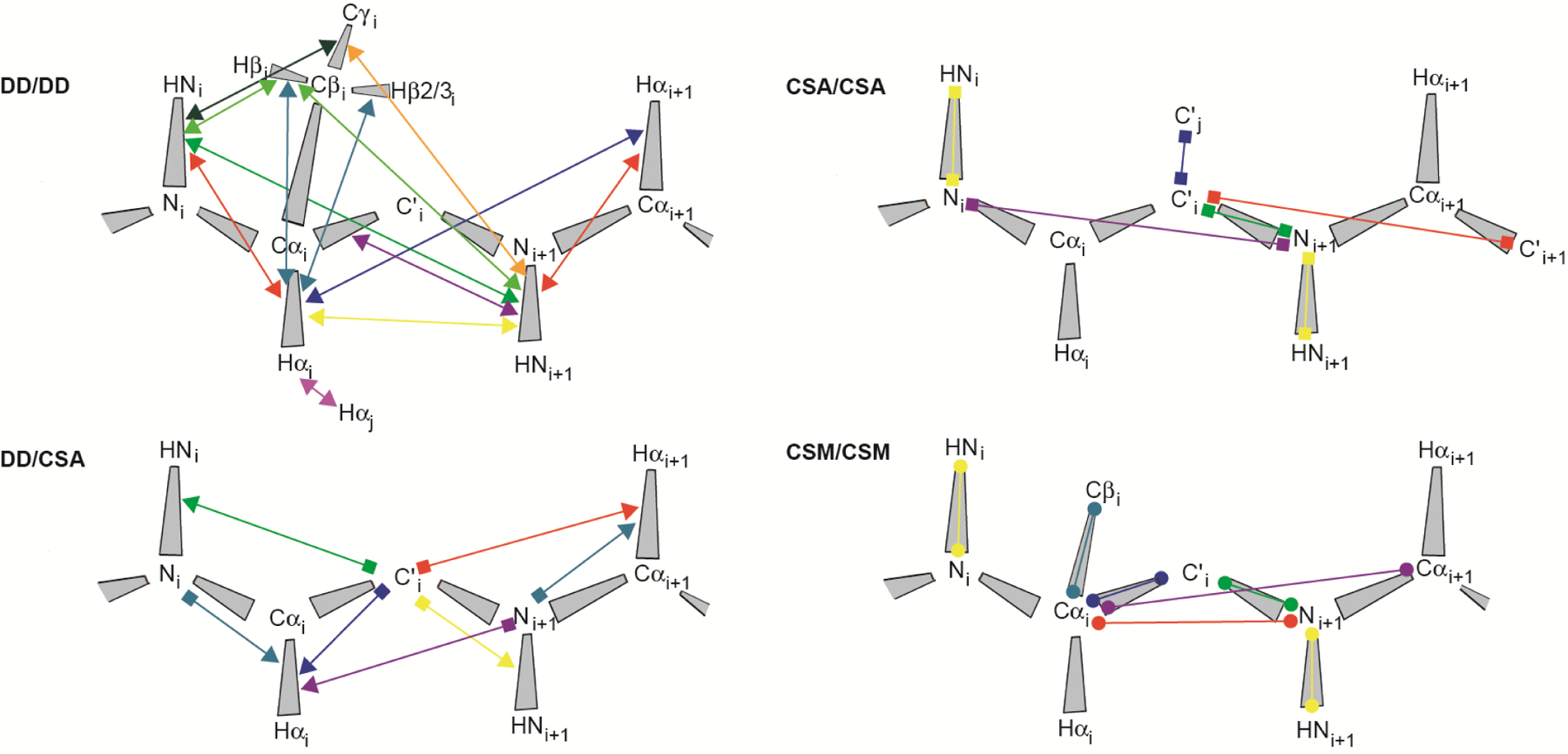
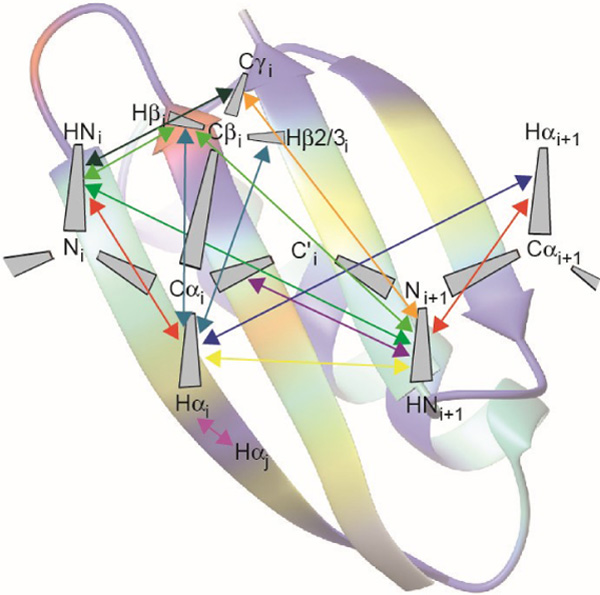
Measured cross-correlated relaxation and isotropic chemical shift modulation. The colored lines connect atoms or atom pairs which are involved in the mechansims giving rise to the interferences. Arrow heads, squares and spheres indicate dipolar interaction (dipole/dipole, DD), chemical shift anisotropy (CSA) and isotropic chemical shift modulation (CSM), respectively. The types of experiment used for measurement and references are given in Table 1.

We distinguish between four different classes of CCR: Interference between two dipole-dipole interactions (DD/DD), between a dipole-dipole interaction and chemical shift anisotropy (DD/CSA), between two chemical shift anisotropies (CSA/CSA), and interference between two isotropic chemical modulations (CSM/CSM). Dipole-dipole interaction is also active between a nucleus and an unpaired electron. In that case, the interaction is referred to as Curie-spin relaxation (CSR).^[21] We do not treat quadrupolar interaction because it vanishes for spins-1/2, of which MQ coherences are typically analyzed in proteins. We denominate the two spins-1/2 being involved in MQ coherence I₁ and S₁. These spins are sufficient to describe CSA and CSM, while for DD interactions, which involve two spins, we assume additional spins I₂ and S₂ in proximity of I₁ and S₁, respectively. As opposed to the distance between I₁ and S₁, the I₁-I₂ and S₁-S₂ distances do impact the CCR rates, which are inversely proportional to the cube of these distances. Although the spatial separation of the two interfering mechanisms giving rise to CCR is unlimited in principle, a practical limitation poses the need to create MQ coherences between spins involved in both interactions. This is highlighted by an overview of all such CCR rates that have been measured in proteins (see Figure 1 and Table 1). The largest separation between almost any two interactions is three covalent bonds for all four classes of CCR translating into distances between the I₁ and S₁ spins of less than 4 Å. The exceptions are CSA(C’)/CSA(C’) and DD(H^αC^α)/DD(H^αC^α) between two neighboring strands in β sheets^[22,23] with associated distances of 4.5–5 Å. Most CCR rates were measured on the protein backbone, while a few share one interaction from the backbone with one in a side chain.^[24–27]

Table 1.

Experiments used for measurement of MQ CCR rates

first mechanism	second mechanism	MQ coherence (I1-S1)	intervening angles	type of experimenta,b	reference
dipole-dipole	dipole-dipole
HNi - Ni	Hαi - Cαi	Ni / Cαi	φ	3D HNCA: DIAI; 3D TROSY-HNCA; 3D HNCA: DIAI; 3D HNCA: ACE; 2D HNCA: DIAI; 3D HNCA: MMQ	45, 46, 47, 48, 49, 50
HNi - Ni	Hβi – Cβi (Ile, Thr, Val)	Ni / Cβi	φ, χ1	3D HN(CA)CB: MMQ	27
HNi - Ni	Cγi – Cβi (aromatic, ASX)	Ni / Cβi	φ, χ1	3D HN(CA)CB: ACE	26
HNi - Ni	HNi+1 - Ni+1	Ni / Ni+1	φ, ω, ψ	2D HN(CACO)N: DIAI; 3D HN(CA)CON: DIAI; 3D HNCA(CO)N: DIAI	17, 50, 50
Hαi - Cαi	Hβ(2,3)i - Cβi	Cαi / Cβi	χ1	3D HBHA(CBCACO)NH: DIAI	25
Hαi - Cαi	HNi+1 - Ni+1	Cαi / Ni+1	ψ, ω	3D HN(CO)CA: ACE, MMQ; 2D HN(CO)CA: DIAI; 3D HNCA: DIAI; 3D TROSY-HNCA; 3D HN(CO)CA: DIAI	4/48/51, 52, 53, 45, 54, 46, 47
Hαi - Cαi	Hαi+1 - Cαi+1	Cαi / Cαi+1	ψ, ω, φ	2D HNCA/CA: DIAI; 3D HNCA(CO)CA	55, 50
Hαi - Cαi	Hαj - Cαj	Hαi / Hαj	N/A	2D HACACAHA: DIAI	23
Hβi – Cβi (Ile, Thr, Val)	HNi+1 - Ni+1	Cβi / Ni+1	ω, ψ, χ1	3D HN(CA)CB: MMQ	27
Cγi – Cβi (aromatic, ASX)	HNi+1 - Ni+1	Cβi / Ni+1	ω, ψ, χ1	3D HN(COCA)CB: ACE	26
Cαi - C’i + Cαi - Ni+1	HNi+1 - Ni+1 + HNi+1 - C’i	C’i / Ni+1	ω	2D H(N)CO: MMQ; 3D HNCO: MMQ; 3D HNCO: ACE, MMQ	56, 56, 57/57
dipole-dipole	CSA
HNi - Ni	C’i	Ni / C’i	φ, ψ	3D HN(CA)CO: MMQ	58
Hαi - Cαi	Ni	Ni / Cαi	φ	3D TROSY-ZQ/DQ-HNCA	46
Hαi - Cαi	C’i	Cαi / C’i	ψ	3D HN(CO)CA: ACE, MMQ, DIAI; 2D HN(CO)CA: ACE	59, 60, 61, 54
Hαi - Cαi	Ni+1	Cαi / Ni+1	ψ, ω	3D HN(CO)CA: ACE; 3D TROSY-ZQ/DQ-HNCA	51, 46
HNi+1 - Ni+1	C’i	C’i / Ni+1	ω	2D HNCO: ACE; 2D H(N)CO: MMQ; 3D HNCO: MMQ	62, 56, 56
Hαi+1 - Cαi+1	C’i	C’i / Cαi+1	ω, φ	3D HNCA/CO: ACE; 2D HNCA: DIAI	63, 49
CSA	CSA
HNi	Ni	HNi / Ni	N/A	2D HN-HMQC: DIAI; 1D HN: ACE	64, 65
Ni	Ni+1	Ni / Ni+1	φ, ψ, ω	2D HN(COCA)N: DIAI	17
Ni+1	C’i	C’i / Ni+1	ω	2D HNCO: ACE	66
C’i	C’i+1	C’i / C’i+1	ω, φ, ψ	3D HNCO/(CA)CO: ACE	22
C’i	C’j	C’i / C’j	across hydrogen bond	3D HNCO/CO: ACE	22
CSM	CSM
HNi	Ni	HNi / Ni		2D HN-HMQC; DIAI	41/42/64/67
Cαi	Cβi	Cαi / Cβi	χ1	3D HN(CO)CACB	24
Cαi	C’i	Cαi / C’i	ψ	2D TROSY-HNCOCA: DIAI	68
Cαi	Ni+1	Cαi / Ni+1	ψ, ω	2D TROSY-HN(CO)CA: DIAI	68
Cαi	Cαi+1	Cαi / Cαi+1	ψ, ω, φ	2D TROSY-HNCA	68/69
C’i	Ni+1	C’i / Ni+1	ω	2D HNCO: DIAI; 2D TROSY-HNCO: DIAI; 2D CON: DIAI	43/44, 68, 69

^aACE (all component evolution) and MMQ (mixed multiple-quantum evolution) experiments employ a J_I1I2- and J_S1S2-resolved constant time evolution period of separate and mixed zero- and double-quantum coherences, respectively; DIAI (double inphase-antiphase inversion) experiments are quantitative Γ experiments, where ‘reference’ and ‘transfer’ subspectra are recorded

^bIn principle, DD(I₁I₂)/CSA(S₁), CSA(I₁)/DD(S₁S₂), CSA(I₁)/CSA(S₁) and CSM(I₁)/CSM(S₁) can also be extracted from an ACE-type experiment designed to measure DD(I₁I₂)/DD(S₁S₂). Similarly, CSM/CSM cannot be separated spectroscopically from CSA/CSA and vice versa, and neither from DD(I₁K)/(S₁K) with any spin K ≠ I₁, S₁. If not explicitly demonstrated in the according publications, these experiments are not listed.

For completeness, we mention that CCR rates have also been measured on RNA (such as DD(HC)/DD(HC) in riboses^[28,29] and in an aminoethoxy side-chain in aminoethoxy-substituted ribose^[30]; DD(HC)/CSA(N) for χ angle determination^[31]; DD(HC)/CSA(N) in bases or between riboses and bases^[32]; DD(HC)/CSA(P) in the phosphodiester backbone^[33]; CSM(N)/CSM(N) across hydrogen bonds in Watson-Crick base pairs^[34] ), carbohydrates ( DD(HC)/DD(HC)^[35] ) and small molecules ( DD(HH)/DD(HC) and DD(HC)/DD(HC) in a η³-allylpalladium complex and its intermediate in a metal-catalyzed substitution reaction^[36,37] ). DD(HC)/DD(HC) CCR have also been used in the context of transferring structural information from a large complex to smaller molecules that are accessible to NMR analysis (‘transferred CCR’),^[38–40] and CSM(H^N)/CSM(N) or CSM(C’)/CSM(N) have been monitored under CPMG conditions^[41–44].

1.1. The cross-correlated relaxation rate constant

The explicit expressions for I₁/S₁ MQ cross-correlated relaxation rate constants for the DD/DD, DD/CSA and CSA/CSA interferences are ^[12,14]

$$R_{\text{DD}({\text{I}}_{\text{1}}{\text{I}}_{\text{2}})\text{/DD}({\text{S}}_{\text{1}}{\text{S}}_{\text{2}})}={\left(\frac{{\mu }_0}{4\pi }\right)}^2\frac{{\gamma }_{{\text{I}}_{\text{1}}}{\gamma }_{{\text{I}}_{\text{2}}}{\gamma }_{{\text{S}}_{\text{1}}}{\gamma }_{{\text{S}}_{\text{2}}}{\text{h}}^{\text{2}}}{\text{10}{\pi }^{\text{2}}}\frac{1}{{(r_{{\text{I}}_{\text{1}}{\text{I}}_{\text{2}}}^{\text{eff}})}^3{(r_{{\text{S}}_{\text{1}}{\text{S}}_{\text{2}}}^{\text{eff}})}^3}{J}_{\text{DD}({\text{I}}_{\text{1}}{\text{I}}_{\text{2}})\text{/DD}({\text{S}}_{\text{1}}{\text{S}}_{\text{2}})}(0)$$ (1)

$$R_{{\text{DD(I}}_{\text{1}}{\text{I}}_{\text{2}}{\text{)/CSA(S}}_{\text{1}})}=\left(\frac{{\mu }_0}{4\pi }\right)\frac{2{\gamma }_{{\text{I}}_{\text{1}}}{\gamma }_{{\text{I}}_{\text{2}}}{\gamma }_{{\text{S}}_{\text{1}}}{\text{hB}}_{\text{0}}}{\text{15}\pi }\frac{1}{{(r_{{\text{I}}_{\text{1}}{\text{I}}_{\text{2}}}^{\text{eff}})}^3}\left[\mathrm{\Delta }{\sigma }_{{\text{S}}_{\text{1}},\text{x}}^{\text{eff}}{J}_{{\text{DD(I}}_{\text{1}}{\text{I}}_{\text{2}}{\text{)/CSA(S}}_{\text{1}})}^{\text{x}}(0)+\mathrm{\Delta }{\sigma }_{{\text{S}}_{\text{1}},\text{y}}^{\text{eff}}{J}_{{\text{DD(I}}_{\text{1}}{\text{I}}_{\text{2}}{\text{)/CSA(S}}_{\text{1}})}^{\text{y}}(0)\right]$$ (2)

$$R_{{\text{CSA(I}}_{\text{1}}{\text{)/CSA(S}}_{\text{1}}\text{)}}=\frac{8{\gamma }_{{\text{I}}_{\text{1}}}{\gamma }_{{\text{S}}_{\text{1}}}{{\text{B}}_{\text{0}}}^2}{\text{45}}\sum _{\mu =\text{x,y}}\sum _{\mu \text{'}=\text{x',y'}}\mathrm{\Delta }{\sigma }_{{\text{I}}_{\text{1}},\mu }^{\text{eff}}\mathrm{\Delta }{\sigma }_{{\text{S}}_{\text{1}},\mu \text{'}}^{\text{eff}}{J}_{{\text{CSA(I}}_{\text{1}}{\text{)/CSA(S}}_{\text{1}}\text{)}}^{\mu ,\mu \text{'}}(0)$$ (3)

γ_X is the gyromagnetic ratio of nucleus X, B₀ the polarizing magnetic field, r_XY^eff is the effective distance between nuclei X and Y (under the assumption that radial and spherical motion of the bond vectors and the CSA tensors are not correlated),^[71,72] μ₀ is the permeability of free space and h denotes Planck’s constant. ${\sigma }_{\text{X,}\mu }^{\text{eff}}$ is the principal component of the effective chemical shift anisotropy tensor of spin X along the μ dimension and $\mathrm{\Delta }{\sigma }_{\text{X},\mu }^{\text{eff}}\equiv {\sigma }_{\text{X},\text{z}}^{\text{eff}}-{\sigma }_{\text{X},\mu }^{\text{eff}}$ (note that chemical shielding and chemical shift anisotropy are closely related and sometimes use the same symbols; for example, following the convention used in reference 73, ${\sigma }_{\text{X,}\mu }^{\text{eff}}$ is the chemical shielding anisotropy and a negative sign would be added to the right-hand side of equation 2). The spectral density functions J are all taken at zero frequency and depend on the orientation and dynamics of the X₁-X₂ bond vectors and ${\sigma }_{\text{X,}\mu }^{\text{eff}}$. In the simplest case of isotropic molecular tumbling with correlation time τ_c and no internal dynamics, the spectral density function is $J=P_2(\cos \theta ){\tau }_{\text{C}}$, where P₂ is the Legendre polynomial of second order and θ the projection angle between the two interaction axes.

Although never reported to our knowledge, the Curie-spin relaxation (CSR) with either DD^[74–76] or CSA^[77] in a three-spin system (two nuclei and one unpaired electron) can be expanded to a four-spin system. In that case, the CCR rates become:

$$R_{\text{DD}({\text{I}}_{\text{1}}{\text{I}}_{\text{2}})\text{/CSR}({\text{S}}_{\text{1}}{\text{S}}_{\text{e}})}={\left(\frac{{\mu }_0}{4\pi }\right)}^2\frac{{\gamma }_{{\text{I}}_{\text{1}}}{\gamma }_{{\text{I}}_{\text{2}}}{\gamma }_{{\text{S}}_{\text{1}}}{\gamma }_{{\text{S}}_{\text{e}}}{\text{h}}^{\text{2}}{\text{g}}_{\text{e}}{\mu }_{\text{e}}{\text{B}}_0{S}_{\text{e}}(S_{\text{e}}+1)}{15{\pi }^{\text{2}}{\text{k}}_{\text{B}}T}\frac{1}{{(r_{{\text{I}}_{\text{1}}{\text{I}}_{\text{2}}}^{\text{eff}})}^3{(r_{{\text{S}}_{\text{1}}{\text{S}}_{\text{e}}}^{\text{eff}})}^3}{J}_{\text{DD}({\text{I}}_{\text{1}}{\text{I}}_{\text{2}})\text{/CSR}({\text{S}}_{\text{1}}{\text{S}}_{\text{e}})}(0)$$ (4)

$$\begin{gathered} R_{\text{CSA}({\text{I}}_{\text{1}})\text{/CSR}({\text{S}}_{\text{1}}{\text{S}}_{\text{e}})}=\left(\frac{{\mu }_0}{4\pi }\right)\frac{4{\gamma }_{{\text{I}}_{\text{1}}}{\gamma }_{{\text{S}}_{\text{1}}}{\gamma }_{{\text{S}}_{\text{e}}}{\text{hg}}_{\text{e}}{\mu }_{\text{e}}{{\text{B}}_0}^2{S}_{\text{e}}(S_{\text{e}}+1)}{45\pi {\text{k}}_{\text{B}}T}\frac{1}{{(r_{{\text{S}}_{\text{1}}{\text{S}}_{\text{e}}}^{\text{eff}})}^3} \\ \times \left[\mathrm{\Delta }{\sigma }_{{\text{I}}_{\text{1}},\text{x}}^{\text{eff}}{J}_{{\text{CSA(I}}_{\text{1}})/{\text{CSR(S}}_{\text{1}}{\text{S}}_{\text{e}}\text{)}}^{\text{x}}(0)+\mathrm{\Delta }{\sigma }_{{\text{I}}_{\text{1}},\text{y}}^{\text{eff}}{J}_{{\text{CSA(I}}_{\text{1}})/{\text{CSR(S}}_{\text{1}}{\text{S}}_{\text{e}}\text{)}}^{\text{y}}(0)\right] \end{gathered}$$ (5)

g_e is the electronic g factor (for simplicity isotropic), μ_e the electronic Bohr magneton, S_e the Curie spin quantum number, and k_B Boltzmann’s constant. Note that the expressions for CSR cannot be obtained by simple substitution of the corresponding constants used for DD. Instead, the electron spin operator must be replaced by an expectation value before commutator rules are applied to calculate the CCR rate.^[21] It is also worth to mention that CCR involving CSR is able to probe long-range effects even when one spin is shared by the two interfering interactions (for example DD(I₁I₂)/CSR(I₁S_e) in single-quantum I₁ relaxation).^[78–81]

Cross-correlated relaxation between two CSR interactions is also possible, as recently measured via transverse relaxation of a single spin.^[82,83] Theoretically, such a CSR/CSR CCR also acts on MQ coherence in a four-spin system:

$$R_{\text{CSR}({\text{I}}_{\text{1}}{\text{I}}_{\text{e}})\text{/CSR}({\text{S}}_{\text{1}}{\text{S}}_{\text{e}})}={\left(\frac{{\mu }_0}{4\pi }\right)}^2\frac{2{\gamma }_{{\text{I}}_{\text{1}}}{\gamma }_{{\text{I}}_{\text{2}}}{\left[{\gamma }_{\text{e}}{\text{hg}}_{\text{e}}{\mu }_{\text{e}}{\text{B}}_0{S}_{\text{e}}(S_{\text{e}}+1)\right]}^2}{45{\left(\pi {\text{k}}_{\text{B}}T\right)}^{\text{2}}}\frac{1}{{(r_{{\text{I}}_{\text{1}}{\text{I}}_{\text{e}}}^{\text{eff}})}^3{(r_{{\text{S}}_{\text{1}}{\text{S}}_{\text{e}}}^{\text{eff}})}^3}{J}_{\text{CSR}({\text{I}}_{\text{1}}{\text{I}}_{\text{e}})\text{/CSR}({\text{S}}_{\text{1}}{\text{S}}_{\text{e}})}(0)$$ (6)

γ_e stands for both γ_Ie and γ_Se, which are identical, and we assumed that the Curie spin quantum numbers are the same for the two electrons, I_e = S_e.

The cross-correlated relaxation rate constant due to CSM/CSM interference is ^[84]

$$R_{\text{CSM}({\text{I}}_{\text{1}})\text{/CSM}({\text{S}}_{\text{1}})}=\left(\frac{1}{2}\right)\left(J_{\text{CSM}({\text{I}}_{\text{1}})\text{/CSM}({\text{S}}_{\text{1}})}(0)+J_{\text{CSM}({\text{S}}_{\text{1}})\text{/CSM}({\text{I}}_{\text{1}})}(0)\right)$$ (7)

Here, the spectral density function J is different from above as it depends on the correlation of the chemical shifts of I₁ and S₁ rather than vectors. No interference between CSM and dipolar interaction or CSA occurs because these interactions have different ranks.

Note that for all CCR rates mentioned above, there are CCR rates caused by other interferences from which they cannot experimentally be separated,^[17,24] which are typically much smaller as long as no CSM/CSM is involved.

2. Cross-correlated relaxation as a probe of dynamics

In this review, we focus on approaches to extracting protein dynamics information from CCR data. While CSM/CSM CCR rates can be directly translated into dynamics information and all studies dedicated to their measurement necessarily obtained such information, most studies using the first three classes of CCR were restricted to obtain structural information at most, that is, average projection angles between the involved interaction axes (bond axis for DD) and tensors (CSA). Generally, interpretation of these CCR rates in terms of dynamics models is non-trivial because dynamics-induced alterations of the rates are typically much smaller than the rates per se. The quantification of the experimental errors are therefore crucial because they may mask the dynamics effects, and considerable effort has been made to estimate these errors.^[85,86] In principle, however, the DD interaction carries the most directly accessible atomistic information as it is directly related to the bond vector connecting the two atoms that interact. The CSA tensor also has a clear formal relationship with the atom geometry, but a reliable tensor (main axis components and orientation) is required for dynamics extraction. In practice, the tensor uncertainties are usually prohibitive as the tensor ultimately depends on the electronic environment. For similar reasons, it is also difficult to translate CSM/CSM data into a structural representation, but it is useful to study temporal aspects of the dynamics. In the following section, the theoretical relationship between the spectral density functions used in equations 1–7 and protein dynamics is outlined. For the sake of compactness and our focus on dynamics studies, we use DD/DD interference to represent the first three classes of CCR. The generalization to DD/CSA and CSA/CSA is straight-forward. If the CSA tensor is axially symmetric the tensor reduces to a vectorial quantity, and is analoguous to the DD interaction with the constants substituted accordingly. If the CSA tensor is anisotropic it can be represented by a sum of two vectorial representations as proposed by Goldman^[12] and done in equations 2, 3 and 5. Then, each summand carries an individual spectral density function with respect to the according direction of the CSA component.

2.1. Spectral density function of cross-correlated relaxation

Dynamic effects are encoded in the spectral density function J_A/B(ω), where A and B are the two interfering interactions giving rise to the CCR. For simplicity, we omit the subscripts from here on. J(ω) is the Fourier transform of the correlation function:^[87]

$$J(\omega )=\underset{-\infty }{\overset{\infty }{\int }}C(t)\cos (\omega t)dt$$ (8)

The correlation function describing dipole/dipole cross-correlated motion between the vectorial tensors A and B can be expressed as:

$$C(t)=\frac{4\pi }{5}\sum _{q=-2}^2\langle \frac{{\left(r_{\text{B}}^{\text{eff}}\right)}^3{\left(r_{\text{A}}^{\text{eff}}\right)}^3}{r_{\text{B}}^3(t)r_{\text{A}}^3(0)}{\text{Y}}_{2q}^{\text{*}}({\theta }_{\text{B}}(t),{\varphi }_{\text{B}}(t)){\text{Y}}_{2q}({\theta }_{\text{A}}(0),{\varphi }_{\text{A}}(0))\rangle$$ (9)

The angular brackets denote ensemble averaging, Y_2q are the second rank spherical harmonics, r_X(t) is the time-dependent length of vector X, and the polar angles θ and ϕ orient the vectors in the laboratory frame. In the case of CSA, (r^eff)³/r(t)³ would be replaced by Δσ(t)/Δσ^eff.

A reasonable assumption is that the fluctuations of the internuclear distances are not correlated with each other and with the orientations of the internuclear vectors. Thus, the dynamics effects may be absorbed into the effective distances used in equation 1 and the correlation function becomes distance independent:

$$C(t)=\frac{4\pi }{5}\sum _{q=-2}^2\langle {\text{Y}}_{2q}^{\text{*}}({\theta }_{\text{B}}(t),{\varphi }_{\text{B}}(t)){\text{Y}}_{2q}({\theta }_{\text{A}}(0),{\varphi }_{\text{A}}(0))\rangle$$ (10)

A slightly different notation of equation 9 is more convenient to express the correlation function.^[19] We assume that the timescales of anisotropic molecular tumbling (τ_k) are at least one order of magnitude different from those of internal motions. In that case, the correlation function can be factorized into contributions from overall tumbling and internal motion if carried out for five summands individually:

$$C(t)=\sum _{k=-2}^2\langle {C_k}^{\mathrm{int}}(t,0)\rangle e^{-t/{\tau }_k}$$ (11)

where τ_k are the inverted eigenvalues of the anisotropic diffusion operator D:^[17,82]

$$\begin{gathered} 1/{\tau }_{-2}=D_{\text{x}}+D_{\text{y}}+4D_{\text{z}} \\ 1/{\tau }_{-1}=D_{\text{x}}+4D_{\text{y}}+D_{\text{z}} \\ 1/{\tau }_0=6(D-\sqrt{D^2-D{\text{'}}^2}) \\ 1/{\tau }_{+1}=4D_{\text{x}}+D_{\text{y}}+D_{\text{z}} \\ 1/{\tau }_{+2}=6(D+\sqrt{D^2-D{\text{'}}^2}) \end{gathered}$$ (12.1–5)

and the coefficients C_k^int(t, 0) contain the angular dependencies on the vectors A and B given by the polar angles (θ_A, ϕ_A) and (θ_B, ϕ_B) in the molecular frame at times 0 and t, respectively:

$$\begin{gathered} {C_{-2}}^{\mathrm{int}}(t,0)=\frac{3}{\text{4}}{\sin }^2{\theta }_{\text{A}}(0){\sin }^2{\theta }_{\text{B}}(t)\sin 2{\phi }_{\text{A}}(0)\sin 2{\phi }_{\text{B}}(t) \\ {C_{-1}}^{\mathrm{int}}(t,0)=\frac{3}{\text{4}}\sin 2{\theta }_{\text{A}}(0)\sin 2{\theta }_{\text{B}}(t)\cos {\phi }_{\text{A}}(0)\cos {\phi }_{\text{B}}(t) \\ {C_0}^{\mathrm{int}}(t,0)=\frac{3{\mu }^2}{{\text{4N}}^{\text{2}}}{\sin }^2{\theta }_{\text{A}}(0){\sin }^2{\theta }_{\text{B}}(t)\cos 2{\phi }_{\text{A}}(0)\cos 2{\phi }_{\text{B}}(t) \\ -\frac{\sqrt{3}\mu \text{w}}{{\text{4N}}^{\text{2}}}\left[{\sin }^2{\theta }_{\text{A}}(0)\cos 2{\phi }_{\text{A}}(0)(3{\cos }^2{\theta }_{\text{B}}(t)-1)+{\sin }^2{\theta }_{\text{B}}(t)\cos 2{\phi }_{\text{B}}(t)(3{\cos }^2{\theta }_{\text{A}}(0)-1)\right] \\ +\frac{{\text{w}}^2}{{\text{4N}}^{\text{2}}}(3{\cos }^2{\theta }_{\text{A}}(0)-1)(3{\cos }^2{\theta }_{\text{B}}(t)-1) \\ {C_{+1}}^{\mathrm{int}}(t,0)=\frac{3}{\text{4}}\sin 2{\theta }_{\text{A}}(0)\sin 2{\theta }_{\text{B}}(t)\sin {\phi }_{\text{A}}(0)\sin {\phi }_{\text{B}}(t) \\ {C_{+2}}^{\mathrm{int}}(t,0)=\frac{3{\text{w}}^2}{{\text{4N}}^{\text{2}}}{\sin }^2{\theta }_{\text{A}}(0){\sin }^2{\theta }_{\text{B}}(t)\cos 2{\phi }_{\text{A}}(0)\cos 2{\phi }_{\text{B}}(t) \\ +\frac{\sqrt{3}\mu \text{w}}{{\text{4N}}^{\text{2}}}\left[{\sin }^2{\theta }_{\text{A}}(0)\cos 2{\phi }_{\text{A}}(0)(3{\cos }^2{\theta }_{\text{B}}(t)-1)+{\sin }^2{\theta }_{\text{B}}(t)\cos 2{\phi }_{\text{B}}(t)(3{\cos }^2{\theta }_{\text{A}}(0)-1)\right] \\ +\frac{{\mu }^2}{{\text{4N}}^{\text{2}}}(3{\cos }^2{\theta }_{\text{A}}(0)-1)(3{\cos }^2{\theta }_{\text{B}}(t)-1) \end{gathered}$$ (13.1–5)

with

$$\begin{array}{ll}\mu =\sqrt{3}\left(D_{\text{x}}-D_{\text{y}}\right);\hfill & \text{w}=2D_{\text{z}}-D_{\text{x}}-D_{\text{y}}+2\mathrm{\Delta };\hfill \\ \mathrm{\Delta }=3\sqrt{D^2-D{\text{'}}^2};\hfill & \text{N}=2\sqrt{\mathrm{\Delta }\text{w}};\hfill \end{array}$$

$$D\text{'}=\sqrt{\frac{D_{\text{x}}{D}_{\text{y}}+D_{\text{x}}{D}_{\text{z}}+D_{\text{y}}{D}_{\text{z}}}{3}};D=\frac{D_{\text{x}}+D_{\text{y}}+D_{\text{z}}}{3}$$

2.2. Lipari-Szabo model-free approximation

Lipari and Szabo proposed a single-exponential approximation for C using an effective correlation time and a generalized order parameter quantifying motion independently of a specific physical model for isotropic overall tumbling.^[87] Analogous application to fully anisotropic tumbling approximates the correlation function as linear superposition of five monoexponential decays

$$C(t)=\sum _{k=-2}^2\left[{S_k}^{\text{2}}+({\langle {C_k}^{\mathrm{int}}({\theta }_{\text{B}}^{\text{av}},{\varphi }_{\text{B}}^{\text{av}};{\theta }_{\text{A}}^{\text{av}},{\varphi }_{\text{A}}^{\text{av}})\rangle }^{\text{slow}}-{S_k}^{\text{2}})e^{-t/{\tau }_{\text{CCR}}}\right]e^{-t/{\tau }_k}$$ (14)

with

$${S_k}^2\equiv {\langle {C_k}^{\mathrm{int}}\rangle }^{\text{fast}}$$ (15)

The internal motion correlation time τ_CCR characterizes the de-correlation process between vectors A and B. S_k² are the generalized order parameters, which are averages of C^int_k over the sub-nanosecond timescale, thus being only sensitive to fast motion. Impact of slow motion, on the other hand, is manifested in the averaging of C_k^int over timescales longer than the overall tumbling time (typically a few nanoseconds). Assuming that the ergodic hypothesis holds, the angled brackets indicate averaging over the fast and slow timescales as indicated by the superscripts. The polar angles (θ^av_A, ϕ^av_A) and (θ^av_B, ϕ^av_B) are averages over the fast time scale.

Fourier transformation of the correlation function gives the spectral density function:

$$J(\omega )=\sum _{k=-2}^2\left[\frac{{S_k}^{\text{2}}{\tau }_k}{1+{(\omega {\tau }_k)}^2}+\frac{({\langle {C_k}^{\mathrm{int}}({\theta }_{\text{B}}^{\text{av}},{\varphi }_{\text{B}}^{\text{av}};{\theta }_{\text{A}}^{\text{av}},{\varphi }_{\text{A}}^{\text{av}})\rangle }^{\text{slow}}-{S_k}^{\text{2}})\tau {\text{'}}_k}{1+{(\omega \tau {\text{'}}_k)}^2}\right]$$ (16)

with

$$\frac{1}{\tau {\text{'}}_k}=\frac{1}{{\tau }_k}+\frac{1}{{\tau }_{\text{CCR}}}$$ (17)

The impact of motion on the CCR rate may be absorbed into a heuristic order parameter:

$$R_{\text{A/B}}={S^2}_{\text{CCR}}{R_{\text{A/B}}}^{\text{rigid}}$$ (18)

where the CCR rate expected for a rigid molecule can easily be calculated by using the following spectral density function:

$$J^{\text{rigid}}(\omega )=\sum _{k=-2}^2\frac{{\tau }_k{C_k}^{\mathrm{int}}({\theta }_{\text{B}}^{\text{av}},{\varphi }_{\text{B}}^{\text{av}};{\theta }_{\text{A}}^{\text{av}},{\varphi }_{\text{A}}^{\text{av}})}{1+{(\omega {\tau }_k)}^2}$$ (19)

2.3. Symmetrically and isotropically tumbling dynamic molecules

More convenient expressions are obtained for simpler models: If the molecular tumbling is axially symmetric, τ_k = τ_-k and equations 11, 14, 16 and 19 can be rewritten as sums over three terms. If the molecular tumbling is isotropic, all τ_k equal the isotropic tumbling time commonly referred to as τ_C, and the summation is replaced by a single expression:

$$J^{\text{iso}}(\omega )=\left(\frac{S^{\text{2}}{\tau }_{\text{C}}}{1+{(\omega {\tau }_{\text{C}})}^2}+\frac{({\langle {\text{P}}_2({\theta }_{\text{AB}}^{\text{proj}})\rangle }^{\text{slow}}-S^{\text{2}})\tau \text{'}}{1+{(\omega \tau \text{'})}^2}\right)$$ (20)

The only remaining C coefficient is the Legendre polynomial P₂ of the cosine of the projection angle between the vectors A and B, and the order parameter S² is its time average over that fast time scale, which is

$$S^2=\frac{4\pi }{5}\sum _{q=-2}^2{\langle {\text{Y}}_{2q}^{\text{*}}({\theta }_{\text{B}},{\varphi }_{\text{B}}){\text{Y}}_{2q}({\theta }_{\text{A}},{\varphi }_{\text{A}})\rangle }^{\text{fast}}$$ (21)

2.4. Internal motion as a two-step process with a quasi-equilibrium

A slightly more complex model of internal motion accounts for fast and slow motion in isotropically tumbling molecules.^[18,89] Internal dynamics is introduced as a two-step process with fast motions with respect to a quasi-equilibrium conformation of a local environment and slow fluctuations of the latter. Both types of motions have a characteristic correlation time, τ_CCR,f and τ_CCR,s, for the fast and slow motion, respectively. There is a correlation function C^int,quasi(t) of the quasi-equilibrium states reached over the fast time scale and therefore associated with the local environment, but which changes over the slow timescale. The fast time scale is faster than the one associated with S², which is per se also faster than τ_C. The slow time scale, on the other hand, is not necessarily slower than τ_C (as opposed to the motion captured by ${\langle ...\rangle }^{\text{slow}}$ in the previous sections). The spectral density function is (compare to equation 20)

$$\begin{gathered} J^{\text{iso}}(\omega )=\frac{S^{\text{2}}{\tau }_{\text{C}}}{1+{(\omega {\tau }_{\text{C}})}^2} \\ +\frac{\tau {\text{'}}_{\text{f}}}{1+{(\omega \tau {\text{'}}_{\text{f}})}^2}\left[{\langle {\text{P}}_2({\theta }_{\text{AB}}^{\text{proj}})\rangle }^{\text{slow}}-S^{\text{2}}-(C^{\text{int,quasi}}(0)-S^{\text{2}})\frac{{\tau }_{\text{CCR,s}}}{{\tau }_{\text{CCR,s}}-{\tau }_{\text{CCR,f}}}\right] \\ +\frac{\tau {\text{'}}_{\text{s}}}{1+{(\omega \tau {\text{'}}_{\text{s}})}^2}\left[(C^{\text{int,quasi}}(0)-S^{\text{2}})\frac{{\tau }_{\text{CCR,s}}}{{\tau }_{\text{CCR,s}}-{\tau }_{\text{CCR,f}}}\right] \end{gathered}$$ (22)

with $\frac{1}{\tau {\text{'}}_{\text{f}}}=\frac{1}{{\tau }_{\text{C}}}+\frac{1}{{\tau }_{\text{CCR,f}}}$ and $\frac{1}{\tau {\text{'}}_{\text{s}}}=\frac{1}{{\tau }_{\text{C}}}+\frac{1}{{\tau }_{\text{CCR,s}}}$

For ${\tau }_{\text{CCR,s}}\gg {\tau }_{\text{C}}$ and ${\tau }_{\text{CCR,f}}\ll {\tau }_{\text{C}}$ we obtain

$$J^{\text{iso}}(\omega )=\frac{C^{\text{int,quasi}}(0){\tau }_{\text{C}}}{1+{(\omega {\tau }_{\text{C}})}^2}$$ (23)

and is further simplified with axially symmetric fast fluctuations:

$$J^{\text{iso}}(\omega )=\frac{S_{\text{A,fast}}{S}_{\text{B,fast}}{\langle {\text{P}}_2({\theta }_{\text{AB}}^{\text{proj}})\rangle }^{\text{slow}}{\tau }_{\text{C}}}{1+{(\omega {\tau }_{\text{C}})}^2}$$ (24)

S_A,fast and S_B,fast are the order parameters of fast motion of the A and B interaction vectors. This result is in agreement with derivations in references 17 and 19, which show that the degree of correlation of slow motion of the vectors A and B alter the spectral density function and thus the CCR rate, but not the correlation of fast motion. A model has been proposed based on a linearized Langevin approach to describe dynamical coupling between two interactions by expressions for correlation functions and their order parameters.^[90] A simple experimentally accessible decomposition can be derived as follows.^[19] Order parameters of the A and B interaction vectors can be derived from residual dipolar couplings (RDCs), which are also sensitive to slow motion (up to tens of milliseconds).^[91] If these motions are axially symmetric and not correlated, they can be used to express the Legendre polynomial in equation 24. Even if the overall tumbling is anisotropic, the following equality holds

$$J(\omega )=S_{\text{A,RDC}}{S}_{\text{B,RDC}}{J}^{\text{rigid}}(\omega )$$ (25)

Any deviation from this equality is indicative of correlation of slow motion of the vectors of interactions A and B.

Finally, we note that the above derivations are all based on the assumption that the overall tumbling and the internal motion can be separated. Expressions for order parameters for CCR relaxation that are not under this restriction have been derived using slowly relaxing local structure (SRLS) theory.^[92]

2.5. Spectral density function of CSM/CSM

CCR induced by CSM/CSM is caused by correlated deviations from the average chemical shifts of spins I₁ and S₁, δω_I1(t) and δω_S1(t). The equivalent to equation 8 is^[24,84]

$$J{(0)}_{\text{CSM(I1)/CSM(S1)}}=\underset{-\infty }{\overset{\infty }{\int }}\langle \delta {\omega }_{\text{I1}}(t)\delta {\omega }_{\text{S1}}(t-\tau )\rangle d\tau$$ (26)

or, when the amplitudes can be clearly defined with means Δω_I1 and Δω_S1

$$J{(0)}_{\text{CSM(I1)/CSM(S1)}}=\mathrm{\Delta }{\omega }_{\text{I1}}\mathrm{\Delta }{\omega }_{\text{S1}}\underset{-\infty }{\overset{\infty }{\int }}\langle C^{\text{CSM/CSM}}(\tau )\rangle d\tau$$ (27)

Here, C^CSM/CSM is the correlation function of the chemical shift fluctuations. As opposed to cross-correlation between DD and/or CSA, the correlation function and therefore also the spectral density function do not depend on the Larmor frequency, and thus we use zero instead of ω (note that in the special case of MQ coherence CCR only the J(0) terms give rise to CCR, although other terms also contribute in other relaxation types).

Explicit expressions can be derived for two-site exchange with populations p₁ and p₂ and the correlation time of exchange τ_ex = 1/(k₁ + k_-1):^[93]

$$\begin{gathered} R_{\text{CSM(I1)/CSM(S1)}}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left(J{(0)}_{\text{CSM(I1)/CSM(S1)}}+J{(0)}_{\text{CSM(S1)/CSM(I1)}}\right)= \\ \frac{1}{\sqrt{8}}{\left\{\frac{1}{{{\tau }_{\text{ex}}}^2}-{\left(\mathrm{\Delta }{\omega }_{\text{I1}}-\mathrm{\Delta }{\omega }_{\text{S1}}\right)}^2+{\left[{\left(\frac{1}{{{\tau }_{\text{ex}}}^2}+{\left(\mathrm{\Delta }{\omega }_{\text{I1}}-\mathrm{\Delta }{\omega }_{\text{S1}}\right)}^2\right)}^2-\frac{16p_1{p}_2{\left(\mathrm{\Delta }{\omega }_{\text{I1}}-\mathrm{\Delta }{\omega }_{\text{S1}}\right)}^2}{{{\tau }_{\text{ex}}}^2}\right]}^{1/2}\right\}}^{1/2} \\ -\frac{1}{\sqrt{8}}{\left\{\frac{1}{{{\tau }_{\text{ex}}}^2}-{\left(\mathrm{\Delta }{\omega }_{\text{I1}}+\mathrm{\Delta }{\omega }_{\text{S1}}\right)}^2+{\left[{\left(\frac{1}{{{\tau }_{\text{ex}}}^2}+{\left(\mathrm{\Delta }{\omega }_{\text{I1}}+\mathrm{\Delta }{\omega }_{\text{S1}}\right)}^2\right)}^2-\frac{16p_1{p}_2{\left(\mathrm{\Delta }{\omega }_{\text{I1}}+\mathrm{\Delta }{\omega }_{\text{S1}}\right)}^2}{{{\tau }_{\text{ex}}}^2}\right]}^{1/2}\right\}}^{1/2} \end{gathered}$$ (28)

In the fast exchange limit this reduces to:^[67,93]

$$R_{\text{CSM(I1)/CSM(S1)}}=2p_1{p}_2\mathrm{\Delta }{\omega }_{\text{I1}}\mathrm{\Delta }{\omega }_{\text{S1}}{\tau }_{\text{ex}}$$ (29)

3. Applications

3.1. Dynamics from DD/DD, DD/CSA, CSA/CSA CCR

3.1.1. First attempts: Gaussian fluctuation models

The first study that examined the impact of motion on MQ CCR rates between DD and/or CSA was a simulation of the effect of Gaussian Axial Fluctuation (GAF) motion^[94,95] of the peptide plane on DD(H^N_iN_i)/CSA(C’_i-1) and CSA(N_i)/CSA(C’_i-1) CCR.^[62,66] In the GAF approach, motions are modeled as angular fluctuations with Gaussian distributed amplitudes around one axis or three orthogonal axes (Theoretical considerations of GAF in the context of CCR can also be found in reference 84). Dynamics was treated according to equation 24, with the fast order parameters set to 1, effectively assuming that all motion takes place on the slow time scale. In the first of the few attempts to obtain dynamical information from measured MQ CCR rates, sums of dipolar H^NN/C’C^α and H^NC^α/C’N CCR rates and sums of dipolar/CSA H^NN/C’ and H^NC’/N CCR rates have been combined with sums of dipolar/CSA N-C^α/N and C’- C^α/C’ CCR rates and compared to a GAF model, but their small size and uncertainty of the CSA tensors prevented a sound interpretation.^[56] Later, five CCR rate types were combined to fit a GAF model to ubiquitin.^[47]

3.1.2. Fitting staggered conformations

The first clear deduction of motion was achieved from four dipolar HC/HC CCR rates in a CH₂-CH₂ group of a aminoethoxy side chain in a ribose:^[30] Carlomagno et al. fitted populations of all three possible staggered conformations and two associated order parameters. Again, no time scales of the motions were modeled, assuming only slow motion in equation 24. A similar approach was then applied to ubiquitin, where order parameters S² were obtained from best fits of the dipolar H^αC^α/H^βC^β CCR rates to χ1 angles when only one H^β was present.^[25] Typical values were 0.7–1 but those for a few residues were less than 0.5. When two H^β protons were present (H^β2 and H^β3) fits to static χ1 angles failed. Instead, the authors assumed GAF around the C^α-C^β axis and fitted χ1 and the amplitudes of the fluctuations of individual staggered conformations simultaneously. These amplitudes ranged from 4 to 30 degrees. Some residues could not be fitted due to conformational averaging. On the other hand, other residues were fitted with three staggered conformations.

3.1.3. Overall heuristic order parameters

A simpler approach than those mentioned above makes use of equation 18. A heuristic CCR order parameter S²_CCR may be determined from the ratio of the experimental CCR rate and the value predicted from a known structure assuming a rigid molecule. S²_CCR of dipolar H^N_iN_i/H^N_i+1N_i+1 CCR rates measured on ubiquitin were found to be ca. 0.75 on average, but with a large variation.^[17] Similar values were obtained for the chicken villin headpiece subdomain, again with large spread of values.^[89] Inspired by equation 24, a slow motion CCR order parameter S²_CCR,slow was then defined as S²_CCR/(S_i,fast)/(S_i+1,fast) and extracted by using relaxation H^NN order parameters for S_fast.^[89] It was shown that slow motion is present in that protein but the degree of correlation is not encoded in S²_CCR,slow. S²_CCR,slow dropped on average from 0.90 to 0.82 when the temperature was raised from 22 to 32 °C. The same technique was applied to the isolated dematin headpiece domain (DHP), where the three helices had S²_CCR,slow averages of 0.57, 0.71 and 0.77.^[96] A mutation having an additional salt bridge was less flexible and raised the figures to 0.80, 0.77 and 0.78.

Measurements of dipolar H^α_iC^α_i/H^α_i+1C^α_i+1 CCR rates have been reported for ubiquitin in reference 55. With an effective H^α-C^α bond length of 1.12 Å, the heuristic CCR order parameter seems frequently to lie outside the range from 0.76 to 1.

As mentioned above, many experiments have been proposed to measure dipolar H^NN/H^αC^α CCR rates. In most publications, it is not clear what effective bond lengths have been used and how accurate the overall correlation time has been. As a consequence, averaged CCR order parameters are generally spread over a range of 0.75–0.95. For the sequential CCR rates (mostly depending on the ψ angle) in ubiquitin and CheY, Yang and Kay appear to have values of 0.95 for less mobile residues.^[52] Other experiments on ubiquitin yielded lower values, either in the range of 0.8–0.9^[45,53] or 0.76^[54]. For intraresidual rates (mostly depending on the φ angle) obtained from ubiquitin, the values are ca. 0.9^[45] or 0.8^[49]. A CCR order parameter relating bonds in different peptide planes in the SH3 domain from spectrin has also been estimated from CSA(C’)/CSA(C’) CCR rates.^[22] The order parameter takes values between 0.47 and 0.92, but the uncertainty in the assumed CSA tensor may be substantial.

In a recent study, we measured sequential H^NN/H^NN, H^αC^α/H^αC^α and intraresidual and sequential H^NN/H^αC^α dipolar CCR rates at high accuracy and precision on GB3.^[50] We measured all CCR rates with at least two methods as different as possible to obtain insight into systematic errors. The overall standard deviations of the averages of the different methods were 0.19, 1.37, 0.20 and 0.26 s⁻¹. Considering ranges of the measured values of 6.73, 43.9, 12.4 and 12.7 s⁻¹, the errors correspond to 2.8, 3.1, 1.6 and 2.1 %. These data sets were then used for comparison to predicted values based on a highly accurate structure. To absorb effects from radial but not spherical fluctuations, we chose values of 1.02 and 1.09 Å for the effective H^N–N and H^α–C^α bond lengths, respectively.^[71,72] A uniform, overall value of the heuristic order parameter S²_CCR introduced in equation 18 is then obtained from the slope of a linear regression in a plot relating the predicted to the experimental CCR rates (Figure 2). As shown in Table 2, the uniform S²_CCR values are 0.72, 0.76, 075 and 0.76 for H^NN/H^NN, H^αC^α/H^αC^α, intraresidual and sequential H^NN/H^αC^α dipolar CCR rates. In order to focus on dynamics corrected for librational motion, effective bond lengths are often set to 1.041 and 1.117 Å.^[71,72] In that case, the order parameters are 0.81, 0.88, 0.86, 0.87.

Figure 2.

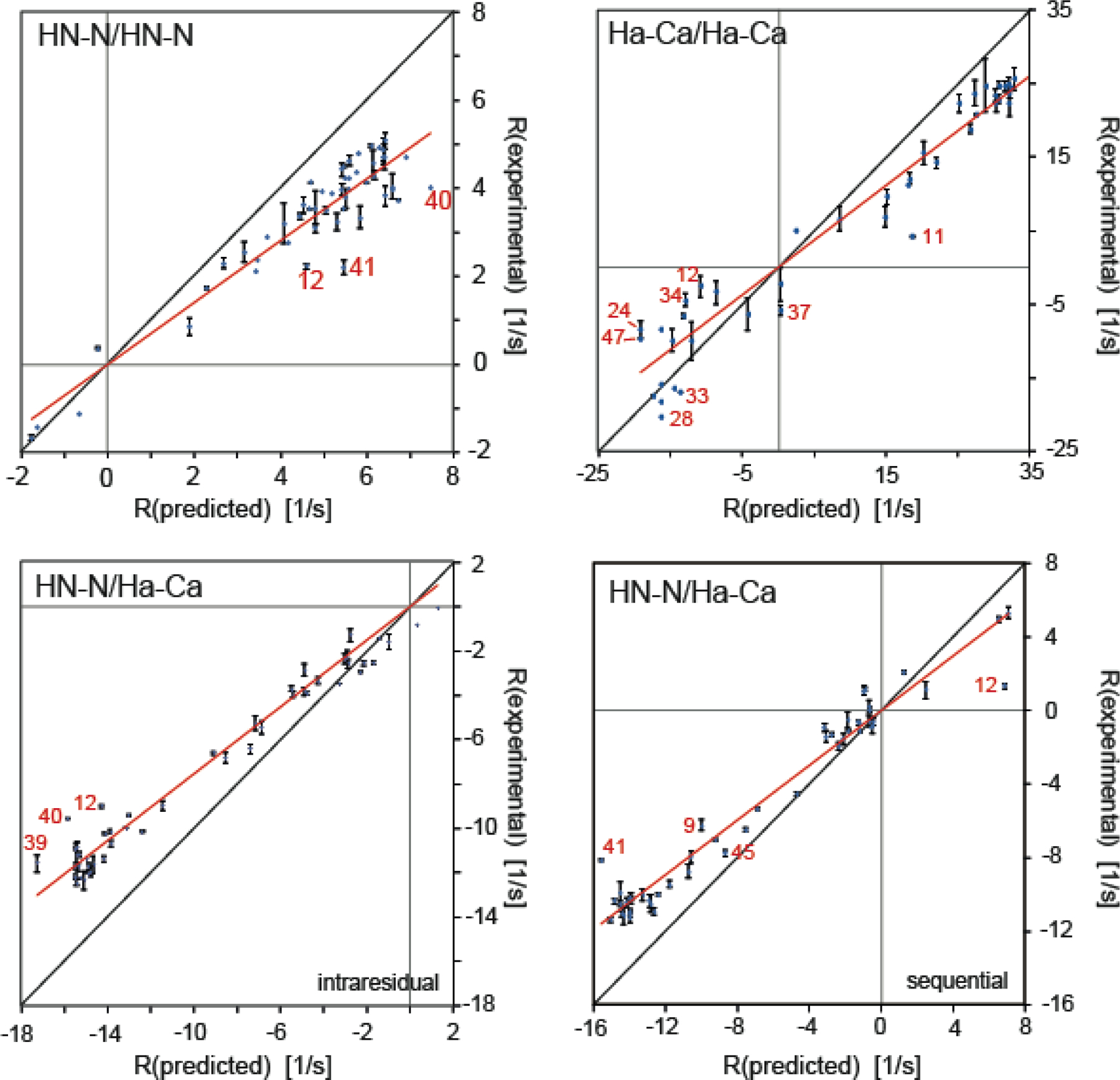
Correlation plots of experimental and predicted dipolar CCR rates based on a rigid GB3 model. R_{DD(I1I2)/DD(S1S2)} + R_{DD(I1S2)/DD(S1I2)} is abbreviated by R. H^NN/H^NN and H^αC^α/H^αC^α rates are shown on the top left and right, respectively, and intraresidual and sequential H^NN/H^αC^α rates at the bottom left and right. The theoretical rates are calculated under the assumption of anisotropic overall tumbling. The effective H^N–N and H^α–C^α bond lengths are 1.02 and 1.09 Å, respectively. Linear regressions shown in red are uniform heuristic order parameters as given in equation 18. The most extreme outliers are indicated in red. The black lines indicate a slope of 1. Reprinted by permission from Springer Nature: B. Vögeli, Cross-correlated relaxation rates between protein backbone H-X dipolar interactions, J. Biomol. NMR 2017, 67, 211–232, copyright 2017.

Table 2.

Slope s and Pearson’s correlation coefficient r between experimental and predicted R = R_{DD(I1I2)/DD(S1S2)} + R_{DD(I1S2)/DD(S1I2)} CCR rates obtained from rigid and dynamic GB3 models.

CCR rate	model	s * †	r *
RDD(HNiNi/HNi+1Ni+1) + RDD(HNiNi+1/HNi+1Ni)	2OED-DIDC, rigid, pairs i = 40, 41 excluded	0.72/0.81	0.96
	2OED-DIDC, S2 §, pairs i = 40, 41 excluded	0.89/1.01	0.97
RDD(HAiCAi/HAi-1CAi-1) + RDD(HAiCAi-1/HAi-1CAi)	2OED-DIDC, rigid, pairs i = 11, 40 excluded	0.76/0.88	0.97
	2OED-DIDC, S2 §, pairs i = 11, 24, 40 excluded	0.90/1.03	0.97
RDD(HNiNi/HAiCAi) + RDD(HAiNi/HNiCAi)	2OED-DIDC, rigid	0.75/0.86	0.98
	2OED-DIDC, S2 §, pairs i = 12, 40 excluded	0.92/1.05	0.98
RDD(HNiNi/HAi-1CAi-1) + RDD(HAi-1Ni/HNiCAi-1)	2OED-DIDC, rigid, pairs i = 12, 41 excluded	0.76/0.87	0.99
	2OED-DIDC, S2 §	0.90/1.03	0.98

^*x axis is the predicted and y axis the experimental rate; coordinates were taken from RDC-refined X-ray structure 2OED^[99], whose H^N and H^α proton positions were subsequently re-optimized with RDCs^[72,100]

^†The first and second entries are calculated with r_HN = 1.02 Å/r_HαCα = 1.09 Å and r_HN = 1.041 Å/r_HαCα= 1.117 Å, respectively.

^§Theoretical CCR rates calculated with r_HN = 1.02 Å and r_HαCα = 1.09 Å are scaled with RDC order parameters, ^[72,100] uncorrelated motion is assumed.

The overall heuristic H^NN/H^NN CCR order parameter S²_CCR of GB3 is in good agreement with the one found for ubiquitin^[17] and for the chicken villin headpiece subdomain^[89]. The H^NN/H^NN S²_CCR are considerably smaller than the Lipari-Szabo relaxation order parameters of a single H^N-N bond (ubiquitin 0.85^[97], GB3 0.83^[98]), suggesting additional motion on the supra-τ_c time scale.

3.1.4. Correlated motion

The first interpretation of correlated motion between the two interaction axes was based on the above mentioned four dipolar HC/HC CCR rates in a CH₂-CH₂ group of an aminoethoxy side chain in a ribose.^[30] As the CCR order parameter was approximately as large as the H-C autocorrelated order parameter, it was concluded that the two internal motions are correlated. Similarly, correlated motion between consecutive peptide planes in ubiquitin has been suggested on the basis of dipolar H^NN/H^NN CCR rates.^[17] The corresponding heuristic CCR order parameters are on average 0.75 (with a large dispersion) and in general smaller than H^N-N relaxation order parameters (average 0.85).

It is clear that for a detailed assessment of the degree of correlation between the motions of the two interaction axes, these motions have to be quantified individually with a probe that is also sensitive to the slow time scale (μs-ms). Building on the idea to relate CCR rates to residual dipolar couplings (RDCs) of the individual bonds as given in equation 25,^[48,89] we have recently mapped out slow correlated motion along the backbone among and between consecutive H^N–N and H^α–C^α bonds of the protein GB3.^[101] For that study, we used the highly accurate and precise H^NN/H^NN, H^αC^α/H^αC^α and intraresidual and sequential H^NN/H^αC^α dipolar CCR rates mentioned above.^[50] In Figure 3, we modified the plot shown in Figure 2 by multiplying the predicted CCR rates for a rigid GB3 model by order parameters derived from RDCs of the individual interaction axes^[72,100]. As explained in the derivation of equation 25, this procedure models a dynamic molecule, where the individual interaction axes are not dynamically correlated (and the motions are approximated as symmetric). In order to correct for libration motions that are not present in static structures, we scaled the linear regressions obtained from the correlation plots in Figure 3 to correspond to 1.041 and 1.117 Å bond lengths of H^N–N and H^α–C^α, respectively.^[71,72] The original and corrected slopes are reported in Table 1. Partial correlation of the interaction axes would cause inequality in equation 25, and consequently deviations of the corrected slopes from a value of 1. To quantify the degree of correlation, we introduced a correlation factor

$$F_{\text{corr,A/B}}=\frac{J_{\text{A/B}}^{\text{exp}}(0)}{S_{\text{A,RDC}}{S}_{\text{B,RDC}}{J}_{\text{A/B}}^{\text{rigid}}(0)},$$ (30)

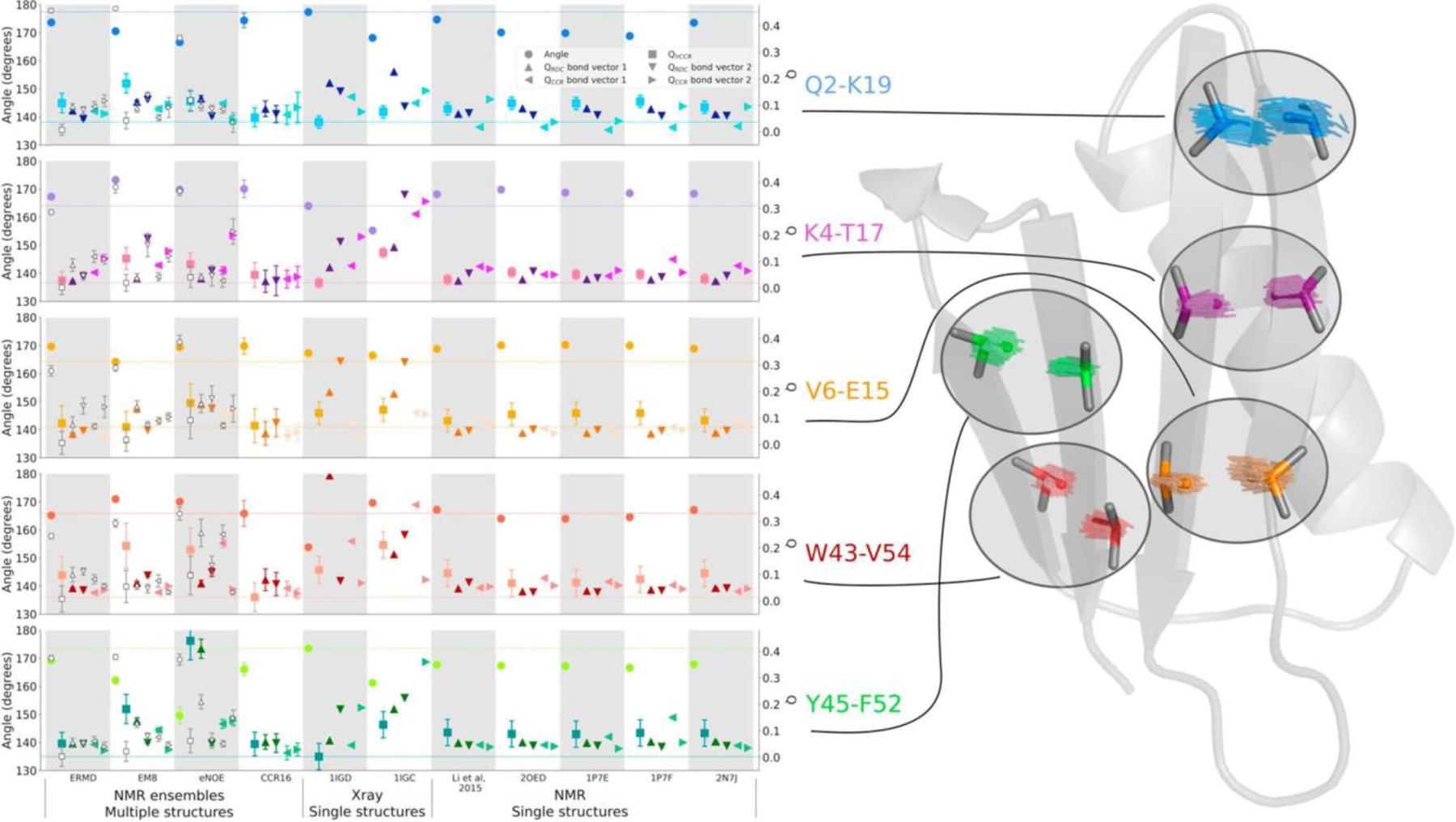
which can be obtained from $\frac{R_{\text{A/B}}^{\text{exp}}}{S_{\text{A,RDC}}{S}_{\text{B,RDC}}{R}_{\text{A/B}}^{\text{predict}}}$ and is plotted in Figure 4. All four types of CCR rates yield on average slopes larger than one, which are indicative of syn-correlated motion (as opposed to anti-correlated motion). The residue-specific correlations are very similar to those observed for a structural ensemble calculated from the same CCR rates, and thus will be further discussed in the ‘Ensemble calculation using CCR restraints’ section. We note that these values critically depend on an overall scaling of the RDC order paramters, which is not a trivial task. The same RDC data set has been used in another study to derive a similar residue-by-residue pattern as the one of the order parameters employed above, but with lower overall values.^[102] These values produce even larger F_corr,A/B factors, which correspond to even stronger correlation of motion (see Figure 4).

Figure 3.

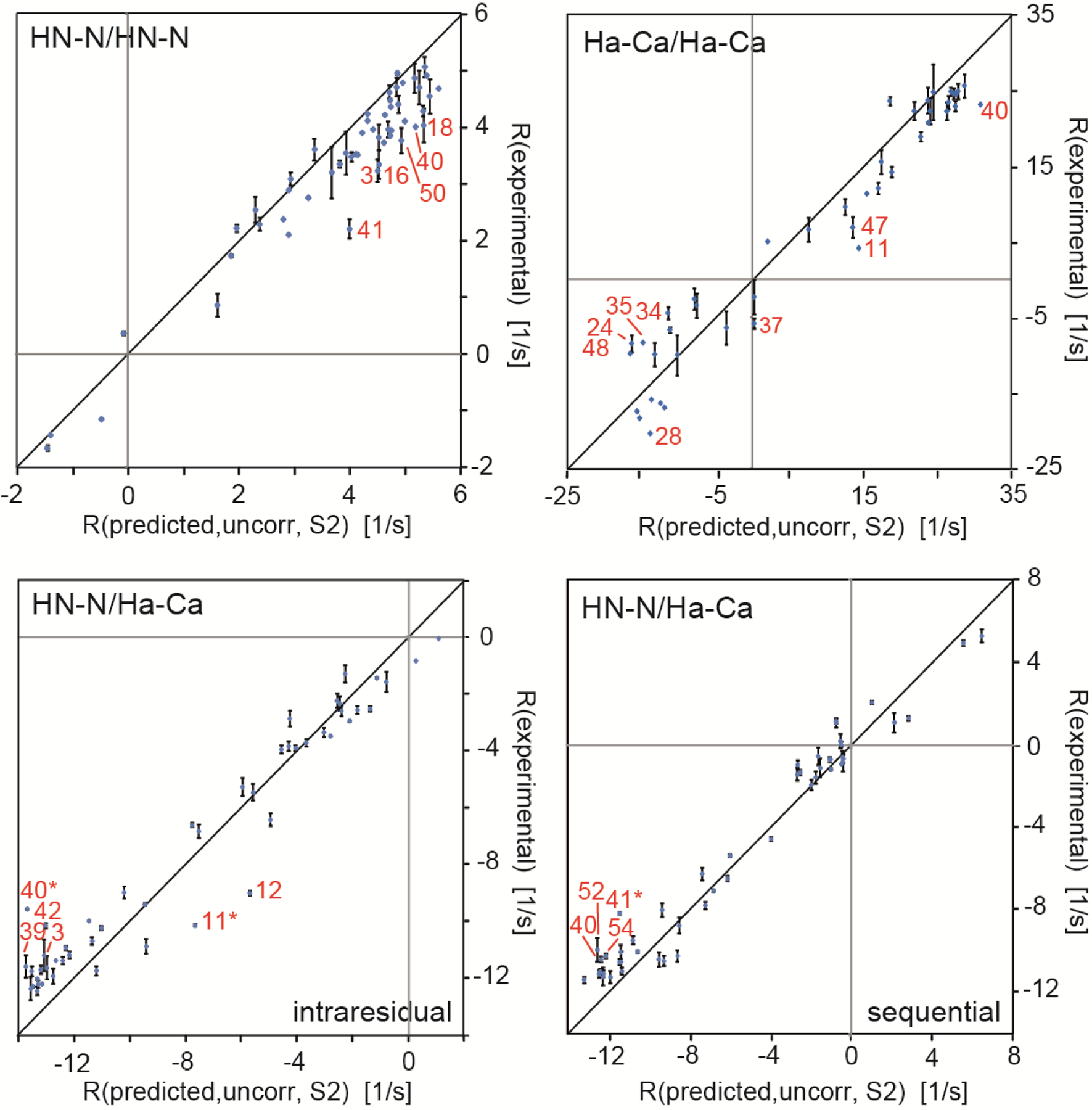
Correlation plots of experimental and predicted dipolar CCR rates based on a dynamic GB3 model. R_{DD(I1I2)/DD(S1S2)} + R_{DD(I1S2)/DD(S1I2)} is abbreviated by R. H^NN/H^NN and H^αC^α/H^αC^α rates are shown on the top left and right, respectively, and intraresidual and sequential H^NN/H^αC^α rates at the bottom left and right. The theoretical rates are calculated under the assumption of uncorrelated motion and anisotropic overall tumbling. The effective H^N–N and H^α–C^α bond lengths are 1.02 and 1.09 Å, respectively. The most extreme outliers are indicated in red. The black lines indicates a slope of 1. Adapted with permission from R.B. Fenwick, C.D. Schwieters, B. Vögeli, Direct investigation of slow correlated dynamics in proteins via dipolar interactions. J. Am. Chem. Soc., 2016, 138, 8412–8421, copyright 2016 American Chemical Society.

Figure 4.

Residue-specific motional correlation factors F_corr,A/B from GB3 versus residue numbers. A/B is H^N_iN_i/H^N_i+1N_i+1 and H^α_iC^α_i/H^α_i-1C^α_i-1 on the top left and right, respectively, and H^N_iN_i/H^α_iC^α_i and H^N_iN_i/H^α_i-1C^α_i-1 on the bottom left and right. Black thick bars connect the lower F_corr,A/B estimate from the RDC order parameters from references 72 and 100 with the higher estimate derived from reference 102. The error bars indicate the propagated errors from the CCR rates and order parameters. The white points indicate the F_corr,A/B values calculated from an ensemble that was restrained with the same CCR and RDC data. Errors for these F_corr,A/B are the r.m.s.d. values from 20 independent ensembles. Reprinted with permission from R.B. Fenwick, C.D. Schwieters, B. Vögeli, Direct investigation of slow correlated dynamics in proteins via dipolar interactions. J. Am. Chem. Soc., 2016, 138, 8412–8421, copyright 2016 American Chemical Society.

3.1.5. Validation of structural ensembles

Another way to identify signatures of dynamics in measured CCR rates is the comparison of the measured rates with rates back-predicted from structural ensembles. The easiest and only approach used so far is based on equation 24 with S_fast set to 1 (or equation 11 with C^int(t,0) at t = 0 in the case of anisotropic overall tumbling). Then, P₂ is simply averaged over each member of the ensemble with equal weight. If there is motional correlation present in the ensemble, it will also be inherent to the back-predicted CCR rate. The first example of this approach was a study of DD(H^NN)/DD(C^βC^γ) CCR rates in aromatic side chains of ubiquitin and GB3.^[26] Although the measured rates are relatively small and therefore have a large relative error, back-prediction from the ubiquitin ensemble agrees better with the experimental rates than from a single-state bundle. For GB3, the two rates involving the side chain of residue 40 indicate correlated motion between the side-chain and backbone torsion angles. The same approach with DD(H^NN)/DD(C^αC’) CCR rates did not result in better agreement when a structural ensemble was used instead of a single structure.^[57] The reason for this failure is that the intervening dihedral angle is the highly rigid ω angle and that these rates are extremely small (−0.2 to 0.2 s⁻¹) because the H^N-N/C^α-C^’ projection angle is close to the magic angle. However, the data confirms previous findings demonstrating that the H^N proton often lies outside the idealized peptide plane. The backbone CCR data set mentioned above (H^NN/H^NN, H^αC^α/H^αC^α, and intraresidual and sequential H^NN/H^αC^α)^[50] also agrees better with an ensemble generated from RDCs, J couplings, ¹⁵N relaxation order parameters and crystallographic B-factors^[103] than with single static structures^[101]. In addition, we have used this CCR data set^[50] to cross-validate a structural bundle of GB3 constructed by a physical force field minimally biased by RDCs.^[104]

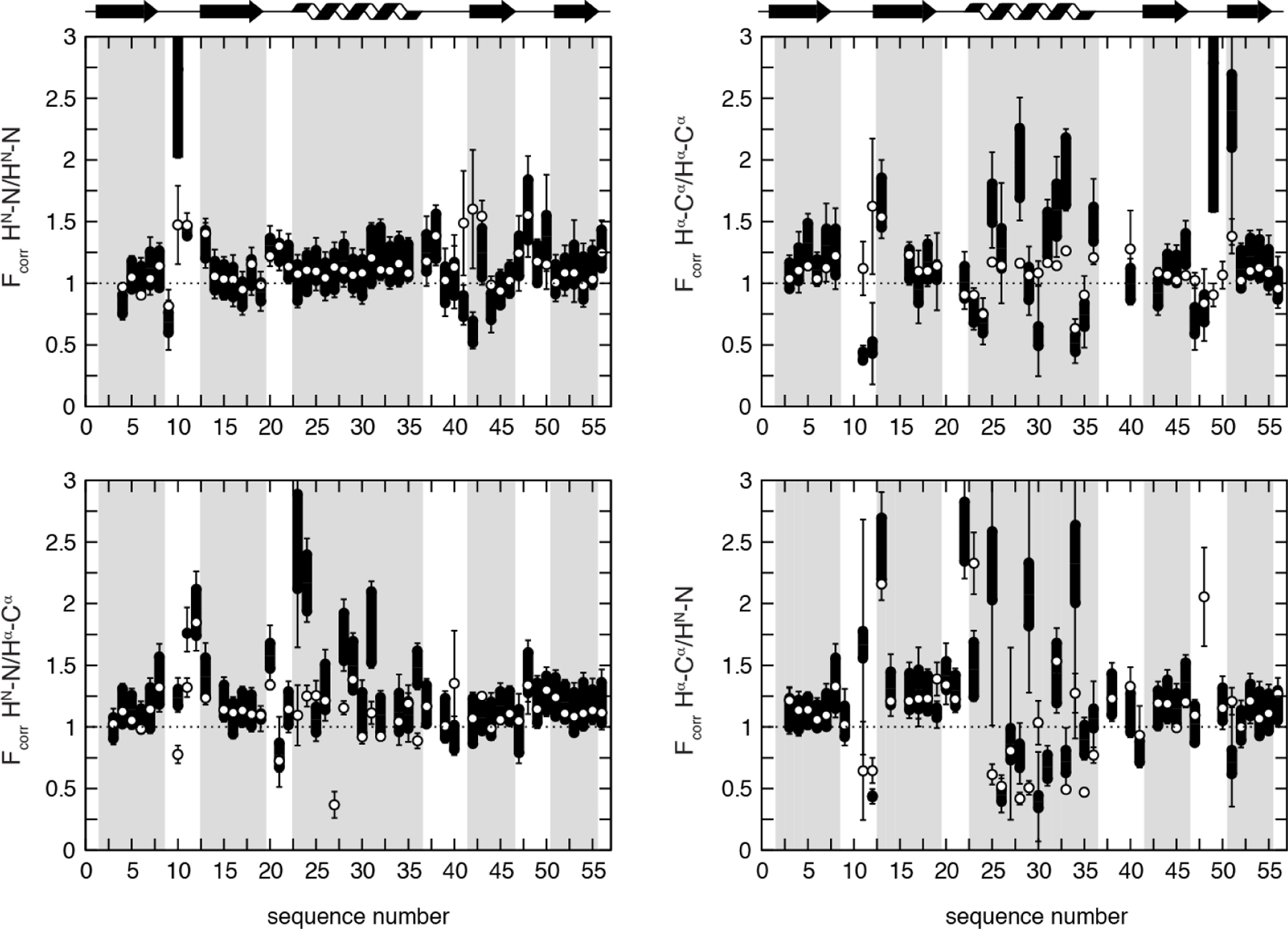
DD(H^NN)/DD(H^βC^β) CCR depends on two or three intervening dihedral angles, which offers a way to probe the motional correlation between the side-chain χ1 and the backbone dihedral angles. We have recently measured the associated CCR rates for Ile, Thr and Val H^β-C^β bonds in GB3 and compared them to various high-resolution single-state structures and ensembles of structures (Figure 5).^[27] Many of these structures were calculated using χ1 angle restraints from the same X-ray structure^[105]. There are many outliers, most notably both CCR rates of residues 42 and 55, but also the ψ-dependent ones of residues 11 and 21, which are dominated by angles that appear to be different in the X-ray crystals than in solution. Indeed, the agreement became much better even when we compared the CCR rates to a single-state bundle^[106] obtained from an accurate data set of unparalleled diversity including exact NOEs (eNOEs), RDCs and J couplings.^[107] Τhe correlation is high (r = 0.93), having only minor outliers like the φ-angle dependent rate of residue 11. A four-state ensemble calculated from the same data set^[106] improves the agreement again substantially with no major outlier. While r only improves slightly to 0.96, the general overestimation of the experimental rates when using the single-state model is substantially reduced. These findings indicate that the single-state model is already a very accurate average structure with a high correlation with the experimental rates. On the other hand, these results also demonstrate that the CCR rates are sensitive to motion as demonstrated by a generally better agreement with the lower rates predicted from the model featuring dynamics.

Figure 5.

Correlation plots of experimental and back-predicted dipolar CCR rates based on four GB3 models. R_{DD(HNN)/DD(CβHβ)} + R_{DD(HNCβ)/DD(NHβ)} is abbreviated by R. The theoretical rates are calculated under the assumption of isotropic (red squares) and anisotropic overall tumbling (blue diamonds). The structural models are: RDC-refined X-ray structure 2OED^[99], where the H^N and H^α proton positions were subsequently re-optimized with RDCs^[72,100] (top left); an eight-state ensemble calculated from RDCs, J couplings, ¹⁵N relaxation order parameters and crystallographic B-factors^[103] (bottom left); single-state structures (top right) and four-state ensembles both from eNOEs, RDCs and J couplings^[106,107] (bottom right). The most extreme outliers are indicated with red residue numbers, where i/j designate the residues of the H^N-N and H^β-C^β vectors. The black lines indicate a slope of 1. Reprinted by permission from John Wiley and Sons: R.B. Fenwick, B. Vögeli, Detection of correlated protein backbone and side-chain angle fluctuations, ChemBioChem, 2017, 18, 2016–2021, copyright 2017.

Next, we tested if the CCR rates are sensitive to the correlation between dihedral angle fluctuations.^[27] We predicted the rates under the assumption that the ϕ and χ1 or ψ and χ1 angles in the four-state ensemble were not correlated by combining all sampled values of the first angle with those of the second. We found relevant differences in the rates as compared to the correlated model for both the ϕ- and ψ-dependent rates of residues 39 and 49, and the ψ-dependent rates of residues 11, 21 and 49. Almost all rates based on the correlated model are in closer agreement with the measured values than those based on the uncorrelated values (Figure 6). The ϕ-dependent rate of residue 39 has the largest difference of all (−1.35 s⁻¹) and the correlated model agrees very well with the experimental value.

Figure 6.

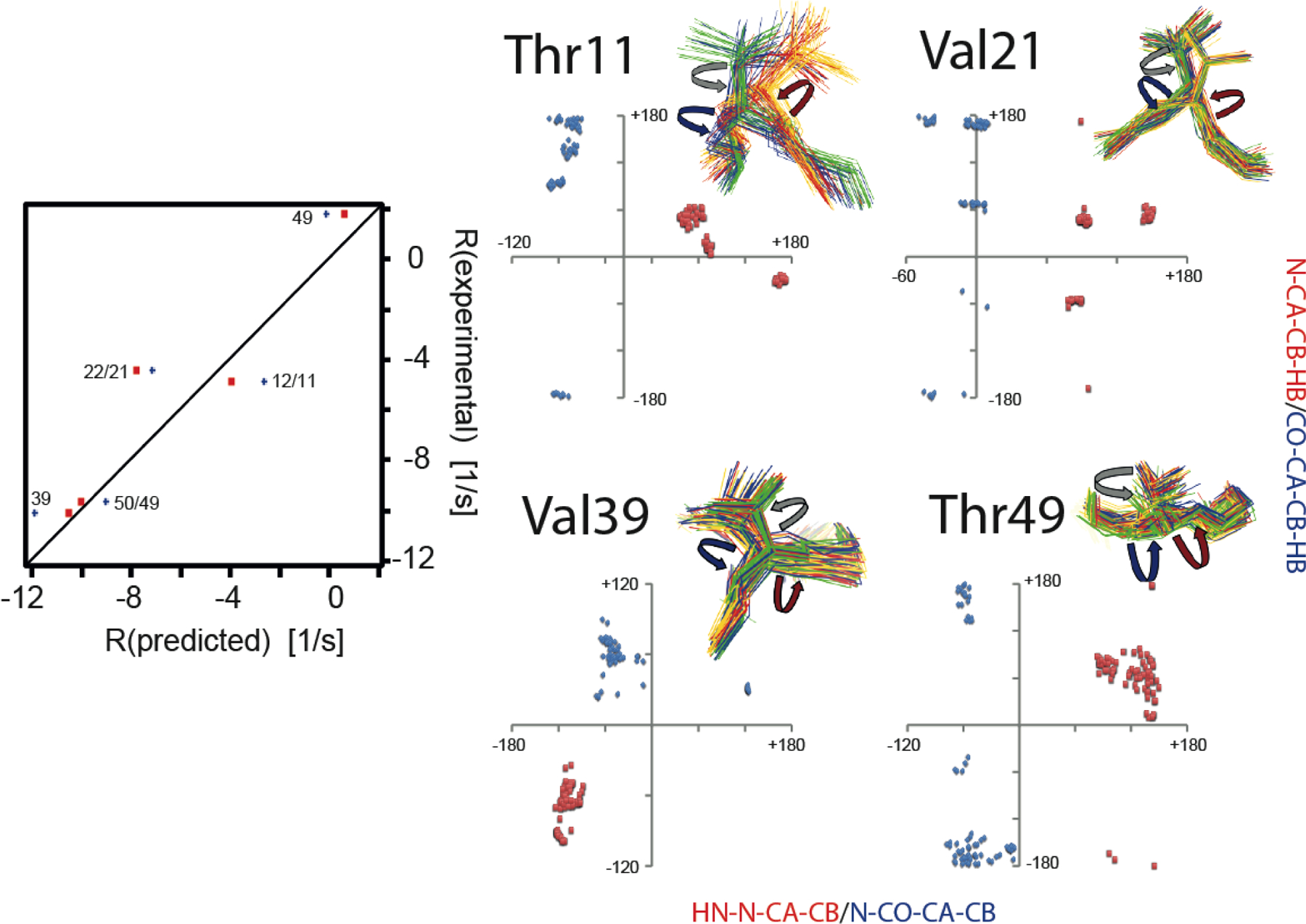
Impact of correlated motion between the ϕ and χ1 or ψ and χ1 angles on CCR. Left panel, correlation plots of experimental and predicted R = R_{DD(HNN)/DD(CβHβ)} + R_{DD(HNCβ)/DD(NHβ)} rates based on ensembles derived from eNOEs, RDCs, and J couplings from GB3.^[106,107] Only rates with changes larger than the experimental error (> 0.59 s⁻¹) are shown. Predicted rates assuming correlated motion are shown in red squares, and those assuming uncorrelated fluctuation in blue diamonds and labeled with the residue number of the involved side-chain and amide bond. Right panel, correlation plots of H^N_i-N_i-C^α_i-C^β_i (≈ϕ+60°) and N_i-C^α_i-C^β_i-H^β_i (≈χ1+120° for Ile, and ≈χ1–120° for Val, Thr) dihedral angles (red squares) and N_i+1-C’_i-C^α_i-C^β_i (≈ψ−240°) and C’_i-C^α_i-C^β_i-H^β_i (≈χ1 for Ile, and ≈χ1–240° for Val, Thr) dihedral angles (blue diamonds). The angles are indicated on the four-state ensembles with red (ϕ), blue (ψ) and grey arrows (χ1). Ensemble states were grouped around residue 9. Reprinted by permission from John Wiley and Sons: R.B. Fenwick, B. Vögeli, Detection of correlated protein backbone and side-chain angle fluctuations, ChemBioChem, 2017, 18, 2016–2021, copyright 2017.

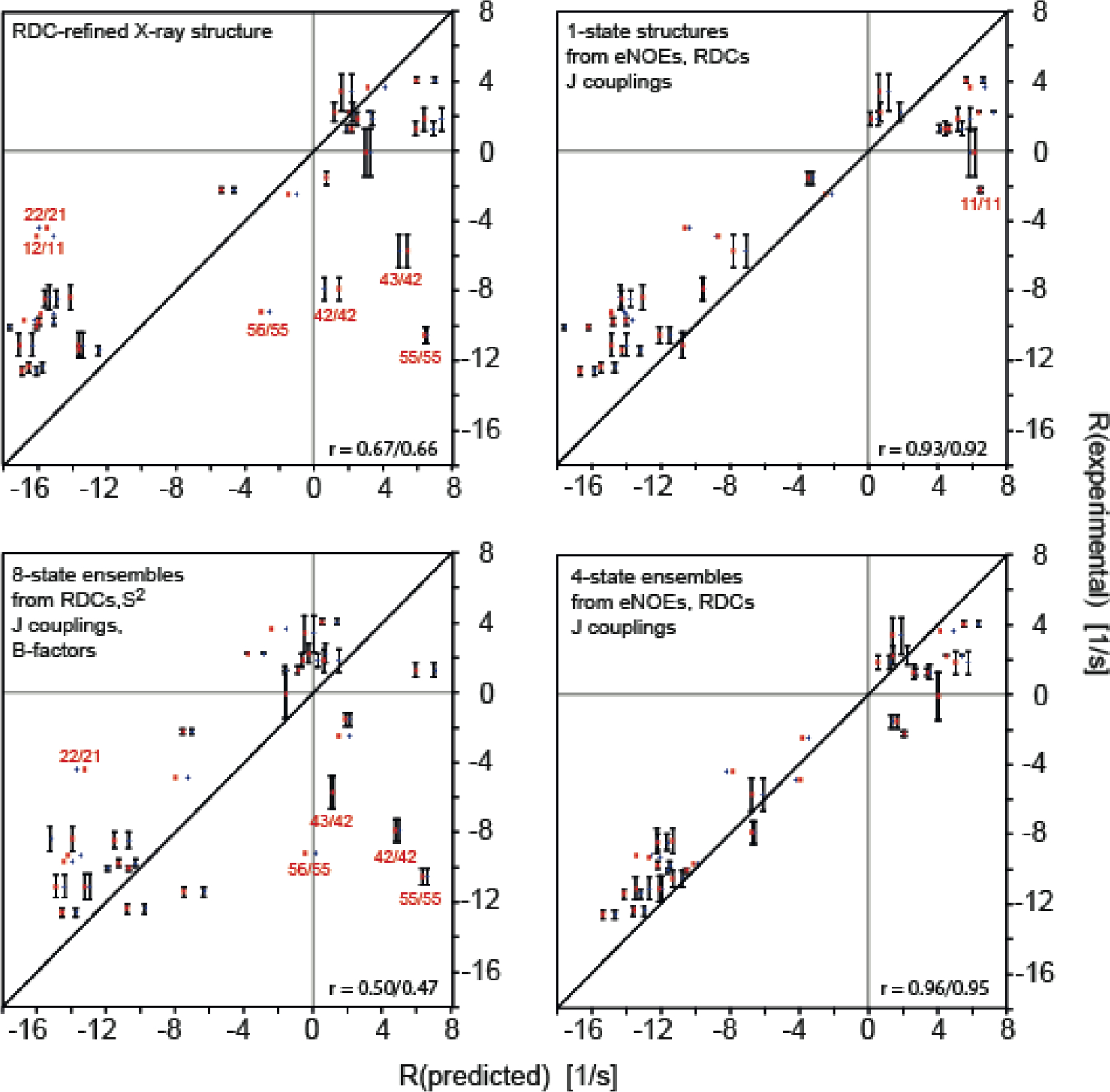
Two studies went beyond straight-forward validation of structural ensembles and used dipolar CCR rates as a selection criterion for realistic NOE-, J coupling-, and RDC-restrained ensembles.^[23,108] In the first study, H^NN/H^NN and H^NN/H^αC^α dipolar CCR rates were used to generate a realistic subensemble of NOE- and RDC-restrained molecular dynamics (MD) ensembles of ubiquitin.^[108] Subsequently, a similar approach has been used with long-range H^αC^α/H^αC^α CCR (lrCCR) rates between opposing antiparallel β strands in GB3.^[23] The measurement required through-space relaxation allowed coherence transfer (RACT), which resulted in relatively low sensitivity and only five lrCCR rate constants were obtained. Nevertheless, this represents an interesting methodological advance. First, various single-state structures and structural ensembles were cross-validated using RDCs and backbone CCR rates (excluding lrCCR) involving the relevant H^α-C^α bonds (Figure 7). Particularly good agreement was observed for the 640-member ERMD ensemble,^[109] and single-state structures and the CCR16 ensemble, both of which have been restrained with these RDCs (and in the case of CCR16 also with the CCRs, under exclusion of the lrCCR; for details on CCR16 see ‘Ensemble calculation using CCR restraints’ section). Typically, these structures are also those that agree well with the lrCCR rates. Surprisingly, X-ray structures^[105] that were in poorer agreement in the local validation of the H^α-C^α bonds showed the best agreement with the lrCCR rates among all structures. Apparently, the relative geometry is properly represented despite of inaccuracies of the individual bond vectors that are necessarily introduced by adding protons to X-ray structures at idealized positions. Finally, new subensembles were generated by selecting two-structure subensembles from the original ensembles that agreed best with the lrCCR rates and adding them one by one to a target subensemble. Those subensembles that reached the best agreement with the RDCs and CCR rates other than the lrCCR were reached at ca. 10% of the original ensemble sizes (white symbols in Figure 7).

Figure 7.

Long-range H^αC^α/H^αC^α dipolar CCR rates compared to H^α-C^α bond vector representations in NMR ensembles, single NMR and X-ray structures and sub-selected ensembles of GB3. The angles between the H^α-C^α bond vectors are depicted by circle symbols (left y-axis), while the quality with which every H^α-C^α bond pair reproduces the measured observables is expressed in terms of Q values (right y-axis). The following Q values were calculated: One Q value for the lrCCR rates for every H^α-C^α bond vector pair (square), two Q values – one for each H^α-C^α bond vector – for the RDCs measured in 17 alignment media (up/down triangle), two Q values for the backbone intra-residue H^NN/H^αC^α, sequential H^NN/H^αC^α and H^αC^α/H^αC^α CCR rates (left/right triangle). The lines in the figure mark the level of the lowest Q value for the lrCCR rate and the inter-vector angle corresponding to that structure or ensemble with the lowest lrCCR Q value. White symbols denote the calculations for the sub-selected ensembles based on the lrCCR rates. Reprinted from M. Sabo, V. Gapsys, K.F.A. Walter, R.B. Fenwick, S. Becker, X. Salvatella, B.L. de Groot, D. Lee, C. Griesinger, Utilizing dipole-dipole cross-correlated relaxation for the measurement of angles between pairs of opposing CαHα-CαHα bonds in anti-parallel β-sheets, Methods, 2018, 138–139, 85–92, with permission from Elsevier.

3.1.6. Ensemble calculation using CCR restraints

Using the high-accuracy H^NN/H^NN, H^NN/H^αC^α and H^αC^α/H^αC^α dipolar CCR rates mentioned above, ^[50] we generated structural models of GB3 and obtained a complex H-X bond motion correlation map.^[101] To that purpose, we introduced a harmonic Xplor-NIH^[110] CCR restraint:

$$E_{\text{corr}}=w_{\text{CCR}}(R_{\text{A/B}}^{\text{calc}}-R_{\text{A/B}}^{\text{restrained}})$$ (31)

where the weighting factor for the potential term w_CCR is set to 0.4, 0.8, 0.8, and 2.0 kcal/mol·s² for H^N_iN_i/H^N_i+1N_i+1, H^N_iN_i/H^α_iC^α_i, H^N_iN_i/H^α_i+1C^α_i+1, and H^α_iC^α_i/H^α_i+1C^α_i+1, respectively. The restraint assumes isotropic overall tumbling. The error introduced by this approximation was reduced by correcting the measured rate for the contribution from anisotropy estimated from a high-resolution structure.

First, we calculated a single-state structure ‘CCR1’ from combined CCR and RDC restraints (Table 3) using Xplor-NIH.^{[101,103,110]} This structure was able to reduce the root-mean-square deviation from the measured CCR values when compared to a previously calculated high-resolution structure (PDB accession code 2OED^[99]). However, independent cross-validation with J couplings that depend on similar angles as the CCR rates were similar (Table 3). As mentioned above, the ensemble generated from RDCs, J couplings, ¹⁵N relaxation order parameters and crystallographic B-factors (‘ENS8’),^[103] is in better agreement with the CCR rates than the single-state structure 2OED, and even better than our CCR-restrained single state structure CCR1 in the case of H^αC^α/H^αC^α. This indicates that the CCR rates can not sufficiently well be represented with static structures. Therefore, we calculated ensemble structures of GB3 restrained by the six sets of both H^N-N and H^α-C^α RDCs^[72,100] and the four sets of CCR rates^[50] mentioned above. The ensemble was determined using Xplor-NIH with the same general protocol previously used to generate ENS8,^[103] but with the CCR restraints added. An optimum ensemble size of 16 members was determined through independent validation with the ³J couplings.

Table 3.

Validation of ensembles and single structures with CCR and ³J coupling data.

structure	CCR rate r.m.s.d. [s−1] a				3J coupling r.m.s.d. [s−1] b
	HNN/HNN	CαHα/CαHα	HNN/CαHα	CαHα/HNN	HN-Hα	C’-C’	HN-C’	HN-Cβ
	Single structures
2OEDc	1.12	4.71	1.68	1.67	0.98	0.41	0.44	1.07
CCR1d	0.65	4.11	0.98	1.23	0.87	0.62	0.63	1.12
	Ensembles
ENS8e	0.78	3.99	1.61	1.28	0.75	0.33	0.40	1.02
CCR16d	0.15	2.02	0.25	0.29	0.55	0.25	0.39	0.72

^aBond lengths of 1.041 and 1.117 Å were used to calculate CCRs from structures to account for libration motions not present in static structures

^bKarplus parameters used were those for the fits to Ace-Ala-NMe,^[111] experimental data^[112,113]

^cCoordinates from RDC-refined X-ray structure,^[99] where H^N and H^α proton positions were subsequently optimized with RDCs^[72,100]

^dEnsemble generated using the CCR data and both 6 sets of H^N-N and H^α-C^α RDCs^[72,100]

^ePreviously determined dynamic ensemble^[103]

Finally, we also calculated F_corr,A/B correlation factors for the CCR16 ensemble. Generally, the values are similar to those calculated in the ‘model-free’ approach described in the ‘Correlated motion’ section, and generally between the two extremes obtained from the different RDC scalings (Figure 4). The F_corr,A/B values derived from CC16 are plotted on the backbone representation of GB3 in Figure 8. In general, we find that the bond motions are on average slightly correlated, and that the local environment dominates many observations. Despite this, some patterns are typical over entire secondary structure elements. In the β sheet, nearly all bonds are weakly correlated and there is an approximately binary alternation in correlation intensity corresponding to the solvent exposure/shielding alternation of the side chains. The average F_corr,A/B value for the consecutive H^N-N bond vectors quantifies the average correlation between neighboring peptide planes and is that closest to 1, indicating that the average degree of correlation between these probes is the weakest. Nevertheless, the H^N-N correlation is also seen in the α helix. The correlation between the side chains probed by the H^αC^α/H^αC^α CCR rates are of intermediate strength as is the sequential H^NN/H^αC^α correlation serving as measure of correlation between the ith side chain and its i+1 peptide plane. The intraresidue H^NN/H^αC^α correlation has the most correlated behavior of all probes. Loops show complex and non-uniform behavior for all four types of CCR rates.

Figure 8.

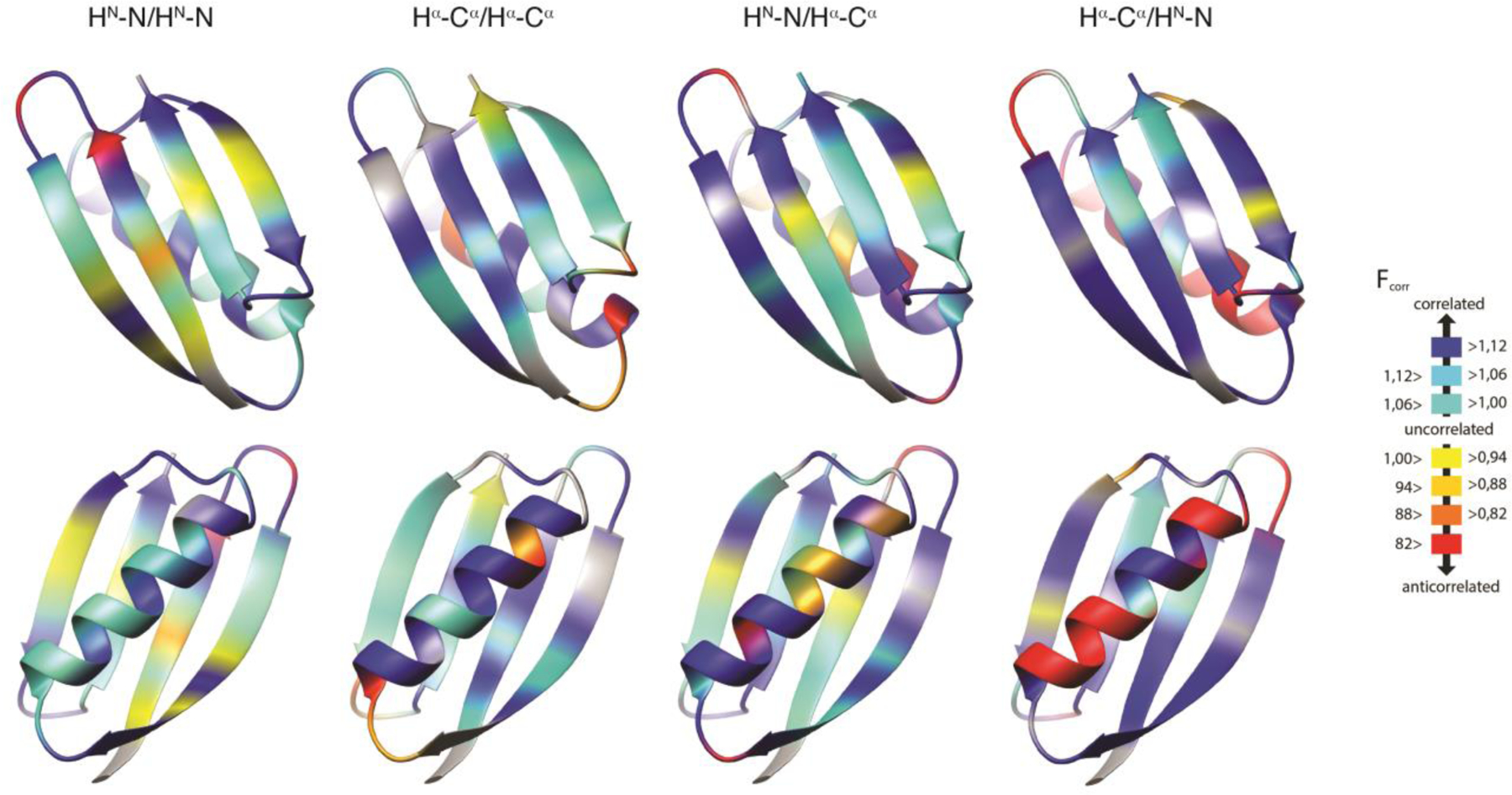
Residue-specific F_corr,A/B values for GB3 from ensemble structure calculation. H^NN/H^NN, H^αC^α/H^αC^α, and intraresidual and sequential H^NN/H^αC^α F_corr,A/B are mapped on 3D ribbon representations of GB3. The β sheet is in the front in the top row, and the α helix in the bottom row. Reprinted with permission from R.B. Fenwick, C.D. Schwieters, B. Vögeli, Direct investigation of slow correlated dynamics in proteins via dipolar interactions. J. Am. Chem. Soc., 2016, 138, 8412–8421, copyright 2016 American Chemical Society.

4. Dynamics from CSM/CSM CCR

Cross-correlated chemical shift modulation (CSM/CSM) is a manifestation of correlation between the local electronic environments of two spins.^[24,69,70] The zero- and double-quantum coherences between the two spins relax at different rates partially due to correlated modulation of the isotropic chemical shifts. The effect is sensitive to motion on the μs-ms time scale, caused by formation and disruption of hydrogen bonds, changes in local geometry by alteration of dihedral angles or changes in local chemical environment by repositioning of neighboring aromtic rings. From the multitude of the applications using CSM/CSM CCR measurements (references 24, 43, 44, 66–69, 93, 96, 114–117), we choose several examples that demonstrate dynamical changes upon mutation, upon interaction with a ligand, as well as changes caused by deuteration of non-exchangeable sites. In general, CSM/CSM experiments are expected to provide complementary information to their more common SQ chemical exchange counterpart, especially for cases in which dynamical changes of interest are anticipated to affect multiple motional modes and be dispersed throughout the protein side-chains and backbone sites.

From a methodological stand-point it is important to note that i) the use of multiple magnetic field strengths enables to pin-point the time scale of the exchange processes, ii) probing the temperature dependence of rates potentially allows for the separation of the rate constant from the static terms, such as p₁p₂ and Δω_I1Δω_S1 (especially in the fast limit given by equation 29), and iii) the comparison between the single-quantum (SQ) and MQ analogs of chemical exchange contributions helps to identify and characterize underlying motional processes.

Insightful work by Wang and Palmer provides theoretical background for the extraction of the chemical exchange time scale of CSM/CSM interactions based on the field dependence of the rates.^[93] Furthermore, the study describes an important comparison of the relative effectiveness of CSM/CSM and SQ chemical exchange measurements in probing motional processes based on the relative values of the chemical shift differences of the two nuclei (Figure 9).

Figure 9.

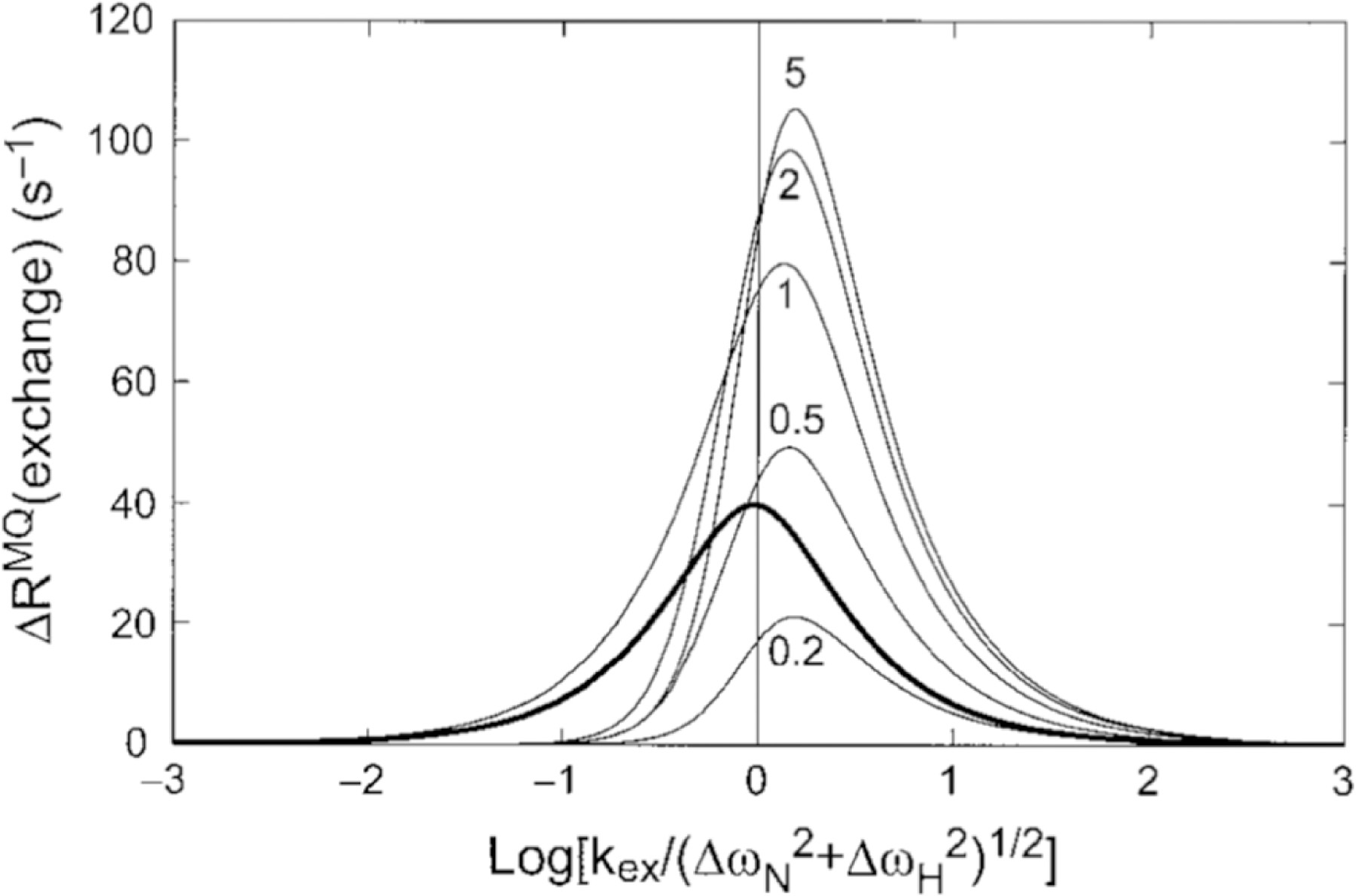
Comparison of MQ CSM(¹⁵N)/CSM(¹H) CCR rates and SQ ¹⁵N exchange contribution. The dependence of ΔR^MQ(exchange) = 2R_{CSM(15N)/CSM(1H)} rates upon the exchange time scale, k_ex = 1/τ_ex, and the ¹H and ¹⁵N chemical shift modulations, Δω_H and Δω_N, respectively, is shown with the thin curves calculated from equation 8 in the study by Wang and Palmer^[93] (Δω_N = 2 ppm at 600 MHz, p₁ = 0.9 and Δω_H/Δω_N ratios equal to 0.2, 0.5, 1,2, 5). The plotted results would be multiplied by −1 if Δω_H and Δω_N had opposite signs. The bold curve shows the exchange contribution to SQ ¹⁵N relaxation, R_ex plotted versus log(k_ex/Δω_N). Reprinted by permission from Springer Nature: C. Wang, A.G. Palmer III, Differential multiple quantum relaxation caused by chemical exchange outside the fast exchange limit. J. Biomol. NMR, 2002, 24, 263–268, copyright 2002.

4.1. CSM/CSM changes upon ligand binding

One exemplary protein studied by CSM/CSM CCR is the major urinary protein (MUP), a pheromone-carrying protein of the lipocalin family.^[115] Isothermal titration calorimetry (ITC) has shown that the affinity of MUP for the pheromone 2-methoxy-3-isobutylpyrazine (IBMP) is primarily driven by enthalpy. However, there is a minor unfavourable contribution from entropy, which can be attributed in part to changes in internal motions of the protein upon binding. Perrazolo et al. have measured CSM(C’)/CSM(N) rates as a function of temperature in MUP with and without IBMP.^[115] Significant dynamical changes were observed upon binding even for residues that were far from the ligand binding sites.

4.2. CSM/CSM changes upon mutation

CSM(C^α_i)/CSM(C^α_i+1) and CSM(¹⁵N)/CSM(¹H^N) experiments on a E140Q mutant of the C-terminal domain of calmodulin have been combined with rotating frame R_1ρ relaxation dispersion measurements of SQ coherences of ¹⁵N, ¹³C^α, and ¹H^N nuclei.^[69,114] Quantitative analysis demonstrated that the mutant protein exchanges between the functionally relevant open (calcium-loaded) and close states of the wild-type variant.

The CSM(¹⁵N)/CSM(¹H^N) CCR rates were measured at three static magnetic field strength values (11.7, 14.1 and 18.8 T).^[114] These rates cannot be spectroscopically separated from CSA(¹⁵N)/CSA(¹H^N) CCR rates and dipolar CCR rates between I₁-K and S₁-K, where K is a neighboring spin. The linear dependence of the effective rates on the squared magnetic field strength indicated that the time scale of exchange is fast on the chemical shift time scales for the majority of the residues. This also means that the dipolar contributions can be separated from the CSM and CSA contributions a posteriori. Furthermore, the ¹⁵N and ¹H^N CSA values were determined separately, and CSA/CSA estimates based on these values were subtracted from the measured rates to obtain the CSM(¹⁵N)/CSM(¹H^N) CCR rates (Figure 10A and B). Using the previously determined residue-specific τ_ex with an average of ca. 20 μs and an average population estimate from ¹⁵N relaxation dispersion R_1ρ measurements, the products of the chemical shift differences could be calculated (Figure 10D, given in units of δσ_Nδσ_HN). For comparison the chemical shift differences between the free and the calcium-saturated wild type is shown, which indicates good agreement for large values of δσ_Nδσ_HN. However, there is disagreement in the calcium binding sites comprising residues 93–104 and 129–140, indicating that the hydrogen bonding pattern in the calcium-binding loops of the mutant remains intact during the exchange process.

Figure 10.

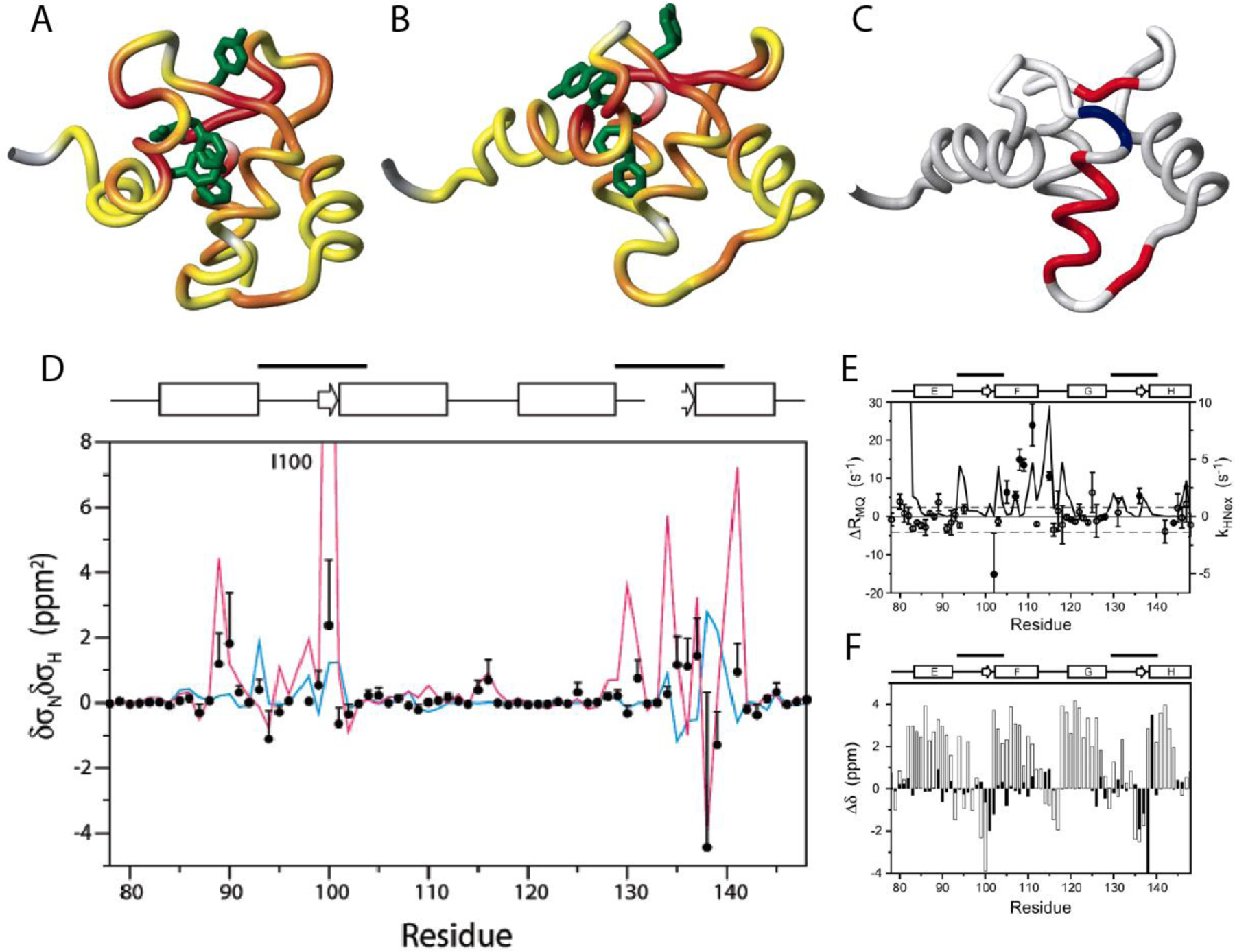
Location of residues exhibiting significant correlated conformational exchange contributions to CSM/CSM CCR rates in the E140Q mutant of the C-terminal domain of calmodulin. A) Residue pairs exhibiting dynamics sensed by CSM(¹⁵N)/CSM(¹H^N) CCR rates in apo wild type are highlighted from yellow to red, for increasing contributions. Residues for which MQ rates could not be measured are shown in gray. B) Same as A) for calcium-loaded wild type. C) Residue pairs exhibiting dynamics sensed by CSM(C^α_i)/CSM(C^α_i+1) CCR rates in calcium-loaded E140Q mutant are highlighted in red or blue, depending on whether the CSM/CSM of the two residues are correlated or anticorrelated. Residues for which MQ rates could not be measured or without significant dynamics are shown in white and gray, respectively. D) δσ_Nδσ_HN values for the of the E140Q mutant extracted from CSM(¹⁵N)/CSM(¹H^N) CCR rates plotted in A) and B) (black dots). The magenta line shows δσ_Nδσ_HN calculated from the chemical shifts of the apo and calcium-loaded wild type (δσ = Δω/γ/Β_ο.). The blue line shows values calculated from δσ_HN ring-current contributions and δσ_N measurements on the mutant. E) Measured differences between DQ- and ZQ-coherence relaxation rates, which are dominated by CSM(C^α_i)/CSM(C^α_i+1) CCR and used for C). For comparison, exchange rates of H^N with the solvent are shown (solid continuous line). F) Secondary ¹³C^α chemical shifts for calcium-loaded E140Q mutant are shown in white bars, and chemical shift differences between apo and calcium-loaded wild type in black bars. C), E) and F) P. Lundström, F.A.A. Mulder, M. Akke, Correlated dynamics of consecutive residues reveal transient and cooperative unfolding of secondary structure in proteins. Proc. Natl. Acad. Sci. USA, 2005, 102, 16984–16989, copyright 2005 National Academy of Sciences. A), B) and D) Reprinted with permission from P. Lundström, M. Akke, Quantitative analysis of conformational exchange contributions to ¹H-¹⁵N multiple-quantum relaxation using field-dependent measurements. Time scale and structural characterization of exchange in a calmodulin C-terminal domain mutant. J. Am. Chem. Soc., 2004, 126, 928–935, copyright 2004 American Chemical Society.

Interestingly, the CSM(C^α_i)/CSM(C^α_i+1) CCR rates are in disagreement with the two-state open-closed transition, as concluded from comparison to wild-type shifts (Figure F).^[69] Instead they suggests that an entire α-helix (helix F) transiently unravels in a cooperative fashion (Figure 10). This notion is supported by ¹H^N exchange measurements (Figure E). Importantly, these motions could not be detected by ¹H^N and ¹⁵N relaxation dispersion R_1ρ measurements.

Vugmeyster and McKnight investigated changes in the dematin headpiece upon S74E mutation, which closely mimics phosphorylation responsible for reversible regulation of actin bundling activity.^[96,116] The results indicated a reduction in mobility upon the mutation in several regions of the protein. The additional salt bridge formed in DHPS74E that links the N- and C-terminal subdomains is likely to be responsible for these changes.

4.3. Effect of deuteration at non-exchangeable sites

In a recent study, Vugmeyster et al. analyzed time scales of chemical exchange in GB3 using CSM/CSM rates in C’-N and C^α-C^β pairs in protonated and deuterated GB3 proteins at two values of static magnetic field strengths.^[118] Significant mobility was observed in the backbone in selected regions of the protein that was obscured in the SQ measurements, especially in the α-helical region. Backbone C’-N dynamics fell into the fast-to-intermediate regime on the chemical shift time scales, whereas C^α-C^β dynamics were determined to be in the intermediate-to-slow time regime. Further, CSM(C^α)/CSM(C^β) measurements indicated that the dynamics at these sites are significantly reduced when non-exchangeable protons are replaced by deuterons (Figure 11).

Figure 11.

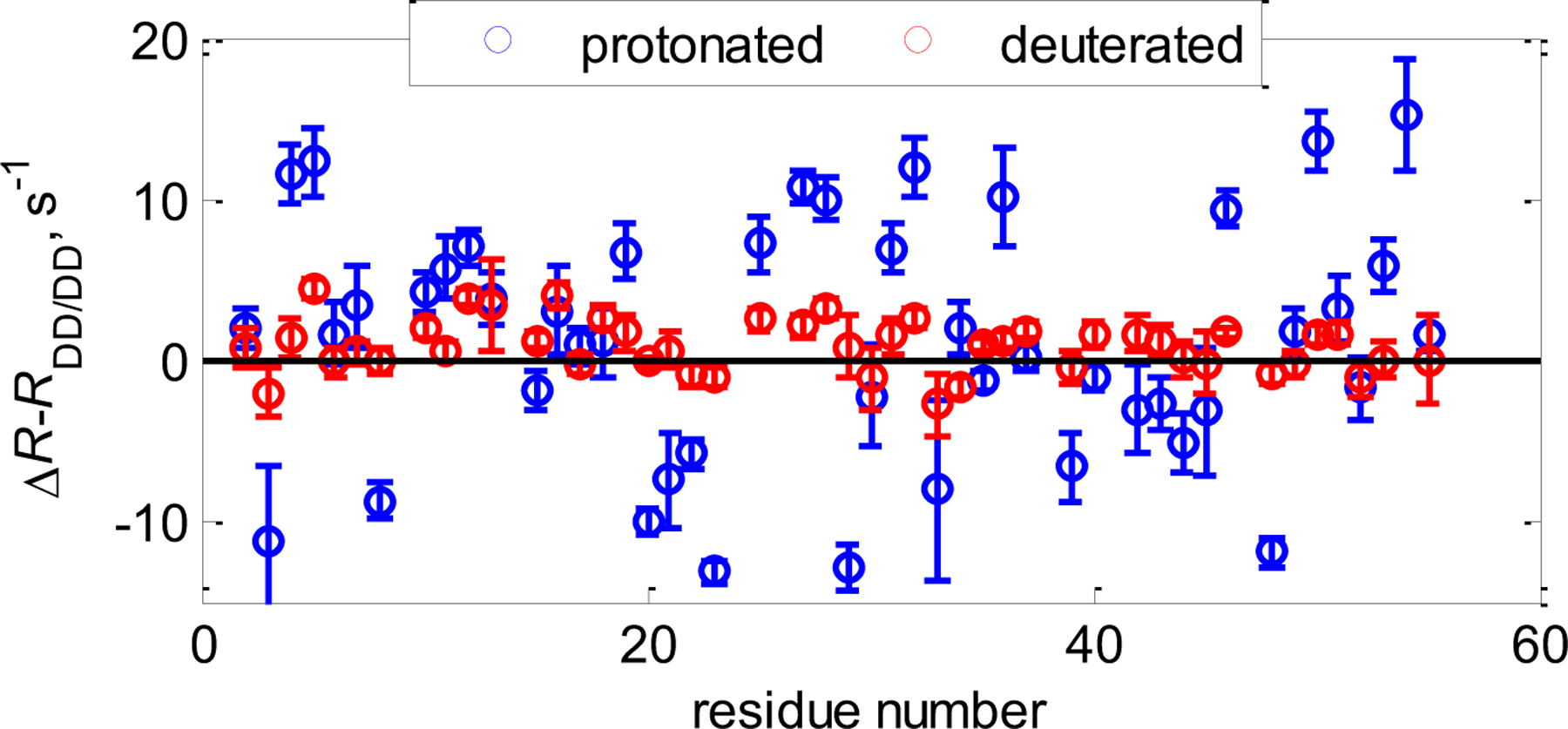
CSM(¹³C^α)/CSM(¹³C^β) interference in GB3. Shown are C^α−C^β ΔR=1/2(R^DQ-R^ZQ) rates with dipolar contributions R_DD/DD subtracted (calculated from structural coordinates) for protonated (blue circles) and deuterated at non-exchangeable sites (red circles) at 25^oC at 900 MHz magnetic field strength. In the deuterated protein the rates are close to zero, indicating a significant reduction in mobility.

5. Summary and Outlook

In summary, we have reviewed the potential of cross-correlated relaxation between two interactions that do not share a common spin for dynamics studies of proteins. Their measurement offers a type of information that is underexplored in structural and dynamics studies, the correlation in time and space of these two interactions. The rates fall into two main categories: CCR rates between rank-two interactions (DD, CSA, CSR) and rank-zero contributions (CSM). DD and CSR report directly on exact atom positions, while CSA and CSM depend on the electronic environment. However, CSM is a very strong probe of temporal aspects.

Although there have been attempts to use CCR rates as structural restraints,^[101,119] they are clearly less explored than other NMR restraints. We foresee two developments that would give multiple-quantum CCR rates novel significance in structure calculation, dynamics studies and molecular dynamics (MD) force field improvement. First, successful modeling of the CCR correlation function from MD trajectories would offer a direct comparison to measured CCR rates that incorporates also temporal properties of correlated motions. Second, reconstruction of CSM/CSM rates from MD trajectories would introduce an unprecedented probe of time correlation. Promising progress has been made in predicting exchange contributions to single-quantum relaxation rates from MD simulations.^[120] Further improvement of the method would open the door to the prediction of correlations between chemical shift fluctuations as well. As opposed to analysis based on NOEs, scalar couplings and RDCs, there is still a need for the development of analytical CCR tools for non-experts.

Another attractive prospect is to probe CCR rates between interactions that are separated by more than 5 Å. This requires the establishment of MQ coherences between spins that are connected be more than three covalent bonds (or separated through space). At least on the GB3 sample that has been used for many of the studies presented here, further INEPT transfer steps are not prohibitive in terms of relaxation. However, many spins in the chain connecting the target spins would have similar chemical shifts to which pulses could not be applied selectively. This may complicate the design of appropriate pulse sequences. Generally, however, there are some limitations to the systems on which CCR rates can be measured with high accuracy. These include solubility at near-mM concentration, protein stability over days and relatively small protein size (even for those CCR rates that are easiest to measure the protein size above 200 residues is problematic).

Finally, we note that almost all studies have focused on the protein backbone. There is no fundamental reason that would prevent further studies on protein side chains, many of which feature more pronounced motions than the backbone, including highly correlated ones.