Changes in neurovascular coupling with cerebral perfusion pressure indicate a link to cerebral autoregulation

Abstract

Cerebral autoregulation ensures a stable average blood supply to brain tissue across steady state cerebral perfusion pressure (CPP) levels. Neurovascular coupling, in turn, relies on sufficient blood flow to meet neuronal demands during activation. These mechanisms break down in pathologies where extreme levels of CPP can cause dysregulation in cerebral blood flow. Here, we experimentally tested the influence of changes in CPP on neurovascular coupling in a hydrocephalus-type non-human primate model (n = 3). We recorded local neural and vascular evoked responses to a checkerboard visual stimulus, non-invasively, using electroencephalography and near-infrared spectroscopy respectively. The evoked signals showed changes in various waveform features in the visual evoked potentials and the hemodynamic responses, with CPP. We further used these signals to fit for a hemodynamic response function (HRF) to describe neurovascular coupling. We estimated n = 26 distinct HRFs at a subset of CPP values ranging from 40–120 mmHg across all subjects. The HRFs, when compared to a subject dependent healthy baseline (CPP 70–90 mmHg) HRF, showed significant changes in shape with increasing CPP (ρ_CPP = −0.55, p-value_CPP = 0.0049). Our study provides preliminary experimental evidence on the relationship between neurovascular coupling and CPP changes, especially when beyond the limits of static autoregulation.

Introduction

The total volume inside the skull remains constant.^1,2 If one of the cerebral constituents, namely, brain tissue, cerebral blood volume, or cerebrospinal fluid changes, the others compensate to maintain a constant intracranial pressure (ICP). However, large ICP increases have been linked to pathologies causing a disruption in cerebral blood inflow and outflow (ischemia/hyperemia), imbalance in cerebrospinal fluid flow (hydrocephalus), or cerebral mass changes (hemorrhage/edema). In these situations, elevated ICP can lead to alterations in cerebral perfusion pressure (CPP), commonly estimated as the difference between mean arterial blood pressure (MAP) and ICP, i.e., CPP = MAP-ICP. Changes in CPP, in turn, have a strong influence on cerebral blood flow (CBF), an inter-relationship first defined by Niels Lassen as cerebral autoregulation. ³ The Lassen’s Curve was thus defined as a tri-phasic curve depicting regions of autoregulation and dysregulation. Cerebral autoregulation happens over a range of CPP, where CBF is maintained, and regions of dysregulation occur below and above this range, where blood flow changes drastically with CPP variations, greatly increasing the risk of cerebral ischemia or hyperemia.

Evaluating autoregulatory health is beneficial in cerebral pathologies. While the Lassen’s Curve has been validated numerous times in animal studies and clinical populations,^4–7 accurate estimation of CBF and CPP lies at the heart of it. Unfortunately, current clinical standards for measuring autoregulation involve either invasive ICP sensors or assume ICP to be constant and use MAP as a surrogate for CPP. On the other hand, measurements of CBF are limited to expensive, sensitive to error, and single-time point measures.^8,9 While alternatives for CBF measurements exist, such as diffuse correlation spectroscopy (DCS), ¹⁰ their clinical translation for autoregulation assessment has been limited so far. Another major caveat of current techniques is the lack of a measure of neural activity or cerebral metabolism which can act as crucial markers of cerebral dysregulation.^4,11 There is a clinical need for a non-invasive biomarker using neural and cerebral vascular changes to assess CPP at the bedside.

Neurovascular coupling, or functional hyperemia is a response to local neural activation, and known to alter the surrounding cerebral tissue perfusion through localized vasodilation. ¹² Additionally, vessels are known to constrict or dilate in response to changing CPP to maintain blood flow. ¹³ Thus, a global change in vasomotor tone (cerebral autoregulation/dysregulation) can likely alter functional hyperemic responses.^14,15 Neurovascular coupling is known to alter in some disease states, especially when vascular integrity and cerebral autoregulation is impaired.^16,17

A hemodynamic response function (HRF) is often used to define neurovascular coupling. When convolved with a neural input, the HRF predicts the hemodynamic response to a stimulus^18,19 which can be local CBF or blood volume changes. The HRF shape is often described by a gamma variate function. ²⁰ The fitting procedure for finding an HRF which best predicts the hemodynamic signal, allows for selection of different shape parameters of this gamma function. Changes in HRF magnitude, time to peak or response duration are linked to changes in neural input (change in response amplitude, latency, duration, etc.) as well as changes in vascular output (amplitude, latency, undershoot, etc.). ¹⁹

Here, we experimentally studied the relationship between neurovascular coupling and CPP using a controlled hydrocephalus-type non-human primate model. We used non-invasive techniques to measure neural (electroencephalogram (EEG)) and vascular (near-infrared spectroscopy (NIRS)) signals at various induced CPP values. We then evaluated an HRF using these signals to study changes in neurovascular coupling at different CPP levels.

Materials and methods

Subjects and procedures

All experimental procedures were approved by the Institutional Animal Care and Use Committee (IACUC) of the University of Pittsburgh and in compliance with the National Institute of Health’s Guide for the Care and Use of Laboratory Animals (2011). The facilities at the University of Pittsburgh are accredited by the Association for Assessment and Accreditation of Laboratory Animal Care International (AAALAC) and in compliance with the Standards for Humane Care and Use of Laboratory Animals of the Office of Laboratory Animal Welfare (OLAW D16-00118). This manuscript is written in compliance with the Animal Research: Reporting In Vivo Experiments (ARRIVE) guidelines. Data reported here was collected from three healthy male non-human primates (Macaca Mulatta; average weight 9.07 ± 0.25 kg and average age 7.14 ± 0.08 years).

Non-human primates were initially sedated using 20 mg/kg Ketamine and 0.04 mg/kg Atropine. During the experiment, the animals were maintained under a combination of fentanyl (∼25 μg/kg/hr) and isoflurane gas (<1%) to avoid the deleterious effects of high concentrations of isoflurane on cerebral autoregulation.^21,22 Additionally, 0.1 mg/kg/hr of Vecuronium Bromide paralytic was administered throughout the experiment to prevent slow shifts in eye position that occur during anesthesia. After sedation, an arterial line was surgically placed in the internal carotid artery to measure MAP and the animals were ventilated at a constant rate of 12 bpm. Two small craniotomies were performed for placement of an ICP sensor (Precision Pressure Catheter, Raumedic Helmbrechts, Germany), placed about 1 cm into the parenchyma, and a catheter (Lumbar catheter, Medtronic, USA) connected to a saline reservoir, inserted about 2.5 cm in the brain to reach the lateral ventricle to manipulate ICP. The craniotomies were sealed using bone wax to avoid cerebrospinal fluid leakage. The animal was placed in the sphinx position in a stereotactic apparatus to face the screen where stimuli were shown. The eyes were held open using wire speculums and rigid gas-permeable contact lenses applied. Regular saline irrigation was used to maintain eye moisture.

Experimental and stimulus protocol

Multiple EEG electrodes (Ag/AgCl electrodes - Grass Instruments, USA) and a NIRS probe were placed in the occipital region over the visual cortex to record visual evoked neural and hemodynamic responses, respectively. EEG was recorded at 1000 Hz (Grapevine, Ripple Neuro, USA) and NIRS was recorded at 50 Hz at a source-detector distance of ∼2 cm (Oxiplex TS, ISS Inc, USA). Additionally, a DCS system built in-house was used to measure CBF at the lateral frontal cortex (away from the region of evoked responses) (Figure 1(a)). We recorded DCS data at 50 Hz at a source to detector fiber distance of 2 cm. (Excelitas Technologies, Canada). More details on the DCS device design has been discussed in a previous paper. ²³ All probes and electrodes were placed directly on the skull, after retracting the scalp to avoid superficial hemodynamic signals from scalp muscles.

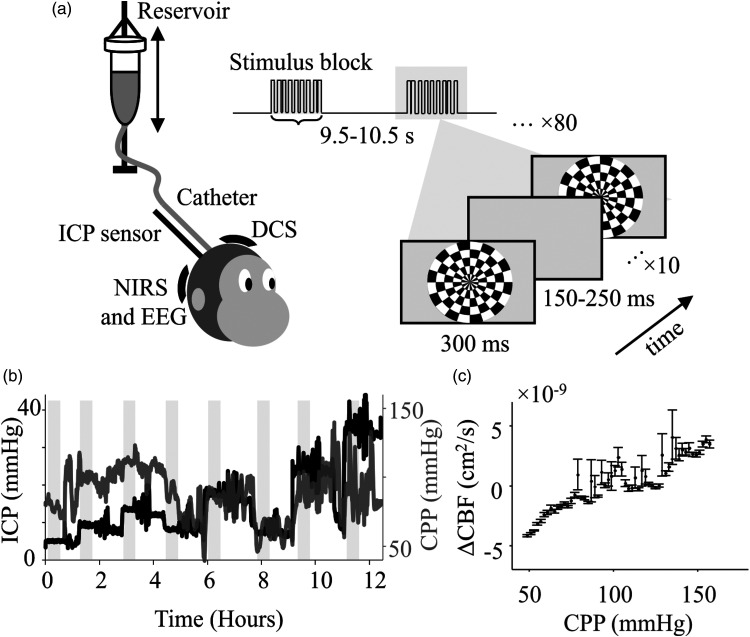
Figure 1.

Testing neurovascular coupling under altered CPP. (a) Schematic representation of the experimental setup. Visual stimulus was presented on a screen in the form of a flashing radial checkerboard at 2 Hz, in a block-design. ICP was altered by changing the position of the reservoir relative to the head before the beginning of each stimulus set. ICP was measured using a parenchymal pressure sensor, and evoked visual responses were recorded using NIRS and EEG. DCS was recorded in the frontal cortex to measure microvascular blood flow changes. MAP was recorded from the carotid artery using an A-line (not shown). (b) Changes in CPP were observed with ICP. ICP was altered in steps (black) and CPP (gray) was measured as the instantaneous difference between MAP and ICP. (c) Average Lassen’s curve (n = 3) evaluated from changes in blood flow measured with DCS across all subjects. The curve follows a typical tri-phasic Lassen’s Curve shape. Each point represents the mean, and the error bars show the s.e.m. in blood flow estimation.

ICP was altered in steps of ∼5 mmHg, from 3 to 30 mmHg, by changing the position of the reservoir to manipulate the hydrostatic pressure and saline flow in the catheter. After each increase, ICP was lowered to 9 mmHg for a full measurement cycle to avoid any additive effects of constantly increasing ICP (Figure 1(b)). For each measurement cycle at every ICP, at least 10 minutes were allowed for pressure to reach a steady state before stimulus presentation. Any periods of data with sudden changes in ICP, MAP, or isoflurane (>1%) were removed from analysis.

The visual stimulus protocol was selected to produce robust responses. Given the temporal difference between the neural and vascular signals, a blocked stimulus protocol was used with inter-block off duration sufficient to ensure singular, non-additive, vascular responses to local neural activation. The Psychtoolbox MATLAB extension ²⁴ was used to present stimuli on a high refresh rate, high resolution monitor (VPixx Technologies, Quebec, Canada) at 100% contrast and 50% average luminance. At each ICP baseline value, 80 blocks of stimuli were shown with an inter-block duration varying randomly between 9.5 and 10.5 s when the screen was gray. Each block of stimulus consisted of 10 counter-phased flashes of radial checkerboards with a duration of 0.3 s for each flash and a blank period between flashes chosen randomly from 0.15 to 0.25 s. (Figure 1(a)). Each visual stimulus protocol lasted ∼22 min at the set ICP baseline. CPP was evaluated as the linear difference between the MAP and the ICP at each time point, for the duration of the experiment (Figure 1(b)).

We analyzed evoked neural and hemodynamic responses to over 430 blocks (4,300 flashes) of visual stimulus presentation, per subject, with CPPs ranging from 40 to 140 mmHg. Further, 26 distinct epochs (15 continuous blocks, ∼3.5 min each) of EEG and NIRS, across all three subjects, were found to produce reliable HRFs. These were then used for further analysis on neurovascular coupling and spanned over a CPP range of 40-120 mmHg.

Neural and hemodynamic signal processing

All data streams were first time-aligned using an external analog marker sent to all devices at the beginning and end of each ICP measurement cycle. The recorded EEG signal was filtered using a 3rd order Butterworth bandpass filter between 0.5–30 Hz with additional notch filters to remove any remaining high frequency noise peaks (“butter” and “iirnotch” respectively, MATLAB2019b, MathWorks Inc.). The EEG data was downsampled to 100 Hz and segmented into epochs corresponding to blocks of stimulus presentation. Any value of EEG voltage exceeding five standard deviations from the mean (z-score > 5) was rejected along with the data in the corresponding stimulus block for EEG, NIRS and CPP. The remaining data was then used for VEP, hemodynamic response and HRF analysis.

A VEP was evaluated as the average voltage response recorded by the occipital electrodes to a flash of stimulus. Each VEP was first baseline corrected by subtracting 0.1 s of pre-flash data and then averaged across the 10 flashes in a block. Signal-to-noise ratio (SNR) for VEPs was estimated as the ratio of the mean amplitude of the N₁₀₀ peak to the standard deviation at that peak for every 10 mmHg in the CPP range of 40 to 140 mmHg.

NIRS data was recorded using two wavelengths, 690 and 830 nm. The modified Beer Lambert law was used to convert the intensity variations into concentration changes. ²⁵ Changes in oxyhemoglobin concentrations (ΔHbO) were used for all evoked vascular response analyses. All linear drifts in the signal were removed by subtracting the first-order polynomial trend from the data. The ΔHbO signal was filtered using a bandpass elliptical filter between 0.05 and 0.2 Hz with a pass ripple of 0.5 dB and a stop band attenuation of 20 dB (“ellipord”, MATLAB2019b, MathWorks Inc.). Additionally, a notch filter at 0.2 Hz was used to remove residual ventilation signal. This filtered signal was then used for evoked and HRF analysis.

Each hemodynamic response (ΔHbO) spanned over a block of stimulation (∼5 s) and ∼10 s of subsequent rest period. These responses were also baseline corrected by subtracting the respective mean of 0.1 s of pre-block-start data from each response. Neural and vascular responses recorded for each block were then sorted based on the average CPP for that block and mean responses calculated at every 10 mmHg in the CPP range of 40 to 140 mmHg. SNR for the evoked hemodynamic responses was estimated as the ratio of the mean amplitude of ΔHbO at the peak to the standard deviation at the peak for each CPP bin.

Lassen’s Curve: DCS was used to measure temporal changes in CBF. The autocorrelation of light intensity changes was used to estimate the scaled diffusion coefficient, αDb, which has been correlated to CBF. ¹⁰ The αDb value was thus used as a proxy for blood flow. The flow data was processed using a moving average filter with a window of 10 s to remove physiological artifacts. Epochs of laser instability were removed from αDb using z-score rejection (z-score > 0.5) corresponding to β-value changes. Here, β-value corresponds to intensity autocorrelation at zero-time delay, subtracted by 1. Additionally, other artifacts such as motion or ambient light were also removed using z-score rejection (z score > 2). The processed αDb value was then averaged in CPP bins of 2 mmHg, followed by mean subtraction and mean division to report ΔCBF per NHP. This was then averaged and plotted against CPP to report the Lassen’s Curve ³ (Figure 1(c)).

HRF estimation

Continuous time traces spanning 15 stimulation blocks (∼3.5 min, 150 flashes) of processed EEG and NIRS signals were used as inputs to a fitting function for estimating an HRF. These epochs were selected where all changes in CPP were within ±5 mmHg. The fitting function employed a gradient-descent based search algorithm (“fmincon”, MATLAB2019b, MathWorks Inc.) to maximize the Pearson’s correlation (r) between the recorded (ΔHbO using NIRS) and estimated hemodynamic signal. The estimated hemodynamic signal was calculated as the convolution product of the square of the neural signal amplitude (EEG), ²⁶ and a six-variable double gamma function HRF given by-

$$\mathit{HRF}\left(t\right)=x_1{\times \left(t\right)}^{x_2}{e}^{-\left(t\right)x_3}-x_4{\times \left(t\right)}^{x_5}{e}^{-\left(t\right)x_6}$$

Here, $t$ denotes time and variables $x_1,\dots ,x_6$ denote the different shape parameters of the HRF, estimated using a fitting function. The “best fit HRF” was selected as the solution with the highest r corresponding to lowest possible first-order optimality measure. Robustness of the solution was checked by comparing actual fits (r_{fit_evoked}) to fits obtained by using the evoked EEG with a set of NIRS data recorded at rest (r_{fit_noise}). Only HRFs with r_{fit_evoked} above the 75^th percentile of the distribution of r_{fit_noise}, were included for further analysis (more details in the Supplementary Text). Finally, this resulted in n = 26 HRFs estimated at different CPPs between 40-120 mmHg, which were used for further analysis.

Estimation of trends

Changes in neural and hemodynamic responses were quantitively analyzed by plotting the amplitude and latency of the VEP N₁₀₀ and the ΔHbO peak respectively, as a function of CPP. The N₁₀₀ feature was identified as the minimum amplitude and maximum slope change in 0.07–0.13 s after stimulus onset. The ΔHbO peak was evaluated as the maximum concentration change within 10 s after stimulus onset. Each feature was evaluated for the mean responses for every 10 mmHg in the CPP range of 40 to 140 mmHg.

For analyzing HRFs, we used normalized root mean square error (NRMSE) defined by-

$$\mathit{NRMSE}=1-\frac{\left|\right|\mathit{xref}-x\left|\right|}{\left|\right|\mathit{xref}-\mathit{mean}\left(\mathit{xref}\right)\left|\right|}$$

Here, $\mathit{xref}$ was taken as the healthy reference signal (mean of HRFs evaluated at CPP 70–90 mmHg) and $x$ as the HRF recorded at different CPP values. The range for healthy responses was selected based on the initial CPPs recorded from the subjects at the beginning of the experiment as well as our autoregulation estimates from the evaluated Lassen’s Curve. NRMSE was used as it ranges between 1 and −∞ and has the benefit of showing semi-bounded errors (unlike mean squared error or root mean square error) as well as being insensitive to reference signal amplitude. An NRMSE of 1 corresponds to “identical to reference” and 0 to “no better than a straight line” and as fits get worse, it tends to −∞. It must be noted that all HRFs were first converted into z-scores, by subtracting the mean and dividing by the standard deviation of the signal, before evaluating the NRMSE. This was done so that remaining analysis only compared HRF shapes and was not biased by amplitude differences (See Supplementary Text). A Spearman’s correlation (ρ) was then used to report trends in NRMSE values.

Results

Across 3 subjects, we evaluated changes in evoked responses (VEP and hemodynamics) over a range of CPP values from 40 to 140 mmHg. Within these ranges, we isolated epochs of EEG and NIRS time traces with distinct CPP values to evaluate HRFs (n = 26) for neurovascular coupling. The average Lassen’s curve estimated using DCS across all three subjects (Figure 1(c)) showed the typical tri-phasic shape with a relatively negligible change in CBF from ∼70−100 mmHg. Regions below and above this range showed greater changes in CBF, potentially indicating impaired cerebral autoregulation.

Changes in evoked visual responses with CPP

We used the local responses to a visual stimulus as indicators of increase in local neuronal activity (VEP) and associated functional hyperemia (ΔHbO). A typical VEP has a distinct shape with prominent positive peaks at ∼50 ms (P₅₀) and ∼150 ms (P₁₅₀), and a large negative amplitude peak at ∼100 ms (N₁₀₀) after stimulus onset. ²⁷ A robust VEP typically shows this P₅₀-N₁₀₀-P₁₅₀ complex, when recorded at the visual cortex, as a response to external stimulus (Figure 2(a) and Supplementary Figure 1). Hemodynamic responses were characterized by an increase in ΔHbO peaking at ∼6 s after the onset of the first flash and settling back to baseline after ∼13 s. We observed an average change in local ΔHbO of ∼0.2 µM, indicating a robust hemodynamic response triggered by the stimulus (Figure 2(b) and Supplementary Figure 1).

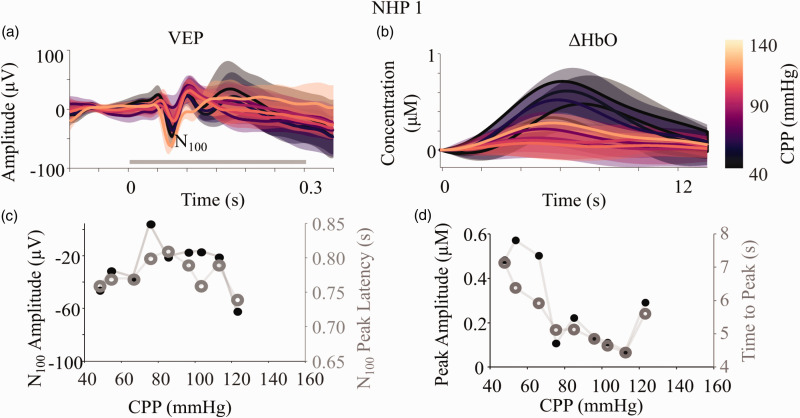
Figure 2.

Changes in evoked neural and vascular responses with CPP. (a) Visual evoked potentials (VEP) were recorded using EEG in the occipital lobe. Each flash of the checkerboard (gray bar from 0-0.3 s) evoked a VEP which was averaged for a block of stimulation and reported as a single VEP. (b) Similarly, block averaged hemodynamic responses were recorded as changes in concentration of oxy-hemoglobin (ΔHbO) using NIRS co-localized with EEG. Each response here, is for a block of stimulation (∼5 s) with ∼10 s of rest. The VEPs and ΔHbO responses were sorted by the recorded CPP for each block and binned in steps of 10 mmHg from 40 to 140 mmHg. The figure shows the mean (bold line) and s.d. (shaded region) for each CPP bin. The common color bar for both the figures is indicated on the right going from black (40 mmHg) to light yellow (140 mmHg). (c) The most negative peak closest to 0.1 s after stimulus onset was selected as the N₁₀₀ peak of the mean VEP at each CPP bin and the latency (gray open circles) and amplitude (black filled circles) plotted as a function of CPP. d) Similarly, the amplitude (black filled circles) and latency (gray open circles) of the highest peak of the ΔHbO response was plotted against CPP. Equivalent plots for all subjects can be found in Supplementary Figure 1.

To quantify changes in the evoked responses as a function of CPP, we isolated specific features and examined their trends with CPP. In VEPs, the N₁₀₀ is an especially robust feature with generally consistent latency which alters with pathology and hence used for clinical diagnosis.^27,28 In NHP1, we observed changes in both the peak amplitude and latency of the N₁₀₀ feature in the VEPs with CPP. For a range of CPP values between 70-100 mmHg, where blood flow was maintained (Figure 1(c)), the average latency was ∼80 ms and the average peak amplitude was ∼−20 µV (Figure 2(c)). At CPP values below ∼70 mmHg and above ∼100 mmHg, the amplitude of the N₁₀₀ became more negative (∼−60 µV) and the latency decreased to ∼75 ms. While the VEP shape in all the subjects were variable, the shape of the N₁₀₀ amplitude and latency curves as a function of CPP showed comparable trends, following an inverted U-shape (Supplementary figure 1).

For hemodynamic responses, the amplitude and latency of the point of maximum change in oxy-hemoglobin concentration were some of the most consistent and prominently changing features with CPP, across all subjects. Changes in hemodynamic responses were thus quantified by plotting these against the reported CPP. For CPP values in the range of 70–100 mmHg, where blood flow was maintained (Figure 1(c)), both the peak amplitude (∼0.1 µM) and time to peak (∼4.5 s) stayed low for NHP 1 (Figure 2(d)). However, at CPP values below ∼70 mmHg and above ∼100 mmHg, both the peak amplitude (∼0.4 µM) and time to peak (∼7 s) of ΔHbO increased. (Figure 2(d)). Similar trends were also observed for the other subjects as seen in Supplementary Figure 1.

In order to account for potential differences in noise between different measurements of VEP and ΔHbO as a function of CPP, we tested for changes in SNR of the responses (VEP and ΔHbO) as a function of CPP (Supplementary Figure 2). We found no significant variation (p-value for all responses≫0.05) in SNR.

While the trends were comparable between all subjects, the selection of only two features (N₁₀₀ for VEPs and peak for ΔHbO) was not sufficient to fully quantify all the differences seen in evoked waveforms across subjects. Additionally, while individual subjects show changes in VEP and ΔHbO, these changes alone do not describe neurovascular coupling. To address this, we evaluated HRFs using a semi-constrained mathematical model, to study changes in neurovascular coupling across subjects.

Estimation of HRF

The HRF was used to define the relationship between simultaneous neural activation and local hemodynamic changes. The best fit HRF was picked as the one that estimated a hemodynamic signal with highest correlation with the recorded ΔHbO (Figure 3(a)).

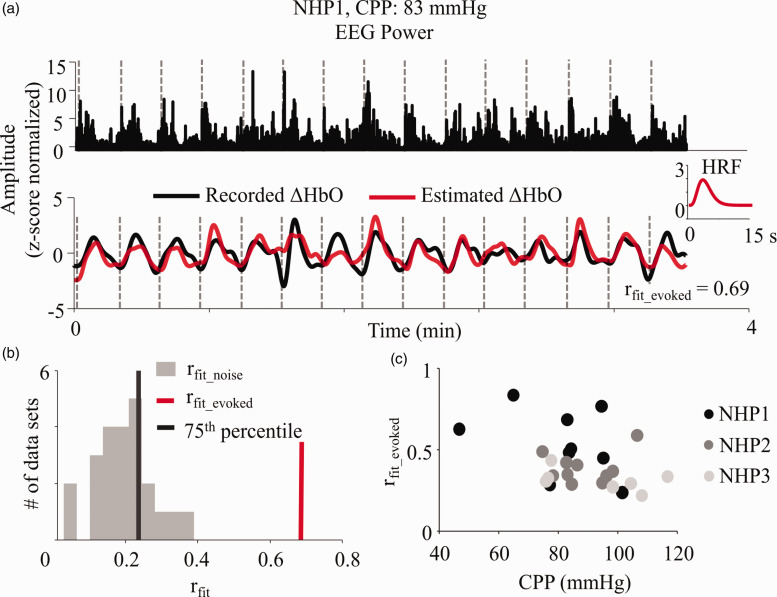
Figure 3.

Estimation of HRF from recorded neural and vascular data. (a) HRF was evaluated by iteratively fitting for a six-variable double gamma function which when convolved with the EEG signal power gave the highest Pearson’s r with the NIRS recorded ΔHbO time trace. EEG and NIRS data containing an equivalent of 15 blocks of stimulation (∼3.5 min) with CPP within 5 mmHg range were selected for HRF evaluation. The plot inset shows the evaluated “best fit” HRF (truncated to 15 s) for NHP1 at CPP of 83 mmHg, which was the average CPP across the 15 blocks. The gray dotted lines show the onset of each block of stimulation. All signals are normalized by their z-scores for comparable visualization. (b) The r_{fit_evoked} for each evaluated HRF was compared against a null distribution (gray bars) formulated by fitting each evoked EEG epoch with a set of temporally unrelated rest data (r_{fit_noise}). Only the r_{fit_evoked} (red vertical line) values which were greater than the 75^th percentile (black vertical line) of the aforementioned distribution were considered reliable fits. (c) The reliable r_{fit_evoked} were also tested for trends with CPP to ensure the fits themselves were not affected by any potential physiological confounds or SNR changes with CPP. All NHPs reported insignificant trends between r_{fit_evoked} and CPP (ρ_NHP1 = −0.47, p-value_NHP1 = 0.21; ρ_NHP2 = −0.03, p-value_NHP2 = 0.94; ρ_NHP3 = −0.21, p-value_NHP3 = 0.66). Here, ρ_i indicates the Spearman’s correlation for the respective subjects.

To eliminate bad fits from further analysis, we tested all our evoked EEG epochs against a noise fit-distribution of r_{fit_noise} that corresponded to “fitting to noise” (see Supplementary Text and Methods and Materials). Only HRFs that had r_{fit_evoked} greater than the 75th percentile of this noise fit-distribution were considered for further analysis (Figure 3(b)). Finally, to ensure there were no CPP related changes in the fits, we tested for changes in r_{fit_evoked} with CPP. None of the subjects showed any significant trends (p-value for all subjects ≫ 0.05) (Figure 3(c)), indicating that the fits were not affected by CPP.

Changes in neurovascular coupling with CPP

The HRFs were estimated using recorded neural (EEG) and vascular (NIRS) signal epochs at different CPP levels for every subject. The HRF typically mimicked the ΔHbO response, peaking in amplitude ∼6 s after stimulus onset and following a typical gamma shape. HRF shapes had a consistent gamma shape, showing altered features above and below the range of autoregulation (Figure 4(b)). An “initial dip” at ∼2 s before the positive rise in the HRF, at very low and very high CPP (Figure 4 and Supplementary Figure 1) was seen across all three subjects.

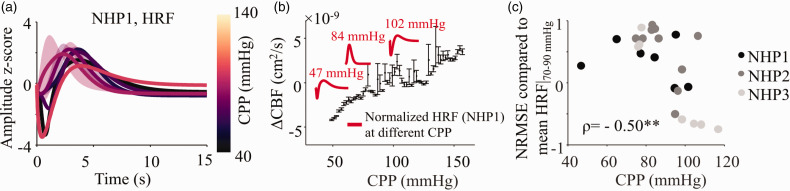
Figure 4.

Changes in HRF with CPP. a) The evaluated HRFs were z-score normalized and plotted as a function of CPP. The HRFs were averaged in CPP bins of 10 mmHg from 40–140 mmHg. The figure shows the mean (bold line) and s.d. (shaded region) for HRF waveforms for NHP1. The equivalent figures for the other two subjects are shown in Supplementary Figure 1. b) The mean Lassen’s Curve from Figure 1(c) overlaid with HRFs. The plots inset show some selected HRFs for NHP1 in red, highlighting shape changes with CPP. c) Each HRF shape across all three subjects were compared to their respective healthy mean HRF recorded at 70–90 mmHg and NRMSE evaluated. NRMSE shows a distinct downward trend (ρ = −0.50, p-value = 0.0097) across all three subjects showing an increasing deviation from the healthy response at higher CPP.

When compared to a healthy baseline HRF (CPP 70–90 mmHg), we observed a negative Spearman’s correlation (ρ = −0.50, p-value = 0.0097) in the NRMSE values across all three subjects (Figure 4(c)). We had only one data point below the lower limit of autoregulation, hence all trends shown here are influenced by autoregulation impairment caused at high CPP. For further analysis, this singular point below the lower limit of autoregulation (NHP1, CPP = 47 mmHg) was omitted.

To test the extent of CPP’s influence in altering HRFs, we ran additional analyses to address confounding factors. We tested for trends in HRFs with experimental factors such as time (affecting duration under anesthesia) and fluctuations in ICP (given the experimental model). We found that HRF changes showed significantly negative trends with only CPP (ρ_CPP = −0.55, p-value_CPP = 0.0049, p-value_ICP and p-value_time >> 0.05) (Supplementary Figure 3a). CPP was also significantly (90^th percentile of the CPP distribution >10^th percentile of either ICP or time distribution) better at predicting changes in neurovascular coupling than either ICP or time (Supplementary Figure 3 b).

Discussion

In this study, we demonstrate that changes in CPP, especially beyond the limits of static autoregulation, are associated with changes in evoked neural and vascular responses, and the coupling between them, as evaluated with an HRF. Through a controlled experimental setup, we altered CPP by inducing ICP changes in a hydrocephalus-type non-human primate model. We non-invasively recorded local responses using EEG and NIRS, to a visual stimulus, and found changes in VEP and ΔHbO waveforms with CPP (Figure 2 and Supplementary Figure 1). We further used these signals to estimate an HRF (Figure 3) which showed significant alterations from its healthy baseline shape, with increasing CPP (Figure 4). Finally, we found that CPP was the best predictor of changes in neurovascular coupling (Supplementary Figure 3). Here, we highlight and contrast our results to existing literature and discuss the implications of this research.

Evoked responses to visual stimuli and neurovascular coupling

Local simultaneous non-invasive recordings of neural and vascular responses have been performed with NIRS and EEG for over two decades. ²⁹ Using external stimuli to evoke responses has the benefit of eliciting robust, repeatable local activity, timed to the external stimuli in a healthy brain. In that regard, the shape and timescale of VEPs and local hemodynamic signals measured in this study (Figure 2, for CPP between 70–100 mmHg) are similar to what has been reported.^30–32 Using task evoked responses has the benefit of contrasting a predictable healthy response to those under pathophysiological conditions. This is seen in our characterization of evoked responses as a function of CPP (Figure 2, Supplementary Figure 1). We see that the shape of VEPs and hemodynamic signals vary from the subject’s healthy normal at extreme CPP values, without significant differences in the SNR (Supplementary Figure 2). It must be noted that VEPs for NHP 3, while following a general P₅₀-N₁₀₀-P₁₅₀ shape, were different at healthy CPP compared to the other two subjects (Supplementary Figure 1). This can be explained by the slight variations in EEG electrode placement or inter-subject variability.^33,34 This, however, did not alter the HRF results as each subject was compared to their respective healthy baseline response or HRF.

The coupling between local neural and vascular responses is often described with an HRF.^19,20 Early studies showed a strong relationship between local field power and local hemodynamic changes which enabled EEG-NIRS based studies to monitor neurovascular coupling. It was noted in fMRI literature that the power of the local neural activity closely resembled the cellular metabolism of the local tissue and hence matched with the consequent blood oxygen level dependent (BOLD) response.^26,35 Multi-modal comparison studies further made it possible to replicate the BOLD signal using NIRS concentration changes.^36,37 In our work, we thus use broadband EEG signal power to convolve with a variable gamma function (HRF) to predict the hemodynamic signal that best matches the recorded ΔHbO using NIRS (Figure 3). ΔHbO particularly has the benefit of high SNR and robust responses (as compared to ΔHbT and ΔHbR) and has also been shown to closely resemble evoked BOLD responses.^36,38

Changes in specific features of the HRF waveform (time-to-peak, initial dip or undershoot, response width, etc.) have been linked to cerebrovascular malfunction in pathologies such as stroke and TBI or with ageing^16,39–41 which are known to alter neurovascular coupling. However, most of these studies model the HRF to represent solely the hemodynamic BOLD signal, assuming no change in neural activity. This has been a common point of criticism for previous HRF literature.^42,43 Hence, here, we attempted to find HRFs by fitting using both recorded local hemodynamic (NIRS) and local neural signals (EEG). Given an estimation of a healthy HRF, alterations in its shape can thus be linked to pathophysiological conditions.

Relationship between neurovascular coupling and CPP

The cascade of events that underlie neurovascular coupling or enable cerebral autoregulation with CPP changes, are too complex to fully discuss in this paper. However, their relationship has been modelled in previous studies.^14,15,44 These models discuss a common cerebral perfusion regulatory mechanism that alters vasomotor tone during CPP variations (cerebral autoregulatory mechanism) and during functional hyperemia (neurovascular coupling). In situations of extreme CPP where the vessel diameter cannot be further altered (fully constricted or dilated), local vascular changes in response to neural activity may be hampered. This can in turn, affect the local oxygenated blood supply and affect subsequent neural response to external stimuli.^45,46 This could explain changes in our evoked neural and vascular responses, and consequently HRFs, with CPP variations, especially at extremes where cerebral autoregulation may be impaired (Figure 2, Figure 4 and Supplementary Figure 1).

One interesting shape feature we observed in HRFs was an increased likelihood of an “initial dip” for CPP outside the autoregulation plateau (Figure 4(a) and (b) and Supplementary Figure 1). This has been modelled before as a mismatch between the cerebral metabolic oxygen need and the commensurate change in blood volume^47,48 which here, could signify a more sluggish evoked hemodynamic change under autoregulatory vasomotor constraints. This delay in volume changes to the stimulus, is also seen in our results as an increase in time-to-peak for the ΔHbO response (Figure 2(d) and Supplementary Figure 1) at the extreme CPP values, potentially corresponding to impaired cerebral autoregulation.

Our experimental paradigm used ICP changes to simulate a hydrocephalus-type model and induce CPP variations. Additionally, we used a controlled level of isoflurane anesthesia (<1%) in combination with fentanyl to minimize the vasodilatory effects of isoflurane in our experiment.^7,22,49,50 A previous study from our group has shown this anesthesia protocol to not impair autoregulation, given the low percentages of isoflurane. ²¹ There are several other factors in addition to CPP that could influence autoregulation (e.g., ICP, end-tidal CO₂ (EtCO₂), time under anesthesia or MAP). We measured changes in HRFs as a function of ICP and time under anesthesia and found no significant trends (Supplementary Figure 3). Since changes in blood gases can also affect cerebrovascular resistance,^51,52 we monitored EtCO₂ and found that it did not vary significantly over the duration of the experiment (25–40 mmHg) and was thus unlikely to substantially affect autoregulation. ⁵³ Lastly, we evaluated whether MAP could explain HRF changes, since CPP is linearly related to MAP (CPP=MAP-ICP). Similar to CPP, HRFs also significantly changed with MAP, albeit showing a slightly lower correlation (ρ_CPP = −0.55, p-value_CPP = 0.0049; ρ_MAP = −0.49, p-value_MAP = 0.0145). Taken together, these analyses support our focus on the relationship between HRF changes and CPP, but additional experiments will be needed to untangle the individual role of ICP and MAP. Overall, this finding aligns with our previous work, ²¹ where we found that CPP was better at distinguishing intact vs. impaired autoregulation, compared to MAP or ICP.

Our work provides preliminary experimental evidence on the relationship between neurovascular coupling and CPP across three male non-human primates, with HRFs estimated at 26 distinct CPP values. Although a larger cohort clinical study with representation from all sexes will be important to extend our observations, our data acquired over a wide range of CPP (40–120 mmHg) provides a unique insight into neurovascular coupling changes with CPP. Such a wide range of CPP cannot be replicated in a clinical setting. In a critical care setting, because it might not be possible to engage subjects in a visual task, assessment of HRF changes with resting state data could be used as an alternative to task induced changes. Finally, while an impairment in neurovascular coupling does not imply altered cerebral autoregulation, in clinical cases with a propensity to have increased CPP, our work experimentally shows that there is a correlation between neurovascular coupling and the state of static autoregulation. Quantification of neurovascular coupling via HRF changes may have potential as a non-invasive biomarker for CPP changes and therefore autoregulatory impairment.