Abstract
Competing risk analyses have been widely used for the analysis of in-hospital mortality in which hospital discharge is considered as a competing event. The competing risk model assumes that more than one cause of failure is possible, but there is only one outcome of interest and all others serve as competing events. However, hospital discharge and in-hospital death are two outcomes resulting from the same disease process and patients whose disease conditions were stabilized so that inpatient care was no longer needed were discharged. We therefore propose to use cure models, in which hospital discharge is treated as an observed “cure” of the disease. We consider both the mixture cure model and the promotion time cure model and extend the models to allow cure status to be known for those who were discharged from the hospital. An EM algorithm is developed for the mixture cure model. We also show that the competing risk model, which treats hospital discharge as a competing event, is equivalent to a promotion time cure model. Both cure models were examined in simulation studies and were applied to a recent cohort of COVID-19 in-hospital patients with diabetes. The promotion time model shows that statin use improved the overall survival; the mixture cure model shows that while statin use reduced the in-hospital mortality rate among the susceptible, it improved the cure probability only for older but not younger patients. Both cure models show that treatment was more beneficial among older patients.
Keywords: competing risk model, mixture cure model, promotion time cure model, observed cure, in-hospital mortality
1. Introduction
Competing risk analyses have been widely used for the analysis of in-hospital mortality or length of stay in hospital, either for patients who were hospitalized for coronavirus disease 2019 (COVID-19),1,2 or for other diseases such as Malaria3 or burns,4 where in-hospital death and hospital discharge are treated as competing events for each other.5 Hospital discharge is treated as a competing instead of a censored event for in-hospital death because the latter approach violates the assumption of non-informative censoring and overestimates the cumulative mortality rate.6 Our work was motivated by a recent study7 conducted by our team of over 4000 COVID-19 patients admitted into Montefiore Medical Center in the Bronx in the spring of 2020, in the epicenter of COVID-19 pandemic in New York City. The study showed that statins, one of the most commonly prescribed medicines to patients with cardiovascular disease and diabetes mellitus, had a beneficial effect on the survival of patients with Type II diabetes.7 During the study's follow-up, about 60% of patients were discharged from the hospital. In this study, in-hospital mortality was the primary outcome of interest, and following the standard competing risk approach, discharge from the hospital was treated as a competing event for in-hospital death.
However, hospital discharge is not the type of competing events commonly seen in competing risk analyses. The competing risk approach typically concerns the situation where more than one cause of failure is possible,8,9 for example, multiple causes of death such as death due to cardiovascular disease or cancer, and only one of the causes is of interest so that the others serve as competing events. On the other hand, hospital discharge and in-hospital death are outcomes resulting from the same disease process. Although hospital discharge does not necessarily imply that the patient was either virus-free or completely free of symptoms, it indicates a well-controlled condition of the patient for whom in-patient care was no longer needed. Thus, it can be considered as “cured” of the disease. In addition, it is of interest to examine not only how statin treatment prolonged survival but also how statin use improved the probability of being cured from the infection. Thus, the cure model seems more suitable here.
Cure models have been used extensively in studies of cancer where some patients of a particular cancer type will never suffer a relapse and hence are cured of the specific cancer type.10–12 There are also applications of cure models among HIV/AIDS patients receiving antiretroviral therapy where there is a substantially large portion of long-term survivors.13 Cure models have rarely been used to examine in-hospital mortality, treating hospital discharge as a cure.14 To the best of our knowledge, our study is among the first to propose to use cure models in this setting.
Standard cure models assume that the cure status is unknown for patients who have not experienced the event of interest during the study follow-up, as one cannot distinguish between cured observations and large censored uncured observations. In our study, we actually observed the cure status of the patients who were discharged from hospital during the follow-up period. Several recently developments in cure models have also considered the case that cure is known for a proportion of the patient population.15 Laska and Meisner16 and Betensky and Schoenfeld17 and others14,18 proposed nonparametric estimations of survival function and cure rate with cure status available for some patients. Nevertheless, the goal of our study is to estimate treatment effects on patient's survival and cure rate rather than the survival function itself. Cure threshold models also consider cure status known as the models assume survival beyond a threshold as cured. For example, it was determined that community acquired pneumonia patients who survived more than 90 days after admittance to the hospital could be considered cured;19,20 pregnant women who did not experience spontaneous abortion (SAB) before 20 weeks were considered cured of SAB.21 Cancer studies have also considered long term survivals as cured.22,23 However, such threshold does not apply to our study, as it is not appropriate to assume a survival beyond certain time as cured. Wu, et al.24 considered a situation when some diagnostic procedures may provide partial information about the cured or the uncured status relative to certain sensitivity and specificity. In this paper, we extend cure models to incorporate the situation that the cure status was truly known for those who were discharged from the hospital during the follow-up period. Furthermore, while a few authors have discussed the connection between the competing risk model and the cure model when the primary interest is to estimate the cumulative incidence function,17,25 to our best knowledge, there has not been much work to examine how treatment effects estimated from a competing risk model when cure is the competing event relate to those estimated from cure models. This paper aims to address this issue as well.
The paper is organized as follows: in Section 2, we start with the competing risk model, next propose the cure models and then demonstrate the relationship between these two approaches in the context of our motivating example. In Section 3, simulation studies are used to examine the performance of the proposed estimation procedure for cure models as well as to verify the relationship established between the competing risk model and the cure model. Then in Section 4, we apply all models to our example cohort of COVID-19 in-hospital patients to examine the effect of statin use on in-hospital mortality. The paper's conclusions are provided in Section 5.
2. Method
2.1. Competing risk model
Let denote time to the event of interest, in the context of our motivating example, it is the time from hospital admission to death in-hospital, and let denote time to hospital discharge for subject i, Let be the right censoring time due to loss to follow-up or end of the follow-up, and denote the failure type so that for censoring if , for death if and for hospital discharge if . Following the standard competing risk approach for in-hospital mortality, with hospital discharge treated as a competing event, the sub-distribution hazard function for in-hospital death is defined as the following
| (1) |
where is the cumulative incidence function of event of interest in the presence of competing events, . The Cox proportional hazards model on sub-distribution hazard function proposed by Fine and Gray26 can be used to examine the association with the cumulative incidence of in-hospital death for variables of interest, denoted by :
| (2) |
where is the baseline sub-distribution hazard function. Here, is the relative risk for in-hospital death associated with X in the presence of the competing event.
2.2. Cure models
Here we propose to use cure models to examine in-hospital mortality, where hospital discharge is treated as an observed cure of the disease rather than a competing event. There are two main classes of cure models, the mixture cure model is the most widely used cure model27–30 and the other class of cure models is called the promotion time cure model.12,31–37 Below we consider the use of these two major classes of cure models.
2.2.1. Mixture cure model
Let , and be the indicator for whether the cure status was observed so that implies a known cured (hospital discharge) or a known uncured (death in hospital) and 0 for unknown cure status. The observed data for subject i is then where and are two covariate vectors.
The mixture cure model models the probability of not being cured, P(Z), and the survival function of the uncured (susceptible) patients, , separately, given covariates X and Z, so that the marginal survivor function is The literature on mixture cure models offers a wide variety of modelling approaches ranging from fully parametric to completely non-parametric. Here we adopt a flexible semiparametric mixture cure model28 which uses a Cox proportional hazards model for time to event among uncured,
| (3) |
and a logistic regression model for the probability of being uncured, ,
| (4) |
where represents the covariate effect among the susceptible patients, also referred to as the latency effect, and represents the covariate effect on the likelihood of uncure; and are may or may not be the same. In our example, we assume
Note that actual time to hospital discharge, , is not incorporated except via such that if When and it can be shown that
where is the density function for Q and is the cumulative distribution function for C. Here we further assume neither the distribution of nor that of depend on covariates. We therefore denote . Thus,
The likelihood function from the ith subject becomes
The expectation and maximization (EM) algorithm for model estimation has been used in standard mixture cure models, which treat the cure status among censored subjects as a latent variable,27,28 and also in the cure threshold models where cure status is partially known.21 We also propose an EM algorithm to estimate the parameters of interest, i.e., where an additional parameter is introduced. Specifically, we use to denote uncured status for subject i so that if not cured and 0 otherwise. Thus, if then and if then When is a latent variable such that
The complete likelihood function conditional on can then be written as:
Therefore, the contribution to the log likelihood function from the ith subject can be broken into the following three parts:
and
and
In the expectation step at the mth iteration of the algorithm, to compute the expectation of the complete-data likelihood given the current values of and the observed data , with respect to the latent variable , we use
while the M-step follows Amico & Keilegom12 to maximize the expected complete data likelihood with respect to the parameters in the model. The baseline survival function, , is estimated by
where is the number of events and is the risk set at time .28 The additional parameter, i.e., the proportion of cures that were observed, , is estimated by the following equation:
With the estimate of , we can then estimate the cure rate for the patient population by .
The algorithm is implemented in R by modifying the smcure package and is available at Github (https://github.com/xiaonanxue/Code). Because of the concerns raised in obtaining the variance estimates based on the EM algorithm,38 the bootstrap method is used to estimate the variances for the parameter estimates.
2.2.2. Promotion time cure model
The promotion time cure model, also called the bounded cumulative hazards model, is defined by an improper survival function
| (5) |
where F(t) is a proper cumulative distribution function such that Thus, is the negative of the log of the cure probability. The promotion time cure model offers a biological interpretation for tumor latency,36,39 where can be interpreted as the tumor cell growth rate. In the context of a viral infection, we can view to be the viral growth rate and model it by
| (6) |
where so that is the baseline cure probability. The improper hazard function defined upon the improper survival function (equation (5)), , can then be modelled as:
where Such modelling allows the use of the proportional hazards model for survival time with cure and the partial likelihood function to estimate .32,40,41
As if X is a binary treatment indicator,
| (7) |
where and are the cure probability for the treated group and the untreated group, respectively. Therefore, is the difference in cure probabilities between the two treatment groups on a complementary log-log scale. Therefore, here contains two types of effects: the effect on the survival among susceptible and the effect on the cure probability, which cannot be separated.
Methods to estimate proportion of long-term survivals, i.e., , and F(t) are available.33,41 Also there are other forms of promotion time cure model. For example, , which also allows covariates in .34,42 The covariate vector Z may or may not be the same as X. However, this model does not respect the proportional hazards assumption because of the presence of covariates in . There are also non-parametric form of .22 These models are beyond the scope of this paper.
It should be noticed that one key issue in cure models is identifiability, as we cannot distinguish censored cured observations from censored uncured observations. The identifiability issue is crucial since the estimation of a cure model can be severely biased if the model is not identifiable. Hanin & Huang43 discussed in detail the identifiability of the mixture cure model. The mixture cure model is identifiable if the survival function among the susceptible (uncured) subjects, i.e., , is proper. Another type of identifiability is related to the uniqueness of the parameters of the model. A key assumption to ensure identifiability of the model is that where for all x where and .44–46 Informally speaking, these assumptions imply that if the survival function has a long plateau, we can be confident that almost all observations in the plateau correspond to cured observations. In our study for patients where were discharged from the hospital during the follow-up, their survival times are assigned to be censored at a fixed value that is much larger than the domain of the distribution of survival time of the uncured subjects, i.e., . Therefore, the assumption of is satisfied.
2.3. Promotion time cure model and competing risk model
Table 1 summarizes data settings for competing risk models, mixture cure models and promotion time cure models for patients who died in the hospital, who were discharged from the hospital during the follow-up and who were censored.
Table 1.
Definitions of event status and observing status and data settings under various models for in-hospital death, hospital discharge and censored patients.
| Scenarios | Definition of Indicators | Data Settings | |||
|---|---|---|---|---|---|
| Event Status | Observed Status | Competing Risk Model | Mixture Cure Model | Promotion Time Cure Model | |
| Died in hospital during follow up | 1 | 1 |
|
|
|
| Discharged from hospital during follow-up | 0 | 1 |
|
|
|
| Censored (cured status unknown) | 0 | 0 |
|
|
|
Note: * is a very large number.
Here we show the competing risk model when cure is the competing event becomes a promotion time cure model. Let denote the subdistribution survival function, i.e., the probability of not developing the event of interest by time t, in the presence of competing events.
Proposition 1 defined in a promotion time cure model so that
Proof: Based on equation (2),
where is the baseline subdistribution survival function and is the baseline cumulative incidence function of the event of interest Let the baseline uncure probability, , the subdistribution survival function can be re-expressed as
| (8) |
Define then is a cumulative distribution function s.t. , increases with t and and . Let equation (8) becomes
which is the same as the improper survival function defined in equation (5) such that and Therefore, when the cure is treated as a competing event, the competing risk model is equivalent to the promotion time cure model. The limit of cumulative incidence function in a competing risk setting, i.e., , equals the uncure probability, i.e., .
The demonstrated equivalence of these two models allows the covariate effect obtained from the competing risk model to have an easier interpretation. Covariate effect from a competing risk model, , is interpreted as the covariate effect on in-hospital mortality in the presence of the likelihood of being cured from the disease. This interpretation is somewhat challenging, particularly since is known to be indirectly affected by the baseline cure rate and the covariate effect on the cure rate.8 The equivalence of and shows that in fact represents the overall covariate effect on for all patients’ survival, including those being cured. In addition, the equivalence of and shows that based on obtained from the promotion time cure model, one can make inference for the covariate effect on the cumulative in-hospital mortality rate over time, taking into account time to cure.9
Note that because the variation for the estimates of in the competing risk model is estimated based on an inverse probability weighted score function,26 while the variation for the estimates of is estimated based on standard score function derived from the partial likelihood function, the variability estimates may be slightly different. The estimates for covariate effects and their variations are further compared in simulation studies.
3. Simulation
In the first set of the simulation, we examined the performance of the EM algorithm developed in Section 2.2.1 for estimating the parameters of interest in the mixture cure model. In each simulated data set, the number of subjects is set to be N = 2000 and the baseline cure probability is set to vary from 0.3 to 0.7. The size of the simulated data set was chosen close to our example. We considered two independent covariates, is a binary variables with and The parameters and and and were set to be pre-selected values so that they are close to the coefficients for the statin use and per standard deviation increase in age in years in our motivating example, respectively. The proportion of observed cures, , is allowed to vary from 0.6 to 0.8. Each simulated data was generated based on the following steps:
Generate the uncure status based on equation (4) with Z = X;
Among cured, i.e., B = 0, generate the status of being observed, ;
For uncured, i.e., B = 1, generate time to event T based on equation (3) with S(t|x) = 1-F(t|x) where the baseline survival function follows a Weibull distribution;
Generate independent censoring time and a and b are chosen to have the censoring proportion to be close to our example;
- For uncured B = 1, observed survival time = min(T,C), if T < C, and otherwise, and ;
- For unobserved cure, B = 0 and observed survival time = C and ;
- For observed cure, B = 0 and .
The EM algorithm developed in Section 2.2.1 was applied to each simulated data set and the bootstrap method was applied to estimate the variance of the parameter estimates. Due to computation intensity, we limited the number of bootstrap samples to be 200 and repeated the simulation for 500 times. The results are summarized in relative bias, coverage probability of the 95% confidence interval in Table 2.
Table 2.
Performances of the estimation of the mixed cure models with cures partially observed: results from 500 simulated data sets of N = 2000 subjects each with one binary random variable () and one continuous random variable () under various levels of baseline cure probability (the cure probability when ) and proportion of the cures that was observed in the study. Time to event was generated based on a Weibull distribution.
| Baseline cure probability = 0.3 | ||||||||||||
| Prob of observed cure = 0.6 | Prob of observed cure = 0.8 | |||||||||||
| Parameters for Models | X 1 | X 2 | Prob of obs cure | X 1 | X 2 | Prob of obs cure | ||||||
| % bias1 | % Cov2 | % bias | % Cov | % bias | % Cov | % bias | % Cov | % bias | % Cov | % bias | % Cov | |
| Prob of Uncure | −0.48 | 93.4 | 0.51 | 96.8 | 0.13 | 97.2 | −0.41 | 94.0 | 0.48 | 95.2 | −0.01 | 96.2 |
| Latency | −0.27 | 94.6 | −0.31 | 95.2 | −0.41 | 94.2 | 0.72 | 93.8 | ||||
| Baseline cure probability = 0.5 | ||||||||||||
| Prob of observed cure = 0.6 | Prob of observed cure = 0.8 | |||||||||||
| Parameters for Models | X 1 | X 2 | Prob of obs cure | X 1 | X 2 | Prob of obs cure | ||||||
| % bias | % Cov | % bias | % Cov | % bias | % Cov | % bias | % Cov | % bias | % Cov | % bias | % Cov | |
| Prob of Uncure | 0.17 | 95.2 | 0.80 | 95.0 | −0.02 | 96.0 | −0.02 | 96.2 | 0.82 | 95.0 | 0.02 | 93.0 |
| Latency | −0.60 | 94.0 | −0.32 | 94.8 | −0.58 | 93.8 | −0.24 | 95.0 | ||||
| Baseline cure probability = 0.7 | ||||||||||||
| Prob of observed cure = 0.6 | Prob of observed cure = 0.8 | |||||||||||
| Parameters for Models | X 1 | X 2 | Prob of obs cure | X 1 | X 2 | Prob of obs cure | ||||||
| % bias | % Cov | % bias | % Cov | % bias | % Cov | % bias | % Cov | % bias | % Cov | % bias | % Cov | |
| Prob of Uncure | 0.65 | 94.6 | 0.25 | 95.8 | 0.33 | 97.2 | 0.61 | 95.2 | 0.25 | 95.2 | 0.14 | 95.2 |
| Latency | 0.73 | 93.8 | −0.32 | 95.6 | 0.68 | 93.2 | −0.21 | 95.6 | ||||
Note. 1. % bias = (estimated parameter-true parameter)/true parameter*100%; 2. % cov = proportion of the true parameter included in the estimated 95% confidence intervals obtained from bootstrapping.
Table 2 shows that the parameters for both the probability of uncure and for latency effects estimated by the proposed EM algorithm are consistent with low bias and the variation of parameter estimates are also consistent so that the nominal coverage probability for the interval estimate is close to its nominal level. The estimate for the proportion of observed cure, , is also consistent. Results are similar when the baseline cure probability and vary.
In the second set of the simulation, we generated cure data based on the promotion time cure model and then applied both the promotion time cure model and the competing risk model. We examined and compared the performance of each model. To simulate time to event data based on the promotion time cure model (equations (5) and (6)), we adopted the approach proposed by Oulhaj and Martin,40 while incorporating the possibility of observed cure. Specifically, we set the number of subjects to be N = 2000 and same as the 1st set of simulations, we considered two independent covariates, and Let the cure probability where and were set to be pre-selected values and the cure rate . The remaining of the parameters including , were chosen to be the same as the first set of the simulations. Then the time to event was generated in the following steps:
Generate the uncure status ;
For cured, i.e., B = 0, generate the observed status ;
- For uncured, i.e., B = 1, generate time to event T: specifically
- Generate calculate and ;
- Let where is the inverse Weibull survival function;
Generate independent censoring time ;
- For promotion time cure model:
- If B = 1, observed survival time = min(T,C), if T < C, and otherwise ;
- If B = 0 and observed survival time = C and ;
- If B = 0 and observed survival time is censored at a very large number, say (),
- For competing risk model
- If B = 1, survival time = min(T,C), if T < C, failure type ; otherwise failure type D = 0;
- If B = 0 and survival time = C and failure type D = 0;
- If B = 0 and discharge time = C and failure type D = 2
We applied the promotion time cure model as well as the competing risk subdistribution hazards model to each simulated data set. We repeated this process for 1000 times and the results were summarized in relative bias, coverage probability of the 95% confidence interval and ratio of sample standard deviation and average estimated standard deviation under each of the model in Table 3.
Table 3.
Comparison between the competing risk and the promotion time cure models: results from 1000 simulated data sets of N = 2000 subjects each with one binary random variable and one continuous random variable under various assumptions on baseline cure probability (the cure probability when ) and proportion of the cures that are observed in the study. Time to event follows a Weibull distribution.
| Baseline cure probability = 0.3 | ||||||||||||
| Prob of observed cure = 0.6 | Prob of observed cure = 0.8 | |||||||||||
| Parameters for Models | X 1 | X 2 | X 1 | X 2 | ||||||||
| % bias1 | ase/sse2 | % Cov3 | % bias | ase/sse | % Cov | % bias | ase/sse | % Cov | % bias | ase/sse | % Cov | |
| Competing risk model | −0.213 | 1.008 | 95.3 | 0.184 | 0.965 | 93.9 | −0.213 | 1.008 | 95.4 | 0.187 | 0.964 | 93.9 |
| Promotion time cure model | −0.213 | 1.009 | 95.2 | 0.184 | 0.966 | 94.1 | −0.213 | 1.009 | 95.5 | 0.187 | 0.966 | 94.1 |
| Baseline cure probability = 0.5 | ||||||||||||
| Prob of observed cure = 0.6 | Prob of observed cure = 0.8 | |||||||||||
| Parameters for Models | X 1 | X 2 | X 1 | X 2 | ||||||||
| % bias | ase/sse | % Cov | % bias | ase/sse | % Cov | % bias | ase/sse | % Cov | % bias | ase/sse | % Cov | |
| Competing risk model | −0.522 | 1.018 | 95.6 | −0.374 | 0.983 | 95.1 | −0.521 | 1.018 | 95.5 | −0.374 | 0.984 | 95.1 |
| Promotion time cure model | −0.520 | 1.018 | 95.6 | −0.374 | 0.983 | 95.1 | −0.520 | 1.018 | 95.7 | −0.374 | 0.984 | 95.0 |
| Baseline cure probability = 0.7 | ||||||||||||
| Prob of observed cure = 0.6 | Prob of observed cure = 0.8 | |||||||||||
| Parameters for Models | X 1 | X 2 | X 1 | X 2 | ||||||||
| % bias | ase/sse | % Cov | % bias | ase/sse | % Cov | % bias | ase/sse | % Cov | % bias | ase/sse | % Cov | |
| Competing risk model | 0.143 | 0.996 | 95.5 | −0.007 | 0.996 | 95.6 | 0.145 | 0.996 | 95.4 | −0.068 | 0.996 | 95.4 |
| Promotion time cure model | 0.144 | 0.996 | 95.5 | −0.007 | 0.997 | 95.4 | 0.146 | 0.996 | 95.4 | −0.068 | 0.996 | 95.4 |
Note. 1. % bias = (estimated parameter-true parameter)/true parameter*100%; 2. ase/sse = average of standard error estimates/sample standard error; 3. % cov = proportion of the true parameter included in the estimated 95% confidence intervals.
Table 3 shows that the promotion time cure model estimated using the standard partial likelihood function results in consistent estimates for the parameters in the model as well as for their variations. Results are similar when the baseline cure probability and the proportion of observed cure varies. The competing risk model provides very close in some scenarios identical parameter estimates as well as variation estimates to those obtained from the promotion time cure model. That is to say, when assessing the overall effect of covariates on survival outcomes with the possibility of being cured from the disease, these two models are numerically equivalent.
4. Application
Our motivating example came from a retrospective cohort of all patients who were admitted into the Montefiore Medical Center in the Bronx between March 1st, 2020 to May 2nd, 2020 with a confirmed COVID-19 diagnosis and were then followed until May 4th of 2020. For this paper, we limited the study population to diabetic patients only. After removing <5% patients with missing BMI information, there were 2159 patients in the study population. Among them 729 (32%) died in hospital, 1349 (62%) were discharged and 188 (8%) remained in the hospital at the end of the follow-up. Note that in our data example there was no patient discharged to hospice care. If there were such observations, then those patients would have been considered as censored for death rather than cured of the disease.
About 44% of patients were treated with statins in this subset. Statins have known anti-inflammatory properties47 and may represent an agent for modulating the host response during COVID-19.48 In this paper, we are interested to evaluate if the impact of statin treatment varied over age. The median age of the patient population was 69 years old, and thus we used age 70 years old as cutoff point to define the two age groups.
4.1. Cure models and competing risk model
We began our analysis by considering the effects of statin use, older age and their interactions while ignoring other covariates. In addition to the competing risk model, we applied both cure models presented in Sections 2.2.1 and 2.2.2 by treating hospital discharge as “cured” of the disease. For the promotion time cure model, we assigned survival time for the observed cured to be censored at 10,000 days. The results are summarized in Table 4a.
Table 4a.
Results from the subset (N = 2399) of the retrospective cohort of COVID-19 patients at montefiore health center at bronx under competing risk model, mixture cure model and promotion time cure model with statin use, older age (age > 70 years old) and their interaction as covariates (Model 1).
| Competing Risk Model | Mixture Cure model | Promotion Time Cure Model | |||||||
| Uncure Probability | In hospital death for uncured | Proportion observed cure | |||||||
|
|
p-value |
|
p-value |
|
p-value | Estimate (95% CI) |
|
p-value | |
| Statin Use | 0.744 (0.579,0.956) |
0.021 | 0.894 (0.682,1.170) |
0.414 | 0.744 (0.555,0.996) |
0.047 | 0.979 (0.956,1.000) |
0.745 (0.577,0.962) |
0.023 |
| Age > 70 vs ≤70 | 2.836 (2.337,3.443) |
<0.001 | 3.144 (2.478,3.989) |
<0.001 | 1.847 (1.434,2.380) |
<0.001 | 2.834 (2.340,3.432) |
<0.001 | |
| Statin &Age group Interaction | 0.555 (0.402,0.767) |
<0.001 | 0.490 (0.335,0.716) |
0.001 | 0.727 (0.511,1.033) |
0.075 | 0.555 (0.401,0.769) |
<0.001 | |
The mixture cure model shows that although statin use did not affect much on the probability of being cured among younger COVID patients (OR for cure = 1.118 (95% CI: 0.854, 1.538), p-value = 0.414), it significantly improved the cure probability among older patients (OR for cure = 1.848 (95% CI: 1.540, 2.223; p-value < 0.001)), ratio of ORs = 2.041 (95% CI: 1.397, 2.985; p-value < 0.001) between older and younger patients. Furthermore, among the uncured, statin use was associated with longer survival (HR = 0.744 (95% CI: 0.555, 0.996; p-value = 0.047)) for younger patients and the effect was about 40% stronger for older patients (HR = 0.541 (95% CI: 0.450, 0.650; p-value < 0.001)) with a borderline statistical significance for the interaction term. Close to 98% of the cured patients were observed, suggesting that the cure probability was about 64% (62%/98%) in this population.
The promotion time cure model combined the effects of statin use on the probability of cure and on survival among those who were not cured and showed an overall HR of 0.745 (CI: 0.577, 0.962, p-value = 0.023) among younger patients and a nearly doubled effect among older patients (HR = 0.413 (95% CI: 0.338, 0.507), p-value < 0.001)), ratio of HRs = 0.555 (95% CI: 0.410, 0.769, p-value < 0.001)) between older and younger patients. As Table 4a indicates, the magnitude of the HR estimate obtained in the promotion time cure model is in between the OR for uncure and the HR for in-hospital death among the uncured obtained from the mixture cure model. The competing risk model, as expected, provided effect estimates very close to those obtained from the promotion time cure model. As discussed in Section 2.3, in this setting a cure model is more natural because it provides a better interpretation for the covariate effect than a competing risk model with cure as the competing event.
4.2. Model fitting
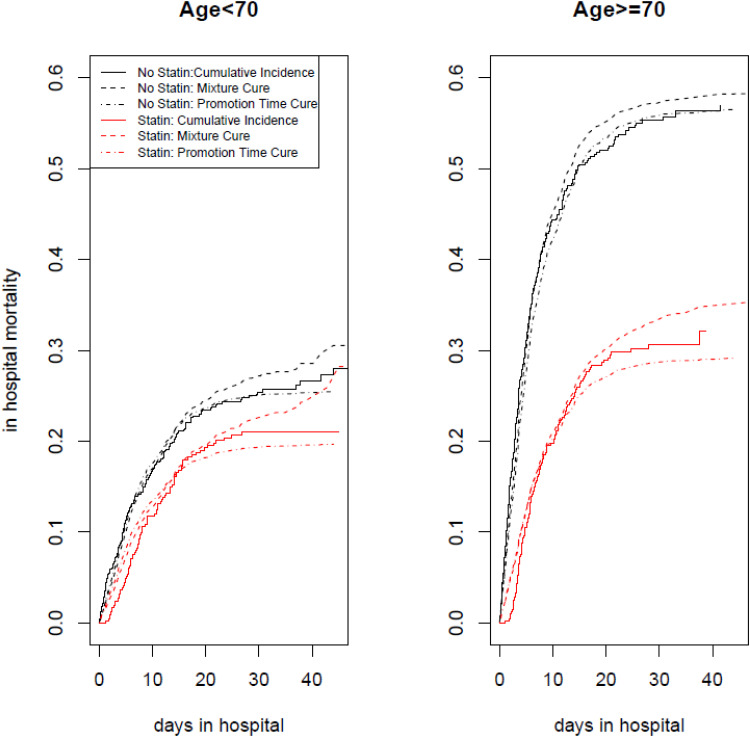
To examine how the models fit the data, in Figure 1 we compared the estimated cumulative incidence of in-hospital mortality under each of the cure models. Figure 1 shows that both cure models fit the cumulative incidence rate very well at short hospital stays with the mixture cure model having a slight advantage. As their hospital stays become longer than 10 to 15 days, both cure models indicate some level of lack of fit with a slightly larger discrepancy for the mixture cure model: the mixed cure models tend to overestimate the cumulative incidence rate while the promotion cure models tend to underestimate the cumulative incidence rate.
Figure 1.
The cumulative incidence rate of in hospital mortality by statin Use. Statin users (red) and Non-Statin users (black) among younger patient population (Age <70) is on the left panel and among older patient population (Age> = 70) is on the right panel. solid line is the non-parametric estimate of cumulative incidence of in hospital mortality, the dashed line is the fitted estimate of cumulative incidence rate based on the mixture cure model and the dotted and dashed line is the fitted estimate of cumulative incidence rate based on the promotion time cure model. Both cure models included statin use, age and their interaction in the model.
To address potential confounding effects and to improve the model fit, we additionally included in the model BMI and the Charlson comorbidity index as continuous variables as well as gender. The results are summarized in Table 4b. Table 4b shows that while male patients did not differ from female patients in survival time, they were less likely to be cured (OR for uncure = 1.572 (95% CI: 1.287, 1.921; p-value < 0.001)); BMI did not affect survival nor the cure probability while the Charlson index predicted both, suggesting patients’ underlying condition played an important role on their COVID outcome. The overall impact of each of these additional variables on COVID survival assessed by the promotion time cure model shows statistical significance. The difference in treatment effects between younger and older patients decreases after the inclusion of these additional variables, implying that the difference observed between age groups is somewhat explained by these variables.
Table 4b.
Results from the subset (N = 2399) of the retrospective cohort of COVID-19 patients at montefiore health center at bronx under competing risk model, mixture cure model and promotion time cure model with covariates in model plus gender, BMI and charlson index. (Model 2).
| Competing Risk Model | Mixture Cure model | Promotion Time Cure Model | |||||||
| Uncure Probability |
In hospital death for uncured | Prop obs cure | |||||||
|
|
p-value |
|
p-value |
|
p-value | Estimate (95% CI) |
|
p-value | |
| Statin Use | 0.631 (0.489,0.814) |
<0.001 | 0.750 (0.561,1.003) |
0.053 | 0.675 (0.516,0.882) |
0.004 | 0.978 (0.954,1.000) |
0.631 (0.488,0.816) |
<0.001 |
| Age > 70 vs ≤70 | 2.242 (1.813,2.773) |
<0.001 | 2.409 (1.853,3.130) |
<0.001 | 1.697 (1.318,2.185) |
<0.001 | 2.239 (1.824,2.749) |
<0.001 | |
| Statin &Age Group Interaction | 0.607 (0.439,0.839) |
0.003 | 0.543 (0.362,0.815) |
0.003 | 0.745 (0.526,1.054) |
0.096 | 0.607 (0.438,0.841) |
0.003 | |
| Male vs Female | 1.396 (1.191,1.636) |
<0.001 | 1.572 (1.287,1.921) |
<0.001 | 1.007 (0.832,1.220) |
0.940 | 1.400 (1.199,1.632) |
<0.001 | |
| BMI | 1.012 (1.001,1.024) |
0.036 | 1.007 (0.993,1.021) |
0.311 | 1.006 (0.993,1.019) |
0.350 | 1.012 (1.001,1.023) |
0.027 | |
| Charlson Score | 1.089 (1.067,1.111) |
<0.001 | 1.096 (1.066,1.127) |
<0.001 | 1.060 (1.034,1.087) |
<0.001 | 1.089 (1.069,1.110) |
<0.001 | |
To examine the fit of the expanded models, we calculated the martingale residuals, which shows the discrepancy between the observed and the expected number of in-hospital deaths given the fitted model. For the mixture cure model, we used the martingale residual for the overall model49 defined as the following:
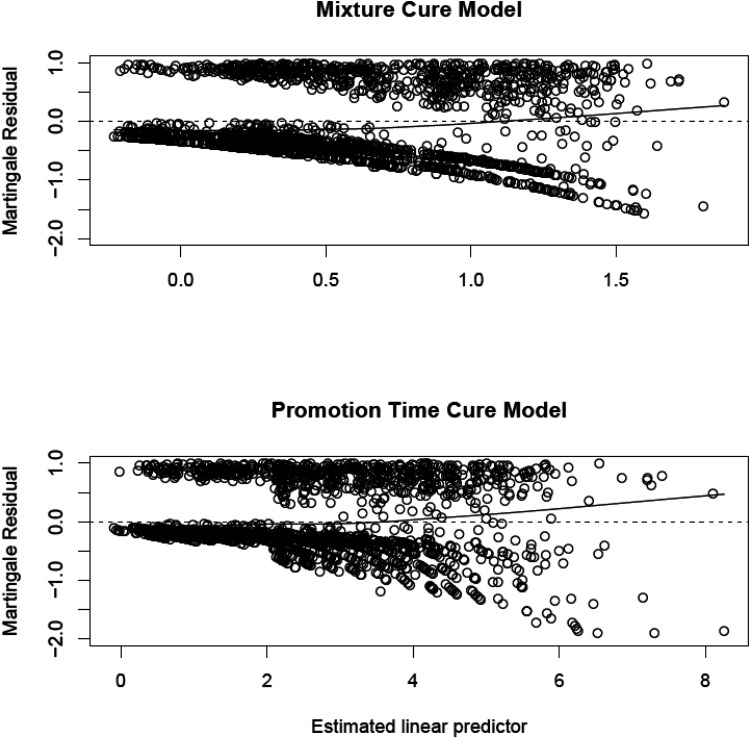
The martingale residual shares some of the properties of the martingale residual for classical survival model: it has mean 0 and is uncorrelated between each other, except that it has a lower bound of . These martingale residuals were then plotted against the estimated linear predictor for the mixture cure model and for the promotion time cure model in Figure 2. Figure 2 indicates that the discrepancy is small for both models with few outliers. When the estimated linear predictor is large, which means higher risk of uncure and earlier death, the mixture cure model has a slight advantage. On the other hand, when the estimated linear predictor is small, the loess smoothed curve for the promotion time cure model is closer to 0 than that for the mixture cure model, indicating a better fit of the promotion time cure model for longer hospital stays. These findings are somewhat consistent with what we have observed in Figure 1. The promotion time cure model has resulted in a few larger residuals (close to −2.0) while the mixture cure model has not, which may result from the fact that the martingale residuals from the mixture cure model have a lower bound and but not those from the promotion time cure model. For the promotion time cure model, we also used Schoenfeld residuals to examine the proportionality assumption graphically and no obvious violation was identified. Overall, as suggested by these residual plots, the two cure models when additional covariates were included fit the data generally well.
Figure 2.
Estimated martingale residuals vs the estimated linear predictor for the retrospective cohort of COVID patients with diabetes. Under the expanded model with additional covariates, the survival part of the mixture cure model is on the top panel and the promotion time cure model is on the bottom panel. Dashed horizon line indicates residual = 0, the solid line is the loess smoothed curve of the residuals.
5. Conclusion and discussion
In this paper, we proposed to use cure models to assess the treatment and disease association for COVID-19 in-hospital patients. Competing risk analyses have been widely used in the literature to model cumulative in-hospital mortality while treating hospital discharge as a competing event. However, unlike a typical situation of multiple types of failures where the competing risk model is used, hospital discharge and in-hospital death reflect two absorbing stages of the same disease. We therefore propose to use the cure model instead, which treats hospital discharge as a “cure”. In standard cure models the cure of the disease, for example, cure of cancer, is not directly observed. While cure threshold models allow cure status known for those whose time to event exceeding a threshold, the model assumption does not apply to our data. In this paper, we extended cure models to allow hospital discharge during the follow-up to be treated as an observed cure. Both the mixture cure model and the promotion time cure model were considered. We developed an EM algorithm to estimate the parameters of interest for the mixture cure model and estimated the parameters of interest for the promotion time cure model via maximizing the standard partial likelihood function. Our simulation studies showed that the proposed algorithms perform well in estimating parameters of interest for both models.
We have shown mathematically as well as numerically that the competing risk model which treats discharges from the hospital as a competing event is equivalent to a promotion time cure model. As we mentioned earlier in the paper, the interpretation of treatment effect under a competing risk model is somewhat challenging when the competing event is the cure of the disease. The equivalence of the competing risk model and the promotion time cure model shows that hazard ratios obtained from the competing risk model capture the global effects of the treatment on time to in-hospital death and on the probability of cure of the disease. The equivalence between the promotion time cure model and the competing risk model also suggests that the promotion time cure model provides an effect estimate on cumulative in-hospital mortality rate over time.
We applied the proposed models to a retrospective cohort of COVID-19 in-hospital patients who were diabetic. The mixture cure model showed that for younger patients (<70) statin use reduced the rate of in-hospital death but did not improve the probability of cure; on the other hand, statin use reduced the rate of in-hospital death as well as improved the probability of cure for older patients. The promotion time model showed that statin use improves the overall survival for both younger and older patients and but statins were much more beneficial among older patients. The findings from our application suggest the administration of statins to COVID-19 patients with diabetes, in particular among older patients.
Comparisons between mixture cure models and promotion time cure models in the literature tended to favor the promotion time cure model for several reasons.39 First, the promotion time cure model respects the proportional hazards assumption thus is easier to compute. Second, the promotion time cure models can be interpreted biologically as we described in Section 2.2.2. Third, Bayesian techniques have been developed for the promotion time cure model not for the mixture cure model. Nevertheless, while studies of chronic diseases including cancer might be more interested to estimate the overall treatment effect on survival, in studies of acute diseases such as COVID-19 infection, the treatment effect on the probability of cure might also be of the primary interest. The mixture cure model distinguishes the treatment effect on the probability of being cured from the treatment effect on the survival function among the uncured patients. On the other hand, in a the promotion time cure model, even by introducing covariates in ,34 it is not possible to separate the effect on cure probability from the effect on survival among those uncured.12 Thus, the mixture cure model is preferred in our data example.
One of the limitation of our mixture cure model is that we assume the probability of observed cure does not depend on covariates. In our future work, we will extend the model to allow to be dependent on X or Z, as treatment and patient characteristics may affect time to hospital discharge.
It is also worth pointing that Yin and Ibrahim50 proposed a unified approach to model time to event data with a cure fraction based on the Box-Cox transformation, in which the mixture cure model and the promotion time cure model are special cases of this unified model.51 Under this approach, the model selection can be based on a test of the Box-Cox transformation parameter: a test of the parameter equal to 1 evaluates the adequacy of the mixture cure model and a test of the transformation parameter equal to 0 evaluates the adequacy of the promotion time cure model. Extension of the approach to our data with partially observed cures is of interest. Furthermore, model fittings should always be examined and used as one of the criteria for model selections.
Footnotes
Declaration of conflicting interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: Dr Xue's work was partially supported by Clinical and Translation Science Award NCATS 5ULTR002556-02 (Keller, Shamoon) and by the Albert Einstein Cancer Center 2P30CA013330-48 (Chu). Dr Saeed was supported by grants from the National Institutes for Health/National Heart, Lung, and Blood Institute (K23HL145140) and the National Center for Advancing Translational Science Clinical and Translational Science Award at Einstein-Montefiore (UL1TR001073). Dr Jorde was supported by the McAdam Family Foundation. Dr Agalliu work was partially supported by the Albert Einstein Cancer Center 2P30CA013330-48 (Chu).
Availability of data and material: The data used as an example in this paper is not publicly available because it is part of an ongoing research study. Research data are not shared.
ORCID iDs: Xiaonan Xue https://orcid.org/0000-0003-2872-8119
Francesco Castagna https://orcid.org/0000-0002-8983-4866
Ilir Agalliu https://orcid.org/0000-0002-6248-5790
References
- 1.Zuccaro V, Celsa C, Sambo M, et al. Competing-risk analysis of coronavirus disease 2019 in-hospital mortality in a northern Italian centre from SMAtteo COvid19 REgistry (SMACORE). Sci Rep 2021; 11: 1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nijman G, Wientjes M, Ramjith J, et al. Risk factors for in-hospital mortality in laboratory-confirmed COVID-19 patients in the Netherlands: a competing risk survival analysis. PloS one 2021; 16: e0249231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Keene CM, Dondorp A, Crawley Jet al. et al. A competing-risk approach for modeling length of stay in severe malaria patients in South-East Asia and the implications for planning of hospital services. Clin Infect Dis 2018; 67: 1053–1062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Taylor SL, Sen S, Greenhalgh DGet al. et al. A competing risk analysis for hospital length of stay in patients with burns. JAMA Surg 2015; 150: 450–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brock GN, Barnes C, Ramirez JAet al. et al. How to handle mortality when investigating length of hospital stay and time to clinical stability. BMC Med Res Methodol 2011; 11: 144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Satagopan JM, Ben-Porat L, Berwick Met al. et al. A note on competing risks in survival data analysis. Br J Cancer 2004; 91: 1229–1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Saeed O, Castagna F, Agalliu I, et al. Statin use and in-hospital mortality in patients with diabetes Mellitus and COVID-19. J Am Heart Assoc 2020; 9: e018475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Putter H, Fiocco M, Geskus RB. Tutorial in biostatistics: competing risks and multi-state models. Stat Med 2007; 26: 2389–2430. [DOI] [PubMed] [Google Scholar]
- 9.Austin PC, Fine JP. Practical recommendations for reporting Fine-Gray model analyses for competing risk data. Stat Med 2017; 36: 4391–4400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Withers HR, Peters LJ, Taylor JM, et al. Local control of carcinoma of the tonsil by radiation therapy: an analysis of patterns of fractionation in nine institutions. Int J Radiat Oncol Biol Phys 1995; 33: 549–562. [DOI] [PubMed] [Google Scholar]
- 11.Tucker SL, Taylor JM. Improved models of tumour cure. Int J Radiat Biol 1996; 70: 539–553. [DOI] [PubMed] [Google Scholar]
- 12.Amico M, Keilegom IV. Cure models in survival analysis. Annu Rev Stat Appl 2018; 5: 311–342. [Google Scholar]
- 13.Varshney M, Grover G, Vajala Ret al. et al. Cure fraction model for the estimation of long-term survivors of HIV/AIDS patients under antiretroviral therapy. J Commun Dis 2018; 50: 1–10. [Google Scholar]
- 14.López-Cheda A, Jácome M-A, Cao Ret al. et al. Estimating lengths-of-stay of hospitalised COVID-19 patients using a non-parametric model: a case study in Galicia (Spain). Epidemiol Infect 2021; 149: e102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Peng Y, Yu B. Cure Models: Methods, Applications, and Implementation. 2021.
- 16.Laska EM, Meisner MJ. Nonparametric estimation and testing in a cure model. Biometrics 1992; 48: 1223–1234. [PubMed] [Google Scholar]
- 17.Betensky RA, Schoenfeld DA. Nonparametric estimation in a cure model with random cure times. Biometrics 2001; 57: 282–286. [DOI] [PubMed] [Google Scholar]
- 18.Safari WC, López-de-Ullibarri I, Jácome MA. A product-limit estimator of the conditional survival function when cure status is partially known. Biometrical Journal Biometrische Zeitschrift 2021; 63: 984–1005. [DOI] [PubMed] [Google Scholar]
- 19.Kellum JA, Kong L, Fink MP, et al. Understanding the inflammatory cytokine response in pneumonia and sepsis: results of the Genetic and Inflammatory Markers of Sepsis (GenIMS) study. Arch Intern Med 2007; 167: 1655–1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bernhardt PW. A flexible cure rate model with dependent censoring and a known cure threshold. Stat Med 2016; 35: 4607–4623. [DOI] [PubMed] [Google Scholar]
- 21.Piao J, Ning J, Chambers CDet al. et al. Semiparametric model and inference for spontaneous abortion data with a cured proportion and biased sampling. Biostatistics (Oxford, England) 2018; 19: 54–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen T, Du P. Promotion time cure rate model with nonparametric form of covariate effects. Stat Med 2018; 37: 1625–1635. [DOI] [PubMed] [Google Scholar]
- 23.Nieto-Barajas LE, Yin G. Bayesian Semiparametric cure rate model with an unknown threshold. Scandinavian Journal of Statistics 2008; 35: 540–556. [Google Scholar]
- 24.Wu Y, Lin Y, Lu SEet al. et al. Extension of a cox proportional hazards cure model when cure information is partially known. Biostatistics (Oxford, England) 2014; 15: 540–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Basu S, Tiwari RC. Breast cancer survival, competing risks and mixture cure model: a Bayesian analysis. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2010; 173: 307–329. [Google Scholar]
- 26.Fine JP, Gray RJ. A proportional hazards model for the subdistribution of a competing risk. J Am Stat Assoc 1999; 94: 496–509. [Google Scholar]
- 27.Peng Y, Dear KBG. A nonparametric mixture model for cure rate estimation. Biometrics 2000; 56: 237–243. [DOI] [PubMed] [Google Scholar]
- 28.Sy JP, Taylor JMG. Estimation in a cox proportional hazards cure model. Biometrics 2000; 56: 227–236. [DOI] [PubMed] [Google Scholar]
- 29.Wang L, Du P, Liang H. Two-Component mixture cure rate model with spline estimated nonparametric components. Biometrics 2012; 68: 726–735. [DOI] [PubMed] [Google Scholar]
- 30.Zhang J, Peng Y. Accelerated hazards mixture cure model. Lifetime Data Anal 2009; 15: 455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tsodikov A. Asymptotic efficiency of a proportional hazards model with cure. Stat Probab Lett 1998; 39: 237–244. [Google Scholar]
- 32.Tsodikov A. A proportional hazards model taking account of long-term survivors. Biometrics 1998; 54: 1508–1516. [PubMed] [Google Scholar]
- 33.Tsodikov A. Estimation of survival based on proportional hazards when cure is a possibility. Math Comput Model 2001; 33: 1227–1236. [Google Scholar]
- 34.Tsodikov A. Semi-parametric models of long- and short-term survival: an application to the analysis of breast cancer survival in utah by age and stage. Stat Med 2002; 21: 895–920. [DOI] [PubMed] [Google Scholar]
- 35.Tsodikov AD, Ibrahim JG, Yakovlev AY. Estimating cure rates from survival data: an alternative to two-component mixture models. J Am Stat Assoc 2003; 98: 1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yakovlev AYAT, A D%A Asselain, B. Stochastic Models of Tumor Latency and Their Biostatistical Applications.
- 37.Diao G, Yuan A. A class of semiparametric cure models with current status data. Lifetime Data Anal 2019; 25: 26–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Peng Y. Estimating baseline distribution in proportional hazards cure models. Comput Stat Data Anal 2003; 42: 187–201. [Google Scholar]
- 39.Chen M-H, Ibrahim JG, Sinha D. A New Bayesian model for survival data with a surviving fraction. J Am Stat Assoc 1999; 94: 909–919. [Google Scholar]
- 40.Oulhaj A, Martin ES. Generating data from improper distributions: application to cox proportional hazards models with cure. J Stat Comput Simul 2014; 84: 204–214. [Google Scholar]
- 41.Zhao X, Zhou X. Proportional hazards models for survival data with long-term survivors. Stat Probab Lett 2006; 76: 1685–1693. [Google Scholar]
- 42.Bremhorst V, Lambert P. Flexible estimation in cure survival models using Bayesian P-splines. Comput Stat Data Anal 2016; 93: 270–284. [Google Scholar]
- 43.Hanin L, Huang L-S. Identifiability of cure models revisited. J Multivar Anal 2014; 130: 261–274. [Google Scholar]
- 44.Patilea V, Van Keilegom I. A general approach for cure models in survival analysis. The Annals of Statistics 2020; 48: 2323–2346, 2324. [Google Scholar]
- 45.Xu J, Peng Y. Nonparametric cure rate estimation with covariates. Canadian Journal of Statistics 2014; 42: 1–17. [Google Scholar]
- 46.Lambert P, Bremhorst V. Estimation and identification issues in the promotion time cure model when the same covariates influence long- and short-term survival. Biometrical Journal Biometrische Zeitschrift 2019; 61: 275–289. [DOI] [PubMed] [Google Scholar]
- 47.Ridker PM, Danielson E, Fonseca FA, et al. Reduction in C-reactive protein and LDL cholesterol and cardiovascular event rates after initiation of rosuvastatin: a prospective study of the JUPITER trial. The Lancet 2009; 373: 1175–1182. [DOI] [PubMed] [Google Scholar]
- 48.Fedson DS, Opal SM, Rordam OM. Hiding in plain sight: an approach to treating patients with severe COVID-19 infection. Mbio 2020; 11(2): e00398-20. 10.1128/mBio.00398-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Peng Y, Taylor JMG. Residual-based model diagnosis methods for mixture cure models. Biometrics 2017; 73: 495–505. [DOI] [PubMed] [Google Scholar]
- 50.Yin G, Ibrahim JG. Cure rate models: a unified approach. Canadian Journal of Statistics 2005; 33: 559–570. [Google Scholar]
- 51.Peng Y, Xu J. An extended cure model and model selection. Lifetime Data Anal 2012; 18: 215–233. [DOI] [PubMed] [Google Scholar]