A unified statistical potential reveals that amino acid stickiness governs nonspecific recruitment of client proteins into condensates

Abstract

Membraneless organelles are cellular compartments that form by liquid–liquid phase separation of one or more components. Other molecules, such as proteins and nucleic acids, will distribute between the cytoplasm and the liquid compartment in accordance with the thermodynamic drive to lower the free energy of the system. The resulting distribution colocalizes molecular species to carry out a diversity of functions. Two factors could drive this partitioning: the difference in solvation between the dilute versus dense phase and intermolecular interactions between the client and scaffold proteins. Here, we develop a set of knowledge‐based potentials that allow for the direct comparison between stickiness, which is dominated by desolvation energy, and pairwise residue contact propensity terms. We use these scales to examine experimental data from two systems: protein cargo dissolving within phase‐separated droplets made from FG repeat proteins of the nuclear pore complex and client proteins dissolving within phase‐separated FUS droplets. These analyses reveal a close agreement between the stickiness of the client proteins and the experimentally determined values of the partition coefficients (R > 0.9), while pairwise residue contact propensities between client and scaffold show weaker correlations. Hence, the stickiness of client proteins is sufficient to explain their differential partitioning within these two phase‐separated systems without taking into account the composition of the condensate. This result implies that selective trafficking of client proteins to distinct membraneless organelles requires recognition elements beyond the client sequence composition.

Statement

Empirical potentials for amino acid stickiness and pairwise residue contact propensities are derived. These scales are unique in that they enable direct comparison of desolvation versus contact terms. We find that partitioning of a client protein to a condensate is best explained by amino acid stickiness.

1. INTRODUCTION

Cellular functions require the spatial and temporal organization of a vast number of molecular components. Cells achieve such organization by complex expression programs, ¹ the use of membrane‐bound compartments, ² chemical gradients, ³ , ⁴ and membraneless organelles that form through a process of phase separation. ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ Membraneless organelles maintain chemical heterogeneity in the cell by exploiting the differences of solubility of nucleic acids, organic molecules, and other proteins in the aqueous and proteinaceous/nucleic acid phases. ¹⁰ , ¹²

Client partitioning within phase‐separated liquid droplets can be used together with other cellular strategies for compartmentalization, as in the distribution of molecular species between the cytosol and the nucleus. For example, transport in and out of the nucleus is mediated by a liquid protein phase composed of intrinsically disordered domains of the nuclear pore complex (NPC). These disordered regions are rich in phenylalanine and glycine residues, and are known as FG domains. Protein cargo must dissolve within the liquid protein phase to gain passage through the pore and entry into the nucleus. ¹³ , ¹⁴

FG domains display sequence properties characteristic of phase‐separating proteins: they have low sequence complexity and contain repeating short linear motifs containing aromatic residues. Early work on the sequence determinants of phase separation established aromatic interactions as important for driving phase separation of proteins. Nott et al. found that mutating phenylalanine residues of the intrinsically disordered protein Ddx4 dramatically increase the threshold concentration required for phase separation. ¹⁵ Similarly, Lin et al. found that tyrosine residues are critical for the phase separation behavior of FUS. ¹⁶ These observations are consistent with π–π interactions being an important attribute of amino acid interactions. Indeed, tyrosine and arginine residues have been observed to be overrepresented in certain proteins prone to undergo phase separation, consistent with the observation that cation–π interactions can also drive condensate formation. ¹⁷

Given that π–π and cation–π interactions are determinants of phase‐separation propensity of scaffold proteins, Wang et al. investigated the sequence properties that establish partitioning of client proteins within liquid droplets made from the protein fused in sarcoma (FUS). ¹⁸ As a first approximation, the authors described the dependence of the partition coefficients on the number of arginine and tyrosine residues in the disordered regions of the client proteins.

Despite the observed similarities between sequence determinants of phase‐separation propensity and client partitioning, it is not necessarily the case that recruitment to condensates is a consequence of interatomic interactions between client and scaffold proteins. Given their distinct physicochemical properties, amino acids have disparate desolvation energies, and are observed to partition to different degrees between bulk water and phases where water could show different properties. Such differences could help to explain divergences in the partitioning of client proteins between the dilute and dense phases in phase‐separated systems, even in the absence of specific recognition elements.

The term “desolvation” in this context refers to the removal from bulk water to an environment of a distinct nature. Such a change would be concomitant with an increased water entropy in the bulk, but does not necessarily involve the complete removal of water from a client's surface, as seen in protein–protein interfaces, for example. Indeed, even in protein crystals, a significant volume is occupied by bulk water. ¹⁹ In one study, the water content in a phase‐separating system composed of ε‐poly‐l‐lysine (εPL) and hyaluronic acid (HA) was measured at 81%. ²⁰

Transfer energies have been extensively studied for individual amino acids, from an aqueous to a nonaqueous environment, resulting in numerous hydrophobicity and hydropathy scales. ²¹ , ²² , ²³ , ²⁴ , ²⁵ One such scale is residue interface propensity, which provides a statistical estimate of transfer free energies of amino acids from solvent to a protein interface of average composition by comparing the frequency of amino acids at the protein surface versus interface. ²⁶ In contrast, amino acid pairwise residue contact propensities have been estimated from over‐ or underrepresentation of contacts in the protein interior, ²⁷ or at protein interfaces. ²⁸ , ²⁹ It was previously observed that a weighted combination of residue interface propensity terms and amino acid pairwise residue contact propensity terms was better at distinguishing true protein–protein interfaces from decoys. ³⁰ Importantly, contact counts (that estimate pairwise residue contact propensity) and frequency counts (that estimate interface propensity and is dominated by desolvation energy) were weighted since the two are different quantities that cannot be compared directly (Figure 1).

FIGURE 1.

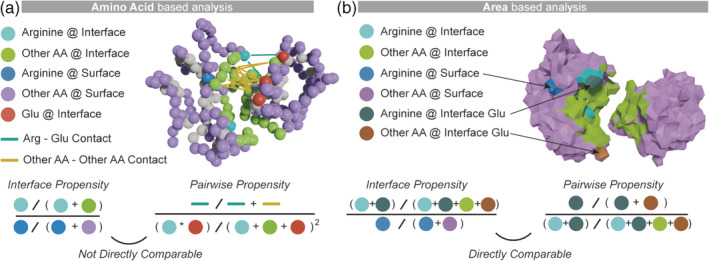
Considering the surface area of amino acids allows a direct comparison of interface propensities and pairwise residue contact propensities. (a) The interface propensity of arginine is the ratio of arginine frequency at the interface relative to its frequency at the surface. The pairwise residue contact propensity between arginine and glutamate is the frequency of their contacts at the interface relative to their frequency at the interface. These two propensities are not directly comparable because the terms used in their derivation are in different units (amino acid frequencies for the former and normalized contact frequencies for the latter). (b) Considering the surface area of amino acids makes interface propensity and contact propensity directly comparable because the same measure (i.e., area fraction) is used to derive all terms. The interface propensity of arginine becomes its fractional area at the interface relative to the surface and the arginine–glutamate contact propensity becomes the fractional area of arginine–glutamate contacts relative to the fractional interface area occupied by arginine

We show here that interface propensity, or “stickiness”, and pairwise residue contact propensity derived from surface areas are directly comparable without arbitrary weighting. To unify these two descriptions into a single energy term, we compared the same quantity – contact surface area – of amino acids at solvated surfaces versus interfaces. The capability of Voronoi tessellation ³¹ , ³² to make both descriptions comparable is illustrated in Figure 1. Voronoi tessellation enables the exact subdivision of any protein surface, making it possible to estimate both interaction propensity (which includes desolvation energy) and pairwise residue contact propensity (which does not include desolvation energy) from fractional amino acid surface areas.

To do so, we used the 3D Complex database ³³ to identify a set of nonredundant heteromeric dimers with high resolution, and a high confidence for correctly annotated assembly. Heteromeric dimers were chosen to eliminate symmetry induced effects. Voronoi contact area statistics were collected from residues at protein–protein interfaces (defined as those with over 25% of their side chain surface exposed in the unbound form, and which bury 50% of the exposed area in the bound form). Solvent exposed surface area statistics were collected from residues with over 25% of their side chain surface exposed in the unbound form, and which bury none of the exposed area in the bound form.

We use the derived potentials to show that the partitioning of client proteins within condensates is best explained by the desolvation energy of the client protein. In contrast, we find that pairwise residue contact propensities between client and scaffold explained the degree of partitioning less well.

2. RESULTS

2.1. A statistical potential unifying residue–solvent and residue–residue interactions

The binding of a protein surface to a partner molecule involves two major energetic components. A first is the desolvation of amino acids forming the new interface, and a second stems from contacts and noncovalent interactions established across the interface. We first aim to derive statistical potentials enabling a direct comparison of the energetic contribution of both of these components. Such comparison is made possible by calculating the ratios of amino acid surface areas, either (i) between protein surfaces and interfaces to estimate desolvation terms or (ii) between total interfaces and a subpart of interfaces composed of a specific amino acid to estimate contact preferences between amino acid residues (Figures 1 and 2a).

FIGURE 2.

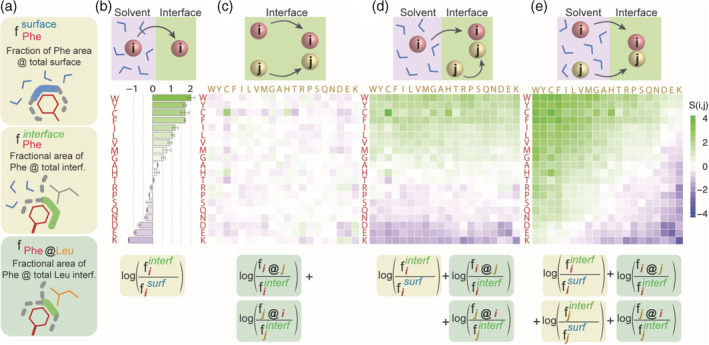
Defining amino acid interface propensities and interaction propensities based on surface areas. (a) We calculate three types of surface areas to derive interface propensities and pairwise residue contact propensities: (i) The area fraction an amino acid occupies at solvated surfaces. Phenylalanine, for example, makes up 1.33% of all protein surfaces in our dataset. (ii) The area fraction an amino acid occupies at interfaces. Phenylalanine, for example, makes up 7.19% of all protein interfaces in our dataset. (iii) The area fraction an amino acid makes up at a subinterface region defined by a particular amino acid. For example, phenylalanine makes up 8.17% of the total leucine interface area. (b) We estimate the free energy of transfer of amino acids from solvent to interface from the statistics of surface areas contributed to both regions. For example, the interface propensity of phenylalanine is log(0.0719/0.0133) = 1.69. (c) We estimate the interaction propensity of amino acids independently of their desolvation component. While the area fraction of phenylalanine at the total interface is 7.19%, it contacts 8.17% of leucine's interface area, highlighting a representation of this contact that is close to a random expectation: log(0.0817/0.0719) = 0.13. (d) We estimate the interaction propensity of amino acids with amino acid i being desolvated (red) and amino acid j (yellow) being already at the interface. (e) Interaction propensity that includes the desolvation component for both amino acids i and j

Calculating the partitioning of amino acid contact areas at interfaces versus at the solvent yields a 1D stickiness scale (Figure 2b, Equation 1). Consistent with previous interface propensity scales, lysine has the lowest propensity followed by negatively charged and polar amino acids, while aromatic and hydrophobic amino acids have the highest. Also consistent with previous scales and observations, arginine is significantly more sticky than lysine despite being highly hydrophilic owing to its increased ability to establish various contacts with partner amino acids. ²⁶ , ³⁴ , ³⁵ , ³⁶

Pairwise interactions are inferred from the area of contact between a pair of amino acids normalized by the area of those amino acids at interfaces (Figure 2c, Equation 6). This is akin to a pairwise residue contact propensity scale. As expected, oppositely charged residues exhibit the highest interaction propensities. Cysteine shows a high favorable self‐interaction potential, as well as a high propensity to interact with histidine, possibly due to its role in forming interfacial metal‐binding sites. ³⁷ Importantly, this observation is not caused by symmetric homodimers as our dataset is composed of heterodimers exclusively (Methods). Important also, unlike the 1D stickiness, these pairwise interactions do not include desolvation and only relate to contact preference within an already formed interface.

Decomposing the interaction propensity into separate terms enables the consideration of the asymmetric interaction between two amino acid residues across a phase boundary. If we consider an environment of reduced hydration, such as the protein dense phase of a phase‐separated system, we can add the desolvation term to only the amino acid residues of the client protein, while considering the desolvation states of the scaffold residues as remaining unchanged (Figure 2D).

Finally, we can add the desolvation term to both amino acids entering in contact, resulting in another familiar form of an interaction matrix that considers desolvation (Figure 2e). The interaction propensities of oppositely charged residues were among the most favorable in the pairwise interaction matrix that does not consider solvation. Interestingly, these favorable interactions are now offset by the unfavorable desolvation energies. Thus, although most pairwise residue potentials would classify a Lys–Asp interaction as favorable, our potential describes it as unfavorable when considering both interaction propensities and desolvation effects. This is reflective of the fact that lysine prefers to be in contact with the solvent, regardless of the existence of favorable electrostatic interactions with glutamate. Similarly Arg–Asp interactions are unfavorable, albeit close to a neutral (zero) value owing to the higher interface propensity of arginine. We see an opposite trend with tyrosine and tryptophan, which show favorable interactions with all amino acids due to a highly positive desolvation term.

Overall, this matrix of pairwise residue contact propensities recapitulates the early observation that desolvation is driving complex formation, whereas electrostatic interactions tune interaction specificity. ³⁸

2.2. Analysis of client partitioning within FG domains of the NPC

The NPC is a large protein complex regulating the transport of biomolecules across the nuclear membrane. A hallmark of the NPC are long disordered regions rich in phenylalanine and glycine (FG domains) that fill up the central cavity and form a gel‐like structure thought to phase separate. ³⁹ , ⁴⁰ , ⁴¹ An important step in the transport of cargo across the nuclear pore is the dissolution of the cargo within the phase‐separated FG domains, which is dependent on the cargo's composition. Frey et al. characterized the partitioning of protein cargo within liquid protein droplets composed of FG domain containing sequences. They found that the partitioning of protein cargo coincided with the passage of cargo across the nuclear pore complex. ⁴² GFP variants that differed only in the identity of a single amino acid type at eight different positions on the protein surface were synthesized, and the partition coefficients of each variant between the dilute phase and the FG domain phase were measured (Figure 3a).

FIGURE 3.

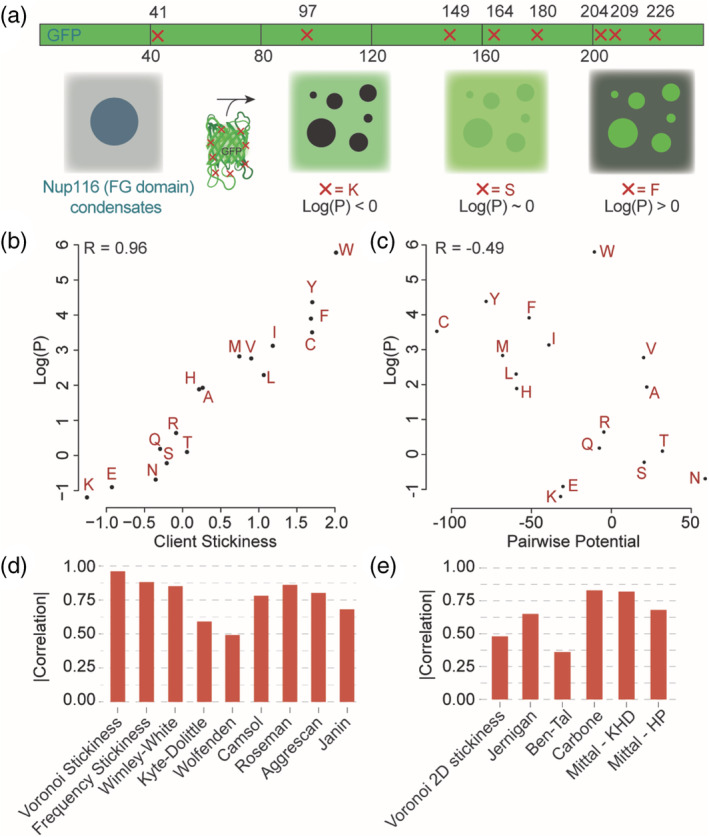
Residue interaction propensity of “stickiness” predicts the dissolution of a protein cargo into FG‐rich condensates better than residue–residue interactions. (a) Frey et al. generated GFP variants harboring eight mutations at their surface. In each variant, all eight mutations were to the same amino acid. They measured the partition coefficient (log(P)) of each variant between bulk and condensates made of a FG‐rich sequence from Nup116. (b) The stickiness scale derived in this work recapitulates the observed partition coefficients well. (c) Pairwise residue contact propensities do not explain the partition coefficients observed, indicating the desolvation energy is driving the dissolution of cargo into these condensates. The Gle2‐binding (GLEB) domain was not included in calculating the interaction potential. (d) We assessed several hydropathy and solubility scales for their ability to recapitulate the observed partition coefficients. (e) We assessed several residue–residue interaction potentials for their ability to recapitulate the observed partition coefficients

We plotted the log values of the partition coefficients with the scores calculated by the use of our derived scales. The derived residue propensity values for each amino acid is highly correlated with the partition coefficient of each of the variants in systems composed of phase‐separated NUP droplets (R = 0.96). This high correlation implies that the desolvation energy of the client protein is the main driver of the partitioning between the two phases. We compared our results to those obtained with other propensity scales and pairwise residue potentials. We first analyzed a set of hydrophobicity scales. These were Wimley–White, ²³ Wolfenden, ²⁵ Kyte–Doolittle, ²¹ CamSol, ⁴³ Roseman, ²² Janin, ⁴⁴ and Aggrescan. ⁴⁵ As can be seen in Figure 2c, our Voronoi‐based residue interface propensity scale is able to capture the partition of proteins to a better degree.

We now consider amino acid pairwise interactions (Figure 2c) between the amino acid of interest and amino acids in the sequence of NUP116, which are summed as described in Equation 11. The total interaction scores so obtained for the different variants correlate negatively with the partition coefficients (R = −0.49). This indicates that the contribution of specific pairwise interactions between the client protein and the scaffold is negligible in establishing the partitioning. We then compared this correlation value to those derived in the same manner (Equation 11), based on several prominent pairwise residue contact propensity scales. These include classical Jernigan potential ²⁷ and the Glaser scale from the Ben‐Tal group. ²⁸ The Mittal group specifically developed one‐dimensional scales for modeling phase separation by protein disordered regions, where pair interactions were calculated as the average single amino acid values, ⁴⁶ the Carbone group developed a scale that combines interaction potential with interface propensity, thus incorporating desolvation energies into each term. ³⁰ Although the pair propensities in Glaser scale reflect the tendency for hydrophobic amino acids to interact at protein interfaces, this scale was designed to capture amino acid interaction propensities without desolvation contributions. This lack of an explicit hydrophobic term is reflected in the reduced performance of this scale compared to scales that account for desolvation, further indicating the desolvation energy is the main driver of the partitioning.

2.3. Analysis of client partitioning within FUS droplets

Liquid droplets formed by the RNA‐binding protein fused in sarcoma (FUS) can recruit client RNA binding proteins through intermolecular interactions between low complexity (LC) domains. ⁴⁷ Wang et al. characterized the partitioning of intrinsically disordered protein cargo between the dilute and the dense phases of phase‐separated FUS. ¹⁸ In these experiments, FUS is fused to a SNAP tag conjugated to a red fluorescent dye, and upon phase separation the dense phase is visible as a red fluorescent droplet. After mixing with various GFP‐fused client proteins, a partition coefficient is calculated from the green fluorescence intensity inside versus outside of droplets (Figure 4).

FIGURE 4.

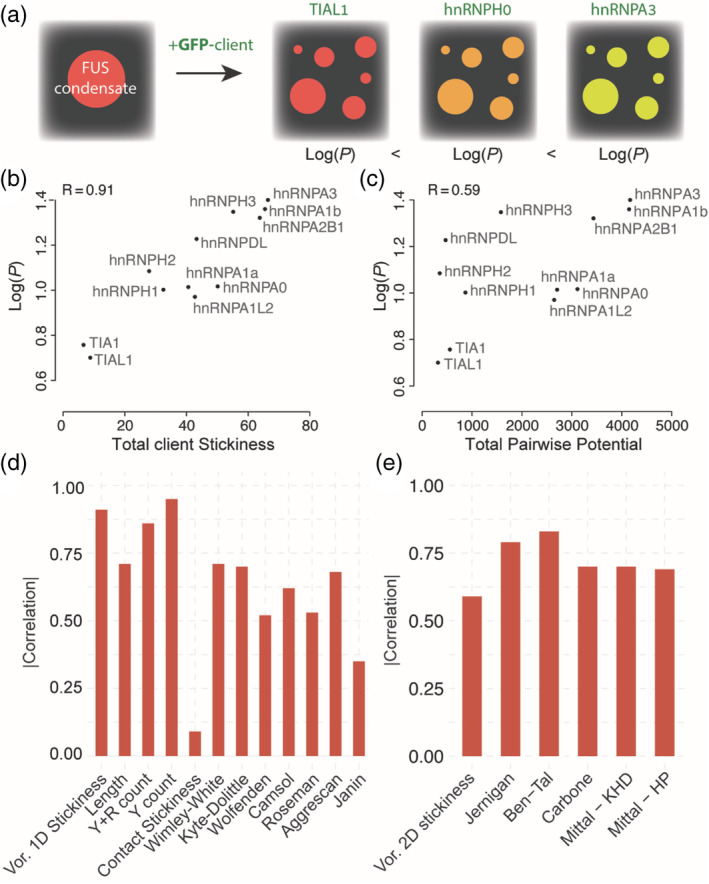
Comparing desolvation energy and residue contact propensities in their ability to predict client recruitment into FUS condensates. (a) FUS condensates exhibiting red fluorescence are mixed with various clients and a partition coefficient is measured for each client. (b) Total stickiness of each client (x‐axis) as a function of the partition coefficient. (c) Total contact preference potential between each client and FUS. (d) Correlation between several client's sequence features and their partition coefficient. Certain features are derived from the sequence directly (e.g., length, Y count), while others correspond to a summed potential based on the same hydropathy and solubility scales used previously. (e) Correlation between log(P) and client–FUS contacts calculated based on several contact potentials

We also observed a Pearson's correlation between client sequence length of disordered regions and the log of the partition coefficients of 0.71. This can be seen as analogous to buried interface surface area in protein complexes. Interestingly, the sole number of tyrosine residues in client proteins was a strong predictor of the partition coefficient (R = 0.95), as were the tyrosine plus arginine counts (R = 0.86).

To shed more light on the sequence dependence of the client in the partitioning within FUS droplets, we correlated the total stickiness of the disordered regions of client proteins to the log values of the measured partition coefficients. We also correlated the stickiness of each client to FUS by summing over all pairwise interactions between client and host. As we saw earlier, the total stickiness mostly captures the desolvation energy of the client, whereas pairwise interactions as shown in Figure 2c and used in Equation 11 reflect residue–residue contact preferences without desolvation being factored in the potential. We observed a high correlation between the total stickiness of the client protein and the log of the partition coefficient (R = 0.91, Figure 4b). In contrast, the contact potential gave a substantially lower correlation (R = 0.59, Figure 4c). While all other pairwise potentials tested performed better than our Voronoi‐derived scale, none of the potentials approached the performance of metrics that only considered client sequence properties. In fact, most of the scales used were predictive to the same degree as client sequence length alone. A simple count of tyrosine residues in the sequence proved to be the best predictor, so that the reason the Glaser scale outperforms in the pairwise case is likely due to the fact that it exhibits strong preferences for interactions involving bulky aromatic amino acids.

A striking result of our analysis was the substantial underperformance of the stickiness scale calculated from interface contact counts. A comparison of the Voronoi 1D stickiness and contact stickiness scales reveals that Gly stickiness differs between the two scales, where Gly is determined to be unfavorable at interfaces when contact counts are used. Given that intrinsically disordered protein segments are rich in glycine residues that confer flexibility, the stickiness value of Gly is a major component of the total stickiness value of each client protein. Replacing the value of Gly stickiness in the contact stickiness scale (−0.1771) by the value in the Voronoi stickiness scale (0.57) results in a correlation of 0.85 between the total stickiness of the client proteins and the log of partition coefficients. This illustrates the importance of considering the physicochemical properties of all residues in phase‐separated systems.

3. DISCUSSION

In vitro condensate formation results in a nonhomogenous solution composed of two distinct chemical environments. Additional molecules are distributed throughout this heterogeneous environment in such a way that minimizes the free energy of the system. The π–π and cation–π interactions play a critical role in the formation of many phase‐separating systems, as evidenced by mutational studies and experiments making use of NMR measurements to detect contact points between specific amino acid residues. Client partitioning into condensates also exhibits a marked dependence on the presence of aromatic residues in the sequence. For example, large values of the partition coefficients were measured for 8F, 8Y, 8W variants of GFP in systems composed of phase‐separated NUP. Similarly, a high degree of correlation is observed between the number of tyrosine residues in a set of IDPs and partition coefficients in systems composed of phase‐separated FUS. These observations are consistent with the hypothesis that the interactions between client and droplet are driven by π–π and cation–π interactions, as in the case of liquid–liquid phase separation.

We sought to investigate an alternative hypothesis that desolvation might explain these phenomena to a large degree. First, a clear dependency on the identity of nonaromatic residues is observed in the partitioning of GFP mutants into NPC droplets. Additionally, aromatic residues exhibit a dominant tendency to sequester from water and form buried surfaces at protein–protein interfaces, irrespective of the amino acid composition of the interacting partner. This suggests specific π–π and cation–π interactions are not necessary for driving the partitioning of aromatic residues between bulk water and protein‐dense phases.

Our results indicate that entropy changes due to water organization around hydrophobic surfaces of client molecules play a significant role in client partitioning into condensates (Figure 5). Classically, desolvation is meant to describe the complete removal of a molecular surface from water, as in protein–protein interactions, drug–protein interactions, ⁴⁸ or protein membrane insertion, ⁴⁹ , ⁵⁰ , ⁵¹ . In that respect, our results appear surprising because condensates are expected to remain highly hydrated. ²⁰ Nevertheless, the nature of the interactions between solutes and water could be different in the condensate phase and in the bulk (Figure 5).

FIGURE 5.

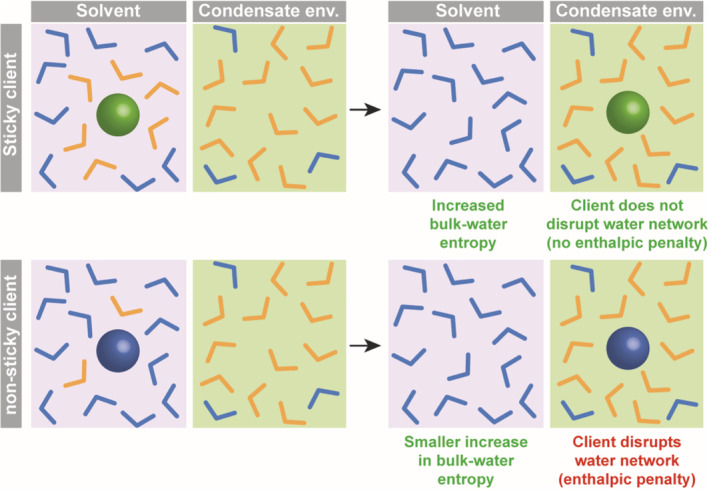
The transfer of a client from bulk water to a condensate environment can be associated with changes in water entropy and enthalpy. The hydrophobicity of nonpolar groups is the result of enthalpic and entropic penalties incurred by the formation of a structured hydration shell. The increase in entropy that results from the release of bound water (orange) lowers the free energy and drives desolvation (orange to blue transition). In contrast to the bulk, water residing within condensates has been experimentally observed to be less dynamic and more densely arranged, ⁶⁶ akin to water molecules on the surface of folded proteins. ⁶⁷ The transfer of amino acids with hydrophobic character from the aqueous phase to the protein dense phase therefore leads to a net increase in entropy by the following mechanism: the replacement of hydration shell water molecules acquired from a highly dynamic environment by hydration shell waters supplied by a more structured environment. By comparison, the gain in water entropy resulting from the transfer of a nonsticky client would be moderate because the hydration shell is more compatible with bulk water. At the same time, the nonsticky client may be less compatible with the overall structure of water in the condensate environment ⁶⁶

In that respect, the desolvation of the client molecules does not only require the client's presence in the dense phase, but also requires interactions with the species forming the condensate. However, our results imply that these interactions are nonspecific in that client partitioning is driven by the increase in the entropy of water within the droplet that occurs as a result.

We reasoned that the interface of protein complexes would provide a reasonable proxy for estimating the chemical environment in the dense phase of biomolecular condensates, while the protein surface would provide the same for the dilute environment. In doing so, we expected that using data extracted from structured protein–protein interfaces would not be an impediment for using such potentials to describe highly dynamic systems, as the underlying physical nature of amino acid desolvation and amino acid pair interactions is the same. Indeed, similar frequencies of amino acids are seen at the interface of complexes between folded proteins and complexes involving disordered regions. ⁵² , ⁵³ We used Voronoi surface area as a quantity that could be used to directly compare amino acid interface and the surface occupancy, and developed a novel interface propensity scale and a pairwise residue contact propensity score. Uniquely, the two potentials are orthogonal to each other and they can be combined as they are derived from the same information type. That is, amino acid surface areas and contact areas.

We find that the interface propensity scores provide good correlation when used to examine the partitioning of client proteins in phase‐separated systems. When we calculated pairwise interaction scores, however, we did not observe the same degree of correlation. This suggests that the main driver of client partitioning is the desolvation energy of going from a dilute environment to a protein dense environment. This is not to say that specific amino acid pair interactions do not contribute anything to the partitioning of client proteins. In fact, a simple count of tyrosine residues outperforms our scale in the case of client IDPs partitioning into FUS droplets. However, this effect can be largely captured by the degree of stickiness of each amino acid sequence, suggesting that specific amino acid pair interactions play a lesser role.

The reduced performance of the pairwise residue contact propensity scale can be partially explained by our lack of explicit sampling of client–droplet configurations, thus ignoring the fact that some specific amino acid pair interactions could be dominant. Nevertheless, the fact that client partitioning correlates to such a large degree with interface propensity implies that the specificity of these interactions have a comparatively small contribution. However, without knowledge of the internal structure of condensates and of client–condensate interactions, the relative enthalpic contributions cannot be precisely determined. Another potential limitation that arises in not performing explicit sampling is the lack of mid‐ to long‐range energy terms, as our potential captures that propensity for residues to be in direct contact. Differences in the dielectric environment between the dilute and condensed phases could exert an effect on the strength of inter‐residue electrostatic interactions, for example. Subsequent studies employing our unified potentials in coarse‐grained or all‐atom simulations in explicit solvent could be used to more accurately estimate these contributions, and rationalize more subtle effects such as charge blockiness on client recruitment. ⁵⁴ Experimental measurements to probe the internal structure of these systems will be needed to further corroborate our hypothesis.

Interestingly, our results indicate that specific interactions between purely disordered sequences may not be sufficient to build selectivity into client partitioning in liquid protein systems. And consequently, additional recognition features are likely required for selectivity.

This notion is in agreement with observations made by Schuster et al., who constructed a model system where globular proteins were used as cargo and proteins composed of phase‐separating RGG domains were used as scaffolds. ⁵⁵ The authors observed that incorporation of recognition elements to both cargo and scaffold proteins substantially increased recruitment to the dense phase. However, even in the absence of recognition elements, proteins of comparable size partitioned to different degrees into droplets composed of RGG domains, suggesting that protein–solvent interactions are a significant driver of this differentiation. This behavior is in contrast to the observations made regarding the sequence determinants of phase‐separation propensities of scaffold proteins, which are not adequately accounted for with desolvation energies alone, ⁵⁶ and where composition as well as sequence patterns play an important role. ⁵⁷ , ⁵⁸ , ⁵⁹

We have presented a unification of the concepts of amino acid interface propensities and pairwise residue contact propensity, and have developed a set of statistical potentials which make the two terms directly comparable. These potentials can be mixed and matched to account for different energetic contributions in amino acid interactions, permitting wide applicability in protein modeling and design. For example, tools for predicting the distribution of species in the complex environment of the cell are crucial for understanding cellular organization as well as pharmacokinetic behavior of therapeutic drugs. The development of potentials that can closely reflect the partitioning of proteins within liquid protein droplets will enable the design of synthetic systems that could be used for the regulation of cellular processes.

4. METHODS

4.1. Dataset

The 3D Complex database ³³ was used to select 1,011 heteromeric dimers from a nonredundant set of proteins. The dataset was divided randomly into three sets, analyses were carried out on each set independently. The resulting scales were the average of the three analyses, which also gave the standard deviation of each propensity value. The dataset consisted of structures with a resolution better than 3.0 Å and was nonredundant at a sequence identity level of 70% as defined in 3D Complex. In order to minimize the number of incorrect biological assemblies, ⁶⁰ we filtered out complexes with a QSbio ⁶¹ error probability greater than 10%. Voronoi surfaces and contact areas were computed on the first chain in the biological assembly, using the command line program CAD score. ⁶² To derive amino acid propensities, we selected surface and interface residues involving significant contact surface area of their side chain with either the solvent or a protein partner. Selected interface residues had to satisfy two criteria: (i) expose over 25% of their surface area in the monomeric state and (ii) 50% of that exposed area had to be buried in the complex. Surface residue also had to satisfy two criteria to be included in the analyses: (i) over 25% of their side chain area was exposed to the solvent and (ii) no surface area was involved at an interface.

4.2. Definition of the propensities

The residue interface propensity scale is calculated as

$$s_i=\log \left(\frac{f_i^{\mathit{\text{interface}}}}{f_i^{\mathit{\text{surface}}}}\right),$$ (1)

where s _i is the interface propensity of amino acid type i , $f_i^{\mathit{\text{interface}}}$ is the area fraction of amino acid type i at the interface, and $f_i^{\mathit{\text{surface}}}$ is the area fraction of amino acid type i at the solvent‐exposed surface. These propensities capture the tendency of amino acids to interact with protein surfaces in general, and as such we also refer to this propensity scale as “stickiness.” ²⁶

The area fraction of amino acid type i at the interface is computed as:

$$f_i^{\mathit{\text{interface}}}=\frac{A_i}{\sum _i{A}_i},$$ (2)

where $\sum _i{A}_i$ is the total interface area and A _i is the surface area of amino acid i at the interface.

The area fraction of an amino acid at the surface is obtained as:

$$f_i^{\mathit{\text{surface}}}=\frac{{\mathit{\text{SASA}}}_i}{\sum _i{\mathit{\text{SASA}}}_i},$$ (3)

where SASA _i is the total surface area of residues of amino acid type i on the first chain in contact with water, as determined by the Voronoi cell capping algorithm. ⁶² These expressions take the familiar forms used originally to estimate interface propensity scales. ⁶³

The use of the Voronoi tessellation allows us to decompose the interface surface area into residue‐level contributions unambiguously. In this manner, we consider an interface as being composed of 20 different subinterfaces, where each subinterface corresponds to a single amino acid type. The subinterface propensity of each amino acid can be calculated as:

$$s_{\mathit{ij}}=\log \left(\frac{f_j^{\mathit{sub}-{\mathit{\text{interface}}}_j}}{f_i^{\mathit{\text{surface}}}}\right),$$ (4)

We can rewrite this expression as:

$$s_{\mathit{ij}}=\log \left(\frac{f_i^{\mathit{sub}-{\mathit{\text{interface}}}_j}}{f_i^{\mathit{\text{surface}}}}\cdot \frac{f_i^{\mathit{\text{interface}}}}{f_i^{\mathit{\text{surface}}}}\right),$$ (5)

resulting in:

$$s_{\mathit{ij}}=\log \left(\frac{f_i^{\mathit{sub}-{\mathit{\text{interface}}}_j}}{f_i^{\mathit{\text{surface}}}}\right)+\log \left(\frac{f_i^{\mathit{\text{interface}}}}{f_i^{\mathit{\text{surface}}}}\right),$$ (6)

This is equivalent to decomposing the expression into the interaction term and the desolvation term, so that we can consider:

$$g_{\mathit{ij}}=\log \left(\frac{f_i^{\mathit{sub}-{\mathit{\text{interface}}}_j}}{f_i^{\mathit{\text{surface}}}}\right),$$ (7)

as the contribution of amino acid i interacting with the subsurface j.

To get the full interaction potential of an amino acid pair, we sum:

$$G_{\mathit{ij}}=\log \left(\frac{f_i^{\mathit{sub}-{\mathit{\text{interface}}}_j}}{f_i^{\mathit{\text{interface}}}}\right)+\left(\frac{f_j^{\mathit{sub}-{\mathit{\text{interface}}}_i}}{f_j^{\mathit{\text{interface}}}}\right),$$ (8)

The numerators can be combined to yield probability of finding amino acid i and amino acid j together at the interface $\left(f_i^{\mathit{sub}-{\mathit{\text{interface}}}_j}\cdot f_j^{\mathit{sub}-\mathit{\text{inte}}{\mathit{\text{rface}}}_i}\right)$, which we can denote as $f_{\mathit{ij}}^{\mathit{\text{interface}}}$. This yields the expression:

$$G_{\mathit{ij}}=\log \left(\frac{f_{\mathit{ij}}^{\mathit{\text{interface}}}}{f_i^{\mathit{\text{interface}}}\cdot f_j^{\mathit{\text{interface}}}}\right),$$ (9)

which is the familiar form for pairwise residue contact propensity normalized by interface frequency. ⁶⁴

4.3. Calculating propensities for specific protein sequences

The stickiness S of a particular protein was calculated as:

$$S=\sum _{n}s\left({\alpha }_n\right),$$ (10)

where α _n is the amino acid identity at residue $n$ of the client protein with $N$ sites and $s$ is the stickiness value of amino acid α _n as obtained from Equation 1 and available in Table S1.

The interaction potential between the client and the droplet is calculated as:

$$G=\sum _n^N\sum _m^{M}s\left({\alpha }_n,{\alpha }_j\right),$$ (11)

where α _n is the amino acid identity at residue $n$ of a client protein with $N$ sites, α _m is the amino acid identity at residue $m$ of the partner protein with $M$ sites, and $G$ is the pairwise potential value. In this equation, we ignore any internal structure in the droplet–client complex and assume that all amino acids of the client and partner interact with equal probability. This is consistent with observations that interactions within biomolecular condensates are heterogenous and not limited to specific pairwise interactions. ⁶⁵

AUTHOR CONTRIBUTIONS

Jose A. Villegas: Conceptualization (equal); data curation (equal); formal analysis (equal); investigation (lead); methodology (equal); writing – original draft (lead); writing – review and editing (equal). Emmanuel D. Levy: Conceptualization (equal); funding acquisition (lead); methodology (equal); project administration (lead); resources (lead); supervision (lead); writing – review and editing (equal).

Supporting information

Appendix S1. Supporting Information

Villegas JA, Levy ED. A unified statistical potential reveals that amino acid stickiness governs nonspecific recruitment of client proteins into condensates. Protein Science. 2022;31(7):e4361. 10.1002/pro.4361