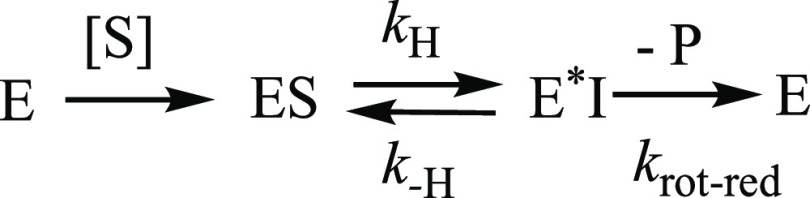Hydride Transfer Mechanism of Enzymatic Sugar Nucleotide C2 Epimerization Probed with a Loose-Fit CDP-Glucose Substrate

Abstract

Transient oxidation–reduction through hydride transfer with tightly bound NAD coenzyme is used by a large class of sugar nucleotide epimerases to promote configurational inversion of carbon stereocenters in carbohydrate substrates. A requirement for the epimerases to coordinate hydride abstraction and re-addition with substrate rotation in the binding pocket poses a challenge for dynamical protein conformational selection linked to enzyme catalysis. Here, we studied the thermophilic C2 epimerase from Thermodesulfatator atlanticus (TaCPa2E) in combination with a slow CDP-glucose substrate (k_cat ≈ 1.0 min^–1; 60 °C) to explore the sensitivity of the enzymatic hydride transfer toward environmental fluctuations affected by temperature (20–80 °C). We determined noncompetitive primary kinetic isotope effects (KIE) due to ²H at the glucose C2 and showed that a normal KIE on the k_cat (^Dk_cat) reflects isotope sensitivity of the hydrogen abstraction to enzyme-NAD⁺ in a rate-limiting transient oxidation. The ^Dk_cat peaked at 40 °C was 6.1 and decreased to 2.1 at low (20 °C) and 3.3 at high temperature (80 °C). The temperature profiles for k_cat with the ¹H and ²H substrate showed a decrease in the rate below a dynamically important breakpoint (∼40 °C), suggesting an equilibrium shift to an impaired conformational landscape relevant for catalysis in the low-temperature region. Full Marcus-like model fits of the rate and KIE profiles provided evidence for a high-temperature reaction via low-frequency conformational sampling associated with a broad distribution of hydride donor–acceptor distances (long-distance population centered at 3.31 ± 0.02 Å), only poorly suitable for quantum mechanical tunneling. Collectively, dynamical characteristics of TaCPa2E-catalyzed hydride transfer during transient oxidation of CDP-glucose reveal important analogies to mechanistically simpler enzymes such as alcohol dehydrogenase and dihydrofolate reductase. A loose-fit substrate (in TaCPa2E) resembles structural variants of these enzymes by extensive dynamical sampling to balance conformational flexibility and catalytic efficiency.

Introduction

Conformational selection enabled by protein flexibility is fundamental to enzyme catalysis.¹⁻⁵ Directed changes in protein conformation (“coupled motions”) enable enzymes to coordinate the immediate catalytic event with other physical steps of the reaction, such as substrate binding and product release.⁴⁻¹¹ In the chemical transformation on the enzyme, stochastic motions enable the dynamical population (“sampling”) of catalytically relevant ground-state conformers to have electrostatics and internuclear distances tuned for bond cleavage/formation.¹²⁻¹⁹ On this dynamic view, conformational selection connects directly to catalytic rate enhancement; and protein flexibility represents an evolutionary target for the optimization of enzyme efficiency.²⁰⁻²² Enzymes of the alcohol dehydrogenase class (ADHs)^8,23−26 as well as several other oxidoreductases (e.g., dihydrofolate reductase,^2,15,27−31 thymidylate synthase,^32,33 formate dehydrogenase,^34,35 flavin-dependent ene-reductases,³⁶⁻³⁹ lipoxygenases^40,41) have been instrumental to link conformational selection to catalysis. ADHs promote hydride transfer between the substrate and nicotinamide coenzyme.^5,24,25,42 Protein flexibility enables ADHs to sample conformers that place the hydride donor in close proximity to the acceptor.^2,23,43−47 Reaction occurs classically over the enthalpic barrier but also by quantum mechanical tunneling.^27,48−51 Conformational selection of donor–acceptor distances (DADs) suitable for tunneling emphasizes dynamic control of the barrier width, in addition to a decrease in the barrier height, as an important element of the ADH catalysis.^{43,45,48,52−58} Extended ADH-type reactions that involve hydride transfer oxidation–reduction in multiple bond-breaking/forming steps pose a conundrum for the enzymes to achieve a well-tuned balance between protein flexibility and catalytic efficiency.⁵⁹⁻⁶¹ Here, we explored dynamical features of catalytic hydride transfer in the context of sugar nucleotide epimerization.

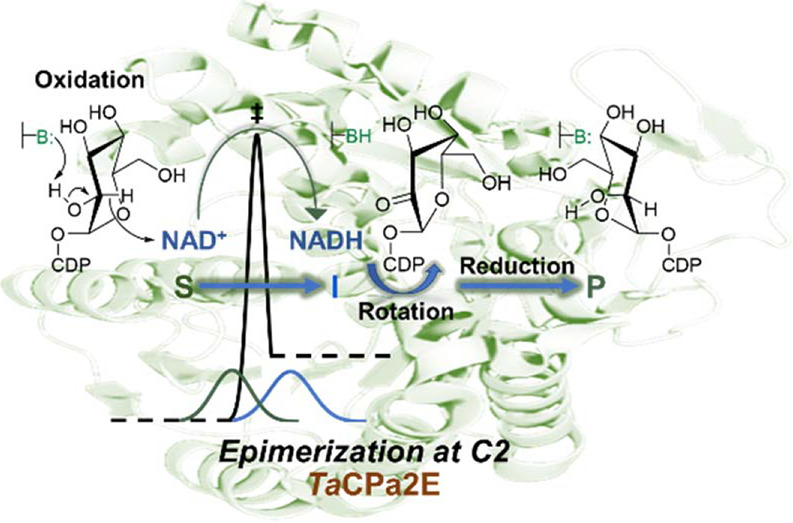
Transient oxidation–reduction via hydride transfer to and from the tightly bound NAD coenzyme is used by a large class of sugar nucleotide epimerases to invert carbon stereocenters in carbohydrate substrates (Scheme 1).⁶¹⁻⁶⁶ The reaction starts with the oxidation of the alcohol group at the targeted stereocenter. Redelivery of the abstracted hydride from enzyme-NADH to the opposite face of the carbonyl in a suitably repositioned keto-intermediate gives the stereo-inverted product.^59,61 The epimerases are unusual among enzymes in their requirement to be non-stereospecific.^59,65,67,68 Their catalysis involves the stabilization of two stereoisomeric transition states for reversible cleavage of C–H bonds at carbon stereocenters. Abstraction and re-addition of the hydride are coordinated with rotation of the transient intermediate in the enzyme binding pocket.^59,65,69 These main elements of epimerase catalysis present a significant challenge for enzyme conformational selection: protein flexibility necessary for the rotation must be aligned with precise positioning of the hydride donor and acceptor in tunneling-ready conformers. Notably, UDP-galactose 4-epimerase binds the 4-keto-pyranosyl moiety of the transient intermediate much more loosely than the corresponding UDP moiety (ΔΔG = −5 kcal/mol).⁶¹ The considerations give rise to the suggestion that catalytic hydride transfer in the epimerase might involve a donor–acceptor distance sampling mode distinct from that of “simple” ADHs. A kinetic isotope effect (KIE) study was designed here to assess the mechanistic implication that the epimerase-catalyzed hydride transfer might be rather sensitive toward environmental fluctuations affected by the temperature. KIEs and their temperature dependence can serve as probes of protein motions that affect the C–H bond activation in enzymatic hydride transfer reactions.^{13,27,33,34,70,71}

Scheme 1. Epimerization of Sugar Nucleotide Substrates via Transient Oxidation–Reduction.

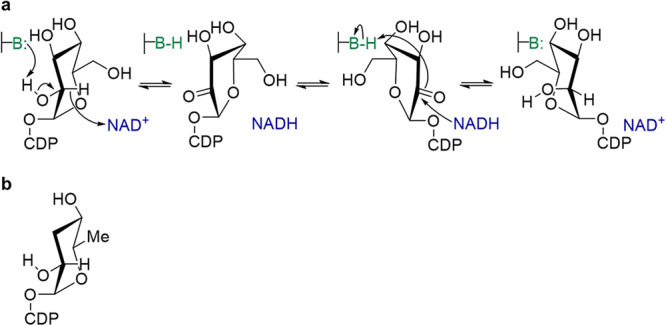
Epimerization shown for the conversion of CDP-glucose into CDP-mannose (a) catalyzed by TaCPa2E (the C2 epimerase from T. atlanticus). CDP-paratose (b) is probably the native substrate of TaCPa2E. It is shown for comparison with CDP-glucose.⁶²

The thermophilic C2 epimerase from Thermodesulfatator atlanticus (TaCPa2E)^72,73 was investigated here in combination with a slow CDP-glucose (CDP-Glc) substrate (Scheme 1a). From its sequence, TaCPa2E belongs to the group of CDP-paratose/CDP-tyvelose epimerases^62,66,74 and is a member of the short-chain dehydrogenase/reductase (SDR) protein superfamily.⁷⁵⁻⁷⁷ The enzyme is a homodimer and each subunit contains tightly bound NAD⁺.⁷² The natural substrate of TaCPa2E is probably CDP-paratose (Scheme 1b), which is 3,6-dideoxygenated compared with CDP-Glc. Reactivity of TaCPa2E with CDP-paratose has not been determined, but the singly deoxygenated CDP-6-deoxy-glucose is ∼5-fold more active than CDP-Glc.⁷² The reason to select TaCPa2E was the ability to specifically interrogate the enzymatic epimerization (CDP-glucose → CDP-mannose) over a broad temperature range (20–80 °C). Seminal research of ADHs^25,78 and also dihydrofolate reductases⁷⁹⁻⁸² has shown that a thermophilic enzyme can offer unique opportunities toward the aim of correlating protein flexibility to the nature of the chemical steps of catalysis. Moreover, the native flexibility of TaCPa2E was unlikely to be optimized for the non-physiological CDP-glucose substrate (Scheme 1). We considered that the “loose fit” CDP-glucose might be instrumental to receive a mechanistically instructive temperature dependence of the KIE.

Evidence is presented that connects changes in the conformational landscape experienced by TaCPa2E in response to the change in temperature with properties of the hydride transfer during transient substrate oxidation, which is shown to be rate-limiting overall. Interestingly, later steps of the catalytic cycle (i.e., keto-intermediate rotation and reduction from enzyme-NADH) do not affect the steady-state rate. Substrate activation for C–H bond cleavage requires partial deprotonation of the glucose 2-OH by an active-site base (Tyr164). Reduced protein flexibility in the low temperature range (≤40 °C) appears to restrict the efficiency of dynamical sampling, via coupled motion, for substrate activation. A model of temperature-dependent equilibration of differently active conformational substates in the conformational ensemble sampled by the enzyme–substrate complex is used to explain an unusual, and to our knowledge unique, kinetic characteristic of the TaCPa2E: the observable KIEs are decreased progressively upon cooling down in the low-temperature region.

Results

C2 Epimerization of CDP-Glucose through Hydrogen Abstraction and Re-addition

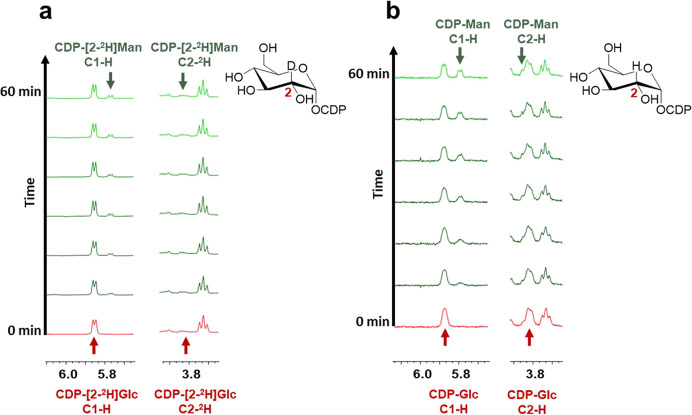
To verify the proposed reaction mechanism of TaCPa2E (Scheme 1), CDP-[2-²H]glucose (CDP-[2-²H]Glc) was synthesized and underwent enzymatic conversion into CDP-mannose (CDP-Man) analyzed by in situ proton NMR in ²H₂O solvent (p²H = 7.5). Time-resolved spectra from the reaction (Figure 1a) showed that the deuterium label at the C2 of the CDP-glucose substrate was retained completely in the CDP-mannose product. Reference reaction with CDP-[¹H]glucose showed that deuterium was not incorporated from the solvent (Figure 1b). These results confirmed CDP-glucose C2 epimerization via hydrogen abstraction from, and re-addition to, the C2 of the d-hexopyranosyl moiety.

Figure 1.

In situ ¹H NMR measurements using TaCPa2E and CDP-[2-²H]Glc (a) or CDP-Glc (b). Only selected spectra (recorded in 10 min intervals) are shown. Signals for C2 (3.80–3.86 ppm) and the anomeric region (5.75–5.90 ppm) are highlighted for both substrate (red) and product (green). The lack of signal in panel (a) at 3.82 ppm for CDP-[2-²H]Glc/Man stems from deuteride incorporation. For the full spectrum, see Figure S4. Reaction conditions: CDP-[2-²H]Glc (2.00 mM) and 50.8 μM TaCPa2E (2.0 mg/mL); CDP-Glc (4.00 mM) and 15.2 μM TaCPa2E (0.6 mg/mL); 60 °C, 50 mM potassium phosphate buffer (p²H = 7.5).

The enzymatic cycle of oxidation–reduction requires catalytic facilitation from a general acid–base, as indicated in Scheme 1. Based on known structure–function relationships of SDR-type epimerases,^65,75,83 Tyr164 was the clear candidate residue of TaCPa2E to fulfill that role. The Y164F variant was generated to replace the tyrosine with a residue minimally disruptive structurally but was incompetent in the proposed catalysis. The purified variant contained tightly bound NAD⁺. In activity assays for a range of protein concentrations (25.4–127 μM) at 60 °C and pH 7.5, the Y164F variant was inactive to epimerize CDP-glucose above the detection limit (≥10⁴-fold decrease in a specific rate compared to wild-type TaCPa2E). Reactions at higher pH (up to 9.5) did not elicit epimerase activity, which was considered possible in the case that the Y164F variant enabled specific base catalysis from H₂O/OH^– similarly to how an analogous Tyr → Phe variant of UDP-glucuronic acid 4-epimerase did.⁶⁴ Collectively, the evidence suggested a classical SDR mechanism (Scheme 1) of C2 epimerization of CDP-glucose by TaCPa2E.

Transient Oxidation of the Substrate Is Rate-Limiting for Overall Epimerization of CDP-Glucose

The noncompetitive KIE on the substrate-saturated rate (k_cat) at 60 °C and pH 7.5 (Figure S1) was determined as 4.3 ± 0.3 (N = 4). The large value of ^Dk_cat implied a substantial contribution from the C–H bond breaking/forming steps of catalysis to the overall rate limitation of enzymatic epimerization. Full Michaelis–Menten kinetics were therefore recorded to also obtain the KIE on the substrate-limited rate (k_cat/K_M). Data were acquired at 60 °C and additionally at the upper and lower limit of the temperature range (20–80 °C) considered for study of the temperature effect on the enzymatic rate (see later). The results are summarized in Table 1. At each temperature, the KIE on the k_cat/K_M was identical within the limits of error of the KIE on the k_cat. This evidence strongly supports the idea of rate limitation by the isotope-sensitive steps of catalysis (for the general case, see ref (84)), independent of the temperature varied between 20 and 80 °C.

Table 1. Kinetic Parameters and their Corresponding Primary KIEs for the Epimerization of CDP-Glc at Distinct Temperatures^a.

T (°C)	substrate	kcat (min–1)	KM (mM)	Dkcat	Dkcat/KM
20	CDP-Glc	(1.20 ± 0.06) × 10–2	0.24 ± 0.05	2.20 ± 0.75	2.06 ± 0.67
	CDP-[2-2H]Glc	(0.62 ± 0.02) × 10–2	0.25 ± 0.03
60	CDP-Glc	0.88 ± 0.03	0.30 ± 0.04	4.30 ± 0.30	3.80 ± 0.40
	CDP-[2-2H]Glc	0.21 ± 0.01	0.26 ± 0.03
80	CDP-Glc	1.31 ± 0.04	0.16 ± 0.03	3.34 ± 0.09	3.19 ± 0.24
	CDP-[2-2H]Glc	0.40 ± 0.02	0.15 ± 0.04

^aThe k_cat and K_M values were determined by a non-linear fit to the specific rates (V/[E], min^–1) dependent on the substrate concentration. Data for the protio and deuterio substrate were fitted separately. The KIEs on k_cat (^Dk_cat) and on k_cat/K_M (^Dk_cat/K_M) were obtained by a global nonlinear fit to the data for both isotopologue substrates. The procedures used are described under Materials and Methods.

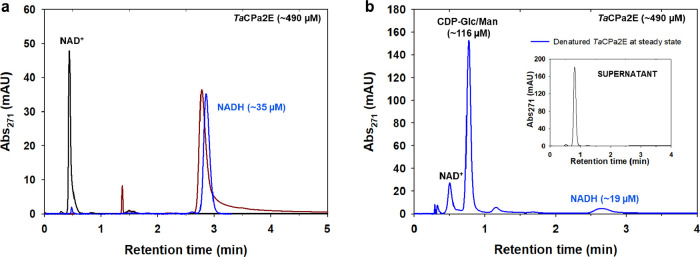
There are two isotope-sensitive steps in the mechanism, one in each half-reaction (Scheme 1). At the steady state of the reaction, the relative rates of transient oxidation and reduction define the portion of total enzyme present in the reduced (NADH) form. Using a rapid-quench assay previously developed for UDP-glucuronic acid 4-epimerase⁶⁴ and here adapted to TaCPa2E (Figure 2), we determined the portion of enzyme-NADH as 2.22% (± 0.5%; N = 4), which was not increased compared to the NADH content of the resting enzyme in the absence of the substrate (4.15 ± 1.0%; N = 4).

Figure 2.

Determination of the steady-state enzyme-NADH in the epimerization of CDP-Glc by TaCPa2E. (a) Overlay of HPLC chromatograms displaying denatured TaCPa2E prior to the reaction (blue), NAD⁺ standard (black), and NADH standard (brown). (b) HPLC chromatogram of denatured TaCPa2E from the reaction at the steady state, showing the enzyme-bound NADH and substrate/product mixture (blue). The NAD⁺ coenzyme is partially released. The inset shows the reaction mixture after 15 min when quenched with methanol and the enzyme removed. The injection volume was half compared to (a). For NADH quantification and method validation, see Figure S5 and Materials and Methods.

Taken in combination, therefore, the high ^Dk_cat (identical with ^Dk_cat/K_M) and the low steady-state portion of enzyme-NADH indicated that the observed KIE arose from C–H bond cleavage in CDP-glucose during rate-limiting transient oxidation of the substrate. The measurement of enzyme-NADH was from the initial-rate phase when the CDP-glucose conversion was just 7–8% of the reaction equilibrium. The K_eq (= [CDP-[2-²H]mannose]^eq/[CDP-[2-²H]glucose]^eq) was 0.67 under the conditions used (60 °C, pH 7.5, Figure S6). The equilibrium position was independent of the 2-²H isotopic substitution of the CDP-glucose substrate (^DK_eq ≈ 1.0). The ratio of CDP-mannose/CDP-glucose associated with the enzyme from rapid-quench processing was 0.163 (± 0.008; N = 4). The corresponding product/substrate ratio in bulk solution was 0.100 (± 0.004; N = 4). Evidence that the enzyme-bound product/substrate ratio was considerably lower than the external equilibrium determined by the K_eq while it was similar to the product/substrate ratio in solution was good support in favor of the suggestion that the kinetic mechanism of TaCPa2E-catalyzed epimerization of CDP-glucose involved rate-limiting oxidation of the substrate.

Temperature Dependence of k_cat

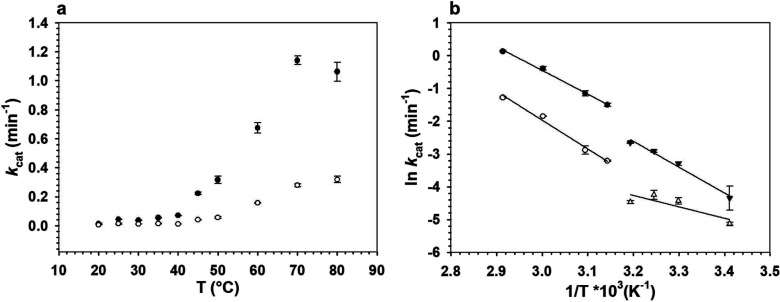
Temperature profiles of k_cat for the reaction with 2-[¹H]- and 2-[²H]-CDP-glucose in the range 20–80 °C (pH 7.5) are displayed in Figure 3. With either substrate, the profile showed a prominent break (abrupt increase in the k_cat by ∼3-fold) in going from 40 to 45 °C. Above and below the break, the profiles featured “Arrhenius-like” (eq 1) behavior and were fitted accordingly (Figure 3), with parameter estimates summarized in Table 2. A possible deviation from linearity is however noted for the Arrhenius plot of the k_cat for the reaction with 2-[²H]-CDP-glucose in the low temperature range (≤40 °C). Clear discrimination between linear and curved dependence was not possible in this range.

1

where k_cat is the rate constant (min^–1), T is temperature [K], R is the gas constant [kJ mol^–1 K^–1], A is an Arrhenius prefactor, and E_A is the activation energy [kJ mol^–1].

Figure 3.

Temperature dependence of k_cat ((a), temperature profile; (b) Arrhenius plots) for the reaction of TaCPa2E with CDP-Glc and CDP-[2-²H]Glc. Epimerizations were analyzed in a temperature range of 20–80 °C using TaCPa2E (1.0 mg/mL; 25.4 μM) and 4.00 mM CDP-Glc (black dots, black triangles) or CDP-[2-²H]Glc (white circles, white triangles). Due to a low coefficient of determination, results for 25 and 80 °C were omitted in (b). Symbols show the experimental data, and error bars show the associated S.D. (N = 4). The lines in panel (b) are straight-line fits with the Arrhenius model (eq 1).

Table 2. Activation Energies E_A and Arrhenius Prefactors A Obtained for CDP-Glc and CDP-[2-²H]Glc for the Temperature Range of 20–40 °C and 45–70 °C^a.

	20–40 °C		45–70 °C
substrate	EA (kJ mol–1)	A (min–1)	EA (kJ mol–1)	A (min–1)
CDP-Glc	+66.7 ± 9.4	(6.9 ± 1.2) × 109	+60.2 ± 3.3	(1.7 ± 0.3) × 109
CDP-[2-2H]Glc	+29 ± 4.5	(9.9 ± 2.6) × 102	+72.9 ± 6.7	(3.8 ± 0.7) × 1010
ΔEA	–36.7 ± 7.6		+12.7 ± 2.6
AH/AD	(7.0 ± 1.1) × 106		0.05 ± 0.007

^aE_A and A (y intercept) were obtained from the slope of the linearized Arrhenius equation (see eq 1). The activation energy difference ΔE_A (= E_A,D – E_A,H) and Arrhenius prefactor ratios A_H/A_D were calculated accordingly. Subscript H and D indicate parameters for the reaction with the protio and deuterio substrate, respectively.

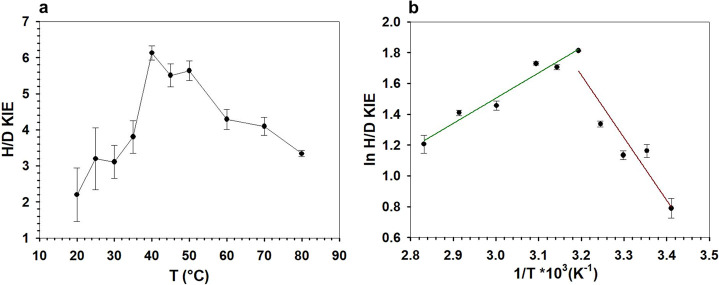
From the results in Figure 3, we also obtained a temperature profile of the KIE, as shown in Figure 4. The ^Dk_cat peaked at 40 °C, with its value of 6.1 approaching the semiclassical limit (∼6.9) of the primary deuterium KIE.^33,85 The result suggested that the chemical step of C–H bond cleavage in the substrate had become unmasked strongly in the measured rate parameter under the conditions used. Figure 4 shows that the ^Dk_cat declined continuously in the temperature ranges above and below the 40 °C peak. We discuss later that the ^Dk_cat decline at low temperature was not consistent with the anticipated effect of environmental cooling on the intrinsic hydride transfer. To clarify whether the decrease in ^Dk_cat could have arisen from a change in the location of the rate-limiting step, we determined the portion of enzyme-NADH at the steady state during the enzymatic reaction at 20 °C. Enzyme-NADH was still present in low amounts (∼3%) and not elevated as compared to the as-isolated TaCPa2E in the absence of the substrate. The result is consistent with the KIE data in Table 1, showing that for the reaction at 20 °C, ^Dk_cat was identical to ^Dk_cat/K_M.

Figure 4.

Temperature dependence of the KIE on k_cat for TaCPa2E. (a) H/D KIE dependent on temperature T (°C) and (b) ln H/D KIE dependent on reciprocal T (1/K). In panel (b), two temperature regimes are highlighted (green: 40–80 °C; brown: 20–40 °C). The straight lines are linear fits of the data. Symbols show the experimental data, and error bars show the associated S.D. (N = 4).

Solvent Isotope Effects

Considering the requirement of proton transfer in the enzymatic oxidation of CDP-Glc (Scheme 1a), we analyzed the effect of solvent deuteration (²H₂O) on the k_cat for the reactions with CDP-Glc and CDP-[2-²H]Glc. The results are summarized in Table 3. Control reactions in ¹H₂O in the presence of 9% v/v glycerol showed no effect on the k_cat (±3%). The result rules out the assumption that the enhanced solvent microviscosity of ²H₂O compared to ¹H₂O could have influenced the measured rates.⁸⁶ With both substrates, the k_cat at 60 °C was independent of the pL (L = ¹H or ²H) in the range 7.0–8.0. The solvent isotope effect (SKIE) on k_cat (^D₂Ok_cat) was therefore also independent of the pL in the range analyzed. Using the protio substrate, the ^D₂Ok_cat was not different from unity within the limits of the experimental error. Using the deuterio substrate, however, the ^D₂Ok_cat was inverse (0.57 ± 0.11; pL 7.5). The KIE from deuteration of the CDP-Glc was therefore solvent-dependent. It was 4.30 (± 0.30) in ¹H₂O as already mentioned, and it was 2.34 (± 0.27) in ²H₂O. The lowering of the ^Dk_cat in ²H₂O could arise if there was a step in the enzymatic mechanism, different from the catalytic step of hydride abstraction to NAD⁺, that was sensitive to solvent deuteration and so became partly rate-limiting in ²H₂O. To explore this possibility, we measured the reduced portion of total enzyme at the steady state during the reaction in ²H₂O at 60 °C. The NADH content in the enzyme sample from the reaction was 1.90% (± 0.60%; N = 4). This was almost identical to the NADH content of the resting enzyme in ²H₂O (2.33 ± 0.88%; N = 4). Moreover, the results in ²H₂O were very similar to the ones in ¹H₂O. Therefore, the evidence implies that the ^D₂Ok_cat in the reaction with CDP-[2-²H]Glc was due to a solvent effect on the transient oxidation catalyzed by the enzyme.

Table 3. Solvent Kinetic Isotope Effects on k_cat for Reactions of TaCPa2E with CDP-Glc and CDP-[2-²H]Glc at Varied Temperatures and pL Values.

substrate	D2Okcat (pL 7.5) 80 °C	D2Okcat (pL 7.0) 60 °C	D2Okcat (pL 7.5) 60 °C	D2Okcat (pL 8.0) 60 °C	D2Okcat (pL 7.5) 20 °C
CDP-Glc	n.d.a	0.97 ± 0.12	1.03 ± 0.13	0.99 ± 0.11	0.49 ± 0.07b
CDP-[2-2H]Glc	0.84 ± 0.03	0.57 ± 0.11	0.57 ± 0.10	0.59 ± 0.10	0.51 ± 0.10

^an.d., not determined.

^bFrom a full Michaelis–Menten analysis performed in these conditions (Figure S3a,b), the ^D₂Ok_cat/K_M was determined as 0.65 (± 0.31).

The SKIE on the k_cat was additionally determined at low (20 °C) and high temperature (80 °C) where the ^Dk_cat decreases strongly, as shown before in Figure 4a. Using CDP-Glc, the ^D₂Ok_cat was inverse (0.49 ± 0.07) at 20 °C, thus substantially different from the ^D₂Ok_cat at 60 °C. Using CDP-[2-²H]Glc, the ^D₂Ok_cat at 20 °C (0.51 ± 0.10) was similar to the ^D₂Ok_cat at 60 °C. In contrast to 60 °C, therefore, the ^Dk_cat at 20 °C was not dependent on the solvent used. Using CDP-[2-²H]Glc at 80 °C, the ^D₂Ok_cat (= 0.84 ± 0.03) was less strongly inverse than at 60 °C.

Discussion

Kinetic Mechanism of TaCPa2E

Evidence was shown that transient oxidation of the substrate is rate-limiting on k_cat for the overall epimerization of CDP-glucose into CDP-mannose (Scheme 1a) over the entire temperature range studied. The chemical step of transient oxidation presumably involves coordinated (i.e., concerted but likely asynchronous^77,87−90) abstraction of the hydride from the C2 and the proton of the 2-OH of the reactive alcohol group, as shown in Scheme 2. A reaction coordinate featuring overlapped timing of proton and hydride transfer is characteristic of metal-independent enzyme catalysis to alcohol oxidation.⁹¹⁻⁹³ It differs from the stepwise catalysis of Zn²⁺-dependent ADHs.⁹⁴ In these ADHs, lowering of the pK_a in the Zn²⁺-bound alcohol strongly activates the substrate for C–H bond cleavage already in the ground-state complex.⁹⁴ Given this major difference in catalysis of the chemical step, the KIE analysis for TaCPa2E was of interest to characterize the metal-independent mechanism of enzymatic alcohol oxidation. Plausible kinetic scenario for the epimerase involves two steps, whereby a relatively slow physical step with a time constant similar to that of catalysis precedes the chemical step of hydride abstraction to NAD⁺ (Scheme 2).^64,95−97 The physical step likely involves coupled motions of the substrate-bound TaCPa2E toward enzyme conformers competent to undergo catalytic conversion. An essential task of this physical step in catalysis would be the precise structural alignment of the substrate’s C2-OH and C2-H with the enzyme’s general base (the ionized side chain of Tyr164) and the C4 of NAD⁺, respectively, to promote the concerted reaction (Scheme 2c). The observable KIE on k_cat is analyzed with eq 2,

2

where ^Dk_H is the isotope effect on the isotope-sensitive step, c_Vf is a constant that compares the rate constant for the isotope-sensitive step with rate constants for all other unimolecular forward steps, c_r is a so-called “commitment” for the reverse direction of the reaction, and ^DK_eq is the equilibrium isotope effect on the step analyzed. The ^DK_eq of hydride transfer oxidation of alcohols by NAD⁺ is in the range 1.1–1.2.⁹⁸⁻¹⁰⁰ Note that ^Dk_H is the intrinsic KIE of the chemical step partly masked by “internal” commitments, like the proposed precatalytic physical step in Scheme 2c.

Scheme 2. Enzyme Strategies to Facilitate Hydride Transfer Oxidation by Deprotonation of the Alcohol Substrate.

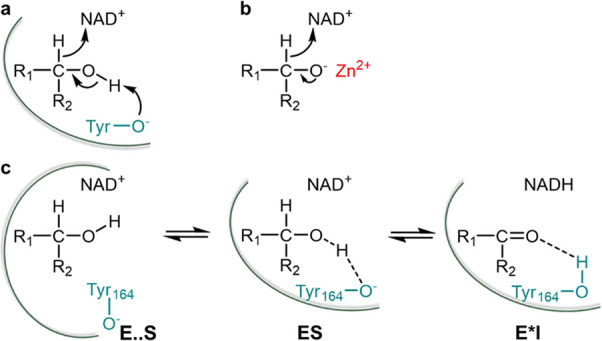
(a) General base catalysis, concerted reaction; (b) electrostatic stabilization by the metal ion, stepwise reaction; (c) two-step catalytic mechanism of substrate oxidation by TaCPa2E, with an initial enzyme–substrate complex (E..S) undergoing coupled motions to populate the reactive enzyme–substrate conformer (ES) that converts chemically to the keto-intermediate complex E*I. A strong (low barrier-like) hydrogen bond may be characteristic of the ES complex, distinct from the “normal” hydrogen bond present in E*I.

We assume in the discussion to follow that the substantially inflated ^Dk_cat of 6.1 at 40 °C implies the intrinsic KIE to have largely been revealed under these conditions. The ^Dk_cat in the temperature range 40–80 °C was therefore considered to show the KIE on the chemical step intrinsically. The evolution of the KIE in the low-temperature regime was unusual and required clarification.

A minimal kinetic scheme consistent with the experimental evidence is Scheme 3, with the important addition that the net rate of conversion of ES into E*I is rate-determining. It follows that c_r = k_–H/k_rot-red and c_Vf = k_H/k_rot-red, where k_–H is the rate constant for the reverse isotope-sensitive step and k_rot-red is a net rate constant for all further unimolecular steps, including rotation, reduction, and product release. Since ^Dk_cat is identical with ^Dk_cat/K_M and no enzyme-NADH accumulates, the c_Vf must be small, with k_H ≪ k_rot-red as discussed. To account for the observed decrease in ^Dk_cat below 40 °C, the c_r would have to increase at low temperature, requiring that the E_A on k_rot-red be larger considerably than the E_A on k_–H According to Scheme 3, the k_cat depends on k_rot-red and k_–H as shown in eq 3a. With the additional assumption of k_H ≪ k_rot-red, one gets the simpler eq 3b.

3a

3b

Scheme 3. Proposed Minimal Kinetic Mechanism of TaCPa2E Used to Analyze the Enzymatic Rates of CDP-Glc Consumption and Their Associated KIEs.

E and E* are enzyme-NAD⁺ and enzyme-NADH, respectively. I stands for the 2-keto intermediate and P for CDP-Man.

The temperature dependence of the k_cat can be expressed by the combined Arrhenius equations of the rate constants, as shown in eq 4.

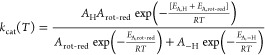4

If as discussed above the steps included in k_rot-red involved a relatively high E_A, k_cat would correspond to ∼k_H at high temperature and to ∼k_Hk_rot-red/k_–H at low temperature. The apparent E_A associated with the k_cat at low temperature would thus be [E_A(k_–H) – E_A(k_rot-red) – E_A(k_H)]. Due to the requirement of c_r that E_A(k_rot-red) > E_A(k_–H), the difference term would yield a negative overall activation energy, which is unreasonable. We thus exclude the possibility that temperature dependence of c_r accounts for the decrease in ^Dk_cat at low temperature.

Next, we consider that the overall catalysis of hydride abstraction by NAD⁺ comprises two steps as indicated in Scheme 2c. The k_H would then be expressed by eq 5

5

where k_con is a precatalytic step (E..S → ES) and k_chem is the chemical step of catalysis (ES → E*I). Since k_con is not isotope-sensitive, it must be the same for the protio and the deuterio substrate. A decrease in the observable KIE on the rate caused by the “kinetic complexity” of k_H must arise from E_A(k_con) larger than E_A(k_chem). At low temperature, therefore, the k_H would gradually become ∼k_con. The Arrhenius plot for k_cat (≈k_H) would be curved downward toward a limiting E_A(k_con). The experimental results for k_cat with both CDP-Glc and CDP-[2-²H]Glc (Figure 3b) are not consistent with the predicted behavior. Overall, therefore, these considerations emphasize the requirement of a different mechanistic model to explain the low-temperature dependence of k_cat and ^Dk_cat. A model based on conformational selection by the enzyme is proposed.

Evidence from Solvent Isotope Effects

Interpretation of the SKIE data is based on the notion from the discussion above that the hydride transfer from substrate to enzyme-NAD⁺ is rate-limiting for the k_cat in the full temperature range from 20 to 80 °C. Evidence that the ^D₂Ok_cat at 20 °C was identical with the protio and deuterio substrate thus suggests that both isotope effects (^D₂Ok_cat, ^Dk_cat) arose from a single rate-limiting step. The implication that the ^D₂Ok_cat is due to a solvent sensitivity of the immediate catalytic step renders the inverse nature of the SKIE of interest. The observable ^D₂Ok_cat can be expressed from the deuterium fractionation factors Φ (i.e., the exchange equilibrium constant between ¹H₂O and ²H₂O solvent) of the ground-state complex ES (Φ_GS) and the relevant enzyme complex involved in the reaction barrier crossing, typically the transition state TS (Φ_TS): ^D₂Ok_cat = Φ_GS/Φ_TS. For the ^D₂Ok_cat to become inverse, the somewhat unusual situation of Φ_GS < Φ_TS must apply. Groups responsible for inverse SKIEs in enzymatic reactions are cysteine (Φ ≈ 0.55¹⁰¹) and metal-bound water,¹⁰² but neither plays a role in the epimerase. An inverse SKIE of 0.6 ± 0.1 on k_cat/K_M was found in the Claisen-like condensation of acetyl-coenzyme A and glyoxylate by malate synthase using the deuterated substrate.¹⁰³ No SKIE was observed with the unlabeled substrate. The authors suggested that metal-bound water or global solvent reorganization enabling a conformational change upon substrate binding might explain these observations. Here, with TaCPa2E, besides a pre-catalytic conformational equilibrium dependent on solvent, a strong (effectively low-barrier)¹⁰⁴ hydrogen bond developed at the ground-state complex between the ionized Tyr164 and the 2-OH of the substrate (Scheme 2c, complex ES) could explain a Φ_GS considerably smaller than unity. The Φ of a negatively charged molecular group of the general form (RO–H–OR) is between 0.27 and 0.47 in a nonaqueous environment (CH₃CN solvent).¹⁰¹ The Φ of a regular hydrogen bond, arguably present at the 2-keto intermediate state (Scheme 2c, complex E*I), is ∼1.0. The requirement of the Φ_TS to be the intermediate between the Φ_GS and the Φ_IS would imply a proton transfer that is advanced considerably and involves the hydride transfer lagging behind at the transition state of the reaction. The catalytic scenario suggested for the epimerase shows a striking analogy to Zn²⁺-ADH catalyzing oxidation of ethanol by NAD⁺: Φ_GS = 0.37 (low-barrier hydrogen bond); Φ_TS = 0.73; Φ_PS = 1 (aldehyde product state).^105,106

The change in the ^D₂Ok_cat with temperature, different for the protio and deuterio substrate, is difficult to interpret with confidence. However, a partially rate-limiting deprotonation of the substrate associated with the hydride transfer appears to be ruled out for the full temperature range examined. Sensitivity to solvent deuteration of the reaction barrier crossing by quantum mechanical tunneling, dependent on the temperature and substrate isotope, could be an interesting topic for further mechanistic study of the epimerase.

Switch to an Impaired Conformational Landscape at Low Temperature

Both k_cat and ^Dk_cat of the TaCPa2E reaction with CDP-glucose showed unusual dependence on the temperature, with abrupt breaks seen at ∼40 °C. Enzyme kinetic behavior at and below the temperature break arose from processes completely reversible upon raising the temperature back to above 40 °C. A plausible explanation for it was a change in the conformational landscape experienced by the enzyme upon cooling-induced loss of structural flexibility. Enzyme conformers may get trapped in regions of conformational space that lead to impaired catalysis. The coupled motion associated with the proposed precatalytic step could arguably be affected by the structural rigidification.

Not only might the coupled motion be slowed down upon the loss of protein flexibility, but it could also become less precise in the positioning for catalysis. Arrhenius profiles of the k_cat in the range 20–40 °C reveal E_A values for the reaction with the ¹H and ²H substrates that differ by as much as −37 kJ mol^–1. Explanation of the result requires the assumption of a heterogeneous population of enzyme molecules differing in their kinetic properties. The simplest case would be that of a two-state equilibrium between enzyme conformers that involve a different nature of the chemical step and thus turn over the product at different rates (Scheme 4). The k_cat is the sum of the individual rate constants weighted by the fraction of total enzyme present in the respective conformer. An observable E_A is then composite of the enthalpic barriers of the chemical steps in the two conformers, but Arrhenius plots are unlikely to be linear over a broad temperature range (see the profile for the ²H substrate in Figure 3).¹⁰⁷ We hypothesize that conformational heterogeneity arises from the effect of low temperature on the conformational sampling achieved by coupled motion. In the proposed scenario, therefore, enzyme conformers featuring impaired positioning in the ground-state complex will experience a substantially elevated enthalpic barrier for the catalytic reaction. Partial loss of catalytic facilitation from proton abstraction to the active-site base can plausibly explain the effect. To undergo chemical conversion, such conformers will rely on a strongly increased contribution from quantum mechanical tunneling to the hydride transfer, compared to conformers that retain precise positioning to enable a lower enthalpic barrier. Lowering the temperature arguably shifts fractional occupation of enzyme conformers toward the ones with non-optimal positioning. The relative contribution to the observable k_cat from turnover of the two types of enzyme conformers will thus depend on temperature, with the reaction from the “tunneling conformer” gaining increased importance as the temperature is lowered. A simple mathematical model shown in Scheme 4 reasonably describes the overall trend of the data (Figure S9). Our two-state model is similar to that of Mulholland and co-workers¹⁰⁸ to explain temperature-dependent KIEs in that it proposes one reactive conformation that proceeds by tunneling and one that passes over the barrier. The output of the proposed model predicts a drop to E_A = 0 for the combined enthalpic barriers in the low temperature regime, suggesting a tunneling controlled reaction and confirming the shift to a tunneling-ready conformer. The obtained equilibrium constant K (= [ES]_GST/[ES]_OTB) converges to ∼1, indicating fractional equality of the two conformers assumed.

Scheme 4. Two-State Equilibrium Model and Presumed Barrier Shapes with Wavefunction Overlap for the Epimerization of CDP-[2-²H]Glc and CDP-Glc.

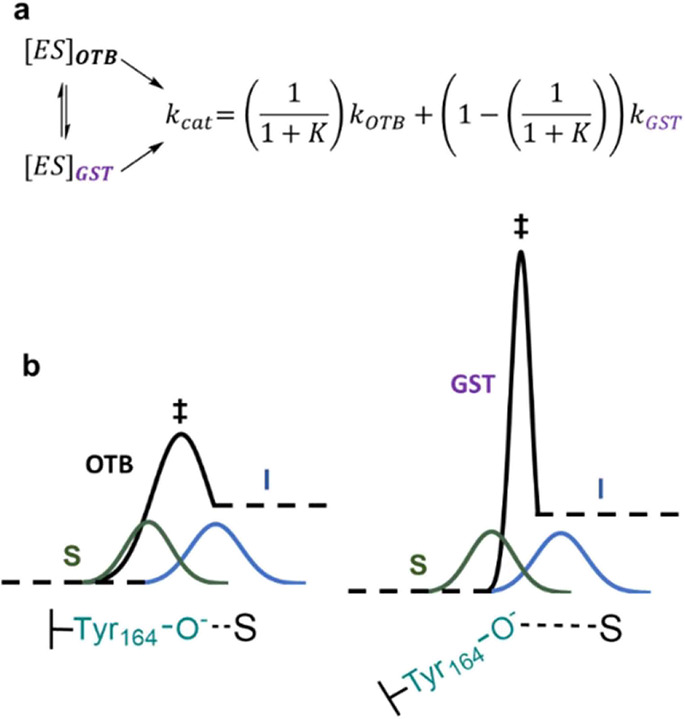
(a) The conformational equilibrium between [ES]_OTB for “over-the-barrier” (OTB) high-temperature epimerization and [ES]_GST being the ground-state tunneling (GST) conformer formed at lower temperature is represented by k_cat as the sum of the weighted reaction rates k_OTB and k_GST. Non-logarithmized experimental data was used for fitting and finding numerical solutions to the model proposed. For details, see Figure S9 and Materials and Methods. (b) Different enthalpic barrier heights/shapes for the OTB (left) and GST (right) conformer during substrate (S) oxidation to the 2-keto intermediate (I). Depictions of Tyr164 locked-on to the substrate in OTB and the moderate interaction in the GST conformer indicate the different levels of coupled motion in the respective substate. The equally overlapping substrate/intermediate wavefunctions (green; blue) allow for the possibility of tunneling controlled reactions in both conformers.

The idea of temperature-dependent equilibration of substates in the conformational ensemble sampled by the TaCPa2E enzyme–substrate complex was built on seminal studies of the thermostable ADH from Bacillus stearothermophilus.^23,25,44 In this ADH, heat is required to promote transition from a conformationally restricted inactive state to a more flexible, active state.^25,43,55TaCPa2E differs from the ADH in that the impaired conformational state retains activity. As discussed above, this unique feature of the TaCPa2E gives rise to an unprecedented temperature dependence of the catalytic rates and their associated KIEs. Important mechanistic insight derives from the evidence showing that the nature of the hydride transfer was fundamentally changed in consequence of the switch to the impaired conformational state at low temperature. Thus, coupled motions enabled by protein flexibility are linked to catalysis of the chemical step in the metal-independent enzymatic mechanism of alcohol oxidation.

Dynamical Properties of Hydride Transfer in the High-Temperature Region

According to the proposed two-state model (Scheme 4), an increase in temperature to 40 °C and higher enables the coupled motion of TaCPa2E to precision in positioning. Catalytically impaired conformers of the enzyme–substrate complex are thus re-equilibrated into the fully active region of the conformational space. From Arrhenius plots of the k_cat, there is a +13 kJ mol^–1 higher E_A for the reaction with ²H compared to the ¹H substrate and the pre-factor A_H/A_D ratio is 0.05. In the semiclassical interpretation of hydride transfer reactions, the A_H/A_D ratio is indicative of the tunneling contribution to the chemical step.^33,108−110 The A_H/A_D ratio below the semiclassical limit of 0.5 suggests a moderate tunneling regime in which tunneling occurs primarily for the light isotope. The very small A_H/A_D ratio found for the TaCPa2E reaction implies a minimal tunneling contribution to the conversion of the deuterated CDP-glucose. The reaction can still occur, however, because the heat provided is sufficient. The inverse SKIE on k_cat with the CDP-[2-²H]Glc substrate suggests increased participation of tunneling to the reaction of the heavier isotope enabled by solvent deuteration. To expand the mechanistic interpretation beyond the limits of semiclassical transition state theory, we applied the Marcus-like full-tunneling model developed by Kohen and co-workers¹³ to describe our experimental data. Generally, models of this type extend the Marcus-theory of electron tunneling to hydrogen atom tunneling (involving proton tunneling) in which heavy-atom reorganization results in tunneling-ready states.^85,111,112 The Kohen model further links the size and temperature dependence of the KIEs to a population distribution for fluctuations of the distance between donor and acceptor atoms.¹³ The data required fitting by a two-population distribution of DADs (Figure S7; fit with a single-population model was unsuccessful), with the long-distance population centered at a value of 3.31 ± 0.02 Å and a Gibbs free energy difference (ΔG) between the two populations of 17.24 ± 2.1 kJ mol^–1. In Kohen’s model,¹³ the ΔG is relative to a short-distance population centered at DAD short enough for ¹H and ²H to cross the dividing surface between the substrate and product with similar probabilities; hence, the KIE associated with the population is unity. Compared to the short-distance population, the second, long-distance population involves lower energy, decreased tunneling probability overall, and larger KIE. Temperature dependence of the KIE is thus explained from the temperature-dependent change in the relative populations present in thermal equilibrium. The ΔG for TaCPa2E is among the largest seen for enzymes catalyzing hydride transfer. Only in one variant of DHFR (M42W-G121V) has a similar ΔG (18.42 kJ mol^–1) been found.³⁰ In both TaCPa2E and DHFR variants, the unusually large ΔG probably reflects a very loose active site that involves substantial fluctuation in DAD for the tunneling ready state. Poor conformational reorganization can result in low-frequency DAD sampling and lead to a wide range of DADs exhibiting temperature dependence of their distribution. The long-distance populations of TaCPa2E and the DHFR variant^13,30 (DAD_L = 3.34 Å) center at similar values to DAD. Since wavefunctions for the substrate and product exhibit a scant overlap for DADs as long as these,¹³ the tunneling probability is low overall and in particular so for the heavy isotope, leading to a large KIE. An increasing temperature populates the short DAD from which the heavy isotope can also be transferred. The relative advantage of ¹H tunneling from the longer DADs is thus lowered, and the KIE decreases in a strongly temperature-dependent manner.

The Loose-Fit CDP-Glucose Substrate Resembles Mutations in Effect on the DAD Coordinate

A number of studies have found that within the limits of the experimental error, wild-type enzymes show temperature-independent KIEs on the hydride transfer.^9,34,113,114 The behavior is generally explained by precise positioning of the substrate in the ground-state complex, leading to a narrow distribution of DADs at the tunneling-ready state of a well-preorganized protein conformation.^13,85 A change in temperature will not cause a DAD population shift, and since both isotopes are affected similarly, the KIE change with temperature will be minimal. Mutations often promote a broader ensemble of conformations representing differently preorganized substates that can give rise to distinct populations along the DAD coordinate.^9,13 Variants of DHFR with substitutions in (e.g., I14G⁹) or distal to the active site (e.g., M42W-G121V; M42W-F125M^7,30,115) reveal the effect dramatically. As shown by phenomenological modeling, they display enhanced conformational flexibility, leading to increased population size and broadening of the DAD distributions. The experimental E_A is +13.8 kJ mol^–1 (I14G),⁹ +15.5 kJ mol^–1 (M42W-G121V),³⁰ and +16.7 kJ mol^–1 (M42W-F125W)¹¹⁵ larger for the reaction with the heavier (³H) isotope substrate. The KIE of TaCPa2E probed with CDP-Glc exhibits a temperature dependence of similar magnitude to (even larger than the ones of) the DHFR variants. The observed ΔE_A is +13 kJ mol^–1 but one must take into account that the ²H KIE instead of the ³H KIE was measured for the epimerase, and the zero-point energy of the ²H-C bond lies +2.26 kJ mol^–1 higher than that of the ³H–C bond. Considering that the TaCPa2E used here is the wild-type enzyme, the strongly inflated ΔE_A warrants further discussion. Its molecular interpretation is that the enzymatic oxidation of CDP-Glc involves extensive dynamical sampling of DADs suitable for tunneling. Requirement for the enzyme to explore a large conformational space in order to promote catalysis is consistent with earlier reported evidence by computational docking. The native 3,6-dideoxygenated substrate CDP-paratose (Scheme 1) fits snugly into the preorganized binding pocket of the TaCPa2E. The CDP-Glc can be accommodated only with substantial structural rearrangements of protein residues, to create sufficient space for the 3-OH and 6-OH sugar substrate groups.⁷² Temperature dependence of the KIE for non-preferred substrates has only been scantly studied with enzymes. Proton transfer by methylamine dehydrogenase involves a KIE that is temperature-independent with the native substrate methylamine but temperature-dependent (ΔE_A = +8.4 kJ mol^–1; A_H/A_D = 0.57) with the slow substrate ethanolamine.¹¹⁶ The increased requirement of active site rearrangements for positioning bulky substrates has been recognized in protein KIE studies of alcohol dehydrogenase.¹¹⁷ The current results emphasize the mechanistic utility of a structurally loose-fit, slowly reacting substrate to probe dynamical features of the chemical step of hydride transfer in enzymatic sugar nucleotide epimerization.

In summary, temperature dependence of the primary deuterium KIE for C2 epimerization of CDP-glucose reveals protein conformational selection linked to catalysis by the thermophilic TaCPa2E. In the multistep catalytic process of the epimerase, the instigating hydride abstraction by enzyme-NAD⁺ is shown to be rate-limiting. A hierarchy of temperature dependent protein motions is necessary for optimal catalysis to the C–H bond cleavage. Evidence suggests that coupled motions achieve precise positioning of the substrate so that partial proton abstraction can effectively initiate the bond breaking. Protein rigidity at low temperature (≤ 40 °C) interferes with conformational sampling by the coupled motion, thus giving rise to catalytically impaired enzyme conformers that lack suitable activation of the proton transfer. Quantum mechanical tunneling associated with the C–H bond cleavage identifies protein dynamics necessary in catalysis. To promote the chemical step in the high temperature region, the epimerase requires extensive dynamical sampling of DADs suitable for tunneling. Due to the high and narrow enthalpic barrier for conversion of the conformationally restricted enzyme substates, the epimerase catalysis is tunneling controlled in the low temperature region. Overall, the contributions of protein dynamics to catalysis of C–H bond cleavage by TaCPa2E show important analogies to ADHs and DHFRs catalyzing the same bond breaking in simpler enzymatic transformations. A loose-fit substrate (in TaCPa2E) resembles structural variants of ADHs and DHFRs in its requirement for extensive dynamical sampling to balance conformational flexibility and catalytic efficiency. Protein motions associated with intermediate rotation and reduction of the epimerase reaction are not revealed at the steady state.

Materials and Methods

Materials

Nucleotides and ¹H-glucose were from Carbosynth (Compton, Berkshire, U.K.). ²H-glucose was from Sigma-Aldrich (Vienna, Austria). Deuterium oxide (99.96% ²H) was from Euriso-Top (Saint-Aubin Cedex, France). All other chemicals and reagents were of the highest available purity. E. coli BL21(DE3) competent cells were prepared in-house. DpnI and Q5 High-Fidelity DNA polymerases were from New England Biolabs (Frankfurt am Main, Germany). For plasmid DNA isolation, a GeneJET Plasmid Miniprep Kit (Thermo Scientific; Waltham, MA, USA) was used.

Enzymes

The TaCPa2E_Y164F variant was prepared via a modified QuikChange protocol. For PCRs, 20 ng of plasmid DNA (template) and 0.2 μM of forward or reverse primer in a total reaction volume of 50 μL were used. DNA amplification was carried out with a Q5 DNA polymerase. Primer sequences used for mutagenesis are shown in Table S2. TaCPa2E wild-type and the Y164F variant were expressed in E. coli BL21 (DE3) cells harboring a pET21a expression vector with the respective gene. Enzyme purification was performed using the C-terminal His-tag. Separate His-tag columns were used for the wild-type TaCPa2E and Y164F variant to traces of one enzyme carried over into the other’s preparation. Molecular mass and purity of the proteins were confirmed by SDS-PAGE (see Figure S10 for the Y164F variant). Detailed information on expression and purification conditions is given elsewhere.⁷²

Substrate Synthesis and Isolation

Details of the enzymatic synthesis of CDP-Glc can be found elsewhere.⁷² The synthesis of CDP-[2-²H]Glc was identical to the synthesis of the unlabeled counterpart (Scheme S1). Briefly, anomeric phosphorylation was carried out using N-acetylhexosamine 1-kinase, ATP, MgCl₂, and [2-²H]glucose in MOPS buffer (100 mM, pH 7.5). The reaction mixture was incubated at 30 °C until ATP was fully depleted. Nucleotidyl transfer from CTP to [2-²H]glucose-1-phosphate was catalyzed by UDP-glucose pyrophosphorylase. An inorganic pyrophosphatase was used for pyrophosphate removal. Product isolation was performed as described elsewhere.⁷² Both CDP-[2-²H]Glc and CDP-Glc were obtained in high purity (≥ 95%) and in amounts of 10–20 mg. The identity of CDP-[2-²H]Glc was confirmed by HPLC and ¹H-NMR (Figures S11 and S12). The ²H content at C2 was 95% or greater.

Determination of Kinetic Isotope Effects

Primary Kinetic Isotope Effects

Primary KIEs on the k_cat were determined by carrying out epimerization reactions of CDP-[2-²H]Glc and CDP-Glc (4.00 mM) for 15 min in MOPS buffer (100 mM, pH 7.5) using purified TaCPa2E (1.0 mg mL^–1; 25.4 μM) at varying temperatures (20–80 °C) in a total reaction volume of 60 μL. CDP-Glc/CDP-[2-²H]Glc (15 μL; 16 mM stock) were added to 45 μL of prepared enzyme solution (10 μL of 6.0 mg mL^–1TaCPa2E + 35 μL buffer). The enzyme solution was equilibrated for 5 min at the desired reaction temperature in a non-agitated thermomixer comfort (Eppendorf AG, Hamburg, Germany). Potential temperature-induced shifts in pH values were ruled out as no changes prior to, or after completion of, the reaction were detected. Samples were taken at 0, 5, and 15 min, and the reaction was quenched by adding 5 μL of sample to 25 μL of doubly distilled water and 30 μL of methanol (1/1 ratio water/methanol). Mixtures were vortexed (10 s), centrifuged for 45 min at 21130g, and analyzed on HPLC. Substrate and enzyme concentrations were kept constant over the entire temperature range to assure the highest reliability and reproducibility of the data. Conversions to the respective D-manno-configured isotopes (0.2–10%) were within the initial rate period (see Figure S2 for 60 °C reaction), which were calculated from the linear segment of the time course by means of dividing the slope of the linear fit (mM min^–1) by the enzyme concentration (mg mL^–1). The apparent k_cat values (min^–1) were calculated from the initial rate (= μmol (min mg_protein)⁻¹) with the molecular mass of the functional enzyme monomer (TaCPa2E_WT: 39362 g mol^–1). Substrate saturating conditions were achieved by using substrate concentrations 12.5-fold above the K_M value (0.32 ± 0.02 mM) at 60 °C. It was further ensured that the increase in the substrate concentration by 0.5 and 1.0 mM did not change the rates obtained at 4.0 mM with limits of error (± 5%). Repeated measurements (N ≥ 4) at a single saturating substrate concentration gave k_cat values determined with high precision. The KIEs (Table S1) were obtained as the ratio of the k_cat for enzymatic reaction with the light (¹H) and heavy (²H) isotope.

The KIE on the k_cat/K_M was determined for reactions at 20, 60, and 80 °C. Initial rates were acquired with TaCPa2E (1.0 mg mL^–1; 25.4 μM) at varying substrate concentration (0.1–5.0 mM) of both CDP-Glc isotopes (Table 2 and Figure S3) in MOPS-H₂O buffer (100 mM, pH 7.5). Samples were taken in 2.5 min intervals and quenched by methanol (1/1 ratio water/methanol). Calculation of the specific rate (V/[E], min^–1) was based on linear correlations of the substrate consumed and the product released within the reaction time. For further experimental details on the kinetic characterization of the enzymatic reaction with CDP-Glc, see ref (72). SigmaPlot 10.0 (Systat Software, Inc.) was used for fitting eq 6 to the experimental data.

6

In eq 6, [A] is the molar concentration of CDP-Glc, K_A is the Michaelis constant, F_i is the fraction of deuterium in the substrate (0.95), and E_V and E_V/K are KIEs minus 1 on k_cat and k_cat/K_M.¹¹⁸ All experiments were performed in triplicate (S.D. shown in Figure S3), and mean values were used for fitting. Note that the KIEs on k_cat determined from fits of eq 6 to the data were in excellent agreement (± 5%) with the corresponding KIEs determined from (repeated) measurements at a single saturating substrate concentration.

Solvent Kinetic Isotope Effects

TaCPa2E (48.0 mg mL^–1; 1.2 mM) was re-buffered to MOPS-²H₂O (100 mM, p²H 7.5) by centrifugation (2100g, 10 °C) using 0.5 mL VivaSpin tubes (10 kDa cutoff) until a dilution factor of 500 was reached. The enzyme was further incubated for 0.25 or 4.5 h at 4 °C. The incubation in ²H2O solvent did not cause loss of enzyme activity (measured in ¹H2O). The substrate preparation, reaction setup, and analysis followed the procedure as described for the determination of primary KIE. CDP-[2-²H]Glc stocks were prepared in MOPS-²H₂O (100 mM). Reactions in MOPS-¹H₂O buffer were carried out with purified TaCPa2E (48.0 mg mL^–1; 1.2 mM) stored in MOPS-¹H₂O (100 mM). SKIEs were determined at pL (L = ¹H or ²H) 7.0, 7.5, and 8.0 at 60 °C and pL 7.5 at 20 °C. Desired pL values were obtained by adjusting MOPS-²H₂O (100 mM) buffers with NaOH dissolved in ²H₂O. The p²H was obtained as a pH meter reading of +0.4. MOPS-¹H₂O (100 mM, pH 7.5) containing 9% v/v glycerol was used as viscosity control.^86,103 It was also shown in kinetic measurements at 60 °C that the time of pre-incubation in ²H₂O (0.25 h, 4.5 h) had no effect on the observable SKIEs within limits of error. All measurements were therefore done with enzyme exchanged in ²H₂O solvent for 4.5 h. Experiments were performed in triplicate. SKIEs (Table 3) were obtained as the ratio of the k_cat for the enzymatic reaction in ¹H₂O and ²H₂O. Superscript D₂O (^D₂Ok_cat) is used to indicate the SKIE.

Determination of Enzyme-Bound NADH/NAD⁺ in the Steady State

Purified TaCPa2E (1.0 mg mL^–1; 25.4 μM) and CDP-Glc (4.00 mM) in a final volume of 1 mL were reacted for 15 min in MOPS-¹H₂O/²H₂O buffer (100 mM, pL 7.5) at 60 °C without agitation (thermomixer comfort; Eppendorf AG, Hamburg, Germany). The reaction was started by adding 200 μL of CDP-Glc (20 mM stock) to 800 μL of equilibrated (5 min, 60 °C) enzyme solution (1.25 mg mL^–1 stock). Control reactions lacking CDP-Glc were prepared using 200 μL of MOPS-¹H₂O/²H₂O buffer (100 mM, pL 7.5) and 800 μL of enzyme solution. The reaction/control was quenched by adding ice-cold acidified MOPS-¹H₂O/²H₂O buffer (100 mM, pL 1.9) in a 1/1 ratio, resulting in a final pL of 5.5 and retaining the enzymes’ solubility while terminating the enzymatic activity. The reaction/control was transferred into ice-cold 5 mL VivaSpin tubes (10 kDa MWCO) and centrifuged at 10 °C (2880g) to a final volume of 0.5 mL. The concentrated reaction/control solution was washed twice by adding 4.5 mL of acidified buffer and repeating the centrifugation step. The flowthroughs were analyzed on HPLC to assure that the reaction equilibrium remained unchanged over the washing process (see Figure S5). The reaction/control (0.5 mL) was transferred into ice-cold 0.5 mL VivaSpin tubes (10 kDa MWCO) and concentrated to a final volume of 50 μL (2880 g, 10 °C), followed by determination of the protein concentrations on a Nanodrop at 280 nm using the TaCPa2E-specific extinction coefficient ε = 16.27 M^–1 cm^–1 (ProtParam tool, Expasy, Swiss Bioinformatics Resource Portal). Protein precipitation was initiated by adding MeOH (50 μL) to the reaction/control and incubation for 2.5 h at 30 °C (no agitation). Afterward, the samples were centrifuged for 45 min at 21130g. The supernatant was withdrawn, and the precipitated enzyme was re-suspended in 50 μL of 6 M urea followed by HPLC analysis. Additionally, NADH stability was tested by subjecting 0.1 mM NADH dissolved in MOPS buffer (100 mM, pH 7.5) to the same procedure as described above. No degradation of the coenzyme was found. Experiments were performed in quadruplicate. Note that based on experiments (N = 8) aimed at showing the reproducibility of the coenzyme extraction method, enzyme-bound NAD⁺ could not be extracted from TaCPa2E reliably (reproducibility ≥28%), whereas extraction of the less tightly-bound NADH proved to be highly dependable (reproducibility of ≥86%). An NADH calibration curve (Figure S5) was used for calculating the concentration of the released NADH (μM). The amount of enzyme-bound NADH (%) was determined by dividing the protein concentration (μM) measured prior to enzyme denaturation (∼96% of the original amount) into the released NADH concentration (μM). Calculation of the amount of CDP-mannose and CDP-glucose (μM) associated with the denatured enzyme (μM) was based on calibration curves for both compounds.

Analytics

HPLC

A Shimadzu Prominence HPLC-UV system equipped with a Kinetex C18 analytical HPLC column was used. Injection volumes were between 5 and 30 μL. For KIE experiments, UV detection at 271 nm using a Kinetex C18 column (150 × 4.6 mm, 5 μm EVO C18 100 Å; Phenomenex, Aschaffenburg, Germany) and an isocratic flow (1 mL/min) at 40 °C with a mobile phase composed of 20 mM potassium phosphate buffer (pH 5.9) containing 40 mM tetrabutylammonium bromide (98%; solvent A) and methanol (2%; solvent B) was applied. HPLC analysis in the course of the rapid-quench assay was performed using a Kinetex C18 column (50 × 4.6 mm, 5 μm 100 Å) and an isocratic flow (2 mL/min) with 40 mM tetrabutylammonium bromide (95%; solvent A) and acetonitrile (5%; solvent B) in 20 mM potassium phosphate buffer (pH 5.9).

¹H-NMR Analysis

The reaction mixture prepared for in situ proton NMR analysis contained 58.4 μM (2.3 mg/mL) TaCPa2E and 2.00 mM CDP-[2-²H]Glc in ²H₂O buffer (50 mM K₂HPO₄/KH₂PO₄, p²H 7.5; p²H = pH meter reading +0.4). The data was acquired at 60 °C on a Varian INOVA 500-MHz NMR spectrometer (Agilent Technologies, Santa Clara, California, USA) in 10 min intervals starting from enzyme addition using VNMRJ 2.2D software. ¹H-NMR spectra (499.98 MHz) were recorded with pre-saturation of the water signal by a shaped pulse on a 5 mm indirect detection PFG probe. Spectra were analyzed using MestReNova 16.0 (Mestrelab Research, S.L.). In situ proton NMR analysis of TaCPa2E/CDP-Glc was described elsewhere.⁷²

Bioinformatic and Computational Tools

Two-State Equilibrium Model

Data fitting was performed using Microsoft Excel’s Solver add-in and the GRG Nonlinear solving method. Constraint precision was set to 10^–6 and convergence to 10^–4. The sum of the relative errors squared was minimized. A unique solution was obtained by multiple fitting events to eqs 7a and 7b.

Fit 1:

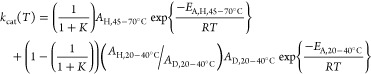7a

Fit 2:

7b

Fitting parameters, constraints, and model outputs including the equilibrium constant K (= [ES]_GST/[ES]_OTB) are presented in Figure S9.

Calculation of Donor–Acceptor Distances

DAD calculations were performed applying the program provided and developed by Roston et al.¹³ at http://chemmath.chem.uiowa.edu/webMathematica/kohen/marcuslikemodel.html.

Enzyme/Substrate Structure model

The PyMOL Molecular Graphics System (Open-Source, Schrödinger, LLC) was used for depicting donor–acceptor distances in TaCPa2E. Structure modeling and ligand docking conducted for Figure S8 were described elsewhere.⁷²

Glossary

Abbreviations

TaCPa2E

Thermodesulfatator atlanticus CDP-paratose 2-epimerase

DAD

donor–acceptor distance

KIE

kinetic isotope effect

CDP-Glc

CDP-α-d-glucose

CDP-Man

CDP-α-d-mannose

CDP-[2-²H]Glc

CDP-[2-²H]α-d-glucose

CDP-[2-²H]Man

CDP-[2-²H]α-d-mannose

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscatal.2c00257.

• Full ¹H NMR spectra, KIE values, HPLC-chromatograms, DAD calculation, PCR method, model output and details of the synthesis and analysis of CDP-[2-²H]Glc; KIE values obtained for reacting TaCPa2E with CDP-Glc or CDP-[2-²H]Glc in the temperature range of 293.15–353.15 K (Table S1); DNA primer sequence for the TaCPa2E_Y164F variant (Table S2) and description of the PCR method; determination of the noncompetitive KIE using CDP-[2-²H]Glc or CDP-Glc (Figure S1); exemplified comparison of the initial rates for the epimerization of CDP-Glc isotopes (Figure S2); kinetic data used for determination of ^Dk_cat/K_M or ^D₂Ok_cat/K_M at different temperatures (Figure S3); complementing full spectrum of in situ ¹H-NMR measurements applying TaCPa2E and CDP-[2-²H]Glc or CDP-Glc (Figure S4); NADH quantification and HPLC analysis of flowthrough and supernatant to assure an unchanged reaction equilibrium of CDP-Glc/CDP-Man in the rapid-quench assay (Figure S5); determination of the reaction equilibrium for TaCPa2E with CDP-[2-²H]Glc (Figure S6); DAD calculation for TaCPa2E obtained by fitting hydrogen/deuterium (H/D) KIEs against the inverse temperature (Figure S7); donor–acceptor distance in the structure model of TaCPa2E (Figure S8); two-state equilibrium model output with fitting parameters and set constraint values (Figure S9); SDS-PAGE result of the purified TaCPa2E_Y164F variant (Figure S10); HPLC chromatogram (Figure S11) and ¹H-NMR spectrum of CDP-[2-²H]Glc (Figure S12); enzymatic synthesis of CDP-[2-²H]Glc (Scheme S1) with short description of the methods used (PDF)

Author Contributions

C.R. and B.N. designed the research. C.R. performed experiments and analyzed the data. C.R. and B.N. wrote the paper.

Financial support from the Austrian Science Fund (FWF) (Project I 3247, EpiSwitch, B.N.) is acknowledged. Open Access is funded by the Austrian Science Fund (FWF).

The authors declare no competing financial interest.