Responsive materials architected in space and time

Abstract

Rationally designed architected materials have attained previously untapped territories in materials property space. The properties and behaviours of architected materials need not be stagnant after fabrication; they can be encoded with a temporal degree of freedom such that they evolve over time. In this Review, we describe the variety of materials architected in both space and time, and their responses to various stimuli, including mechanical actuation, changes in temperature and chemical environment, and variations in electromagnetic fields. We highlight the additive manufacturing methods that can precisely prescribe complex geometries and local inhomogeneities to make such responsiveness possible. We discuss the emergent physics phenomena observed in architected materials that are analogous to those in classical materials, such as the formation and behaviour of defects, phase transformations and topologically protected properties. Finally, we offer a perspective on the future of architected materials that have a degree of intelligence through mechanical logic and artificial neural networks.

Architected materials are a class of materials with structures intermediate in scale between atomic arrangement and bulk dimensions; this additional degree of freedom enables unique properties and functionalities. This Review describes the state of the art in architected materials that are responsive to various stimuli.

Introduction

Throughout history, materials have been gathered, mined, alloyed and synthesized to substantiate every step of societal development from the Bronze Age to modern-day Silicon Valley. The essential goal of materials science is to predict and create materials with ever-improving properties and new functionalities through manufacturable, sustainable and economical pathways. For example, building materials have evolved from stones, bricks and wood, to stronger and cheaper engineered materials such as steel, plastics and reinforced concrete, and to synthetic functional materials such as the lightweight, durable and translucent polymer membranes used in retractable stadium roofs. Key to materials science is the relationship between a material’s microstructure at the atomic and molecular level and its properties; this understanding has led to world-changing material discoveries in mechanics^1,2, computing³ and energy storage⁴.

The development of architected materials — structures with mesoscale, microscale and even nanoscale components designed into particular spatial arrangements — introduces a new architectural degree of freedom with which to encode properties that differ from or surpass those of their constituent materials. Prominent examples include solids that deform like a fluid with near-zero shear-to-bulk modulus ratio⁵, and typically brittle ceramics that instead deform and recover upon compression⁶. Advances in fabrication technologies, especially in additive manufacturing, have allowed material components to be spatially varied across multiple length scales, enabling the rational design of architected materials that have enhanced properties and novel functionalities. Architected materials are populating previously untapped territories in the materials property space, such as ultralow thermal conductivity⁷ and simultaneous low density and high strength⁸, and they often possess exotic properties such as negative Poisson’s ratio⁹ and mechanical invisibility¹⁰, earning their description as ‘metamaterials’.

This Review looks beyond the static properties of architected materials and encompasses progress in architected materials that can evolve over time by following a pre-programmed trajectory. These dynamic materials, architected in both space and time, challenge the conventional perception that materials are stagnant once the components are manufactured. They can respond to a broad range of stimuli, reconfigure to different geometries or adapt to the surrounding environment. When triggered, architected materials can attain different mechanical properties^11,12 or chemical reactivity¹³, release carried cargos via structural changes^14,15 or fail at designated locations¹⁶. This built-in responsiveness could enable novel functionalities in ‘smart’ materials that react, deploy and evolve in specific environments or conditions directly at the material level. For example, architected materials can hide and reveal information through structural transformation on demand^17,18; untethered moving robots can be powered by temperature changes¹⁹, guided by light²⁰ or manipulated by magnetic fields¹⁴; self-regulated chemomechanical systems can maintain a homeostatic temperature range against environmental perturbations¹³.

We categorize responsive architected materials on the basis of four distinct activation mechanisms: mechanical actuation, heat transfer, chemomechanical transformation and electromagnetic interaction (Table 1). We focus on materials with rationally designed architectures that define their properties and temporal responses; in a few cases, we highlight the intrinsic responsiveness of certain materials that could be integrated into architected systems in the future. Throughout the discussion, we describe the fabrication techniques that produce the desired architecture and build inhomogeneities into material properties within that architecture, which together enable the tailored responsiveness. We then describe the emerging physics phenomena in architected materials that find analogy to those in classical materials. We end by offering a vision for how materials architected in space and time may one day lead to a certain degree of materials intelligence.

Table 1.

Comparison of representative activation mechanisms as building blocks for responsive architected materials

Activation mechanism		Typical materials	Fabrication methods	Response speeda	Advantages	Limitations
Mechanical actuation		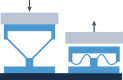Elastomers, polymers, papers, metals	DIW, SLA, PolyJet, DLP, TPL, SLS, machining	Fast	Mature fabrication and advanced design methods; easy mechanical control; marginal sensitivity to surrounding environment; stable reconfigurability	Difficult to deploy or modulate remotely; response depends on specific loading conditions (such as uniaxial loading)
Heat transfer	Phase change	Polymers, metals, polymer-filler composites, LCEs, SMPs, hydrogels	DIW, DLP, TPL, microfabrication, machining	Slow to medium	Remote activation by temperature; thermal expansion is universal and can be modelled systematically; phase-changing materials have substantial thermal expandability and programmable anisotropy; SMPs can be willfully deformed after fabrication and achieve nearly full shape recovery	Limited to specific temperatures and environments (for example, cannot operate when temperature cannot be changed); may require large temperature change and long heating or cooling time
	Shape memory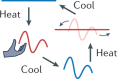
Chemomechanical transformation	Swelling	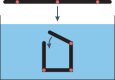Hydrogels, hydrogel-filler composites, polymers, multi-material composites	DIW, DLP, microfabrication, machining	Slow to medium	Large, programmable structural changes; easy activation by wetting	Transformation speed limited by mass transport; require large environmental changes
	Chemistry	Hydrogels	DLP, TPL, microfabrication, machining	Medium to fast	Chemical activation is useful for biomedical applications; autonomous feedback can be achieved via chemical reactions	Require specific reactions and relevant materials synthesis to respond to different chemical cues
	Electrochemistry	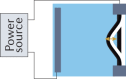Electrochemically active materials (such as conjugated polymers, battery electrode materials)	Machining, microfabrication, TPL	Slow to medium	Structure and property retention upon stimulus removal; continuous control of transformation; potential to simultaneously store energy	Typically require two electrodes, a liquid or gel electrolyte, and a power source; 3D structuring methods are not fully developed
Electromagnetic interactions	Magnetic field	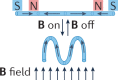Polymers with embedded magnetic particles	DIW, DLP, microfabrication	Fast	Fast, remote activation (typically <1 s); complex, reversible, and programmable structural changes	Require strong magnetic fields (typically >0.1 T); mostly soft materials
	Electric field	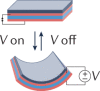Ionic hydrogels, dielectric elastomers, piezoelectric composites	DLP, moulding, machining, microfabrication	Medium to fast	Dielectric elastomers integrate into electronic control circuits for autonomous devices; piezoelectric materials can measure strain	Require additional electrodes and electronic control
	Light	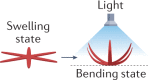Polymers with light-absorbing nanoparticles, azobenzene-containing liquid crystal polymers	DIW, microfabrication, machining	Medium to fast	Fast, remote activation and active manipulation; independent control of shape changes by different polarizations and wavelengths	Limited 3D patterning methods; cannot function without a light source and sufficient transmission

DIW, direct ink writing; DLP, digital light processing; LCE, liquid crystal elastomer; SLS, selective laser sintering; SMP, shape memory polymer; TPL, two-photon lithography. ^aResponse speed is compared in relative terms between representative responsive materials with similar dimensions; the demonstrated response speed of specific responsive architected materials examples depends on both the activation mechanism and the architecture’s geometry and feature sizes. Illustration in row 1 adapted with permission from ref.²⁴, Wiley. Illustration in row 5 adapted from ref.⁹⁶, Springer Nature Limited. Illustration in row 7 adapted from ref.¹⁴, Springer Nature Limited. Illustration in row 9 adapted from ref.¹⁴⁷, Springer Nature Limited.

Responsive mechanisms of architected materials

Here we describe current progress in each category of responsive architected materials, explain their unique programming and transformation approaches, and offer examples of their potential applications. Table 1 offers a comprehensive comparison of representative implementations of various response mechanisms. Mechanically responsive architected materials exhibit dramatic and programmable structural changes beyond the linear elastic regime, often through purposefully incorporated mechanical instabilities^17,21–25. Their development has benefited from the manufacturability of complex 3D architectures, established analytical frameworks, and systematic design tools. Their structural and property modulation generally requires direct physical contact. Thermo- and chemo-responsive architected materials are triggered by temperature or chemical cues from the surrounding environment. Their structures can transform conditionally in response to a changing local environment; for example, they may release a drug at a certain temperature and/or pH. Electromagnetically responsive architected materials can be manipulated remotely with a short response time by a magnetic field, an electric field or light. Active modulation of the electromagnetic fields gives these materials more complex temporal trajectories, enabling them to perform remotely prescribed tasks such as picking up an object and delivering it to a specific location¹⁴. When designing functional responsive materials, the specific objectives — for instance, response time, local environment, or need for remote deployment — provide guidance for one or more of these activation mechanisms to be integrated into the architectural design for desired spatiotemporal responses.

Mechanical actuation

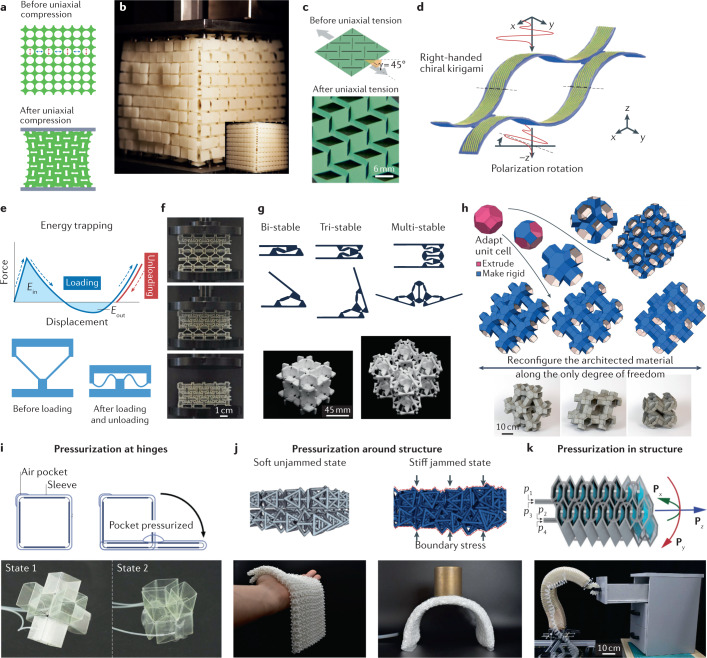
Architected materials have demonstrated static mechanical properties⁸ superior to those of traditional materials or composites, such as light weight²⁶, high specific stiffness²⁷ and near-theoretical strength²⁸. Beyond the linear elastic regime, architected materials can exhibit further programmable structural transformations and nonlinear responses induced by mechanical actuation. For example, designed buckling instabilities can trigger dramatic and reversible structural changes in response to modest applied forces^{17,21–23,29–31}. Slender elements, such as beams or ligaments, can be systematically embedded in architected materials at specific sites or throughout the sample to program coordinated instabilities in a predictable fashion. A simple demonstration of this strategy is in elastomeric cellular sheets with a periodic arrangement of holes, creating narrow sections that are prone to buckling upon uniaxial compression^21–23 (Fig. 1a). The displacements of slender elements are coupled with those of the neighbouring elements, and the collective buckling response induces pattern transformations as the holes collapse into mutually orthogonal or other correlated directions. Such cellular materials have been demonstrated to exhibit auxetic behaviour^21,22, which can be utilized to modulate acoustic bandgaps³². Auxetic materials have a negative Poisson’s ratio, which means that when they are stretched along a particular direction, they expand in the transverse direction instead of exhibiting typical Poisson contraction. Similar coordinated buckling can be extended to 3D elastomeric architectures with a high degree of programmability by exploring symmetry groups³³ and by engineering compositions of multiple materials, each with a distinct stiffness³⁴ or viscoelastic property³⁵. Architected materials with tailored and entangled buckling instabilities have been designed to exhibit strain-dependent twisting upon compression³⁴, to localize deformation and failure by controlling the structure’s states of self-stress¹⁶, to function as reusable lightweight shock absorbers³⁶ and to program pattern formation and recognition through a combinatorial algorithm¹⁷ (Fig. 1b).

Fig. 1. Architected materials with tailored mechanical responses and reconfigurability.

a | Illustration of coordinated buckling of elastomeric cellular solids upon compression²¹. b | Programmed pattern formation of voxelated mechanical metamaterials¹⁷. c | Illustration of buckling-induced structural transformation of kirigami-based metamaterials before and after tensile loading at an angle γ with respect to the cutting direction³⁸. d | Illustration of a stretched kirigami polarization modulator that can rotate the polarization of a terahertz wave by various degrees depending on the applied mechanical strain⁴¹. The kirigami substrate with herringbone-shaped gold patterns is a topologically equivalent helix structure with right-handed chirality. e | Force–displacement curve of a reconfigurable unit cell with snap-through instabilities that retain the deformed geometry upon unloading²⁴. f | Time-lapse images of a compressive loading experiment on an elastic multi-stable structure, which exhibits self-similar layer-by-layer collapse and retains its deformed shape after unloading²⁴. g | Reconfiguration of 3D architected materials based on modular bi-stable, tri-stable and multi-stable hinges²⁵. h | Reconfigurable prismatic architectures based on numerical analysis of space-filling tessellation of polyhedra⁵². i | Illustration and images of structural transformation of origami-inspired metamaterials induced by pressurized air pockets at selected hinges⁵⁵. j | Illustration and images of the stiffening and reconfiguration of architected chainmail fabrics by external pressurization through an enclosing envelope⁵⁶. k | Illustration of a honeycomb pneumatic network that can bend (P_x and P_y degrees of freedom) and elongate (P_z degree of freedom) by controlled inflation of embedded air pockets through four pressurized tubes (p₁–p₄), and an image showing that a soft robotic arm based on honeycomb pneumatic networks can open a drawer⁵⁸. Panel a adapted with permission from ref.²¹, Royal Society of Chemistry. Panel b reprinted from ref.¹⁷, Springer Nature Limited. Panel c adapted with permission from ref.³⁸, American Physical Society. Panel d reprinted from ref.⁴¹, Springer Nature Limited. Panels e and f adapted with permission from ref.²⁴, Wiley. Panel g reprinted with permission from ref.²⁵, Wiley. Panel h reprinted from ref.⁵², Springer Nature Limited. Panel i adapted from ref.⁵⁵, CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/). Panel j adapted from ref.⁵⁶, Springer Nature Limited. Panel k reprinted from ref.⁵⁸, copyright © 2021 by SAGE Publications; reprinted by permission of SAGE Publications.

To elicit even larger programmable deformation, architected materials can be designed with thin sheets or shells that energetically favour out-of-plane bending or buckling. When the constitutive building blocks are made sufficiently thin, the architected materials they comprise can withstand strains in excess of 100%³⁷ and reversibly morph into complex 3D geometries without fracturing^30,31. Inspired by kirigami, the Japanese art of paper cutting, mechanical metamaterials can be created by simply introducing an array of hierarchical cuts into a thin sheet³⁸ (Fig. 1c). They can be inversely designed to conform to prescribed target shapes in two and three dimensions³⁹. Local out-of-plane buckling facilitates different deformation patterns at programmed levels of strains, as characterized by two distinct stress plateaux in the stress–strain data.²⁹ The unique simplicity in fabrication of kirigami patterns has rendered them easy to adopt in creating stretchable, conductive nanocomposites³⁷; friction-enhancing shoe grips⁴⁰; dynamic terahertz polarization modulators⁴¹ (Fig. 1d); and strain-tunable diffraction gratings⁴². Another way to use thin materials components to prompt structural transformations is by microfabricating patterned thin films on a pre-stretched elastomeric substrate with discrete film-to-substrate adhesion points, and then releasing the substrate to shrink. This shrinking drives coordinated out-of-plane buckling, twisting and translational motion of the now free-standing film strips to form 3D structures such as helices, conical spirals and flowers^30,31. To push the thickness limit further, nanolattices created by wrapping nanometre-thick ceramic shells around sacrificial 3D templates have demonstrated extreme mechanical resilience to shell buckling and nanomaterial size effects, recovering nearly fully to their original shape after compression in excess of 50%, in contrast to the typical brittle behaviour of their ceramic constituents^6,43,44.

Reconfigurability

Mechanically responsive architected materials can morph into a particular shape and then maintain the reconfigured geometry even after the stimulus is removed. A simple reconfigurable form consists of multiple levels of rigid polygons connected by narrow, deformable hinges^45–47. Such patterns can be transformed into desired geometries through synchronized rotation of the rigid units around the hinges; the reconfigured patterns are essentially held together by friction, which renders them susceptible to perturbation. The reconfigurability can be made more robust by incorporating snap-through instabilities into elastic beams that comprise the material’s unit cells, whose trapped elastic energy states preserve the deformed geometry²⁴ (Fig. 1e). Translated arrays of such bistable unit cells, whose geometries vary between two stable ‘on’ and ‘off’ states, produce an elastically multi-stable structure, which can exhibit layer-by-layer collapse upon uniaxial compression and retains its shape at discrete compressed levels after unloading²⁴ (Fig. 1f). Rotational bi-stability — the type of instability in a structure that leads to rotation rather than collapse — has been demonstrated in architected materials built from symmetrically interconnected triangular plates with soft hinges at each vertex. When this material is stretched along a particular direction, the triangular plates rotate collectively, causing auxetic expansion in the direction perpendicular to loading, and remain stable upon unloading^48,49. So-called ‘magnetoelastic metamaterials’ instead achieve reconfigurability through permanent magnets at interfacing hinges; upon compression, coordinated hinge bending draws pairs of neighbouring magnets together until magnetic forces bring them into contact, setting a stable reconfiguration of the lattice structure⁵⁰.

Although individual examples of reconfigurable structures are being routinely reported, more general design approaches and structure-searching algorithms are needed to eventually solve the inverse problem of encoding the desired reconfiguration in tailor-made architectures. For example, modular systems combine versatile building blocks — such as compliant rolling-contact joints⁵¹ or bi-stable triangular hinges²⁵ (Fig. 1g) — into networks that prescribe multiple degrees of freedom in 2D and 3D structural transformation. Numerical analysis of space-filling tessellations of polyhedra can search through a large design space to predict a wide range of origami-inspired reconfigurable prismatic architectures⁵² (Fig. 1h), which could function as switchable and tunable acoustic waveguides⁵³.

Pressurization is an alternative way to induce and to maintain structural transformations in architected materials. In many cases, it can be activated remotely using tubes with controlled gas pressure. The Buckliball⁵⁴ is a class of elastomeric, perforated spherical shells containing symmetrically patterned circular voids covered by thin membranes. Reducing the pressure inside these shapes causes the ligaments surrounding the voids to buckle cooperatively, leading to a reduction of the total shell volume by up to 54%. More sophisticated designs utilize air pockets at specific hinges (Fig. 1i), surrounding the exterior of the structure (Fig. 1j), or as integrated components throughout the entire structure (Fig. 1k). For example, small air pockets placed at the hinges of origami-inspired metamaterials can remotely actuate geometric transformations across multiple configurations⁵⁵ (Fig. 1i). When an enclosing envelope applies external pressure to architected chainmail fabrics composed of interlocking octahedral units, the originally soft fabrics undergo a jamming transition to gain up to 25 times the bending stiffness and lock in the pre-pressurization geometry, which can be erased and reconfigured upon relaxation of the applied pressure⁵⁶ (Fig. 1j). In a different example of exterior pressurization, kirigami sheets are wrapped around the inside of an elastomeric balloon. Upon inflation, the pre-cut kirigami pattern can induce bending, twisting or shape morphing of the balloon⁵⁷. Pressurization-controlled actuation of architected materials finds functional applications in soft robotic arms made of honeycomb pneumatic networks that elongate and bend as the embedded air pockets are inflated and deflated⁵⁸ (Fig. 1k). Using multi-level control algorithms based on reinforcement learning, such robotic arms have the ability to perform daily interaction tasks such as opening drawers and unscrewing bottle caps⁵⁸.

Thermally activated transformation

Thermal expansion

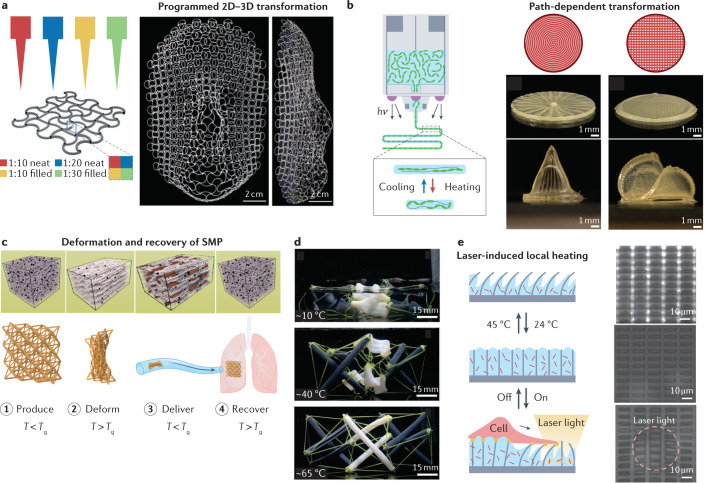
Heat transfer is one of the most common interactions between a material and its surrounding environment. Bimetallic strips with deliberately distinct thermal expansion coefficients have long been used to convert temperature changes into mechanical displacement in thermometers and circuit breakers. Architected materials can also be rationally designed with compositional variations to induce programmed and anisotropic structural changes through thermal expansion. For example, bi-material 3D lattices have been demonstrated⁵⁹ and systematically designed⁶⁰ to exhibit tunable, negative or directional thermal expansion. These properties are attained by constructing individual beams of the lattice structure from materials with different coefficients of thermal expansion, such that an increase in temperature triggers parts of the structure to rotate or bend internally, rather than expanding at the lattice level. A multi-material 3D-printing method⁶¹ has enabled the fabrication of multiplexed bilayer cellular patterns composed of four materials with different elastic moduli and thermal expansion coefficients, providing access to an even wider range of 3D shape changes. Using this method, a planar lattice was encoded to morph into a 3D human face in response to a temperature change of 250 °C (ref.⁶¹) (Fig. 2a).

Fig. 2. Architected materials that can undergo temperature-induced shape changes.

a | Programmable shape morphing of multiplexed bilayer lattices that are 3D-printed by direct ink writing of four different ink formulations with different elastic moduli and thermal expansion coefficients⁶¹. b | Printing direction encodes liquid crystalline domain alignment in 3D-printed liquid crystal elastomer (LCE) structures⁶² so that two similarly shaped disks can morph into different 3D structures upon heating⁶³. c | Shape programming and recovery of a 3D-printed shape memory polymer (SMP) lattice with illustration of the polymer network microstructures at different stages¹¹. The as-fabricated SMP has randomly distributed chain segments connected by a network of crosslinked netpoints (shown as block dots) (stage 1). When heated above its glass transition temperature (T_g), the SMP reaches a rubbery state and can be deformed easily to a programmed shape that is often smaller than its original shape (stage 2). After cooling under stress to a temperature below T_g, local domains of chain segments crystallize (shown as brown packets) so that the temporary shape is maintained upon removal of applied force. In this state, the deformed SMP can be delivered to an enclosed region with a small entrance for deployment (stage 3). At the desired location with T > T_g, the SMP will recover its original shape, fulfilling its designed functionality (stage 4). d | Two-step self-assembly of a tensegrity structure composed of shape memory polymer struts with two shape recovery temperatures⁶⁸. e | Localized photothermal heating and structural transformation of a hybrid architected material system with polymeric microstructures and light-absorbing gold nanorods embedded in a thermally responsive hydrogel matrix⁸¹. This allows for micro-manipulation of individual living cells that are grown on top of the architected system. Panel a adapted with permission from ref.⁶¹, National Academy of Sciences. Panel b adapted with permission from ref.⁶³, Wiley. Panel c adapted with permission from ref.¹¹, Royal Society of Chemistry, and adapted from ref.⁷², Springer Nature Limited. Panel d adapted from ref.⁶⁸, CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/). Panel e adapted from ref.⁸¹, CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).

Thermally activated phase changes

An inevitable drawback of thermal-expansion-driven reconfigurations is that the material deforms by a limited amount, typically no more than a few per cent within a practical temperature range. As an alternative, materials that change phase with temperature can produce large deformations or property changes with modest thermal stimuli. Liquid crystal elastomers (LCE), which are composed of crosslinked polymer networks with aligned liquid crystalline domains along specific directions at room temperature, are one example of such phase-change materials. When the temperature is raised beyond the nematic-to-isotropic transition temperature (T_NI), LCEs can contract by up to 40% in the direction of alignment with a high degree of reversibility. During 3D printing of LCEs by a direct ink writing process, controlling the printing direction in combination with ultraviolet crosslinking of polymer near the extrusion nozzle can define the nematic phase alignment⁶² (Fig. 2b); optimizing printing speed and extrusion temperature can further program the degree of nematic order⁶³. Careful design and optimization of the printing parameters allows for prescribing reversible and substantial structural transformation of complex architectures in response to temperature changes⁶³. For example, a 3D-printed LCE disk can morph into either a cone or a saddle shape, depending on the printing path⁶³ (Fig. 2b). Multi-material printing of LCE ink formulations with tunable T_NI (ref.⁶⁴) enable sequential actuation in untethered robots with temperature-controlled shape morphing and propulsion¹⁹. Permanent locking of either the entire structure or some sections of the transformed geometry has also been demonstrated by designing crosslinking chemistry that is also sensitive to post-printing ultraviolet exposure⁶⁵. Whereas direct ink writing can prescribe only 2D nematic orientation profiles, which are particularly suitable for 2D-to-3D transformations, two-photon lithography has achieved voxel-by-voxel encoding of nematic alignment in 3D vector fields, enabling higher degrees of freedom in 3D-to-3D transformations⁶⁶.

Shape memory effect

Shape memory polymers (SMP) are another class of thermally activated phase-change materials that enable structural transformation (Fig. 2c). SMPs are polymer networks composed of flexible chain segments subtended across a network of crosslinked netpoints, which define their permanent shape. When an SMP is heated to a temperature above its glass transition temperature (T_g), the polymer network becomes rubbery and can be mechanically deformed into a temporary, often more compact, shape. After cooling under stress to a temperature below T_g, local domains of chain segments crystallize or vitrify, so that the temporary shape is maintained upon removal of applied force. The so-called shape memory effect manifests itself when the temporary shape is heated back to above T_g, which releases the phase-transformed domains and returns the SMP to its original permanent shape.

3D printing makes it possible to define complex permanent shapes and architectures of SMPs with dimensions between approximately 10 μm and 10 cm, which can be mechanically programmed into any temporary state and eventually recover its original form upon heating^11,67–69. The structure-level stiffness of SMP-based materials can be tuned by over two orders of magnitude, from 3.0 GPa at 30 °C (glassy) to 6.4 MPa at 90 °C (rubbery)¹¹. The flexibility and large deformability enabled by direct mechanical programming is particularly attractive for stents⁶⁷, modular structures⁶⁸ (Fig. 2d), and other deliver-and-deploy devices. For biomedical applications, biodegradable SMPs can be synthesized with a T_g close to body temperature^70,71. Although the shape memory effect in SMPs is typically one-way (recovering the permanent shape and erasing the temporary shape) reversible or two-way actuation is also possible⁷². Two types of control unit must be designed into the SMP, such as chain segments with dissimilar crystallization temperatures⁷³ and polymer networks with distinct thermo- or photo-reversible bonds⁷⁴. Such SMPs have exhibited reversible structural transformation in a soft gripper⁷³ and a folded crane with flapping wings⁷⁴ in response to cyclic temperature changes.

Localized heating

When the ambient temperature must remain stable, localized heating mechanisms such as Joule heating or photothermal heating can be adopted to induce shape changes in architected materials. Conductive fillers can be uniformly dispersed in SMPs^75,76 and LCEs⁷⁷ to reduce electrical resistivity for efficient Joule heating. Metal wires embedded in a thermally responsive host material enable Joule heating of the overall structure, as well as of the specific sections to actuate bending of soft grippers or walking motion in robots⁷⁸. One interesting and relatively unexplored direction is to use the architecture itself to define specific heating and strain profiles. For example, conductive components can be overlaid onto an otherwise passive architected network: applying a voltage at discrete points in the network induces electrical current to flow along an architecture-defined trajectory; complex strain profiles arise from local Joule heating and concurrent thermomechanical responses⁷⁹. Laser irradiation of thermo-responsive architected materials can also produce site-specific structural changes through photothermal effects⁸⁰. One such system — of polymeric microstructures encased in a thermo-responsive hydrogel matrix loaded with light-absorbing Au nanorods⁸¹ — can support biological cell adhesion and growth on its surface, and deform locally in response to heating by a near-infrared laser (Fig. 2e). These properties allow for micro-manipulation of individual living cells by up to 45% strain at 0.1 Hz (ref.⁸¹) with no obvious degradation in the cells’ vitality.

Chemomechanical transformation

Liquid-uptake-induced swelling

Architected materials can undergo changes in their chemical composition to transform and adapt to the environment. Soft materials, such as polymers and hydrogels, can swell through liquid uptake when placed in water or solvents. Photoresists patterned with regions of variable crosslinking density can swell inhomogeneously in a solvent and self-assemble into a variety of 3D structures⁸². Bi-material structures with different stiffnesses and swelling capabilities can also prescribe shape morphing^83,84, symmetry-breaking transformations⁸⁵ and negative effective swelling⁸⁶. Cellulose hydrogel composites fabricated through a biomimetic 3D-printing method can transform in shape when placed in water⁸⁷; the printing process aligns cellulose fibrils such that they exhibit localized anisotropic swelling behaviour. 3D geometries resembling various flowers can be encoded in printed bilayer lattice structures using predictive design, with the programmed structural transformation activated upon immersion in water (Fig. 3a). One limitation of swelling-induced responsiveness is that the transformed geometries generally revert to their original form upon drying or de-solvation. To overcome this limitation, capillary forces arising during liquid evaporation can be used to apply pressure and thus retain certain structures upon drying. For example, base-attached triangular cellular microstructures composed of a liquid crystalline polymer soften and swell upon contact with solvents like acetone. When the solvent evaporates, capillary forces at the localized air–liquid interfaces within the liquid-filled architecture ‘zip’ the edges of the softened lattice into a hexagonal structure, which subsequently re-stiffens and remains kinetically trapped in a fully dried state⁸⁸ (Fig. 3b).

Fig. 3. Architected materials that undergo chemomechanical transformations.

a | Cellulose fibrils aligned by programmed printing direction within 3D-printed hydrogel composites that encode complex geometric transformations, such as morphing of an interlacing bilayer pattern into a 3D flower, activated by immersion in water⁸⁷. b | A base-attached triangular cellular microstructure softens and swells upon contact with acetone, converts to a hexagonal structure by capillary forces when the solvent evaporates, and re-stiffens in the persistently transformed structure after complete drying⁸⁸. c | A chemo-responsive bi-material hydrogel micro-umbrella that can reversibly fold and unfold in response to pH changes⁸³. d | Illustration and a representative temperature profile of a homeostatic chemomechanical feedback system that maintains a stable environment against external perturbation¹³. The hybrid system contains an array of microscopic fins embedded in a responsive hydrogel and a phase-separated liquid bilayer. When either the pH or the temperature changes, the hydrogel swells and forces the micro-fins to straighten, inserting their chemically active tops into the overlying liquid and triggering a pre-designed chemical reaction to restore the original pH or temperature. e | Illustration of representative actuation mechanisms of electrochemically active architected materials¹⁰⁰. When the active–inactive bilayer electrode is constrained at one end, electrochemically induced volume changes of the active material causes bending of the active electrode (mechanism 1). When the active–inactive bilayer electrode is constrained at both ends, electrochemically induced volume expansion of the active material causes buckling of the active electrode (mechanism 2). Both the positive and the negative electrode can be integrated into the active structure while being separated by an inactive structural component. The electrochemical reaction will cause one electrode to expand and the other to contract, leading to a bending motion of the active structure (mechanism 3). Ion transport of the electrochemical reaction can be conducted by a solid or gel electrolyte sandwiched by the two active electrodes. This enables freestanding, electrochemically actuated structures that do not have to be immersed in a liquid electrolyte (mechanism 4). f | Microrobots with metallic current collectors, conjugated polymer actuators, and electrochemically inactive structural components can grab and lift a 100-µm glass bead via electrochemical control¹⁰². g | Electrochemically reconfigurable microlattices that consist of a 3D polymer scaffold conformally coated with thin layers of metal (current collector) and silicon (active material). The beams in these architected electrodes undergo cooperative buckling in response to electrochemically induced silicon–lithium alloying reactions¹⁸. Panel a adapted from ref.⁸⁷, Springer Nature Limited. Panel b adapted from ref.⁸⁸, Springer Nature Limited. Panel c adapted from ref.⁸³, CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/). Panel d adapted from ref.¹³, Springer Nature Limited. Panel e adapted with permission from ref.¹⁰⁰, Wiley. Panel f reprinted with permission from ref.¹⁰², AAAS. Panel g adapted from ref.¹⁸, Springer Nature Limited.

Physicochemical responses in hydrogels

Hydrogels immersed in an aqueous environment can change volume by swelling and contracting in response to physical or chemical stimuli, such as the temperature or concentration of specific ions and molecules. This unique property, combined with their fabrication flexibility and low toxicity, makes responsive hydrogels particularly attractive for functioning in a biological environment^87,89–92. Hydrogels’ solubility in water is sensitive to temperature^93,94 and ionic strength^91,95, and as solubility is reduced, the hydrogel expels water, shrinking and structurally transforming as prescribed by the architectural design^{83,91,93–95}. Hydrogels can also deform in response to a change in pH, which causes pendant functional groups to ionize and the polymer chains to electrostatically repel each other. pH-sensitive hydrogels enable reversibly folding-and-unfolding micro-umbrellas⁸³ (Fig. 3c), microfluidics with autonomous flow control⁹⁶ and self-releasing drug delivery capsules¹⁵. Leveraging the physicochemical responsiveness of hydrogels, a homeostatic chemomechanical feedback system can be built to maintain a stable environment against external perturbation¹³. The hybrid system contains an array of microscopic fins embedded in a responsive hydrogel and a phase-separated liquid bilayer. When either the pH or the temperature changes, the hydrogel swells and forces the micro-fins to straighten, inserting their chemically active tops into the overlying liquid and triggering a pre-designed chemical reaction to restore the original pH or temperature (Fig. 3d). A similar chemomechanical shuttling system in a bi-phasic environment can also be used for catch-and-release biomolecule sorting⁹⁷. The composition of responsive hydrogels is not limited to a few basic formulations; they are highly versatile and adaptable to biological environments. For example, supramolecular hydrogels containing specifically engineered host–guest complexes exhibit large volumetric changes in the presence of targeted guest molecules like adamantane under physiological conditions⁹⁰. They are useful for mechanical stimulation of single cells triggered by chemical cues⁹⁰. Chemo-responsive hydrogels may also find application as more lifelike engineered tissues, as with DNA-encoded, cell-loaded hydrogel sheets that can morph, through cell contractility, into origami-inspired 3D patterns that emulate the complex surface texture of biological organs⁹⁸.

Electrochemical reactions

Electrochemical reactions represent a unique route to reversibly and continuously modulate structural transformation of architected materials (Fig. 3e). Electrochemistry allows the extent of a chemical reaction to be precisely controlled through the applied current’s magnitude and duration; turning the current off locks in the transformed geometry and properties even if the surrounding environment continues to change. The voltage required to activate electrochemically active materials is typically low, of the order of a few volts or less; the accumulated charge that is transferred during the redox reaction determines the extent of the chemical changes and thus the overall degree of deformation. Conjugated polymers such as polypyrrole and polyaniline are among the earliest electrochemically deformable materials. In these intrinsically conductive polymers, electrochemical doping and undoping of mobile ions from the electrolyte triggers reorganization of the polymer network and concurrent volume changes^99,100. Microfabricated devices that contain metallic current collectors, conjugated polymer actuators and electrochemically inactive structural components can function as microrobots that selectively and reversibly fold and unfold multiple arms, as well as manipulate small objects^101,102 (Fig. 3f).

Redox couples that have been investigated in conventional electrochemical systems, such as batteries, provide a material inventory for this type of programmed structural transformation. For example, in response to an electrochemically driven silicon–lithium alloying reaction, a polymer microlattice coated with thin layers of nickel and silicon converts from tetragonal into mutually orthogonal sinusoidal patterns through cooperative beam buckling¹⁸ (Fig. 3g). Controlling the mechanical constraints and the relative ratio between the polymer scaffold and the active material can achieve different reconfigurational degrees of freedom: rotation, bending, out-of-plane buckling and expansion¹⁸. Numerous electrochemical reactions are associated with reversible volumetric changes and can drive actuation in reconfigurable architected materials such as molybdenum disulfide (MoS₂) nanosheets¹⁰³, black phosphorus–carbon nanotube composites¹⁰⁴ and graphdiyne¹⁰⁵.

Key to electrochemically induced functionality is the incorporation of an electrolyte, a medium that facilitates ion transfer and prohibits electron transfer. Electrochemically active architected materials can be fully immersed in an organic¹⁸, ionic liquid¹⁰⁶, or aqueous electrolyte^101,102, including bodily fluids for biomedical applications¹⁰⁷; alternatively, they can function in a dry state with a solid or gel electrolyte component integrated into the architecture^104,105,108 (Fig. 3e). Because the surrounding electrolyte can influence the onset and the extent of an electrochemical reaction, electrochemically active material systems can take on sensing capabilities as measured by structural changes¹⁰⁹ and enable conditional chemomechanical responses depending on the chemical environment.

Electromagnetic interactions

Magnetic fields

Architected materials can also respond to electromagnetic fields, offering the benefits of remote control and short response time. The materials can be made magnetically responsive by infilling or embedding them with magnetic fluids¹² or nanoparticles¹¹⁰, enabling tuning of effective stiffness by an applied magnetic field¹² or inductive heating of SMPs by an alternating magnetic field¹¹⁰. Integrating electromagnets into architected materials also allows for electrical control of their magnetically induced responsiveness¹¹¹.

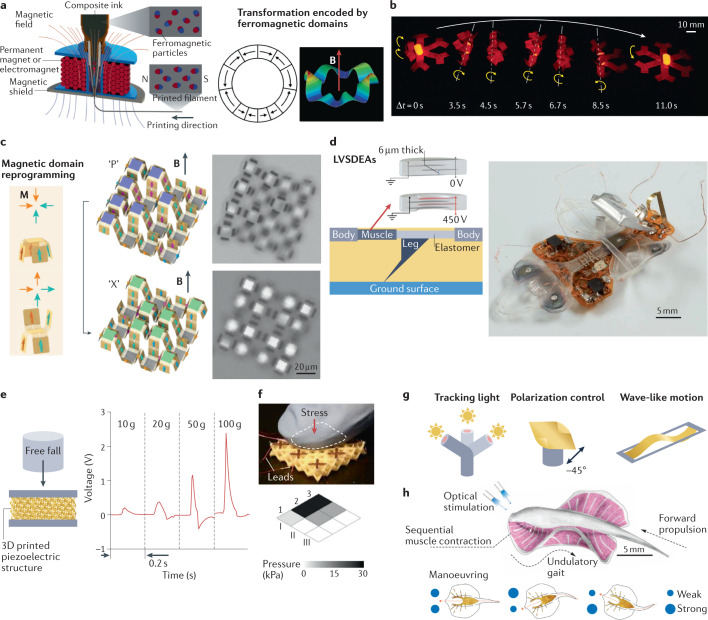
To program complex structural transformations in response to magnetic fields, ferromagnetic domains can be spatially distributed in a soft magnetic composite through direct ink writing. Positioning a permanent magnet or an electromagnet at the extrusion nozzle aligns the ferromagnetic particles in the ink formulation with the printing direction. Under applied magnetic fields, the 3D-printed architectures change shape almost instantaneously (<1 s)¹⁴ (Fig. 4a). Figure 4b showcases a hexapedal structure that catches, moves and releases small objects under the control of a magnetic field over the course of 11 s (ref.¹⁴). Magnetically responsive metamaterials have also been demonstrated to transform asymmetrically, with widely tunable stiffness and acoustic bandgaps, in response to positive and negative magnetic fields¹¹². Whereas the magnetization prescribed by direct ink writing is confined to the lateral plane, a projection-based printing system that uses a permanent magnet with multi-axis rotational control can program 3D magnetization profiles that allow higher-order bending and torsion¹¹³.

Fig. 4. Architected materials that interact with electromagnetic fields.

a | 3D-printed elastomers with spatially varied ferromagnetic domains display complex shape changes under applied magnetic fields¹⁴. b | A magnetically controlled hexapedal structure that can catch, move and release small objects¹⁴. c | A shape-morphing micromachine that consists of single-domain nanomagnet arrays can be programmed to display different letters by following a specific sequence of switching magnetic fields¹¹⁶. d | An autonomous untethered fast soft robotic insect driven by low-voltage stacked dielectric elastomer actuators (LVSDEAs) with integrated optical sensors, a microcontroller and a battery¹²⁵. e | 3D-printed piezoelectric structures generate different voltage outputs in response to free-fall impacts of different weights¹³². f | Piezoelectric architectures with spatially distributed readout electrodes can function as pressure sensors for tactile mapping¹³³. g | Examples of unique mechanical responses in photo-sensitive materials. Sunflower-mimicking phototropic light tracking through photothermal effects¹³⁴ (left). Directed bending of an azobenzene-containing liquid-crystal polymer film by linearly polarized light with different angles of polarization¹³⁹ (middle). A photoactive polymer walker that exhibits continuous, directional, macroscopic mechanical wave motion under constant light illumination through a feedback loop driven by self-shadowing¹⁴² (right). h | A tissue-engineered soft-robotic ray can swim and follow light cues through an obstacle course; it is fabricated by patterning dissociated rat cardiomyocytes onto an elastomeric body enclosing a gold skeleton²⁰. Panel a adapted from ref.¹⁴, Springer Nature Limited. Panel b reprinted from ref.¹⁴, Springer Nature Limited. Panel c adapted from ref.¹¹⁶, Springer Nature Limited. Panel d adapted with permission from ref.¹²⁵, AAAS. Panel e adapted from ref.¹³², Springer Nature Limited. Panel f reprinted from ref.¹³³, Springer Nature Limited. Panel g, left, adapted from ref.¹³⁴, Springer Nature Limited. Panel g, middle, adapted from ref.¹³⁹, Springer Nature Limited. Panel g, right, adapted from ref.¹⁴², Springer Nature Limited. Panel h adapted with permission from ref.²⁰, AAAS.

To operate at a practical magnetic field, these magnetically deformable materials are composed mostly of soft elastomers, with stiffnesses of the order of 100 kPa (refs^14,112,113). In one promising stiffening mechanism, ferromagnetic domains are encoded inside 3D-printed SMP-based composites, which deform in response to an applied magnetic field only at elevated temperatures when the SMP is in its rubbery state. Cooling the composite to below the T_g under applied magnetic field locks in the stiff, reconfigured structure, which persists after removing the field^112,114. Embedding a second type of low-coercivity magnetic particle into a magnetic SMP composite allows for inductive heating under a high-frequency magnetic field, which enables magnetically controlled recovery of the original structure upon heating¹¹⁵. Further programming of the magnetic response after fabrication can be accomplished in spatially organized single-domain nanomagnet arrays with different switching field thresholds¹¹⁶. Applying a specific sequence of switching magnetic fields reprograms these shape-morphing arrays to display different letters (Fig. 4c).

Electric fields

Applied electric fields can also trigger recombination of structure, motion and property in architected materials. For example, when ionic electroactive polymers consisting of polyelectrolyte hydrogels with ionized groups (such as carboxylates) are immersed in a liquid electrolyte (such as NaCl aqueous solution), a large amount of mobile counterions (Na⁺) are generated inside the hydrogels¹¹⁷. When an electric field is applied, the mobile ions move directionally inside the hydrogels, setting up an osmotic pressure difference that causes the hydrogel to bend towards the direction of ion motion. The degree of deformation depends on the structures’ aspect ratios (such as the length-to-width ratio of a beam) and on the magnitude of the applied field, and the response time is usually of the order of a few minutes^117–119. Lithography¹¹⁸, moulding¹¹⁷ or 3D printing¹¹⁹ can create ionic hydrogel structures that can move, grip and transport small objects under a modulating electric field.

Another class of electric-field-responsive materials, dielectric elastomer films, are typically sandwiched between compliant electrode materials (such as carbon-impregnated grease) and electrostatically compressed under applied voltage, inducing a lateral expansion of up to over 100% strain¹²⁰. This voltage-based actuation mechanism with integrated electrodes is easier to connect to an electrical control circuit and can achieve fast response times of <1 ms, but it requires a high operation voltage in the range of hundreds or thousands of volts^120,121. Such an assembly of dielectric elastomer films and electrodes can be patterned in 2D and positioned at specific locations within an otherwise non-electroactive 2D- or 3D-structured frame to enable soft grippers^122–124, untethered walking¹²⁵ (Fig. 4d) or swimming^126,127 robots, and haptic display arrays¹²⁸. Replacing the dielectric elastomer with dielectric liquids enclosed in a flexible structure can amplify the electrostatically triggered actuation by hydraulic forces, which provides a pathway to robotic arms with strain-sensing capabilities^129,130.

Piezoelectric materials are also voltage-responsive, serving as the foundation of several active and reconfigurable acoustic metamaterials¹³¹. Even though piezoelectric materials have an attainable strain of usually <1%, their crystallographically driven conversion between strain and voltage is active in both directions, meaning that an applied strain will cause a voltage response, which provides an opportunity to accurately detect impacts and measure deformation with an electrical output. Additive manufacturing of piezoelectric nanocomposites based on lead zirconate titanate has produced metamaterials with piezoelectric coefficients fully defined by their 3D geometry, which makes them useful for simultaneous impact absorption and monitoring¹³² (Fig. 4e). By selectively metallizing specific locations within the device to serve as readout electrodes, such piezoelectric architectures can function as prosthetic pressure sensors with tailored geometries and mechanical properties for tactile mapping¹³³ (Fig. 4f).

Light

Architected materials can also be directly stimulated, reconfigured and maneuvered by light through distinct actuation mechanisms (Fig. 4g) that often mimic biological organisms like sunflowers¹³⁴ and ray fish²⁰. Photoabsorbers embedded in thermally responsive precursors, such as SMPs, liquid-crystal polymers and hydrogels, enable light-induced shape recovery¹³⁵, tensegrity-based rolling robots¹³⁶ and phototropic light tracking¹³⁴ through photothermal effects. Light can also interact with materials at the molecular level directly: an important class of photo-responsive molecules is azobenzene and its derivatives, which isomerize when exposed to light of appropriate wavelengths. In azobenzene-containing liquid crystal networks, for example, light-induced trans-to-cis isomerization of azobenzene units triggers polarization-dependent movement of the liquid crystalline domains and collapses the alignment order. The materials then reversibly contract¹³⁷, bend^138–140, coil^138,141 or propagate mechanical waves¹⁴² upon appropriate illumination with a response time as low as 100 ms (ref.¹⁴⁰), enabling light-driven walkers^142,143 and grippers¹⁴⁴. Shape memory effects can be induced by light, rather than temperature, by photocleaving and photofixing of grafted or interpenetrating polymer networks with both permanent and photo-responsive crosslinks¹⁴⁵, a phenomenon that serves as the foundation of self-folding photo-origami¹⁴⁶.

Photo-responsive architected materials often draw inspiration from biological systems. For example, a soft-robotic ray can be assembled from rat heart muscle cells, cardiomyocytes, that have been genetically engineered to respond to light and patterned onto an elastomeric body enclosing a microfabricated gold skeleton²⁰. The artificial ray swims in water by light-induced sequential muscle activation, mimicking the motion of a ray fish, and maneuvers through an obstacle course guided by light cues²⁰ (Fig. 4h). At the molecular level, the integration of supramolecular structures and covalent polymers contributes to the responsive behaviour of biological membranes, muscles and tendons¹⁴⁷. By emulating these living systems, hydrogels that contain both supramolecular and covalent interactions are able to expel water in response to visible light, and compose structures that can deform, crawl and rotate through light modulation¹⁴⁷.

Analogy between classical and architected materials

Responsive architected materials bring about intriguing physics phenomena that are analogous to those governing classical materials, such as defect nucleation and propagation, phase transformation and topological properties. Understanding these principles at the fundamental level can inspire, improve, and simplify architectural design, as freeform computational optimization^148,149 becomes increasingly expensive for large, complex and multi-physics materials systems.

Defects and domains

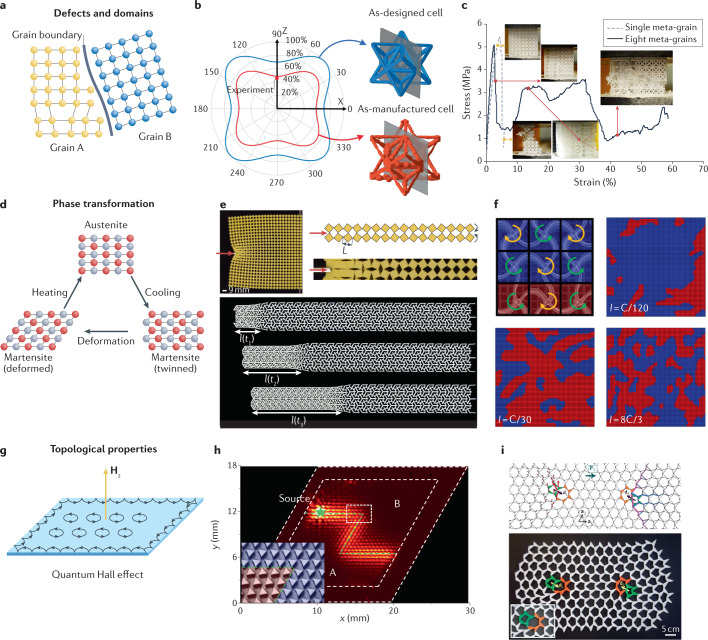
The mechanical properties of crystalline materials are largely dictated by imperfections such as point defects, dislocations and grain boundaries (Fig. 5a) through well established laws such as Taylor hardening¹⁵⁰ and Hall–Petch plasticity^1,2. Architected materials are also inherently imperfect because of limitations in the fabrication processes, such as scalloped surfaces from layer-by-layer printing, unwanted curvatures owing to residual stress during curing or coating, and non-uniform features as a result of unstable melt pools for selective laser melting, which generally leads to a reduction in measured material properties¹⁵¹ (Fig. 5b).

Fig. 5. Analogy between classical materials and architected materials.

a | Illustration of a domain boundary and a dislocation in a classical crystalline material. b | A polar plot that illustrates a reduction in the normalized Young’s modulus of an as-manufactured aluminium alloy octet lattice with fabrication defects (reconstructed by computed tomography) compared to that of an as-designed perfect lattice¹⁵³. c | Comparison of compressive stress–versus–strain responses of 3D-printed polymer face-centred-cubic lattices with one and eight meta-grains, showing that the architected domain boundaries can effectively deflect crack propagation¹⁵⁵. d | Illustration of crystallographic phase transformation between austenite, deformed martensite and twinned martensite phases of shape memory alloys driven by deformation and temperature changes. e | A gradual decay of rotation-based mechanisms with a structure-dependent characteristic length scale when a metamaterial consisting of square rubber plates of width L connected by slender hinges in a diamond pattern is locally compressed at an exterior hinge¹⁵⁶ (top). 1D propagation of the phase-transformation front from an expanded configuration to a collapsed one within bistable architected materials (the collapsed length l as a function of time t) can be described quantitatively as a propagating shock front¹⁵⁷ (bottom). f | The statistical distribution of differently sized, bistable deformation domains (shown in red and blue) in cooperatively buckled tetragonal microlattices can be controlled by the applied current during electrochemically induced reconfiguration¹⁸. Within each domain, all beams are deformed via mode-I buckling and all neighbouring vertical posts rotate in opposite directions (clockwise (yellow arrow), anticlockwise (green arrow)); across the domain boundary, the interfacing beams between two vertical posts rotating in the same direction are deformed via mode-II buckling with a higher elastic energy. I= 1 C represents a constant current under which the full electrochemical reaction will be completed in one hour. g | Illustration of the topologically protected electron edge states in a physical phenomenon called the quantum Hall effect. h | Topologically protected edge states for elastic wave propagation in a phononic crystal that consists of a hexagonal array of triangular Si pillars, which is analogous to the edge-state current in topological insulators¹⁶⁶. Brightness corresponds to the measurement intensity of the edge state. The green star represents the source of the elastic wave. The Z-shaped interface between phase A and phase B is marked by the green dotted line. The inset shows an enlarged image of the interface enclosed by the white dotted box. i | Topological defects in a deformed kagome lattice composed of stiff elements connected by free hinges allow for localized motion in the interior of an otherwise rigid, isostatic lattice¹⁷⁰. a₁ and a₂ are the primitive vectors of the deformed kagome lattice. d_L and d_R represent the equal and opposite dipole moments of the pair of dislocations that are topological defects. P_T is the topological polarization. Panel b reprinted from ref.¹⁵³, Springer Nature Limited. Panel c reprinted from ref.¹⁵⁵, Springer Nature Limited. Panel e, top, reprinted from ref.¹⁵⁶, Springer Nature Limited. Panel e, bottom, reprinted from ref.¹⁵⁷, CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/). Panel f adapted from ref.¹⁸, Springer Nature Limited. Panel h reprinted from ref.¹⁶⁶, Springer Nature Limited. Panel i reprinted from ref.¹⁷⁰, Springer Nature Limited.

Topology optimization is one way to produce structures that are robust against defects by accounting for geometric uncertainties. For example, a perturbation approach typically leads to architectures with redundant load paths that dramatically improve structural stiffness and stability^152–154. Damage tolerance of crystal-inspired lattice structures can also be improved by incorporating architectural features that mimic crystalline discontinuities — twinning, grain boundaries, precipitates and separate phases¹⁵⁵ — which induce hardening and toughening behaviours. This enhanced damage tolerance is seen in a mesoscale polymer lattice containing eight meta-grains with high-angle boundaries¹⁵⁵; compared to a singly oriented lattice, the polycrystal-like structure is able to stop and deflect crack propagation at grain boundaries, increasing the energy absorption of the material by about 5.7 times (Fig. 5c).

Phase transformation

To continue the analogy to crystalline materials, structural transformations of architected materials activated by mechanical or environmental stimuli can be viewed as phase transformations between different geometric and energetic states (Fig. 5d). Within an architected material’s interwoven geometric framework, the mechanical response of each individual building block (beams, walls, shells and unit cells) is constrained by those of its neighbours, such that local perturbations establish a characteristic correlation length scale that represents the affected distance¹⁵⁶ (Fig. 5e). When a 1D tessellation of multi-stable architected materials is deformed to a lower energy state at one end, coupled near-neighbour interactions drive the phase-transformation front forward, which can be quantitatively described as propagating shock fronts¹⁵⁷ (Fig. 5e) or transition waves¹⁵⁸. In 2D or 3D networks, the defect landscape influences the propagation of such phase transitions, and prescribed defects can be used to guide the evolving domain distribution^159,160. In an electrochemically reconfigurable network, the spontaneous bi-stable phase separation can be controlled by the magnitude of the applied current, which dictates the deformation rate¹⁸ (Fig. 5f), with higher rates forming smaller domains, a process analogous to rapid quenching of a molten crystalline solid. The stochastic distribution of the domain sizes can be analysed by statistical mechanics and is subject to the influence of random and prescribed defects as well as reaction temperature.

Topological properties

Topologically protected properties in the mechanical response of architected materials can be explored in the context of their electronic counterparts, such as the quantum Hall effect (Fig. 5g) and the quantum spin Hall effect in topological insulators. Mechanical metamaterials have been demonstrated to contain topologically protected edge states of the elastic and acoustic wave propagation, which can travel through the defects and sharp features without backscattering, analogously to the edge-state current in topological insulators^161–166 (Fig. 5h). Mechanical¹⁶⁷ or circuit^168,169 reconfiguration can reprogram the domain boundaries along which such topological edge states propagate. Topological defects placed at specific dislocations in an otherwise rigid structure also allow localized motion. When designed into a deformed kagome lattice, composed of stiff elements connected by free hinges with equal number of constraints and degrees of freedom everywhere, the defects permit motion only near the dislocation sites¹⁷⁰ (Fig. 5i). In another mechanical metamaterial analogous to a spin system with tunable ferromagnetic and antiferromagnetic interactions, topological defects can separate and steer deformations and stresses to distinct regions of the architected network in response to external actuation at specific sites¹⁷¹. Other topological properties explored in architected mechanical networks include static non-reciprocity¹⁷², topological negative refraction¹⁷³, nonlinear soliton conduction¹⁷⁴ and higher-order mechanical topological insulators^175,176.

Outlook: towards materials intelligence

Logic

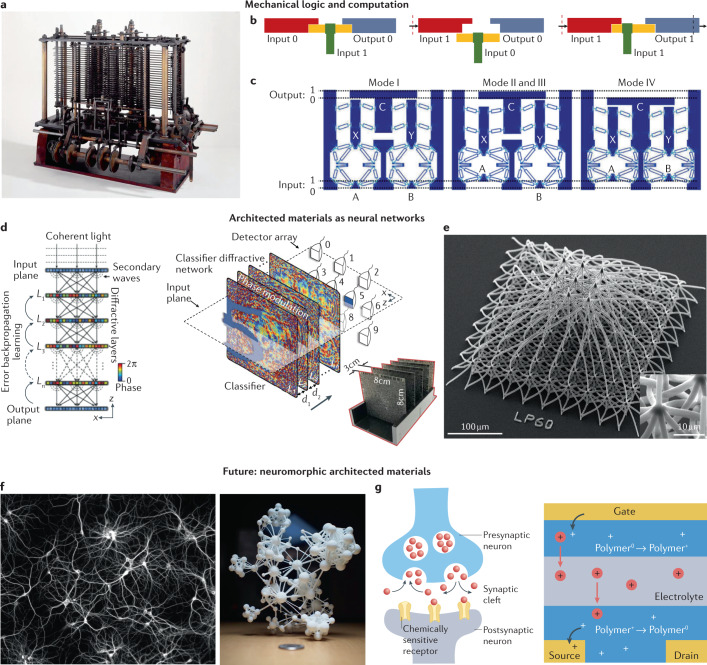
As architected materials become more sophisticated and autonomous, a natural question arises: can they exhibit any degree of materials intelligence through pre-programmed logic or by actively drawing inferences, tasks that are normally performed by computers and neural networks? The earliest programmable computer design is the Analytical Engine, a grand, intricate architecture of hinges, gears and other mechanisms envisioned by Charles Babbage and Ada Lovelace in the 1830s^177,178 (a trial model of a small section of Babbage’s Analytical Engine is shown in Fig. 6a). Though never completed, the Analytical Engine, which is designed to be powered by a steam engine, incorporated an arithmetical unit, integrated memory, punch card inputs (numbers, variables and operations), an output printer, and microprogramming capabilities such as conditional branching and loops. Its conceptual ingenuity was acknowledged by prominent computer pioneers Alan Turing¹⁷⁹ and Vannever Bush¹⁸⁰ roughly a hundred years later. This mechanical computer can perform logic operations owing to its conditional arm, which mechanically triggers different instructions depending on whether or not a control lever is inserted into its opening¹⁸¹ (Fig. 6b). Similar concepts of mechanical logic gates have been implemented in additively manufactured architectures that incorporate multi-stable mechanisms at centimetre and micrometre scales, yielding a variety of functionally complete logic gates that output specific displacement based on mechanical^182,183 (Fig. 6c) or chemical¹⁸⁴ inputs. Structural transformations in architected logic devices can also encode electrical¹⁸⁵ and pneumatic¹⁸⁶ outputs. In theory, a combination of such functionally complete mechanical logic gates could produce arbitrarily diverse digital logic circuits to execute pre-programmed tasks, as showcased in the simple demonstrations of an autonomous ‘flytrap’¹⁸⁴ and an leading-edge detector¹⁸⁶. Their large-scale integration into a useful and robust system remains a challenge, however, in practice.

Fig. 6. Responsive architected materials with emergent materials intelligence.

a | A trial model of a section of the Analytical Engine, a proposed mechanical general-purpose computer designed by Charles Babbage and Ada Lovelace, displayed at the Science Museum, London. b | Illustration of a conditional arm that functions as an AND gate, which enables the Analytical Engine’s microprogramming capabilities such as conditional branching and loops¹⁸¹. c | Design of a 3D-printed mechanical logic gate driven by flexural mechanisms, with mechanical deformation as input¹⁸². This is a NAND gate, which is functionally complete, meaning that an entire processor can be created using NAND gates alone. d | Illustration and an image of an all-optical diffractive neural network consisting of multiple diffractive layers that can be trained in computer simulations and then 3D-printed to classify handwritten digits, using projected letter images as input¹⁹³. e | 3D waveguide interconnects for photonic neural networks that demonstrate a scaling advantage compared to 2D networks in a crossbar configuration¹⁹⁹. The image shown is of nine parallel 1-to-81 couplers featuring two bifurcation layers. Inset: zoomed-in image of a splitter node. f | Comparison between the complex 3D architectures of biological neural networks and architected materials networks. A fluorescence image of a dissociated culture of rat hippocampal neurons, showing a complex biological neural network¹⁹⁷ (left). A 3D-printed model representing a complex network structure¹⁹⁶ (right). g | Comparison between biological synapses and artificial synapses updating their synaptic weights. Left: illustration of how biological neurons modulate synaptic weight by releasing neurotransmitters²⁰⁵. Right: illustration of a non-volatile artificial synapse in which conductance between source and drain can be modulated by electrochemical doping of an organic mixed ionic/electronic conductor between them²⁰⁶. Panel a from Babbage’s Analytical Engine, CC BY-NC-SA 4.0. Panel c reprinted from ref.¹⁸², CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/). Panel d reprinted with permission from ref.¹⁹³, AAAS. Panel e adapted with permission from ref.¹⁹⁹, Optica Publishing Group. Panel f, left, reprinted with permission from ref.¹⁹⁷, © The Optical Society. Panel f, right, reprinted from ref.¹⁹⁶, Springer Nature Limited. Panel g, left, adapted from ref.²⁰⁵, Springer Nature Limited. Panel g, right, reprinted from ref.²⁰⁶, Springer Nature Limited.

Training

A potentially transformative approach to designing architected materials is through machine learning from a large training data set without explicit, rule-based programming, especially using a class of machine-learning algorithms called deep neural networks. These algorithms, inspired by biological neural networks in animal brains, use multiple data-processing layers that consist of hierarchically interconnected nodes to represent highly nonlinear relations. Machine learning has enabled the efficient design of architected materials with superior mechanical responses, including programmable 2D¹⁸⁷ and 3D¹⁸⁸ elastic stiffness tensors, composites with high toughness and strength^189,190 and lattice-based actuators with orthogonal input–output movement¹⁹¹. Generative adversarial networks, a class of deep neural network originating from the computer vision community, can learn geometric features from a set of training images and then generate images based on these features. Generative adversarial networks have been particularly successful at designing freeform optical metasurfaces because they can be trained by a set of high-efficiency device images and generate near-optimal, topologically complex yet manufacturable designs that are not constrained to specific geometric frameworks¹⁹². One common feature of all the above-mentioned examples of machine-learning-based architected material design is that the training data can be generated by accurate, established simulation frameworks, such as finite-element-based mechanical and electromagnetic solvers, without the need for extensive experimental testing. The machine-learning-predicted architectures can either be validated experimentally, or be fed back into the simulation framework to generate more training data for the neural network in an iterative process that continues to improve the architecture design.

Inference

Intriguingly, machine learning can also design architected materials that physically represent the computationally trained neural networks, capable of performing real-time inference tasks as sound or light propagates through its layered^193,194 or volumetrically multiplexed^194,195 construct. A conspicuous example is an all-optical diffractive neural network¹⁹³ that consists of multiple diffractive layers. The layers are first trained by electromagnetic simulations and then physically 3D-printed to implement specific pre-assigned computations based on optical inputs, such as handwritten digit classification (Fig. 6d,e). Similarly, a spatially varied acoustic medium can directly perform vowel classification of a human voice¹⁹⁵. These efforts represent an exciting research frontier of artificial-intelligence-based inference implemented by architected physical kernels in real time, eliminating the need to first convert the input into digital signals and then process them in computers as in typical implementations of artificial neural networks.

Neuromorphism

Finally, we speculate whether architected materials could eventually evolve to be neuromorphic — that is, actively learn from past or current experience by emulating, to some degree, both the structure and the functionality of biological neural networks. Architected materials have two defining features that are conducive to neuromorphism: hierarchical connectivity¹⁹⁶ and weighted coupling of every nodal pair within the network, which correspond, respectively, to the architecture of biological neurons¹⁹⁷ (Fig. 6f) and the synaptic weights between neurons (Fig. 6g).

Photonic neural networks are a promising hardware implementation of artificial neural networks for neuromorphic computation, and may offer high processing speed and massive parallelization¹⁹⁸. To represent neural networks’ hierarchical topology with a large number of inputs and outputs, 3D photonic routing is crucial because the area of a 3D integrated system scales linearly with the number of inputs and outputs, whereas that of a 2D integrated system scales parabolically¹⁹⁹. Additively manufactured 3D-architected optical interconnects, including arrays of 1-to-81 splitters (Fig. 6e) and Boolean Haar filters, have been demonstrated for scalable integration of photonic neural networks with up to 225 inputs in a footprint area of 460 × 460 µm² (ref.¹⁹⁹).

A neuromorphic architecture must also be able to update and store synaptic weights among neurons. This could enable so-called in-memory computing, which is substantially more energy-efficient than traditional digital computers for implementing machine learning algorithms²⁰⁰ and has been demonstrated by processing systems modulated in a variety of ways. For example, in photonic neural networks, the synaptic weights can be modulated by programmable Mach–Zehnder interferometers with thermo-optic phase shifters²⁰¹. In electronic neuromorphic systems, the conduction level of memristors — a class of nonlinear electrical components whose resistance can be programmed (resistor function) by their voltage or current history and subsequently remains stored (memory function) — can represent synaptic weights. 2D crossbar arrays²⁰² or 3D architectures of staircase electrodes in row banks²⁰³ with memristor cross-points can implement highly efficient vector-matrix multiplication, a particularly computationally intensive task in deep learning algorithms. Beyond traditional memristors are electrochemical artificial synapses (Fig. 6g), whose conductance can be linearly adjusted to more than 500 distinct, non-volatile states by electrochemical doping of an organic mixed ionic-electronic conductor²⁰⁴. These electrochemical artificial synapses more faithfully mimic the neurotransmitter-mediated synaptic plasticity in biological systems, and they can be directly integrated with biological cells that produce neurotransmitters, such as dopamine, for potential applications in prosthetic sensors and brain–machine interfaces^205,206.

The capabilities described here, of building complex networks and updating the weights between nodal pairs, provide a wealth of opportunities to create architected material systems that can potentially learn and evolve ‘on the fly’ in response to various forms of stimuli. Therefore, we find it intriguing to wonder whether neuromorphic materials of the future might react in a sentient way by developing preferences for certain stimuli from past experiences. In this way, they could potentially provide an idealized framework within which to further the neurological understanding of the human brain.

Author contributions

All authors contributed equally to the preparation of this manuscript.

Peer review

Peer review information

Nature Reviews Materials thanks Qi Ge and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Competing interests

The authors declare no competing interests.