LEARNING TO WAIT FOR MORE LIKELY OR JUST MORE: GREATER TOLERANCE TO DELAYS OF REWARD WITH INCREASINGLY LONGER DELAYS

Abstract

Little research has focused on training greater tolerance to delays of rewards in the context of delayed gratification. In delayed gratification, waiting for a delayed outcome necessitates the ability to resist defection for a continuously available smaller, immediate outcome. The present research explored the use of a fading procedure for producing greater waiting in a video-game based, delayed gratification task. Participants were assigned to conditions in which either the reward magnitude, or the probability of receiving a reward, was a function of time waited and the delay to the maximum reward was gradually increased throughout this training. Waiting increased for all participants but less for those waiting for a greater reward magnitude than a greater reward probability. All participants showed a tendency to wait in a final testing phase, but training with probabilistic outcomes produced a significantly greater likelihood of waiting during testing. The behavioral requirements of delay discounting versus delay gratification are discussed, as well as the benefits of training greater self-control in a variety of contexts.

Impulsive choice is a widely studied phenomenon that has taken many procedural forms over the years. While there is debate regarding whether or not some of the most commonly used ways of measuring impulsive choice are tapping into the same construct (Evenden, 1999), two common behavior assessments measure how long someone will wait for a larger reward before reversing their preference and taking a smaller reward much sooner. In delay discounting (DD) tasks, an organism is presented a choice between a smaller immediate outcome and a larger delayed outcome. After a choice has been made, the organism is forced to commit to that choice: There is no opportunity to later reverse it. The variable of interest from such tasks is the point of indifference between a smaller immediate outcome and a larger delayed outcome—the adjusted amount of an immediate alternative that is equally attractive as a larger delayed alternative. The indifference point reflects how much the larger delayed outcome is devalued as a function of its temporal distance, which is typically arrived at through the assessment of choice over multiple trials (e.g., Rachlin, Raineri, & Cross, 1991; Du, Green, & Myerson, 2002). In delayed gratification (DG) tasks, the organism must endure the delay to the better outcome while the immediate outcome is always available. The dependent measure in DG tasks is commonly the duration of time waited for the better outcome (Mischel & Ebbesen, 1970); these tasks often entail one-shot decisions, and waiting time provides a continuous measure of impulsivity in one assessment. Regardless of whether these tasks measure the same construct, both provide a meaningful index of impulsivity that is relevant to life outcomes.

The degree to which individuals devalue future outcomes and their ability to wait for more preferred, delayed outcomes correlate with behaviors related to health and well-being. For instance, individual differences in DD correlate with smoking status (Bickel, Odum, & Madden, 1999), body fat percentage (Rasmussen, Lawyer, & Reilly, 2010), presence of alcoholism (Petry, 2001), the problematic use of illicit drugs (Kirby & Petry, 2004) and other behaviors such as pathological internet use (Saville, Gisbert, Kopp, & Telesco, 2010). Waiting times in DG tasks obtained at approximately 4 years old correlate with academic success in high school (as measured by SAT scores), ratings of ability to cope with stressful situations and resist temptation (Shoda, Mischel, & Peake, 1990), and with shorter defection times and cocaine use in early adulthood (Ayduk et al., 2000). There is additional research that suggests that these early measures are also correlated with self-reported body mass index 30 years after their initial assessment (Schlam, Wilson, Shoda, Mischel, & Ayduk, 2013). Given the variety of health and quality of life outcomes these measures of impulsivity have been shown to predict, it is of no surprise that there has been increasing interest in developing methods for reducing impulsivity (e.g., Morrison, Madden, Odum, Friedel, & Twohig, 2014; Radu, Yi, Bickel, Gross, & McClure, 2011; Stein et al., 2013).

Research aimed at uncovering variables that influence impulsive choice has revealed a variety of factors that alter preferences between smaller immediate rewards and larger delayed ones. These variables include reinforcer magnitude (Green, Fristoe, & Myerson, 1994; Green, Myerson, & McFadden, 1997), the quality of the reinforcer (Forzano & Logue, 1995; Forzano, Porter, & Mitchell, 1997; King & Logue 1990), and the likelihood of receiving a delayed reward (Mischel & Grusec, 1967; Vanderveldt, Green, & Myerson, 2014), among others (e.g., Berry, Sweeney, Morath, Odum, & Jordan, 2014).

Procedures with the explicit aim to train greater self-control in DD contexts have successfully used fading procedures in which either a) both outcomes are delayed and the smaller outcome’s delay is gradually reduced across trials (e.g., Mazur & Logue 1978), or b) both outcomes are immediate, and the delay to the larger–later is gradually increased across trials (e.g., Dixon et al., 1998). The use of fading procedures in which participants are exposed to increasingly longer delays of reinforcement has also increased waiting in subsequent DG assessments (e.g., Newman & Kanfer, 1976; Newman & Bloom, 1981). Yet, while other variables affecting waiting in DG contexts have been examined, such as attention (Mischel & Ebbesen, 1970), task instructions (Mischel, Ebbesen, & Zeiss, 1972), and the reliability of the experimenter (Kidd, Palmeri, & Aslin, 2013), many of the procedural manipulations that have altered choice in DD have seldom been applied for training greater waiting in DG scenarios where obtaining the smaller immediate outcome is not precluded by an initial choice to wait for a better delayed outcome.

Accumulation Tasks—a DG Variation

The lack of studies on promoting greater waiting in DG scenarios is likely due to procedural limitations. There are few tasks with which delayed gratification can be easily studied in humans beyond an early age because the delays necessary to induce defection for a smaller, immediate reward would be difficult to arrange in the experimental context (see Paglieri, 2013 for further discussion of this topic). One existing procedure that is able to measure this behavior in human adults is the Escalating Interest task (EI task; Young, Webb, & Jacobs, 2011). The EI task has been typically implemented in a video game, in which the reward is the magnitude of weapon damage. The amount of time a participant waits between firing his or her weapon dictates the amount of damage that the participant’s weapon can produce. This sort of task is best understood as an accumulation task, where the amount of the immediately available reward increases as a function of time waited (cf., Anderson, Kuroshima, and Fujita, 2010; Beran, 2002; Pelé, Dufour, Micheletta, & Thierry, 2010).

Experiments using the video game implementation of the EI task have varied the rate of weapon damage accumulation to produce differential incentives for waiting. The available weapon damage is visible on a “charge bar” on the screen that gradually fills over time. In most implementations of the task, the bar is filled after 10 s have elapsed since the previous shot and thus waiting longer than 10 s is never beneficial. The rate at which the charge bar fills (and as a result, the damage that could be produced when the weapon is fired) has been determined using a superellipsoid feedback function:

$$damage=100*{\left(1-{\left(\frac{10-t}{10}\right)}^{power}\right)}^{\frac{1}{power}}$$ (1)

where t is the time in seconds waited since the last shot was fired, power is a parameter that changes the rate of damage growth, and 10 indicates the time in seconds until maximum damage. For example, when power is equal to a value less than 1.00, the growth rate is positively accelerating. Damage growth over a 10 s maximum charge interval with two values of power less than 1.00 is shown in Figure 1 (the dashed and dashed-dotted lines); the increase in damage accumulated is initially slow and becomes more rapid as time waited increases. Under these conditions, it is beneficial to wait because firing quickly reduces the density of damage that is produced (thus, resulting in more time to complete the task). When power is greater than 1.00, the growth rate is negatively accelerating and it is best to fire rapidly because this maximizes damage density. Damage growth with a value of power equal to 1.25 is shown by the dotted line in Figure 1; the increase in damage accumulated is initially rapid and slows as time waited increases—the converse of power values less than 1.00. When power is equal to 1.00, the growth rate is linear (a slope of 1, shown by the solid line in Fig. 1) and the density of damage accumulated is not dependent on the amount of time waited between shots. Thus, regardless of how long a participant waits when the power is 1.00, the rate of damage production is constant and time waited does not matter (with the caveat that, so long as the participant does not wait longer than the duration of time it takes for damage to reach the maximum). While wait times do not affect damage density when the growth rate of weapon damage is linear, how quickly one fires under such conditions is mildly correlated with rate of delay discounting—as do wait times with other growth rates where the differential contingency to fire quickly or rapidly is moderate (Young, Webb, Rung & Jacobs, 2013).

Fig. 1.

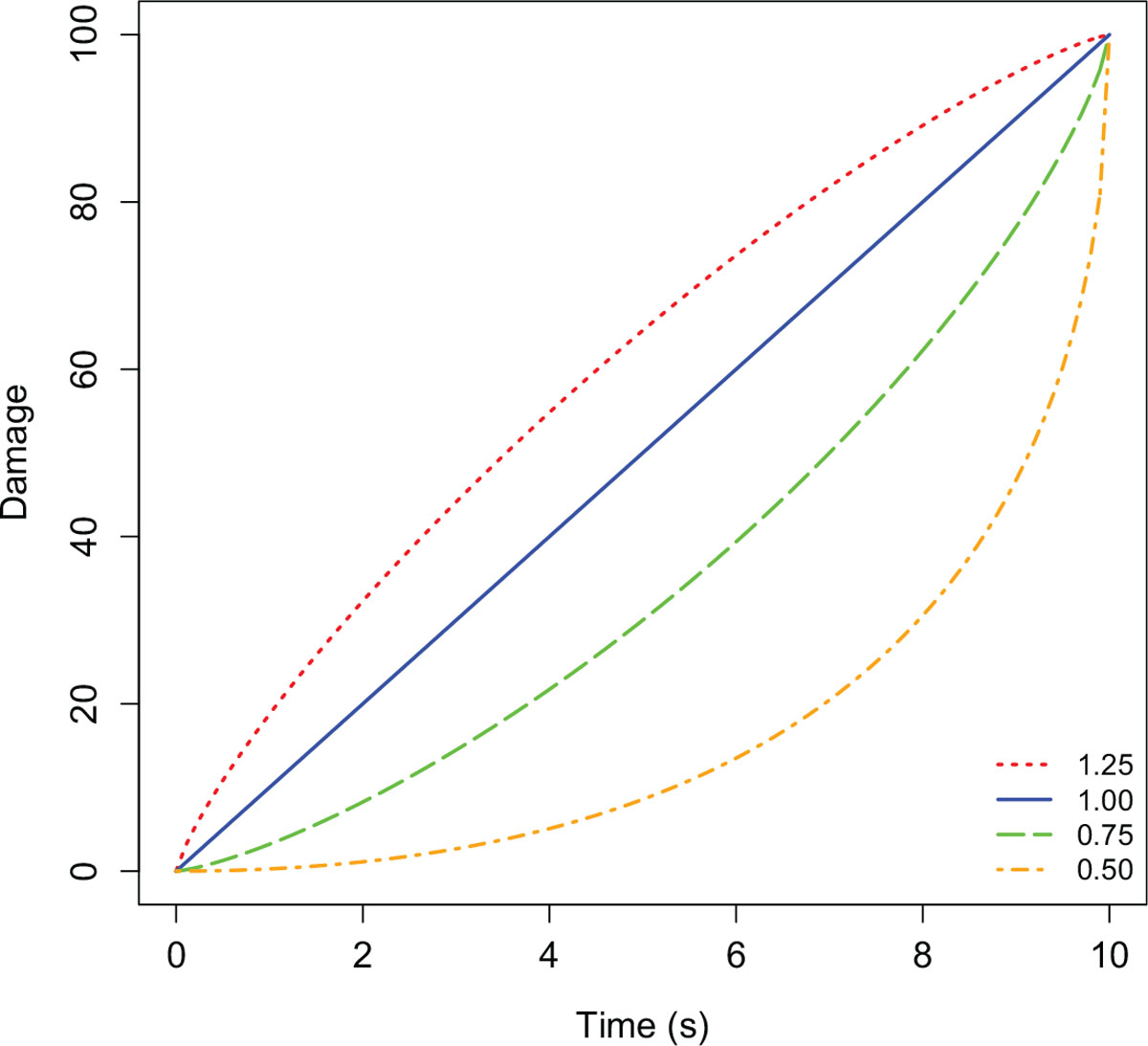
Currently available damage as a function of time waited since the last shot fired. In this graph, the maximum damage is accumulated after waiting 10 s since the previous shot. The curves illustrate the rate of damage accumulation according to four different values of power, as indicated in the legend.

In the EI task, participants tend to show good sensitivity to changes in the growth rate of weapon damage, which is evidenced by appropriate changes in interresponse times (IRTs) for the currently experienced value of power in Equation 1 (Young et al., 2011; Young, Webb, Sutherland, & Jacobs, 2013). IRTs are, however, also influenced by the order in which the different values of power are experienced (Young et al., 2013), as well as by the duration of time that a participant experiences them (Rung & Young, 2014). Specifically, Rung and Young exposed participants to a prolonged duration of gameplay with one of three power values (two positively accelerating damage growth rates, powers of 0.50 and 0.75, and one linear growth rate, power of 1.00) during the first half of the game. They assessed the effects of this experience on subsequent behavior during the second half of the game when the growth rate was always linear, or in other words, when the contingency to fire slowly was removed. Overall, participants assigned to conditions with positively accelerating growth rates (the experimental groups) continued to wait longer when the increase became linear than did participants assigned to linear growth rates for the entirety of the game (the control group). Waiting gradually decreased in this latter phase indicating that the initially trained tolerance to delay was not fully maintained when the delay contingency was removed, but the experimental groups continued to wait longer than the control group throughout its duration.

The persistent order effects found in Rung and Young (2014) are similar to those found in a study using similar contingencies with primates as subjects in a food accumulation task. Anderson et al. (2010) aimed to assess the ability of two species of monkeys (squirrel monkeys and capuchins) to delay gratification. In this type of accumulation task, a piece of food was presented after fixed intervals of time until either the maximum number of pieces was achieved or the subject took the currently available reinforcers. A majority of the monkeys across both species did not accumulate many pieces, but after experience in a condition where the magnitude of food pieces increased after each successive presentation, half of all subjects began to reliably accumulate more pieces than when the magnitude of the reinforcers was constant. The increase in number of items accumulated by subjects continued in subsequent follow-up assessments and in unpublished observations by the researchers.

Training Participants to Wait When It Is Optimal to Do So

The lasting effects on waiting, arising from experience with contingencies in which the density of reinforcement increases with time, show promise for a behavioral means of training greater tolerance to delays of reinforcement. While Rung and Young (2014) were successful in training humans to wait longer after prolonged training, and this behavior persisted when the contingency was removed (albeit with a slow loss of control as time passed), it is unclear whether or not this arrangement of contingencies would produce the same effects if the duration of time to reach the maximum reward were extended to periods greater than 10 s. While participants have demonstrated sensitivity to the differing growth rates of weapon damage at longer charge durations (17–20 s) than those used in the Rung and Young study, sensitivity to the different growth rates was superior when the charge intervals were shorter (Young et al., 2013). Therefore, it was unknown if participants could be trained to consistently wait much longer than 10 s in the video game EI task. Moreover, while the effects of exposure to positively accelerating growth rates did result in overall longer IRTs by participants in the latter phase of Rung and Young, those who had been assigned to the condition with the most steeply positively accelerating growth rate (i.e., provided the lowest reward for suboptimal IRTs) evidenced a contrast effect when the contingency to fire slowly was removed. Despite the fact that those participants waited significantly longer than controls, there was a sudden and significant decrease in the likelihood of producing a long IRT in the second half of the game. The decrease in the likelihood of producing a long IRT was not significant for the group assigned to a more moderate positively accelerating growth rate in the first half of the game.

Thus, in the present experiment we sought to examine the efficacy of the previously established training effect with a longer maximum delay. To increase sensitivity to positively accelerating growth rates of weapon damage at longer charge intervals, we used a fading procedure throughout the first three-quarters of the game in which the charge interval was gradually increased from 5 s to 20 s. Longer IRTs were differentially reinforced during this period by either a moderately positively accelerating growth rate of damage magnitude (magnitude condition), or by a moderately positively accelerating growth rate of the likelihood of producing maximum damage (probability condition). While we expected that participants would show sensitivity to the growth rate of magnitude and probability by waiting longer as the charge interval increased, we also expected that those assigned to the probability condition would show longer IRTs because previous research indicates that people wait longer to obtain a higher probability of an outcome than an equivalent certain magnitude (Young et al., 2011; Young, Webb, Rung, & McCoy, 2014; Webb & Young, in press). Notably, unlike Rung and Young (2014); we opted to use a moderately positively accelerating growth rate in lieu of more extreme rates because subsequent changes to the contingencies in the final phase would be less salient (visually cued by the charge-bar). As such, we expected that using moderate growth rates of weapon damage would result in a smaller contrast effect—and ultimately a smaller decrease in IRT duration, if one were to occur—when the waiting contingency was removed in the final quarter of the game.

The sustained efficacy of the fading procedure and previously assigned contingencies (growth rate of magnitude or probability) were examined in the final quarter of the game. This generalization test was done by making the rate of damage accumulation linear, in which maximum damage increased over 20 s, and the outcome had a constant probability of 1.0 regardless of the prior contingency on damage production in the fading procedure. The change to linear growth rate of weapon damage is synonymous with the removal of the differential contingency to produce long IRTs: When the growth rate of weapon damage is linear, there is no incentive to wait, because responding quickly or slowly does not affect damage density in this free-operant preparation. We expected that participants in both the magnitude and probability conditions would continue to wait during this final phase of the experiment, but that those in the probability condition would wait longer than those in the magnitude condition. Finally, we did not know whether control would be lost during this final phase (as in Rung and Young) or be maintained throughout.

It should be noted that we opted not to include a control group in which there was no differential contingency to encourage waiting (i.e., a power of 1.0) during the training period. Previous research has shown participants nearly exclusively fire rapidly when the growth rate of weapon damage is linear. This finding is robust and has been demonstrated whether participants experience different values of power rapidly (changing after every two enemies are eliminated; Young et al., 2011), for a quarter of the task (Young et al., 2013), or for the entirety of the game (Rung & Young, 2014). Thus, we chose not to include such a control group in order to better allocate our resources and increase the power of the study to make the more critical comparisons between the probability and magnitude conditions.

In addition to the video game task, participants completed a brief demographics questionnaire that assessed sex and prior video game playing experience, a hypothetical money DD task (Johnson & Bickel, 2002), and a self-assessment measure of impulsivity (Lynam, Smith, Whiteside, & Cyders, 2006). In previous studies, individual differences variables have been idiosyncratically related to behavior in the video game (Young et al., 2011; Young et al., 2013; Young et al., 2013). The differences in relations across studies are likely due to procedural variations, which complicate a more general understanding of their relevance to behavior in the game. We included these additional measures here in the hope that they would indicate whether individuals showing greater impulsivity by other measures would display the same sensitivity and behavioral change as those who were less impulsive.

Method

Participants

Forty-three college students were recruited from introductory psychology courses and received course credit as compensation for their voluntary participation. Sessions lasted approximately 1 hr. All procedures were approved by the Institutional Review Board of Southern Illinois University at Carbondale.

Procedure

At the beginning of a session, the research assistant reviewed experimental procedures and obtained informed consent from participants. Subsequently, all participants completed the video game task, a brief demographics questionnaire, the UPPS-P (Lynam et al., 2006), and a delay-discounting task. Half of the participants completed the last three tasks after the video game, and half of them completed the last three tasks prior to the video game. All four portions of the experiment were completed on a computer; the last three tasks were presented on a computer using PsyScope (Cohen, MacWhinney, Flatt, & Provost, 1993).

Participants were randomly assigned to one of two conditions in the video game. In the magnitude condition, waiting increased the magnitude of the damage dealt by a shot of the participants’ equipped weapon. In the probability condition, waiting increased the probability of a successful shot while the magnitude of damage was held constant at the programmed maximum. Each condition was matched in terms of expected value of the outcome. A more detailed description of each of the tasks is provided below.

Video Game

The video game task was a modified version of the EI Task (Young et al., 2011) embedded in a video game using the Torque game engine (www.garagegames.com). In the EI task, the participant plays as an “orc” in a virtual village that is under attack by enemy orcs. Participants are instructed to protect the village by eliminating all of the enemy orcs in each level (or block) of the game by the use of an equipped weapon. Depending upon the assigned condition, participants were told that the charge bar indicated either the currently available amount of damage (magnitude condition) or the likelihood that their weapon would fire (probability condition). Enemy orcs fired weapons at buildings in the village. Orcs were eliminated by successful shots of the player’s equipped weapon, with the number of shots it takes to eliminate an orc dependent on the damage that the weapon produced. There were 14 enemy orcs in each of the four blocks of the game and all orcs appeared in pairs dispersed throughout the environment. After a participant eliminated all of the 14 orcs in a game block, the next block began by resetting the game environment and repopulating the orcs. The blocks were identical, but the placement of the orc pairs varied, as well as the starting location of the participant’s character.

The video game progressed through two phases: the first phase was a fading procedure (hereafter referred to as “training”) which took place over the first three blocks of the game, and the second phase was an assessment phase in which the efficacy of the fading procedure and previously assigned weapon contingencies were evaluated for training longer IRTs. A visual outline depicting the programmed contingencies at the beginning of each game block, as well as the contingencies in place at the end of the third block and for the duration of the final block are given in Figure 2. In the training phase, regardless of group, the first block began with a 5 s charge interval. In the magnitude group, the magnitude of weapon damage increased as a function of time waited between shots according to Equation 2:

$$magnitudeorprobability=100\times \frac{t_{\text{max}}}{20}\times {\left(1-{\left(\frac{t_{\max }-t}{t_{\max }}\right)}^{power}\right)}^{\frac{1}{power}}$$ (2)

where t_max was the currently programmed delay to maximum charge (5 s at the beginning of training) and power was 0.75; in the probability group, the probability of dealing maximum damage increased in the same fashion. Because growth rates of magnitude and probability were the same, the two groups were matched in expected value as a function of time waited: The proportion of maximum damage available in the magnitude group always mirrored the probability of a full shot in the probability group at the same charge interval duration. For instance, imagine that the total possible damage with a maximum charge interval of 10 s was 100. If waiting 7 s in the magnitude group resulted in the accumulation of 85 points of damage, the probability of producing maximum damage after 7 s in the probability group was 0.85. The expected value of damage in the magnitude group would be 85 (with a constant probability of 1.00: 1.00 × 85 pts = 85), and the expected value of damage in the probability group would also be 85 (with a probability of .85 of producing maximum damage: .85 × 100 pts = 85). After every two orcs were eliminated, t_max increased. The increase was gradual (0.71 s), such that by the beginning of the next block, the time to maximum charge was 5 s longer than its initial value in the preceding block. Thus, t_max began at 5 s in the first block, 10 s in the second block, and 15 s in the third. With every increase in t_max, the maximum possible damage also increased; this modification allowed the damage per unit time waited (or the maximum damage at 100% probability) to remain constant as t_max increased.

Fig. 2.

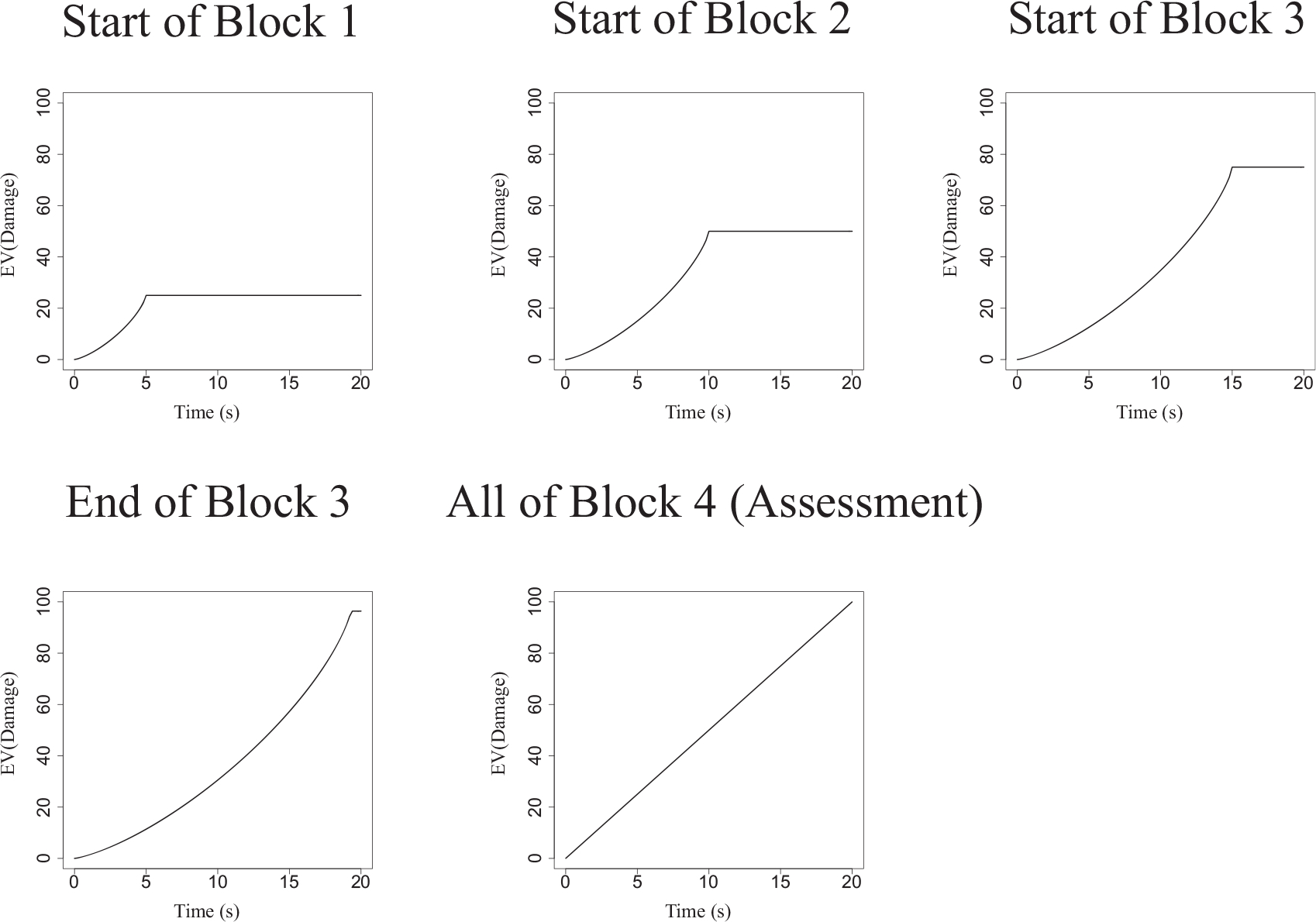
Snapshots of the programmed increase in magnitude or probability as a function of time waited (depending on condition) throughout the first three blocks of training. The y-axis represents the expected value of damage, which is the product of the probability of a successful shot and the available damage; for the magnitude condition, the expected value is the currently available damage (probability is a constant 100%), and for the probability condition the expected value is the maximum damage times the current probability. In the final block, magnitude increased linearly for both the magnitude and probability conditions while the probability was 100%.

After the training phase was completed, the assessment phase began (the fourth block). Regardless of the condition participants were assigned to, the growth rate of weapon damage was a linear function of time (i.e., where power = 1.00), the weapon always worked (probability of 1.00), and the delay to maximum charge (t_max) was 20 s throughout. It is important to note that the contingencies in the training phase for participants in the magnitude condition were more similar to the conditions under which they were subsequently tested in the assessment phase, in that across both the training and assessment phases, only the growth rates of weapon damage and charge interval were manipulated. For the probability condition, participants were first trained with increasing probability of weapon damage over increasingly longer charge intervals, and then tested under conditions where magnitude of weapon damage increased with time waited—not probability.

Demographics

Participants were asked to report their sex and the frequency at which they played nine different types of video games (e.g., musical/rhythm, first-person shooter) over the last four years (see Young et al., 2011 for further details). Frequencies were rated on a 7-point scale, ranging from 0 (never) to 6 (daily), with a score of 3 corresponding to monthly.

UPPS-P

The UPPS-P (Lynam et al., 2006) is a 59-item questionnaire that assesses five dimensions of impulsive behavior: urgency, (lack of) premeditation, (lack of) perseverance, sensation-seeking, and positive urgency. Items were scored 1 to 4, with 1 indicating “agree strongly” and 4 indicating “disagree strongly”. For this questionnaire, a composite score is not typical. Instead, the mean score is calculated for each of the five dimensions.

Delay Discounting

The delay discounting task was an adjusting-immediate-amount procedure. Participants were asked to choose between a smaller amount of money available immediately (randomly determined on the first trial) and $1000 after a delay. The amount of the immediate money varied according to the double-limit choice algorithm developed by Johnson and Bickel (2002). An indifference point was equal to a chosen immediate amount of money that caused the outer upper and outer lower limits to be adjusted such that their difference was less than $10 (see Johnson & Bickel, 2002 for details). After an indifference point was obtained, the delay to the larger amount of money was increased to the next delay in the series. The delays at which indifference points were obtained were 1 week, 1 month, 3 months, 1 year, and 5 years.

The dependent measure in the DD task was area under the curve (AUC). AUC is an atheoretical metric of the degree to which an individual discounts (for details, see Myerson, Green, and Warusawitharana, 2001). Participants who provided nonsystematic data (i.e., when the subjective value at any delay other than the first was greater than the previous by an amount greater than 10% of the delayed reward) were excluded from analyses that included AUC as a predictor (Johnson & Bickel, 2008). While participants who do not discount the delayed reward are also often excluded, we opted to keep these data in our analyses because of the possibility that these are choices participants would actually make over the range of delays tested herein.

Results

Of the 43 participants, 3 were excluded from the analysis due to their experiencing technical difficulties during the video game task. Of the remaining 40 participants, there were 10 females in the magnitude group, and 11 females in the probability group. All participants completed the video game, DD task, UPPS-P, and demographics questionnaires within the allotted time of 1 hr and were included in the analysis.

To ensure that random assignment equated groups in terms of individual differences variables, differences between groups on these variables were analyzed with t-tests or a nonparametric equivalent (Wilcoxon rank sum test) in instances where the distributions violated assumptions of normality. There were no significant differences between groups on measures of AUC or UPPS-P subscales (all ps > .05). Participants across groups were equivalent on all measures of video game play frequency (ps > .05), with the following two exceptions: participants in the probability condition more frequently played both puzzle and casino games (χ²(1) = 5.26, p =.02) and musical/rhythm games (χ²(1) = 11.19, p < .001). While the self-reported frequencies across groups were significantly different, these differences were fairly small: The mean frequency ratings of playing puzzle/casino games and musical/rhythm games were 2.20 (SD = 1.70) and 1.80 (SD = 1.70), respectively, for the probability group, and 1.22 (SD = 1.93) and 0.32 (SD = 0.82), respectively, for the magnitude group. On average, both groups played these types of games at a low frequency (less than monthly, but more than never). Scale ratings other than 0 (never), 3 (monthly), and 6 (daily), were not explicitly anchored, but it is apparent from the low scores and small differences that these frequencies indicated marginal differences in game play.

The dependent variable used in all analyses was a dichotomized function of IRT. IRTs are highly bimodal in this preparation; Figure 3 illustrates the distributions of IRTs at each charge interval (expressed as raw IRTs on the left, and as a proportion of the programmed maximum charge on the right), in which the width of the plot at each interval indicates the frequency of the corresponding IRT. In addition to Figure 3, two figures provided as supplemental materials (Figs. 1A and 2A) show the individual participant data for each portion of the game. In Figure 3, the bimodal nature of the distribution can easily be discerned by the increased widths near proportions of 0 and 1.00, with the contour narrowing in the middle. Because the data are bimodal, responses were classified into those with IRTs less than half the programmed t_max (which increased as the experiment progressed) and those greater than half. We classify these responses as not-waited versus waited, respectively. In addition, IRTs greater than twice the programmed full charge interval were excluded from analyses; these long IRTs likely reflect inattention to the task or extensive travel time in the gaming environment. Excluding these IRTs produced a 4% reduction in the number of trials with no more than 10% lost for any single participant. This approach is consistent with prior research using the video game EI task (e.g., Young et al., 2011; Young et al., 2013; Young et al., 2013; Rung & Young, 2014).

Fig. 3.

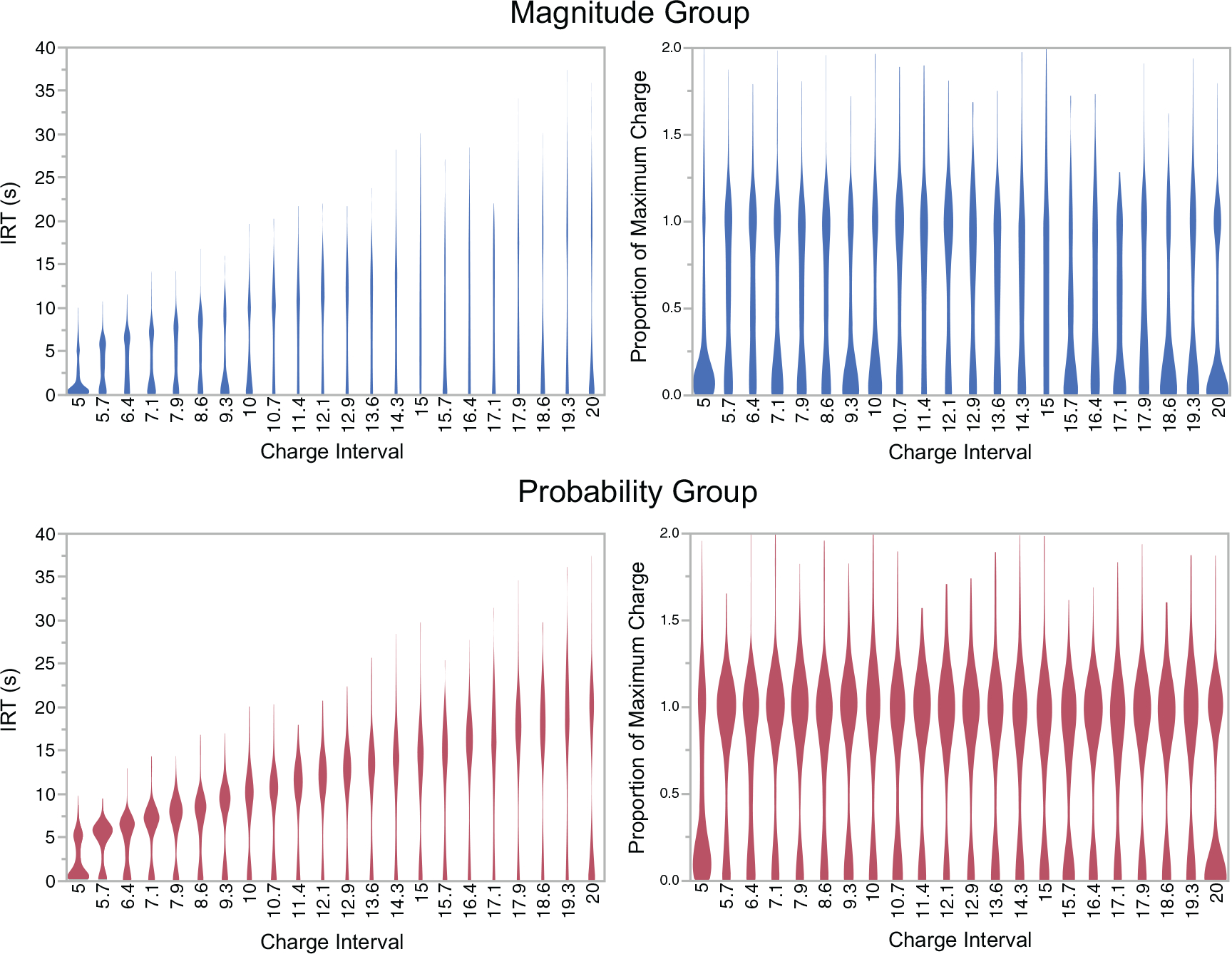
Distributions of IRTs (on the left) and IRTs expressed as a proportion of the charge interval (on the right) for each condition. The width of the plot corresponds to the frequency with which that IRT occurred. On the left, the width of the plots decreases as the charge interval increases due to the increases in IRTs (i.e., the elongation of the plot). Note that, for the plots of proportions at a charge interval of 20 s, the proportion of short IRTs appears inflated compared to other plots; this is a by-product of a longer duration of the game played with this particular charge interval compared to others.

The data were analyzed with a linear mixed effects (i.e., multilevel or random coefficients) analysis using R’s lmer function and specifying a binomial error distribution (Pinheiro & Bates, 2004). This analysis can be conceptualized as a repeated measures logistic regression. A mixed effects analysis uses maximum likelihood estimation to address the highly unbalanced data generated by a free operant task (Laird & Ware, 1982). In addition, the analysis allows the fitting of individual regression curves for participants. Continuous variables were centered to avoid multi-collinearity issues, and categorical variables were effect-coded because all main effects and interactions were examined in the model.

Training (Blocks 1 through 3)

We adopted a model comparison approach to the analysis by examining a series of nested models of theoretical interest and identifying the best fitting model. The base model included condition (magnitude vs. probability), block as a categorical predictor (1, 2, or 3), the proportion of time spent in a block (ranging from 0 to 1), and all of their two- and three-way interactions; individual differences variables were considered in a second set of models. The time in block was individually rescaled for each participant for each block; for example, a score of 0.5 on the proportion of time in block indicates the performance halfway through the block. We chose block and time in block as independent predictors to capture the discontinuities in behavior across blocks of training (recall that the game resets by repopulating the orcs between game blocks). Using the programmed t_max (delay to maximum reward) as a predictor would have necessitated the use of nonlinear functions to capture these discontinuities.

Multilevel modeling requires the consideration of random effect components—within-subject factors that might vary across participants. In order to find the best fitting model for predicting the likelihood of waiting, we examined random effects of intercept, time in block (slope), and block (slope). In other words, we evaluated whether participants significantly varied from each other in their overall tendency to wait (intercept random effect), their rate of change across the blocks (time in block slope random effect), and the differences in behavior across blocks (block slope random effect). The best fitting model included all three random effects, determined by the lowest Akaike Information Criterion (AIC; Akaike, 1974). Because fit indices like R² are not suitable for nonlinear models given the lack of a consensus on their relative strengths, such metrics are not provided.

Figure 4 shows each participant’s model fits of the probability of waiting as the game progressed for the two conditions. The model performs the equivalent of a piecewise linear regression in which each block is fitted separately, thus allowing for discontinuities between blocks of the game. The sigmoidal functions evident for some participants are a by-product of the use of logistic regression. In the probability condition, although participants began with a range of waiting times at the beginning of the task, they converged on very similar behavioral profiles throughout the rest of the task. Most participants waited until the charge bar was full or nearly so, even as the duration of the time to maximum reward was increasing within a block and across blocks. There is some evidence of a loss of control by the contingencies at the beginning of the third block, but control was rapidly re-established. In the magnitude condition, a wide range of waiting probabilities was evident throughout the entire task. Although there was a general increase in the likelihood of waiting for the second block, this tendency was not maintained in the third block where there was also some evidence of a loss of control.

Fig. 4.

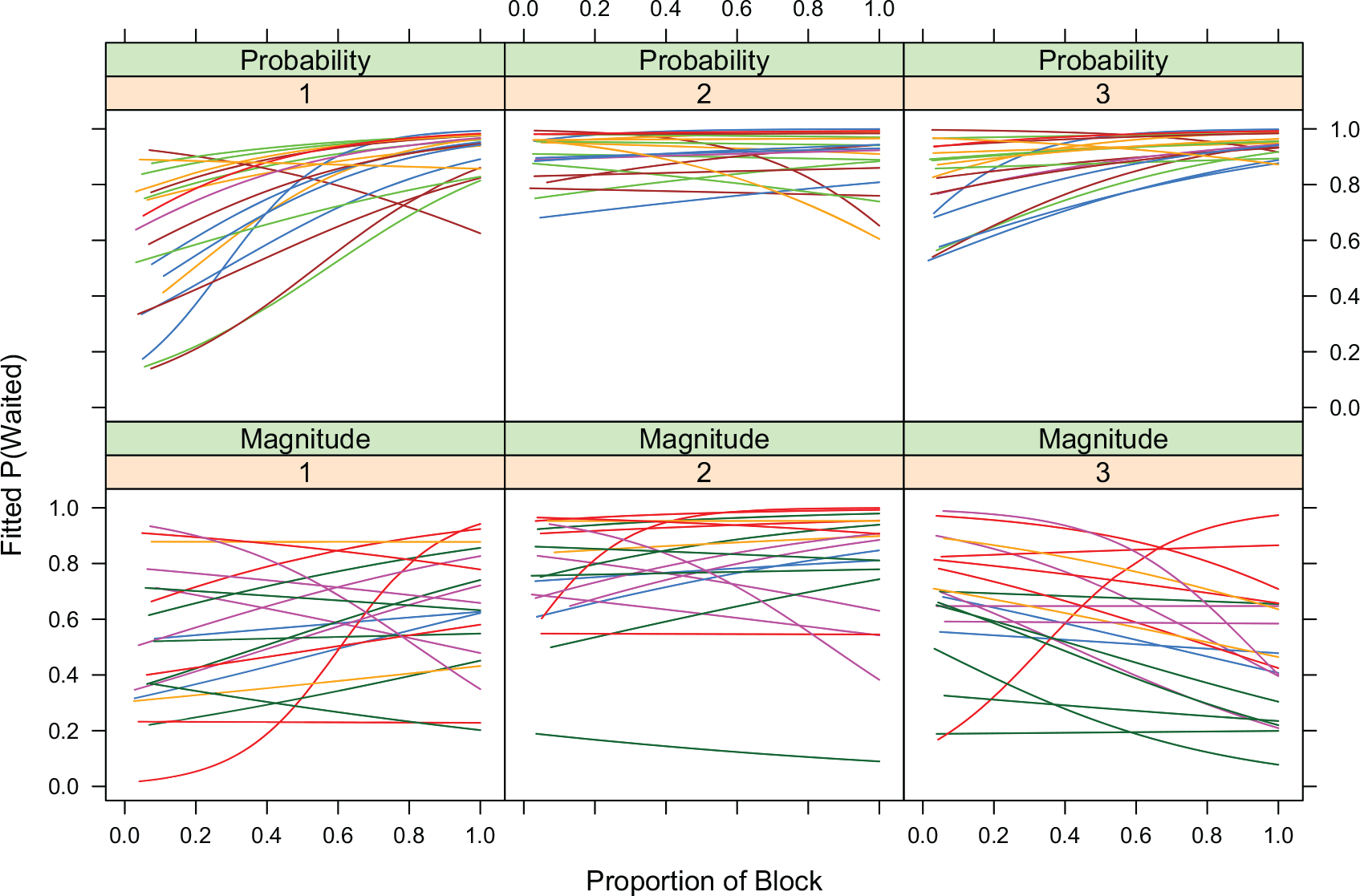
Individual participant model fits of the probability of waiting as a function of the proportion of the block, block, and condition. The delay to maximum reward was [5.0, 9.3] in the first block, [10.0, 14.3] in the second block, and [15.0, 19.3] in the third block and systematically increased from the lowest value at the beginning of each block to the highest value by the end (indicated respectively in brackets).

Figure 5 depicts the same behavior by plotting mean IRT as a function of the increasing delays to maximum reward. Smoothed spline fits are used to capture the nonlinearities in these relationships. This figure illustrates both the higher variability in the magnitude condition, the earlier cash-ins relative to the optimal wait time (illustrated by the heavy dashed line), and the increasing interval strain as the duration of the interval to maximum reward was increased.

Fig. 5.

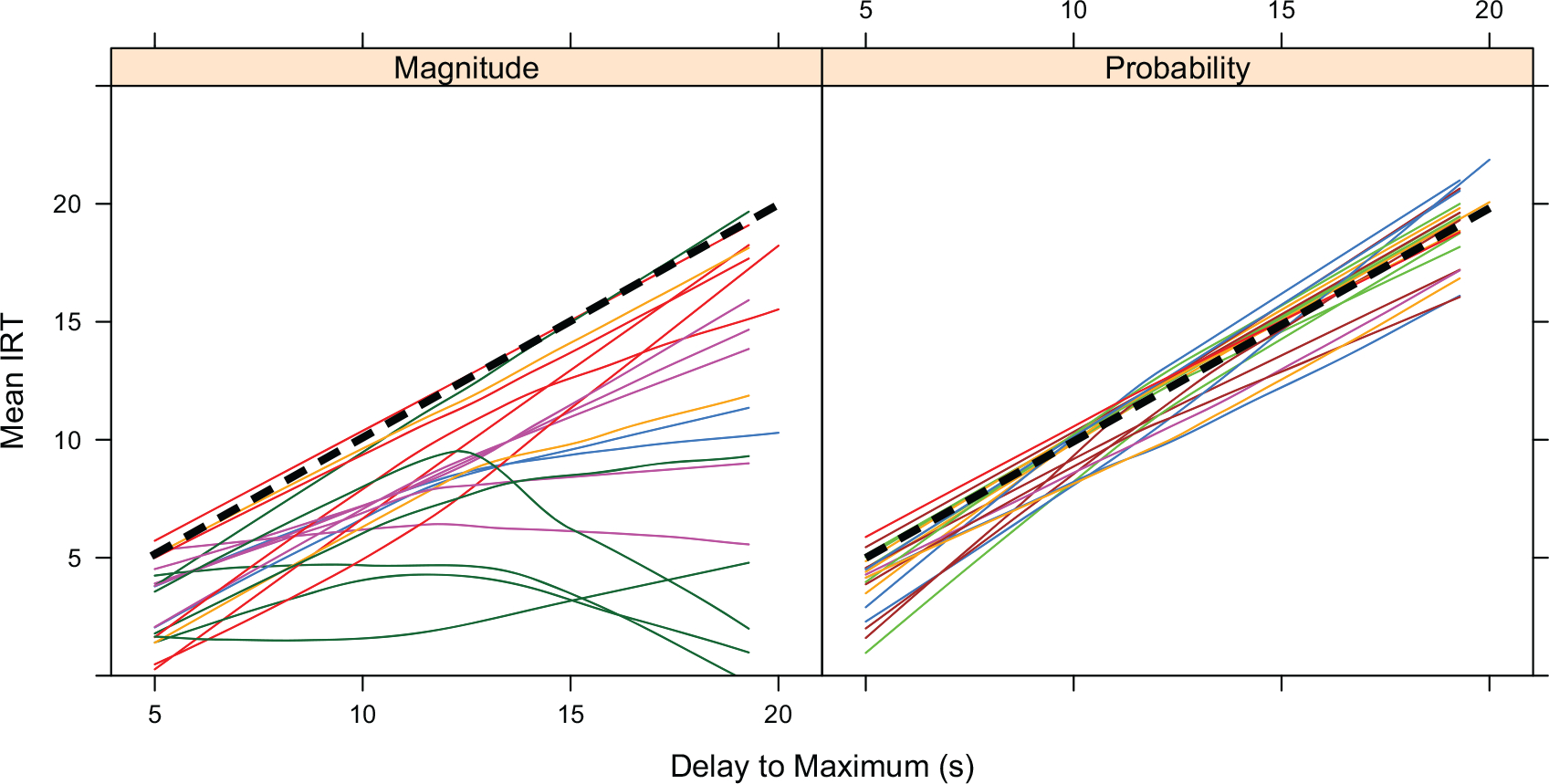
Individual participant smoothed spline fits of the probability of waiting as a function of the delay to maximum reward across conditions. The dashed line designates optimal behavior.

The mixed effects analysis of the probability of waiting (Fig. 4) confirmed main effects of condition (z = 4.62, p < .01), block (F(2, 78) = 84.9, p < .01), and proportion of time in the block (z = 2.08, p < .05). These main effects are qualified by the presence of significant interactions of Condition × Block (F(2, 78) = 19.22, p < .01), Block × Time in Block (F(2, 78) = 18.66, p < .01), and Condition × Block Time in Block (F(2, 78) = 11.66, p < .01); the Condition × Time in Block interaction did not reach significance (z = 1.88, p > .05).

The best fitting intercepts and slopes from this model are shown in Tables 1 and 2. The intercepts estimate the mean likelihood of waiting for each condition in each block of the experiment. The slopes estimate the change in the likelihood of waiting for each condition in each block. All comparisons of interest were statistically significant. The intercept analysis confirmed that people waited longer in the probability condition in all three blocks with the gap growing smaller in the second block but increasing again in the third block when the delay to maximum charge was greater than 15 s. The slope analysis clearly showed faster increases in the likelihood of waiting in the probability condition for the first block, little change in the second block for either condition, and a small but significant upward trend for the probability condition in the third block accompanied by a slight downward trend for the magnitude condition.

Table 1.

Intercepts from the best-fitting mixed-effects logistic regression analysis with condition, block, and time in block as predictors of the likelihood of producing a long IRT during training. Larger intercepts indicate a greater likelihood of waiting as indicated by the accompanying percentages derived using the best-fitting logistic function.

	Block
	1	2	3
Magnitude	0.35 (58%)	1.67 (84%)	0.48 (62%)
Probability	1.57 (83%)	2.77 (94%)	2.54 (93%)

SE=.31

Table 2.

Slopes from the best-fitting mixed-effects logistic regression analysis with condition, block, and time in block as predictors of the likelihood of producing a long IRT during training. More positive slopes indicate a greater increase in the probability of waiting as the block progressed.

	Block
	1	2	3
Magnitude	0.61	0.62	−0.35
Probability	2.63	0.16	0.77

SE=.36

Finally, we evaluated whether adding AUC, the five UPPS-P scores, the nine video game experience metrics, or sex improved the model fits. To avoid overfitting, each of these classes of predictors was only considered as a main effect rather than as moderators of the independent variables, and each model included only one of these categories of predictors. For example, one model included the original three predictors and their interactions plus AUC. Another model included the original three predictors and their interactions plus the five UPPS-P scores. Six participants did not produce valid AUC data (two due to program error, four due to nonsystematic behavior on the DD task) and were excluded from the AUC analysis.

Only the model that added AUC as a predictor produced a significantly better fit of the data (χ²(1) = 11.88, p < .01); notably, this was true whether all 40 participants were included or only the 34 with valid AUC data. Higher AUC scores were associated with a greater likelihood of waiting in the video game (r(34) = 0.45, z = 3.78, p < .01). To make the strength of this relationship more concrete, the regression equation predicts a 76% likelihood of waiting for participants with an AUC at the 25^th percentile (AUC = .17) and an 88% likelihood of waiting for participants with an AUC at the 75^th percentile (AUC = .77).

Assessment (Block 4)

We conducted a full factorial multilevel logistic regression of behavior in the final block using condition (probability vs. magnitude), proportion of time in block (as a continuous variable) and their interaction as fixed effects, and intercept and proportion of time in the block as random effects. Individual model fits for each participant are shown in Figure 6.

Fig. 6.

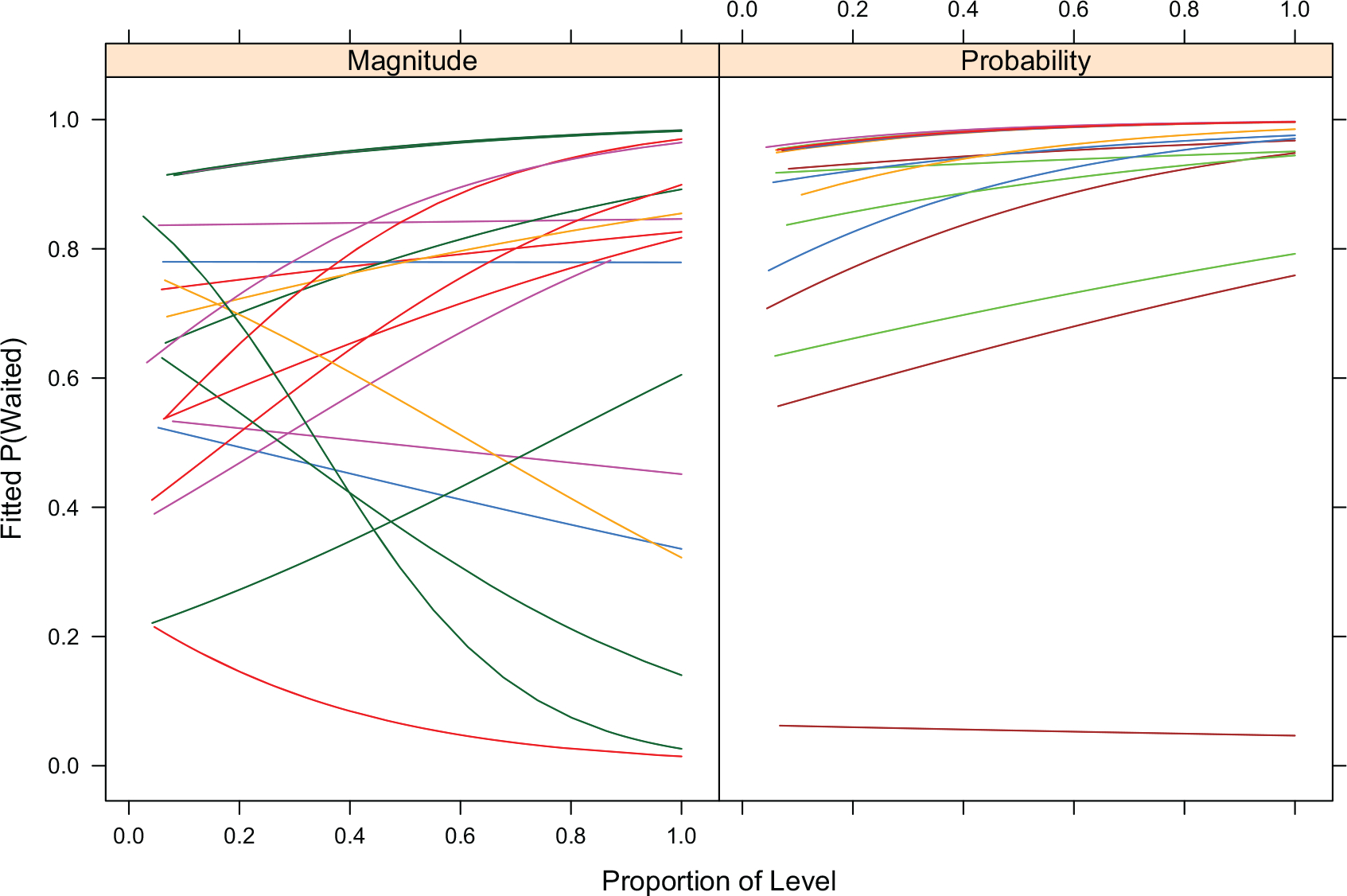
Individual participant model fits of the probability of waiting as a function of the proportion of time in the fourth block across conditions. The delay to maximum reward was 20 s throughout, and the task was the same for each condition in this block (see Figure 2 and text for details).

There was a main effect of condition, with participants trained in the magnitude condition in the first three blocks showing less waiting than those trained in the probability condition (73% vs. 96%, respectively; z = −3.22, p < .01). There was also a main effect of time in block with a greater likelihood of waiting as the block progressed (b = 1.46, z = 2.25, p < .05). The Condition × Time in Block interaction was not statistically significant (b = −.88, z = −1.36, p = .17). This basic model was subsequently compared to a series of models adding AUC, sex, UPPS-P, or the video game variables. The addition of these predictors did not improve the basic model. Although AUC was still positively related to the likelihood of waiting, the predictor did not reach statistical significance (r(40) = 0.34, z = 1.54, p = .12).

Discussion

The results of the present study show that when probability of damage increased rather than an equivalent magnitude as a function of time waited, participants not only waited longer (replicating), but also that it was easier to train participants to wait for higher probabilities at increasingly longer durations to the maximum reward (up to 20 s) and that this behavior was more likely to be sustained when the incentives to wait were removed (Tables 1 and 2; Figs. 4, 5, and 6). Participants’ behavior in the probability condition also came under control of the contingencies faster, and individual differences were significantly reduced after this initial exposure.

In the final block of the game where the disincentive to fire rapidly was removed and the probability of producing weapon damage was a constant 1.0, participants across both conditions showed a tendency to produce longer IRTs. There was, however, greater between-subjects variability in the propensity to wait in the magnitude condition: Slightly more than half the participants showed a relatively high probability of waiting, and the remaining participants showed differing levels of relatively low probabilities of waiting. Participants in the probability condition, however, had a very high likelihood of waiting. All but three participants in the probability condition showed at least a 90% chance of waiting by the end of the final block.

Perhaps one of the most intriguing results is that, unlike Rung and Young (2014), the propensity to wait was sustained for nearly all participants throughout the final block, independent of the assigned condition. Additionally, the likelihood of waiting increased as time in the final block progressed. This is also in contrast to Rung and Young, who found a decrease in the likelihood of waiting across the final testing blocks. In their study, while waiting was still higher in both experimental groups compared to the control group during assessment, there was a significant decreasing trend of the likelihood of waiting. It should be noted that the assessment phase used in their study was twice as long (two blocks) as that used in the present study (one block). An ideal direction for future research would be to have a prolonged assessment phase, as in Rung and Young, in order to increase the opportunity for participants to sample the consequences of shorter IRTs in the assessment phase, as well as to better determine the longevity of the training effect. Nevertheless, as can be discerned from Figure 6, the tendency to wait—and to wait longer—was strong across the majority of participants during the assessment.

The variety of individual differences variables we included in our analyses revealed only one significant predictor of the likelihood of producing long IRTs: rate of discounting in a hypothetical money choice task. It is possible that this relation was detectable because we used a moderately positively accelerating growth rate. Young, Webb, Rung et al. (2013) found a similar result: The propensity to wait in conditions where the growth rate of weapon damage was either moderately positively accelerating (power =.75) or linear (power = 1.00) was also correlated with rate of delay discounting. However, unlike Young, Webb, Rung, et al. (2013), the relation between discounting and the likelihood of waiting was no longer significant in the present experiment during the final block of the game, where the value of power was changed to 1.00. Participants in both conditions (and especially in the probability condition) showed a relatively high likelihood of waiting that increased slightly as time in block progressed. It appears that, independent of discount rate, this type of training was largely successful in producing greater waiting during the assessment phase regardless of initial differences in behavior.

While random assignment did, for the most part, equate our groups on the individual differences predictors we measured, there were some differences in frequency of video game play between the magnitude and probability groups. These differences, however, were relatively small, both in terms of the differences in ratings themselves and the frequencies that corresponded to those ratings. Previous research has shown that these variables tend to be either unrelated to behavior in the EI task (Young et al., 2014), or that when they are, they are only weakly related (see Young et al., 2011; Young, Webb, Rung, et al., 2013; Rung & Young, 2014). Because of these previous findings, and that the inclusion of these variables in our models did not account for a significant proportion of variance above and beyond those that we manipulated, we believe it is unlikely that the differences between groups on these variables significantly impacted the results.

The Efficacy of Increasing Probability rather than Magnitude

The strong preference for higher probability events has been well documented as the certainty effect (Kahneman & Tversky, 1979). Participants prefer a smaller certain outcome over a larger uncertain one, even when the expected value of the uncertain outcome is larger than that for the certain outcome. Thus, the longer waiting to obtain certainty may reflect another demonstration of the certainty effect (also see Webb & Young, in press; Young et al., 2011; Young et al., 2014).

It should be noted that it is possible that participants in the probability condition were unaware of the change from increasing probability to increasing magnitude in the assessment phase. These participants were instructed at the beginning of the game that the charge bar indicated the likelihood their weapon would produce damage, and no further instruction was given regarding subsequent changes. Participants in the probability condition showed a very high likelihood of waiting throughout the second and third training blocks, and this behavior continued through the beginning of the fourth block. As such, participants may not have sufficiently sampled the consequences for waiting a short period of time in order to detect the change in contingencies. Indeed, when inspecting the raw data, this appears to be the case for many of the participants in the probability condition.

While participants in the probability condition may have been unaware of the change in contingencies, this does not explain the increase in the likelihood of waiting throughout the final block—for either the probability or magnitude conditions. As previously mentioned, the increase in charge interval duration also led to an increase in maximum possible damage. A by-product of greater waiting in both conditions, then, was that participants were able to eliminate enemies with fewer shots as the charge interval increased. In the assessment block, waiting the maximum time allowed participants to eliminate enemies with one shot: This is a qualitatively different reward for waiting than reducing the enemies’ remaining health alone. While we cannot be certain this was the case, we believe the qualitatively different reward was the likely cause of the increase in waiting during the final block, and that this outcome was an efficacious consequence for waiting that may have led to little sampling of shorter IRTs in the probability condition.

Lastly, the procedures used were designed to answer which manipulation—probability or magnitude—could produce greater waiting that subsequently generalized to a context in which waiting was no longer differentially reinforced. All else being equal, behavior was more sensitive to the probability manipulation and this behavior generalized to the nondifferential contingency. However, the design used leaves open the possibility that a functionally based fading procedure could have produced equivalent performance in the probability and magnitude conditions (i.e., increasing the charge interval only after consistently producing long IRTs at the currently programmed interval). We regard this as an interesting avenue for future research, because it would provide additional information on the differential efficiency of probability and magnitude manipulations. Regardless, it is evident from the results that behavior was more sensitive to probability in the acquisition of generalized waiting for a larger–later reward.

Self Control: Waiting versus Choosing

Developing an organism’s predilection to wait for a greater delayed consequence has implications for increasing the likelihood of attaining greater life outcomes. The behaviors with which impulsive choice correlate appear vast, and while there has been increased attention and focus on reducing impulsivity in the context of discounting, research on how to improve the ability to endure the delay to a better outcome (DG) appears sparse. Improving the propensity to choose a delayed outcome in a prospective scenario such as delay discounting is undoubtedly important, but there are also many real-life situations where an individual is not committed to a choice for a larger delayed outcome once it has been made. Being able to tolerate the delay to the better outcome can be paramount in following through with such decisions. For example, a drug abuser may prefer to quit using in order to improve health, relationships, and quality of living, but whether that individual can tolerate the delay for those outcomes upon initiating abstinence—and for outcomes that could undoubtedly take a prolonged period to achieve—may hinge upon functionally different behaviors than those of just making the choice to do so.

Regardless of whether delay discounting and delayed gratification are based on the same or different processes, the development of methods to reduce impulsivity across both contexts can provide a holistic approach to seeking ways to improve the human condition. The greater the knowledge that scientists have about how to improve behavior across these different contexts, the more efficacious our future developments can be for reducing the likelihood of maladaptive behavior.

Supplementary Material

supinfo2

Figure S2: Boxplots of IRTs as a function of the proportion of time in the assessment phase (block 4) for each participant.

supinfo1

Figure S1: Boxplots of IRTs as a function of the current charge interval in the training phase (blocks 1–3) for each participant.