Abstract
In conventional classification, soft robots feature mechanical compliance as the main distinguishing factor from traditional robots made of rigid materials. Recent advances in functional soft materials have facilitated the emergence of a new class of soft robots capable of tether-free actuation in response to external stimuli such as heat, light, solvent, and electric or magnetic fields. Among the various types of stimuli-responsive materials, magnetic soft materials have shown remarkable progress in their design and fabrication, leading to the development of magnetic soft robots with unique advantages and potential for many important applications. However, the field of magnetic soft robots is still in its infancy and requires further advancements in terms of design principles, fabrication methods, control mechanisms, and sensing modalities. Successful future development of magnetic soft robots would require a comprehensive understanding of the fundamental principle of magnetic actuation as well as the physical properties and behavior of magnetic soft materials. In this review, we discuss recent progress in the design and fabrication, modeling and simulation, and actuation and control of magnetic soft materials and robots. We then give a set of design guidelines for optimal actuation performance of magnetic soft materials. Lastly, we summarize potential biomedical applications of magnetic soft robots and provide our perspectives on next-generation magnetic soft robots.
1. Introduction
Composed of materials with moduli close to those of soft biological materials (i.e., 104 to 109 Pa), soft-bodied robots hold great promise for many important applications, particularly in biomedical areas because of their inherent mechanical compliance that can lead to enhanced safety during their operation. The use of soft materials helps to prevent tissue damage while interacting with biological tissues or organs,1–3 by allowing for continuous deformation4,5 and ensuring the mechanical similarities to the interfacing tissue. Despite the purported advantages of soft robots and burgeoning efforts to utilize them in biomedical applications, the field of soft robotics is still faced with a set of key challenges. First, conventional soft robots based on pneumatic or hydraulic actuation (i.e., fluid-driven) or antagonistic pairs of mechanical wires (i.e., tendon-driven) are mostly heavily tethered for connection to the driving actuators and supporting hardware.1,6,7 This limits their practical use in applications where tether-free actuation is required or preferred, such as implantable devices for internal organ support or controlled drug release and minimally invasive devices for therapeutic or diagnostic operations. Second, most soft robots are difficult to accurately model and control, because their actuation mechanisms often rely on highly nonlinear deformation or even instabilities while requiring complex structural designs with many passive degrees of freedom.1,3,5,8 This elusive nature of soft robots renders the traditional model-based approach for controlling rigid robots largely inapplicable.9 Third, mainstream soft robots with conventional actuation mechanisms are difficult to miniaturize down to sub-millimeter scales, because their fabrication methods are often unfavorable to such small size.3,9,10
The invention of “stimuli-responsive” or “functional” (also referred to as “smart” or “active” in the field) soft materials has led to the development of soft actuators or artificial muscles that can be controlled remotely by means of external stimuli such as heat, light, solvent, or electric or magnetic field.11 Composed of soft polymers (e.g., elastomers or hydrogels) with integrated micro- or nanomaterials as functional components, most stimuli-responsive soft materials by themselves are not new in the field of materials science. However, the recent progress in advanced fabrication techniques for functional soft materials has enabled previously inaccessible and more sophisticated designs across various length scales, facilitating the development of small-scale, untethered soft robots with programmable shape-changing capabilities.2,12,13 Among the various types of soft materials that self-actuate in response to external stimuli, magnetically responsive soft materials have shown remarkable progress in terms of both their design and fabrication, leading to the development of magnetically actuated and controlled soft robots.14–16 These magnetic soft robots possess great potential for biomedical applications because of a set of unique advantages of magnetic actuation. First, natural tissues and organs are transparent to static and low-frequency magnetic fields,17 and magnetic fields can be remotely applied without causing any adverse effects on biological systems over a wide range of actuating field strengths and frequencies.18 Second, magnetic fields are relatively easy to control in that their magnitude, phase, and frequency can be modulated accurately and rapidly.19 For these reasons, magnetic fields can offer a safe and effective means of manipulating untethered soft robots in confined spaces inside the human body.20
The potential of magnetic soft robots for biomedical applications has been demonstrated in a number of impressive examples. For instance, self-folding “origami” robots have been reported that can crawl through the gut, patch wounds, and dislodge swallowed objects;21,22 and soft “capsule” robots have been made that roll along the inner surface of the stomach and can perform biopsies and deliver medicine.23–25 Magnetically steerable robotic catheters have also been developed, which can perform minimally invasive therapeutic or diagnostic operations on the heart26–29 or in the lung airways.30 Much thinner thread-like robots have also been developed that can navigate the narrow and complex vasculature of the brain to treat intracranial aneurysms or stroke.31 Ranging from hundreds of micrometers to a few centimeters in diameter, these small-scale robots would not damage interfacing tissues owing to their soft and flexible nature. Despite the promising developments and demonstrated potential of magnetic soft robots, much work still needs to be done to make them practically useful and applicable in clinical settings. Further advancements in the field of magnetic soft materials and robots would require a comprehensive understanding of physical and chemical properties of magnetic materials and fundamental principles of magnetic actuation as well as quantitative modeling of the behavior of magnetic soft materials under applied magnetic fields. Identifying key scientific and technical challenges that remain to be overcome will also be important for developing next-generation magnetic soft materials and robots.
In this review, we discuss recent developments in the field of magnetic soft materials and robots. We first discuss various types of magnetic soft materials with different characteristics depending on the chosen magnetic and polymeric substances as well as their microscopic morphologies and configuration in the composite. Then, we discuss common strategies and underlying principles for different types of magnetic soft actuators, based on which we further discuss the quantitative modeling of magnetic soft materials and robots. We also review recent developments in the related areas of additive manufacturing and microfabrication as well as magnetic manipulation platforms as they pertain to the design, fabrication, actuation, and control of magnetic soft materials and robots. We then discuss applications of magnetic soft materials to soft robotic or electronic devices and also highlight their biomedical applications, in which we see the greatest potential of magnetic soft robots for societal impact. Finally, we provide considerations for future developments of next-generation magnetic soft materials and robots, focusing on unmet needs and remaining challenges.
2. Composition, Structure, and Properties
2.1. Classification of Magnetic Soft Materials
Historically, magnetically responsive soft materials in the form of elastically deformable solids have been referred to by a variety of terms such as magnetorheological,32–36 magnetoactive,37,38 or magnetosensitive39–41 elastomers or gels or, simply ferrogels,42–45 depending on their applications or the type of materials used. For simplicity, we refer to such elastic solids with mechanical softness or compliance as well as magnetic properties as magnetic soft materials. In our definition, and throughout this review, the term “magnetic” generally implies “strongly magnetic”. Accordingly, we will use the term “magnetic materials” to generically refer to “ferromagnetic” or “ferrimagnetic” materials that are strongly attracted to a magnet due to spontaneous magnetization (i.e., magnetic moments present in the material even in the absence of an external magnetic field). Magnetic soft materials in general have at least two constituent materials to form a composite, in which magnets of varying sizes (from nanometers to millimeters) are attached to or integrated into deformable bodies made of soft materials or flexible structures.20
Depending on the composite structure, magnetic soft materials can be classified into either discrete or continuous systems. Discrete systems have one or a few finite-sized magnets or some patches of magnetic composite attached to or embedded in the deformable body21,22,24,25,46 and hence feature highly concentrated and localized magnetic moments (Figure 1a). Continuous systems have dispersed magnetic materials usually in the form of micro- or nanoscale particles, which give rise to diluted and distributed magnetic moments throughout the composite matrices (Figure 1b). Continuous magnetic soft materials can be further divided into either isotropic or anisotropic composites, depending on the distribution and orientation of the embedded magnetic particles in the composite matrix. In isotropic composites, the magnetic particles are uniformly dispersed and randomly oriented (Figure 1c), regardless of whether the particles themselves are isotropic or anisotropic in shape. In anisotropic composites, however, the embedded magnetic particles are either connected to form microscopic chains that are aligned in the same direction or all oriented toward the same direction (Figure 1d), both of which can result from an external magnetic field applied during the solidification of the soft polymer matrix to immobilize the aligned particles.
Figure 1. Classification and composition of magnetic soft materials.
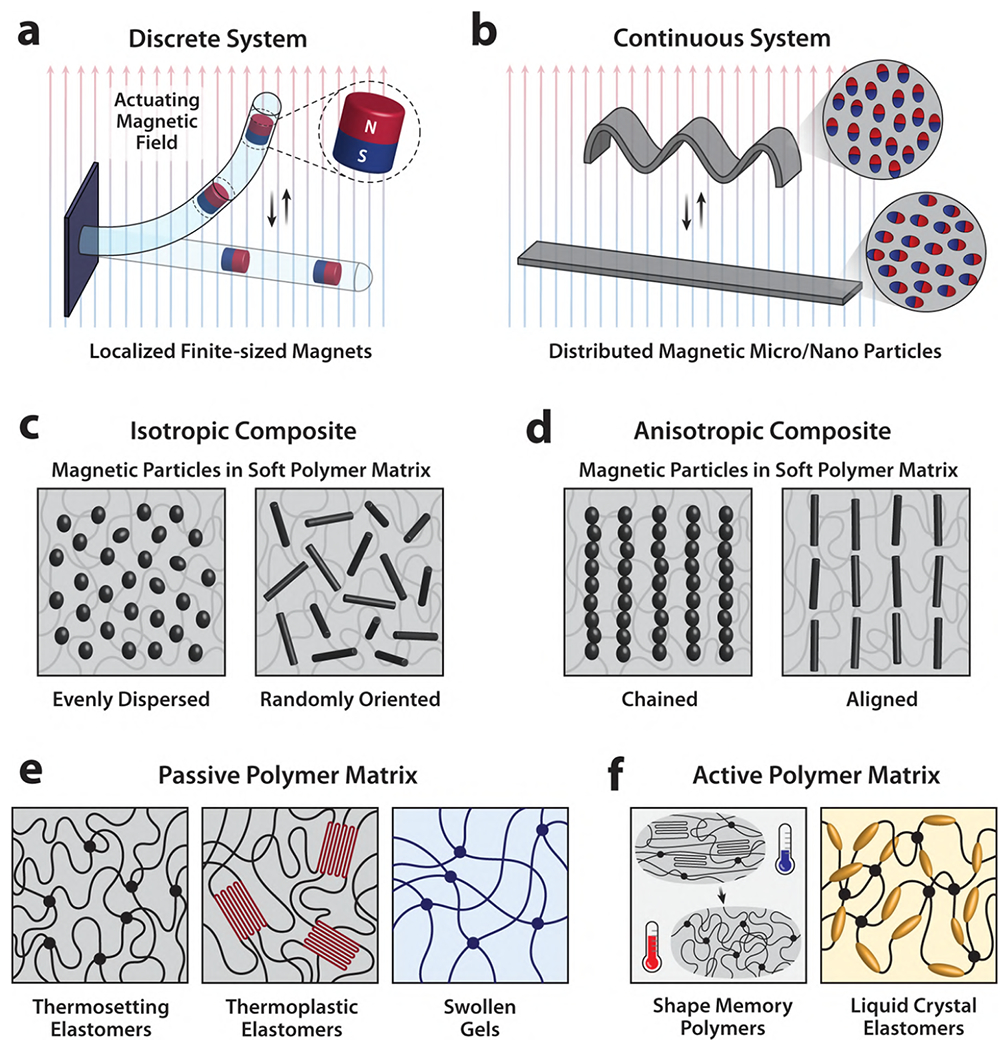
Magnetic soft materials can be classified into either (a) discrete or (b) continuous systems depending on whether the magnetic components are in the form of finite-sized magnets embedded in the flexible structure or micro- or nanoparticles dispersed in the soft polymer matrix. Continuous magnetic soft materials can be further categorized into either (c) mechanically isotropic or (d) anisotropic composites depending on the microscopic structure or arrangement of the magnetic filler particles in the host polymer matrix. The polymeric component of magnetic soft materials can be classified into either (e) passive polymeric materials such as thermosetting or thermoplastic elastomers and swollen gels or (f) active polymeric materials such as shape memory polymers or liquid crystal elastomers depending on whether the polymer matrices themselves are responsive to external stimuli to change their physical properties or produce actuation via deformation.
In the following sections, we summarize some common types of magnetic materials as functional components and discuss their physical properties and magnetic characteristics in the context of actuating magnetic soft materials. We then discuss common materials for host polymers or flexible substrates of magnetic soft materials and robots across various length scales.
2.2. Magnetic Components
Among the different classes of magnetic materials, the focus here is primarily on ferromagnetic or ferrimagnetic substances, which are generally considered “magnetic” due to their strong response to an externally applied magnetic field. Depending on the magnetization characteristics, these strongly magnetic materials can be classified into three categories: soft-magnetic, hard-magnetic, and superparamagnetic. The key difference among these types of magnetic materials can be described by the qualitatively different features of their magnetization curves (Figure 2, a–c). In doing so, two quantities of particular importance are the remanence (or remanent magnetization), Mr, and the coercivity (or coercive field), Hc. The remanence denotes the magnetization that remains in the material even in the absence of external actions once the material is magnetized by a large magnetic field. The coercivity represents the resistance to being demagnetized and measures the magnetic field strength required to reverse the remanent magnetization in the material. Other important parameters are the magnetic susceptibility χm, and the saturation magnetization Ms. The magnetic susceptibility indicates how much of the material of interest will be magnetized in a given applied magnetic field and corresponds to the slope of the magnetization curve (i.e., , where M is the induced magnetization and H is the applied magnetic field) in a differential sense for magnetically isotropic materials. As the field strength H increases, the material becomes further magnetized and eventually saturated when all moments are aligned substantially with the applied magnetic field, with the induced magnetization, M(H), approaching the saturation magnetization Ms.
Figure 2. Classification of magnetic materials and characteristics of magnetic particles with different sizes and shapes.
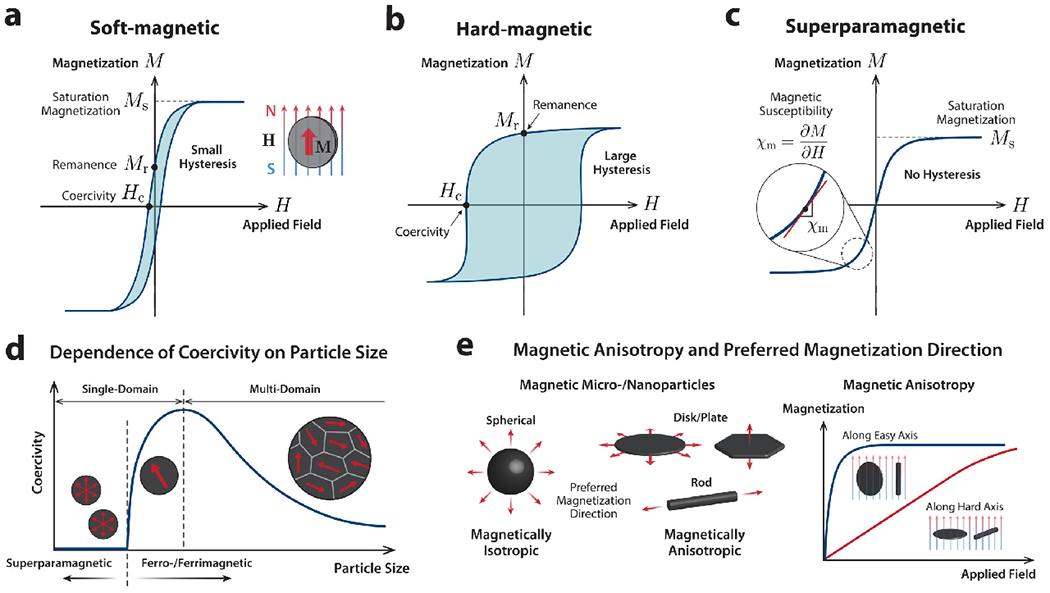
(a-c) Magnetic component of magnetic soft materials can be divided into three categories (soft-magnetic, hard-magnetic, and superparamagnetic) depending on their magnetization characteristics. In general, soft-magnetic materials are characterized by their high saturation magnetization (Ms), low coercivity (Hc), and low remanence (Mr) with narrow hysteresis curves, whereas hard-magnetic materials are characterized by large hysteresis due to their high coercivity and remanence. Superparamagnetic materials exhibit no hysteresis and become quickly saturated under relatively low fields. (d) Qualitative behavior of coercivity of magnetic particles depending on their size. The coercivity increases as the particles become smaller to approach the single-domain regime, but the coercivity disappears below a certain critical size to enter the superparamagnetic regime as the smaller particles become more susceptible to thermal fluctuation and hence cannot retain stable magnetism in the absence of external fields. (e) Magnetic particles can also be classified into magnetically isotropic or anisotropic particles depending on their particle morphology and preferred magnetization direction.
2.2.1. Soft-Magnetic Materials
Soft-magnetic materials such as iron and nickel- or silicon-based alloys of iron are characterized by high magnetic susceptibility and saturation magnetization but relatively low remanence and coercivity (Figure 2a). Owing to these properties, soft-magnetic materials are strongly attracted to a magnet and easy to magnetize, but at the same time, they are easily demagnetized as well by a relatively weak magnetic field. Conventional magnetic soft composites based on magnetorheological elastomers and ferrogels mostly use carbonyl iron or iron oxide particles embedded in soft polymer matrices. This type of composite exhibits soft-magnetic characteristics (i.e., low remanence and low coercivity) while being mechanically soft (i.e., low Young’s modulus), and we therefore refer to this type as soft-magnetic soft materials.
In general, the response of soft-magnetic soft materials to externally applied magnetic fields is complex and largely dependent on the microstructure of the composite as well as the concentration and configuration of the embedded soft-magnetic particles.47–49 Our focus here is on the qualitative description of the most representative behavior of soft-magnetic soft materials. In an unstructured isotropic composite, the application of a uniform magnetic field induces dipole-dipole interactions between the neighboring particles that are magnetized by the applied field, provided that the particles are close enough to each other due their sufficient volume fraction (Figure 3a). Under a sufficiently strong field, the magnetized particles tend to align themselves with the applied field, causing changes in their microscopic arrangement in the composite matrix and associated physical interaction between the particles and the polymer matrix. The microscopic rearrangement of the magnetized particles leads to macroscale material response, causing the matrix to elongate in the applied magnetic field direction (Figure 3a).50 Such magnetically induced deformation is often referred to as “magnetostriction” in the literature.38,47,49–52
Figure 3. Traditional magnetic soft materials and their response to externally applied magnetic fields.
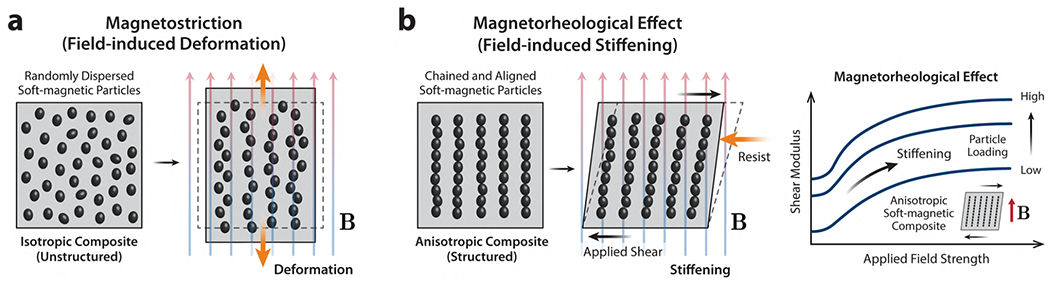
(a) Field-induced deformation (magnetostriction) of isotropic soft-magnetic soft materials with randomly dispersed particles. (b) Field-induced stiffening (magnetorheological effect) of anisotropic soft-magnetic soft materials with chained particles.
Anisotropic composites with chain-like microstructures can be obtained by applying an external magnetic field to the uncured mixture of soft-magnetic particles and polymer resin/solution during the fabrication process (Figure 3b). The applied field magnetizes the particles and induces dipolar coupling between the magnetized particles during the solidification of the composite mixture, after which the particle chains are immobilized within the polymer matrix, resulting in an anisotropic (or transversely isotropic) composite. When an external magnetic field is subsequently applied to this anisotropic composite along the chained particles, magnetic forces arise from the dipole-dipole interaction between the magnetized particles and help them maintain the interparticle orientation to oppose mechanical deformations, thereby increasing the apparent stiffness or modulus of the composite (Figure 3b),36,38,53 which is often termed the “magnetorheological effect” or field-induced stiffening. Owing to their ability to rapidly modulate the viscoelastic properties (stiffness and damping) in a reversible and controllable manner, magnetorheological elastomers and gels have found utility in vibration isolation or absorption applications.54–59
In the context of soft robotic applications, however, traditional soft-magnetic soft materials in the form of magnetostrictive or magnetorheological elastomers and gels have somewhat limited utility in terms of creating useful functions to perform a set of different tasks. For instance, it is challenging to reproduce walking gaits or grasping tasks, which typically utilize bending motions or complex shape changes, using the simple deformation based on uniaxial elongation of isotropic composites (Figure 3a). Magnetic torques can help to increase the level of complexity in terms of available actuation modes and achievable shapes by introducing additional degrees of freedom associated with the rotation of body parts. However, when the embedded soft-magnetic particles have spherical shapes, the individual particles cannot produce magnetic torques. This is because the induced magnetic moment in each particle is always aligned with the applied magnetic field, meaning zero torque, as a consequence of the spherical particles being magnetically isotropic to have no preferred magnetization direction (Figure 2e). For this reason, typical magnetosensitive elastomers and gels based on isotropic soft-magnetic soft materials have utilized force-driven magnetic actuation to create material deformation (shortening,60 elongation,42 or bending61) (Figure 4b) based on the attractive force acting on the magnetized particles under spatially nonuniform actuating fields (Figure 4a). Another force-driven actuation mode for isotropic soft-magnetic soft materials in the shape of a cylindrical rod utilizes buckling and coiling instability in the presence of confinement under a strong magnetic field,62–64 which leads to contraction of the rod in the axial direction to function as an artificial muscle (Figure 4b).
Figure 4. Different actuation modes of soft-magnetic soft materials.
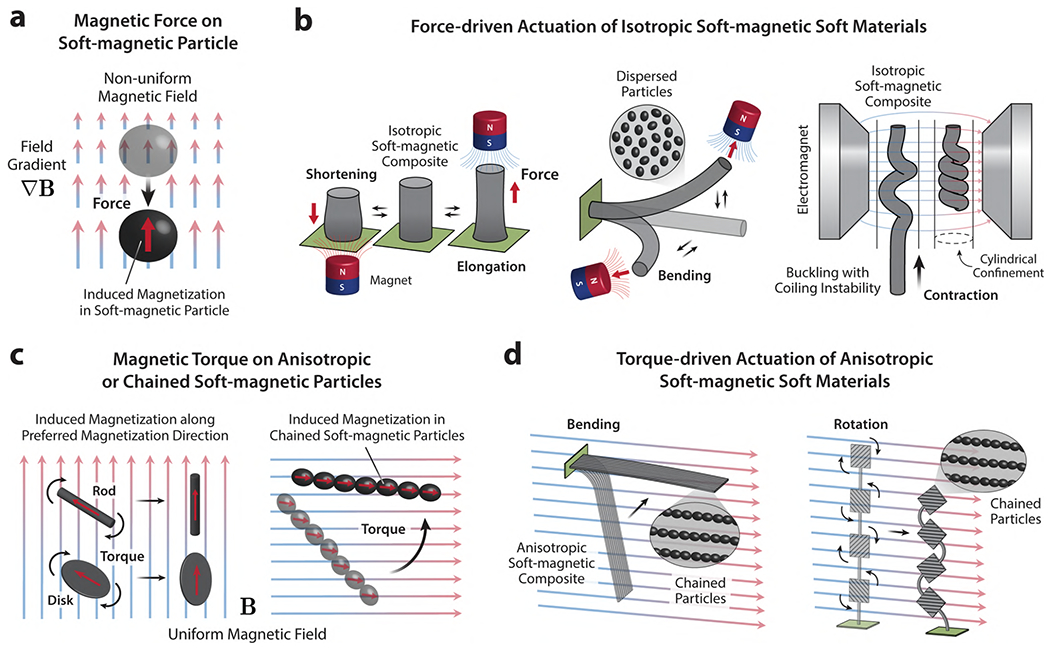
(a) Magnetic force acting on a single soft-magnetic particle under spatially nonuniform magnetic fields. (b) Force-driven actuation modes for isotropic soft-magnetic soft composites under spatially nonuniform actuating fields: shortening,60 elongation,42 bending,61 and contraction based on buckling and coiling instability.62–64 (c) Magnetic torque acting on anisotropic or chained soft-magnetic particles under spatially uniform magnetic fields. (d) Torque-driven actuation of anisotropic soft-magnetic soft composites with chained soft-magnetic particles.65–67 It should be noted that the principle of torque-driven actuation of anisotropic composites based on chained soft-magnetic microparticles65 also holds for superparamagnetic nanoparticles.66,67
To produce magnetic torques from soft-magnetic materials, one needs to break the symmetry in their response to an externally applied magnetic field by introducing some form of magnetic anisotropy in the composite matrix. Such magnetic anisotropy can be introduced by either forming chains of isotropic particles to create asymmetry at the composite level65–67 (Figure 4c,d) or employing anisotropic filler particles with nonspherical shapes (e.g., rods, spheroids, platelets)68–71 to produce local asymmetry at the particle level (Figure 2e).18,69,72 However, the magnetic torque arising from the broken symmetry due to either anisotropic particle arrangement or anisotropic particle shape is intrinsically nonlinear and hence nontrivial.73 Unlike isotropic particles in which the magnetization is always induced along the applied field, the induced magnetization in a chain of spherical particles or in a non-spherical particle (Figure 4c) is largely dependent on their shape and orientation relative to the applied magnetic field. The magnetic torque produced by a chain of isotropic soft-magnetic particles or an anisotropic particle under an applied actuating field will be described more quantitatively in Section 3.2.2, where we discuss the principles of torque-driven actuation for anisotropic soft-magnetic materials based on idealized magnetic constitutive laws.
2.2.2. Hard-Magnetic Materials
The most distinctive feature of hard-magnetic materials is that they can become a stable and permanent source of magnetic field after being magnetized, due to their large magnetic hysteresis characterized by the high coercivity and high remanence (Figure 2b). For example, the coercivities of alnico (iron alloys consisting of aluminum, nickel, cobalt, and copper) range from 30 to 150 kAm−1, which is orders of magnitude greater than that of soft-magnetic materials. In hexagonal ferrites, such as barium hexaferrite (BaFe12O19)34,46,74 or strontium hexaferrite (SrFe12O19), the coercivity can be around 300 kAm−1. It can even exceed 1000 kAm−1 in rare-earth magnets such as samarium-cobalt (SmCo5 or Sm2Co17) or neodymium-iron-boron (Nd2Fe14B). The high coercivity allows them to be relatively insensitive to external conditions (e.g., temperature and magnetic fields) and have much greater resistance to being demagnetized when compared with soft-magnetic materials. In other words, hard-magnetic materials can retain their high remanent magnetization even when exposed to external magnetic fields (below the coercive field at which the magnetization reversal occurs) or elevated temperature (below the Curie point at which the material begins to lose its remanence). When hard-magnetic particles are incorporated into a soft polymer matrix, the resulting composite can exhibit hard-magnetic characteristics (i.e., high remanence and high coercivity) while being mechanically soft, acting as a flexible and deformable permanent magnet. We refer to this type of magnetic soft composite as hard-magnetic soft materials.
One of the unique advantages of using hard-magnetic materials is that magnetic torques can be readily exploited from individual magnetic dipole moments, which act as distributed and stable actuation sources under spatially uniform magnetic fields (Figure 5a). Once the embedded hard-magnetic particles are magnetized to saturation, their remanent magnetization can be considered almost independent of the external actuating field below the coercivity. The implication of this stable remanence is that the magnetic torque acting on the material linearly increases with the applied field within the actuation range below the coercivity. As a representative example of hard-magnetic soft actuators, we consider a simple rectangular beam composed of a hard-magnetic soft material that is uniformly magnetized to have its remanent magnetization formed along the length direction (Figure 5b). Under a spatially uniform actuating field that is applied perpendicularly to the beam, the embedded hard-magnetic particles tend to align their remanent magnetization with the actuating field due to the magnetic torques, creating bending actuation of the beam toward the applied field direction (Figure 5b). Under spatially nonuniform magnetic fields, magnetic forces as well as the magnetic torques act on the particles such that they are attracted toward the direction in which the field strength increases (Figure 5c), which helps to further increase the deflection of the beam (Figure 5d).
Figure 5. Torque- and force-driven bending actuation of hard-magnetic soft materials.
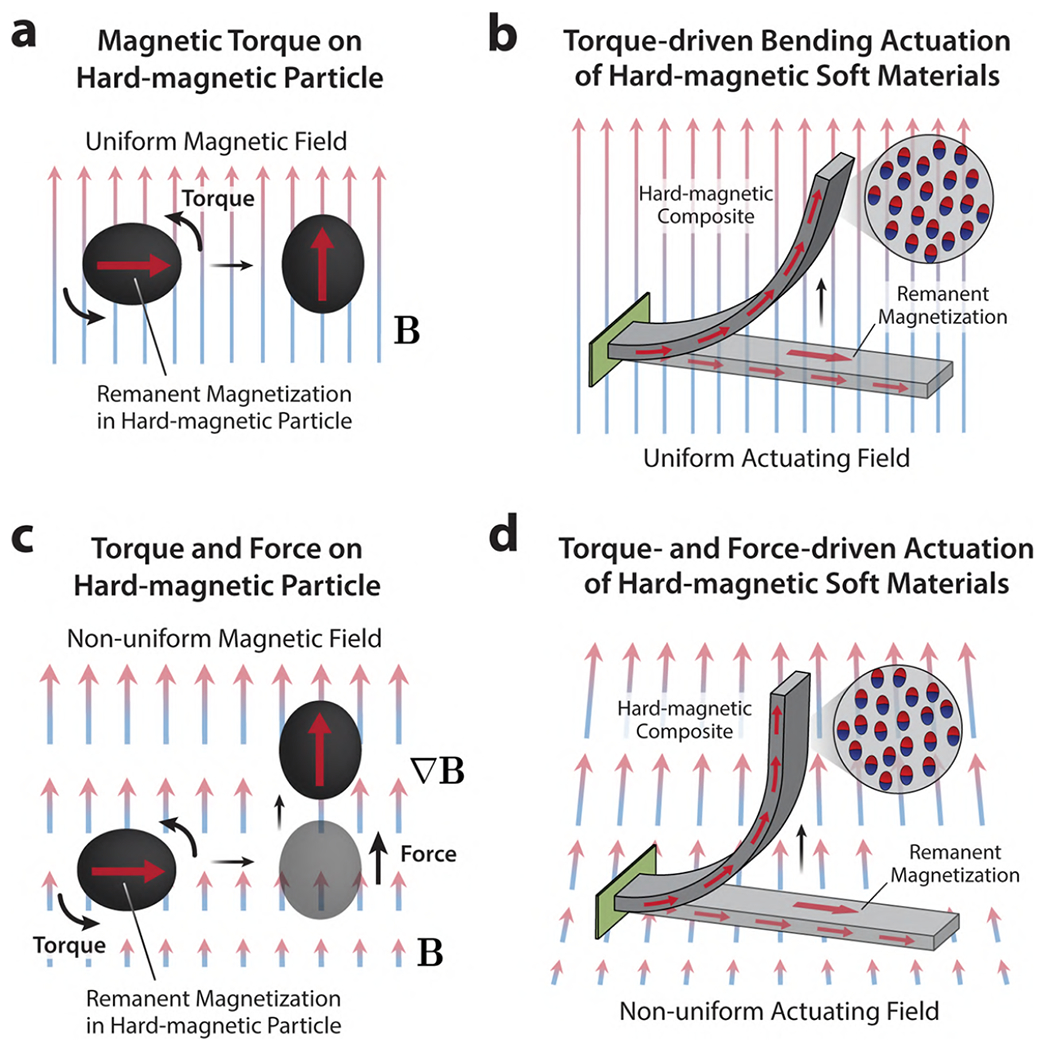
(a) Magnetic torque acting on a magnetized hard-magnetic particle under a spatially uniform magnetic field. (b) Rectangular beam made of a hard-magnetic soft composite that is uniformly magnetized along the length direction and its torque-driven bending actuation under a uniform actuating field that is applied perpendicularly to the beam’s remanent magnetization. (c) Magnetic torque and force acting on a magnetized hard-magnetic particle under a spatially nonuniform magnetic field, in which the particle not only rotates due to the magnetic torque but also moves toward the direction of the increasing field due to the attractive magnetic force. (d) Bending actuation of hard-magnetic soft materials under nonuniform actuating fields is initially driven by the magnetic torque and further supported by the increasing magnetic force as the body deforms to align its remanent magnetization with the applied field.
For such bending actuators, either isotropic or anisotropic hard-magnetic particles can be used. When using magnetically anisotropic hard-magnetic particles as distributed actuation sources (e.g., platelet-shaped barium hexaferrite particles), the neighboring particles should be oriented toward the same direction (Figure 1d) to be able to create macroscale bending actuation of the composite using the magnetic torques generated by the particles. This is because the preferred magnetization directions of magnetically anisotropic particles are constrained to their easy axes due to the shape-induced or magnetocrystalline anisotropy (Figure 2e). If the magnetized rods or platelets were randomly oriented in the composite (Figure 1c), with their magnetic moments pointing in different directions, the magnetic torques produced by the particles would cancel each other out to yield zero net torque at the composite level. The necessity of such particle alignment in the composite to produce a nonzero net torque implies that the composite is likely mechanically anisotropic to have greater stiffness along the aligned particles which essentially act as rigid, reinforcing elements.
For simplicity, it is also possible to use magnetically isotropic hard-magnetic materials such as rapidly solidified (e.g., melt-spun or gas-atomized) neodymium-iron-boron microparticles.75–77 Upon rapid quenching of the molten alloy, the solidified microparticles can develop nanocrystalline or amorphous microstructure with nanoscale grain size comparable to or less than a single magnetic domain, giving rise to their isotropic magnetization properties. Therefore, when magnetically isotropic hard-magnetic particles are used, the magnetic torque can be readily exploited regardless of the shape and orientation of the embedded particles, and thus the remanent magnetization within the composite matrix can be designed in a more flexible manner. Recent advances in the fabrication techniques have facilitated engineering hard-magnetic soft materials with programmable, complex shape-changing capabilities by enabling design of intricate magnetization patterns within the composite matrix. The resulting structures, as we shall see later, have demonstrated a rich array of actuation behavior due to the additional degrees of freedom controlled by the magnetic torque.
2.2.3. Superparamagnetic Materials
It is worth noting that the magnetization characteristics of certain magnetic materials are not necessarily their intrinsic material properties. That is, the same magnetic material can exhibit different magnetization behavior depending on its size, shape, crystalline microstructure, etc. For example, typical soft-magnetic materials such as iron, nickel, and cobalt can have relatively stable remanent magnetization when they are in the form of single-domain particles with anisotropic shape (e.g., nanorods or nanowires) due to the enhanced coercivity, which increases with their aspect ratios.78–81 The coercivity of magnetic materials is largely dependent on the particle size as well. When the size is sufficiently small (e.g., below a micrometer in diameter), magnetic particles prefer to stay uniformly magnetized and to avoid the formation of magnetic domains, exhibiting single-domain characteristics with high remanence. However, when the particles become smaller than a certain critical size, the coercivity starts to decrease drastically as the particles become more susceptible to thermal fluctuation and relaxation (Figure 2d). Hence, ferro- or ferrimagnetic particles smaller than the critical size would behave in a way analogous to paramagnetic materials with no hysteresis (i.e., no remanence in the absence of an external magnetic field), except for the fact that it still retains relatively high magnetic susceptibility (i.e., remaining strongly magnetic in the presence of an external field). For this reason, this type of behavior has been denominated as superparamagnetism. The magnetization curve of a superparamagnetic particle is characterized by the near absence of remanence and coercivity and is therefore typically modeled with the Langevin function (Figure 2c). Iron oxide nanoparticles, particularly magnetite (Fe3O4), are most commonly used for biomedical applications because of their biocompatibility.82–84
Magnetic soft composites with embedded superparamagnetic nanoparticles, which we refer to as superparamagnetic soft materials, are similar to soft-magnetic soft materials in the sense that they cannot produce magnetic torques without columnar microstructures of chained particles for providing magnetic anisotropy. Magnetic torques generated by the chained superparamagnetic nanoparticles have been demonstrated to be an effective means for driving small-scale soft bending actuators (Figure 4d).67,85,86 However, the maximum particle loading at which the nanoparticles are uniformly dispersed in the soft polymer matrix is in general far lower (i.e., typically below 10 vol%) than that of soft- or hard-magnetic microparticles.87,88 This can be attributed in part to the propensity of nanoscale magnetic particles to cluster and aggregate due to attractive van der Waals forces between the particles when the interparticle distance decreases as the particle volume fraction increases.89–91 For better dispersion and colloidal stability, magnetic nanoparticles need to be coated or functionalized with polymers to have thin shells to increase the electrostatic repulsion and steric interaction to balance the attractive forces.88–92 With the relatively low particle concentration, the field-induced stiffening or elongation behavior under an applied field is generally less pronounced in superparamagnetic soft materials than in magnetorheological elastomers or gels based on soft-magnetic microparticles. For these reasons, previously reported superparamagnetic soft materials mostly utilized magnetic forces acting on the embedded particles in the presence of field gradients (i.e., under nonuniform magnetic fields) to induce deformations at the composite level (Figure 2c),60,61,93,94 commonly in the form of macroporous sponge-like composites to maximize the strain. Overall, the relatively low particle concentration in superparamagnetic soft materials leads to low magnetic moment density per unit volume and therefore low magnetic torque and force densities in general, when compared with the other types of magnetic soft materials.
Although superparamagnetic nanoparticles may not be ideal for producing actuation due to the limitations discussed above, they could offer a unique advantage in converting electromagnetic energy into heat via thermal relaxation under an alternating magnetic field.83,95,96 Ferromagnetic microparticles can also produce heat by dissipating energy through other mechanisms such as magnetic hysteresis, where the area of the hysteresis loop is proportional to the dissipated energy. However, the energy dissipation in ferromagnetic microparticles during the cycle of magnetization and demagnetization would require either high field strength due to their greater coercivity or low frequency due to the longer time scale in their magnetization/demagnetization behavior, rendering it less effective and energy-efficient than generating heat using superparamagnetic nanoparticles. When superparamagnetic nanoparticles are incorporated into thermally responsive polymeric materials, such as shape memory polymers,97–102 liquid crystal elastomers,103,104 and temperature-sensitive hydrogels,105,106 internal heating through the released energy from the nanoparticles under alternating magnetic fields can be harnessed to induce programmed shape changes (Figure 6a) or control swelling/deswelling behavior of the composite (Figure 6b), producing indirect actuation that is different from direct magnetic actuation based on magnetic forces or torques.
Figure 6. Magnetothermal actuation of superparamagnetic soft materials based on thermally responsive polymer matrices.
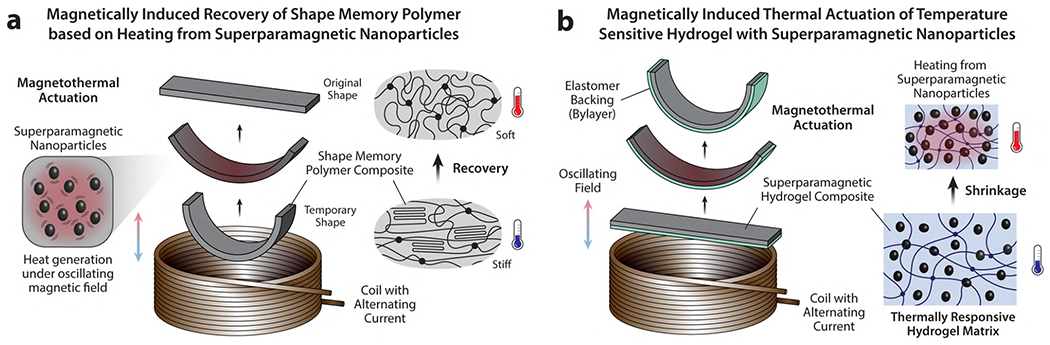
The programmed shape changes of the composite structures are triggered by field-induced heating through thermal relaxation of the embedded superparamagnetic nanoparticles under alternating fields, which leads to (a) recovery of the shape memory polymer into the original shape or (b) deswelling (shrinkage) of the temperature-sensitive hydrogel in the form of bilayer structure.
2.3. Polymeric Components
Polymeric components of magnetic soft materials account for the elasticity of the composite matrices in which the magnetic filler particles are embedded. Forces and torques acting on the individual particles under an external magnetic field generate internal mechanical stresses, causing the soft polymer matrix to deform, the extent of which is determined by how soft or flexible the material or structure is and how the polymeric material behaves under the applied stress. A variety of soft elastomers and gels can be used as host polymers for the embedded magnetic fillers, and the choice of polymeric substances depends on various factors: desired mechanical (viscoelastic) properties of the composite, physicochemical properties of the chosen polymers and their compatibility with magnetic filler particles (especially when the particles are surface-treated or functionalized), required functions and target applications, environmental conditions, fabrication schemes, and so on. In the traditional sense of magnetic soft materials, polymeric components are mostly passive (Figure 1e), while the activeness comes only from the embedded magnetic particles in response to the actuating field. More recent studies have demonstrated multifunctional magnetic soft materials that utilize thermal or photothermal actuation in tandem with magnetic actuation by using stimuli-responsive materials such as shape memory polymers107–111 and liquid crystal elastomers112 as active polymeric components (Figure 1f). In the following sections, we discuss some commonly used soft polymeric materials and their characteristics in the context of magnetic soft actuators.
2.3.1. Passive Polymer Matrices
2.3.1.1. Elastomers
Among the various types of rubber-like soft materials, silicone-based thermosetting elastomers (Figure 1e) have been most commonly used as host polymers for magnetic soft materials, primarily because they are relatively easy to handle during the fabrication process for producing composite materials. In addition, there is a wide range of commercial products with different mechanical properties available off the shelf. Some of the representative products include Sylgard 184 (Dow Chemical), Ecoflex 00-10/00-20/00-30 (Smooth-On, Inc), and Elastosil RT604/RT625/RT745 or M4601/M4644 (Wacker Chemie AG), which are addition-curing type silicone elastomers that can be cured at either elevated temperature (faster curing) or room temperature (slower curing) upon the addition of platinum-based catalysts. Unless too heavily loaded, magnetic particles can be mixed easily with the base liquid of uncured silicone resin using a planetary centrifugal mixer before adding the catalysts. However, it is worth noting that microparticles or agglomerates of nanoparticles can settle in the uncured mixture after some time due to gravitational sedimentation of the dispersed particles, leading to phase separation in the composite mixture. For composites based on hard-magnetic microparticles, it has been shown that the uncured composite mixture can become a thixotropic paste when the dispersed particles are permanently magnetized, which helps to prevent the sedimentation of the dispersed particles over time.31 After mixing with the curing agent (catalysts), the composite mixture can be cast, molded, or printed to obtain desired shapes upon curing and solidification. The inclusion of rigid filler particles generally leads to the reinforcement of the elastomer, making the composite stiffer and less stretchable than unfilled elastomers. The increased stiffness and reduced stretchability can be compensated to some extent by lowering the cross-linking density of the silicone elastomer network by reducing the amount of the cross-linking agent during the fabrication process.
Thermoplastic elastomers have also been used as the host polymers for magnetic soft composites, where common types of materials include thermoplastic polyurethane65,66,113 and styrene-ethylene-butylene-styrene (SEBS),114–116 which are essentially block copolymers with alternating rigid and flexible segments. The rigid crystalline segments serve as physical cross-links to form a copolymer network (Figure 1e), while the flexible amorphous segments provide the network with elasticity.117 At elevated temperature, the rigid segment becomes disentangled and softer, making the polymers melt-processable. Upon cooling, the rigid segment solidifies again, and the material regains its strength and elasticity. Magnetic particles can be mixed into the molten thermoplastic elastomers through a process called melt blending or compounding, typically using a twin-screw extruder, and then formed into desired shapes through different manufacturing processes such as extrusion, injection, blowing, and compression molding. However, such melt-processing requires dedicated facilities that are often too bulky and costly for a single laboratory to have for research purposes. Hence, it is not uncommon to use organic solvents (i.e., tetrahydrofuran65 or dimethylformamide31) to dissolve the thermoplastic elastomers for blending with magnetic particles as well as processing at room temperature. The mixture can be cast, molded, or printed into desired forms that solidify upon evaporation of the solvent. This method, so-called solvent casting, however, inevitably entails a certain level of shrinkage of the composite volume during the solidification process as a result of the evaporation of the solvent molecules.
Thermoplastic elastomers in general have more desirable mechanical properties in terms of the strength and toughness and are hence more durable than silicone elastomers. However, magnetic soft composites based on thermoplastic elastomers generally exhibit smaller deformations due to their higher modulus values, when compared with softer silicone-based composites under the same conditions in terms of the geometry, magnetic particle concentration, and actuating field strength. Therefore, when it comes to design and actuation, magnetic soft materials and robots based on thermoplastic elastomers often require their structural rigidity (i.e., bending stiffness) to be smaller or the actuating magnetic fields to be stronger when compared with silicone-based magnetic soft materials and robots. In the context of biomedical applications, there exist medical-grade silicone and thermoplastic elastomers that are mechanically soft while at the same time biocompatible to be used for medical devices. Being thermosetting polymers, silicone elastomers are resistant to heat, and hence silicone-based magnetic soft materials can be readily sterilized by heat (dry heat or steam autoclave). When hard-magnetic components are used, however, elevated temperature can potentially affect the programmed magnetization pattern and the magnetization strength due to thermal relaxation and randomization as discussed earlier. Therefore, if applicable, the heat sterilization should precede the magnetization process during the fabrication; otherwise, other sterilization methods such as ethylene oxide treatment are preferred. Electron beam or gamma ray irradiation can be used, in principle, but these sterilization methods based on ionizing radiation can cause changes in the mechanical properties of silicone and thermoplastic elastomers,118,119 which may affect the actuation performance as well.
2.3.1.2. Gels
Gels generically refer to semisolids composed of cross-linked or colloidal polymer networks with entrapped liquids throughout the entire volume of the swollen polymer network (Figure 1e). With a relatively low polymer content, gels are generally much softer than elastomers. The focus here, in the context of magnetic soft materials and robots, is primarily on cross-linked gels (elastic solids), which exhibit much greater elasticity than colloidal gels (complex fluids with finite yield stresses). Composed of hydrophilic polymers, gels containing water as a swelling agent are referred to as hydrogels, while gels swollen in organic solvents or oils are referred to as organogels. Organogels based on styrenic block copolymers such as styrene-ethylene-butylene-styrene (SEBS) or styrene-butadiene-styrene (SBS) swollen in paraffin or mineral oils120–122 as well as polyurethane or silicone gels123 have been used with carbonyl iron particles, mostly for vibration isolation and absorption applications. For biomedical applications such as targeted drug delivery, hydrogels have been more commonly used because of their purported advantages in terms of biocompatibility or biodegradability.124 As the host polymers for magnetic filler particles, hydrogels based on naturally occurring polysaccharides such as alginate,60,93 carrageenan,59,125–127 and scleroglucan128 or hydrogels based on synthetic polymers such as poly(vinyl alcohol),43,129–131 poly(N-isopropylacrylamide),105,132–134 and polyacrylamide135–137 have been used. Poly(N-isopropylacrylamide) has been used to design thermally responsive magnetic soft robots with dual (magnetic and photothermal) actuation for multimodal locomotion134 or thermal actuation combined with magnetic guidance or navigation.132 When compared with elastomers, hydrogels are in general mechanically weak and brittle138,139 due mainly to their high water content (i.e., low polymer content), and so are most of the hydrogel-based magnetic soft composites. To improve their mechanical robustness while maintaining the softness, highly stretchable and tough hydrogels based on double networks of polyacrylamide-alginate61 or physically cross-linked poly(N,N-dimethylacrylamide) by nanoclays140 have also been adopted for magnetic soft materials.
For hydrogel-based magnetic soft materials, it should be noted that ferromagnetic particles can be corroded in the aqueous environment of hydrogels (Figure 7a). The corrosion process can be accelerated in the presence of dissolved ions which are used as physical cross-linkers for ionically cross-linked hydrogels (e.g., alginate, chitosan, hyaluronan, etc.). Partly because of this corrosion problem, relatively inert (i.e., already oxidized) iron oxide nanoparticles have been more commonly used as filler particles for magnetic soft composites based on hydrogels. To prevent corrosion of ferromagnetic particles in hydrogels, protective coating can be applied to the particle surface (Figure 7b) through different methods. As an example, microparticles of carbonyl iron141–143 and neodymium-iron-boron31 can be coated with a thin layer of silica (SiO2) through hydrolysis and condensation of tetraethyl or tetramethyl orthosilicates (TEOS/TMOS), also known as the Stober method, followed by the nucleation of silica around the magnetic particles (Figure 7d). Other methods for introducing an inert passivation layer on the surface of ferromagnetic particles include plasma electrolytic deposition,144 atomic layer deposition,145,146 chemical vapor deposition,147 and those based on chemical reactions for surface polymerization and polymer grafting.148–150 Anti-corrosion coating is also useful for elastomer-based composites, when they are coated with hydrogel skin (Figure 7c) to enhance lubrication and biocompatibility for biomedical applications.31
Figure 7. Silica coating on magnetic particles for corrosion prevention.
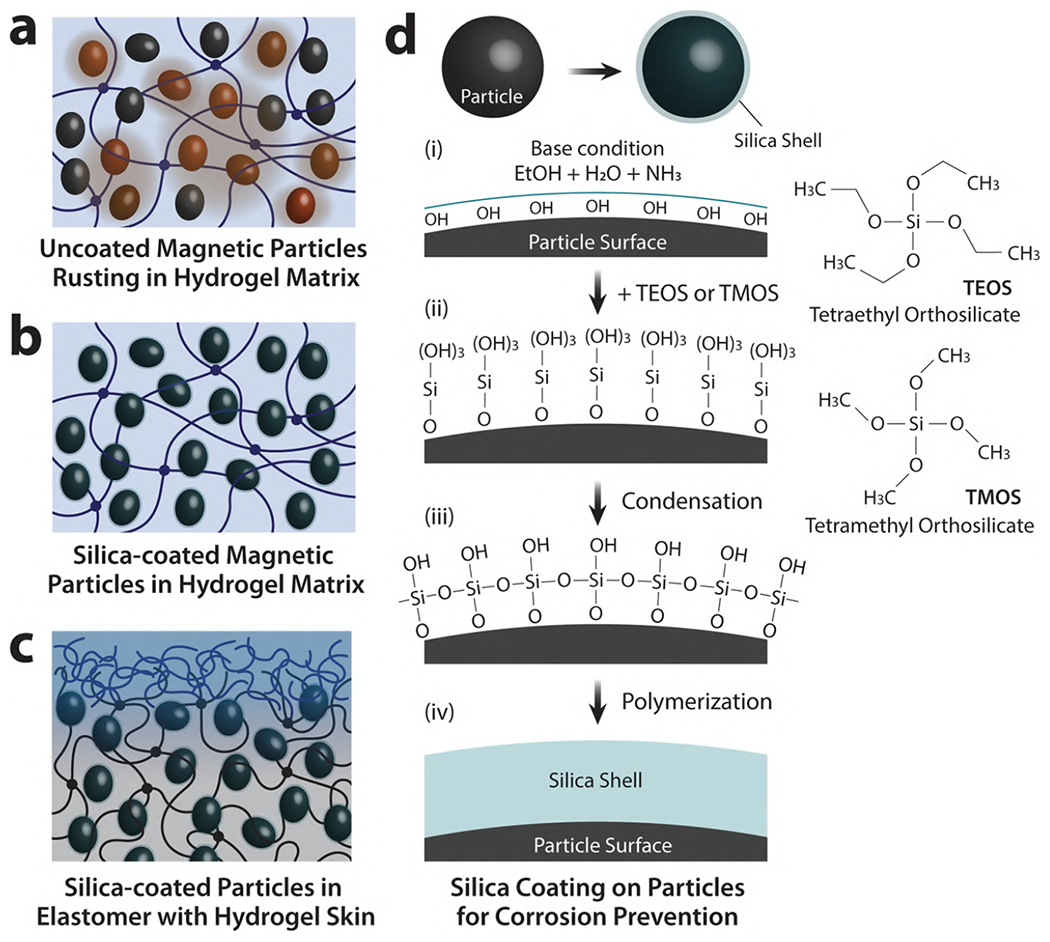
(a) Corrosion of ferromagnetic particles in the aqueous environment of magnetic soft composites based on hydrogels. Silica-coated ferromagnetic particles for corrosion prevention in (b) hydrogel-based composites or (c) elastomer-based composites with hydrogel skin for biocompatibility and lubrication. (d) Schematic of the polycondensation reaction of tetraethyl and tetramethyl orthosilicate (TEOS/TMOS) in the presence of catalysts under basic conditions, in which the nucleation and polymerization of TEOS/TMOS give rise to cross-linked layers of silica around the magnetic particles.31
2.3.2. Active Polymer Matrices
Magnetic soft composites based on passive polymer matrices (i.e., elastomers or gels) undergo elastic deformation under an externally applied field and revert to their original shape upon the removal of the applied field. The fact that the deformed state can be maintained only in the presence of an external actuating field may in some cases be considered an inherent limitation of magnetic soft materials for their applications to where semipermanent shape changes are preferred.
Aimed at enabling magnetic soft materials to maintain their actuated state or deformed shape without continuously applying an actuating field, thermally responsive shape memory polymers (Figure 1f) have been adopted as the polymeric component of both soft- and hard-magnetic soft materials.107–111 Thermally activated shape memory polymers are generally stiff below the transition temperature and become softer and more malleable when heated to reach the transition point. When soft-magnetic or hard-magnetic particles are incorporated as distributed actuation sources in shape memory polymers, the composite can be deformed at or above the transition temperature into a desired shape through force- or torque-driven actuation under externally applied magnetic fields. Upon cooling below the transition point, the composite becomes stiffer again to maintain the deformed shape. The deformed composite can revert to its original shape when heated above the transition temperature in the absence of external fields or deform into a new temporary shape when heated in the presence of another actuating field to magnetically induce the deformation. It is worth noting that there is a key difference between this type of magnetically deformable shape memory polymer with shape-locking ability and the conventional type of magnetically activated shape memory polymers97–102 discussed earlier (see Section 2.2.3). The conventional type mostly used heat generated by the embedded superparamagnetic nanoparticles under oscillating fields to trigger the shape memory effect to recover its original shape from the temporary shape (Figure 6a) as an indirect means of magnetic actuation. When the two approaches are combined by adding different types of magnetic particles, such as hard-magnetic microparticles for magnetic actuation and superparamagnetic nanoparticles for magnetic heating, it has been shown that the composite can provide fully magnetically controlled actuation with shape-locking capability.107
Another class of stimuli-responsive polymeric substances for magnetic soft materials is liquid crystal elastomers, which are loosely cross-linked soft polymers containing anisotropic (rod-like) molecules called mesogens that are covalently attached to the polymers96,151 either as side chains or within the main chains (Figure 1f). When heated above their transition temperature, liquid crystal elastomers undergo a large contraction along the direction of mesogen alignment, as the mesogens undergo a phase transition from an ordered (nematic) state to a disordered (isotropic) state. Complex shape changes can be programmed into liquid crystal elastomers by controlling the mesogen alignment in the nematic phase. Unlike shape memory polymers with mostly one-way actuation, liquid crystal elastomers can produce large deformation in a reversible manner. As is the case with shape memory polymers, liquid crystal elastomers have also been used along with superparamagnetic nanoparticles to exploit magnetic heating for triggering the nematic-isotropic phase transition103,104 as discussed in Section 2.2.3. Recently, hard-magnetic soft composites based on liquid crystal elastomers have been used to develop small-scale untethered soft robots capable of distinct locomotion in different environments, such as walking on a solid surface or swimming by helical propulsion in a warm liquid after thermally induced shape change.112
3. Modeling of Magnetic Soft Materials
A comprehensive understanding of the fundamental principles for magnetic actuation, as well as the physical properties and behavior of magnetic materials, plays a key role in the design of magnetic soft materials and robots. When the behavior of magnetic soft materials is modeled, the different magnetic characteristics and constitutive relations for the chosen magnetic and polymeric components should be considered. For example, magnetized hard-magnetic particles can produce torques under externally applied fields, whereas soft-magnetic or superparamagnetic particles do not generate torques unless there is some form of magnetic anisotropy. Therefore, to exploit torque-based actuation with soft-magnetic or superparamagnetic materials, one needs to use particles with asymmetrical shapes or chained particles. In the following sections, we first review some of the fundamental magnetostatic relations and discuss how the magnetic force and torque can be formulated for hard-magnetic, soft-magnetic, and superparamagnetic soft materials.
3.1. Principles of Magnetic Actuation
3.1.1. Force and Torque on a Magnetic Dipole
The actuation of magnetic soft materials relies on forces and torques acting on the embedded magnetic components under externally applied magnetic fields. When a magnetic dipole (point-like source) with the magnetic moment m is located at the position x in free space under an externally applied magnetic field B, it possesses the magnetic potential energy um (also known as Zeeman energy) defined as the dot product of the two vector quantities as
| (1) |
A small variation in the position and orientation of the magnetic moment, with the constraint of fixed magnitude |m|, causes the change in the potential energy, which can be expressed as
| (2) |
For irrotational (i.e., curl-free) magnetic fields with no free electric currents (see Eq.(10) below), Eq.(2) can be transformed using relevant vector and tensor identities into an equivalent form as
| (3) |
where δx is the change in the magnetic moment position, and δθ is a vector that points along the axis of rotation with its magnitude corresponding to the angle of rotation of the magnetic moment m. In Eq. (3), grad B represents the spatial gradient of the applied magnetic field with respect to the point x. It is worth noting that the infinitesimal rotation of the magnetic moment δm is related to δθ by the following cross-product relation: δm = δθ × m. From Eq. (3), the magnetic force, fm, acting on the magnetic moment is given by
| (4) |
while the magnetic torque, τm, acting on the magnetic moment is given by
| (5) |
It is worth noting that Eq.(4) can be expressed equivalently as
| (6) |
using a more common expression in the literature based on the vector operator ∇ = (∂/∂xi) ei (also called the nabla operator), where ei represents the three Cartesian basis vectors (i = 1, 2, 3).
From Eq.(5) we know that the magnetic torque vanishes when the magnetic moment m is aligned (either parallel or antiparallel) with the actuating field B. We also know from Eq.(4) (or equivalently from Eq.(6)) that the magnetic force fm exists only in the presence of magnetic field gradients. This implies that the actuation based on spatially uniform magnetic fields is driven solely by the magnetic torque τm. Under spatially nonuniform actuating fields, magnetic forces as well as torques can contribute to the actuation of magnetic soft materials. In Eq.(6), (m · ∇) denotes the directional derivative in the direction of m multiplied by its magnitude. Physically, this implies that the magnetic force can be produced when there is a variation in the applied field in the direction of the magnetic moment. In general, it is the magnetic torque that drives the actuation by rotating the magnetic object to align its remanent or induced magnetic moment with the applied field, while the magnetic force attracts the aligned object in the direction of increasing field strength (Figure 5, c,d), usually toward the external source of actuating magnetic fields.
3.1.2. Fundamental Equations in Magnetostatics
In the presence of homogeneous magnetizable media, it is often more convenient to introduce an additional field, the H field, which shares with B the name and the status of magnetic field (for differentiation, B is usually termed the magnetic induction or flux density, while H is called the magnetic field).152 B and H fields are related by
| (7) |
where μ0 is the magnetic permeability of free space (vacuum) and M is the magnetization that measures the average magnetic moment density in the magnetic media (per unit volume). The magnetization vector at a material point x can be defined such that
| (8) |
where m is the total magnetic moment and V is the volume of the magnetic media. When the material is uniformly magnetized, Eq.(8) becomes m = VM. It is worth noting that B and H fields are simply related by B = μ0H in the absence of magnetizable media, under which Eqs.(1) to (6) can also be written in terms of H fields.
For magnetostatic systems with no time variation of the pertinent electromagnetic quantities, the Maxwell’s equations in differential forms can be stated as
| (9) |
| (10) |
where div B denotes the spatial divergence of B fields, curl B denotes the spatial curl of B fields, and J is the electric current density. The boundary conditions corresponding to Eqs.(9) and (10) are given by
| (11) |
| (12) |
where n is the outward unit normal to the boundary, ⟦ ⟧ denotes the jump of the field at the interface (i.e., ⟦B⟧ = Bout − Bin), and K denotes the surface current density. Eq.(9) is also known as Gauss’s law for magnetism and states that no magnetic monopoles exist and suggests that B fields should be solenoidal (divergence-free).
Substituting Eq.(7) into Eq.(9) leads to the definition of magnetic charge density, ρm, in the material (per unit volume) which is given by
| (13) |
from the analogy to the description of the electric charge density in electrostatics, except for the absence of magnetic monopoles, which are analogous to unpaired electric charges. Although they have no physical existence, the concept of magnetic charges often provides a useful abstraction when understanding the behavior of a magnetized body (Figure 8).152 Eq.(10) is usually referred to as Ampere’s law and can also be expressed by using Eq.(7) as
| (14) |
where Jf denotes the free electric current density, along with the definition of the magnetization current density Jm given by
| (15) |
with the total current density given by the sum of two: J = Jf + Jm. Eq.(14) requires H fields to be irrotational (curl-free) when there is no free current (i.e., Jf = 0), while Eq.(15) allows the magnetization to be treated as a current.
Figure 8. Graphical representation of a uniformly magnetized body.
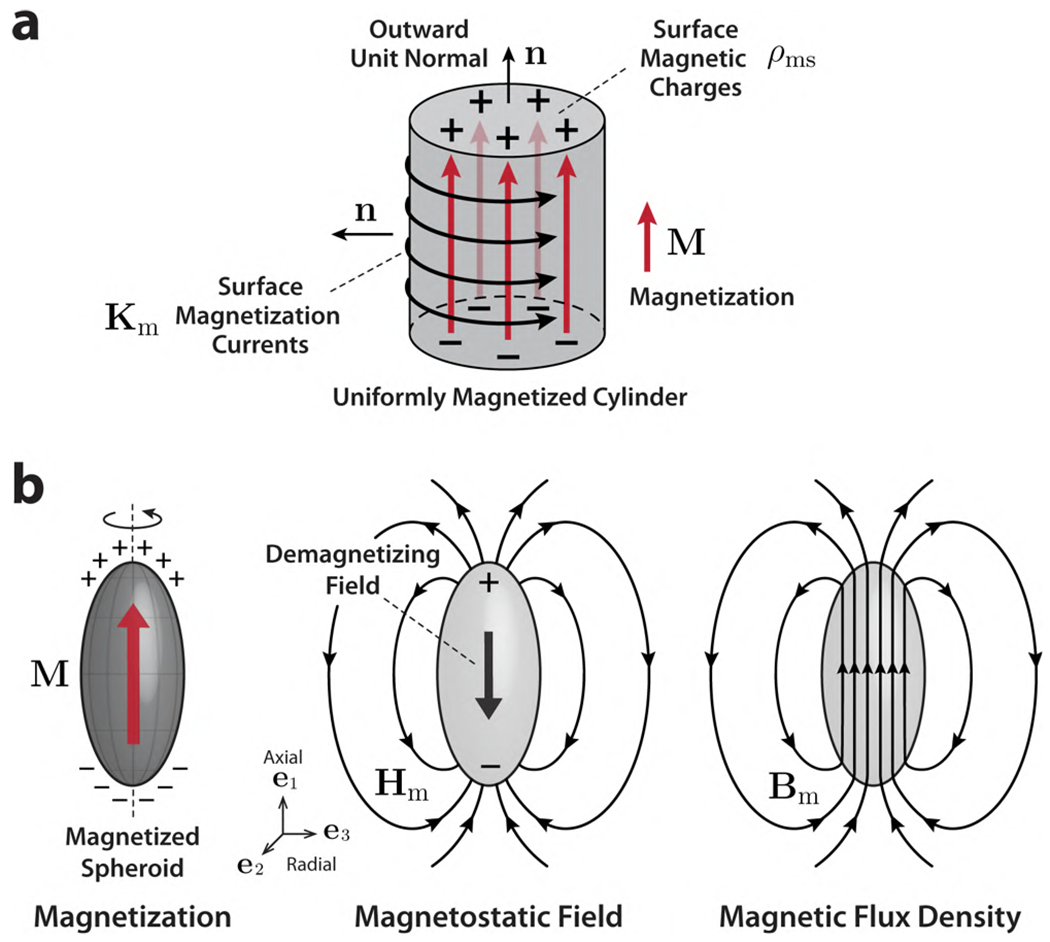
(a) Uniformly magnetized cylinder with graphical representations of the surface magnetic charges (ρms) and the magnetization currents (Km). (b) Magnetization (M), magnetostatic field (Hm), and magnetic flux density (Bm) of a uniformly magnetized spheroid, which represent the effect of a demagnetizing field inside the magnetized body.
At the material surface, the magnetic surface charge density (per unit area), denoted by ρms, can be defined from Eq.(13) as
| (16) |
while the boundary conditions for Eqs. (14) and (15) are given by
| (17) |
| (18) |
where Kf denotes the free surface current density and Km is the surface magnetization current density. Since the magnetization is zero outside the body (Figure 8a), which yields ⟦M⟧ = −M, the boundary conditions for a magnetized body given in Eqs. (16) and (18) can be simplified as ρms = μ0M · n and Km = M × n, respectively.
The H fields being irrotational in the absence of free electric currents from Eq.(14) implies that the magnetic scalar potential, denoted by Φ, can be defined such that
| (19) |
from the vector identity, curl (grad f) = ∇ × (∇f) ≡ 0, which holds for any scalar field f(x). Then, from Eqs.(13) and (19), it follows that the magnetic scalar potential Φ obeys Poisson’s equation:
| (20) |
which reduces to ∇2Φ = 0 for uniformly magnetized materials with no divergence (∇ · M = 0).
3.1.3. Magnetostatic and Demagnetizing Fields
In the absence of magnetizable media (i.e., M = 0), the externally applied magnetic field in empty space can be expressed as Ba = μ0Ha from Eq.(7), with the subscript a used to denote the applied fields. When a magnetizable body is introduced into the space, it becomes magnetized by the externally applied field Ha to have the induced magnetization M inside the body. Then, it follows from Eq.(16) that positive and negative magnetic surface charges are induced on its top and bottom surfaces, respectively (Figure 8b). The surface charges induce another magnetic field, often termed the magnetostatic field and denoted by Hm, originating from the positive charge at the top and terminating on the negative charge at the bottom. Then, the total magnetic field H can be expressed as
| (21) |
and from Eq.(7), the corresponding B field (magnetic flux density) becomes
| (22) |
with Bm = μ0 (M + Hm) inside the body and Bm = μ0Hm outside the body and with Ba = μ0Ha everywhere. It is worth noting that because ∇ · Ba = ∇ · μ0Ha = 0 from Eq.(9), that Eqs.(13) and (16) can be expressed in terms of the magnetostatic field Hm by simply replacing H with Hm.
In a uniformly magnetized body, the magnetostatic field Hm acts to oppose the magnetization M and hence reduces the overall magnetization (Figure 8b). For this reason, the magnetostatic field Hm inside the body is often termed the demagnetizing field and is given by
| (23) |
where denotes the demagnetizing tensor. When the coordinate frame is chosen such that the Cartesian axes are aligned with the principal axes of the magnetized body, the demagnetizing tensor becomes diagonal in the following matrix form:
| (24) |
where Ni (i = 1, 2, 3) represents the three eigenvalues that correspond to the demagnetizing factors associated with each of the principal axes. These demagnetizing factors obey the general constraint N1 + N2 + N3 = 1, which suggests that N1 = N2 = N3 = 1/3 when the body is of spherical shape due to symmetry. For an ellipsoidal body with axial symmetry (i.e., the spheroid in Figure 8b), the demagnetizing factors are further constrained by N2 = N3 = (1 – N1)/2, with N1 denoting the demagnetizing factor along the axis of symmetry and N2 = N3 denoting the factors along the radial directions perpendicular to the symmetry axis.
In an idealized sense, a magnetic body can be considered an assembly of magnetic moments that are subject to magnetostatic interactions with each other. Then, the mechanical work spent in building the body by assembling the elementary magnetic moments can be represented by the magnetostatic energy, which is determined by the spatial distribution of the magnetization and by the geometric shape of the magnetic body. The magnetostatic energy density (per unit volume) is defined by
| (25) |
which is calculated as when the coordinate frame is aligned with the principal axes of the body. For isotropic (spherical) particles, the magnetostatic energy density can be expressed as with M denoting the magnitude of the magnetization.
3.2. Modeling of Magnetic Actuation
3.2.1. Idealized Magnetic Constitutive Laws
The constitutive law of a magnetic medium describes the material’s response to the magnetic field acting on it and can be stated in the form of either M(H) or B(H), with H denoting the field experienced by the material. In general, the constitutive laws for ferromagnetic materials can be quite complex when the magnetization process exhibits anisotropic, nonlinear, and hysteretic behavior. Therefore, to simplify the analysis without loss of generality, it is often practically more advantageous to idealize the constitutive laws for typical magnetic materials.
In soft-magnetic materials, the induced magnetization is largely dependent on the applied field and hence the magnetization process should be taken into account when modeling their behavior. In the presence of magnetic anisotropy, the induced magnetization is dependent on the particle orientation and can occur in directions other than that of the applied magnetic field. Ideal soft-magnetic materials are assumed to have no hysteresis (i.e., zero remanence and zero coercivity) as superparamagnetic particles (Figure 2c). In addition, at low fields below the saturating field, Hsat, the induced magnetization M in ideal soft-magnetic materials is assumed to increase linearly with the magnetic field H experienced by the material (Figure 9a), until it reaches the saturation magnitude (denoted Ms in Figure 9a). The constitutive law for such linearly magnetic materials can be stated as
| (26) |
where χm denotes the magnetic susceptibility of the soft-magnetic particle under the applied field and Ms represents the saturation magnetization of the particle. It is worth noting that χm is a dimensionless constant on the order of 103 to 106 for typical soft-magnetic materials. It is also worth noting that the graphical representation of the constitutive law for ideal soft-magnetic materials in Figure 9a shows the representative magnetization curve where both the induced magnetization M and the applied magnetic field Ha point along the same direction.
Figure 9. Idealized magnetic constitutive laws for soft-magnetic and hard-magnetic materials.
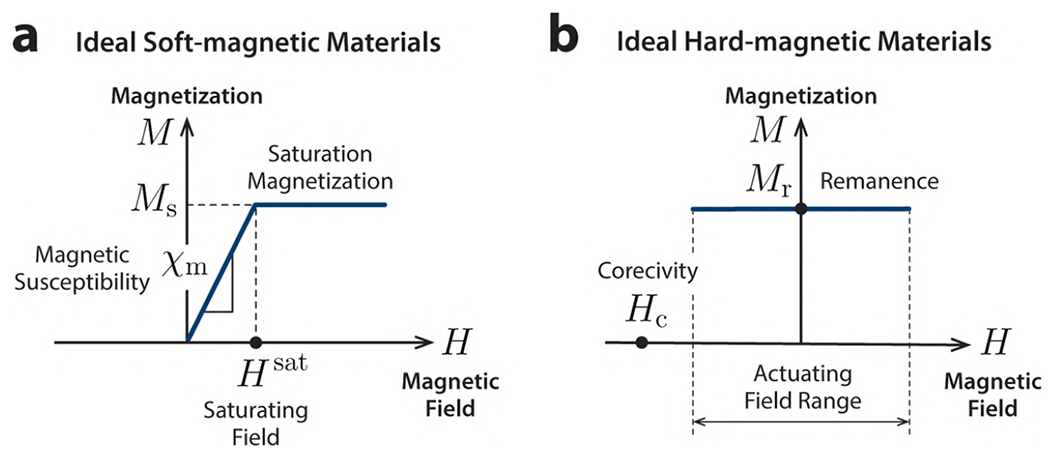
(a) Ideal soft-magnetic materials are characterized by the linear relationship between the induced magnetization and the magnetic field with constant magnetic susceptibility before saturation and constant magnetization after saturation without magnetic hysteresis (zero remanence and coercivity). (b) Ideal hard-magnetic soft materials are characterized by large magnetic hysteresis (high remanence and coercivity) to maintain the remanence under an actuating field below the coercivity.
In contrast to soft-magnetic materials, ideal hard-magnetic materials are considered to have strong hysteresis (i.e., high remanence and high coercivity). When hard-magnetic particles are magnetized to saturation, they can be regarded as small permanent magnets whose magnetic moments (or remanent magnetization) are independent of the actuating field below coercivity, Hc (Figure 9b). Thus, in the context of magnetic actuation, the constitutive law for ideal hard-magnetic materials can be expressed as
| (27) |
where Mr is the remanent magnetization of the hard-magnetic particle after magnetization. The constitutive law for ideal hard-magnetic soft materials in Eq.(27) implies that there is no energy transformation related to the magnetization process taking place during actuation.
3.2.2. Ideal Soft-Magnetic Materials
3.2.2.1. Shape-Induced Magnetic Anisotropy
The induced magnetization in soft-magnetic materials is largely dependent on the particle orientation due to the magnetic anisotropy and hence is not necessarily collinear with the applied magnetic field. Among the different causes of magnetic anisotropy, our focus here is on the shape-induced anisotropy, which originates from the magnetostatic energy when the particles are not of spherical shape. Applying the relations given in Eqs.(21) and (23), the linear constitutive law for soft-magnetic particles in Eq.(26) (for ) can be written as
| (28) |
which can be rearranged and expressed as a function of the externally applied field Ha as
| (29) |
where I denotes the identity tensor and is defined for convenience as the apparent magnetic susceptibility tensor,73 which relates the induced magnetization M in an anisotropic particle with the applied magnetic field Ha. Then the idealized constitutive law for soft-magnetic particles can be expressed in terms of the applied field Ha as
| (30) |
with denoting the applied field at which saturation takes place.
For isotropic soft-magnetic particles of spherical shape, the apparent magnetic susceptibility tensor is given by , which makes the two vectors M (induced magnetization) and Ha (applied magnetic field) collinear so as to produce no magnetic torques. For anisotropic (i.e., nonspherical) soft-magnetic particles, the susceptibility tensor is largely dependent on the particle shape as well as its orientation and hence can be complicated in general. To simplify the analysis while illustrating the soft-magnetic characteristics without loss of generality, we can assume that the particles are of ellipsoidal shape, for which the demagnetizing factors are known to have tractable analytical expressions.153 To make the problem even simpler, we can further assume that the ellipsoidal particles have axial symmetry to be essentially spheroids (Figure 8b). There are two types of spheroids: prolate spheroids have symmetry around their long (i.e., easy) axes (Figure 10a), whereas oblate spheroids are symmetric around their short (i.e., hard) axes (Figure 10b). When the coordinate frame is chosen to be aligned with the principal axes of the spheroidal particle, such that its symmetry axis lies with the Cartesian basis e1 (Figure 10), the demagnetizing tensor becomes diagonal as given in Eq.(24). Then, the apparent susceptibility tensor also takes the diagonal matrix form, which is given by
| (31) |
with N1 = NA denoting the magnetization factor along the symmetry axis of the spheroidal soft-magnetic particle and N2 = N3 = NR along the radial directions perpendicular to the symmetry axis under the constraint NA + 2NR = 1.
Figure 10. Anisotropic soft-magnetic particles of spheroidal shape.
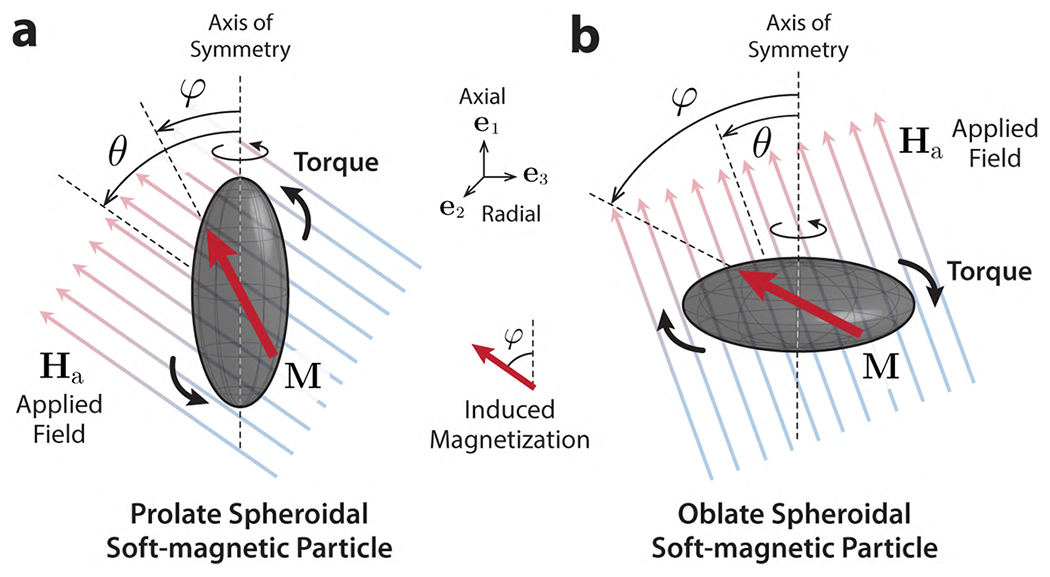
(a) Prolate and (b) oblate spheroidal (ellipsoid with axis symmetry) soft-magnetic particles under externally applied magnetic fields (at an angle θ relative to the symmetry axis) and the induced magnetization (at an angle φ relative to the symmetry axis) that is not parallel to the applied field due to the presence of shape anisotropy.
3.2.2.2. Induced Magnetization Direction
When an actuating magnetic field Ha is applied to a spheroidal soft-magnetic particle at an angle θ with respect to the particle’s axis of symmetry (Figure 10), the magnetization M is induced toward the long axis (i.e., easy axis), forming an angle φ relative to the symmetry axis. Then, from Eqs.(29) and (31), it can be shown that the magnetization direction φ is related to the field angle θ by
| (32) |
where the approximation made can be considered reasonable because the magnetic susceptibility χm is typically very large (χm > 103) for soft-magnetic materials. We know from Eq.(32) that the magnetization direction φ for a given applied field at an angle θ relative to the particle’s axis of symmetry is determined by the ratio of the demagnetization factors along the axial and radial directions (NA/NR) at low fields before saturation (i.e., ).
At high fields beyond the saturating point (i.e., ), the magnetization direction φ can be determined such that it minimizes the magnetic energy. The magnetostatic energy density due to the demagnetizing field can be expressed (per unit volume of the particle) as
| (33) |
from the definition given in Eq.(25), with from Eq.(23) and the magnetization M replaced by the saturation magnetization Ms. For the given configuration in Figure 10, in which the principal axes of the spheroidal soft-magnetic particle are aligned with the coordinate frame to yield , the magnetostatic energy density can be calculated as
| (34) |
where denotes the magnitude of the saturation magnetization vector. The magnetized particle under the applied field Ba = μ0Ha possesses the magnetic potential energy density as well, expressed per unit volume and denoted by Um, which can be given from Eqs.(1) and (8) as
| (35) |
which holds for both the prolate and oblate spheroidal particle configurations in Figure 10. Then the total magnetic energy density is given by the sum of the magnetostatic energy density in Eq.(34) and the magnetic potential energy density Um in Eq. (35). Taking the derivative of this sum with respect to the magnetization direction φ, we know that the total magnetic energy density is minimized at φ = φ* which satisfies the following transcendental equation:
| (36) |
When the applied field is strong enough, we know from Eq.(36) that the induced magnetization direction φ* in the saturated particle approaches the applied field direction θ (i.e., φ* → θ), if the particle is fixed not to rotate despite the influence of magnetic torque.
3.2.2.3. Magnetic Torque on Anisotropic Particles
The magnetic force and torque density (per unit volume) acting on a soft-magnetic particle with the induced magnetization M can be expressed in terms of the applied field Ha as
| (37) |
| (38) |
with the bar symbol used to denote the force and torque density per unit volume, by replacing m with M and B with μ0Ha in Eqs.(4) to (6). Our focus here is on the modeling of the torque-driven actuation of soft-magnetic materials (Figure 4c,d). For the spheroidal soft-magnetic particle in Figure 10, the torque density can be calculated as , where the induced magnetization M is given as a function of the applied field Ha in Eq.(30).
Before saturation (i.e., ), the magnetic torque acting on the spheroidal particle per unit volume can be calculated using the apparent susceptibility tensor given in Eq.(31) as
| (39) |
which can be simplified as
| (40) |
for typical soft-magnetic materials with high magnetic susceptibility χm (e.g., χm > 103). From the equation above, we know that the magnetic torque on the particle is maximized at θ = 45°, when the actuating field (below the saturating field) is applied obliquely to the particle with an angle of 45° relative to the particle’s axis of symmetry (Figure 10).
At high fields beyond the saturating field (i.e., ), the magnetic torque density on the saturated spheroidal particle in Figure 10 can be expressed as
| (41) |
with φ* denoting the magnetization direction in the saturated particle. Using the relation given in Eq.(36), the torque in Eq.(41) can be expressed equivalently as
| (42) |
Since the saturation magnetization Ms and the applied field Ha become collinear at sufficiently high fields (i.e., φ* → θ), we can consider that the magnetic torque is maximized at θ ≈ 45° when the applied field strength is sufficiently high.
It is worth noting that, even when the particles are not of exact spheroidal shape, practical approximation can be made to simplify the analysis. For example, rod-like particles and disk-like particles (Figure 4c) can be approximated as prolate spheroids (Figure 10a) and oblate spheroids (Figure 10b), respectively. When the aspect ratio (i.e., the ratio of the long and short axes) is large enough, the demagnetizing factors for rod-like particles (very slender prolate spheroids) can be approximated as NA = 0 and NR = 0.5, whereas those for disk-like particles (very flat oblate spheroids) can be approximated as NA = 1 and NR = 0.18 Then, for rod-like particles, the magnetic torque density before and after saturation can be approximated from Eqs.(39) and (42) as
| (43) |
Likewise, for disk-like soft-magnetic particles, the magnetic torque density can be expressed as
| (44) |
For both the rod-like and disk-like particles (Figure 4c), the magnetic torque is maximized when θ = 45°, with the long axes of the particle misaligned by 45° from the actuating field below the saturating field (). Before saturation takes place, it is evident from Eq.(32) that the magnetization is induced preferentially along the long dimension of the particles with high aspect ratios, with φ = 0° for rod-like particles and φ = 90° for disk-like particles. When the particles are saturated, we know from Eqs.(41) and (42) that the magnetic torque can still be maximized when θ ≈ 45°, provided that the applied field is sufficiently high.
It should be noted that the analysis above is the first-order approximation that holds for ideal soft-magnetic materials, which are assumed to have no hysteresis, even when the particles are of anisotropic shape, to suppress the highly nonlinear and complex nature of magnetic hysteresis. As discussed in Section 2.2.3, single-domain soft-magnetic particles of anisotropic shape with high aspect ratios (e.g., nanorods or nanowires) can exhibit hysteresis, which is more pronounced in particles with higher aspect ratios.78–81 These single-domain soft-magnetic particles with high aspect ratios can be reasonably considered to have hard-magnetic characteristics, in the context of magnetic actuation, as permanently magnetized particles. When compared with typical hard-magnetic particles, however, they can be more easily demagnetized or remagnetized by lower fields, because their coercivity is not as high as that of typical hard-magnetic materials. For these reasons, the use of anisotropic soft-magnetic particles as distributed actuation sources has been limited mostly to small, thin features that require relatively weak magnetic torques for actuation. The fact that the coercivity of soft-magnetic nanorods varies with their aspect ratios has recently been employed as a strategy for selective magnetic programming in microfabricated shape-morphing structures with patterned nanomagnet arrays80 (see Figure 21a).
Figure 21. Applications of magnetic soft materials for magnetically reconfigurable active origami and metamaterials.
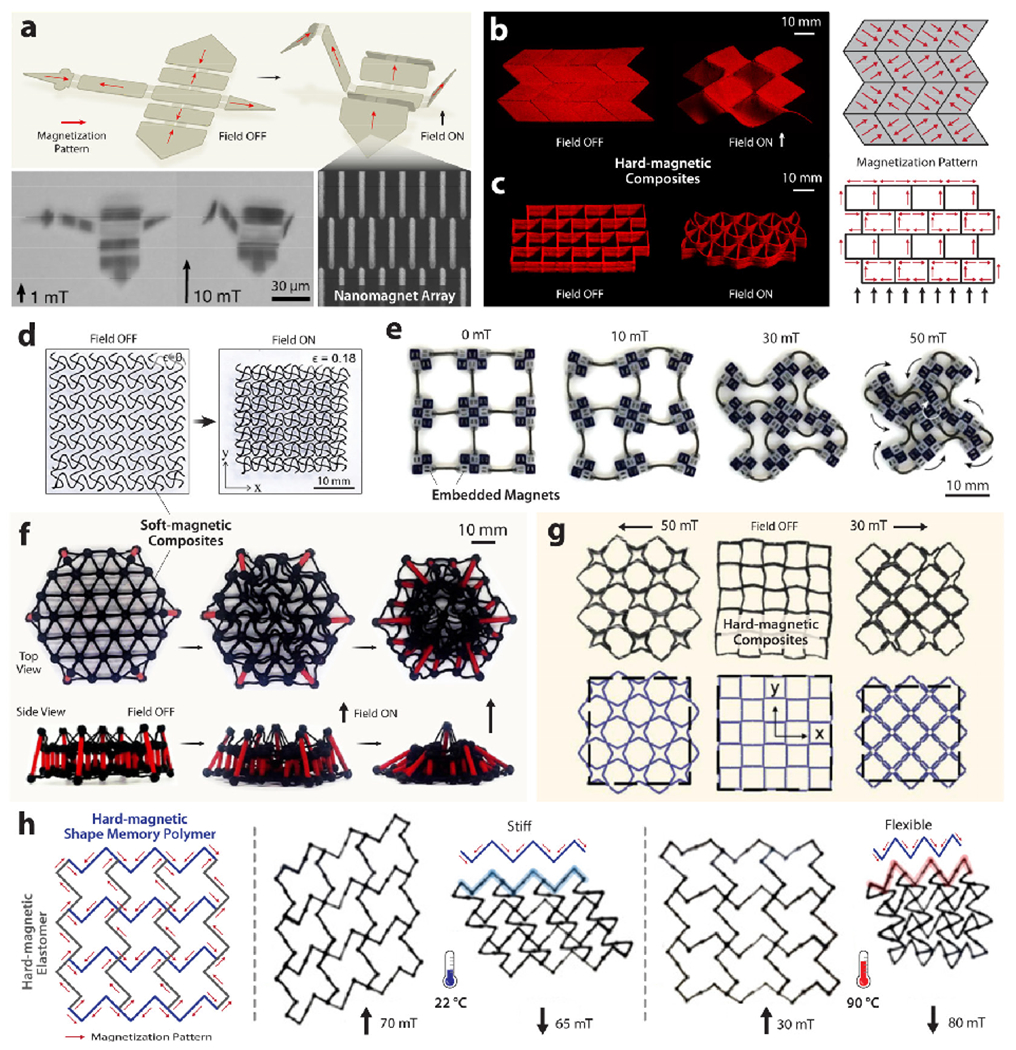
(a) Rigid panels with patterned nanomagnet arrays connected by microfabricated hinges morphing into a microscopic crane upon the application of an external magnetic field. (b) Miura-ori fold made of a hard-magnetic soft composite encoded with alternating oblique patterns of magnetic polarities. Auxetic structures with negative Poisson’s ratios based on 3D-printed (c) hard-magnetic (torque-driven) and (d) soft-magnetic (force-driven) composites exhibiting shrinkage in both length and width under applied magnetic fields. (e) Torque-driven auxetic behavior of a manually assembled structure based on embedded magnets connected by flexible members. (f) Tensegrity structure based on injection-molded soft-magnetic soft composites exhibiting force-driven auxetic behavior under an applied magnetic field. (g) 2D lattice structure based on manually assembled hard-magnetic composites connected by asymmetrically bendable joints exhibiting different torque-driven auxetic behavior depending on the applied field direction for magnetically tunable acoustic properties. (h) 3D-printed 2D lattice structure based on hard-magnetic elastomer and shape memory polymer exhibiting temperature-dependent torque-driven auxetic behavior. Panel (a) is reproduced with permission from refs 80 and 20 (Copyright 2019 Springer Nature); panels (b) and (c) from ref 156 (Copyright 2018 Springer Nature); panel (d) from ref 173 (Copyright 2019 Wiley); panel (e) from ref 212 (Copyright 2019 American Association for the Advancement of Science); panel (f) from ref 162 (Copyright 2020 American Association for the Advancement of Science); panel (g) from ref 324 (Copyright 2021 Wiley); and panel (h) from ref 110 (Copyright 2021 American Chemical Society).
3.2.2.4. Chained Isotropic Soft-Magnetic Particles
As discussed earlier, no magnetic torque is generated by a single isotropic (i.e., spherical) soft-magnetic particle because the induced magnetization M (or the magnetic moment m) is always aligned with the applied field Ha. Isotropic soft-magnetic particles can produce magnetic torques when they are connected and aligned to form chains to create magnetic anisotropy (Figure 4c,d).65–67,108,109 To model the magnetic torque acting on the chained soft-magnetic particles, we consider a long chain of spherical particles (each of which has a diameter of d) under a uniform magnetic field Ha that is applied obliquely to the chain with an angle of θ (Figure 11a). The dipole-dipole interaction between the neighboring particles causes the induced magnetization in each particle to form an angle φ relative to the chain (Figure 11a), which can be determined such that it minimizes the magnetic energy, as was the case with spheroidal soft-magnetic particles.
Figure 11. Modeling of the magnetic torque produced by chained soft-magnetic particles.
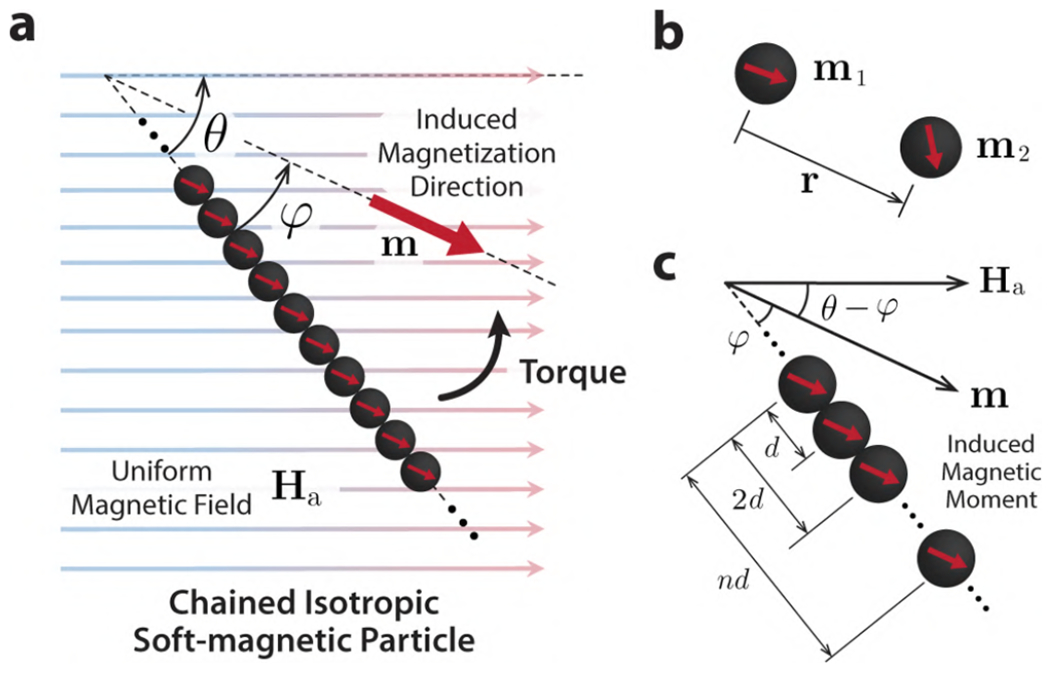
(a) Isotropic (spherical) soft-magnetic particles connected to form a chain. The chain of identical isotropic particles as a whole can be considered a rod-like anisotropic particle that produces induced magnetization (at an angle φ relative to the chain) under an applied uniform field (at an angle θ relative to the chain) to generate the magnetic torque. (b) Magnetostatic interaction between two magnetic dipoles under the influence of their dipolar fields on each other. (c) Modeling the magnetostatic dipolar interaction of a particle in the chain with its neighboring particles on both sides at distances of d, 2d, …, nd under the assumption of a sufficiently long chain.
We first consider the magnetostatic energy associated with building up the chain by bringing the magnetized particles, each of which in an idealized sense can be treated as a magnetic dipole (point-like source), one after the other from infinity to their current position. A magnetic dipole with the magnetic moment m generates the dipolar field given by
| (45) |
at any position r from the dipole. When two magnetic dipoles with magnetic moments m1 and m2 are separated by distance r (with the corresponding position vector r) as depicted in Figure 11b, their dipolar interaction energy (denoted e12) is given by
| (46) |
from the magnetic potential energy (defined in Eq.(1)) of either dipole under the field produced by its counterpart. Within a long chain consisting of a great number of particles (Figure 11a), the dipolar interaction energy of each particle can be calculated by considering its interaction with the neighboring particles in both sides at distances of d, 2d, …, nd (Figure 11c) as
| (47) |
where m denotes the magnitude of the particle’s magnetic moment (m = |m|). For sufficiently long chains (n ≫ 15), Eq.(47) can be simplified as
| (48) |
using the fact that for n > 15 (note: ).66 If the chain consists of N particles, the total dipolar interaction energy can be expressed as
| (49) |
Next, we consider the magnetic potential energy of the chained particles due to the externally applied field Ha which can be expressed from Eq.(1) as
| (50) |
Then, the magnetization direction φ can be determined by finding φ = φ* that minimizes the total magnetic energy. For the derivative of the sum of Eqs.(49) and (50) to be zero at φ = φ*, the following transcendental equation should be satisfied:
| (51) |
where the single particle’s magnetic moment m was replaced by the magnetization M (magnetic moment density) using the relation . When the particles are magnetically saturated (i.e., M = Ms), the magnetization direction can be identified based on the material’s property Ms and the actuating field strength |Ha| and direction θ from Eq.(51). Then the magnetic torque density acting on the chained particles per unit volume can be expressed as
| (52) |
It is worth noting that the individual isotropic particles in the chain can be considered each as an assembly of elementary magnetic moments as discussed in Section 3.1.3. As given in Eq.(25), the magnetostatic energy density for individual isotropic particles in the chain is , which, unlike that of an anisotropic particle given in Eq.(34), does not vary with the applied field direction θ and remain constant even when the magnetization direction φ changes. Therefore, the magnetostatic energy of individual particles does not contribute to the magnetic torque produced from the chained particles. This is why the magnetostatic energy of individual particles was not considered when deriving Eq.(51) for finding the magnetization direction φ* that minimizes the total magnetic energy of the chained particles.
From the analysis above, we know that the behavior of chained soft-magnetic particles is close to that of anisotropic particles discussed earlier in terms of the magnetic torque produced under a uniform actuating field. This implies that the chained isotropic soft-magnetic particles can be approximated as a rod-like particle with a high aspect ratio, as can be compared from Eq.(43) and Eq.(52). It is also worth noting that the analysis and equations presented above can be applied to modeling of the magnetic torque produced by chained superparamagnetic nanoparticles.66,67
3.2.3. Ideal Hard-magnetic Materials
Ideal hard-magnetic materials are characterized by their remanent magnetization Mr, which remains constant and independent of the applied field within the actuating field range below the coercivity (Figure 9b), as described in the constitutive law in Eq.(27). This implies that there is no energy transformation related to the magnetization process taking place during actuation. In other words, within the actuating field range below the coercivity, the magnetostatic energy plays no role in generating magnetic forces and torques. Therefore, the magnetic force and torque acting on a hard-magnetic particle (Figure 5a,c) per unit volume can be expressed simply as
| (53) |
| (54) |
by replacing m with M = Mr and B with Ba = μ0Ha in Eqs.(4) and (5), respectively. It is worth emphasizing that the remanent magnetization Mr independent of the applied field Ha greatly simplifies the calculation of the magnetic force and torque for hard-magnetic soft materials.
3.3. Continuum Mechanical Framework
For magnetic soft materials and robots with one or a few rigid, finite-sized magnets attached to or incorporated in a deformable body (Figure 1a), the magnetic force and torque generated by the magnet can be considered a point load acting on the center of the magnet. For such discrete systems with simple geometry, theoretical models can be derived by considering the global force and moment balance of the structure to find its deformed configuration in static equilibrium.154 For continuous systems with dispersed magnetic particles in the polymer matrices (Figure 1b and Figure 5b,d), the composite can be treated as a homogenized continuum that exhibits both elastic and magnetic characteristics simultaneously (Figure 12a). Modeling of such continuous systems can be formulated in a continuum mechanical framework by considering the local force and moment balance that holds at every point of the composite.
Figure 12. Continuum mechanical framework for magnetic soft materials.
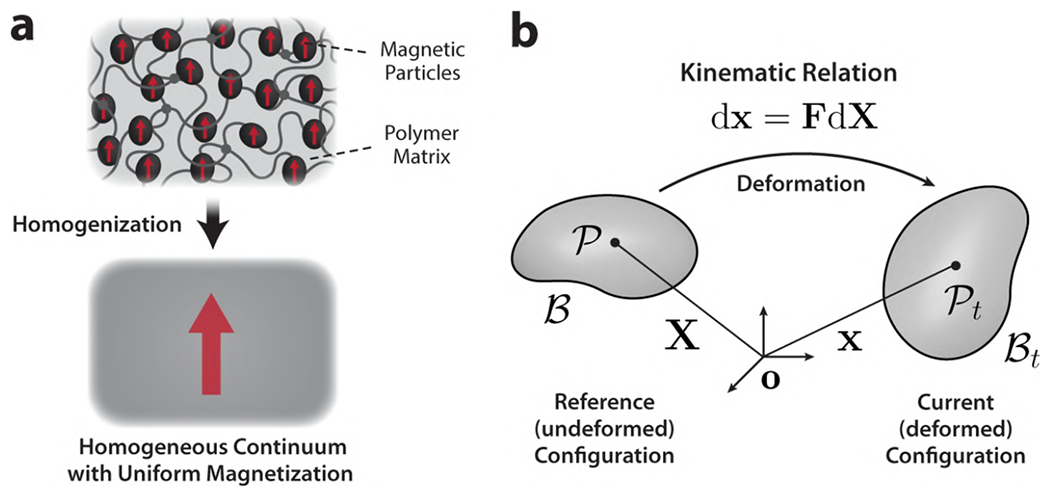
(a) Treatment of magnetic soft composites based on polymer matrices with filler particles as a homogeneous continuum with uniform magnetization for continuum mechanical approaches. (b) Kinematic relation for deformable solids in the continuum mechanical framework.
When a continuum (denoted by ) deforms (Figure 12b), a material point X (denoted by ) on the body in its reference (undeformed) configuration is mapped to a spatial point x (denoted by ) on the deformed body (denoted by ) in the current configuration. The deformation of the body can be measured by the deformation gradient tensor F which is defined by
| (55) |
The deformation gradient is a linear transformation that maps the infinitesimal line elements dX and dx between the reference and current configurations and hence serves as a primary measure of deformation. The determinant of the deformation gradient characterizes the change in volume during the deformation as
| (56) |
which is termed the volumetric Jacobian that relates the infinitesimal volume elements dV and dυ in the reference and current configurations, respectively.
For quasi-static equilibrium, the principle of linear momentum balance reduces to the force balance equation that holds for each point x:
| (57) |
which is also known as Cauchy’s equilibrium equation, where σ is the Cauchy stress, with div σ denoting its spatial divergence with respect to the point x, and is the body force density (per unit volume of the continuum) exerted by the environment on x (including the gravitational body force). For a polar continuum with distributed body torque density (per unit volume of the continuum), the balance of angular momentum reduces to the following moment balance:
| (58) |
where is the third-order permutation tensor with εijk being the permutation (also known as Levi-Civita) symbol and the operator ® denoting the tensor (dyadic) product. σ⊤ is the transpose of the Cauchy stress tensor, and the operator : denotes the double contraction of the two tensors. When there is no body torque, Eq.(58) requires the Cauchy stress to be symmetric: σ = σ⊤. In the presence of body torques, however, the Cauchy stress may no longer be symmetric.
The mechanical behavior of the composite matrix can be described by relevant constitutive models for hyperelastic solids, such as neo-Hookean, Mooney-Rivlin, Gent, and Arruda-Boyce models, to name a few. The material model defines the Helmholtz free energy per unit reference volume (also called the strain energy density), denoted by , as a function of the deformation gradient F. For hyperelastic solids with no internal energy dissipation in isothermal conditions, the mechanical stress in the referential form can be directly obtained from the derivative of the Helmholtz free energy density as
| (59) |
which is termed the first Piola-Kirchhoff stress, or simply the Piola stress, which measures the force acting on the deformed material per unit reference (undeformed) area. The Piola stress is related to the Cauchy stress σ (force per unit current area) by P = JσF−⊤ which leads to
| (60) |
Substituting this into the equilibrium equation in Eq.(57) and solving it for the deformation gradient F, typically through the finite element method with relevant boundary conditions taken into account, the deformed configuration of the material in equilibrium can be found.
It should be noted that the magnetic force and torque densities calculated in Sections 3.2.2 and 3.2.3 measure the force and torque on a single particle per unit volume of the particle. When they are multiplied by the particle’s volume fraction, denoted by ϕ, the magnetic body force and torque densities per unit volume of the composite can be obtained, under the assumption of homogeneous continua (Figure 12a) discussed above. Then, the magnetic body force and torque densities (per unit volume of the homogenized composite) can be substituted into Eqs. (57) and (58).
4. Design, Fabrication, and Characterization
Material design and fabrication schemes have been central to the development of magnetic soft materials and robots with complex shapes and sophisticated functions. Remarkable progress in the field has been made lately by actively adopting emerging fabrication techniques in additive manufacturing (Table 1). The technical developments have been focused on the incorporation of magnetic components into polymer matrices or flexible substrates and their alignment to achieve desired magnetization patterns or profiles within the composite structures across different scales. In the following sections, we discuss how the field of magnetic soft materials and robots has been evolving with advances in design and fabrication techniques.
Table 1.
Comparison of Representative Fabrication and Programming Methods for Magnetic Soft Materials and Robots.
| Fabrication | Material Composition | Magnetization Programming | Shape | Magnetization | Scale | Resolution | Refs |
|---|---|---|---|---|---|---|---|
| Molding and casting | Hard-magnetic (NdFeB) microparticles uniformly dispersed in silicone elastomers | Template-assisted magnetization of composite while deformed into temporary shapes | 2D | Continuous, 3D | 5~100 mm | ~0.5 mm | 164–166 |
| Extrusion-based 3D printing | Hard-magnetic (NdFeB) microparticles uniformly dispersed in silicone elastomers | In situ alignment of magnetized particles in printed fibers while depositing composite inks | 3D | Discrete, 2D | 10~100 mm | ~100 μm | 156 |
| Light-based 3D printing | Hard-magnetic (NdFeB) microparticles chained and aligned in photocurable elastomers | In situ alignment of magnetized particles in printed areas while curing with patterned UV light | 2D | Discrete, 3D | 2~10 mm | ~100 μm | 178 |
| Micro-molding and assembly | Hard-magnetic (NdFeB) microparticles uniformly dispersed in silicone elastomers | Assembly of microscale building blocks made of magnetized composite into 3D structures | 3D | Discrete, 3D | 0.5~5 mm | ~50 μm | 194 |
| UV photolithography | Superparamagnetic (iron oxide) nanoparticles aligned in photocurable hydrogels | In situ chain formation and alignment of particles in while curing with patterned UV light | 2D | Discrete, 3D | 50~500 μm | ~1.5 μm | 67,200,201 |
| Electron-beam lithography | Single-domain anisotropic nanomagnets (cobalt) aligned on thin, flexible silicon substrates | Patterning arrays of nanomagnets with different aspect ratios and selective magnetization | 2D | Discrete, 2D | 10~100 μm | ~0.1 μm | 80 |
4.1. Optimal Design Strategies
As discussed in the previous section on the modeling of magnetic actuation, magnetic soft materials can be considered essentially bending actuators driven by the magnetic torque. From a materials design perspective, it is worth discussing the strategies to optimize the performance of magnetic soft actuators. Our focus here is on the hard-magnetic soft materials, which provide simple and effective bending actuation. To achieve optimal actuation performance, a good balance between the mechanical resistance of the composite structure and the driving magnetic torque is required. For composites based on soft polymers with embedded hard-magnetic particles, both the mechanical and magnetic properties of the composite vary with particle volume fraction ϕ.
For a uniformly magnetized homogeneous continuum (Figure 12a), we can assume that the magnetization of the composite M is proportional to the particle volume fraction ϕ (Figure 13a):
| (61) |
where Mp represents the magnetization of an individual particle. The shear modulus of the filled composite, denoted by G, increases nonlinearly with the particle concentration (Figure 13a). This nonlinear dependence can be expressed as
| (62) |
which is known as the Mooney model for spherical particles with G0 denoting the shear modulus of an unfilled elastomer.155
Figure 13. Design optimization of magnetic composites based on soft polymers with embedded hard-magnetic particles.
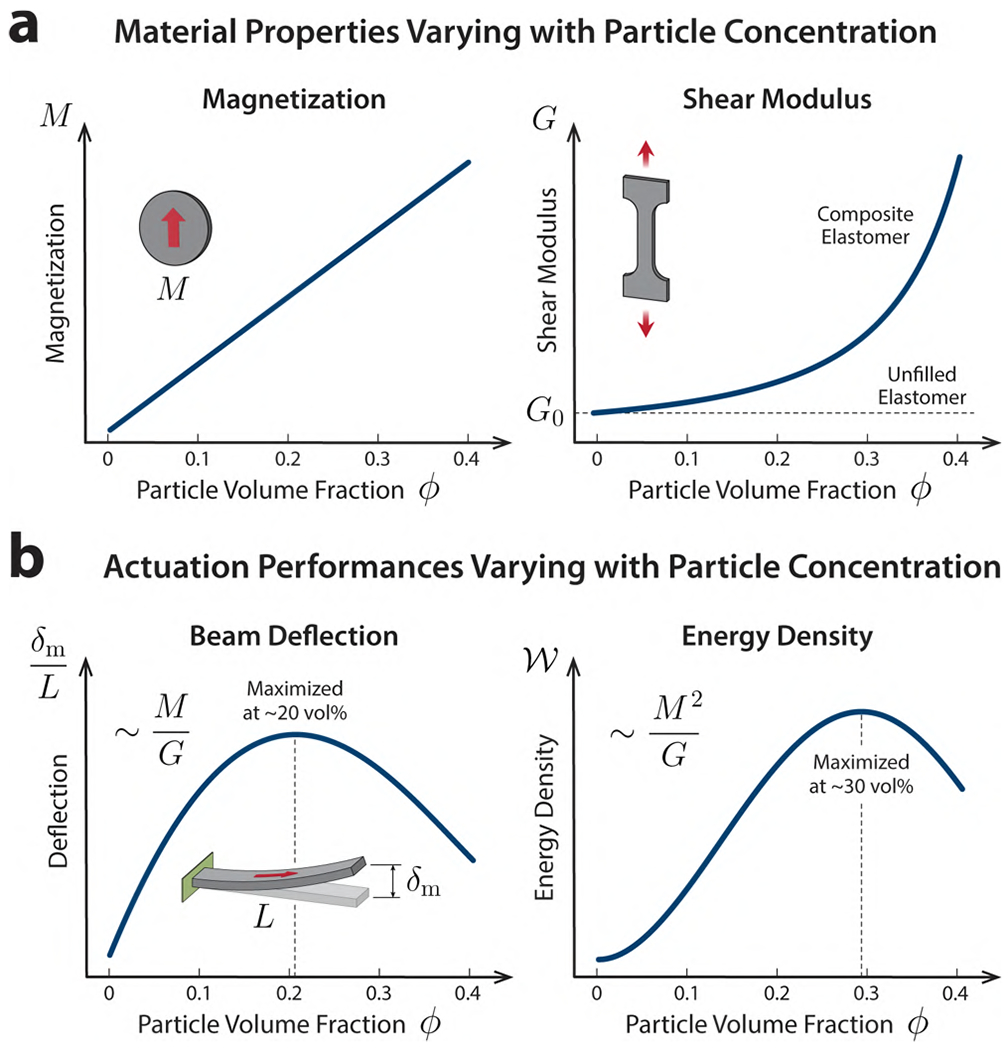
(a) Material properties (magnetization and shear modulus) of magnetic soft composites varying with the particle volume fraction. (b) Actuation performance of magnetic soft bending actuators in terms of the free-end deflection (normalized by the beam length L) and energy density varying with the particle volume fraction.
For a beam made of hard-magnetic soft composite under small bending, the deflection of the beam, δm, due to the applied magnetic field B can be modeled with the following scaling relation:156
| (63) |
where L and D are the length and diameter (or thickness) of the beam, respectively, and M is the magnetization of the beam along its length direction. In Eq.(63), the dimensionless number MB/G, which represents the applied field B normalized by the material properties M and G, characterizes the competition or balance between the magnetic interaction and the elasticity of the composite. L/D is the aspect ratio of the bending actuator that contributes to the structural bending stiffness. Substituting Eqs. (61) and (62) into Eq.(63), it can be analytically shown that the deflection is maximized when the particle volume fraction is around 20% (ϕ = 0.207; Figure 13b). Although the scaling in Eq.(63) holds only for small deflection, it has been shown that the overall tendency and the optimal concentration to maximize the deflection hold true for large deformation as well.31
When the actuation force is of greater importance than the large deflection under the given applied field B, the material design can be optimized in terms of the energy density to maximize the mechanical work that can be produced per unit volume during actuation. For hard-magnetic soft bending actuators with small deflection, the energy density (denoted by ) scales with31
| (64) |
Then, the optimal particle volume fraction that maximizes the energy density under the given conditions is calculated to be around 30% (ϕ = 0.293; Figure 13b).
From Eq.(63), we know that the geometric factor L/D (aspect ratio) also plays an important role in determining how much the beam would bend under the applied field B. This implies that fine features with high aspect ratios, such as magnetic cilia,109,157–161 would require significantly lower field strength to induce the bending actuation. It is worth noting, however, that such slender structures can be more susceptible to sagging due to gravity and their self-weight because of the small structural rigidity. The competition between the gravitational body force and the magnetic interaction can be characterized from the following scaling relation:
| (65) |
where δg denotes the deflection of the beam due to gravity, with ρ, g, and L denoting the mass density of the composite material, the gravitational acceleration, and the free length of the bending actuator, respectively. This can be derived from standard beam equations along with Eq.(63).
4.2. Fabrication and Magnetic Programming
4.2.1. Molding and Casting
Molding and casting have been the most common fabrication method for conventional magnetic soft materials with relatively simple geometry, usually in the form of blocks or sheets (Figure 14a). When soft-magnetic or superparamagnetic soft materials are molded, chained microstructures can be introduced by applying a uniform magnetic field along the desired direction in which the chains are to be formed. Molding has also been used to fabricate magnetically responsive mechanical metamaterials based on 3D-printed lattice structures into which magnetorheological fluids or elastomers with soft-magnetic particles are injected to impart magnetic responsiveness.162,163
Figure 14. Fabrication and magnetic shape-programming methods for magnetic soft materials.
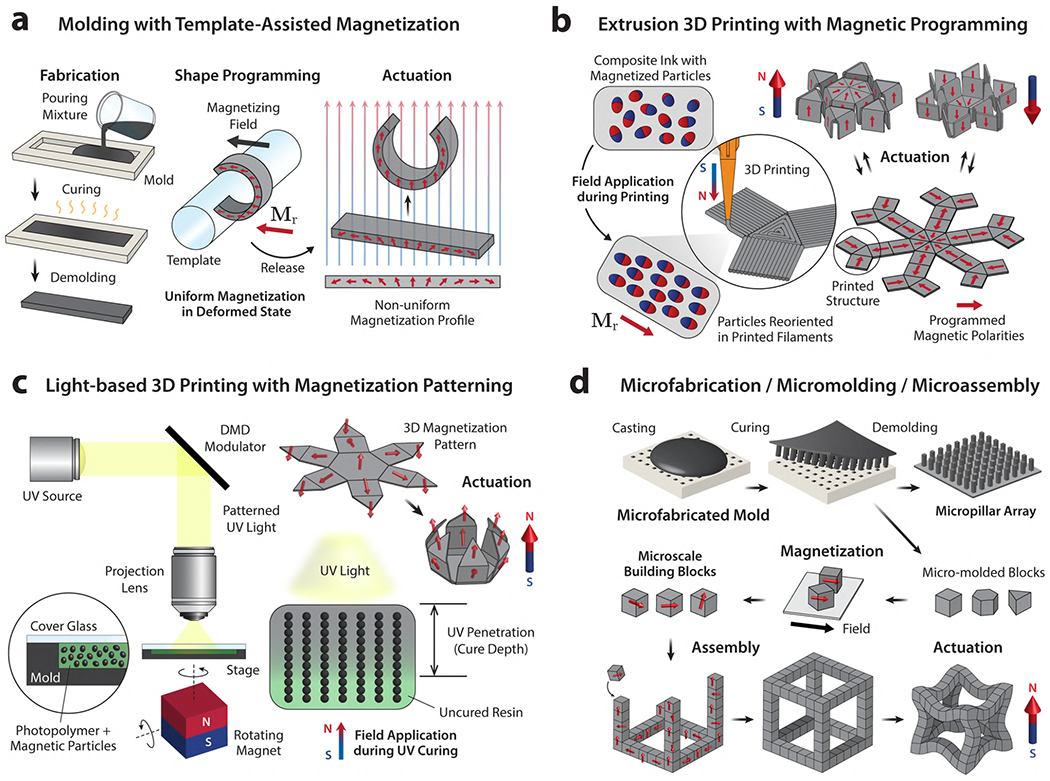
(a) Molding and casting for fabrication and templated-assisted magnetization for shape programming to obtain a nonuniform magnetization profile.166 (b) Extrusion-based 3D printing of magnetic composites containing magnetized particles that can be reoriented by the applied magnetic field during the printing process to program desired magnetization patterns in the printed structure.156 (c) Light-based 3D printing or UV photolithography of magnetic composites based on photocurable resins mixed with magnetic particles, which can be aligned to form chains along the applied field direction during the UV curing process to create desired magnetization patterns in the printed structure.178 (d) Fabrication of micropillar arrays193 or microscale building blocks194 through molding of magnetic soft composites using microfabricated molds. Microscale building blocks based on hard-magnetic composites can be magnetized and assembled into 3D structures capable of programmed shape changes under applied magnetic fields due to the designed magnetization patterns.194
When hard-magnetic soft materials are molded or cast into planar structures or flat beams, they are usually magnetized after curing on purpose for shape-programming. The fabricated (cured) composite with magnetizable hard-magnetic particles is first deformed into a desired temporary shape using a fixture or template and then magnetized to saturation by a strong magnetic field in the deformed state (Figure 14a and Table 1). This leads to nonuniform magnetization profile in the composite structure, which tends to revert to the programmed shape when an actuating field is applied (see examples in Figure 19, b to d).164–169 This template-aided magnetization and shape-programming strategy is often useful for planar structures with relatively simple geometry. However, it should be noted that the programmed shape may not always be achievable (especially when the desired shape requires large deflection from the original shape). There often can exist some gap between the desired shape and the actual shape upon magnetic actuation, partly because the actuating field has an upper limit below the coercivity.
Figure 19. Magnetic actuation and manipulation platforms based on electromagnets.
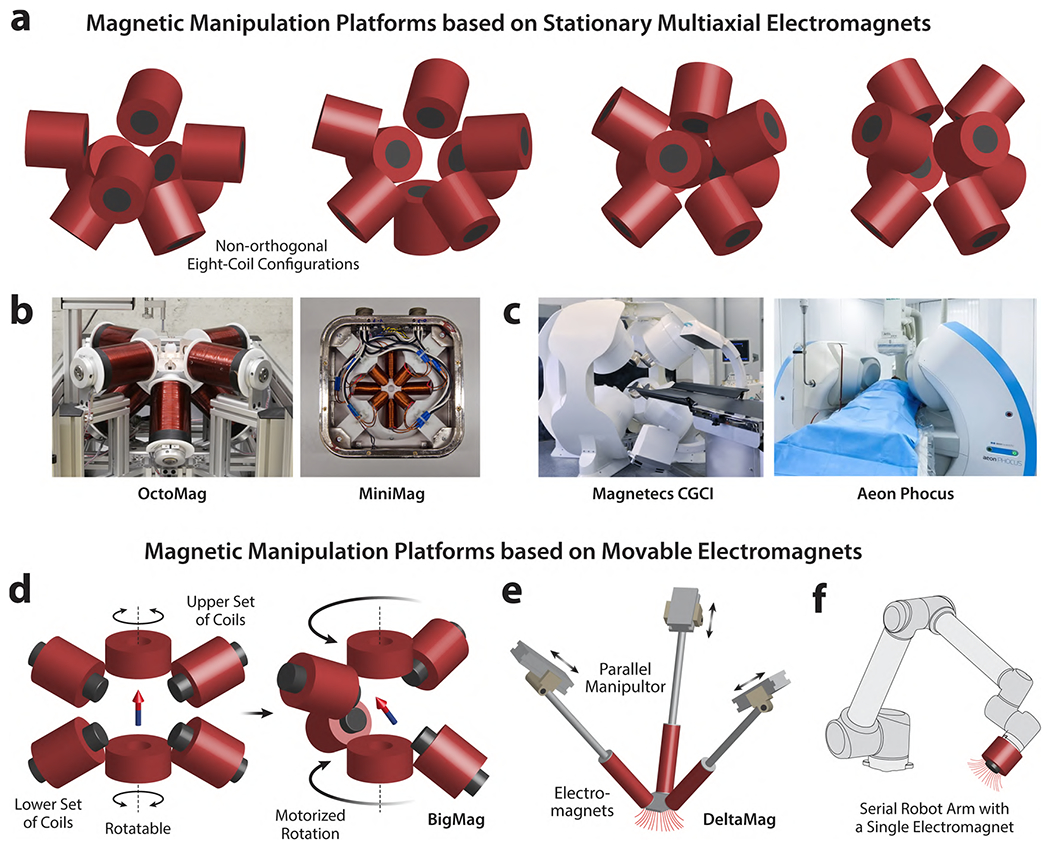
(a) Representative examples of magnetic actuation and manipulation platforms based on stationary multiaxial electromagnets in nonorthogonal eight-coil configurations258,295 and commercially available systems for (b) table-top296–298 and (c) human-body scales. Magnetic manipulation platforms based on movable electromagnets: (d) motorized actuation of rotatable electromagnets168,300 and (e) a parallel297,298 or (f) a serial303–306 robot manipulator for controlling the position and orientation of the actuating electromagnet in the workspace. Photo on the right in panel (b) reproduced with permission from ref 298. Copyright 2014 Springer Nature.
Unlike other fabrication techniques based on additive manufacturing, which often require certain material properties (i.e., optical transparency of resins for light-based 3D printing or thixotropy of ink materials for extrusion-based 3D printing; see Section 4.2.2) for compatibility with their fabrication process, molding and casting are generally applicable to a wide range of elastomers and hydrogels with minimal material modifications. Contrary to the 3D printing techniques, which are often sensitive to the rheological properties of the ink materials, molding and casting can be used without the need to carefully tune the rheological properties. Therefore, molding and casting are most commonly used when developing new magnetic soft composites with unconventional functionalities by including additional components due to their wide applicability and procedural simplicity. For magnetorheological elastomers, as an example, adding a liquid phase such as glycerol-based ferrofluids into the elastomer matrix has been shown to enable exceptional stiffening due to the enhanced mobility of the embedded soft-magnetic particles.170,171 For validation of such new materials and approaches, the uncured composites are usually molded into sheets to prepare testing samples with simple geometry. Similar examples of adding phase-changing materials in hard-magnetic soft materials to facilitate magnetic reprogramming (see Section 4.3) also utilized the simple molding and casting technique for sample preparation and fabrication.
4.2.2. Additive Manufacturing
Recent advances in additive manufacturing for soft materials have accelerated progress in the design and fabrication of magnetic soft materials and robots with more complex shapes and more sophisticated actuation and functions. Widely used additive manufacturing techniques such as extrusion-based 3D printing (e.g., direct ink writing156,172–174 and fused deposition modeling175,176) and light-based 3D printing177–180 have been adopted for fabricating different types of magnetic soft materials and robots (Figure 14b,c, and Table 1).
4.2.2.1. Extrusion-Based 3D Printing
Among different extrusion-based 3D printing techniques, our focus here is on direct ink writing which enables 3D printing of viscoelastic inks composed of uncured polymer resins and magnetic particles. By extrusion of the composite inks through deposition nozzles under applied pressure and arrangement of the deposited filaments in each layer, 2D or 3D structures can be fabricated in a layer-upon-layer fashion. For 3D-printed hard-magnetic soft materials, it has been shown that the magnetization pattern can be controlled at the filament level by applying weak magnetic fields during printing to align the magnetized particles in the printed composite fibers (Figure 14b).156 This technique has demonstrated its ability to fabricate magnetic soft materials with complex shape-changing capabilities due to the intricate patterns of magnetic polarities in the printed structures, including mechanical metamaterials with negative Poisson’s ratios (see Section 6.1.2), and has recently been adopted for hard-magnetic shape memory polymers110 as well.
For magnetic soft composites based on anisotropic filler particles, alignment of the particles is required to induce collective macroscale response of the printed structure, because the magnetic torque is dependent on the particle orientation relative to the actuating field direction (see Section 3.2.2). For composite inks containing rod-shaped magnetic particles, the particles undergo shear-induced alignment as the ink flows through the printing nozzle,181–184 and hence the alignment can be obtained naturally while printing. For disk-shaped particles (e.g., alumina platelets coated with iron oxide nanoparticles185,186), it has been shown that the particles can be aligned while printing under a weak rotating magnetic field.172 It is worth noting that the aligned anisotropic particles lead to mechanical anisotropy with increased stiffness along the aligned particles.81,182,185
To use the direct ink writing method, the composite ink should possess thixotropic properties, meaning that the material should maintain a stable form at rest but become a fluid that can flow when agitated by externally applied stresses. In most cases, the un-cross-linked or uncured polymer base resin mixed with magnetic particles can be considered a Newtonian fluid,172 a viscous but freely flowing fluid with a constant viscosity, unless it is heavily loaded with the particles (e.g., ϕ > 0.3). Therefore, rheological modifiers such as fumed silica nanoparticles (for silicone elastomers) or nanoclays such as Laponite (for hydrogels) are often added to impart desired ink properties such as shear thinning and shear yielding to ensure that the composite ink can be extruded easily through the nozzle when pressurized and that the deposited inks maintain their shapes even when stacked up to multiple layers.187,188 For hard-magnetic composite inks, it has also been shown that the ink materials can exhibit thixotropic properties when the embedded hard-magnetic particles are magnetized,31,189 even without the addition of rheological modifiers, and hence become printable for the extrusion-based processes. For soft-magnetic composite inks, it has been shown that the capillary forces between the liquid phase (uncured polymer resin) and the solid phase (polymer beads encasing magnetic particles) due to wetting (solid beads connected to each other by binding liquid) can provide thixotropic properties190,191 to obtain printability for direct ink writing without rheological modification.173,192
4.2.2.2. Light-Based 3D Printing
In addition to extrusion-based methods, light-based 3D printing techniques have also been used to fabricate magnetic soft materials and robots. Light-based 3D printing uses photopolymerizable or photocurable polymer resins that can solidify upon the application of patterned ultraviolet (UV) light or focused laser light, and this light-based 3D printing includes stereolithography (SLA) and continuous liquid interface production (CLIP)195 techniques. SLA 3D printing based on digital light processing (DLP) has been adopted for fabrication of hard-magnetic and soft-magnetic soft materials by coupling a permanent magnet178 or electromagnetic coils177 beneath or around the printing platform to control the alignment of the embedded magnetized or magnetizable particles while selectively curing the photopolymer resin using patterned UV light (Figure 14c). This DLP-based 3D printing is similar to UV photolithography (see Section 4.2.3) in terms of the fabrication process when printing 2D (single-layer) structures. BothSLA/DLP 3D printing and CLIP 3D printing have been adopted to fabricate flexible magnetic actuators and grippers using 3D-printed isotropic superparamagnetic soft composites based on photopolymerizable materials containing uniformly dispersed iron oxide nanoparticles.179,180,196
When compared with the direct ink writing method discussed above, where the programmed magnetization patterns lie on the printing plane onto which the inks are deposited (Figure 14b), the light-based 3D printing methods provide greater degrees of freedom in terms of the achievable magnetization direction in printed structures (i.e., 3D magnetization patterns in printed 2D or 3D structures), allowing for programming complex shape changes in hard-magnetic soft materials (Figure 14c). However, the maximum thickness of UV-curable layer (i.e., cure depth) is limited because the photocurable resin containing light-absorbing magnetic particles is no longer optically transparent, with the UV penetration depth decreasing rapidly with the particle concentration. For example, the cure depth is below 200 μm when the concentration of Nd2Fe14B microparticles is 50% by mass (around 13% by volume) or below 100 μm when the concentration is 60% by mass (around 18% by volume),178 which may potentially affect the scalability of the light-based 3D printing techniques for magnetic soft materials due to the limited processable layer thickness.
4.2.3. Microfabrication and Microassembly
The above-mentioned additive manufacturing techniques are mostly limited to millimeter or centimeter scales in terms of the typical feature size. For fabricating small-scale magnetic soft materials in size of tens or hundreds of micrometers, different types of microfabrication techniques have been adopted. To realize magnetically controlled microgrippers197 or micropillar or microplate arrays157,193,198,199 using magnetic soft materials, microscale molding and casting has been used. For this, microfabrication techniques such as photolithography or femtosecond laser writing have been used to prepare micromolds, into which uncured composite mixture is poured, followed by curing and demolding processes (Figure 14d).
UV photolithography has been used to fabricate small-scale magnetic soft materials and robots based on poly(ethylene glycol) diacrylate (PEGDA) hydrogels and superparamagnetic (iron oxide) nanoparticles. The superparamagnetic nanoparticles are chained and aligned by externally applied magnetic fields while the photocurable pregel solution is selectively cross-linked through patterned (either masked or digitally modulated) UV light to inscribe desired magnetic or mechanical anisotropy patterns in the fabricated structures for actuation purposes.67,200,201 As mentioned earlier, it is worth noting that maskless photolithography based on digitally modulated patterned UV light67 is similar to the DLP-based 3D printing (Figure 14c) in terms of their working principles for magnetic programming. Standard photolithography has shown that fabricated microcubes can build magnetically reconfigurable microstructures that are capable of self-assembly under externally applied fields, when the microcube building blocks are coated with thin layers of cobalt to impart magnetic responsiveness.202,203 Electron-beam lithography has also been used to fabricate magnetically controlled microstructures with complex shape-changing capabilities by depositing micropatterned arrays of nanoscale magnets (e.g., single-domain cobalt with anisotropic shape) onto flexible structures with microfabricated hinges.80
The two-photon polymerization technique, also known as direct laser writing,204 has been widely used to fabricate helical microstructures that can be driven magnetically for drug or cell delivery purposes.205–210 However, despite the unique advantage of two-photon polymerization among other microfabrication techniques in terms of the ability to produce complex 3D microstructures, the technique has demonstrated limited applicability to the fabrication of shape-shifting magnetic soft materials and robots, possibly because of the incompatibility of the opaque composite mixture with the two-photon polymerization process beyond a certain size limit. Instead, the technique has been used to fabricate micromolds for tiny building blocks of magnetic soft materials, which can be manually assembled under a microscope to build 3D structures with 3D magnetization patterns (Figure 14d),194 similarly to large-scale assembly of magnetic building blocks to realize 3D shapes or magnetization patterns.211–213 Lacking an automated workflow, however, the microassembly process based on micromolding, magnetization, and manual assembly of the building blocks piece by piece to build 3D objects can be labor-intensive and hence is not likely scalable. Thus far, to the best of our knowledge, there is currently no automated fabrication technique to realize small-scale magnetic soft materials and robots in fully 3D shapes with 3D magnetization patterns to achieve complex transformation, which will be an important area of research and development for next-generation magnetic soft robots with more advanced and sophisticated functions.
4.3. Magnetic Reprogramming Strategies
As discussed earlier in Sections 2.2.2 and 3.2.1, the high coercivity of typical hard-magnetic materials used for magnetic soft composites allows them to be stable and reliable sources of torque-driven magnetic actuation within the actuating field range below the coercivity (Figure 9b). This also means, however, that it is not easy to reprogram the magnetization pattern of hard-magnetic soft materials. For example, common hard-magnetic materials of rare-earth type (e.g., NdFeB and SmCo; see Section 2.2.2) require strong magnetizing fields due to their high coercivity values.
Different strategies have been proposed to enable facile reprogramming of the magnetization patterns of hard-magnetic soft materials. One strategy is to use magnetic materials with relatively low Curie temperature, above which the material loses its remanent magnetization. Such materials include chromium dioxide (CrO2), the Curie point of which is around 118 °C, which is far lower than that of typical magnetic materials (e.g., iron, nickel, and cobalt) that ranges from 300 to 1200 °C. It has been shown that magnetic soft composites based on CrO2 can be readily demagnetized through either global heating or localized laser heating and then remagnetized upon cooling while applying an external magnetic field.214,215 It has also been shown that the demagnetization and remagnetization can be done in a spatially selective manner by applying a focused laser beam for localized heating (Figure 15a) to create intricate 3D magnetization patterns in planar structures.215 Magnetic materials with low Curie temperature such as CrO2, however, have in general relatively low remanence and coercivity as well, which can limit the actuation performance. Microparticles of CrO2 microparticles (~10 μm) have the remanence of around 75 kAm−1 (8 times lower than that of NdFeB particles of similar size) and the coercivity of around 50 mT (12 times lower than that of NdFeB particles of similar size),214 and hence the maximum magnetic torque density can be substantially lower (i.e., 96 times) than that of NdFeB microparticles of similar size.
Figure 15. Head-assisted magnetic reprogramming strategies for hard-magnetic soft materials.
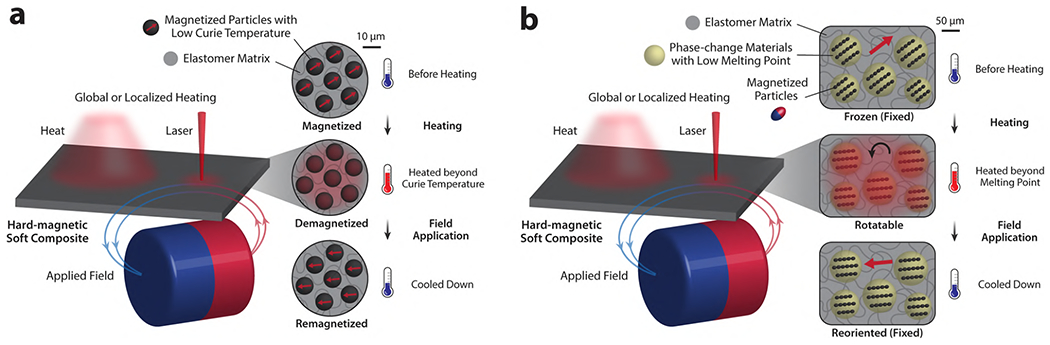
(a) Magnetic materials with low Curie temperature (above which the material loses its remanent magnetization) can be easily demagnetized upon global heating or localized laser heating above the Curie point and then remagnetized by an externally applied magnetic field during cooling.215 (b) Hard-magnetic particles encapsulated in phase-change materials with low melting temperature can temporarily move and rotate when heated above the melting point to reorient themselves along the applied field during the heating process. Upon cooling, the reoriented particles are immobilized within the solidified phase-change material to yield a newly programmed magnetization direction in the composite.216,217
Another heat-assisted reprogramming strategy for hard-magnetic soft materials is to use phase-change materials with relatively low melting temperature, such as poly(ethylene glycol) (PEG)216 or polycaprolactone (PCL),217 to encapsulate the magnetized particles incorporated in the elastomer matrix (Figure 15b). Below the melting temperature, which is around 60 °C for PEG and PCL, the particles are enclosed and fixed within the solid PEG or PCL. When heated above the melting point, through either global heating or localized laser heating, the particles enclosed in the molten (i.e., liquid) PEG or PCL can temporarily move and reorient when an external magnetic field is applied simultaneously during heating.216,217 Upon cooling, the reoriented particles are immobilized within the solidified PEG or PCL, yielding a newly programmed magnetization direction in the composite matrix (Figure 15b). Allowing the use of magnetized particles with high remanence and coercivity, this reprogramming method based on solid-liquid phase transition would not inherently sacrifice the actuation performance of hard-magnetic soft composites in terms of the torque density. It is likely, however, that the increase in the average size of particulate fillers due to the inclusion of the meltable solid phase (i.e., the phase-changing beads encasing the magnetic particles) in an elastomer matrix may affect the mechanical properties and behavior of the composite,218,219 such as more pronounced softening after stretching due to the Mullins effect.220
4.4. Characterization Methods
4.4.1. Magnetic Characterization
Magnetic properties of composite samples can be measured using different magnetometry techniques. One of the most common ways to measure the magnetization properties of a sample is using a vibrating sample magnetometer (VSM).221,222 In typical VSM settings, a magnetizable or already magnetized sample is placed in a spatially uniform magnetic field between a pair of electromagnets and then vibrated perpendicularly to the applied field at a prescribed frequency and amplitude (Figure 16a). The vibrating motion (usually vertical) of the magnetized sample causes the magnetic flux entering the pickup coil to change, which in turn creates an induced voltage in the coil that is proportional to the sample’s magnetic moment. By measuring the induced voltage while varying the applied field strength over a range, the hysteresis curve can be obtained for ferromagnetic materials. For already magnetized samples, the measurement should be performed under weak magnetic fields to ensure that the sample’s remanent magnetization remains unaffected by the applied field. It is also worth noting that the sample’s orientation matters when characterizing samples with anisotropic soft-magnetic particles or magnetized hard-magnetic particles, because what is measured from the VSM is the component of the sample’s magnetic moment vector, which is perpendicular to the pickup coil.156 For small-scale samples, which require higher sensitivity in measurement, more recent characterization methods, such as using a superconducting quantum interference device (SQUID), can be used.80,221,223 SQUID magnetometers allow the measurement of the sample’s magnetization as a function of temperature as well as the applied magnetic field.223 Characterization of even smaller magnetic materials such as nanomagnet arrays79,80,224 requires optical magnetometry techniques based on the magneto-optical Kerr effect, which describes the changes to polarized light when it is reflected from a magnetized surface.225 Magneto-optical sensors can also be useful when visualizing the complex magnetization patterns programmed in hard-magnetic soft materials with planar geometry (see Figure 22f).178,215
Figure 16.
(a) Magnetic characterization of magnetic materials using a vibrating sample magnetometer (VSM) and (b) mechanical characterization of elastomeric composites through tensile testing, where the obtained stress-strain curve can be fitted with hyperelastic constitutive models such as Gent or neo-Hookean models.
Figure 22. Applications of magnetic soft materials for programmable and reconfigurable surfaces.
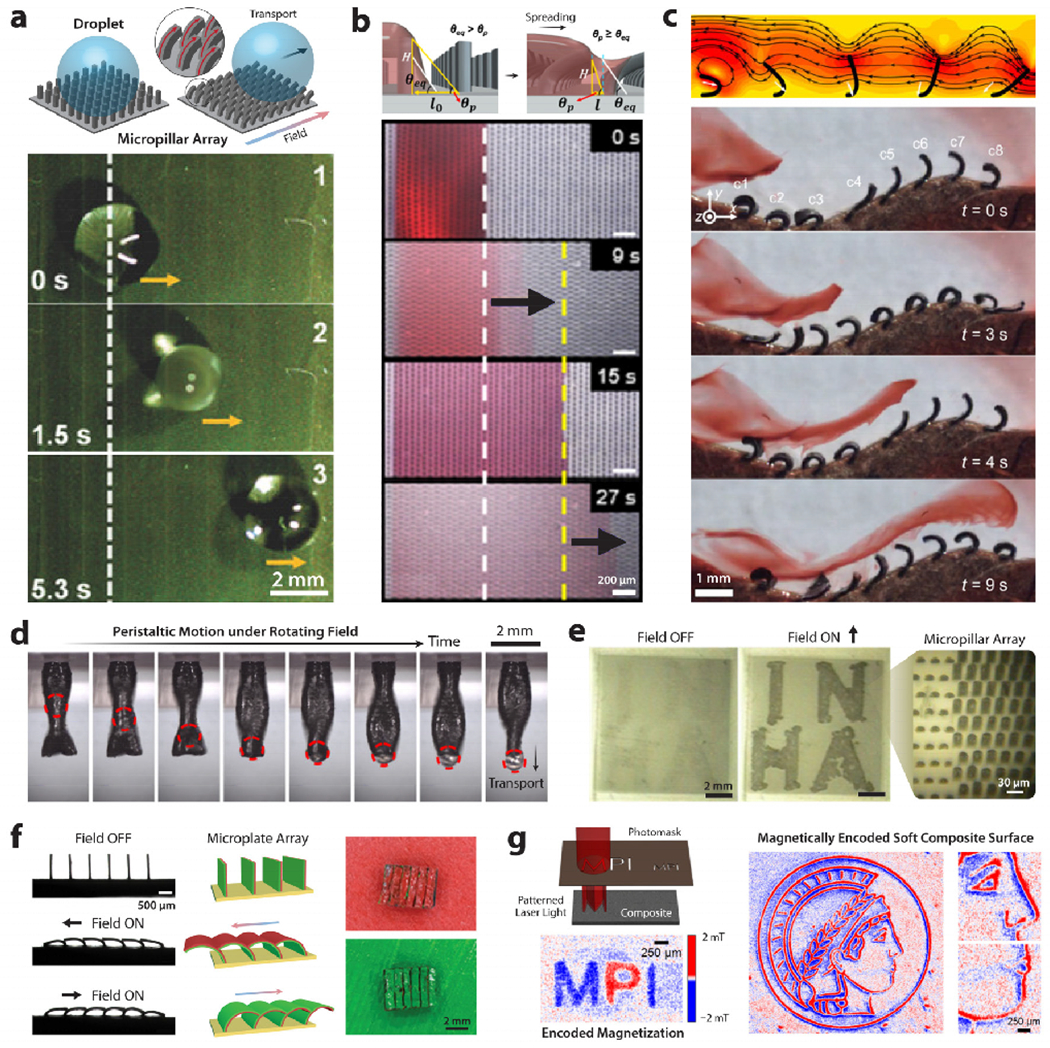
Hard-magnetic micropillar arrays (a) transporting liquid droplets and (b) spreading liquids using magnetically controlled deformation of the pillars. (c) Hard-magnetic cilia transporting fluids through traveling metachronal waves under rotating magnetic fields. (d) Peristaltic pump based on microassembled hard-magnetic composites for transporting particles or liquids under rotating magnetic fields. (e) Hard-magnetic micropillar array with encrypted patterns that can be revealed under an applied magnetic field. (f) Hard-magnetic microplate array with each side of the plate colored differently to realize magnetically controlled active camouflage. (g) Hard-magnetic soft composite based on materials with low Curie point (e.g., CrO2) and laser-assisted heating for spatially selective remagnetization (left). A magnetic soft composite surface encoded with a complex magnetization pattern through contact transfer of the magnetization profile from a magnetic master under global heating of the composite while in contact with the master surface (right). Panel (a) is reproduced with permission from ref 193 (Copyright 2018 Wiley); panel (b) from ref 198 (Copyright 2020 American Chemical Society); panel (c) from refs 158 and 330 (Copyrights 2020 American Association for the Advancement of Science and 2011 Cambridge University Press); panel (d) from ref 194 (Copyright 2021 American Association for the Advancement of Science); panel (e) from ref 198 (Copyright 2020 American Chemical Society); panel (f) from ref 199 (Copyright 2019 Wiley); and panel (g) from ref 215 (Copyright 2020 American Association for the Advancement of Science).
4.4.2. Mechanical Characterization
Mechanical properties of magnetic soft materials are as important as their magnetic properties in determining the performance and characteristics of the magnetically driven soft actuators. Our focus here is primarily on the mechanical response of the magnetic soft composite at zero field (i.e., purely mechanical response). For magneto-mechanical characterization of the field-induced stiffening of traditional magnetorheological elastomers, the reader is encouraged to consult other reviews more specifically focused on magnetorheological elastomers and gels.226–230 As mentioned earlier in Section 3.3, the mechanical response of magnetic soft composites can be described by hyperelastic constitutive models. The neo-Hookean model provides the simplest form of strain energy density (Helmholtz free energy per unit reference volume) function, which for isotropic and incompressible (J = 1) solids is given by
| (66) |
where G is the shear modulus of the material and I1 = tr(F⊤F) is the trace of the right Cauchy-Green tensor F⊤F. It is worth noting that most rubber-like materials can be reasonably considered to be incompressible because their bulk modulus values are typically orders of magnitude greater than their shear modulus values.231 For incompressible solids, the constitutive equation in Eq.(60) is modified with the additional constraint of incompressibility taken into account as
| (67) |
where p is often termed the hydrostatic pressure, a scalar quantity that can be determined from the equilibrium equations and the boundary conditions. Substituting Eq.(66) into Eq.(67) gives the following form of the Cauchy stress for incompressible neo-Hookean solids:
| (68) |
Under uniaxial loading, the deformation gradient F can be expressed in terms of the principle stretches as . With the incompressibility constraint (), the deformation gradient tensor can be expressed in the matrix form as
| (69) |
with λ1 = λ and λ2 = λ3 = λ−1/2. Then, from Eqs.(68) and (69), each component of the Cauchy stress is calculated as σ11 = Gλ2 − p and σ22 = σ33 = Gλ−1 − p. With the traction-free boundary condition σ22 = σ33 = 0, which gives p = G/λ, the true tensile stress can then be expressed as
| (70) |
which measures the true stress (force per unit current area) in the elongated specimen. In practice, the engineering or nominal stress, which characterizes the force per unit reference (undeformed) area, is easier to measure. From the relation between the Piola stress and the Cauchy stress in Eqs.(59) and (60) (i.e., P = Jσ−⊤), the engineering tensile stress can be expressed as
| (71) |
By fitting the experimentally obtained stress-stretch curve with Eq.(71), one can find the shear modulus of the material that is assumed to be an incompressible neo-Hookean hyperelastic solid (Figure 16b). In general, the neo-Hookean model captures the experimental data reasonably well for relatively small deformation (i.e., λ ≤ 1.5). At higher stretch levels, the neo-Hookean fails to predict the stiffening behavior that is observed in most rubber-like materials, and therefore other hyperelastic models (e.g., Gent, Mooney-Rivlin, Ogden, etc.) should be used along with additional fitting parameters. Given that the local maximum strain is typically around 30% (i.e., λ ≤ 1.3) even for large bending, it is reasonable to use the neo-Hookean model to find the material property (i.e., shear modulus G) when characterizing the mechanical response of magnetic soft bending actuators. It is worth noting that, for magnetic soft materials with mechanical anisotropy due to the aligned anisotropic particles, the strain energy density function should be chosen accordingly to account for their anisotropic mechanical response. Such anisotropic composites with directional mechanical properties can be regarded as transversely isotropic materials in general and treated similarly as fiber-reinforced composite materials in their modeling and characterization.81
5. Magnetic Actuation and Manipulation Platforms
Magnetic actuation utilizes torques and forces generated from the embedded magnetic particles under an applied magnetic field and therefore requires an external magnetic source that generates the actuating field. Manipulation of magnetic soft materials and robots can be achieved through the spatiotemporal control of the actuating magnetic field. Magnetic actuation and manipulation platforms can be categorized into different groups depending on the type of magnetic sources (permanent magnet or electromagnets) and their configuration (single, paired, or multiaxial), the characteristics of the actuating fields (spatially uniform or nonuniform, static or time-varying), and the mobility of the magnetic source (moving or stationary). In the following sections, we discuss some of the common types of magnetic actuation platforms that have been proposed for manipulation and control of magnetic objects in space for different applications.
5.1. Platforms Based on Permanent Magnets
One of the advantages of using a permanent magnet comes from the fact that it can give rise by itself to a static and relatively strong magnetic field in outer space. Contrary to electromagnets with current-carrying coils, which are subject to heat loss, permanent magnets do not experience heat loss and hence are generally more energy-efficient than electromagnets in generating magnetic fields of the same strength. Typical electromagnets are based on stacking multiple coils around a highly permeable soft-magnetic core to concentrate the magnetic flux. Even in the presence of a core, however, the field of a permanent magnet can in general exceed that of an electromagnet of the same size by up to an order of magnitude.232
For this reason, a single permanent magnet has been commonly used to actuate magnetic soft materials and robots as well as rigid magnetic objects or devices in different forms (e.g., pills or capsules). Magnetic manipulation can be achieved through spatial positioning of the actuating magnet while changing the position and orientation of the magnet relative to the object being manipulated. It is not uncommon to see a hand-held magnet being used to manipulate small magnetic objects in the literature, usually for validation of the proposed concepts or devices, for different applications such as capsule endoscopy,233–237 therapeutic delivery,60,131,238 endovascular navigation,31 and other general soft robotic applications.156,194 For more precise and reliable manipulation, it is also common to use a serial robot arm manipulator with multiple degrees of freedom (DOFs) to carry the actuating magnet and place it around the object being manipulated (Figure 17a). While in early days heavy and bulky industrial robot manipulators were employed,239–247 recently more compact and lightweight robot arms have been used for magnetic manipulation in medical applications.248–250
Figure 17. Magnetic actuation and manipulation platforms based on permanent magnets.
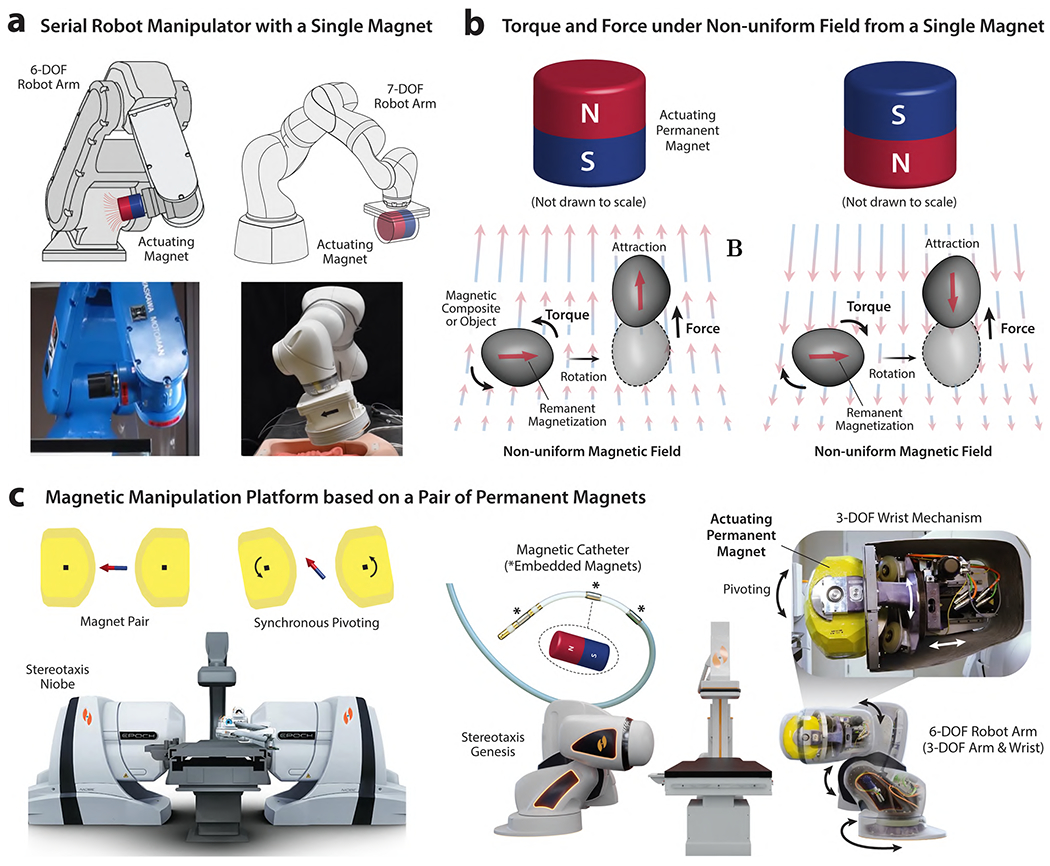
(a) Multi-DOF serial robot manipulators with a single actuating magnet attached at the end for steering untethered or tethered magnetic devices. (b) Magnetic torque and force on a hard-magnetic object in spatially nonuniform fields from a single actuating magnet. (c) Stereotaxis Niobe and Genesis platforms based on a pair of large permanent magnets for steering magnetic catheters by changing the applied field direction through synchronous pivoting of the actuating magnets. Panel (a) reproduced with permission from refs 243 and 249. Copyright 2016 SAGE Publications and 2019 American Association for the Advancement of Science.
A single permanent magnet, however, produces spatially nonuniform magnetic fields, and the presence of field gradients gives rise to the magnetic force as well as the magnetic torque acting on the object being manipulated (Figure 17b). The coupled interaction of magnetic force and torque, along with the complex geometry of the magnetic fields that depends on the shape of the magnet, make it nontrivial or rather difficult to precisely manipulate magnetic objects in many cases. One way to mitigate the geometrical complexity is to make the field symmetric by choosing an actuating magnet of simple symmetrical shape (e.g., cylindrical or spherical) with its remanent magnetization along the axis of symmetry. Then, the rotation of the magnet around its symmetry axis causes no change in the actuating magnetic field, which effectively reduces the DOFs involved in the manipulation of the magnet to 5 (3 for translations and 2 for rotations). Accordingly, for an untethered magnetic object (e.g., a magnetic capsule or pill containing a small magnet) with uniform magnetization in an unrestricted workspace, the number of DOFs that can be controlled by a single actuating magnet is at most five.243,251 The reduction of the effective DOFs due to the symmetry of the actuating magnet is equivalent to having kinematic redundancy when using a serial robot arm to spatially manipulate the magnet. This allows for more flexible operation of the robot arm when controlling a magnetic body through spatial positioning of the actuating magnet while avoiding collision with surrounding obstacles and other constraints such as kinematic singularity and joint limits.
In addition to having symmetry in the actuating field, magnetic manipulation can be further simplified by effectively decoupling the magnetic torque and force acting on the magnetic object by design. We know from Eq.(4) that the magnetic force can be suppressed by minimizing the effect of field gradients while reducing the strength of the object’s magnetic moment. When the magnetic object is sufficiently smaller than the actuating magnet and manipulated at sufficiently large distance from the magnet, the field gradients become substantially weaker due to the nature of the dipole field,252 for which the field gradient decays rapidly with the distance from the source (i.e., inversely proportional to the fourth power).17 Furthermore, by reducing the strength of the magnetic moment through dispersing small magnetic particles instead of embedding finite-sized permanent magnets, magnetic forces acting on the object can be suppressed. It has been shown, for example, that sub-millimeter-scale soft continuum robots based on hard-magnetic soft materials can be steered easily and intuitively with a single magnet.31,253 By design, such continuum devices with uniformly distributed magnetic particles have much diluted magnetization across the device, whereas conventional magnet-tipped devices, which contain one or a few embedded magnets, have highly concentrated and localized magnetic moments. Because the magnetic force always tends to attract the embedded magnets toward the actuating magnet (Figure 17b), steering control of the magnet-tipped devices using a single magnet can be easily complicated by the coupled interaction from the magnetic torques and forces. By contrast, the continuum devices based on hard-magnetic soft materials can utilize the magnetic torque as the primary source of actuation in steering control while experiencing negligible influence from the magnetic force.
For purely torque-based actuation and manipulation, spatially uniform magnetic fields can be created when two permanent magnets are configured in such a way that their opposite poles face each other. Commercially available magnetic actuation platforms based on spatially uniform fields include the Niobe and Genesis systems (Stereotaxis Inc.), which use a pair of large permanent magnets (Figure 17c). These systems have been used mostly for cardiac electrophysiology to treat heart arrhythmia using magnetic ablation catheters with a few rigid magnets incorporated in the distal portion for steering purposes.26,28 By synchronously rotating the two actuating magnets, each around its pivot inside the casing, these magnetic actuation platforms can create relatively uniform magnetic fields of 80-100 mT in any direction in the workspace between the magnets and hence enable force-free, intuitive steering control of the magnetic catheters (Figure 17c).28,254–257
5.2. Platforms Based on Electromagnets
While current-carrying coils are generally less energy-efficient in producing magnetic fields than permanent magnets, magnetic actuation platforms based on electromagnets offer several benefits that make them preferable to permanent magnets in many practical applications. Electromagnets provide a larger design space, with a variety of possible configurations of multiaxial coils, and a larger control space as well due to the ability to quickly turn on and off each coil or reverse the magnetic polarities of the individual coils to create complex (rotating or oscillating) fields without the need to move the set of coils physically. Furthermore, magnetic actuation platforms based on electromagnets can be designed to provide the capability to control both the magnetic force and torque either independently or simultaneously,154,258,259 to enable more flexible and sophisticated manipulation of magnetic objects within the workspace. To date, numerous types of magnetic actuation and manipulation systems based on electromagnets have been developed, which vary in the shape, number, and configuration of the current-carrying coils. According to the classification used by Abbott et al.,258 magnetic actuation and manipulation platforms based on electromagnets can be categorized into magnetically orthogonal systems or magnetically nonorthogonal systems.
5.2.1. Magnetically Orthogonal Systems
Magnetically orthogonal systems utilize special types of electromagnets, based on either circular or saddle coils arranged in pairs, which are designed to produce spatially uniform fields or constant field gradients in the workspace. When two identical circular coils are separated coaxially by a distance equal to their radius r and carry equal currents in the same direction, the field produced between the two coils in the axial direction (z-axis) is nearly uniform (Figure 18a). This is known as the Helmholtz coil configuration, and a pair of coils in such an arrangement is commonly called a Helmholtz coil-pair.260 The magnitude of the uniform field is proportional to the current strength i and inversely proportional to the radius r (i.e., Bz ~ i/r), and a Helmholtz coil-pair can be used to apply a uniform torque on a magnetic object in the workspace. When the two circular coils are separated further by a distance and carry equal currents in the opposite direction (Figure 18b), the pair of coils can generate a nearly constant field gradient in the axial direction (∂Bz/∂z), the magnitude of which is proportional to the current i and inversely proportional to the square of the radius r (i.e., ∂Bz/∂z ~ i/r2). Such an arrangement is called the Maxwell coil configuration,261 which can be used to apply a uniform force on a magnetic object in the workspace. These circular coil-pairs are easy to construct and offer good accessibility to the workspace of cylindrical shape.
Figure 18. Magnetic actuation and manipulation platforms based on orthogonally arranged or specially shaped electromagnetic coils.
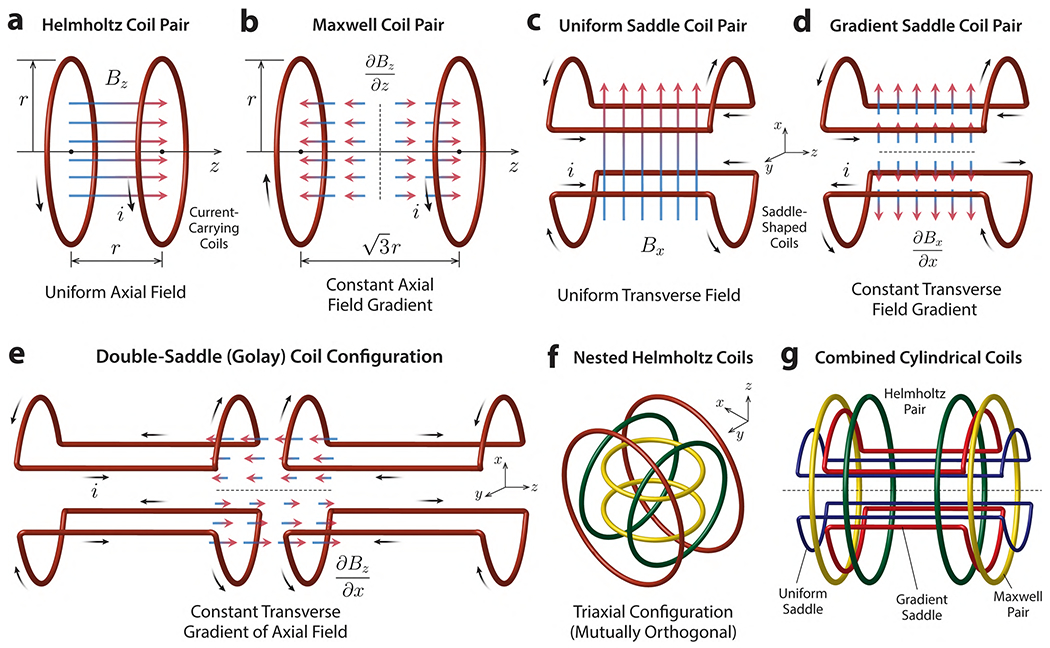
(a) Helmholtz and (b) Maxwell coil pairs for creating a uniform axial field (Helmholtz) or field gradient (Maxwell). Saddle-shaped coil pair for creating (c) a uniform transverse field or (d) a constant transverse field gradient depending on the direction of currents. (e) Golay coil configuration based on two saddle coil pairs for creating a constant transverse gradient of the axial magnetic field. (f) Nested Helmholtz coils in mutually orthogonal triaxial configuration for creating uniform actuating fields in three different directions. (g) Combination of different coil-pair types for multi-DOF magnetic manipulation based on magnetic torques and forces in a cylindrical workspace.
When it is desired to have an actuating magnetic field perpendicular to the symmetry axis of the cylindrical workspace, a pair of saddle-shaped coils can be used. In the saddle coil-pair system, two saddle-shaped coils that are confined to a thin cylindrical shell (i.e., coils wound on the surface of a cylinder) carry equal currents either in the same (parallel) direction to produce a uniform field (Figure 18c) or in the opposite (antiparallel) direction to produce a uniform field gradient (Figure 18d).262 It is worth noting, however, that the symmetry of the actuating field can be reduced with the saddle coil-pair system, when compared with the circular coil-pair system.263 When two saddle coil-pairs are aligned to have a common symmetry axis of the arcs, forming a specific configuration called Golay or double-saddle coils (Figure 18e),261,264 a uniform field gradient can be generated in the transverse direction (∂Bz/∂x or ∂Bz/∂y) depending on their orientation.
To increase the controllable DOFs, Helmholtz or Maxwell coil pairs can be nested in a mutually orthogonal fashion such that the symmetry axes of the coil pairs intersect at the common center (Figure 18f),265–268 where each coil pair independently produces a uniform field (Helmholtz) or field gradient (Maxwell) along its axial direction. For example, one or two Maxwell coil pairs can be incorporated into a triaxial Helmholtz coil system to apply forces in one or two directions in addition to torques in three directions on a magnetic object in the workspace.269,270 However, the available workspace for such orthogonally nested coil pairs is constrained to the workspace of the innermost (smallest) coil pair, which often leads to the scalability issue,259 given that both the field strength (~ r−1) and the field gradient (~ r−2) decrease as the coil radius r increases under the same current strength. When saddle coil pairs are combined with circular Helmholtz and Maxwell coil pairs, a spatially more compact system with a cylindrical workspace (Figure 18g) can be designed to enable multi-DOF magnetic manipulation.271–275 Lacking soft-magnetic cores, however, magnetically orthogonal systems based on nested Helmholtz/Maxwell or saddle coil pairs are usually suitable for applications with relatively small workspace. This is because the generated field strength is limited by the coil radius, while the problem of overheating276 precludes the use of large currents to produce stronger fields unless the setup is equipped with a cooling system like clinical magnetic resonance imaging (MRI) scanners.
In the clinical MRI scanner, field gradients can be generated in the bore by two pairs of Golay coils (for transverse gradients) and one pair of Maxwell coils (for axial gradient), in addition to the strong and uniform bore field in the axial direction generated by the main superconducting electromagnet. Therefore, clinical MRI scanners have been proposed as a magnetic manipulation platform with integrated imaging capabilities in many studies,258,277,278 despite some image artifacts that can be caused by magnetic objects,17 and used after minor hardware/software modifications for wireless actuation of magnetically controlled medical robots or devices based on magnetic forces generated through the gradient coils.279–287 Instead of using the field and field gradients in the bore, it has also been proposed that the strong fringe fields emanating from the clinical MRI scanner can be used to steer a magnet-tipped continuum device (e.g., guidewire), for which an industrial robot arm was employed for spatial positioning of the patient table around the MRI scanner as a large stationary magnet.288
5.2.2. Magnetically Nonorthogonal Systems
Another class of magnetic actuation and manipulation platforms, termed the magnetically nonorthogonal system,258 utilizes multiple columnar coils with soft-magnetic cores that are arranged around the workspace such that they all point to the center of the workspace. The fields generated by individual electromagnets are superimposed to create desired fields and field gradients for manipulation, and hence all electromagnets are active in general. It is known that in general at least eight coils are needed to control the five DOFs of an unconstrained magnetic object (i.e., three translations and two rotations except one rotation around the magnetization axis due to symmetry) independently without orientation-dependent singularities,289 at which the system loses the ability to generate magnetic force or torque on the object.259 Various designs of magnetic manipulation platforms based on eight electromagnets (Figure 19a) have been developed,29,197,290–294 which have different characteristics and performances in terms of torque- and force-generation capabilities and the accessibility of the workspace surrounded by the electromagnets.258,295 For small scales (i.e., table-top), the MagnebotiX OctoMag296 or MFG-100297 (or MiniMag298) systems based on eight stationary electromagnets are commercially available (Figure 19b). For human-body scale, clinical magnetic manipulation platforms based on eight stationary electromagnets include the Magnetecs (Neuro-Kinesis) CGCI (Catheter Guidance Control and Imaging)26,27,290 and the Aeon Phocus29,292 systems (Figure 19c), which have been used for cardiac electrophysiology as the Stereotaxis Niobe/Genesis system. These products are capable of independently controlling both the field and field gradient at any location in the workspace.154,234
The number of coils can be increased for systems based on stationary electromagnets to have manipulation redundancy258,299 or to enable spatially selective magnetic actuation.266,268 The number of coils can be reduced as well by adding motorized actuators168,300 (Figure 19d) or a parallel robot manipulator301,302 (Figure 19e) to rotate or move the electromagnets, which helps to increase the available workspace by reducing the number of electromagnets. A 6-DOF serial robot arm with a single electromagnet at its end-effector (Figure 19f) has also been proposed and demonstrated as a magnetic manipulation platform for steering tethered magnetic devices such as a magnet-tipped catheter.303–306 Instead of employing a multi-DOF serial robot arm to change the position and orientation of a single electromagnet, a simple passive arm has been used to carry and hold a cube-shaped electromagnet consisting of three nested mutually orthogonal coils, also known as Omnimagnet,307,308 to control a magnetically steerable cochlear implant (see Figure 25g in Section 6.2.2).309 When compared with the platforms based on multiple stationary electromagnets (Figure 19a–c), these mobile electromagnetic actuation platforms can provide a larger workspace for more flexible operation with increased compatibility with external imaging or sensing devices.
Figure 25. Applications of magnetic soft materials and robots for minimally invasive interventions.
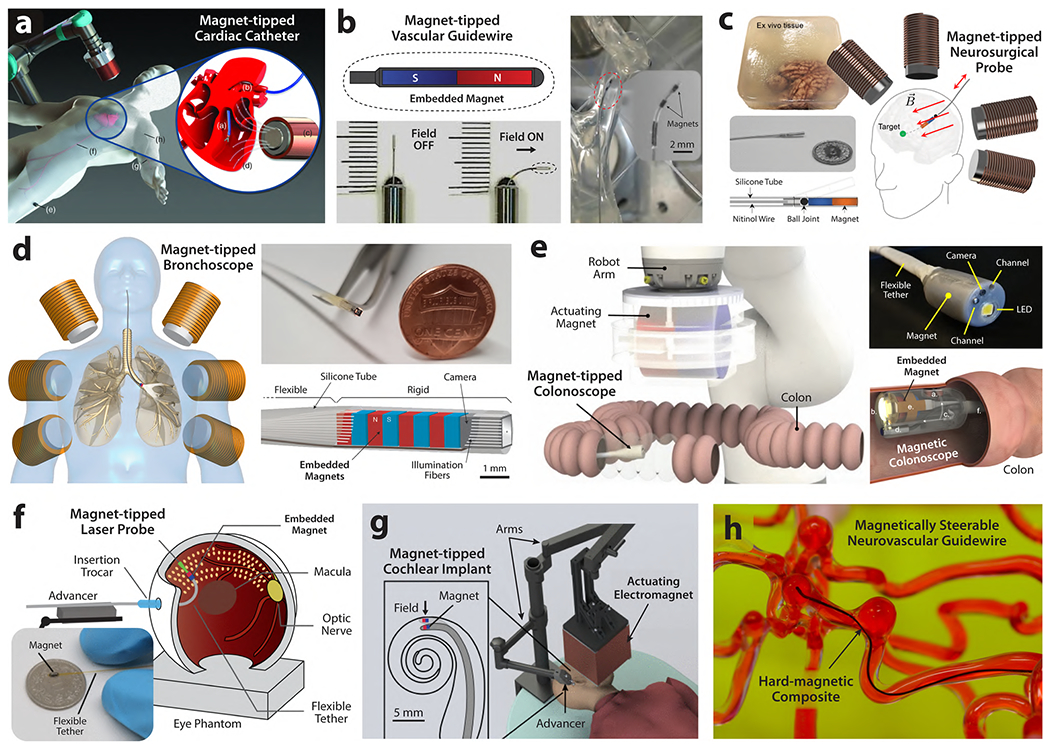
(a) Magnet-tipped catheters for cardiac applications, (b) magnet-tipped guidewires for endovascular navigation, (c) magnet-tipped flexible needles for minimally invasive neurosurgical applications. Magnetically steerable endoscopes for (d) lung airway (i.e., bronchoscope) and (e) colon lumen (i.e., colonoscope) inspections based on flexible tethered devices with embedded finite-sized magnets. (f) Magnetically steerable laser probe for ophthalmic surgical applications to treat retinal diseases. (g) Magnet-tipped cochlear implants for magnetically controlled robotic insertion. (h) Magnetically steerable guidewires based on hard-magnetic soft composites for navigation in the complex neurovasculature. Panel (a) is reproduced with permission from ref 303 (Copyright 2018 IEEE); panel (b) from refs 254 and 355 (Copyrights 2006 Springer Nature and 2018 MDPI); panel (c) from ref 350 (Copyright 2021 IEEE); panel (d) from ref 30 (Copyright 2018 World Scientific Publishing); panel (e) from refs 248,249,359 (Copyrights 2019 IEEE, 2019 American Association for the Advancement of Science, and 2020 Springer Nature); panel (f) from ref 352 (Copyright 2019 IEEE); panel (g) from ref 309 (Copyright 2020 IEEE); and panel (h) from ref 31 (Copyright 2019 American Association for the Advancement of Science).
6. Applications of Magnetic Soft Materials and Robots
The recent progress in materials design, modeling, and fabrication techniques for magnetic soft materials and robots and the advances in the magnetic actuation platforms have collectively broadened their boundary of applications in different areas, which is in contrast with traditional magnetorheological elastomers whose applications have developed somewhat narrowly in the field of vibration isolation or absorption. In the following sections, we discuss the emerging applications of magnetic soft materials and robots by grouping them into a few categories depending on their purposes. First, we will discuss general soft-robotic concepts and devices based on magnetic soft materials, which are not necessarily in biomedical areas in terms of their target applications. Then, we will review those that have been more specifically proposed and demonstrated for biomedical applications in the literature.
6.1. General Applications
6.1.1. Small-Scale Untethered Soft Robots
Magnetic actuation has been a fast and effective means of manipulating untethered small-scale magnetic soft robots. In fluidic environments, in which the viscous drag becomes more significant or dominant than the inertial force (i.e., with low Reynolds number) due to the size effects, swimming strategies have often been adopted based on those of living microorganisms.17 Inspired by sperm cells, for example, which utilize traveling waves from the head toward the tail for propulsion, soft or flexible magnetic filaments have been used to create undulating motion under an oscillating magnetic field to produce thrust.310–313 The helical propulsion of bacterial flagella has also been adopted to small-scale magnetic soft robots which are designed to mimic the screw-like motion to propel themselves under rotating magnetic fields (Figure 20a).200,201 Millimeter-scale magnetic soft robots have also been designed to mimic the jellyfish and successfully demonstrated a life-like swimming motion under oscillating magnetic fields (Figure 20b).167 Such bioinspired magnetic soft robots have been developed for locomotion in solid environments as well, including the millipede- or centipede-inspired soft-robotic crawlers that utilize traveling metachronal waves under rotating magnetic fields (Figure 20c).159,168,314 Shape-programmable magnetic soft materials can be designed to exhibit different modes of deformations depending on the applied field strength and direction, and their shape-changing capabilities can be used to enable multiple modes of locomotion when combined with spatiotemporal control of the actuating magnetic fields. Magnetic soft robots of relatively simple geometry (e.g., a planar beam) with non-uniform magnetization patterns have demonstrated a series of multimodal locomotion and transition in fluid and/or solid environments (Figure 20d).164–166,315 The advanced fabrication techniques based on 3D printing (see Section 4.2.2) have increased the level of complexity in the design of magnetic soft robots and provided them with flexible appendages, which help to achieve more sophisticated functions while interacting with other objects or environments at millimeter or centimeter scales (Figure 20, e and f).156,178,316
Figure 20. Small-scale untethered soft robots based on magnetic soft materials.
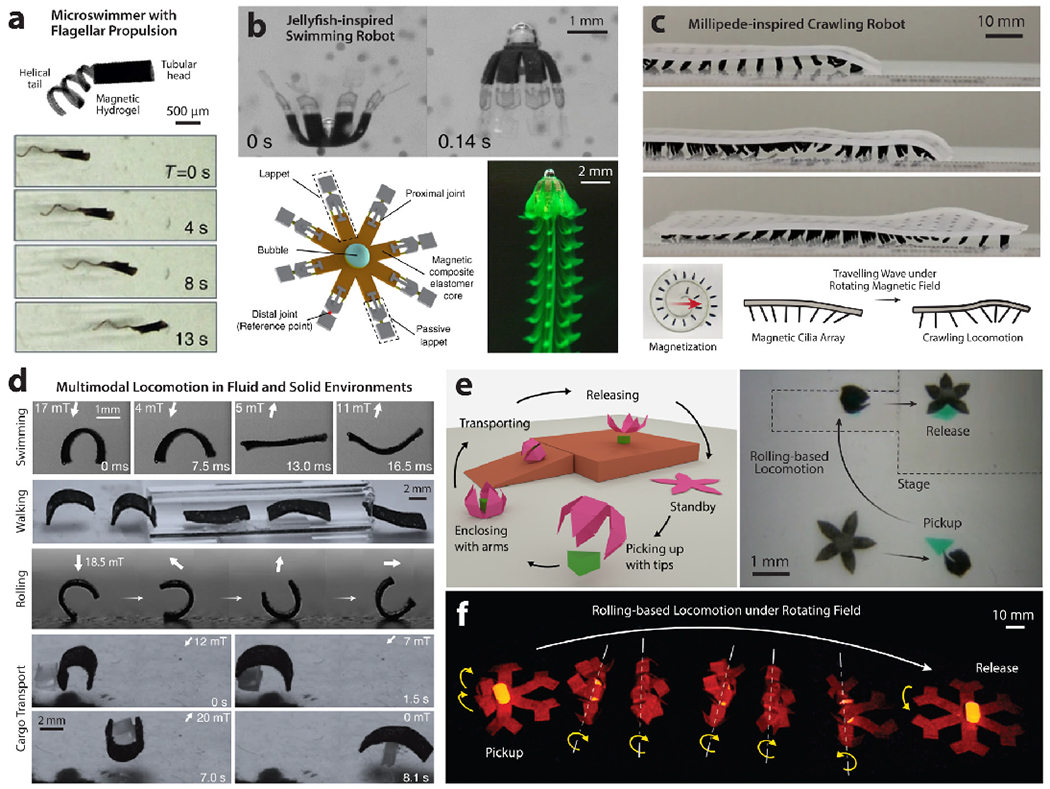
(a) Microswimmer based on magnetic hydrogel mimicking the helical propulsion of bacterial flagella under rotating magnetic fields. (b) Bioinspired magnetic soft robots based on hard-magnetic soft composites mimicking the swimming motion of a jellyfish under alternating magnetic fields. (c) Millipede-inspired crawling robot with an array of hard-magnetic cilia with different magnetization directions to produce traveling waves under a rotating magnetic field for crawling locomotion. (d-f) Magnetic soft robots based on hard-magnetic composites exhibiting multimodal locomotion such as swimming, walking, and rolling in fluid/solid environments as well as cargo transport through spatiotemporal control of the actuating magnetic fields. Panel (a) reproduced with permission from ref 200 (Copyright 2016 Springer Nature); panel (b) from ref 167 (Copyright 2019 Springer Nature); panel (c) from ref 159 (Copyright 2020 Springer Nature); panel (d) from ref 166 (Copyright 2018 Springer Nature); panel (e) from ref 178 (Copyright 2019 American Association for the Advancement of Science); and panel (f) from ref 156 (Copyright 2018 Springer Nature).
6.1.2. Active Origami and Metamaterials
Earlier forms of magnetically controlled origami robots317 have used small permanent magnets embedded in passive origami structures for magnetic manipulation and localization.21,22,46,318,319 Using distributed magnetic torques and local rotations under an applied field, magnetic soft materials have been shown to enable magnetically controlled folding and unfolding of origami-type structures across different scales.80,156,216,320 For example, a magnetically controlled microscopic crane has been designed and fabricated based on patterned nanomagnet arrays connected by flexible hinges (Figure 21a), which produces flapping movements under an alternating magnetic field.80 The classic Miura-ori pattern has also been reproduced with magnetic soft materials156,319 (Figure 21b), which is essentially a type of mechanical metamaterial that shrinks in both length and width directions, exhibiting a negative in-plane Poisson’s ratio.321,322 Various structures with negative Poisson’s ratios (often referred to as auxetic metamaterials322) whose auxetic behaviors can be controlled magnetically have been realized, through either extrusion-based 3D printing156,173 (Figure 21c,d), manual assembly194,212,215,323,324 (Figure 21e,g), or injection molding162 (Figure 21f) approaches, highlighting the utility of shape-programmable magnetic soft materials in the design of active mechanical metamaterials. By integrating shape memory polymer components into magnetic soft composites via multimaterial 3D printing, mechanical metamaterials with temperature-dependent magnetic response have also been realized110 (Figure 21h). Other types of magnetically controlled mechanical metamaterials, which utilize field-induced stiffening to exhibit field-dependent structural properties or behaviors in response to applied static or dynamic mechanical loads, have been demonstrated.163,325,326 Active metamaterials made of magnetic soft materials have demonstrated potential for applications in unconventional soft robotics,156,162 acoustic metastructures with tunable bandgap,324 and vibration-resistant structures.326
6.1.3. Programmable and Reconfigurable Surfaces
Arrays of micropillars or microplates based on magnetic soft materials have been used to create magnetically reconfigurable surfaces for different purposes. Through the superhydrophobic nature of micropillar arrays made of magnetic soft materials, for example, it has been shown that small liquid droplets or particles can be transported and manipulated on the arrays by controlling the applied magnetic field (Figure 22a).157,193,327,328 Similarly, magnetically reconfigurable surfaces based on micropillar or microplate arrays have been used for fluid transport (spreading, pumping, mixing) through magnetically induced topographical and wettability changes (Figure 22b)198,199,329 or using dynamic metachronal waves created by magnetic cilia under rotating fields (Figure 22c).158–160,330,331 Fluid transport has also been demonstrated with circular tubes made of magnetic soft materials that are designed to mimic the peristaltic motion under traveling or rotating magnetic fields (Figure 22d)194,332 or using a miniaturized centrifugal pump based on magnetic soft composites.333
Other potential applications of reconfigurable surfaces based on magnetic pillar arrays have been proposed as well. As an example, creation of arrays of micropillars with different responses or reactivity to an applied field to enable selective deformation of the pillars, it has been shown that the micropillar arrays can be encoded or encrypted with designed patterns that are visible only under an applied magnetic field (Figure 22e).157,198 Actively reconfigurable surfaces based on magnetic microplate arrays have also been applied to active camouflage by coloring each side of the arrayed microplates differently (Figure 22f).199 Similarly, application of hydrophilic coating to one side and superhydrophobic coating to the other side of the arrayed microplates, it has also been shown that such a Janus-type microplate array can be used to create reconfigurable surfaces with magnetically switchable wettability.199
Instead of using reconfigurable micropillar arrays, it has also been shown that the surface of a magnetic soft composite sheet can be encoded with intricate magnetization patterns, which can be seen only under a magneto-optical sensor (Figure 22g),215 using magnetic particles with low Curie temperature (e.g., CrO2) along with the laser-assisted reprogramming technique discussed in Section 4.3 to selectively demagnetize and remagnetize the embedded particles.
6.1.4. Soft and Flexible Electronic Devices
Previously, magnetically guided self-assembling structures based on flexible planar substrates containing patches of magnetic soft composites and electronic components were shown to form 3D flexible electronic devices.211 More recently, magnetic soft materials have been used to demonstrate magnetically reconfigurable soft/flexible electronic devices by integrating electronic components and circuitry into 3D-printed structures or molded sheets based on hard-magnetic soft composites with nonuniform magnetization patterns. Such soft devices exhibit different electronic functions that correspond to their deformed states under applied magnetic fields156 (Figure 23a), where such a concept of functionally reconfigurable electronic devices was previously demonstrated by means of passive buckling of patterned flexible circuits upon the release of prestretched elastomer substrates,334 or reconfigure themselves into different states through programmed shape changes to control light beams emitted from the attached LEDs335 (Figure 23b). Magnetic soft composites with an integrated miniature magnetic sensor and circuitry have been proposed as a tactile sensor, which utilizes the change in the measured magnetic flux density due to the change in the position and orientation of the embedded hard- or soft-magnetic filler particles under local deformations (Figure 23c–e).174,336–339 Similarly, it has been shown that tactile or pressure sensors can be designed based on micropillar or microstructural arrays of hard-magnetic soft composites, either on top of a miniature magnetic sensor78,340 or with a flexible coil between them,341 to measure the change in magnetic flux during bending of the magnetized pillars upon the applied pressure. Magnetic soft materials have also been used to build a flexible vibration sensor by integrating pickup coils to measure the rate of change in the magnetic flux during the vibration of a substrate or an object onto which the sensor is mounted (Figure 23f).342
Figure 23. Applications of magnetic soft materials for soft and flexible electronic devices.
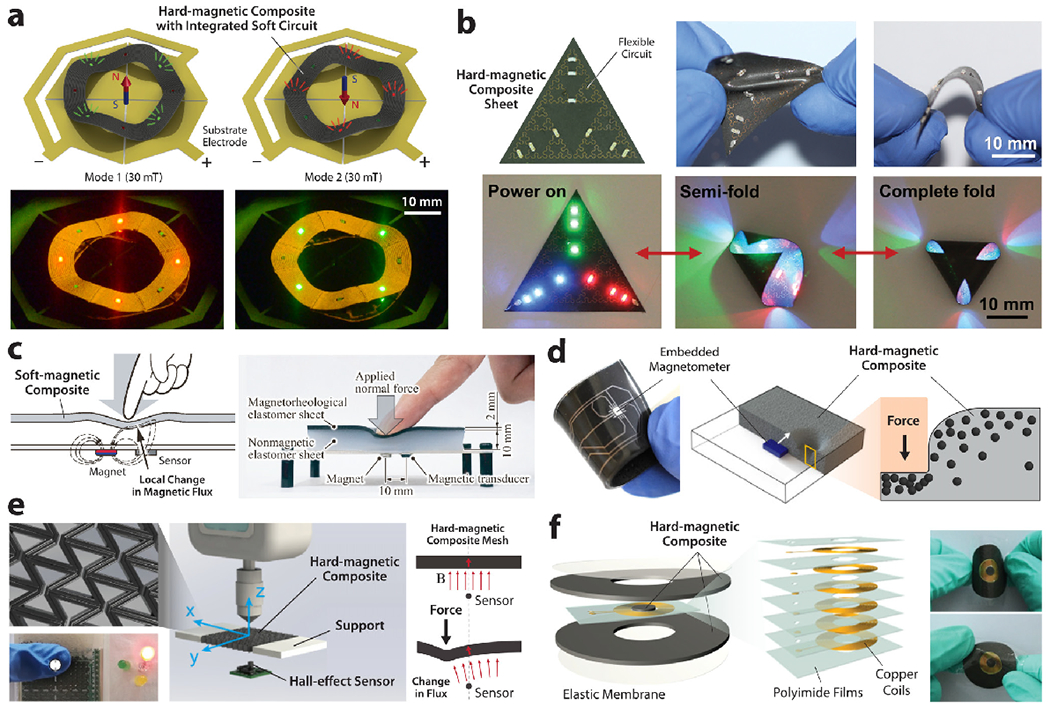
(a) Magnetically reconfigurable soft electronic device based on 3D-printed hard-magnetic composite (Figure 9b) with an integrated soft circuit to exhibit different functions corresponding to its shapes under the applied fields. (b) Hard-magnetic composite with electroplated flexible (serpentine) circuits. Tactile sensors based on (c) soft-magnetic and (d) hard-magnetic composite sheets and (e) 3D-printed hard-magnetic composite mesh with integrated hall-effect sensors to measure the change in the magnetic flux density due to the change in the position and orientation of the embedded hard- or soft-magnetic filler particles under local deformations. (f) Flexible vibration sensor based on hard-magnetic composites with integrated flexible coils. Panel (a) is reproduced with permission from ref 156 (Copyright 2018 Springer Nature); panel (b) from ref 335 (Copyright 2021 Wiley); panel (c) from ref 336 (Copyright 2018 MDPI); panel (d) from ref 337 (Copyright 2019 Wiley); panel (e) from ref 174 (Copyright 2021 Elsevier); and panel (f) from ref 342 (Copyright 2020 Wiley).
6.2. Biomedical Applications
6.2.1. Targeted Delivery of Therapeutics
Magnetic microrobots have displayed great potential for localized delivery of therapeutics usually in the form of rigid carriers for drugs, cells, or genes.205,208,343–346 As the cargo capacity of a single microrobot is limited, multiple robots are often employed as a swarm to improve the delivery performance.347 At millimeter scales, shape-programmable magnetic soft robots have also been proposed for targeted drug or cell delivery. As an example, magnetically active porous hydrogels have been demonstrated as carriers for therapeutic agents, which can be released on demand as the scaffold deforms upon the application of magnetic fields (Figure 24a).60,93 Magnetic hydrogels have also been used as carriers for diagnostic microbes for targeted transport and retention in gastrointestinal tract (Figure 24b).131 Magnetically controlled capsule devices based on a flexible body with embedded magnets (Figure 24c) have demonstrated their capabilities for imaging, biopsy, and therapeutic delivery under magnetic control.23–25,348 Magnetic capsule robots composed of fully soft materials have recently been demonstrated and are capable of rolling-based locomotion on rough surfaces (e.g., stomach wall) and release of the drugs by squeezing themselves under applied magnetic fields (Figure 24d).194 The magnetically controlled release of therapeutic agents upon the deformation of the soft carriers has proven more effective and controllable than passive release based on molecular diffusion or cell migration.60,94
Figure 24. Applications of magnetic soft materials and robots for targeted delivery of therapeutics.
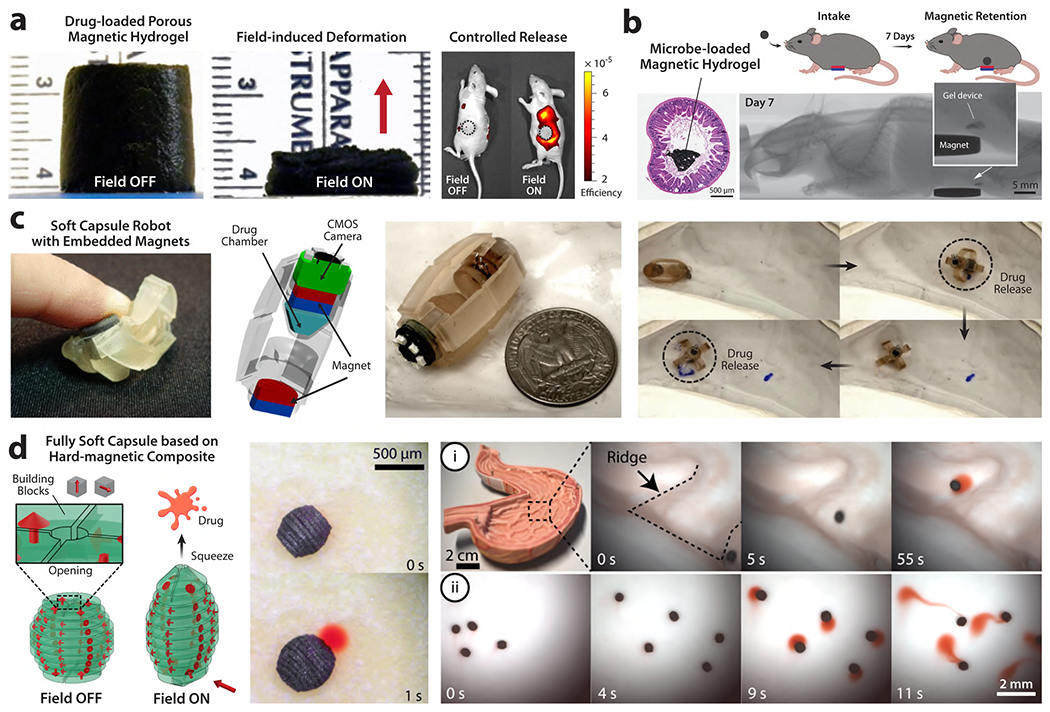
(a) Macroporous magnetic hydrogel for on-demand drug or cell delivery based on field-induced deformation. (b) Microbe-loaded magnetic hydrogel device for magnetically controlled transport and retention in the gastrointestinal tract. (c) Magnetic soft capsule robot with embedded magnets for targeted drug delivery and endoscopic imaging. (d) Magnetic soft capsules based on microassembled hard-magnetic composites (Figure 14d) that roll under weak rotating magnetic fields and squeeze themselves under a strong field to release liquid drugs. Panel (a) is reproduced with permission from ref 60 (Copyright 2011 National Academy of Sciences); (b) from ref 131 (Copyright 2021 Wiley); (c) from ref 23 (Copyright 2012 IEEE); and (d) from ref 194 (Copyright 2021 American Association for the Advancement of Science).
6.2.2. Minimally Invasive Procedures
Magnetically steerable tethered devices in the form of magnet-tipped catheters or guidewires have been used for minimally invasive cardiac or vascular interventional procedures (Figure 25a,b),254–257 utilizing the remotely controlled steering of the device based on the magnetic torque or force generated by the embedded magnet under externally applied actuating fields. The advances in hard-magnetic materials and manipulation platforms have facilitated the application of magnetically steerable devices in different types of minimally invasive surgery, which include stereotactic neurosurgical procedures for biopsy or deep brain stimulation (Figure 25c),349,350 endoscopy for lung airway30 or colon lumen248,249 inspections (Figure 25d,e), eye surgery for treating retinal diseases or cataracts (Figure 25f),351–353 robotic insertion of cochlear-implants (Figure 25g),309,354 and endovascular navigation.31,288,355–357 While the majority of magnetically steerable tethered devices utilize one or a few small magnets embedded in the distal portion, it has recently been shown that hard-magnetic soft composites can be used to realize sub-millimeter-scale magnetic soft continuum robots with omnidirectional steering and navigational capabilities (Figure 25h) for neuroendovascular applications.31,250,358 When compared with the “magnet-tipped” design for conventional magnetically controlled intravascular devices, the “soft continuum” design based on soft composites with distributed magnetic particles can facilitate the miniaturization of the device while obviating the potential risks of embolization due to mechanical failure of the finite-sized magnet attached at the end of the device.31,288
7. Considerations for Future Developments
Despite the recent progress in magnetic soft materials and robots and their demonstrated potential for future therapies, much work needs to be done to address remaining challenges in the design, fabrication, sensing, and control of magnetic soft robots. In the following section, we highlight underexplored areas of research in the field of magnetic soft materials and robots and suggest directions for future developments (Figure 26). We also discuss from clinical translation perspectives the biocompatibility of magnetic soft materials for their medical applications.
Figure 26.
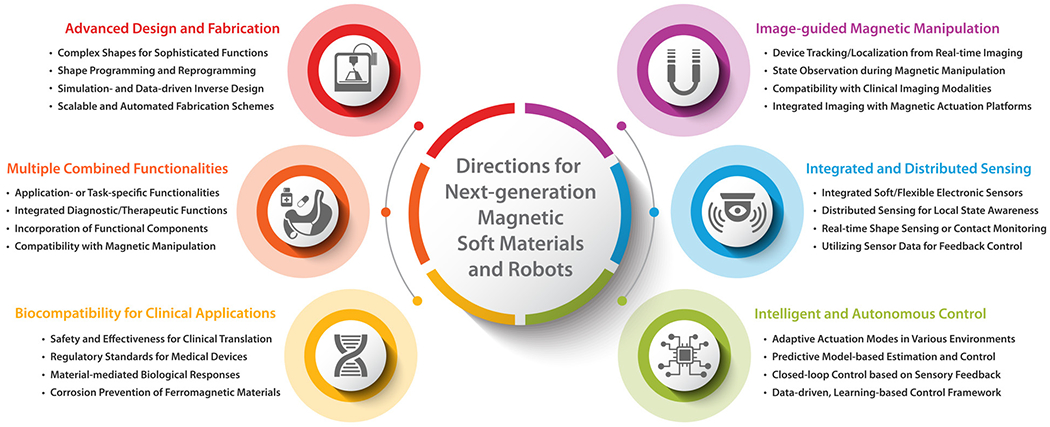
Future developments and research directions for next-generation magnetic soft materials and robots.
7.1. Advanced Design and Fabrication
As discussed in Section 4.2, the advances in fabrication techniques have increased the level of complexity in the design of magnetic soft materials and robots, enabling complex shape changes programmed by means of intricate magnetization patterns. Even for a single magnetic object that is not designed to morph into programmed shapes, the magnetization profile can play an important role in terms of enabling more sophisticated manipulation by increasing the number of controllable DOFs. As discussed earlier in Section 5.1, a uniformly magnetized object with axial symmetry has at most five controllable DOFs in free space, as the symmetry around the magnetization direction reduces one rotational DOF, and so do typical untethered magnetic objects such as magnetic capsule robots. Aimed at enabling more dexterous manipulation of magnetic objects, it has been shown that the controllable DOFs of an untethered magnetic object can be increased to six by creating a complex magnetization pattern achieved from assembling a few pieces of composites with nonuniform magnetization into a single object.251,360 In terms of fabrication, the magnetic 3D printing techniques discussed in Section 4.2.2 can be used to build objects with such intricate magnetization patterns more easily.
When it comes to design, however, finding the required magnetization patterns to achieve the desired shape changes or functions can be nontrivial in many cases, especially when the geometry becomes complicated. For simple geometries such as beams or rods, numerical solutions of their governing equations based on the force and moment balances165,253 can be used to find the optimal magnetization profile to program the desired shape.165 For high-dimensional geometries with complex programmed shape changes, however, there is no unified framework for design, which has often relied on heuristic approaches based on trial and error. While finite element simulations based on the continuum mechanical models (see Section 3.3) can be used to find the equilibrium state when the object geometry and magnetization profile are given and the actuating magnetic field and boundary conditions are specified, solving the inverse problem is challenging. However, given that large quantities of data can be easily generated from finite element simulations for the forward problems, machine learning approaches can be used to solve the inverse-design problems by utilizing the collected data set for training learning networks, which have shown promising results in designing functional composite materials.358,361–363 In doing so, the limitations of the existing fabrication methods discussed in Section 4.2 will need to be considered, given that they are not without limitations in terms of their achievable level of complexity in the programmed magnetization pattern and the fabricated object geometry. In other words, advanced fabrication techniques to realize the optimized design should be developed in parallel to be able to leverage such learning-based design frameworks for next-generation magnetic soft materials and robots. As mentioned in Section 4.2.3, developing a scalable and automated fabrication method to realize 3D magnetization patterns in 3D structures will thus be an important area of future exploration.
7.2. Multiple Combined Functionalities
As shown in many examples discussed in Section 6.2, biomedical applications of magnetic soft materials and robots require additional functionalities for therapeutic or diagnostic purposes in addition to magnetic actuation and control for device manipulation and deployment. In some cases, some of the device functions can be directly achieved through the programmed shape changes of the device under magnetic actuation, as was the case with the soft capsule robots that can release drugs through squeezing action while deforming under an externally applied field (Figure 24d).194 In many other cases, however, the magnetically driven transformation alone may not be sufficient to perform sophisticated diagnostic or therapeutic tasks. For example, a biopsy requires high enough forces to extract cells or tissues for sampling, which can be challenging for soft-bodied robots to generate or exert on the targeted tissue. One possible approach could be to incorporate magnetically controlled microneedles296 or thermally activated microgrippers24 inside the soft robot that can be delivered and released on demand at the targeted site to perform the biopsy task and safely retrieved.2
When compared with discrete systems based on one or a few finite-sized magnets incorporated into the robot’s deformable body (Figure 1a), continuous systems based on soft composites with dispersed magnetic particles (Figure 1b) could offer greater flexibility in the design and fabrication of magnetic soft robots with multiple combined functionalities. In the field of intravascular or endoluminal soft-robotic devices, for example, the magnetically steerable soft continuum robots for endovascular navigation (Figure 25h) have demonstrated an additional capability of steerable laser delivery by incorporating an optical fiber as a functional core inside the composite polymer jacket.31 Since the actuating magnetic field does not affect the transmission of laser light through the optical fiber core, such devices could potentially be used for laser-assisted endovascular therapy such as laser atherectomy for removing plaque from blood vessels to treat obstructive vascular diseases. When the functional core is in the form of a fiber-optic shape sensor based on fiber Bragg grating (FBG) arrays,364 real-time shape sensing and device tracking or localization could be realized for magnetically steerable soft continuum robots to enable feedback control.
7.3. Biocompatibility for Clinical Applications
While great potential of magnetic soft materials and robots for biomedical applications has been demonstrated in many proof-of-concept studies, as discussed in Section 6.2, much work is needed to ensure their safety and effectiveness for successful clinical translation. In the context of the regulatory process for medical devices, different levels of biocompatibility are required for the device materials depending on the level of interaction with the human body, considering the type and duration of contact with biological materials (e.g., tissues, cells, blood), following relevant standards such as the ISO 10993 series365–368 and the related Food and Drug Administration (FDA) guidance369 for 510(k) premarket notification or premarket approval (PMA) processes depending on the device classification for FDA regulatory pathways.
As mentioned earlier, iron oxide nanoparticles are considered biocompatible82–84 and hence have been most commonly used for biomedical applications such as magnetic hyperthermia for cancer treatment. While common host polymers for magnetic soft materials and robots based on silicone or polyurethane elastomers and hydrogels are generally known to be biocompatible with no acute cytotoxicity,138,370–374 ferromagnetic materials including iron and iron-based alloys can be cytotoxic due to their corrosive nature.375–377 It has been shown from cell viability testing that, for relatively short-term (i.e., 24 hours) exposure to aqueous environments, magnetic soft composites based on silicone elastomers containing bare (uncoated) neodymium-iron-boron (NdFeB) microparticles are biocompatible,378 which can be attributed to the fact that the particles are contained within the polymer matrix. For hydrogel-based composites, in which the uncoated NdFeB microparticles are directly exposed to the aqueous environment of the hydrogel matrix, it has been shown that 90% of cells can remain alive in a similar testing condition with short-term exposure (24 hours).137 However, the particles will eventually become corroded residing in the aqueous environment for extended periods of time because the silicone elastomers are permeable to gas and water vapor, and the corrosion products can cause cytotoxic effects. For this reason, the anticorrosion coatings for magnetic particles (see Section 2.3.1.2) will be required for biomedical applications with long-term exposure to physiological environments such as tissue scaffolds or implantable devices. It has recently been reported that composites based on poly(vinyl alcohol) hydrogels and silica-coated NdFeB particles did not result in cytotoxic effects even when in contact with mammalian cells or living bacteria for several days.131 Although uncoated samarium cobalt (SmCo) alloys have been reported to show a greater tendency for corrosion and cytotoxicity, when compared with uncoated NdFeB alloys, it has been shown that different types of anticorrosion coatings can be applied to make the material nontoxic.379,380
For clinical applications that involve contact of the device with circulating blood, such as the magnetically guided intravascular devices, hemocompatibility should also be evaluated to ensure that the device materials cause no adverse responses such as thrombosis, coagulation, hemolysis, and complement activation during their intended uses. For example, thrombosis on the robot can impede robotic functionality (e.g., increasing the mechanical rigidity) and may lead to distal tissue ischemia, while complement activation may not only render the robot nonfunctional but also cause systemic impacts due to the subsequent inflammatory response.381 Material-mediated complement activation is a complex process that depends on multiple factors such as the physical and chemical properties of the material and the surface area and surface architecture of the device.369,382 Further studies will be required to evaluate such material-mediated biological and physiological responses to evaluate both short-term and long-term systemic responses and thereby to ensure the safety of magnetic soft materials and robots for their applications to blood-contacting medical devices.
7.4. Image-Guided Magnetic Manipulation
For magnetic capsule robots or magnet-tipped tethered devices for medical applications, whose size can range from a few millimeters to centimeters in terms of the device diameter, localization and tracking of the device have been obtained from internal or external sensing (e.g., embedded Hall-effect sensors and inertial measurement units247,249,383 or externally arranged Hall-effect sensor arrays25,299,384–386) or real-time imaging (e.g., internal imaging using endoscopy cameras;30,359 external imaging through optical or stereocameras,242,243,300,301 x-ray fluoroscopy,249,387 magnetic resonance imaging,287 or ultrasound305). The state observation from device tracking and localization through real-time sensing or visual feedback through imaging allows for the implementation of closed-loop feedback control or learning-based, data-driven control386 for intelligent magnetic manipulation. For small-scale magnetic soft robots, however, device tracking and localization for closed-loop control and advanced manipulation through internal or external sensing can be challenging due to their constrained size, and the state observation would rely mostly on the visual feedback from real-time external imaging.
When it comes to clinical applications of magnetic soft robots, such as for minimally invasive interventions, x-ray fluoroscopy could offer reliable real-time imaging for state observation of the device being manipulated inside the human body, because a device with distributed magnetic particles will be naturally visible under x-ray due to the presence of radiopaque magnetic particles. Another important point is that externally applied magnetic fields do not cause interference on x-ray imaging, which is why the commercialized magnetic manipulation systems (Figures 17c and 19c) have been used along with a C-arm fluoroscope for real-time x-ray imaging. However, the fact that x-ray fluoroscopy provides only planar 2D projection imaging at a time implies that an integrated imaging and actuation platform will be needed to facilitate flexible and dexterous manipulation of magnetic soft robots in 3D environments. The C-arm fluoroscopy system has been evolving into essentially a multi-DOF robotic platform capable of automated rotation and angulation with flexible maneuverability for complex image-guided interventions. In this regard, we envision that next-generation magnetic manipulation platforms will have an integrated robotic imaging system that can be synchronized with magnetic actuation. However, the previously developed or existing magnetic manipulation systems are mostly based on either a pair of large permanent magnets (Figures 17a) or a set of multiaxial electromagnets (Figures 19a–d), for which the C-arm angulation and rotation is greatly limited due to the confined space between the magnets or electromagnetic coils.254 When compared with these relatively bulky systems, compact platforms based on a serial robot arm manipulator with a single actuating magnet at the end of its end-effector (Figures 17a and 19f) could allow wider C-arm rotation angles for better state observation and hence suggest a cost-efficient alternative to the existing magnetic actuation and manipulation systems for clinical applications.
7.5. Integrated and Distributed Sensing
Recent advances in soft electronic sensors and circuits based on semiconducting or conductive soft materials with percolating networks of conductive phases suggest potential for integration with magnetic soft robots for distributed sensing capabilities in the form of stretchable electronic skin7,111,388,389 or integrated soft and flexible circuits in the soft-bodied robots390,391. The use of multimaterial 3D printing would facilitate seamless integration of the sensing and actuating components, where the addition of the sensing elements should ideally not affect or sacrifice the actuation performance due to the additional mechanical resistance that needs to be overcome by magnetic torques or forces during actuation. In this light, highly compliant, stretchable conductive polymers or hydrogels based on poly(3,4-ethylenedioxythiophene) poly(styrene sulfonate) (PEDOT:PSS)392–394 can be potentially useful for integration as sensing elements in small-scale magnetic soft robots, because of their lightness as well as good electrical performance. The sensory skin with distributed sensing elements can also be used to collect environmental signals such as temperature or pressure for monitoring and diagnosis purposes. In addition, given the absence of well-defined kinematics for soft-bodied robots, whose elastic deformation can involve virtually infinite DOFs, the advances in integrated or distributed sensing modalities will be conducive to developing better control strategies for magnetic soft robots. For example, the integrated or distributed sensing capabilities would allow for measuring mechanical strains for shape sensing or locating applied stresses for contact monitoring,395–397 where the sensory feedback can provide local state awareness of the robot during the actuation or operation to realize autonomous or semiautonomous control of magnetic soft robots. Magnetic actuation coupled with such integrated and distributed sensing capabilities will further enable more effective control of the robot’s dynamic interactions with the environment.
7.6. Intelligent and Autonomous Control
For magnetic soft devices and robots with complex and continuous shape changes that involve a large number of DOFs, it can be even more difficult to use traditional control methods based on sensory feedback. Alternatively, a quantitative predictive model can be constructed from finite element simulations in the continuum mechanical framework and used for open-loop control of magnetic soft robots, particularly for quasi-static problems with negligible dynamic or inertial effects in relatively unrestricted environments with well-defined boundary conditions. However, when dynamic tasks are of concern or when operating in unstructured or constrained environments, learning-based control will offer an advantage over the model-based approach, provided that a sufficient amount of data can be generated and collected experimentally. It has recently been shown that a probabilistic learning approach can be applied to gait control of untethered small-scale magnetic soft robots to optimize locomotion performance with a relatively small amount of training data obtained from physical experiments.398 Although not much work has been done in this direction thus far, this will be an important and promising area for future exploration toward the intelligent and autonomous control of magnetic soft robots. Collective efforts will be needed to develop more robust and effective control strategies for magnetic soft robots to turn their complex morphological properties into dexterous manipulation and sophisticated functions.
8. Concluding Remarks
There is rather long and checkered history of utilizing magnetism for medical applications,399 including the magnetically guided tethered devices for vascular exploration and treatment.255,400–407 Unfortunately, most of them have “faded into oblivion”408,409 with no successful adoption. Fueled by recent advances in the development of materials design and fabrication techniques for magnetic soft materials, we are moving away from attaching small pieces of iron or magnets to such devices toward building actively reconfigurable soft-bodied robots capable of complex shape changes to enable more advanced and sophisticated functions. Over the past few years, we have seen many exciting advances and examples in the field of magnetic soft materials and robots that suggest great potential for many important applications including biomedical areas. While many of the advantages of magnetic soft materials and robots for biomedical applications are considered unique, there are still a number of challenges that remain to be overcome to make them widely adopted as practical tools for real-world applications, as discussed above. To avoid sharing the fate of their predecessors, magnetic soft materials and robots must go beyond materials development and proof-of-principle demonstrations through both fundamental and applied research focused on realizing the required level of complexity and performance in their functions for practical applications. To this end, a close collaboration among researchers in academia and industry with different expertise across diverse fields will be needed, given the multidisciplinary nature of this emerging field at the intersection of materials science, chemistry, physics, mechanics, robotics, and biomedicine.
Acknowledgements
This work was supported by the National Science Foundation (EFRI-1935291) and National Institutes of Health (1R01HL153857-01). Y.K. acknowledges funding through scholarships from ILJU Academy and Culture Foundation and MIT School of Engineering MathWorks Fellowship.
Biographies
Yoonho Kim is a Ph.D. candidate in the Department of Mechanical Engineering at Massachusetts Institute of Technology (MIT). He earned his B.S. degree in mechanical and aerospace engineering from Seoul National University in 2013 and S.M. degree in mechanical engineering from MIT in 2016. His research focuses on the advanced fabrication, design, and mechanics of functional soft materials and applying them to medical robotics toward next-generation soft robots for biomedical applications. He is a recipient of 2019 Materials Research Society Graduate Student Gold Award and 2020-2021 MIT School of Engineering MathWorks Fellowship and is a Graduate Finalist of 2020 Collegiate Inventors Competition.
Xuanhe Zhao is Professor of Mechanical Engineering and Principal Investigator of the Zhao Lab (http://zhao.mit.edu) at MIT. The mission of the Zhao Lab is to advance science and technology on the interfaces between humans and machines for addressing grand societal challenges in health and sustainability with integrated expertise in mechanics, materials, and biotechnology. A major focus of the Zhao Lab’s current research is the study and development of soft materials and systems. He is the recipient of the NSF CAREER Award, ONR Young Investigator Award, SES Young Investigator Medal, ASME Hughes Young Investigator Award, Adhesion Society’s Young Scientist Award, Materials Today Rising Star Award, and Web of Science Highly Cited Researcher.
Footnotes
The authors declare the following competing financial interest(s): Yoonho Kim and Xuanhe Zhao are inventors on patents and patent applications from Massachusetts Institute of Technology that describe fundamental principles and fabrication techniques for 3D-printed magnetic soft actuators and magnetically steerable soft continuum robots.
References
- (1).Rus D; Tolley MT Design, Fabrication and Control of Soft Robots. Nature 2015, 521, 467–475. [DOI] [PubMed] [Google Scholar]
- (2).Sitti M Miniature Soft Robots — Road to the Clinic. Nat. Rev. Mater 2018, 3, 74–75. [Google Scholar]
- (3).Cianchetti M; Laschi C; Menciassi A; Dario P Biomedical Applications of Soft Robotics. Nat. Rev. Mater 2018, 3, 143–153. [Google Scholar]
- (4).Ilievski F; Mazzeo AD; Shepherd RF; Chen X; Whitesides GM Soft Robotics for Chemists. Angew. Chem. Int. Ed 2011, 50, 1890–1895. [DOI] [PubMed] [Google Scholar]
- (5).Laschi C; Mazzolai B; Cianchetti M Soft Robotics: Technologies and Systems Pushing the Boundaries of Robot Abilities. Sci. Robot 2016, 1, eaah3690. [DOI] [PubMed] [Google Scholar]
- (6).Tolley MT; Shepherd RF; Mosadegh B; Galloway KC; Wehner M; Karpelson M; Wood RJ; Whitesides GM A Resilient, Untethered Soft Robot. Soft Robot. 2014, 1, 213–223. [Google Scholar]
- (7).Rich SI; Wood RJ; Majidi C Untethered Soft Robotics. Nat. Electron 2018, 1, 102–112. [Google Scholar]
- (8).Kim S; Laschi C; Trimmer B Soft Robotics: A Bioinspired Evolution in Robotics. Trends. Biotechnol 2013, 31, 287–294. [DOI] [PubMed] [Google Scholar]
- (9).Polygerinos P; Correll N; Morin SA; Mosadegh B; Onal CD; Petersen K; Cianchetti M; Tolley MT; Shepherd RF Soft Robotics: Review of Fluid-Driven Intrinsically Soft Devices; Manufacturing, Sensing, Control, and Applications in Human-Robot Interaction Adv. Eng. Mater 2017, 19, 1700016. [Google Scholar]
- (10).Ranzani T; Russo S; Bartlett NW; Wehner M; Wood RJ Increasing the Dimensionality of Soft Microstructures through Injection-Induced Self-Folding. Adv. Mater 2018, 30, 1802739. [DOI] [PubMed] [Google Scholar]
- (11).Shen Z; Chen F; Zhu X; Yong K-T; Gu G Stimuli-Responsive Functional Materials for Soft Robotics. J. Mater. Chem. B 2020, 8, 8972–8991. [DOI] [PubMed] [Google Scholar]
- (12).Yang G-Z; Fischer P; Nelson B New Materials for Next-Generation Robots. Set. Robot 2017, 2, eaap9294. [DOI] [PubMed] [Google Scholar]
- (13).Li M; Ostrovsky-Snider NA; Sitti M; Omenetto FG Cutting the Cord: Progress in Untethered Soft Robotics and Actuators. MRS Adv. 2019, 4, 2787–2804. [Google Scholar]
- (14).Bira N; Dhagat P; Davidson JR A Review of Magnetic Elastomers and Their Role in Soft Robotics. Front. Robot. AI 2020, 7, 588391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Chung H-J; Parsons AM; Zheng L Magnetically Controlled Soft Robotics Utilizing Elastomers and Gels in Actuation: A Review. Adv. Intell 2020, 2000186. [Google Scholar]
- (16).Wu S; Hu W; Ze Q; Sitti M; Zhao R Multifunctional Magnetic Soft Composites: A Review. Multifunct. Mater 2020, 3, 042003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Nelson BJ; Kaliakatsos IK; Abbott JJ Microrobots for Minimally Invasive Medicine. Annu. Rev. Biomed. Eng 2010, 12, 55–85. [DOI] [PubMed] [Google Scholar]
- (18).Erb RM; Martin JJ; Soheilian R; Pan C; Barber JR Actuating Soft Matter with Magnetic Torque. Adv. Func. Mater. 2016, 26, 3859–3880. [Google Scholar]
- (19).Hines L; Petersen K; Lum GZ; Sitti M Soft Actuators for Small-Scale Robotics. Adv. Mater 2017, 29, 1603483. [DOI] [PubMed] [Google Scholar]
- (20).Zhao X; Kim Y Soft Microbots Programmed by Nanomagnets. Nature 2019, 575, 58–59. [DOI] [PubMed] [Google Scholar]
- (21).d’Argentré A. d. P.; Perry S; Iwata Y; Iwasaki H; Iwase E; Fabozzo A; Will I; Rus D; Damian DD; Miyashita S Programmable Medicine: Autonomous, Ingestible, Deployable Hydrogel Patch and Plug for Stomach Ulcer Therapy. 2018 IEEE International Conference on Robotics and Automation (ICRA), 2018, 1511–1518. [Google Scholar]
- (22).Miyashita S; Guitron S; Yoshida K; Shuguang L; Damian DD; Rus D Ingestible, Controllable, and Degradable Origami Robot for Patching Stomach Wounds. 2016 IEEE International Conference on Robotics and Automation (ICRA), 2016, 909–916. [Google Scholar]
- (23).Yim S; Sitti M Design and Rolling Locomotion of a Magnetically Actuated Soft Capsule Endoscope. IEEE Trans. Robot 2012, 28, 183–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Yim S; Gultepe E; Gracias DH; Sitti M Biopsy using a Magnetic Capsule Endoscope Carrying, Releasing, and Retrieving Untethered Microgrippers. IEEE Trans. Biomed, Eng 2014, 61, 513–521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Son D; Gilbert H; Sitti M Magnetically Actuated Soft Capsule Endoscope for Fine-Needle Biopsy. Soft Robot. 2020, 7, 10–21. [DOI] [PubMed] [Google Scholar]
- (26).Nguyen BL; Merino JL; Gang ES Remote Navigation for Ablation Procedures - A New Step Forward in the Treatment of Cardiac Arrhythmias. Eur. Cardiol. 2010, 6, 50–56. [Google Scholar]
- (27).Filgueiras-Rama D; Estrada A; Shachar J; Castrejón S; Doiny D; Ortega M; Gang ES; Merino JL Remote Magnetic Navigation for Accurate, Real-time Catheter Positioning and Ablation in Cardiac Electrophysiology Procedures. J. Vis. Exp 2013, e3658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Bassil G; Markowitz SM; Liu CF; Thomas G; Ip JE; Lerman BB; Cheung JW Robotics for Catheter Ablation of Cardiac Arrhythmias: Current Technologies and Practical Approaches. J. Cardiovasc. Electrophysiol 2020, 31, 739–752. [DOI] [PubMed] [Google Scholar]
- (29).Chautems C; Tonazzini A; Boehler Q; Jeong SH; Floreano D; Nelson BJ Magnetic Continuum Device with Variable Stiffness for Minimally Invasive Surgery. Adv. Intell 2020, 2, 1900086. [Google Scholar]
- (30).Edelmann J; Petruska AJ; Nelson BJ Estimation-based Control of a Magnetic Endoscope without Device Localization. J. Med. Robot. Res 2018, 03, 1850002. [Google Scholar]
- (31).Kim Y; Parada GA; Liu S; Zhao X Ferromagnetic Soft Continuum Robots. Sci. Robot 2019, 4, eaax7329. [DOI] [PubMed] [Google Scholar]
- (32).Jolly MR; Carlson JD; Muñoz BC A Model of the Behaviour of Magnetorheological Materials. Smart Mater. Struct 1996, 5, 607–614. [Google Scholar]
- (33).Davis LC Model of Magnetorheological Elastomers. J. Appl. Phys 1999, 85, 3348–3351. [Google Scholar]
- (34).von Lockette PR; Lofland SE; Biggs J; Roche J; Mineroff J; Babcock M Investigating New Symmetry Classes in Magnetorheological Elastomers: Cantilever Bending Behavior. Smart Mater. Struct 2011, 20, 105022. [Google Scholar]
- (35).Galipeau E; Ponte Castaáeda P A Finite-Strain Constitutive Model for Magnetorheological Elastomers: Magnetic Torques and Fiber Rotations. J. Mech. Phys. Solids 2013, 61, 1065–1090. [Google Scholar]
- (36).Han Y; Hong W; Faidley LE Field-Stiffening Effect of Magneto-Rheological Elastomers. Int. J. Solids Struct. 2013, 50, 2281–2288. [Google Scholar]
- (37).Bustamante R Transversely Isotropic Nonlinear Magneto-Active Elastomers. Acta Mech. 2010, 210, 183–214. [Google Scholar]
- (38).Han Y; Mohla A; Huang X; Hong W; Faidley LE Magnetostriction and Field Stiffening of Magneto-Active Elastomers. Int. J. Appl. Mech 2014, 07, 1550001. [Google Scholar]
- (39).Brigadnov IA; Dorfmann A Mathematical Modeling of Magneto-Sensitive Elastomers. Int. J. Solids Struct 2003, 40, 4659–4674. [Google Scholar]
- (40).Dorfmann A; Ogden RW Nonlinear Magnetoelastic Deformations of Elastomers. Acta Mech. 2004, 167, 13–28. [Google Scholar]
- (41).Bustamante R; Dorfmann A; Ogden R Universal Relations in Isotropic Nonlinear Magnetoelasticity. Q. J. Mech. Appl. Math 2006, 59, 435–450. [Google Scholar]
- (42).Zrínyi M; Barsi L; Büki A Deformation of Ferrogels Induced by Nonuniform Magnetic Fields. J. Chem. Phys 1996, 104, 8750–8756. [Google Scholar]
- (43).Zrínyi M; Barsi L; Büki A Ferrogel: A New Magneto-Controlled Elastic Medium. Polym. Gels Networks 1997, 5, 415–427. [Google Scholar]
- (44).Han Y; Hong W; Faidley L Coupled Magnetic Field and Viscoelasticity of Ferrogel. Int. J. Appl. Mech 2011, 03, 259–278. [Google Scholar]
- (45).Gebhart P; Wallmersperger T A General Framework for the Modeling of Porous Ferrogels at Finite Strains. J. Mech. Phys. Solids 2019, 122, 69–83. [Google Scholar]
- (46).Bowen L; Springsteen K; Feldstein H; Frecker M; Simpson TW; von Lockette P Development and Validation of a Dynamic Model of Magneto-Active Elastomer Actuation of the Origami Waterbomb Base. J. Mech. Robot 2015, 7. [Google Scholar]
- (47).Ginder JM; Clart SM; Schlotter WF; Nichols ME Magnetostrictive Phenomena in Magnetorheological Elastomers. Int. J. Mod. Phys. B 2002, 16, 2412–2418. [Google Scholar]
- (48).Schumann M; Odenbach S In-situ Observation of the Particle Microstructure of Magnetorheological Elastomers in Presence of Mechanical Strain and Magnetic Fields. J. Magn. Magn. Mater 2017, 441, 88–92. [Google Scholar]
- (49).Martin JE; Anderson RA; Read D; Gulley G Magnetostriction of Field-Structured Magnetoelastomers. Phys. Rev. E 2006, 74, 051507. [DOI] [PubMed] [Google Scholar]
- (50).Danas K; Kankanala SV; Triantafyllidis N Experiments and Modeling of Iron-Particle-Filled Magnetorheological Elastomers. J. Mech. Phys. Solids 2012, 60, 120–138. [Google Scholar]
- (51).Bednarek S The Giant Magnetostriction in Ferromagnetic Composites within an Elastomer Matrix. Appl. Phys. A 1999, 68, 63–67. [Google Scholar]
- (52).Guan X; Dong X; Ou J Magnetostrictive Effect of Magnetorheological Elastomer. J. Magn. Magn. Mater 2008, 320, 158–163. [Google Scholar]
- (53).Varga Z; Filipcsei G; Zrínyi M Magnetic Field Sensitive Functional Elastomers with Tuneable Elastic Modulus. Polymer 2006, 47, 227–233. [Google Scholar]
- (54).Deng H-X; Gong X-L; Wang L-H Development of an Adaptive Tuned Vibration Absorber with Magnetorheological Elastomer. Smart Mater. Struct 2006, 15, N111–N116. [Google Scholar]
- (55).Hoang N; Zhang N; Du H A Dynamic Absorber with a Soft Magnetorheological Elastomer for Powertrain Vibration Suppression. Smart Mater. Struct 2009, 18, 074009. [Google Scholar]
- (56).Opie S; Yim W Design and Control of a Real-Time Variable Modulus Vibration Isolator. J. Intell. Mater. Syst. Struct 2011, 22, 113–125. [Google Scholar]
- (57).Li Y; Li J; Tian T; Li W A Highly Adjustable Magnetorheological Elastomer Base Isolator for Applications of Real-time Adaptive Control. Smart Mater. Struct 2013, 22, 095020. [Google Scholar]
- (58).Liao GJ; Gong X-L; Xuan SH; Kang CJ; Zong LH Development of a Real-time Tunable Stiffness and Damping Vibration Isolator Based on Magnetorheological Elastomer. J. Intell. Mater. Syst. Struct 2012, 23, 25–33. [Google Scholar]
- (59).Kim HK; Kim HS; Kim Y-K Stiffness Control of Magnetorheological Gels for Adaptive Tunable Vibration Absorber. Smart Mater. Struct 2017, 26, 015016. [Google Scholar]
- (60).Zhao X; Kim J; Cezar CA; Huebsch N; Lee K; Bouhadir K; Mooney DJ Active Scaffolds for On-Demand Drug and Cell Delivery. Proc. Natl. Acad. Sci. U. S. A 2011, 108, 67–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (61).Haider H; Yang CH; Zheng WJ; Yang JH; Wang MX; Yang S; Zrínyi M; Osada Y; Suo Z; Zhang Q et al. Exceptionally Tough and Notch-Insensitive Magnetic Hydrogels. Soft Matter 2015, 11, 8253–8261. [DOI] [PubMed] [Google Scholar]
- (62).Zrinyi M Magnetically Responsive Polymer Gels and Elastomers: Properties, Synthesis and Applications In Smart Polymers and their Applications; Aguilar MR;San Román J, Eds.;Woodhead Publishing, 2014. [Google Scholar]
- (63).Nguyen VQ; Ramanujan RV Novel Coiling Behavior in Magnet-Polymer Composites. Macromol. Chem. Phys 2010, 211, 618–626. [Google Scholar]
- (64).Nguyen VQ; Ahmed AS; Ramanujan RV Morphing Soft Magnetic Composites. Adv. Mater 2012, 24, 4041–4054. [DOI] [PubMed] [Google Scholar]
- (65).Schmauch MM; Mishra SR; Evans BA; Velev OD; Tracy JB Chained Iron Microparticles for Directionally Controlled Actuation of Soft Robots. ACS Appl. Mater. Interfaces 2017, 9, 11895–11901. [DOI] [PubMed] [Google Scholar]
- (66).Mishra SR; Dickey MD; Velev OD; Tracy JB Selective and Directional Actuation of Elastomer Films using Chained Magnetic Nanoparticles. Nanoscale 2016, 8, 1309–1313. [DOI] [PubMed] [Google Scholar]
- (67).Kim J; Chung SE; Choi S-E; Lee H; Kim J; Kwon S Programming Magnetic Anisotropy in Polymeric Microactuators. Nat. Mater 2011, 10, 747–752. [DOI] [PubMed] [Google Scholar]
- (68).Ozaki M; Kratohvil S; Matijevic E Formation of monodispersed spindle-type hematite particles. J. Colloid Interface Sci 1984, 102, 146–151. [Google Scholar]
- (69).Roeder L; Bender P; Tschöpe A; Birringer R; Schmidt AM Shear modulus determination in model hydrogels by means of elongated magnetic nanoprobes. J. Polym. Sci. B Polym. Phys 2012, 50, 1772–1781. [Google Scholar]
- (70).Lisjak D; Mertelj A Anisotropic magnetic nanoparticles: A review of their properties, syntheses and potential applications. Prog. Mater. Sci 2018, 95, 286–328. [Google Scholar]
- (71).Seifert J; Roitsch S; Schmidt AM Covalent Hybrid Elastomers Based on Anisotropic Magnetic Nanoparticles and Elastic Polymers. ACS Appl. Polym. Mater. 2021, 3, 1324–1337. [Google Scholar]
- (72).von Lockette PR; Lofland SE Role of Magnetization Anisotropy in the Active Behavior of Magnetorheological Elastomers. ASME 2011 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, 2011, 459–463. [Google Scholar]
- (73).Abbott JJ; Ergeneman O; Kummer MP; Hirt AM; Nelson BJ Modeling Magnetic Torque and Force for Controlled Manipulation of Soft-Magnetic Bodies. IEEE Trans. Robot 2007, 23, 1247–1252. [Google Scholar]
- (74).Crivaro A; Sheridan R; Frecker M; Simpson TW; Von Lockette P Bistable Compliant Mechanism using Magneto Active Elastomer Actuation. J. Intell. Mater. Syst. Struct 2016, 27, 2049–2061. [Google Scholar]
- (75).Ma BM; Herchenroeder JW; Smith B; Suda M; Brown DN; Chen Z Recent Development in Bonded NdFeB Magnets. J. Magn. Magn. Mater 2002, 239, 418–423. [Google Scholar]
- (76).Brown DN; Wu Z; He F; Miller DJ; Herchenroeder JW Dysprosium-Free Melt-Spun Permanent Magnets. J. Phys. Condens. Matter 2014, 26, 064202. [DOI] [PubMed] [Google Scholar]
- (77).Sarriegui G; Martín JM; Ipatov M; Zhukov AP; Gonzalez J Magnetic Properties of NdFeB Alloys Obtained by Gas Atomization Technique. IEEE Trans. Magn 2018, 54, 1–5. [Google Scholar]
- (78).Alfadhel A; Kosel J Magnetic Nanocomposite Cilia Tactile Sensor. Adv. Mater 2015, 27, 7888–7892. [DOI] [PubMed] [Google Scholar]
- (79).Luo Z; Dao TP; Hrabec A; Vijayakumar J; Kleibert A; Baumgartner M; Kirk E; Cui J; Savchenko T; Krishnaswamy G et al. Chirally Coupled Nanomagnets. Science 2019, 363, 1435–1439. [DOI] [PubMed] [Google Scholar]
- (80).Cui J; Huang T-Y; Luo Z; Testa P; Gu H; Chen X-Z; Nelson BJ; Heyderman LJ Nanomagnetic Encoding of Shape-Morphing Micromachines. Nature 2019, 575, 164–168. [DOI] [PubMed] [Google Scholar]
- (81).Li C; Lau GC; Yuan H; Aggarwal A; Dominguez VL; Liu S; Sai H; Palmer LC; Sather NA; Pearson TJ et al. Fast and Programmable Locomotion of Hydrogel-Metal Hybrids under Light and Magnetic Fields. Sci. Robot 2020, 5, eabb9822. [DOI] [PubMed] [Google Scholar]
- (82).Mody VV; Singh A; Wesley B Basics of magnetic nanoparticles for their application in the field of magnetic fluid hyperthermia. Eur. J. Nanomed 2013, 5, 11–21. [Google Scholar]
- (83).Shasha C; Krishnan KM Nonequilibrium Dynamics of Magnetic Nanoparticles with Applications in Biomedicine. Adv. Mater 2021, 33, 1904131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (84).Krishnan KM Biomedical Nanomagnetics: A Spin Through Possibilities in Imaging, Diagnostics, and Therapy. IEEE Trans. Magn 2010, 46, 2523–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (85).Shcherbakov VP; Winklhofer M Bending of Magnetic Filaments under a Magnetic Field. Phys. Rev. E 2004, 70, 061803. [DOI] [PubMed] [Google Scholar]
- (86).Dzhezherya YI; Xu W; Cherepov SV; Skirta YB; Kalita VM; Bodnaruk AV; Liedienov NA; Pashchenko AV; Fesych IV; Liu B et al. Magnetoactive Elastomer based on Superparamagnetic Nanoparticles with Curie Point Close to Room Temperature. Mater. Des 2021, 197, 109281. [Google Scholar]
- (87).Fahrni F; Prins MWJ; van Ijzendoorn LJ Magnetization and actuation of polymeric microstructures with magnetic nanoparticles for application in microfluidics. J. Magn. Magn. Mater 2009, 321, 1843–1850. [Google Scholar]
- (88).Evans BA; Fiser BL; Prins WJ; Rapp DJ; Shields AR; Glass DR; Superfine R A Highly Tunable Silicone-based Magnetic Elastomer with Nanoscale Homogeneity. J. Magn. Magn. Mater 2012, 324, 501–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (89).Lalatonne Y; Richardi J; Pileni MP Van der Waals versus dipolar forces controlling mesoscopic organizations of magnetic nanocrystals. Nat. Mater 2004, 3, 121–125. [DOI] [PubMed] [Google Scholar]
- (90).Ditsch A; Laibinis PE; Wang DIC; Hatton TA Controlled Clustering and Enhanced Stability of Polymer-Coated Magnetic Nanoparticles. Langmuir 2005, 21, 6006–6018. [DOI] [PubMed] [Google Scholar]
- (91).Kumar S; Ravikumar C; Bandyopadhyaya R State of Dispersion of Magnetic Nanoparticles in an Aqueous Medium: Experiments and Monte Carlo Simulation. Langmuir 2010, 26, 18320–18330. [DOI] [PubMed] [Google Scholar]
- (92).Eberbeck D; Wiekhorst F; Steinhoff U; Trahms L Aggregation behaviour of magnetic nanoparticle suspensions investigated by magnetorelaxometry. J. Phys. Condens. Matter 2006, 18, S2829–S2846. [Google Scholar]
- (93).Cezar CA; Kennedy SM; Mehta M; Weaver JC; Gu L; Vandenburgh H; Mooney DJ Biphasic Ferrogels for Triggered Drug and Cell Delivery. Adv. Healthc. Mater 2014, 3, 1869–1876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (94).Kennedy S; Roco C; Déléris A; Spoerri P; Cezar C; Weaver J; Vandenburgh H; Mooney D Improved Magnetic Regulation of Delivery Profiles from Ferrogels. Biomaterials 2018, 161, 179–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (95).Deatsch AE; Evans BA Heating Efficiency in Magnetic Nanoparticle Hyperthermia. J. Magn. Magn. Mater 2014, 354, 163–172. [Google Scholar]
- (96).Ji Y; Marshall JE; Terentjev EM Nanoparticle-Liquid Crystalline Elastomer Composites. Polymers 2012, 4, 316–340. [Google Scholar]
- (97).Mohr R; Kratz K; Weigel T; Lucka-Gabor M; Moneke M; Lendlein A Initiation of Shape-Memory Effect by Inductive Heating of Magnetic Nanoparticles in Thermoplastic Polymers. Proc. Natl. Acad. Sci. U. S. A 2006, 103, 3540–3545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (98).Schmidt AM Electromagnetic Activation of Shape Memory Polymer Networks Containing Magnetic Nanoparticles. Macromol. Rapid Commun 2006, 27, 1168–1172. [Google Scholar]
- (99).Kumar UN; Kratz K; Wagermaier W; Behl M; Lendlein A Non-contact Actuation of Triple-Shape Effect in Multiphase Polymer Network Nanocomposites in Alternating Magnetic Field. J. Mater. Chem 2010, 20, 3404–3415. [Google Scholar]
- (100).Kumar UN; Kratz K; Heuchel M; Behl M; Lendlein A Shape-Memory Nanocomposites with Magnetically Adjustable Apparent Switching Temperatures. Adv. Mater 2011, 23, 4157–4162. [DOI] [PubMed] [Google Scholar]
- (101).Razzaq MY; Behl M; Lendlein A Magnetic Memory Effect of Nanocomposites. Adv. Func. Mater 2012, 22, 184–191. [Google Scholar]
- (102).Razzaq MY; Behl M; Kratz K; Lendlein A Multifunctional Hybrid Nanocomposites with Magnetically Controlled Reversible Shape–Memory Effect. Adv. Mater 2013, 25, 5730–5733. [DOI] [PubMed] [Google Scholar]
- (103).Kaiser A; Winkler M; Krause S; Finkelmann H; Schmidt AM Magnetoactive Liquid Crystal Elastomer Nanocomposites. J. Mater. Chem 2009, 19, 538–543. [Google Scholar]
- (104).Winkler M; Kaiser A; Krause S; Finkelmann H; Schmidt AM Liquid Crystal Elastomers with Magnetic Actuation. Macromol. Symp 2010, 291-292, 186–192. [Google Scholar]
- (105).Ghosh S; Cai T Controlled Actuation of Alternating Magnetic Field-Sensitive Tunable Hydrogels. J. Phys. D Appl. Phys 2010, 43, 415504. [Google Scholar]
- (106).Thévenot J; Oliveira H; Sandre O; Lecommandoux S Magnetic Responsive Polymer Composite Materials. Chem. Soc. Rev 2013, 42, 7099–7116. [DOI] [PubMed] [Google Scholar]
- (107).Ze Q; Kuang X; Wu S; Wong J; Montgomery SM; Zhang R; Kovitz JM; Yang F; Qi HJ; Zhao R Magnetic Shape Memory Polymers with Integrated Multifunctional Shape Manipulation. Adv. Mater 2020, 32, 1906657. [DOI] [PubMed] [Google Scholar]
- (108).Liu JA-C; Gillen JH; Mishra SR; Evans BA; Tracy JB Photothermally and Magnetically Controlled Reconfiguration of Polymer Composites for Soft Robotics. Sci. Adv 2019, 5, eaaw2897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (109).Liu JAC; Evans BA; Tracy JB Photothermally Reconfigurable Shape Memory Magnetic Cilia. Adv. Mater. Technol 2020, 5, 2000147. [Google Scholar]
- (110).Ma C; Wu S; Ze Q; Kuang X; Zhang R; Qi HJ; Zhao R Magnetic Multimaterial Printing for Multimodal Shape Transformation with Tunable Properties and Shiftable Mechanical Behaviors. ACS Appl. Mater. Interfaces 2021, 13, 12639–12648. [DOI] [PubMed] [Google Scholar]
- (111).Ha M; Canon Bermudez GS; Liu JAC; Oliveros Mata ES; Evans BA; Tracy JB; Makarov D Reconfigurable Magnetic Origami Actuators with On-Board Sensing for Guided Assembly. Adv. Mater 2021, 33, 2008751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (112).Zhang J; Guo Y; Hu W; Soon RH; Davidson ZS; Sitti M Liquid Crystal Elastomer-Based Magnetic Composite Films for Reconfigurable Shape-Morphing Soft Miniature Machines. Adv. Mater 2021, 33, 2006191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (113).Wu J; Gong X; Fan Y; Xia H Anisotropic Polyurethane Magnetorheological Elastomer Prepared through In Situ Polycondensation under a Magnetic Field. Smart Mater. Struct 2010, 19, 105007. [Google Scholar]
- (114).Zajac P; Kaleta J; Lewandowski D; Gasperowicz A Isotropic Magnetorheological Elastomers with Thermoplastic Matrices: Structure, Damping Properties and Testing. Smart Mater. Struct 2010, 19, 045014. [Google Scholar]
- (115).Lu X; Qiao X; Watanabe H; Gong X; Yang T; Li W; Sun K; Li M; Yang K; Xie H et al. Mechanical and Structural Investigation of Isotropic and Anisotropic Thermoplastic Magnetorheological Elastomer Composites Based on Poly(Styrene-b-Ethylene-co-Butylene-b-Styrene) (SEBS). Rheol. Acta 2012, 51, 37–50. [Google Scholar]
- (116).Qiao X; Lu X; Gong X; Yang T; Sun K; Chen X Effect of Carbonyl Iron Concentration and Processing Conditions on the Structure and Properties of the Thermoplastic Magnetorheological Elastomer Composites based on Poly(Styrene-b-Ethylene-co-Butylene-b-Styrene) (SEBS). Polym. Test 2015, 47, 51–58. [Google Scholar]
- (117).Domansky K; Sliz JD; Wen N; Hinojosa C; Thompson G; Fraser JP; Hamkins-Indik T; Hamilton GA; Levner D; Ingber DE SEBS Elastomers for Fabrication of Microfluidic Devices with Reduced Drug Absorption by Injection Molding and Extrusion. Microfluid. Nanofluidics 2017, 21, 107. [Google Scholar]
- (118).Murray KA; Kennedy JE; McEvoy B; Vrain O; Ryan D; Cowman R; Higginbotham CL Effects of Gamma Ray and Electron Beam Irradiation on the Mechanical, Thermal, Structural and Physicochemical Properties of Poly (Ether-Block-Amide) Thermoplastic Elastomers. J. Mech. Behav. Biomed. Mater 2013, 17, 252–268. [DOI] [PubMed] [Google Scholar]
- (119).Ashfaq A; Clochard M-C; Coqueret X; Dispenza C; Driscoll MS; Ulański P; Al-Sheikhly M Polymerization Reactions and Modifications of Polymers by Ionizing Radiation. Polymers 2020, 12, 2877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (120).An H-N; Sun B; Picken SJ; Mendes E Long Time Response of Soft Magnetorheological Gels. J. Phys. Chem. B 2012, 116, 4702–4711. [DOI] [PubMed] [Google Scholar]
- (121).An H-N; Picken SJ; Mendes E Direct Observation of Particle Rearrangement during Cyclic Stress Hardening of Magnetorheological Gels. Soft Matter 2012, 8, 11995–12001. [Google Scholar]
- (122).Venkateswara Rao P; Maniprakash S; Srinivasan SM; Srinivasa AR Functional Behavior of Isotropic Magnetorheological Gels. Smart Mater. Struct 2010, 19, 085019. [Google Scholar]
- (123).Fuchs A; Xin M; Gordaninejad F; Wang X; Hitchcock GH; Gecol H; Evrensel C; Korol G Development and Characterization of Hydrocarbon Polyol Polyurethane and Silicone Magnetorheological Polymeric Gels. J. Appl. Polym. Sci 2004, 92, 1176–1182. [Google Scholar]
- (124).Weeber R; Hermes M; Schmidt AM; Holm C Polymer Architecture of Magnetic Gels: A Review. J. Phys. Gondens. Matter 2018, 30, 063002. [DOI] [PubMed] [Google Scholar]
- (125).Mitsumata T; Abe N Giant and Reversible Magnetorheology of Carrageenan/Iron Oxide Magnetic Gels. Smart Mater. Struct 2011, 20, 124003. [Google Scholar]
- (126).Mitsumata T; Honda A; Kanazawa H; Kawai M Magnetically Tunable Elasticity for Magnetic Hydrogels Consisting of Carrageenan and Carbonyl Iron Particles. J. Phys. Chem. B 2012, 116, 12341–12348. [DOI] [PubMed] [Google Scholar]
- (127).Ikeda J; Takahashi D; Watanabe M; Kawai M; Mitsumata T Particle Size in Secondary Particle and Magnetic Response for Carrageenan Magnetic Hydrogels. Gels 2019, 5, 39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (128).François NJ; Allo S; Jacobo SE; Daraio ME Composites of polymeric gels and magnetic nanoparticles: Preparation and drug release behavior. J. Appl. Polym. Sci 2007, 105, 647–655. [Google Scholar]
- (129).Lin H; Watanabe Y; Kimura M; Hanabusa K; Shirai H Preparation of Magnetic Poly(Vinyl Alcohol) (PVA) Materials by In Situ Synthesis of Magnetite in a PVA Matrix. J. Appl. Polym. Sci 2003, 87, 1239–1247. [Google Scholar]
- (130).Reséndiz-Hernández PJ; Rodríguez-Fernández OS; García-Cerda LA Synthesis of Poly(Vinyl Alcohol)–Magnetite Ferrogel Obtained by Freezing–Thawing Technique. J. Magn. Magn. Mater 2008, 320, e373–e376. [Google Scholar]
- (131).Liu X; Yang Y; Inda ME; Lin S; Wu J; Kim Y; Chen X; Ma D; Lu TK; Zhao X Magnetic Living Hydrogels for Intestinal Localization, Retention, and Diagnosis. Adv. Func. Mater 2021, 31, 2010918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (132).Breger JC; Yoon C; Xiao R; Kwag HR; Wang MO; Fisher JP; Nguyen TD; Gracias DH Self-Folding Thermo-Magnetically Responsive Soft Microgrippers. ACS Appl. Mater. Interfaces 2015, 7, 3398–3405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (133).Tang J; Yin Q; Qiao Y; Wang T Shape Morphing of Hydrogels in Alternating Magnetic Field. ACS Appl. Mater. Interfaces 2019, 11, 21194–21200. [DOI] [PubMed] [Google Scholar]
- (134).Du X; Cui H; Xu T; Huang C; Wang Y; Zhao Q; Xu Y; Wu X Reconfiguration, Camouflage, and Color-Shifting for Bioinspired Adaptive Hydrogel-based Millirobots. Adv. Func. Mater 2020, 30, 1909202. [Google Scholar]
- (135).Hu X; Nian G; Liang X; Wu L; Yin T; Lu H; Qu S; Yang W Adhesive Tough Magnetic Hydrogels with High Fe3O4 Content. ACS Appl. Mater. Interfaces 2019, 11, 10292–10300. [DOI] [PubMed] [Google Scholar]
- (136).Mayer CR; Cabuil V; Lalot T; Thouvenot R Magnetic Nanoparticles Trapped in pH 7 Hydrogels as a Tool to Characterize the Properties of the Polymeric Network. Adv. Mater 2000, 12, 417–420. [Google Scholar]
- (137).Sun B; Jia R; Yang H; Chen X; Tan K; Deng Q; Tang J Magnetic Arthropod Millirobots Fabricated by 3D-Printed Hydrogels. Adv. Intell n/a, 2100139. [Google Scholar]
- (138).Zhao X; Chen X; Yuk H; Lin S; Liu X; Parada G Soft Materials by Design: Unconventional Polymer Networks Give Extreme Properties. Chem. Rev 2021, 128, 4309–4372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (139).Liu X; Liu J; Lin S; Zhao X Hydrogel Machines. Mater. Today 2020, 36, 102–124. [Google Scholar]
- (140).Lee JH; Han WJ; Jang HS; Choi HJ Highly Tough, Biocompatible, and Magneto-Responsive Fe3O4/Laponite/PDMAAm Nanocomposite Hydrogels. Sci. Rep 2019, 9, 15024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (141).Liu YD; Fang FF; Choi HJ Core–Shell-Structured Silica-Coated Magnetic Carbonyl Iron Microbead and Its Magnetorheology with Anti-Acidic Characteristics. Colloid Polym. Sci 2011, 289, 1295–1298. [Google Scholar]
- (142).Zhu J; Wei S; Lee IY; Park S; Willis J; Haldolaarachchige N; Young DP; Luo Z; Guo Z Silica Stabilized Iron Particles toward Anti-Corrosion Magnetic Polyurethane Nanocomposites. RSC Adv. 2012, 2, 1136–1143. [Google Scholar]
- (143).Malecki P; Krolewicz M; Hiptmair F; Krzak J; Kaleta J; Major Z; Piglowski J Influence of Carbonyl Iron Particle Coating with Silica on the Properties of Magnetorheological Elastomers. Smart Mater. Struct. 2016, 25, 105030. [Google Scholar]
- (144).Zhang Y; Bu A; Xiang Y; Yang Y; Chen W; Cheng H; Wang L Improving Corrosion Resistance of Carbonyl Iron Powders by Plasma Electrolytic Deposition. Mater. Des 2020, 188, 108480. [Google Scholar]
- (145).Weimer AW Particle Atomic Layer Deposition. J. Nanoparticle Res 2019, 21, 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (146).Li C-F; Li L-X; Liu Y-F; Wang Y-Y Corrosion Resistance and Wave Absorbing Property of Carbonyl Iron Powder Coating with Alumina by Atomic Layer Deposition. J. Inorg. Mater 2017, 32, 751–757. [Google Scholar]
- (147).Pu H; Jiang F; Wang Y; Yan B Soft Magnetic Composite Particles of Reduced Iron Coated with Poly(p-xylylene) via Chemical Vapor Deposition Polymerization. Colloids Surf, A Physicochem. Eng. Asp 2010, 361, 62–65. [Google Scholar]
- (148).Behrooz M; Sutrisno J; Zhang L; Fuchs A; Gordaninejad F Behavior of Magnetorheological Elastomers with Coated Particles. Smart Mater. Struct 2015, 24, 035026. [Google Scholar]
- (149).Cvek M; Mrlik M; Ilcikova M; Mosnacek J; Babayan V; Kucekova Z; Humpolicek P; Pavlinek V The Chemical Stability and Cytotoxicity of Carbonyl Iron Particles Grafted with Poly(glycidyl methacrylate) and the Magnetorheological Activity of their Suspensions. RSC Adv. 2015, 5, 72816–72824. [Google Scholar]
- (150).Jamari SKM; Nordin NA; Ubaidillah; Aziz SAA; Nazmi N; Mazlan SA Systematic Review on the Effects, Roles and Methods of Magnetic Particle Coatings in Magnetorheological Materials. Materials 2020, 13, 5317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (151).Kularatne RS; Kim H; Boothby JM; Ware TH Liquid Crystal Elastomer Actuators: Synthesis, Alignment, and Applications. J. Polym. Sci. B Polym. Phys 2017, 55, 395–411. [Google Scholar]
- (152).Bertotti G Hysteresis in Magnetism: For Physicists, Materials Scientists, and Engineers; Elsevier Science, 1998. [Google Scholar]
- (153).Osborn JA Demagnetizing Factors of the General Ellipsoid. Phys. Rev 1945, 67, 351–357. [Google Scholar]
- (154).Edelmann J; Petruska AJ; Nelson BJ Magnetic Control of Continuum Devices. Int. J. Robot. Res 2017, 36, 68–85. [Google Scholar]
- (155).Ahmed S; Jones FR A Review of Particulate Reinforcement Theories for Polymer Composites. J. Mater. Sci 1990, 25, 4933–4942. [Google Scholar]
- (156).Kim Y; Yuk H; Zhao R; Chester SA; Zhao X Printing Ferromagnetic Domains for Untethered Fast-Transforming Soft Materials. Nature 2018, 558, 274–279. [DOI] [PubMed] [Google Scholar]
- (157).Wang Z; Wang K; Liang D; Yan L; Ni K; Huang H; Li B; Guo Z; Wang J; Ma X et al. Hybrid Magnetic Micropillar Arrays for Programmable Actuation. Adv. Mater 2020, 32, 2001879. [DOI] [PubMed] [Google Scholar]
- (158).Dong X; Lum GZ; Hu W; Zhang R; Ren Z; Onck PR; Sitti M Bioinspired Cilia Arrays with Programmable Nonreciprocal Motion and Metachronal Coordination. Sci. Adv 2020, 6, eabc9323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (159).Gu H; Boehler Q; Cui H; Secchi E; Savorana G; De Marco C; Gervasoni S; Peyron Q; Huang T-Y; Pane S et al. Magnetic Cilia Carpets with Programmable Metachronal Waves. Nat. Comm 2020, 11, 2637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (160).Hanasoge S; Hesketh PJ; Alexeev A Metachronal Actuation of Microscale Magnetic Artificial Cilia. ACS Appl. Mater. Interfaces 2020, 12, 46963–46971. [DOI] [PubMed] [Google Scholar]
- (161).Evans BA; Shields AR; Carroll RL; Washburn S; Falvo MR; Superfine R Magnetically Actuated Nanorod Arrays as Biomimetic Cilia. Nano Lett. 2007, 7, 1428–1434. [DOI] [PubMed] [Google Scholar]
- (162).Lee H; Jang Y; Choe JK; Lee S; Song H; Lee JP; Lone N; Kim J 3D-Printed Programmable Tensegrity for Soft Robotics. Sci. Robot 2020, 5, eaay9024. [DOI] [PubMed] [Google Scholar]
- (163).Jackson JA; Messner MC; Dudukovic NA; Smith WL; Bekker L; Moran B; Golobic AM; Pascall AJ; Duoss EB; Loh KJ et al. Field Responsive Mechanical Metamaterials. Sci. Adv 2018, 4, eaau6419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (164).Diller E; Zhuang J; Zhan Lum G; Edwards MR; Sitti M Continuously Distributed Magnetization Profile for Millimeter-Scale Elastomeric Undulatory Swimming. Appl. Phys. Lett 2014, 104, 174101. [Google Scholar]
- (165).Lum GZ; Ye Z; Dong X; Marvi H; Erin O; Hu W; Sitti M Shape-Programmable Magnetic Soft Matter. Proc. Natl. Acad. Sci. U. S. A 2016, 113, E6007–E6015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (166).Hu W; Lum GZ; Mastrangeli M; Sitti M Small-Scale Soft-Bodied Robot with Multimodal Locomotion. Nature 2018. , 554 , 81–85. [DOI] [PubMed] [Google Scholar]
- (167).Ren Z; Hu W; Dong X; Sitti M Multi-functional Soft-bodied Jellyfish-like Swimming. Nat. Comm 2019, 10, 2703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (168).Venkiteswaran VK; Tan DK; Misra S Tandem Actuation of Legged Locomotion and Grasping Manipulation in Soft Robots using Magnetic Fields. Extreme Mech. Lett 2020, 41, 101023. [Google Scholar]
- (169).Gong X; Tan K; Deng Q; Shen S Athermal Shape Memory Effect in Magnetoactive Elastomers. ACS Appl. Mater. Interfaces 2020, 12, 16930–16936. [DOI] [PubMed] [Google Scholar]
- (170).Testa P; Style RW; Cui J; Donnelly C; Borisova E; Derlet PM; Dufresne ER; Heyderman LJ Magnetically Addressable Shape-Memory and Stiffening in a Composite Elastomer. Adv. Mater 2019, 31, 1900561. [DOI] [PubMed] [Google Scholar]
- (171).Testa P; Chappuis B; Kistler S; Style RW; Heyderman LJ; Dufresne ER Switchable Adhesion of Soft Composites Induced by a Magnetic Field. Soft Matter 2020, 16, 5806–5811. [DOI] [PubMed] [Google Scholar]
- (172).Kokkinis D; Schaffner M; Studart AR Multimaterial Magnetically Assisted 3D Printing of Composite Materials. Nat. Comm 2015, 6, 8643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (173).Roh S; Okello LB; Golbasi N; Hankwitz JP; Liu JAC; Tracy JB; Velev OD 3D-Printed Silicone Soft Architectures with Programmed Magneto-Capillary Reconfiguration. Adv. Mater. Technol 2019, 4, 1800528. [Google Scholar]
- (174).Zhang X; Hu H; Tang D; Zhang C; Fu J; Zhao P Magnetic Flexible Tactile Sensor via Direct Ink Writing. Sens. Actuators A 2021, 327, 112753. [Google Scholar]
- (175).Von Petersdorff-Campen K; Hauswirth Y; Carpenter J; Hagmann A; Boës S; Schmid Daners M; Penner D; Meboldt M 3D Printing of Functional Assemblies with Integrated Polymer-Bonded Magnets Demonstrated with a Prototype of a Rotary Blood Pump. Appl. Sci 2018, 8, 1275. [Google Scholar]
- (176).Chatzipirpiridis G; Gervasoni S; Fischer C; Ergeneman O; Pellicer E; Nelson BJ; Pané S 3D Printing of Thermoplastic-Bonded Soft- and Hard-Magnetic Composites: Magnetically Tuneable Architectures and Functional Devices. Adv. Intell 2019, 1, 1900069. [Google Scholar]
- (177).Martin JJ; Fiore BE; Erb RM Designing Bioinspired Composite Reinforcement Architectures via 3D Magnetic Printing. Nat. Comm 2015, 6, 8641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (178).Xu T; Zhang J; Salehizadeh M; Onaizah O; Diller E Millimeter-Scale Flexible Robots with Programmable Three-Dimensional Magnetization and Motions. Sci. Robot 2019, 4, eaav4494. [DOI] [PubMed] [Google Scholar]
- (179).Shao G; Ware HOT; Li L; Sun C Rapid 3D Printing Magnetically Active Microstructures with High Solid Loading. Adv. Eng. Mater 2020, 22, 1900911. [Google Scholar]
- (180).Shao G; Ware HOT; Huang J; Hai R; Li L; Sun C 3D printed magnetically-actuating micro-gripper operates in air and water. Addit. Manuf 2021, 38, 101834. [Google Scholar]
- (181).Compton BG; Lewis JA 3D-Printing of Lightweight Cellular Composites. Adv. Mater 2014, 26, 5930–5935. [DOI] [PubMed] [Google Scholar]
- (182).Sydney Gladman A; Matsumoto EA; Nuzzo RG; Mahadevan L; Lewis JA Biomimetic 4D Printing. Nat. Mater 2016, 15, 413–418. [DOI] [PubMed] [Google Scholar]
- (183).Boley JW; van Rees WM; Lissandrello C; Horenstein MN; Truby RL; Kotikian A; Lewis JA; Mahadevan L Shape-Shifting Structured Lattices via Multimaterial 4D Printing. Proc. Natl. Acad. Sci. U. S. A 2019, 116, 20856–20862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (184).Smay JE; Cesarano J; Lewis JA Colloidal Inks for Directed Assembly of 3-D Periodic Structures. Langmuir 2002, 18, 5429–5437. [Google Scholar]
- (185).Erb RM; Libanori R; Rothfuchs N; Studart AR Composites Reinforced in Three Dimensions by Using Low Magnetic Fields. Science 2012, 335, 199–204. [DOI] [PubMed] [Google Scholar]
- (186).Erb RM; Sander JS; Grisch R; Studart AR Self-shaping Composites with Programmable Bioinspired Microstructures. Nat. Comm 2013, 4, 1712. [DOI] [PubMed] [Google Scholar]
- (187).Wehner M; Truby RL; Fitzgerald DJ; Mosadegh B; Whitesides GM; Lewis JA; Wood RJ An Integrated Design and Fabrication Strategy for Entirely Soft, Autonomous Robots. Nature 2016, 536, 451–455. [DOI] [PubMed] [Google Scholar]
- (188).Lewis JA Direct Ink Writing of 3D Functional Materials. Adv. Func. Mater 2006, 16, 2193–2204. [Google Scholar]
- (189).Cao L; Yu D; Xia Z; Wan H; Liu C; Yin T; He Z Ferromagnetic Liquid Metal Putty-Like Material with Transformed Shape and Reconfigurable Polarity. Adv. Mater 2020, 32, 2000827. [DOI] [PubMed] [Google Scholar]
- (190).Koos E; Willenbacher N Capillary Forces in Suspension Rheology. Science 2011, 331, 897–900. [DOI] [PubMed] [Google Scholar]
- (191).Schneider M; Koos E; Willenbacher N Highly Conductive, Printable Pastes from Capillary Suspensions. Sci. Rep 2016, 6, 31367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (192).Roh S; Parekh DP; Bharti B; Stoyanov SD; Velev OD 3D Printing by Multiphase Silicone/Water Capillary Inks. Adv. Mater 2017, 29, 1701554. [DOI] [PubMed] [Google Scholar]
- (193).Lin Y; Hu Z; Zhang M; Xu T; Feng S; Jiang L; Zheng Y Magnetically Induced Low Adhesive Direction of Nano/Micropillar Arrays for Microdroplet Transport. Adv. Func. Mater 2018, 28, 1800163. [Google Scholar]
- (194).Zhang J; Ren Z; Hu W; Soon RH; Yasa IC; Liu Z; Sitti M Voxelated Three-Dimensional Miniature Magnetic Soft Machines via Multimaterial Heterogeneous Assembly. Sci. Robot 2021, 6, eabf0112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (195).Tumbleston JR; Shirvanyants D; Ermoshkin N; Janusziewicz R; Johnson AR; Kelly D; Chen K; Pinschmidt R; Rolland JP; Ermoshkin A et al. Continuous Liquid Interface Production of 3D Objects. Science 2015. , 347, 1349–1352. [DOI] [PubMed] [Google Scholar]
- (196).Lantean S; Barrera G; Pirri CF; Tiberto P; Sangermano M; Roppolo I; Rizza G 3D Printing of Magnetoresponsive Polymeric Materials with Tunable Mechanical and Magnetic Properties by Digital Light Processing. Adv. Mater. Techno 2019, 4, 1900505. [Google Scholar]
- (197).Diller E; Sitti M Three-Dimensional Programmable Assembly by Untethered Magnetic Robotic Micro-Grippers. Adv. Func. Mater 2014. , 24 , 4397–4404. [Google Scholar]
- (198).Jeon J; Park JE; Park SJ; Won S; Zhao H; Kim S; Shim BS; Urbas A; Hart AJ; Ku Z et al. Shape-Programmed Fabrication and Actuation of Magnetically Active Micropost Arrays. ACS Appl. Mater. Interfaces 2020, 12, 17113–17120. [DOI] [PubMed] [Google Scholar]
- (199).Jiang S; Hu Y; Wu H; Zhang Y; Zhang Y; Wang Y; Zhang Y; Zhu W; Li J; Wu D et al. Multifunctional Janus Microplates Arrays Actuated by Magnetic Fields for Water/Light Switches and Bio-Inspired Assimilatory Coloration. Adv. Mater 2019, 31, 1807507. [DOI] [PubMed] [Google Scholar]
- (200).Huang H-W; Sakar MS; Petruska AJ; Pan73é S; Nelson BJ Soft Micromachines with Programmable Motility and Morphology. Nat. Comm 2016, 7, 12263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (201).Huang H-W; Huang T-Y; Charilaou M; Lyttle S; Zhang Q; Pané S; Nelson BJ Investigation of Magnetotaxis of Reconfigurable Micro-Origami Swimmers with Competitive and Cooperative Anisotropy. Adv. Func. Mater 2018, 28, 1802110. [Google Scholar]
- (202).Han K; Shields CW; Bharti B; Arratia PE; Velev OD Active Reversible Swimming of Magnetically Assembled “Microscallops” in Non-Newtonian Fluids. Langmuir 2020, 36, 7148–7154. [DOI] [PubMed] [Google Scholar]
- (203).Han K; Shields CW; Diwakar NM; Bharti B; López GP; Velev OD Sequence-encoded Colloidal Origami and Microbot Assemblies from Patchy Magnetic Cubes. Sci. Adv 2017, 3, e1701108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (204).Anscombe N Direct Laser Writing. Nat. Photon, 2010, 4, 22–23. [Google Scholar]
- (205).Tottori S; Zhang L; Qiu F; Krawczyk KK; Franco-Obregón A; Nelson BJ Magnetic Helical Micromachines: Fabrication, Controlled Swimming, and Cargo Transport. Adv. Mater 2012, 24, 811–816. [DOI] [PubMed] [Google Scholar]
- (206).Peters C; Hoop M; Pané S; Nelson BJ; Hierold C Degradable Magnetic Composites for Minimally Invasive Interventions: Device Fabrication, Targeted Drug Delivery, and Cytotoxicity Tests. Adv. Mater 2016, 28, 533–538. [DOI] [PubMed] [Google Scholar]
- (207).Bozuyuk U; Yasa O; Yasa IC; Ceylan H; Kizilel S; Sitti M Light-Triggered Drug Release from 3D-Printed Magnetic Chitosan Microswimmers. ACS Nano 2018, 12, 9617–9625. [DOI] [PubMed] [Google Scholar]
- (208).Ceylan H; Yasa IC; Yasa O; Tabak AF; Giltinan J; Sitti M 3D-Printed Biodegradable Microswimmer for Theranostic Cargo Delivery and Release. ACS Nano 2019, 13, 3353–3362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (209).Dong M; Wang X; Chen X-Z; Mushtaq F; Deng S; Zhu C; Torlakcik H; Terzopoulou A; Qin X-H; Xiao X et al. 3D-Printed Soft Magnetoelectric Microswimmers for Delivery and Differentiation of Neuron-Like Cells. Adv. Func. Mater 2020, 30, 1910323. [Google Scholar]
- (210).Lao Z; Xia N; Wang S; Xu T; Wu X; Zhang L Tethered and Untethered 3D Microactuators Fabricated by Two-Photon Polymerization: A Review. Micromachines 2021, 12, 465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (211).Boncheva M; Andreev SA; Mahadevan L; Winkleman A; Reichman DR; Prentiss MG; Whitesides S; Whitesides GM Magnetic Self-Assembly of Three-Dimensional Surfaces from Planar Sheets. Proc. Natl. Acad. Sci. U. S. A 2005, 102, 3924–3929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (212).Gu H; Boehler Q; Ahmed D; Nelson BJ Magnetic Quadrupole Assemblies with Arbitrary Shapes and Magnetizations. Sci. Robot 2019, 4, eaax8977. [DOI] [PubMed] [Google Scholar]
- (213).Niu R; Du CX; Esposito E; Ng J; Brenner MP; McEuen PL; Cohen I Magnetic Handshake Materials as a Scale-Invariant Platform for Programmed Self-Assembly. Proc. Natl. Acad. Sci. U. S. A 2019, 116, 24402–24407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (214).Li M; Wang Y; Chen A; Naidu A; Napier BS; Li W; Rodriguez CL; Crooker SA; Omenetto FG Flexible Magnetic Composites for Light-controlled Actuation and Interfaces. Proc. Natl. Acad. Sci. U. S. A 2018, 115, 8119–8124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (215).Alapan Y; Karacakol AC; Guzelhan SN; Isik I; Sitti M Reprogrammable Shape Morphing of Magnetic Soft Machines. Sci. Adv 2020, 6, eabc6414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (216).Song H; Lee H; Lee J; Choe JK; Lee S; Yi JY; Park S; Yoo J-W; Kwon MS; Kim J Reprogrammable Ferromagnetic Domains for Reconfigurable Soft Magnetic Actuators. Nano Lett. 2020, 20, 5185–5192. [DOI] [PubMed] [Google Scholar]
- (217).Deng H; Sattari K; Xie Y; Liao P; Yan Z; Lin J Laser Reprogramming Magnetic Anisotropy in Soft Composites for Reconfigurable 3D Shaping. Nat. Comm 2020, 11, 6325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (218).Mermet-Guyennet MRB; Gianfelice de Castro J; Varol HS; Habibi M; Hosseinkhani B; Martzel N; Sprik R; Denn MM; Zaccone A; Parekh SH et al. Size-dependent Reinforcement of Composite Rubbers. Polymer 2015, 73, 170–173. [Google Scholar]
- (219).Mermet-Guyennet M; Dinkgreve M; Habibi M; Martzel N; Sprik R; Denn M; Bonn D Dependence of Nonlinear Elasticity on Filler Size in Composite Polymer Systems. Rheol. Acta 2017, 56, 583–589. [Google Scholar]
- (220).Qian M; Zou B; Chen Z; Huang W; Wang X; Tang B; Liu Q; Zhu Y The Influence of Filler Size and Crosslinking Degree of Polymers on Mullins Effect in Filled NR/BR Composites. Polymers 2021, 13, 2284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (221).Sandler SE; Fellows B; Mefford OT Best Practices for Characterization of Magnetic Nanoparticles for Biomedical Applications. Anal. Chem 2019, 91, 14159–14169. [DOI] [PubMed] [Google Scholar]
- (222).Chantrell RW; O’Grady K Magnetic Characterization of Recording Media. J. Phys. D Appl. Phys 1992, 25, 1–23. [Google Scholar]
- (223).Buchner M; Höfler K; Henne B; Ney V; Ney A Tutorial: Basic Principles, Limits of Detection, and Pitfalls of Highly Sensitive SQUID Magnetometry for Nanomagnetism and Spintronics. J. Appl. Phys 2018, 124, 161101. [Google Scholar]
- (224).Lambert C-H; Mangin S; Varaprasad BSDCS; Takahashi YK; Hehn M; Cinchetti M; Malinowski G; Hono K; Fainman Y; Aeschlimann M et al. All-Optical Control of Ferromagnetic Thin Films and Nanostructures. Science 2014. , 345, 1337–1340. [DOI] [PubMed] [Google Scholar]
- (225).Qiu ZQ; Bader SD Surface Magneto-Optic Kerr Effect. Rev. Sci. Instrum 2000, 71, 1243–1255. [Google Scholar]
- (226).Bastola AK; Hossain M A Review on Magneto-Mechanical Characterizations of Magnetorheological Elastomers. Compos. B. Eng 2020, 200, 108348. [Google Scholar]
- (227).Kang SS; Choi K; Nam J-D; Choi HJ Magnetorheological Elastomers: Fabrication, Characteristics, and Applications. Materials 2020, 13, 4597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (228).Li Y; Li J; Li W; Du H A State-of-the-art Review on Magnetorheological Elastomer Devices. Smart Mater. Struct 2014, 23, 123001. [Google Scholar]
- (229).Brancati R; Di Massa G; Pagano S Investigation on the Mechanical Properties of MRE Compounds. Machines 2019, 7, 36. [Google Scholar]
- (230).Arslan Hafeez M; Usman M; Umer MA; Hanif A Recent Progress in Isotropic Magnetorheological Elastomers and Their Properties: A Review. Polymers 2020, 12, 3023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (231).Tabor D The Bulk Modulus of Rubber. Polymer 1994, 35, 2759–2763. [Google Scholar]
- (232).Erni S; Schürle S; Fakhraee A; Kratochvil BE; Nelson BJ Comparison, Optimization, and Limitations of Magnetic Manipulation Systems. J. Microbio Robot 2013, 8, 107–120. [Google Scholar]
- (233).Rahman I; Pioche M; Shim CS; Lee SP; Sung I-K; Saurin J-C; Patel P Magnetic-Assisted Capsule Endoscopy in the Upper GI Tract by Using a Novel Navigation System. Gastrointest. Endosc 2016, 83, 889–895.e881. [DOI] [PubMed] [Google Scholar]
- (234).Shamsudhin N; Zverev VI; Keller H; Pane S; Egolf PW; Nelson BJ; Tishin AM Magnetically Guided Capsule Endoscopy. Med. Phys 2017, 44, e91–e111. [DOI] [PubMed] [Google Scholar]
- (235).Keller J; Fibbe C; Volke F; Gerber J; Mosse AC; Reimann-Zawadzki M; Rabinovitz E; Layer P; Swain P Remote Magnetic Control of a Wireless Capsule Endoscope in the Esophagus is Safe and Feasible: Results of a Randomized, Clinical Trial in Healthy Volunteers. Gastrointest. Endosc 2010. , 72, 941–946. [DOI] [PubMed] [Google Scholar]
- (236).Keller J; Fibbe C; Volke F; Gerber J; Mosse AC; Reimann-Zawadzki M; Rabinovitz E; Layer P; Schmitt D; Andresen V et al. Inspection of the Human Stomach using Remote-Controlled Capsule Endoscopy: A Feasibility Study in Healthy Volunteers. Gastrointest. Endosc 2011, 73, 22–28. [DOI] [PubMed] [Google Scholar]
- (237).Hale MF; Rahman I; Drew K; Sidhu R; Riley SA; Patel P; McAlindon ME Magnetically Steerable Gastric Capsule Endoscopy is Equivalent to Flexible Endoscopy in the Detection of Markers in an Excised Porcine Stomach Model: Results of a Randomized Trial. Endoscopy 2015, 47, 650–653. [DOI] [PubMed] [Google Scholar]
- (238).Yang X; Shang W; Lu H; Liu Y; Yang L; Tan R; Wu X; Shen Y An Agglutinate Magnetic Spray Transforms Inanimate Objects into Millirobots for Biomedical Applications. Sci. Robot 2020, 5, eabc8191. [DOI] [PubMed] [Google Scholar]
- (239).Ciuti G; Donlin R; Valdastri P; Arezzo A; Menciassi A; Morino M; Dario P Robotic Versus Manual Control in Magnetic Steering of an Endoscopic Capsule. Endoscopy 2010, 42, 148–152. [DOI] [PubMed] [Google Scholar]
- (240).Ciuti G; Valdastri P; Menciassi A; Dario P Robotic Magnetic Steering and Locomotion of Capsule Endoscope for Diagnostic and Surgical Endoluminal Procedures. Robotica 2010, 28, 199–207. [Google Scholar]
- (241).Tognarelli S; Castelli V; Ciuti G; Di Natali C; Sinibaldi E; Dario P; Menciassi A Magnetic Propulsion and Ultrasound Tracking of Endovascular Devices. J. Robot. Surg 2012, 6, 5–12. [DOI] [PubMed] [Google Scholar]
- (242).Mahoney AW; Abbott JJ Generating Rotating Magnetic Fields With a Single Permanent Magnet for Propulsion of Untethered Magnetic Devices in a Lumen. IEEE Trans. Robot 2014, 30, 411–420. [Google Scholar]
- (243).Mahoney AW; Abbott JJ Five-Degree-of-Freedom Manipulation of an Untethered Magnetic Device in Fluid using a Single Permanent Magnet with Application in Stomach Capsule Endoscopy. Int. J. Robot. Res 2015, 35, 129–147. [Google Scholar]
- (244).Wright SE; Mahoney AW; Popek KM; Abbott JJ The Spherical-Actuator-Magnet Manipulator: A Permanent-Magnet Robotic End-Effector. IEEE Trans. Robot 2017, 33, 1013–1024. [Google Scholar]
- (245).Kratchman LB; Bruns TL; Abbott JJ; Webster RJ Guiding elastic rods with a robot-manipulated magnet for medical applications. IEEE Trans. Robot 2017, 33, 227–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (246).Slawinski PR; Taddese AZ; Musto KB; Obstein KL; Valdastri P Autonomous Retroflexion of a Magnetic Flexible Endoscope. IEEE Robot. Autom. Lett 2017, 2, 1352–1359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (247).Taddese AZ; Slawinski PR; Pirotta M; De Momi E; Obstein KL; Valdastri P Enhanced Real-Time Pose Estimation for Closed-Loop Robotic Manipulation of Magnetically Actuated Capsule Endoscopes. Int. J. Robot. Res 2018, 37, 890–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (248).Pittiglio G; Barducci L; Martin JW; Norton JC; Avizzano CA; Obstein KL; Valdastri P Magnetic Levitation for Soft-Tethered Capsule Colonoscopy Actuated With a Single Permanent Magnet: A Dynamic Control Approach. IEEE Robot. Autom. Lett 2019, 4, 1224–1231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (249).Norton JC; Slawinski PR; Lay HS; Martin JW; Cox BF; Cummins G; Desmulliez MPY; Clutton RE; Obstein KL; Cochran S et al. Intelligent Magnetic Manipulation for Gastrointestinal Ultrasound. Sci. Robot 2019, 4, eaav7725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (250).Zhao X; Kim Y Magnetically Steerable Continuum Robotic Guidewires for Neurovascular Applications. U.S. Patent 11,103,324, August 31, 2021.
- (251).Diller E; Giltinan J; Lum GZ; Ye Z; Sitti M Six-Degree-of-Freedom Magnetic Actuation for Wireless Microrobotics. Int. J. Robot. Res 2015, 35, 114–128. [Google Scholar]
- (252).Zhou H; Mayorga-Martinez CC; Pané S; Zhang L; Pumera M Magnetically Driven Micro and Nanorobots. Chem. Rev 2021, 121, 4999–5041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (253).Wang L; Kim Y; Guo CF; Zhao X Hard-Magnetic Elastica. J. Mech. Phys. Solids 2020, 142, 104045. [Google Scholar]
- (254).Krings T; Finney J; Niggemann P; Reinacher P; Lück N; Drexler A; Lovell J; Meyer A; Sehra R; Schauerte P et al. Magnetic versus Manual Guidewire Manipulation in Neuroradiology: In Vitro Results. Neuroradiology 2006, 48, 394–401. [DOI] [PubMed] [Google Scholar]
- (255).Ramcharitar S; Patterson MS; van Geuns RJ; van Meighem C; Serruys PW Technology Insight: Magnetic Navigation in Coronary Interventions. Nat. Clin. Pract. Cardiovasc. Med 2008, 5, 148–156. [DOI] [PubMed] [Google Scholar]
- (256).Schiemann M; Killmann R; Kleen M; Abolmaali N; Finney J; Vogl TJ Vascular Guide Wire Navigation with a Magnetic Guidance System: Experimental Results in a Phantom. Radiology 2004, 232, 475–481. [DOI] [PubMed] [Google Scholar]
- (257).Tsuchida K; García-García HM; van der Giessen WJ; McFadden EP; van der Ent M; Sianos G; Meulenbrug H; Ong ATL; Serruys PW Guidewire Navigation in Coronary Artery Stenoses using a Novel Magnetic Navigation System: First Clinical Experience. Catheter. Cardiovasc. Interv 2006, 67, 356–363. [DOI] [PubMed] [Google Scholar]
- (258).Abbott JJ; Diller E; Petruska AJ Magnetic Methods in Robotics. Annu. Rev. Control Robot. Anton. Syst 2020, 3, 57–90. [Google Scholar]
- (259).Yang Z; Zhang L Magnetic Actuation Systems for Miniature Robots: A Review. Adv. Intel 2020, 2, 2000082. [Google Scholar]
- (260).Purcell EM Helmholtz Coils Revisited. Am. J. Phys 1989, 57, 18–22. [Google Scholar]
- (261).Turner R Gradient Coil Design: A Review of Methods. Magn. Reson. Imaging 1993, 11, 903–920. [DOI] [PubMed] [Google Scholar]
- (262).Ginsberg DM; Melchner MJ Optimum Geometry of Saddle Shaped Coils for Generating a Uniform Magnetic Field. Rev. Sci. Instrnm 1970, 41, 122–123. [Google Scholar]
- (263).Hanssum H The Magnetic Field of Saddle-Shaped Coils. I. Symmetry of the Magnetic Field around the Coil Centre. J. Phys. D Appl. Phys 1984, 17, 1–18. [Google Scholar]
- (264).Hidalgo-Tobon SS Theory of Gradient Coil Design Methods for Magnetic Resonance Imaging. Concepts Mag. Res. A 2010, 36A, 223–242. [Google Scholar]
- (265).Abbott JJ Parametric Design of Tri-Axial Nested Helmholtz Coils. Rev. Sci. Instrnm 2015, 86, 054701. [DOI] [PubMed] [Google Scholar]
- (266).Rahmer J; Stehning C; Gleich B Spatially Selective Remote Magnetic Actuation of Identical Helical Micromachines. Sci. Robot 2017, 2, eaal2845. [DOI] [PubMed] [Google Scholar]
- (267).Nothnagel N; Rahmer J; Gleich B; Halkola A; Borgert J; Buzug TM Steering of Magnetic Devices with a Magnetic Particle Imaging System. 2013 International Workshop on Magnetic Particle Imaging (IWMPI), 2013, 1–1. [DOI] [PubMed] [Google Scholar]
- (268).Rahmer J; Stehning C; Gleich B Remote Magnetic Actuation using a Clinical Scale System. PLOS ONE 2018, 13, e0193546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (269).Yu C; Kim J; Choi H; Choi J; Jeong S; Cha K; Park J.-o.; Park S Novel Electromagnetic Actuation System for Three-Dimensional Locomotion and Drilling of Intravascular Microrobot. Sens. Actuators A 2010, 161, 297–304. [Google Scholar]
- (270).Choi H; Cha K; Jeong S; Park J; Park S 3-D Locomotive and Drilling Microrobot Using Novel Stationary EMA System. IEEE ASME Trans. Mechatron 2013, 18, 1221–1225. [Google Scholar]
- (271).Choi H; Cha K; Choi J; Jeong S; Jeon S; Jang G; Park J.-o.; Park S EMA System with Gradient and Uniform Saddle Coils for 3D Locomotion of Microrobot. Sens. Actuators A 2010, 163, 410–417. [Google Scholar]
- (272).Jeon S; Jang G; Choi H; Park S Magnetic Navigation System With Gradient and Uniform Saddle Coils for the Wireless Manipulation of Micro-Robots in Human Blood Vessels. IEEE Trans. Magn 2010, 46, 1943–1946. [Google Scholar]
- (273).Jeon SM; Jang GH; Choi JH; Park SH; Park JO Precise Manipulation of a Microrobot in the Pulsatile Flow of Human Blood Vessels using Magnetic Navigation System. J. Appl. Phys 2011, 109, 07B316. [Google Scholar]
- (274).Lee C; Choi H; Go G; Jeong S; Ko SY; Park J; Park S Active Locomotive Intestinal Capsule Endoscope (ALICE) System: A Prospective Feasibility Study. IEEE ASME Trans. Mechatron 2015, 20, 2067–2074. [Google Scholar]
- (275).Go G; Choi H; Jeong S; Lee C; Ko SY; Park J; Park S Electromagnetic Navigation System Using Simple Coil Structure (4 Coils) for 3-D Locomotive Microrobot. IEEE Trans. Magn 2015, 51, 1–7.26203196 [Google Scholar]
- (276).Pourkand A; Abbott JJ Magnetic Actuation With Stationary Electromagnets Considering Power and Temperature Constraints. IEEE Robot. Autom. Lett 2020, 5, 6964–6971. [Google Scholar]
- (277).Martel S Beyond Imaging: Macro- and Microscale Medical Robots Actuated by Clinical MRI Scanners. Sci. Robot 2017, 2, eaam8119. [DOI] [PubMed] [Google Scholar]
- (278).Erin O; Boyvat M; Tiryaki ME; Phelan M; Sitti M Magnetic Resonance Imaging System–Driven Medical Robotics. Adv. Intell 2020, 2, 1900110. [Google Scholar]
- (279).Mathieu J; Beaudoin G; Martel S Method of Propulsion of a Ferromagnetic Core in the Cardiovascular System through Magnetic Gradients Generated by an MRI System. IEEE Trans. Biomed, Eng 2006, 53, 292–299. [DOI] [PubMed] [Google Scholar]
- (280).Martel S; Mathieu J-B; Felfoul O; Chanu A; Aboussouan E; Tamaz S; Pouponneau P; Yahia LH; Beaudoin G; Soulez G et al. Automatic Navigation of an Untethered Device in the Artery of a Living Animal using a Conventional Clinical Magnetic Resonance Imaging System. Appl. Phys. Lett 2007, 90, 114105. [Google Scholar]
- (281).Pouponneau P; Leroux J-C; Soulez G; Gaboury L; Martel S Co-encapsulation of Magnetic Nanoparticles and Doxorubicin into Biodegradable Microcarriers for Deep Tissue Targeting by Vascular MRI Navigation. Biomaterials 2011, 32, 3481–3486. [DOI] [PubMed] [Google Scholar]
- (282).Vartholomeos P; Bergeles C; Qin L; Dupont PE An MRI-Powered and Controlled Actuator Technology for Tetherless Robotic Interventions. Int. J. Robot. Res 2013, 32, 1536–1552. [Google Scholar]
- (283).Muthana M; Kennerley AJ; Hughes R; Fagnano E; Richardson J; Paul M; Murdoch C; Wright F; Payne C; Lythgoe MF et al. Directing Cell Therapy to Anatomic Target Sites In Vivo with Magnetic Resonance Targeting. Nat. Comm 2015, 6, 8009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (284).Felfoul O; Becker AT; Fagogenis G; Dupont PE Simultaneous Steering and Imaging of Magnetic Particles using MRI toward Delivery of Therapeutics. Sci. Rep 2016, 6, 33567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (285).Liu T; Jackson R; Franson D; Poirot NL; Criss RK; Seiberlich N; Griswold MA; Cavusoglu MC Iterative Jacobian-Based Inverse Kinematics and Open-Loop Control of an MRI-Guided Magnetically Actuated Steerable Catheter System. IEEE ASME Trans. Mechatron 2017, 22, 1765–1776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (286).Folio D; Ferreira A Two-Dimensional Robust Magnetic Resonance Navigation of a Ferromagnetic Microrobot Using Pareto Optimality. IEEE Trans. Robot 2017, 33, 583–593. [Google Scholar]
- (287).Erin O; Antonelli D; Tiryaki ME; Sitti M Towards 5-DoF Control of an Untethered Magnetic Millirobot via MRI Gradient Coils. 2020 IEEE International Conference on Robotics and Automation (ICRA), 2020, 6551–6557. [Google Scholar]
- (288).Azizi A; Tremblay CC; Gagné K; Martel S Using the Fringe Field of a Clinical MRI Scanner Enables Robotic Navigation of Tethered Instruments in Deeper Vascular Regions. Sci. Robot 2019, 4, eaax7342. [DOI] [PubMed] [Google Scholar]
- (289).Petruska AJ; Nelson BJ Minimum Bounds on the Number of Electromagnets Required for Remote Magnetic Manipulation. IEEE Trans. Robot 2015, 31, 714–722. [Google Scholar]
- (290).Gang ES; Nguyen BL; Shachar Y; Farkas L; Farkas L; Marx B; Johnson D; Fishbein MC; Gaudio C; Kim SJ Dynamically Shaped Magnetic Fields: Initial Animal Validation of a New Remote Electrophysiology Catheter Guidance and Control System. Circ. Arrhythm. Electrophysiol 2011, 4, 770–777. [DOI] [PubMed] [Google Scholar]
- (291).Khalil ISM; Magdanz V; Sanchez S; Schmidt OG; Misra S Three-Dimensional Closed-Loop Control of Self-Propelled Microjets. Appl. Phys. Lett 2013, 103, 172404. [Google Scholar]
- (292).Charreyron SL; Boehler Q; Kim B; Weibel C; Chautems C; Nelson BJ Modeling Electromagnetic Navigation Systems. IEEE Trans. Robot 2021, 1–13. [Google Scholar]
- (293).Le VNT; Nguyen NH; Alameh K; Weerasooriya R; Pratten P Accurate Modeling and Positioning of a Magnetically Controlled Catheter Tip. Med. Phys 2016, 43, 650–663. [DOI] [PubMed] [Google Scholar]
- (294).Li J; Wang H; Cui J; Shi Q; Zheng Z; Sun T; Huang Q; Fukuda T Magnetic Micromachine Using Nickel Nanoparticles for Propelling and Releasing in Indirect Assembly of Cell-Laden Micromodules. Micromachines 2019, 10, 370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (295).Pourkand A; Abbott JJ A Critical Analysis of Eight-Electromagnet Manipulation Systems: The Role of Electromagnet Configuration on Strength, Isotropy, and Access. IEEE Robot. Autom. Lett 2018, 3, 2957–2962. [Google Scholar]
- (296).Kummer MP; Abbott JJ; Kratochvil BE; Borer R; Sengul A; Nelson BJ OctoMag: An Electromagnetic System for 5-DOF Wireless Micromanipulation. IEEE Trans. Robot 2010, 26, 1006–1017. [Google Scholar]
- (297).Koepele CA; Guix M; Bi C; Adam G; Cappelleri DJ 3D-Printed Microrobots with Integrated Structural Color for Identification and Tracking. Adv. Intell 2020, 2, 1900147. [Google Scholar]
- (298).Kratochvil BE; Kummer MP; Erni S; Borer R; Frutiger DR; Schürle S; Nelson BJ MiniMag: A Hemispherical Electromagnetic System for 5-DOF Wireless Micromanipulation In Experimental Robotics: The 12th International Symposium on Experimental Robotics; Khatib O;Kumar V;Sukhatme G, Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2014, DOI:10.1007/978-3-642-28572-1_22 10.1007/978-3-642-28572-1_22. [Google Scholar]
- (299).Son D; Dong X; Sitti M A Simultaneous Calibration Method for Magnetic Robot Localization and Actuation Systems. IEEE Trans. Robot 2019, 35, 343–352. [Google Scholar]
- (300).Sikorski J; Denasi A; Bucchi G; Scheggi S; Misra S Vision-based 3-D Control of Magnetically Actuated Catheter Using BigMag—An Array of Mobile Electromagnetic Coils. IEEE ASME Trans. Mechatron 2019, 24, 505–516. [Google Scholar]
- (301).Yang L; Du X; Yu E; Jin D; Zhang L DeltaMag: An Electromagnetic Manipulation System with Parallel Mobile Coils. 2019 International Conference on Robotics and Automation (ICRA), 2019, 9814–9820. [Google Scholar]
- (302).Wang B; Chan KF; Yuan K; Wang Q; Xia X; Yang L; Ko H; Wang Y-XJ; Sung JJY; Chiu PWY et al. Endoscopy-Assisted Magnetic Navigation of Biohybrid Soft Microrobots with Rapid Endoluminal Delivery and Imaging. Sci. Robot 2021, 6, eabd2813. [DOI] [PubMed] [Google Scholar]
- (303).Heunis C; Sikorski J; Misra S Flexible Instruments for Endovascular Interventions: Improved Magnetic Steering, Actuation, and Image-Guided Surgical Instruments. IEEE Robot. Autom. Mag 2018, 25, 71–82. [Google Scholar]
- (304).Sikorski J; Heunis CM; Franco F; Misra S The ARMM System: An Optimized Mobile Electromagnetic Coil for Non-Linear Actuation of Flexible Surgical Instruments. IEEE Trans. Magn 2019, 55, 1–9. [Google Scholar]
- (305).Heunis CM; Wotte YP; Sikorski J; Furtado GP; Misra S The ARMM System - Autonomous Steering of Magnetically-Actuated Catheters: Towards Endovascular Applications. IEEE Robot. Autom. Lett 2020, 5, 705–712. [Google Scholar]
- (306).Heunis CM; Barata BF; Furtado GP; Misra S Collaborative Surgical Robots: Optical Tracking During Endovascular Operations. IEEE Robot. Autom. Mag 2020, 27, 29–44. [Google Scholar]
- (307).Petruska AJ; Abbott JJ Omnimagnet: An Omnidirectional Electromagnet for Controlled Dipole-Field Generation. IEEE Trans. Magn 2014, 50, 1–10. [Google Scholar]
- (308).Petruska AJ; Mahoney AW; Abbott JJ Remote Manipulation With a Stationary Computer-Controlled Magnetic Dipole Source. IEEE Trans. Robot 2014, 30, 1222–1227. [Google Scholar]
- (309).Bruns TL; Riojas KE; Ropella DS; Cavilla MS; Petruska AJ; Freeman MH; Labadie RF; Abbott JJ; Webster RJ Magnetically Steered Robotic Insertion of Cochlear-Implant Electrode Arrays: System Integration and First-In-Cadaver Results. IEEE Robot. Autom. Lett 2020, 5, 2240–2247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (310).Dreyfus R; Baudry J; Roper ML; Fermigier M; Stone HA; Bibette J Microscopic Artificial Swimmers. Nature 2005, 437, 862–865. [DOI] [PubMed] [Google Scholar]
- (311).Khalil ISM; Dijkslag HC; Abelmann L; Misra S MagnetoSperm: A microrobot that navigates using weak magnetic fields. Appl. Phys. Lett 2014, 104, 223701. [Google Scholar]
- (312).Khalil ISM; Fatih Tabak A; Klingner A; Sitti M Magnetic Propulsion of Robotic Sperms at Low-Reynolds Number. Appl. Phys. Lett 2016, 109, 033701. [Google Scholar]
- (313).Magdanz V; Khalil ISM; Simmchen J; Furtado GP; Mohanty S; Gebauer J; Xu H; Klingner A; Aziz A; Medina-Sánchez M et al. IRONSperm: Sperm-templated Soft Magnetic Microrobots. Sci. Adv. 2020, 6, eaba5855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (314).Lu H; Zhang M; Yang Y; Huang Q; Fukuda T; Wang Z; Shen Y A Bioinspired Multilegged Soft Millirobot that Fnctions in Both Dry and Wet Conditions. Nat. Comm 2018, 9, 3944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (315).Zhang J; Diller E Untethered Miniature Soft Robots: Modeling and Design of a Millimeter-Scale Swimming Magnetic Sheet. Soft Robot. 2018, 5, 761–776. [DOI] [PubMed] [Google Scholar]
- (316).Goudu SR; Yasa IC; Hu X; Ceylan H; Hu W; Sitti M Biodegradable Untethered Magnetic Hydrogel Milli-Grippers. Adv. Func. Mater 2020, 30, 2004975. [Google Scholar]
- (317).Rus D; Tolley MT Design, Fabrication and Control of Origami Robots. Nat. Rev. Mater 2018, 3, 101–112. [Google Scholar]
- (318).Miyashita S; Guitron S; Li S; Rus D Robotic Metamorphosis by Origami Exoskeletons. Sci. Robot 2017, 2, eaao4369. [DOI] [PubMed] [Google Scholar]
- (319).Cowan B; von Lockette PR Fabrication, Characterization, and Heuristic Trade Space Exploration of Magnetically Actuated Miura-Ori Origami Structures. Smart Mater. Struct 2017, 26, 045015. [Google Scholar]
- (320).Novelino LS; Ze Q; Wu S; Paulino GH; Zhao R Untethered Control of Functional Origami Microrobots with Distributed Actuation. Proc. Natl. Acad. Sci. U. S. A 2020, 117, 24096–24101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (321).Schenk M; Guest SD Geometry of Miura-Folded Metamaterials. Proc. Natl. Acad. Sci. U. S. A 2013, 110, 3276–3281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (322).Bertoldi K; Vitelli V; Christensen J; van Hecke M Flexible Mechanical Metamaterials. Nat. Rev. Mater 2017, 2, 17066. [Google Scholar]
- (323).Wu S; Ze Q; Zhang R; Hu N; Cheng Y; Yang F; Zhao R Symmetry-Breaking Actuation Mechanism for Soft Robotics and Active Metamaterials. ACS Appl. Mater. Interfaces 2019, 11, 41649–41658. [DOI] [PubMed] [Google Scholar]
- (324).Montgomery SM; Wu S; Kuang X; Armstrong CD; Zemelka C; Ze Q; Zhang R; Zhao R; Qi HJ Magneto-Mechanical Metamaterials with Widely Tunable Mechanical Properties and Acoustic Bandgaps. Adv. Func. Mater 2021, 31, 2005319. [Google Scholar]
- (325).Chen T; Pauly M; Reis PM A Reprogrammable Mechanical Metamaterial with Stable Memory. Nature 2021, 589, 386–390. [DOI] [PubMed] [Google Scholar]
- (326).Pierce CD; Willey CL; Chen VW; Hardin JO; Berrigan JD; Juhl AT; Matlack KH Adaptive Elastic Metastructures from Magneto-Active Elastomers. Smart Mater. Struct 2020, 29, 065004. [Google Scholar]
- (327).Drotlef D-M; Blümler P; Papadopoulos P; del Campo A Magnetically Actuated Micropatterns for Switchable Wettability. ACS Appl. Mater. Interfaces 2014, 6, 8702–8707. [DOI] [PubMed] [Google Scholar]
- (328).Yang Z; Park JK; Kim S Magnetically Responsive Elastomer–Silicon Hybrid Surfaces for Fluid and Light Manipulation. Small 2018, 14, 1702839. [DOI] [PubMed] [Google Scholar]
- (329).Zhu Y; Antao DS; Xiao R; Wang EN Real-Time Manipulation with Magnetically Tunable Structures. Adv. Mater 2014, 26, 6442–6446. [DOI] [PubMed] [Google Scholar]
- (330).Khaderi SN; den Toonder JMJ; Onck PR Microfluidic Propulsion by the Metachronal Beating of Magnetic Artificial Cilia: A Numerical Analysis. J. Fluid Mech 2011, 688, 44–65. [Google Scholar]
- (331).Hanasoge S; Hesketh PJ; Alexeev A Microfluidic Pumping using Artificial Magnetic Cilia. Microsyst. Nanoeng 2018, 4, 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (332).Wu C; Zhang Q; Fan X; Song Y; Zheng Q Smart magnetorheological elastomer peristaltic pump. J. Intell. Mater. Syst. Struct 2019, 30, 1084–1093. [Google Scholar]
- (333).Zhou M; Qi Z; Xia Z; Li Y; Ling W; Yang J; Yang Z; Pei J; Wu D; Huo W et al. Miniaturized Soft Centrifugal Pumps with Magnetic Levitation for Fluid Handling. Sci. Adv 2021, 7, eabi7203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (334).Fu H; Nan K; Bai W; Huang W; Bai K; Lu L; Zhou C; Liu Y; Liu F; Wang J et al. Morphable 3D Mesostructures and Microelectronic Devices by Multistable Buckling Mechanics. Nat. Mater 2018, 17, 268–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (335).Qi Z; Zhou M; Li Y; Xia Z; Huo W; Huang X Reconfigurable Flexible Electronics Driven by Origami Magnetic Membranes. Adv. Mater. Technol 2021, 6, 2001124. [Google Scholar]
- (336).Kawasetsu T; Horii T; Ishihara H; Asada M Mexican-Hat-Like Response in a Flexible Tactile Sensor Using a Magnetorheological Elastomer. Sensors 2018, 18, 587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (337).Hellebrekers T; Kroemer O; Majidi C Soft Magnetic Skin for Continuous Deformation Sensing. Adv. Intell 2019, 1, 1900025. [Google Scholar]
- (338).Wu Y; Liu Y; Zhou Y; Man Q; Hu C; Asghar W; Li F; Yu Z; Shang J; Liu G et al. A Skin-inspired Tactile Sensor for Smart Prosthetics. Sci. Robot 2018, 3, eaat0429. [DOI] [PubMed] [Google Scholar]
- (339).Yan Y; Hu Z; Yang Z; Yuan W; Song C; Pan J; Shen Y Soft Magnetic Skin for Super-resolution Tactile Sensing with Force Self-decoupling. Sci. Robot 2021, 6, eabc8801. [DOI] [PubMed] [Google Scholar]
- (340).Ge J; Wang X; Drack M; Volkov O; Liang M; Cañón Bermúdez GS; Illing R; Wang C; Zhou S; Fassbender J et al. A Bimodal Soft Electronic Skin for Tactile and Touchless Interaction in Real Time. Nat. Comm 2019, 10, 4405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (341).Li Y; Chen Z; Zheng G; Zhong W; Jiang L; Yang Y; Jiang L; Chen Y; Wong C-P A Magnetized Microneedle-Array Based Flexible Triboelectric-Electromagnetic Hybrid Generator for Human Motion Monitoring. Nano Energy 2020, 69, 104415. [Google Scholar]
- (342).Zhao Y; Gao S; Zhang X; Huo W; Xu H; Chen C; Li J; Xu K; Huang X Fully Flexible Electromagnetic Vibration Sensors with Annular Field Confinement Origami Magnetic Membranes. Adv. Func. Mater 2020, 30, 2001553. [Google Scholar]
- (343).Kim S; Qiu F; Kim S; Ghanbari A; Moon C; Zhang L; Nelson BJ; Choi H Fabrication and Characterization of Magnetic Microrobots for Three-Dimensional Cell Culture and Targeted Transportation. Adv. Mater 2013, 25, 5863–5868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (344).Qiu F; Fujita S; Mhanna R; Zhang L; Simona BR; Nelson BJ Magnetic Helical Microswimmers Functionalized with Lipoplexes for Targeted Gene Delivery. Adv. Func. Mater 2015, 25, 1666–1671. [Google Scholar]
- (345).Qiu F; Nelson BJ Magnetic Helical Micro- and Nanorobots: Toward Their Biomedical Applications. Engineering 2015, 1, 021–026. [Google Scholar]
- (346).Jeon S; Kim S; Ha S; Lee S; Kim E; Kim SY; Park SH; Jeon JH; Kim SW; Moon C et al. Magnetically Actuated Microrobots as a Platform for Stem Cell Transplantation. Sci. Robot 2019, 4, eaav4317. [DOI] [PubMed] [Google Scholar]
- (347).Peyer KE; Zhang L; Nelson BJ Bio-inspired Magnetic Swimming Microrobots for Biomedical Applications. Nanoscale 2013, 5, 1259–1272. [DOI] [PubMed] [Google Scholar]
- (348).Yim S; Sitti M Shape-Programmable Soft Capsule Robots for Semi-Implantable Drug Delivery. IEEE Trans. Robot 2012, 28, 1198–1202. [Google Scholar]
- (349).Petruska AJ; Ruetz F; Hong A; Regli L; Sürücü O; Zemmar A; Nelson BJ Magnetic Needle Guidance for Neurosurgery: Initial Design and Proof of Concept. 2016 IEEE International Conference on Robotics and Automation (ICRA), 2016, 4392–4397. [Google Scholar]
- (350).Hong A; Petruska AJ; Zemmar A; Nelson BJ Magnetic Control of a Flexible Needle in Neurosurgery. IEEE Trans. Biomed, Eng 2021, 68, 616–627. [DOI] [PubMed] [Google Scholar]
- (351).Charreyron SL; Boehler Q; Danun AN; Mesot A; Becker M; Nelson BJ A Magnetically Navigated Microcannula for Subretinal Injections. IEEE Trans. Biomed, Eng 2021, 68, 119–129. [DOI] [PubMed] [Google Scholar]
- (352).Charreyron SL; Gabbi E; Boehler Q; Becker M; Nelson BJ A Magnetically Steered Endolaser Probe for Automated Panretinal Photocoagulation. IEEE Robot. Autom. Lett 2019, 4. [Google Scholar]
- (353).Ullrich F; Lussi J; Chatzopoulos V; Michels S; Petruska AJ; Nelson BJ A Robotic Diathermy System for Automated Capsulotomy. J. Med. Robot. Res 2017, 03, 1850001. [Google Scholar]
- (354).Leon L; Warren FM; Abbott JJ Optimizing the Magnetic Dipole-Field Source for Magnetically Guided Cochlear-Implant Electrode-Array Insertions. J. Med. Robot. Res 2018, 03, 1850004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (355).Hoshiar AK; Jeon S; Kim K; Lee S; Kim J.-y.; Choi H Steering Algorithm for a Flexible Microrobot to Enhance Guidewire Control in a Coronary Angioplasty Application. Micromachines 2018, 9, 617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (356).Jeon S; Hoshiar AK; Kim K; Lee S; Kim E; Lee S; Kim J.-y.; Nelson BJ; Cha H-J; Yi B-J et al. A Magnetically Controlled Soft Microrobot Steering a Guidewire in a Three-Dimensional Phantom Vascular Network. Soft Robot. 2018, 6, 54–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (357).Pancaldi L; Dirix P; Fanelli A; Lima AM; Stergiopulos N; Mosimann PJ; Ghezzi D; Sakar MS Flow Driven Robotic Navigation of Microengineered Endovascular Probes. Nat. Comm 2020, 11, 6356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (358).Lloyd P; Hoshiar AK; Veiga T. d.; Attanasio A; Marahrens N; Chandler JH; Valdastri P A Learnt Approach for the Design of Magnetically Actuated Shape Forming Soft Tentacle Robots. IEEE Robot. Autom. Lett 2020, 5, 3937–3944. [Google Scholar]
- (359).Martin JW; Scaglioni B; Norton JC; Subramanian V; Arezzo A; Obstein KL; Valdastri P Enabling the Future of Colonoscopy with Intelligent and Autonomous Magnetic Manipulation. Nat. Mach. Intell 2020, 2, 595–606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (360).Xu C; Yang Z; Lum GZ Small-Scale Magnetic Actuators with Optimal Six Degrees-of-Freedom. Adv. Mater 2021, 33, 2100170. [DOI] [PubMed] [Google Scholar]
- (361).Gu GX; Chen C-T; Buehler MJ De Novo Composite Design based on Machine Learning Algorithm. Extreme Mech. Lett 2018, 18, 19–28. [Google Scholar]
- (362).Gu GX; Chen C-T; Richmond DJ; Buehler MJ Bioinspired Hierarchical Composite Design using Machine Learning: Simulation, Additive Manufacturing, and Experiment. Mater. Horiz 2018, 5, 939–945. [Google Scholar]
- (363).Mao Y; He Q; Zhao X Designing Complex Architectured Materials with Generative Adversarial Networks. Sci. Adv 2020, 6, eaaz4169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (364).Jackle S; Eixmann T; Schulz-Hildebrandt H; Hüttmann G; Patz T Fiber optical shape sensing of flexible instruments for endovascular navigation. Int. J. Comput. Assist. Radiol. Surg 2019, 14, 2137–2145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (365).ISO 10993-5 Biological Evaluation of Medical Devices – Part 5: Tests for In Vitro Cytotoxicity. 2009.
- (366).ISO 10993-12 Biological Evaluation of Medical Devices – Part 12: Sample Preparation and Reference Materials. 2012.
- (367).ISO 10993-1 Biological Evaluation of Medical Devices – Part 1: Evaluation and Testing within a Risk Management Process. 2018.
- (368).ISO 10993-4 Biological Evaluation of Medical Devices – Part 4: Selection of Tests for Interactions with Blood. 2017.
- (369).U.S. Food and Drug Administration (FDA), Center for Devices and Radiological Health Use of International Standard ISO 10993-1, “Biological Evaluation of Medical Devices - Part 1: Evaluation and Testing within a Risk Management Process”. 2016. [Google Scholar]
- (370).Yoda R Elastomers for Biomedical Applications. J. Biomater. Sci. Polym. Ed 1998, 9, 561–626. [DOI] [PubMed] [Google Scholar]
- (371).Fallahi D; Mirzadeh H; Khorasani MT Physical, Mechanical, and Biocompatibility Evaluation of Three Different Types of Silicone Rubber. J. Appl. Polym. Sci 2003, 88, 2522–2529. [Google Scholar]
- (372).Rahimi A; Mashak A Review on Rubbers in Medicine: Natural, Ssilicone and Polyurethane Rubbers. Plast. Rubber Compos 2013, 42, 223–230. [Google Scholar]
- (373).Rajan KP; Al-Ghamdi A; Parameswar R; Nando GB Blends of Thermoplastic Polyurethane and Polydimethylsiloxane Rubber: Assessment of Biocompatibility and Suture Holding Strength of Membranes. Int. J. Biomater 2013, 2013, 240631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (374).Alexandre N; Ribeiro J; Gärtner A; Pereira T; Amorim I; Fragoso J; Lopes A; Fernandes J; Costa E; Santos-Silva A et al. Biocompatibility and Hemocompatibility of Polyvinyl Alcohol Hydrogel used for Vascular Grafting—In Vitro and In Vivo Studies. J. Biomed. Mater. Res. A 2014, 102, 4262–4275. [DOI] [PubMed] [Google Scholar]
- (375).Donohue VE; McDonald F; Evans R In Vitro Cytotoxicity Testing of Neodymium-Iron-Boron Magnets. J. Appl. Biomater 1995, 6, 69–74. [DOI] [PubMed] [Google Scholar]
- (376).Francis A; Yang Y; Virtanen S; Boccaccini AR Iron and Iron-based Alloys for Temporary Cardiovascular Applications. J. Mater. Sci. Mater. Med 2015, 26, 138. [DOI] [PubMed] [Google Scholar]
- (377).Eliaz N Corrosion of Metallic Biomaterials: A Review. Materials 2019, 12, 407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (378).Li Y; Qi Z; Yang J; Zhou M; Zhang X; Ling W; Zhang Y; Wu Z; Wang H; Ning B et al. Origami NdFeB Flexible Magnetic Membranes with Enhanced Magnetism and Programmable Sequences of Polarities. Adv. Func. Mater 2019, 29, 1904977. [Google Scholar]
- (379).Bondemark L; Kurol J; Wennberg A Orthodontic Rare Earth Magnets—In Vitro Assessment of Cytotoxicity. Br. J. Orthod 1994, 21, 335–341. [DOI] [PubMed] [Google Scholar]
- (380).Hopp M; Rogaschewski S; Groth T Testing the cytotoxicity of metal alloys used as magnetic prosthetic devices. J. Mater. Sci. Mater. Med 2003, 14, 335–345. [DOI] [PubMed] [Google Scholar]
- (381).Gunduz S; Albadawi H; Oklu R Robotic devices for minimally invasive endovascular interventions: a new dawn for interventional radiology. Adv. Intell 3, 2000181. [Google Scholar]
- (382).Moghimi SM; Andersen AJ; Ahmadvand D; Wibroe PP; Andresen TL; Hunter AC Material properties in complement activation. Adv. Drug Deliv. Rev 2011, 63, 1000–1007. [DOI] [PubMed] [Google Scholar]
- (383).Natali CD; Beccani M; Valdastri P Real-Time Pose Detection for Magnetic Medical Devices. IEEE Trans. Magn 2013, 49, 3524–3527. [Google Scholar]
- (384).Chao H; Max Qinghu M; Mandal M Efficient Magnetic Localization and Orientation Technique for Capsule Endoscopy. 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2005, 628–633. [Google Scholar]
- (385).Hu C; Meng MQ; Mandal M The Calibration of 3-Axis Magnetic Sensor Array System for Tracking Wireless Capsule Endoscope. 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2006, 162–167. [Google Scholar]
- (386).Turan M; Almalioglu Y; Gilbert HB; Mahmood F; Durr NJ; Araujo H; Sari AE; Ajay A; Sitti M Learning to Navigate Endoscopic Capsule Robots. IEEE Robot. Autom. Lett 2019, 4, 3075–3082. [Google Scholar]
- (387).Laulicht B; Gidmark NJ; Tripathi A; Mathiowitz E Localization of Magnetic Pills. Proc. Natl. Acad. Sci. U. S. A 2011, 108, 2252–2257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (388).Liu X The More and Less of Electronic-Skin Sensors. Science 2020, 370, 910–911. [DOI] [PubMed] [Google Scholar]
- (389).Sim K; Rao Z; Ershad F; Yu C Rubbery Electronics Fully Made of Stretchable Elastomeric Electronic Materials. Adv. Mater 2020, 32, 1902417. [DOI] [PubMed] [Google Scholar]
- (390).Muth JT; Vogt DM; Truby RL; Mengüç Y; Kolesky DB; Wood RJ; Lewis JA Embedded 3D Printing of Strain Sensors within Highly Stretchable Elastomers. Adv. Mater 2014, 26, 6307–6312. [DOI] [PubMed] [Google Scholar]
- (391).Truby RL; Wehner M; Grosskopf AK; Vogt DM; Uzel SGM; Wood RJ; Lewis JA Soft Somatosensitive Actuators via Embedded 3D Printing. Adv. Mater 2018, 30, 1706383. [DOI] [PubMed] [Google Scholar]
- (392).Wang Y; Zhu C; Pfattner R; Yan H; Jin L; Chen S; Molina-Lopez F; Lissel F; Liu J; Rabiah NI et al. A Highly Stretchable, Transparent, and Conductive Polymer. Sci. Adv 2017, 3, e1602076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (393).Lu B; Yuk H; Lin S; Jian N; Qu K; Xu J; Zhao X Pure PEDOT:PSS Hydrogels. Nat. Comm 2019, 10, 1043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (394).Yuk H; Lu B; Lin S; Qu K; Xu J; Luo J; Zhao X 3D Printing of Conducting Polymers. Nat. Comm 2020, 11, 1604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (395).Truby RL; Santina CD; Rus D Distributed Proprioception of 3D Configuration in Soft, Sensorized Robots via Deep Learning. IEEE Robot. Autom. Lett 2020, 5, 3299–3306. [Google Scholar]
- (396).Santina CD; Truby RL; Rus D Data–Driven Disturbance Observers for Estimating External Forces on Soft Robots. IEEE Robot. Autom. Lett 2020, 5, 5717–5724. [Google Scholar]
- (397).Stottlemire BJ; Miller JD; Whitlow J; Huayamares SG; Dhar P; He M; Berkland CJ Remote Sensing and Remote Actuation via Silicone–Magnetic Nanorod Composites. Adv. Mater. Technol 2021, 6, 2001099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (398).Culha U; Demir SO; Trimpe S; Sitti M Learning of Sub-optimal Gait Controllers for Magnetic Walking Soft Millirobots. Robot. Sci. Syst 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (399).Hafeli U The History of Magnetism in Medicine In Magnetism in Medicine, 2nd ed.; Wilfried A;Nowak H, Eds.; Wiley-VCH, 2006. [Google Scholar]
- (400).Tillander H Magnetic Guidance of a Catheter with Articulated Steel Tip. Acta Radiol. 1951, 35, 62–64. [DOI] [PubMed] [Google Scholar]
- (401).Alksne JF Magnetically Controlled Intravascular Catheter. Surgery 1968, 64, 339–345. [PubMed] [Google Scholar]
- (402).Yodh SB; Pierce NT; Weggel RJ; Montgomery DB A New Magnet System for ‘Intravascular Navigation’. Med. Biol. Eng 1968, 6, 143–147. [DOI] [PubMed] [Google Scholar]
- (403).Molcho J; Karny HZ; Frei EH; Askenasy HM Selective Cerebral Catheterization. IEEE Trans. Biomed, Eng 1970, 17, 134–140. [DOI] [PubMed] [Google Scholar]
- (404).Cares HL; Hale JR; Montgomery DB; Richter HA; Sweet WH Laboratory Experience with a Magnetically Guided Intravascular Catheter System. J. Neurosurg 1973, 38, 145–154. [DOI] [PubMed] [Google Scholar]
- (405).Hilal SK; Michelsen WJ; Driller J; Leonard E Magnetically Guided Devices for Vascular Exploration and Treatment. Radiology 1974, 113, 529–540. [DOI] [PubMed] [Google Scholar]
- (406).Ram W; Meyer H Heart Catheterization in a Neonate by Interacting Magnetic Fields: A New and Simple Method of Catheter Guidance. Catheter. Cardiovasc. Interv 1991, 22, 317–319. [DOI] [PubMed] [Google Scholar]
- (407).Grady MS; Howard MA; Dacey RG; Blume W; Lawson M; Werp P; Ritter RC Experimental Study of the Magnetic Stereotaxis System for Catheter Manipulation within the Brain. J. Neurosurg 2000, 93, 282–288. [DOI] [PubMed] [Google Scholar]
- (408).Frickel S; Gross N A General Theory of Scientific/Intellectual Movements. Am. Sociol. Rev 2005, 70, 204–232. [Google Scholar]
- (409).Hawkes EW; Majidi C; Tolley MT Hard Questions for Soft Robotics. Sci. Robot 2021, 6, eabg6049. [DOI] [PubMed] [Google Scholar]


