Abstract
Complex networks have been used widely to model a large number of relationships. The outbreak of COVID-19 has had a huge impact on various complex networks in the real world, for example global trade networks, air transport networks, and even social networks, known as racial equality issues caused by the spread of the epidemic. Link prediction plays an important role in complex network analysis in that it can find missing links or predict the links which will arise in the future in the network by analyzing the existing network structures. Therefore, it is extremely important to study the link prediction problem on complex networks. There are a variety of techniques for link prediction based on the topology of the network and the properties of entities. In this work, a new taxonomy is proposed to divide the link prediction methods into five categories and a comprehensive overview of these methods is provided. The network embedding-based methods, especially graph neural network-based methods, which have attracted increasing attention in recent years, have been creatively investigated as well. Moreover, we analyze thirty-six datasets and divide them into seven types of networks according to their topological features shown in real networks and perform comprehensive experiments on these networks. We further analyze the results of experiments in detail, aiming to discover the most suitable approach for each kind of network.
Keywords: Link prediction, Complex networks, Data mining, Network analysis
Introduction
With the development of network analysis, many complex systems can be described as networks [1]. Networks are a natural and powerful tool for characterizing a large number of social, biological, and information systems composed of interacting elements, and network science is one of the most active interdisciplinary fields of research today. A typical network consists of nodes and edges, where nodes denote various entities in real systems and edges represent the relationships between entities. Treating individuals as nodes for example, and associations between corresponding persons as edges, social relations could be abstracted as a network. Protein–protein interactions form a network where nodes denote proteins and edges denote interactions among them. In addition, the hyperlink structure of the Internet can be modeled as a directed graph. These complex networks have many significant statistical properties, such as the small-world effects and the scale-free properties.
Related Works A number of problems related to complex networks are being studied, including community detection and structural network analysis. In recent years, link prediction on complex networks attracts more and more concerns. Link Prediction is a fundamental problem that attempts to estimate the likelihood of the existence of a link between two nodes [2], which makes it easier to understand the association between two specific nodes and how the entire network evolves.
The problem of link prediction over complex networks can be categorized into two classes. One is to reveal the missing links. The other is to predict the links that may exist in the future as the network evolves [3]. Previous studies [4–6] suggest that there may be mechanisms to guide the formation of networks; it is therefore important to investigate the evolution of networks, as well as networks’ characteristics and structures.
Link prediction has been widely applied to a variety of fields. In biology, it is used to predict unobserved links in PPI (protein–protein interaction) networks [7–10]. In terms of social networks [11–13], link prediction algorithms help to recommend friends with similar interests or goods that one may purchase [14]. There have been several reviews on link prediction analysis in social networks [15–17]. As for the Internet, researchers use link prediction to realize web page personalization [18].
There are a large number of link prediction methods. Malhi et al [19] give a review on various link prediction algorithms. It focuses on evaluating shortcomings of link prediction methods. However, it does not provide any evaluation results, and the information it provides is rather limited. Lü et al [2] present an excellent survey by summarizing different approaches; introducing typical applications; and outlining future challenges of link prediction algorithms. However, the methods presented in this paper are somewhat antiquated. Martínez et al [20] add to the review of some more recent methods, as well as a more detailed experimental comparison of the similarity-based methods, while the specific data used for the experiments are not analyzed or categorized. As experimentally demonstrated in this survey, it is difficult to give a method that has the best performance in all complex networks, which strongly depends on the structural properties of the network. Therefore, an empirical study of discovering the most suitable link prediction methods for different kinds of networks is desirable. To the best of our knowledge, we are the first to review link prediction methods, including the state-of-the-art network embedding-based methods, on top of a comprehensive evaluation result.
Contributions The evaluation comparison of the most advanced network embedding-based link prediction methods is included in this paper, as well as other popular traditional methods. We also summarize and analyze the trade-offs among different methods. This work has greatly compensated for the shortcomings of previous research articles. In this work, we divide the complex networks involved in some common applications into seven categories and analyze their characteristics by calculating their attributes. The structural features of different kinds of networks are also extracted. On the basis of comprehensive experiments, we recommend appropriate link prediction methods for each type of networks.
In this study, we focus on the link prediction problem on undirected networks which can be formulated as follows. Consider an undirected network G(V, E), where V represents a set of nodes and E stands for a set of edges. Using U to denote the set of all possible links, the target of link prediction is to infer the missing links or links that will arise in the future in . Our contributions are summarized as follows:
A rational categorizing for link prediction methods is suggested, and a thorough study of the representative link prediction approaches and methods, including the state-of-the-art network embedding-based methods, is performed. Due to the emergence of the large number of the network embedding (graph representation learning)-based methods in recent years, we are not able to make a comprehensive summary of them all. Instead, we selected several representative methods for investigation, reflecting the commonness of this kind of methods. The characteristics of these methods are summarized and compared (Sect. 2)
We present the properties used to classify complex networks and introduce the characteristics of each type. A new taxonomy of complex networks is then proposed (Sect. 3)
To the best of our knowledge, this survey is the first comprehensive evaluation of a broad spectrum of link prediction methods and includes the evaluation comparison of the state-of-the-art network embedding methods. A mass of real datasets are comprehensively tested to compare a large number of link prediction methods. A rounded analysis is conducted according to the experimental results for each type of networks, which is able to give instructional selection advice for different link prediction tasks (Sect. 4)
Methods for Link Prediction
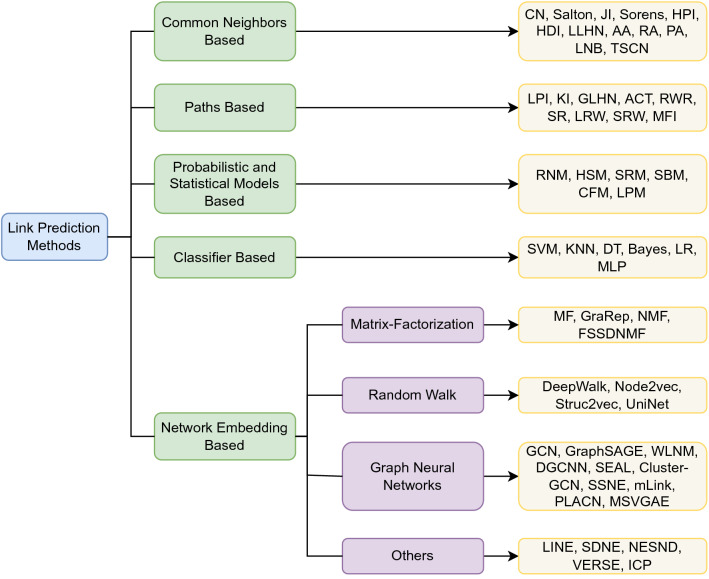
Researchers have proposed a variety of link prediction techniques, ranging from the simplest heuristic methods of counting common neighbors between two nodes to the current popular network embedding-based methods. Most of them calculate the similarities or the probabilities of forming links between nodes by capturing the structural features of the network. In this section, we perform a comprehensive overview of representative link prediction approaches and propose a new taxonomy for link prediction methods (as shown in Fig. 1), including common neighbor-based, path-based, probabilistic and statistical models-based, classifier-based, and network embedding-based methods. In Sect. 2.6, a more detailed comparison among different methods are given, including time complexity and scalability, etc. Table 1 explains the meaning of the common notations that will be used in this survey.
Fig. 1.
Taxonomy for link prediction methods
Table 1.
A summary of common notations
| G(V, E) | Undirected network |
|---|---|
| V | Set of nodes |
| E | Set of edges |
| n | Number of nodes |
| m | Number of edges |
| Similarity score of node x and node y | |
| Maximum degree of a network | |
| Minimal degree of a network | |
| d(v) | Number of edges connecting to node v |
| Set of neighbors of node x | |
| l | Number of random walk steps |
| L | Laplacian matrix |
| S | Similarity matrix |
| M | Direct similarity |
| A | Adjacent matrix |
| I | Identity matrix |
| Parameters | |
| P | Transition probability matrix |
| Probability of a walker starting from x and locating at y |
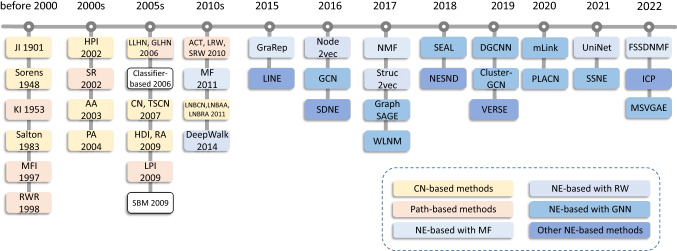
The timeline for the development of link prediction methods is organized in Fig. 2. As can be seen from the figure, before 2010, the traditional link prediction methods were the mainstream methods, such as common neighbor-based and path-based methods, which were widely applied because of their simplicity, interpretability, high efficiency, and high accuracy. However, these methods fail to make full use of nodes and network structure information. With the rapid development of Internet technology and big data, the scale of the network continues to expand. The traditional adjacency matrix representing graph structure information presents high-dimensional and sparse characteristics, which poses a challenge to the research on large-scale networks. Probabilistic and statistical-based methods are time-consuming and computationally expensive, making them unsuitable for large-scale networks. Classifier-based methods [21] face class imbalance due to the sparsity of real networks, that is, the number of nonexistent links between nodes far exceeds the number of existing links. The network embedding methods, also known as graph representation learning, effectively address the deficiencies of the traditional methods. Using the network embedding methods with powerful representation ability, on the premise of retaining the network structure information, the nodes are mapped into the low-dimensional space, and the low-dimensional and dense continuous feature vector representation of each node is obtained. DeepWalk [22] is the first method to use deep learning for network embedding. It obtains a linear sequence of network structure through random walk and further uses the SkipGram model in word representation learning to learn the representation of nodes in the network. On the basis of DeepWalk, after 2015, with the development of graph representation learning, more and more network embedding methods have been applied to link prediction tasks. As a representative class of methods, the graph neural network methods are extremely effective methods to solve the problem of graph learning by adding graph operations to the traditional deep learning model and applying the structural information and attribute information of the graph to deal with the complexity of graph data.
Fig. 2.
Timeline of link prediction methods
Methods Based on Common Neighbor
Common neighbor(CN)-based methods assign a score for each pair of nodes x and y, which is proportional to the probability that there exists an edge between x and y. It is an apparent intuition that two nodes x and y are more likely to form a link in the future, if their neighbors have large overlap. The simplest technique of measuring common neighbor is counting the shared neighbors directly which is called Common Neighbors (CN). As a basis of research work presented later, it is also applied to the study of graph streams [23] and dynamic social networks [24]. It can be computed as Equation (1). For a node x, let denote the neighbors of x in G(V, E).
Other representative methods of calculating based on common neighbor are Salton Index (Salton) [25], Jaccard Index (JI) [26], Sørensen Index (Sørensen) [27], Hub Promoted Index (HPI) [28], Hub Depressed Index (HDI) [29], Local Leicht–Holme–Newman (LLHN) [30], Adar-Adamic Index (AA) [13], Resource Allocation (RA) [29], Preferential Attachment (PA) [31]. In summary, these metrics are variations based on the CN method, which are normalized or take into account the importance of neighbors in order to minimize biases due to node degree skewness. They are calculated as follows.
Local Naive Bayes (LNB) [32] It is a method based on the Bayesian theory, while combining the idea that different shared neighbors play different roles. The formula of the connection likelihood is
| 11 |
where f has three forms, which are , , and , corresponding to the CN, AA and RA measurements, respectively. In Equation (11), a is a constant for a given training set and is the role function of the node w, which can be defined as in [20]:
| 12 |
Transfer Similarity (TS) [33] Direct similarities are less accurate when a network is sparse. Thus, transfer similarity that properly integrates the high-order correlations is proposed [34]. The self-consistent definition of this index is
| 13 |
where M represents the direct similarity, such as common neighbor (TSCN) or Pearson correlation coefficient, and is the rate of information aging when the information is further transferred.
Methods Based on Path
The common neighbor-based approaches ignore the global similarities between nodes and can only capture limited local structural information. In contrast, the path-based methods formulate similarity measurements according to the paths between nodes and take care of more high-order information, which greatly alleviate the previous problem. We let measure the possibility of the appearance of a link between x and y which has the same meaning as in Sect. 2.1. In this subsection, A, I, and S represent the adjacent matrix, identity matrix, and similarity matrix of G(V, E), respectively.
Katz Index (KI) [35] Katz index is defined as
| 14 |
where is the number of the l-length paths between nodes x and y, and is a damping factor used to control the attenuation pace (). The Katz index for all pairs of nodes can be computed by
| 15 |
Local Path Index (LPI) [3] This index takes local paths into consideration [20]. It reduces the complexity of Katz index at the cost of accuracy by only focusing on the paths whose length are 2 or 3, which can be defined as
| 16 |
where is a free parameter like .
Global Leicht–Holme–Newman (GLHN) [30] The definition of this index consists of two parts: the neighbor term, and the self similarity. The initial guess is
| 17 |
where is the Korenecker’s function [36], while and are free parameters that control the balance of the two parts.
Local Random Walk (LRW) [37] Random walk is a process that a walker starts from a source and chooses one of the neighbors randomly as his next step [11]. It can be described by a Markov chain and its transition probability matrix. We use P to denote the transition probability matrix, and to denote the probability that a walker starts from node x and reaches the node y after l steps [37]; thus We have
| 18 |
where is a vector of length |V| with the x-th element equals to 1 and others to 0.
The similarity is calculated as
| 19 |
It reduces the computational cost by limiting the random walk steps l. A shortcoming of this metric is its sensitivity to the regions far away from the target [11].
Superposed Random Walk (SRW) [37] To counteract the dependency of local random walk, Liu et al proposed to continuously release the walkers at the source. By superposing the contribution of each walker, the similarity index is
| 20 |
Random Walk with Restart (RWR) [38] Staring from a node in G, each step has two choices: return to the source node with probability or go to its neighbors randomly with probability . There is an iterative equation:
| 21 |
where is a vector whose term is the probability of the walker locating at the corresponding node when the walking process reaches a steady state, while is a vector of length n with the x-th element equals to 1 and others to 0. Finally, use denotes the probability of a random walker starting from x and locating at y in the steady state, and the random walk with restart similarity is defined as
| 22 |
Average Commute Time (ACT) [37] The average commute time between x and y is the sum of the average steps from x to y, and from y to x, which can be computed by the pseudoinverse of the Laplacian matrix . Therefore, the average commute time can be expressed as
| 23 |
SimRank (SR) [39] Suppose two random walkers start from x and y, respectively, this index reflects the time that they are expected to meet. A recursive equation for is
| 24 |
where C is a constant between 0 and 1.
Others Matrix Forest Index (MFI) [40]: This index is also a method of calculating similarities and is proposed based on matrix-forest theorem which can be written as
| 25 |
Methods Based on Probabilistic and Statistical Models
Probabilistic and statistical methods provide a way to extract the underlying structure from a network. They build a model and estimate the model parameters which can best fit the data of the network, and then predict the formation probability of the missing links. These methods are highly time-consuming for model training, so they are impractical for large networks. Moreover, they only have mediocre prediction results. On the other hand, they do provide valuable insights into the network structure. Based on the above considerations, we only conduct experiments on the stochastic block model (SBM) as a representative.
Stochastic Block Model (SBM) [41]: In a stochastic block model, nodes are divided into different groups and the probability that two nodes are connected relies only on the groups which they belong to. This model is based on three properties: Nodes in real networks (1) are usually organized in communities, (2) play distinct roles, and (3) connect to each other based on these rules. The probability that a link truly exists requires to calculate all possible partitions of the network. Thus, Metropolis sampling algorithm [42] can be used to correctly sample relevant partitions and obtain an estimation of the link probability in practice. When the number of possible partitions is very large, this approach is computationally expensive.
Others Here is a brief introduction of other selective probabilistic and statistical-based methods. Relational network model (RNM) [17, 43] is originally designed for attribute prediction over a database. Due to the difference of trained models, RNM can be divided into Relational Bayesian Networks (RBN) [44], Relational Markov Networks (RMN) [45] and Relational Dependency Networks (RDN) [46]. Hierarchical structure model (HSM) [47] is suitable for networks which exhibit hierarchical organizations such as metabolic networks. In Stochastic Relational Model (SRM) [48], the relationships between nodes are modeled by a tensor interaction of multiple Gaussian processes. Huang [49] proposes a framework of predicting links, cycle formation model (CFM), based on the cycle formation which relates to the generalized clustering coefficient measure. Local probabilistic model (LPM) [50] learns a local Markov random field model constrained on non-derivable frequent itemsets from the local neighborhood and forms the co-occurrence probability feature.
Methods Based on Classifier
Link prediction can be studied as a supervised or semi-supervised learning task. A plethora of classification algorithms are applicable for link prediction [21]. Choosing appropriate features is the most critical part of a supervised learning algorithm. Due to the large number of classification methods, we choose six representative classifiers for evaluation, including Support Vector Machine (SVM) [51], K-Nearest Neighbors (KNN) [52], Decision Tree (DT) [53], Naive Bayes (Bayes) [54], Logistic Regression (LR) [55], and Multilayer Perceptron (MLP) [56], where the training features include the indices mentioned in Sects. 2.1 and 2.2 . The indices with a high time complexity are not considered, such as TS, GLHN, SRW, RWR, ACT, SR, and MFI. Other classifier based methods are introduced as follows.
Hasan et al [21] choose proximity features, aggregated features, and topological features. Lichtenwalter et al [57] provide a general, high-performance supervised framework for the prediction task, and try to overcome the imbalance by oversampling and undersampling. De Sá et al [58] use the metrics computed from the network structure, and the weights of links are taken into consideration. In addition, Doppa et al [59] propose a learning algorithm based on the chance constrained programs which exhibit all the properties needed for a good link predictor. The idea of Chen et al [60] is to reduce the computation cost by combining multiple classifiers while maintaining the accuracy of predictions.
Kashima et al [61] propose a semi-supervised link prediction method called Link Propagation by applying the label propagation technique, where the Kronecker sum similarity is used as the similarity matrix. However, the time complexity and the space complexity makes it unrealistic to deal with large networks. Raymond et al [62] extend the semi-supervised learning algorithm [61] to solve the link prediction problem approximately on large-scale dynamic graphs by using a non-trivial combination of techniques in the linear algebra. Moreover, Zeng et al [63] give a new semi-supervised learning approach SLiPT. The entire algorithm is based on the temporal features.
Methods Based on Network Embedding
The emergence of large-scale complex networks has led to dimensionality explosion, so network embedding(NE)-based methods are needed to reduce the dimensionality, and capture the charactersitcis and attributes of the network at the same time; therefore they can be applied to link prediction. Different from the traditional adjacency matrix, network embedding aims to effectively preserve rich topological and structural information such as links, neighbors, and high-order proximities [64, 65] by embedding nodes into a low-dimensional space to predict the possible future links. The previous high-dimensional sparse feature vectors can be represented by the low-dimensional dense embedding vectors.
A good network embedding method should be able to capture the internal structure of the network well to predict the possible future links. We divide network embedding methods into shallow and deep network embedding techniques according to their different encoding methods. It can also be subdivided into matrix factorization based, random walk based, graph neural network based, and other methods.
Network Embedding with Matrix Factorization
The traditional algorithms of network embedding consider the problem of network embedding as matrix decomposition or matrix dimensionality reduction, and reduce the dimensionality of the adjacency matrix of the graph by matrix decomposition or singular value decomposition, so that the original network structure can be easily restored by learning the embedding vectors. Matrix factorization-based network embedding is widely applied to recommender systems [66]. It represents the attributes of the network (such as the similarities of node pairs) in the form of a matrix, which is factored to obtain node embeddings. Inspired by traditional dimensionality reduction techniques, network embedding can be regarded as a dimensionality reduction problem with retained structure.
MF [67] Menon and Elkan propose a latent feature learning method which extends matrix factorization to solve structural link prediction problems in graphs. It extracts the latent features of nodes and use them for prediction tasks. The similarity matrix S is factorized to
| 26 |
where we have , , and is a link function. Each node x will have a latent vector , where k is the number of latent features [67, 68]. The similarity is calculated as
| 27 |
GraRep [69] It considers the k order (k>2) similarity. Although GraRep can get the node representation with stronger expression ability, it takes a lot of time to calculate the power of a matrix and SVD. GraRep similarly exploits node co-occurrence information at different scales by raising the graph adjacency matrix to different powers. Singular value decomposition (SVD) is applied to the powers of the adjacency matrix to obtain a low-dimensional representation of nodes.
FSSDNMF [70] To address the network noise problem, a novel link prediction model based on deep nonnegative matrix factorization is proposed, which elegantly fuses topological and sparse constraints to perform the link prediction task. The observed link information of each hidden layer is fully exploited by deep nonnegative matrix factorization. The similarity score is then calculated and mapped to a multilayer low-dimensional latent space using the common neighbor method to obtain topological information for each hidden layer. At the same time, a norm-constrained factor matrix is used at each hidden layer to remove random noise.
In practical applications, nonnegative matrix factorization (NMF) and singular value decomposition (SVD) are usually used to get the approximation of S, whose time complexity is . Duan et al [71] applied the structural bagging to decompose the link prediction problem into smaller pieces, and use NMF to factorize the adjacency matrix, which addresses the top-k problem in link prediction.
Network Embedding with Random Walk
Only decomposing the adjacency matrix can only take into account the influence of the direct neighbor on the current node, which is very limited. Random walk is used to generate the context of nodes which makes up for the deficiency of matrix factorization. Then the node sequences can be treated as sentences to take advantage of natural language processing methods to get node embeddings. Under this circumstance, the more times two nodes appear in the same random walk, the more similar their embeddings will be.
DeepWalk [22] This method is the pioneering work to learn nodes’ vector representations using random walks which obtains local information by truncated random walks to generate the context of nodes and thereby learns latent representations by treating node sequences as sentences. It provides a new idea for network embedding algorithms, which is often used as a benchmark model for this kind of method. By performing random walks on the network, the node sequence is obtained, and the vector representation of the node is learned by using the skip-gram model in natural language processing.
Node2vec [72] Grover et al proposed Node2vec, which learns continuous feature representations of nodes. It further utilizes a biased random walk strategy that combines breadth-first search(BFS) and depth-first search(DFS) neighborhood exploration to capture a more flexible contextual structure on the basis of DeepWalk. Nodes that are “close” in the network will tend to be “close” in the latent representation space.
Struc2vec [73] Struc2vec pays attention to the structural identity and uses a hierarchical metric to measure node similarity at different scales by constructing a weighted multilayer graph to generate context. It defines vertex similarity from the perspective of spatial structural similarity.
UniNet [74] The existing network embedding models based on random walk are unified into an optimized framework which can be effectively used for large-scale network. The Metropolis-Hastings sampling is adopted for edge sampling, which greatly improves the efficiency of random walk generation in network representation learning model.
However, the above approaches merely provide the embedding vectors for subsequent analysis tasks, and we still need to apply similarity calculation and so on for link prediction. For example, Euclidean distance, standardized Euclidean distance, Chebyshev distance, and cosine distance can be used to compute the similarities. In a previous set of experiments, we have evaluated the results of using different distance metrics in different network embedding methods for link prediction. The results did not reflect a significant influence among different distance metrics. Since cosine similarity is the most commonly used metric in network embedding literature, we apply cosine distance between two nodes to quantify their similarities in this work as well.
Network Embedding with Graph Neural Networks
Graph neural networks (GNNs) are proposed based on convolutional neural networks (CNNs) and graph embedding. Firstly, traditional CNNs can only operate on regular Euclidean space-based data such as images and text, while complex networks are non-Euclidean data structures. Secondly, although shallow encoding methods such as DeepWalk and Struc2vec have achieved breakthroughs in graph embedding, many of them still suffer from their shallow learning mechanisms, the network embedding quality can hardly be further improved. Thus GNNs are brought forward to solve the above problems [75]. There are three most popular downstream graph analysis tasks, namely node classification, graph classification, and link prediction. While there is abundant literature on the first two, GNNs for link prediction is relatively less studied and less understood. The following lists some representative methods of them.
Graph Convolutional Networks(GCN) [76] This model is based on an efficient variant of CNNs for semi-superivised learning on graph data. It learns hidden layer representations that encode both local graph structure and features of nodes, so that we can use these characteristics to complete the tasks such as node classification, graph classification, and link prediction.
GraphSAGE [77] It is an inductive learning framework that can efficiently generate the unknown vertex embedding vectors by learning a function that aggregates the neighbor vertices.
WLNM [78] This is a new link prediction framework proposed to automatically learn network topology features. The framework first extracts a enclosing subgraph for each target link, and then encodes the subgraph into an adjacency matrix. Finally, the neural network is trained on these adjacency matrices and the prediction model is learned. A fast hashing-based Weisfeiler-Lehman (WL) algorithm is proposed to mark vertices according to their structural roles in subgraph while preserving the inherent directionality of the subgraph.
DGCNN [79] Zhang et al proposed a novel end-to-end deep learning architecture for graph classification, called Deep Graph Convolutional Neural Network. Since features can be extracted using a novel spatial graph convolution layer, it also can be used for link prediction. It learns from the topology of the global graph by sorting vertex features rather than adding them together, which is supported by the new SortPooling layer.
SEAL [80] SEAL extracts local subgraphs that preserve rich information and learns heuristics suitable for the current graph by a GNN. It will obtain a function that takes local enclosing subgraphs as input and outputs the possibility that the links exist. SEAL is flexible with which GNN or node embeddings to use. We follow the default setting of original paper, that is, choose DGCNN as the default GNN and select Node2vec as the default embeddings.
Cluster-GCN [81] It is an efficient algorithm for training deep and large GCN. Cluster-GCN works as the following: at each step, it samples a block of nodes that associate with a dense subgraph identified by a graph clustering algorithm, and restricts the neighborhood search within this subgraph. This simple but effective strategy has made significantly improvement on memory and computational efficiency, while being able to achieve comparable test accuracy with previous algorithms.
Others [82] introduces Attention Mechanisms into Graph Neural Networks which is called GAT. Each layer learns the contribution of each neighbor of the node to its new feature generation, and aggregates the neighbor features according to the contribution degree to generate new aggregated features for downstream tasks. Cai et al [83] introduce a new method for node aggregation, mLink, which can transform the enclosing subgraph to different scales while preserving the network structure information, thus providing supplementary information for link prediction. In order to solve low accuracy on some networks, [84] proposed a method of extracting subgraph for target link based on common neighbors on the basis of WLNM and SEAL, which is called PLACN. After labeling the extracted subgraphs based on the average hop number and average weight, the feature matrix is constructed and finally the convolutional neural network is trained. Guo et al [85] proposes a novel graph embedding framework, called Multiscale Variational Graph Autoencoder (MSVGAE), which learns multiple sets of low-dimensional vectors of different dimensions to represent the mixed probability distribution of the original graph data by the graph encoder. Perform multiple sampling on each dimension. In addition, a self-supervised learning strategy (ie, graph feature reconstruction-assisted learning) is introduced to make full use of graph attribute information to help graph structure learning.
GNNs have become powerful tools for learning over graph-structured data since they showed up, and have been successfully used in link prediction as well. A large number of experiments show that GNN-based methods can learn more effective link representations than previous methods.
Other Methods
We present other representative network embedding-based methods which can hardly be divided into any of the previous categories in the last subsection.
LINE [86] This method learns a d-dimensional feature representations in two separate phases. In the first phase, it learns d/2 dimensions by BFS-style simulations over immediate neighbors of nodes. In the second phase, it learns the next d/2 dimensions by sampling nodes strictly at a 2-hop distance from the source nodes. Additionally, it adopts negative sampling [87] to optimize the skip-gram model, compared with the hierarchical softmax [88] used in DeepWalk.
SDNE [89] This algorithm extends the traditional deep autoencoder to preserve the proximity between 2-hop neighbors. It is the first method to introduce the deep learning model into the network representation learning which optimizes first-order and second-order similarity simultaneously. It learns node representations using semi-supervised learning. On the one hand, supervised learning is used to get the local structure from the adjacency matrix to achieve the first-order similarity. On the other hand, unsupervised learning is used to obtain the global structure to meet the second-order similarity. In this way, SDNE can preserve the highly-nonlinear local-global network structure well and address sparsity problems.
NESND [90] It compares the structural similarity algorithm and the network embedding algorithm. On this basis, Cao et al present a new method to supplement local structure information with network embedding algorithm. While this method is only a combinatorial optimization of the existing methods, its characteristics are not listed separately.
VERSE [91] Tsitsulin et al propose a scalable algorithm for graph embeddings, which is extremely efficient and can reach linear time complexity. It falls in between deep learning approaches and the direct decomposition of the similarity matrix. It explicitly learns the distribution of any chosen vertex similarity measure for each graph vertex by training an expressive single-layer neural network.
ICP [93] A novel link prediction method ICP based on inductive matrix completion is proposed, which recovers the node connection probability matrix by applying node features to a low-rank matrix. The method first explores comprehensive node feature representations by combining different structural topology information with node importance attributes through feature construction and selection. The selected node features are then used as input for a supervised learning task of solving low-rank matrices. The node connection probability matrix is finally recovered by a bilinear function that predicts the connection probability between two nodes and its features and a low-rank matrix.
Summary
In this section, a new taxonomy is proposed to scientifically divide link prediction methods into five categories. As far as we know, there has been no experimental survey of network embedding-based link prediction methods, especially GNN based, which have currently widely been used for a variety of tasks. In order to address this problem, we have carried out an extensive experimental study on network embedding methods, which are refined to matrix decomposition based, random walk based, graph neural network based, etc. Table 2 provides a clear comparison among the methods from multiple perspectives and offers instructive suggestions for method selection by summarizing the common characteristics of different methods. It can be learned whether the method captures local or global topology information from the aspect of preserved proximity. The time complexities of the link prediction methods mentioned in this section are shown in the fourth column, where “-” indicates that there is no clear time complexity to refer to. The S column stands for the scalability of a method, which is limited by the memory requirements and time costs needed for training. The last column represents the learning models of the methods.
Table 2.
A summary of methods
| Category | Method | Preserved proximity | Time complexity | S | Learning model |
|---|---|---|---|---|---|
| Common neighbor based | order | Unsupervised | |||
| AA [13], RA [29], LNBAA [32], LNBRA [32] | order | Unsupervised | |||
| TSCN [33] | order | Unsupervised | |||
| Path Based | LPI [3] | order | Unsupervised | ||
| order | Unsupervised | ||||
| LRW [37], SRW [37] | order | Unsupervised | |||
| Probabilistic and statistical models based | SBM [41] | order | – | Supervised | |
| Classifier based | order | Supervised | |||
| Network embedding based | MF [67] | order | Supervised | ||
| GraRep [69] | order | Supervised | |||
| DeepWalk [22] | order | Unsupervised | |||
| Node2vec [72] | order | Semi-supervised | |||
| Struc2vec [73] | Structural Identity | Unsupervised | |||
| UniNet [74] | order | – | Semi-supervised | ||
| GCN [76] | order | Semi-supervised | |||
| GraphSAGE [77] | order | Unsupervised | |||
| WLNM [78] | order | – | Supervised | ||
| DGCNN [79] | order | – | Semi-supervised | ||
| SEAL [80] | order | – | Semi-supervised | ||
| Cluster-GCN [81] | order | Semi-supervised | |||
| LINE [86] | order | Supervised | |||
| SDNE [89] | order | O(mn) | Semi-supervised | ||
| VERSE [91] | order | Semi-supervised |
Let denotes the maximum degree of a network, l denotes the number of the random walk steps. For embedding approaches, denotes the dimensionality of embedding vector, is number of layers, r is the number of sampled neighbors per node
Complex Networks
Complex networks have been used widely to model a large number of relationships. A typical network consists of nodes and edges, where nodes denote various entities in real systems and edges represent the relationships between entities. In this study, we focus on the link prediction problem on undirected homogeneous networks. That is, there is no difference between the edge from u to v and the edge from v to u; both are the edge u, v. Consider a simple network G(V, E), where V and E are collections of nodes and links, respectively, the directionality and weight of links are ignored, and multiple links and self-connections are not allowed. By observing many properties of actual networks and combining them with link prediction application areas, we roughly categorize the well-known applications into seven kinds of complex networks according to their natural meanings: coauthorship networks, computer networks, infrastructure networks, interaction networks involving people, protein–protein interaction networks, offline social networks, and online social networks.
Properties
As stated by Newman [94], many studies have proposed some topological features where different types of networks may share a different set of common features. We describe six properties in this paper to distinguish different types of networks. We are mainly concerned with representative features and examine their relationship with link prediction. Common notations are listed in Table 1. We next describe the six properties as following:
Average Degree (AD) Node degree is a basic feature which reflects local information of a node by counting the number of links connected to the node. Average degree is the average of all nodes’ degrees , which measures the overall connectivity of a network and characterizes the intensiveness of connections between nodes. It is defined as
| 28 |
Networks with higher AD usually have higher cohesion and therefore algorithms that can capture local information are more advantageous in such networks.
Clustering Coefficient (CC) Clustering coefficient is a main index to measure clustering numerically, which can only be applied to unipartite networks. The local clustering coefficient is defined as the probability that two randomly chosen neighbors of a node v are connected. Global clustering coefficient is defined as the probability that two incident edges are completed by a third edge to form a triangle [95]. It can be expressed as [96]
| 29 |
where means there is a connection between two nodes, and means node v and w are not the same one. The value of CC is between 0 and 1. A larger CC indicates that there are more triangles in the network and the greater the aggregation degree of nodes.
Assortativity Coefficient () Assortativity is used to observe whether nodes with similar degrees tend to connect to each other. Assortativity coefficient is a Pearson correlation coefficient based on degree. Newman et al [97] propose the correlation function as
| 30 |
where is the normalized distribution of the remaining degree, and is computed as
| 31 |
and is a variance of the distribution of , computed as
| 32 |
Choosing an edge randomly, is the joint probability that the degrees of the two endpoints are j and k, respectively. In general, is between -1 and 1. A positive indicates that the network has good assortativity, and a negative reveals that the network is negatively correlated.
Power Law Exponent (PLE) A network follows power law if its degree distribution follows
| 33 |
where the constant is the power law exponent [98]. If is fixed, C is determined by the requirement that the sum of p(x) is 1. Complex networks obeyed power law distribution are referred as scale-free networks. A greater implies a weaker scale-free network. Given a network, there are multiple ways to estimate . A robust method [99] calculates as
| 34 |
Edge Distribution Entropy (EDE) Entropy is used to measure the randomness of a system. Particularly, for a network, edge distribution entropy is computed as
| 35 |
It equals to one if all nodes have the same degree and is close to zero when all edges connect to a single node [126].
Algebraic Connectivity () The algebraic connectivity is the second-smallest eigenvalue of the Laplacian matrix of a graph [127]. This measurement is greater than zero if and only if the graph is connected. Since the real networks do not always meet this condition, we consider the Largest Connected Component (LCC) instead of the entire network. It is used to analyze the robustness and the synchronizability of a network [128]. A higher algebraic connectivity suggests a better network connectivity.
Datasets
In this section, we introduce the thirty-six datasets we used in experiments and divide them into seven types of complex networks according to their natural meaning. We also show the features of each type of networks we find from mining the datasets. Based on the statistical information in Table 3, the key characteristics of each type of complex networks are extracted, which lays an important foundation for the analysis of experimental results in Sect. 4.
Table 3.
Properties of complex networks (datasets used in experiments)
| Category | Datasets | |V| | |E| | AD | CC | PLE | EDE | ||
|---|---|---|---|---|---|---|---|---|---|
| Coauthorship | APH [100] | 18,771 | 198,050 | 22.0044 | 0.6328 | 0.2013 | 1.4245 | 0.9340 | 0.0272 |
| CM [100] | 23,133 | 93,439 | 8.5462 | 0.6417 | 0.1253 | 1.5908 | 0.9525 | 0.0459 | |
| GQ [100] | 5241 | 14,484 | 6.4560 | 0.5569 | 0.6392 | 1.7423 | 0.9341 | 0.0353 | |
| HPH [100] | 12,006 | 118,489 | 20.9959 | 0.6216 | 0.6295 | 1.5142 | 0.8788 | 0.0355 | |
| HTH [100] | 9875 | 25,973 | 5.7435 | 0.4816 | 0.2389 | 1.7642 | 0.9512 | 0.0244 | |
| Computer | CAD [100] | 26,475 | 53,381 | 4.0326 | 0.2082 | –0.1946 | 2.5086 | 0.8381 | 0.0204 |
| GNT [101] | 62,586 | 147,892 | 4.7275 | 0.0055 | –0.0927 | 2.0625 | 0.9485 | – | |
| RT [100] | 6474 | 12,572 | 3.8838 | 0.2522 | –0.1818 | 2.4616 | 0.8396 | 0.0880 | |
| Infrastructure | CHO [102] | 1467 | 1298 | 1.9976 | 0.0000 | –0.7248 | 4.7986 | 0.9124 | 0.0031 |
| EUR [103] | 1174 | 1417 | 2.5120 | 0.0189 | 0.0900 | 2.2170 | 0.9854 | 0.0012 | |
| OFS [104] | 2939 | 15,677 | 10.7711 | 0.4555 | 0.0489 | 1.7168 | 0.8719 | 0.0408 | |
| PG [95] | 4941 | 6594 | 2.6691 | 0.0801 | 0.0035 | 2.2468 | 0.9783 | 0.0008 | |
| USA [105] | 1574 | 17,215 | 21.9008 | 0.5048 | –0.1134 | 1.5462 | 0.8486 | 0.2180 | |
| Interaction Involving People | CHS [106] | 7301 | 55,899 | 15.6793 | 0.1794 | 0.3705 | 1.4959 | 0.9248 | 0.0696 |
| CRE [107] | 829 | 1473 | 3.5537 | 0.0058 | –0.1645 | 2.0134 | 0.9584 | 0.2364 | |
| UCI [108] | 899 | 7019 | 15.6151 | 0.0705 | –0.0945 | 1.4763 | 0.9256 | 0.3739 | |
| Protein–Protein Interaction | FGS [109] | 2239 | 6432 | 5.7898 | 0.0403 | –0.3318 | 2.0840 | 0.8550 | 0.1025 |
| STL [110] | 1702 | 3155 | 3.8464 | 0.0063 | –0.2020 | 2.2983 | 0.9007 | 0.0257 | |
| VDL [111] | 3023 | 6149 | 4.3169 | 0.0715 | –0.1366 | 2.0531 | 0.9235 | 0.0698 | |
| YST [112] | 1846 | 2203 | 2.6722 | 0.0708 | –0.2095 | 2.6030 | 0.9398 | 0.0213 | |
| Offline Social | ADE [113] | 2539 | 10,455 | 8.2355 | 0.1467 | 0.2513 | 1.5141 | 0.9824 | 0.2997 |
| IFT [114] | 410 | 2765 | 13.4878 | 0.4558 | 0.2258 | 1.4241 | 0.9677 | 0.1945 | |
| JAZ [115] | 198 | 2742 | 27.6970 | 0.6175 | 0.0202 | 1.3293 | 0.9615 | 0.5720 | |
| PHY [116] | 217 | 1839 | 16.9493 | 0.3628 | 0.0960 | 1.4928 | 0.9815 | 1.7137 | |
| RSD [117] | 241 | 923 | 7.9487 | 0.2192 | –0.0842 | 1.7995 | 0.9748 | 1.4240 | |
| Online Social | AVG [118] | 5155 | 39,285 | 15.5601 | 0.2527 | –0.0957 | 1.5627 | 0.8926 | 0.1206 |
| BK [119] | 58,228 | 214,078 | 7.5061 | 0.1734 | 0.0096 | 1.8880 | 0.9027 | – | |
| DNC [120] | 906 | 10,429 | 24.4617 | 0.5072 | –0.1331 | 1.5529 | 0.8549 | 0.1405 | |
| DB [121] | 154,908 | 327,162 | 4.2240 | 0.0161 | –0.1803 | 2.9706 | 0.8897 | – | |
| EPN [122] | 75,879 | 405,740 | 10.6947 | 0.1378 | –0.0406 | 2.0258 | 0.8471 | – | |
| FB [123] | 2888 | 2981 | 2.0644 | 0.0272 | –0.6682 | 25.5893 | 0.7087 | 0.0024 | |
| G+ [123] | 23628 | 39,194 | 3.3187 | 0.1742 | –0.3887 | 3.9819 | 0.7677 | 0.0114 | |
| GWL [119] | 196,591 | 950,327 | 9.6681 | 0.2367 | –0.0293 | 1.7307 | 0.9043 | – | |
| HSS [124] | 2426 | 16,630 | 16.0970 | 0.5401 | 0.0227 | 1.4541 | 0.9281 | 0.1029 | |
| LMC [121] | 104,103 | 2,193,083 | 42.1329 | 0.0544 | –0.1468 | 1.3828 | 0.9003 | – | |
| PRT [125] | 10,680 | 24,316 | 4.5536 | 0.2659 | 0.2382 | 2.1092 | 0.9219 | 0.0112 |
The first column of the table is the network category, and the second one is a more specific classification. The properties measured from left to right are: number of nodes, number of edges, Average Degree, Clustering Coefficent, Assortativity Coefficient, Power Law Exponent, Edge Distribution Entropy, and Algebraic Connectivity. In each column, high values are highlighted in bold and low values are indicated by an underscore. High and low values are compared for categories by taking their mean values
Coauthorship Networks In coauthorship networks [100, 129], nodes stand for a set of authors who have written papers together, and edges represent their collaboration relationships. AstroPh (APH) [100] is in the field of Astro Physics. CondMat(CM) [100] describes the collaborations of papers submitted to Condense Matter. GrQc (GQ) [100] is a coauthorship network of General Relativity and Quantum Cosmology. HepPh (HPH) [100] and HepTh (HTH) [100] show the collaborations between authors related to High Energy Physics and its theory category, respectively.
Higher clustering coefficients than most of the other networks imply that the small-world effect is significant in coauthorship networks. They have the highest and positive assortativity coefficient which shows their strong assortative. In other words, well-known authors tend to associate with each other.
Computer Networks Due to the huge scales of computer networks, we conduct experiments on datasets named CAIDA (CAD) [100]: comes from a project that has the same name as the dataset; Route (RT) [100]: a communication network of autonomous systems collected from Route Views Project; and Gnutella (GNT) [101]. Nodes in computer networks are hosts or autonomous systems of the Internet. They exchange information through connections and form routing mechanisms.
According to the low power law exponent and the edge distribution entropy of computer networks, the edge distribution is skewed. In addition, negative assortativity coefficient shows that low-degree nodes prefer to connect with high-degree nodes.
Infrastructure Networks An infrastructure network consists of physical engineering facilities that provide public services. Chicago (CHO) [102] shows the road transportation in the Chicago region, and Euroroad (EUD) [130] is an international E-road network. OpenFlights (OFS) [104] contains the information of flights collected by the OpenFlight project. PowerGrid (PG) [95] is an undirected network about the electrical grid of the Western US. USAir (USA) [105] shows a network of flights between US airports. These datasets compose the infrastructure networks used in the experiments.
Electric networks are similar to road networks. Their average degree is pretty low. The power law exponent and the edge distribution entropy are obviously higher than any other categories of networks, which indicates the edge distribution of this kind of network is more uniform. The connection between nodes only passes through a small number of local neighbors, resulting in a relatively small algebraic connectivity. Airline networks show different properties from them. Their average degrees are higher, and the edge distributions are more nonuniform which can be reflected by the power law exponents.
Interaction Networks Involving People Most of the interaction networks involving people are bipartite networks that consist of people and items, where each edge represents an interaction [96]. For interaction networks, we use the following datasets : Chess (CHS) [106], Crime (CRE) [107] and UC Irvine (UCI) [108]. Chess is an anonymous dataset that represents the gaming relationships of chess players. Crime is a bipartite network, where nodes denote people or crimes. UC Irvine shows the forum messages posted by the students in the University of California, Irvine.
The degree distributions and the average degrees of interaction networks do not show a distinctive feature as the three networks mentioned earlier. There is no particularly distinctive features about this type of network.
Protein–Protein Interaction Networks This kind of networks can be represented by a graph, where nodes and edges represent proteins and the interactions between them, respectively [131]. Figeys (FGS) [109], Stelzl (STL) [110], and Vidal (VDL) [111] are three PPI networks focusing on homo sapiens. Yeast (YST) [112] is a network of protein interactions in yeast.
We can draw a conclusion from Table 3 that the relationships between the proteins are sparse, and the probability that two proteins have no interaction even though they both interact with a third protein, is high. The assortativity coefficients are negative for four PPI networks, which implies that the molecules with high degrees tend to associate with low degrees.
Offline Social Networks Offline social networks reflect the actual contacts between people, such as talking to each other, participating in activities together, or being physically close. The face-to-face interactions of people participating in big events, and the collaborations of musicians are typical offline social networks. Adole (ADE) [113] captures the connections between students in 1994/1995, and Infectious (IFT) [114] describes the face-to-face behaviors of visitors in the Infectious exhibition. Jazz (JAZ) [115] is a network that shows the collaborations between the Jazz musicians who have played in a band. Physicians (PHY) [116] is a directed network of physicians who are friends or interested in a discussion. Residence (RSD) [117] is a friendship network between the residents living in a residence hall located at an Australian university campus.
Statistics show that most of offline social networks are highly assortative which means people are more likely to associate with people of their own rank in real life. In addition, it is worth noting that the offline social networks have extremely strong scale-free characteristics and high edge distribution entropy which indicates a uniform degree distribution. The high average degrees and clustering coefficients indicate that the central network has obvious hierarchical characteristics. High algebraic connectivities means that all networks are well connected.
Online Social Networks Online social networks consist of individuals and their connections in online social networking platforms and email systems. Plenty of platforms have become increasingly popular, such as Facebook, Twitter and YouTube [16]. Advogato (AVG) [118] is the trust network of an online community platform for the software developers. Brightkite (BK) [119] contains the friendship relations from a location-based social network. The network of Douban(DB) [121] comes from a Chinese online recommendation site. The data of DNC (DNC) [120] are generated from the Democratic National Committee email leak. Epinions (EPN) [122] is the trust network from the online social network Epinions. Facebook(FB) [123] consists of the friend lists. Each list comes from the survey participants using Facebook app. Google+ (G+) [123] is a network of Google+ user-user links. Gowalla (GWL) [119] is the friendship network of a namesake website. Hamsterster (HSS) [124] contains the contacts between users of the website Hamsterster. Livemocha (LMC) [121] is the network of an online language learning community. Pretty (PRT) [125] represents the interactions of people who use the Pretty Good Privacy algorithm.
Different from offline social networks, the assortativity coefficients of most networks are negative. It means that online networks break down invisible barriers between social classes, and the virtual relationships formed in social networks make it easier for ordinary people to connect with celebrities.
Resources
This subsection summarizes valuable resources for investigating complex networks, including network datasets and network visualization tools.
Collections of Network Data
SNAP [132]. A collection of more than 50 large network datasets from tens of thousands of nodes and edges to tens of millions of nodes and edges, including social networks, web graphs, road networks, internet networks, citation networks, collaboration networks, and communication networks. KONECT [133]. The KONECT project has 1,326 network datasets in 24 categories. They have computed 56,300 graph statistics and generated 92,074 plots. AMiner Dateset [134]. The site offers datasets on COVID-19, scientific collaboration networks, multi-relationship networks, dynamic social networks, and many more related to machine learning and knowledge graph. Datasets Released for Reproducibility [135]. The website organized by the comunelab group provides a large number of multi-relational networks of varying degrees of complexity, including social networks and biological networks. Pajek datasets [136]. Many datasets in the early research of complex networks are derived from this collection. Network Repository [137]. The first interactive data and network data repository with real-time visual analytics. Network repository is not only the first interactive repository, but also the largest network repository with thousands of donations in 30+ domains (from biological to social network data). The Internet Topology Zoo [138]. This is an ongoing project to collect data network topologies from around the world. It currently has over two hundred and fifty networks in the Zoo, in a variety of graph formats for statistical analysis, plotting, or other network research.
Tools of Network Data
The research of complex network is inseparable from the statistics, calculation and drawing of various real or simulated networks. For general work, it can be done with software such as Pajek, Netdraw and Ucinet. Figure 3 is an example of visualizing the EUR network using GraphVis [137]. However, in some special scenarios, such as new models developed by oneself, corresponding modeling or calculation needs to be performed through programming. These two types of tools are summarized below.
Fig. 3.
EUR network visualization using GraphVis
NetworkX [139]. This is a Python package for the creation, manipulation, and study of the structure, dynamics, and functions of complex networks. igraph [140].It is a collection of network analysis tools with the emphasis on efficiency, portability and ease of use. It can be programmed in R, Python, Mathematica and C/C++. statnet [141]. statnet is a suite of R packages for the management, exploration, statistical analysis, simulation and vizualization of network data.
Gephi [142]. Gephi is a tool for data analysts and scientists keen to explore and understand all kinds of graphs and networks. GraphVis [137]. GraphVis is a platform for interactive visual graph mining and relational learning. MuxViz [143]. The platform for visualization and analysis of interconnected multilayer networks. It can be used as a library for the implementation of custom analysis or through an interactive browser-based graphical user interface to provide access to many customizable graphic options to render multilayer networks.
Experiments and Analysis
In this section, we evaluate the methods mentioned in Sect. 2 on datasets of seven types of complex networks described in Sect. 3.2. The evaluation results1 will then be presented along with analysis which combine the properties of complex networks in a groundbreaking way.
Evaluation Metrics
There are many evaluation methods of link prediction technology. In this paper, AUC [144], MRR [145] and HR@K are considered to evaluate the link prediction methods which measure results from different perspectives. AUC measures the quality of the method from the overall level. MRR focuses on the ranking of the edges which . HR@K considers the probability of existence of the edges in the first K position.
Area Under the ROC Curve (AUC) [144] AUC is the most suitable and commonly used metric to assess link prediction methods. This is owing to the imbalance distribution of link prediction datasets whose existing edges are notably less than absent edges, while AUC is unaffected by the distribution of the classes. It is tested as following: select one edge randomly from the test set, and select a non-existent edge randomly. Then we compare the scores of the two edges. If the former is greater than the latter, we add 1 to ; If the two are equal, we add 1 to . Finally, the number of comparison time is t, and AUC can be computed as:
| 36 |
Mean Reciprocal Rank (MRR) [145] It is usually used to measure searching algorithms. If the content to be searched matches the first result, the score adds 1. If the content to be searched matches the second result, the score adds 0.5. If the content to be searched matches the nth result, the score adds 1/n. if there is no matching result, the score adds 0.
Hit Ratio@K (HR) [146] HR is often used to calculate the recall rate of the recommendation system. In general, the larger the index, the better the recommendation system. It can be computed as:
| 37 |
The denominator is the total number of neighbors of a given node in the verification set, and the molecular is the number of neighbors belonging to a given node in the verification set in the first K prediction results.
System Setup
To construct a training set and a testing set, all existing links are randomly divided in a 9:1 ratio. We use AUC, MRR and HR@K(K= 1, 5, 10) to evaluate the performance of different approaches. Each experiment is repeated five times, and we use the average as the final result.
Most hyperparameters are inherited from the original paper of each method. Considering the time complexity and the settings of previous works, we reasonably hand-picked different parameters as follows. The parameter in KI is set to 0.01 and 0.001. In LPI, is fixed to 0.001. The value of in GLHN is tested for 0.9, 0.95 and 0.99. For RWR, the damping factor is set to 0.85 and 0.95. LRW and SRW with set to 0.85 are tested for the step length in 3, 4 and 5. The distance r is set to 5 in SR. MF is implemented by libFM, where the number of latent factors is fixed to . For DeepWalk, Node2vec, LINE and other network embedding methods, we end up with 128-dimensional embeddings and calculate the cosine distance of two nodes’ embedding as a link’s embedding. Paremeter tuning itself is a complex process. Since we would like to provide a quick and easy method which works for different types of networks, we only provide preliminary results where the parameters are set according to their original papers. Further adjustment may needed during one’s actual practice. All methods are implemented in Matlab and Python.
Results and Analysis
For the methods with multiple tested parameters, the best results are selected to report. Due to the limitations of space and time, we only evaluate a portion of the methods over large datasets of online social networks. The AUC values and the best methods are reported for each category of complex networks in all datasets. Some methods ran longer than 24 hours on some datasets, thus we terminate those methods, and represent the results as “-”. Surprisingly, some ground-breaking conclusions could be drawn from the empirical results. Due to space constraints, we show the AUC results of all methods on all kinds of networks, and combine the analysis of the attributes of the datasets in Sect. 3 to analyze the results in detail. MRR and HR are omitted for clarity and the complete results are publicly available at [147] for reference. We first analyze various methods and show their efficiency from an overall perspective, and then analyze particular performances of link prediction methods on different types of networks.
Overall Effects
Table 4 shows the number of times each approach ranks first, second, third, top five and top ten on all networks except for big datasets of online social networks. As we concentrate on network embedding-based methods, we show the average rank of other types of methods as a comparison.
Table 4.
Statistics of methods appearing in the top ten of the results
| Methods/rank | 1st | 2nd | 3rd | Top5 | Top10 | AvgRank |
|---|---|---|---|---|---|---|
| Common neighbor based | 0 | 0.1 | 0 | 0.3 | 2.1 | 24 |
| Path based | 0 | 0.4 | 0.4 | 3.1 | 10.2 | 17.8 |
| SBM | 0 | 0 | 2 | 4 | 12 | 12.9 |
| Classifier based | 0 | 0 | 0.4 | 1 | 3.3 | 26.7 |
| MF | 1 | 6 | 3 | 17 | 22 | 6.8 |
| DeepWalk | 0 | 0 | 0 | 0 | 2 | 30.8 |
| Node2vec | 1 | 7 | 4 | 15 | 21 | 10.7 |
| Struc2vec | 1 | 4 | 5 | 18 | 25 | 7.1 |
| GCN | 0 | 0 | 0 | 0 | 0 | 35.8 |
| GraphSAGE | 0 | 0 | 1 | 1 | 2 | 26.1 |
| WLNM | 0 | 1 | 0 | 1 | 7 | 20.8 |
| DGCNN | 0 | 1 | 1 | 5 | 14 | 14.6 |
| SEAL | 0 | 6 | 3 | 17 | 25 | 5.9 |
| LINE | 0 | 0 | 1 | 2 | 4 | 25.9 |
| SDNE | 0 | 0 | 6 | 10 | 15 | 16.3 |
| VERSE | 28 | 1 | 1 | 30 | 31 | 1.3 |
It can be clearly seen from the Table 4 that the methods based on network embedding have the best performance, and their performance are less affected by network attributes which is due to its excellent ability to preserve network information. Examples of these excellent methods are VERSE, SEAL and Struc2vec, which capture network topology information very well and were developed specifically for link prediction task. It is worth noting that VERSE has outstanding performance and ranks first on almost every dataset. It rebuilds the similarity distribution between nodes by training a simple but expressive single-layer neural network, which is very effective in terms of accuracy and time efficiency. MF and Node2vec rely less on network properties and therefore perform well as well. Degree distribution does not affect the efficiency of the method based on matrix factorization. Since shallow encoders optimize an unique embedding vector for each node individually, the shortcoming of shallow network embedding methods comes from that no parameters are shared between nodes, and this will cause a sharp increase in parameter numbers and low computational efficiency. Different from shallow embedding methods, graph neural network-based methods use node features or local graph structures around each node as input to generate embeddings. Different graph neural network methods have different node representation capabilities, resulting in different performances.
As a summary, methods based on common neighbors are quite effective link prediction methods and are suitable for large-scale networks. When compared with advanced network embedding-based methods, they still have competitive performances on networks with high aggregation coefficients. However, due to the limited amount of information such methods preserve, the prediction accuracy of common neighbor-based methods is slightly lower than those of global indicators. Path-based methods also have mediocre performance, while ACT is not affected since it is based on the multiple-route distance diminishment. Path-based approaches take more information into consideration than common neighbor-based approaches, and the former can capture more global structures. The prediction results of probabilistic and statistical models are quite good, due to the reason that some additional information about network structures can be obtained by sampling the fitting and configuration of parameters. On the other hand, a key disadvantage is that the computation is extremely complex, thus it cannot be used to handle large-scale networks at present. Networks with higher aggregation coefficients are found to have a modular structure, so SBM performs better on this type of network. The performance of the methods based on classifier are generally poor, possibly owing to the imbalance of categories. Unlike similarity or probabilistic and statistical models-based methods which rank possible links based on the similarity between nodes or probability of link formation, the predicted number of links in each category cannot be well controlled.
Efficiency Evaluation
Table 5 lists the run time results of representative methods on datasets with comparative significance. We can analyze the scalability of each method through this set of experiments. SBM is extremely sensitive to the number of edges, so it is not suitable for datasets with large number of edges. On the contrary, for DGCNN, the increase of the edge amount does not affect the running time much. WLNM is not sensitive to the number of vertices but is sensitive to the number of edges, while VERSE is completely opposite to WLNM. GraphSAGE is not sensitive to vertex number increasing, and thus is suitable for datasets with a large number of vertices. From the perspective of time consumption, the average run time of common neighbor-based methods is the shortest, among which TSCN is the longest. When there is a need to get an initial result very quickly and does not have a strict restriction on accuracy, a common neighbor-based approach is a good choice. The methods based on probabilistic and statistical models can extract the underlying structure and obtain additional information of the networks by fitting the parameters, while they are time-consuming and are not applicable to deal with large-scale networks. Network embedding-based methods can achieve superior results, while the time consumption is acceptable meanwhile. Methods based on graph neural network run a little longer than other network embedding methods, while it could capture more abundant network information.
Table 5.
Runtime results(s)
| GQ | RT | OFS | USA | CHS | CRE | UCI | ADE | IFT | JAZ | AVG | DNC | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CN | 124.21 | 194.54 | 67.28 | 39.34 | 821.95 | 1.95 | 9.22 | 33.79 | 1.29 | 0.52 | 389.44 | 9.65 |
| Salton | 124.79 | 195.04 | 83.55 | 35.99 | 825.22 | 1.98 | 7.47 | 37.28 | 1.34 | 0.48 | 399.78 | 9.50 |
| JI | 124.46 | 223.07 | 71.88 | 35.83 | 829.50 | 2.00 | 7.56 | 35.08 | 1.37 | 0.48 | 418.16 | 9.73 |
| Sorens | 126.25 | 208.23 | 70.62 | 35.96 | 829.19 | 1.99 | 7.65 | 35.43 | 1.37 | 0.48 | 392.20 | 9.83 |
| HPI | 128.06 | 229.47 | 62.81 | 37.14 | 828.63 | 2.01 | 7.33 | 34.99 | 1.40 | 0.49 | 400.10 | 9.98 |
| HDI | 125.88 | 198.49 | 62.94 | 34.43 | 829.92 | 2.00 | 7.29 | 35.00 | 1.37 | 0.48 | 381.07 | 9.90 |
| LLHN | 121.78 | 197.09 | 61.23 | 33.92 | 822.72 | 1.95 | 7.46 | 34.38 | 1.41 | 0.48 | 383.64 | 9.88 |
| AA | 121.43 | 202.08 | 62.69 | 34.06 | 822.55 | 1.96 | 7.18 | 34.71 | 1.40 | 0.48 | 427.55 | 9.83 |
| RA | 120.72 | 191.37 | 67.22 | 33.58 | 824.08 | 1.95 | 7.21 | 34.56 | 1.36 | 0.48 | 398.08 | 9.62 |
| PA | 152.58 | 229.16 | 86.64 | 35.71 | 1021.88 | 2.08 | 7.82 | 40.14 | 1.41 | 0.48 | 445.87 | 9.67 |
| LNBCN | 121.05 | 194.31 | 83.59 | 33.62 | 822.94 | 1.95 | 7.53 | 33.93 | 1.36 | 0.48 | 386.68 | 9.58 |
| LNBAA | 120.47 | 190.72 | 69.02 | 33.75 | 822.87 | 1.95 | 7.58 | 34.32 | 1.35 | 0.47 | 385.93 | 9.82 |
| LNBRA | 241.59 | 381.55 | 134.23 | 67.81 | 1648.95 | 3.89 | 14.91 | 68.65 | 2.71 | 0.95 | 778.96 | 19.38 |
| TSCN | 195.59 | 797.75 | 105.83 | 55.25 | 2508.02 | 2.17 | 12.21 | 85.97 | 1.60 | 0.52 | 1084.99 | 15.21 |
| LPI | 122.66 | 210.41 | 67.20 | 35.51 | 938.39 | 1.95 | 7.45 | 35.58 | 1.41 | 0.47 | 429.35 | 9.66 |
| KI | 147.31 | 228.50 | 76.01 | 38.98 | 1031.91 | 2.08 | 8.15 | 42.09 | 1.39 | 0.66 | 462.51 | 10.29 |
| GLHN | 157.12 | 259.91 | 73.36 | 36.36 | 1050.12 | 2.14 | 9.39 | 42.71 | 1.43 | 0.78 | 484.94 | 10.59 |
| ACT | 195.35 | 359.22 | 83.06 | 37.59 | 1209.19 | 1.75 | 9.01 | 47.57 | 1.37 | 0.52 | 560.75 | 10.28 |
| RWR | 154.52 | 233.36 | 73.64 | 46.23 | 1122.68 | 1.67 | 8.38 | 46.38 | 1.35 | 0.51 | 509.63 | 10.08 |
| SR | 173.20 | 408.23 | 82.65 | 38.71 | 1141.32 | 1.85 | 8.03 | 43.54 | 1.36 | 0.51 | 528.61 | 10.77 |
| LRW | 124.27 | 210.68 | 65.92 | 35.47 | 941.17 | 1.61 | 7.93 | 34.94 | 1.20 | 0.49 | 438.03 | 10.81 |
| SRW | 123.86 | 208.96 | 68.22 | 38.00 | 944.38 | 1.95 | 7.53 | 35.07 | 1.20 | 0.49 | 430.63 | 10.11 |
| MFI | 148.67 | 224.34 | 70.02 | 48.72 | 1063.05 | 2.07 | 7.68 | 40.62 | 1.21 | 0.48 | 548.67 | 9.74 |
| SBM | 2164.01 | 25672.40 | 3628.33 | 1670.13 | 6707.33 | 240.09 | 656.54 | 1229.14 | 155.72 | 93.99 | 4420.39 | 922.64 |
| Struc2Vec | 153.72 | 164.48 | 93.44 | 55.54 | 838.63 | 3.33 | 12.89 | 54.34 | 2.33 | 1.13 | 409.51 | 19.24 |
| GraphSAGE | 1079.19 | 847.21 | 1236.27 | 1319.22 | 4379.00 | 112.35 | 358.64 | 614.30 | 145.14 | 153.84 | 3647.11 | 527.61 |
| WLNM | 816.10 | 7789.45 | 2349.60 | 5858.12 | – | 72.06 | 544.47 | 517.47 | 210.10 | 264.18 | 9500.13 | 2907.10 |
| DGCNN | 694.41 | 525.44 | 787.62 | 791.45 | 26738.46 | 64.67 | 289.21 | 489.54 | 113.08 | 105.23 | 2197.41 | 413.38 |
| LINE | 151.33 | 160.43 | 91.98 | 53.96 | 824.54 | 3.02 | 12.95 | 53.76 | 2.29 | 1.11 | 407.72 | 18.93 |
| VERSE | 129.67 | 152.72 | 73.78 | 43.69 | 194.27 | 22.29 | 22.33 | 57.92 | 10.94 | 4.97 | 127.39 | 25.27 |
Particular Performances on Different Types of Networks
The AUC results of coauthorship networks, computer networks and infrastructure networks are reported in Table 6. Table 7 shows the results on interaction networks involving people, protein–protein interaction networks and offline social networks. Tables 8 and 9 show the outcomes of small and large datasets of online social networks, respectively. We will analyze particular performances of some methods on different types of networks, where the inconsistency comes from different characteristics of different kinds of networks. Methods that are not affected by network attributes are mentioned in Sect. 4.3.1 and will not be repeated here. For example, VERSE performs well on any kind of networks and will not be discussed in this section.
Table 6.
AUC results of coauthorship networks, computer networks and infrastructure networks
| Coauthorship Networks | Computer Networks | Infrastructure Networks | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Methods | APH | CM | GQ | HPH | HTH | CAD | GNT | RT | CHO | EUR | OFS | PG | USA |
| CN | 0.9854 | 0.9647 | 0.9145 | 0.9799 | 0.9000 | 0.9599 | 0.6887 | 0.7040 | 0.4980 | 0.5137 | 0.9364 | 0.5951 | 0.9534 |
| Salton | 0.9863 | 0.9651 | 0.9165 | 0.9796 | 0.9013 | 0.9602 | 0.6702 | 0.6827 | 0.4980 | 0.5134 | 0.9364 | 0.5893 | 0.9404 |
| JI | 0.9856 | 0.9646 | 0.9161 | 0.9797 | 0.9025 | 0.9699 | 0.6715 | 0.6821 | 0.4980 | 0.5132 | 0.9346 | 0.5968 | 0.9377 |
| Sorens | 0.9855 | 0.9652 | 0.9164 | 0.9796 | 0.9002 | 0.9601 | 0.6719 | 0.6835 | 0.4981 | 0.5153 | 0.9383 | 0.5956 | 0.9359 |
| HPI | 0.9861 | 0.9649 | 0.9181 | 0.9795 | 0.8993 | 0.9603 | 0.6846 | 0.6923 | 0.4976 | 0.5134 | 0.9346 | 0.5954 | 0.9079 |
| HDI | 0.9861 | 0.9651 | 0.9184 | 0.9796 | 0.9042 | 0.9598 | 0.6728 | 0.6836 | 0.4977 | 0.5141 | 0.9339 | 0.5914 | 0.9367 |
| LLHN | 0.9858 | 0.9648 | 0.9166 | 0.9793 | 0.9023 | 0.9596 | 0.6683 | 0.6805 | 0.4980 | 0.5134 | 0.9275 | 0.5949 | 0.8449 |
| AA | 0.9863 | 0.9653 | 0.9215 | 0.9794 | 0.9055 | 0.9602 | 0.6923 | 0.7072 | 0.4975 | 0.5121 | 0.9407 | 0.5895 | 0.9570 |
| RA | 0.9857 | 0.9654 | 0.9161 | 0.9798 | 0.9017 | 0.9604 | 0.6920 | 0.7019 | 0.4980 | 0.5141 | 0.9462 | 0.5966 | 0.9615 |
| PA | 0.9463 | 0.9126 | 0.7428 | 0.9561 | 0.7273 | 0.9124 | 0.8316 | 0.7467 | 0.2205 | 0.3036 | 0.8640 | 0.4540 | 0.9298 |
| LNBCN | 0.9862 | 0.9651 | 0.9194 | 0.9782 | 0.9025 | 0.9602 | 0.6927 | 0.7011 | 0.4979 | 0.5138 | 0.9418 | 0.5954 | 0.9547 |
| LNBAA | 0.9863 | 0.9653 | 0.9167 | 0.9800 | 0.9023 | 0.9604 | 0.6921 | 0.7030 | 0.4979 | 0.5135 | 0.9431 | 0.5934 | 0.9568 |
| LNBRA | 0.9865 | 0.9650 | 0.9178 | 0.9808 | 0.9062 | 0.9601 | 0.6923 | 0.7084 | 0.4980 | 0.5139 | 0.9415 | 0.5911 | 0.9617 |
| TSCN | 0.5438 | 0.7392 | 0.6369 | 0.5138 | 0.7562 | 0.5129 | 0.5102 | 0.5291 | 0.4720 | 0.6459 | 0.4944 | 0.6452 | 0.4390 |
| LPI | 0.9893 | 0.9716 | 0.9329 | 0.9841 | 0.9233 | 0.9694 | 0.7879 | 0.7624 | 0.4945 | 0.5371 | 0.9465 | 0.6482 | 0.9545 |
| KI | 0.9905 | 0.9757 | 0.9166 | 0.9849 | 0.8972 | 0.9731 | 0.7988 | 0.6939 | 0.4565 | 0.6451 | 0.9308 | 0.6602 | 0.1754 |
| GLHN | 0.9907 | 0.9793 | 0.8914 | 0.9862 | 0.8748 | 0.9757 | 0.7147 | 0.4394 | 0.7130 | 0.6128 | 0.8584 | 0.6492 | 0.6913 |
| ACT | 0.9485 | 0.9384 | 0.8103 | 0.9711 | 0.7764 | 0.9362 | 0.9359 | 0.8279 | 0.9847 | 0.9075 | 0.8896 | 0.9540 | 0.9304 |
| RWR | 0.9914 | 0.9761 | 0.9161 | 0.9853 | 0.8966 | 0.8481 | 0.8396 | 0.7798 | 0.4551 | 0.6594 | 0.9334 | 0.6697 | 0.9514 |
| SR | 0.9912 | 0.9759 | 0.9188 | 0.9851 | 0.8945 | 0.7816 | 0.7481 | 0.5942 | 0.4716 | 0.7021 | 0.9159 | 0.7689 | 0.8507 |
| LRW | 0.9913 | 0.9757 | 0.9318 | 0.9857 | 0.9215 | 0.8466 | 0.8338 | 0.7833 | 0.4950 | 0.5401 | 0.9545 | 0.6522 | 0.9616 |
| SRW | 0.9915 | 0.9755 | 0.9302 | 0.9859 | 0.9229 | 0.8427 | 0.8310 | 0.7813 | 0.4932 | 0.5392 | 0.9504 | 0.6521 | 0.9604 |
| MFI | 0.9902 | 0.9748 | 0.9103 | 0.9842 | 0.8977 | 0.8286 | 0.8022 | 0.7054 | 0.4536 | 0.6472 | 0.9237 | 0.6650 | 0.9236 |
| SBM | – | – | 0.8939 | – | 0.8517 | – | 0.9375 | 0.9391 | 0.8835 | 0.6823 | 0.9373 | 0.6534 | 0.9688 |
| SVM | 0.7324 | 0.8346 | 0.8619 | 0.7726 | 0.8845 | 0.7295 | 0.8197 | 0.7864 | 0.8097 | 0.6111 | 0.8063 | 0.5002 | 0.7152 |
| KNN | 0.8391 | 0.8980 | 0.9043 | 0.7818 | 0.9027 | 0.6302 | 0.6244 | 0.5549 | 0.5846 | 0.5485 | 0.7847 | 0.5970 | 0.7153 |
| DT | 0.5972 | 0.5998 | 0.5883 | 0.6053 | 0.5869 | 0.5588 | 0.5708 | 0.5233 | 0.5386 | 0.5812 | 0.5135 | 0.5494 | 0.5917 |
| Bayes | 0.9667 | 0.9611 | 0.9394 | 0.9268 | 0.9277 | 0.9110 | 0.9056 | 0.7967 | 0.5248 | 0.5030 | 0.8761 | 0.7629 | 0.7966 |
| LR | 0.7584 | 0.6853 | 0.6879 | 0.8791 | 0.5618 | 0.9191 | 0.8602 | 0.7861 | 0.4157 | 0.3385 | 0.6842 | 0.4572 | 0.7430 |
| MLP | 0.7233 | 0.7659 | 0.7768 | 0.6305 | 0.7308 | 0.6857 | 0.8034 | 0.7655 | 0.4209 | 0.3426 | 0.6807 | 0.4634 | 0.7451 |
| MF | – | – | 0.9188 | 0.9628 | 0.9206 | 0.9782 | 0.9745 | – | 0.9699 | 0.8416 | 0.9619 | 0.8942 | 0.9702 |
| DeepWalk | 0.6935 | 0.7250 | 0.7753 | 0.6829 | 0.6718 | 0.5919 | 0.5784 | 0.6702 | 0.8873 | 0.7848 | 0.6896 | 0.7251 | 0.6021 |
| Node2vec | 0.9925 | 0.9701 | 0.9349 | 0.9407 | 0.9264 | 0.9722 | 0.9518 | 0.9617 | 0.9889 | 0.9805 | 0.9588 | 0.9904 | 0.8544 |
| Struc2vec | 0.9931 | 0.9832 | 0.9458 | 0.9497 | 0.9399 | 0.9835 | 0.9597 | 0.9739 | 0.8671 | 0.8973 | 0.9598 | 0.8257 | 0.9235 |
| GCN | 0.6372 | 0.5730 | 0.5685 | 0.5587 | 0.5960 | 0.6410 | 0.5900 | 0.6896 | 0.4970 | 0.5338 | 0.5962 | 0.5144 | 0.5356 |
| GraphSAGE | 0.8002 | 0.7508 | 0.7730 | 0.8939 | 0.7323 | 0.8356 | 0.7923 | 0.7988 | 0.6743 | 0.6515 | 0.8536 | 0.6851 | 0.8758 |
| WLNM | 0.8563 | 0.8819 | 0.9269 | – | 0.8821 | 0.7268 | 0.7441 | 0.8802 | 0.9149 | 0.7042 | 0.9319 | 0.7701 | 0.9088 |
| DGCNN | 0.9169 | 0.9161 | 0.9100 | 0.9168 | 0.8404 | 0.8632 | 0.9232 | 0.9108 | 0.9789 | 0.9667 | 0.9406 | 0.9259 | 0.9311 |
| SEAL | 0.9925 | 0.9913 | 0.9793 | 0.9902 | 0.9659 | – | 0.9587 | – | 0.9705 | 0.7796 | 0.9730 | 0.7864 | 0.9600 |
| LINE | 0.9261 | 0.9691 | 0.9615 | 0.9598 | 0.9366 | 0.5659 | 0.5484 | 0.5285 | 0.4253 | 0.5957 | 0.8275 | 0.7311 | 0.4646 |
| SDNE | 0.8814 | 0.8625 | 0.7518 | 0.8325 | 0.8172 | 0.9609 | 0.9498 | 0.9503 | 0.9655 | 0.9695 | 0.9253 | 0.9648 | 0.9054 |
| VERSE | 0.9992 | 0.9994 | 0.9979 | 0.9992 | 0.9978 | 0.9977 | 0.9853 | 0.9965 | 0.9655 | 0.9863 | 0.9956 | 0.9948 | 0.9928 |
Table 7.
AUC results of interaction networks involving people, protein–protein interaction networks and offline social networks
| Interaction networks involving people | Protein–protein interaction networks | Offline social networks | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Methods | CHS | CRE | UCI | FGS | STL | VDL | YST | ADE | IFT | JAZ | PHY | RSD |
| CN | 0.8783 | 0.5043 | 0.7262 | 0.5526 | 0.5238 | 0.6162 | 0.5917 | 0.7652 | 0.9362 | 0.9576 | 0.9085 | 0.8407 |
| Salton | 0.8784 | 0.5051 | 0.6923 | 0.5474 | 0.5229 | 0.6169 | 0.5894 | 0.7695 | 0.9367 | 0.9659 | 0.9208 | 0.8394 |
| JI | 0.8779 | 0.5045 | 0.6998 | 0.5486 | 0.5253 | 0.6153 | 0.5881 | 0.7700 | 0.9401 | 0.9580 | 0.9212 | 0.8365 |
| Sorens | 0.8828 | 0.5043 | 0.6905 | 0.5485 | 0.5249 | 0.6146 | 0.5897 | 0.7678 | 0.9369 | 0.9615 | 0.9156 | 0.8376 |
| HPI | 0.8747 | 0.5036 | 0.6924 | 0.5506 | 0.5248 | 0.6179 | 0.5904 | 0.7647 | 0.9321 | 0.9484 | 0.9166 | 0.8389 |
| HDI | 0.8796 | 0.5057 | 0.6945 | 0.5479 | 0.5242 | 0.6179 | 0.5899 | 0.7712 | 0.9358 | 0.9487 | 0.9135 | 0.8333 |
| LLHN | 0.8740 | 0.5052 | 0.6643 | 0.5473 | 0.5252 | 0.6157 | 0.5894 | 0.7710 | 0.9246 | 0.9031 | 0.8955 | 0.8357 |
| AA | 0.8814 | 0.5054 | 0.7316 | 0.5561 | 0.5272 | 0.6176 | 0.5878 | 0.7726 | 0.9352 | 0.9611 | 0.9179 | 0.8399 |
| RA | 0.8787 | 0.5061 | 0.7269 | 0.5537 | 0.5246 | 0.6176 | 0.5920 | 0.7661 | 0.9368 | 0.9694 | 0.9207 | 0.8437 |
| PA | 0.9316 | 0.6189 | 0.8369 | 0.8080 | 0.6890 | 0.7463 | 0.4885 | 0.6147 | 0.7134 | 0.7671 | 0.6212 | 0.5200 |
| LNBCN | 0.8787 | 0.5056 | 0.7345 | 0.5783 | 0.5278 | 0.6138 | 0.5890 | 0.7699 | 0.9327 | 0.9594 | 0.9125 | 0.8407 |
| LNBAA | 0.8828 | 0.5060 | 0.7294 | 0.5742 | 0.5268 | 0.6170 | 0.5873 | 0.7701 | 0.9386 | 0.9636 | 0.9194 | 0.8470 |
| LNBRA | 0.8788 | 0.5040 | 0.7282 | 0.5765 | 0.5256 | 0.6148 | 0.5894 | 0.7748 | 0.9356 | 0.9726 | 0.9113 | 0.8368 |
| TSCN | 0.5362 | 0.5507 | 0.5231 | 0.4760 | 0.5737 | 0.5144 | 0.5747 | 0.6996 | 0.5365 | 0.5141 | 0.6266 | 0.8891 |
| LPI | 0.9391 | 0.5876 | 0.8016 | 0.8016 | 0.7156 | 0.7667 | 0.6178 | 0.8430 | 0.9526 | 0.9509 | 0.9055 | 0.9062 |
| KI | 0.9311 | 0.5770 | 0.8087 | 0.7550 | 0.6546 | 0.7507 | 0.5742 | 0.8844 | 0.9525 | 0.9425 | 0.9039 | 0.9164 |
| GLHN | 0.9099 | 0.5022 | 0.5586 | 0.4939 | 0.5635 | 0.6513 | 0.5031 | 0.8786 | 0.9362 | 0.8082 | 0.8379 | 0.9062 |
| ACT | 0.8555 | 0.7001 | 0.8349 | 0.8982 | 0.8421 | 0.8162 | 0.7681 | 0.6570 | 0.8088 | 0.7773 | 0.6581 | 0.5290 |
| RWR | 0.9468 | 0.5870 | 0.8037 | 0.8031 | 0.6777 | 0.7727 | 0.5803 | 0.9047 | 0.9606 | 0.9500 | 0.9118 | 0.9194 |
| SR | 0.9398 | 0.4834 | 0.6586 | 0.3261 | 0.5220 | 0.7006 | 0.5845 | 0.9022 | 0.9510 | 0.8991 | 0.9057 | 0.9193 |
| LRW | 0.9444 | 0.5881 | 0.8151 | 0.8494 | 0.7220 | 0.7684 | 0.6184 | 0.8471 | 0.9613 | 0.9529 | 0.9221 | 0.9149 |
| SRW | 0.9440 | 0.5893 | 0.7863 | 0.8353 | 0.7089 | 0.7665 | 0.6134 | 0.8433 | 0.9647 | 0.9663 | 0.9246 | 0.9163 |
| MFI | 0.9417 | 0.5538 | 0.7774 | 0.7453 | 0.6419 | 0.7347 | 0.5755 | 0.9041 | 0.9534 | 0.9222 | 0.9129 | 0.9121 |
| SBM | 0.9015 | 0.6562 | 0.8370 | 0.9532 | 0.8557 | 0.8206 | 0.7966 | 0.8360 | 0.9423 | 0.9172 | 0.8599 | 0.8891 |
| SVM | 0.7586 | 0.6429 | 0.7157 | 0.8864 | 0.7568 | 0.8125 | 0.6518 | 0.7316 | 0.7175 | 0.7023 | 0.7359 | 0.7618 |
| KNN | 0.7315 | 0.5824 | 0.6038 | 0.7316 | 0.5873 | 0.7519 | 0.5940 | 0.6657 | 0.7191 | 0.7524 | 0.7742 | 0.7369 |
| DT | 0.5200 | 0.5109 | 0.5347 | 0.5021 | 0.6195 | 0.5472 | 0.5268 | 0.5268 | 0.5481 | 0.5816 | 0.5364 | 0.5660 |
| Bayes | 0.8126 | 0.6318 | 0.6234 | 0.7964 | 0.7122 | 0.8195 | 0.7616 | 0.7586 | 0.7499 | 0.8978 | 0.9005 | 0.8993 |
| LR | 0.7557 | 0.6291 | 0.6809 | 0.8149 | 0.7233 | 0.7157 | 0.5763 | 0.6584 | 0.6815 | 0.9038 | 0.7125 | 0.7067 |
| MLP | 0.7250 | 0.6314 | 0.6922 | 0.8075 | 0.7354 | 0.7341 | 0.6008 | 0.6596 | 0.6971 | 0.7833 | 0.7654 | 0.8050 |
| MF | 0.9368 | 0.8925 | 0.8953 | 0.9657 | 0.8904 | 0.9026 | 0.9269 | 0.8925 | 0.9431 | 0.9784 | 0.9529 | 0.9211 |
| DeepWalk | 0.6259 | 0.6152 | 0.5264 | 0.5639 | 0.5967 | 0.6654 | 0.6872 | 0.6562 | 0.7254 | 0.6533 | 0.6194 | 0.8582 |
| Node2vec | 0.9436 | 0.9643 | 0.6366 | 0.8700 | 0.9416 | 0.9497 | 0.9765 | 0.9623 | 0.9378 | 0.9046 | 0.9297 | 0.9658 |
| Struc2vec | 0.9466 | 0.9713 | 0.8533 | 0.9488 | 0.8815 | 0.9108 | 0.9340 | 0.9737 | 0.9604 | 0.9325 | 0.9308 | 0.9655 |
| GCN | 0.6901 | 0.5475 | 0.6481 | 0.6140 | 0.5795 | 0.6054 | 0.5043 | 0.5153 | 0.5505 | 0.5967 | 0.5359 | 0.6056 |
| GraphSAGE | 0.7904 | 0.6012 | 0.7261 | 0.7339 | 0.6898 | 0.6624 | 0.6819 | 0.7066 | 0.8083 | 0.7958 | 0.7478 | 0.6740 |
| WLNM | 0.5406 | 0.5984 | 0.6994 | 0.8230 | 0.7369 | 0.7823 | 0.7506 | 0.7940 | 0.8457 | 0.8459 | 0.7677 | 0.7634 |
| DGCNN | 0.9139 | 0.8714 | 0.9361 | 0.9382 | 0.8399 | 0.8199 | 0.9114 | 0.8873 | 0.9406 | 0.9190 | 0.9108 | 0.9067 |
| SEAL | 0.9651 | 0.8127 | 0.8597 | 0.9593 | 0.9128 | 0.9017 | 0.9051 | 0.8961 | 0.9528 | 0.9539 | 0.8898 | 0.9124 |
| LINE | 0.8119 | 0.5690 | 0.5169 | 0.5214 | 0.5599 | 0.6960 | 0.7596 | 0.8274 | 0.9514 | 0.8838 | 0.8696 | 0.9023 |
| SDNE | 0.9312 | 0.9576 | 0.6153 | 0.8975 | 0.9217 | 0.9366 | 0.9518 | 0.9549 | 0.9421 | 0.9133 | 0.9152 | 0.9267 |
| VERSE | 0.9930 | 0.9687 | 0.9686 | 0.9915 | 0.9815 | 0.9897 | 0.9938 | 0.9909 | 0.9925 | 0.9701 | 0.9698 | 0.9714 |
Table 8.
AUC results of small datasets of online social networks
| Methods/datasets | AVG | DNC | FB | G+ | HSS | PTY |
|---|---|---|---|---|---|---|
| CN | 0.9008 | 0.9667 | 0.5033 | 0.9549 | 0.9616 | 0.8466 |
| Salton | 0.8834 | 0.9319 | 0.5249 | 0.9628 | 0.9703 | 0.8462 |
| JI | 0.8812 | 0.9309 | 0.4837 | 0.9626 | 0.9694 | 0.8468 |
| Sorens | 0.8803 | 0.9317 | 0.5061 | 0.9627 | 0.9691 | 0.8471 |
| HPI | 0.8798 | 0.8256 | 0.4969 | 0.9625 | 0.9675 | 0.8470 |
| HDI | 0.8827 | 0.9267 | 0.5276 | 0.9626 | 0.9712 | 0.8466 |
| LLHN | 0.8707 | 0.8074 | 0.4739 | 0.9625 | 0.9627 | 0.8468 |
| AA | 0.9009 | 0.9717 | 0.4965 | 0.9627 | 0.9709 | 0.8472 |
| RA | 0.9076 | 0.9714 | 0.5142 | 0.9624 | 0.9746 | 0.8474 |
| PA | 0.8946 | 0.9325 | 0.4590 | 0.9112 | 0.9447 | 0.8453 |
| LNBCN | 0.9033 | 0.9681 | 0.4879 | 0.9629 | 0.9704 | 0.8471 |
| LNBAA | 0.9036 | 0.9695 | 0.5384 | 0.9627 | 0.9705 | 0.8471 |
| LNBRA | 0.9063 | 0.9716 | 0.5168 | 0.9628 | 0.9736 | 0.8472 |
| TSCN | 0.5061 | 0.5077 | 0.5485 | 0.5137 | 0.5394 | 0.5925 |
| LPI | 0.9296 | 0.9629 | 0.4861 | 0.9705 | 0.9827 | 0.8579 |
| KI | 0.9262 | 0.9515 | 0.4327 | 0.9754 | 0.9835 | 0.8503 |
| GLHN | 0.6796 | 0.6327 | 0.4692 | 0.9792 | 0.9826 | 0.8618 |
| ACT | 0.8969 | 0.9532 | 0.9875 | 0.9829 | 0.9466 | 0.9622 |
| RWR | 0.9290 | 0.9617 | 0.4526 | 0.7304 | 0.9843 | 0.8505 |
| SR | 0.8637 | 0.8190 | 0.4368 | 0.6765 | 0.9802 | 0.8534 |
| LRW | 0.9302 | 0.9668 | 0.4457 | 0.7658 | 0.9855 | 0.8641 |
| SRW | 0.9292 | 0.9660 | 0.5135 | 0.7653 | 0.9807 | 0.8638 |
| MFI | 0.9115 | 0.9519 | 0.4983 | 0.7222 | 0.9814 | 0.8507 |
| SBM | 0.9105 | 0.9810 | 0.9856 | – | – | – |
| SVM | 0.6523 | 0.8546 | 0.8367 | 0.9116 | 0.8382 | 0.7878 |
| KNN | 0.6849 | 0.8367 | 0.5543 | 0.6946 | 0.9017 | 0.7896 |
| DT | 0.5694 | 0.6318 | 0.5230 | 0.6353 | 0.6006 | 0.6253 |
| Bayes | 0.8368 | 0.8416 | 0.6644 | 0.9651 | 0.9485 | 0.9003 |
| LR | 0.6316 | 0.8564 | 0.5891 | 0.9799 | 0.8847 | 0.5842 |
| MLP | 0.5849 | 0.8648 | 0.4492 | 0.8836 | 0.7934 | 0.7197 |
| MF | 0.9628 | 0.9837 | 0.9918 | – | 0.9572 | 0.9156 |
| DeepWalk | 0.5533 | 0.6352 | 0.8029 | 0.5697 | 0.6984 | 0.7932 |
| Node2vec | 0.8869 | 0.7138 | 0.9821 | 0.9602 | 0.9526 | 0.9859 |
| Struc2vec | 0.9044 | 0.9703 | 0.9762 | 0.9674 | 0.9701 | 0.9537 |
| GCN | 0.5831 | 0.7647 | 0.5694 | 0.5981 | 0.5630 | 0.6079 |
| GraphSAGE | 0.7591 | 0.9162 | 0.9954 | 0.8835 | 0.7794 | 0.7988 |
| WLNM | 0.8823 | 0.9497 | 0.9987 | 0.7756 | 0.9269 | 0.9537 |
| DGCNN | 0.9439 | 0.9420 | 0.9066 | 0.9131 | 0.9605 | 0.9226 |
| SEAL | 0.9486 | 0.9763 | 0.9898 | – | 0.9833 | 0.9684 |
| LINE | 0.7040 | 0.6775 | 0.5861 | 0.4669 | 0.8998 | 0.9218 |
| SDNE | 0.8725 | 0.7076 | 0.9309 | 0.9536 | 0.9475 | 0.9802 |
| VERSE | 0.9910 | 0.9970 | 0.9997 | 0.9998 | 0.9978 | 0.9916 |
Table 9.
AUC results of big datasets of online social networks
| Methods/datasets | BK | DB | EPN | GWL | LMC |
|---|---|---|---|---|---|
| CN | 0.8194 | 0.5978 | 0.8685 | 0.8837 | 0.7826 |
| Salton | 0.8565 | 0.6059 | 0.9131 | 0.8972 | 0.7634 |
| JI | 0.8216 | 0.5999 | 0.8607 | 0.8775 | 0.7781 |
| Sorens | 0.8217 | 0.5797 | 0.8609 | 0.8773 | 0.7795 |
| HPI | 0.8542 | 0.6214 | 0.9012 | 0.8901 | 0.7783 |
| HDI | 0.8186 | 0.5830 | 0.8620 | 0.8775 | 0.7774 |
| LLHN | 0.8569 | 0.6163 | 0.9088 | 0.8907 | 0.7653 |
| AA | 0.8205 | 0.5886 | 0.8709 | 0.8801 | 0.7829 |
| RA | 0.8197 | 0.5879 | 0.8716 | 0.8806 | 0.7812 |
| PA | 0.8312 | 0.6691 | 0.8901 | 0.8674 | 0.9215 |
| LNBCN | 0.8201 | 0.5877 | 0.8725 | 0.8761 | 0.7903 |
| LNBAA | 0.8193 | 0.5874 | 0.8707 | 0.8757 | 0.7899 |
| LNBRA | 0.6400 | 0.5876 | 0.8724 | 0.8760 | 0.7886 |
| DeepWalk | 0.6426 | 0.5437 | 0.6028 | 0.6514 | 0.5386 |
| Node2vec | 0.9731 | 0.9714 | 0.9269 | 0.9794 | 0.8239 |
| Struc2vec | 0.9783 | 0.9796 | 0.9298 | 0.9852 | 0.8315 |
| GCN | 0.6563 | 0.6047 | 0.7937 | – | – |
| DGCNN | 0.9276 | 0.9444 | 0.9520 | 0.9419 | 0.9298 |
| LINE | 0.8383 | 0.6234 | 0.6454 | 0.8098 | 0.6875 |
| SDNE | 0.9705 | 0.9685 | 0.9193 | 0.9718 | 0.8197 |
| VERSE | 0.9969 | 0.9970 | 0.9964 | 0.9980 | 0.9865 |
Coauthorship Networks SEAL performs well on all tested datasets. LINE, Node2vec and Struc2vec follow closely behind, which reveals that network embedding methods are suitable for coauthorship networks. High clustering coefficients and average node degrees ensure that subgraphs of coauthorship networks preserve sufficient local information. Therefore, methods based on local information such as common neighbor-based methods perform well. For coauthorship networks, authors who belong to the same organization have a high probability of publishing papers together. However, there is a considerable portion of links between different organizations. Hence, path-based methods are also competitive. In a word, when meets time and space consumptions, SEAL is recommended for coauthorship networks with high clustering coefficients, assortativity coefficients, and strong scale-free features.
Computer Networks Computer networks present the properties of low average degree, weak connectivity and skewed degree distribution, resulting in the difficulty to predict links by obvious topology information. In view of this situation, Struc2vec performs surprisingly well on CAD, RT and shows competitive performance on GNT. Skewed degree distributions lead to apparent community structure properties, which contributes to the good performance of Struc2vec. In addition, MF, Node2vec and SDNE also achieve good performances. According to above analysis, network embedding methods with matrix factorization and random walk are recommended for computer networks.
Infrastructure Networks According to the network attributes shown in Table 3, the airlines network has a high average degree and a low power law exponent with a high clustering coefficient. In terms of the overall effects, DGCNN has the most competitive performance on this kind of networks. Node2vec and SDNE work well in electrical networks and roads networks, while have an average performance on airlines datasets. Because of the uniform degree distribution, low clustering coefficient and numerous low-degree nodes which make it difficult to capture local information well, common neighbor-based methods and most path-based methods show bad results in infrastructure networks. However, ACT is based on the multiple-route distance diminishment, which makes ACT will not be affected by those properties of infrastructure networks.
Interaction Networks Involving People Except for VERSE, there is no single method that performs well on all three datasets. This may be caused by inconsistent statistical properties. Methods based on network embedding with random walk are worth of attentions, especially Struc2vec, which performs better than other methods on the CRE dataset and shows competitive performance on other datasets as well. On the whole, DGCNN performs best among all the methods. Thus Struc2vec and DGCNN can be considered as a quick-pick method for this kind of networks. For bipartite datasets, there is no common neighbor between different roles, which makes it difficult to predict these links for the methods based on common neighbors.
Protein–protein Interaction Networks Although Node2vec obtains the most impressive results on three datasets, it has a mediocre performance on the FGS dataset. Considering the results of protein–protein interaction networks and infrastructure networks jointly, MF is also an excellent method when a network shows less connectivity and low cluster coefficient. LINE performs poor on the PPI networks because of the low cluster coefficient, while Struc2vec, SEAL, and SDNE have a better performance. To sum up, methods based on matrix factorization and random walk tend to be more suitable for link prediction tasks on PPI networks.
Offline Social Networks Methods for each dataset in Table 7 do not show a consistent trend. Uniform degree distribution, high assortativity and good connectivity indicate that the information of offline social networks are evenly distributed. Methods based on network embedding, especially random walk-based approaches generally work well on offline social networks. The reason may be that the coverage of random walk is wider and more comprehensive.
Online Social Networks Table 8 shows the AUC results of small online social networks. High average degree and cluster coefficient provide enough information for link prediction on online social networks. However, some path-based methods involve too much noise. Unbalanced degree distribution and strong scale-free lead to the fact that there is no single method performs well on all datasets. Although MF and SEAL do not obtain the best results in all datasets, their performance are generally very close to the best methods. As can be seen from the table, network embedding-based link prediction methods performs well on this kind of networks and are excellent methods to choose from.
For big online social networks, we show the results in Table 9. We only show a portion of the methods over large datasets of online social networks, while the rests cannot complete the task with time and space limitations. VERSE kept its usual dominant position. Other than that, DGCNN performs best among these networks since it can learn more expressive representations than others. Node2vec and Struc2vec perform better than other methods on all datasets. This is reasonable because Node2vec and Struc2vec capture more information than common neighbor-based methods, which is achieved at the cost of more time consumption. For common neighbor-based methods, PA, which only considers the degree of nodes, has surprisingly good performance in LMC. When PA appears as the best method, it is significantly better than other methods. It can be found that LMC has extremely high average degree, which compromises the performance of other common neighbor-based methods.
Conclusions
In this survey, we have conducted, as far as we know, the most comprehensive experimental overview of the link prediction methods that have been proposed till now on complex networks. We propose a scientific taxonomy, which reasonably classifies the representative link prediction methods according to their internal principles. We then divide thirty-six datasets into seven different types of networks according to their natural meaning, and extract network property features for each type of the networks. Next, we analyze the properties of different type of networks in detail. Full-scale experiments have been performed for forty-two link prediction methods on above mentioned thirty-six datasets. On the basis of statistical analysis of the experimental results, we further analyze them in detail in order to reveal the methods with good performance and recommend appropriate link prediction methods for each type of networks. In addition, observing that the methods based on network embedding provide new solutions for the tasks of link prediction, while the complete investigation of such methods has been missing. One of the important contributions of this paper is to fill in the gap of the research of link prediction methods based on network embedding.
Acknowledgements
This work was supported in part by NSFC (national science foundation of China) under the grants 62172237, U1936206, U1936105 and 62077031; NSF (national science foundation) grant IIS-1633271, IIS-2124704, OAC-2106740; and the New England Transportation Consortium project 20-2.
Author Contributions
Haixia Wu contributed to evaluation and writing; Chunyao Song contributed to methodology, evaluation, writing, supervision, and funding acquisition; Yao Ge contributed to evaluation and writing; Tingjian Ge contributed to writing-review and editing and supervision.
Availability of data and materials
Statements and Declarations
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
All datasets, codes and complete results are publicly available at https://github.com/whxhx/Link-Prediction-Methods.
References
- 1.Amaral LA, Ottino JM. Complex networks. Eur Phys J B. 2004;38(2):147–162. doi: 10.1140/epjb/e2004-00110-5. [DOI] [Google Scholar]
- 2.Lü L, Zhou T. Link prediction in complex networks: A survey. Physica A. 2011;390(6):1150–1170. doi: 10.1016/j.physa.2010.11.027. [DOI] [Google Scholar]
- 3.Lü L, Jin C-H, Zhou T (2009) Similarity index based on local paths for link prediction of complex networks. Phys Rev E 80(4):046122 [DOI] [PubMed]
- 4.Uchida M, Shirayama S. Formation of patterns from complex networks. J Visual. 2007;10(3):253–255. doi: 10.1007/BF03181690. [DOI] [Google Scholar]
- 5.Liu Z, He J-L, Srivastava J (2013) Cliques in complex networks reveal link formation and community evolution. Comput Sci
- 6.Kossinets G, Watts DJ. Empirical analysis of an evolving social network. Science. 2006;311(5757):88–90. doi: 10.1126/science.1116869. [DOI] [PubMed] [Google Scholar]
- 7.Lei C, Ruan J. A novel link prediction algorithm for reconstructing protein-protein interaction networks by topological similarity. Bioinformatics. 2012;29(3):355–364. doi: 10.1093/bioinformatics/bts688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Franceschini A, Szklarczyk D, Frankild S, Kuhn M, Simonovic M, Roth A, Lin J, Minguez P, Bork P, Von Mering C, et al (2012) String v9. 1: protein-protein interaction networks, with increased coverage and integration. Nucl Acids Res 41(D1):D808–D815 [DOI] [PMC free article] [PubMed]
- 9.Szklarczyk D, Franceschini A, Wyder S, Forslund K, Heller D, Huerta-Cepas J, Simonovic M, Roth A, Santos A, Tsafou KP, et al. String v10: protein-protein interaction networks, integrated over the tree of life. Nucl Acids Res. 2015;43(D1):D447–D452. doi: 10.1093/nar/gku1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Szklarczyk D, Morris JH, Cook H, Kuhn M, Wyder S, Simonovic M, Santos A, Doncheva NT, Roth A, Bork P et al (2016) The string database in 2017: quality-controlled protein–protein association networks, made broadly accessible. Nucl Acids Res gkw937 [DOI] [PMC free article] [PubMed]
- 11.Liben-Nowell D, Kleinberg J. The link-prediction problem for social networks. J Am Soc Inform Sci Technol. 2007;58(7):1019–1031. doi: 10.1002/asi.20591. [DOI] [Google Scholar]
- 12.Bonchi F, Castillo C, Gionis A, Jaimes A. Social network analysis and mining for business applications. ACM Trans Intell Syst Technol. 2011;2(3):22. doi: 10.1145/1961189.1961194. [DOI] [Google Scholar]
- 13.Adamic LA, Adar E. Friends and neighbors on the web. Soc Netw. 2003;25(3):211–230. doi: 10.1016/S0378-8733(03)00009-1. [DOI] [Google Scholar]
- 14.Chen H, Li X, Huang Z (2005) Link prediction approach to collaborative filtering. In: Proceedings of the 5th ACM/IEEE-CS joint conference on digital libraries, pp 141–142
- 15.Daud NN, Hamid S, Saadoon M, Sahran F, Anuar NB (2020) Applications of link prediction in social networks: a review. J Netw Comput Appl 166:102716
- 16.Nandi G, Das A. A survey on using data mining techniques for online social network analysis. Int J Comput Sci Iss. 2013;10(6):162. [Google Scholar]
- 17.Al Hasan M, Zaki MJ (2011) A survey of link prediction in social networks. Soc Netw Data Analyt 243–275
- 18.Vinupriya A, Gomathi S (2016) Web page personalization and link prediction using generalized inverted index and flame clustering. In: Proceedings of the 2016 international conference on computer communication and informatics, pp 1–8
- 19.Heemakshi Malhi MA. A survey of various link prediction algorithms in complex networks. Int J Comput Sci Mob Comput. 2016;5(6):244–250. [Google Scholar]
- 20.Martínez V, Berzal F, Cubero J-C. A survey of link prediction in complex networks. ACM Comput Surv (CSUR) 2016;49(4):69. [Google Scholar]
- 21.Al Hasan M, Chaoji V, Salem S, Zaki M (2006) Link prediction using supervised learning. Proceedings of SDM Workshop on Link Analysis Couterterrorism & Security 30(9):798–805
- 22.Perozzi B, Alrfou R, Skiena S (2014) Deepwalk: Online learning of social representations. In: Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining
- 23.Zhao P, Aggarwal C, He G (2016) Link prediction in graph streams. In: Proceedings of the 32nd IEEE International Conference on Data Engineering, pp 553–564
- 24.Yao L, Wang L, Pan L, Yao K. Link prediction based on common-neighbors for dynamic social network. Procedia Comput Sci. 2016;83:82–89. doi: 10.1016/j.procs.2016.04.102. [DOI] [Google Scholar]
- 25.Salton G, McGill MJ. Introduction to modern information retrieval. Auckland: MuGraw-Hill; 1986. [Google Scholar]
- 26.Jaccard P. Étude comparative de la distribution florale dans une portion des alpes et des jura. Bulletin de la Societe Vaudoise des Science Naturelles. 1901;37(142):547–579. [Google Scholar]
- 27.Sorensen TA. A method of establishing groups of equal amplitude in plant sociology based on similarity of species content and its application to analyses of the vegetation on danish commons. Biologiske Skrifter. 1948;5:1–34. [Google Scholar]
- 28.Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabási A-L. Hierarchical organization of modularity in metabolic networks. Science. 2002;297(5586):1551–1555. doi: 10.1126/science.1073374. [DOI] [PubMed] [Google Scholar]
- 29.Zhou T, Lü L, Zhang Y-C. Predicting missing links via local information. Eur Phys J B. 2009;71(4):623–630. doi: 10.1140/epjb/e2009-00335-8. [DOI] [Google Scholar]
- 30.Leicht EA, Holme P, Newman ME (2006) Vertex similarity in networks. Phys Rev E 73(2):026120 [DOI] [PubMed]
- 31.Mitzenmacher M. A brief history of generative models for power law and lognormal distributions. Internet Math. 2004;1(2):226–251. doi: 10.1080/15427951.2004.10129088. [DOI] [Google Scholar]
- 32.Liu Z, Zhang Q-M, Lü L, Zhou T. Link prediction in complex networks: a local naïve bayes model. Europhys Lett. 2011;96(4):48007. doi: 10.1209/0295-5075/96/48007. [DOI] [Google Scholar]
- 33.Stojmirović A, Yu Y-K. Information flow in interaction networks. J Comput Biol. 2007;14(8):1115–1143. doi: 10.1089/cmb.2007.0069. [DOI] [PubMed] [Google Scholar]
- 34.Sun D, Zhou T, Liu J-G, Liu R-R, Jia C-X, Wang B-H (2009) Information filtering based on transferring similarity. Phys Rev E 80(1):017101 [DOI] [PubMed]
- 35.Katz L. A new status index derived from sociometric analysis. Psychometrika. 1953;18(1):39–43. doi: 10.1007/BF02289026. [DOI] [Google Scholar]
- 36.Kronecker L (1882) Grundzüge einer arithmetischen theorie der algebraischen grössen... von L. Kronecker, G. Reimer
- 37.Liu W, Lü L (2010) Link prediction based on local random walk. Europhys Lett 89(5):58007–58012(6)
- 38.Brin S, Page L (1998) The anatomy of a large-scale hypertextual web search engine. In: Proceedings of the International Conference on World Wide Web, pp 107–117
- 39.Jeh G, Widom J (2002) Simrank: a measure of structural-context similarity. In: Proceedings of the eighth ACM SIGKDD international conference on knowledge discovery and data mining, pp 538–543
- 40.Chebotarev P, Shamis E. The matrix-forest theorem and measuring relations in small social groups. Autom Rem Control. 1997;58(9):1505–1514. [Google Scholar]
- 41.Guimerà R, Sales-Pardo M (2009) Missing and spurious interactions and the reconstruction of complex networks. In: Proceedings of the National Academy of Science, pp 22073–22078 [DOI] [PMC free article] [PubMed]
- 42.Hastings WK (1970) Monte Carlo sampling methods using Markov chains and their applications
- 43.Friedman N, Getoor L, Koller D, Pfeffer A (2001) Learning probabilistic relational models with structural uncertainty. In: Proceedings of the International Conference on Machine Learning
- 44.Jaeger M (1997) Relational bayesian networks. In: Proceedings of the 13th Conference on Uncertainty in Artifical Intelligence, pp 266–273
- 45.Taskar B, Abbeel P,Wong M-F, Koller D (2007) Relational Markov networks. Introduction to Statistical Relational Learning 175–200
- 46.Neville J, Jensen D. Relational dependency networks. J Mach Learn Res. 2001;8(2):653–692. [Google Scholar]
- 47.Clauset A, Moore C, Newman ME. Hierarchical sturcture and the prediction of missing links in networks. Nature. 2008;453(7191):98. doi: 10.1038/nature06830. [DOI] [PubMed] [Google Scholar]
- 48.Yu K, Chu W, Yu S, Tresp V, Xu Z (2006) Stochastic relational models for discriminative link prediction. In: Proceedings of the international conference on neural information processing systems. pp 1553–1560
- 49.Huang Z Link prediction based on graph topology: the predictive value of generalized clustering coefficient. Social Science Electronic Publishing
- 50.Wang C, Satuluri V, Parthasarathy S (2007) Local probabilistic models for link prediction. In: Proceedings of the IEEE international conference on data mining, pp 322–331
- 51.Cortes C, Vapnik V. Support-vector networks. Mach Learn. 1995;20(3):273–297. [Google Scholar]
- 52.Keller JM, Gray MR, Givens JA. A fuzzy k-nearest neighbor algorithm. IEEE Trans Syst Man Cybern. 1985;4:580–585. doi: 10.1109/TSMC.1985.6313426. [DOI] [Google Scholar]
- 53.Safavian SR, Landgrebe D. A survey of decision tree classifier methodology. IEEE Trans Syst Man Cybern. 1991;21(3):660–674. doi: 10.1109/21.97458. [DOI] [Google Scholar]
- 54.Rish I et al (2001) An empirical study of the naive bayes classifier. In: IJCAI 2001 workshop on empirical methods in artificial intelligence, vol 3, pp 41–46
- 55.Hosmer Jr D W, Lemeshow S, Sturdivant RX (2013) Applied logistic regression, vol 398. Wiley
- 56.Mitra S, Pal SK. Fuzzy multi-layer perceptron, inferencing and rule generation. IEEE Trans Neural Networks. 1995;6(1):51–63. doi: 10.1109/72.363450. [DOI] [PubMed] [Google Scholar]
- 57.Lichtenwalter RN, Lussier JT, Chawla NV (2010) New perspectives and methods in link prediction. In: Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp 243–252
- 58.De Sá HR, Prudêncio RB (2011) Supervised link prediction in weighted networks. In: Proceedings of the International Joint Conference on Neural Networks, pp 2281–2288
- 59.Doppa JR, Yu J, Tadepalli P, Getoor L (2009) Chance-constratined programs for link prediction. In: Proceedings of the NIPS Workshop on Analyzing Networks and Learning with Graphs
- 60.Chen Y-L, Chen M-S, Philip SY (2015) Ensemble of diverse sparsifications for link prediction in large-scale networks. In: Proceedings of the IEEE International Conference on Data Mining, pp 51–60
- 61.Kashima H, Kato T, Yamanishi Y, Sugiyama M, Tsuda K (2009) Link propagation: a fast semi-supervised learning algorithm for link prediction. In: Proceedings of the 2009 SIAM international conference on data mining, pp 1100–1111
- 62.Raymond R, Kashima H (2010) Fast and scalable algorithms for semi-supervised link prediction on static and dynamic graphs. In: Proceedings of the joint European conference on machine learning and knowledge discovery in databases, pp 131–147
- 63.Zeng Z, Chen K-J, Zhang S, Zhang H (2013) A link prediction approach using semi-supervised learning in dynamic networks. In: Proceedings of the Internation Conferennce on Advanced Computational Intelligence, pp 276–280
- 64.Cui P, Wang X, Pei J, Zhu W. A survey on network embedding. IEEE Trans Knowl Data Eng. 2019;31(5):833–852. doi: 10.1109/TKDE.2018.2849727. [DOI] [Google Scholar]
- 65.Zhang D, Yin J, Zhu X, Zhang C. Network representation learning: a survey. IEEE Trans Big Data. 2020;6(1):3–28. doi: 10.1109/TBDATA.2018.2850013. [DOI] [Google Scholar]
- 66.Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems. Computer. 2009;42(8):30–37. doi: 10.1109/MC.2009.263. [DOI] [Google Scholar]
- 67.Menon AK, Elkan C (2011) Link prediction via matrix factorization. In: Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pp 437–452
- 68.Chen B, Li F, Chen S, Hu R, Chen L. Link prediction based on non-negative matirx factorization. PLoS ONE. 2017;12(8):e0182968. doi: 10.1371/journal.pone.0182968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Shaosheng Cao QX, Lu Wei (2015) Grarep: learning graph representations with global structural information. In: Proceedings of the 24th ACM International on Conference on Information and Knowledge Management, pp 891–900
- 70.Chen G, Wang H, Fang Y, Jiang L (2022) Link prediction by deep non-negative matrix factorization. Expert Syst Appl 188:115991
- 71.Duan L, Ma S, Aggarwal C, Ma T, Huai J. An ensemble approach to link prediction. IEEE Trans Knowl Data Eng. 2017;29(11):2402–2416. doi: 10.1109/TKDE.2017.2730207. [DOI] [Google Scholar]
- 72.Grover A, Leskovec J (2016) node2vec: Scalable feature learning for networks. In: Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, pp 855–864 [DOI] [PMC free article] [PubMed]
- 73.Leonardo DR, Ribeiro FR, Savarese Pedro HP (2017) struc2vec: learning node representations from structural identity. In: Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining, pp 385–394
- 74.Yao X, Shao Y, Cui B, Chen L (2021) Uninet: scalable network representation learning with metropolis-hastings sampling. In: Proceedings of the 37th IEEE international conference on data engineering, pp 516–527
- 75.Zhou J, Cui G, Zhang Z, Yang C, Liu Z, Wang L, Li C, Sun M (2019) Graph neural networks: a review of methods and applications. arXiv:1812.08434
- 76.Kipf TN, Welling M (2016) Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907
- 77.Hamilton W, Ying Z, Leskovec J. Inductive representation learning on large graphs. Adv Neural Inf Process Syst. 2017;30:1. [Google Scholar]
- 78.Zhang M, Chen Y (2017) Weisfeiler-Lehman neural machine for link prediction. In: Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp 575–583
- 79.Mahjoub AB, Atri M. An efficient end-to-end deep learning architecture for activity classification. Analog Integrated Circuits Signal Process. 2019;99:23–32. doi: 10.1007/s10470-018-1306-2. [DOI] [Google Scholar]
- 80.Zhang M, Chen Y (2018) Link prediction based on graph neural networks. In: Advances in Neural Information Processing Systems, pp 5165–5175
- 81.Chiang W-L, Liu X, Si S,Li Y, Bengio S, Hsieh C-J (2019) Cluster-gcn: An efficient algorithm for training deep and large graph convolutional networks. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp 257–266
- 82.Veličković P, Cucurull G, Casanova A, Romero A, Lio P, Bengio Y (2017) Graph attention networks. arXiv preprint arXiv:1710.10903
- 83.Cai L, Ji S (2020) A multi-scale approach for graph link prediction. In: Proceedings of the 34th AAAI Conference on Artificial Intelligence, 2020, pp 3308–3315
- 84.Ragunathan K, Selvarajah K, Kobti Z (2020) Link prediction by analyzing common neighbors based subgraphs using convolutional neural network. In: the 24th European Conference on Artificial Intelligence, vol 325, pp 1906–1913
- 85.Guo Z, Wang F, Yao K, Liang J, Wang Z (2022) Multi-scale variational graph autoencoder for link prediction. In: Proceedings of the 15th ACM International Conference on Web Search and Data Mining, pp 334–342
- 86.Jian Tang M W e a , Qu Meng (2015) Line: Large-scale information network embedding. In: Proceedings of the 24th International Conference on World Wide Web, pp 1067–1077
- 87.Mikolov T, Sutskever I, Chen K, Corrado G, Dean J (2013) Distributed representations of words and phrases and their compositionality. In: Proceedings of the 26th International Conference on Neural Information Processing Systems - Volume 2, NIPS’13, Curran Associates Inc., Red Hook, NY, USA, pp 3111–3119
- 88.Mikolov T, Chen K, Corrado G, Dean J (2013) Efficient estimation of word representations in vector space. In: Proceedings of Workshop at ICLR
- 89.Wang D, Cui P, Zhu W (2016) Structural deep network embedding. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp 1225–1234 [DOI] [PMC free article] [PubMed]
- 90.Ren-Meng C, Liu S-Y, Xu X-K (2019) Network embedding for link prediction: the pitfall and improvement. Chaos: Interdiscip J Nonlinear Sci 29:103102. 10.1063/1.5120724 [DOI] [PubMed]
- 91.Tsitsulin A, Mottin D, Karras P, Müller E (2018) Verse: Versatile graph embeddings from similarity measures. In: Proceedings of the 2018 World Wide Web Conference, WWW ’18, International World Wide Web Conferences Steering Committee, Republic and Canton of Geneva, Switzerland, pp 539–548. 10.1145/3178876.3186120
- 92.Newman ME (2001) Clustering and preferential attachment in growing networks. Phys Rev E 64(2):025102 [DOI] [PubMed]
- 93.Zhao Z, Gou Z, Du Y, Ma J, Li T, Zhang R (2022) A novel link prediction algorithm based on inductive matrix completion. Expert Syst Appl 188:116033
- 94.Newman ME. The structure and function of complex networks. SIAM Rev. 2003;45(2):167–256. doi: 10.1137/S003614450342480. [DOI] [Google Scholar]
- 95.Watts DJ, Strogatz SH. Collective dynamics of small-world networks. Nature. 1998;393(6684):440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 96.Kunegis J (2013) http://konect.cc/statistics/clusco#b736
- 97.Newman ME (2002) Assortative mixing in networks. Phys Rev Lett 89(20):208701 [DOI] [PubMed]
- 98.Newman ME. Power laws, pareto distributions and Zipf’s law. Contemp Phys. 2005;46(5):323–351. doi: 10.1080/00107510500052444. [DOI] [Google Scholar]
- 99.Kunegis J (2013) http://konect.cc/statistics/power
- 100.Leskovec J, Kleinberg J, Faloutsos C. Graph evolution: densification and shrinking diameters. ACM Trans Knowl Discov Data. 2007;1(1):1–40. doi: 10.1145/1217299.1217301. [DOI] [Google Scholar]
- 101.Ripeanu M, Foster I (2002) Mapping the gnutella network: macroscopic properties of large-scale peer-to-peer systems. In: International Workshop on Peer-to-Peer systems. Springer, pp 85–93
- 102.Boyce DE, Chon KS, Ferris M, Lee YJ, Lin K, Eash R (1985) Implementation and evaluation of combined models of urban travel and location on a sketch planning network. Chicago Area Transportation Study
- 103.Kunegis J (2013) http://konect.cc/networks/subelj_euroroad
- 104.Opsahl T, Agneessens F, Skvoretz J. Node centrality in weighted networks: generalizing degree and shortest paths. Soc Networks. 2010;3(32):245–251. doi: 10.1016/j.socnet.2010.03.006. [DOI] [Google Scholar]
- 105.Opsahl T (2011) Why anchorage is not that important : Binary ties and sample selections. https://toreopsahl.com/2011/08/12/why-anchorage-is-not-that-important-binary-ties-and-sample-selection/
- 106.Kunegis J (2013) http://konect.cc/networks/chess
- 107.Kunegis J (2013) http://konect.cc/networks/moreno_crime
- 108.Opsahl T. Triadic closure in two-mode networks: redefining the global and local clustering coefficients. Soc Networks. 2011;35(2):159–167. doi: 10.1016/j.socnet.2011.07.001. [DOI] [Google Scholar]
- 109.Ewing RM, Chu P, Elisma F, Li H, Taylor P, Climie S, McBroom-Cerajewski L, Robinson MD, O’Connor L, Li M, et al. Large-scale mapping of human protein-protein interactions by mass spectrometry. Mol Syst Biol. 2007;3(1):89. doi: 10.1038/msb4100134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Stelzl U, Worm U, Lalowski M, Haenig C, Brembeck FH, Goehler H, Stroedicke M, Zenkner M, Schoenherr A, Koeppen S, et al. A human protein-protein interaction network: a resource for annotating the proteome. Cell. 2005;122(6):957–968. doi: 10.1016/j.cell.2005.08.029. [DOI] [PubMed] [Google Scholar]
- 111.Rual J-F, Venkatesan K, Hao T, Hirozane-Kishikawa T, Dricot A, Li N, Berriz GF, Gibbons FD, Dreze M, Ayivi-Guedehoussou N, et al. Towards a proteome-scale map of the human protein–protein interaction network. Nature. 2005;437(7062):1173–1178. doi: 10.1038/nature04209. [DOI] [PubMed] [Google Scholar]
- 112.Han J-DJ, Dupuy D, Bertin N, Cusick ME, Vidal M. Effect of sampling on topology predictions of protein–protein interaction networks. Nat Biotechnol. 2005;23(7):839–844. doi: 10.1038/nbt1116. [DOI] [PubMed] [Google Scholar]
- 113.Moody J. Peer influence groups: identifying dense clusters in large networks. Soc Netw. 2001;23(4):261–283. doi: 10.1016/S0378-8733(01)00042-9. [DOI] [Google Scholar]
- 114.Isella L, Stehlé J, Barrat A, Cattuto C, Pinton J-F, Van den Broeck W. What’s in a crowd? Analysis of face-to-face behavioral networks. J Theor Biol. 2011;271(1):166–180. doi: 10.1016/j.jtbi.2010.11.033. [DOI] [PubMed] [Google Scholar]
- 115.Gleiser PM, Danon L. Community structure in Jazz. Adv Complex Syst. 2003;6(4):565–573. doi: 10.1142/S0219525903001067. [DOI] [Google Scholar]
- 116.Coleman J, Katz E, Menzel H. The diffusion of an innovation among physicians. Sociometry. 1957;20(4):253–270. doi: 10.2307/2785979. [DOI] [Google Scholar]
- 117.Freeman LC, Webster CM, Kirke DM. Exploring social structure using dynamic three-dimensional color images. Soc Networks. 1998;20(2):109–118. doi: 10.1016/S0378-8733(97)00016-6. [DOI] [Google Scholar]
- 118.Massa P, Salvetti M, Tomasoni D (2009) Bowling alone and trust decline in social network sites. In: Proceedings of the IEEE International Conference on Dependable, Autonomic and Secure Computing, pp 658–663
- 119.Cho E, Myers SA, Leskovec J (2011) Friendship and mobility: User movement in location-based social networks. In: Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp 1082–1090
- 120.Kunegis J (2013) http://konect.cc/networks/dnc-corecipient
- 121.Zafarani R, Liu H (2009) Social computing data repository at asu. http://socialcomputing.asu.edu
- 122.Richardson M, Agrawal R, Domingos P (2003) Trust management for the semantic web. In: The Semantic Web-ISWC 2003, Springer, pp 351–368
- 123.Leskovec J, Mcauley JJ (2012) Learning to discover social circles in ego networks. In: Advances in neural information processing systems, pp 539–547
- 124.Kunegis J (2013) http://konect.cc/networks/petster-friendships-hamster
- 125.Boguñá M, Pastor-Satorras R, Díaz-Guilera A, Arenas A (2004) Models of social networks based on social distance attachment. Phys Rev E Stat Nonlinear Soft Matter Phys 70(5):056122 [DOI] [PubMed]
- 126.Kunegis J, Preusse J (2012) Fairness on the web: alternatives to the power law. In: Proceedings of the 4th Annual ACM Web Science Conference, pp 175–184
- 127.Fiedler M. Algebraic connectivity of graphs. Czechoslov Math J. 1973;23(2):298–305. doi: 10.21136/CMJ.1973.101168. [DOI] [Google Scholar]
- 128.https://en.wikipedia.org/wiki/Algebraic_connectivity (2020)
- 129.Newman ME (2004) Coauthorship networks and patterns of scientific collaboration. In: Proceedings of the National Academy of Sciences, pp 5200–5205 [DOI] [PMC free article] [PubMed]
- 130.Šubelj L, Bajec M. Robust network community detection using balanced propagation. Eur Phys J B. 2011;81(3):353–362. doi: 10.1140/epjb/e2011-10979-2. [DOI] [Google Scholar]
- 131.Ji J, Zhang A, Liu C, Quan X, Liu Z (2014) Survey: functional module detection from protein–protein interaction networks. In: Proceedings of the IEEE Transactions on Knowledge and Data Engineer, pp 261–277
- 132.Leskovec J, Krevl A (2014) SNAP Datasets: stanford large network dataset collection. http://snap.stanford.edu/data
- 133.Kunegis J (2013) KONECT—The Koblenz Network Collection. In: Proceedings of International Conference on World Wide Web Companion, pp 1343–1350. http://dl.acm.org/citation.cfm?id=2488173
- 134.Tang J (2006) Aminer dataset. https://www.aminer.cn/data/ (May )
- 135.Domenico MD (2017) Datasets released for reproducibility. https://manliodedomenico.com/data.php
- 136.Batagelj V, Mrvar A (2006) Pajek datasets. http://vlado.fmf.uni-lj.si/pub/networks/data/
- 137.Rossi RA, Ahmed NK (2015) The network data repository with interactive graph analytics and visualization. In: Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence. http://networkrepository.com
- 138.Knight S (2011) The internet topology zoo. http://topology-zoo.org/dataset.html
- 139.Hagberg A, Swart P, Chult DS (2008) Exploring network structure, dynamics, and function using networkx, Tech. rep., Los Alamos National Lab.(LANL), Los Alamos, NM (United States)
- 140.Csardi G, Nepusz T, et al. The igraph software package for complex network research. InterJ Complex Syst. 2006;1695(5):1–9. [Google Scholar]
- 141.Handcock MS, Hunter DR, Butts CT, Goodreau SM, Morris M. statnet: Software tools for the representation, visualization, analysis and simulation of network data. J Stat Softw. 2008;24(1):1548. doi: 10.18637/jss.v024.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Bastian M, Heymann S, Jacomy M (2009) Gephi: an open source software for exploring and manipulating networks. In: Proceedings of the international AAAI conference on web and social media, vol 3, pp 361–362
- 143.De Domenico M, Porter MA, Arenas A. Muxviz: a tool for multilayer analysis and visualization of networks. J Complex Netw. 2015;3(2):159–176. doi: 10.1093/comnet/cnu038. [DOI] [Google Scholar]
- 144.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (roc) curve. Radiology. 1982;143(1):29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- 145.Chakrabarti S, Khanna R, Sawant U, Bhattacharyya C (2008) Structured learning for non-smooth ranking losses. In: Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’08, Association for Computing Machinery, New York, NY, USA, pp 88–96. 10.1145/1401890.1401906
- 146.Bordes A, Usunier N, Garcia-Duran A, Weston J, Yakhnenko O. Translating embeddings for modeling multi-relational data. Adv Neural Inf Process Syst. 2013;26:1. [Google Scholar]
- 147.https://github.com/whxhx/Link-Prediction-Methods (2021)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.