Removal of Partial Fourier-Induced Gibbs (RPG) Ringing artifacts in MRI

Abstract

Purpose:

To investigate and remove Gibbs-ringing artifacts caused by partial Fourier (PF) acquisition and zero filling interpolation in MRI data.

Theory and Methods:

Gibbs ringing of fully sampled data, leading to oscillations around tissue boundaries, is caused by the symmetric truncation of k-space. Such ringing can be removed by conventional methods, with the local subvoxel shifts method being the state-of-the-art. However, the asymmetric truncation of k-space in routinely used PF acquisitions leads to additional ringings of wider intervals in the PF sampling dimension that cannot be corrected solely based on magnitude images reconstructed via zero filling. Here, we develop a pipeline for the Removal of PF-induced Gibbs ringing (RPG) to remove ringing patterns of different periods by applying the conventional method twice. The proposed pipeline is validated on numerical phantoms, demonstrated on in vivo diffusion MRI measurements, and compared with the conventional method and neural network-based approach.

Results:

For PF = 7/8 and 6/8, Gibbs-ringings and subsequent bias in diffusion metrics induced by PF acquisition and zero filling are robustly removed by using the proposed RPG pipeline. For PF = 5/8, however, ringing removal via RPG leads to excessive image blurring due to the interplay of image phase and convolution kernel.

Conclusions:

RPG corrects Gibbs-ringing artifacts in magnitude images of PF acquired data and reduces the bias in quantitative MR metrics. Considering the benefit of PF acquisition and the feasibility of ringing removal, we suggest applying PF = 6/8 when PF acquisition is necessary.

1. Introduction

By encoding images in the Fourier domain (k-space) with applied magnetic field gradients, MRI serves as a super-resolution medical imaging technique probing anatomical structure much smaller than radiofrequency wavelength. However, constraints of scan time and singal-to-noise level limit the amount of the k-space data that can be sampled. The maximal spatial frequency ±K_max of the sampled data leads to a sharp edge in the Fourier domain and subsequent Gibbs-ringing artifacts in the image space(Wilbraham, 1848; Gibbs, 1898).

Conventionally, the k-space data is acquired symmetrically around the low frequency k = 0 domain in a Cartesian grid (line by line), resulting in a symmetric truncation of the k-space data, usually dubbed “fully”-sampled data. Many algorithms have been proposed to correct the Gibbs-ringing artifacts due to this symmetric truncation in k-space. The early approaches include the Lanczos-type local averaging method(Jerri, 2000) and the hybrid Gegenbauer reconstruction(Archibald & Gelb, 2002). Later on, total variation (TV) approaches have been applied to jointly reduce noise and ringings(Sarra, 2006; Block et al., 2008; Perrone et al., 2015; Veraart et al., 2016); the choice of regularization factors for TV or total generalized variation (TGV) necessitates the noise level estimation and noise reduction during the ringing removal. Alternatively, as the image is reconstructed on a discretized grid, the image can be re-interpolated on the local subvoxel-shifts to sample the ringing pattern at the zero-crossings of the oscillation kernel (sinc function)(Kellner et al., 2016). In early works, the idea of global subvoxel-shifts implemented by using the translational phase-shift in k-space has been applied to reduce the partial volume effect in MR angiography(Du et al., 1994) and functional MRI(Du et al., 2014); subsequently, the dark rim artifact in myocardial perfusion MRI was suggested to be due to Gibbs-ringing, the degree of which was attributed to subvoxel-shifts relative to the endocardial border(Ferreira et al., 2009). Recently, a convolutional neural network (CNN) has been used to remove the Gibbs-ringing either with(Muckley et al., n.d.) or without(Wang et al., 2017) adding noise into the training data.

Partial Fourier (PF) is a common technique to accelerate MRI acquisition and shorten echo time (TE)(Sotiropoulos et al., 2013). Due to the MR data redundancy (e.g., smoothly varying image phase), it is possible to restore nearly half of the k-space data instead of acquiring it; such PF acquisition leads to an asymmetric truncation in the k-space and complicates the ringing artifacts. The easiest way to remove the ringings for such data is to recover fully sampled k-space data by using PF reconstruction algorithms, such as Margosian and Projection Onto Convex Sets (POCS) methods(McGibney et al., 1993), and perform above-mentioned ringing removal pipelines (Figure 1). However, this PF reconstruction method requires the knowledge of image phase map or k-space data, which is often unavailable for public MRI databases and clinical data reconstructed by simply using zero filling. Lately, Muckley et al.(Muckley et al., n.d.) used CNN to jointly remove Gibbs-ringings and the noise for PF acquired data of magnitude or complex images reconstructed via zero filling; ringings in PF acquired complex images were robustly removed as expected, whereas ringings of PF acquired magnitude images were only partially removed, especially for highly undersampled data.

Figure 1.

Numerical simulations of Gibbs-ringing removal in 2D magnitude images of the Shepp-Logan phantom with the additional phase (Section 3.4.2). The first row shows magnitude images reconstructed by using zero filling interpolation without corrections, and the second and third rows show images processed by applying PF reconstruction (Margosian or POCS) (McGibney et al., 1993) and local subvoxel-shifts (SuShi) ringing removal(Kellner et al., 2016) on the complex data. The red arrows indicate that the Margosian method leads to biased image intensity in phase-wrapping regions; in contrast, POCS does not. Conventionally, with the knowledge of image phase map or k-space data, POCS+SuShi is the most robust way of removing ringings in PF acquired data. However, the complex-valued data is often unavailable for public MRI databases and clinical data. SI is the sharpness index(Vu et al., 2011).

Gibbs ringing around sharp edges in MRI has been shown to bias diffusion metrics around, for example, the boundary between cerebrospinal fluid (CSF) and brain white matter (WM)(Perrone et al., 2015; Veraart et al., 2016; Kellner et al., 2016). In particular, for PF acquired data reconstructed via zero filling, the underestimated mean diffusivity (MD) in genu and splenium of the corpus callosum (CC) has been reported as spurious dark bands in WM around the CSF in MD map(Kellner et al., 2016). These banding artifacts are wider than ordinary Gibbs ringings of fully sampled data, and cannot be corrected by pipelines targeting ringings of fully sampled data. Yet, PF acquisition has been widely used in diffusion MRI (dMRI) to shorten the TE for achieving higher signal-to-noise ratios (SNR). Besides, zero filling is sometimes preferred since PF reconstruction can be vulnerable to motion during the echo train of echo-planar imaging (EPI)(Sotiropoulos et al., 2013; Bammer et al., 2010). For instance, dMRI data in Human Connectome Project were obtained using PF acquisition of 6/8 and zero filling interpolation, and only magnitude images were made publicly available for dMRI(Sotiropoulos et al., 2013). To achieve fast and accurate quantitative analysis for such data, it is essential to develop an efficient and robust pipeline to correct the “unconventional”, PF-induced Gibbs ringing.

Here, we analytically investigate the origin of Gibbs ringing patterns caused by the PF acquisition and zero filling interpolation, and propose a pipeline for the Removal of PF-induced Gibbs ringing (RPG), based on any conventional (fully-sampled) unringing method, to correct the extra ringing arising in PF-acquired magnitude images. While the RPG pipeline is in principle independent of the choice of the conventional unringing method, here we employ the local subvoxel-shifts method(Kellner et al., 2016) as a current state-of-the-art. We demonstrate the RPG pipeline in magnitude signals of numerical phantoms and of in vivo human brain dMRI data, and observe the effect of the ringing removal on diffusion metrics. We emphasize that the RPG pipeline is applicable not just to EPI-acquired dMRI data but also to MRI of other contrasts acquired using PF Cartesian k-space sampling, such as anatomical MRI or functional MRI. The main advantage of our approach is in its theoretical foundation alleviating the need for adjustable parameters, training data, or complex-valued data, making it a straightforward method to correct magnitude images.

2. Theory

To understand ringing patterns due to the PF acquisition and zero filling, we explore the point spread function (PSF), i.e., oscillating convolution kernel in image space, caused by the asymmetric k-space truncation. For PF acquisition of factor pf, the k-space data is asymmetrically truncated at cutoffs k = −νK_max and +K_max (Figure 2a), where

$$v=2pf-1<1,\frac{1}{2}<pf<1.$$

Figure 2.

The theory of Gibbs-ringing artifacts due to the PF acquisition and zero filling interpolation. a. For PF acquisition of factor pf, the k-space data is asymmetrically truncated at k = −(2pf − 1) · K_max and +K_max. b. This modulation in k-space leads to multiple zeros in the point spread function in Equations (1) and (5), i.e., oscillating convolution kernel in image space. Positions of these zeros correspond to oscillation patterns of different intervals x_r and x_ν in Equations 3 and 6 in the image space, indicated by blue and red curves (sinc functions) respectively.

The Fourier transform of this k-space modulation yields a PSF P_ν(x) accounting for the Gibbs-ringing patterns in image space. By definition, P_ν(x) is a result of the cutoffs in the delta-function at x = 0:

$$P_{\nu }\left(x\right)\equiv {\int }_{-\nu K_{\mathrm{m}\mathrm{a}\mathrm{x}}}^{K_{\mathrm{m}\mathrm{a}\mathrm{x}}}\frac{dk}{2\pi }{e}^{ikx}=\frac{1}{2\pi ix}\left(e^{i{K}_{\mathrm{m}\mathrm{a}\mathrm{x}}x}-e^{-i\nu K_{\mathrm{m}\mathrm{a}\mathrm{x}}x}\right).$$ (1)

This function has sinusoidal oscillations at both cutoffs, with periods 2π/K_max and 2π/νK_max. Given that the voxel size

$$\Delta x=\frac{\pi }{K_{\mathrm{m}\mathrm{a}\mathrm{x}}}$$ (2)

is half the smallest period, we see that ringing patterns correspond to intervals

$$x_r=\Delta x$$ (3)

and

$$x_{\nu }=\frac{\Delta x}{\nu }=\frac{\Delta x}{2pf-1}>\Delta x.$$ (4)

Here, we defined the interval of a ringing pattern as the distance of peak-to-valley or valley-to-peak along x- and/or y-directions in the magnitude image, such that the distance from the central peak to the first zero of the convolution kernel (sinc function) is the same as the interval of the ringing pattern.

The real part of the PSF in Equation 1 is an even function and it is nonzero at x = 0. In contrast, the imaginary part of the PSF is an odd function and it is equal to zero at x = 0. In other words, for the most part, the ringings patterns arise by the convolution with PSF’s real part,

$$Re{P}_{\nu }\left(x\right)=\frac{1}{2\Delta x}\left[\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\left(\pi \frac{x}{x_r}\right)+\nu \cdot \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\left(\pi \frac{x}{x_{\nu }}\right)\right],$$ (5)

where sinc(x ) ≡ sinx/x. Interestingly, the first ringing pattern of interval x_r is exactly the same as the ordinary Gibbs-ringing of fully sampled data (with half the amplitude), and the second ringing pattern has an interval x_ν wider than the first one. The first ringing pattern arises as the result of the ordinary rectangular modulation at k = +K_max (denoted by “r”), and the second ringing pattern is the consequence of the asymmetric truncation at k = −νK_max (denoted by “ν”). Here, we list x_ν for commonly used under-sampling factors:

$$x_{\nu }=\left\{\begin{array}{ll}\frac{4}{3}\Delta x,& pf=7/8;\\ 2\Delta x,& pf=6/8;\\ 4\Delta x,& pf=5/8.\end{array}\right.$$ (6)

PSF’s real part in Equation 5 is the superposition of two sinc functions, indicating that the two ringing patterns can be independently removed by applying conventional algorithms twice. However, PSF’s imaginary part is negligible only when the image phase map (the ideal one without k-space truncation) smoothly varies over the image space in a length scale much longer than ringing intervals. This is empirically true for pf = 7/8 and 6/8, whose ringing intervals are relatively short. However, for pf = 5/8, the wide ringing interval x_ν = 4Δx potentially breaks this assumption in experimental data.

Most algorithms correcting Gibbs-ringing artifacts focus only on the oscillations of interval x_r in Equation 3 (blue curves in Figure 2b), while oscillations of interval x_ν in Equation 6 (red curves in Figure 2b) have been considered as anatomical structures and left untreated.

3. Methods

Our innovation is to recognize and remove the two distinct ringing patterns, with intervals x_r and x_ν, by employing the conventional method twice. The identification and removal of the x_ν pattern will be done by resampling the image in such a way that the problem gets reduced to removing the conventional pattern x_r in the resampled image. In this way, the PF-specific Gibbs pattern (with interval x_ν) can be removed both in 1-dimensional (1D) and in 2D magnitude images.

Since we employ the local subvoxel-shifts method(Kellner et al., 2016) as the state-of-the-art for the conventional Gibbs pattern, we first briefly outline the idea behind it, then describe our RPG pipeline, and finally validate it on numerical phantoms and on in vivo dMRI data of a human brain.

3.1. Recap: Local subvoxel-shifts

Let us briefly recap the idea of local subvoxel-shifts method for the ringing removal of fully sampled data (Kellner et al., 2016). The k-space modulation in fully sampled data is symmetrically truncated at k = ±K_max, leading to a convolution kernel of a sinc function of ringing interval Δx in image space. The prior knowledge of the shape of this specific ringing pattern, under the assumption of no oscillation in a “perfect” image, allows one to identify the position of the boundary to a subvoxel precision, analogous to the idea of super-resolution. After shifting the image by a subvoxel amount through Fourier interpolation, the optimal shift t for each voxel can be individually determined by minimizing the local signal oscillation (e.g., TV) around the voxel. Based on the optimal subvoxel-shift and its subsequent signal with locally minimized oscillations, the signal at the original position is linearly re-interpolated to the grid before shifting.

Since, according to Equation 4, the PF and regular ringing patterns due to a given tissue boundary interfere additively, the local subvoxel-shifts (t_r, t_ν) are not independent, and should be proportional to the corresponding ringing intervals (x_r, x_ν), such that

$$\frac{t_{\nu }}{t_r}=\frac{x_{\nu }}{x_r}=\frac{1}{2pf-1}.$$ (7)

As shown in simulations in Supporting Information (Figure S1), the shift ratio t_ν/t_r, for the case when the shift is nonzero, generally obeys Equation 7. Of course, the shifts widely fluctuate between voxels, such that for some there is no shift at all, but when the shift is actually needed, the above ratio holds to a reasonable numerical accuracy. Given the known PSF shape, one may attempt to design a procedure to self-consistently determine both shifts for both ringing patterns simultaneously. Practically, however, we found it difficult to use Equation 7 to regularize and optimize both local shifts in ringing removal pipeline at the same time, due to image phase and noise in actual data. Hence, in what follows, we remove the two kinds of ringing independently from each other. The benefit of this approach is in the decoupling of the RPG pipeline from a particular conventional Gibbs pattern removal algorithm.

3.2. Removal of partial Fourier-induced Gibbs-ringing (RPG)

The RPG pipeline consists of two steps: We first remove the ringing of interval x_ν given by Equation 6, and then remove the ringing of interval x_r given by Equation 3.

3.2.1. 1D case

The 1D case of ringing removal is relatively simple. Given that the 1D image (N_x × 1 array) is obtained by using PF acquisition and zero filling in k-space, we introduce the 1D RPG pipeline for pf = 7/8, 6/8, and 5/8 as follows:

• For pf = 7/8, we first remove the ringing of interval $x_{\nu }=\frac{4}{3}\Delta x$ in Equation 6. To do so, we use nearest neighbor to up-sample the 1D image by 3 fold (3N_x × 1 array) and divide it into 4 smaller sub-images (taking one array element for every 4 elements, i.e., (4n + i)th element, n = 0,1,2,..., $⌊\frac{3N_x}{4}⌋$, and i = 1,2,3,4 for each sub-image), where the ringing interval becomes x_ν′ = Δx. Then we apply the ordinary local subvoxel-shifts method in the 4 sub-images respectively to remove ringings of interval x_ν′. After combining the corrected sub-images together and use nearest neighbor to down-sample the combined image by 3 fold (N_x × 1 array), we again use the local subvoxel-shifts method to remove the remaining ringing of interval x_r = Δx.

• For pf = 6/8, we first target the ringing of interval x_ν = 2Δx in Equation 6; we divide the 1D image into 2 smaller sub-images (taking the odd and even elements respectively), where the ringing interval becomes x_ν′ = Δx. Then we apply the local subvoxel-shifts method in the 2 sub-images respectively to remove ringings of interval x_ν′. After combining the corrected sub-images together, we again use the local subvoxel-shifts method to remove the remaining ringing of interval x_r = Δx.

• For pf = 5/8, we first focus on the ringing of interval x_ν = 4Δx in Equation 6; we divide the 1D image into 4 smaller sub-images (taking one element for every 4 elements, i.e., (4n + i)th element, n = 0,1,2,..., $⌊\frac{N_x}{4}⌋$, and i = 1,2,3,4 for each sub-image), where the ringing interval becomes x_ν′ = Δ. Then we apply the local subvoxel-shifts method to the 4 sub-images respectively to remove ringings of interval x_ν′. After combining the corrected sub-images together, we again apply the local subvoxel-shifts method to remove the remaining ringing of interval x_r = Δx.

Using ideas similar to those in ref. 9, we generalize the above 1D pipeline to 2D magnitude images.

3.2.2. 2D case

As discussed in ref. 9, generalizing the algorithm to the 2D case by applying 2D-shift cannot remove ringings of checkerboard-like pattern caused by diagonal edges in images. For the fully acquired data, instead, Kellner et al. introduced the “weighting” filter functions with a saddle-like structure in Fourier domain(Kellner et al., 2016):

$$\begin{array}{rr}{G}_x& =\frac{1+\mathrm{c}\mathrm{o}\mathrm{s}{k}_y}{(1+\mathrm{c}\mathrm{o}\mathrm{s}{k}_y)+(1+\mathrm{c}\mathrm{o}\mathrm{s}{k}_x)},\\ G_y& =\frac{1+\mathrm{c}\mathrm{o}\mathrm{s}{k}_x}{(1+\mathrm{c}\mathrm{o}\mathrm{s}{k}_y)+(1+\mathrm{c}\mathrm{o}\mathrm{s}{k}_x)},\end{array}$$ (8)

where G_x + G_y = 1 for any (k_x, k_y), and Δx = Δy = 1 for simplicity. After applying the filter G_x to the original image I, the ringing is suppressed in y direction and enhanced in x direction in the filtered image I_x, and vice versa for the G_y and I_y(Kellner et al., 2016):

$$\begin{array}{r}{I}_x={\mathrm{F}\mathrm{T}}^{-1}\left\{\mathrm{F}\mathrm{T}\right\{I\}\cdot G_x\},\\ I_y={\mathrm{F}\mathrm{T}}^{-1}\left\{\mathrm{F}\mathrm{T}\right\{I\}\cdot G_y\},\end{array}$$ (9)

where FT{⋅} is the Fourier transform. Removing ringings in I_x using local subvoxel-shifts along x-direction (denoted as “unring x”) results in a corrected image J_x. Similarly, applying local subvoxel-shifts along y-direction (“unring y”) to the I_y leads to a corrected image J_y. Their sum yields the final corrected image J = J_x + J_y, which is well-normalized due to G_x + G_y = 1. Here we emphasize that unring x and unring y do not include the filter smoothing, but only the local subvoxel-shifts searching of ringing removal. For simplicity, we denote the above local bvoxel-fts pipeline for 2D fully sampled data as “SuShi” (see FIG. 3 in ref. 9).

Figure 3.

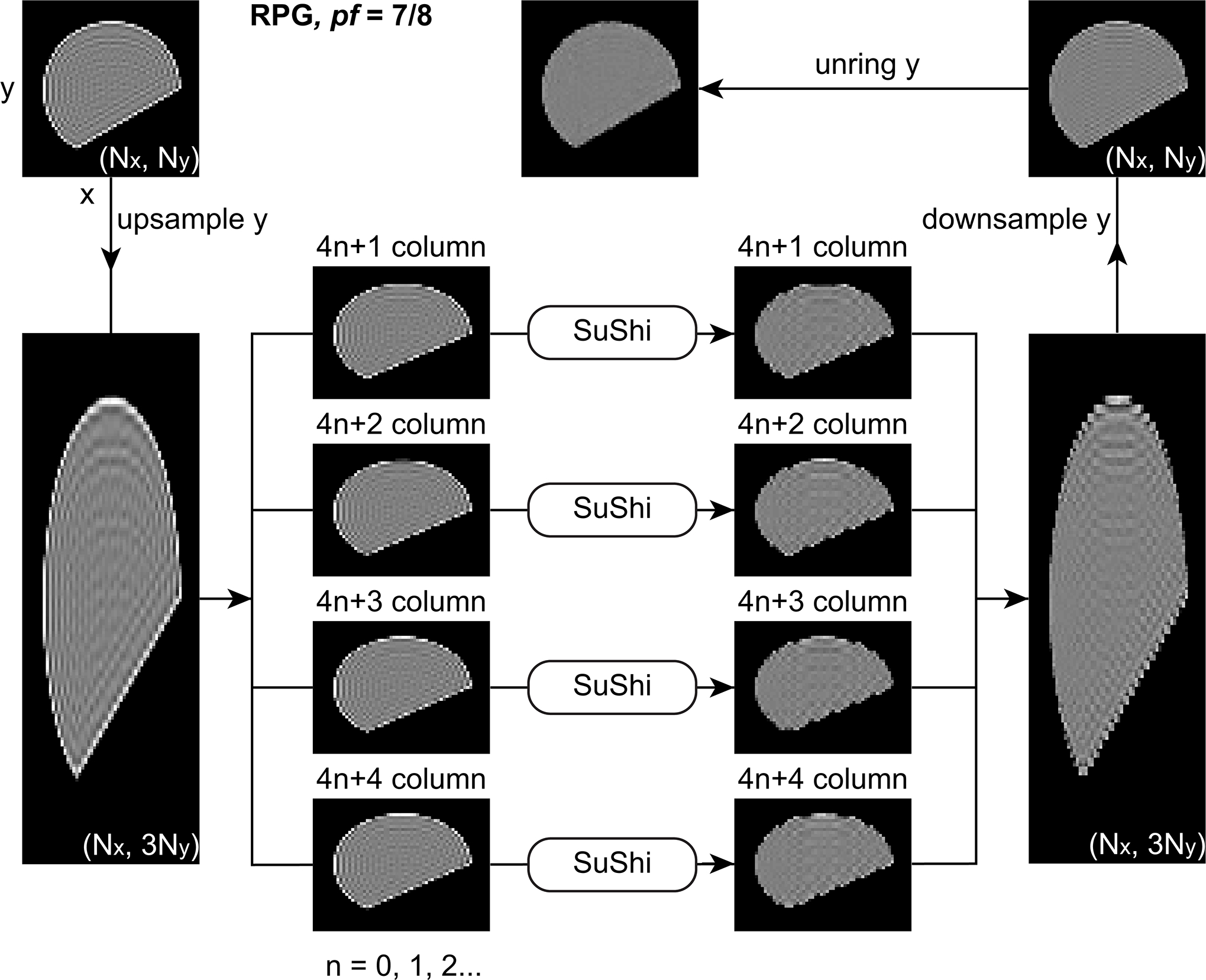
Removing Gibbs-ringing in 2D images. Removal of PF induced Gibbs-ringing (RPG) of pf = 7/8. Reconstructing PF acquired k-space data with zero filling leads to extra ringings of interval $\frac{4}{3}\Delta y$ in phase-encoding (y) direction. To remove ringings, we up-sample the image in y direction by 3 fold and divide it into 4 smaller sub-images (taking one column for every 4 columns). After applying local subvoxel-shifts (SuShi) on the 4 sub-images, ringings of interval Δx and $\frac{4}{3}\Delta y$ are removed. After combining the 4 sub-images and down-sample it in y direction by 3 fold, we apply ordinary unring y to remove ringings of interval Δy. In this figure, each image is rotated by 90°, and the column in each image is in a horizontal direction.

For PF acquired 2D magnitude images, we assume that k-space data is asymmetrically sampled in k_y-direction, and thus the ringing induced by PF acquisition and zero filling is in y-direction in the images. The original image is a N_x × N_y matrix, with a voxel size of (Δx, Δy) in x- and y-directions. Here we focus on the removal of three ringing patterns, including ringings of intervals x_r = Δx and y_r = Δy in x- and y-directions, and of interval y_ν in Equation 6 in y-direction. Our 2D RPG pipeline is described as follows (Figures 3, 4, and S4):

• For pf = 7/8 (Figure 3, Table S1), we first remove the ringings of interval x_r = Δx in x-direction and of interval $y_{\nu }=\frac{4}{3}\Delta y$ in y-direction. To do so, we use nearest neighbor to up-sample the 2D image by 3 fold in y-direction (N_x × 3N_y matrix), and divide it into 4 smaller sub-images (taking one column for every 4 columns, i.e., (4n + i)th column, n = 0,1,2,..., $⌊\frac{3N_y}{4}⌋$, and i = 1,2,3,4 for each sub-image), where the ringing interval in y-direction becomes y_ν′ = Δy, and the ringing interval x_r = Δx in x-direction is kept unchanged. Then we apply the original SuShi method in the 4 sub-images respectively to remove the ringings of interval x_r in x-direction and of interval y_ν′ in y-direction. After combining the corrected sub-images together and using nearest neighbor to down-sample the combined image by 3 fold in y-direction (N_x × N_y matrix), we use the 1D local subvoxel-shifts in y-direction (unring y) to remove the remaining ringing of interval y_r = Δy in y-direction.

• For pf = 6/8, naively it makes sense to remove Gibbs-ringing similarly to the case of pf = 7/8, i.e., by dividing the 2D image into 2 smaller sub-images (consisting of odd and even columns respectively) and applying SuShi to the two sub-images to remove ringings of intervals y_ν′ = Δy and x_r = Δx, and then combining the two sub-images and applying the 1D local sub-voxel shifts (unring y) to remove the remaining ringing of interval y_r = Δy. This approach, as shown in Supporting Information, introduces excessive image blurring; in this study, it is dubbed as an alternative approach and detailed in Figures S2 and S3. Instead, it turns out that image blurring and performance of ringing removal are best balanced by first applying the weighting filters (G_x, G_y) and only then searching for local subvoxel-shifts. This is our primary pipeline for pf = 6/8 (Figure 4, Table S2).

• To begin, we apply weighting filter functions G_x and G_y in Equation 8 to the original image I, resulting in filtered images I_x and I_y in Equation 9. On the one hand, for I_y, the ringing of interval x_r = Δx in x-direction is suppressed by G_y, and the ringing of interval y_r = Δy in y-direction is subsequently removed by using 1D local subvoxel-shifts (unring y), yielding an intermediate image J_y. To remove the ringing of interval y_ν = 2Δy in y-direction, we further divide the J_y into two sub-images by taking the odd and even columns respectively, and apply 1D local subvoxel-shifts (unring y) to each of them. Combining the two corrected sub-images, we obtain the first corrected image ${\tilde{J}}_y$. On the other hand, for I_x, the ringing of interval y_r = Δy in y-direction is suppressed by G_x, and the ringing of interval x_r = Δx in x-direction is subsequently removed by using 1D local subvoxel-shifts (unring x), leading to the second corrected image J_x. Particularly, in J_x, the ringing of interval y_ν = 2Δy is left untouched because it is difficult to define a filter to simultaneously suppress the ringings of intervals y_r = Δy and y_ν = 2Δy in y-direction. Finally, the sum of the two corrected images yields the final output $J={\tilde{J}}_y+J_x$.

• For pf = 5/8 (Figure S4, Table S3), we first remove the ringings of interval x_r = Δx in x-direction and of interval y_ν = 4Δy in y-direction. Dividing the original image into 4 sub-images (taking one column for every 4 columns, i.e., (4n + i)th column, n = 0,1,2,..., $⌊\frac{N_y}{4}⌋$, and i = 1,2,3,4 for each sub-image), we apply SuShi to 4 sub-images respectively to remove ringings of interval x_r in x-direction and of interval y_ν′ = Δy in y-direction. After combining sub-images together, we use the 1D local subvoxel-shifts in y-direction (unring y) to remove the remaining ringing of interval y_r = Δy in y-direction.

Figure 4.

Removing Gibbs-ringing in 2D images (continued). RPG of pf = 6/8. The PF acquisition and zero filling induce extra ringings of interval 2Δy in phase-encoding (y) direction. The ringing removal pipeline has two steps: First, the weighting filter G_y is applied to the Fourier domain of the original image, smoothing out ringings of interval Δx in x-direction. The remaining ringings of interval Δy in y direction are subsequently removed by applying unring y to the image, and ringings of interval 2Δy are removed by applying unring y to sub-images consisting of odd columns and even columns respectively. Combining the two sub-images, we obtain the first corrected image. Secondly, the weighting filter G_x is applied to the Fourier domain of the original image, smoothing out ringings of interval Δy in y direction. The remaining ringings of interval Δx in x direction are further removed by applying unring x to the image, and ringings of interval 2Δy in y direction are kept untreated. Then we obtain the second corrected image. Finally, the average of two corrected images yields the output image. In this figure, each image is rotated by 90°, and the column in each image is in a horizontal direction.

In the above pipelines for 1D and 2D images, we ignore the effect of image phase variations on the ringing pattern. In other words, we assume that the image phase varies smoothly over a length scale longer than the ringing interval y_ν in Equation 6. This assumption seems empirically valid for pf = 7/8 and 6/8, but less so for pf = 5/8 due to the wide interval y_ν = 4Δy. In the following sections, we will test our RPG pipeline in 1D and 2D magnitude images with no additional phase, and further demonstrate the applicability of RPG to 2D magnitude images modulated by the interplay of added image phase map and PSF in Equation 1.

3.3. Atypical partial Fourier factor

In addition to common PF factors (pf = 7/8, 6/8, 5/8), the RPG pipeline could potentially be generalized for any PF factors of rational number (e.g., pf = 0.6 on Philips MRI machines, and pf = 5.5/8 on GE MRI machines)(Casey et al., 2018): For ν ≡ 2pf − 1 = p/q with coprime positive integers p and q (p < q), one could first remove the ringings of interval x_r = Δx in x-direction and of interval y_ν = Δy/ν in y-direction in Equation 4. Further, one could use nearest neighbor to up-sample the 2D image by p fold in y-direction (N_x × pN_y matrix), and divide it into q smaller sub-images (taking one column for every q columns, i.e., (qn + i)th column, $n=\mathrm{0,1},2,...,⌊\frac{p{N}_y}{q}⌋$, and i = 1,2,...,q for each sub-image), where the ringing interval in y-direction becomes y_ν′ = Δy, and the ringing interval x_r = Δx in x-direction is kept unchanged. Then one could apply the original SuShi method in the q sub-images respectively to remove the ringings of interval x_r in x-direction and of interval y_ν′ in y-direction. After combining the corrected sub-images together and using nearest neighbor to down-sample the combined image by p fold in y-direction (N_x × N_y matrix), one could use the 1D local subvoxel-shifts in y-direction (unring y) to remove the remaining ringing of interval y_r = Δy in y-direction.

3.4. Numerical phantoms

3.4.1. 1D phantom

The 1D phantom was a rectangular function of 64 pixels wide in a 128 × 1 array, i.e., field-of-view (FOV) = 128 pixels, with no additional image phase:

$$S_0\left(x\right)=\left\{\begin{array}{ll}0.2& x\notin \left[\mathrm{32,95}\right],\\ 1& x\in \left[\mathrm{32,95}\right].\end{array}\right.$$ (10)

To induce Gibbs-ringings in the 1D phantom, we created a ground truth/high resolution image of a rectangular function of 640 pixels wide in a 1280 × 1 array, and took only its center k-space data (128 × 1 array), where we defined the range of spatial frequencies k ∈ [−K_max, +K_max]. The center k-space data was further zeroed for k ∈ [−K_max, −νK_max] to simulate the data of PF acquisition of factor pf = 7/8, 6/8, and 5/8 (Figure 2a). Here we did not apply any PF reconstruction to recover the zeroed k-space data; instead, we applied Fourier transform and took the magnitude image. To remove Gibbs-ringings due to the asymmetric k-space truncation (PF acquisition and zero filling), we applied our 1D pipeline in Section 3.2.1 to the magnitude image. As a reference, we also applied the original local subvoxel-shifts method to the magnitude image of fully sampled data.

To analyze the spatial frequencies of removed ringings, we calculated the power-spectrum |FT{ΔI}|² of the image residual ΔI ≡ J − I before and after the ringing removal. The Gibbs-ringing of interval x_r in Equation 3 has a period of 2x_r (twice of the ringing interval), corresponding to a peak at the spatial frequency

$$k=\frac{2\pi }{2x_r}=K_{\mathrm{m}\mathrm{a}\mathrm{x}}$$ (11)

in the power spectrum of the image residual. Similarly, the PF induced Gibbs-ringing of interval x_ν in Equation 6 has a period of 2x_ν (twice of the ringing interval), corresponding to a peak at the spatial frequency

$$k=\frac{2\pi }{2x_{\nu }}=\nu K_{\mathrm{m}\mathrm{a}\mathrm{x}}=(2pf-1)\cdot K_{\mathrm{m}\mathrm{a}\mathrm{x}}$$ (12)

in the power spectrum of the image residual, i.e., k/K_max = 3/4, 1/2, and 1/4 for pf = 7/8, 6/8, and 5/8.

To further simulate the effect of Gibbs-ringings on diffusion metrics, we assigned diffusivities D(x) and kurtosis K(x) for this 1D phantom:

$$\begin{array}{r}\begin{array}{l}D(x)=\left\{\begin{array}{ll}1\mu m^2/ms& x\notin \left[\mathrm{32,95}\right],\\ 3\mu m^2/ms& x\in \left[\mathrm{32,95}\right],\end{array}\right.\\ K(x)=\left\{\begin{array}{ll}1& x\notin \left[\mathrm{32,95}\right],\\ 0& x\in \left[\mathrm{32,95}\right],\end{array}\right.\end{array}\end{array}$$ (13)

where the values D(x) = 1 μm²/ms and K(x) = 1 correspond to tissue properties in white matter, and the values D(x) = 3 μm²/ms and K(x) = 0 correspond to properties of cerebrospinal fluid. The diffusion-weighted signals were generated by using a cumulant expansion truncated at the kurtosis term (Jensen et al., 2005):

$$S(b,x)=S_0\left(x\right)\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left(-bD\left(x\right)+\frac{1}{6}{b}^2{D}^2\left(x\right)K\left(x\right)\right),$$ (14)

where the non-diffusion-weighted signal S₀ was given by Equation 10, and diffusion weightings (b-values) were b = [0.25,1,2] ms/μm², matching the in vivo MRI protocol in Section 4.2. For signals S₀ and S, we induced Gibbs-ringings due to the asymmetric k-space truncation (PF acquisition and zero filling), and applied local subvoxel-shifts method or our 1D RPG pipeline in Section 3.2.1 to remove ringings in magnitude signals. The signals before and after ringing removal yielded estimated mean diffusivity and mean kurtosis (Figure S5) from Equation 14 via linear least squares method.

3.4.2. 2D phantom

The 2D phantom was a 90 × 90 Shepp-Logan phantom. To induce Gibbs-ringings in the 2D phantom, we created a ground truth/high resolution image of a 900 × 900 Shepp-Logan phantom with additional phase (Chiew, n.d.)

$$\varphi =2\pi \cdot \left[1.35\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{\sqrt{(x-338{)}^2+(y-338{)}^2}}{150}\right)+0.9\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{(x-525{)}^2}{{338}^2}\right)\right].$$ (15)

We then took only its center k-space data (90 × 90 matrix), where we defined the range of spatial frequencies k_x,y ∈ [−K_max, +K_max]. The center k-space data was further zeroed in k_y ∈ [−K_max, −νK_max] to simulate the data of PF acquisition of factor pf = 7/8, 6/8, and 5/8 in the phase-encoding direction. We did not recover the zeroed k-space data using PF reconstruction; instead, we applied Fourier transform and took the magnitude image. To remove Gibbs-ringing due to the asymmetric k-space truncation (PF acquisition and zero filling), we applied the 2D RPG pipeline in Section 3.2.2 to the magnitude image. As a reference, we also applied the original local subvoxel-shifts method(Kellner et al., 2016) or magnitude-input CNN (MCNN)(Muckley et al., n.d.) to the magnitude image of fully sampled data and PF acquired data.

Furthermore, in addition to the noiseless case, we explore the effect of noise on ringing removal pipeline by adding Gaussian noise of standard deviation σ = [0.02,0.05,0.10] in k-space data (cf. 2D phantom’s image intensity ∈[0,1]), simulating the case of different SNR.

3.5. In vivo MRI

A 27-year-old female underwent imaging on a 3T Siemens Prisma scanner (Erlangen, Germany) with a 20-channel head coil after obtaining informed consent as approved by our Institutional Review Board. Diffusion MRI measurements using a monopolar pulsed-gradient spin echo sequence were repeated for fully sampled k-space data and PF acquisition of factor pf = 7/8, 6/8, and 5/8 respectively. Images were reconstructed by simply using zero filling. For each scan, we obtained 4b = 0 non-diffusion-weighted images (non-DWIs) and 84 DWIs of b-values b = [0.25,1,2] ms/μm² along [4,20,60] gradient directions for each b-shell, with an anisotropic resolution of 1.7 × 1.7 × 3 mm³ and a FOV of 220 × 220 mm². The whole brain volume was scanned within 50 slices, aligned parallel to the anterior commissure-posterior commissure (AC-PC) line. GRAPPA with acceleration factor = 2 and multiband with acceleration factor = 2 were used. All scans were performed with the same TR/TE (repetition time/echo time) = 3700/96 ms and readout bandwidth = 1480 Hz/pixel. We also acquired an additional b = 0 image with the same sequence parameters except the opposing polarity of phase-encoding direction for the susceptibility-induced distortion correction. The total scan time is about 30 minutes.

Our image processing DESIGNER pipeline was based on ref. 22 and included five steps: denoising(Veraart et al., 2016), Gibbs-ringing removal (local subvoxel-shifts(Kellner et al., 2016) or MCNN(Muckley et al., n.d.) for fully sampled data and PF acquired data; RPG for PF acquired data), susceptibility-induced distortion correction(Andersson et al., 2003), eddy current and motion correction(Andersson & Sotiropoulos, 2016), and Rician noise correction(Koay & Basser, 2006). For comparison, an alternative image processing pipeline excluding Gibbs-ringing removal was also applied. For each voxel, we estimated the diffusion and kurtosis tensors using weighted linear least squares with the constraint of positive apparent kurtosis(Veraart et al., 2013). Maps of MD, fractional anisotropy (FA), and mean kurtosis (MK) were calculated accordingly(Jensen et al., 2005; Basser et al., 1994).

To further demonstrate the effect of ringing removal on diffusion metrics in the area close to ventricles, we segmented the CC and parcellated it into multiple regions-of-interests (ROIs) based on the distance from the CSF: The subject’s FA map of fully sampled data was registered to FSL’s standard FA map with FMRIB’s linear and non-linear registration tools (FLIRT, FNIRT)(Jenkinson & Smith, 2001; Andersson et al., 2007). We retrieved the transformation matrix (FLIRT) and the warp (FNIRT) to inversely transform Johns Hopkins University (JHU) DTI-based WM atlas ROIs to the subject space(Mori et al., 2005) and obtained the CC ROI. The CSF mask was obtained by thresholding the MD >1.5 μm²/ms of fully sampled data. We then applied a distance transform to the CSF mask to obtain a distance map showing the distance from the CSF (in a unit of voxels). The CC ROI was further segmented into multiple ROIs based on the distance map from the CSF (Figure S9). The influence of ringing removal on diffusion metrics (MD, FA, MK) was shown in each CC ROI.

3.6. Image sharpness assessment

Ringing removal algorithms inevitably induce image blurring due to the application of weighted filter and/or the TV/TGV as the cost function or regularization. To evaluate the image blurring introduced by ringing removal, we define the sharpness index (SI) based on the S3 metric(Vu et al., 2011), which incorporates two sharpness estimators: (1) a spectral-based estimator according to the slope of the local magnitude spectrum, and (2) a spatial-based estimator according to the local total variation. The higher the SI is, the sharper (and less smoother) the image is.

4. Results

In what follows, we demonstrate the applicability of the proposed ringing removal pipeline in 1D/2D numerical phantoms and in vivo dMRI data.

4.1. Numerical phantoms

Numerical simulations of Gibbs-ringing removal in 1D magnitude signal of a rectangular function showed that ringings of targeted intervals due to PF acquisition and zero filling in Equations 3 and 6 were properly removed by the proposed 1D RPG pipeline in Section 3.2.1 (Figure 5a–b). The power spectrum analysis of the image residual further demonstrated the spatial frequency of removed ringings (Figure 5c): For fully sampled data, the original 1D local subvoxel-shifts method removes the ringing of interval Δx, leading to a peak at k = K_max in the power spectrum, according to Equation 11. Similarly, for PF acquired data, the RPG pipeline removes both ringings of intervals x_r and x_ν, leading to two peaks at k = K_max and (2pf − 1)⋅K_max in the power spectrum, based on Equations 11 and 12 respectively.

Figure 5.

Numerical simulations of Gibbs-ringing removal in 1D magnitude signals of a phantom of rectangular function in Equation 10. a. Signals before (black) and after (red) Gibbs-ringing removal using 1D local subvoxel-shifts (unring x) for fully sampled data and RPG for PF acquired data reconstructed via zero fillling. b. The zoom in of top of the signals in panel a. c. The power spectrum of the signal residual before and after Gibbs-ringing removal, shown in the spatial frequency domain. The targeted ringing frequency in Equations 11 and 12 is indicated by red solid lines.

In addition to the 1D b = 0 signal phantom, we also demonstrated our 1D RPG pipeline on a data set of 1D diffusion weighted phantom in Equation 14 (Figure S5). Simulation results showed that 1D local subvoxel-shifts method removed most ringings in MD and MK maps of fully sampled data, while ringings of PF acquired data were not corrected properly. In contrast, our 1D RPG pipeline removed most ringings in MD and MK maps of PF acquired data, especially for the correction of undershooting in the “white matter” region, where D(x) = 1 μm²/ms and K(x) = 1.

For 2D magnitude images of the Shepp-Logan phantom with additional phase in Equation 15, our 2D RPG pipeline properly removed most Gibbs-ringings due to the PF acquisition for pf = 7/8 and 6/8 (Figure 6). However, for pf = 5/8, the image corrected by RPG was excessively blurred with remaining ringings. Similarly, MCNN removed most ringings for pf = 7/8 and 6/8, but not for pf = 5/8. In contrast, local subvoxel-shifts corrected only ringings of interval x_r in Equation 3 and left ringings of interval x_ν in Equation 6 untreated.

Figure 6.

Numerical simulations of Gibbs-ringing removal in 2D magnitude images of the Shepp-Logan phantom with the additional phase in Equation 15. The first row shows images of the signal magnitude before ringing removal, and the second, third and forth rows show images after ringing removal by using magnitude-input CNN (MCNN), local subvoxel-shifts (SuShi) and RPG. For PF acquired data, SuShi can only correct the ordinary ringings of interval x_r in Equation 3, but not PF-induced ringings of interval x_ν in Equation 6. In contrast, for pf = 7/8 and 6/8, both MCNN and RPG pipelines robustly remove PF-induced ringings, whereas for pf = 5/8 the corrected image still has non-trivial amount of ringings, potentially caused by the interaction of the image phase in high resolution ground truth and the convolution kernel in Equation 1. SI is the sharpness index(Vu et al., 2011).

Further, we tested the stability of RPG pipeline in 2D phantom images of different SNR in Figures S6, S7 and S8. For pf = 7/8 and 6/8 at the noise level σ = 0.02 and 0.05 (cf. image intensity ∈ [0,1]), the RPG pipeline robustly removed PF-induced ringings, whereas for pf = 5/8 the corrected image still had non-trivial amount of ringings. At σ = 0.10, the effect of ringing removal was not obvious due to the low SNR.

4.2. In vivo MRI

For PF acquired data of pf = 7/8, 6/8, and 5/8, the b = 0 images (Figure 7) and MD maps (Figure 8) have ringing artifacts due to PF acquisition and zero filling that e.g. manifest as dark bands surrounding ventricles in MD maps, especially in genu and splenium of CC. While these cannot be corrected by using the original local subvoxel-shifts method, we can see that the 2D RPG pipeline largely removes the additional ringings in b = 0 images and MD maps for pf = 7/8 and 6/8. For pf = 5/8, the b = 0 image and MD map are both excessively blurred by using RPG, potentially caused by the interaction between the image phase map and the PSF in Equation 1. Furthermore, though the MCNN successfully removes ringing artifacts for pf = 7/8, extra spurious ringings in the corpus callosum adjacent to the ventricles are observed in b = 0 images and MD maps after applying the MCNN for pf = 6/8 and 5/8, potentially related with the increase of the sharpness index in b = 0 images.

Figure 7.

Non-diffusion-weighted (b = 0) images before and after Gibbs-ringing removal using magnitude-input CNN (MCNN), local subvoxel-shifts (SuShi) and RPG. For pf = 7/8 and 6/8, RPG robustly removes Gibbs-ringings around ventricles (e.g., genu/splenium of corpus callosum), whereas MCNN (pf = 6/8) and SuShi (pf = 7/8, 6/8) cannot. For pf = 5/8, however, none of the methods can correct the ringings solely based on magnitude images. SI is the sharpness index(Vu et al., 2011).

Figure 8.

Mean diffusivity (MD) map based on DWIs before and after Gibbs-ringing removal using magnitude-input CNN (MCNN), local subvoxel-shifts (SuShi) and RPG. For pf = 7/8 and 6/8, RPG robustly corrects underestimated MD around ventricles (e.g., genu/splenium of corpus callosum), whereas MCNN (pf = 6/8) and SuShi (pf = 7/8, 6/8) cannot. For pf = 5/8, however, none of the methods can correct the ringings solely based on magnitude images. The unit of MD is μm²/ms.

For MK maps (Figure 9), Gibbs-ringings lead to physically implausible values of MK >3 (varying from 3 to about 1000), that can be largely corrected by using the original local subvoxel-shifts method, even for PF acquired data. Compared with the original local subvoxel-shifts method, the RPG pipeline further reduces unrealistically high MK-values in voxels around the ventricles. However, after the ringing removal using RPG for pf = 5/8, the MK values are lowered not only around ventricles but also in major WM tracts, such as the central region of genu in corpus callosum. In contrast, the MCNN reduces unrealistically high MK-values around the ventricles for pf = 7/8 and 6/8, but not for pf = 5/8.

Figure 9.

Mean kurtosis (MK) map based on DWIs before and after Gibbs-ringing removal using magnitude-input CNN (MCNN), local subvoxel-shifts (SuShi) and RPG. The red pixels indicate voxels with very high MK >3. For pf = 7/8 and 6/8, all methods decrease the number of voxels with high MK values. For pf = 5/8, however, only SuShi appropriately decreases the number of voxels with high MK values (cf. MCNN) without changing the contrast (cf. RPG).

To study the effect of Gibbs-ringing removal on diffusion metrics in more detail, we compared changes of MD, FA, and MK before and after ringing removal in the CC. The CC was segmented into multiple ROIs based on the distance from the CSF, being the major source of clear-cut edges in b = 0 images and DWIs and resulting Gibbs-induced ringings. Before ringing removal for PF acquired data, MD is underestimated in WM close to the CSF, shown as dark bands surrounding ventricles in MD maps (Figure 8). The ROI analysis of CC showed that the local subvoxel-shifts method only slightly corrected the underestimated MD in WM voxels close to the CSF (Figure 10a). In contrast, the RPG pipeline resulted in stronger corrections on the underestimated MD in voxels close to the CSF. Similarly, the MCNN led to the MD corrections comparable with the RPG for pf = 7/8, but not for pf = 6/8 and 5/8. Furthermore, the local subvoxel-shifts method decreased FA values in WM voxels close to the CSF (Figure 10c), and the RPG pipeline decreased the FA values even further. This FA value reduction could be caused by the ringing removal and/or the additional smoothing introduced by local subvoxel-shifts or RPG pipeline. The MCNN, however, had similar FA reduction effect for pf = 7/8, but not for pf = 6/8 and 5/8. Finally, for pf = 7/8 and 6/8, both local subvoxel-shifts method and RPG pipeline similarly reduced MK values in WM voxels close to the CSF (Figure 10b), whereas the RPG of pf = 5/8 led to excessive reductions in MK, compared with the local subvoxel-shifts method. And yet the MCNN led to reduced MK values in voxels slightly away from the CSF (distant from the CSF for about 2–3 voxels).

Figure 10.

The differences of mean diffusivity (ΔMD), mean kurtosis (ΔMK), and fractional anisotropy (ΔFA) before and after ringing removals in corpus callosum ROIs consisting of voxels distant from the ventricles by 1–4 voxels (Figure S9). The a. MD, b. MK and c. FA were calculated based on b = 0 images and DWIs before and after ringing removals using magnitude-input CNN (MCNN), local subvoxel-shifts (SuShi) or RPG. The diffusion metrics after ringing removals are subtracted by those before ringing removals.

5. Discussion

Asymmetric truncation in k-space due to PF acquisition and zero filling induces additional Gibbs-ringing artifacts with ringing intervals determined by the PF factor pf in Equations 3 and 6, as compared to fully sampled data. Such artifacts are not trivial to recognize due to their wider ringing intervals as opposed to the regular Gibbs-ringing in acquisitions with no PF.

In numerical simulations and in vivo MRI data, we show that these additional ringings can be robustly removed by the proposed RPG pipeline for pf = 7/8 and 6/8, with the assumption of a smoothly varying image phase. Indeed, PF induced Gibbs-ringings resulted in reduction of MD in WM close to CSF, and these spurious dark bands are robustly removed by RPG for pf = 7/8 and 6/8, but not by the ordinary local subvoxel-shifts method(Kellner et al., 2016)(pf = 7/8, 6/8) or MCNN(Muckley et al., n.d.) (pf = 6/8). In contrast, PF induced Gibbs-ringings have relatively small influence on MK even in WM close to the CSF, and local subvoxel-shifts, MCNN and RPG all had relatively small impact on MK-values.

For pf = 6/8, the residual of PF-induced ringing after applying RPG (Figure 6) mainly comes from the “unring x” pathway in Figure 4, i.e., the route with the weighted filter G_x. Ideally, we could adapt the filter G_x to suppress the ringing of intervals Δy and 2Δy along the PF dimension (y-direction) in this pathway. However, it is difficult to create such modified G_x since the constraint of G_x + G_y = 1 needs to be satisfied at the same time, ensuring proper scaling of image intensity. Therefore, the optimization of weighted filters (G_x, G_y) for pf = 6/8 is non-trivial and left to be solved in future study.

For pf = 5/8, RPG ringing removal may lead to excessive image blurring due to the interaction between image phase map and complex PSF in Equation 1 (we only consider its real part contribution in RPG pipeline), as shown in numerical simulations. In the in vivo brain MRI, we noticed a unreasonable reduction of MK values in CC after applying RPG. The wide ringing interval x_ν = 4Δx of pf = 5/8 could break the assumption of smoothly varying phase over a length scale longer than the ringing interval. Previous work using MCNN(Muckley et al., n.d.) for Gibbs-ringing correction and noise removal also shows that it is practically impossible to correct the ringing artifacts for pf = 5/8 without knowledge of the image phase map or k-space data. Therefore, it is not recommended to employ PF acquisition of pf = 5/8 without using a dedicated PF reconstruction, such as Margosian or POCS methods(McGibney et al., 1993).

The PF-induced Gibbs-ringing in images of relatively high SNR ~20 (e.g., non-DWI) can be reliably removed by the RPG pipeline. In contrast, the ringing artifact is minor in images of low SNR (e.g., DWI)(Perrone et al., 2015), and the ringing removal pipeline would only lead to slight image blurring due to the application of weighted filters. However, it is still not harmful to apply the RPG pipeline to images of low SNR except the limited blurring effect.

Theoretically, the RPG pipeline can be generalized for any PF factors of rational number. Practically, the RPG is particularly well-suited for removing ringings in PF acquired magnitude images of pf = 6/8, because (1) for pf = 7/8, the bias of additional ringings due to PF is relatively small, and (2) for pf = 5/8, it is very difficult for any algorithm to remove ringings without knowing the phase map. Considering the balance between undersampling efficiency (e.g., to shorten TE in EPI sequence) and applicability of ringing removal in magnitude images, we suggest to perform PF acquisitions of pf = 6/8, which is already adopted as the default in dMRI protocols of many large preclinical and clinical studies including the Human Connectome Project(Sotiropoulos et al., 2013), Adolescent Brain Cognitive Development study (Siemens protocol)(Casey et al., 2018), and UK Biobank(Alfaro-Almagro et al., 2018).

One interesting future direction is to fine-tune the RPG pipeline for better performance. For example, the implementation of the RPG pipeline could potentially be based on any other ringing removal method targeting the ordinary Gibbs-ringing in fully sampled data. Furthermore, the image subsampling in RPG pipeline is currently performed in the image space (Figure 3), whereas it may be possible to achieve higher-quality image subsampling in a wavelet domain. Optimizing each component in RPG pipeline may improve the results at extreme PF factors.

Compared with the previous study using MCNN(Muckley et al., n.d.) to remove PF induced Gibbs-ringings in magnitude images, the RPG pipeline is a fast and straightforward method that requires neither training data nor tuning parameters for the correction kernels. Extending the theoretical understanding of PF acquisition (Section 2) and the well-established local subvoxel-shifts method(Kellner et al., 2016), we can robustly remove these ringing artifacts in magnitude images. Even without applying any ringing removal pipelines, the knowledge of ringing patterns resulting from PF acquisitions and zero filling is potentially valuable for radiologists to distinguish ringing artifacts from anatomical structures.

6. Conclusion

Gibbs-ringing artifacts in magnitude images obtained by using PF acquisition and zero filling interpolation were theoretically modeled, and a correction pipeline based on modifying the local subvoxel-shifts method is proposed. With the understanding of oscillating convolution kernels due to the PF acquisition, the ringings in magnitude images can be robustly removed without the need of complicated models and/or tuning parameters trained with a non-trivial amount of data. The effects of ringings on diffusion metrics were compared to the original local subvoxel-shifts method and a magnitude-input CNN in numerical phantoms and in vivo diffusion data. The proposed RPG pipeline not just removes most ringings in magnitude DWIs of PF factors pf = 7/8 and 6/8, but also stabilizes estimations of diffusion metrics around anatomical boundaries.

Data availability statement

The source code of the Gibbs-ringing removal pipeline will be released on our Github page (https://github.com/NYU-DiffusionMRI).