Abstract
Recent literature has revealed a growing interest in methods for anticipating the demand for medical items and personnel at hospital, especially during turbulent scenarios such as the COVID-19 pandemic. In times like those, new variables appear and affect the once known demand behavior. This paper investigates the hypothesis that the combined Prophet-LSTM method results in more accurate forecastings for COVID-19 hospital Intensive Care Units (ICUs) demand than both standalone models, Prophet and LSTM (Long Short-Term Memory Neural Network). We also compare the model to well-established demand forecasting benchmarks. The model is tested to a representative Brazilian municipality that serves as a medical reference to other cities within its region. In addition to traditional time series components, such as trend and seasonality, other variables such as the current number of daily COVID-19 cases, vaccination rates, non-pharmaceutical interventions, social isolation index, and regional hospital beds occupation are also used to explain the variations in COVID-19 hospital ICU demand. Results indicate that the proposed method produced Mean Average Errors (MAE) from 13% to 45% lower than well established statistical and machine learning forecasting models, including the standalone models.
Keywords: Neural networks, Forecasting, Time series, Machine learning, Decision support systems
1. Introduction
Uncertainty is a constant in the hospital environment. One of the main issues hospitals face is uncertainty over demand for their services [1]. The number of incoming patients varies substantially over time, impacting the number of beds and items needed. Nevertheless, even socially-driven industries, such as hospitals, are still interested in improving their business performance [2]. On the one hand, over-forecasting the demand may waste resources that could be used elsewhere within the hospital. On the other, under-forecasting may pull the hospital away from its purposes, such as to provide excellent and efficient patient care [3] or care for everyone who come to them [1]. Moreover, hospital performance is closely inspected by government and society: generally its primary stakeholders. Thus, the task of balancing service and costs is notably challenging during turbulent scenarios, such as global healthcare crises, when hospitals may face disruptions in the upstream and over-demand in the downstream [4].
The COVID-19 pandemic is the most significant global healthcare crisis of the last century. Despite HID/AIDS being associated with more deaths (32 mi since 1981),1 the COVID-19 pandemic is a natural disaster with no precedents to our generation, due to its great transmissibility and severe economic impact [4]. It has been causing recessions, damage to people’s health and jobs, and overcrowding hospitals worldwide.2 Those impacts are amplified in developing countries, where social and hospital infrastructure are generally under stress even during regular times [5]. Unfortunately, SARS-CoV-2 variants are still emerging, such as Omicron, reducing the certainties that we may have regarding an imminent end to this pandemic [6]. Additionally, COVID-19 does not seem to be a standalone episode, and the chances of other pandemics striking humanity soon may to be increasing [7], [8]. Thus, operating under strict budgetary limits and high volatility in demand may become more frequent to hospitals in general, even in developed countries [3], [4].
Ex-ante forecasts are those made using only the information that is available at the time of the forecast. In contrast, ex-post forecasts use later information on the predictors, beyond the time at which the forecast is made [9], [10], [11]. Generally, researchers employ regression approaches to tackle ex-post forecasting problems. At the same time, ex-ante forecasts may be performed by classical time series forecasting approaches [9]. However, choosing between classical forecasting or regression approaches may lead researchers to perform simplifications that make the forecast lack precision. Selecting a subset of all relevant variables available, lagging the variables beyond its optimum lag window, or discarding temporal patterns that the target variable may have, are examples of such simplifications. To Ioannidis et al. [12] those may be causes for COVID-19 forecasting models to fail.
This paper presents the applicability of an Integrated Multivariate Prophet-LSTM approach to forecasting ICU beds, considering traditional time series patterns and explanatory and correlated variables with different optimal time lags. The addressed hypothesis is that Prophet-LSTM, a hybrid ex-ante/ex-post forecasting approach, results in better ICU bed forecasts during the COVID-19 pandemic than standalone Prophet and LSTM approaches. This modeling was motivated on the premises that Prophet performs well on capturing time series components and linear relationships between the demand and ex-post variables. On the other hand, LSTM efficiently captures additional non-linearities and correlations between the ICU demand and ex-ante variables. Besides the univariate time series components, several additional variables that partially explain the variations in the target variable are considered: the current number of daily COVID-19 cases, vaccination rates, non-pharmaceutical interventions, social isolation index, and regional hospital beds occupation. Also, this paper presents a comparative analysis between the proposed model and benchmark models, typically used in hospital demand and COVID-19 forecasting, namely Autoregressive Integrated Moving Average (ARIMA), Holt-Winters, Random Forest Regressor (RFR), K-Nearest Neighbors Regressor (KNN), Gated Recurrent Units (GRU) and Simple Recurrent Neural Networks (Simple RNN). To the best of our knowledge, no study has yet investigated a similar approach to the case of hospital demand forecasting. The main contributions of this paper can be summarized as follows:
-
•
It provides a thorough analysis of the correlation between new ICU entrances (target variable) and daily COVID-19 new cases, vaccination rates, non-pharmaceutical interventions, regional hospital beds occupation, and social isolation indexes. Other variables that do not display significant correlation to the target variable are also mentioned.
-
•
It uses the variables mentioned earlier to predict daily ICU entrances in all hospitals of a large Brazilian municipality, aggregated to the city level.
-
•
It loosely couples Prophet and LSTM, two trending Machine Learning (ML) approaches, to incorporate ex-post and ex-ant variables.
-
•
It shows that proposed Prophet-LSTM reduces MAE metrics of Prophet and LSTM in 14.2% and 17.3%, respectively, when feeding all three models with the same inputs.
-
•
It shows that the proposed Prophet-LSTM produces Mean Average Error (MAE) metrics 30%, 27%, 45%, and 34% smaller than univariate Holt-Winters, ARIMA, RFR, and KNN models, respectively.
-
•
The proposed Prophet-LSTM produces Mean Average Error (MAE) metrics 13% and 14% smaller than multivariate GRU and Simple RNN models, respectively.
The remainder of this paper is organized as follows: Section 3 introduces the data and the data treatments, and analyses we perform. Next, Section 4 proposes the two-stage model hybridizing Prophet and LSTM. Then, Section 5 presents the results from Prophet-LSTM and the benchmark models, and the discussions concerning the results. Finally, Section 6 shows the conclusions and future work directions.
2. Related work
Demand forecasting plays a central role in hospital applications. Despite forecasting not being a novel topic to statistics, nor to healthcare sciences and hospitals [13], [14], it has been constantly improved and adjusted to solve current problems [15].
During the COVID-19 pandemic, forecasting models that once were kept in vaults as strategic secrets became available to society, as part of a worldwide effort to suppress this crisis through knowledge sharing and science. Recently, many researchers have investigated and created forecasting approaches to predict the numbers related to COVID-19, such as: when the pandemic will peak, how long it will last, how many will be infected or die, and how big will be the demand for hospital beds, ventilators, and PPE (Personal Protective Equipment) [4], [15], [16], [17], [18], [19].
As soon as new pieces of data, estimates and conditions are made available, researchers create new models that accommodate those variables to better forecast the problems at hand. In the context of COVID-19, many variables were investigated to explain how the hospital demand could evolve in the future, such as the hospital carrying capacity [20], [21], the daily number of COVID-19 deaths [18], [20], [21], new COVID-19 confirmed cases [18], [19], [22], ICU new hospital entrances [19], [22], percentage of ICU occupancy [21], lockdowns and non-pharmaceutical interventions [18], [23], patients’ age [22], and vaccination rates [23]. Thus, depending on when and how strongly the effect of those variables reflect upon the target variable, researchers choose between different forecasting approaches [9].
Hospital demand and occupancy have become even more critical during the COVID-19 pandemic. A few researchers have recently aimed to tailor forecasting models to address hospital needs. Capistran et al. [18] presented a forecasting model to predict hospital occupancy in Mexican metropolitan areas during the COVID-19 pandemic. The model is based on the Susceptible–Exposed–Infected–Recovered–Dead (SEIRD) model, but also considers lockdowns and lockdown-relaxations as two kinds of interventions that affect the transmission rates and effective population size. A more straightforward modeling approach was used by Rivera and Urdinola [24] to forecast hospital demands in Colombia. The authors used an SEIR model to indirectly estimate the hospital demand from the number of infected people, which may fall into three groups: those that can stay at home, people who need regular hospital beds, and patients who need ICU treatment. Similarly, Massonnaud et al. [25] forecasted hospital needs in France, using an SEIR model, but with short-term goals.
Apart from compartmental models, commonly used to model medium-long term infectious diseases, other statistical models have also gained space in forecasting COVID-19 hospital numbers, especially for short-term predictions. Nguyen et al. [26] used a Vector Error Correlation Model (VECM), a multivariate time series model, that is a restricted Vector Autoregression (VAR) model designed to be used with non-stationary data that are known to be cointegrated. The authors present a case for hospital census in the Charlotte metropolitan area of North Carolina. They introduce infection rates as additional variables as a scientific contribution of the method. According to the authors, the need for a stable long-run relationship and the assumption that case severity does not change in time are limitations of the model. A very similar approach was presented one year earlier by Berta et al. [27], but to the case of Italy, Switzerland and Spain. The authors use publicly available data on the number of COVID-19 cases as supporting variables.
The next section introduces the COVID-19 data used for the forecasting in the present study.
3. Case study: The data
This section introduces the investigated data and the pre-processing methodology employed to the data treatment before forecasting. Fig. 1 summarizes the content of this section and the two to follow.
Fig. 1.
The methodology of the proposed approach.
3.1. Data acquisition
Up to July 2021, Brazil was the country with the third-highest number of accumulated cases and the second in the number of COVID-19 accumulated deaths worldwide [28]. Among all Brazilian states, São Paulo had the highest absolute numbers of COVID-19 cases and deaths [29]. Due to the high infection rates, new SARS-COV-2 variants have emerged in the country, such as the more aggressive lineage called P.1. From November 2020, P.1. became dominant in the country [30]. Large cities, such as state capitals, are the most affected ones by the pandemic in Brazil [17]. This is also the case of large inland cities, such as São José dos Campos, in the state of São Paulo.
São José dos Campos is the largest city in the Vale do Paraíba region and a local medical reference. The city has around 731,000 inhabitants and holds the 24th and 19th highest Brazilian HDI (0.807) and annual GDP (US$ 7 billion), respectively [31]. During the COVID-19 pandemic, the city has also served as a scape valve to other parts of the Vale do Paraíba region, which has around 3.3 million inhabitants, by receiving COVID-19 patients from less affluent cities.
The primary data source is the municipality of São José dos Campos, which provided to us, under confidentiality agreement, a desegregated dataset to the patient level, reporting all COVID-19 cases in the city and how they have evolved. This data was partially used in a recent study [32]. Thus, we aggregated all the information on a daily level and produced the following first two variables described in each subsection that follows. Besides, several pieces of information were obtained from data freely available online and compiled by the state’s COVID-19 contingency center of the state of São Paulo [33]. From this data, we produced the remaining variables of the introduced forecasting model. Fig. 2 graphically shows how each variable, briefly described in the following subsections, evolves in time.
Fig. 2.
Target and additional variables used for forecasting.
3.1.1. ICU-in
The variable ICU-in accounts for the number of daily entrances in COVID-19 ICUs in all hospitals located in the city. ICU-in is the target variable in this study; all other variables are predictors.
3.1.2. Cases
The variable Cases represents the number of COVID-19 daily cases in the city since the first tracked case on March 05, 2020. Only reported cases are considered, and this variable does not cover sub-notifications.
3.1.3. SII
SII stands for Social Isolation Index and represents the daily percentage of people under social isolation in São José dos Campos. This index is produced by telephonic companies that operate within the state.
3.1.4. RHBO
RHBO stands for Regional Hospital Beds Occupation and refers to the daily percentage of hospital beds in usage in the whole Vale do Paraíba region, including São José dos Campos. For comparison purposes, the population of São José dos Campos represents 22% of the entire population in the Vale do Paraíba region.
3.1.5. Plano-SP
Plano-SP is the state government’s color-based reopening plan that grades the regions of São Paulo from red (under severe mobility restrictions) to blue (free of mobility restrictions). This means that cities of a same region have the same mobility restrictions. In particular, Vale do Paraíba is one of the state regions.
Recently, the state government introduced a new phase with more mobility restrictions than the red phase, the “Emergency” phase, as well as two intermediate phases between Red/ Emergency and Orange/Red [34]. In this paper, the phases were converted into a linear numeric scale ranging from 0 to 6, with higher values associated with more restricting phases.
3.1.6. Vax
The variable Vax regards an artificial index created in this paper to reflect the percentage of the population that is likely to need an ICU bed. This index is an aggregation of several parameters and variables. It also decreases with the advance of vaccination. It is calculated considering the four types of vaccines available in Brazil, their protection indexes against severe hospitalization after first and second doses. Moreover, since there is a clear relation between people from age groups and the likelihood of them to need an ICU bed due to the COVID-19 infection, we divided the population into age groups, where .
Roughly, the index Vax consists of an estimation on the number of people requiring an ICU bed from each age group, here denoted by , multiplied by the probability of someone needing an ICU bed, denoted by . Eq. (1) presents the proposed index.
| (1) |
where is the size of the population in age group . The probability is calculated considering the previous available data regarding ICU hospitalizations. To estimate , we consider the size of the population in age group minus the estimated size of the population who do not need an ICU bed due to vaccination, here denoted by . Therefore, . The value of takes into account parameters and , that represent the proportion of people (from any age group) that will not develop severe COVID-19 after one and two shots, respectively. Therefore, can be calculated as in Eq. (3).
| (2) |
where , , and represent the population inside the age segment that took, respectively, two, one, or none of the doses of vaccine . Therefore, , where is the number of available vaccines, and, thus
| (3) |
The index considering every age group is, therefore, calculated as indicated in Eq. (4).
| (4) |
The total number of vaccines available is . The values for and reflect the state’s policies in the beginning of vaccination. Also, all vaccines have different immunization coefficients, which are provided by the companies that produced them and according to the tested population. These coefficients increase with more vaccine doses taken and vary from vaccine makers, as shown in Table 1. Thus, the first dose has a percentage of immunization , whereas the second dose has a percentage of immunization . However, even after immunization, different age segments have different probabilities of needing an ICU bed if infected by COVID-19. Thus a coefficient , obtained from the municipal data prior vaccination, representing the probability of hospitalization for age segment is also employed in the calculations. Vaccination started on January 18, 2021, thus Vax is constant up to this day, when it starts decreasing.
The main idea behind Equation (4) is to better address the target variable of this paper, the vaccination rates. It is constructed in this manner to reflect the impact of vaccination rates over ICU bed demand, which is our target variable in this paper. Additionally, we only use vaccines as source of immunity for two reasons. First, the percentage of the city’s population that contracted COVID-19, by the time this work was performed, was relatively low; and second due to the fact that a single person may be reinfected by different SARS-COV-2 variants, which may implicate in hospitalization.
Table 1.
Vaccine percentage of immunization by doses taken and vaccine maker.
| Vaccine | 1st dose | 2nd dose |
|---|---|---|
| Pfizer | 89% | 92% |
| Coronavac | 42.7% | 86% |
| AstraZeneca | 76% | 81% |
| Janssen | 85.4% | – |
3.2. Data analysis
We start by empowering the relevance of the predictor variables in describing the behavior of the target variable. To do so, we maximize the correlation coefficient (CC) between the number of ICU new entrances (ICU-in) and other variables that may be relevant to the predictive analysis. To maximize the CC, we remove anomalies from the data, lag the variables according to ranges prescribed in the literature, and detached seasonal effects that may make noise to predictions.
3.2.1. Seasonal analysis
The target variable does not display a continuous and consistent weekly seasonal pattern, unlike what was observed on the variable Cases. Fig. 3 exhibits a graphical analysis of the weekly seasonal components of the variables by using radar charts to illustrate how the seasonality of each variable evolves in time. Each set of lines connecting dots in each graph represents the seasonality pattern in a given period of time. The more consistent the seasonality pattern is, the more parallel the set lines are, and less area of the graph is occupied by the lines. On the other hand, the less consistent the seasonality pattern is, the more frequent lines will cross each other and occupy other areas of the graph.
Fig. 3.
Seasonal pattern.
We notice that as well as the target variable, RHBO, Plano-SP, and Vax also do not seem to display a consistent weekly seasonal pattern along the months. However, the opposite is true for Cases and SII variables, which show a consistent weekly seasonal pattern.
We also perform a linear regression to determine whether seasonal components are relevant to describe the variables in an overall manner. First, each variable is seasonally decomposed by taking the 7 day-moving average of the series as a trend component, and the additive and multiplicative seasonalities are computed. We then regress the original variable on its trend and compute the R-squared metric. Finally, we regress the original variable on its trend adjusted by the seasonal component and verify if there is any considerable improvement in the R-squared. The ordinary least squares (OLS) linear regression was used in both cases. The higher the gain, the more relevant the variable’s weekly seasonal component. As shown by Table 2, seasonal components are more relevant in Cases and SII variables.
Table 2.
R-squared improvement with additive and multiplicative seasonalities over the decomposed trend.
| Variable | Additive | Multiplicative |
|---|---|---|
| ICU-in | 2.31% | 2.61% |
| Cases | 5.23% | 6.69% |
| SII | 44.35% | 44.16% |
| RHBO | 0.03% | 0.02% |
| Plano-SP | 0.07% | 0.05% |
| Vax | 0 | 0 |
We assume that the target variable does not show a consistent and relevant seasonal component when looking at both analyses. Thus we deseasonalize both the variables Cases and SII before lagging them.
3.2.2. Lagging the variables
Despite all the variables considered in our analysis being collected daily, their influence over ICU new entrances (ICU-in) lags in time. Recent studies point out incubation periods (from infection to symptom onset) for SARS-COV-2 ranging from 4 to 6 days [35], [36], [37]. Besides, the interval between symptom onset and hospitalization seems to range from 2 to 10 days [38], [39]. Especially in the Brazilian case, testings for COVID-19 are not coincident with symptom onset. In fact, tests happen on average 10 days after the first symptoms [40].
Thus, the correlation analysis performed in this paper also aims to find the best lag to each predictor variable, respecting the ranges found in the literature regarding the target variable. The tested lag ranges we test are shown in Table 3.
Table 3.
Optimal time lags and Spearman correlation coefficients (CC) with the target variable.
| Variable | Lag range tested | Optimal lag | CC |
|---|---|---|---|
| Cases | 0–10 days | 0 days | 0.69 |
| SII | 6–16 days | 9 days | −0.07 |
| RHBO | 0–10 days | 0 days | 0.51 |
| Plano-SP | 4–16 days | 6 days | 0.53 |
| Vax | 7–21 days | 19 days | 0.15 |
3.2.3. Correlation analysis
We use the Spearman correlation, a non-parametric test commonly employed in the context of time series analysis. For this, first consider the Spearman rank correlation coefficient (), in Eq. (5):
| (5) |
where is the pairwise difference between the ranks of samples, and is the number of samples [17]. The ranks of the samples are obtained from the raw daily data. In the case where, for a given predictor variable, ranks are not distinct integers, a more general correlation measure must be used, presented in Eq. (6).
| (6) |
where is the Pearson correlation coefficient between the rankings of the predictor and target variables, is the covariance of the rank variables, and and are the standard deviations of the rank variables [41]. In both formulations, a negative value of indicates inversely proportional variables, and a positive value of indicates directly proportional variables.
Table 3 resumes the optimal time lag for each variable, as well as the correlation coefficient found to the optimal time lag. The p-values for all correlations are less than or equal to 0.01, which means that the correlations are statistically significant.
Table 3 suggests that the most correlated predictor is the number of daily COVID-19 cases in the city, and SII is the less correlated. Since the forecasting approach proposed in the next section is non-linear, even variables with small linear correlation coefficients may bring relevant information to the predictions. Therefore, we deliberately chose to keep all variables, even those with small correlation coefficients, since they may also carry information pertinent to the models.
4. The proposed integrated approach
The approach proposed in this paper integrates the Prophet and LSTM models to tackle the problem of demand forecasting under the influence of independent variables with different optimal time lags.
In the first stage, we run Prophet taking as exogenous variables those with optimum time lag (), with , where is the forecasting horizon. The introduced model then collects the Prophet fitted values for the training set (), Prophet predicted values () for the forecasting horizon , and Prophet residuals for the training set (), with , where refers to the target value for observation in the training set, and refers to each observation being predicted, with , , and .
Then, an LSTM model is applied in the second stage. In this model, the target variables are the set of residuals from Prophet, . Besides the residuals, the LSTM model also takes variables those whose as input. The LSTM model then returns the predicted values () for the forecasting horizon . The residuals from Prophet and LSTM are aggregated, producing the Prophet-LSTM predicted values (), described in Eq. (7):
| (7) |
Algorithm 1 presents a pseudocode of the Prophet-LSTM integration.
More details about the Python implementation of the analyses and models are given in Appendix section.
4.1. Fitting and forecasting
Both models, Prophet and LSTM, are explained in the following subsections. In addition, details on how the models were set to the studied data are also provided.
4.2. First stage: Prophet
Prophet is a recent forecasting model introduced by Facebook [42]. The model was originally proposed to forecast daily demands under the effect of different seasonal patterns, such as weekly and annual seasonalities, plus holiday effects [9]. Despite its novelty, it has been used to tackle demand forecasting problems. For example, Guo et al. [43] used Prophet to forecast the maximum power demand in China. In another Chinese case study, Guo et al. [44] integrated Prophet to Support Vector Regression (SVR) to predict product demands. The proposed integrated model uses SVR to capture nonlinearities in the residuals generated by Prophet. In the case of COVID-19, Prophet has been mainly used to forecast the COVID-19 number of new cases [45], [46].
To generate forecasts, Prophet first decomposes the time series in trend (), seasonality (), and holidays (), which are given by Eq. (8) [42], [43].
| (8) |
where is the residual from the decomposition at time . In the case of multiplicative seasonalities, and include log transformations.
The trend, , may be described as a piecewise-linear or non-linear function with saturated logistic growth. In this paper, we use Prophet to model a piecewise-linear function, thus:
| (9) |
where is a basic trend growth rate and is a offset parameter. For each of the changes in the trend, a changepoint at time is set, with . Thus, a vector of growth rate adjustments is defined, where is the change rate at time . The rate at any time will be the base rate plus all changes up to : . In a cleaner way, a vector can be defined, such that:
| (10) |
Thus the rate at time is . To each change in , must also be updated, in order to connect the segments endpoints. To adjust , a vector is also employed, whose elements .
The changepoints are automatically selected by putting a sparse prior on . Thus, to choose the changepoints from several candidates, Prophet uses the prior , where the parameter sets the model’s flexibility in altering the rate.
Additional regressors, such as Cases and Vax, are treated as supporting terms in Eq. (9), similarly to tabular supervised settings. Thus, extra regressors need to be known in all future dates for which the target variables will be predicted.
Smoothed weekly seasonality is computed as a Fourier series, given by:
| (11) |
where is the regular period we expect in the case of weekly seasonalities associated with the COVID-19 time series presented, and is a smoothing parameter that regulates how quickly seasonal patterns are fit. Thus, increasing also increases the risk of overfitting. Fitting seasonality also requires estimating the parameters . All Prophet constants are manually set or automatically found via grid search or optimization approaches.
4.2.1. Second stage: LSTM
Neural Networks are the backbones of many Artificial Intelligence (AI) algorithms, which play an important role on daily economic activities [47], [48]. Long–Short Term Memory Neural Networks (LSTM) are the most popular deep learning subset of models for time series forecasting [49]. LSTMs are extensions of Recurrent Neural Networks (RNN). The main difference between LSTM and RNN is that an LSTM can store time-dependent information, mapping non-linear relationships between inputs and outputs [50]. Recently, especially after the development of open-source libraries and the improvements in computational power, LSTMs have mainly been used to tackle demand forecasting problems, such as ultra-short-term industrial power demand [51], highly fluctuating product demand [50], and hourly natural gas demand [52]. Similarly to Prophet, during the COVID-19 pandemic, LSTM has been mainly used to forecast the number of COVID-19 new cases [53], [54].
LSTM cells and gates form LSTM units, that are merged to compose the LSTM layers of an LSTM neural network. The LSTM units are formed by three main types of gates, that regulate the information flow, and a memory cell. This structure allows an LSTM to decide which information will be forgotten and which will be remembered, promoting the learning process of long-term dependencies [55]. The main gates of an LSTM are the input, output, and forget gates. Associated with these gates, there are the input activation vector , output activation vector and forget activation vector . The first one, along with a second gate , determines which information is stored in the memory state vector at time . The forget gate determines which information must be kept or erased from the memory cell in period . Finally, the output gate decides which information will be used as an output of the memory cell. The architecture of the LSTM model adopted in this paper is explained by Eqs. (12)–(17).
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
where is an input vector to the LSTM unit, is the output vector of the LSTM unit, is the LeakyReLU activation function, is the linear activation function, is a hyperbolic tangent activation function, and are weight matrices to be learned, whose indexes , , and refer to the gate or cell the matrices are associated within each step. Finally, is a bias vector parameter to be learned.
Appendix presents details on the implementation of the method.
5. Results and discussion
This section presents how the experiments were configured and the results obtained. The process starts with the configuration of the first stage, Prophet, and the analysis of its residuals and prediction errors. Then, the second stage, LSTM, is set and the combined Prophet-LSTM metrics are presented. Finally, the performances of Prophet-LSTM and both standalone models are compared with classic univariate models.
5.1. First stage: Prophet output
First, the experiment we carried out using Prophet has as inputs the variables whose optimum correlation with the target variable presented a time lag of 7 days or more, which is the size of the forecasting horizon. Thus, the variables SII and Cases were lagged 7 days ahead, and the variables Vax and Plano-SP were lagged 21 days ahead. All variables were standardized before utilization.
In the upper part of Fig. 4, one may observe how the average MAE evolves in time after each feeding forward cross-validation run, where successive training sets are supersets of those that come before them. Thus, in run 99, the model attempts to predict the last 7 observations available (from 0, the last dataset observation, to −7 days) and with a given MAE. In run 98, the model tries to predict 7 observations of the target variable but between days −8 to −1. This way, in CV run 0, we compute the MAE for the prediction of days −106 to −99, using as the training set all data-points available before day-106. One may also observe the impact of incrementally adding characteristics, different exogenous variables, and data pre-processing strategies to the Prophet modeling. Thus, the results referred to as “a. Trend” represents a model that only accounts for the trend in the data. The results indicated by “b. Seasonality” display the MAE values for the Prophet model accounting for trend and seasonality. The same is true for all other lines. In particular, the results indicated by “g. MA7” refers to the MAE for the Prophet model that accounts for Trend and Seasonality, and variables Cases, SII, Vax, and Plano-SP. Moreover, this prediction also considers a 7-day Moving Average (MA7) on all exogenous variables series. It is worth mentioning that in the results enumerated from c. to f., the exogenous variables are only standardized and still bring information about their own seasonalities. As observed, taking the moving average of the variables (“g. MA7”), and adding the variables Cases (“c. Cases”) and Vax (“e. Vax”) are the improvements that have greater impacts on Prophet forecasting accuracy. Also, the improvements brought by the components stabilize after CV run 69.
Fig. 4.
MAE for feeding forward cross-validation for different Prophet approaches.
The bottom of Fig. 4 shows the predicted values evolving with the addition of new components and variables to the Prophet modeling. Those relations are extracted by looking inside CV 98, the run with lower MAE. However, the actual values are always the same. Despite the decrease in MAE and RMSE metrics, it is visually possible to notice how the predictions improve after each increment.
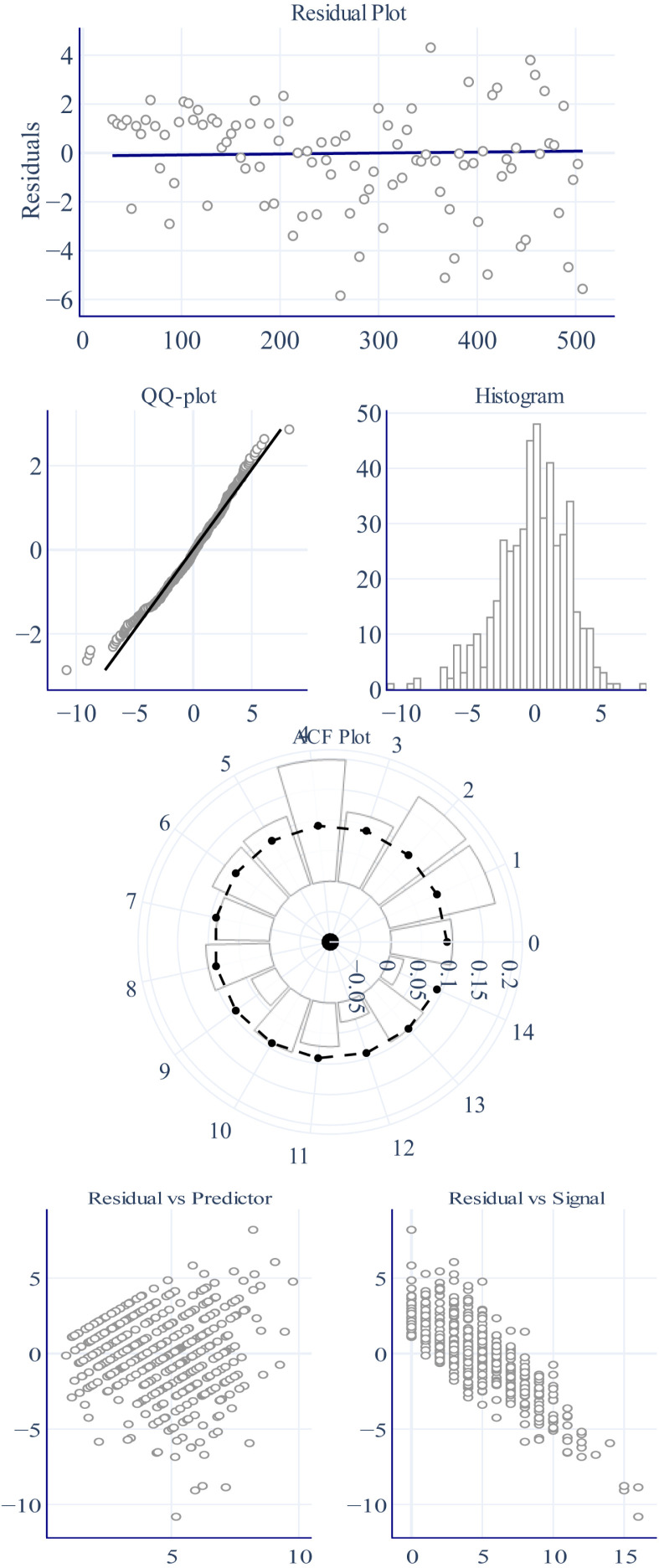
As observed in Fig. 5, the residuals look stationary (ADF-statistic is −6.377, with a -value of 0.0, for a 5.0% significance level), which means they have constant mean, constant variance (homoscedastic), and are free of seasonality. This is graphically represented in Fig. 5 - Residual Plot, which displays a non-repetitive pattern in the observed residuals and mean equal to zero. The residuals also seem to be free of autocorrelation of the first order (DW-statistic of 1.8). Finally, according to the Shapiro–Wilk test for a 5.0% significance level, despite the bell shape in Fig. 5 - Histogram, the residuals are not normally distributed, displaying a W-statistic of 0.975 but a -value close to zero. Therefore, the residuals may be treated as white noise in a general classification. The residuals also do not display a significant correlation with the predicted values (See Fig. 5 - Residual vs. Predictor).
Fig. 5.
Residual analysis after first stage with Prophet.
However, despite the improvements and quality of the residuals, there is still room for improvements in the model. For example, a Pearson’s correlation of −0.82 is observed between the residuals and the target variable (See Fig. 5 - Residual vs. Signal). Also, the autocorrelation of orders higher than one was found, as observed in Fig. 5 - ACF Plot. Those realizations may indicate some information left over that should be accounted for, such as those that may be brought by additional independent variables or hidden seasonal components. Thus, to tackle this issue we run the second stage of the proposed method, which relies on a LSTM neural network.
5.2. Second stage: LSTM output
The LSTM multivariate model takes the residuals from the Prophet training set as the target variable. The LSTM model explains the variations in the residuals in terms of the residuals themselves and the variables Cases and RHBO. The variables Cases and RHBO are in their raw form, with no lags applied to them nor variance smoothing with moving averages.
After manually searching, the LSTM architecture was configured as follows: batch size of 5, input layer with 50 neurons, two hidden layers with 50 and 25 neurons each, LeakyReLU as activation function (), and a dropout rate of 0.1. We set Mean Squared Error (MSE) as the loss function, Adam as optimizer, and RMSE as the evaluation metric. The models were also set to train for 200 epochs but with early stopping.
Fig. 6 compares the performances of the proposed Prophet-LSTM integration and standalone models Prophet (MA7) and a pure LSTM model running all variables with no lags and following the same architecture as the one used for the integrated approach. Prophet-LSTM outperformed standalone Prophet and LSTM in 87% of the runs. One can also notice that Prophet and LSTM change positions during the runs in a non-consistent pattern. The average MAE for all runs of Prophet-LSTM is 0.99, whereas the MAE for Prophet and LSTM was 1.15 and 1.20, respectively. Thus, the Prophet-LSTM integration to the case of hospital ICU demand forecasting during COVID-19 in a Brazilian municipality reduces standalone Prophet and LSTM MAEs by 14.2% and 17.3%, respectively. This posterior treatment of Prophet residuals with LSTM has a greater impact over the proposed model MAE than the pre-treatment performed in the data, which were performed to lag the variables and remove unwanted seasonal patterns.
Fig. 6.
Target and additional variables used for forecasting.
Regarding the computational time taken to perform the models, each CV run of standalone Prophet takes in average (with standard deviation (s) of and Coefficient of Variation (CV) of 0.12). As expected, the models running neural nets are considerably more time consuming than Prophet. Standalone LSTM performs each CV run in (with and ), while the Prophet-LSTM model performs each CV run in (with and ). Since Prophet-LSTM sequentially performs both standalone Prophet and LSTM approaches, its total running time is a rough aggregation of both models individual times. On the other hand, Prophet-LSTM CV roughly weights the CVs of both Prophet and LSTM individual models, thus a CV falling in between the CVs of both individual models was expected. Despite the longer time taken by Prophet-LSTM to train and predict the data, especially in comparison to standalone Prophet (almost ten times more time consuming), the total Prophet-LSTM computational running time still seems to have almost no impact over the hospitals demand forecasting routines. It still runs in a scale of seconds.
It is also noticeable how the performance of Prophet-LSTM improves over time, as soon as more training samples are available. However, despite this apparent continuous extension of the model’s knowledge, Prophet-LSTM do not seem appropriate to incremental learning tasks, mainly because it is considerably dependent on hyperparameter tuning and feature engineering. Additionally, Prophet-LSTM may also face difficulties in handling intermittent demand or in forecasting time series whose behavior is not partially explained by a set of independent variables.
5.3. Benchmarking
In addition to Prophet and LSTM standalone models, we also compare the results from Prophet-LSTM to other models commonly employed in demand forecasting and to predict COVID-19 numbers. The four univariate forecasting models are Holt-Winters, ARIMA, KNN, and RFR, and the two multivariate models are the GRU and Simple RNN. A good explanation of those models and their main mathematical formulations are presented by Souza et al. [56], Kadri and Abdennbi [57], and Sezer et al. [49]. Table 4 summarizes the average MAE for all models and their respective MAE coefficient of variance, considering the results of all 30 cross-validation runs.
Table 4.
Comparison of forecasting models.
| Model | Average MAE | MAE CV |
|---|---|---|
| Prophet-LSTM | 0.99 | 0.25 |
| Prophet | 1.16 | 0.22 |
| LSTM | 1.20 | 0.31 |
| GRU | 1.13 | 0.40 |
| Simple RNN | 1.16 | 0.43 |
| Holt-Winters | 1.43 | 0.34 |
| ARIMA | 1.37 | 0.31 |
| KNN | 1.51 | 0.63 |
| RFR | 1.82 | 0.52 |
In general, Prophet-LSTM outperforms all models, presenting smaller MAE, RMSE, and sMAPE metrics, also displaying MAE with a smaller coefficient of variation (CV). These results suggest that the model is both more accurate and more stable.
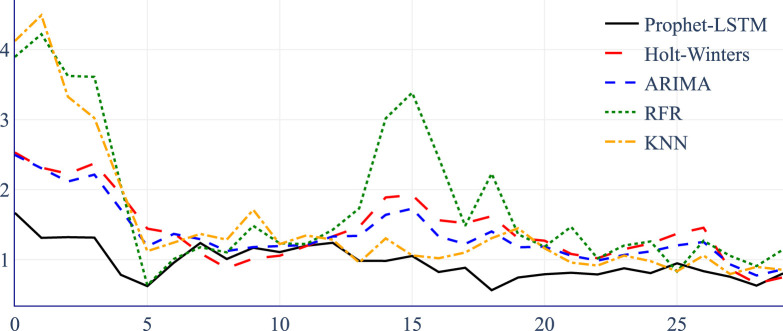
Fig. 7 graphically summarizes how the MAE of the univariate models and Prophet-LSTM varies on time.
Fig. 7.
MAE over time for benchmark models.
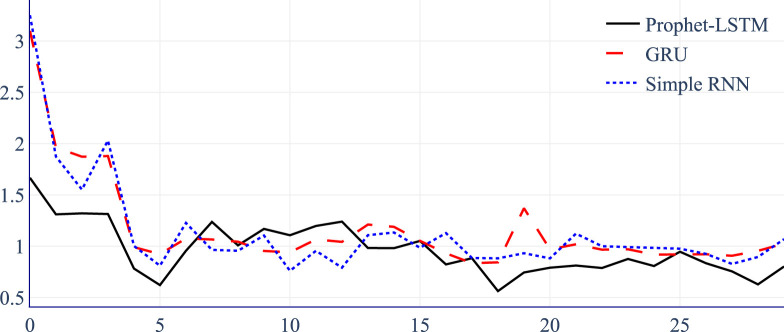
Fig. 8 graphically summarizes how the MAE of the multivariate models and Prophet-LSTM varies with time. Notice that despite the better performance of the multivariate models, especially in contrast to the performance of univariate models, the two multivariate benchmarks are considerably less stable than Prophet-LSTM, displaying a much higher MAE CV, as shown by Table 4.
Fig. 8.
MAE over time for benchmark models.
Finally, we also run Mann–Whitney U Tests to all cross-validation runs, comparing Prophet-LSTM to the other models. The null hypothesis (H) assumes no significant difference between the two series. The alternative hypothesis (H) investigates if the series are different. The H is accepted in all cases for p-values . In detail, the -value of Prophet is 0.008; LSTM is 0.012; GRU is 0.018; Simple RNN is 0.045; Holt-Winters, ARIMA, and RFR are 0.000; KNN is 0.002.
6. Conclusions
In this paper, we showed that a two-stage integrated approach of Prophet and LSTM models results in significantly (max -value 0.012) better COVID-19 ICU demand forecastings than both standalone models, Prophet and LSTM, and also four univariate benchmarks (ARIMA, Holt-Winters, RFR, and KNN) and two multivariate benchmarks (GRU and Simple RNN). During the Prophet stage, the variables Cases and Vax showed the most significant impact on the model performance. After the second stage, the MAE CV was also improved in relation to standalone LSTM. Despite the smaller forecasting errors, the Prophet-LSTM model is also more time-consuming than both standalone models. Thus, running this model for several time series may demand simplifications or the usage of hierarchical structures. In contrast to Prophet, Prophet-LSTM also significantly increases the time needed to set the optimal parameters before the final forecast. However, in the case of COVID-19 ICU forecasting, the model appears to be an interesting option that could potentially be replicated to other municipalities with similar data available.
CRediT authorship contribution statement
Dalton Borges: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing – original draft, Writing – review & editing, Project administration. Mariá C.V. Nascimento: Validation, Resources, Writing – review & editing, Supervision, Funding acquisition.
Declaration of Competing Interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Dalton Garcia Borges de Souza reports financial support was provided by Coordination for the Improvement of Higher Education Personnel (CAPES).
Acknowledgments
The authors would like to thank the Brazilian Coordination for the Improvement of Higher Education Personnel (CAPES), Brazil for fully supporting this work through the Call CAPES-Print 2020 and Grant: 88887.507037/2020-00.
Footnotes
HIV/AIDS vs. COVID: https://time.com/5915401/world-aids-day-covid-coronavirus-pandemic/.
OCDE’s Economic Outlook: https://www.oecd.org/newsroom/global-economy-faces-a-tightrope-walk-to-recovery.htm.
Appendix. Implementation
All data acquisition, analysis, and treatment, as well as the models, are implemented in Python. Fig. A.9 shows the main libraries, modules and the flow in which the analysis and experiments were performed. The framework of Fig. A.9 follows a similar distribution of the processes presented in Fig. 1.
Fig. A.9.
Main libraries and modules used to implement the analyses and forecasting models in Python.
In the first implementation block, regarding data acquisition and anomaly detection, the framework acquires the data (approximately 40 GB) and preprocesses it to patient-level variables in a tabular format. The library Dask is widely used in this step, taking raw data from hospitals and the government as input. Then, data preprocessing occurs by removing simple anomalies, such as patients with dissonant ages and incorrect dates. Finally, the variables for the models are created and consolidated in a daily granularity. This step is performed primarily through the use of the libraries pandas and NumPy, taking patient-level variables as input.
The next stage of the framework consists of data analysis and treatment. It searches for seasonal components in the data and removes them when needed. The libraries used in these steps are StatsModels, mainly the module seasonal_decompose, and Plotly, for data visualization. The primary input data for the functions of both libraries are the dependent and independent variables. Finally, the modules Linear Regression, of Sklearn library, and Spearmanr, of Scipy library are used to check the optimal correlation between the dependent and independent variables, which are also their primary data input. For the Spearman test, , the threshold value used to judge whether a test statistic is statistically significant, was set to 0.05.
For the Prophet implementation block, the Sktime library is employed to split the data into training and testing sets, taking the set of target and exogenous variables as input. Then, the Prophet function initiates the model. Its inputs are the growth model (linear in our case), the width of the confidence interval (95% in the case), and Boolean variables indicating the set of seasonalities used. After that, function add.regressor add the exogenous variables to the model and the function fit trains the model, taking as inputs the instantiated model and the training set of the target variable. Finally, the function predict is used to predict future values with the fitted model, the test set, and the size of the forecasting horizon. The framework collects the RMSE, MAE, and SMAPE using the Scikit-learn library.
After Prophet, the framework performs the following tests for the residual analysis:
-
•
Augmented Dickey–Fuller Test, Autocorrelation Test, and Durbin Watson Statistic (functions adfuller, acfn and durbin_watson of Statsmodels library), taking the series of residuals, an of 0.05 and, in the case of Autorrelation Test, a given number of lags to be mapped (15, in the case) as input.
-
•
The Shapiro–Wilk test (function shapiro of Scipy library), which takes as input the series of residuals and of 0.05. The residual graphs are then drawn with the libraries Plotly (graph_objects module) and Scikit-learn (LinearRegression module), taking are primary inputs the target variable series of values and the series of residuals.
The LSTM implementation block relies primarily on Keras and TensorFlow libraries. However, for the data preparation, the framework employs the library Sktime to split the data into training and testing sets, taking the set of target and explanatory variables as input, and the library Sklearn (MinMaxScaler function) to normalize the explanatory variables between 0 and 1. The module TimeseriesGenerator of Keras is also employed to prepare the data, taking the window length (5 in the case), sampling_rate (1 in the case), batch_size (5 in the case), and a set of explanatory and target variables as input. The model is then created, and a set of LSTM, LeakyRelu, Dropout, and Dense layers are added through keras.layers modules of Library Keras. The model is then compiled (function compile of Tensorflow, taking the mean squared error as loss function, Adam as optimizer, and RMSE as metric) and fit to the data (function fit_generator of Tensowflow, taking as inputs 100 epochs with early_stopping and the data prepared previously). Finally, predictions are made with module predict_generator.
After running the LSTM model, the Prophet-LSTM model is simply built with Pandas and Numpy operations. Finally, the full integration is analyzed with metrics drawn from Scikit-learn libraries, through the module metrics.
The benchmark implementation block re-implements the Prophet and LSTM models, in the same way they were implemented before; however, taking the whole set of variables is available as input. The Simple RNN and GRU models follow similar implementations as the LSTM model, but with GRU and RNN gates, instead of LSTM gates. Finally, the Univariate models are implemented with Sktime library. The data is first split into training and testing sets (function temporal_train_test_ split), the training set is used to train the modules (forecaster.fit), and the trained model and testing sets are used to make the predictions (forecaster.fit).
Once the predicted values are collected from Prophet-LSTM, Prophet and LSTM standalone models, and all benchmark models, they are compared using the module metrics of Scikit-Learn and Mann–Whitney U Test (function stats.mannwhitneyu of Scipy library). Finally, we draw the comparison graphs with Library Plotly (graph_objects module).
References
- 1.Gaynor M., Anderson G.F. Uncertain demand, the structure of hospital costs, and the cost of empty hospital beds. J. Health Econ. 1995;14(3):291–317. doi: 10.1016/0167-6296(95)00004-2. [DOI] [PubMed] [Google Scholar]
- 2.Raju P., Lonial S.C., Gupta Y.P. Market orientation and performance in the hospital industry. Mark. Health Serv. 1995;15(4):34. [PubMed] [Google Scholar]
- 3.Abraham G., Byrnes G.B., Bain C.A. Short-term forecasting of emergency inpatient flow. IEEE Trans. Inf. Technol. Biomed. 2009;13(3):380–388. doi: 10.1109/TITB.2009.2014565. [DOI] [PubMed] [Google Scholar]
- 4.Nikolopoulos K., Punia S., Schäfers A., Tsinopoulos C., Vasilakis C. Forecasting and planning during a pandemic: COVID-19 growth rates, supply chain disruptions, and governmental decisions. European J. Oper. Res. 2021;290(1):99–115. doi: 10.1016/j.ejor.2020.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Egger D., Miguel E., Warren S.S., Shenoy A., Collins E., Karlan D., Parkerson D., Mobarak A.M., Fink G., Udry C., et al. Falling living standards during the COVID-19 crisis: Quantitative evidence from nine developing countries. Sci. Adv. 2021;7(6):eabe0997. doi: 10.1126/sciadv.abe0997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Karim S.S.A., Karim Q.A. Omicron SARS-CoV-2 variant: a new chapter in the COVID-19 pandemic. Lancet. 2021;398(10317):2126–2128. doi: 10.1016/S0140-6736(21)02758-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dodds W. The World’s Worst Problems. Springer; 2019. Disease now and potential future pandemics; pp. 31–44. [Google Scholar]
- 8.Castillo-Chavez C., Curtiss R., Daszak P., Levin S.A., Patterson-Lomba O., Perrings C., Poste G., Towers S. Beyond Ebola: Lessons to mitigate future pandemics. Lancet Global Health. 2015;3(7):e354–e355. doi: 10.1016/S2214-109X(15)00068-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hyndman R.J., Athanasopoulos G. OTexts; 2018. Forecasting: Principles and Practice. [Google Scholar]
- 10.Chan N.H. John Wiley & Sons; 2011. Time Series: Applications to Finance with R and S-Plus, Vol. 837. [Google Scholar]
- 11.Hyndman R.J., Fan S. Density forecasting for long-term peak electricity demand. IEEE Trans. Power Syst. 2009;25(2):1142–1153. [Google Scholar]
- 12.Ioannidis J.P., Cripps S., Tanner M.A. Forecasting for COVID-19 has failed. Int. J. Forecast. 2020 doi: 10.1016/j.ijforecast.2020.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhu X., Zhang G., Sun B. A comprehensive literature review of the demand forecasting methods of emergency resources from the perspective of artificial intelligence. Nat. Hazards. 2019;97(1):65–82. [Google Scholar]
- 14.Gul M., Celik E. An exhaustive review and analysis on applications of statistical forecasting in hospital emergency departments. Health Syst. 2020;9(4):263–284. doi: 10.1080/20476965.2018.1547348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rahimi I., Chen F., Gandomi A.H. A review on COVID-19 forecasting models. Neural Comput. Appl. 2021:1–11. doi: 10.1007/s00521-020-05626-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.de Souza D.G.B., Júnior F.T.A., Soma N.Y. Forecasting COVID-19 cases at the Amazon region: a comparison of classical and machine learning models. BioRxiv. 2020 [Google Scholar]
- 17.da Silva T.T., Francisquini R., Nascimento M.C. Meteorological and human mobility data on predicting COVID-19 cases by a novel hybrid decomposition method with anomaly detection analysis: a case study in the capitals of Brazil. Expert Syst. Appl. 2021 doi: 10.1016/j.eswa.2021.115190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Capistran M.A., Capella A., Christen J.A. Forecasting hospital demand in metropolitan areas during the current COVID-19 pandemic and estimates of lockdown-induced 2nd waves. PLoS One. 2021;16(1) doi: 10.1371/journal.pone.0245669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Koç E., Türkoğlu M. Forecasting of medical equipment demand and outbreak spreading based on deep long short-term memory network: the COVID-19 pandemic in Turkey. Signal Image Video Process. 2021:1–9. doi: 10.1007/s11760-020-01847-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.COVID I., Murray C.J., et al. Forecasting the impact of the first wave of the COVID-19 pandemic on hospital demand and deaths for the USA and European economic area countries. MedRxiv. 2020 [Google Scholar]
- 21.COVID I., Murray C.J., et al. Forecasting COVID-19 impact on hospital bed-days, ICU-days, ventilator-days and deaths by US state in the next 4 months. MedRxiv. 2020 [Google Scholar]
- 22.Goic M., Bozanic-Leal M.S., Badal M., Basso L.J. COVID-19: Short-term forecast of ICU beds in times of crisis. PLoS One. 2021;16(1) doi: 10.1371/journal.pone.0245272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Borchering R.K., Viboud C., Howerton E., Smith C.P., Truelove S., Runge M.C., Reich N.G., Contamin L., Levander J., Salerno J., et al. Modeling of future COVID-19 cases, hospitalizations, and deaths, by vaccination rates and nonpharmaceutical intervention scenarios—United States, April–September 2021. Morb. Mortal. Wkly. Rep. 2021;70(19):719. doi: 10.15585/mmwr.mm7019e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rivera-Rodriguez C., Urdinola B.P. Predicting hospital demand during the COVID-19 outbreak in Bogota, Colombia. Front. Public Health. 2020;8:710. doi: 10.3389/fpubh.2020.582706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Massonnaud C., Roux J., Crépey P. COVID-19: Forecasting short term hospital needs in France. Medrxiv. 2020 [Google Scholar]
- 26.Nguyen H.M., Turk P.J., McWilliams A.D. Forecasting COVID-19 hospital census: A multivariate time-series model based on local infection incidence. JMIR Public Health Surveill. 2021;7(8) doi: 10.2196/28195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Berta P., Paruolo P., Verzillo S., Lovaglio P.G. A bivariate prediction approach for adapting the health care system response to the spread of COVID-19. Plos One. 2020;15(10) doi: 10.1371/journal.pone.0240150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.WHO . 2021. Coronavirus disease 2019 (COVID-19) pandemic. URL: https://covid19.who.int/. Accessed on 30.07.2021. [Google Scholar]
- 29.Ministry of Health of Brazil . 2021. Painel coronavírus. URL: https://covid.saude.gov.br/. Acessed on 30.07.2021. [Google Scholar]
- 30.Faria N.R., Mellan T.A., Whittaker C., Claro I.M., Candido D.d.S., Mishra S., Crispim M.A., Sales F.C., Hawryluk I., McCrone J.T., et al. Genomics and epidemiology of the P. 1 SARS-CoV-2 lineage in Manaus, Brazil. Science. 2021;372(6544):815–821. doi: 10.1126/science.abh2644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.IBGE . 2021. IBGE cidades 2021. URL: https://cidades.ibge.gov.br/. Accessed on 30.07.2021. [Google Scholar]
- 32.Francisquini R., Lorena A.C., Nascimento M.C.V. Community-based anomaly detection using spectral graph filtering. Appl. Soft Comput. 2022 doi: 10.1016/j.asoc.2022.108489. [DOI] [Google Scholar]
- 33.CCE-SP . 2021. Centro de conntingência do Estado de São Paulo. URL: https://www.saopaulo.sp.gov.br/coronavirus/. Accessed on 30.07.2021. [Google Scholar]
- 34.CCE-SP . 2021. Plano São Paulo. URL: https://www.saopaulo.sp.gov.br/planosp/. Accessed on 30.07.2021. [Google Scholar]
- 35.Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Azman A.S., Reich N.G., Lessler J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann. Int. Med. 2020;172(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dos Santos L.A., de Góis Filho P.G., Silva A.M.F., Santos J.V.G., Santos D.S., Aquino M.M., de Jesus R.M., Almeida M.L.D., da Silva J.S., Altmann D.M., et al. Recurrent COVID-19 including evidence of reinfection and enhanced severity in thirty Brazilian healthcare workers. J. Infect. 2021;82(3):399–406. doi: 10.1016/j.jinf.2021.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.He W., Yi G.Y., Zhu Y. Estimation of the basic reproduction number, average incubation time, asymptomatic infection rate, and case fatality rate for COVID-19: Meta-analysis and sensitivity analysis. J. Med. Virol. 2020;92(11):2543–2550. doi: 10.1002/jmv.26041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Faes C., Abrams S., Van Beckhoven D., Meyfroidt G., Vlieghe E., Hens N., et al. Time between symptom onset, hospitalisation and recovery or death: Statistical analysis of belgian covid-19 patients. Int. J. Environ. Res. Public Health. 2020;17(20):7560. doi: 10.3390/ijerph17207560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Thompson R.N., Lovell-Read F.A., Obolski U. Time from symptom onset to hospitalisation of coronavirus disease 2019 (COVID-19) cases: implications for the proportion of transmissions from infectors with few symptoms. J. Clin. Med. 2020;9(5):1297. doi: 10.3390/jcm9051297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lima F.E.T., Albuquerque N.L.S.d., Florencio S.d.S.G., Fontenele M.G.M., Queiroz A.P.O., Lima G.A., Figueiredo L.M.d., Amorim S.M.C., Barbosa L.P. Time interval between onset of symptoms and COVID-19 testing in Brazilian state capitals, August 2020. Epidemiol. Serv. Saúde. 2020;30 doi: 10.1590/S1679-4974202100010002. [DOI] [PubMed] [Google Scholar]
- 41.Myers J.L., Well A., Lorch R.F. Routledge; 2010. Research Design and Statistical Analysis. [Google Scholar]
- 42.Taylor S.J., Letham B. Forecasting at scale. Amer. Statist. 2018;72(1):37–45. [Google Scholar]
- 43.Guo C., Ge Q., Jiang H., Yao G., Hua Q. Maximum power demand prediction using fbprophet with adaptive Kalman filtering. IEEE Access. 2020;8:19236–19247. [Google Scholar]
- 44.Guo L., Fang W., Zhao Q., Wang X. The hybrid PROPHET-SVR approach for forecasting product time series demand with seasonality. Comput. Ind. Eng. 2021;161 [Google Scholar]
- 45.Battineni G., Chintalapudi N., Amenta F. Forecasting of COVID-19 epidemic size in four high hitting nations (USA, Brazil, India and Russia) by Fb-Prophet machine learning model. Appl. Comput. Inform. 2020 [Google Scholar]
- 46.Indhuja M., Sindhuja P. Prediction of covid-19 cases in India using prophet. Int. J. Stat. Appl. Math. 2020;5(4) [Google Scholar]
- 47.Lu H., Li Y., Chen M., Kim H., Serikawa S. Brain intelligence: go beyond artificial intelligence. Mob. Netw. Appl. 2018;23(2):368–375. [Google Scholar]
- 48.Chen Z., Lu H., Tian S., Qiu J., Kamiya T., Serikawa S., Xu L. Construction of a hierarchical feature enhancement network and its application in fault recognition. IEEE Trans. Ind. Inf. 2020;17(7):4827–4836. [Google Scholar]
- 49.Sezer O.B., Gudelek M.U., Ozbayoglu A.M. Financial time series forecasting with deep learning: A systematic literature review: 2005–2019. Appl. Soft Comput. 2020;90 [Google Scholar]
- 50.Abbasimehr H., Shabani M., Yousefi M. An optimized model using LSTM network for demand forecasting. Comput. Ind. Eng. 2020;143 [Google Scholar]
- 51.Tan M., Yuan S., Li S., Su Y., Li H., He F. Ultra-short-term industrial power demand forecasting using LSTM based hybrid ensemble learning. IEEE Trans. Power Syst. 2019;35(4):2937–2948. [Google Scholar]
- 52.Su H., Zio E., Zhang J., Xu M., Li X., Zhang Z. A hybrid hourly natural gas demand forecasting method based on the integration of wavelet transform and enhanced Deep-RNN model. Energy. 2019;178:585–597. [Google Scholar]
- 53.Chimmula V.K.R., Zhang L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals. 2020;135 doi: 10.1016/j.chaos.2020.109864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Kırbaş İ., Sözen A., Tuncer A.D., Kazancıoğlu F.Ş. Comparative analysis and forecasting of COVID-19 cases in various European countries with ARIMA, NARNN and LSTM approaches. Chaos Solitons Fractals. 2020;138 doi: 10.1016/j.chaos.2020.110015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Livieris I.E., Pintelas E., Pintelas P. A CNN–LSTM model for gold price time-series forecasting. Neural Comput. Appl. 2020;32(23):17351–17360. [Google Scholar]
- 56.de Souza D.G.B., dos Santos E.A., Alves Júnior F.T., Nascimento M.C.V. On comparing cross-validated forecasting models with a novel fuzzy-TOPSIS metric: A COVID-19 case study. Sustainability. 2021;13(24):13599. [Google Scholar]
- 57.Kadri F., Abdennbi K. RNN-based deep-learning approach to forecasting hospital system demands: application to an emergency department. Int. J. Data Sci. 2020;5(1):1–25. [Google Scholar]