Analysis of complexity in the EEG activity of Parkinson’s disease patients by means of approximate entropy

Abstract

The objective of the present study is to explore the brain resting state differences between Parkinson’s disease (PD) patients and age- and gender-matched healthy controls (elderly) in terms of complexity of electroencephalographic (EEG) signals. One non-linear approach to determine the complexity of EEG is the entropy. In this pilot study, 28 resting state EEGs were analyzed from 13 PD patients and 15 elderly subjects, applying approximate entropy (ApEn) analysis to EEGs in ten regions of interest (ROIs), five for each brain hemisphere (frontal, central, parietal, occipital, temporal). Results showed that PD patients presented statistically higher ApEn values than elderly confirming the hypothesis that PD is characterized by a remarkable modification of brain complexity and globally modifies the underlying organization of the brain. The higher-than-normal entropy of PD patients may describe a condition of low order and consequently low information flow due to an alteration of cortical functioning and processing of information. Understanding the dynamics of brain applying ApEn could be a useful tool to help in diagnosis, follow the progression of Parkinson’s disease, and set up personalized rehabilitation programs.

Introduction

Parkinson’s disease (PD) is a common progressive neurodegenerative disorder [1] which affects about 1% of the population over 55 years of age worldwide [2]. PD results from a complicated interaction of genetic and environmental factors affecting numerous cellular processes and leading to a progressive degeneration of dopaminergic neurons in the substantia nigra of the midbrain and related neural -including cortical- networks [3].

The series of symptoms and signs associated with PD are predominantly characterized by motor dysfunction, such as gait disturbance, bradykinesia, muscle rigidity, resting tremor, and postural instability [1, 4, 5] and non-motor deficits such as autonomic dysfunction, cognitive impairments, or psychiatric disturbances [6, 7].

The neurodegeneration is working in the darkness—namely without evident clinical symptoms—for many years until the percentage of degenerated neurons in the substantia nigra is remarkably high. Therefore, early diagnosis—hopefully in a stage in which symptoms are approximately absent—would be highly desirable, but difficult to be reached in the early stage with the presently available technologies [6–8] and when it is based on clinical exam looking for the presence of both cardinal motor dysfunction and response to levodopa [9]. PD disorders were largely studied by functional imaging methods, whereas there are still few scientific contributions exploring the disease using neurophysiological techniques such as magnetoencephalography (MEG) or electroencephalography (EEG), probably because it is assumed that PD is mainly due to subcortical relays degeneration (i.e., basal ganglia). However, this is not a real obstacle since such relays are heavily and mutually connected with cortical areas (the main source of EEG signals for the brain complexity) and symptoms are mainly stemming from disruption of such connection, leading to full support the idea of using the scalp EEG recordings for the evaluation of brain activity modulation due to subcortical deregulation in PD. Furthermore, new approaches are required to improve PD early detection in order to set up an efficient treatment and intervention on risk factors at the earliest possible time of neurodegeneration. As said above, one of such approaches could be the EEG, a non-invasive technique able to depict brain electric activity with high temporal resolution and high test–retest reliability [10, 11]. In the last decades, clinical and basic research quantifying EEG rhythms led to obtain important biomarkers for several neurological disorders, such as schizophrenia, major depressive disorder, Alzheimer’s disease, and epilepsy [12–16].

Many studies have focused on EEG abnormalities in PD patients by using traditional spectral analysis. With such a method of analysis, different pathological brain features associated with PD have been identified; in particular, a generalized slowing of EEG activity in comparison to elderly healthy controls has been described [17–21]. Recently, a mathematical model of architecture of brain functional organization, the graph theory, has been employed to analyze EEG data for the investigation of network differences between PD patients and healthy elderly subjects [22]. The small-world parameter, that reflects the balance between local processing and global integration and model the architecture of brain centers connectivity, has been found lower in theta and higher in alpha 2 EEG frequency bands which highlighted the presence of significant modifications at EEG level due to the disease.

These studies indicate that quantifying EEG may be also useful in describing the PD alterations. Therefore, it would be still necessary to use new analysis methods to explore EEG signals of PD patients, which may contribute to reveal other features of brain organization and more important information underlying brain dysfunctions. Non-linear signal analysis is a different way of dealing with EEG complexity, considering the latter as the result of nonlinear deterministic dynamics, possibly representing a chaotic process [23–25]. For example, Lainscsek and collaborators [26] used a non-linear dynamical analysis, based on delay differential equations (DDE), to characterize and distinguish the EEG changes of PD patients from healthy controls providing the basis for a novel approach for the evaluation of the dynamics of neural activity in patients with PD.

A non-linear approach to determine the complexity of EEG signals is a measure based on the patterns of recorded times series, specifically the entropy. Initially, the term “entropy” was introduced in thermodynamics in the nineteenth century, and only later in 1948, this measure was adapted for information theory and signal analysis. Entropy was first defined as a measure of information comprised in a given amount of signals and as a measure of how information within a signal can be quantified with absolute precision as the amount of unexpected data contained in the signal itself. In this case, entropy represents and describes the irregularity, complexity, or unpredictability characteristics of a signal [27]. In general, as neural systems have been shown to exhibit some kind of nonlinear chaotic behavior, it can be reasonable to apply methods from the theory of nonlinear dynamics to the EEG signals to detect its variability that can emerge from neuronal circuits and extend over the entire brain. The entropic brain hypothesis suggests that any given mental state can be indexed by a quantitative measure of the magnitude of entropy as a parameter to describe spontaneous brain activity, for example, recorded with EEG [28]. So, entropy represents a powerful approach for EEG analysis, and it can be used to quantify brain functions and alteration across brain areas related to altered state, for example, due to a neurodegenerative disease [25, 29, 30].

In the past decades, several entropy measures (i.e., sample entropy, approximate entropy, Tsallis entropy, permutation entropy, multiscale entropy) have been introduced to study brain activity, some of which have already been applied to PD patients’ EEGs even if the investigation of these associated with PD is still in its infancy [31, 32].

In the present study, we selected approximate entropy (ApEn) compared to other measures of entropy, because of the properties that facilitate its use: it can be applied with good reproducibility to time series [25], it is almost unaffected by noise, it is finite for composite, stochastic, and noisy deterministic processes [33], and it detects the changes in underlying episodic behavior undetected by peak occurrences or amplitudes [34]. Moreover, ApEn has been extensively used in studies of time series of physiologic parameters to assess their degree of randomness [35, 36]. For all the exposed reasons, ApEn would be extremely helpful in brain function understanding, given the complex and dynamical characteristics of the cerebral systems.

Within this theoretical frame, the aim of the present study was to explore the resting state brain activity differences between PD patients and age- and gender-matched healthy subjects (elderly) applying the ApEn analysis. In particular, the current study expands the existing research literature, investigating the complexity of EEG activity in different brain areas, selecting 10 cerebral networks, 5 for each hemisphere (frontal, central, parietal, occipital, temporal), to explore the brain abnormalities due to PD, compared to a healthy brain.

Subjects and methods

Participants

Two groups of Parkinson’s patients (n = 13) and healthy subjects (n = 15) matched for sex (8 female) and age (61,54 ± 2,47 (mean ± standard error)) were enrolled.

The informed consent of each participant was obtained according to the Code of Ethics of the World Medical Association (1997), and the experimental procedures were carried out conforming to the Declaration of Helsinki. The EEG recordings were performed following the safety guidelines procedures.

For each PD patient included, the disease was diagnosed taking into account the medical history and neurological and physical examinations as well as response to levodopa drugs. Exclusion criteria included atypical Parkinsonism, neuroleptic drug use, antidepressants, dopamine blocking agents, alcohol abuse, presence of other neurological or psychiatric conditions, and any other severe illness. As measure of severity of motor disability, the Unified Parkinson’s Disease Rating Scale-III (UPDRS) was used. The UPDRS score was 15.1 $\pm$ 1.2 (mean $\pm$ standard error). All PD patients underwent the MMSE scales, showing a mean score of 28.2 $\pm$ 0.3 (mean $\pm$ standard error).

For the control group, the subjects were physically and intellectually healthy with no symptoms or history of any neuropsychiatric disorder.

Data recordings and preprocessing

Each subject underwent EEG clinical recordings measured at rest in eyes-closed condition, without performing any tasks, for at least 6 min. The EEG recording was conducted after about 1–2 h from administration of morning medications. During the recording, subjects were seated in a comfortable armchair. EEG signals were recorded using 19 electrodes for PD group and 32 electrodes for elderly, positioned according to the International 10–20 system.

Vertical and horizontal EOGs separate channels were used to monitor eyes blinking. Impedance was kept below 5 KΩ and the sampling rate frequency was set up at 256 Hz.

The data were processed in Matlab (MathWorks, Natick, MA) using scripts based on EEGLAB toolbox (Swartz Center for Computational Neurosciences, La Jolla, CA) [37–39].

The data were band-pass filtered from 0.2 to 47 Hz using a finite impulse response (FIR) filter. EEG recordings were processed segmenting the signal in 2-s duration epochs in order to remove principal artifacts, such as eye movements, scalp muscle contraction, and cardiac activity first by an EEG expert visual inspection, and then with Infomax ICA algorithm [40, 41], that allows the separation of statistically independent sources from multichannel EEG recordings [42–46] as implemented in the EEGLAB. At the end of the artifact removal procedure, at least 5 min EEG recordings remained for subjects.

Entropy analysis

Entropy analysis was computed on the artifact free epochs by means of a homemade software developed in Matlab. The core of the software is the ApEn evaluation, which was realized by using the algorithm already implemented in Matlab: approximate entropy (ApEn) function estimates the approximate entropy of the uniformly sampled time-domain signal by reconstructing the phase space. The software is implemented as follows: for each channel and for each epoch, a value of ApEn is computed; then, those values are averaged among the epochs in order to obtain only one ApEn value for each channel and for each EEG session [24, 25, 47].

Two input parameters, the window length m and tolerance factor r, are specified to compute it. r is also called similarity factor used to detect a range in which data points are similar. The ApEn generates values from 0 to 2: an ApEn value equal to 0 corresponds to a time series that is perfectly regular, whereas an ApEn value equal to 2 is produced by random time series [48]. The ApEn is computed as in the study of Lee and collaborators [49]: the first segment of length m is compared to all the other sequences of the same length point by point. A point of a sequence is similar to its corresponding point in the original sequence, when its value is not above its original value plus the tolerance factor r. The same process is applied to sequences of length m + 1, starting with the first sequence of m + 1 points. The process is repeated for all possible sequences. All results are summed and normalized with respect to the total number of data samples N.

In summary, the ApEn is calculated as $ApEn={\mathrm{\Phi }}_m-{\mathrm{\Phi }}_{m+1}$:

$${\mathrm{\Phi }}_m={(N-m+1)}^{-1}\sum _{i=1}^{N-m+1}\log (N_i)$$

where $N_i$ represents the amount of points that are within r of their corresponding point in the original sequence Y, at point i:

$${\mathrm{N}}_i=\sum _{i=1,i\ne k}^N({\Vert Y_i-Y_k\Vert }_{\infty }<r)$$

In the present study, the Matlab default values for the input parameters were selected: so m was equal to 2 and r to 0.2*variance(x) [49–52], where x is a 2-s long epoch of a specific channel.

These well-established values are selected because they have been demonstrated to produce good statistical reproducibility for time series of length N > 60 [53]. Normalizing r in this manner gives ApEn a translation and scale invariance; in this way, it remains unchanged under uniform process magnification, reduction, or constant shift to higher or lower values [54]. In the current study, since the sampling frequency was set to 256 Hz, time series of 2 s were 512 points long.

Through the homemade software, ApEn was evaluated on each single epoch for each channel. Only later, the ApEn values were averaged over the epochs, in order to get a single value of ApEn for each channel [55].

Once computed, in order to obtain a single value of entropy for each region of interest (ROI), the ApEn values evaluated in each electrode were averaged over ten ROIs (five left and five right: frontal, central, parietal, occipital; temporal), grouping the electrodes as shown in Table 1 referred to 32 electrodes’ montage [24, 25, 56]. The electrodes along the midline were excluded (Fig. 1).

Table 1.

The table shows the grouping of the electrodes for each region of interest (ROI) and for each hemisphere

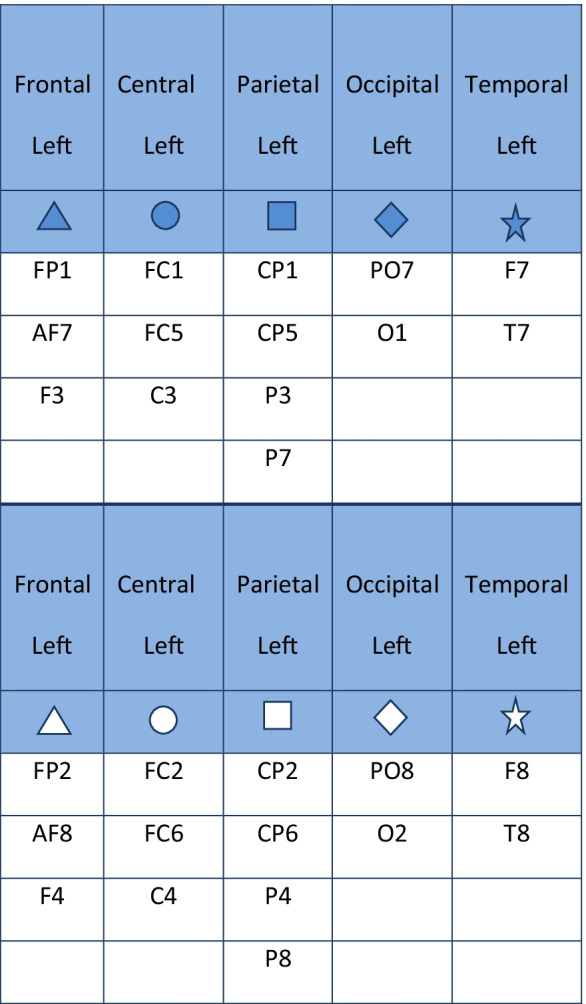
Fig. 1.

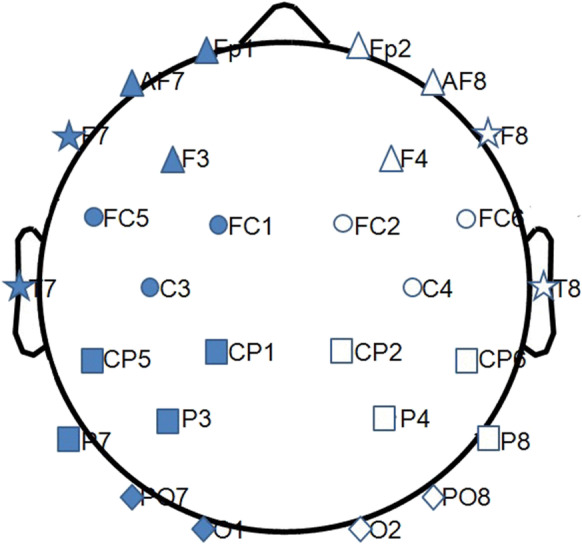
The figure shows the grouping of the electrodes for the regions of interest (ROIs of the brain networks) explored the two groups of subjects: full shapes for the left hemisphere, empty shapes for the right hemisphere. Triangle for frontal, circle for central, square for parietal, rhombus for occipital, and star for temporal ROI

Statistical evaluation

A statistical ANOVA design was addressed for the ApEn between the factor group (PD, elderly), hemisphere (left, right), and ROI (frontal, central, parietal, occipital, temporal). The normality of the data was tested using the Kolmogorov–Smirnov test, and the hypothesis of Gaussianity could not be rejected. Greenhouse and Geisser correction was used for the protection against a possible violation of the sphericity assumption in the repeated measure ANOVA. Besides, post hoc analysis with the Duncan’s test and significance level at 0.05 was performed. To confirm the ability of ApEn to distinguish PD group from elderly, the probability of PD was estimated from the given set of features, coming from ApEn values for each ROI (frontal, central, parietal, occipital, temporal) and each hemisphere (left, right), for a total of 10 predictors. The features are used to train a binary classifier based on support vector machine (SVM). To realize this approach, the dataset was split into training set, used to train the model, and test set, to evaluate the model performances, in particular classification accuracy. In order to have a complete model evaluation, we followed a cross-validation technique (i.e., fivefold): the dataset was randomly split in 80% training set and 20% test set.

Results

The ANOVA for the evaluation of ApEn index showed a statistically significant main effect (F(1, 26) = 55.517, p < 0.00001) for the factor group (PD, elderly) as illustrated in the Boxplot reported in Fig. 2. The Duncan post hoc testing showed statistic differences between PD and elderly; in particular, ApEn in Parkinson shows higher values in PD patients than in controls (p < 0.05). Although the limited number of samples must be taken into consideration and the following result is only preliminary to future research, the resulting classifier based on SVM showed 96.4% of accuracy and the average receiver operating characteristic (ROC) had an area under the curve equal to 1, indicating very high classification power of PD respect to control subjects.

Fig. 2.

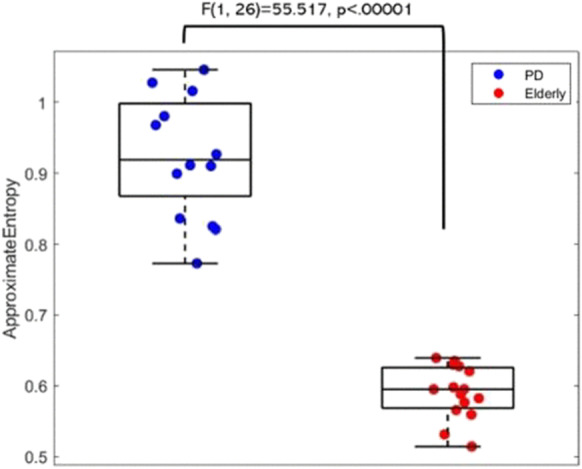
Boxplot of the approximate entropy (ApEn) values for the two groups (PD, Elderly). The middle line represents the median of the ApEn values, the box represents the quartile, and the whiskers represent the range

Discussion

Parkinson’s disease (PD) is a neurodegenerative disorder caused by major alteration in the basal ganglia function [57], which may also result in changes of the brain activity recorded by EEG.

In the past decades, electrophysiological techniques and mathematical analysis approaches have been applied to identify in the EEG signals the characteristics of cortical dynamics of PD patients. Among these, from the idea that human brain can be modeled as a highly complex dynamical system, in the last decade, non-linear measures have been increasingly used to understand the nature of both physiological and pathological conditions. In this framework, non-linear analysis have proven to be a powerful and innovative tool to describe eventual changes of the dynamics in EEG, providing novel evidence about the alterations in such neurodegenerative process, for example, associated with the Parkinsonian condition. Among these, entropy is an innovative non-linear parameter used to measure the irregularity, the complexity, and therefore the unpredictability and randomness of a time series; in particular, greater entropy has been associated with randomness and less regular system.

On this context, the present study aimed to investigate the brain complexity differences between PD patients and healthy elderly subjects, in particular by means of approximate entropy (ApEn) measures applied on closed eyes, resting state EEG recordings, with the aim of evaluating the PD influence on brain dynamics with respect to a healthy brain condition. ApEn appears to be one of the finest indexes for its properties that facilitate its use for EEG non-linear analysis [24, 25, 56].

The main novelty of the present study has been the computation of the novel method of ApEn selecting ten cerebral regions of interest (ROIs), five for each hemisphere (frontal, central, parietal, occipital, temporal), allowing to probe the effect of PD on EEG activity with a relatively fine topography, as well as more specific in the investigation of possible differences across the entire brain.

Because of the relatively limited sample size (still larger than the majority of studies in the literature with EEG), this study can be considered a pilot study.

The result of the current research showed that PD patients presented statistically significant higher ApEn than age- and gender-matched healthy participants in all the brain areas confirming the hypothesis that, also at non-linear level, PD is characterized by a remarkable modification of the entire brain complexity. The brain chaotic behavior has been revealed in all the explored regions confirming that there is not a specific brain area or hemisphere with a different behavior during the eyes-closed resting state EEG recording condition.

In line with our study, Pezard and collaborators examined both linear and nonlinear EEG characteristics in a smaller number of non-demented patients in the early stages of PD (n = 9) and showed that the local entropy of EEGs was increased in PD patients compared to healthy controls [23]. In a further study, brain activity abnormality of PD was investigated by means of alternative type of entropy, called “wavelet packet entropy,” which indicated that the EEG signals for PD patients were more complex and less predictable than in controls [58]. Moreover, Muller and colleagues [59] analyzed the resting state EEGs of PD patients and healthy subjects by the dimensional analysis of correlation, which determines the number of state variables required to describe the EEG signals, revealing slight differences, but not significant, between the two groups.

Although it is notable that EEG signals present an entropy increase in PD patients, there is still a lack of information on the relationship between higher entropy and what happens at the neural circuit level. Some results of previous studies have suggested a causative relationship between beneficial effects of anti-Parkinsonian treatments and a decrease in the complexity of dynamic firing of neuronal assemblies in the basal ganglia [60]. This finding, by Lafreniere-Roula and collaborators [60], demonstrated that the administration of apomorphine, a rapidly acting alkaloid used in the treatment of PD (e.g., administered during deep brain stimulation [DBS] surgical procedure), decreases neuronal entropy of the signals, recorded by depth electrodes in the subthalamic nucleus, helping for the first time to link neurotransmission and neuronal entropy.

We can speculate that these results obtained at neuronal level may reflect a network disorganization and an increase in the complexity of the signal recorded through the EEG.

In general, an increase of complexity, namely higher entropy, is interpreted by the hypothesis of Shannon–Brillouin as a condition of low knowledge, low order, and consequently low information flow/processing [61]. The hypothesis is that when synaptic structures are deteriorating, new different synapses or vicarious connections can be established to fill the gap, to change connection pathway limiting order and organization. Thus, this reduction of information and disruption of cerebral rhythms might be interpreted as an alteration of cortical functioning and processing of information [62].

In summary, although the present pilot study is largely speculative, it expands the existing research literature, demonstrating that the resting state EEG complex dynamical analysis by means of ApEn could be an easily available and powerful tool to distinguish PD patients from elderly healthy controls. Certainly, some potential methodological limitations should be taken into account, first of all the small sample size or, for example, the volume conduction error, which intrinsically affecting each EEG experiment [63]. Although the electrodes cannot be placed in the same fixed position for all the participants, we can perform such an approximation, computing the value of ApEn in each ROI as the average of the ApEn values of each electrode. Accordingly, the localization error was minimized as the values of the ApEn come from a set of averaged electrodes representative of a larger brain area and not only from a single electrode. Moreover, the same approach should be attempted in neurodegenerative disease different from PD (e.g., Alzheimer) in order to test the specificity of the present findings.

Altogether, we conclude that ApEn parameters could represent in a near future a way to find an innovative biomarker to support PD diagnosis in the early stages and individualized rehabilitation treatments.

Conclusion

Parkinson’s disease is a complex neurodegenerative disease of unknown etiology. In future studies, it could be interesting to study the ApEn from EEG signals during other conditions, such as the eyes open condition. It could be also interesting to evaluate its power of PD’s biomarker, for instance, following the stages of disease and assessing the patients through EEGs recorded in various follow-ups. It will be also crucial to deepen the ApEn classification power, first of all increasing the number of participants. Surely, as a step forward, the results of the present research showed that resting brain networks exhibit a different degree of entropy between Parkinson’s patients and control subjects in all the regions analyzed, without differences between hemispheres, suggesting that Parkinson globally modulates the underlying organization of the entire brain. In conclusion, entropy could be a useful parameter to help in a diagnosis and follow the progression of Parkinson’s disease and plan rehabilitation interventions.

Author contribution

CP: Conceptualization, Methodology, Writing—Original draft preparation.

FM: Supervision, Writing—Reviewing and Editing.

MC: Writing—Reviewing and Editing.

PMR: Writing—Reviewing and Editing.

FV: Conceptualization, Methodology, Writing—Reviewing and Editing.

Funding

This work was partially supported by the Italian Ministry of Health for Institutional Research (Ricerca corrente) and by Toto Holding.

Data availability

The data that support the findings of this study are available on request from the corresponding author.

Declarations

Conflict of interests

The authors declare no competing interests.