Light flashes and the geometry of specular fish schools

Abstract

The risk of predation presents a difficult challenge in environments that offer no physical shelter, such as the open waters of the world's seas. In the absence of hiding places, many marine fishes turn to two main anti-predator strategies: aggregation and camouflage, which, mostly, have been studied separately. Here, we consider both aspects together and examine the visual imprint of fish schools of different sizes and geometries, given that camouflage is attained by specular (mirror-like) skin texture. To do so, we developed ray-tracing simulations that model the passage of sunbeams as they go through an optically realistic aquatic environment and reflect off the skins of the fish. We find that due to frequent high-intensity specular reflections (light flashes), the marginal increase in detectability with increasing school size is significantly higher than previously estimated under the assumption of diffusive reflection. However, we also find that by increasing density and alignment the fish can mitigate the detectability of individuals, albeit at the expense of the detectability of the school as a whole. Our findings provide a new perspective on documented responses to threat by schooling pelagic fishes and underscore the importance of the optical signature of animals in structuring their behaviour.

1. Introduction

Active formation of groups is ubiquitous across animals. Pelagic fishes are a notable example, with most species forming aggregates, shoals or schools during some stage of their life cycle [1–4]. Of the various possible advantages of aggregation, the abatement of predation risk (e.g. through risk dilution, predator confusion and increased vigilance, or through reduction of available targets [5]) seems the most dominant [6]. Yet, for large fish groups, which often exceed several thousand [7], the utility of aggregation in terms of reduced risk of predation is somewhat enigmatic; especially if the conspicuousness of the group as a whole was to increase with its size [8]. Recent theoretical analyses found a low marginal increase in the visual detectability with increasing aggregate size; with a mere twofold increase in the maximum detection distance for a 100-fold increase in the number of fish [6]. Such estimates underlie the generally accepted understanding that the detectability-cost of group-living is likely to be outweighed by its benefits [5]. For clarity, we will simply refer to all forms of fish collectives or aggregates as schools.

Most discussions on group detectability implicitly assume that individuals have matt skin texture, i.e. they are treated as diffusive reflectors that reflect light at many angles (figure 1a). This is not the case for many open-water marine fishes, which are typically silver-coloured and specular—i.e. mirror-like [9–12]. Under ideal conditions, specularity is hypothesized to provide camouflage in open waters by reflecting the same light intensity as the background (figure 1b) [13–15]. Yet, under direct sunlight, specular skins may reflect direct sunlight or surface illumination to produce high-intensity flashes (figure 1c) [13]. Thus, specularity may be highly disadvantageous when the fish are near the surface, where reflected sunlight or surface light are significantly more intense than the ambient and contrast with the diffusive background light of the ocean [16] (see electronic supplementary material, figure S1 for a graphical explanation). Given the conspicuousness of the light flashes reflected by specular skin, it is surprising that their potential effect on the structure and dynamics of fish schools received little attention. In the analysis presented below we account for the specularity of open-water fishes and examine how it affects the detectability of individual members and of the school as a whole.

Figure 1.

Reflectance of light from fish. (a) Diffusive reflections: a schematic drawing of a cross-section of an ideal diffusive (matt-textured) fish and its reflection of a sun ray. The orientation of the fish does not affect the light intensity that arrives to an arbitrary observer (compare (i) and (ii)). (b) Specular reflections: (i) as light intensity in the water is approximately uniformly distributed in the horizontal dimension, an upright specular fish acts as a vertical mirror that reflects light at the same intensity as found behind it. (ii) In near-surface conditions, slight changes in the orientation of a fish can result in high-intensity flashes. (c) A school of the hardyhead silverside Atherinomorus lacunosus (total length: approx. 5–15 cm) off the coast of Eilat, Israel, showing high-contrast flashes that are highly visible against the background (water depth: approx. 1 m). The mean Weber's contrast of the non-flashing fish is at least an order of magnitude lower than that of flashing fish (see electronic supplementary material, figure S1). The image is for demonstrative purposes only.

The main goal of the study described herein is to understand the effect of specularity on group detectability. To this end, we simulated static ‘snapshots’ of schools of specular and diffusive fish. Our simulations assume a light source that sends rays into the ocean and track their propagation as they reflect off the fish. Known properties of light propagation in the ocean and models of specular fish skins allow a realistic analysis of the visual signature of schools, under different scenarios. In particular, we apply our simulations to evaluate the detectability of silvery fish under different light conditions and school properties, such as their geometry, density, size and internal alignment. We calibrated our simulations on the measured contrast of the hardyhead silverside (Atherinomorus lacunosus) and proceed to use them to explore how specular fish may adjust the properties of the school in order to reduce detectability.

2. Methods

We investigated the visual signature of flashes by tracing the trajectories of up to 10⁷ simulated light rays, as they shine on approximately 5000 specular fish and, for comparison, on similarly configured schools of diffusive fish. Simulated schools are defined by specifying the three-dimensional positions of all fish centres, and two sets of normalized (orthogonal) direction vectors specifying the direction of the head and back (the side that normally points upwards) of each fish. We assume that fish are placed on a (randomly perturbed) tetrahedral grid that is cropped according to the defined idealized geometry of the school. We focus on a few typical school shapes. When fish try to stay together, they often form dense ball-shaped schools. Along the shore or when moving, schools can become elongated, which we represent as a cylindrical shaped school. Alternatively, when the school stays close to the water surface, it may take the shape of a thin filled circle, which we term pancake-like. The direction in which the fish are facing is specified according to a prescribed alignment—‘polarized’, where all fish face the same direction, or ‘circular’ with the fish rotated around the z-axis. The back of the fish typically points upward. We assume that fish bodies are elongated and flattened ellipsoids of size 50 × 10 × 5 mm, whose axes are given by the direction of the head and back. Small, random noise was added to the direction of both the head and back of the fish (default normal distribution with a standard deviation of π/30, see electronic supplementary material, S2 for cases with different values).

Ray-tracing consists of generating light rays of equal intensity that start at the water surface (z = 0), at random (x, y) locations above the school. These rays point in random directions, according to the prescribed light conditions: centred around a single direction to simulate noontime, or randomly scattered from Snell's window (a 96 degrees cone of light) to simulate dusk. Light rays propagate in straight lines with exponentially decreasing intensities, according to the water's absorption and scattering properties [17–20]. The typical distance at which light is attenuated was determined from previous experimental measurement [20]. If a ray hits a fish, it is either absorbed, with a fixed probability, or reflected according to the prescribed skin type: diffusive or specular [9]. For diffusive reflections, we assume that the fish skin is an ideal diffuser, which implies that incoming rays split into several weaker ones, at random directions. To be precise, each ray is split into a number (n = 100) of rays whose intensity is the corresponding fraction (1/n) of the incoming intensity. Given the intersection point between the incoming ray and the ellipsoid describing the fish, the directions of reflected rays are distributed uniformly across a half unit sphere, which is centred at this intersection point and tangent to the fish surface. For specular reflections, rays are reflected by a mirror which is vertical to the fish normal, i.e. aligned with its back direction, in accordance with realistic specular fish skins [10]. A cartoon of both types of reflections is shown in figure 1a,b. See the section on ‘Fish-ray collisions’ in electronic supplementary material, S1a for a detailed description of the implementation.

To quantify the extent by which reflected rays are distinguishable from the background, we used the Weber contrast, which has been shown to be a key component in the predators prey detection capabilities [21],

$$W={\displaystyle \frac{N_{\mathrm{f}}-N_0}{N_0},}$$

where N_f and N₀ are the intensity of a flash and the background, respectively (see electronic supplementary material, figure S1 for a graphical explanation). The flash intensity N_f, observed by a fixed observer looking at a given direction $\hat{v}$, was calculated as the average intensity of all beams arriving to the observer at an angle of 1° compared with $\hat{v}$. The background intensity N₀, was similarly defined by using a wider angle of 5° compared with $\hat{v}$. Reflected light rays, be they specular or diffusive, were considered ‘detectable’ if their Weber contrast exceeded a specified threshold. Since we are unaware of published estimates of the detection thresholds of piscivorous marine fish, we use 0.3 as an approximation (measured for the coral-reef dwelling triggerfish, Rhinecanthus aculeatus (van den Berg et al. 2020 [21])). A comparison with the expectation under a lower detectability threshold is presented in electronic supplementary material, figure S2.

A virtual school of approximately 5000 fish has a diameter of about 1 m. Although real schools can get significantly larger, this size was found to be qualitatively representative for larger schools, as will be shown below. To quantify the optical signature of the virtual school, we placed a dome-shaped viewing field approximately 2 m away from the centre of the aggregate. Again, this is relatively a short distance. However, as the density of rays per unit area on the viewing field decreases approximately as the square of the distance, larger viewing fields are significantly more computationally expensive. Since light intensity decays (approximately) exponentially with distance, we can extrapolate results on longer distances by artificially increasing the contrast threshold of detectability. For example, given the attenuation coefficient used, a threshold of 5.0 (instead of the default value of 0.3) corresponds to about 30 m between the school and viewing field. In most cases, the viewing field was placed perpendicular to the direction of the incoming light (specified in the text if different). As a result, the view from the complementary dome, which would complete a full-sphere viewing field, is the same. The viewing field, projected stereographically on a two-dimensional plane, was divided into 128 × 128 bins, yielding an area of approximately 5 × 5 cm per bin (figure 2). The visual information reaching the viewing field was analysed using two types of statistics that summarize what an observer situated at a specified position on the field would see: (i) the flux (number/area) of supra-threshold flashes (in terms of the contrast) arriving at each position and (ii) the contrast of the brightest among those flashes.

Figure 2.

Ray-tracing simulations and its analysis. A few rays (for example, the yellow lines c₁ and c₂) are reflected from fish towards an observer located at point P on the viewing field D. The viewing field is mapped onto a plane using a stereographic projection; i.e. by extending lines from a focal point O, located approximately 2 m behind the school, to points on D that intersect the projection plane L. For example, point P is projected onto point I. The collection of all the projected points maps a circular region on L, which is truncated at the water surface and appears as a shaded region at the top of the contrast maps. For each projected bin on the viewing field, we consider: (i) the flash flux, i.e. the number of supra-threshold reflections (in terms of contrast) arriving from the direction of the school and (ii) the magnitude of the strongest flash. See electronic supplementary material, figure S7 for further details.

As a measure of detectability, we used two quantities that relate directly to the rate at which individuals or schools are detected: (i) the average flash flux: the total number of flashes crossing the viewing field divided by its area, which describes the probability that an individual within the school will be registered as a flash (individual detectability) and (ii) the solid angle, which equals the proportion of the viewing field that registers supra-threshold reflections, which is proportional to the probability of the school being detected by an observer that is randomly placed on the viewing field (group detectability). To clarify, the viewing field is divided into equal-area bins, and the intensities of light rays hitting each bin (which may come from multiple fish) are summed and subtracted from the background to obtain the contrast. Bins that reach supra-threshold levels ‘light up’ (figure 2) and contribute to the solid angle. The greater the proportion of the viewing field which is ‘lit’, the greater the number of directions from which the school can be detected. We complement the latter by considering also the ‘maximal detection distance’, beyond which the solid angle of the aggregate drops to below a specified value; e.g. 0.3.

The simulation was written in Matlab. The code is provided in the electronic supplementary material, S3, description of the simulation in the electronic supplementary material, S1a and a full list of parameter configurations in the electronic supplementary material, S2.

Seeing that natural aggregates may differ in properties such as size, shape, alignment or density, we decided to consider how variation along these properties may affect detectability of specular and diffusive aggregates. Each of these variations was simulated once. The simulation size (here, the number of rays) was increased until the results were stabilized. See electronic supplementary material, S1b for analysis of the sensitivity of the simulation to initial parameters.

3. Results

Comparing specular and diffusive schools of identical size and geometry (here, spherical with circular alignment), we see that diffusive groups reflect relatively low-intensity light beams, but in a wide range of directions (figure 3a–c), as expected from a single opaque and reflective solid body [5]. Hence, such schools will create weak contrasts on the background of the water towards a wide range of directions. On the other hand, schools of specular fish reflect fewer beams but of significantly higher contrast (figure 3d–f). This means that a specular school will be easier to detect, but from fewer directions. The implication of this difference is that while the detectability of diffusive fish schools declines rapidly with distance, the detectability of specular fish schools remains consistently high across a wide range of distances (figure 3g). In the further configurations we analyse, we relate to larger distance (approx. 30 m) which is more relevant to predation scenarios. At such large distances, diffusive schools are practically invisible. The geometric shape of the school, and the orientation of the fish within it, affect detectability in terms of both the solid angle (figure 4a) and the average flash flux (figure 4b), but to a lesser extent than specularity itself. The differential sensitivity of diffusive and specular schools to its geometric and structural properties is far from trivial and, as we exemplify below, bears on possible strategies to mitigate conspicuousness at the individual and school level.

Figure 3.

The visual signature of a school. The visibility of a spherical school of approximately 5000 circularly aligned fish. The blue cartoon (above (a)) depicts a three-dimensional view of the ball-shaped school, slightly from above, showing the circular orientation of the fish around the z-axis. Results with diffusive (a–c) and specular (d–f) fish, viewed from different locations on a dome-shaped viewing field. In plots (a) and (d), the wavy blue line marks the water surface; grey and black lines depict diffusive and specular reflections, respectively. Contrast maps show the flash flux, i.e. the number of detectable flashes per unit area (b,e) and the Weber contrast of the most intense flash (c,f). Diffusive schools emit a large number of low-intensity beams across a wide range of directions. By contrast, specular schools emit a smaller number of flashes, but each is highly visible. Additionally, since the specular fish are not perfect reflectors, the specular schools also emit some low-intensity beams but less than the diffusive schools. (g) The change in average solid angle (extracted from the maps in plots (c) and (f)) with increasing distance between the observer and the schools. The high-intensity flashes emitted by the specular fish cause a plateau in the detection angle across a wide range of viewing distances. The contribution to the solid angle of specular fish, appearing above the dashed red line, is due to the additive effect of diffusive reflections (see electronic supplementary material, figure S3 for more details).

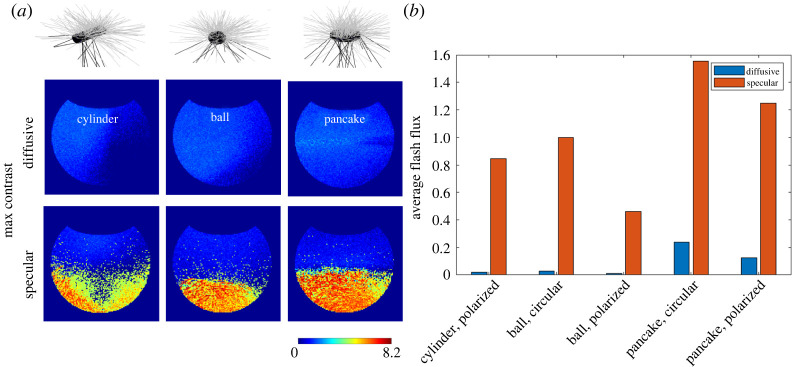
Figure 4.

The effect of school shape. (a) Contrast maps depict the Weber's contrast of the most intense flash registered per bin of the viewing field, for diffusive (top) and specular (bottom) schools of different shapes: cylinder, ball and pancake. Grey and black lines emanating from the differently shaped schools depict diffusive and specular reflections, respectively. The fish in the ball- and pancake-shaped schools are aligned circularly (‘rotating’ around the z-axis), while those in the cylinder schools are arranged in a polarized alignment (aligned along the main axis of the cylinder). (b) The effect of specularity on the average number of flashes per bin, for schools of different shape and internal alignment. The influences of additional parameters (fish shape and colour) are demonstrated in electronic supplementary material, figures S4 and S5.

School density also appears to be a major factor affecting detectability, but has a different effect on specular and diffusive schools. We examined the detectability of sparse (inter-individual distance between fish is three times larger than the default configuration) and dense (inter-individual distance is 0.5 of the default configuration) on detectability as a function of the school size. For sparse specular schools, the average flash flux increases approximately linearly with the size. By contrast, it is largely insensitive to the size of diffusive schools (figure 5a). This increase in flux, however, does not translate linearly to an increase in the solid angle (figure 5b), as many of the accumulating flashes fall in areas of the viewing field that have registered at least one other flash at smaller school sizes. With dense specular schools, we see an increase of the average flash flux with school size (figure 5a), but the slope is decreasing as shorter inter-individual distances imply that reflected rays are more likely to merge and produce a supra-threshold flash. In these dense schools, however, light occlusion becomes significant and the flux quickly saturates with increased size (figure 5a). On the other hand, the solid angle associated with dense schools is considerably higher than that of sparse ones (figure 5b) as the merging-together of rays produce supra-threshold flashes in areas on the viewing field that otherwise would have received only low-contrast reflections. This conflicting effect of density on flash flux and solid angle indicates a trade-off between individual detectability and group detectability, which is absent if the specular nature of the fish is ignored. The maximal distance at which a specular school is detectable as a function of its size increases faster compared with diffusive ones (figure 5c). As light intensity in water decays approximately exponentially, the dependence of the contrast of the brightest flash will decay accordingly.

Figure 5.

Detectability as a function of school size and density. (a) The average flash flux reaching a dome-shaped viewing field around the school. Results for specular (red) and diffusive (blue) schools of different sizes, at high (solid) and low (dashed) densities. The radius of the viewing field is approximately 4 m. (b) The corresponding effect of school size on the solid angle. In simulations, the fish were arranged in a spherical school and linearly aligned perpendicular to the sun. Inter-fish distances were three (sparse) and one (dense) body lengths. (c) The maximal distance at which a school is detectable from at least 5% of the viewing field, for specular-sparse (red) and diffusive-dense schools, as a function of its size. See electronic supplementary material, figure S6 for the solid angle as a function of distance.

Finally, we consider the effect of the alignment of individuals within the school. In the diffusive case, flash flux was affected by the time-of-day and orientation-to-sun but not by the variability in alignment (i.e. in the amount of added noise). Albeit, the low baseline levels of flux emanating from diffuse schools renders these effects negligible. By contrast, we find that subject to direct sunlight, specular fish can greatly reduce their detectability, both in terms of the average flash flux and the solid angle, by aligning their longitudinal axis with the direction of the sun and minimizing their roll around that axis (figure 6). Importantly, the effect varies in extent with the angular distribution of the incident light rays and, hence, with the time of day. In the absence of direct light (e.g. dusk or dawn), flashes are caused by reflecting any part of the sky that refracts into the water through Snell's window. Under these conditions, alignment along the yaw axis contributes little to the reduction in detectability, rendering the alignment around the longitudinal (roll) axis the most influential.

Figure 6.

The effect of fish alignment. Specular fish can decrease their detectability by orienting in the same direction and increasing their alignment. (a) The average flash flux under different lighting conditions, with the ‘noise’ in the orientation of fish silenced along specified rotation axes—yaw, pitch, roll or all three (aligned). Noise levels on each axis were normally distributed with zero mean and a standard deviation of approximately 20°. Light conditions varied between ‘noon front’ (the sun at approx. 30° from the zenith and the fish face the sun), ‘noon-side’ (fish direction is perpendicular to the sun) and dusk (approximating a uniformly lit sky with light entering through Snell's window). (b) (i–iv) Maximum contrast maps, showing the effect of alignment by specular fish under direct and indirect light conditions. (v,vi) The differences in light conditions (noon versus dusk) are exemplified by the reflections from a submerged Styrofoam ball (diameter 10 cm) covered by flat 0.5 × 0.5 cm mirrors. At noon, a strong reflection of the direct sunlight comes from a few mirrors (directions; (v)), while at dusk many mirrors reflect the relatively weak sky glow (vi).

4. Discussion

Fish are highly visual organisms and, as such, light and optics play a crucial role in their behaviour and ecology [22]. Clearly, the flashes of light produced by schools of specular fish are a salient visual feature of the realm within which they live. Yet, this feature has been largely neglected by ecologists, and the question remains as to whether it is also ignored by the natural observers of these flashes—the fish that produce them and their predators. As we note below, certain aspects in the behavioural response to threat by pelagic fish are consistent with our findings—namely, increased aggregate density and alignment—suggesting that these flashes may be of ecological consequence.

Our modelling predicts that individual and, to some degree, group detectability of specular fish should increase significantly with school size (figure 5); particularly when it is sparse. This is important as the accepted view, based on analytical models that implicitly assume diffusive reflection, predicts a rapid decline in the marginal detectability-cost of forming increasingly larger schools [5]; as seen also in our simulations (figure 5). Thus, the trade-off between the potential benefits of being in a larger group (e.g. increased vigilance, dilution, etc.) and the cost of increasing detectability is expected to be far more severe when allowing for specularity. This in turn, would suggest that, given specular skins, fish face a greater need to find ways to reduce detectability than would be expected when considering only diffusive reflections.

The organization of individuals in schools of a particular shape and internal structure depends on a variety of behavioural, physiological and hydrodynamic considerations [23,24]. Faced with heightened threat, for example, wild schools of pelagic fish tend to increase both their density and level of alignment [8,24,25]. The reasons for these behaviours may include increased predator confusion [26]; enhanced information transfer during collective evasive manoeuvres [27,28]; reduced probability of being targeted as the ‘odd one out’ [6,29] and, specifically with increased density, the minimization of the individual's ‘domain of danger’ (e.g. [30]). Our simulations present a new, complementary perspective of changes in density and alignment at times of elevated predation risk, whereby the increase in both can act as a pre-emptive strategy to reduce individual detectability (figures 5 and 6). Accordingly, and contingent on its size, schools that increase their density and level of alignment can reduce the average flash flux (figure 5a) and lower the individual probability of being detected; even if increased density, by itself, would increase the solid angle over which the school can be detected (figure 5b). It would seem, therefore, that flashes of reflected light could play a significant role in structuring predator–prey dynamics of specular marine fish, opening intriguing questions as to what other aspects of their behaviour may be similarly affected.

To the best of our knowledge, this study is the first to explore the seemingly twofold implication of specularity in marine fish. Clearly, a fuller treatment should include analyses of other parameters like fish size, body motions and more complex school geometries. Above-water perspective and the effect of different textures of the water surface also leave room for further investigations. Finally, addressing the effect of specularity on the visual signature of the school should go beyond our current ‘snapshot’ perspective and consider the temporal dynamics of the flashes reflected off these fish—for example, the magnificent phenomenon of ‘shimmering waves’ propagating across schools [31].

Data accessibility

All data generated or analysed during this study are included in this published article (and its supplementary information files [32]).

Authors' contributions

A.P.: conceptualization, data curation, formal analysis, methodology, resources, software, validation, visualization, writing—original draft and writing—review and editing; G.A.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing—original draft and writing—review and editing; M.K.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing—original draft and writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

This research received no specific grant from any funding agency in the public, commercial or not-for-profit sectors.