Comparing the Real-World Performance of Exponential-family Random Graph Models and Latent Order Logistic Models for Social Network Analysis

Summary.

Exponential-family Random Graph models (ERGM) are widely used in social network analysis when modelling data on the relations between actors. ERGMs are typically interpreted as a snapshot of a network at a given point in time or in a final state. The recently proposed Latent Order Logistic model (LOLOG) directly allows for a latent network formation process. We assess the real-world performance of these models when applied to typical networks modelled by researchers. Specifically, we model data from an ensemble of articles in the journal Social Networks with published ERGM fits, and compare the ERGM fit to a comparable LOLOG fit. We demonstrate that the LOLOG models are, in general, in qualitative agreement with the ERGM models, and provide at least as good a model fit. In addition they are typically faster and easier to fit to data, without the tendency for degeneracy that plagues ERGMs. Our results support the general use of LOLOG models in circumstances where ERGMs are considered.

1. Introduction

Social network analysis has become increasingly important in recent decades, with particular need in the social sciences to elucidate relational structure (Goldenberg et al., 2010). However developing generative models for social networks has proven challenging (Chatterjee and Diaconis, 2013). Here we consider a social network a collection of fixed nodes, each with fixed covariates and with edges stochastically present or absent between every pair of nodes. The chief problems for modelling such data are the vast space of possible networks and the likely highly complex dependence structures of the network edges.

The Exponential-family Random Graph Model (ERGM) framework is widely used to represent the stochastic process underlying social networks (Frank and Strauss, 1986; Hunter and Handcock, 2006). ERGMs allow researchers to quantitatively evaluate the impact of local social processes and nodal attributes on the probability of edges between nodes forming. However these models are prone to near-degeneracy (Handcock, 2003) and can not naively be applied to large networks (Schweinberger, 2011; Chatterjee and Diaconis, 2013). Model degeneracy is the application specific tendency of the model to concentrate probability mass on a small subset of graphs, especially those which are not similar to realistic networks for that application.

Much progress has been made on managing model degeneracy by introducing local neighbourhood structures (Schweinberger and Handcock, 2015) or tapering (Fellows and Handcock, 2017). The presence of degeneracy in many fitted ERGMs motivates the search for alternative model classes with similar or complementary modelling capacity that are less susceptible to these challenges.

While ERGMs are descriptive, they are often embedded as the equilibrium distribution of a social process. The Latent Order Logistic model (LOLOG) (Fellows, 2018b) is a related model that uses an edge formation process to develop a general probability model over the space of graphs. It is motivated by using the so-called change statistics, the change in the specified graph statistics resulting from toggling an edge on or off, as predictors in a sequential logistic regression for each possible edge. Noting that an ERGM specified with independent tie variables, reduces to a sequential logistic regression on its change statistics, ERGM and LOLOG are equivalent in the independent dyad case (Fellows, 2018b). LOLOG models also allow non-independent dyads, and graph statistics that depend on the order of edge formation, which result in different models than ERGM.

LOLOG models have the advantage that they are straightforward to sample from, and can be used with simpler model terms, that would for an ERGM almost certainly result in near-degeneracy. This allows for a fast and user friendly fitting procedure, with easily interpretable model terms.

How can we assess and compare differing model classes? Both ERGM and LOLOG are fully general and able to represent arbitrary distributions over the set of graphs (Fellows, 2018b, Theorem 1). As ERGMs are the equilibrium distribution of a relatively general Markov chain Monte Carlo (MCMC) process, there are many mechanisms that can lead to them, as there are for LOLOG. Hence both model classes have strong theoretical and modelling motivations, although the ERGM class to this point has been much more extensively explored (Schweinberger and Stewart, 2020; Schweinberger et al., 2020). In this paper, we provide a separate and novel contribution to the assessment on the model classes. Our objective is to compare the models by a pairwise assessment on the population of networks that the research community would choose to fit them on. The idea here is to move the perspective from that of the model viewpoint (i.e., given we have a model, what can we fit with it?) to a data-centric view point (i.e., given that this is the data we have, what are the best modelling approaches?). The latter is the question facing the real-world users of these models, while the “inverse problem” addressed by the former is commonly taken as it does not require the population of networks to be specified.

However, to take the data-centric viewpoint, we need to specify the population. We operationalised this in this paper by taking a population of networks that ERGM models have been applied to in the premier journal for publishing social network analyses, Social Networks (Everett and Valente, 2020). Social Networks is an interdisciplinary journal for those with “interest in the study of the empirical structure of social relations and associations that may be expressed in network form”. While the sub-population of networks in Social Networks for which ERGMs have been fit is a sample of the population of interest, we believe that it is a salient and (non-statistical) representative sub-population of the broader population.

Our selection of ERGM papers was at first a census of papers in the journal Social Networks using the ERGM framework, published from the journal’s founding in 1979 up to and including the January 2016 issue. Note that we have chosen a population of networks that are biased toward ERGM. These networks have successfully completed the peer-review process of Social Networks. In particular, the ERGM fit and analyses have passed peer-review and are deemed of sufficient scientific interest to appear in this premier journal. Clearly this is not sufficient to ensure the fit and models are appropriate for the data, although they represent a strong selectiveness relative to the population of networks that researchers would consider for analysis (without regard to a model class choice). Hence a comparable or competitive fit for LOLOG models to this sub-population presents stronger evidence for the value of LOLOG models than a comparison to the broader population. In particular it seems likely that in papers published that fit an ERGM model, ERGM performs well on this data set, thus we expect a publication bias towards networks that suit ERGM well, which may not necessarily suit LOLOG well. We therefore suggest that good performance on data published with ERGM fits is a conservative indicator that LOLOG is a useful model for analysing social networks.

Identifying, assembling and fitting ERGMs and LOLOGs to an ensemble of networks, analysing their goodness of fit (GOF) and interpreting the results, is a significant undertaking. For brevity we give the fit of networks from a case-study (Sailer and McCulloch, 2012) in detail and provide summaries for the remaining networks in the supplement.

The structure of this paper is as follows. In Section 2 we briefly introduce ERGMs and LOLOG models, reviewing work in Fellows (2018b) as well as discussing the theoretical similarities and differences. Section 3 gives a description of the ensemble of networks and discusses the motivation for selecting such an ensemble. Section 4 shows both the LOLOG and ERGM fit of office layout networks with the data from Sailer and McCulloch (2012). Section 5 presents a summary of all the LOLOG and ERGM fits to each of the networks in the ensemble. Section 6 discusses the results of the fitting, as well as its implications regarding the utility of the LOLOG model.

2. ERGM and LOLOG Model Classes

Let Y be a random graph whose realisation is $y\in \mathcal{Y}=\{a\in {\mathbb{R}}^{n\times n}\mid \forall i,j{y}_{i,i}=0y_{i,j}\in \{0,1\}\}$. We regard the number of nodes and any nodal covariates as fixed and known. For undirected networks the additional restriction that y_i,j = y_j,i ∀i,j can be added. Let ∣y∣ = n(n − 1) denote the number of possible edges in y (∣y∣ = n(n − 1)/2 for undirected graphs). A dyad in a graph is a sub-graph of two nodes and any ties between them.

2.1. Model Specification

LOLOG and ERGM are alternative specifications of the distribution of Y. An ERGM for the network can be expressed as

$$p_E(y\mid \theta )=\frac{\text{exp}(\theta \cdot g(y))}{c(\theta )}y\in \mathcal{Y}$$ (1)

where g(y) is a d–vector valued function defining a set of sufficient statistics; $\theta \in {\mathbb{R}}^d$ is a vector of parameters; and c(θ) the normalising constant. Each ERGM family is defined by the choice of sufficient statistics. These are chosen by the researcher, depending on domain knowledge, to specify the generating social processes. They can be any statistical summary of network properties and are typically motivated by social theory (Goodreau et al., 2009) or symmetry arguments (Strauss, 1986). In this way, ERGMs constitute a family of models across different choices of the sufficient statistics.

Typically graph statistics are the density and degree counts, as well as nodal or edge covariate terms such as sociability and homophily (Morris et al., 2008). Geometrically weighed edgewise shared partner (GWESP) and geometrically weighted degree (GWDEG) terms are often included (Snijders et al., 2006) as they capture complex structure while reducing the effects of near degeneracy (Handcock, 2003). A very large number of terms are used by researchers in applications. Explicit definitions of almost all terms used in this paper can be found in Morris et al. (2008) or the documentation of Handcock et al. (2018). Regardless of which sufficient statistics are used, the ERGM will have the maximal entropy of any distribution satisfying the d-dimensional mean constraints placed on g(y), E[g(y)] = μ.

LOLOG models posit the existence of a latent discrete temporal dimension, t = 1, … , ∣y∣ so that the edges form in a sequence. Fellows (2018b) defines the latent random variables Y_t, t = 1,…, ∣y∣ representing the sequential formation of Y. Y_t has exactly t edges and is formed from Y_t−1 by the addition of an edge. A LOLOG model is specified by two components, The first is the probability of observing a graph given a specified order of edge formation, s:

$$p(y\mid s,\theta )=\prod _{t=1}^{\mid y\mid }\frac{1}{Z_t(s)}\text{exp}(\theta \cdot C_{s,t})$$ (2)

where $s=\{s_1,s_2,\dots ,s_{\mid y\mid }\}\in {\mathcal{I}}_{\mid y\mid }$ is the set of possible edge formation orders with ∣y∣ dyads, and

$$C_{s,t}=g(y_t,s_{\le t})-g(y_{t-1},s_{\le t-1})$$ (3)

where s_≤t denotes the first t elements of $s\in {\mathcal{I}}_{\mid y\mid }$. The C_s,t are the difference in the graph statistics from the y_t−1 network to the y_t network and are informally called the “change statistics” of the formation process. The Z_t(s) sequentially specify the normalising constants. Let $y_t^{+}$ be the graph y_t−1 with the edge s_t added, then

$$Z_t(s)=\text{exp}(g(y_t^{+},s_{\le t})-g(y_{t-1},s_{\le t-1}))+1$$ (4)

The second component is the model for the edge order permutations, p(s). The LOLOG distribution for Y is:

$$\begin{gathered} p_L(y\mid \theta )=\sum _{s}p(y\mid s,\theta )p(s) \\ =\sum _s\left(p(s)\prod _{t=1}^{\mid y\mid }\frac{1}{Z_t(s)}\text{exp}(\theta \cdot C_{s,t})\right) \end{gathered}$$ (5)

2.2. Model Interpretation

For the LOLOG model, conditioning on an edge permutation s, at each step t, we have logit $(p(y_t^{+}\mid s_{\le t},y_{t-1},\theta ))=\theta \cdot C_{s,t}$. Thus at each time t, conditional on the network already formed by that point, each dyad is a logistic regression on the change statistics associated with the edge. For ERGMs, equation (1) yields the auto-logistic interpretation of the θ parameter $\log \left(\frac{p(y_{i,j}^{+}\mid y_{i,j}^c,\theta )}{p(y_{i,j}^{-}\mid y_{i,j}^c,\theta )}\right)=\theta \cdot (g(y_{i,j}^{+})-g(y_{i,j}^{-}))$, where $y_{i,j}^c$ is $y\setminus y_{i,j},y_{i,j}^{+}=y_{i,j}^c\cup \{y_{i,j}=1\}$ and $y_{i,j}^{-}=y_{i,j}^c\cup \{y_{i,j}=0\}$. Thus, conditional on the rest of the graph, each dyad can be thought of as an (auto)-logistic regression on change statistics. This gives a helpful interpretation for the parameters, but does not help interpret the probability distribution of each edge unconditional of the rest of the graph.

2.3. Model Estimation

Due to the intractability of summing over all possible edge permutations in the LOLOG model, the likelihood or likelihood ratio, cannot be evaluated and the maximum likelihood estimate (MLE) is intractable. Fellows (2018b) proposed a method of moments (MOM) approach to estimate model parameters. The idea is to seek θ_MOM such that $g(y)-{\mathbb{E}}_{{\theta }_{\text{MOM}}}[g(y)]=0$. Fellows (2018b) developed a Newton-Raphson approach as it is possible to differentiate the ${\mathbb{E}}_{{\theta }_{\text{MOM}}}[g(y)]$ with respect to θ and approximate its value by sampling from the LOLOG model. Along with introducing LOLOG models in Fellows (2018b), the lolog R package (Fellows, 2018a) provides a sophisticated, fast and user friendly method to fit LOLOG models to data.

ERGM parameters are typically estimated using an MCMC procedure to estimate the MLE (Snijders, 2002; Hunter and Handcock, 2006). This is computationally demanding and there are sophisticated R packages available to perform this estimation (Handcock et al., 2018).

For both LOLOG and ERGM models we approximate standard errors derived from MCMC estimated inverse Fisher information matrices.

2.4. Model Discussion

A key advantage of the LOLOG model is the ease of simulation from the model. To simulate a network we simply draw s from p(s) and perform a sequential logistic regression simulation on the change statistics (Fellows, 2018a). The ERGM by comparison requires a full MCMC procedure to simulate networks (Handcock et al., 2018).

For LOLOG models we are required to model p(s) the probability mass function (PMF) on the space of possible edge permutations. In the absence of strong substantive reason for a particular partial ordering of the edges, a uniform PMF can be used. However many natural reasons exist to constrain the edge ordering. For example, in schools that welcome a new cohort each year, edges in upper years could reasonably be constrained to have been formed before edges in lower years.

For ERGMs the interpretation is conditional on the entire rest of the network, whilst for LOLOG models with a specified edge ordering, the interpretation is conditional only on the network formed up until that point. We emphasise that the network formed up until that point will depend on the particular edge permutation. We note that in the case where the tie variables are independent, the edge ordering s does not matter (as the dyads do not depend on each another) and LOLOG reduces to logistic regression on change statistics, as does ERGM and to the same model.

We may also compare dyad-dependent ERGM and LOLOG models through their simulation algorithms A network from an ERGM is simulated through an MCMC procedure where dyads are considered conditional on the rest of the network. Often many thousands of steps are required to converge to the stationary distribution. As noted above, the log odds is equal to the inner product of the parameter and the change statistics of that dyad. The LOLOG model is formed by first sampling a dyad ordering, then starting with an empty network, adding an edge based on the log odds (being the inner product of the parameter and the change statistic). Each dyad is considered for edge formation and then the process is terminated leaving the simulated graph.

LOLOG considers each dyad exactly once, whereas the ERGM process can consider dyads multiple times for both edge formation and dissolution. We suggest a reason that LOLOG models do not suffer from the same degeneracy is that, in the simulation, each dyad is considered exactly once. This limits the scope for the explosive edge formation or deletion that often occurs when simulating from ERGM models.

More broadly we argue that the LOLOG, motivated as a model with an easy simulation method with parameters that remain interpretable, is more desirable than ERGM. Whilst ERGMs are straightforward to write down, they require MCMC procedures to simulate from.

2.5. Assessing Goodness of Fit

For the interpretation of model parameters to be valid, we must show that the model is a plausible generating process for the observed network. In Section 4 we follow the goodness of fit procedure as in Hunter et al. (2008). That is, we graphically compare the simulated distribution of chosen graph statistics to the observed values of those graph statistics. Whilst our models are highly parsimonious representations of complex social processes, the goodness of fit method highlights, that at a minimum, we should expect the observed statistics to be plausible realisations from a well fitting model.

3. Description of the Ensemble

We considered papers in the journal Social networks where ERGMs were fit to data. We included papers up to and including the January 2016 issue. There were 45 such papers, of which we selected 18 papers as follows. First, we excluded bipartite ERGMs (5), we then included all networks with publicly available data (7) and selected a further 11 papers out of the remaining 33 based on their, subjectively assessed, novelty as well as the likely availability and ability to share data. We contacted the authors of the 11 papers and received the data for 7 of the papers. This gave an ensemble of 137 networks in 14 peer reviewed published papers, as many papers contained multiple networks. We note that 102 of these networks were from a single paper (Lubbers and Snijders, 2007), which were omitted from our analyses, leaving 35 networks. Table 1 shows a brief summary for each of the networks.

Table 1.

Properties of each network contained in the ensemble. The ensemble includes directed and undirected networks from various applications ranging in size from 16 nodes to 1681 nodes

Description	Network	Nodes	Edges	Directed	Citation
Add Health		1681	1236	Undirected	Harris et al. (2007)
School Friends		Various	Varies	Directed	Lubbers and Snijders (2007)
Kapferer’s Tailors		39	267	Undirected	Robins et al. (2007)
Florentine Families		16	15	Undirected	Robins et al. (2007)
German Schoolboys		53	53	Directed	Heidler et al. (2014)
Employee Voice	1	27	104	Directed	Pauksztat et al. (2011)
Employee Voice	2	24	53	Directed	Pauksztat et al. (2011)
Employee Voice	3	30	126	Directed	Pauksztat et al. (2011)
Employee Voice	4	31	139	Directed	Pauksztat et al. (2011)
Employee Voice	5	37	149	Directed	Pauksztat et al. (2011)
Employee Voice	6	39	155	Directed	Pauksztat et al. (2011)
Office Layout	University	67	211	Directed	Sailer and McCulloch (2012)
Office Layout	University	69	203	Directed	Sailer and McCulloch (2012)
Office Layout	Research	109	458	Directed	Sailer and McCulloch (2012)
Office Layout	Publisher	119	872	Directed	Sailer and McCulloch (2012)
Disaster Response		20	148	Directed	Doreian and Conti (2012)
Company Boards	2007	808	1997	Undirected	Wonga et al. (2015)
Company Boards	2008	808	1740	Undirected	Wonga et al. (2015)
Company Boards	2009	808	1682	Undirected	Wonga et al. (2015)
Company Boards	2010	808	1622	Undirected	Wonga et al. (2015)
Swiss Decisions	Nuclear	24	282	Directed	Fischer and Sciarini (2015)
Swiss Decisions	Pensions	23	294	Directed	Fischer and Sciarini (2015)
Swiss Decisions	Foreigners	20	169	Directed	Fischer and Sciarini (2015)
Swiss Decisions	Budget	25	224	Directed	Fischer and Sciarini (2015)
Swiss Decisions	Equality	24	248	Directed	Fischer and Sciarini (2015)
Swiss Decisions	Education	20	227	Directed	Fischer and Sciarini (2015)
Swiss Decisions	Telecoms	22	256	Directed	Fischer and Sciarini (2015)
Swiss Decisions	Savings	19	138	Directed	Fischer and Sciarini (2015)
Swiss Decisions	Persons	26	280	Directed	Fischer and Sciarini (2015)
Swiss Decisions	Schengen	26	316	Directed	Fischer and Sciarini (2015)
University Emails		1133	10903	Undirected	Toivonen et al. (2009)
School Friends	grade 3	22	177	Directed	Anderson et al. (1999)
School Friends	grade 4	24	161	Directed	Anderson et al. (1999)
School Friends	grade 5	22	103	Directed	Anderson et al. (1999)
Online Links	Hyperlinks	158	1444	Directed	Ackland and O’Neil (2011)
Online Links	Framing	150	1382	Undirected	Ackland and O’Neil (2011)

Our selection of ERGM papers was at first a census of papers in the journal Social Networks using the ERGM framework. The conclusions drawn from this study should be considered stronger than if the networks selected were sampled at random or through convenience. We do note that we did take a selective sample as described above as a first wave of networks to request data for, though this was also chosen based on our thoughts on which networks the authors would be able and willing to share.

We considered papers that used ERGMs for their statistical analyses as the ERGM class of models is arguable the most widely used descriptive statistical model for network analyses (Amati et al., 2018). Both LOLOG models and ERGMs are typically used to model global network structure using local network structure, thus comparing the two models is appealing. While both LOLOG and ERGM can represent any given PMF over the space of networks (Fellows, 2018b), specifying interpretable models that fit the data is often the practical challenge. There is no obvious reason to suspect similar performance in terms of fit and interpretability, when fit with similar network statistics, on the same network. In particular it seems likely that in papers published that fit an ERGM, ERGM should perform well thus we expect a publication bias towards networks that suit ERGM well compared to LOLOG. We therefore suggest that good performance on data published with ERGM fits, is a conservative indicator that LOLOG is a useful model for analysing social networks.

We also note that the LOLOG model allows for the consideration of information on the order of the edge formation within a network the researcher may have. This is currently implemented by allowing edge orderings to be constrained to those orderings compatible with the sequential adding of nodes to the network, followed by the consideration of all possible new edges. This is not possible in ERGM and few of the available networks had plausible ordering mechanisms. However this may not be entirely due to the lack thereof: without the ability to model such an ordering process with ERGM, it seems likely that even if there is a compelling sequential node adding process the data would not be reported or even collected.

4. Case Study of LOLOG and ERGM fits: Complex networks where ERGM is insufficient

In this section we consider a case study from a single published paper where the networks in question are sufficiently complex to demonstrate that ERGM can be insufficient and LOLOG can help in modelling social network data.

We consider four networks of daily social interactions between workers within four different office spaces. An ERGM based analysis was originally carried out in Sailer and McCulloch (2012). Ties are present between person i and person j if person i reported daily social interaction with person j. Two of the networks are of a British university faculty before and after an office refurbishment, the remaining two are a German research institute and a corporate publishing company. The networks are directed and have 69, 63, 109 and 120 people/nodes, respectively.

The research question of interest in Sailer and McCulloch (2012) was the effect of spatial distance in the formation of social interactions within an office environment. The authors specified an ERGM with terms to represent the potential complex structure. These are listed in the first column of Table 2 and detailed here. The edges term models the overall propensity for social interactions, it has a similar role to an intercept term in regression. The reciprocity term measures the propensity for both people in a dyad to report social interaction with the other. The GWESP term, with decay parameter 0.5, is an integrated measure of the transitivity of social interactions (See Snijders et al., 2006, for a detailed explanation). The usefulness term is an edge-covariate term, with value equal to the sum over edges of the usefulness measure: for dyad (i, j) being person i’s self reported perception of the usefulness of person j. It measures the direct dependence of the propensity to have a social interaction on the usefulness of the person nominated. The team match term is the number of ties between people from the same team. It measures the propensity of teams to influence the density of social interaction. floor match is similar to team match, except it measures the importance of being on the same floor for social interaction. The metric distance term is the sum of the shortest walking distance in meters between the socially interacting peoples normal place of work. Similarly, the topo distance is the sum of measures of how far the desks could be perceived to be apart given the topography of the office (See Sailer and McCulloch, 2012, for precise definitions). The coefficients of the metric and topo distances measure the increase in log-odds of a social interaction given the distance they are apart. These coefficients are generally negative, indicating that social interactions become less common as the distance increases.

Table 2.

Sailer’s office layout ERGM fits as per the published results. In all cases the selected measure of distance is negative and significant suggesting that close office workers, are more likely to interact, even after allowing for team, floor, usefulness as well as social structure in the form of reciprocity and transitivity.

	University 2005	University 2008	Research Institute	Publisher
Edges	−3.4 (0.37)***	−4.41 (0.2)***	−4.1 (0.12)***	−5.07 (0.15)***
Reciprocity	0.38 (0.45)	0.62 (0.31)***	2.39 (0.2)***	−1.26 (0.19)***
GWESP(0.5)	1.36 (0.14)***	1.24 (0.11)***	0.92 (0.07)***	2.09 (0.09)***
Usefulness	0.7 (0.15)***	0.54 (0.11)***	0.81 (0.04)***	1.31 (0.05)***
Team Match	0.78 (0.18)***	0.56 (0.1)***	NA	NA
Floor Match	0.15 (0.26)	0.58 (0.14)***	NA	NA
Metric Distance	−0.04 (0.01)***	−0.01 (0)***	−0.01 (0)***	NA
Topo Distance	NA	NA	NA	−0.06 (0)***

^***p-value < 0.001

^**p-value < 0.01

^*p-value < 0.05

The best fitting model was then selected using the Akaike Information Criterion (AIC) and then a variety of different distance metrics were added individually as edge-covariates. The best model in terms of AIC was once again selected and analysed. Notably no analysis of the goodness of fit for the models was provided.

4.1. Model Fits

We were able to recreate the selected ERGM fit for all four networks, shown in Table 2. The reciprocity coefficient is positive in two of the networks, indicating that the conditional log-odds of a social interaction is positive if the social interaction is mutual. The GWESP coefficient is positive for all four networks, indicating that the log-odds of a social interaction existing is positive if the social interaction increases this measure of transitivity. The usefulness coefficient is positive for all four networks, indicating that the log-odds of a social interaction existing is positively related to the usefulness of the nominated person. The team match coefficient is positive for all four networks, indicating that the log-odds of a social interaction existing is positive if the social interaction is within the same team (as distinct from between people in different teams). Floor match coefficients are also positive, indicating that the log-odds of a social interaction existing is positive if the social interaction is within the same floor (as distinct from between people in different floors). The metric and topo coefficients are generally negative, indicating that social interactions become less common as the distance increases.

Overall, the Sailer and McCulloch (2012) concluded that daily social interactions of people in offices exhibit a tendency for mutuality and social closure. Interactions are also more likely to occur where there is a high level of usefulness of the receiver to the sender as well as within teams. While being on the same floor plays a role in some cases, the distance apart plays a role in all cases, with social interactions more likely for people closer together.

We were able to obtain LOLOG fits with the same covariates, as the ERGM fits for all networks, we summarise the fits in Table 3. In addition we show the LOLOG fit using GWESP, 2- and 3- in- and out-stars, together with all covariate matches and metric distance in Table 4. For k = 1, 2,…, a k-in-star centred on a node i and a set of k different nodes {i₁,…,i_k} such that the tie from i to i_j exists for j = 1,…, k. The k-in-star statistic is the number of distinct k-in-stars in the network (i.e., summing over the centring nodes). The k-out-star statistic is the same except the ties from i_j to i must exist for j = 1,…,k (rather than the in-ties to i). As noted in Section 2.2, the qualitative interpretation of the LOLOG coefficients is similar to ERGM with the primary difference being the log-odds is conditional on the network at the point the edge is added. We directly compare the qualitative fits in Section 4.3.

Table 3.

Sailers office layout networks LOLOG fits with same terms as published ERGM. Shows broad quantitative agreement with the published results using ERGM in Table 2

	University 2005	University 2008	Research Institute	Publisher
Edges	−1.69 (0.38)***	−3.67 (0.36)***	−3.18 (0.13)***	−1.63 (0.09)***
Reciprocity	1.99 (0.34)***	1.96 (0.31)***	3.9 (0.25)***	0.64 (0.2)***
GWESP(0.5)	0.55 (0.12)***	0.87 (0.13)***	0.73 (0.09)***	−0.22 (0.06)***
Usefulness	1.02 (0.15)***	0.81 (0.14)***	1.21 (0.05)***	1.89 (0.06)***
Team Match	1.29 (0.19)***	0.72 (0.19)***	NA	NA
Floor Match	−0.28 (0.3)	1.08 (0.29)***	NA	NA
Metric Distance	−0.07 (0.01)***	−0.02 (0.01)***	−0.02 (0)***	NA
Topo Distance	NA	NA	NA	−0.1 (0)***

^***p-value < 0.001

^**p-value < 0.01

^*p-value < 0.05

Table 4.

Sailer’s office layout networks LOLOG fit with GWESP and 2- and 3- in- and out-stars. Significant out-star terms may suggest there is social structure unaccounted for with just the published ERGM terms. Despite additional significant structural terms, the LOLOG models still show broad quantitative agreement with the published results using ERGM

	University 2005	University 2008	Research Institute	Publisher
Edges	−3.2 (0.67)***	−5.04 (0.59)***	−4.04 (0.22)***	−4.87 (1.19)***
Reciprocity	2.03 (0.77)***	1.11 (0.45)***	4.7 (0.52)***	3.16 (1.27)***
GWESP(0.5)	0.33 (0.2)	0.49 (0.16)***	0.77 (0.11)***	0.01 (0.26)
Out-2-Star	1.39 (0.26)***	0.65 (0.16)***	0.41 (0.07)***	0.69 (0.15)***
Out-3-Star	−0.28 (0.07)***	−0.07 (0.03)***	−0.04 (0.01)***	−0.02 (0)***
In-2-Star	0.26 (0.22)	0.25 (0.15)	0.21 (0.12)	0.73 (0.54)
In-3-Star	−0.04 (0.05)	−0.03 (0.02)	−0.09 (0.03)***	−0.18 (0.1)
Usefulness	1.07 (0.2)***	0.75 (0.16)***	1.28 (0.07)***	2.98 (0.61)***
Team Match	1.93 (0.31)***	1.14 (0.25)***	NA	NA
Floor Match	−0.24 (0.47)	1.35 (0.43)***	NA	NA
Metric Distance	−0.09 (0.01)***	−0.02 (0.01)***	−0.02 (0)***	NA
Topo Distance	NA	NA	NA	−0.24 (0.06)***

^***p-value < 0.001

^**p-value < 0.01

^*p-value < 0.05

We were also able to fit LOLOG models to each of the networks when the GWESP term is replaced with a triangle term. This is not possible with ERGM due to near-degeneracy. We summarise this in Table 5. The estimated standard errors for the Publisher network are very high, suggesting there is great uncertainty in the data generating process. The estimated standard errors for the mutual and triangle terms for the University in 2005 and 2008 are also high though not as severe and they fall out of significance for these model fits. As the triangle term increases the estimated standard errors and does not improve the GOF (see next section), we suggest using the GWESP term.

Table 5.

Office Layout LOLOG fit with triangles instead of gwesp term, hows broad quantitative agreement with the published results on nodal covariates, however suggests little tendency for reciprocity and transitivity in the university networks.

	University 2005	University 2008	Research Institute	Publisher
Edges	−2.05 (0.82)***	−3.9 (0.67)***	−3.36 (0.15)***	−5.4 (49.3)
Reciprocity	−2.96 (5.83)	−0.08 (1.6)	3.34 (0.36)***	−24.8 (367.3)
Triangles	2.69 (2.95)	1.2 (0.73)	0.61 (0.13)***	3.71 (50.63)
Usefulness	1.35 (0.53)***	0.83 (0.16)***	1.21 (0.06)***	6.57 (88.39)
Team Match	1.8 (0.85)***	0.9 (0.35)***	NA	NA
Floor Match	−0.29 (0.88)	1.07 (0.46)***	NA	NA
Metric Distance	−0.1 (0.05)***	−0.02 (0.01)***	−0.02 (0)***	NA
Topo Distance	NA	NA	NA	−0.39 (5.82)

^***p-value < 0.001

^**p-value < 0.01

^*p-value < 0.05

We also fitted the LOLOG model where the people are added in the order of their average usefulness, as reported by the other people. As we suspect more useful people may have been in the office longer or should be the first point of contact for new employees we suggest this as a plausible ordering mechanism. The fit was comparable to the fit without the ordering, and the GOF was not improved, so we do not consider it further.

We tried to fit an ERGM model with the in- and out- geometrically weighted degree (GWDEG) terms but this was degenerate for the University 2005 and 2008 networks. The in-GWDEG term adds one network statistic to the model equal to a weighted sum of the in-degree counts with weights decreasing geometrically. The out-GWDEG is similar with the out-degree counts (See Hunter, 2007, for a detailed explanation). For the Research institute and Publisher out-GWDEG was negative and significant, in line with the LOLOG model positive 2-star and negative 3-star parameters. However, the fit was still poor and inferior to the LOLOG model. We do not comment further on this, though it is reassuring that the ERGM with GWDEG gives similar interpretations to LOLOG with star terms. The GWDEG terms were not discussed in Sailer and McCulloch (2012).

We note the computation time difference in the LOLOG and ERGM parameter estimation. We ran each with a single core with Intel(R) Xeon(R) Platinum 8160 CPU @ 2.10GHz processor. The recreated ERGM took around 35 seconds, and the LOLOG took around 8 seconds. For larger networks, we found parallelisation in the network simulation step of the fit to be extremely helpful for both the LOLOG and ERGM models. From our experience for larger networks the performance differential between LOLOG and ERGM can be much greater, in particular when the ERGM MCMC simulation is computationally expensive.

4.2. Goodness of Fit

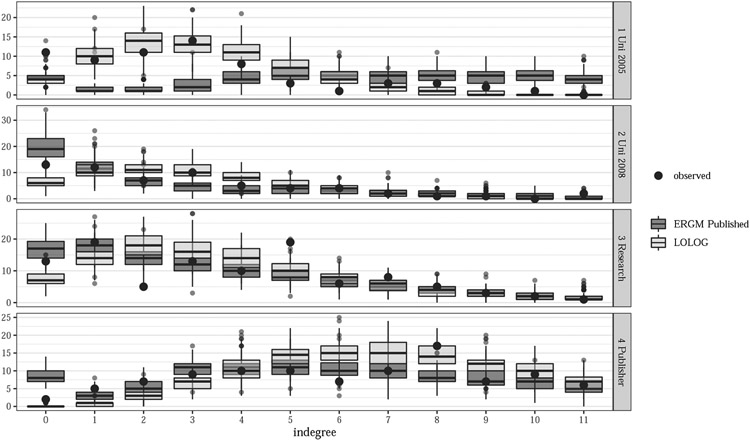
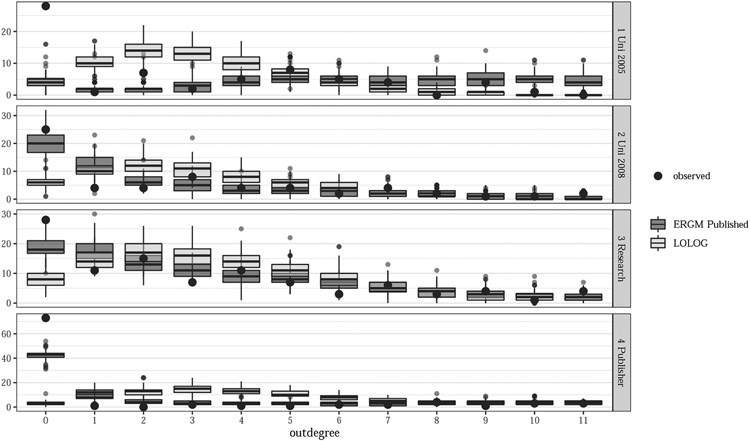
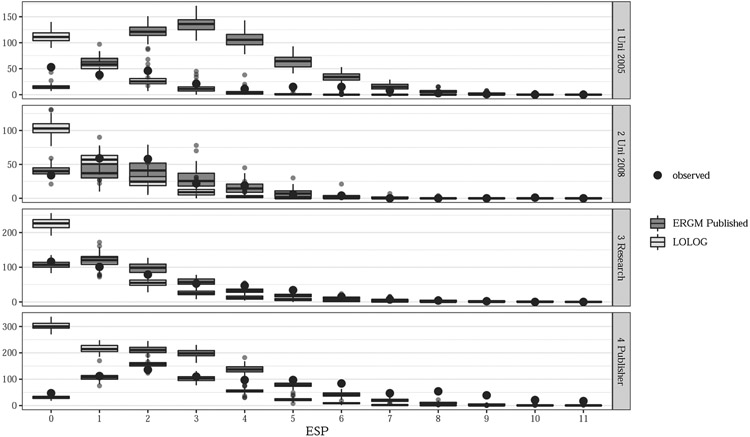
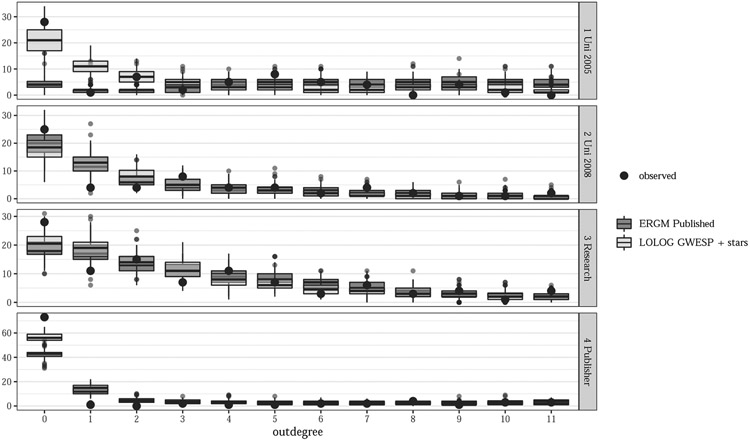
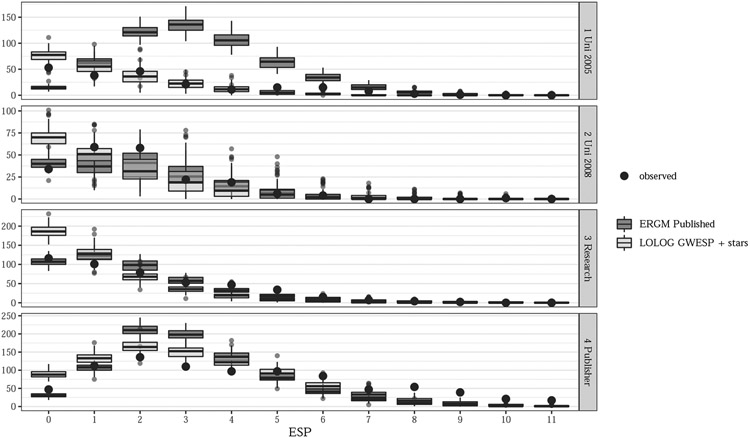
Firstly we consider the goodness of fit for the published ERGM model, and the LOLOG model with the same terms. Figures 1 show the comparison of simulated distribution of the in-degree with the observed network statistics. Figures 3 and 4 contained in Appendix A show the same comparison for edgewise shared partners (ESP) and out-degree.

Fig. 1.

In-degree goodness of fit comparison plot for Sailer’s office layout networks. The comparison is between ERGM and LOLOG fits both using the published ERGM terms

Table 4.2 shows comments on the goodness of fit for each network, using the recreated published ERGM and the LOLOG model with published ERGM terms. Where no comment is made for any of the goodness of fit terms or any model, the model fits well on that statistic.

All models for all networks have a least one of the in-degree, out-degree or ESP statistic of the observed network not being a typical value for the fitted models. As a result the models do poorly on recreating networks similar to the observed, and thus inference based on the parameter estimates and standard errors should be treated with caution. In particular we note that the LOLOG model with identical terms to the published ERGM does not seem to help improve the fit for any of the networks in question here.

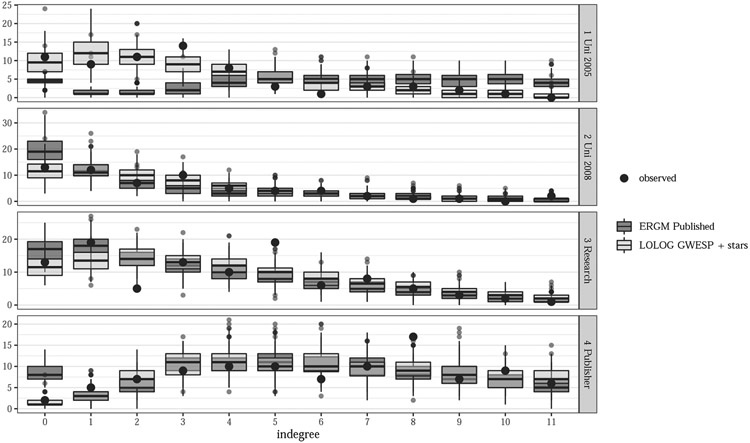
We also show the GOF for in-degree the LOLOG model with GWESP and 2- and 3- in- and out-stars for each model in Figure 2. Figures 5 and 6 contained in Appendix A show the plots for out-degree and ESP. We note here that all models fit the in-degree distribution well, all models except for the Publisher network fit the out-degree distribution well and the University 2005 and 2008 models fit well on the ESP distribution. This is an improvement in all cases versus the ERGM models published in Sailer and McCulloch (2012).

Fig. 2.

In-degree goodness of fit comparison plot for Sailer’s office layout networks. The comparison is between the published ERGM and LOLOG fits with GWESP and stars terms included.

4.3. Model Comparison

These networks are of particular interest as they represents a real world cases of applied researchers seeking a statistical tool to represent and test their social hypotheses and analyse their collected data. Good performance in such settings for the LOLOG model suggests the model could be of real use to the applied social network research community. Using these four complex networks as an example, helps us to present the the utility of the LOLOG model. The ERGM and LOLOG models with the terms as in Sailer and McCulloch (2012) produced the same qualitative interpretation.

However it is important to note that neither the specific LOLOG or the ERGM fitted the data well in terms of all in-degree, out-degree and ESP distributions. Therefore the models are not capturing basic aspects of the observed network data and the above interpretation should be treated with caution. In particular the Publisher network proved especially hard to fit.

Using the triangle term in the LOLOG model in place of the GWESP term did not improve the fit. Including 2- and 3- in- and out-star terms yields models that fit much better on the in- and out-degree distribution as well and the ESP distribution. We therefore have a stronger belief that inferences from these models are valid. They show similar conclusions to the published ERGM, though in addition we observe a significant positive out-2-star coefficient and a significant negative out-3-star coefficient, suggesting that there is a tendency for some people to have social interactions with many more people that others. This tendency for super-daily interactors was not captured in the published ERGM fit. We also note that the lack of a significant in-2-star parameter suggests that there is not a corresponding tendency for some people to attract more interactions, when their usefulness had already been accounted for. We can infer that perhaps there is a surplus of unwanted daily interaction due to people with a tendency for high out-degree. Thus the LOLOG model allowed for a better fit, as well as a deeper interpretation of the social interaction process.

5. Summary of Results for the Ensemble

The comparison of the value of models rarely will come down to a quantitative measure on a single dimension. The social processes that produce network data are typically complex and our choice of which data to analyse tends to favour complex structures. The models typically only approximate that structure and some features of the data are not represented in the models. Scientists that model social network data typically have multiple objectives with some models more suited to some of those objectives rather than others. Having said this, we constructed a rubric of criteria to assess the models, both relatively and absolutely. We follow each criterion with a brief justification for why it was included.

1. Are we able to recreate the published ERGM qualitatively?

   We asked this to screen out network data where our usage differs qualitatively from the original, for whatever reason. This is to help ensure we were using the data correctly, so that our comparison is valid.

2. Do the recreations of the published ERGM fit the network well?

   This is to assess the validity of the published ERGM results, and to assess if ERGM is a good model for the published case study.

3. Are we able to fit the LOLOG with the published ERGM terms?

   This is to assess the LOLOG on terms likely favourable to the ERGM. Typically, published ERGM will have undergone model selection criteria to choose terms that had good fit compared to other possible ERGM. This criteria assesses the flexibility of the LOLOG model class.

4. Does the LOLOG model with the published ERGM terms fit well?

   This is an absolute measure of the LOLOG goodness-of-fit with the ERGM terms.

5. Are we able to fit the LOLOG model with ERGM Markov terms (that are often degenerate in ERGM)?

   Markov terms, such as k-stars and triangles, often lead to near-degenerate models despite their conceptual appeal (Frank and Strauss, 1986). This criteria assesses if the LOLOG can aid in interpretability by using simpler terms that are not possible in ERGM.

6. Is a better fit achieved with LOLOG than the published ERGM?

   This is a direct comparison to judge if the LOLOG is a better model for the observed data than the published ERGM.

7. Do the published ERGM and best-fitting LOLOG models have consistent interpretations?

   This assesses if qualitative substantive conclusions draw from each model are consistent with the other. If affirmative, this gives some confidence that qualitative conclusions are not simply an artifact of the chosen modelling approach.

8. Which model do we believe to be more useful?

   This is a subjective judgement criterion. A major component is the goodness-of-fit criteria (Section 2.5). These criteria measure the degree that important statistical characteristics of the network data are reproduced by the model. These focus on characteristics not explicitly in the model. A second component is the substantive interpretability of the terms (i.e., are they socially salient). A third is the complexity of the model terms (i.e., the value of simplicity).

Table 7 provides a summary of the ERGM and LOLOG model fits for the networks in our ensemble, the columns are binary answers (1=Yes, 0 = No), to the above criteria. The fits were carried out in R using the ergm package (Handcock et al., 2018), and the lolog package (Fellows, 2018a). For the GWESP, GWDSP and GWDEG terms decay parameters were used as stated. If they where not available, α = 0.5 was used.

Table 7.

Summary table for LOLOG and ERGM Fits

Description	Network	Nodes	a	b	c	d	e	f	g	h
Add Health		1618	1	0	1	0	1	1	1	LOLOG
School Friends		Various
Kapferer’s Tailors		39	1	0	1	0	1	1	0	LOLOG
Florentine Families		16	1	1	1	1	1	1	0	ERGM
German Schoolboys		53	1	1	0	NA	1	1	1	Both
Employee Voice	1	27	0	NA	1	1	1	1	NA	LOLOG
Employee Voice	2	24	1	1	0	NA	0	0	NA	ERGM
Employee Voice	3	30	0	NA	1	1	1	1	NA	LOLOG
Employee Voice	4	31	0	NA	1	1	1	1	NA	LOLOG
Employee Voice	5	37	0	NA	1	1	1	1	NA	LOLOG
Employee Voice	6	39	0	NA	1	1	1	1	NA	LOLOG
Office Layout	University	67	1	0	1	0	1	1	1	LOLOG
Office Layout	University	69	1	1	1	0	1	1	1	LOLOG
Office Layout	Research	109	1	1	1	0	1	1	1	LOLOG
Office Layout	Publisher	119	1	0	1	0	1	1	1	LOLOG
Disaster Response		20	0	0	0	0	1	1	0	LOLOG
Company Boards	2007	808	0	0	0	0	1	1	NA	LOLOG
Company Boards	2008	808	0	0	0	0	1	1	NA	LOLOG
Company Boards	2009	808	0	0	0	0	1	1	NA	LOLOG
Company Boards	2010	808	0	0	0	0	1	1	NA	LOLOG
Swiss Decisions	Nuclear	24	0	1	0	NA	1	1	1	ERGM
Swiss Decisions	Pensions	23	0	1	1	0	1	0	0	ERGM
Swiss Decisions	Foreigners	20	0	1	0	NA	1	0	0	ERGM
Swiss Decisions	Budget	25	0	1	0	NA	1	1	0	ERGM
Swiss Decisions	Equality	24	0	0	0	NA	1	1	0	LOLOG
Swiss Decisions	Education	20	0	0	1	0	1	1	NA	LOLOG
Swiss Decisions	Telecoms	22	0	0	0	NA	1	1	NA	LOLOG
Swiss Decisions	Savings	19	1	1	0	NA	1	1	0	ERGM
Swiss Decisions	Persons	26	0	1	0	NA	1	1	0	ERGM
Swiss Decisions	Schengen	26	0	0	0	0	1	1	NA	LOLOG
University Emails		1133	0	0	0	0	0	0	NA	Neither
School Friends	grade 3	22	1	0	0	0	1	1	NA	LOLOG
School Friends	grade 4	24	1	0	0	0	1	1	NA	ERGM
School Friends	grade 5	22	1	0	0	0	1	1	NA	ERGM
Online Links	Hyperlinks	158	1	0	1	0	1	1	1	LOLOG
Online Links	Framing	150	1	0	1	0	1	0	1	LOLOG
Column Proportion	NA	NA	0.43	0.37	0.46	0.23	0.94	0.86	0.5	NA

Finally, we make some general comments regarding the significant amount of information on the hundreds of models fitted to the data that we gathered, more detailed summaries for each individual network are contained the supplement. More detailed overall comments on the study are in the discussion in Section 6.

Overall we see that in many cases, we were not able to recreate the published ERGM (Table 7 column a), and often when we could, the model did not fit the data well using the GOF methodology of Hunter et al. (2008) (Table 7 column b). We were sometimes able to use the same terms as the published ERGM to fit a LOLOG model, however there were also some networks where we could not fit the LOLOG model with ERGM terms.

Where a LOLOG model with ERGM terms was able to be fit it usually did not fit the data well (Table 7 column c). However in almost all cases we were able to fit the LOLOG model, with terms that usually result in degenerate ERGMs e.g. triangles and stars (Table 7 column e), and usually could achieve at least as good a fit as the published ERGM (Table 7 column f). Where is was possible to fit both a LOLOG and ERGM model the qualitative interpretations were equivalent on all parameters for half of the networks (Table 7 column g).

In general our experience in fitting the LOLOG model was that it was easier and faster to fit that ERGM (Table 7 column h), with the MOM estimation typically requiring little to no tuning, in contrast to ERGM models. In addition the triangles and star terms that can be readily fit with LOLOG models provide a simple and intuitive interpretation for users of the model.

6. Discussion

We have shown that the LOLOG model can be fit to most members of an ensemble of network data sets that have published ERGM fits in the journal Social Networks. We report a case-study of a complex data set and show that the LOLOG model is at least the equal of the ERGM, in terms of goodness of fit and interpretability. We carried out fits to 35 networks in total and gave a summary of each of the networks’ fits. We regard this as strong evidence that the LOLOG model is a useful model for modelling real social network data, as journal articles with published ERGM fits likely have a selection bias towards data sets that are well suited to ERGMs.

In carrying out this study we have gained a great deal of practical experience in the types of tasks for which ERGMs are used, as well as practical problems in fitting them, in particular code run time and degeneracy issues. We have found the LOLOG model to be in general more user friendly and faster to fit, leading to easier identification of poor models, and a much faster data analysis procedure. The benefits of this should not be overlooked, in particular when social network analyses are often of interest to applied researchers whose expertise is not statistical modelling. As a result LOLOG models seem particularly better suited to feasibly analysing larger networks, which whilst possible to fit with ERGMs (Stivala et al., 2020), often require significant tuning and computational resources.

LOLOG models can usually be fit with terms that are almost always degenerate for ERGMs on even small networks. Using this greater flexibility of specification, we were often able to achieve a better fit. In addition the need to use complex geometrically weighted statistics is reduced, aiding interpretability of the LOLOG model. In practice we also believe LOLOG models could facilitate more robust model selection procedures. The degeneracy issues of ERGM as well as the time taken to fit the model, can result in researchers omitting terms based on their degeneracy, as well as considering fewer models than they would want. The fast fit and robust to degeneracy properties of the LOLOG model should help alleviate these practical issues. This should increase the scope of terms that researchers use, as they can focus on their representation of the underlying social processes rather than being restricted by computational and class specific representation issues.

We have also seen that qualitative interpretations of analyses carried out with both ERGMs and LOLOG models are generally in agreement. We do note, however, from our experiences that the LOLOG model applied to small networks can result in parameter estimates with high variance, where the ERGM model parameters have lower variances, more amenable to interpretation.

Goodness of fit of LOLOG models also compares favourably with the ERGMs, with little drop in quality, for the same terms. In particular with the ability to use simpler terms for the LOLOG model we were often able to achieve improved fit over the published ERGMs in the ensemble of networks that we fit.

The LOLOG model has the advantage of being able to account for edge orderings. We believe that this may be helpful for analysing network data, although we have not seen clear benefits in the ensemble of network data in this study. It is worth noting that there are many settings where the ability to model the edge ordering process is a great advantage of the LOLOG model. A clear case is citation networks where the temporal directional is fundamental (McLevey et al., 2018). Another case is where preferential attachment type processes are thought to be strong. A third is where the edge ordering is known exactly, or thought to be strongly influenced by a covariate or contingency. The further consideration of edge ordering processes is beyond the scope of this paper. However, we hope that the availability of a latent ordering network model like LOLOG available will spur the development of edge ordering processes models. We also note that the LOLOG model is a fully general model in the sense that it can represent any PMF over the space of networks. Therefore even if it is hard to justify such an edge formation procedure, the LOLOG model may still be a useful approach to understanding the social processes producing network data.

All analysis was done in the R environment (R Core Team, 2020) primarily with the lolog (Fellows, 2018a) and ergm packages (Handcock et al., 2018). The code and available data to reconstruct the analyses of this paper are available at https://github.com/duncan-clark/lolog_catalog_paper/tree/main/example_fit.

Table 6.

Summary of GOF for ERGM and LOLOG with published terms for Sailer’s office layout networks. For all networks neither the LOLOG model or ERGM provide satisfactory fit.

Network	ERGM	LOLOG
2005 University	Fits poorly on out-degree	Fits poorly on in-degree
	Fits poorly on ESP	Fits poorly on ESP but much better than ERGM
2008 University	Fits poorly on out-degree	ERGM convex, LOLOG concave on in-degree
	Fits poorly on ESP	Fits poorly on out-degree
		Fits poorly on ESP
Research Institute	Fits poorly on out-degree	Fits poorly on in-degree
	Fits poorly on ESP	Fits poorly on out-degree
		Fits poorly on ESP
Publisher	Fits poorly on in-degree	Fits poorly on in-degree
	Fits poorly on out-degree	Fits poorly on out-degree
	Fits poorly on ESP	Fits poorly on ESP

Appendices

A. Additional Goodness of Fit Figures

Fig. 3.

Out-degree goodness of fit comparison plot for Sailer’s office layout networks. The comparison is between ERGM and LOLOG fits both using the published ERGM terms

Fig. 4.

ESP goodness of fit comparison plot for Sailer’s office layout networks. The comparison is between ERGM and LOLOG fits both using the published ERGM terms

Fig. 5.

Out-degree goodness of fit comparison plot for Sailer’s office layout networks. The comparison is between the published ERGM and LOLOG fits with GWESP and stars terms included.

Fig. 6.

ESP goodness of fit comparison plot for Sailer’s office layout networks. The comparison is between the published ERGM and LOLOG fits with GWESP and stars terms included.

B. Links to publically available data

Table 8 provides hyperlinks to the publicly available datasets used in our ensemble.

Table 8:

Links to publicly available datasets

Network	Links
Add Health	addhealth.cpc.unc.edu/
Elementary School	moreno.ss.uci.edu/data.html#children
Florentine Families	sites.google.com/site/ucinetsoftware/datasets/padgettflorentinefamilies
Kapferer’s Tailors	sites.google.com/site/ucinetsoftware/datasets/kapferertailorshop
Natural Disasters	vlado.fmf.uni-lj.si/pub/networks/data/GBM/kansas.htm
German Schoolboys	github.com/gephi/gephi/wiki/Datasets
Company Boards	corp.boardex.com