Recurrent ancient geomagnetic field anomalies shed light on future evolution of the South Atlantic Anomaly

Significance

Earth’s magnetic field, which is generated through convection in the liquid iron–rich outer core, acts as a shield against harmful particle radiation. During the past two centuries, the field strength has decreased rapidly as an area of weak field has expanded over the South Atlantic Ocean. The decreased shielding effect of the magnetic field in this area has important implications for low Earth-orbiting satellites and space travel. Using archeological and geological records, we have reconstructed the variations of Earth’s magnetic field over the past 9,000 y. We find evidence for recurrent magnetic field anomalies, similar to the present-day South Atlantic Anomaly, which provides insights into underlying geodynamo processes that may help predict the future development of Earth’s magnetic field.

Abstract

The strength of the geomagnetic field has decreased rapidly over the past two centuries, coinciding with an increasing field asymmetry due to the growth of the South Atlantic Anomaly. The underlying processes causing the decrease are debated, which has led to speculation that the field is about to reverse. Here, we present a geomagnetic field model based on indirect observations over the past 9,000 y and identify potential ancient analogs. The model is constructed using a probabilistic approach that addresses problems with age uncertainties and smoothing of sedimentary data that have hampered previous attempts. We find evidence for recurrent hemispherical field asymmetries, related to quasiperiodic millennial-scale variations in the dipole moment. Our reconstruction indicates that minima in the dipole moment tend to coincide with geomagnetic field anomalies, similar to the South Atlantic Anomaly. We propose that the period around 600 BCE, characterized by a strongly asymmetric field, could provide an analog to the present-day field. The analogy implies that the South Atlantic Anomaly will likely disappear in next few hundred years, accompanied by a return to a more symmetric field configuration and possibly, a strengthening of the axial dipole field.

The strength of the axial dipole part of the geomagnetic field has been decreasing at an average rate of 16 nT/y over the past 180 y (1), for which there are direct measurements of field intensity. This period of rapid decay has coincided with the expansion of the South Atlantic Anomaly (SAA), which has been proposed as a possible precursor to a polarity reversal (2). The weak intensities associated with the anomaly can be traced to several reverse flux patches between South America and Africa at the core–mantle boundary (CMB) (3). It has been proposed that the rapid decrease of the dipole field is caused by the growth and/or poleward migration of some of these reverse flux patches (4). Overall, the decrease of the dipole moment (DM) is primarily traced to field structures in the Southern Hemisphere of the core and also, involves increased transport of normal flux toward the equator (5).

Recent core flow inversions (6, 7) have highlighted the importance of a planetary-scale westward eccentric gyre in the liquid outer core. The dominantly axially symmetric gyre circles the inner core tangent cylinder in the Pacific Hemisphere and reaches lower latitudes in the Atlantic Hemisphere, leading to predominantly meridional flow along the eastern (equatorward) and western (poleward) limbs of the gyre. The presence of this gyre, coupled with the asymmetry in the field due to the SAA, is able to account for the majority of the dipole decay since 1840 CE through an average poleward transport of reversed flux along the gyre’s western limb and equatorward transport of normal flux along the gyre’s eastern limb (8). This hypothesis is supported by core flow models suggesting that the gyre has persisted over at least the past 140 y, during which the flow can be reliably reconstructed (9). Similar flow structures have been reproduced in coupled Earth dynamo simulations through a combination of heterogeneous lower-mantle heat flux and asymmetric inner core growth (10). This implies that the planetary gyre may persist or recur over much longer timescales, which could be tested with improved paleomagnetic field reconstructions.

Indirect geomagnetic field measurements obtained from burnt archaeological artifacts, volcanic rocks, and sediments suggest that the axial dipole field may have been continuously decreasing at similar rates as today over the past 300 to 1,000 y (11–13). Recent models show that the SAA emerged around 1800 CE but also, suggest that it developed from the remnants of a previous weak field anomaly that first appeared in the Indian Ocean region around 600 CE and proceeded to drift westward (11, 14). Despite the considerable progress that has been made over the past two decades, significant differences between different Holocene geomagnetic field models remain. Neither the recent dipole decay nor the appearance of SAA-type field asymmetries appear to be unusual features of the ancient geomagnetic field (15–17), but it is currently not clear if the former is always associated with the latter. Several studies have also suggested that the South Atlantic may represent a region of unusual field behavior (18, 19). Such observations are important for understanding the underlying mechanisms and to predict the future evolution of the SAA and the current dipole decay.

The challenges with Holocene geomagnetic field reconstructions are mainly related to the 1) sparse data distribution, 2) chronological data uncertainties, and 3) temporal smoothing due to the gradual process by which sediments acquire a magnetization. Here, we present a (2nd generation) paleomagnetic field model for the past 9000 y (pfm9k.2) based on a probabilistic approach (Materials and Methods) that addresses all of these problems (20). A key feature of this model is the coestimation of geomagnetic field and the age of the archeo-/paleomagnetic data. In addition to independent chronologic constraints, the model uses information on the spatial and temporal variability of the geomagnetic field to synchronize available archeo-/paleomagnetic data in time. Furthermore, smoothing effects associated with the gradual process by which sediments acquire a magnetization are also accounted for in the geomagnetic field model. The model takes advantage of the most up-to-date archeomagnetic data compilation (21) and paleomagnetic directions from 10 sediment records, strategically selected based on data quality and geographic location (SI Appendix, Figs. S1–S11). The shortcomings in data coverage are accounted for by the modeling approach, resulting in large model uncertainties in regions that are not populated by data (20). The model allows us to resolve structures in the geomagnetic field that have previously been obscured by excessive model smoothing caused by apparent data inconsistencies.

In this study, we will investigate variations in the DM over the past 9,000 y and potential links to hemispherical field asymmetries, such as the SAA, and discuss potential underlying mechanisms. We purposely focus on geomagnetic features of spherical harmonic degree 1 to 2 that should be adequately recovered by the model (20).

Variations in the DM

Reconstructing changes in the DM over the Holocene is challenging, primarily due to the general lack of absolute paleointensity data from the Southern Hemisphere (22). Our model is in principle able to account for this (20), but the method is sensitive to the prior assumptions about the variance and rates of change of the Gauss coefficients that are used to describe the geomagnetic field (Materials and Methods). The prior distributions of the Gauss coefficients are mainly derived from the relatively short record of direct measurements, which means that the large-scale and slowly evolving properties of the field (e.g., the axial dipole [$g_1^0$ coefficient]) are the least well constrained. To illustrate this, we compare the DM variations over the past 9,000 y from our model based on three different priors for $g_1^0$ (Fig. 1). In all three cases, $g_1^0$ is described by a stationary stochastic process with a covariance function defined by either two or three parameters (23). The first case (pfm9k.2A) uses the same prior that was used for the geomagnetic field model COV-OBS.x2 (24), based on observational data. This can be considered quite a conservatory prior with purposely low secular variation variance ${({\sigma }_{{\dot{g}}_1^0})}^2={(10\text{nT/y})}^2$ chosen to ensure the stability of the modeled axial dipole. The second case (pfm9k.2B) uses the $g_1^0$ prior as described in ref. 20 and can be considered as a more relaxed alternative with ${\sigma }_{{\dot{g}}_1^0}=17\text{nT/y}$. The third and preferred case (pfm9k.2) uses an intermediate prior with ${\sigma }_{{\dot{g}}_1^0}=13.5\text{nT/y}$, defined the same way as in ref. 24 but with different parameters (SI Appendix, Fig. S12). The rates of change of the axial dipole based on the conservative prior (pfm9k.2A) are consistent with published Holocene geomagnetic field models that include sedimentary data. We argue that these estimates should be considered as a lower boundary due to the effects of chronologic uncertainties and inherent smoothing of the sedimentary data. Published archeomagnetic models typically exhibit larger-amplitude variations on millennial timescales, which are consistent with the more relaxed prior (pfm9k.2B) (SI Appendix, Fig. S15). For the remainder of this study, unless otherwise stated, we only show results from our preferred case pfm9k.2 but note that this choice does not have an impact on our overall conclusions.

Fig. 1.

Reconstructions of the DM over the past 9,000 y using three different priors for the axial dipole ($g_1^0$). Thick lines show the posterior mean, and the semitransparent lines show 100 samples from the posterior distribution of each case. In addition, thin black lines show the 95% credible interval of the preferred pfm9k.2 case. Vertical dotted black lines are added to illustrate the ∼650- and ∼1,300-y quasiperiodic variations in the reconstructed DM.

As shown in Fig. 1, the long-term variations in the DM are similar for all three cases, but there are substantial differences in the amplitude of variations on timescales of 100 to 1,000 y. The differences are mainly due to a redistribution of power from the axial dipole $g_1^0$ to coefficients $g_1^1,g_2^0,g_2^1$, and $g_3^0$. This is particularly evident around 3,000 y ago, where the DM fluctuates between a minimum at 1300 BCE, a maximum at 1000 BCE, and another minimum at 700 BCE. Absolute average rates of change of $g_1^0$ based on the different cases range from 4 to 16 nT/y (equivalent of $1\times {10}^{19}$ to $4\times {10}^{19}$ Am²/y) during both the growth phase (1300 to 1000 BCE) and the decay phase (1000 to 700 BCE), which is in line with the recent dipole decay rates. The minimum in the DM around 700 BCE is different from the predictions of most published models, some of which show the highest DM during the Holocene around the same time (SI Appendix, Fig. S15). The discrepancy is traced to the axial DM ($g_1^0$) and its role in explaining strong intensities in western Eurasia at 700 BCE (e.g., ref. 25). Our model is able to capture previously unresolved steep inclinations in Scandinavia and shallow inclinations in the Arctic, which demonstrates that the strong intensities in western Eurasia have to be explained by higher moments (SI Appendix, Fig. S16). Similar arguments have previously been put forward in refs. 26 and 27, invoking the role of the equatorial dipole to explain the discrepancy, but here, we show that the quadrupole field is more important (see below).

The centennial fluctuations in the DM around 1000 BCE are part of a quasiperiodic variation with recurrent peaks (or minima) every ∼650 y, which is present in all three cases but most clearly seen in pfm9k.2B over the past 4,000 y. Prior to 3000 BCE, the DM shows similar periodic variations but with twice as long of a period (∼1,300 y), potentially due to data limitations that inhibit the model from resolving variations on shorter timescales. Similar periodicities have previously been observed in paleomagnetic reconstructions associated with the axial dipole and octupole terms (600 to 800 y) and the equatorial dipole and quadrupole terms (1,000 to 1,400 y) (e.g., refs. 26 and 28). The identified periodic variations are also supported by comparisons with independent records of cosmogenic radionuclide production, which are inversely related to the strength of the geomagnetic field. While the production rate signal of the observed oscillations is relatively small, roughly 10% of the full range due to solar modulation, we detect variations that are both in phase and with similar amplitudes within the same frequency band range in both geomagnetic and radionuclide-based records (SI Appendix, Fig. S17).

East–West Hemispherical Field Asymmetries

The period of (potentially) large fluctuations in DM around 1000 BCE coincides with a period of strong quadrupole field. The quadrupole contribution to the field is here illustrated through the eccentric dipole (29), which is the best-fitting dipole field moved away from the Earth’s center, constituting a combination of spherical harmonic degrees 1 and 2. Fig. 2A shows the radial distance of the eccentric dipole from the rotation axis. The eccentric dipole variations in Fig. 2A are traced almost entirely to variations in the $g_2^1$ and $h_2^1$ Gauss coefficients, which in combination with $g_1^0$, produce an east–west hemispherical field asymmetry. The $g_2^1$ and $h_2^1$ coefficients have previously also been noted as important to account for the observed paleosecular variation at high latitudes over the past 5 My (30–32). Shifts along the z axis (away from the equatorial plane) are predominantly toward the Northern Hemisphere, implying persistent north–south asymmetry in the field (i.e., due to a persistent $g_2^0$ component) (e.g., ref. 33). Such north–south field asymmetries could potentially be caused by the Northern Hemisphere bias in data distribution (34), although tests using synthetic data do not support this (20, 35). While similar artifacts cannot be ruled out for the location of the eccentric dipole in the equatorial plane, they are less likely due to the relatively even longitudinal distribution of data (SI Appendix, Fig. S1).

Fig. 2.

(A) Radial distance of the eccentric dipole from the rotation axis (s_c) based on 1,000 samples from the pfm9k.2 posterior distribution (semitransparent black lines) and the posterior mean (thick black line). Also shown is the posterior mean contribution from Gauss coefficients $g_2^1$ and $h_2^1$ (dashed red line, upper x axis). (B) Time–longitude density plot of the eccentric dipole locations projected onto the equatorial plane (i.e., ignoring the z component) based on 1,000 posterior samples. Horizontal dotted black lines are added to illustrate the identified ∼1,300-y quasiperiodic variations in both the DM and the eccentric dipole location. (C) The eccentric dipole locations projected onto the equatorial plane based on 1,000 posterior samples (every 50 y) and the posterior mean model (black line), both over the period 7000 BCE to 1850 CE. The eccentric dipole determined from COV-OBS.x2 for years 1840 to 2000 CE (blue line) is shown for reference. Red and green stars mark the locations of the eccentric dipole at 2020 CE and 600 BCE, respectively.

During the past 9,000 y, two periods of pronounced east–west field asymmetries are clearly resolved by the model: from 1600 to 300 BCE and from 1000 CE to present. The eccentric dipole, located in the Atlantic and the Pacific Hemispheres, respectively, was in both cases drifting westward, generating a distinctive “s-shape” in the time–longitude plot (Fig. 2B). Overall, there is a pattern of recurrent “eccentric phases” with similar signatures in the time–longitude plot (Fig. 2B) roughly every 1,300 y, consistent with (or twice the length of) the identified periodic variations in DM. This hints at similarities in the field around 600 BCE with the present-day field (i.e., 1,000 y after the onset of respective eccentric phase). Prior to 1600 BCE, the eccentric dipole location is generally less well resolved (and we, therefore, focus less on this time period), but it is still possible to distinguish three clusters in the time–longitude plot (Fig. 2B) more or less consistent with the same periodic pattern (around 6100, 4800, and 3500 BCE). While the identified eccentric phases are individually characterized by westward drift, the eccentricity centers appear to propagate eastward with each new phase. This is consistent with a similar eastward propagation in the occurrence of high-latitude weak/reverse flux in the Northern Hemisphere of the core over the past four millennia (36). The high-latitude weak/reverse flux patches appear toward the end of each eccentric phase, roughly 180${}^{°}$ away from the eccentric dipole location and as previously noted (36), tend to coincide with large dipole tilts (SI Appendix, Fig. S18). There are indications in our model but also, in previous reconstructions (14, 37), that the weak/reverse flux patches first appear at low latitudes several centuries earlier and then, migrate poleward, which suggests that they could be linked to the growth and decay of the east–west hemispherical field asymmetries.

There is tendency that the eccentric dipole, at least during more eccentric phases, is preferentially located either in the first (0${}^{°}$ to 90${}^{°}$E) or third quadrant (180${}^{°}$ to 270${}^{°}$E) of the equatorial plane (Fig. 2C). We note, however, that the location of the eccentric dipole over the historical era is moving into the second quadrant, deviating from this general pattern. The distinctive s-shapes in the time–longitude plots (Fig. 2B) are caused by a slight interruption of the westward motion of the eccentric dipole location, which also tends to occur at specific longitudes ($\sim {50}^{°}$E and $\sim {200}^{°}$E). Such preferential longitudes of the eccentric dipole are likely due to some external forcing factors influencing the geodynamo (e.g., ref. 38). While this could potentially also be caused by a bias in the data distribution, we think this is unlikely as we do not see any indications for such artifacts in our tests based on synthetic data (20).

Recurrent Geomagnetic Field Anomalies

The dipole eccentricity of the geomagnetic field during the historical era is attributed to the asymmetric distribution of high-latitude, high-intensity flux patches at the CMB, with on average more intense magnetic field in the Pacific Hemisphere compared with the Atlantic Hemisphere (e.g., refs. 2 and 34). The dipole eccentricity has been increasing over the past two centuries due to the growth of reverse flux beneath the South Atlantic region of the CMB coinciding with the decline in the DM (39). This has led to a more pronounced field asymmetry in the Southern Hemisphere of the core and the development of the SAA at Earth’s surface (Fig. 3 A and B).

Fig. 3.

Maps of geomagnetic field intensity (F) at Earth’s surface and radial field (B_r) at the CMB based on model averages of (A and B) COV-OBS.x2 at 2020 CE and (C and D) pfm9k.2 at 600 BCE. The geomagnetic field at 600 BCE serves as a potential ancient analog to the present. The projection in B and D maps (600 BCE) has been rotated 100${}^{°}$ toward the east to align the eccentric dipole axis location with A and C (red star in Fig. 2B). (C and D) Gray shaded areas, which represent regions where the model SD exceeds 5 and 120 µT, respectively, are added to highlight the large model uncertainties, particularly in the Southern Hemisphere field predictions. Movies S1 and S2 have more detailed information on the model uncertainties.

Our results suggest that the geomagnetic field has remained more or less asymmetric over the past 1,000 y ago starting with the development of an equatorial geomagnetic field anomaly around the Indian Ocean (11, 14). The geomagnetic anomaly reached its maximum extent in the Indian Ocean around 1100 CE and then, proceeded to drift westward (similarly to the eccentric dipole) (Fig. 2B) toward the Atlantic Ocean, where it again deepened (Movie S1). As previously described (14), the evolution of the anomaly can be traced to reverse flux that appears at the equator beneath the Indian Ocean and migrates southwestward, reaching the region beneath Africa around 1300 CE, coinciding with a minimum in the DM, and eventually moving further westward into the South Atlantic region of the CMB. Also previously noted (14) is the synchronous (potentially related) emergence of a reverse flux patch at the equator beneath the Atlantic Ocean, which migrates toward high northern latitudes between 1000 and 1700 CE (Movie S2). It is important, however, to stress that the ability to resolve distinct flux patches at the CMB and their movement (as opposed to the growth and decay of different flux patches) is severely limited by the low resolution of archeo-/paleomagnetic field models.

Between 1600 and 300 BCE, the east–west hemispherical field asymmetry can be traced to the growth and decay of two weak field anomalies in the Pacific Hemisphere, coinciding with minima in the DM at 1300 and 700 BCE (Movie S1). The anomaly at 1300 BCE is mainly associated with a field asymmetry in the Southern Hemisphere, while the anomaly at 700 BCE is due to a field asymmetry in the Northern Hemisphere, with unusually high intensities in Europe and the Middle East (Fig. 3C) (e.g., ref. 40). Fig. 4 shows the reconstructed variations in intensity in North America and the Middle East over the past 9,000 y, which illustrate this large-scale field asymmetry in the Northern Hemisphere field around 1000 to 500 BCE (vertical gray bands). According to our model, the high intensities in the Middle East around this time are due to a concentration of intense flux beneath this region of the core (Fig. 3D), similar to the present-day situation beneath the Indian Ocean (Fig. 3B). The field variations in the Middle East during this time period have also been associated with unusually high rates of change, so-called geomagnetic spikes (41), but due to the prior constraints and the 50-y sampling rate, the model is likely not able to capture such proposed rapid field variations.

Fig. 4.

Model–data comparison of variations in geomagnetic field intensity over the past 9,000 y in (A) North America and (B) the Middle East. The vertical gray shaded bands between 1000 and 500 BCE are added to highlight the large Northern Hemisphere asymmetry in the field during this time. Model predictions are represented by 100 samples from the posterior distribution (semitransparent black lines) and the 95% credible intervals (red lines). The archeomagnetic data (black dots; plotted on the maximum posterior probability ages) were selected from radii of 30${}^{°}$ and 10${}^{°}$, respectively, and relocated assuming an axial dipole field. The large radii used to select the data, chosen to obtain a reasonable amount of data for the comparison, can be justified on account that the model resolution is limited to spherical harmonic degree 5 (i.e., spatial wavelengths of 72${}^{°}$). Error bars represent 1-σ uncertainties. Note that the y-axes limits have been adjusted to highlight the main features of the field variation, thereby omitting four and three unusually high-intensity data, respectively.

Both the 1300 and 700 BCE weak field anomalies appear to be related to the appearance of weak/reverse flux at the equator beneath the western coast of South America, which then migrates to higher southern or northern latitudes, respectively (Movie S2). There are also indications of weak/reverse flux appearing beneath Australia that likely contributes to the surface field anomalies. In terms of paleomagnetic data, the Pacific weak field anomalies are largely traced to shallow inclinations in North America and the Canadian Arctic (e.g., refs. 42 and 43) and consistently low intensities in Mexico between 1500 and 500 BCE (Fig. 4A) (44).

Discussion

Ancient Analogs of the Present Day.

We find evidence for recurrent east–west hemispherical geomagnetic field asymmetries linked to weak field anomalies at Earth’s surface and quasiperiodic fluctuations in the DM over the past 9,000 y. Understanding the underlying mechanisms of these recurrent events may help to predict how the SAA is likely to evolve. Based on the similarities in the variations of the eccentric dipole, the period between 1600 and 300 BCE could potentially serve as an ancient analog of the geomagnetic field changes over the past 1,000 y (i.e., controlled by similar underlying core processes). The observed periodicity of these eccentric phases (Fig. 2) suggests an average length of 1,300 y. This would imply that the present-day geomagnetic field is approaching the end of such an eccentric phase (equivalent to the year 600 BCE) (Fig. 3) and that the field will return to more symmetric conditions in the next ∼300 y, possibly with a strengthening of the DM through a shift of quadrupole to dipole energy. However, we note that the DM is still decreasing without showing signs of slowing down, which is not consistent with the proposed ancient analog and highlights its limitations.

Eccentric Planetary Gyre.

It has been demonstrated that the eccentric planetary-scale gyre in Earth’s core can explain the current dipole decay through an advective transfer of energy from dipole to nondipole field (8). A key aspect of the proposed mechanism is the presence of a field asymmetry, such as the SAA, which causes an imbalance in the meridional transport of flux. In the present-day case, this leads to an on average greater transport of reverse flux poleward and normal flux equatorward, resulting in axial dipole decay. The same mechanism could, however, also explain a rapid dipole growth with a different field configuration. Our results suggest that there are millennial-scale periodicities in the variation of the DM over the past 9,000 y and that these are related to a recurrent pattern of field asymmetries, similar to the present-day SAA. We speculate that the mechanism proposed in ref. 8 may also provide an explanation for the evolution of the DM during the past 9,000 y. Of particular interest is the period between 1600 and 300 BCE, which shows both large hemispherical field asymmetries (Fig. 2) and rapid fluctuations in the DM (Fig. 1). It is possible that core flow during this period may have been characterized by a similar eccentric planetary-scale gyre as today, facilitating rapid fluctuations in the axial dipole through increased meridional flux advection along its eastern and western limbs. According to this hypothesis, the concentration of intense flux beneath the Middle East, starting to build up around 1300 BCE (Movie S2), may partially have resulted from preferential equatorward flow (i.e., along the gyre’s eastern limb). While there are some indications of this, we note that such observations are generally beyond the resolution of the current model.

High-Latitude Westward Drift.

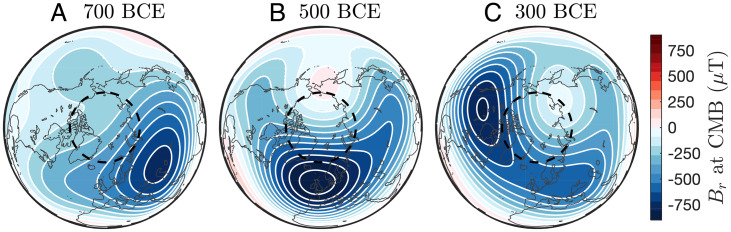
As shown in Fig. 2, the eccentric dipole location is generally drifting westward, but the eccentric phases instead show a slow eastward progression, similar to the occurrence of high–northern latitude weak/reverse flux at the CMB (36). This slow eastward propagation is potentially related to the superposition of two distinct westward drift signals (0.09${}^{°}$/y and 0.25${}^{°}$/y) observed at high northern latitudes at the CMB (36). It has been suggested (36) that the observed westward drift may represent magnetic Rossby waves riding on top of the background flow (45), corresponding to the slower drift rate. Alternatively, the faster drift rates could potentially also be explained by the presence of a planetary-scale gyre that itself is drifting westward along with the background flow, consistent with similar flow structures reproduced in numerical simulations (10). Such flow structures would give rise to localized intense westward drift at high latitudes at the CMB in the hemisphere where the gyre approaches the inner core tangent cylinder. A possible example of this is a period of exceptionally rapid westward drift observed at high latitudes in the Atlantic Hemisphere between 700 and 300 BCE (Fig. 5).

Fig. 5.

Northern Hemisphere polar maps of the radial field (B_r) at the CMB at (A) 700 BCE, (B) 500 BCE, and (C) 300 BCE. The CMB expression of the inner core tangent cylinder (dashed black lines) is shown for reference.

This period of rapid high-latitude westward drift coincides with the return to a more symmetric field configuration (Fig. 2A). The drift rates, initially as high as 0.5${}^{°}$/y to 1${}^{°}$/y (SI Appendix, Fig. S19), are similar to those observed over the past 20 y beneath the Canadian Arctic region of the core, which have been attributed to an accelerating core flow jet (46). As shown in Fig. 5, the drift is related to an intense flux patch beneath Europe, which splits into two patches, similar to the present day (47), with one part moving rapidly toward North America. The rapid movement can be traced to the characteristic westward swing in declination data from Europe (e.g., ref. 48), which previous models have not been able to capture in full extent (SI Appendix, Fig. S19). If we assume that this westward drift is caused by a planetary gyre–type structure, this implies that the gyre around this time period extended toward the Pacific Hemisphere, approaching the inner core tangent cylinder in the Atlantic Hemisphere.

Evidence for External Forcing Mechanisms.

Our results suggest that the eccentric dipole is preferentially located in the first or third quadrant of the equatorial plane (Fig. 2C), related to geomagnetic anomalies occurring in the opposite hemisphere. These observations are consistent with locations of the eccentric dipole in numerical dynamo simulations, including a combination of heterogeneous heat flow across the CMB (based on variations in shear-wave velocity at lower mantle) and more importantly, an asymmetric inner core with two (opposite) preferred growth directions (38). The comparison suggests that the asymmetric inner core growth may be an important factor to consider in order to explain the recurrent east–west asymmetries. However, while reorientations of the fastest inner core growth direction have been proposed (38), they are thought to be due to changes in flow in the inner core, which would imply much longer timescales than considered here (49). Interestingly, we also note that the weak/reverse flux associated with the Pacific geomagnetic field anomalies (e.g., Fig. 3D) appears to occur around the edges of the lower-mantle large low–shear velocity zones. These have been proposed to represent areas of increased upwelling (50, 51), highlighting the potential role of the lower mantle as well.

Materials and Methods

The method used to construct the time-varying geomagnetic field model over the past 9,000 y is described in detail in ref. 20. Briefly summarized, the model is based on a compilation of archeomagnetic data and 10 strategically selected sediment records from the GEOMAGIA50.v3 database (21, 52) (SI Appendix). The model is built following a Bayesian approach, and we use a Hamiltonian Monte Carlo algorithm (53) to generate $M=1,000$ samples from the joint posterior probability distribution. The geomagnetic field prior is encoded using a spherical harmonic decomposition of the scalar potential for the field $B=-\nabla \varphi$, with each Gauss coefficient expanded in time using Gaussian processes (e.g., ref. 11). The a priori variance and characteristic timescales for all coefficients of degree $l\ge 2$ were determined based on the historical era model COV-OBS.x2 (24), while the dipole coefficients, l = 1, were treated separately (SI Appendix). The spherical harmonic expansion of the field is truncated at $L=5$, evaluated every 50 y, and constrained to COV-OBS.x2 (24) from 1850 to 2000 CE. The data ages are included as unknown model parameters. Archeomagnetic ages are assumed to be normally distributed, while sedimentary ages are parameterized using a modified version of the Bayesian age-depth model Bacon (54), which incorporates both independent chronologic constraints and stratigraphic information. To account for the smoothing and temporal offset of postdepositional remanent magnetizations associated with the gradual processes by which sediments record the field, the likelihood function is adapted based on the method in ref. 55. Model parameters are also introduced to account for potential systematic errors that affect declination (e.g., coring related) and/or inclination data (e.g., due to compaction) from the same sediment record. Finally, a Student’s t error distribution is used to account for data outliers (56).

The model description allows us to plot maps (Figs. 3 and 5) and time series (Fig. 4) of the field observed at Earth’s surface and the radial magnetic field (B_r) at the CMB. Movies of the intensities at Earth’s surface (Movie S1) and B_r at the CMB (Movie S2) as well as the model uncertainties are provided in SI Appendix. The DM plotted in Fig. 1 is given by

$$DM=\frac{4\pi }{{\mu }_0}{a}^3\sqrt{{(g_1^0)}^2+{(g_1^1)}^2+{(h_1^1)}^2},$$ [1]

where μ₀ is the permeability of free space and $a=6,371.2$ km is the mean radius of the Earth. The geocentric Cartesian coordinates ($x_c,y_c,z_c$) of the best-fitting eccentric dipole plotted in Fig. 2 are (29)

$$x_c=a\frac{(L_1-E{g}_1^1)}{3m^2},y_c=a\frac{(L_2-E{h}_1^1)}{3m^2},z_c=a\frac{(L_0-E{g}_1^0)}{3m^2},$$ [2]

where

$$\begin{array}{ll}\hfill & L_0=2g_1^0{g}_2^0+\sqrt{3}(g_1^1{g}_2^1+h_1^1{h}_2^1),\hfill \\ \hfill & L_1=-g_1^1{g}_2^0+\sqrt{3}(g_1^0{g}_2^1+g_1^1{g}_2^2+h_1^1{h}_2^2),\hfill \\ \hfill & L_2=-h_1^1{g}_2^0+\sqrt{3}(g_1^0{h}_2^1+g_1^1{h}_2^2-h_1^1{g}_2^2),\hfill \\ \hfill & E=\frac{(L_0{g}_1^0+L_1{g}_1^1+L_2{h}_1^1)}{4m^2},\hfill \\ \hfill & m^2={(g_1^0)}^2+{(g_1^1)}^2+{(h_1^1)}^2.\hfill \end{array}$$ [3]

Data Availability

Model parameters and data have been deposited in the EarthRef.org Digital Archive (https://earthref.org/ERDA/2522) (57).