Crosslinguistic word order variation reflects evolutionary pressures of dependency and information locality

Significance

Many languages have subject–verb–object order, while many others have subject–object–verb order. Why do languages vary in the way they do, and how does word order evolve? We present a theory postulating that each language exhibits the basic word order it has due to two evolutionary pressures that trade off against each other; some languages prefer to keep syntactically related elements close together, while others prefer to keep elements together if they are informative about each other. Using phylogenetic analyses, we show that our theory explains the crosslinguistic frequency variation in word order and the historical trajectories of word order change. Our findings suggest that grammar and usage coadapt in word order to support efficient communication.

Abstract

Languages vary considerably in syntactic structure. About 40% of the world’s languages have subject–verb–object order, and about 40% have subject–object–verb order. Extensive work has sought to explain this word order variation across languages. However, the existing approaches are not able to explain coherently the frequency distribution and evolution of word order in individual languages. We propose that variation in word order reflects different ways of balancing competing pressures of dependency locality and information locality, whereby languages favor placing elements together when they are syntactically related or contextually informative about each other. Using data from 80 languages in 17 language families and phylogenetic modeling, we demonstrate that languages evolve to balance these pressures, such that word order change is accompanied by change in the frequency distribution of the syntactic structures that speakers communicate to maintain overall efficiency. Variability in word order thus reflects different ways in which languages resolve these evolutionary pressures. We identify relevant characteristics that result from this joint optimization, particularly the frequency with which subjects and objects are expressed together for the same verb. Our findings suggest that syntactic structure and usage across languages coadapt to support efficient communication under limited cognitive resources.

The world’s languages show considerable variation in syntactic structure (1–3). A key syntactic dimension that languages vary along is word order. Linguists have long classified languages according to their basic word order or the order in which they typically order verbs, subjects, and objects (1). About 40% of the world’s languages are classified as following subject–verb–object (SVO) order (as in English: “dogs bite people”), and 40% are classified as following subject–object–verb (SOV) order (as in Japanese: inu-wa hito-o kamimasu [“dogs people bite”]) (4) (Fig. 1 has an illustration). Other orders, such as verb–subject–object (VSO; as in Modern Standard Arabic: taʕad^ʕ:u l-kila:bu n-na:sa [“bite dogs people”]), are much less common. Many languages have more than one ordering or exhibit historical change in their word order, although typically with one of the orderings being the most common. This ordering is considered the basic word order of a language in the typological literature (1, 5). Why do languages vary in word order the way they do, and what explains the evolution of word order? Here, we present a unified theory that addresses these long-standing questions.

Fig. 1.

Illustrations of crosslinguistic word order variation and the theoretical proposal. (A) English (SVO; Center) and Japanese (SOV; Right) linearize different syntactic structures into strings of words. Numbers below arcs indicate dependency length. Syntactic structures in A, 1 contain both a subject and an object; those in A, 2 only express one of the two. The percentage bars show relative usage frequencies computed from large-scale English and Japanese text corpora (SI Appendix, Fig. S9). In A, 1, English achieves shorter dependency length: two compared with three in Japanese. In A, 2, both languages achieve the same dependency length. Therefore, structures as those in A, 2 are more favorable for dependency length minimization in SOV languages than those in A, 1. Structures, such as those in A, 2, are considerably more frequently expressed in Japanese. (B) SOV makes the beginning and end of clauses more predictable from the local context. For instance, in this example, the end of a clause is always a verb, increasing the mutual information with the subsequent word, irrespective of whether the clause expresses both subject and object as in B, 1, or only one of the two, as in B, 2. Therefore, SOV tends to be more favorable for IL.

Different theories have been proposed for the word order variation across languages. The low frequency of object-initial orderings (e.g., object–subject–verb [OSV]; “human–dog–bites”) arguably has satisfactory explanations in terms of the meanings and functions typically associated with objects and subjects (e.g., ref. 6), but there is no consensus on the frequency distribution of SVO and SOV. Some work has argued that SOV is the default order in the history of language and that SVO emerged later (7–11), although phylogenetic simulation suggests that languages can cycle between these two orders in their historical development (12). Other work suggests there is a tension between different cognitive pressures that favor SVO and SOV (13, 14), but these accounts do not predict word order on the level of individual languages. So far, there exists no theory that coherently explains the principles underlying both crosslinguistic variation and evolution in word order.

One promising view suggests that crosslinguistic variation is constrained by the functional pressures of efficient communication under limited cognitive resources (15–18). Under this view, the structure of language in part reflects the way that language is used (19–22) and adapts to optimize informativeness and effort for human communication (23–25). Work in this paradigm has argued that many properties of language arise because they make language efficient for human language use and processing. Several studies have shown in various domains that the grammars of human languages are more efficient than the vast majority of other logically possible grammars (26–29). Prior work has also shown that several of the known near-universal properties of languages hold in most logically possible languages that are also highly efficient and used this fact to argue that evolution toward efficiency explains why these properties are near universal (30–33). However, existing efficiency-based approaches to grammatical typology leave open two key questions. First, work in this paradigm focuses on cross-sectional studies, suggesting that languages are relatively efficient typically without answering how languages come to be efficient over time. Second, the idea that languages are shaped by efficiency optimization does not directly explain why they vary in their grammatical structure: for instance, why both SVO and SOV are frequently attested across the world’s languages. In some domains, differences among languages have been interpreted as reflecting different optima or points along a Pareto frontier (17, 31). However, it is currently unknown whether this perspective also applies to syntax and word order and in particular, to basic word order.

Theoretical Proposal

We address the open questions regarding word order variation and evolution using a large-scale phylogenetic analysis of 80 languages from 17 families and contributing the following theoretical view. We propose that crosslinguistic variation in word order reflects a tendency for languages to trade off competing pressures of communicative efficiency. This tendency is a product of an evolutionary process, whereby different languages are functionally optimized in both their grammatical structure and the way they are used. As such, grammar and usage should evolve together to jointly maintain efficiency, reflecting a process of coadaptation between grammar and usage.

Our proposal is grounded in prominent efficiency-based accounts of word order that are centered around various locality principles. These accounts assert that syntactic elements are ordered closer together when they are more strongly related in terms of their meaning and function (23, 34–37). Recent work has specifically established two locality principles in word order typology. The first principle is dependency locality (DL), which is the observation that languages tend to order words to reduce the overall distance between syntactically related words (23, 26, 27, 36, 38). DL can be justified in terms of parsing efficiency (23), memory efficiency (39), and general communicative efficiency (33). The second locality principle is information locality (IL), which holds that words are close together if they contain predictive information about each other (29, 40–42). IL is grounded in the well-established finding that words are hard to process for humans to the extent that they are hard to anticipate from preceding context (43, 44) under constraints of human memory (41). Both principles have individually received substantial support from crosslinguistic corpus studies (26, 27, 29). In a recent study, Gildea and Jaeger (28) even showed for five languages that they optimize a trade-off of DL and an IL-like quantity, although this finding has not been replicated on a larger sample yet.

The two locality principles we described can make opposing predictions concerning basic word order (Fig. 1). DL should tend to favor SVO order over SOV (14) because it ensures that subject (S) and object (O) are both close to the verb (V). In contrast, IL may tend to favor SOV order over SVO because uniform placement of S and O makes the beginning and end of each sentence easier to predict from local information. We thus hypothesize that the crosslinguistic variation in basic word order emerges from an evolutionary process in which languages resolve the tension between these two pressures in different ways.

To illustrate our proposed theory, we consider a simple transitive sentence, such as dogs bite people (Fig. 1A). DL is defined formally in terms of dependency grammar (45–49). In this formalism, the syntactic structure of a sentence is drawn with directed arcs linking words—called heads—to those words that are syntactically subordinate to them—called dependents. For instance, arcs link the verb “bite” to its subject “dogs” and object “people.” The length of an arc is one plus the number of other words that it crosses. The dependency length of an entire sentence is the sum of the lengths of all dependency arcs.

The grammars of languages specify how such syntactic structures are linearized into strings of words. Fig. 1 shows how the same syntactic structures are linearized differently by the grammars of English (SVO) and Japanese (SOV). In a simple sentence as illustrated in Fig. 1A, SVO order results in overall lower dependency length than SOV (five instead of six).

The extent to which these general predictions are valid in a particular language will depend on the precise frequency at which speakers of a language use different syntactic structures. For example, the difference between SVO and SOV order is neutralized for DL in sentences like in Fig. 1 A and 2, where only a subject or an object is expressed. Conversely, there are also syntactic structures where SOV achieves strictly shorter dependency lengths. Therefore, DL favors SVO more strongly when a language frequently coexpresses both the subject and object of the same verb (Fig. 1).

IL is defined in terms of the information-theoretic predictability of words from their recent prior context. We adopt a simple formalization in terms of maximizing the mutual information between adjacent words; SI Appendix, section S1.1 has other operationalizations of IL. SOV can be advantageous for IL because a uniform verb-final ordering makes the beginning and end of each clause more predictable (Fig. 1B).

Which pressure will prevail in shaping a language depends not only on which pressure the language optimizes more strongly but also, on the frequency with which different syntactic structures are used. The average values for DL and IL achieved for a language depend on both the linearizations provided by grammars and the frequencies at which different syntactic structures are used. Languages differ not only in the ways that they linearize these syntactic structures but also, in the frequencies at which speakers utilize them. For instance, syntactic structures, such as those in Fig. 1 A, 1 and B, 1, are used at significantly higher frequencies by speakers of English than speakers of Japanese. Given a distribution over syntactic structures, we can identify which grammar orders them in such a way to achieve optimal average dependency length, optimal average IL, or any linear combination of the two. This gives rise to a Pareto frontier of grammars.

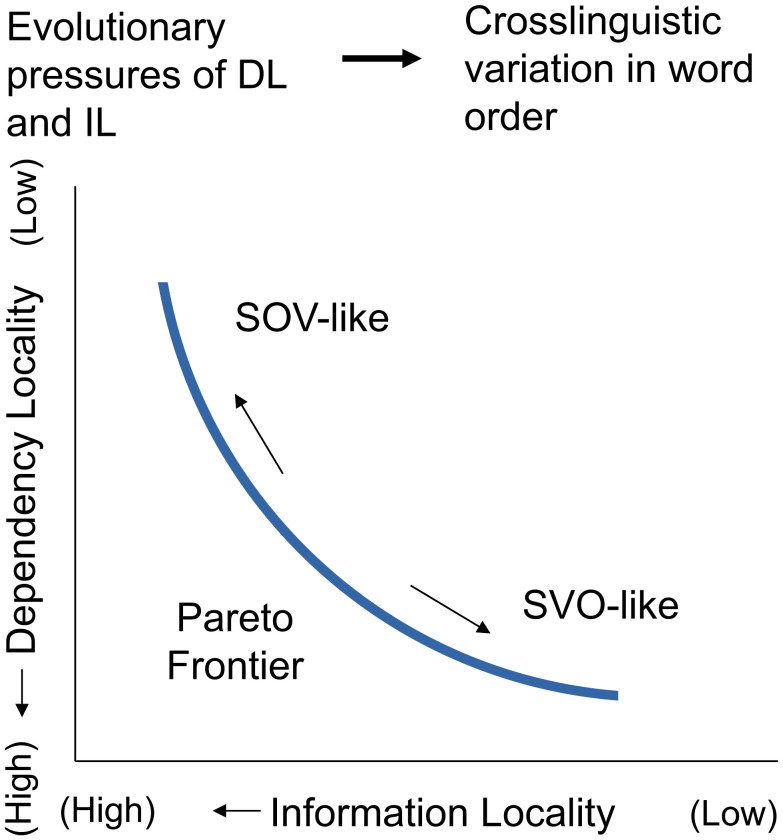
We summarize our proposal with the following two theoretical predictions (Fig. 2). First, languages evolve to maintain a relatively efficient balance between DL and IL, and second, this evolutionary process jointly affects usage frequencies (which syntactic structures are chosen by speakers) and grammar (how they are linearized). This means that the actual word orders used by languages should be close to the most efficient possible grammar given the distribution over syntactic structures.

Fig. 2.

Illustration of our theoretical proposal. Our theory postulates that word orders of languages trade off the competing evolutionary pressures of DL and IL. The space of logically possible word orders is bounded by a Pareto frontier of optimal orders. Along the Pareto frontier, SVO-like orders tend to optimize DL more strongly than SOV-like orders do. The precise distribution of orderings along the frontier is determined by language-specific usage frequencies, which evolve together with word order in a process of coadaptation so that the real order used in a language resembles the orderings more prevalent along the frontier.

Results

We first evaluate our proposed theory in a synchronic setting using data from 80 languages. We compute, for each language, which basic word orders are most efficient given its usage distribution as recorded in large-scale text corpora. We then use a diachronic model of drift on phylogenetic trees to assess whether languages have evolved historically toward states where syntactic usage frequency and basic word order are aligned.

To begin with, we compared the efficiency of the attested orderings with both a null distribution of baseline grammars and the Pareto frontier of optimized grammars. We represent grammars using the established model of counterfactual order grammars introduced by Gildea and Temperley (50). These are simple parametric models specifying how the words in a syntactic structure are linearized depending on their syntactic relations. They specify the orders not only of subjects and objects but also, of all other syntactic relations annotated in the syntactic structures, such as adpositions, adjectival modifiers, or relative clauses. For instance, such a grammar may specify that subjects follow or precede verbs, that adpositions are pre- or postpositions, and that adjectival modifiers follow or precede nouns (Materials and Methods has details). Given a frequency distribution over syntactic structures, any grammar achieves a certain average dependency length and IL across the syntactic structures from that distribution.

We compare two groups of word orders: SVO-like order, where S and O are ordered on different sides of the verb, and SOV-like order, where S and O are ordered on the same side of the verb. Languages can fall on a spectrum between languages with entirely strict SVO order and languages with entirely strict SOV order (51). English is close to one end of the spectrum with dominant SVO order, with rare exceptions (e.g., stylistically marked verb–subject (VS) order in “then came a dog”). Japanese falls entirely on one end of the spectrum, allowing only SOV and OSV order. Many languages occupy intermediate positions. For instance, in Russian, all logically possible orderings of S, V, and O can occur, although with different frequencies.

We quantify the position of an individual language on the continuum between SVO and SOV using a quantitative corpus-based metric called subject–object position congruence. This metric indicates the chance that two randomly selected instances of S and O from a corpus—not necessarily from the same sentence—are on the same side of their respective verbs. This number is 1 in strict SOV languages, like Japanese; close to 0.5 in languages with flexible word order; and close to 0 in English.

Word Order Variation Reflects Competing Pressures.

Fig. 3A shows the positions of the 80 languages in the efficiency plane spanned by IL and DL. In order to make efficiency planes comparable across different corpora, we rescaled the distance between the optimal IL (DL) value and the mean of the baseline to one. Contour lines indicate the density of sampled possible grammars; the vast majority of the $\approx {10}^{43}$ possible grammars concentrates in a range of IL and DL separated from the Pareto frontier, and only a vanishing proportion of grammars extends to the frontier. Consistent with findings from prior work on IL and DL (28, 29, 52), the attested grammars occupy the range between the baseline samples and the frontier, making them more efficient than almost all other possible grammars. Each language outperformed at least either $\ge$ 90% of baselines on DL or $\ge$ 90% on IL. All languages outperformed the median baseline on DL, and all but three outperformed the median baseline on IL. Some languages are beyond the average curve because their frontiers are to the left of the average curve. There are also languages that are more efficient than all computationally optimized grammars within the formalism of word order grammars, suggesting they achieve even higher efficiency through flexibility in word order (SI Appendix, section S28).

Fig. 3.

Summary of the efficiency analysis of crosslinguistic word order variation. (A) All 80 languages in the plane spanned by IL (x axis) and DL (y axis), with 12 languages annotated (SI Appendix, Fig. S16 shows results with all language names). IL and DL are scaled to unit length across languages; SI Appendix, section S22 has raw results. Positions closer to the lower left corner indicate higher efficiency. Colors indicate subject–object position congruence as attested in corpus data. The contour lines indicate a Gaussian fit to the distribution of baseline grammars averaged across languages. The curve indicates the average of the Pareto frontier across all 80 languages. Some languages are beyond the curve because they utilize word order flexibility to achieve higher efficiency than any fixed ordering grammar. Colors along the frontier indicate the average subject–object position congruence of counterfactual grammars along the frontier of maximally optimal grammars. (B) The same information as shown in A with languages classified as SOV (Left) and SVO (Right) in the typological literature. The distribution of optimal grammars along the frontier overrepresents SOV-like grammars in SOV languages and SVO-like grammars in SVO languages.

The attested grammars of the languages and the possible counterfactual grammars along the Pareto frontier are colored by their subject–object position congruence as found in corpus data. DL was correlated with congruence, such that languages with higher subject–object position congruence optimized DL less strongly ($R=-0.47$, 95% CI $[-0.63,-0.28],\hspace{0.17em}P={10}^{-5}$; Spearman’s $\rho =0.45,\hspace{0.17em}P=3·{10}^{-5}$). This agrees with recent findings that SOV languages optimize DL less strongly (27, 53). To account for the statistical dependencies between related languages more rigorously, we grouped the 80 languages into 17 maximal families (or phyla) describing maximal units that are not genetically related to each other (Materials and Methods) and performed a regression analysis where we entered per-family random slopes and intercepts. This analysis confirmed a significant effect of congruence on DL [$\beta =-0.37$, 95% credible interval (CrI) $[-0.62,-0.08],\hspace{0.17em}P(\beta \ge 0)=0.009$, Bayesian $R^2=0.45$]. Subject–object position congruence did not correlate with IL (R = 0.09, P > 0.05).

Fig. 3 also shows an analogous result for the counterfactual grammars along the frontier. Among those, subject–object position congruence is higher when DL is not optimized and IL is strongly optimized; it is lower when DL is most optimized. In a mixed effects analysis with per-family random effects, subject–object position congruence was significantly higher at the end optimizing for IL (on the left) than at the end optimizing for DL [on the bottom; difference between the two: $\beta =0.38$, 95% CrI $[0.25,0.53],\hspace{0.17em}P(\beta \le 0)<0.0001$].

In Fig. 3B, we plot these results specifically for languages classified as SOV and SVO in the typological literature (54, 55). SVO languages tend to optimize DL more strongly. Note that some of the 80 languages belong to less common categories, such as VSO; SI Appendix, Fig. S17 shows results for those categories. We also observe that subject–object position congruence tends to be higher along the frontier for SOV languages than SVO languages. This observation suggests coadaptation. Language users tend to produce frequency distributions of syntactic structure for which the real word order of the language is efficient.

To test this idea about coadaptation more rigorously, we computed the average subject–object position congruence along the frontier. In Fig. 4A, we compare average congruence along the frontier with attested congruence. The correlation between the average congruence and the attested congruence was R = 0.49 (95% CI $[0.31,0.65],\hspace{0.17em}P=4·{10}^{-6}$; Spearman’s $\rho =0.49,\hspace{0.17em}P=4·{10}^{-6}$). The correlation was substantially lower when considering the density not along the full frontier but at the two end points, where only IL or DL is optimized (Fig. 4 B and C). The correlation between the average density and the congruence was significant in a by-families mixed effects regression predicting the attested congruence from the average density [$\beta =0.62$, 95% CrI $[0.28,1.0],\hspace{0.17em}P(\beta \le 0)=0.0011$, Bayesian $R^2=0.52$]. Analogous regressions predicting the attested congruence from the density at either of the end points yielded inferior model fit (Bayes factor 32 compared with the IL-optimized end point, 101 compared with the DL-optimized end point). A possible concern is that a majority of the 80 languages belongs to the Indo-European family. We confirmed the presence of coadaptation in an analogous analysis excluding Indo-European [$\beta =0.72$, 95% CrI $[0.25,1.18],\hspace{0.17em}P(\beta \le 0)=0.0026$, Bayesian $R^2=0.74$], showing that this result is not driven by this family.

Fig. 4.

Coadaptation between grammar and usage (SI Appendix, Fig. S11 has further results). Real subject–object position congruence (x axis) is compared against the average subject–object position over the entire Pareto frontier (A), at the end optimizing only for IL (B), and at the end optimizing only for DL (C). The lines indicate the diagonal. Optimizing for IL or DL tends to over- and underpredict SOV-like orderings, respectively. Considering the joint optimization of both factors results in better prediction of real orderings.

Word Order Evolves to Maintain Communicative Efficiency.

We have provided evidence that variability in basic word order reflects competing pressures of IL and DL resolved differently across languages through coadaptation of grammar and usage. However, this does not rule out the possibility that the observed correlations are artifacts of the common histories of languages descended from common ancestors.

To test whether the observed patterns arise from the process of language evolution, we performed a phylogenetic analysis on the evolution of efficiency and word order. Phylogenetic analyses have previously been applied to studying the historical evolution of languages (e.g., refs. 56–59), including the evolution of word order patterns (12, 60).

A phylogenetic analysis allows us to construct an explicit model of language change drawing on two sources of information. First, in several cases, our dataset includes data from different stages of the same language (such as Ancient Greek and Modern Greek). Such datasets provide direct evidence of historical development. Second, using phylogenetic information, the model can also draw strength from contemporary language data. Data from related languages may permit inferences about their (undocumented) common ancestor and thus, about possible trajectories of historical change (12, 60, 61).

In order to understand how basic word order evolves, we used a model of drift (or random walks) on phylogenetic trees (61–63) to model how grammar and usage frequencies of a language evolve over time. We describe the state of a language L at time t as a vector ${\xi }_{L,t}$ encoding 1) the efficiency of the language as parameterized by IL and DL, 2) its subject–object position congruence, and 3) the average subject–object position congruence along the frontier. Whenever a language splits into daughter languages, the point ${\xi }_{L,t}$ continues to evolve independently in each daughter language. As the components of ${\xi }_{L,t}$ are continuous, we model their change over time using a random walk given by an Ornstein–Uhlenbeck process (64–66) (Materials and Methods has details). This process is parameterized by rates of change in the traits, correlations between the changes in different traits, and the long-term averages of the traits (62, 65, 67). This model allows us to model the development of word order both in the real language and across the optimization landscape within a single model.

We obtained phylogenetic trees for the 80 languages in our sample from Glottolog (68) (Materials and Methods) and inserted historical stages as inner nodes in these trees. We fitted the parameters of the model using Hamiltonian Monte Carlo methods (Materials and Methods has details).

The long-term behavior of the Ornstein–Uhlenbeck model is encoded in its stationary distribution, which describes the likely outcomes of long-term language evolution (69). First, language evolution maintains relative efficiency; the mean of the stationary distribution was estimated at $\mu =0.35$ (95% CrI $[0.22,0.45]$) of the distance between the maximum IL and the mean of the baselines for IL and $\mu =0.28$ (95% CrI $[0.21,0.35]$) of the distance between the maximum DL and the baseline mean for DL, with SDs 0.36 (95% CrI $[0.3,0.44]$) for IL and 0.24 (95% CrI $[0.2,0.3]$) for DL well separated from the less efficient bulk of possible grammars. High congruence was correlated with decreased efficiency in DL [$R=-0.31$, 95% CrI $[-0.48,-0.14],\hspace{0.17em}P(R>0)=0.0004$]. Second, attested and average congruences were substantially correlated [R = 0.36, 95% CrI $[0.19,0.53],\hspace{0.17em}P(R\le 0)<0.0001$], confirming the presence of coadaptation between word order and usage frequencies in resolving the competing pressures of IL and DL. When excluding the Indo-European family, there continued to be a correlation between congruence and DL [$R=-0.33$, 95% CrI $[-0.61,0.00],\hspace{0.17em}P(R\ge 0)=0.026$] and—more importantly—substantial evidence for the presence of coadaptation [correlation between attested and average optimized congruence: R = 0.39, 95% CrI $[0.10,0.65],\hspace{0.17em}P(R\le 0)=0.005$] (SI Appendix, section S8 has further details).

While the model shows that evolution maintains efficiency, it might be the case that, once languages are close to the frontier, most possible changes would keep languages in that area so that apparent optimization might be simply the result of neutral drift rather than a pressure toward increasing efficiency. To rule out this possibility, we compared the model with neutral drift, which we simulated by iteratively flipping randomly chosen pairs of syntactic relations with minimally differing weights in the grammar. Results are shown in Fig. 5A (SI Appendix, section S9 has further results). For each grammar, we created 30 chains with 200 changes each. Grammars close to the frontier quickly and consistently move toward the baseline distribution, with very few chains improving efficiency even temporarily. We contrast this with sample trajectories from the fitted phylogenetic model (Fig. 5B); these stay along the frontier and move toward it when grammars are inefficient. This provides evidence that language evolution selects specifically for grammatical changes that maintain or increase efficiency.

Fig. 5.

A comparison of fitted phylogenetic drift model (B) against random mutations in grammars (A). The analysis is for 40 grammars close to the frontier (orange) and 40 samples from the baseline distribution (red), each evaluated on the tree structure distribution of 1 of the 80 languages. Arrows denote sampled change due to 200 mutations (A) or $\approx$ 200 y of language change (B). The fitted model predicts that grammars stay along the frontier and that inefficient grammars move toward it. In contrast, random mutations drive grammars toward the baseline distribution.

We visualize the model fit on language families in our sample in Fig. 6. We plot maximal families (phyla) except within the well-represented Indo-European family, where we plot smaller units. In addition to the attested languages, we also show historical trajectories as reconstructed by the phylogenetic analysis. For each family, we show the average congruence across languages.

Fig. 6.

Historical evolution within language families. All families (maximal phyla or subgroups within the well-represented Indo-European family) with at least three attested languages in the dataset are shown. Panels 2 to 6 show subgroups of Indo-European. For each family, we show the average of the Pareto frontier and of the average congruence on the frontier and behind it. Large full dots indicate attested languages, while small faint dots indicate positions and orderings of historical stages as inferred by the phylogenetic analysis. Languages evolve in the area between the baselines and the frontier. Basic word order tends to match the order most prevalent among optimal grammars. The prevalence of orderings along the frontier varies between families, indicating coadaptation between grammar and usage.

The families illustrate the findings of the analysis. First, languages evolve in the area between the baseline samples and the frontier. Second, evolution toward higher DL goes hand in hand with lower subject–object position congruence. Third, languages with high subject–object position congruence, such as the Turkic languages, also represent such possible grammars more strongly along the Pareto frontier of optimal possible grammars. SI Appendix, section S24 has analyses of historical change in individual languages, which suggest that they either change toward the optimal frontier or stay near optimal throughout history.

A well-known variable covarying with word order is case marking. Languages with case marking are more likely to have free word order, and loss of case marking has been argued to correlate with word order becoming more fixed or shifting toward SVO (70); conversely, SOV languages mostly have case marking (1). This has a clear functional motivation because case marking can distinguish subjects and objects when order does not. This raises the question of whether our results can be explained away by assuming that both grammar and usage change in response to changes in case marking. We coded the 80 languages for the presence of case marking distinguishing subjects from objects (71). We then conducted a version of the phylogenetic analysis where languages are allowed to concentrate in different regions depending on the presence of case marking. The rates of change and the long-term averages were allowed to depend on the presence or absence of case marking, and only the correlations between short-term changes in the different traits remained independent of case marking. We found that the phylogenetic analysis continued to predict correlations in changes of word order and DL and in changes of usage and word order (SI Appendix, section S12). Changes were correlated in DL and congruence [$R=-0.39$, 95% CrI $[-0.60,-0.18],\hspace{0.17em}P(R\ge 0)<0.0001$] and in attested and average optimized congruence [R = 0.49, 95% CrI $[0.29,0.67],\hspace{0.17em}P(R\le 0)<0.0001$].

Relation between Usage and Word Order.

Our results provide evidence that variation in basic word order results from an evolutionary process trading off competing pressures of DL and IL and that languages resolve these via coadaptation between usage and basic word order. In what aspects of usage do languages vary or change that reflect this coadaptation? We predict that languages favor SOV-like orders more when they do not frequently coexpress subjects and objects on a single verb. Indeed, it has been argued, based on evidence from Turkish and Japanese, that SOV languages omit arguments or use intransitive structures more frequently than SVO languages do (72–74), although this might not hold for Basque (75). We tested this idea on a larger scale using the corpora in our sample. We calculated what fraction of verbs simultaneously realize a subject and an object, out of all verbs realizing at least one of them. In a linear mixed effects models, with the by-family intercept and slope, attested subject–object position congruence was predictive of this fraction [$\beta =-0.11$, SE = 0.04, 95% credible interval $[-0.20,-0.03],\hspace{0.17em}\text{P}(\beta >0)=0.006$, Bayesian $R^2=0.18$] (Materials and Methods has details). Optimized subject–object position congruence was also predictive of this fraction [$\beta =-0.23$, SE = 0.05, 95% credible interval $[-0.33,-0.13],\hspace{0.17em}\text{P}(\beta >0)<0.0001$, Bayesian $R^2=0.32$]. This shows that languages differ in the rate at which they coexpress subjects and objects and that this is a factor through which frequency and word order can influence each other.

We also found an association between order and coexpression within individual languages. Languages with word order flexibility tend to order subjects differentially depending on the presence or absence of an object in a way that is consistent with optimizing DL (SI Appendix, section S14).

Discussion

We have investigated the frequency distribution and historical evolution of word order across languages. Languages evolve to maintain relative efficiency for IL and DL compared with the vast majority of other logically possible grammars. We found that variation in basic word order emerges from these two competing pressures, resolved differently across languages through a process of coadaptation between grammar and usage.

Our results go beyond existing efficiency-based accounts of word order in two ways. First, extending the cross-sectional synchronic comparison, we explicitly model the evolutionary process through which languages maintain efficiency. Second, we make specific predictions for individual languages based on their distributions of syntactic structures. Ref. 76 proposes that the frequency of different basic word order patterns is predicted by a tendency to avoid peaks and troughs in the rate at which information is transmitted (although ref. 77 reports a replication with diverging results). The model in ref. 76 accounts for the low frequency of object-initial orders, but it underpredicts SOV and predicts SVO as the most efficient order even when it is applied to Japanese (i.e., an exemplary language for SOV order). In comparison, our account explains the language dependence of basic word order. For Japanese, SOV-like orderings are predominant along the Pareto frontier (SI Appendix, section S22), in contrast with the model in ref. 76 that predicts SVO across languages.

Among the previous efficiency-based proposals, the one most closely related to our study, ref. 14, agrees with our proposal that SVO is favored by DL but proposes that SOV is favored by a pressure toward predictability of the final verb. Despite the seeming similarity to our theoretical proposal, there are several key differences. First, the underlying psycholinguistic theories (43, 44) refer to the predictability of all words in a sentence and do not warrant the assumption that it is specifically the verb that should be more predictable. Second, while the arguments in ref. 14 were theoretical in nature, our proposal here is grounded in large-scale empirical evidence, including both synchronic and diachronic analyses. Specifically, our work reveals strong empirical evidence for coadaptation as a key factor in resolving competing pressures.

The variation between SOV and SVO basic word orders stands in interesting contrast to some other aspects of word order, where a clear preference is observed across languages. While the relative position of the subject relative to the object is variable, several other syntactic relations have a typologically stable position relative to the object (1, 78). These patterns, known as Greenberg’s correlation universals, are predicted uniformly by both DL (23, 36, 37) and IL (SI Appendix, section S21). The interaction of IL and DL thus explains both why the order of those syntactic relations shows uniformity across languages and why basic word order shows variability. The process of coadaptation that we discover in basic word order might also operate in other aspects of grammar, and it might explain the observation that language families appear to systematically differ in which subset of Greenberg’s correlations they support (60).

Our results on coadaptation do not speak to the causal direction between usage and grammar in changes in individual languages. The process of coadaptation as we identified is consistent with causal influence in different directions, with the possibility of a third hidden causal factor. In the future, the availability of more historical data with high temporal resolution might make it possible to explore the causal direction of change in individual languages. This might also make it possible to determine whether further aspects of usage beyond the coexpression of subjects and objects are affected by coadaptation.

A limitation of our work is that corpus data with syntactic annotation are available primarily for European and Asian languages. Alternative approaches to estimating usage distributions could leverage either manual annotation of text for relevant quantities, such as subject–object coexpression, or automatically projecting syntactic annotation to other languages on multilingual text, such as Bible translations. However, those approaches would either not reflect usage distributions in sufficient detail to identify optimized orderings or risk reflecting nonidiomatic properties of translated text.

Our phylogenetic analysis confirmed that grammar and usage patterns evolve together so that the real order distribution found in a language tends to resemble that dominating along the Pareto frontier of optimal orderings. This process of coadaptation highlights that grammar and usage frequencies can interact in the evolution of language. This finding has connections to findings in some other areas. Existing work has suggested that communicative need, or how frequently a linguistic element is used by its speakers, differs across languages and that this is responsible for some of the differences observed among the structures of different languages (79–81). Ref. 79 provides evidence that differences in social structure account for differences in the complexity of deictic inflection across languages; ref. 80 shows that languages in small-scale societies tend to have higher inflectional complexity. It has been argued that color-naming systems are influenced by the way color names are used (82). Ref. 81 suggests that color-naming systems differ between industrialized and nonindustrialized societies due to differences in the usefulness of color in a society, and ref. 83 shows that vocabulary about the environment depends on the climatic conditions in which a language is spoken. In syntax, recent work argues that adjective use (84) and comprehension (85) interact with word order in a way beneficial for communicative efficiency. The coadaptation account is also compatible with evidence that human language comprehension itself adapts to the statistics of the language (86). Related to our findings on the correlation between DL and subject–object position congruence, ref. 87 finds that SOV languages tolerate longer head-final dependencies, attributing this to adaptation of the human language processing system.

It has been argued that there is an inherent directionality in the evolution of basic word order and that SOV is the default or original order in the history of language. Many historically documented word order changes have gone from SVO to SOV, and the protolanguages of several extant families are thought to have been SOV (7, 9, 12). However, only a small fraction of all word order changes is directly documented through written evidence of historical languages. Ref. 12, using phylogenetic modeling, found that languages can cycle between SOV and SVO over long-term development, with little bias toward either order. The strongest evidence that SOV might be the “default” order comes from recently emerged sign languages (8, 88–90) and from gesturing tasks (10, 13). If this is true, then our proposed theory would predict that emerging languages tend to use those structures that maximize the IL advantages of SOV languages. Indeed, multiple studies report high frequencies of utterances where only one argument is expressed in recently emerged sign languages and home-sign systems (88, 89, 91, 92) and in sign languages more generally (93).

Assuming that SOV is the historically earlier order, some studies have further argued that SVO order later arises to avoid ambiguity in communicating reversible events (11, 94) or to communicate more complex structures (13, 14, 95) and intensional predicates (96, 97). In agreement with our proposed theory, this view also explains the distribution of SOV and SVO in terms of a tension between distinct cognitive and communicative pressures favoring SOV and SVO, respectively (13). However, those proposals do not explain the fine-grained per-language distribution of word order patterns since they do not explain why specific languages have SVO or SOV order. Our theory provides a more precise account of the fine-grained distribution because it explicitly accounts for the language dependence of word order, providing per-language predictions of optimal word orders through the process of coadaptation between grammar and usage.

Our work combines evidence from richly annotated syntactic corpora with phylogenetic modeling. This approach can be generally useful for characterizing the fine-grained evolution of grammar in the world’s languages.

Materials and Methods

Ordering Grammars.

The counterfactual order grammars have a weight in $[-1,1]$ for every 1 of the 37 syntactic relations annotated in the Universal Dependencies 2.8 corpora (e.g., subject, object). Dependents of a head are ordered around it in order of these weights; dependents with negative weights are placed to the left of the head, and others are to its right. SI Appendix, section S2 has more details and examples.

Locality Principles.

We compute dependency length in terms of the Universal Dependencies 2.8 representation format.

IL can be formalized in multiple ways grounded in information-theoretic models of human language processing (29, 41). We adopt a simple formalization in terms of maximizing $\text{I}[X_t:X_{t+1}]$ or the mutual information between adjacent words. SI Appendix, section S1.1 has other formalization choices.

Inferring Frontier and Congruence along Frontier.

We create approximately optimal grammars using the hill-climbing method in ref. 50 and the gradient descent method in ref. 33. The hill-climbing method is applicable to IL and DL and any combination; the gradient descent method is fast but only applicable to DL. SI Appendix, section S2.2 has details. These optimization methods result in approximately optimal grammars populating the area between the baselines and the Pareto frontier. We ran these optimization methods at linear combinations $(1-\lambda )·\text{DL}+\lambda ·\text{IL}$ for $\lambda =0,0.25,0.5,0.75,1$, obtaining at least 150 approximately optimal samples per language. Due to the difficulty of high-dimensional combinatorial optimization, determining the exact Pareto frontier is not feasible; we thus approximated it as the convex hull of the approximately optimized grammars. For each language, we further randomly constructed at least 75 baseline ordering grammars. For each language, we interpolated subject–object position congruence throughout the efficiency plane using a Gaussian kernel applied to the approximately optimized grammars and the baseline grammars, with scales chosen for each language using leave-one-out cross-validation (SI Appendix, section S3). SI Appendix, section S22 has raw results.

Data.

We drew on the Universal Dependencies 2.8 tree banks (98), including every language for which data with at least 10,000 words were available while excluding code-switched text, text produced entirely by nonnative speakers, and text only reflecting specific types of sentences (e.g., questions). Data for one further language (Xibe) became available after completion and were included. For the phylogenetic analysis, we included additional historical languages as follows. In addition to the data available in Universal Dependencies 2.6, we added Old English, Medieval Spanish, and Medieval Portuguese dependency tree banks in a slightly different but comparable version of dependency grammar (99). We further split two tree banks spanning multiple centuries (Icelandic and Ancient Greek) into multiple stages based on documented word order changes (SI Appendix, section S25). While there are some other historical tree banks, such as the Penn Parsed Corpora of Historical English (100), they are not in the Universal Dependencies format; calculating dependency length is highly nontrivial without a high-quality conversion.

We obtained the topology of phylogenetic trees from Glottolog (68), inserted documented historical languages as inner nodes, and assigned dates for the other inner nodes based on the literature (SI Appendix, section S6 has details).

Bayesian Regression Analyses.

We conducted Bayesian inference for mixed effects analyses using Hamiltonian Monte Carlo in Stan (101–103). We assumed the prior N(0, 1) for the fixed effects slopes, $N(0.5,1)$ for the intercepts, weakly informative Student’s t priors (ν = 3 degrees of freedom, location 0, and scale $\sigma =2.5$) for the SDs of the residuals and the random effects, and a Lewandowski–Kurowicka–Joe prior with parameter 1 (104) for the correlation matrix of random effects. SI Appendix, section S16 has details and results with more strongly regularizing priors. We computed Bayesian R² values following ref. 105. We report $P(\beta \le 0)$, the posterior probability that the coefficient is not positive, to quantify the fraction of the posterior supporting the hypothesis of a positive coefficient. The families in the random effects structure correspond to the maximal subgroups in the phylogenetic trees described in Data.

Model of Language Change.

We model the state of a language L as a tuple ${\xi }_L\in {\mathbb{R}}^4$ consisting of the position of the language in the efficiency plane spanned by DL and IL, the observed subject–object position congruence, and the average subject–object position congruence of optimized grammars.

A common choice in phylogenetic modeling of coevolving traits is correlated Brownian motion, also known as the independent contrasts model (62, 67). This model can quantify the correlation between pairs of traits (e.g., DL and position congruence) in evolution. To enable the model to capture biases toward specific parts of the parameter space (e.g., toward regions of high or low efficiency), we added a drift term that can model drift into a specific region. This leads to an Ornstein–Uhlenbeck process (64–66) described by the following stochastic differential equation for the instantaneous change of the state ${\xi }_{L,t}$ of a language L at a given time t:

$$\text{d}{\xi }_{L,t}=\mathrm{\Gamma }·({\xi }_{L,t}-\mu )\text{d}t+\sqrt{\mathrm{\Sigma }}\text{d}{B}_t,$$

where $\mu \in {\mathbb{R}}^4$ is a vector, $\mathrm{\Sigma }\in {\mathbb{R}}^{4\times 4}$ is a covariance matrix, $\mathrm{\Gamma }\in {\mathbb{R}}^{4\times 4}$ is diagonal with negative entries, B_t is Brownian motion in four dimensions, and $\sqrt{\mathrm{\Sigma }}\in {\mathbb{R}}^{4\times 4}$ is positive definite and symmetric such that ${(\sqrt{\mathrm{\Sigma }})}^2=\mathrm{\Sigma }$.

The first term, $\mathrm{\Gamma }·({\xi }_{L,t}-\mu )\text{d}t$, encodes deterministic drift and describes which region $\mu \in {\mathbb{R}}^4$ of parameter space languages tend to concentrate around in the long run.

The dynamics of stochastic change are described by the second term, $\sqrt{\mathrm{\Sigma }}\text{d}{B}_t$. Σ is the covariance matrix of instantaneous changes (69); its diagonal entries encode rates of random change in each dimension. The off diagonals Σ_ij encode correlations between the instantaneous changes in different dimensions (62, 67). Standard results (69) imply that the long-term stationary distribution is a Gaussian centered around the vector μ with a covariance Ω given as (SI Appendix, section S7.1)

$${\mathrm{\Omega }}_{ij}=\frac{{\mathrm{\Sigma }}_{ij}}{{\mathrm{\Gamma }}_{ii}+{\mathrm{\Gamma }}_{jj}}.$$

The Pearson correlation coefficient R between the ith and jth components (e.g., DL and position congruence) is then obtained by normalizing the corresponding off-diagonal entry by the individual variances of the two components:

$$R_{ij}=\frac{{\mathrm{\Omega }}_{ij}}{\sqrt{{\mathrm{\Omega }}_{ii}{\mathrm{\Omega }}_{jj}}}.$$

Without the first term (i.e., with $\mathrm{\Gamma }=0$), the simpler independent contrasts model (62, 67) would result. SI Appendix, section S10 has results from that simpler model and model comparison.

In the version controlling for case marking, the parameters $\mu ,\mathrm{\Gamma }$ are allowed to depend on the presence or absence of case marking. This model has no unique stationary covariance Ω across languages with and without case marking; hence, we computed the correlation coefficient R using the covariance matrix Σ of instantaneous changes instead of using Ω.

SI Appendix, section S7.1 has more on the calculation of the long-term stationary distribution, and SI Appendix, section S7.3 has the calculation of the correlations between short-term changes in different traits.

We conducted Bayesian inference using Hamiltonian Monte Carlo in Stan (101, 102). SI Appendix, section S7.2 has implementation details.

Data Availability

Optimized grammars for 80 languages have been deposited in GitLab (https://gitlab.com/m-hahn/efficiency-basic-word-order/) (106).