The stability and dynamics of computationally designed proteins

Abstract

Protein stability, dynamics and function are intricately linked. Accordingly, protein designers leverage dynamics in their designs and gain insight to their successes and failures by analyzing their proteins’ dynamics. Molecular dynamics (MD) simulations are a powerful computational tool for quantifying both local and global protein dynamics. This review highlights studies where MD simulations were applied to characterize the stability and dynamics of designed proteins and where dynamics were incorporated into computational protein design. First, we discuss the structural basis underlying the extreme stability and thermostability frequently observed in computationally designed proteins. Next, we discuss examples of designed proteins, where dynamics were not explicitly accounted for in the design process, whose coordinated motions or active site dynamics, as observed by MD simulation, enhanced or detracted from their function. Many protein functions depend on sizeable or subtle conformational changes, so we finally discuss the computational design of proteins to perform a specific function that requires consideration of motion by multi-state design.

Graphical Abstract

Graphical Abstract.

Introduction

Proteins are dynamic molecules, and their dynamics are critical to their functions. Enzyme active sites may close around their substrates, transporters change shape as they move substrates across a membrane, signaling proteins change conformation to bind a receptor or not and intrinsically disordered regions may organize in the presence of a particular substrate. Designed proteins adopt these sorts of motions too, some of which may have been intentionally engineered by the designer, and some not. Recent studies probing the dynamics of computationally designed proteins have begun to shed light on how designed proteins move, how their dynamics affect their stabilities and functions, and how their stability and dynamics depend on the technique by which they were designed. As protein designers work towards a particular functional goal or stability requirement, they may want to select a design strategy that produces protein dynamics compatible with these goals.

We will discuss here proteins designed using two general computational strategies, structure-based and sequence-based, and begin with a brief summary of these techniques. First, structure-based protein design begins with a preexisting or designed backbone scaffold, then computationally optimizes the amino acid side chain and its conformation at each position (Das and Baker, 2008; Huang et al., 2016; Korendovych and DeGrado, 2020). Alternatively, the critical residues may be oriented, the backbone designed to accommodate them and finally the remaining residues packed in Kries et al. (2013). Design of proteins to adopt multiple conformations requires modeling of the various states (Davey and Chica, 2017; Korendovych, 2018; Mandell and Kortemme, 2009). Second, consensus design and ancestral sequence reconstruction (ASR) are two sequence-based, computational techniques that use phylogenetic information from multiple sequence alignments (MSAs). Consensus design takes in the sequences of a family of proteins, aligns them in an MSA and assigns each residue of the new, consensus protein to be the most frequent amino acid found at that position (Lehmann et al., 2000; Porebski and Buckle, 2016; Sternke et al., 2020). ASR again takes in sequences of related proteins, builds a phylogenetic tree and predicts the protein sequences at the nodes, representing common ancestors (Risso and Sanchez-Ruiz, 2017; Thornton, 2004). Based on the reconstructed tree, it is possible to predict at what point in time the common ancestors could have existed.

Computational protein design occurs at the atomic- and residue-scale, and molecular dynamics (MD) simulations provide detailed structural and dynamic data at these scales. MD simulations can provide relevant insight to the success of the proteins in maintaining their designed conformations as well as data on the dynamics and conformations populated over time. MD simulations use Newtonian mechanics along with a force field and energy function to calculate the movements of a molecule’s atoms over time (Allen and Tildesley, 1989). These simulations provide structural data on the atomic level and femtosecond-to-microsecond timescales, allowing scientists to assess local and global protein properties (Hollingsworth and Dror, 2018; Karplus and McCammon, 2002). Although we focus this review on proteins assessed by MD, MD data becomes even more powerful when it can be validated and enhanced by complimentary experimental data to paint a full picture of protein stability and dynamics (Bottaro and Lindorff-Larsen, 2018).

In this review, we first discuss the structural basis of stability in computationally designed proteins as investigated by MD simulations. Next, we compare the dynamics of designed proteins, including coordinated motions and active site accessibility and preorganization, when dynamics were not explicitly considered in the design process. Finally, we discuss proteins designed to perform a function where the function depends on a conformational change or where insight to the functional success was provided by analysis of the protein’s dynamics. In conclusion, we discuss common stabilizing and dynamic properties of designed proteins based on the design strategy (Table I).

Table I.

Dynamic properties of computationally designed proteins

Designed protein	Design strategy	Dynamic properties	Reference(s)
Alpha-carbonic anhydrase	Insertion of strategic point mutations inspired by MD of a thermophilic homologue	Decreased RMSD/F, decreased SASA	Bharatiy et al., 2016
T4 lysozyme	Proteus-designed point mutant pairs	Increased interresidue contacts; Some stabilizing (ProTherm ΔΔG)	Barroso et al., 2020
Conserpin	Consensus design	More conformationally homogeneous (PCA), thermostable (Tm from CD), decreased salt bridges, decreased H-bonds, decreased SASA, decreased RMSF	Porebski et al., 2016
Consensus-HD	Consensus design	Decreased backbone motion (15N NMR), more stable (ΔG from CD)	Tripp et al., 2017
UVF	De novo design	Increased RMSD/F, increased unique side-chain contacts	Nguyen et al., 2019
15 scFvs and scAbs	RosettaAntibody	Some more thermostable (Tm from DSFa); Some resistant to heat deactivation at 70 °C (ELISA)	Lee et al., 2020
AYEdes	Rosetta de novo	Decreased RMSD/F, decreased SASA, increased secondary structure retention, increased contacts, more stable (ΔG from CD)	Dantas et al., 2007; Gill and McCully, 2019
Flu and botulism antigen-binding mini proteins	Rosetta de novo design, including backbone	Generally thermostable (Tm from CD); Antigen-binding residues were less dynamic in successful designs (backbone/side-chain RMSD)	Chevalier et al., 2017
7896 pocket proteins	Rosetta de novo design, including backbone	Stability score was correlated with total sequence hydrophobicity, Rosetta energy score, local sequence-structure agreement; Those that expressed tended to be thermostable (Tm from CD)	Basanta et al., 2020
ASR, consensus EF-Tu	ASR, consensus design	ASRs were more rigid (RMSD/F); Consensus had dynamic properties unlike naturally occurring proteins (PCA)	Okafor et al., 2018
AncSR1, AncSR2 steroid receptors	ASR	Older ASR had several highly dynamic regions (RMSD/F); ASRs maintained extant contact networks to mediate an allosteric conformational change	Okafor et al., 2020
Ancestral glycosidase	ASR	ASR was more flexible near the active site but core was equally rigid as extant (RMSF, b-factor, proteolysis)	Gamiz-Arco et al., 2021
Precambrian β-lactamases	ASR	Older ASRs were more flexible globally and in/around the catalytic pocket (RMSF, DFIb)	Zou et al., 2015; Risso et al., 2017
AncHLD-RLuc	ASR	ASR was less dynamic than extant proteins, and a highly mobile helix/loop led to increased active site accessibility (RMSD, Caver)	Chaloupkova et al., 2019
Nitrating P450 TxtE mutants	MD/HMMc-informed site-saturating mutagenesis	Mutants’ F/G loop stayed in the closed conformation more often (HMM,c TTN,d KD)	Dodani et al., 2016
4 LinB mutants	Caver + site-saturating mutagenesis	Mutant’s active site tunnel was open more often (MD, Caver, SAe)	Brezovsky et al., 2016
2 successful, 2 unsuccessful DIG-binding proteins (DIG10.2, DIG10.3, DIG12, DIG16)	Rosetta de novo	Successful designs had more rigid cavity entrances (RMSF), better-organized hydrophobic cores (SASA), smaller cavity volumes (POVME, RMSF), preorganized ligand-binding side chains (dihedral angles), stationary ligand in holo simulations (RMSD)	Tinberg et al., 2013; Barros et al., 2019
DFSc	Rational coiled-coil design	Preorganization of SQ•-compatible Zn2+ coordination state improves binding	Reig et al., 2012; Ulas et al., 2016
PS1	Rational coiled-coil design, Rosetta	Hydrophobic core is structured and ligand-binding region is flexible (HDX, water locations from MD)	Polizzi et al., 2017
ABLE	Rational coiled-coil design, COMBS, van der Mers, Rosetta	Preorganization of rotamers in the ligand-binding site except for two residues (crystal structure)	Polizzi and DeGrado, 2020

^a Differential scanning fluorimetry.

^b Dynamic Flexibility Index.

^c Hidden Markov Models.

^d Total turnover numbers.

^e Specific activity.

Assessment of Designed Proteins’ Stability

Protein folding is driven by burial of hydrophobic surface area away from ordered water and favorable arrangements of charged and nonpolar residues (Dill, 1990). Secondary structure and tertiary contacts form, and most are maintained as the protein moves towards the native structure (Fersht, 2008; Shea and Brooks III, 2001). Proteins constantly experience thermal fluctuations that may enhance or detract from their ability to remain in the folded, native state (Dill and MacCallum, 2012). Proteins found in thermophilic organisms are thermostabilized through a variety of methods including rigidification and shortening of loops, addition of surface salt bridges and helix–dipole interactions, optimization of core packing and increasing burial of hydrophobic surface area (Jaenicke and Böhm, 1998; Russell and Taylor, 1995). Computationally de novo designed proteins often end up being extremely stable or thermostable (Baker, 2019), but it is not obvious whether they are thermostable for the same reasons as those that are naturally occurring. In this section, we review the structural bases of stability (ΔG) and thermostability (T_m) in engineered proteins that were designed without function in mind.

Backbone rigidity is associated with thermo/stability

Decreased backbone dynamics and conformational heterogeneity were observed in MD simulations of conserpin, a protein designed from the consensus sequence of the serpin family, relative to wild type serpins (Porebski et al., 2016). These decreased dynamics were associated with an increase in thermostability, measured experimentally. Consensus-HD, another consensus protein designed based on the homeodomain family, has a decrease in ps–ns backbone dynamics as measured by ¹⁵N NMR relaxation studies, and it is more stable than engrailed-HD, one of the wild type sequences in the family, by 5 kcal/mol (Tripp et al., 2017).

Although MD simulations may be used to assess the stability of a designed protein, they also provide data that can be leveraged in designing proteins to be more stable. When the goal of protein design is to stabilize a protein, this stability may be assessed by quantifying the backbone motion of the protein and residue contact frequencies. Analysis of salt bridge networks in MD simulations of thermophilic carbonic anhydrases (CAs) suggested three point mutations that were inserted into a mesophilic CA to increase thermostability (Bharatiy et al., 2016; Fig. 1a). These mutations successfully increased its conformational stability, as measured by RMSD/F of the backbone in high-temperature MD simulations.

Fig. 1.

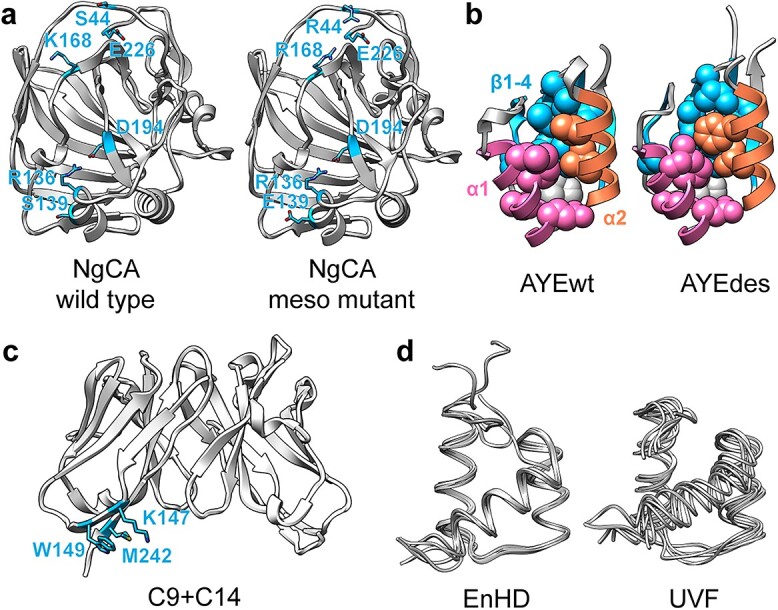
Structural and dynamic sources of thermo/stability in designed proteins. (a) Wild type NgCA (left, PDB 1koq) and mutant NgCA (right, added Ser44Arg, Ser139Glu and Lys168Arg mutations) with its designed salt bridge networks. Also showing Arg136, Asp194 and Glu226 in sticks. (b) Wild type AYE (right, PDB 1aye) and designed AYEdes (left, PDB 2gjf) colored by secondary structure and showing hydrophobic core packing (AYEdes residues 6, 8, 10, 15, 16, 19, 22, 36, 43, 45, 47, 55 and 59). (c) Designed scFv C9 + C14 (PDB 6p79) with core-adjacent hydrophobic cluster (Ser147Lys, Ser149Trp and Glu242Met) shown in blue sticks. (d) Structures from MD simulations of wild-type EnHD (right, PDB 1enh) and UVF (left, PDB 2p6j) showing differences in native dynamics.

Protein design often optimizes core packing and contacts

Structure-based protein design algorithms tend to optimize for tight core packing and increased core contacts. Most energy functions do not explicitly reward tight core packing, but tightly packed cores score well based on the attractive energies between atoms and exclusion of solvent (Alford et al., 2017). Total protein hydrophobicity is one of the best predictors of experimental success in expressing and purifying a de novo designed protein (Basanta et al., 2020). Likewise, burial of large swaths of hydrophobic surface area and tightly packed hydrophobic cores are also properties observed in the proteins of thermophilic organisms (Jaenicke and Böhm, 1998; Russell and Taylor, 1995).

Proteins designed using Rosetta should therefore have tightly packed cores, but it is important to check whether the packing is maintained in vitro or in silico, as designed. AYEdes, a Rosetta de novo design, has a tightly packed hydrophobic core in MD simulations based on contacts and buried SASA, and it also has decreased backbone motion relative to the wild type template (Gill and McCully, 2019; Fig. 1b). These properties likely contribute to its increased stability of ΔΔG = −10.3 kcal/mol relative to its wild type backbone template (Dantas et al., 2007). MD simulations of proteins containing a subset of the mutations in AYEdes showed that core packing was increased but between different regions than was expected based on the Rosetta models (Gill and McCully, 2019).

Redesigning the entire protein may not be necessary to increase stability, as tighter packing and increasing burial of hydrophobic surface area is stabilizing when applied to small clusters of residues only. Although protein cores are often already optimally packed, there may be more room for improvement in surface-proximal regions. Indeed, increasing the packing by adding bulky hydrophobic residues in clusters of <5 residues resulted in higher melting temperatures in several antibodies designed with Rosetta (Lee et al., 2020; Fig. 1c). The Protein Engineering Supporter (Proteus) web tool leverages the Protein Databank (PDB) to build a database of interacting residues, which can replace non-interacting residue pairs in a provided protein structure if their backbone geometries match (Barroso et al., 2020). Mutations to lysozyme designed by Proteus also increased the number of contacts beyond the mutated residue or pair, and four were found in the ProTherm database to be stabilizing.

Thermo/stability is not necessarily associated with rigidity and tightly packed cores

Although protein design algorithms often produce tightly packed cores, loose, dynamic cores are also possible outcomes and may impart stability themselves. UVF, a de novo designed, thermostable protein, has a highly dynamic and fully hydrophobic core as measured by increased backbone RMSD/F and unique side-chain contact pairs in MD simulations (McCully et al., 2013; Nguyen et al., 2019). At high temperature, UVF maintained these heightened dynamics without unfolding. Rather than interpreting heightened dynamics as destabilizing, however, we hypothesized that these dynamics explain UVF’s thermostability by imparting entropic stability (Fig. 1d). Sequence-based design methods, such as consensus design, do not optimize for core packing and residue contacts. Indeed, conserpin has fewer salt bridges, hydrogen bonds and SASA than extant serpins, but it is still more stable and thermostable (Porebski et al., 2016). Conserpin’s stability is due to smoothing of its energy landscape from the addition of stabilizing contacts that discourage aggregation-prone conformations.

For these reasons, it may not be accurate to infer thermo/stability from the level of dynamics or contact/packing patterns observed in MD simulations of proteins, designed or otherwise. Analysis of traditional MD simulations to infer thermostability should focus on detecting the early stages of the unfolding pathway in elevated-temperature simulations. Alternately, MD simulation in combination with enhanced sampling methods may calculate a protein’s T_m or ΔG more directly (Miao and McCammon, 2016).

Assessment of Designed Proteins’ Dynamics

Protein function may depend on coordinated motion within a region of a protein (e.g. binding site accessibility) or between regions across a protein structure (e.g. signal transduction, regulation and motor functions; Berendsen and Hayward, 2000). Therefore, proteins designed to complete these sorts of functions may need to do so via coordinated motions. Studying coordinated motions in naturally occurring proteins has provided much insight to enzyme biochemistry, cellular biology and disease (Grant et al., 2010; Olsson et al., 2006; Papaleo et al., 2016). For proteins that bind a ligand, such as sensors or enzymes, accessibility of the active site is essential and often under control of surrounding loop, flap or cap regions.

Analyzing the similarities and differences between the motions of proteins that are subject to natural evolutionary forces versus those that were computationally designed may provide insight to essential or novel mechanisms. Dynamics are difficult to rationally design, and we will address this challenge in Section ‘Proteins designed for dynamic function’ of this review. In this section, however, we review mechanisms of coordinated motion, active site accessibility and active site preorganization in designed proteins where motion was not explicitly considered in the design process.

Coordinated motions

ASR is a sequence-based protein design technique that attempts to predict a natural sequence rather than engineer one. ASR proteins shed light on protein evolution and are attractive starting points for protein design projects due to their heightened thermostabilities (Nguyen et al., 2017). Beyond their use as templates, investigation of their dynamics provides insight to how coordinated motions evolved.

In investigating the stability and dynamics of six EF–Tu proteins: three ASRs, one consensus, one mesophilic and one thermophilic; Okafor et al. (2018) found that heightened dynamics in Domain 1 was correlated with lower thermostability for both the naturally occurring and designed proteins. Similarly, lower dynamics in Domain 2 at high temperature were observed in ASRs of the two oldest common ancestors, which might be expected to be thermostable based on their computed age (Nguyen et al., 2017). The heightened dynamics in the most recent ASR were associated with loss of these ionic interactions in favor of interactions with the Domains 1–2 hinge peptide, leading to a major reorientation of Domain 2 relative to Domain 1 (Fig. 2a). Based on a community analysis, the ASR designs’ dynamics were most similar to the naturally thermostable EF–Tu. Consensus EF–Tu was the least coordinated and most disparate of the set of EF–Tus, which was predicted to explain its relatively lower function.

Fig. 2.

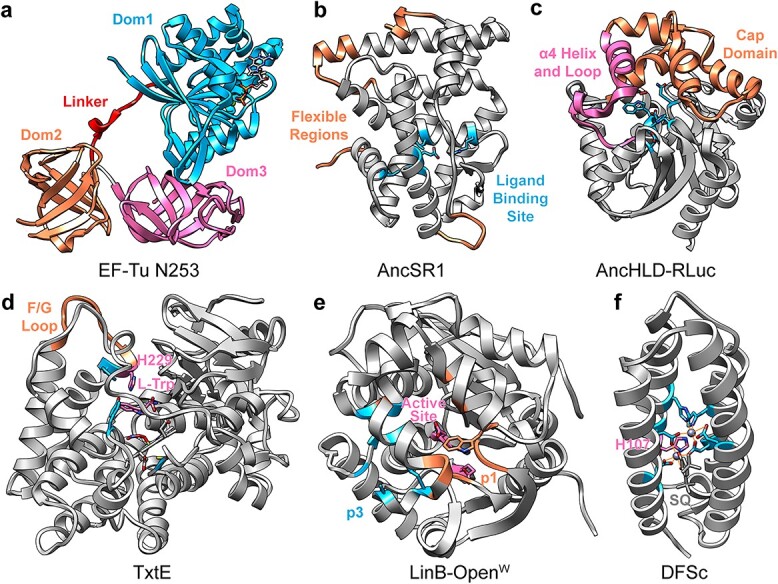
Flexible regions and stabilizing features arising from consensus designs and ancestral sequence reconstructions. (a) ASR EF-Tu N253 with GDP and Mg²⁺ (PDB 5w76) colored by domain with the flexible linker shown in red. (b) Model of AncSR1 (personal communication) showing the most dynamic regions (residues 1–7, 28–35, 155–168 and 245–249) and ligand-binding site (Ala47, Glu50, Leu84, Arg91 and Leu237). (c) AncHLD-RLuc (PDB 6g75) with catalytic residues (Asn51, Asp118, Trp119, Glu142 and His284), O₂ substrate, α4 helix and adjacent loop (residues 142–167) and cap domain (residues168–222) shown. (d) Closed-lid TxtE (MD structure (Dodani et al., 2016)) with F/G loop (residues 175–186), wild type His229, active site residues (Tyr89, Tyr175, Cys357), L-Trp substrate and heme cofactor shown. (e) LinB-Open^W (PDB 5lka) with the native, blocked p1 tunnel (Leu177Trp), designed p3 tunnel (Trp140Ala, Phe143Leu and Ile211Leu) and active site (residues Asp108 and Asp132) shown. (f) Model of DFSc bound to semiquinone (personal communication) with Zn²⁺-coordinating residues (Glu11, Glu44, Glu74, His77, His100 and Glu104) and His107 shown.

Investigation of ASRs of steroid receptors by MD simulation identified crucial contact networks maintained across evolutionary time (Okafor et al., 2020). These networks provide allosteric communication mediating activation of a conformational switch upon ligand binding. Different classes of ligands trigger different allosteric pathways and conformational changes incompatible with function. These insights provide useful information for those wishing to exploit steroid receptors as an engineered biosensor. Looking to the dynamics of the ASRs, the older ancestor (AncSR1) had a higher RMSD than the more recent ancestor (AncSR2), but these heightened dynamics were concentrated in several loop, terminal and helix-terminal regions that were distal from the ligand-binding site (Fig. 2b). When removing these highly dynamic regions from the calculation, the overall core RMSDs were similar between AncSR1 and AncSR2.

Active site dynamics and accessibility

Heightened dynamics, especially in the catalytic pocket, may be advantageous when designing a protein with promiscuous function. In multiple studies of proteins designed by ASR, heightened dynamics in the active site has been observed (Gamiz-Arco et al., 2021) and linked with promiscuous function (Chaloupkova et al., 2019; Zou et al., 2015), but it is not always associated with heightened dynamics globally.

This promiscuity of ASR proteins can be leveraged as a starting point for the design of new enzymatic function. In replica exchange MD simulations of three ASR Precambrian β-lactamases and one modern (TIM-1), the two oldest ancestral enzymes, based on predicted ages from the reconstruction (PNCA and GNCA), were the most flexible and had the most flexible catalytic pocket, whereas the most recent ancestor (ENCA) and extant TIM-1 were more rigid (Risso et al., 2017). Furthermore, the active site moved more independently in the older enzymes, suggesting a mechanism for the promiscuity of the older enzymes (PNCA and GNCA) via heightened dynamics and independent motion of the active site to accommodate a more diverse set of substrates. Similarly, the reconstructed common ancestor of haloalkane dehalogenases (HLDs) and Renilla reniformis luciferase (RLuc) was promiscuous, able to catalyze the reactions of both HLDs and RLuc (Chaloupkova et al., 2019). The reconstructed protein, AncHLD-RLuc, had the most dynamic α4 helix and adjacent loop in MD simulation, which allowed increased accessibility in the main tunnel to the active site (Fig. 2c), but globally it was the least dynamic of the three.

The dynamics of the region providing access to an enzyme’s active site may be exploited to design new enzyme function. Creation of a differentially substituted product was possible through leveraging the F/G loop dynamics of the nitrating P450 TxtE from Saccharomyces scabies (Dodani et al., 2016). Mutation of His176 on this loop to bulky, hydrophobic residues (Phe/Trp/Tyr) stabilizes the active site lid in the closed conformation, resulting in a differently substituted product with a longer retention time (Fig. 2d). Brezovsky et al. (2016) controlled access to the active site of haloalkane dehalogenase LinB by blocking the native tunnel with a Leu177Trp mutation and opening a new tunnel with three mutations identified via high-throughput mutagenesis: Trp140Ala, Phe143Leu and Ile211Leu (Fig. 2e). The mutant’s tunnel spent more time in an open conformation in MD simulations, and the protein had increased activity for 20/30 substrates relative to the wild-type enzyme.

Active site preorganization in ligand-binding proteins

In addition to detailing active site accessibility, MD studies may be used to assess differences between successful and unsuccessful designs. Whereas flexible active sites promote promiscuous function in ASR-based proteins, preorganized active sites are correlated with increased activity when optimizing for a single function. Tinberg et al. (2013) used Rosetta to design a β-barrel protein to bind digoxigenin (DIG) by placing three ligand-binding residues in known protein scaffolds. As static structures and energy scores did not provide satisfying explanations to why 15/17 high-scoring proteins were not functional experimentally, Barros et al. (2019) leveraged MD simulations to explore the dynamics of two successful and two unsuccessful designs in both the apo and holo forms. Non-binders had the largest fluctuations in both cavity volume and backbone motion around the cavity entrance. Once again, preorganization of the three ligand-binding residues in the apo simulations helped discriminate between the binders and non-binders.

Likewise, optimizing metal-coordination geometry, based on mutations suggested by QM/MM simulations, was successful in speeding the reaction of a Zn²⁺-binding de novo designed four-helix bundle protein that stabilized the formation of a semiquinone radical (Fig. 2f; Ulas et al., 2016). Similarly, in MD simulations of proteins designed using Rosetta to bind a flu antigen, those whose antigen-binding residues moved less were more likely to bind, suggesting that preorganization of the binding site is beneficial (Chevalier et al., 2017).

Although active site preorganization is important for high activity, it is energetically favorable for proteins to bind their ligand as the last step in protein folding. Polizzi et al. (2017) built a four-helix bundle scaffold around a porphyrin first then subsequently packed in surrounding residues in designing PS1. In another study, they used their van der Mers database to build a four-helix bundle scaffold that properly oriented the backbone relative to several chemical groups in their ligand (Polizzi and DeGrado, 2020). The active site residues of this protein, ABLE, largely adopted binding-compatible rotamers in the apo form. Conversely, PS1 folded to form its hydrophobic core in half of the bundle, whereas the largely polar binding site in the other half remained open and highly flexible, clamping down upon porphyrin binding.

The main feature of Rosetta design is selecting amino acids and placing their side chains in orientations that pack well. When particular side-chain geometries are required, as when designing a ligand-binding site into a pocket, it may be necessary to move the protein backbone to achieve the ideal side-chain geometries without introducing strain. Two recent developments for exploring backbone geometries similar to a template structure involve using the CoupledMoves/KIC method within Rosetta and providing MD-generated structures as input to Rosetta design (Löffler et al., 2017; Loshbaugh and Kortemme, 2020; Ludwiczak et al., 2018). Experimental information such as X-ray diffraction data may be incorporated to restrain MD simulations and generate ensembles of backbone templates without strain for use in enzyme design (Broom et al., 2020).

Proteins Designed for Dynamic Function

Proteins that are designed to perform a function, such as transport a ligand, bind a molecule or change conformation, pose an additional challenge beyond designing a stable protein. Protein designers attempting these challenges must consider the dynamics of the active site, multiple productive conformations and potentially negative design of unproductive conformations. We begin by discussing multistate design, which is used to favor or disfavor functionally relevant conformations. Then, we review the design and analysis of several fold-switching proteins.

Design of dynamic function by multi-state design

To rationally design a protein to adopt multiple states, the scoring function must reward sequences that adopt all desired conformations, as well as perhaps penalize those that favor undesired conformations. (Joh et al., 2014) worked from a four-helix-bundle backbone structure to design a Zn²⁺ transporter with an alternating-access mechanism by optimizing for the energy difference between the singly bound (asymmetric, desired) and doubly bound (symmetric, undesired) states. Although scoring functions can reward or penalize specific states, at times it is necessary to tune the relative balance between these states experimentally. Once a protein is designed to occupy two populations, mutations may be strategically introduced to adjust the balance between two populations such that the conformation/function is tunable by e.g. light (Stone et al., 2019; Teets et al., 2020), ligand-binding (Ha and Loh, 2017; Wei et al., 2020) or temperature (Campos et al., 2019).

Subtle changes such as the flipping of the Trp43 rotamer in Gβ1 on the millisecond timescale may be precisely engineered via multistate design (Davey et al., 2017). The multistate design considered the six rotamers for Trp43, two of which were favored (core-buried and surface-exposed), one assigned the transition state, and the remaining three disfavored, including the wild-type rotamer. The design, DANCER-2, allowed exchange of Trp43 between the core-buried and surface-exposed rotamers, as confirmed by NMR (Fig. 3b). Consideration of all six states and >16 million designed structures and energies was necessary to sufficiently sample the energy landscape and select sequences that could exchange between the desired states while avoiding others.

Fig. 3.

Proteins designed for dynamic function. (a) XAA_GDVQ in the short (top, PDB 6nz1/6nxm) and long (bottom, PDB 6ny8) forms with the GDVQ hinge region (residues 73–76), Ca²⁺-coordinating residues (Asp75), and polar networks (Asn54, Asn55, Ser92 and Asn61, Asn62, Gln85) shown. (b) DANCER-2 with Trp43 in its major/exposed (PDB 5uce) and minor/buried (PDB 5ucf) state shown. (c) G_A88 (PDB 2jws) and G_B88 (PDB 2jwu) shown with Thr1 and Glu19, which interact in the G_B88 denatured state (MD simulation).

Fold-switching proteins

The Paracelsus challenge, to change one protein’s conformation into another while retaining at least 50% of the sequence identity (Rose and Creamer, 1994), was accomplished for the first time in 1997 (Dalal et al., 1997). Since then, protein designers have become quite efficient at designing pairs of proteins with high or complete sequence identity that adopt disparate folds. The perhaps surprising ease of developing these proteins pairs and fold-switchers may be explained by the common existence of fold-switching proteins in nature (Porter and Looger, 2018).

Inspired by viral fusion proteins, Wei et al. (2020) designed a six-helix bundle fold-switching protein, the C-terminal end of which could switch to a ‘long’ three-helix bundle conformation. They incorporated a hydrogen-bonding network to destabilize the short state and make the helices more soluble in the long state, and they designed flexible loops that could coordinate Ca²⁺ in the three-helix bundle state, creating a Ca²⁺-dependent switch (Fig. 3a). The G_A/G_B set of proteins are perhaps the most true to the Paracelsus challenge, where G_A88 and G_B88 have 88% sequence identity but fold to either an all-α (G_A88) or α + β (G_B88) conformation (Alexander et al., 2007). Gianni et al. (2018) identified an interaction between Thr1 and Glu19 in MD simulations of the denatured state of G_B88 that they hypothesized primed formation of the β1/β2 hairpin and predisposed G_B88 to adopt the α + β vs. all-α conformation (Fig. 3c). Indeed, MD simulations of a G_B88-E19Q mutant showed inhibition of the Thr1–Glu19 interaction in the denatured state, and NMR experiments showed adoption of the all-α fold.

Conclusions and Future Directions

Protein dynamics studies have shown that hydrophobic surface area burial, secondary structure packing, backbone strain minimization, loop and helix edge stabilization and active site preorganization tend to be associated with successful, stable protein designs (Table I). On the other hand, heightened dynamics and loosely packed hydrophobic cores may also be compatible with—if not responsible for—thermostability in other designed proteins. If the goal is to design a protein that is rigid and thermo/stable, Rosetta de novo design or consensus design are strategic choices. For a protein that is thermostable but dynamic, a fully hydrophobic core may be leveraged.

Proteins designed by de novo computational methods tend to be very stable when successful or fail to fold properly when they are not. This dichotomy suggests there is still much to be learned about how designed proteins are stabilized and the implications of optimizing for known stabilization strategies. Atomic-level investigations of the dynamics of designed proteins, especially in comparison with similar naturally occurring mesophilic and thermophilic proteins, will continue to shed light on the structural basis of thermostability in designed proteins. Interpretation of heightened dynamics in MD simulations should be taken with care, as they are not necessarily evidence of instability. Instead, evidence of the early steps in unfolding or lack thereof should be identified.

Consideration of protein dynamics may provide further insight to differentiate successful from unsuccessful designs when static structures and energy scores cannot, particularly when the designed protein carries out a particular function. Ligand binding and catalysis tend to be most efficient with a preorganized active site (Table I). Highly dynamic proteins may spend minimal time in functionally compatible conformations, lowering activity. However, heightened dynamics may be associated with functional promiscuity, especially in the active sites of enzymes designed by ASR. If the design goal is a protein that acts on a variety of substrates or has a slightly different function than a known protein, ASR is a strategic choice of design method. For a function that requires multiple protein conformations to carry out, designing in a fully hydrophobic region to act as an entropy sink may provide thermo/stability. Iteration of design with MD could assess whether a particular sequence/structure produces the appropriate level of dynamics in the desired regions without evidence of unfolding.

Proteins have been designed to catalyze reactions, transport molecules, report the presence of a ligand and change conformation in the presence of light or temperature. Designing proteins that adopt multiple conformations as part of their function requires weighting desired states, negative design of unproductive states and consideration of the paths between them. MD may be used to assess whether a protein stays in a desired versus unproductive state and give insight to the pathways between states that might need to be stabilized or avoided. Multistate design may leverage structures produced by MD simulations or other perturbation methods to design amino acid sequences compatible with both function and backbone dynamics concurrently.

As proteins are inherently dynamic molecules, investigation of designed proteins’ dynamics is essential to understanding why they are at times unsuccessful at folding stably or performing a desired function, especially when analysis of static structures or energy scores do not offer satisfying explanations. Sharing both the structures of designed proteins—both successful and not—and data from their molecular dynamic simulations would facilitate large-scale analysis of their dynamic properties.

Authors’ Contributions

All authors performed a literature search, MEM wrote the initial manuscript draft, and all authors edited the manuscript.

Funding

This work was supported by the DeNardo Research Foundation, the Santa Clara University REAL Program, and the National Institute of General Medical Sciences of the National Institutes of Health (award number R15-GM134439).

Conflicts of Interest

None declared.