Abstract
Background
One measure to quantify the degree of dysregulation is allostatic load (AL). Typically, AL incorporates information on diverse biomarkers and is associated with health outcomes such as cardiovascular diseases or the incidence of coronary events (C-E).
Aims
This study investigates the predictive performance of different AL scoring methods on the incidence of coronary events (C-E). This study also elaborates sex differences in the baseline risks of C-E and the AL associated risks of C-E.
Design
Longitudinal data analysis of the Heinz Nixdorf Recall Study (Risk Factors, Evaluation of Coronary Calcification, and Lifestyle) of 4327 participants free of C-E at study baseline aged 45–75. The data contains over 13 biomarkers measuring AL.
Methods
After conducting multiple imputations on missing values on AL for 826 participants, the analysis sample consisted of N = 4327 participants. We applied the two most commonly used methods of AL scoring AL (count-based and Z-score) and a recently developed logistic regression weighting method (LRM) approach. Cox regression was used to predict the incidence of C-E for each AL score. Results were estimated without (M0) and with (M1) covariate adjustment, and in a final model (M2), with an interaction between AL and sex.
Results
We found no violation of the proportional hazard assumption and significant differences in the survival curves between the sexes for C-E (Log-rank test: prob. > Chi2 = 0.000). In M0, all AL-scoring methods predicted C-E significantly, with the LRM based AL-score having the best performance (hazard ratio = 3.133; CI: [2.630, 3.732]; Somer's D = 0.717). After covariate inclusion, differences between the scoring methods levelled, though the count-based method and LRM performed better than the Z-scoring method. The interaction analysis in M2 showed a significant multiplicative interaction for the count-based method (1.254; [1.066, 1.475]) and for the LRM (1.746; [1.132, 2.692]). The additive relative excess risk due to interaction (RERI) measure was negative for the count-based method (RERI = −1.967; [-3.778; −0.156]) and the LRM (RERI = −1.909 [-3.910; 0.091]), indicating subadditivity.
Conclusion
AL scores are suitable for predicting C-E. Differences between the AL-scoring algorithms were only present after including interactions. We value the count-based method as suitable for clinical practice since its calculation is relatively simple, and performance was among the best. Interaction analysis revealed that despite strong sex differences in baseline C-E, the effect of AL is more pronounced for females at high levels of AL; thus, females could benefit more from a potential intervention on AL. We suggest further investigation of sex differences concerning the mediation by physiological and psychological intermediates.
Keywords: Allostatic load, Biomarkers, Sex interaction, Cardiovascular diseases, Hazard Cox regression, Older adults
1. Introduction
McEwen and Stellar [1] introduced the concept of allostatic load (AL) to consider the impact of long-term stress on physiological aspects of health. AL combines stress theory with the concept of allostasis. The concept of allostasis differentiates between homeostasis and allostasis. Homeostasis describes the regulatory processes of the organism to maintain optimal stability. Allostasis is the reaction to changing environments that affects multiple biological systems [2]. The linkage between homeostasis, allostasis and stress theory exists in the stressor evaluation of the organism. McEwen and Gianaros [3] further differentiated the involvement of the brain in the allodynamic processes. Here, allostasis is the short-term adaption, while AL is the long-term maladaptation. More precisely, the primary outcomes of the adaption process are the acute responses of the organism to the stressor, which, e.g., expresses through anti-inflammatory reactions. Secondary outcomes result from chronic exposition to stress, concurrently chronic exposition to primary outcomes. Secondary outcomes induce changes in various regulatory processes, such as the metabolism and the cardiovascular system, that mutually reinforce each other. The adaption process to stress results in pathophysiological adaptions of the organism if exposition to secondary outcomes is permanent and not followed by recovery [4].
AL measures the pathophysiological adaptions of the organism through various biomarkers. Initially, Seeman [21] presented a summary score of ten biomarkers corresponding to different health domains to measure AL. The AL scores have been applied to predict numerous diseases, such as cardiovascular diseases (CVD), mortality, diabetes, depressive symptoms and cognitive limitations (for systematic reviews, see: [5,6]).
1.1. AL – C-E and sex
Regarding AL and its impact on mortality, it is vital to highlight its association with coronary events (C-E) and CVD because these are major causes of mortality [7]. Many empirical studies have confirmed the association of stress, AL and C-E/CVD (e.g., Ref. [8]). Research has shown that the association of AL and C-E/CVD seems sensitive towards stress intersections with race and deprivation (e.g. Refs. [[9], [10], [11]]. Gianaros and Jennings [12] provided biological evidence that further supports stress's impact on the body. They identified neurobiological mechanisms from brain to body and body to brain. Such insights provide a deeper understanding of the reciprocal pathophysiological processes causing C-E/CVD. Especially in the face of the increased prevalence of C-E/CVD among males, such processes can be different between the sexes, biologically and psychologically. McEwen [13] discussed biological sex differences in the autonomic nervous system (ANS) and hypothalamic–pituitary–adrenal (HPA) axis between the sexes, which has been proven to be more robust in females mice than in males mice [14]. Psychologically, gendered coping patterns and stress responses have been associated with increased AL levels [15,16]. However, research so far also found mixed evidence for differences by sex in the effects of AL on health outcomes [[17], [18], [19], [20]]. Still, there is a lack of research on the sex gradient in incidence of C-E/CVD that integrates AL.
1.2. Scoring methods for AL
While the implications of AL on the organism are undoubted, the scoring algorithms of AL are not. Since the AL score's initial presentation by Seeman [21]; different AL scoring methods have evolved with mixed predictive performances (e.g., Refs. [[22], [23], [24]]). Due to AL combining multisystem information (e.g., neuroendocrine, metabolic, inflammatory), some challenges in constructing appear. First, the technical calculation of the index. Second, the relative importance of each biomarker in the AL score. Third, the amount of biomarker information from each domain in the final AL score. Fourth, the standardization of the AL scores within the population.
1.3. The present study
This study utilizes information on a total set of 13 biomarkers. It compares the most commonly used AL-scoring methods (count-based and Z-scoring method) and the recently developed logistic regression weighting method (LRM) by Li et al. [23]. This study also compares the predictive performance of different AL scoring algorithms on the incidence of cardiovascular events. We emphasize sex differences in the analysis due to the higher prevalence of C-E for males. This study contributes to the methodological discussion of scoring AL and investigates the suitability of the AL concept for predicting C-E in general and between the sexes.
2. Material and methods
2.1. Sample
We used the Heinz Nixdorf Recall (HNR) study (Risk Factors, Evaluation of Coronary Calcification, and Lifestyle) as the database for the analysis. The data consists of randomly selected participants aged 45–75 years from mandatory residence registries of three adjacent cities in the Ruhr area (Bochum, Essen and Mülheim). Between 2000 and 2003, 4814 individuals were enrolled with a recruitment efficacy proportion of 56% [25]. After enrolment, study participants completed questionnaires, blood samples were drawn, and urine was taken. The questionnaires were conducted by computer-assisted personal interviews (CAPI) and contained information on health behaviours, social contexts, attitudes and sociodemographics [26]. Laboratory blood and urine tests provided pathophysiological information. In total, we observed 13 biomarkers relevant for scoring AL. The HNR study aimed to provide information on the first occurrence of nonfatal myocardial infarction and cardiac death. More detailed descriptions of the sampling process of the HNR study are available elsewhere [27,28].
2.2. Study endpoints
The endpoint was defined as incident coronary events (C-E), including unequivocally documented death related to coronary artery disease or incident nonfatal myocardial infarction that met the predefined study criteria [27,28]. The HNR-study asked participants to give medical records information to document emerging conditions during the observation period and validate self-reported diagnoses. Myocardial infarction was validated based on electrocardiographic signs, enzymes (creatinine kinase), troponin T or I and necropsy as nonfatal or fatal myocardial infarction. The outcome measure is binary, with a value of 1 indicating the onset of the condition. The incidence surveillance is ongoing. More details on sample characteristics, outcome and covariate distribution are displayed in Table 1.
Table 1.
Descriptive statistics of outcome and covariates.
| Measures | N | Mean (SD)/% |
|---|---|---|
| Outcome: | ||
| Incidence of C-E*: | 4327 | 100% |
| Does not apply | 4054 | 93.69% |
| Applies | 273 | 6.31% |
| Years to event | 273 | 7.95 (4.66) |
| Males: Incidence of C-E*: | 2050 | 100% |
| Does not apply | 1864 | 90.93% |
| Applies | 186 | 9.07% |
| Years to event | 186 | 7.77 (4.51) |
| Females: Incidence of C-E*: | 2309 | 100% |
| Does not apply | 2190 | 96.18% |
| Applies | 87 | 3.82% |
| Years to event | 87 | 8.32 (4.98) |
| Socio-demographic and -economic confounders: | ||
| Age | 4327 | 59.18 (7.74) |
| Born in Germany | 4327 | 100% |
| Yes | 4016 | 92.81% |
| No | 311 | 7.19% |
| Maritial Status | 4327 | 100% |
| Married/living with partner | 3444 | 79.59% |
| Living alone/divorced | 883 | 20.41% |
| ISCED-97 (0–4) | 4327 | 100% |
| 0 | 47 | 1.09% |
| 1 | 441 | 10.19% |
| 2 | 2416 | 55.84% |
| 3 | 126 | 2.91% |
| 4 | 1297 | 29.97% |
| Health-behavioural confounders | ||
| Smoking status | 4327 | 100% |
| Currently not Smoking | 3310 | 76.50% |
| Currently Smoking | 1017 | 23.50% |
| Sports (Chruch-Index) | 4327 | 100% |
| Sports | 2357 | 54.37% |
| No Sports | 1970 | 45.53% |
| Health-related confounders | ||
| Diabetes | 4327 | 100% |
| Does not apply | 4021 | 92.93% |
| Applies | 306 | 7.07% |
| Heart related medication | 4327 | 100% |
| Does not apply | 3176 | 73.40% |
| Applies | 1151 | 26.60% |
2.3. Biomarkers
The 13 biomarkers represent different health domains, dividing into metabolic, immune-inflammatory, cellular, cardiovascular and renal systems. Information on the metabolic system stems from low-density lipoprotein cholesterol (LDL-C) (1) and high-density lipoprotein cholesterol (HDL-C) (2), triglycerides (3), blood glucose (4) and waist-hip ratio (5). C-reactive protein (6) and the glycoprotein fibrinogen (7) reflect immune-inflammatory processes. Dehydroepiandrosterone – sulphate (DHEA-S) measures cellular ageing (8) and homocysteine vascular cell damages (9). Systolic (10) and diastolic (11) blood pressure measures the cardiovascular system. The renal system contains information on serum albumin (12) and urine creatinine (13). Higher values of HDL-C and DHEA-S do not correspond to higher AL; therefore, we reverse-coded HDL-C and DHEA-S, according to previous studies on AL (e.g., Ref. [[23], [24]]). High values on the biomarkers correspond to high values on the AL scores. More details on origin, related health domain, measurement and distribution of the biomarkers are described in Table 2.
Table 2.
Biomarker and allostatic load score distribution between sexes.
| All | ||||||||
|---|---|---|---|---|---|---|---|---|
| Domain | Biomarker | Unit | Mean | Std. Dev. | p90 | Min | Max | N |
| (1) | LDL-C | mg/dl | 147.018 | 36.123 | 193 | 4 | 360 | 4315 |
| (1) | HDL-C* | mg/dl | 58.765 | 17.182 | 81 | 7 | 171 | 4326 |
| (1) | Triglyceride | mg/dl | 147.819 | 102.038 | 247 | 13 | 1846 | 4324 |
| (1) | Glucose | mg/dl | 110.487 | 26.588 | 130 | 48 | 459 | 4323 |
| (1) | Waist-Hip-Ratio | cm/cm | 0.909 | 0.092 | 1.026 | 0.529 | 1.281 | 4315 |
| (2) | C-reactive Protein | g/l | 0.299 | 0.634 | 0.65 | 0.01 | 14 | 4315 |
| (2) | Fibrinogen | mg/dl | 332.834 | 75.606 | 434 | 124 | 876 | 4287 |
| (3) | DHEA-S* | μg/dl | 844.911 | 118.767 | 953 | 0 | 1000 | 4034 |
| (3) | Homocysteine | μmol/l | 11.565 | 4.288 | 15.74 | 4.04 | 100 | 3985 |
| (4) | Sys. blood Pressure | mmHg | 132.788 | 20.78 | 158.5 | 70 | 229 | 4326 |
| (4) | Dias. blood Pressure | mmHg | 81.572 | 10.859 | 95.5 | 44 | 133.5 | 4326 |
| (5) | Albumin | g/dl | 34.438 | 273.805 | 44.5 | 5.4 | 13100 | 4128 |
| (5) | Creatinine | mg/dl | 0.923 | 0.22 | 1.13 | 0.2 | 7.12 | 4323 |
| Raw | Z-Score | AL score | −0.115 | 5.128 | 6.05 | −14.738 | 57.757 | 3499 |
| Imputed | Z-Score | AL score | −0.077 | 4.796 | 5.476 | −14.738 | 57.757 | 4327 |
| Raw | Count score (p90) | AL score | 1.255 | 1.379 | 3 | 0 | 9 | 3499 |
| Imputed | Count score (p90) | AL score | 1.259 | 1.279 | 3 | 0 | 9 | 4327 |
| Raw | LRM score | AL score | −0.011 | 0.65 | 0.783 | −5.007 | 3.674 | 3499 |
| Imputed | LRM score | AL score | −0.006 | 0.618 | 0.744 | −5.007 | 3.674 | 4327 |
| Males | ||||||||
| (1) | LDL-C | mg/dl | 147.491 | 35.286 | 191 | 38 | 360 | 2044 |
| (1) | HDL-C* | mg/dl | 51.633 | 14.496 | 70 | 7 | 155 | 2049 |
| (1) | Triglyceride | mg/dl | 164.938 | 121.382 | 275 | 17 | 1846 | 2048 |
| (1) | Glucose | mg/dl | 114.336 | 29.519 | 136 | 55 | 459 | 2049 |
| (1) | Waist-Hip-Ratio | cm/cm | 0.978 | 0.061 | 1.055 | 0.544 | 1.238 | 2046 |
| (2) | C-reactive Protein | g/l | 0.302 | 0.657 | 0.65 | 0.01 | 13.7 | 2043 |
| (2) | Fibrinogen | mg/dl | 326.219 | 75.8 | 425 | 124 | 876 | 2031 |
| (3) | DHEA-S* | μg/dl | 807.933 | 130.081 | 932 | 0 | 996 | 1910 |
| (3) | Homocysteine | μmol/l | 12.208 | 3.891 | 16.38 | 4.75 | 57.72 | 1894 |
| (4) | Sys. blood Pressure | mmHg | 137.971 | 19.248 | 163 | 70 | 219.5 | 2049 |
| (4) | Dias. blood Pressure | mmHg | 84.441 | 10.471 | 98 | 44 | 133.5 | 2049 |
| (5) | Albumin | g/dl | 43.581 | 252.691 | 58.6 | 5.4 | 8480 | 1946 |
| (5) | Creatinine | mg/dl | 1.004 | 0.189 | 1.2 | 0.32 | 4.46 | 2049 |
| Raw | Z-Score | AL score | 2.068 | 4.609 | 7.501 | −11.691 | 28.956 | 1652 |
| Imputed | Z-Score | AL score | 2.107 | 4.239 | 6.895 | −11.691 | 28.956 | 2050 |
| Raw | Count score (p90) | AL score | 1.611 | 1.521 | 4 | 0 | 9 | 1652 |
| Imputed | Count score (p90) | AL score | 1.614 | 1.393 | 3 | 0 | 9 | 2050 |
| Raw | LRM score | AL score | 0.351 | 0.536 | 0.972 | −3.996 | 3.674 | 1652 |
| Imputed | LRM score | AL score | 0.355 | 0.498 | 0.936 | −3.996 | 3.674 | 2050 |
| Females | ||||||||
| (1) | LDL-C | mg/dl | 146.592 | 36.863 | 194 | 4 | 277 | 2271 |
| (1) | HDL-C* | mg/dl | 65.183 | 16.879 | 87 | 8 | 171 | 2277 |
| (1) | Triglyceride | mg/dl | 132.415 | 77.629 | 216 | 13 | 1390 | 2276 |
| (1) | Glucose | mg/dl | 107.02 | 23.102 | 124 | 48 | 380 | 2274 |
| (1) | Waist-Hip-Ratio | cm/cm | 0.848 | 0.069 | 0.932 | 0.529 | 1.281 | 2269 |
| (2) | C-reactive Protein | g/l | 0.296 | 0.612 | 0.66 | 0.01 | 14 | 2272 |
| (2) | Fibrinogen | mg/dl | 338.789 | 74.949 | 440 | 128 | 738 | 2256 |
| (3) | DHEA-S* | μg/dl | 878.162 | 96.148 | 963 | 0 | 1000 | 2124 |
| (3) | Homocysteine | μmol/l | 10.983 | 4.541 | 14.8 | 4.04 | 100 | 2091 |
| (4) | Sys. blood Pressure | mmHg | 128.123 | 21.005 | 154 | 78 | 229 | 2277 |
| (4) | Dias. blood Pressure | mmHg | 78.99 | 10.551 | 92.5 | 50 | 121 | 2277 |
| (5) | Albumin | g/dl | 26.285 | 291.164 | 31.2 | 5.9 | 13100 | 2182 |
| (5) | Creatinine | mg/dl | 0.849 | 0.22 | 1.01 | 0.2 | 7.12 | 2274 |
| Raw | Z-Score | AL score | −2.067 | 4.77 | 3.565 | −14.738 | 57.757 | 1847 |
| Imputed | Z-Score | AL score | −2.044 | 4.401 | 3.141 | −14.738 | 57.757 | 2277 |
| Raw | Count score (p90) | AL score | 0.936 | 1.148 | 3 | 0 | 7 | 1847 |
| Imputed | Counts core (p90) | AL score | 0.939 | 1.07 | 2 | 0 | 7 | 2277 |
| Raw | LRM score | AL score | −0.334 | 0.568 | 0.385 | −5.007 | 2.795 | 1847 |
| Imputed | LRMs core | AL score | −0.331 | 0.528 | 0.335 | −5.007 | 2.795 | 2277 |
Note: *Values reversed during calculation of AL scores.
2.4. Scoring methods
2.4.1. Z-scoring method
The Z-scoring method Z-standardized each biomarker to a mean of 0 and a standard deviation of 1 and then calculates the sum-score (e.g., Ref. [29]). The obtained Z-standardized biomarker values are comparable to one another but not directly interpretable, though higher values on the Z-standardized AL score correspond to higher levels of AL. The Z-scoring method requires continuously measured biomarkers and accounts for variances in the biomarkers. However, each biomarker's relative importance and the number of biomarkers from certain health domains remain unreflected.
2.4.2. Count-based method
The simplest and most applied method to score AL is the count-based method. The count-based method relies on building risk quartiles for the biomarkers in the study sample [21]. If an individual's biomarker value falls into the risk quartile, the individual receives the value "1"; if not, the value is "0". The overall sum of the dichotomized biomarkers represents the AL score. We used the 90th percentile sample distribution of each biomarker as the cut-off values. Most studies so far used the 75th or 90th risk percentile as the cut-off values of the biomarkers [[21], [23], [24]]. Subsequently, we summarized the dichotomized biomarkers into one AL score. A value of 13 indicates the highest AL and zero the lowest AL. Another issue of the count-based method is the potential loss of information due to the dichotomization of the biomarkers. The count-based method does also not adjust for the relative importance of each biomarker for the AL score and the number of biomarkers from each health domain.
2.4.3. The logistic regression method
The LRM addresses the relative importance of each biomarker for the AL score. We applied the LRM according to Li et al. [23]. First, a logistic regression on the outcome (C-E) with all Z-standardized biomarkers as predictors were calculated. Second, the Z-standardized biomarkers with their respective coefficient were multiplied and, third, summarized to an AL score. Thus, the LRM addresses an important issue the two most commonly applied AL-scoring methods do not address.
2.5. Confounding factors and covariate selection
To investigate the AL – C-E/CVD association, we also adjusted for confounding variables. These variables simultaneously affect the exposure (AL) and the outcome (C-E) and can confound any observed association between AL and C-E. We identify four primary confounding sources: (1) socio-demographic, (2) socio-economic, (3) health-behavioral and (4) health-related. Table 1 gives a detailed overview of the distributional properties of all measures.
-
(1)
Age is an apparent socio-demographic confounder since it increases AL and the probability of experiencing a C-E simultaneously. Living alone at an older age or the experience of a marital disruption have been found to increase AL and the likelihood of cardiovascular diseases [30], especially for males [31,32]. We used a continuous measure for age and a binary measure for marital status.
-
(2)
The migration background is often accompanied by lower social status and a higher stress exposition due to racial discrimination [33]. Similarly, socio-economic factors, such as the educational level, can influence the AL and C-E through health-behavioural pathways [34]. We added information on the direct migration background (binary), and we used the International Standard Classification of Education (ISCED) as a proxy for social status (categorical).
-
(3)
Health-behavioural confounders may affect AL and C-E positively or negatively [35], and therefore confound the association. Hence, we added information on the current smoking status (binary) and the sport participation (binary).
-
(4)
Health-related conditions, such as certain conditions and medications, could also confound the AL – C-E association. To account for confounding pre-existing health conditions, we added diabetes (binary) and any heart-related medication (binary) as covariates in the models.
2.6. Sample selection and missing values
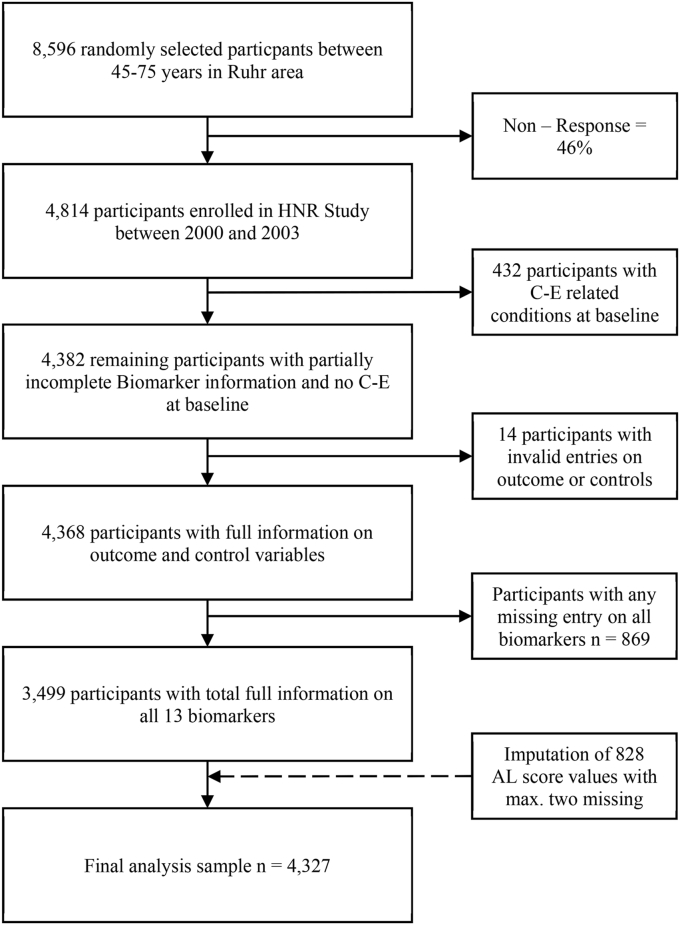
The sample selection process is shown in Fig. 1. We addressed potential reverse causalities by excluding 432 participants reporting physician-diagnosed coronary artery disease (i.e., history of myocardial infarction or coronary revascularization) at baseline, resulting in a sample of 4482 remaining participants. Only 14 participants were excluded due to missing values on the outcome or control variable (N = 4368).
Fig. 1.
Flowchart of sample selection and imputation.
Due to the nature of sum-scoring, complete information on all biomarkers was required for the AL scores. However, 80.11% had full information, and 16.76% had only one and 2.20% only two missing values on all 13 biomarkers; thus, over 99% of the study participants had at least 11 out of 13 valid entries on the AL score. We imputed missing values on the AL scores for individuals with at least 11 or more valid entries on the biomarker and assumed missingness at random for the remaining biomarker information. In sum, 828 values for the participants with only one or two incomplete entries on the AL score were imputed, resulting in a final analysis sample of 4327 study participants. We used the multiple imputations (MI) procedure as an imputation technique in Stata 16.1 (StataCorp LP, College Station, Texas, USA). This MI procedure is based on Rubin [36]; and we included all covariates and the outcome in the imputation model as predictors. We also supplement the imputation model with the incidence of CVD as an auxiliary variable. Auxiliary variables can reduce the bias in imputation. According to the overall missingness of approx. 20% on the AL score, we calculated 20 MI datasets [37]. Robertson et al. [38] conducted a similar MI approach on imputing AL scores.
2.7. Statistical methods
We investigated the AL-associated hazard of C-E with Cox regression modelling [39]. Cox regressions are commonly applied in analyzing events, such as the incidence of C-E (e.g., Ref. [40]). We checked the proportional hazards assumption and the linear relation assumption by inspecting the Kaplan-Meier curve and the Schoenfeld residual plot and test [41]. We provide results before (M0) and after (M1) covariate inclusion for each AL-scoring method.
We evaluated the performance of the AL-scoring techniques by comparing the estimated hazard ratios and the model-fit parameters. As model-fit parameters, we reported Harell's C and Somers' D. The first expresses the balance between concordant and discordant pairs, and the latter is the correlation between predicted risk observed survival. Additionally, we inspected the receiver operator characteristic (ROC). The ROC displays the positive cases (incidence of C-E) that the models correctly classified (sensitivity) and the negative cases that the model correctly classified (specificity). We contrasted the sensitivity and specificity of the scoring methods by testing the equality in the ROC-curves between the scoring methods. Further, we reported pseudo-R2 and the Akaike Information Criterion (AIC). Lower AIC values correspond to increases in model fit, and pseudo-R2 values can be used to compare the models between one another.
We investigated sex differences through sex separated Kaplan-Meier curves and the log-rank test to compare the survival curves between females and males. In addition, we performed the analysis of the interaction between AL and sex in M2. As demonstrated by Vatcheva et al. [42]; considering interactions in hazard Cox regression can substantially improve the prediction of the main effects. We reported additive and multiplicative interaction measures. As a multiplicative measure, we included the product of sex and AL as a predictor in the hazard Cox regression. For the additive interaction measures, we followed the recommendation by Anderson et al. [43] and constructed a composite variable of sex and AL. For sex, we define female sex as the low-risk category, and for AL, we define having an AL score above the 90th percentile as the high-risk category. The risk combinations are then defined ordinally. The value 1, the reference category, equals the lowest risk combination (being female sex and not having high AL) and the value of 4, the highest risk combination (being male sex and having high AL). As additive interaction measures, we reported the relative excess risk due to interaction (RERI), the synergy index S and the attributable proportion (AP) due to interaction [43].
3. Results
3.1. Descriptive results
Table 1 presents the sample characteristics of the analysis sample after imposing the selection criterion (Fig. 1) and imputation of the AL score values. The analysis sample consisted of 4327 participants, with 2050 males and 2227 females. The incidence of C-E was observed more often in males (9.07%) than in females (3.82%). On average, it took about eight years after study participation if a C-E occurred. For males, this duration was slightly lower than for females (7.77–8.32). The mean age of the analysis sample was 59.18 (SD = 7.74), and the majority of the analysis sample were married or cohabiting (79.59%), had no direct migration background (92.81%), were currently not smoking (76.50%) and had no diabetes (92.93%). Although we restricted the analysis sample to participants with no baseline C-E or CVD, 26.60% of the analysis sample had heart-related medications prescripted.
Table 2 shows the distribution of the biomarkers and AL scores. A more detailed table on the missing values of the biomarkers and AL score is available in Appendix Tables 1 and 2. Overall, the biomarkers values indicated higher levels of AL for males than for females, except for fibrinogen. Also, the raw HDL-C and DHEA-S values were lower for males than for females; however, higher values for these biomarkers correspond to a lower AL, and the HDL-C and DHEA-S values were reversed during the AL score calculation. Logically, males also had higher values on the AL scores. For the count-based scoring method, the mean AL score was 1.259, whereas the mean value for males was 1.614 and 0.939 for females. Similarly, the signs of the AL scores based on Z-standardization (Z-score and LRM) showed in opposite directions between the sexes, with a negative sign for females and a positive sign for males. We found no significant difference between raw and imputed AL scores in an unpaired t-test for mean differences (see also, Appendix Table 2).
3.2. Hazard Cox regressions on C-E
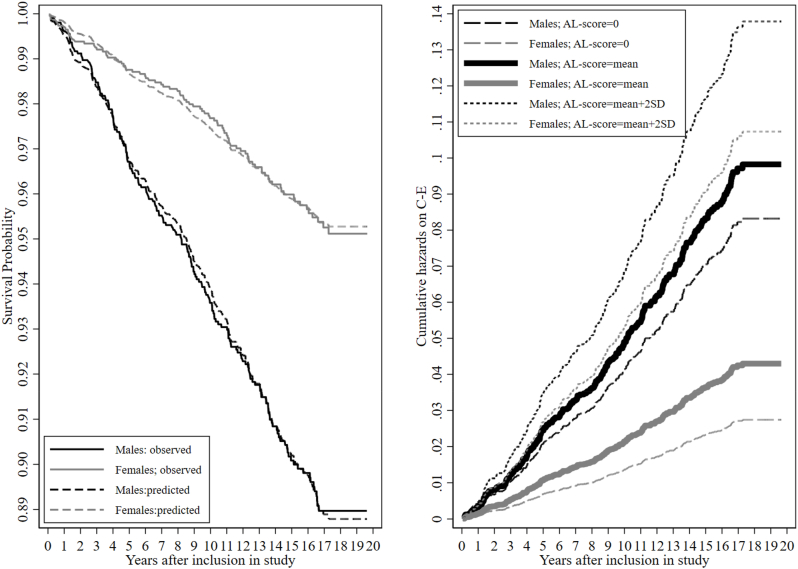
Fig. 2a shows the Kaplan-Meier curve for the observed (bolt lines) and predicted (dashed lines) values of the C-E between males (black colour) females (grey colour). Fig. 2a clearly illustrates a gap between the sexes in the survival probability for the predicted and observed values. The gap between the sexes further increased with the observation duration. For example, after ten years of observation, males had at least a 0.05 lower survivability than females. The log-rank test for equality of survival curves was also highly significant (prob. > Chi2 = 0.000), confirming significant differences in the survival function between the sexes. Fig. 2a also visually checked the proportional-hazards assumption and the linear relation. The larger the gap between observed and predicted lines within the sex, the more likely the violation of the proportional-hazards assumption. The Kaplan-Meier curve indicated no violation of the proportional-hazards assumption with a continuously decreasing trend in the survival for both sexes, which plateaued after 17 years of observation.
Fig. 2.
a: Kaplan-Meier survival curve between sexes b: Cumulative hazards between sexes at different levels of AL. Note: a: relative hazards for males: 1.6167; relative hazards for females = 0.6582; Cox regression-based test for equality of survival: Log-rank Chi2(1) = 51.78; prob. > Chi2 = 0.000. Note: b: Estimated cumulative hazards at different levels of the count-based AL-scoring method between the sexes. Mean AL = 1.258; SD = 1.278.
Table 3 summarizes the hazard Cox regression models for each AL score, where M0 consists only of the AL scores, M1 includes the covariates, and M2 includes the covariates and an interaction term between AL scores and sex. In M0, the AL score of the LRM overall provided the best model fits, with the lowest AIC, the highest pseudo-R2 and a ROC-Area of 0.703. Z-scoring method and count-based method performed fairly similar, however the model fit statistics pseudo-R2 and AIC indicated a slightly better performance for the count-based method (Z-scoring: pseudo-R2 = 0.017; AIC = 4375.6; Count-based: pseudo-R2 = 0.020; AIC = 4365.8). The Kendall rank parameters indicated a good fit for all models, with Harrell's C > 0.5 and Somer's D > 0.35. However, the ROC-test for equality between the models revealed significant differences (prob. > Chi2 = 0.012) in the sensitivity and specificity of the predictions between the scoring methods.
Table 3.
Estimates and fit statistics of AL scoring methods on C-E with and without covariate inclusion.
| M0 without controls | Z-Scoring | Count-based | LRM |
| AL HR | 1.085*** [1.071,1.100] | 1.450*** [1.352,1.556] | 3.133*** [2.630,3.732] |
| Somers' D | 0.378 | 0.357 | 0.434 |
| Harrell's C | 0.689 | 0.678 | 0.717 |
| AIC | 4375.6 | 4365.8 | 4308.9 |
| Pseudo-R2 | 0.017 | 0.020 | 0.032 |
| ROC-Area [CI] | 0.673 [0.644, 0.703] | 0.671 [0.635, 0.697] | 0.703 [0.674, 0.734] |
| ROC-M0 equality test: |
Chi2 = 8.81; prob > Chi2 = 0.012 |
||
|
M1 with controls |
Z-Scoring |
Count-based |
LRM |
| AL HR | 1.047*** [1.020,1.072] | 1.213*** [1.114,1.321] | 1.939*** [1.499,2.508] |
| Somers' D | 0.467 | 0.482 | 0.476 |
| Harrell's C | 0.733 | 0.741 | 0.738 |
| AIC | 4279.5 | 4271.8 | 4266.3 |
| Pseudo-R2 | 0.043 | 0.045 | 0.046 |
| ROC-Area [CI] | 0.723 [0.694,0.753] | 0.731 [0.702,0.760] | 0.727 [0.698,0.756] |
| ROC-M1 equality test |
Chi2 = 6.32; Prob > Chi2 = 0.042 |
||
|
M2 multiplicative interaction |
Z-Scoring |
Count-based |
LRM |
| AL HR | 1.031 [0.997, 1.066] | 1.142** [1.035, 1.260] | 1.568** [1.147, 2.143] |
| Sex = Female (2) HR | 0.471*** [0.346, 0.640] | 0.330*** [0.220, 0.495] | 0.568*** [0.406, 0.794] |
| AL-sex interaction HR | 1.030 [0.987, 1.075] | 1.254** [1.066, 1.475] | 1.746* [1.132, 2.692] |
| Somers' D | 0.469 | 0.485 | 0.481 |
| Harrell's C | 0.742 | 0.743 | 0.740 |
| AIC | 4279.7 | 4266.9 | 4262.1 |
| Pseudo-R2 | 0.044 | 0.046 | 0.047 |
| ROC-Area [CI] | 0.724 [0.695,0.753] | 0.732 [0.703,0.761] | 0.730 [0.700,0.759] |
| LR-Test M1 nested in M2: Prob > Chi2 | 0.188 | 0.008 | 0.012 |
| ROC-M2 equality test:Prob > Chi2 | Chi2 = 5.11; Chi2 = 0.077 | ||
| M2 additive interaction measures | Z-Scoring | Count-based | LRM |
| Female; low AL (1; reference) | 1 | 1 | 1 |
| Female; high AL (2; one risk factor) | 1.277 [0.583; 2.795] | 3.254*** [1.996; 5.306] | 2.715** [1.371; 5.377] |
| Male; low AL (3; the other risk factor) | 2.475*** [1.836; 3.338] | 2.938*** [2.129; 4.056] | 2.672*** [1.971; 3.622] |
| Male; high AL (4; all risk factors) | 2.529*** [1.686; 3.792] | 3.226*** [2.152; 4.837] | 2.477*** [1.641; 3.738] |
| RERI | −0.223 [-1.541; 1.095] | −1.967* [-3.778; −0.156] | −1.909 [-3.910; 0.091] |
| AP | −0.088 [-0.623; 0.447] | −0.610 [-1.245; 0.026] | −0.771 [-1.663; 0.122] |
| S | 0.873 [0.186; 1.559] | 0.531*** [0.247; 0.815] | 0.436** [0.116; 0.757] |
Note: 95% confidence intervals in brackets * p < 0.05, **p < 0.01, ***p < 0.001.
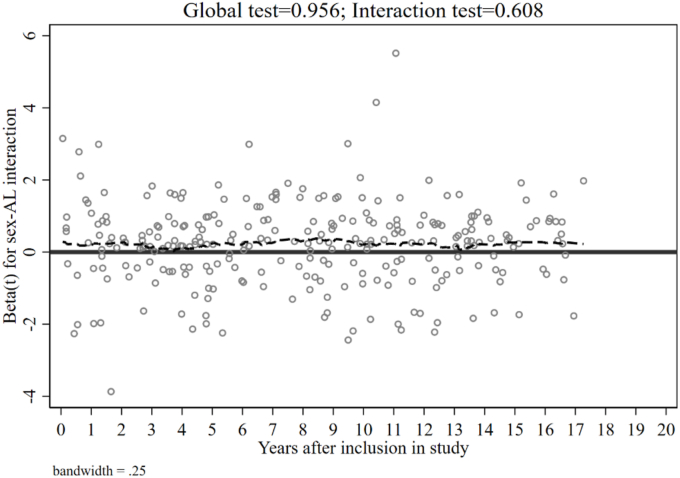
Adding covariates in M1 improved all models and levelled most of the initial differences in M0 between the AL scores, and all estimated hazard ratios remained highly significant. After covariate inclusion, the Z-scoring and count-based methods' AIC decreased by nearly 100. Somer's D increased by almost 0.1 to 0.467 for the Z-scoring method and 0.482 for the count-based method. Pseudo-R2 values ranged from 0.043 to 0.046. The estimated ROC-Area was at least above 0.720 for all scoring methods. However, the ROC-test of equality between the models remained significant (prob. > Chi2 = 0.046), indicating significant differences in the ROC-area between the scoring methods. In Appendix Fig. 1, we also present additional diagnostics for the PH assumption of M2 by displaying the Schoenfeld residuals graph. The global test was 0.950, and the single test for the interaction term was 0.644, indicating no violation of the PH assumption in M2.
M2 added the multiplicative interaction between AL score and sex (1 = male; 2 = female) to test if the effect of AL is different across sexes. All model-fit parameters increased in comparison to M1 for all scoring methods. The ROC-test for equality between the models turned insignificant (prob. > Chi2 = 0.077), indicating no differences in sensitivity and specificity between the scoring methods in M2. The LR-test confirmed the increased fit of M2 over M1, which indicated that M1 is nested in M2 except for the Z-scoring method. Regarding the AL-sex interaction, the multiplicative interaction was insignificant for the Z-scoring method (1.030; p > 0.05) but significant for the count-based method (1.254**: p < 0.01) and LRM (1.746*; p < 0.05). The hazard ratio for the multiplicative interaction effect was >1, while the hazard ratio for sex was <1, indicating that the AL hazard ratio effect is stronger for females than males.
To further illustrate the interaction between AL and sex, we plotted the cumulative hazards in Fig. 2b. It displays the cumulative hazards for males (black lines) and females (grey lines) for the best performing method in M2 (count-based method). The cumulative hazards on the bolt solid lines were calculated by the mean score of the count-based AL score (1.259). The dotted lines were calculated by the cumulative hazards with two SD units increase from the mean (SD = 1.29; AL score∼3.9), reflecting the cumulative hazards for individuals with high levels of AL. The dashed lines are the cumulative hazards where the AL score was set to "0" to reference individuals with no AL. The difference between the bold black solid line (mean AL and males) and the bold grey solid line (mean AL and female) were much larger than the difference between the dotted black (high AL and male) and dotted grey line (high AL and female). The decrease in the differences of the cumulative hazards between the sexes at higher AL scores visualizes that although males have a much higher baseline hazard for experiencing C-E, the relative increase in hazards that is due to increased AL is larger for females than for males. Therefore, the interaction showed that the more elevated the AL score, the lesser the differences between the sexes in the cumulative hazards of C-E.
Following the recommendations of VanderWeele and Knol [44]; the inspection of additive interaction is recommended when the baseline risk for one group is higher than for the other group. We calculated additive interactions measures with the composite variable of AL and sex (Table 3; Model 2b) [43]. The hazard ratios for the composite variable are estimated in reference to the expected lowest risk group, which were females with low AL. For females with high AL, the Z-scoring method predicted a hazard ratio of 1.277, while for the count-based method, the hazard ratio was 3.254***, and for the LRM, the hazard ratio was 2.715***. For the count-based method and the LRM, being male sex and having high AL (highest risk group) had a lower hazard ratio than being female and having high AL. The relative excess risk due to interaction (RERI) is < 0, indicating sub-additivity of the interaction, which means that the increase in hazards is not consistent with the increase in risk groups. The attributable proportion due to interaction (AP) shows that 61% of the observed C-E incidences are due to interaction for the count-based method. This amount even increased for the LRM to 77%. The synergy index (S) expresses whether the combinations of the hazard ratios of the risk groups is greater than the separate hazard ratios; in cases where the RERI is < 0, S would indicate no synergy when S = 1 or S = 0. For the count-based method, S = 0.531*** and S = 0.436***for the LRM, but S is insignificant S = 0.873 for the Z-scoring method, and its upper C.I. includes values above 1. Overall, the additive interaction analysis confirmed Fig. 2b's illustration; at high levels of AL, the relative increase in hazards is more substantial for females than for males.
4. Discussion
This study investigated the predictive performance of three AL-scoring algorithms on the incidence of C-E. using hazard Cox regression models. The data used for analysis was the HNR study, which is an ongoing surveillance of participants aged 45 to 75 living in Germany. The HNR study examined over 13 biomarkers related to the concept of AL, observed any incidence of C-E and CVD and enabled us to apply hazard Cox modelling on the C-E incidence.
This study highlighted sex differences between the incidence of C-E and the effect of AL by providing measures of multiplicative and additive interaction. Irrespective of the scoring algorithms, we found that AL is a solid predictor for the incidence of C-E. This study also contributes to AL being valid for predicting heart-related diseases [45] and to the recent discussions on the differences in performance of various AL-scoring algorithms [[22], [23], [24]].
In the naïve model without covariate inclusion, the LRM outperformed the other methods. With covariates, the AL scores remained highly significant, and the differences between the scoring methods were reduced. In the final adjusted models with an interaction between AL and sex, all scoring methods model fits increased even further, leading to insignificant differences in sensitivity and specificity between the models. Nevertheless, the interaction for the Z-scoring method was insignificant, whereas the interactions for the count-based method and LRM were significant. In covariate-adjusted models, the differences between AL-scoring methods are minor, but the range of the AL score should be reflected when incorporating interaction terms. We also confirmed substantial sex differences in the incidence of C-E, with males having a higher probability of a C-E incidence. However, with increasing levels of AL we found that the relative increase in hazards is larger for females than for males.
4.1. Strengths and limitations
One strength of this study is comparing three different AL scoring algorithms based on the same set of 13 biomarkers. There numerous other scoring AL scoring techiques that either rely on Z-standardization of the biomarkers, such as the factor loading method (e.g. Ref. [46]), or defininig risk-profiles, such as the grade of membership method (e.g., Ref. [47]). However, with increasing amount of specifications in scoring the comprabibility decreases. Recently, McLoughlin et al. [24] presented a genuine discussion and comparison of different scoring algorithms in a nationally representative cohort of older persons living in community-dwellings. They advocated the use of standardized, comparable AL scores across investigations. At the same time, they also recommended using sex-specific AL scores and incorporating medication information either directly in the AL-scoring procedure or as a covariate, as done by Piazza et al. [48]. Recently, Liu et al. [49] even introduced a scoring procedure of AL using the item response theory, which shows that the discussions on optimal AL scoring algorithms are still ongoing. With our chosen scoring methods, we achieved comparability across previous studies, and we also included heart-related medication as a covariate. Though, we did not provide sex-specific AL scores because we investigated sex differences through modelling interactions between AL and sex.
The analysis of interaction is another strength of our study. Interaction analysis allowed us to investigate sex differences in the AL related hazards of C-E incidence. Following the recommendations of VanderWeeele and Knol [44]; we provided measures of multiplicative and additive interactions, which is important for three reasons. Although multiplicative interactions are most commonly used when assessing interactions, their interpretations can be biased when baseline risks between groups differ largely. The Kaplan-Meier curve revealed that the baseline hazards for experiencing C-E were substantially higher for males; thus, the multiplicative interaction measures could be biased. Secondly, it is possible to observe null or negative multiplicative interactions while also having positive additive interactions. Therefore, relying solely on multiplicative interaction could lead to wrong conclusions [44]. Thirdly, the interpretation of additive interactions is of high public health relevancy. The additive interaction measures identify the sub- or riskgroups for whom an intervention is more effective.
Without the interaction analysis, the large sex differences in the C-E incidence and AL levels could lead to the conclusion that AL is more important in males than in females. Our analysis revealed that for C-E prevention, females could benefit more from a potential allostatic load intervention than males, despite having lower baseline risks than males. Reporting additive and multiplicative interaction measures should become standard practice.
Our study confirms the applicability of the AL concept for predicting coronary events and diseases because our study finds comparable predictive performances to traditional C-E/CVD risk scores. For instance, in the study, Erbel et al. [28] had a similar predictive performance on C-E for the Framingham risk score (FAS) using the same data. Unlike traditional C-E/CVD risk scores such as the FAS, AL is not restricted to and specifically designed to predict C-E/CVD risk. However, we evaluate the similarity in the predictive performance as additional validity for AL predicting C-E and CVD.
To address potential reverse-causality issues between high AL and C-E, we excluded those study participants with a C-E related condition at baseline. Still, we did not exclude individuals that have had heart-related drugs already prescribed at baseline. In this sense, the analysis is not entirely free of reverse-causality issues.
A limitation to this finding is that the Z-scoring method did not provide significant interactions. The Z-score ranges from −14.738 to 57.757, and we assume that the insignificance of the interaction is partly caused by the relatively large range. The LRM is based on the Z-scores of the biomarkers and, overall, provided better performances and significant interactions. We view that the causes of both aspects are the lower range of the LRM based AL score (−3.996 to 3.674) and the LRM AL score weights for the relative importance of each biomarker for the C-E incidence.
Another challenge of our study was the relatively large amount of missing values (n = 869) on the AL scores, which we addressed with multiple imputations. The vast majority of the individuals with missing values on the AL score had only one or two missing values on the AL scores (n = 828); thus, excluding those individuals from the analysis would equal the exclusion of study participants of whom 11 out of 13 valid information on the biomarkers were available. We found no significant mean differences between the imputed and unimputed AL scores (see Appendix; Table 2). Furthermore, missing values were only slightly more common in Albumin, Homocysteine and DHEA-S (see Appendix; Table 1). We can neither empirically nor logically find evidence for these missing values to be systematically correlated with the incidence of C-E; thus, we evaluate the assumption of completely missing at random as justified.
The outcome measure C-E also posits a challenge due to the relative rarity (n = 273). This measure was a predefined study criterion restricted to unequivocally documented death related to coronary artery disease or incident nonfatal myocardial infarction [27,28]. To test the restrictiveness of our findings to C-E as an outcome, we provided the same analysis with a looser outcome that measures any incidence of CVD (n = 655). In Appendix Table 3, we applied the same analysis as in Table 3 for the CVD outcome and found similar results in hazards and interaction, but overall lower model fits. With this comparison, we view our results supported.
Concerning the causal character of our study, a limitation is the missing incorporation of time-varying measures. For instance, observing the AL score on multiple points in time would allow more sophisticated modelling to detect time-varying effects on the C-E incidence. Likewise, time-varying confounding could also change the association of AL and C-E. Although we tried to adjust for socio-demographic/economic, health-behavioural and health-related confounders between AL and C-E, we did not analyze time-varying measures for these confounders since they were unavailable to us. The issue of time-varying measures also highlights the importance of process-oriented analysis, which would allow investigation of mediation and moderation on the AL – C-E association over time and could also determine the influence of gendered coping responses to stress on the sex differences in C-E incidence and AL [15,16]. Such process-oriented analysis could also help to explain the substantial higher baseline hazards in C-E for males.
4.2. Conclusion
Our study contributes to three research subjects: First, on the discussion of AL scoring algorithms. Second, the applicability of the AL concept on C-E and related conditions. Third, the sex differences in C-E and AL. We conclude that the commonly used methods perform well. The simplicity of the count-based method has the advantage that it can be easily adapted to clinical practices; thus, we recommend using the count-based method for these settings. Our results give strong support for AL to be a valid predictor of C-E. In all models and irrespective of the scoring methods, AL remained a significant predictor of C-E. Concerning the sex differences in the C-E incidence, we showed with multiplicative and additive interaction analysis that at low levels of AL, the sex differences are larger, and at high levels of AL are lower. The additive interaction indicated that, despite the higher baseline risk for males experiencing C-E, females could benefit more from a potential intervention on AL. However, we would like to emphasize that more research on the physiological and psychological origins of the sex gap in the C-E incidence is needed and would suggest the analysis of time-varying AL levels and intermediate factors such as gendered stress coping patterns.
Funding
The authors thank the Heinz Nixdorf Foundation [Chairman: Martin Nixdorf; Past Chairman: Dr jur. Gerhard Schmidt (†)], for their generous support of this study. Parts of the study were also supported by the German Research Council (DFG) [DFG project: EI 969/2–3, ER 155/6-1;6-2, HO 3314/2-1;2-2;2–3;4-3, INST 58219/32-1, JO 170/8-1, KN 885/3-1, PE 2309/2-1, SI 236/8-1;9-1;10-1,], the German Ministry of Education and Science [BMBF project: 01EG0401, 01GI0856, 01GI0860, 01GS0820_WB2-C, 01ER1001D, 01GI0205], the Ministry of Innovation, Science, Research and Technology, North Rhine-Westphalia (MIWFT-NRW), the Else Kröner-Fresenius-Stiftung [project: 2015_A119] and the German Social Accident Insurance [DGUV project: FF-FP295]. Furthermore the study was supported by the Competence Network for HIV/AIDS, the deanship of the University Hospital and IFORES of the University Duisburg-Essen, the European Union, the German Competence Network Heart Failure, Kulturstiftung Essen, the Protein Research Unit within Europe (PURE), the Dr. Werner-Jackstädt Stiftung and the following companies: Celgene GmbH München, Imatron/GE-Imatron, Janssen, Merck KG, Philips, ResMed Foundation, Roche Diagnostics, Sarstedt AG&Co, Siemens HealthCare Diagnostics, Volkswagen Foundation.
Statement
The corresponding author has full access to all data in the study and final responsibility for the submission of the article for publication. Due to data security reasons (i.e., data contain potentially participant identifying information), the HNR Study does not allow sharing data as a public use file. Data requests can also be addressed to: recall@uk-essen.de.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors express their gratitude to all study participants of the Heinz Nixdorf Recall (HNR) Study, the personnel of the HNR study center and the EBT-scanner facilities, the investigative group and all former employees of the HNR study. The authors also thank the Advisory Board of the HNR Study: T. Meinertz, Hamburg, Germany (Chair); C. Bode, Freiburg, Germany; P.J. de Feyter, Rotterdam, Netherlands; B. Güntert, Hall i.T., Austria; F. Gutzwiller, Bern, Switzerland; H. Heinen, Bonn, Germany; O. Hess (†), Bern, Switzerland; B. Klein (†), Essen, Germany; H. Löwel, Neuherberg, Germany; M. Reiser, Munich, Germany; G. Schmidt (†), Essen, Germany; M. Schwaiger, Munich, Germany; C. Steinmüller, Bonn, Germany; T. Theorell, Stockholm, Sweden; and S.N Willich, Berlin, Germany.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.cpnec.2021.100089.
Appendix.
Appendix Table 1.
Missing Values in Analysis Sample.
| Biomarker | MV | % of TS (N = 4368) |
|---|---|---|
| LDL-C | 21 | 0.48 |
| HDL-C* | 33 | 0.76 |
| Triglyceride | 22 | 0.50 |
| Glucose | 23 | 0.53 |
| Waist-Hip-Ratio | 12 | 0.27 |
| C-reactive Protein | 31 | 0.71 |
| Fibrinogen | 212 | 4.85 |
| DHEA-S* | 76 | 1.74 |
| Homocysteine | 330 | 7.55 |
| Sys. blood Pressure | 378 | 8.65 |
| Dias. blood Pressure | 4 | 0.09 |
| Albumin | 4 | 0.09 |
| Creatinine | 212 | 4.85 |
| Allostatic load | 869 | 19.89 |
Appendix Table 2. Unpaired t-test of AL scores before and after imputation
| Unpaired t-test | Ha: diff <0; Pr(T < t) | Ha: diff ! = ; 0 Pr(|T | > |t |) | Ha: diff >0; Pr(T > t) |
|---|---|---|---|
| Z-scoring | 0.631 | 0.739 | 0.369 |
| Count-based | 0.555 | 0.889 | 0.444 |
| LRM | 0.637 | 0.726 | 0.363 |
Appendix Table 3. Estimates and fit statistics of AL scoring methods on CVD with and without covariate inclusion
| M0 without controls | Z-Scoring | Count-based | LRM |
|---|---|---|---|
| Hazard Ratio [CI] | 1.084*** [1.075,1.094] | 1.420*** [1.355,1.489] | 2.704*** [2.438,2.999] |
| Somers' D | 0.373 | 0.314 | 0.408 |
| Harrell's C | 0.686 | 0.657 | 0.704 |
| AIC | 10475.1 | 10483.4 | 10340.8 |
| Pseudo-R2 | 0.017 | 0.017 | 0.030 |
| ROC-Area [CI] | 0.673 [0.644, 0.703] | 0.671 [0.635, 0.697] | 0.703 [0.660, 0.720] |
| ROC-M0 equality test: | Chi2 = 3.53; prob > Chi2 = 0.170 | ||
| M1 with controls | Z-Scoring | Count-based | LRM |
| Hazard Ratio [CI] | 1.055*** [1.039,1.071] | 1.206*** [1.141,1.276] | 1.814*** [1.559,2.112] |
| Somers' D | 0.453 | 0.459 | 0.457 |
| Harrell's C | 0.726 | 0.729 | 0.728 |
| AIC | 10261.5 | 10259.0 | 10243.7 |
| Pseudo-R2 | 0.039 | 0.039 | 0.041 |
| ROC-Area [CI] | 0.715 [0.685, 0.745] | 0.7237 [0.693, 0.753] | 0.714 [0.684, 0.744] |
| ROC-M1 equality test | Chi2 = 6.37; Prob > Chi2 = 0.041 | ||
| M2 AL-sex interaction | Z-Scoring | Count-based | LRM |
| AL- Hazard Ratio [CI] | 1.044*** [1.022,1.067] | 1.155*** [1.083,1.232] | 1.643*** [1.369,1.971] |
| Sex = Female (2) - Hazard Ratio [CI] | 0.473*** [0.388,0.576] | 0.350*** [0.271,0.453] | 0.588*** [0.472,0.731] |
| AL-sex interaction Hazard Ratio [CI] |
1.019 [0.992,1.047] | 1.181** [1.060,1.317] | 1.314* [1.010,1.710] |
| Somers' D | 0.453 | 0.460 | 0.457 |
| Harrell's C | 0.726 | 0.730 | 0.728 |
| AIC | 10261.7 | 10252.4 | 10241.6 |
| Pseudo-R2 | 0.039 | 0.040 | 0.041 |
| ROC-Area [CI] | 0.724 [0.695,0.753] | 0.732 [0.703,0.761] | 0.730 [0.700,0.759] |
| ROC-M2 equality test | Chi2 = 5.11; Prob > Chi2 = 0.077 | ||
Note: 95% confidence intervals in brackets * p < 0.05, **p < 0.01, ***p < 0.001.
Appendix Fig. 1.
Schoenfeld residual plot of M2 Table 3. Note: Scaled Schoenfeld residuals for the sex-AL interaction. The dashed line expresses the slope. A nonzero slope would equal a violation of the PH assumption and imply time-dependency.
Appendix B. Supplementary data
The following is/are the supplementary data to this article:
References
- 1.McEwen B.S., Stellar E. Stress and the individual. Mechanisms leading to disease. Arch. Intern. Med. 1993;153(18):2093–2101. https://doi:10.1001/archinte.1993.00410180039004 [PubMed] [Google Scholar]
- 2.Schulkin J. MIT Press; Cambridge, MA, US, xvi: 2003. Rethinking Homeostasis: Allostatic Regulation in Physiology and Pathophysiology; p. 296. [Google Scholar]
- 3.McEwen B.S., Gianaros P.J. Stress- and allostasis-induced brain plasticity. Annu. Rev. Med. 2011;62:431–445. doi: 10.1146/annurev-med-052209-100430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.McEwen B.S. Brain on stress: how the social environment gets under the skin. Proc. Natl. Acad. Sci. Unit. States Am. 2012;109(Suppl 2):17180–17185. doi: 10.1073/pnas.1121254109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Beckie T.M. A systematic review of allostatic load, health, and health disparities. Biol. Res. Nurs. 2012;14(4):311–346. doi: 10.1177/1099800412455688. [DOI] [PubMed] [Google Scholar]
- 6.Guidi J., Lucente M., Sonino N., Fava G.A. Allostatic load and its impact on health: a systematic review. Psychother. Psychosom. 2020;1–17 doi: 10.1159/000510696. [DOI] [PubMed] [Google Scholar]
- 7.Lozano R., Naghavi M., Foreman K., Lim S., Shibuya K., Aboyans V., Murray J.L.C. Global and regional mortality from 235 causes of death for 20 age groups in 1990 and 2010: a systematic analysis for the Global Burden of Disease Study 2010. Lancet. 2012;380(9859):2095–2128. doi: 10.1016/S0140-6736(12)61728-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ohlin B., Nilsson P.M., Nilsson J.-A., Berglund G. Chronic psychosocial stress predicts long-term cardiovascular morbidity and mortality in middle-aged men. Eur. Heart J. 2004;25(10):867–873. doi: 10.1016/j.ehj.2004.03.003. [DOI] [PubMed] [Google Scholar]
- 9.Chyu L., Upchurch D.M. A longitudinal analysis of allostatic load among a multi-ethnic sample of midlife women: findings from the study of women's health across the nation. WHI. 2018;28(3):258–266. doi: 10.1016/j.whi.2017.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Danese A., McEwen B.S. Adverse childhood experiences, allostasis, allostatic load, and age-related disease. Physiol. Behav. 2012;106(1):29–39. doi: 10.1016/j.physbeh.2011.08.019. [DOI] [PubMed] [Google Scholar]
- 11.Gillespie S.L., Anderson C.M., Zhao S., Tan Y., Kline D., Brock G., Joseph J.J. Allostatic load in the association of depressive symptoms with incident coronary heart disease: the Jackson Heart Study. Psychoneuroendocrinology. 2019;109:104369. doi: 10.1016/j.psyneuen.2019.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gianaros P.J., Jennings J.R. Host in the machine: a neurobiological perspective on psychological stress and cardiovascular disease. Am. Psychol. 2018;73(8):1031–1044. doi: 10.1037/amp0000232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.McEwen B.S. Sex, stress and the hippocampus: allostasis, allostatic load and the aging process. Neurobiol. Aging. 2002;23(5):921–939. doi: 10.1016/S0197-4580(02)00027-1. [DOI] [PubMed] [Google Scholar]
- 14.Oyola M.G., Handa R.J. Hypothalamic–pituitary–adrenal and hypothalamic–pituitary–gonadal axes: sex differences in regulation of stress responsivity. Stress. 2017;20(5):476–494. doi: 10.1080/10253890.2017.1369523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Williams D.R. The health of men: structured inequalities and opportunities. Am. J. Publ. Health. 2008;98(Supp 1):150–157. doi: 10.2105/AJPH.98.Supplement_1.S150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Juster R.P., Pruessner J.C., Desrochers A.B., Bourdon O., Durand N., Wan N., Lupien S.J. Sex and gender roles in relation to mental health and allostatic load. Psychosom. Med. 2016;78(7):788–804. doi: 10.1097/PSY.0000000000000351. [DOI] [PubMed] [Google Scholar]
- 17.Mair C.A., Cutchin M.P., Peek M.K. Allostatic load in an environmental riskscape: the role of stressors and gender. Health Place. 2011;17(4):978–987. doi: 10.1016/j.healthplace.2011.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Juster R.P., Lupien S. A sex-and gender-based analysis of allostatic load and physical complaints. Gend. Med. 2012;9(6):511–523. doi: 10.1016/j.genm.2012.10.008. [DOI] [PubMed] [Google Scholar]
- 19.Seeman T.E., Singer B.H., Ryff C.D., Love G.D., Levy-Storms L. Social relationships, gender, and allostatic load across two age cohorts. Psychosom. Med. 2002;64(3):395–406. doi: 10.1097/00006842-200205000-00004. [DOI] [PubMed] [Google Scholar]
- 20.Brooks K.P., Gruenewald T., Karlamangla A., Hu P., Koretz B., Seeman T.E. Social relationships and allostatic load in the MIDUS study. Health Psychol. 2014;33:1373–1381. doi: 10.1037/a0034528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Seeman T.E. Price of adaptation—allostatic load and its health Consequences. Arch. Intern. Med. 1997;157(19):2259. doi: 10.1001/archinte.1997.00440400111013. [DOI] [PubMed] [Google Scholar]
- 22.Duong M.T., Bingham B.A., Aldana P.C., Chung S.T., Sumner A.E. Variation in the calculation of allostatic load score: 21 examples from NHANES. J. of Racial and Ethnic Health Disparities. 2017;4(3):455–461. doi: 10.1007/s40615-016-0246-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Li Y., Rosemberg M.-A.S., Dalton V.K., Lee S.J., Seng J.S. Exploring the optimal allostatic load scoring method in women of reproductive age. J. Adv. Nurs. 2019;75(11):2548–2558. doi: 10.1111/jan.14014. [DOI] [PubMed] [Google Scholar]
- 24.McLoughlin S., Kenny R.A., McCrory C. Does the choice of Allostatic Load scoring algorithm matter for predicting age-related health outcomes? Psychoneuroendocrinology. 2020;120:104789. doi: 10.1016/j.psyneuen.2020.104789. [DOI] [PubMed] [Google Scholar]
- 25.Stang A., Moebus S., Dragano N., Beck E.M., Möhlenkamp S., Schmermund A., Jöckel K.H. Heinz Nixdorf recall study investigation group. Baseline recruitment and analyses of nonresponse of the Heinz Nixdorf recall study: identifiability of phone numbers as the major determinant of response. Eur. J. Epidemiol. 2005;20(6):489–496. doi: 10.1007/s10654-005-5529-z. [DOI] [PubMed] [Google Scholar]
- 26.Dragano N., Verde P.E., Moebus S., Stang S., Schmermund A., Roggenbuck U., Siegrist J. Subclinical coronary atherosclerosis is more pronounced in men and women with lower socioeconomic status: associations in a population-based study Coronary atherosclerosis and social status. Eur. J. Cardiovasc. Prev. Rehabil. 2007;14(4):568–574. doi: 10.1097/HJR.0b013e32804955c4. [DOI] [PubMed] [Google Scholar]
- 27.Schmermund A., Möhlenkamp S., Stang A., Grönemeyer D., Seibel R., Hirche H.…Erbel R. Assessment of clinically silent atherosclerotic disease and established and novel risk factors for predicting myocardial infarction and cardiac death in healthy middle-aged subjects: rationale and design of the Heinz Nixdorf RECALL Study. Risk Factors, Evaluation of Coronary Calcium and Lifestyle. Am. Heart J. 2002;144(2):212–218. doi: 10.1067/mhj.2002.123579. [DOI] [PubMed] [Google Scholar]
- 28.Erbel R., Möhlenkamp S., Moebus S., Schmermund A., Lehmann N., Stang A., Jöckel K.-H. Coronary risk stratification, discrimination, and reclassification improvement based on quantification of subclinical coronary atherosclerosis. J. Am. Coll. Cardiol. 2010;56(17):1397–1406. doi: 10.1016/j.jacc.2010.06.030. [DOI] [PubMed] [Google Scholar]
- 29.Hawkley L.C., Lavelle L.A., Berntson G.G., Cacioppo J.T. Mediators of the relationship between socioeconomic status and allostatic load in the Chicago health, aging, and social relations study (CHASRS) Psychophysiology. 2011;48(8):1134–1145. doi: 10.1111/j.1469-8986.2011.01185.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rote S. Marital disruption and allostatic load in late life. J. Aging Health. 2017;29(4):688–707. doi: 10.1177/0898264316641084. [DOI] [PubMed] [Google Scholar]
- 31.Gandhi S., Goodman S.G., Greenlaw N., Ford I., McSkimming P., Ferrari R., Udell J.A. Living alone and cardiovascular disease outcomes. Heart. 2019;105(14):1087–1095. doi: 10.1136/heartjnl-2018-313844. [DOI] [PubMed] [Google Scholar]
- 32.Kandler U., Meisinger C., Baumert J., Löwel H. Living alone is a risk factor for mortality in men but not women from the general population: a prospective cohort study. BMC Publ. Health. 2007;7(1):1–8. doi: 10.1186/1471-2458-7-335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ryan A.M., Gee G.C., Laflamme D.F. The Association between self-reported discrimination, physical health and blood pressure: findings from African Americans, Black immigrants, and Latino immigrants in New Hampshire. J. of Healthc. for the Poor and Underserved. 2006;17(2):116–132. doi: 10.1353/hpu.2006.0092. [DOI] [PubMed] [Google Scholar]
- 34.Petrovic D., Pivin E., Ponte B., Dhayat N., Pruijm M., Ehret G., Stringhini S. Sociodemographic, behavioral and genetic determinants of allostatic load in a Swiss population-based study. Psychoneuroendocrinology. 2016;67:76–85. doi: 10.1016/j.psyneuen.2016.02.003. [DOI] [PubMed] [Google Scholar]
- 35.Howell B.R., Sanchez M.M. Understanding behavioral effects of early life stress using the reactive scope and allostatic load models. Dev. Psychopathol. 2011;23(4):1001–1016. doi: 10.1017/S0954579411000460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rubin D.B. John Wiley & Sons; New York: 1987. Multiple Imputation for Nonresponse in Surveys. [Google Scholar]
- 37.Graham J.W., Olchowski A.E., Gilreath T.D. How many imputations are really needed? Some practical clarifications of multiple imputation theory. Prev. Sci. 2007;8(3):206–213. doi: 10.1007/s11121-007-0070-9. [DOI] [PubMed] [Google Scholar]
- 38.Robertson T., Beveridge G., Bromley C. Allostatic load as a predictor of all-cause and cause-specific mortality in the general population: evidence from the Scottish Health Survey. PLoS One. 2017;12(8) doi: 10.1371/journal.pone.0183297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cox D.R., Oakes D. Chapman and Hall; London: 1984. Analysis of Survival Data. [Google Scholar]
- 40.Malik S., Wong N.D., Franklin S.S., Kamath T.V., L'Italien G.J., Pio J.R., Williams G.R. Impact of the metabolic syndrome on mortality from coronary heart disease, cardiovascular disease, and all causes in United States adults. Circulation. 2004;110(10):1245–1250. doi: 10.1161/01.CIR.0000140677.20606.0E. [DOI] [PubMed] [Google Scholar]
- 41.Schoenfeld D. Partial residuals for the proportional hazards regression model. Biometrika. 1982;69(1):239–241. doi: 10.1093/biomet/69.1.239. [DOI] [Google Scholar]
- 42.Vatcheva K.P., Lee M., McCormick J.B., Rahbar M.H. The effect of ignoring statistical interactions in regression analyses conducted in epidemiologic studies: an example with survival analysis using Cox proportional hazards regression model. Epidemiol. Open Access. 2016;6(1) doi: 10.4172/2161-1165.1000216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Anderson D.G., Putnam D., Lavik E.B., Mahmood T.A., Langer R. Biomaterial microarrays: rapid, microscale screening of polymer–cell interaction. Biomaterials. 2005;26(23):4892–4897. doi: 10.1016/j.biomaterials.2004.11.052. [DOI] [PubMed] [Google Scholar]
- 44.VanderWeele T.J., Knol M.J. A tutorial on interaction. Epidemiol. Methods. 2014;3(1):33–72. doi: 10.1515/em-2013-0005. [DOI] [Google Scholar]
- 45.Logan J.G., Barksdale D.J. Allostasis and allostatic load: expanding the discourse on stress and cardiovascular disease. J. Clin. Nurs. 2008;17(7B):201–208. doi: 10.1111/j.1365-2702.2008.02347.x. [DOI] [PubMed] [Google Scholar]
- 46.Seeman T.E., Gruenewald T., Karlamangla A., Sidney S., Liu K., Schwartz J. Modeling multisystem biological risk in young adults: the coronary artery risk development in young adults study. Am. J. Hum. Biol. 2010;22(4):463–472. doi: 10.1002/ajhb.21018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Seplaki C.L., Goldman N., Weinstein M., Lin Y.-H. Measurement of cumulative physiological dysregulation in an older population. Demography. 2006;43(1):165–183. doi: 10.1353/dem.2006.0009. [DOI] [PubMed] [Google Scholar]
- 48.Piazza J.R., Stawski R.S., Sheffler J.L. Age, daily stress processes, and allostatic load: a longitudinal study. J.of Aging & Health. 2019;31(9):1671–1691. doi: 10.1177/0898264318788493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Liu S.H., Juster R.P., Dams-O’Connor K., Spicer J. Allostatic load scoring using item response theory. Compr. Psychoneuroendocr. 2021;5:100025. doi: 10.1016/j.cpnec.2020.100025. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.