Two-dimensional reciprocal cross entropy multi-threshold combined with improved firefly algorithm for lung parenchyma segmentation of COVID-19 CT image

Abstract

The lesions of COVID-19 CT image show various kinds of ground-glass opacity and consolidation, which are distributed in left lung, right lung or both lungs. The lung lobes are uneven and it have similar gray value to the surrounding arteries, veins, and bronchi. The lesions of COVID-19 have different sizes and shapes in different periods. Accurate segmentation of lung parenchyma in CT image is a key step in COVID-19 detection and diagnosis. Aiming at the unideal effect of traditional image segmentation methods on lung parenchyma segmentation in CT images, a lung parenchyma segmentation method based on two-dimensional reciprocal cross entropy multi-threshold combined with improved firefly algorithm is proposed. Firstly, the optimal threshold method is used to realize the initial segmentation of the lung, so that the segmentation threshold can change adaptively according to the detailed information of lung lobes, trachea, bronchi and ground-glass opacity. Then the lung parenchyma is further processed to obtain the lung parenchyma template, and then the defective template is repaired combined with the improved Freeman chain code and Bezier curve. Finally, the lung parenchyma is extracted by multiplying the template with the lung CT image. The accuracy of lung parenchyma segmentation has been improved in the contrast clarity of CT image and the consistency of lung parenchyma regional features, with an average segmentation accuracy rate of 97.4%. The experimental results show that for COVID-19 and suspected cases, the method has an ideal segmentation effect, and it has good accuracy and robustness.

1. Introduction

1.1. Background problem domain

COVID-19 is an acute respiratory infectious disease caused by the type of new coronavirus infection, which is highly contagious [1], [2]. Until October 6, 2021, there have been more than 235.67 million confirmed cases of COVID-19 worldwide and 4.81 million cases died. With the rapid development of CT, CT images have been able to provide high-definition lung images with high contrast among lung tissues [3]. Therefore, high-resolution CT images are gradually used for the diagnosis of COVID-19 [4]. Computer aided detection (CAD) technology can effectively detect various ground-glass opacity from lung CT images, so as to lay a foundation for the early diagnosis and treatment of COVID-19 [5]. The main processes of CAD technology based on CT images include preprocessing, lung parenchyma segmentation, candidate lesion segmentation, feature extraction and optimal selection, disease classification, etc [6]. Among them, the most important step is lung parenchyma segmentation, and it is also a key link affecting the stability and accuracy of CAD. Rapid and accurate segmentation of lung parenchyma from CT images is the key to the diagnosis of COVID-19, which has very important practical significance and clinical value.

1.2. Review of literature

The main clinical symptoms of COVID-19 are fever, cough and fatigue, which may lead to acute respiratory distress syndrome (ARDS) [7], [8]. The main obstacle to controlling the spread of this disease is the lack of efficient detection methods. Reverse transcription polymerase chain reaction (RT-PCR) is the gold standard for the diagnosis of COVID-19, but it takes 4–6 h to obtain the results, and the RT-PCR test also has a high false negative rate [9]. It takes several times of RT-PCR test every few days to confirm the diagnostic results [10]. In addition, RT-PCR reagents are also insufficient in many severely epidemic areas [11]. In contrast, CT examination has been widely used in various hospitals. In clinical practice, CT is a more efficient and safer method to diagnose COVID-19 by combining clinical symptoms and signs [12]. At the same time, CT images can also be used in the tracking and prognosis of COVID-19. The size and shape of COVID-19 ground-glass opacity (GGO) are the main factors for COVID-19 tracking and prognosis. In the early stage of COVID-19, the density of GGO is low. The GGO is not obvious, and it is easy to cause the miss diagnosis. The CAD technology based on CT images can accurately classify COVID-19, and the real time observation of GGO changes can improve prognosis and reduce mortality. The GGO of COVID-19 involve both lungs. The manifestations of the lesions are diverse, and the CT images of GGO change rapidly. Therefore, CT diagnosis and timely treatment for COVID-19 patients are very important to improve tracking and prognosis of COVID-19. The lung image of early patients show multiple small patchy opacities. Advanced patients show multiple GGO and infiltration shadow of both lungs, and severe patients can have lung consolidation [13]. In conclusion, medical imaging plays a vital role in limiting virus transmission and diagnosing COVID-19.

In the medical image diagnosis of COVID-19, due to the need to screen and treat a large number of patients, in order to reduce the workload of doctors, artificial intelligence technology can be used to automatically diagnose the medical images and calculate the severity of infection [14], [15]. Jin [16] has designed an AI-assisted diagnosis system, which can achieve comparable performance to that of doctors, and the system has been deployed to many hospitals. In addition, self-diagnosis technology can also predict high-risk patients according to the clinical characteristics of COVID-19, which can help doctors find and treat the disease [17]. Wang [18] proposed the PatchShuffle convolutional neural network (PSCNN) and applied it for COVID-19 image classification to highlight the influence of neighboring pixels on the classification results of central pixels, so as to improve the classification accuracy of COVID-19. Zhang [19] divides the COVID-19 image into self-similar blocks and non-self-similar blocks by using the Pseudo Zernike moment and deep stacked sparse autoencoder. The Pseudo Zernike moments of the self-similar blocks are calculated to select the most robust moment. The CT image of COVID-19 is diagnosed by quantizing and modulating the amplitude of the pseudo Zernike moments.

In the lung CT image, the structure of each tissue is complex and the shape is different. The difference of gray contrast between the lung and the surrounding tissues (muscles, blood vessels) is low. These factors increase the difficulty of lung parenchymal segmentation. Threshold segmentation is a method of image segmentation, which segments the target and background in the image by selecting an appropriate threshold. The threshold segmentation method divides the original CT image pixel into several subsets by setting a threshold to segment the lung parenchyma. It mainly uses the difference in grayscale between the lung parenchyma to be extracted from the CT image and the lung organs to perform image segmentation. The traditional segmentation threshold method of lung images with a small time complexity, but its stability is not high [20]. When the threshold is not selected properly, it is easy to ignore the edge lesions and the surrounding tissues. The gray contrast is not obvious and the region of interest may be over segmented. The appropriate threshold method can achieve better segmentation, and it segments the CT image into lung parenchyma target region and background region. When the image is complex or there are many target objects [21], [22], the multi-threshold segmentation is needed. It aims to effectively segment background and multiple targets, which is an extension of single threshold segmentation.

The traditional threshold segmentation methods find the appropriate threshold by setting specific criteria, and the operation speed is slow, such as Otsu method [23], minimum error method [24], image entropy method [25] and so on. Many scholars have proposed improved algorithms to increase the speed of segmentation. Raja [26] used particle swarm optimization (PSO) with improved inertia factors to optimize the Otsu threshold segmentation method. Rajinikanth [27] proposed a fast threshold segmentation method based on Otsu criterion and line intercept histogram. Wang [28] proposed an improved adaptive genetic algorithm, combined with the two-dimensional fisher image segmentation evaluation function for global optimization, in order to improve the speed of the segmentation threshold. In recent years, image entropy threshold segmentation has been widely used in image segmentation. Zhou [29] used the maximum entropy of one-dimensional grayscale to segment gray image effectively, but the algorithm is sensitive to noise. In order to overcome the noise sensitivity, Estanon [30] proposed a threshold segmentation method of two-dimensional entropy. This method makes full use of the gray value and local spatial information of the image, and it can achieve good segmentation results. But this method still has the problem of time-consuming.

Most of the threshold segmentation methods are time-consuming, while the multi-threshold segmentation method has a larger amount of calculation, so its calculation time is longer and it occupies more memory. Aiming at this problem, many scholars combine the multi-threshold segmentation with the optimization algorithm. Chakraborty [31] used PSO algorithm, Darwin particle swarm optimization (DPSO) and fractional order Darwin particle swarm optimization (FODPSO) to find the optimal threshold under the criterion of maximum variance between classes respectively. Horng [32] proposed to find the optimal threshold under the minimum cross entropy by using the honey-bee mating optimization (ABCA) algorithm. Ozyurt [33] combined genetic algorithm (GA) and improved maximum fuzzy entropy for multi-threshold segmentation. These methods improve the speed of finding multi-threshold, but PSO, GA and ABCA algorithm are easy to fall into local extremum, which makes the optimization results inaccurate.

Hrosik [34] proposed a firefly algorithm (FA) for multi-mode optimization. The algorithm is optimized by the phototaxis between fireflies, and it has the ability of fast global search. Wu [35] solved multiple constrained optimization problems by using firefly algorithm. Horng [36] combined the firefly algorithm and the minimum cross entropy criterion for image multi-threshold segmentation, and it achieved a good result. In this paper, the firefly algorithm is combined with two-dimensional entropy multi-threshold segmentation method to segment multi-target images.

There are some state-of-the-art methods about image segmentation algorithm reported. Alqazzaz [37] proposed an improved SegNet model for image segmentation. Through the global gray information to guide the curve to approach the target edge, it has stronger segmentation adaptability for the image with uneven foreground gray level. However, this model does not abstract the higher-level semantic features for image segmentation. Therefore, when the target size is small, the background is complex, and the features are not significant, the image segmentation effect is still not good. Ghaffari [38] proposed a fast and robust fuzzy c-means clustering algorithm (FRFCM) based on the morphological reconstruction and membership filtering. This algorithm effectively uses the local spatial information of the image and it replaces the traditional distance calculation with the membership filtering to ensure the superiority of anti-noise performance. But the clustering result is too smooth, and too much detailed information will be lost. Li [39] proposed a contextualized convolutional neural network (Co-CNN) structure. This method integrates the multi-level image content into a unified network, and the weighted multiscale features are trained at each pixel position. However, this method is realized by introducing different scales of input, which cannot realize the human-like attention mechanism, and the algorithm runs for a long time. Basukala [40] proposed a dual tree-complex wavelet transform (DT-CWT) image segmentation algorithm. MRF sequences are constructed in wavelet domain multi-resolution, which are nested with each other, and this method realizes the effective image segmentation by recursive operation between adjacent scales in the wavelet domain. This algorithm not only represents the image structure information, but also better describes the instability of the image. However, the wavelet transform lacks translation invariance, and it can only model the feature information of the image in the horizontal, vertical and 45 directions. Therefore, the continuity of image segmentation based on wavelet is not ideal in obtaining the target edge, and there is a certain “hole” phenomenon in the detection result. Yan [41] proposed a GAN-Unet image segmentation method. This model consists of two parts including 2D and 3D Unet. The 2D part extracts the features in the slice, and the 3D part integrates the information of the slice. The network can be used for organ and lesion segmentation. However, because the model uses 3D convolutional network, it becomes difficult to train and it requires higher demand for hardware.

1.3. Highlights

The highlights of this work can be summarized as the following: (i) a multi-threshold segmentation method based on two-dimensional reciprocal cross entropy is proposed to make up for the problem of undefined and zero value of Shannon cross entropy due to logarithm operation; (ii) aiming at the problem the traditional histogram only considers the background and the target area, the edge and the noise information are ignored. This paper improves the segmentation of the binary histogram that is divided the four-region histogram into two-region of the target and the background, and the gray information is fully considered; (iii) traditional threshold segmentation algorithms only use the value of gray level in the image without considering the spatial neighborhood information of pixels, which greatly increases the ratio of misclassification between the target and the background of the gray image. Aiming at this problem, a weighted fuzzy threshold segmentation based on the spatial neighborhood information is proposed; (iv) aiming at the problem that the standard firefly algorithm is easy to fall into local optimization, this paper improves the attraction term by using exponential distribution in the position movement and the exponential decreasing inertia weight to enhance the global detection ability. The step size monotone decreasing mode is used to improve the random item to enhance the local mining ability in the later stage of the optimization; (v) the lung parenchyma template is repaired by the proposed eight-direction Freeman chain code combined with quadratic Bezier curve can make up for the under-segmentation problem when repairing large-area defects with straight lines. It has flexible adjustment to better meet the characteristics of lung parenchyma edge, which can achieve a good repair effect.

1.4. Paper structure

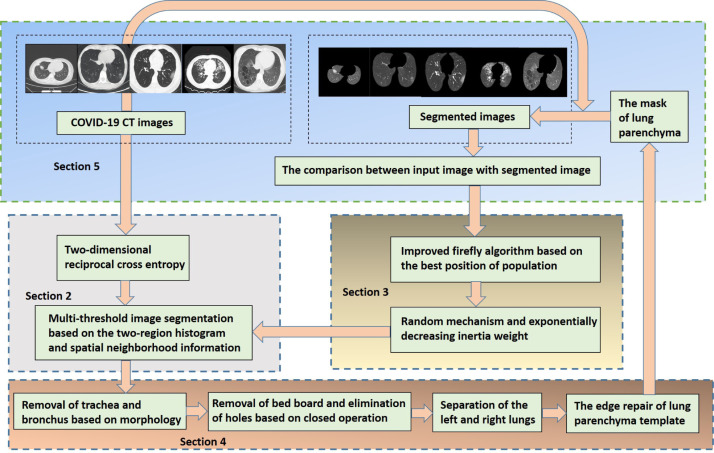
The rest of this paper is organized as follows. Section 2 describes the two-dimensional reciprocal cross entropy multi-threshold image segmentation based on the two-region histogram and spatial neighborhood information. In Section 3, we propose the improved firefly algorithm to optimize the parameters of the two-dimensional reciprocal cross entropy. Section 4 describes the refinement segmentation of lung parenchyma. The defective template is repaired combined with the improved Freeman chain code and Bezier curve, and then the lung parenchyma is extracted by multiplying the template with the lung CT image. In Section 5, we show the simulation experiments for the different kinds of COVID-19 CT images. The paper is structured as shown in Fig. 1.

Fig. 1.

Paper structure.

2. Two-dimensional reciprocal cross entropy image segmentation

2.1. Two-dimensional reciprocal cross entropy single-threshold image segmentation

The size of the gray image $I$ is set to $M\times N$. $I(x,y)$ represents the gray value of the pixel $(x,y)$ in the image $I$. $1\le x\le M$, $1\le y\le N$, and the gray level of the image is $L$. The average gray value of the $n\times n$ neighborhood corresponding to each pixel $(x,y)$ of the image $I$ is defined as $G(x,y)$, and its mathematical expression is: $G(x,y)=\frac{1}{n^2}{\sum }_{i=-n/2}^{n/2}{\sum }_{j=-n/2}^{n/2}I(x+i,y+j)$.

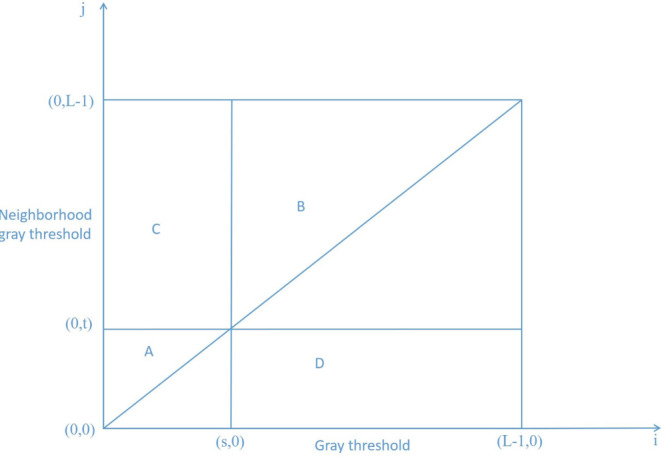
The frequency of simultaneous occurrence of the pixel gray value $i$ at a certain position in the image $I(x,y)$ and the pixel gray value $j$ at the corresponding position of the neighborhood average gray image $G(x,y)$ is set as $r_{ij}$. The corresponding joint probability density is defined as $p_{ij}=r_{ij}/(M\times N)(i,j=0,1,\dots ,L-1)$. Where: ${\sum }_{i=0}^{L-1}{\sum }_{j=0}^{L-1}{p}_{ij}=1$. $p_{ij}$ constitutes a two-dimensional histogram of the image, as shown in Fig. 2. Zone $A$ and zone $B$ represent the background and goal respectively; Zone $C$ and zone $D$ represent the edge and noise respectively (zone $C$ and zone $D$ are usually ignored when calculating the reciprocal cross entropy). The probabilities of zone $A$ and zone $B$ are: $P_A={\sum }_{i=0}^s{\sum }_{j=0}^t{p}_{ij}$, $P_B={\sum }_{i=s+1}^{L-1}{\sum }_{j=t+1}^{L-1}{p}_{ij}$.

Fig. 2.

Two-dimensional histogram.

The normalized probabilities corresponding to the gray level in zone $A$ and zone $B$ are: $P_{ij}^A=\frac{p_{ij}}{{\sum }_{i=0}^s{\sum }_{j=0}^t{p}_{ij}}$, $P_{ij}^B=\frac{p_{ij}}{{\sum }_{i=s+1}^{L-1}{\sum }_{j=t+1}^{L-1}{p}_{ij}}$.

The reciprocal cross entropy of the image corresponding to the threshold $(s,t)$ is defined as:

$$H(s,t)=H\left(A\right)+H\left(B\right)=-\sum _{i=0}^s\sum _{j=0}^t\frac{i\cdot j\cdot p_{ij}}{1+\frac{i\cdot j}{P_{ij}^A}}-\sum _{i=s+1}^{L-1}\sum _{j=t+1}^{L-1}\frac{i\cdot j\cdot p_{ij}}{1+\frac{i\cdot j}{P_{ij}^B}}$$ (1)

When $H(s,t)$ takes the minimum value, the best single threshold of the two-dimensional reciprocal cross entropy can be obtained: $(\dot{s},\dot{t})=arg{min}_{0\le s\le L-1}{min}_{0\le t\le L-1}H(s,t)$.

2.2. Two-dimensional reciprocal cross entropy multi-threshold image segmentation based on the improved histogram

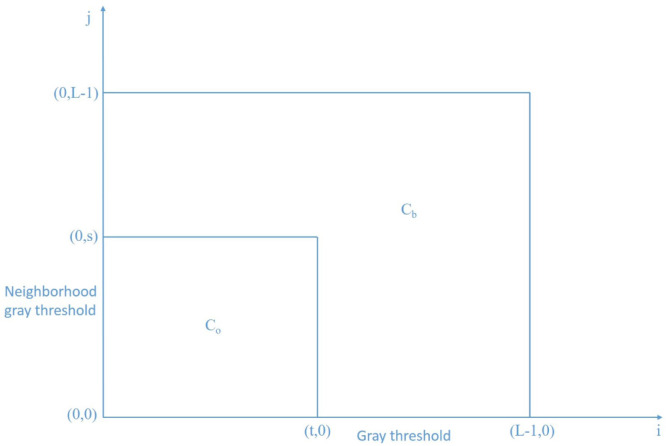
The traditional histogram only considers the background and the target area, but the edge and the noise information in area $C$ and $D$ are ignored, resulting in poor effect of the image segmentation. When calculating the optimal threshold, if the area C and D are ignored, the points with large difference between the pixel gray level and the average gray level of the neighborhood are not fully considered. These points may exist in area C and D, and the calculated optimal threshold will be biased and the segmentation results are inaccurate. In order to improve the quality of segmentation, this paper improves the division of the binary histogram, as shown in Fig. 3.

Fig. 3.

Segmentation of improved histogram.

In Fig. 3, $C$, $C_o$ and $C_b$ represent the whole area, target and background area respectively. The equations are:

$$C=\left\{(i,j)\right|i=0,1,\dots ,L-1;j=0,1,\dots ,L-1\}=\text{{}(x,y)|I(x,y)=0,1,\dots ,L-1;$$$$G(x,y)=0,1,\dots ,L-1\text{}}$$ (2)

$$C_o=\left\{(i,j)\right|i=0,1,\dots ,t;j=0,1,\dots ,s\}=\text{{}(x,y)|I(x,y)=0,1,\dots ,t;$$$$G(x,y)=0,1,\dots ,s\text{}}$$ (3)

$$C_b=C\setminus C_o$$ (4)

Where, $I(x,y)$ represents the gray value of the pixel $(x,y)$ in the image $I$; $G(x,y)$ represents the average gray value of the $n\times n$ neighborhood corresponding to each pixel $(x,y)$ of the image $I$. The threshold is used to change the four-region segmentation of the histogram into two-region segmentation of the target and the background, and the gray information of the target and the background is fully considered, then the normalized probabilities corresponding to the gray level in zone $o$ and zone $b$ are: $P_{ij}^o=\frac{p_{ij}}{{\sum }_{i=0}^t{\sum }_{j=0}^s{p}_{ij}}$, $P_{ij}^b=\frac{p_{ij}}{{\sum }_{i=t+1}^{L-1}{\sum }_{j=s+1}^{L-1}{p}_{ij}}$.

The two-dimensional reciprocal cross target entropy and background entropy are respectively: $H\left(o\right)=-{\sum }_{i=0}^t{\sum }_{j=0}^s\frac{i\cdot j\cdot p_{ij}}{1+\frac{i\cdot j}{P_{ij}^o}}$, $H\left(b\right)=-{\sum }_{i=t+1}^{L-1}{\sum }_{j=s+1}^{L-1}\frac{i\cdot j\cdot p_{ij}}{1+\frac{i\cdot j}{P_{ij}^B}}$. The total entropy of two-dimensional reciprocal cross is: $H(t,s)=H\left(o\right)+H\left(b\right)$.

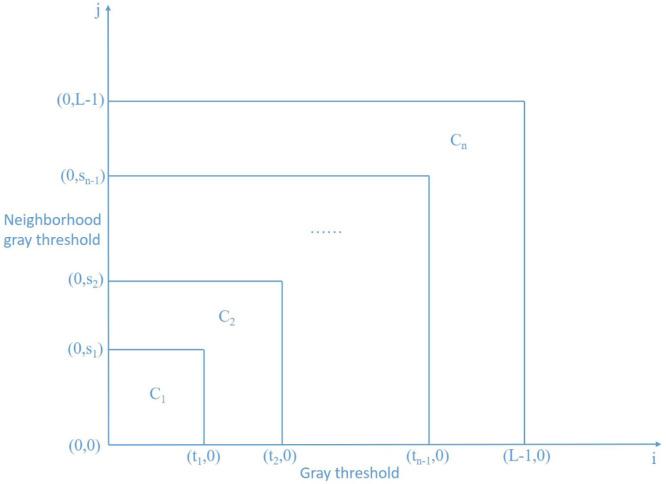
The lesions of COVID-19 CT image showed various ground-glass opacity and consolidation. The lung lobe is uneven and it has similar gray value to the surrounding arteries, veins and bronchus. Aiming at the problems of low contrast and fuzzy boundary in the traditional two-dimensional single-threshold lung image segmentation algorithm, it is proposed to extend the two-dimensional reciprocal cross entropy single-threshold to multi-threshold segmentation. The image $I$ is segmented by $n-1$ gray levels, and the two-dimensional reciprocal cross entropy single-threshold segmentation is extended to multi-threshold. The values of the threshold are ($t_1$, $s_1$)($t_2$, $s_2$)...($t_{n-1}$, $s_{n-1}$).

As shown in Fig. 4, the image $P$ is segmented into n classes $\{C_1,C_2,\dots ,C_n\}$. The normalized probability corresponding to the gray level $C_k(k=1,2,\dots ,n)$ is:

$$P_{ij}^{C_k}=\frac{p_{ij}}{\sum _{i=t_{k-1}+1}^{t_k}\sum _{j=s_{k-1}+1}^{s_k}{p}_{ij}}$$ (5)

Fig. 4.

Segmentation of two-dimensional multi-threshold histogram.

Assuming that {$i_1$, $i_2$, …, $i_{m+1}$} is a subset of $\{1,2,\dots ,n\}$, and the total entropy of the two-dimensional reciprocal cross is:

$$H(t_1,s_1,t_2,s_2,\dots ,t_{n-1},s_{n-1})=H\left(C_1\right)+H\left(C_2\right)+\cdots +H\left(C_n\right)=-\sum _{i=0}^{t_1}\sum _{j=0}^{s_1}\frac{i\cdot j\cdot p_{ij}}{1+\frac{i\cdot j}{P_{ij}^{C_1}}}-\sum _{i=t_1+1}^{t_2}\sum _{j=s_1+1}^{s_2}\frac{i\cdot j\cdot p_{ij}}{1+\frac{i\cdot j}{P_{ij}^{C_2}}}-\cdots -\sum _{i=t_k+1}^{L-1}\sum _{j=s_k+1}^{L-1}\frac{i\cdot j\cdot p_{ij}}{1+\frac{i\cdot j}{P_{ij}^{C_n}}}$$ (6)

2.3. Calculation of spatial neighborhood information

The traditional image threshold segmentation method only uses the gray value information in the image pixels but ignores the influence of the spatial information between the pixels, which makes the segmentation not very effect. In this paper, a threshold segmentation algorithm combined with fuzzy theory is proposed. The algorithm comprehensively uses the gray value and the spatial neighborhood information of image pixels to design the membership function and the evaluation standard of fuzzy distance to solve the optimal threshold solution.

2.3.1. Calculation of similarity between pixels in spatial neighborhood

This function is to calculate the similarity between the pixels in the neighborhood of the window and the central pixel. For $\forall x(m,n,f_{mn})\in W_{(x,y)}$, there is the following equation:

$$w(I(x,y),x(m,n,f_{mn}))=1-{|I(x,y)-x(m,n,f_{mn})|}_{\sigma }=1-\sum _{t=0}^n{\sigma }^{\left(t\right)}|I{(x,y)}^{\left(t\right)}-x{(m,n,f_{mn})}^{\left(t\right)}|=1-(0.5\times d_1(I(x,y),x(m,n,f_{mn}))\times h+0.5\times d_2(I(x,y),x(m,n,f_{mn}))\times c)$$ (7)

Where, $I(x,y)$ means that the value of pixel in the position $(x,y)$. $W_{(x,y)}$ represents the range of window centered on pixel $I(x,y)$, this paper selects eight neighborhoods for the range of window. $x(m,n,f_{mn})$ represents the pixels within the window. $w(I(x,y)$, $x(m,n,f_{mn}))$ represents the similarity weight between the pixels in the neighborhood of the window and the center pixel. ${\sigma }^{\left(t\right)}$ is the weight in the $t$th similarity measure. In this paper, two measures are taken: the geometric distance between the central pixel and the neighborhood pixels, the Euclidean distance of the gray value. $n$ is the number of the similarity measure; $|I{(x,y)}^{\left(t\right)}-x{(m,n,f_{mn})}^{\left(t\right)}|$ represents the similarity degree of the t-th similarity measure between pixels; $h$ is the maximum geometric distance from the central pixel in the neighborhood; $c$ is the normalization factor.

2.3.2. Calculation of fuzzy membership degree of spatial neighborhood information

This function is to calculate the membership degree of the spatial neighborhood information: in region $C_i$, the similarity of the pixels is calculated whose gray value is less than or equal to $(t_i,s_i)$ in the neighborhood of the center pixel as shown in Eq. (7), then sum and its calculation is shown in Eq. (8). Similarly, the similarity of the pixels is calculated whose gray value in the neighborhood of the window is greater than $(t_i,s_i)$ as shown in Eq. (9). Finally, the spatial neighborhood information is transformed into the range of (0,1) by normalization processed according to Eq. (10) and Eq. (11).

$${\mu }_{nsum1}=\sum _{s=0}^{n1}w(I(x,y),x(m,n,f_{mn}))$$ (8)

$${\mu }_{nsum2}=\sum _{s=0}^{n2}w(I(x,y),x(m,n,f_{mn}))$$ (9)

$${\mu }_{n1}=\frac{{\mu }_{nsum1}\times n1}{1+{\mu }_{nsum1}\times n1+{\mu }_{nsum2}\times n2}$$ (10)

$${\mu }_{n2}=\frac{{\mu }_{nsum2}\times n2}{1+{\mu }_{nsum1}\times n1+{\mu }_{nsum2}\times n2}$$ (11)

Where, $n1$ and $n2$ are the number of pixels in the window neighborhood under the conditions of Eq. (8) and Eq. (9) respectively.

2.3.3. Calculation of fuzzy membership function of gray value information

In the region $C_i$, the gray histogram of the image is calculated, and the whole gradient image is divided into two categories by using the threshold $(t_i,s_i)$. The value of threshold less than or equal to $(t_i,s_i)$ is called background, and the value of threshold greater than $(t_i,s_i)$ is called foreground. On this basis, the calculation of the mean value ${\mu }_0$ for the background class can be obtained:

$${\mu }_0=\frac{\sum _{i=t_{i-1}+1}^{t_i}\sum _{j=s_{i-1}+1}^{s_i}I(x,y)\times hist\left(I(x,y)\right)}{\sum _{i=t_{i-1}+1}^{t_i}\sum _{j=s_{i-1}+1}^{s_i}hist\left(I(x,y)\right)}$$ (12)

Similarity, the calculation of the mean value ${\mu }_1$ for the foreground class can be obtained:

$${\mu }_1=\frac{\sum _{i=t_i+1}^{t_{i+1}}\sum _{j=s_i+1}^{s_{i+1}}I(x,y)\times hist\left(I(x,y)\right)}{\sum _{i=t_i+1}^{t_{i+1}}\sum _{j=s_i+1}^{s_{i+1}}hist\left(I(x,y)\right)}$$ (13)

Where, $I(x,y)$ in Eq. (12) and Eq. (13) means that the value of pixel in the position $(i,j)$ is $f_{ij}$. $hist\left(I(x,y)\right)$ is the number of pixels whose value of pixel at $(i,j)$ is $f_{ij}$.

The fuzzy membership of the gray information of the image pixels is calculated: the maximum and minimum gray values are counted by scanning the gray information of each pixel in the image. In the region $C_i$, assuming that the threshold is $(t_i,s_i)$, the mean value is solved by Eq. (12) and Eq. (13), and then the gray information value of each pixel is taken out. The fuzzy membership degree of the gray information of the corresponding image pixels is calculated by Eq. (14) and Eq. (15), and the form is following:

$${\mu }_{g1}\left(I(x,y)\right)=1-\frac{|I(x,y)-{\mu }_0|}{I{(x,y)}^{f_{max}}-I{(x,y)}^{f_{min}}}$$ (14)

$${\mu }_{g2}\left(I(x,y)\right)=1-\frac{|I(x,y)-{\mu }_1|}{I{(x,y)}^{f_{max}}-I{(x,y)}^{f_{min}}}$$ (15)

Where, $I{(x,y)}^{f_{max}}$ is the maximum gray value of the image pixel; $I{(x,y)}^{f_{min}}$ is the minimum gray value of the image pixel; the maximum gray value and the minimum gray value are not equal; $0\le {\mu }_{gi}\left(I(x,y)\right)\le 1,i=1,2$.

2.3.4. The total membership function of pixels

In region $C_i$, the sum of the total membership degree of the image pixels greater than the threshold $(t_i,s_i)$ and less than the threshold $(t_i,s_i)$ is calculated respectively. Firstly, each pixel in the image is scanned, then the gray information and the spatial neighborhood information of the pixel are calculated respectively. The membership degree of the pixel that is less than the threshold $(t_i,s_i)$ is counted in Eq. (16). The membership degree of the pixel that is greater than the threshold $(t_i,s_i)$ is counted in Eq. (17). Finally, the values of the two parts are compared. If the result of Eq. (16) is greater than or equal to the result of Eq. (17), the pixel belongs to the class less than or equal to $(t_i,s_i)$, otherwise it belongs to class greater than $(t_i,s_i)$. The calculation is as following:

$$\mu \left(I(x,y)\right)=({\mu }_{n1}+{\mu }_{g1}\left(I(x,y)\right))/2$$ (16)

$$\mu \left(I(x,y)\right)=({\mu }_{n2}+{\mu }_{g2}\left(I(x,y)\right))/2$$ (17)

2.3.5. Calculation of the optimal threshold

Fuzzy distance is defined: $A$ is the discrete fuzzy set defined on interval [${\mu }_{min}$, ${\mu }_{max}$], and ${\mu }_A\left(u\right)$ is its membership function, then defining:

$$\varphi \left(A\right)=\frac{\sum _{i=0}^n{\mu }_i}{{\mu }_{max}-{\mu }_{min}}$$ (18)

$${\varphi }^{\prime }\left(A\right)=\frac{\varphi \left(A\right)}{\varphi \left(U\right)}$$ (19)

Where, $U$ is a finite element fuzzy set on [${\mu }_{min}$, ${\mu }_{max}$] and $\mu \left(u\right)=1\forall u\in U$, namely:

$$\varphi \left(U\right)=\sum _{f=f_{min}}^{f_{max}}hist\left(I{(x,y)}^{\left(f\right)}\right)$$ (20)

Where, $hist\left(x(i,j,f_{ij}^{\left(f\right)})\right)$ represents the number of pixels whose pixel value is $f$ in the image. The distance between fuzzy sets $A$ and $B$ is defined as:

$$d(A,B)=\frac{|\varphi \left(A\right)-\varphi \left(B\right)|}{1+{\varphi }^{\prime }\left(A\right)+{\varphi }^{\prime }\left(B\right)}$$ (21)

$\varphi \left(A\right)$ and $\varphi \left(B\right)$ can be regarded as the quotient of the membership degree and its membership span of all elements in fuzzy sets $A$ and $B$. When ${\varphi }^{\prime }\left(A\right)$ and ${\varphi }^{\prime }\left(B\right)$ are constant, $d(A,B)$ increases with the increase of the absolute value of the difference between $\varphi \left(A\right)$ and $\varphi \left(B\right)$. ${\varphi }^{\prime }\left(A\right)$ and ${\varphi }^{\prime }\left(B\right)$ are approximately equal to the average value of the membership degrees of all elements in the set $A$ and $B$. When the absolute value of the difference between $\varphi \left(A\right)$ and $\varphi \left(B\right)$ is the same, the larger the ${\varphi }^{\prime }\left(A\right)$ and ${\varphi }^{\prime }\left(B\right)$ are, and the smaller the $d(A,B)$ is. It can be seen that the greater the $d(A,B)$, the greater the distance between the two sets is. The greater the value of distance, the clearer the difference between the image target and the background is, and the better the image segmentation effect is. Therefore, maximizing the distance between the two sets means minimizing the probability of misclassification between the target and the background.

The total entropy of the two-dimensional reciprocal cross based on the two-region histogram and the spatial neighborhood information is:

$$H(t_1,s_1,t_2,s_2,\dots ,t_{n-1},s_{n-1})=d(C_1,C_2)\cdot H\left(C_1\right)+d(C_1,C_2)$$$$\cdot H\left(C_2\right)\cdot d(C_2,C_3)+d(C_2,C_3)\cdot H\left(C_3\right)\cdot d(C_3,C_4)+...+d(C_{n-1},C_n)\cdot H\left(C_n\right)=-\frac{|\varphi \left(C_1\right)-\varphi \left(C_2\right)|}{1+{\varphi }^{\prime }\left(C_1\right)+{\varphi }^{\prime }\left(C_2\right)}\cdot \sum _{i=0}^{t_1}\sum _{j=0}^{s_1}\frac{i\cdot j\cdot p_{ij}}{1+\frac{i\cdot j}{P_{ij}^{C_1}}}-$$$$\frac{|\varphi \left(C_1\right)-\varphi \left(C_2\right)|}{1+{\varphi }^{\prime }\left(C_1\right)+{\varphi }^{\prime }\left(C_2\right)}\cdot \sum _{i=t_1+1}^{t_2}\sum _{j=s_1+1}^{s_2}\frac{i\cdot j\cdot p_{ij}}{1+\frac{i\cdot j}{P_{ij}^{C_2}}}\cdot \frac{|\varphi \left(C_2\right)-\varphi \left(C_3\right)|}{1+{\varphi }^{\prime }\left(C_2\right)+{\varphi }^{\prime }\left(C_3\right)}-$$$$\frac{|\varphi \left(C_2\right)-\varphi \left(C_3\right)|}{1+{\varphi }^{\prime }\left(C_2\right)+{\varphi }^{\prime }\left(C_3\right)}\cdot \sum _{i=t_2+1}^{t_3}\sum _{j=s_2+1}^{s_3}\frac{i\cdot j\cdot p_{ij}}{1+\frac{i\cdot j}{P_{ij}^{C_3}}}\cdot \frac{|\varphi \left(C_3\right)-\varphi \left(C_4\right)|}{1+{\varphi }^{\prime }\left(C_3\right)+{\varphi }^{\prime }\left(C_4\right)}-......-\frac{|\varphi \left(C_{n-1}\right)-\varphi \left(C_n\right)|}{1+{\varphi }^{\prime }\left(C_{n-1}\right)+{\varphi }^{\prime }\left(C_n\right)}\sum _{i=t_k+1}^{L-1}\sum _{j=s_k+1}^{L-1}\frac{i\cdot j\cdot p_{ij}}{1+\frac{i\cdot j}{P_{ij}^{C_n}}}$$ (22)

The criterion of two-dimensional reciprocal cross entropy multi-threshold image segmentation is to find the threshold $(\dot{t_1},\dot{s_1})(\dot{t_2},\dot{s_2})...({\dot{t}}_{n-1},{\dot{s}}_{n-1})$ to minimize the two dimensional reciprocal cross entropy $H(t_1,s_1,t_2,s_2,\dots ,t_{n-1},s_{n-1})$.

3. Two-dimensional reciprocal cross entropy multi-threshold image segmentation combined with improved firefly algorithm

In order to solve the problems of large amount of calculation and time-consuming in the multi-threshold image segmentation method, by improving the firefly algorithm, this paper proposes the two- dimensional reciprocal cross entropy multi-threshold image segmentation combined with the improved firefly algorithm, so as to transform the calculation of the multi-threshold segmentation into the optimization of the two-dimensional reciprocal cross entropy function $H(t_1,s_1,t_2,s_2,\dots ,t_{n-1},s_{n-1})$ by the firefly algorithm.

The firefly algorithm is a bionic optimization method whose principle is to simulate individual firefly individuals in nature with points in the search space [42]. By using the phototaxis of fireflies in the process of optimization, the objective function of solving the problem is transformed into finding the firefly with the largest brightness. In each iteration, the position of the firefly is updated by attracted and moving to find the firefly with the greatest brightness [43]. Therefore, the firefly algorithm can carry out the global optimization quickly. The formula for the movement of the firefly $i$ to the brighter firefly $j$ is defined as:

$$X_i(t+1)=X_i\left(t\right)+\beta \left(\gamma \right)\times (X_j\left(t\right)-X_i\left(t\right))+\alpha \times (rand-0.5)$$ (23)

Where, $X_i$ and $X_j$ represent the position of firefly $i$ and firefly $j$ respectively; $\beta \left(\gamma \right)={\beta }_0{e}^{-\gamma {\gamma }_{ij}^2}$ is the attraction of firefly $j$ to firefly $i$; ${\gamma }_{ij}$ is the distance between fireflies $i$ and $j$, ${\gamma }_{ij}=\Vert X_i-X_j\Vert$; ${\beta }_0$ is the degree of attraction when ${\gamma }_{ij}$ is zero; $\gamma$ is the absorption coefficient of light intensity; $\alpha$ is the step factor and it is a constant within [0,1]; rand is a random factor submitted to uniform distribution on [0,1]; $\alpha \times (rand-0.5)$ is the perturbation term, which is used to avoid falling into local optimization too early.

3.1. Limitation analysis of traditional firefly algorithm

The firefly algorithm mainly relies on the best individual in the field to guide the optimization. Once the field is an empty set, the algorithm will stagnate, which greatly reduces the optimization efficiency [44]. In addition, the location update formula of the algorithm is too simple and the search step is fixed, so that the algorithm cannot quickly optimize the optimal solution [45]. The lesions of COVID-19 CT image can be seen in left lung, right lung or both lungs. Aiming at the problems of complex structure and uneven gray distribution of various tissues in lung CT image, it is difficult to accurately segment and extract lung parenchyma and lesions. The exponentially decreasing inertia weight and random mechanism are proposed to make the segmentation threshold change adaptively according to the detailed information of lung lobes, trachea, bronchi and carina. The attraction term of firefly algorithm is matched and switched by combining exponential distribution and weber distribution, so as to obtain more accurate contour boundaries of each target with relatively fewer iterations.

3.2. Improved firefly algorithm based on the best position of the population

The principle of the improved firefly algorithm based on the optimal position of the population is shown in Fig. 5.

Fig. 5.

Improved firefly algorithm based on the best position of population.

The position update formula of the firefly $i$ under the influence by the optimal position of the population is:

$$X_i(t+1)=X_i\left(t\right)+{\beta }_0\times e^{-\gamma R_{ij}^2}\times (X_j\left(t\right)-X_i\left(t\right))+$$$${\beta }_0\times e^{-\gamma R_{i,best}^2}\times (X_{best}\left(t\right)-X_i\left(t\right))+\alpha \times (rand-0.5)$$ (24)

Where, ${\beta }_0\times e^{-\gamma R_{i,best}^2}\times (X_{best}\left(t\right)-X_i\left(t\right))$ represents the update position of firefly $i$ under the influence by the optimal position of the population.

3.3. Improved firefly algorithm based on random mechanism

The balance between detection and search ability is the core issue of the firefly algorithm. The detection ability can be improved by the random mechanism, which can make the algorithm jump out of the local optimization with a greater probability to realize the global search. The improvement of search ability depends on local information, such as gradient, mode and the historical information in the process of the algorithm.

Aiming at the problem of traditional firefly algorithm that is easy to fall into local optimality, the attraction is improved by using exponential distribution in the position movement formula, so as to enhance the global detection. In addition, the random item is improved by the step-size monotonous decreasing mode to enhance the local mining ability in the later stage of the algorithm. In this paper, random factor is added to disturb the attraction coefficients and it enhances the ability to jump out of the local optima. The expression of $\beta$ is:

$$\beta ={\beta }_0{e}^{-\gamma {\gamma }_{ij}^2}{R}_i$$ (25)

Where, $R_i$ is the exponential distribution. If the step factor $\alpha$ takes a fixed value, the detection and search ability of the algorithm cannot be effectively adjusted. In this paper, $\alpha$ is decremented so that the random function has a large random step at the beginning of iteration, and the algorithm can search better in the global scope. The step size is gradually reduced in the later stage of the iteration, so that the algorithm can refine the search in the local scope. The expression of $\alpha$ is:

$$\alpha ={\alpha }_0{\delta }^{t}S,0<\delta <1$$ (26)

Where, ${\alpha }_0$ is the initial random step size, $\delta$ is the cooling coefficient, 0¡$\delta$¡1, $S$ is the step factor. In the early stage of the algorithm, the larger step search is required to traverse a wide range of feasible solutions. In the later stage of the algorithm, the position function has slowly converged near the optimal solution. At this time, a small step is required to search. According to this improved idea, it can be found that in the tangent function $tan\left(x\right)$, when the independent variable $x$ is 0.785, the value of function is 1, which decreases with the decrease of the independent variable, and the reduction rate also decreases gradually. Therefore, the tangent function is introduced into the step factor, and the expression is:

$$S=tan(0.785\times \frac{t_{max}-t}{t_{max}})\cdot s_0$$ (27)

Where, $t_{max}$ is the maximum number of iterations; $t$ is the maximum number of iterations; $s_0$ is the fixed step parameter.

3.4. Exponentially decreasing inertia weight

The inertia weight $w\left(t\right)$ is used to control the influence on the current position by the previous position of the firefly, which adjusts the global optimization. At the beginning, the inertia weight is large, which makes the relative attraction small. The global optimization is enhanced and the local search ability is weakened. On the contrary, with the increase of the iteration, the inertia weight gradually decreases, and the local search ability is enhanced, so as to avoid repeated oscillation on the extreme point due to the excessive movement of the firefly. According to the idea of linear decline, combined with the random and exponential inertia weight in particle swarm optimization, an improved exponential decline inertia weight is proposed, and the random disturbance term is added for adjustment. The weight formula is expressed as:

$$w\left(t\right)=w_{min}\cdot {\left(\frac{w_{max}}{w_{min}}\right)}^{1-\frac{t}{T}}+rand\cdot w_{min}$$ (28)

Where, $t$ is the current number of iteration, and $w_{max}=0.8$, $w_{min}=0.2$, $T=150$. rand is the random number between [0,1] to ensure $w\left(t\right)\in (0,1)$. In summary, the position movement formula of the improved firefly algorithm is:

$$X_i(t+1)=w\left(t\right)X_i\left(t\right)+{\beta }_0\cdot e^{-\gamma R_{ij}^2}{R}_i\cdot (X_j\left(t\right)-X_i\left(t\right))+$$$${\beta }_0\cdot e^{-\gamma R_{i,best}^2}{R}_i\cdot (X_{best}\left(t\right)-X_i\left(t\right))+{\alpha }_0{\delta }^{t}S\cdot (rand-0.5)$$ (29)

Where: $X_i(t+1)$ is the location of the firefly after updating; $X_{best}\left(t\right)$ is the optimal individual of the current population.

3.5. Time computational complexity of improved firefly algorithm

For the time computational complexity, $O\left(f\right)$ is set as the time computational complexity in each iteration of each firefly, then it can be seen that the time computational complexity of the traditional firefly algorithm is $O\left(T\cdot N\cdot f\right)$. Where, $T$ is the maximum number of iteration and $N$ is the maximum population size. For the traditional firefly algorithm, the value of the inertia weight in each iteration remains unchanged, so there is $O\left(f_1\right)=O\left(f_2\right)=\cdots =O\left(f_T\right)=O\left(f\right)$. For the proposed firefly algorithm, the value of the inertia weight gradually decreases with the increase of iteration, so there is $O\left(f_1\right)\ge O\left(f_2\right)\ge \cdots \ge O\left(f_T\right)$. It can be seen from the above analysis that compared with the traditional firefly algorithm, the proposed firefly algorithm greatly reduces the time computational complexity.

3.6. Steps and flow chart of multi-threshold image segmentation method

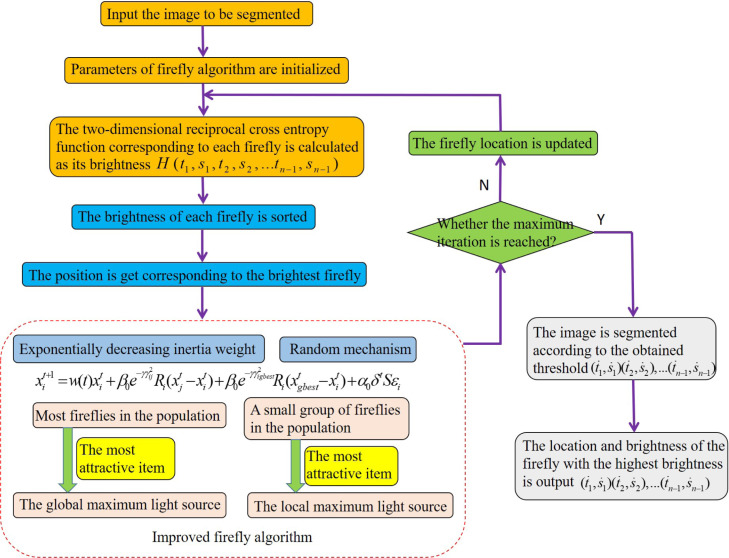
The two-dimensional reciprocal cross entropy $H(t_1,s_1,t_2,s_2,\dots ,t_{n-1},s_{n-1})$ is set as the objective function of the firefly algorithm, and the optimization result is the firefly position $X(\dot{t_1},\dot{s_1},\dot{t_2},\dot{s_2},\dots ,{\dot{t}}_{n-1},{\dot{s}}_{n-1})$ with the highest brightness. Where: $k$ is the number of threshold, $(\dot{t_1},\dot{s_1})(\dot{t_2},\dot{s_2})...({\dot{t}}_{n-1},{\dot{s}}_{n-1})$ is the required threshold.

The steps of the two-dimensional reciprocal cross entropy multi-threshold combined with improved firefly algorithm are as following:

(1) The parameters of firefly algorithm are initialized, including the number of fireflies $n$, the initial position $X_i(t_{i1},s_{i1},t_{i2},s_{i2},\dots ,t_{i(n-1)},s_{i(n-1)})$, the initial attraction ${\beta }_0$, the light intensity absorption $\gamma$, the step factor ${\alpha }_0$, and the maximum number of iteration $T$, the fixed step parameter $s_0$. We use the horizontal test [46] to obtain the combination with the most occurrences of the optimal solution, then the number of fireflies n and the maximum number of iteration $T$ are fixed. The enumeration method [47] is used to obtain the range of a series optimal value combinations for the initial attraction ${\beta }_0\in [0,2]$, the light intensity absorption $\gamma \in [0.01,10]$, the step factor ${\alpha }_0\in [0,1]$, and the fixed step parameter $s_0\in [0,0.8]$. Finally, we analyze the results to obtain the optimal parameters of the improved firefly algorithm. ${\beta }_0=1$, ${\alpha }_0=0.5$, $n=100$, $T=150$, $\gamma$=1, $s_0=0.4$;

(2) The two-dimensional reciprocal cross entropy function $H_i(t_{i1},s_{i1},t_{i2},s_{i2},\dots ,t_{i(n-1)},s_{i(n-1)})$ is calculated. We sort the value of objective function to obtain the position of the firefly with the largest brightness;

(3) We judge whether the maximum number of iteration $T$ is reached. If it is reached, turn to Step.(4), otherwise turn to Step.(5);

(4) The position of the firefly with the highest brightness is output, and the calculated is used as the threshold to segment the image;

(5) The position of the firefly is updated according to Eq. (29), randomly disturb the fireflies in the best position, increase the search times by 1, and turn to Step.(2) for the next search.

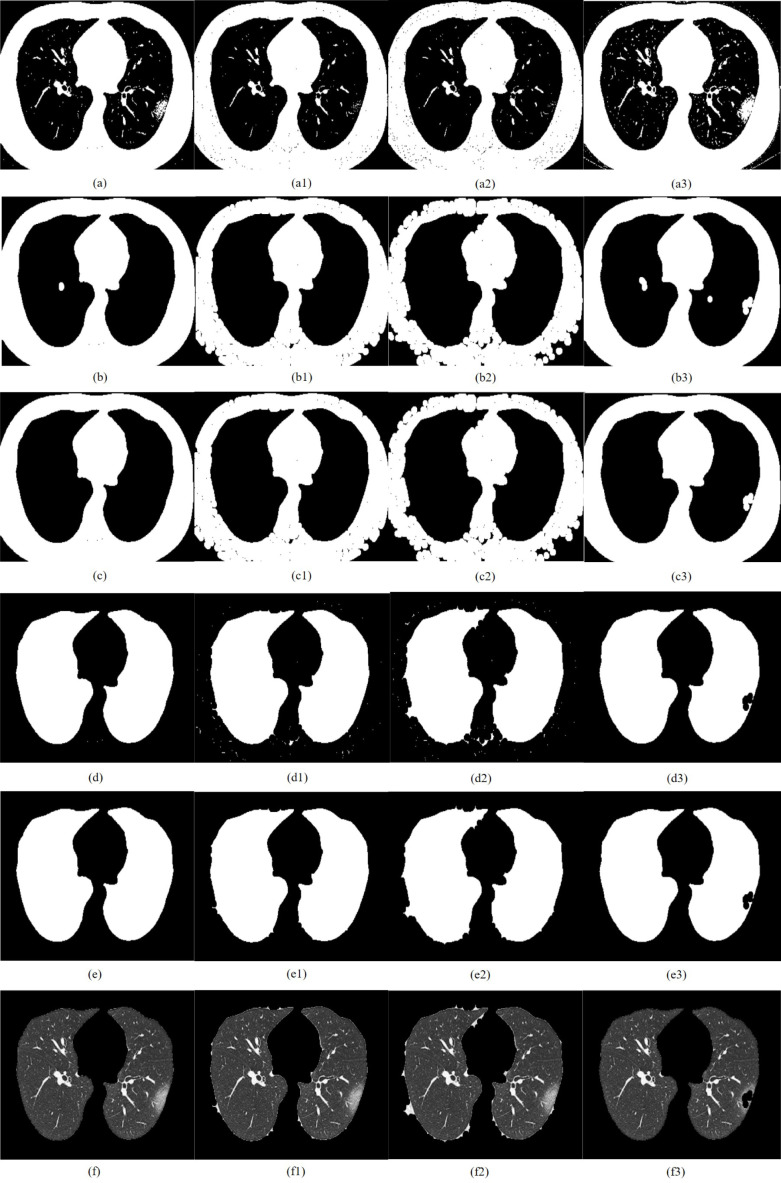
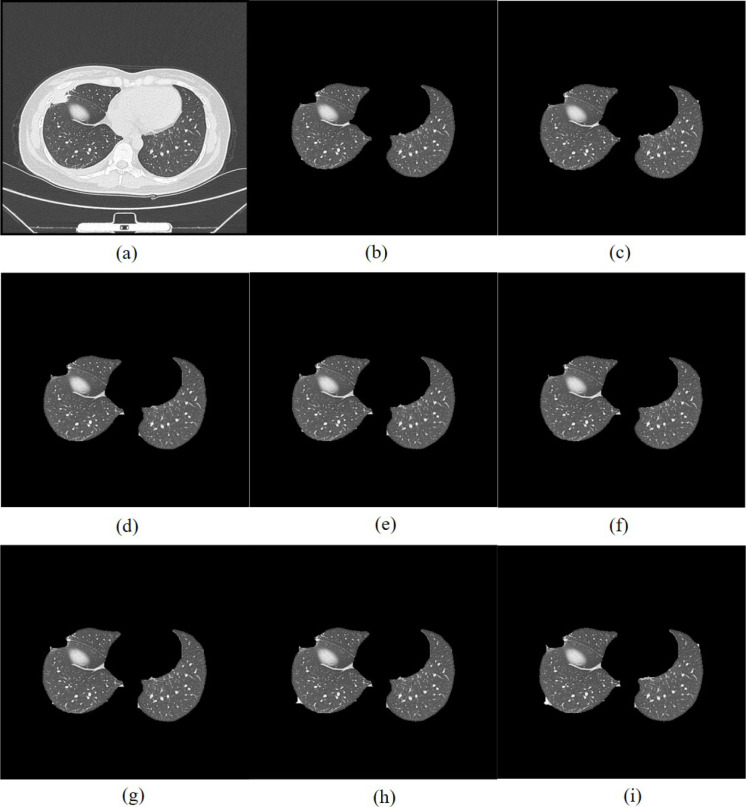
The flow chart is shown in Fig. 6. Taking early COVID-19 as an example, the CT image after multi-threshold image segmentation is shown in Fig. 11(a).

Fig. 6.

The flow chart of two-dimensional reciprocal cross entropy multi-threshold combined with improved firefly algorithm for image segmentation.

Fig. 11.

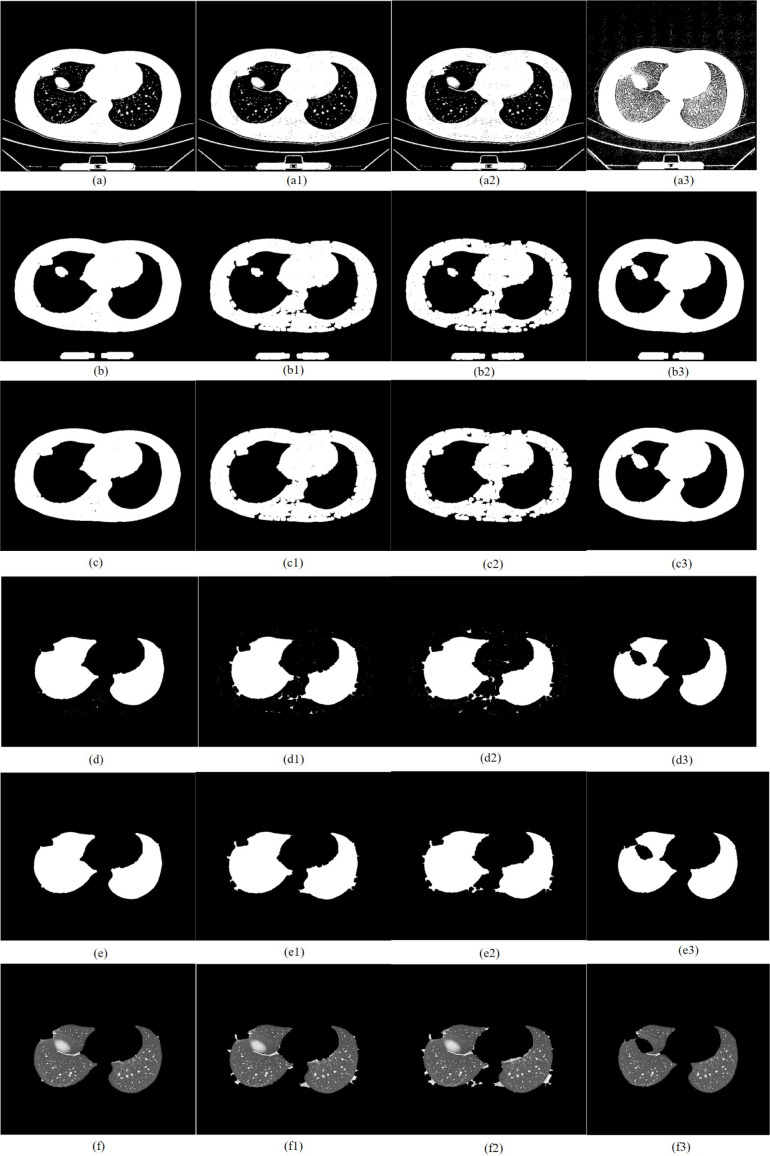
CT image of early COVID-19 segmented by TDRMFA: (a)binarized segmentation; (b)removal of trachea and bronchus; (c)removal of bed board and elimination of holes; (d)separation of the left and right lungs; (e)edge repair; (f)lung parenchyma segmentation. CT image of early COVID-19 segmented by SFTM: (a1)binarized segmentation; (b1)removal of trachea and bronchus; (c1) removal of bed board and elimination of holes; (d1)separation of the left and right lungs; (e1)edge repair; (f1)lung parenchyma segmentation. CT image of early COVID-19 segmented by PTEM: (a2) binarized segmentation; (b2)removal of trachea and bronchus; (c2)removal of bed board and elimination of holes; (d2)separation of the left and right lungs; (e2)edge repair; (f1)lung parenchyma segmentation. CT image of early COVID-19 segmented by PDEE: (a3)binarized segmentation; (b3) removal of trachea and bronchus; (c3)removal of bed board and elimination of holes; (d3)separation of the left and right lungs; (e3)edge repair; (f3)lung parenchyma segmentation.

4. Refinement segmentation of lung parenchyma

4.1. Removal of trachea and bronchus based on morphology

The lung parenchyma is more obvious after the initial segmentation of CT image through the above optimal threshold iterative method, but the presence of blood vessels and trachea in the image has a great impact on the accurate segmentation of the lung area. Therefore, the processed binary image is separated from the trachea adhering to the lung parenchyma by mathematical morphology [48]. Then combined with the hole filling algorithm to remove the lung trachea tree and small-area lung parenchyma holes, the strel function expansion corrosion is used to remove the boundary irrelevant to the lung parenchyma in the image and smooth the edge of the lung parenchyma, in order to obtain a complete lung parenchyma template. Taking early COVID-19 as an example, the CT image after removal of the trachea and bronchi is shown in Fig. 11(b).

4.2. Removal of bed board and elimination of holes based on closed operation

It can be seen from the binary image of lung parenchyma that there are a large number of holes inside the lung parenchyma and bed shadow outside the lung parenchyma. Moreover, due to the existence of X-ray pulse interference, there are many isolated noises in CT images. Therefore, in order to improve the quality of image, the holes inside the lung parenchyma are filled, the boundary of the lung parenchyma is smoothed, and the shape and size of the lung parenchyma remain unchanged. This paper proposes the closed operation of binary morphology to further process the lung parenchyma image obtained in Section 4.1.

The closed operation in binary morphology is defined as a mathematical morphological operator that uses the same structure element to perform the dilation and erosion operations on binary images successively. Where, the structural elements are the basic operators in binary morphology. Through the specific logical operation with the surrounding area of each pixel in the lung parenchyma image, the new value of each pixel is obtained. The structural elements include circle, rectangle, diamond, straight line and other shapes. In view of the advantages of isotropy and strong operability for the square structural elements, the closed operation is carried out by using the square structural elements.

According to the sequence of the closed operation, the lung parenchyma image is expanded firstly. The expansion operation can fill the holes in the lung parenchyma and smooth the boundary of the lung parenchyma. Assuming that the lung parenchyma image is $F$ and the structural element is $J$, the structural element $J$ is moved sequentially on the image plane. When passing through each pixel, $J\left[s\right]$ has the following three states: $\left(1\right)J\left[s_1\right]\subseteq F$; $\left(2\right)J\left[s_2\right]\subseteq F^c$; $\left(3\right)J\left[s_3\right]\cap F\ne \varnothing ,J\left[s_3\right]\cap F^c\ne \varnothing$; as shown in Fig. 7.

Fig. 7.

Three possible states of $J\left[s\right]$.

The expansion operation corresponds to the third state above. $J\left[s\right]$ is related to part $F$, and each pixel in $F$ is expanded into structural element $J$ to obtain a new image, which can be described as:

$$F\oplus J=\left\{s\right|J\left[s\right]\cap F\ne \varnothing \}$$ (30)

The erosion operation can remove the isolated noise and restore the size of lung parenchyma at the same time. The erosion operation corresponds to the first state above, and $J\left[S\right]$ is most correlated to $F$. The image after the erosion operation can be described as:

$$F⊛J=\left\{s\right|J\left[s\right]\subseteq F\}$$ (31)

In summary, the image obtained after the closed operation is:

$$CLOSE\left(F\right)=(F\oplus J)⊛J$$ (32)

Taking early COVID-19 as an example, the CT image after removal of bed board and elimination of holes is shown in Fig. 11(c).

4.3. Separation of the left and right lungs

Due to the complex structure of the two lung regions, and the similar tissue gray levels or the influence of lung disease, it is difficult to define the edges of the two lung regions, which will interfere with the detection of lung disease in the later stage. Therefore, it is necessary to separate the left and right lungs in the process of lung parenchyma segmentation. In this paper, the two lung regions are separated by combining the grayscale integral projection and scanning algorithm [49]. Firstly, whether there is adhesion between the left and right lungs is judged, and each connected domain in the image is marked and then its size in descending order is arranged. The ratio of the minimum and maximum area of the pixel column coordinate connected domain is recorded as $S_1$, and the ratio of the minimum and maximum area of the pixel row coordinate connected domain is recorded as $S_2$. When $S_1>0.5$ and $S_2>0.5$, it is judged that the left and right lungs are separated, otherwise, the left and right lungs are adhered. Secondly, the position of the connection between the two lungs is determined according to the gray scale integral projection feature of the image. Finally, the two lung regions are made independent by the rule-based row and column scanning. Taking early COVID-19 as an example, the result of lung parenchyma separation is shown in Fig. 11(d).

4.4. The edge repair template of lung parenchyma

If the edge of the processed lung parenchyma template is complete and smooth, it indicates that there is no nodule at the edge, which does not affect the integrity of the lung parenchyma and it is directly saved as a template. If the edge of the template is rough and concave at this time, there may be neglected fuzzy problems such as edema, inflammation or nodules. At this time, the template needs to be repaired.

The convex hull algorithm [50] fails to achieve the desired ideal effect when inpainting the lung parenchyma template of large area lesions. The rolling ball method cannot accurately determine the size of the defect when repairing the edge of the lung parenchyma template, and it is difficult to accurately set the radius of the sphere. If the radius is not selected properly, it is easy to have the problem of under segmentation or over segmentation.

The Freeman chain code can provide sufficient information about the target image and it is not affected by image noise. It represents the boundary of the image by line segments of unit length and preset direction. In this paper, the Freeman chain code and the difference of chain code are used to describe the concavity and convexity of the boundary to find the defect position of the template. Firstly, the starting position of the chain code needs to be determined and marked. For each point on the boundary there is a chain code $A\left(i\right)$ that directs from the preset point to that point, and the chain code $A\left(i1\right)$ directs to the point next to the current point. In this paper, an edge repair algorithm based on the combination of the eight-direction Freeman chain code and the difference of triple chain code is proposed. This method has a good repair effect on the loss of lung parenchyma edges, especially the vascular depression, and it is not easily affected by noise. The Freeman chain code is divided into eight-direction connection chain code and four-direction connection chain code, as shown in Fig. 8.

Fig. 8.

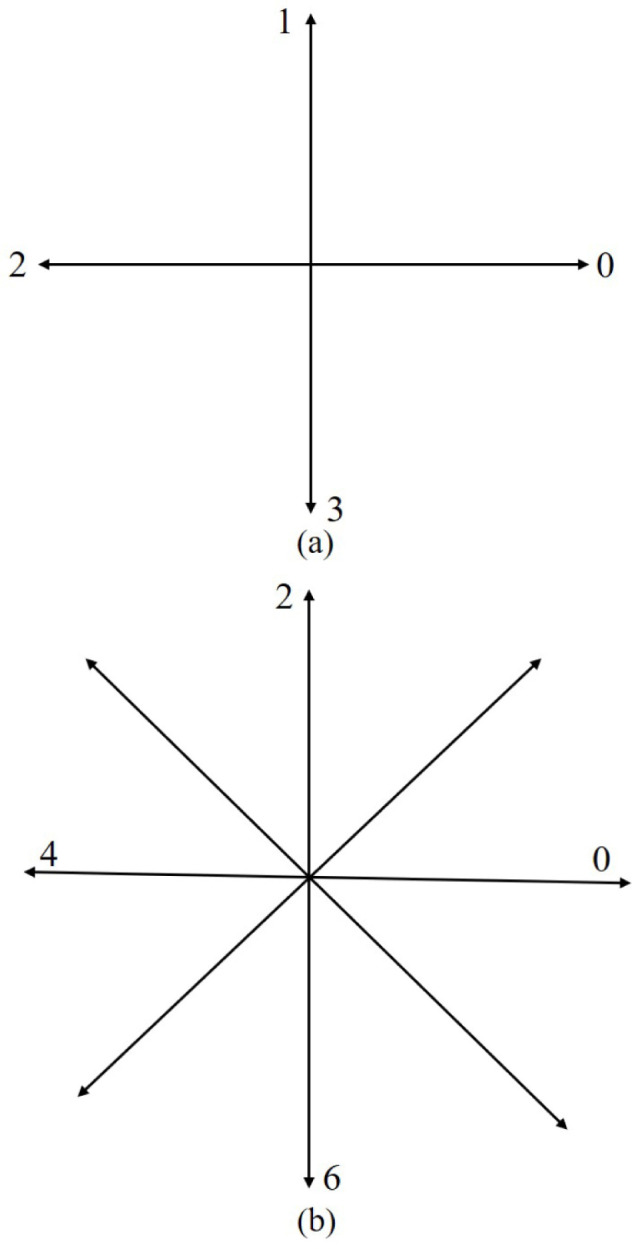
Freeman chain code (a)four-direction connection chain code; (b)eight-direction connection chain .

The corresponding relationship between the chain code value and the boundary coordinates $(x,y)$ when the eight-connection chain code describes the boundary is shown in Table 1.

Table 1.

Correspondence between the chain code value of eight neighborhood and the boundary coordinates (x, y).

x offset	y offset	The value of chain code
1	0	0
1	1	1
0	1	2
−1	1	3
−1	0	4
−1	−1	5
0	−1	6
1	−1	7

Rotating clockwise from the preset point to traverse the edges in the image. The value of the chain code increases by 1 for every 45°rotation, and the difference $Diff\left(i\right)$ of the chain code is calculated by each point on the boundary. The threshold is set according to the different characteristics of chain code. When $Diff\left(i\right)<-1$, the point is convex. When $Diff\left(i\right)>2$, the point is concave, and then the concave boundary of the lung parenchyma is repaired according to the convex and concave points. Ayerbe et al. [51] proposed Bresenham straight line algorithm to repair the defects of lung parenchyma. The repair effect is better for defects with small fissures in the lung parenchyma, while the outline of the lung parenchyma is generally curvilinear, which is not ideal for repairing large-area edge lesions. In this paper, a connection method based on the quadratic Bezier curve fitting interpolation is proposed. The primary Bezier curve is a line segment connecting the beginning and the end points, such as the line segment $P_0{P}_2$ in Fig. 9, and its expression is:

$$B\left(t\right)=(1-t)P_0+t{P}_2,t\in [0,1]$$ (33)

Fig. 9.

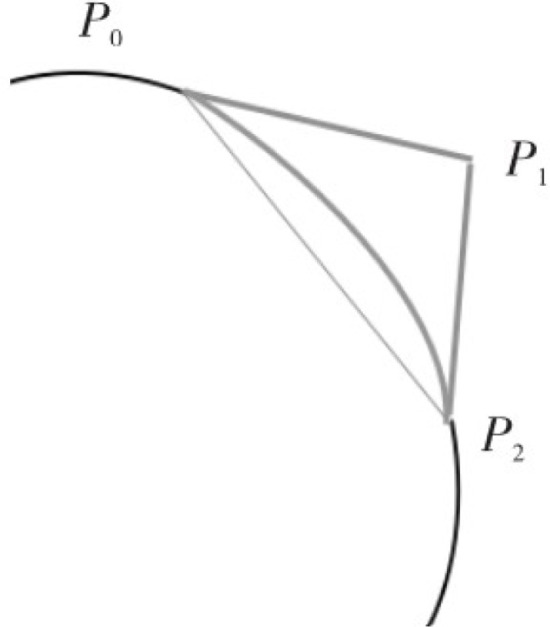
Bezier curve interpolation defect .

The quadratic Bezier curve is a curve segment drawn by three points, and its expression is:

$$B\left(t\right)={(1-t)}^2{P}_0+2t(1-t)P_1+t^2{P}_2,t\in [0,1]$$ (34)

Among them, an interpolation curve is required between point $P_0$ and point $P_2$. $P_1$ is the directional control point at a certain distance from the midpoint of the line segment on the vertical bisector of the line $P_0{P}_2$. The distance is the optimal fixed value selected through testing, which can minimize the fitting interpolation error as much as possible. Through these three points, the curve interpolated to the position of the lung parenchyma will be drawn to complete the repair of lung parenchyma. Bezier curve patching is shown in Fig. 9.

The lung parenchyma template is repaired by Freeman chain code combined with quadratic Bezier curve can make up for the under-segmentation problem when repairing large-area defects with straight lines. At the same time, it has flexible adjustment to better meet the characteristics of lung parenchyma edge, which can achieve a good repair effect. Taking early COVID-19 as an example, the edge repair template of the lung parenchyma is shown in Fig. 11(e). Finally, the template is multiplied with the lung CT image, which can preserve a good effect of the preset ideal segmentation. It ensures the integrity of the lung parenchyma and do a good work for the subsequent detection of lung disease.

5. Analysis of experimental results

Aiming at the different kinds of COVID-19 CT images including early COVID-19, early asymptomatic COVID-19, resolution COVID-19, adenovirus pneumonia (suspected cases of COVID-19), staphylococcal pneumonia (suspected cases of COVID-19) are tested by the Intel E8200 CPU 2.5 GHz, RAM 8G, Matlab 2016a. The size of the image is 512 × 512, and the tested images and the golden standard segmented images of the lung parenchyma by doctors are shown in Fig. 10. The COVID-19 CT images tested in this paper are from COVID-19 CT segmentation dataset (https://medicalsegmentation.com/covid19/) and LIDC-IDRI (https://paperswithcode.com/dataset/lidc-idri). Two-dimensional entropy exhaustive segmentation(TDEE) [20], PSO two-dimensional entropy multi-threshold segmentation(PTEM) [52], standard firefly two-dimensional entropy multi-threshold segmentation (SFTM) [53], two-dimensional reciprocal cross entropy multi-threshold combined with improved firefly algorithm(TDRMFA, paper method) are used for simulation comparison tests.

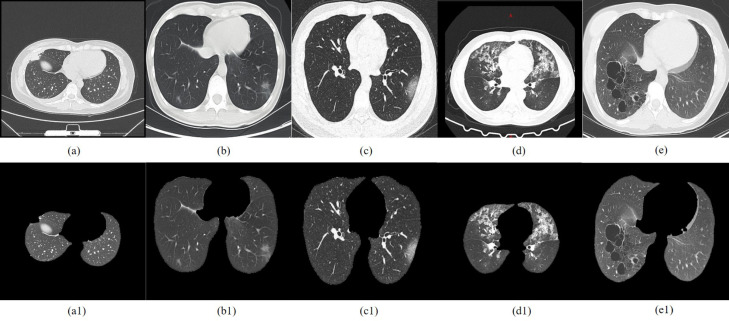
Fig. 10.

Original COVID-19 CT images: (a)early COVID-19; (b)early asymptomatic COVID-19; (c)resolution COVID-19; (d)adenovirus pneumonia; (e)staphylococcal pneumonia; Golden standard segmented images of the lung parenchyma by doctors: (a1)early COVID-19; (b1)early asymptomatic COVID-19; (c1)resolution COVID-19; (d1)adenovirus pneumonia; (e1)staphylococcal pneumonia.

The experimental results show that the fixed threshold and the histogram threshold are easy to skip some areas adhered to the lung wall, and the segmentation effect is not ideal. If the threshold is not selected properly, it is easy to ignore the marginal nodules, and the gray contrast is not obvious, so it is impossible to observe the lesions comprehensively. The optimal threshold method proposed in this paper can perform the initial segmentation of the lungs more accurately. When the extracted lung parenchyma is repaired for defects, the convex hull algorithm cannot achieve the expected ideal effect when repairing the lung parenchyma template of large-area lesions. The rolling ball method cannot accurately determine the size of the defect when repairing the edge of the lung parenchyma template, and it is difficult to accurately set the radius of the sphere. If the radius is not selected properly, it is easy to have the problem of under segmentation or over segmentation. This paper improves this problem by calculating the Dice similarity coefficient ($DSC$) and $sensitivity$ of image segmentation effect to verify the effectiveness of the experimental methods. The Dice similarity coefficient can be obtained by measuring the overlap between the segmentation results of the paper method and the manual segmentation results of experts, namely:

$$DSC=\frac{2\times |u\cap v|}{\left|u\right|+\left|v\right|}$$ (35)

Where, $u$ represents the segmentation result of this article, and $v$ represents the golden standard segmentation result by doctor.

The $sensitivity$ is obtained by measuring the ratio of the segmentation results of the paper method and the expert manual segmentation results to correctly segment the lung parenchyma area, namely:

$$Sensitivity=\frac{|u\cap v|}{\left|u\right|}$$ (36)

Where, $u$ represents the segmentation result of this article, and $v$ represents the golden standard segmentation result by doctor. The improved segmentation method in this paper has better indicators for the $DSC$ and the $sensitivity$. The segmented lung parenchyma image can fully and clearly show the lesions, which is helpful to improve the accuracy and sensitivity of nodules detection. The extraction of lung parenchyma for different kinds of COVID-19 CT images are shown in Fig. 11, Fig. 12, Fig. 13, Fig. 14, Fig. 15.

Fig. 12.

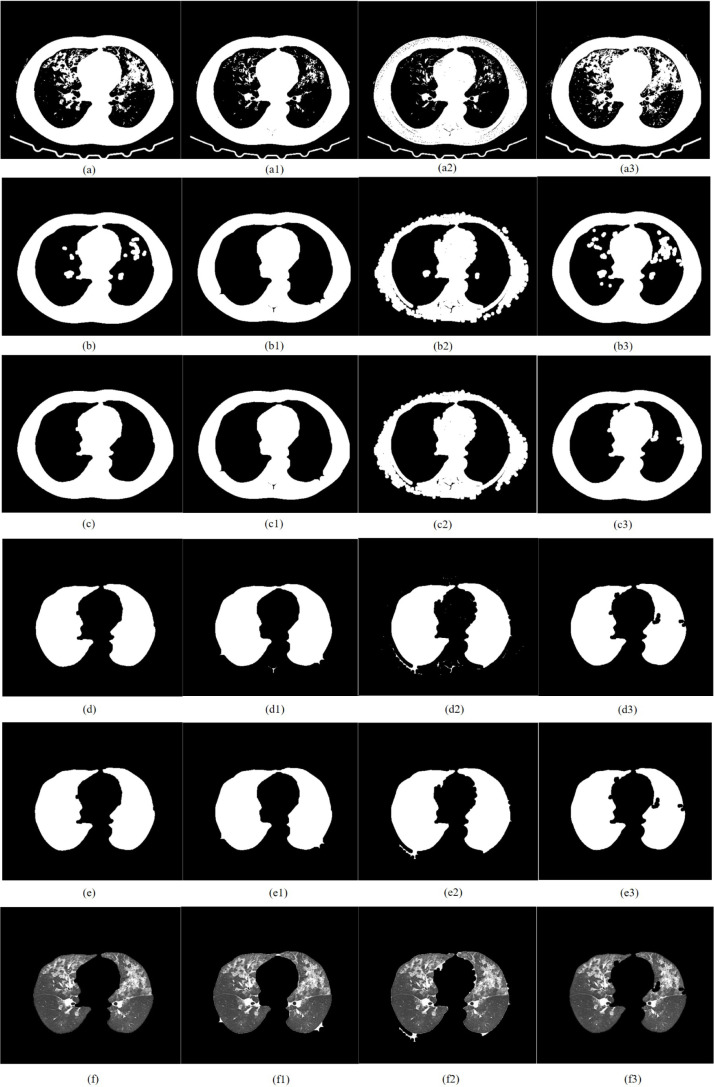
CT image of early asymptomatic COVID-19 segmented by TDRMFA: (a)binarized segmentation; (b)removal of trachea and bronchus; (c)removal of bed board and elimination of holes; (d)separation of the left and right lungs; (e)edge repair; (f)lung parenchyma segmentation. CT image of early asymptomatic COVID-19 segmented by SFTM: (a1)binarized segmentation; (b1)removal of trachea and bronchus; (c1) removal of bed board and elimination of holes; (d1)separation of the left and right lungs; (e1)edge repair; (f1)lung parenchyma segmentation. CT image of early asymptomatic COVID-19 segmented by PTEM: (a2)binarized segmentation; (b2)removal of trachea and bronchus; (c2)removal of bed board and elimination of holes; (d2)separation of the left and right lungs; (e2)edge repair; (f1)lung parenchyma segmentation. CT image of early asymptomatic COVID-19 segmented by PDEE: (a3)binarized segmentation; (b3) removal of trachea and bronchus; (c3)removal of bed board and elimination of holes; (d3)separation of the left and right lungs; (e3)edge repair; (f3)lung parenchyma segmentation.

Fig. 13.

CT image of resolution COVID-19 segmented by TDRMFA: (a)binarized segmentation; (b)removal of trachea and bronchus; (c)removal of bed board and elimination of holes; (d)separation of the left and right lungs; (e)edge repair; (f)lung parenchyma segmentation. CT image of resolution COVID-19 segmented by SFTM: (a1)binarized segmentation; (b1)removal of trachea and bronchus; (c1) removal of bed board and elimination of holes; (d1)separation of the left and right lungs; (e1)edge repair; (f1)lung parenchyma segmentation. CT image of resolution COVID-19 segmented by PTEM: (a2)binarized segmentation; (b2)removal of trachea and bronchus; (c2)removal of bed board and elimination of holes; (d2)separation of the left and right lungs; (e2)edge repair; (f1)lung parenchyma segmentation. CT image of resolution COVID-19 segmented by PDEE: (a3)binarized segmentation; (b3) removal of trachea and bronchus; (c3)removal of bed board and elimination of holes; (d3)separation of the left and right lungs; (e3)edge repair; (f3)lung parenchyma segmentation.

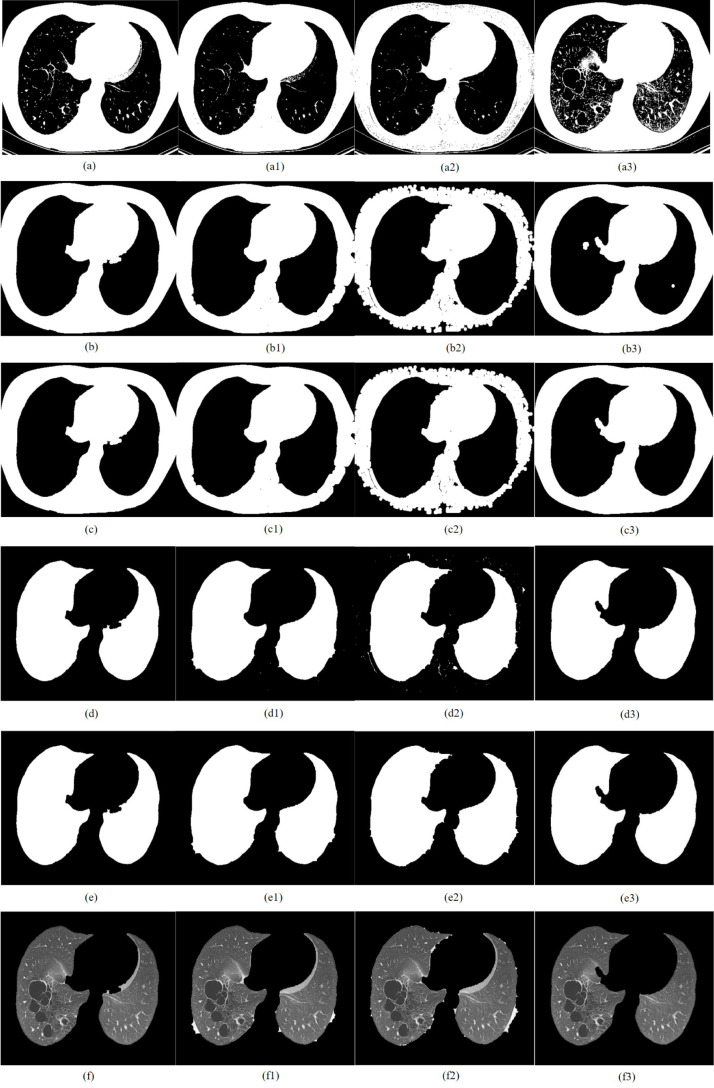
Fig. 14.

CT image of adenovirus pneumonia segmented by TDRMFA: (a)binarized segmentation; (b)removal of trachea and bronchus; (c)removal of bed board and elimination of holes; (d)separation of the left and right lungs; (e)edge repair; (f)lung parenchyma segmentation. CT image of adenovirus pneumonia segmented by SFTM: (a1)binarized segmentation; (b1)removal of trachea and bronchus; (c1) removal of bed board and elimination of holes; (d1)separation of the left and right lungs; (e1)edge repair; (f1)lung parenchyma segmentation. CT image of adenovirus pneumonia segmented by PTEM: (a2)binarized segmentation; (b2)removal of trachea and bronchus; (c2)removal of bed board and elimination of holes; (d2)separation of the left and right lungs; (e2)edge repair; (f1)lung parenchyma segmentation. CT image of adenovirus pneumonia segmented by PDEE: (a3)binarized segmentation; (b3) removal of trachea and bronchus; (c3)removal of bed board and elimination of holes; (d3)separation of the left and right lungs; (e3)edge repair; (f3)lung parenchyma segmentation.

Fig. 15.

CT image of staphylococcal pneumonia segmented by TDRMFA: (a)binarized segmentation; (b)removal of trachea and bronchus; (c)removal of bed board and elimination of holes; (d)separation of the left and right lungs; (e)edge repair; (f)lung parenchyma segmentation. CT image of staphylococcal pneumonia segmented by SFTM: (a1)binarized segmentation; (b1)removal of trachea and bronchus; (c1) removal of bed board and elimination of holes; (d1)separation of the left and right lungs; (e1)edge repair; (f1)lung parenchyma segmentation. CT image of staphylococcal pneumonia segmented by PTEM: (a2)binarized segmentation; (b2)removal of trachea and bronchus; (c2)removal of bed board and elimination of holes; (d2)separation of the left and right lungs; (e2)edge repair; (f1)lung parenchyma segmentation. CT image of staphylococcal pneumonia segmented by PDEE: (a3)binarized segmentation; (b3) removal of trachea and bronchus; (c3)removal of bed board and elimination of holes; (d3)separation of the left and right lungs; (e3)edge repair; (f3)lung parenchyma segmentation.

This paper compares with the comparative methods and uses the accuracy $IOU$ index to objectively evaluate the experimental results:

$$IOU=\frac{N_{11}+N_{10}}{N_{11}+N_{10}+N_{01}+N_{00}}$$ (37)

Where, $N_{11}$ represents the correctly segmented lung parenchyma region. $N_{10}$ represents the correctly segmented background region. $N_{01}$ represents the incorrectly segmented lung parenchyma region and $N_{00}$ represents the incorrectly segmented background region. The greater the accuracy $IOU$, the more accurate the image segmentation is and the closer to the standard segmentation. The calculation results are shown in Table 2, Table 3, Table 4, Table 5, Table 6.

Table 2.

Comparison of TDRMFA with different methods for CT image of early COVID-19.

Segmented method	Dice	Sensitivity	IOU
PDEE	0.7732	0.7898	0.8113
PTEM	0.8214	0.8342	0.8643
SFTM	0.8543	0.8623	0.8932
TDRMFA	0.9221	0.9353	0.9632

Table 3.

Comparison of TDRMFA with different methods for CT image of early asymptomatic COVID-19.

Segmented method	Dice	Sensitivity	IOU
PDEE	0.8037	0.8145	0.8544
PTEM	0.8465	0.8530	0.8865
SFTM	0.8748	0.8865	0.9134
TDRMFA	0.9346	0.9484	0.9783

Table 4.

Comparison of TDRMFA with different methods for CT image of resolution COVID-19.

Segmented method	Dice	Sensitivity	IOU
PDEE	0.7992	0.8067	0.8488
PTEM	0.8591	0.8662	0.8974
SFTM	0.8856	0.8982	0.9274
TDRMFA	0.9284	0.9334	0.9675

Table 5.

Comparison of TDRMFA with different methods for CT image of adenovirus pneumonia.

Segmented method	Dice	Sensitivity	IOU
PDEE	0.7994	0.8038	0.8453
PTEM	0.8365	0.8430	0.8865
SFTM	0.8784	0.8885	0.9164
TDRMFA	0.9374	0.9474	0.9765

Table 6.

Comparison of TDRMFA with different methods for CT image of staphylococcal pneumonia.

Segmented method	Dice	Sensitivity	IOU
PDEE	0.7738	0.7819	0.8259
PTEM	0.8183	0.8274	0.8679
SFTM	0.8547	0.8683	0.8982
TDRMFA	0.9193	0.9243	0.9584

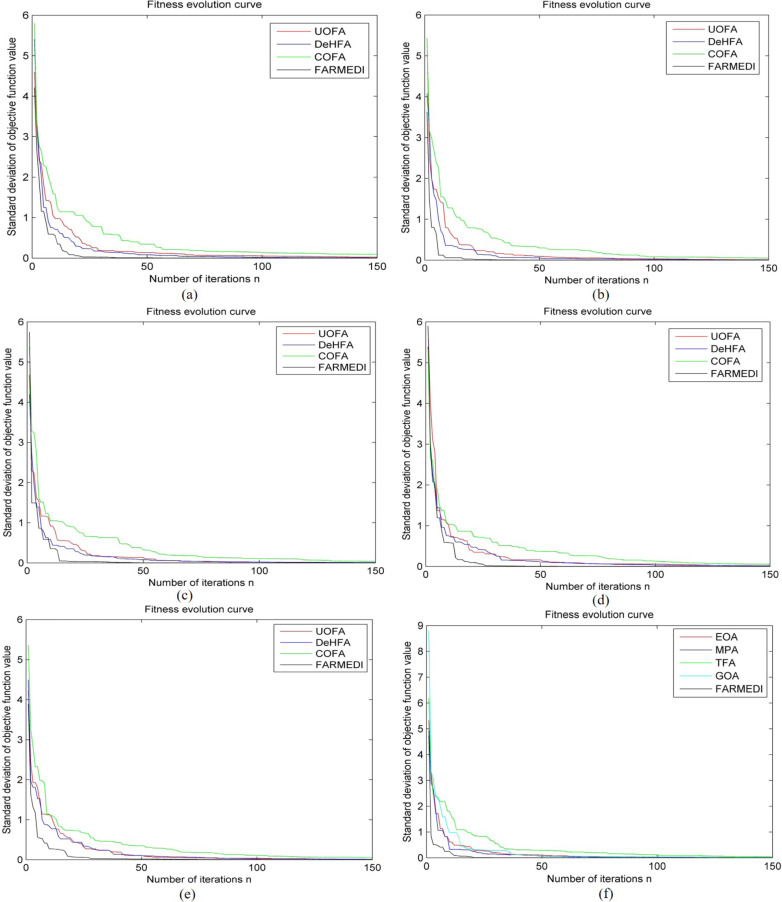
Aiming at the different kinds of COVID-19 CT images, diversity-enhanced hybrid firefly algorithm (DeHFA) [54], uniform orthogonal firefly algorithm (UOFA) [55], chaos optimization firefly algorithm (COFA) [44], firefly algorithm based on the random mechanism and exponentially decreasing inertia weight (FARMEDI, paper method) are used for simulation comparison tests of segmentation parameters optimization. Moreover, aiming at the early COVID-19 CT image, we use the meta-heuristic algorithms to optimize image segmentation, including grasshopper optimization algorithm (GOA) [56], equilibrium optimization algorithm (EOA) [57], [58], marine predators algorithm (MPA) [59], [60] and traditional firefly algorithm (TFA). The fitness evolution curve for different COVID-19 CT images are shown in Fig. 16. The evaluation index of the optimization performance under different methods are shown in Table 7.

Fig. 16.

Fitness evolution curve of segmented parameters optimization for different CT images: (a)Early COVID-19;(b)Early asymptomatic COVID-19;(c)Resolution COVID-19;(d)Adenovirus pneumonia;(e)staphylococcal pneumonia;(f)Early COVID-19.

Table 7.

Comparison of algorithm optimization performance.

CT image	Algorithm	Average	Std	Time processing
Early COVID-19	DeHFA	0.2853	0.0203	3.33
	UOFA	0.4135	0.0582	3.47
	COFA	0.5309	0.0947	4.71
	FARMEDI	0.0901	0.0056	2.74
Early asymptomatic COVID-19	DeHFA	0.3898	0.0106	3.56
	UOFA	0.5435	0.0508	3.82
	COFA	0.6140	0.0614	4.46
	FARMEDI	0.0640	0.0043	2.69
Resolution COVID-19	DeHFA	0.3731	0.0421	3.34
	UOFA	0.6945	0.0458	3.76
	COFA	0.8018	0.0751	4.48
	FARMEDI	0.0517	0.0089	2.76
Adenovirus pneumonia	DeHFA	0.2455	0.0116	3.46
	UOFA	0.2508	0.0614	3.54
	COFA	0.4335	0.0853	4.78
	FARMEDI	0.0656	0.0034	2.82
Staphylococcal pneumonia	DeHFA	0.3889	0.0391	3.35
	UOFA	0.5345	0.0407	3.43
	COFA	0.7018	0.0818	4.65
	FARMEDI	0.0642	0.0047	2.89
Early COVID-19	MPA	0.2738	0.0018	3.27
	EOA	0.3949	0.0052	3.39
	GOA	0.5543	0.0086	4.82
	TFA	0.8632	0.0083	5.29
	FARMEDI	0.0901	0.0056	2.74

It can be seen from Fig. 16 and Table 7 that with the increase of the number of iterations, the standard deviation of the objective function value is gradually reduced and the processing time is gradually increased under different parameters optimization methods. Compared with the different comparison methods, the value of average and standard deviation for “FARMEDI” is still the smallest, and the processing time of “FARMEDI” is still the fastest. In conclusion, the paper method (FARMEDI) significantly improves the segmentation effect for different kinds of COVID-19 CT images of parameters optimization.

We compared the TDRMFA with 6 state-of-the-art approaches including Inf-Net [61], Chain code-SVM [62], CNN-Clustering [63], MLT [64], GAN-Unet [41], U-Net++ [65] to do segmentation simulations on the CT image of early COVID-19, and further comparing and analyzing the Dice, Sensitivity and $IOU$ under different segmentation methods. The comparative CT image segmentation simulations of early COVID-19 are shown in Fig. 17. The evaluation index values are shown in Table 8.

Fig. 17.

CT image of early COVID-19 (a)original CT image; (b)golden standard segmented image; (c)segmented by TDRMFA; (d)segmented by GAN-Unet; (e)segmented by U-Net++; (g)segmented by MLT; (h)segmented by CNN-Clustering; (i)segmented by Chain code-SVM; (j)segmented by Inf-Net.

Table 8.

Comparison of TDRMFA with segmented SOTA methods for CT image of early COVID-19.

Segmented method	Dice	Sensitivity	IOU
Inf-Net	0.8494	0.8549	0.9254
Chain code-SVM	0.8519	0.8673	0.9372
CNN-Clustering	0.8626	0.8713	0.9443
MLT	0.8632	0.8784	0.9464
U-Net++	0.8753	0.8814	0.9532
GAN-Unet	0.8786	0.8843	0.9536
TDRMFA	0.8872	0.9871	0.9667

From the change trend of the data in Table 8, compared with the comparative segmentation methods, TDRMFA has increased the value of $Dice$ by about 0.0086, the value of $Sensitivity$ has been increased by about 0.1028, the value of $IOU$ has been increased by about 0.0131. It can be seen that the segmentation effect for the CT image of early COVID-19 under TDRMFA is the best. The early COVID-19 is characterized by the small number of lesion and the density is low. The TDRMFA method improves the segmentation accuracy for the CT image of early COVID-19 and reduces the missed diagnosis for the early lesions.

6. Conclusion

In view of the large computational and time-consuming problem for lung parenchymal segmentation of COVID-19, two-dimensional reciprocal cross entropy multi-threshold combined with improved firefly algorithm is proposed. The reciprocal cross entropy proposed in this paper solves the problem of the undefined and zero value of the logarithmic function. A weighted fuzzy threshold segmentation based on the spatial neighborhood information comprehensively considers the gray value and the spatial neighborhood information of image pixels, which improves the effect of image segmentation. In the process of calculating the optimal multi-threshold, the improved firefly algorithm is used to further improve the computational efficiency. The repair of lung parenchyma defects by Freeman chain code and Bezier curve is ideal, which can improve the accuracy of lung parenchyma segmentation and solve the problem of missed lesions. The experimental results for different kinds of COVID-19 CT images show that compared with the comparison methods, the performance of the paper method is the best. It not only segments COVID-19 lung parenchyma more accurately but also requires less running time. Thus, the time for doctors to sketch COVID-19 lesions is reduced, and it realizes the purpose of fully automatic segmentation of the COVID-19 lung parenchyma. However, there is a certain degree of difference in the structural characteristics of each person’s chest, so each lung parenchyma segmentation method has a limitation of robustness. In the segmentation results of the paper method, there is also a difference in segmentation accuracy for different CT images, which is the direction that needs to be researched in the future.

CRediT authorship contribution statement

Guowei Wang: Writing - original draft, Methodology, Software, investigation, validation. Shuli Guo: Conceptualization, Data curation. Lina Han: Writing - review & editing. Anil Baris Cekderi: Visualization.

Declaration of Competing Interest

No author associated with this paper has disclosed any potential or pertinent conflicts which may be perceived to have impending conflict with this work. For full disclosure statements refer to https://doi.org/10.1016/j.bspc.2022.103933.