Applicability of an Arrhenius Model for the Combined Effect of Temperature and CO₂ Packaging on the Spoilage Microflora of Fish

Abstract

The temperature behavior of the natural microflora on the Mediterranean fish red mullet (Mullus barbatus) was examined as a case study. The growth of the spoilage bacteria Pseudomonas spp., Shewanella putrefaciens, Brochothrix thermosphacta, and lactic acid bacteria was modeled as a function of temperature and the concentration of carbon dioxide in modified atmosphere packaging. Combined models were developed and comparatively assessed based on polynomial, Belehradek, and Arrhenius equations. The activation energy parameter of the Arrhenius model, E_A, was independent of the packaging atmosphere and ranged from 75 to 85 kJ/mol for the different bacteria, whereas the preexponential constant decreased exponentially with the packaging CO₂ concentration. We evaluated the applicability of the models developed by using experimental bacterial growth rates obtained from 42 independent experiments performed with three Mediterranean fish species and growth rates predicted from the models under the same temperature and packaging conditions. The accuracy factor and bias factor were used as statistical tools for evaluation, and the developed Arrhenius model and the Belehradek model were judged satisfactory overall.

Predictive modeling is currently accepted as a useful method for describing quantitatively the effects of ecological determinants (e.g., temperature, water activity) on bacterial growth (20, 28). In particular, predictive microbiology has been used to predict the growth of specific spoilage microorganisms in order to determine the shelf life of various fish products (3, 22). However, the development of specific spoilage bacteria in a fish ecosystem is a result of both environmental conditions and microbial competition (7, 16). In fish packed aerobically competition occurs between members of an aerobic gram-negative flora (mainly pseudomonads and Shewanella putrefaciens). In fish packed under modified atmosphere packing (MAP) conditions competition occurs between members of a facultatively anaerobic gram-positive flora (such as Brochothrix thermosphacta and lactic acid bacteria). The bacteria mentioned above have been reported to be important specific spoilage bacteria of Mediterranean fish stored under MAP conditions or aerobically (6, 13, 22, 23). Selection of a specific microflora eventually leads to spoilage at a rate that depends on pretreatment, packaging conditions, and temperature conditions during distribution and storage in the chill chain. Modeling the behavior of this microflora and quantitatively correlating it with shelf life can provide an effective tool for predicting chilled fish quality. To achieve this, it is necessary not only to identify the specific spoilage organisms but also to define the spoilage domain (i.e., the range of conditions, including microbial interactions, in which different groups of microorganisms are responsible for spoilage) (3). Most mathematical modeling studies have not allowed workers to predict quantitatively the growth behavior of a mixed naturally existing flora consisting of spoilage organisms in the actual food matrix. This is mainly because most of these studies were performed primarily with liquid growth media or simulated foods (5, 27). Potentially, this approach has the advantage of producing well-developed and statistically sound models; however, it has been shown that these models often overestimate the growth of microorganisms that actually occurs in real food as they do not take into account the effects of important factors, such as structure, possible microbial interaction, or minor constituents, which cumulatively can provide significant hurdles to growth (2, 12). In liquid media bacterial growth occurs planktonically, while on or in a solid matrix, such as a solid food, like fish, the environment may lead to bacteria that form discrete colonies or biofilms (18). In this case, the spatial relationship between colonies can be a crucial feature for selection of the spoilage bacteria, and interactions can depend on the population density, as well as on the structure per se and oxygen limitation due to diffusion factors (21, 25). This situation may account for the observation of Gram and Melchiorsen (11), who reported that the maximum cell density of S. putrefaciens and the growth rate were reduced when the organism was growing together with pseudomonads in fish. It is, therefore, necessary for the experimental conditions to be as similar as possible to the real conditions in order to obtain meaningful predictions, since identical ecological determinants (e.g., temperature, CO₂ concentration, etc.) may have different effects (e.g., on the rate of growth) on the same bacteria in different ecosystems.

So far, despite the increasing importance of MAP technology in the food and fish industry, only a limited number of models that have included the effect of temperature and gas concentration in the packaging environment have been proposed for different spoilage microorganisms (such as pseudomonads, lactic acid bacteria, S. putrefaciens, Photobacterium phosphoreum) (3–5, 22, 27), and even fewer models have been applied to fish (3). The objectives of the present study were to express quantitatively the combined effects of temperature and packaging gas on the natural microflora of an actual fish product by using predictive microbiology methods and to evaluate the applicability of alternative models to other fish systems based on independent experiments.

MATERIALS AND METHODS

Experimental design.

With the approach and methods used, we aimed to assess the reliability of models for the fish species tested and the whole relevant range of conditions. Red mullet (Mullus barbatus), a Mediterannean fish that is consumed in large quantities and is commercially important in Greece, was studied.

The storage experiments were carried out with fresh red mullet (M. barbatus). Fish caught from offshore fishing boats that set out from harbor at 2 or 3 a.m. and returned after about 3 h were obtained. The fish were kept in ice in a local fish shop until they were bought within 4 to 9 h after they were caught, and they were transported in ice within 30 min of purchase to the laboratory. The fish were then stored in individual pouches aerobically and under four different MAP conditions (25% CO₂–75% air, 50% CO₂–50% air, 80% CO₂–20% air, and 100% CO₂) by using Suprovac polyamide laminate (thickness, 90 μm; gas permeability at 20°C and 50% relative humidity, ca. 25, 90, and 6 cm³/m² per day/10⁵ Pa for CO₂, O₂, and N₂, respectively). After the bags were sealed, they were stored under controlled isothermal conditions (0, 4, 10, 15, and 20°C) in high-precision (±0.2°C) low-temperature incubators (model MIR 153; Sanyo Electric Co., Ora-Gun, Gunma, Japan). Samples were taken at appropriate time intervals to allow for efficient kinetic analysis of microbial growth. The same approach and method were used for validation studies performed with three different fish species, gilthead seabream (Sparus aurata), boque (Boops boops), and red mullet (M. barbatus). Boque and red mullet were obtained as described above, whereas gilt-head seabream was a marine cultured fish that was transported to the laboratory in ice boxes by air within 12 h after harvest.

Sample preparation and microbiological analysis.

A fish sample (25 g) was transferred to a stomacher bag (Seward Medical, London, United Kingdom), 225 ml of 0.1% peptone water supplemented with salt (0.85% [wt/vol] NaCl) was added, and the preparation was homogenized for 60 s with a stomacher (Lab Blender 400; Seward Medical).

Samples (0.1 ml) of serial dilutions of fish homogenates prepared as described above were spread onto the surfaces of dried media in petri dishes for enumeration, as follows. (i) Total viable counts were determined on modified Long-Hammer agar (26), which was incubated at 10°C for 7 days. This medium contained (per liter of distilled water) 20 g of proteose peptone (catalog no. P 0431; Sigma Chemical Co., St. Louis, Mo.), 40 g of gelatin (catalog no. 4070; Merck, West Point, Pa.), 1 g of K₂HPO₄, 10 g of NaCl, 15 g of agar (catalog no. L11; Oxoid, Basingstoke, United Kingdom), and 0.25 g of ammonium ferric citrate. (ii) Pseudomonads were enumerated on centrimide-fusidin-cephaloridine agar (catalog no. CM 559; Oxoid) supplemented with SR 103 (Oxoid), which was incubated at 20°C for 2 days (14). (iii) Brochothrix thermosphacta was enumerated on streptomycin sulfate-thallous acetate-cycloheximide (Acti-Dione) agar (catalog no. CM 881; Oxoid) supplemented with SR 151 (Oxoid), which was incubated at 20°C for 3 days (8). For lactic acid bacteria and hydrogen sulfide-producing bacteria 1.0-ml portions were inoculated into 10-ml portions of molten (45°C) MRS agar (lactobacillus MRS agar; catalog no. CM 361; Oxoid) and iron agar (catalog no. CM 867; Oxoid), respectively. After the medium set, a 10-ml overlay consisting of molten medium was added. For the lactic acid bacteria the preparations were incubated at 25°C for 5 days (15). Iron agar plates were incubated at 20°C for 4 days (13). Black colonies formed by the production of H₂S were enumerated after 2 or 3 days (9). Three replicates of at least three appropriate dilutions were enumerated. All plates were examined visually for typical colony types and morphological characteristics that were associated with each growth medium. In addition, the selectivity of each medium was checked routinely by Gram staining and microscopic examination of smears prepared from randomly selected colonies obtained from all media.

Model development.

A standard two-stage method was used to obtain a model for the influence of temperature and CO₂ concentration on the growth of red mullet microflora. Estimates of the lag phases and maximum specific growth rates were obtained with the log-transformed form of the four parameter logistic model (equation 1) (17) by using nonlinear regression.

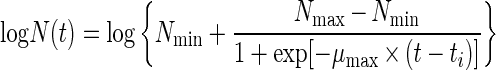1

In equation 1, t is the time (in hours), N(t) is the number of microorganisms at time t (in CFU per gram), N_max and N_min are the maximum and minimum asymptotic numbers of microorganisms (in CFU per gram), t_i is the time at which N(t) = N_max/2, and μ_max is the maximum specific growth rate (in hours⁻¹). The four-parameter logistic model was used for modeling all of the experimentally obtained growth curves. When no lag phase was exhibited, the fourth parameter (N_min), which was not significant, was omitted by the statistical software used in the fitting process.

The estimates of μ_max obtained were then fitted to secondary models. Three different models describing the individual and combined effects of temperature and CO₂ concentration were used and comparatively evaluated.

One of the models was a quadratic response surface model which corresponded to the following equation:

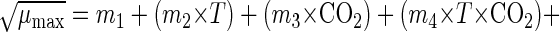2

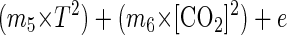where T is the temperature (in degrees Centigrade), CO₂ is the concentration of carbon dioxide in the package (expressed as a percentage), m₁ through m₆ are estimated coefficients, and e is random error.

Another model was an extended Ratkowsky model (17) based on the general Belehradek equation for biological growth rate (1):

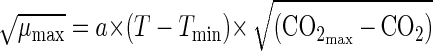3

where T is the temperature (in degrees Centigrade), CO₂ is the concentration of carbon dioxide in the package (expressed as a percentage), a is a constant, and T_min and CO_2max are the theoretical minimum temperature (in degrees Centigrade) and maximum carbon dioxide concentration (expressed as a percentage) for growth of the organism, respectively, as estimated by extrapolation of the regression line to √μ_max = 0.

We also used an Arrhenius model

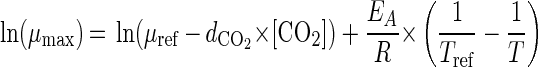4

where T is the absolute temperature (in Kelvins), [CO₂] is the concentration of carbon dioxide in the package (expressed as a percentage), E_A is the activation energy (in kilojoules per mole), R is the universal gas constant, T_ref is the reference temperature (273 K), μ_ref is the μ_max under reference storage conditions (T_ref, [CO₂] = 0) (in hours⁻¹), and d_CO2 is a constant expressing the effect of carbon dioxide on the μ_max.

Standard software (FigP; Biosoft, Cambridge, United Kingdom) was used to fit the primary growth model (equation 1) and the secondary growth models (equations 2 to 4) and for an analysis of variance. The statistically significant parameters of the models were determined by stepwise regression (F value).

Validation of the applicability of the predictive models.

Equations 2 to 4 were tested by comparing predicted growth rates and growth rates observed in independent storage experiments. Product validation experiments were carried out with different fish species (red mullet [M. barbatus], gilthead seabream [S. aurata], boque [B. boops]) stored at various temperature and under MAP conditions. The experimental conditions used for the validation experiments are shown in Table 1. Accuracy and bias factors (19) were used to comparatively assess the models' applicability. Accuracy and bias factors provided an indication of the average deviation between the model predictions and observed results (19), and the closeness to a value of 1 was an effective and practical measure of predictive model validity. The bias and accuracy factors were defined as follows:

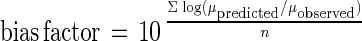5

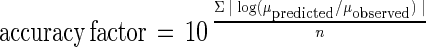6

where μ_observed is the μ_max that was experimentally observed (in hours⁻¹), μ_predicted is the μ_max that was predicted from the model (in hours⁻¹), and n is the number of observations.

TABLE 1.

Fish species and storage conditions used in the experiments performed to validate the models for each microorganism

Species	Atmosphere	Temp (°C)	No. of exptsa
			Pseudomonads	S. putrefaciens	B. thermosphacta	Lactic acid bacteria
M. barbatus	Air	0	+	+++	+++	+++
	Air	5	+	+	+	+
	Air	10	+	+	+	+
	Air	15	+	+	+	+
	20/80/0b	0	+	+	+	+
	50/50/0	0	+	+	+	+
	40/30/30	3	+	+	+	+
S. aurata	Air	0	+++	+++	++	−c
	Air	3	+	+	+	−
	Air	8	+++	+++	+++	−
	Air	15	+++	+++	+++	−
	5/90/5	0	+	+	+	+
	40/30/30	0	+	+	+	+
	40/30/30	3	+	+	+	+
	50/50/0	10	+	+	+	+
	100/0/0	3	++	+	++	++
B. boops	Air	0	+	+	−	+
	Air	3	++	++	−	++
	Air	7	++	++	−	++
	Air	10	++	++	−	++
	20/80/0	3	+	+	+	+
	100/0/0	3	+	+	+	+
	100/0/0	10	+	+	+	+

^aNumber of experiments in which growth of the bacterium or bacterial group was monitored during storage. 

^bPercentage of CO₂/percentage of N₂/percentage of O₂. 

^c−, no enumeration was performed. 

RESULTS AND DISCUSSION

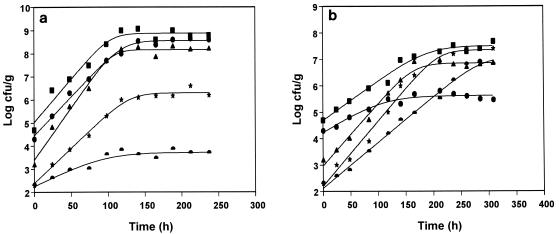
Changes in the microbial flora of red mullet during storage under aerobic and MAP conditions at 4°C are shown in Fig. 1. It is evident that when the fish was stored aerobically, pseudomonads and S. putrefaciens were the dominant bacteria. This is in agreement with the results obtained with other fish species (10, 13). In contrast, as the concentration of CO₂ increased, the growth rate of pseudomonads decreased significantly. When 50 and 80% CO₂ were used, codominance of B. thermosphacta and S. putrefaciens was evident, especially at low temperatures, while the levels of pseudomonads remained low. This could be attributed to the fact that the CO₂ tolerance of B. thermosphacta and S. putrefaciens was greater than that of pseudomonads. The level of B. thermosphacta in the initial fish population was low, but the contribution of this organism to the final population was great, which suggests that an ecosystem in which CO₂ is enriched favors growth of B. thermosphacta. Also, lactic acid bacteria play a secondary role in the spoilage process, which becomes more pronounced as the CO₂ concentration increases. When the fish was stored under 100% CO₂ conditions, growth of all bacteria was inhibited significantly, and the levels remained low. Evidently, CO₂ affected the development of the microbial association on Mediterranean red mullet, and the selection of dominant bacteria changed as the percentage of CO₂ increased. Inhibition of pseudomonads and codominance of B. thermosphacta and S. putrefaciens in samples stored under MAP conditions have been reported in previous studies on Mediterranean fish (6, 9, 13).

FIG. 1.

Development of the natural microflora of Mediterranean red mullet (M. barbatus) stored aerobically (a) and under MAP conditions (50% CO₂, 50% air) (b) at 4°C. Symbols: ■, total viable count; ●, pseudomonads; ▴, S. putrefaciens; ★, B. thermosphacta; ◗, lactic acid bacteria.

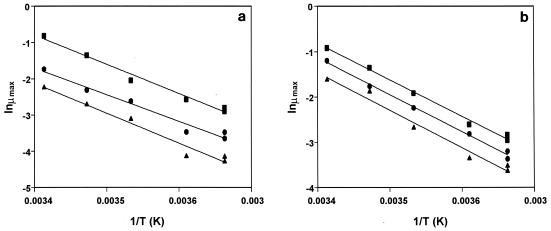
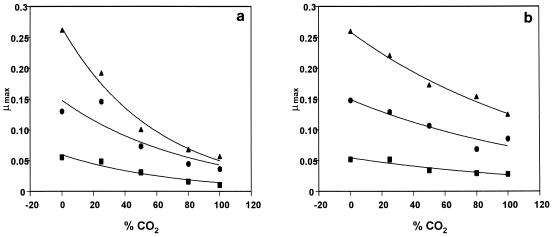
The experimental data for growth of the different bacteria were fitted to the logistic equation, and the estimated μ_max for each combination of temperature and CO₂ is shown in Table 2. We noted that a significant lag phase was not observed except under the most constraining conditions, 80 and 100% CO₂ at 0°C. Furthermore, the temperature dependence of growth was modeled by using the Arrhenius equation (Fig. 2). The relative parallel positions of the regression lines in the Arrhenius plots for all of the microorganisms tested, as expressed by statistically invariant E_A, led to the conclusion that the temperature dependence of the red mullet microflora growth rate is not affected significantly by the atmosphere. The effect of CO₂ concentration, as expressed through an effect on the exponential factor of the Arrhenius type of equation, was also examined. This effect is shown in Fig. 3, in which the growth rate is plotted versus the CO₂ concentration under constant-temperature conditions. The effect can be described by an exponential decrease in the rate as the CO₂ concentration increased. The relative effects of CO₂ are different for different bacterial species. These observations led to the proposed Arrhenius type of model (equation 4).

TABLE 2.

μ_max of the natural microflora of Mediterranean red mullet stored by using various combinations of temperature and atmospheric conditions, as estimated with the logistic equation

Temp (°C)	CO2 concn (%)	μmax (h−1)
		Pseudomonads	S. putrefaciens	B. thermosphacta	Lactic acid bacteria
0	0	0.056	0.067	0.052	0.034
0	0	0.061	0.073	0.059	0.044
4	0	0.077	0.104	0.074	0.041
10	0	0.130	0.160	0.148	0.107
15	0	0.261	0.338	0.259	0.159
20	0	0.443	0.515	0.400	0.260
0	25	0.049	0.066	0.052	0.040
0	25	0.052	0.060	0.059	0.038
4	25	0.065	0.070	0.075	0.045
10	25	0.146	0.151	0.129	0.134
15	25	0.191	0.296	0.220	0.174
20	25	0.368	0.500	0.393	0.269
0	50	0.031	0.032	0.035	0.026
0	50	0.026	0.033	0.041	0.030
4	50	0.031	0.055	0.060	0.041
10	50	0.073	0.086	0.107	0.106
15	50	0.100	0.189	0.172	0.143
20	50	0.177	0.368	0.302	0.199
0	80	0.016	0.029	0.030	0.025
0	80	0.014	0.025	0.026	0.018
4	80	0.016	0.040	0.035	0.031
10	80	0.045	0.065	0.069	0.056
15	80	0.067	0.116	0.153	0.128
20	80	0.107	0.223	0.199	0.144
0	100	0.010	0.031	0.028	0.023
0	100	0.012	0.031	0.023	0.021
4	100	0.021	0.030	0.032	0.039
10	100	0.036	0.072	0.085	0.053
15	100	0.056	0.138	0.124	0.128
20	100	0.075	0.227	0.219	0.158

FIG. 2.

Arrhenius plots showing the temperature dependence of μ_max (h⁻¹) of pseudomonads (a) and B. thermosphacta (b) growing on red mullet stored under different atmospheric conditions. Symbols: ■, aerobic storage; ●, storage in 50% CO₂–50% air; ▴, storage in 80% CO₂–20% air. T, temperature.

FIG. 3.

Effect of the concentration of carbon dioxide on μ_max of pseudomonads (a) and B. thermosphacta (b) growing on red mullet stored at different temperatures. Symbols: ■, 0°C; ●, 10°C; ▴, 15°C.

In order to describe the combined effect of temperature and CO₂ on the growth of the microorganisms tested, the parameters of the Arrhenius equation were determined. Similarly, parameters of the polynomial and Belehradek models (equations 2 and 4), which are commonly used in predictive microbiology, were determined. The values for the model parameters and the results of the statistical analysis are summarized in Tables 3 and 4 for the bacteria which made up the spoilage microflora. The confidence intervals at the 95% level are shown for all of the parameters estimated.

TABLE 3.

Estimated values and statistics for the coefficients of three models for the μ_max of maximum growth rates pseudomonads and S. putrefaciens growing on Mediterranean red mullet stored by using different combinations of temperature and atmospheric conditions

Equation type	Parameter	Pseudomonads		S. putrefaciens
		Estimated valuea	r2b	Estimated valuea	r2b
Polynomial	m1	2.35 × 10−1 ± 2.62 × 10−2		2.58 × 10−1 ± 2.6 × 10−2
	m2	1.27 × 10−2 ± 5.12 × 10−3		9.31 × 10−3 ± 4.39 × 10−3
	m3	−1.26 × 10−3 ± 4.00 × 10−4	0.970	−1.00 × 10−3 ± 3.90 × 10−4	0.979
	m4	−1.20 × 10−4 ± 4.00 × 10−5		−8.90 × 10−5 ± 3.10 × 10−5
	m5	3.94 × 10−4 ± 2.47 × 10−4		7.43 × 10−4 ± 2.39 × 10−4
	m6	P > 0.05c		P > 0.05
Belehradek	a	1.73 × 10−3 ± 2.47 × 10−4		1.85 × 10−3 ± 2.88 × 10−4
	Tmin (°C)	−11.4 ± 2.61	0.942	−9.93 ± 2.18	0.940
	CO2max	120.9 ± 8.79		156.4 ± 23.9
Arrhenius	μref (h−1)	6.11 × 10−2 ± 7.40 × 10−3		0.065 ± 8.20 × 10−3
	EA (kJ/mol)	65.4 ± 5.53	0.973	70.3 ± 5.72	0.966
	dCO2	1.69 × 10−2 ± 1.80 × 10−3		1.03 × 10−2 ± 1.70 × 10−3

^aEstimated value ± 95% confidence limit. 

^bCorrelation coefficient. 

^cP > 0.05 indicates that the parameter was not significant at the 95% level. 

TABLE 4.

Estimated values and statistics for the coefficients for three models for the μ_max of B. thermosphacta and lactic acid bacteria growing on Mediterranean red mullet stored by using different combinations of temperature and atmospheric conditions

Equation	Parameter	B. thermosphacta		Lactic acid bacteria
		Estimated valuea	r2b	Estimated valuea	r2b
Polynomial	m1	2.38 × 10−1 ± 1.74 × 10−2		1.86 × 10−1 ± 2.41 × 10−2
	m2	1.07 × 10−2 ± 3.42 × 10−3		1.62 × 10−2 ± 2.17 × 10−3
	m3	−8.20 × 10−4 ± 2.70 × 10−4	0.987	−4.80 × 10−4 ± 3.80 × 10−4	0.958
	m4	−5.20 × 10−5 ± 2.50 × 10−5		−3.7 × 10−5 ± 3.50 × 10−5
	m5	4.72 × 10−4 ± 1.64 × 10−4		P > 0.05
	m6	P > 0.05c		P > 0.05
Belehradek	a	1.45 × 10−3 ± 1.00 × 10−4		1.11 × 10−3 ± 2.06 × 10−4
	Tmin (°C)	−10.89 ± 1.64	0.966	−11.35 ± 1.84	0.958
	CO2max	187.4 ± 30.1		231.7 ± 62.6
Arrhenius	μref (h−1)	5.56 × 10−2 ± 4.98 × 10−3		3.78 × 10−2 ± 4.78 × 10−3
	EA (kJ/mol)	68.2 ± 4.02	0.981	67.5 ± 5.79	0.958
	dCO2	8.15 × 10−3 ± 1.27 × 10−3		5.76 × 10−3 ± 1.82 × 10−3

^aEstimated value ± 95% confidence limit. 

^bCorrelation coefficient. 

^cP > 0.05 indicates that the parameter was not significant at the 95% level. 

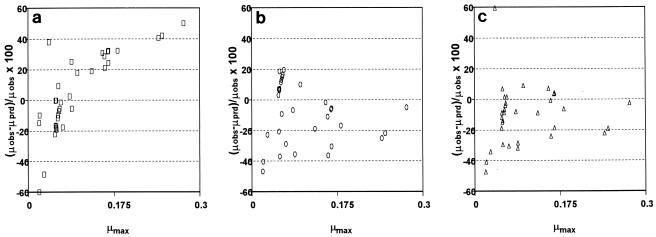
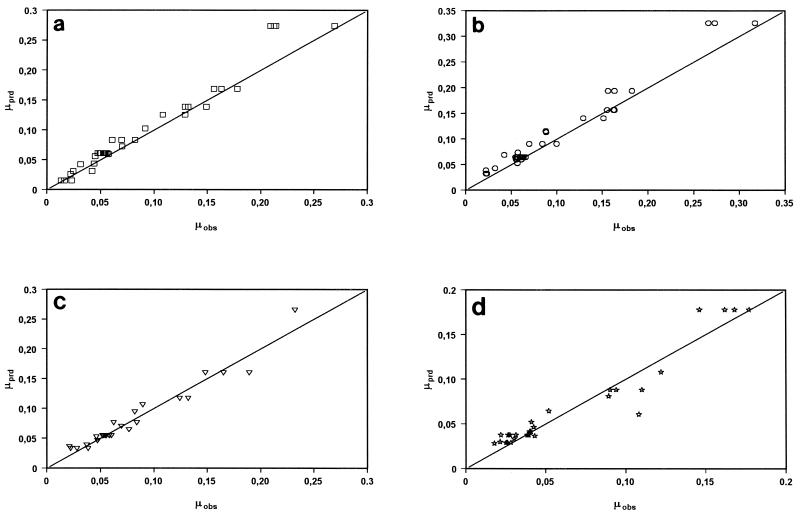
We evaluated the applicability of the models as practical prediction tools for different Mediterranean fish by comparing the predicted growth rates and the growth rates observed in independent storage experiments. Product validation experiments were carried out with three fish species, red mullet (M. barbatus), gilthead seabream (S. aurata), and boque (B. boops), which were stored at various temperatures and under MAP conditions. In Fig. 4 the percent deviations for the μ_max of S. putrefaciens predicted by using the three different models tested in this study are compared with the growth rates observed in the independent experiments. The data show that with the polynomial model there was a systematic difference between the predicted and observed values. The Arrhenius and Belehradek models revealed no systematic bias, and more Arrhenius predictions fell in the 20% range. Figure 5 shows another comparison of the μ_max of all of the microorganisms tested as predicted by the Arrhenius model and the observed growth rates in the independent experiments. Satisfactory agreement is shown by the spread of the points close to the diagonal.

FIG. 4.

Difference between the observed μ_max of S. putrefaciens (μ_obs) and the predicted μ_max (μ_prd), as estimated with the polynomial (a), Belehradek (b), and Arrhenius (c) models for different Mediterranean fish species.

FIG. 5.

Plots of predicted μ_max (μ_prd) versus observed μ_max (μ_obs) of pseudomonads (a), S. putrefaciens (b), B. thermosphacta (c), and lactic acid bacteria (d) growing on different Mediterranean fish species stored by using various combinations of temperature and atmospheric conditions. The predicted values were obtained by using the Arrhenius model.

The applicability of the models was also quantitatively evaluated by comparing the bias and accuracy factors for each model (Table 5). Overall, in most cases the accuracy factor values for the Arrhenius model were closer to 1. The bias factor values of the Belehradek and Arrhenius models were greater than 1, and the Belehradek model values were slightly closer to 1. These values indicate that there was a small error on the safe side (i.e., a tendency that would lead to a slight underprediction of the remaining shelf life rather than an overprediction that could lead to spoiled products and dissatisfied consumers before the predicted time).

TABLE 5.

Evaluation of model applicability by using bias and accuracy factors

Organism(s)	Polynomial model		Belehradek model		Arrhenius model
	Bias factor	Accuracy factor	Bias factor	Accuracy factor	Bias factor	Accuracy factor
Pseudomonads	0.93	1.22	1.02	1.16	1.11	1.17
S. putrefaciens	0.91	1.28	1.13	1.22	1.15	1.17
B. thermosphacta	0.95	1.22	1.05	1.16	1.06	1.13
Lactic acid bacteria	1.14	1.22	1.02	1.37	1.09	1.19

In conclusion, the combined models that have been developed provide practical tools for predicting the growth of microorganisms important in the spoilage of aerobically and MAP-packed Mediterranean fish. The polynomial model is the least preferred model; it adds two or three parameters without exhibiting improved predictive ability and was rated worse than the other models on the basis of all of the criteria used. The Belehradek type of model was judged satisfactory overall. The Arrhenius-based model had a good rating in the applicability evaluation, and it allows expression of the temperature dependence of microbial growth in terms like the E_A parameter, which is widely used in kinetic modeling of physicochemical phenomena, including food deterioration reactions (24). Although it has to be recognized that for most complex food and biological systems the equation is empirical rather than based on the theoretical foundation upon which it was developed, it gives a common quantitative point of reference for assessment of the relative temperature sensitivities of different phenomena or reactions of interest. The applicability of the same equations for growth of the microorganisms studied in different fish species under similar growing conditions (e.g., moderate-temperature water of the Mediterranean basin) is not surprising based on previous studies on the development of a single empirical shelf life model for moderately cold-water fish (3) or reports of E_A values for the microorganisms studied in different fish (23; European FAIR project CT95-1090, unpublished data). The proposed models, in combination with an increased understanding of the microbial associations in the target fish and establishment of the specific spoilage bacteria and domain and correlation with the organoleptic expression of spoilage, give a reliable and practical tool for predicting the shelf life of MAP-packed fish.